Abstract
We describe statistical methods that extend the application of admixture mapping from unrelated individuals to nuclear pedigrees, allowing existing pedigree-based collections to be fully exploited. Computational challenges have been overcome by developing a fast algorithm that exploits the factorial structure of the underlying model of ancestry transitions. This has been implemented as an extension of the program ADMIXMAP. We demonstrate the application of the method to a study of sarcoidosis in African Americans that has previously been analyzed only as an admixture mapping study restricted to unrelated individuals. Although the ancestry signals detected in this pedigree analysis are generally similar to those detected in the earlier analysis of unrelated cases, we are able to extract more information and this yields a much sharper exclusion map; using the classical criterion of an LOD score of minus 2, the pedigree analysis is able to exclude a risk ratio of 2 or more associated with African ancestry over 96% of the genome, compared with only 83% in the earlier analysis of unrelated individuals only. Although the pedigree extension of ADMIXMAP can use ancestry-informative markers only at relatively low density, it can use imputed ancestry states from programs such as WINPOP or HAPMIX that use dense SNP marker genotypes for admixture mapping. This extends both the efficiency and the range of application of this powerful gene mapping method.
Keywords: admixture, ancestry, pedigrees, linkage, sarcoidosis, African American, hidden Markov models
Introduction
Where large admixed populations are available, admixture mapping is the most direct method of localizing genes that underlie ethnic variation in disease risk [McKeigue, 2005]. A key advantage of admixture mapping over genome-wide single nucleotide polymorphism (SNP) association mapping is that it is not affected by allelic heterogeneity. Standard panels of ancestry-informative markers are now widely available, and statistical methods to infer locus ancestry and test for linkage with a disease or quantitative trait are implemented in programs such as ADMIXMAP [Hoggart et al., 2004] and ANCESTRYMAP [Patterson et al., 2004]. However, these programs can be used only with samples of unrelated individuals. Many existing collections of clinical data and DNA from admixed populations consist of pedigrees with multiple affected members, originally collected for linkage studies. Standard programs for pedigree linkage analysis such as GENEHUNTER [Kruglyak and Lander, 1995] cannot model the linkage disequilibrium that is generated by admixture. To apply admixture mapping in these collections, it has been necessary to restrict the analysis to a subset of unrelated individuals. In principle, it is possible to extend the statistical theory underlying admixture mapping to pedigrees. In this paper, we describe the extension of the statistical and computational methods for admixture mapping to nuclear pedigrees, and apply these methods to the AMASS (Ancestry Mapping of African genes of Sarcoidosis Susceptibility) study from which we have previously reported an analysis restricted to unrelated individuals [Rybicki et al., 2011]. The rationale for applying admixture mapping to this disease is based on the higher risk in people of west African ancestry than in people of European ancestry living in the same countries [Edmondstone and Wilson, 1985; Rybicki et al., 1997; Sartwell and Edwards, 1974].
Methods
Statistical Model for Admixture and Linkage
To model admixture in pedigrees, we have to combine two families of models, each of which is well established in statistical genetics: a hidden Markov model (HMM) for segregation indicators in pedigrees, and a HMM for locus ancestry in admixed individuals.
The classical HMM for segregation indicators was first described by Lander and Green, and later used in programs such as GENEHUNTER [Kruglyak and Lander, 1995] for linkage analysis in pedigrees. In this model, each meoisis is represented by a sequence of segregation indicators, one for each locus, that take value 0 or 1 according to whether the paternally derived or maternally derived copy is transmitted at the locus. The stochastic variation of segregation indicators between states 0 and 1 on each gamete is generated by two independent Poisson arrival processes each with intensity one per morgan. This is equivalent to the Haldane mapping function. For a single gamete, the probability of transition to state j at locus t + 1 given state j at locus t as , where δij is an indicator variable taking value 1 if i = j and 0 otherwise, g = exp(−2x), and x is the map distance in morgans from locus t to locus t + 1. For a pedigree with M meioses in the pedigree, the joint state space of the segregation indicators is of size 2M. The transition probabilities between these 2M joint states can be calculated as products of the corresponding transition probabilities for each meiosis. The probability of the observed genotypes given each joint state (emission probabilities) can be calculated from the allele frequencies. This is a HMM in which the hidden state at each locus is defined by the vector of segregation indicators, the transition probabilities are known (given the map distances), and the observations are the unphased marker genotypes. The probability distribution of the hidden states given the observations can be calculated by standard algorithms.
A HMM for ancestry at linked loci in a population formed by admixture between K ancestral populations [McKeigue, 1998] has been implemented for unrelated individuals in programs such as STRUCTURE [Pritchard et al., 2000], AD-MIXMAP [Hoggart et al., 2004], and ANCESTRYMAP [Patterson et al., 2004]. In this model, stochastic variation of ancestry across each of the two parental gametes in each individual is generated by K -independent Poisson arrival processes, with total intensity ρ per morgan. This model specifies the probability of transition to ancestry state j at locus t + 1 given ancestry state j at locus t as f δij + (1 – f)μj, where f = exp(−ρx) and μj is the proportion of the parental genome that has ancestry from the kth population. The locus ancestry states on each gamete thus arise from a Markov process with stationary distribution probabilities (μ1,…, μK). The Haldane mapping function can be viewed as a special case of this model in which K = 2, ρ = 2 and the two arrival processes each have intensity 1. The transition matrices depend on the model parameters (μ1,…, μK) and ρ, which can be learned from the data. The parameter ρ can be interpreted as the effective number of generations back to unadmixed ancestors.
To model admixture in a pedigree with F founder gametes and M meioses, we combine these two model families in a factorial HMM, in which the hidden states are generated by F + M independent Markov processes. “Factorial” means that the Markov processes are independent (unless we condition on the observed genotypes). At each locus, there are KF possible states for founder ancestry, and 2M possible states of the segregation indicators, so the hidden state space is of size KF 2M. For an African American sib pair, there are four founder gametes (F = 4), two ancestral populations (K = 2), and four meioses (M = 4) so there are 4224 = 256 states. For affected-only analyses, we can model nonshared ancestors as contributing only a single founder gamete and no meioses: thus for a pair of half-sibs, there are only four founder gametes (one from each nonshared parent, two from the shared parent) and two meioses.
At any locus, the ancestry states in the F founders and the segregation indicators for the M meioses specify the locus ancestry states for all individuals in the pedigree. The transition probabilities between joint states of the HMM are the products of the corresponding terms for the F + M individual processes. Given the ancestry-specific allele frequencies (probabilities of each allele given each locus ancestry state), we can specify for each hidden state the emission probability (probability of the observed genotypes given the hidden state) as a sum of phased genotype probabilities (calculated as products of allele frequencies) taken over all phased founder genotypes that are compatible with the observed unphased genotypes given the segregation indicators. This accounts for phase uncertainty in the observed genotypes.
A few other modifications of the standard model of admixture are required to handle pedigrees. We constrain the admixture proportions to be the same for both gametes in each parent, as there is not usually enough information in the data to infer whether the two gametes in a parent (not directly genotyped in most pedigrees) differ in their admixture proportions. For the same reason, the total arrival rate ρ is constrained to be the same for all individuals. As with unrelated individuals, we introduce an additional global parameter ψ to allow for unequal sex ratio in the founder populations [Rybicki et al., 2011]. ψj is the odds ratio for female sex in the j th ancestral population compared with the reference population. From previous studies of mitochondrial and Y chromosomal lineages [Lind et al., 2007; Parra et al., 1998], we estimate this parameter to be about 10 for female vs. male sex in African vs. European founders of the modern African American population. Given average autosomal European admixture proportions of 0.20, this is approximately equivalent to a 20 to 1 ratio of Africans to Europeans among unadmixed females who contributed gametes to the modern African American gene pool, compared with a 2 to 1 ratio of Africans to Europeans among unadmixed male founders. In principle, it should be possible to learn the parameter ψ from comparing ancestry state frequencies on the X chromosome with frequencies on the autosomes. In practice, a very large sample size is required for ψ to be inferred accurately, as large changes in ψ correspond to fairly small changes in the X chromosome admixture proportions. For instance, with autosomal European admixture proportions of 0.20, the expected X chromosome admixture proportion would vary only from 0.20 to 0.13 as ψ varies from 1 to infinity. As in the dataset used for this study (described below) there was not enough information for ψ to be inferred reliably, we therefore specified a Gaussian prior on log ψ with mean 2.4 and variance 0.01. This forces the value of ψ to be close to 10 in accordance with estimates based on mitochondrial and Y chromosome lineages.
Computational Methods
As each pedigree is represented as a HMM, a standard HMM forward recursion algorithm can in principle be applied to compute the likelihood P (y | μ,ρ) at any value of the admixture proportions μ and ancestry arrival rate ρ, given the observed genotypes y. For a fully Bayesian approach, we can sample the posterior distribution of these parameters using a Metropolis algorithm, rather than just maximize their likelihood as in classical machine learning applications that use HMM methods. At each realization of the model parameters, the forward and backward probability vectors can be used to calculate for each locus the marginal posterior distribution of hidden states, conditional on the model parameters. The standard algorithm for recursive computation of the forward and backward probabilities of a HMM entails at each locus multiplication of the transition matrix by a vector, as described in the Appendix. As the order of the transition matrix is equal to the size of the hidden state space, this matrix multiplication has time complexity that scales with the square of the size of the hidden state space.
Faster algorithms have been developed for special cases of the hidden Markov model. Two special cases are classical multipoint linkage analysis with unadmixed founders (K = 1), and admixture mapping of unrelated individuals (F = 2,ρM = 0). In classical linkage analysis, the transition probabilities for each segregation indicator are of the form , and the forward and backward recursions can be computed efficiently with a Hadamard transform [Kruglyak and Lander, 1998]. For admixture mapping with unrelated individuals, there are only two Markov processes each with transition probabilities of the form f δij + (1 – f)μj, and the time complexity can be reduced from O(K 4) to O(K) by using an algorithm that computes expectations of products from the product of expectations plus the covariance. This is implemented in ADMIXMAP for analysis of unrelated individuals. However, neither of these algorithmic speedups can be extended to the combined model of segregation and admixture that is required to model data on admixed pedigrees. We have therefore developed a more general algorithm for factorial HMMs where on each chain the stochastic transitions between states are generated by independent Poisson arrival processes, giving rise to transition probabilities of the form f δij + (1 – f)μj. This algorithm, described in the Appendix, achieves a speedup of about 100-fold compared with the standard HMM algorithm. This has been implemented in an updated version of the ADMIXMAP program for analysis of nuclear pedigrees including half-sibships.
Model parameters are updated with Metropolis algorithms, using a stochastic approximation algorithm to tune the step size automatically for each parameter [Atchade and Rosenthal, 2005]. For founder admixture proportions, the Metropolis proposals are generated by a Hamiltonian leapfrog algorithm which uses gradient information to propose states that have higher probability [MacKay, 2003]. Sampling algorithms are documented in more detail in the source code.
As a pedigree consisting of a single individual is just a special case of a nuclear pedigree, a collection that combines unrelated individuals and multimember pedigrees can be handled with the same algorithm. The only exception to this is the modeling of ancestry-specific allele frequencies. When ADMIXMAP is used to model unrelated individuals, the ancestry-specific allele frequencies are generated from their posterior distribution. The priors on the allele frequencies are based on the observed counts in samples from un-admixed modern populations such as the HapMap reference panels. This allows the program to learn the allele frequencies from the admixed population under study, rather than relying only on samples from modern populations that may differ from the ancestral populations that contributed to the admixed population. By sampling the joint posterior distribution of allele frequencies, we ensure that uncertainty in these nuisance parameters is integrated out in accordance with the rules of Bayesian inference. With unrelated individuals, it is possible to use an efficient sampling algorithm that integrates over phase in heterozygous individuals. This sampling algorithm cannot easily be extended to pedigrees, so instead we resort to an approximation of the fully Bayesian procedure in which the allele frequencies are fixed at the posterior mean computed from an initial run of ADMIXMAP with unrelated individuals only. In a large sample (as in the study reported here), this effect of this approximation on tests for linkage is likely to be small.
Testing for Linkage of Disease Status With Locus Ancestry
In admixture mapping, the effect of locus ancestry on disease risk is measured by the ancestry risk ratio parameter r: the ratio of risk in those with 2 copies that have ancestry from the high-risk population to risk in those with 0 copy [McKeigue, 1998]. For a rare disease with low penetrance, the ancestry frequencies at the disease susceptibility locus will differ only slightly between unaffected individuals and the general population. This can be seen by reversing the labeling of the diseased and nondiseased states to define “risk” as the probability of the nondiseased state. If the disease is rare and has low penetrance, the “risk” ratio associated with 2 vs. 0 copy of the high-risk ancestry state will be close to 1. Thus, very little information is lost by restricting the test for linkage to affected pedigree members.
The likelihood P (A, S | x, r) for an affected pedigree with disease states x given founder ancestry states A and segregation indicators S at the locus under study can be factored as P (S | A, x, r) P (A | x, r). In words, the likelihood factors into the contribution of segregation indicators S and the contribution of founder ancestry states A.
We consider the simple case in which high-risk and low-risk alleles are each fixed in one of the two ancestral populations. Under this assumption, the score test previously derived for unrelated individuals under a multiplicative model for penetrances [Hoggart et al., 2003] can be extended to related individuals. With individuals who have 0 copy of the high-risk allele as baseline, the risk ratios associated with 1 and 2 copies of the high-risk allele are, respectively, and r. The likelihood as a function of r, given the observed founder ancestry states, segregation indicators, and disease status in pedigree members can then be calculated by application of the rules of conditional probability. For affected half-sibs, the likelihood is evaluated as the sum of the contribution of meioses in the shared parent, the contribution of locus ancestry in the shared parent, and the contribution of the gametes transmitted to affected individuals from the non-shared parents. For n affected offspring of a founder parent, the contributions of segregation indicators and founder ancestry states to the likelihood are as follows:-
Contribution of segregation indicators to the likelihood conditional on founder ancestry states: P (S | A, n, r) Only meioses in parents who are heterozygous for ancestry (locus ancestry from high-risk population on one gamete, low-risk population on other gamete) contribute to this component. This is analogous to the transmission disequilibrium test [Spielman et al., 1993], in which only parents heterozygous at the locus under study contribute to the likelihood conditional on parental genotype. Given a parent heterozygous for ancestry at the locus under study who transmits the copy with ancestry from the high-risk population m times, the log-likelihood of the ancestry risk ratio parameter r is m log π+ (n – m) log (1 – π), where .
-
Contribution of parental locus ancestry to the likelihood: P (A | n, r)
This is evaluated as Σm P ((A, m,ρ| n, r). Expressions for this component of the log-likelihood are given in Table 1.
Table 1.
Likelihood as function of ancestry risk ratio r, score and information (at r = 1 with respect to log r) given n affected offspring and parental locus ancestry (0, 1, or 2 copies from high-risk population)
| Parental ancestry | Likelihood | Score | Information | |||
|---|---|---|---|---|---|---|
| 0 copy |
|
|
|
|||
| 1 copy |
|
|
|
|||
| 2 copies |
|
|
|
To construct a classical score test, we evaluate the score (gradient of the log-likelihood at the null) and information (minus the second derivative of the log-likelihood at the null) with respect to log r. We use the logarithm of the rate ratio because in this basis the quadratic approximation to the log-likelihood (on which the score test depends) is more accurate [Kirkwood and Sterne, 2003].
At log r = 0, the segregation indicators for meioses in a parent heterozygous for ancestry at the locus under study contribute to the score and n/16 to the information. Expressions for the contribution of parental locus ancestry to the score and information are given in Table 1. Each gamete from a nonshared parent with admixture proportions μ contributes to the score and to the information, where A is an indicator variable for locus ancestry (0 for ancestry from low-risk population, 1 for ancestry from high-risk population). These expressions are equivalent to those derived previously for admixture mapping in unrelated individuals [Hoggart et al., 2003].
Comparison of Information From Different Study Designs
We can compare the information from different study designs in the limiting case that segregation indicators and founder ancestry can be inferred without uncertainty. This is the Fisher information (minus the expectation of the second derivative of the log-likelihood) with respect to the parameter under test. This is relevant because the total information content of the study design determines the statistical power of the study: a fourfold increase in information content is required to halve the size of effect that can be detected. The statistical power to detect an effect of given size can be calculated from the information content of the study design as described previously [Hoggart et al., 2003].
Using the expressions in Table 1, we can calculate the expected information contributed by parental locus ancestry from one parent of n affected offspring (where the expectation is over the probability distribution of parental locus ancestry) as . Thus, for an affected sibship of size n, the expected information is from the 2n segregation indicators, and from locus ancestry in both parents. For a single individual (n = 1), this evaluates to as derived previously [Hoggart et al., 2003]. For an affected sib-pair (n = 2), this evaluates to one and a half times the information contributed by two unrelated individuals. Larger affected sibships are even more informative: thus an affected sib-trio contributes twice as much information as three unrelated individuals.
Score Test Algorithm
Using the expressions derived above for the score and information given the hidden states (segregation indicators and locus ancestry) and model parameters, we can evaluate the score and information given the observed data by averaging over the posterior distribution. For any realization of the hidden states and model parameters, we can calculate the complete data score U and the information V by summing over all pedigrees. Standard results [Dempster et al., 1977] yield the observed score as the posterior expectation of U, the missing information as the posterior variance of U, and the complete information as the posterior expectation of V. The observed information is calculated by subtracting the missing information from the complete information. A useful by-product of this algorithm is that the ratio of observed to complete information (proportion of information extracted) can be used to assess the efficiency of the study in relation to an ideal design in which all pedigree members are typed with a perfectly informative marker panel.
The expectations of U, U2, and V are evaluated in two steps:-
At each realization of the model parameters, accumulate the conditional expectations of U, U2, and V over the probability distribution of hidden states given by the HMM algorithm (elementwise product of the forward and backward probability vectors at the locus).
At the end of the sampling run, calculate the observed score as the average (over all samples) conditional expectation of U, and the complete information as the average (over all samples) of the conditional expectation of V.
Calculate the missing information (posterior variance of the score) as the sum of the variance of the conditional expectation of U and the expectation of the conditional variance of U. Using angle brackets to denote expectation:-Varθ(U) = Varθ(〈 U〉) + 〈Var(U | θ〉 θ.
This algorithm is computationally efficient because the conditional expectations at each realization of the model parameters can be calculated exactly, and sampling is required only to average over the posterior distribution of model parameters. A useful by-product of the algorithm is that the ratio of observed to complete information (proportion of information extracted) can be used to assess the efficiency of the study in relation to an ideal design in which all pedigree members are typed with a perfectly informative marker panel. The missing information can be partitioned into two components: information missing because of uncertainty about model parameters (Varθ(〈 U 〉)), and information missing because of uncertainty about locus ancestry and segregation indicators (〈 Var(U | θ;〉 θ).
Effect estimates for the log ancestry risk ratio and standard errors can be calculated from the score and information using a quadratic approximation to the log-likelihood. The same approximation can be used to calculate an exclusion map as described elsewhere [Hoggart et al., 2003].
Description of Study Dataset
The AMASS study comprises three datasets: a multisite case-control study (ACCESS) [Rybicki et al., 2001], a multi-site affected sib-pair study (SAGA) [Rybicki et al., 2005], and a single institution family-based study [Iannuzzi et al., 2003]. All three studies had informed consent for use of data and genetic material for future studies, and the admixture mapping study underwent human subjects review (Henry Ford Human Subjects Assurance number FWA00005846, AMASS IRB protocol number 4466). The dataset is available on request for sharing subject to a safeguards agreement. Our previously reported admixture mapping analysis of this study was restricted to 1,026 unrelated sarcoidosis cases and 316 unrelated controls [Rybicki et al., 2011]. This included all individuals from the ACCESS study (272 cases and 286 controls). For the two family-based designs, the probands were preferentially sampled for analysis (754 cases), and the eldest unaffected individual (30 controls) was sampled from families where DNA was no longer available from the affected family members. For the pedigree admixture analysis reported here, an additional 935 subjects (329 affected and 606 unaffected) were included from the two family-based studies, increasing the total number of cases by 32% to 1,355 in comparison with the earlier analysis of unrelated individuals only. Inclusion of additional unaffected pedigree members does not contribute directly to the affected-only test but helps to reduce the uncertainty in inference of segregation indicators within the pedigree. From the two family-based studies, 257 pedigrees contributed additional affected full- or half-sib pairs beyond the index case, and those families are categorized as follows: 165 had a single affected full-sib pair; 55 had a single affected half-sib pair; and 37 had more than one full-sib or half-sib pair. These individuals were typed for 1,384 SNPs informative for ancestry as described previously [Rybicki et al., 2011]. For the current analyses of unrelated and related subjects, we genotyped an additional 32 SNPs around our strongest ancestry peak on chromosome 6 in attempt to further refine the signal, giving a total of 1,416 SNPs in the final analysis map. All markers had passed diagnostic tests (implemented in ADMIXMAP) for lack of fit to Hardy-Weinberg equilibrium in a model that allows for population stratification, for mis-specification of allele frequency priors, and for residual linkage disequilibrium between adjacent pairs of loci conditional upon locus ancestry. This last diagnostic test is equivalent to testing for linkage disequilibrium within the ancestral subpopulations.
Results
Information Content and Model Parameters
To keep memory and CPU time requirements within bounds, unaffected pedigree members were omitted from the analysis where necessary so as to limit the maximum sibship size to seven. Analysis with 200 iterations for burn-in and 1,000 iterations for inference took 32 hr on 12 × 86–64 cores. From the affected-only test, we computed at each locus the complete information (the Fisher information that we would have if founder ancestry states, segregation indicators, and founder admixture proportions were directly observed) the observed information, and the proportion of information extracted. As the score test is computed with respect to the natural logarithm of the ancestry risk ratio, the information is expressed in natural log units (nats) to the power of minus 2. Over all autosomal loci, the mean complete information was 110 nats−2, and the mean proportion of information extracted was 74%. Only 1% of information was missing because of uncertainty about model parameters. For comparison, with unrelated individuals only, the mean complete information was 70, and the mean proportion of information extracted was 69%. Modeling the pedigree structure thus increased the effective sample size (indexed by the observed information) by nearly 70% (from 48 (69% of 70) to 81 nats−2, even though the number of affected individuals in the dataset increased only by 32%. The posterior mean of the proportion of European admixture in the population was 0.18 (95% CI 0.17–0.18). The total arrival rate parameter was 4.7 per morgan (95% CI 4.7–4.8). This parameter can be interpreted as the effective number of generations back to unadmixed ancestors. In the pedigree ADMIXMAP model, this parameter is specified for gametes transmitted from grandparents of the sibs. In the earlier study restricted to unrelated individuals, this parameter was estimated to be 5.2 per morgan on gametes transmitted from the parents of the genotyped individuals. As in a population with admixture proportions (0.2/0.8), the arrival rate increases by about 0.6 per generation, the estimate for parental and grandparental gametes are consistent.
Results of Admixture Scan
Figure 1 shows a QQ plot of the affected-only test for linkage with sarcoidosis, comparing the analysis of the full AMASS dataset including pedigrees results with those reported earlier based on unrelated cases and controls only [Rybicki et al., 2011]. The outliers on the right tail of the distribution of test statistics correspond to the signals of linkage with African ancestry on chromosomes 6p and 17p described below. When chromosomes that show possible signals of linkage (Table 2)–2, 3, 5, 6, and 17—are excluded, there is no remaining overdispersion of the test statistic.
Figure 1.
QQ plot of affected-only test statistics: model with unrelated individuals only in blue, model with all pedigrees (including unrelated cases) in red.
Table 2.
Comparison between ancestry risk ratio estimates from unrelated cases only and estimates from the full AMASS dataset for the strongest associations reported by Rybicki et al. [2011]
| Cytogenetic location | dbSNP | Unrelated only
|
Pedigree
|
||||
|---|---|---|---|---|---|---|---|
| aRRa | 95% CI | P-value | aRR | 95% CI | P-value | ||
| 2p13.3–2q12.1 | rs1444543 | 0.69 | 0.53–0.90 | 0.006 | 0.74 | 0.61–0.91 | 0.003 |
| 2q35.2–q36.3 | rs4674659 | 0.70 | 0.54–0.92 | 0.011 | 0.86 | 0.70–1.06 | 0.16 |
| 4q31.21–4q34.1 | rs1530044 | 1.53 | 1.15–2.05 | 0.004 | 1.22 | 0.98–1.51 | 0.07 |
| 5p13.2–5p13.3 | rs35397 | 1.47 | 1.13–1.91 | 0.004 | 1.28 | 1.05–1.56 | 0.02 |
| 5q23.1–5q31.2 | rs30533 | 0.68 | 0.52–0.89 | 0.006 | 0.79 | 0.65–0.97 | 0.02 |
| 6p12.1–6p24.3 | rs2844463b | 1.97 | 1.51–2.58 | 6 × 10−7 | 1.75 | 1.43–2.16 | 9 × 10−8 |
| 6q23.3–6q25.2 | rs276497 | 0.68 | 0.52–0.88 | 0.004 | 0.73 | 0.60–0.89 | 0.002 |
| 8p11.21–8p21.3 | rs1462906 | 0.67 | 0.51–0.87 | 0.003 | 0.82 | 0.67–1.00 | 0.06 |
| 17p13.1–17p13.3 | rs8070464 | 1.70 | 1.27–2.27 | 0.0003 | 1.5 | 1.21–1.86 | 0.0002 |
Ancestry risk ratio.
In the previously published analysis of unrelated individuals only [Rybicki et al., 2011], the additional 32 ancestry-informative markers included in this analysis had not been typed and rs11966463 had the highest level of statistical significance in this region (aRR=1.90; 95% CI = 1.36–2.64; P = 2 × 10−4).
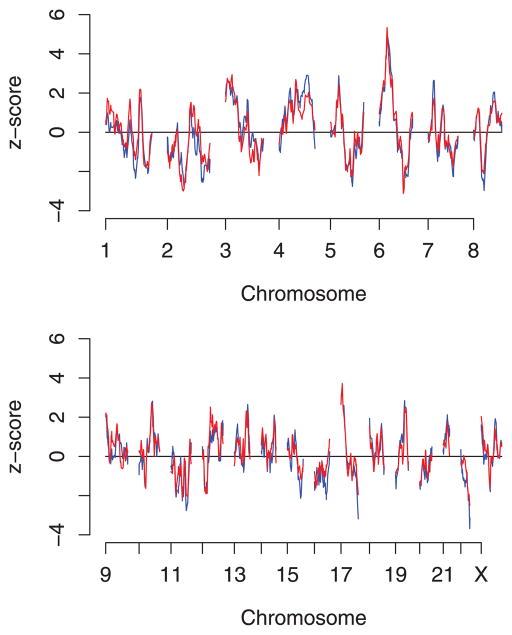
Figure 2 shows a plot of the z scores by map position, comparing previous results with unrelated individuals only (blue) with those obtained using all pedigrees (red). As the pedigree analysis contains 70% more information than the analysis with unrelated individuals only, we expect it to perform better at distinguishing true linkage signals from false-positive signals. Table 2 compares the results of affected-only tests between unrelated-only and full pedigree analysis at those loci which showed the most extreme results in the analysis of unrelated individuals reported previously. The most extreme P-values in that analysis were in the region 6p12.1–6p24.3, with a minimum value of 2 × 10−4 at rs11966463 where the estimated ancestry risk ratio was 1.90 (95% CI 1.36–2.64) [Rybicki et al., 2011]. With the additional 32 markers typed in this region for this analysis, the most extreme P-value in this region was at rs2844463, where the ancestry risk ratio estimate based on unrelated individuals was 1.97 (95% CI 1.49–2.59, P = 6 × 10−7) at this locus. With pedigrees included, the estimated ancestry risk ratio at this locus was 1.75 (95% CI 1.43–2.16, P = 9 × 10−8). This more extreme P-value despite a smaller effect size estimate reflects the increase in information obtained with the pedigree analysis. Over the rest of the genome, chromosome 17p13.1–13.3 (Fig. 2 and Table 2) now stands out more clearly than before as the only other region where there is suggestive evidence (P = 0.0002) of linkage with African ancestry.
Figure 2.
Affected-only test statistics by map position: unrelated individuals only in blue, analysis with pedigrees (including unrelated cases) in red.
Exclusion Mapping
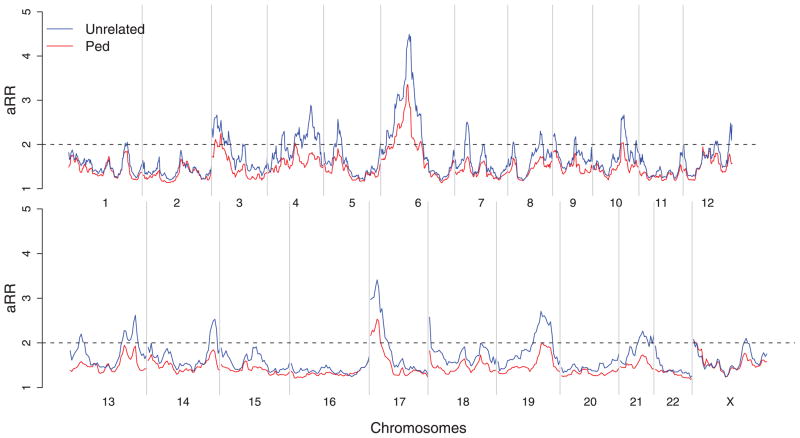
The exclusion map calculation, which takes into account not only the P-value but also the amount of information, shows in Figure 3 how extra information has been gained by the full pedigree analysis in comparison with an analysis of unrelated individuals only. We have used the classical criterion of a likelihood ratio less than 0.01 (LOD score less than minus 2) to exclude linkage. From the pedigree analysis, a risk ratio greater than or equal to 2 associated with African ancestry could be excluded at an LOD score of minus 2 over all but four regions on the genome: chromosome 3 (10–43 cM), chromosome 6 (37–82 cM), chromosome 10 (112–115 cM), and chromosome 17 (3–19 cM). In comparison with the earlier analysis of unrelated individuals only, the proportion of the genome excluded was increased from 87% to 96%.
Figure 3.
Exclusion map: unrelated individuals only in blue, analysis with pedigrees (including unrelated cases) in red.
Discussion
Although family-based designs are more difficult to assemble than case-control collections, many existing case collections in admixed populations are based on sib-pairs or other nuclear pedigrees. Our calculations show that for admixture mapping with a given number of affected individuals, affected sibships contribute more information than collections of unrelated cases. The extent to which the genotyping workload is also reduced depends upon whether parents and other unaffected pedigree members are genotyped also. In principle, the affected sibship design is more robust than the unrelated case-only design to violations of the assumptions on which the affected-only test for effect of locus ancestry depends. This is because the affected-only test in an affected sibship uses not only the likelihood given parental locus ancestry states (which depends upon the assumption that ancestry state frequencies do not vary systematically across the genome within the admixed population under study), but also the likelihood given the segregation indicators, which does not depend upon any assumptions other than the absence of ancestry-related segregation distortion. When five chromosomes showing signals of linkage are excluded, the distribution of affected-only test statistics in this analysis is a close fit to the theoretical distribution under the null, implying that there is no serious violation of model assumptions.
As in the previous analysis of unrelated individuals [Rybicki et al., 2011] an effect of African ancestry on sarcoidosis risk is detected in the human leukocyte antigen (HLA) region on chromosome 6p but the estimated ancestry risk ratio at this peak is only 1.75. As the risk ratio between Africans and Europeans is much larger than this, other regions must account for most of the excess risk of sarcoidosis associated with west African descent. In this example, the main advantage of using the pedigree-based analysis is that we are able to exclude an African ancestry risk ratio of 2 or more over all but three regions on the genome apart from chromosome 6p: 3p25.3–26.2, 3p24.3, 10q23.1, and 17p13.1–13.3. These regions are now being investigated more intensively with tag SNP genotyping.
The main limitation of the modeling approach used in AD-MIXMAP and in similar programs such as ANCESTRYMAP is that it assumes no linkage disequilibrium within the ancestral populations. This limits the density of markers that can be used to about 1 per cM, and this in turn generally limits the efficiency of the marker panel (proportion of information extracted) to about 80% even with markers that have been selected to be informative for ancestry. Alternative modeling approaches, such as those used in HAPAA [Sundquist et al., 2008], LAMP/WINPOP [Pasaniuc et al., 2009], and HAPMIX [Price et al., 2009] can extract more than 95% of information about locus ancestry using all the genotype data from a dense panel of SNPs used for genome-wide association studies. HAPAA and HAPMIX model the genotypes as generated by a mosaic of source haplotypes in the ancestral populations, while LAMP and WINPOP use a sliding window to combine information about locus ancestry from multiple SNPs. However, these programs have not been extended to handle pedigree data. In principle, any of these programs could be used with ADMIXMAP for a pedigree analysis by a two-stage procedure as follows. In the first step, the dense SNP genotype data are used to infer locus ancestry states of each typed individual, ignoring the pedigree data. In the second step, the inferred locus ancestry states (at a thinned subset of marker loci) can be used as pseudo-genotypes (scored as 0, 1, 2 copies from the high-risk population) in a pedigree analysis with ADMIXMAP with the corresponding ancestry-specific “allele” frequencies set to be close to 0 or 1. By allowing the pseudo-markers to be less than perfectly informative for locus ancestry (“alleles” are not differentially fixed in the ancestral subpopulations), we allow for incorrectly imputed ancestry states. ADMIXMAP can then generate score tests for linkage based on averaging over the joint distribution of founder locus ancestry states and segregation indicators. Although this procedure has yet to be demonstrated, it is possible in principle using existing software tools. It would not be so straightforward to extend to admixed pedigrees the joint test developed by Pasaniuc et al. [2011]. This test combines the likelihood given locus ancestry in affected individuals with the likelihood given case-control genotypes conditioned on locus ancestry, assuming a single causal variant with the same odds ratio for disease in each ancestral subpopulation. To extend this argument to admixed pedigrees would require integrating over the joint posterior distribution of founder genotypes and segregation indicators, rather than the joint posterior distribution of founder locus ancestry and segregation indicators generated by AD-MIXMAP. An alternative approach would be to use a mixed model to test for allelic association, in which kinships are used to correct for stratification and relatedness [Astle and Balding, 2009].
Acknowledgments
The authors would like to recognize the contributions of the NHLBI-funded ACCESS and SAGA research groups in original data collection efforts. The AMASS study was supported by NIH R01HL092576 and R56AI072727 (B. A. R.) and NIH/NHLBI RC2 HL101499-01 (C. G.-M.).
Appendix A
The forward recursion of a HMM with hidden states h and observations x is given by
| (A1) |
where , and the emission probability . Equation (A1) may be expressed in matrix form as
| (A2) |
where [T(t)]ij = p (h (t+1) = i|h(t) = j) = at(j i), [b(t+1)]i = bt+1(j), [α(t+1)]j = αt+1(j), and a ○ b denotes the element-wise product of vectors a and b. The computations in (A2) are dominated by the matrix product Tα ~ O(n2), where T ∈ ℝn×m, α∈ℝn×1, and n is the number of states of the latent variable h.
The combined model for linkage and admixture is a special case of a HMM, with two properties that make it possible to implement a faster algorithm. First, the underlying Markov process is generated by several parallel (marginally independent) Markov chains: one for each segregation indicator and one for ancestry on each founder gamete. This is a factorial hidden Markov model. Second, the transitions on each of these chains are generated by independent Poisson arrival processes, so that the transition probabilities on each chain have the form
| (A3) |
where is the state of the ith chain at locus t, is the probability of 0 arrivals between loci t and t + 1, and is the probability of state k in the stationary distribution of this chain.
For the founder ancestry chains, is the proportion of ad-mixture from population k on gamete i, and k, l ∈{1,…, ni} are ancestry states at loci t + 1 and t, respectively, For the segregation indicator chains, the number of states ni = 2, and . Without loss of generality, we will treat founder and segregation chains similarly, assuming that the segregation variables are binary with equal proportions μ.
Appendix B: Forward Recursion for Factorial HMMs
Notation
Let vector h(t) denote both hidden founder states and indicators at locus t, where different components of h(t) may have different semantics and cardinality. The vector of the corresponding observations will be given by x(t). For T loci, the total collection of observations and hidden variables will be denoted as {x} and {h}, respectively.
If each latent variable hi forms a marginally independent Markov chain, the structure is a factorial HMM. The joint likelihood is given by
| (B1) |
where the state variables are marginally independent, i.e.
| (B2) |
Here corresponds to the j th component of the hidden vector h(t) at locus t, and defines the transitions of the j th chain. By analogy with (A2), the forward α-recursion of the factorial HMM is defined by
| (B3) |
where , and each latent variable hj of the j th chain takes values in {1, …, nj }. The transition probability matrix T in (B3) is given as
| (B4) |
where is the effective cardinality of the state space, Ti ∈ ℝ ni ×ni is the transition matrix for the ith chain, and A ⊗ B is the matrix Kronecker product1 (note the fixed ordering of the states h). In general, computational complexity of (B3) is ~ O(N2), which is prohibitively expensive in situations when the number of chains |h| is large.
For the considered construction (A3), it is easy to see that if we were able to treat each ith chain independently of the others, the cost of computing Tiαi would be linear (rather than quadratic) in the number of states ni of each hidden variable hi. Indeed, each factor in (B4) can be expressed as
| (B5) |
where I ∈ ℝni ×ni is the unit matrix, 1 ∈1 ni ×1 is the column vector of ones, and
| (B6) |
is the diagonal matrix of the admixture proportions for all ni states. Clearly, T defined according to (B4) and (B5) is in general nonsymmetric, so that fast algorithms for the α-recursion using Fourier transforms [Kruglyak and Lander, 1998] cannot be easily applied.
For a single variable h1 with
| (B7) |
the matrix product in the α-recursion (B3) would result in
| (B8) |
where , with the complexity of computing (B8) ~ O(n1) (rather than as one would expect for the general construction). Computational advantage may be carried forward to the multifactor case (|h| > 1) by assuming a simple recursion on the factors hi.
Algorithm: Define to be the vector of joint probabilities spanning the complete state space for variables . Also define to be the vector of probabilities spanning the space for hi–1,…, h1 when , so that
| (B9) |
| (B10) |
Here we have assumed the descending ordering of the variables hi,…, h1 and ascending ordering of the states 1,…, ni for each variable, consistent with definitions in (B3) and (B7). (This ordering is important, because Kronecker products in (B4) are in general noncommutative.)
The recursive algorithm is summarized in Algorithm 1. It is assumed that the algorithm has access to and for all factors i = 1,…, |h|, states j = 1,…, ni, and loci t. At the top level of recursion, one needs to execute ComputeLevel ( ,|h|), which returns Tα (t) ∈ ℝ N×1 with T defined according to (B4).
Algorithm 1.
ComputeLevel ( , i)
| {Compute Tα(t) recursively} |
| if i>1 then |
| for all j=1: ni do |
| , i−1) |
| end for |
| else |
| {see Equation (B8)} |
| end if |
| return res |
The computations at the inner levels of the recursion are straightforward and analogous to (B5)–(B8). Note that the vec operation concatenates its arguments to a single column vector.
Appendix C: Analysis of Computational Complexity
Algorithm 1 computes the product (B3) by assuming that at each ith level of the recursion, variables h|h|,…, hi+1 remain fixed at some unknown values (set at the outer levels of the recursion), and hi takes each of ni possible values. Thus, on the ith level of the recursion tree, there are computations of . By analogy with (B8), each call ComputeLevel ( , i–1) is linear in dimensionality of and has the complexity of (indeed, summations, scalar products of the vectors, and vector-rearrangement operations vec in the body of the recursion are linear in the size of the function’s argument). Thus, each level i = 1, …, |h| of the recursion is , with the overall computational costs scaling as O(|h|N) for each locus t.
Clearly, in the special case when hidden states of all variables hi have the same cardinality, i.e. ∀i ∈ {1,…, |h|}.ni =n, the α-recursion will scale as O(|h|n|h|). For example, assume that we are dealing with four founder chains and four ancestry states per gamete. When recursion level i = 2, the algorithm would generate n3 calls to Compute Level ( , 1) for each setting of h4, h3, and h2 = j ∈1,…, n, with each call costing O(n) according to Equation (B8). For i = 3, there would be n2 calls costing O(n2) each. At the outer level, there would be n O(n3) calls for each setting of h4, with the rearrangement operations costing O(n4), resulting in total cost of O(4 × 44) (instead of O(48) as in the general unstructured case). A more detailed analysis of the number of summations, multiplications, and memory access operations can be performed similarly.
Unless there is an exploitable factorial structure in the emissions p (x|h), probabilities p (h1,…, h|h|, x) of the forward-recursion do not factorize in h. This means that despite the marginal independence of the hidden variables, the chains cannot be handled independently. This explains why the algorithm is more expensive than , and motivates the recursion for the settings of the components of h(t). However, the resulting algorithm appears to be more appealing than O N2 ≡ O ((Πi ni)2) in situations when N is large, both in terms of speed and memory efficiency. For example, dealing with eight chains of cardinality four would result in 216 effective states of the hidden vectors, and even storing the transition matrix T ∈ ℝ216×216 in memory could pose a challenge for modern desktops. In contrast, construction (B4) and Algorithm 1 only need to deal with eight matrices Ti ∈ℝ4×4, and a vector α ∈R216×1.
Note that in situations when the number of states is small, the costs of performing the recursion and/or memory operations may potentially compromise the efficiency of Algorithm 1. The algorithm could potentially be improved by constraining the model further, i.e. by assuming that some of the arrival probabilities or admixture proportions are fixed for some of the latent chains. Even more efficient code could potentially be produced by unrolling the recursion for some special case of interest, and improving memory indexing for accessing p (hi = a, hi–1 =,…, h1 = {x}). A simple implementation of the general algorithm checking the consistency of the computations in MATLAB®/Octave is available online at http://homepages.ed.ac.uk/pmckeigu/admixmap/tools/TransRecursion.tar.gz.
Footnotes
If A ∈ ℝm×n, B ∈ ℝ p×q, and C = A ⊗B, then C ∈ ℝmp×nq is the block matrix such that Ci j = Ai j B ∈ ℝp×q. It is clear that in general A⊗B ≠ B ⊗ A.
Web Resources
The ADMIXMAP program is available at http://www.homepages.ed.ac.uk/pmckeigu/admixmap
References
- Astle W, Balding DJ. Population structure and cryptic relatedness in genetic association studies. Statist Sci. 2009;4:451–471. [Google Scholar]
- Atchade YF, Rosenthal JS. On adaptive Markov chain Monte Carlo algorithms. Bernoulli. 2005;11:815–828. [Google Scholar]
- Dempster A, Laird NM, Rubin DB. Maximum likelihood from incomplete data via the EM algorithm. J R Stat Soc B. 1977;39:1–38. [Google Scholar]
- Edmondstone WM, Wilson AG. Sarcoidosis in Caucasians, Blacks and Asians in London. Br J Dis Chest. 1985;79(1):27–36. doi: 10.1016/0007-0971(85)90004-x. [DOI] [PubMed] [Google Scholar]
- Hoggart CJ, Parra EJ, Shriver MD, Bonilla C, Kittles RA, Clayton DG, McKeigue PM. Control of confounding of genetic associations in stratified populations. Am J Hum Genet. 2003;72(6):1492–1504. doi: 10.1086/375613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoggart CJ, Shriver MD, Kittles RA, Clayton DG, McKeigue PM. Design and analysis of admixture mapping studies. Am J Hum Genet. 2004;74(5):965–978. doi: 10.1086/420855. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iannuzzi MC, Maliarik MJ, Poisson LM, Rybicki BA. Sarcoidosis susceptibility and resistance HLA-DQB1 alleles in African Americans. Am J Respir Crit Care Med. 2003;167(9):1225–1231. doi: 10.1164/rccm.200209-1097OC. [DOI] [PubMed] [Google Scholar]
- Kirkwood BR, Sterne JAC. Essential Medical Statistics. 2. Oxford, UK: Blackwell; 2003. [Google Scholar]
- Kruglyak L, Lander ES. High-resolution genetic mapping of complex traits. Am J Hum Genet. 1995;56(5):1212–1223. [PMC free article] [PubMed] [Google Scholar]
- Kruglyak L, Lander ES. Faster multipoint linkage analysis using Fourier transforms. J Comput Biol. 1998;5(1):1–7. doi: 10.1089/cmb.1998.5.1. [DOI] [PubMed] [Google Scholar]
- Lind JM, Hutcheson-Dilks HB, Williams SM, Moore JH, Essex M, Ruiz-Pesini E, Wallace DC, Tishkoff SA, O’Brien SJ, Smith MW. Elevated male European and female African contributions to the genomes of African American individuals. Hum Genet. 2007;120(5):713–722. doi: 10.1007/s00439-006-0261-7. [DOI] [PubMed] [Google Scholar]
- MacKay DJC. Information Theory, Inference and Learning Algorithms. Cambridge, UK: Cambridge University Press; 2003. [Google Scholar]
- McKeigue PM. Mapping genes that underlie ethnic differences in disease risk: methods for detecting linkage in admixed populations, by conditioning on parental admixture. Am J Hum Genet. 1998;63(1):241–251. doi: 10.1086/301908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McKeigue PM. Prospects for admixture mapping of complex traits. Am J Hum Genet. 2005;76(1):1–7. doi: 10.1086/426949. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parra EJ, Marcini A, Akey J, Martinson J, Batzer MA, Cooper R, Forrester T, Allison DB, Deka R, Ferrell RE, et al. Estimating African American admixture proportions by use of population-specific alleles. Am J Hum Genet. 1998;63(6):1839–1851. doi: 10.1086/302148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pasaniuc B, Sankararaman S, Kimmel G, Halperin E. Inference of locus-specific ancestry in closely related populations. Bioinformatics. 2009;25(12):i213–i221. doi: 10.1093/bioinformatics/btp197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pasaniuc B, Zaitlen N, Lettre G, Chen GK, Tandon A, Kao WHL, Ruczinski I, Fornage M, Siscovick DS, Zhu X, et al. Enhanced statistical tests for GWAS in admixed populations: assessment using African Americans from CARe and a breast cancer consortium. PLoS Genet. 2011;7(4):e1001371. doi: 10.1371/journal.pgen.1001371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patterson N, Hattangadi N, Lane B, Lohmueller KE, Hafler DA, Oksenberg JR, Hauser SL, Smith MW, O’Brien SJ, Altshuler D, et al. Methods for high-density admixture mapping of disease genes. Am J Hum Genet. 2004;74(5):979–1000. doi: 10.1086/420871. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price AL, Tandon A, Patterson N, Barnes KC, Rafaels N, Ruczinski I, Beaty TH, Mathias R, Reich D, Myers S. Sensitive detection of chromosomal segments of distinct ancestry in admixed populations. PLoS Genet. 2009;5(6):e1000519. doi: 10.1371/journal.pgen.1000519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pritchard JK, Stephens M, Donnelly P. Inference of population structure using multilocus genotype data. Genetics. 2000;155(2):945–959. doi: 10.1093/genetics/155.2.945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rybicki BA, Hirst K, Iyengar SK, Barnard JG, Judson MA, Rose CS, Donohue JF, Kavuru MS, Rabin DL, Rossman MD, et al. A sarcoidosis genetic linkage consortium: the sarcoidosis genetic analysis (SAGA) study. Sarcoidosis Vasc Diffuse Lung Dis. 2005;22(2):115–122. [PubMed] [Google Scholar]
- Rybicki BA, Iannuzzi MC, Frederick MM, Thompson BW, Rossman MD, Bresnitz EA, Terrin ML, Moller DR, Barnard J, Baughman RP, et al. Familial aggregation of sarcoidosis. a case-control etiologic study of sarcoidosis (ACCESS) Am J Respir Crit Care Med. 2001;164(11):2085–2091. doi: 10.1164/ajrccm.164.11.2106001. [DOI] [PubMed] [Google Scholar]
- Rybicki BA, Levin AM, McKeigue P, Datta I, Gray-McGuire C, Colombo M, Reich D, Burke RR, Iannuzzi MC. A genome-wide admixture scan for ancestry-linked genes predisposing to sarcoidosis in African-Americans. Genes Immun. 2011;12(2):67–77. doi: 10.1038/gene.2010.56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rybicki BA, Major M, Popovich J, Maliarik MJ, Iannuzzi MC. Racial differences in sarcoidosis incidence: a 5-year study in a health maintenance organization. Am J Epidemiol. 1997;145(3):234–241. doi: 10.1093/oxfordjournals.aje.a009096. [DOI] [PubMed] [Google Scholar]
- Sartwell PE, Edwards LB. Epidemiology of sarcoidosis in the U.S. navy. Am J Epidemiol. 1974;99(4):250–257. doi: 10.1093/oxfordjournals.aje.a121609. [DOI] [PubMed] [Google Scholar]
- Spielman RS, McGinnis RE, Ewens WJ. Transmission test for linkage disequilibrium: the insulin gene region and insulin-dependent diabetes mellitus (IDDM) Am J Hum Genet. 1993;52(3):506–516. [PMC free article] [PubMed] [Google Scholar]
- Sundquist A, Fratkin E, Do CB, Batzoglou S. Effect of genetic divergence in identifying ancestral origin using HAPAA. Genome Res. 2008;18(4):676–682. doi: 10.1101/gr.072850.107. [DOI] [PMC free article] [PubMed] [Google Scholar]