The valuation system: A coordinate-based meta-analysis of BOLD fMRI experiments examining neural correlates of subjective value

Abstract

Numerous experiments have recently sought to identify neural signals associated with the subjective value (SV) of choice alternatives. Theoretically, SV assessment is an intermediate computational step during decision making, in which alternatives are placed on a common scale to facilitate value-maximizing choice. Here we present a quantitative, coordinate-based meta-analysis of 206 published fMRI studies investigating neural correlates of SV. Our results identify two general patterns of SV-correlated brain responses. In one set of regions, both positive and negative effects of SV on BOLD are reported at above-chance rates across the literature. Areas exhibiting this pattern include anterior insula, dorsomedial prefrontal cortex, dorsal and posterior striatum, and thalamus. The mixture of positive and negative effects potentially reflects an underlying U-shaped function, indicative of signal related to arousal or salience. In a second set of areas, including ventromedial prefrontal cortex and anterior ventral striatum, positive effects predominate. Positive effects in the latter regions are seen both when a decision is confronted and when an outcome is delivered, as well as for both monetary and primary rewards. These regions appear to constitute a "valuation system," carrying a domain-general SV signal and potentially contributing to value-based decision making.

1. Introduction

Many psychological and economic theories of decision making are couched within the framework of value maximization (e.g., Kahneman and Tversky, 1979; Samuelson, 1937). According to such a framework, an organism facing a choice first determines the scalar subjective value (SV) of each available alternative, and then selects the alternative with the greatest SV. SV serves as a common currency, allowing complex and qualitatively different alternatives to be compared on a common scale. Stable assessments of SV can support consistent decision behavior over time and across contexts.

Although there are noted and well-studied anomalies (see, e.g., Tversky and Kahneman, 1974), value maximization has been an enormously productive framework for understanding learning and decision making. As such, a major objective in decision neuroscience has been to uncover neural signals associated with the computation and representation of SV. A growing number of studies have used fMRI to measure blood oxygenation level dependent (BOLD) signal from the brain while human participants perform evaluation and decision-making tasks, comparing BOLD response amplitudes across outcomes or prospects that differ in SV. Qualitative reviews of this work (e.g., Delgado, 2007; Grabenhorst and Rolls, 2011; Kable and Glimcher, 2009; Knutson and Cooper, 2005; Levy and Glimcher, 2012; Montague and Berns, 2002; O'Doherty, 2004; Peters and Büchel, 2010) have concluded that: (1) BOLD signal in a small number of regions, including ventral striatum (VS), ventromedial prefrontal cortex (VMPFC) and (in some cases) posterior cingulate cortex (PCC) scales with the SV of the available alternatives during choice; (2) the same regions also respond when a reward is received, implicating a common set of regions in the evaluation of both prospects and outcomes; (3) these regions respond to outcomes in multiple domains (e.g., primary rewards such as food, secondary rewards such as money, social rewards, etc.), as would be required for any domain-general common currency signal.

Though many studies support this consensus, there remains a risk that qualitative reviews have either overestimated the support for prevailing hypotheses or overlooked unanticipated but reliable findings. Such selectivity certainly can occur in individual studies, which may focus discussion on regions identified a priori while ignoring equally strong results elsewhere. In the present work we use meta-analytic techniques to quantify the state of the evidence for the above three claims. Quantitative meta-analysis offers a complementary perspective to well-designed individual experiments and qualitative reviews, allowing a large and diverse array of existing findings to be aggregated, regardless of how each experiment was originally interpreted.

We perform a series of coordinate-based meta-analyses of published fMRI findings relating to the neural correlates of SV. Our examination focuses on four specific questions.

Question 1: In what regions does BOLD correlate positively or negatively with SV? Our first step tests for reliable BOLD correlates of SV. Previous reviews have tended to emphasize BOLD responses that scale positively with SV. At the single neuron level, however, there seem to be roughly equal numbers of neurons that increase or decrease firing as SV changes (Kennerley et al., 2009). There have been preliminary suggestions, from both fMRI and electrophysiological studies, that these positively and negatively directed responses may be anatomically dissociable (Monosov and Hikosaka, 2012; O'Doherty et al., 2001).

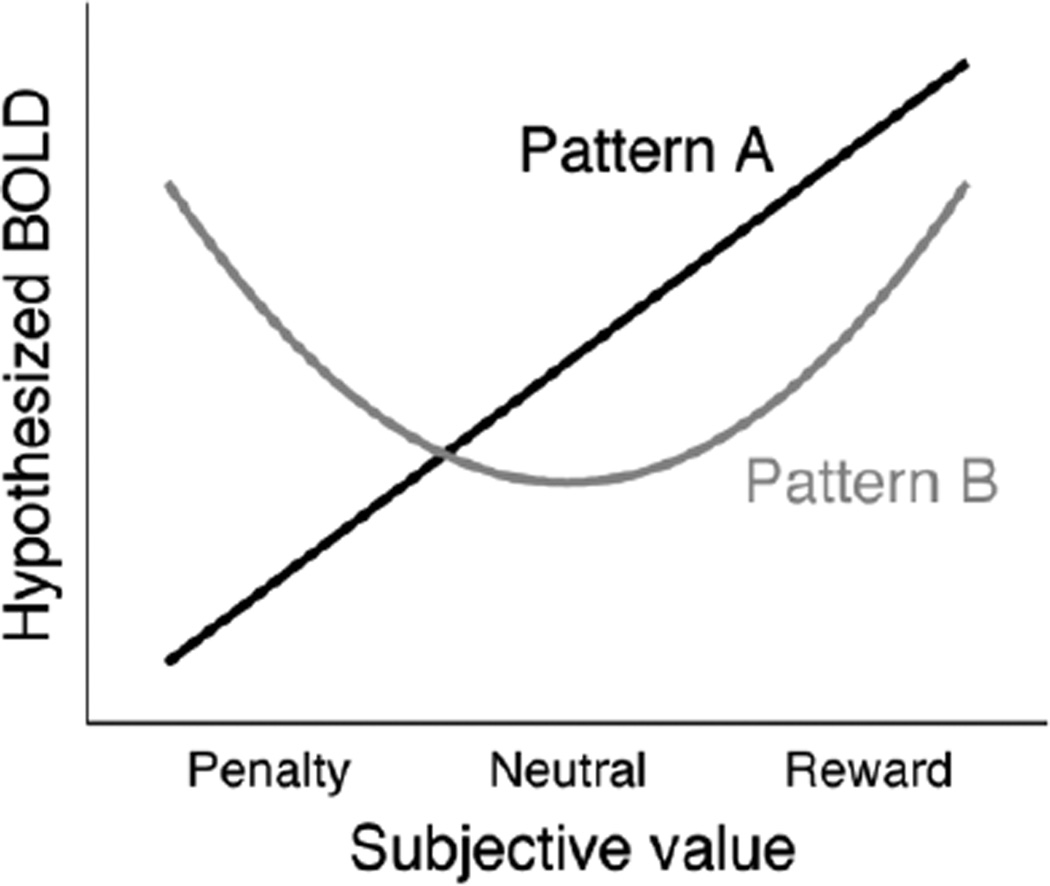
Question 2: Do neural responses follow a linear or nonlinear function of SV? A second question is whether neural correlates of SV can be distinguished from potentially related signals of arousal or salience (cf. Zink et al., 2004). Figure 1 illustrates two possible ways in which a neural response might vary across different levels of SV. Pattern A shows a response rising linearly with SV, while Pattern B shows a U-shaped response that is maximal either for extreme positive or extreme negative values. The linear pattern is more properly a correlate of SV, while the U-shaped pattern might be better described as a signal of arousal or salience. A source of difficulty in disambiguating these patterns is that their predictions overlap in experiments that only involve rewards. Neural structures that appear reward-responsive in such experiments may also respond strongly to penalties (Carretié et al., 2009; Levita et al., 2009). Previous work suggests it may be possible to distinguish areas that show either or both of the activity profiles in Figure 1 (Litt et al., 2011).

Figure 1.

Two hypothetical profiles for regional BOLD as a function of SV. Pattern A (linear) represents a monotonically increasing response for more valuable outcomes, while Pattern B (quadratic) represents a greater response to more extreme outcomes, either rewards or penalties.

Question 3: Do the same regions encode SV when a decision is made and when an outcome is experienced? We next ask whether the neural correlates of SV during decision-making are similar or different from SV responses during the receipt of an outcome (cf. "decision utility" vs. "experienced utility"; Kahneman et al., 1997). Numerous experiments have demonstrated that neural correlates of SV can indeed be identified during decision making (Kable and Glimcher, 2007; Knutson et al., 2007; Plassmann et al., 2007; Tom et al., 2007), and the same general regions are active when rewards are experienced. However, there is also evidence that neural responses during choice and during outcome delivery may be anatomically dissociable (Knutson et al., 2001b; Smith et al., 2010).

Question 4: Is SV encoded differently for primary versus secondary incentives? An important question is to what extent the neural representation of SV is domain-specific versus domain-general. Many studies targeting this question have investigated whether secondary rewards (e.g., money) are evaluated using the same neural architecture as primary rewards (e.g., juice). A number of studies have concluded that different categories of rewards recruit at least partially overlapping neural substrates (Chib et al., 2009; Kim et al., 2011; Valentin and O'Doherty, 2009). Partial overlap has also been noted for primary and secondary aversive outcomes (Delgado et al., 2011). Other work has reached the conclusion that neural mechanisms involved in evaluating primary and secondary incentives are dissociable (Sescousse et al., 2010).

Previous meta-analyses have examined subsets of the above questions in more restricted databases. Both Knutson and Greer (2008) and Diekhof and colleagues (2012) focused on the passive anticipation of rewards, comparing SV responses associated with outcome anticipation and delivery. Peters and Büchel (2010) and Levy and Glimcher (2012) presented anatomically circumscribed meta-analyses in VMPFC and adjacent regions, showing overlap between activation coordinates associated with multiple forms of SV. The present investigation extends previous work by examining all four of the above questions simultaneously across the entire brain in a large corpus of published studies. Our sample size affords us the statistical power to conduct comprehensive and rigorous inferential tests at the meta-analytic level.

Across the present meta-analyses, we find evidence for reliable positive correlates of SV in VMPFC and anterior VS. We find that these can be distinguished from responses in anterior insula, other striatal regions, and dorsomedial prefrontal cortex (DMPFC), which seem more related to arousal or salience. We find overlapping responses in VMPFC and VS to decision and experienced SV, as well as overlapping responses to both primary and secondary incentives. These results bolster the conclusion that VMPFC and VS form the core of a “valuation system” believed to play a critical role in value-based learning and decision-making.

2. Materials and Methods

2.1. Coordinate-based meta-analysis

The importance of quantitatively synthesizing the findings of independent experiments is well recognized across scientific domains. Quantitative meta-analysis poses unique challenges in the context of neuroimaging. Neuroimaging results are conventionally reported in terms of the anatomical location of peak statistical effects, expressed using a stereotactic system such as Talairach (Talairach and Tournoux, 1988) or Montreal Neurological Institute (MNI) coordinate space.

This reporting convention has motivated the development of specialized methods for performing coordinate-based meta-analysis (CBMA; Chein et al., 2002; Fox et al., 1998; Turkeltaub et al., 2002). As Fox and colleagues (1998) point out, neuroimaging findings are more amenable to an “effect-location meta-analysis” rather than the “effect-size meta-analysis” common in other domains. The objective of CBMA is not to estimate the magnitude of an effect across studies, but rather to identify anatomical locations in which an effect is observed consistently. This emphasis renders CBMA robust to certain pitfalls of effect-size meta-analysis. For example, publication bias (underreporting of null results) systematically inflates estimates of effect size, but is less likely to bias estimates of effect location (Fox et al., 1998).

Several specific approaches to CBMA have been developed and popularized in recent years. One is activation likelihood estimation (ALE; Eickhoff et al., 2012; Eickhoff et al., 2009; Turkeltaub et al., 2002; Turkeltaub et al., 2012), implemented in a freely available software package (“GingerALE”; http://brainmap.org/). The objective of ALE is to estimate, for each voxel, the probability that at least one activation focus from a collection of experiments truly lies at that voxel’s location, given Gaussian assumptions about spatial uncertainty. A second approach is multilevel kernel density analysis (MKDA; Wager et al., 2007; Wager et al., 2009), which quantifies the proportion of studies that report activation foci within some radius (e.g., 10mm) of each voxel. Direct comparison of ALE and MKDA suggests their results are qualitatively similar (Salimi-Khorshidi et al., 2009).

The present meta-analyses largely adhere to the strategy of MKDA, based on our judgment that this technique yields a more readily interpretable meta-analytic test statistic. However, as described in detail below, we refine our methods using insights gained in both these threads of methodological development.

2.2. Developing a corpus of experimental findings

2.2.1. Identifying candidate studies

The present meta-analyses are based on a corpus of 206 published fMRI experiments. Candidates for inclusion were initially identified using a PubMed search on the keywords "fMRI" and "reward," which returned 1,121 records on Nov. 15, 2011. We also explored several additional sources, which added relatively few (<30) studies to the eventual corpus. These additional sources included (1) the BrainMap database (http://brainmap.org), (2) work cited in review papers (e.g., Grabenhorst and Rolls, 2011; Kable and Glimcher, 2009; Knutson and Cooper, 2005; O'Doherty, 2004; Peters and Büchel, 2010); (3) existing in-house reference libraries, and (4) direct searches on the names of frequently occurring authors.

2.2.2. Selection criteria

Candidate papers identified in the above manner were evaluated for inclusion in the corpus according to a series of selection criteria. As initial criteria, we restricted our sample to English-language papers that used fMRI to measure brain-based BOLD signal in healthy young-adult human participants.

We required that a study report a directional change in BOLD as a function of SV. The relevant statistical comparison could be either a binary contrast or a continuous parametric analysis. Because one objective of the present research is to examine neural coding of SV across various contexts, we imposed few restrictions on the specific task events that could qualify as carriers of SV, and there was considerable heterogeneity among the studies ultimately included. Different studies involved outcomes consisting of monetary payoffs, consumable liquids, arousing pictures, social feedback, and a variety of other types of events. Outcomes could consist of either rewards or penalties. There was likewise considerable variation in the nature of the experimental tasks, including tasks both with and without elements of choice, risk, or learning.

Two specific outcome domains were excluded: penalties that consisted of physical pain, and rewards that consisted of psychoactive drug administration. Each of these domains has a large dedicated scientific literature. In the case of physical pain, at least one comprehensive meta-analysis of neuroimaging findings is already available (Peyron et al., 2000).

We judged two outcomes as differing in SV if participants preferred (i.e., would choose) one outcome relative to another. In some cases such a preference could be inferred a priori. For example, we regarded larger monetary rewards as higher-SV than smaller rewards, all else equal. For more idiosyncratic kinds of outcomes (e.g., music or flavors), we included a comparison as long as accompanying behavioral data (e.g., choices or ratings) clearly established differences in preference. We took care to exclude cases in which differences in SV were inferred on the basis of the neuroimaging findings themselves. To illustrate, in one example (Kampe et al., 2001), the pattern of BOLD response in VS was taken to suggest that the reward value of viewing a human face depended on an interaction between the face's attractiveness and its gaze direction. This conclusion capitalizes on a presumed link between SV and striatal BOLD rather than counting, for our purposes, as independent evidence for such a link.

We required that peak activation foci be reported in stereotactic spatial coordinates (i.e., Talairach or MNI space), together with the direction of the effect (positive or negative). We did not impose specific requirements regarding statistical threshold levels or correction for multiple comparisons, deferring instead to the judgment of the original authors and reviewers. However, we did require that the same threshold be applied uniformly across the whole brain. Results derived from region-of-interest (ROI) or small-volume-correction (SVC) analyses were excluded, even if spatial coordinates were provided. Because our meta-analytic statistical tests assume foci are spatially random under the null hypothesis, it is important to avoid experimenter-imposed bias in the locations at which effects can be identified.

The above restrictions often led us to include only a subset of a given study's findings. For clinical studies, we often could include results pertaining exclusively to a healthy control group. For example, in one instance (Stoy et al., 2011) we included results solely from a group of healthy individuals, excluding results from groups suffering from attention deficit hyperactivity disorder. When a study’s main findings were based on tests of ROIs (e.g., Smith et al., 2009) we often could still include foci derived from supplementary whole-brain exploratory analyses.

2.2.3. Coding study results

Coordinate foci that met our inclusion criteria were entered into a spreadsheet. Coordinates originally reported in Talairach space were converted to MNI space using the transformation proposed by Lancaster (2007), as implemented in GingerALE software (http://brainmap.org). Each focus was coded according to whether the direction of the effect was positive or negative. Regardless of the nominal directionality of the original statistical contrast, we defined effects as positive if greater BOLD signal was associated with higher SV, and negative if greater BOLD signal was associated with lower SV. Foci were also coded for attributes of the task, including the choice stage (e.g., decision time vs. outcome receipt), the qualitative valence of the outcomes (e.g., rewards vs. penalties), and the specific type of outcome involved (e.g., monetary vs. primary rewards).

We developed in-house software to query the spreadsheet on the basis of these attributes. A query could return a list of foci, organized by study, that met criteria for inclusion in a given meta-analysis.

2.2.4. Final corpus

The final corpus of 206 publications included a total of 348 analysis contrasts, 3,857 participants, and 3,933 activation foci. The number of participants per study ranged from 6–76 (median = 17, interquartile range [IQR] = 12.5–20). The studies in the corpus are listed in Appendix 1.

2.3. Meta-analytic statistical procedures

2.3.1. General considerations

As described above, our meta-analyses do not estimate the magnitude of signal change, but rather the density with which foci from different studies are clustered in the vicinity of given voxel. Among the studies that report effects somewhere in the brain, our goal is to assess the consistency of the reported effect locations.

Given this emphasis, particular care is required in incorporating information about the directionality of BOLD signal change. Our strategy will be to treat positive and negative effects as categorically distinct. Where we directly compare positive and negative effects at the meta-analytic level, we will be comparing the degree of spatial clustering for each category. It is logically possible for both positive and negative effects to cluster in the same location.

2.3.2. Indicator maps

We converted each study's results to an indicator map (IM). One IM was generated for each publication, using all of the foci in that paper that met the criteria for a given meta-analysis. IMs were constructed using a binary indicator function, similarly to the procedure in MKDA (Salimi-Khorshidi et al., 2009; Wager et al., 2007; Wager et al., 2009). A voxel held a value of 100 if an activation focus fell within 10mm of that voxel, or a value of zero otherwise. IMs used 2mm-voxel resolution, with coordinate locations rounded to the nearest voxel center. The sphere of positive indicator values surrounding a single focus point had a volume of 515 voxels (4.12cm³).

The binary indicator statistic has several advantages. First, it ensures that the range of values in a study’s IM does not increase merely as a result of within-study overlap, so studies that report large numbers of nearby foci are not unduly influential. The importance of this consideration is widely recognized in the literature on CBMA methods (Turkeltaub et al., 2012; Wager et al., 2007). The binary approach provides a "multi-level" or "random-effects" meta-analytic test, placing principal emphasis on cross-study consistency.

A second advantage is that averaging a group of binary IMs yields a concretely interpretable meta-analytic statistic. The mean IM in a given voxel equals the percent of studies that report an activation focus within 10mm. In interpreting our results, it is important to keep in mind that this statistic represents the density of foci in an area, not the amplitude of BOLD signal change.

Several techniques have previously been proposed for differentially weighting the relative contribution of individual studies to a meta-analysis. For example, it seems theoretically appropriate to down-weight studies that use fixed-effects rather than random-effects group-level analyses (Wager et al., 2007; Wager et al., 2009), or to apply a more spatially diffuse kernel to studies with fewer participants (Eickhoff et al., 2009). However, despite careful efforts to quantify certain sources of uncertainty (Eickhoff et al., 2009), it remains difficult, in our view, to determine confidently the appropriate degree (or form) of weighting. Because of this, together with the recognition that we are unlikely to identify all factors relevant to adjudicating a study's relative credibility, we refrain from applying nonuniform weights to studies in our meta-analyses. We focus on identifying cross-study consistencies, while taking the results of individual studies largely at face value provided they pass our inclusion criteria. A key benefit of this approach is that the mean-IM statistic retains its literal interpretation as the percent of studies reporting foci within 10mm.

2.3.3. Inference overview

Our meta-analytic conclusions at the whole-brain level rest on two qualitatively different types of inferential test. The first involves testing a single set of studies. For example, we might wish to test for above-chance clustering of foci across all studies that report positive effects of SV on BOLD. The second involves comparing two sets of studies. For example, we might wish to determine whether the foci associated with SV during decision making and during reward receipt are clustered differently. The following two sections describe each test in detail.

2.3.4. Single-category tests

The objective of single-category tests is to determine whether effects occur in consistent locations. An initial statement of the relevant null hypothesis (which we shall refine below) is as follows: foci are located randomly, with no systematic anatomical correspondence across studies. We wish to draw conclusions only if foci are clustered densely enough to cast doubt on this null hypothesis. The test needs to be conducted in a manner that controls familywise error (FWE) rate, accounting for the fact that all voxels in the brain are tested simultaneously.

We constructed an IM for each study as described above, and averaged them to yield a mean-IM map. We assessed statistical significance using permutation testing (Nichols and Holmes, 2002). Procedures were implemented in Matlab (The Mathworks, Natick, MA). Consistent with previous work on CBMA (Turkeltaub et al., 2002; Wager et al., 2007), we simulated null-hypothesis conditions by assigning foci to random locations while maintaining the true number of studies and foci per study. We then ran the full analysis on the randomized data and identified the maximum statistic in the resulting brain image. Repeating this procedure many times yielded a null distribution for the imagewise maximum, which could then be used to assign corrected p values to the unpermuted results. For example, a p value of 0.01 at a given voxel would signify that only 1% of the random permutations produced a value anywhere in the image that exceeded that voxel’s value in the real data.

This basic procedure forms the core of our approach. We next describe two additional refinements.

The first refinement relates to the exact specification of the null hypothesis. Even if the results of individual studies were essentially random, we still would not necessarily expect foci to be distributed uniformly throughout the brain. Even spurious foci might occur more often in gray matter than white matter. This consideration has led previous investigators to restrict meta-analyses to a gray-matter mask. There are practical difficulties in identifying such a mask, however, and the masks used in previous research tend to be fairly liberal. For example, the GingerALE software package uses a mask thresholded at a gray-matter probability of 0.10 and subsequently dilated, ultimately including 96.9% of the voxels in a whole-brain mask.² A liberal mask risks underestimating how densely foci might cluster by chance alone.

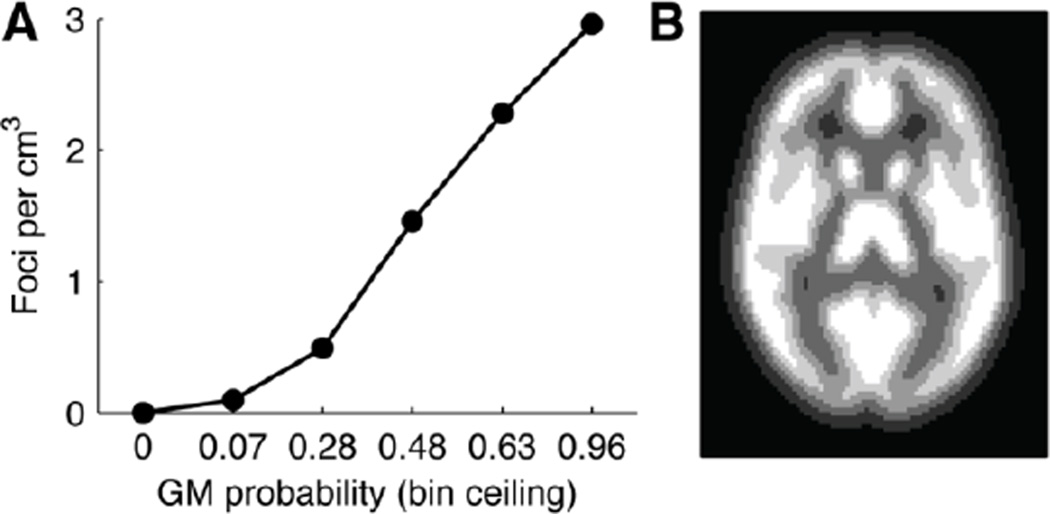
We suspected a more graded relationship might hold between a voxel's gray-matter probability (henceforth denoted pGM) and the frequency of activation foci. We examined this possibility using all the foci in our database together with the pGM map distributed with the SPM software package (derived from the ICBM Tissue Probabilistic Atlases; http://www.loni.ucla.edu/ICBM). This map identifies 338,634 voxels (at 2x2x2mm resolution; 2709.1 cm³) with pGM > 0. We divided these voxels into 5 equal-sized bins and tabulated the number of foci in our entire corpus that fell within each bin. As shown in Figure 2A, this reveals a continuous relationship between pGM and foci density.

Figure 2.

Effect of gray-matter probability (pGM) on the density of reported activation foci, across all results in our corpus. A: Voxels with nonzero pGM were divided into five equal-sized bins. Foci density increased as a function of pGM. We therefore account for pGM in our null hypothesis. B: Illustration of the pGM bins (lighter color denotes higher pGM).

In light of this observation, we adopted a modified null hypothesis: foci are distributed randomly, conditional on pGM. Testing this version of the null hypothesis required only a small modification to the procedure described above. On each iteration of the permutation test, each focus was assigned to a random location within its original pGM bin (see Figure 2B). The randomized data thus preserve the tendency for foci to fall more densely in high-pGM locations, providing for an appropriately conservative test.

Our second refinement of the basic permutation procedure relates to defining the test statistic. Recent work (Eickhoff et al., 2012) indicates that coordinate-based meta-analyses can achieve considerably improved sensitivity by incorporating spatial clustering (cf. Forman et al., 1995). We therefore use cluster mass (i.e., the sum of all the statistical values in a cluster), rather than mean IM value, as our primary test statistic for evaluating statistical significance (Bullmore et al., 1999).

Cluster-mass thresholding requires first specifying a "primary" or "cluster-forming" threshold,³ which we set to uncorrected p < 0.01. Implementing this threshold in turn requires an additional step, given that we would not otherwise compute uncorrected p values. We focused on voxels in the highest pGM bin, where high mean-IM values are the most likely to occur by chance. For each study in a given meta-analysis, we calculated the proportion of voxels in this bin with a positive IM value. By treating the proportions from different studies as independent probabilities, we could calculate the mean-IM value that would be exceeded with a probability of less than 0.01 by chance alone. This value, specific to each single-category analysis, served as the cluster-forming threshold. (Our approach is equivalent to the "histogram integration" procedure recommended by Eickhoff et al., 2012 for setting primary thresholds, but much simpler because our IM statistic is binary rather than continuous.)

The primary threshold was applied to the results of each random permutation, and the largest cluster mass was recorded in the null distribution. The same primary threshold was then applied to the real data, and the resulting clusters were assigned corrected p values based on the frequency of equal or larger clusters in the null distribution. All reported results are based on 5000 permutations. The nonrandomized data were included as one of these permutations, so our smallest possible corrected p value is 0.0002. We applied a threshold of corrected p = 0.05. A one-tailed test is appropriate here because we place no interpretive significance on a finding of less dense clustering than expected by chance.

2.3.5. Between-category comparisons

A second meta-analytic objective involves comparing two sets of experimental findings to assess whether they involve topographically different response patterns.

Between-category comparisons involve different inferential logic and a different null hypothesis from single-category tests. The null hypothesis here is that category labels are exchangeable. Specifically, in voxelwise independent-samples t-tests comparing two categories of IMs, the null hypothesis is that the observed statistical values are no greater than would be expected if IMs were assigned to categories randomly. Here again, permutation testing provides a natural way to evaluate the null hypothesis while controlling for multiple comparisons. Rather than randomize the spatial locations of foci, here we leave the original IMs intact but shuffle their category assignments. In this way we can estimate the imagewise maximum t statistic expected by chance alone (Nichols and Holmes, 2002).

This type of independent-samples permutation test is widely applicable beyond CBMA (the same test applies to comparisons between groups of participants), and software to perform it is readily available. We implemented 2-sample permutation tests using the "randomise" utility in the FSL package (Smith et al., 2004).

Because the IMs are binary, we technically are testing whether, at each voxel, two categories differ in the proportion of studies with nearby activation foci. The correct test would therefore be a chi-square or related exact test. For simplicity, and to take advantage of standard software, we used an independent-samples t-test as an approximation. The approximation is valid because we derive accurate whole-brain-corrected p values via permutation testing. (Note that voxelwise chi-square tests would still not yield valid parametric p values because cell-size requirements would not always be met.) Variance was spatially smoothed (σ = 5mm), so the resulting statistic is a “pseudo-t” (Nichols and Holmes, 2002).

Results are based on 5000 permutations. As above, the primary (cluster-forming) threshold was set at the nominal p = 0.01 level, and corrected significance levels were assessed on the basis of cluster mass. On each random permutation the mass of the largest suprathreshold cluster was recorded in the null distribution, and this distribution was then used to assign corrected p values to suprathreshold clusters in the unpermuted data. Because we care about differences in both directions, we ran the permutation test separately for positive and negative differences and applied a significance threshold of p = 0.025 to each set of results.

2.3.6. Region-of-interest analyses

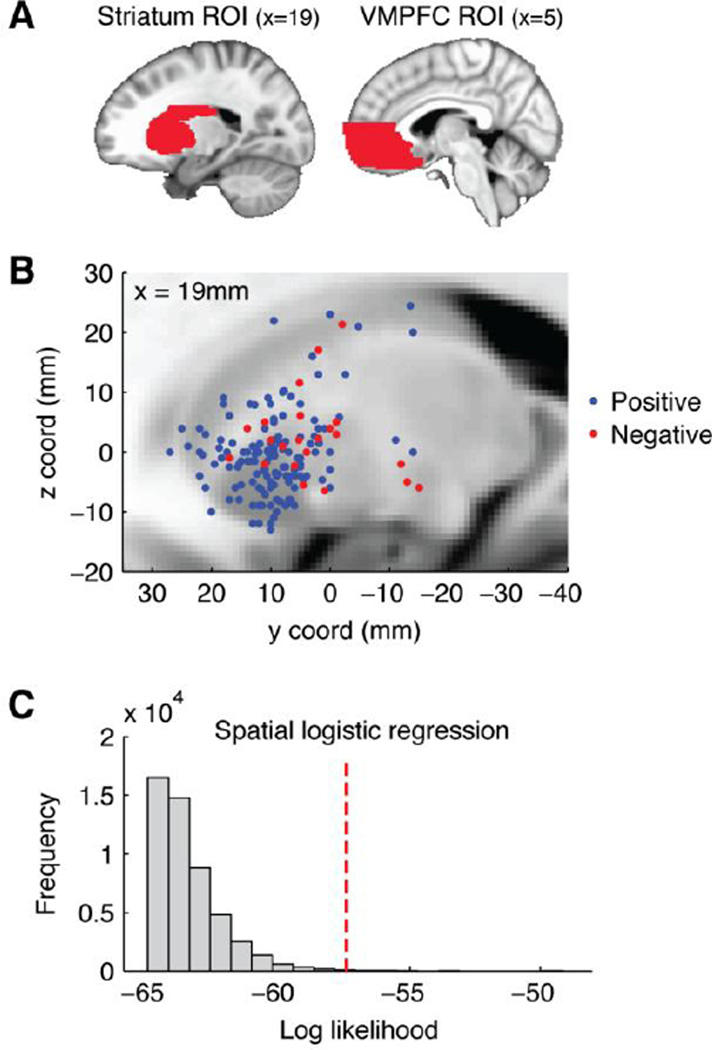
Additional analyses focused in detail on two specific regions of interest (ROIs): (1) striatum, and (2) VMPFC. Both these regions are considered integral in representing SV, and their internal organization is a topic of growing interest (e.g., Seymour et al., 2007; Smith et al., 2010; Tanaka et al., 2004; Voorn et al., 2004). We addressed this issue meta-analytically by analyzing the spatial distribution of foci within each ROI.

ROIs were defined using anatomical atlas labels (Tzourio-Mazoyer et al., 2002). The striatum ROI was created by combining bilateral atlas regions labeled as caudate, putamen, and pallidum (these regions also encompass nucleus accumbens, which is not labeled separately in this atlas). The VMPFC ROI included regions labeled as medial orbitofrontal and gyrus rectus. It also included portions of two additional areas ("anterior cingulum" and "superior medial frontal"), truncated dorsally at an MNI coordinate of z = +10mm (note, however, that excluding these latter two areas from the ROI leads to similar conclusions). ROI masks (1mm resolution) were made symmetrical by taking the union of the original and left/right reversed masks, and then dilated by one voxel. Volumes of the resulting bilateral ROIs were 57.20 cm³ for VMPFC and 60.44 cm³ for striatum.

Analyses were conducted for each ROI separately. For results in a given category, we identified foci that fell inside the ROI. Foci were projected into a single hemisphere by using the absolute value of the x coordinate, thereby encoding medial-lateral rather than hemispheric organization. Within-ROI foci from the same study were averaged, so each study contributed a single centroid location to the meta-analysis. This step ensures that each point represents unique data, and studies with more foci are not unduly influential.

Different categories of foci (e.g., positive vs. negative effects) were then compared. The simplest factor to compare is the proportion of contrasts that report foci in the ROI at all. This analysis can test, for example, whether two types of effect have different probabilities of falling within the striatum. Rates were compared using Fisher's exact test.

In addition to comparing whether studies report foci in an ROI, we can also compare where in the ROI these foci lie (again projecting all foci to a single hemisphere). For example, do positive and negative effects consistently occur in different parts of the striatum? We tested spatial discriminability using logistic regression. For a given pair of categories, category label was the outcome variable and |x|, y, and z spatial coordinates were predictors. We assessed the log likelihood (LL) of the data under the fitted logistic model. This value was compared to a permutation-based null distribution, generated by repeatedly fitting the model with randomly shuffled category labels and recording the resulting LL values (50,000 iterations). If the empirical LL exceeded the 95th percentile of the null distribution, we judged that the two categories of foci were significantly discriminable within the ROI on the basis of their spatial coordinates. Significant results were followed up with Wilcoxon rank-sum tests, individually comparing |x|, y, and z coordinate values between the two categories. Finally, to examine potential hemispheric lateralization, we separately tested the signed x coordinates against zero for each group of studies using a Wilcoxon signed-ranks test, and between categories of studies using Wilcoxon rank-sum tests.

3. Results

3.1. Positive and negative effects of SV on BOLD

3.1.1. Whole-brain meta-analysis

We first examine overall associations between SV and BOLD. Here we organize experimental findings solely according to the direction of the reported effects (positive or negative), aggregating across other attributes. An effect was coded as positive if a greater BOLD response was observed for more rewarding (or less aversive) outcomes; it was coded as negative if a greater BOLD response was observed for less rewarding (or more aversive) outcomes. Our corpus contains 200 studies that report positive effects and 77 studies that report negative effects. (Seventy-one of these studies report both positive and negative effects and therefore contribute different data to both categories.)

We first describe single-category analyses examining the spatial distributions of positive and negative effects separately. As described above, these analyses sought to identify regions in which foci clustered more densely than chance alone would predict.

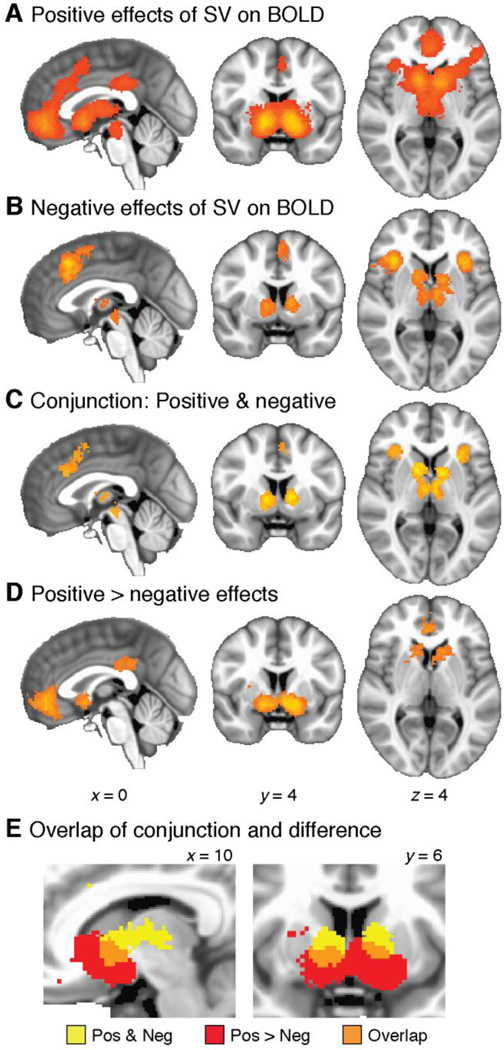
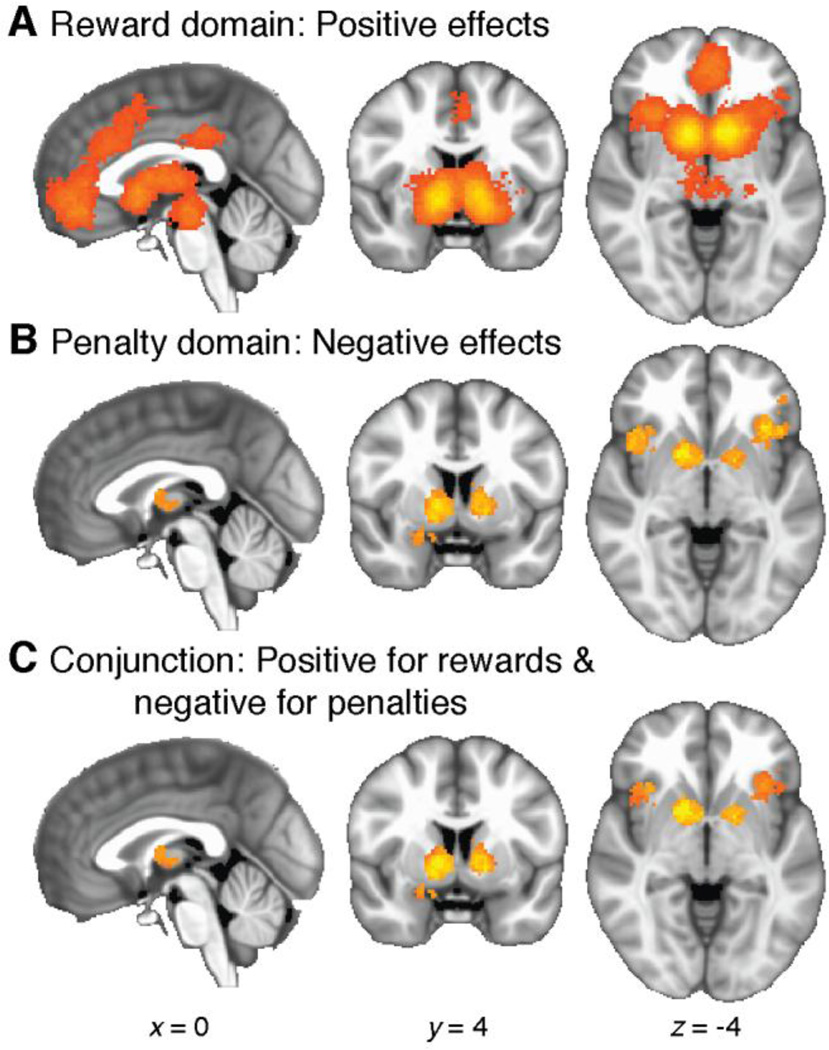
Foci for positive effects showed significant clustering in a large connected area of medial prefrontal cortex and nearby cortical and subcortical regions (12981 voxels, 103.85 cm³, cluster-corrected p = 0.0002), as well as posterior cingulate cortex (467 voxels, 3.74 cm³, p = 0.0208; see Figure 3A and Table 1). As described above, the meta-analytic statistic corresponds to the percent of included studies that report an activation focus within 10mm of a given voxel. Local maxima for this statistic were as follows: 42.0 in left striatum, 40.5 in right striatum, 23.5 in VMPFC, 15.0 in left anterior insula, 16.0 in right anterior insula, 13.5 in posterior cingulate, 12.0 in brainstem, 12.0 in anterior cingulate cortex (ACC), and 11.0 in pre-supplementary motor area (pre-SMA).

Figure 3.

Whole-brain meta-analysis of positive and negative responses. A: Significant clustering of positive responses. B: Significant clustering of negative responses. C: Conjunction maps, showing regions with significant clustering for both positive and negative responses. D: Results of a between-category comparison, showing regions with significantly greater clustering for positive than negative effects. E: Detail of the striatum, illustrating overlap between the conjunction map (Panel C) and the difference map (Panel D). In the overlapping region (orange), positive effects cluster more densely than negative effects, which in turn still cluster more densely than expected by chance.

Table 1.

SV effects

Description	X	Y	Z	Peak meta- analytic statistic
Positive effects of SV on BOLD
L Striatum	−12	12	−6	42.0
R Striatum	12	10	−6	40.5
VMPFC	2	46	−8	23.5
L Anterior Insula	−30	22	−6	15.0
R Anterior Insula	32	20	−6	16.0
PCC	−4	−30	36	13.5
Brainstem	−2	−22	−12	12.0
ACC	−2	28	28	12.0
Pre-SMA	−2	16	46	11.0
Negative effects of SV on BOLD
L Anterior Insula	−36	20	−6	26.0
R Anterior Insula	40	22	−6	24.7
DMPFC	4	22	44	22.1
L Thalamus	−6	−8	6	18.2
R Thalamus	6	−8	6	14.3
L Striatum	−12	4	2	14.3
R Striatum	12	10	−2	15.6
Conjunction: Positive and negative effects
L Anterior Insula	−30	22	−6	15.0
R Anterior Insula	32	20	−6	16.0
L Striatum	−12	4	2	14.3
R Striatum	12	10	−2	15.6
L Thalamus	−4	−12	6	14.3
R Thalamus	6	−8	6	13.0
ACC	4	28	26	11.0
Comparison: Positive > negative effects
L Striatum	−12	12	−6	7.11
R Striatum	14	12	−10	6.23
VMPFC	2	46	−8	5.28
PCC	2	−36	32	3.91

Note: Coordinates are in MNI space. For single-category analyses, the meta-analytic statistic is the percent of studies reporting an activation focus within 10mm. For conjunctions, the statistic is the minimum meta-analytic statistic across both tests. For between-group comparisons, the meta-analytic statistic is the pseudo-t (see text for details). Abbreviations: L, left; R, right; ACC, anterior cingulate cortex; DMPFC, dorsomedial prefrontal cortex; PCC, posterior cingulate cortex; pre-SMA, pre-supplementary motor area; VMPFC, ventromedial prefrontal cortex

Foci for negative effects were significantly clustered in DMPFC (1423 voxels, 11.38 cm³, p = 0.0002), left anterior insula (1111 voxels, 8.89 cm³, p = 0.0002), right anterior insula (1195 voxels, 9.56 cm³, p = 0.0002), and bilateral striatum and thalamus (1610 voxels, 12.88 cm³, p = 0.0002; see Figure 3B and Table 1). Local maxima for the meta-analytic statistic were as follows: 26.0 in left anterior insula, 24.7 in right anterior insula, 22.1 in DMPFC, 18.2 in left thalamus, 14.3 in right thalamus, 14.3 in left striatum, and 15.6 in right striatum.

In some cases, positively and negatively signed effects appeared to cluster in the same regions. Indeed, most of the areas that showed negative effects overlapped with areas that also showed positive effects. We confirmed this by calculating the conjunction map for significant clustering of both positive and negative effects. The conjunction test accepts voxels that are significant at FWE-corrected p < 0.05 in both analyses. Clusters passing the conjunction test occurred in DMPFC (454 voxels, 3.63 cm³), left anterior insula (542 voxels, 4.34 cm³), right anterior insula (697 voxels, 5.58 cm³), and bilateral thalamus and striatum (1248 voxels, 9.98 cm³; see Figure 3C and Table 1).

Finally, we pitted positive effects against negative effects in a between-category comparison. This comparison examines whether a given region is associated with different degrees of clustering for positively vs. negatively signed responses. As detailed above, this test compares the density of foci, not the amplitudes of BOLD responses. The results identified several regions in which positive effects clustered more densely than negative effects: bilateral VS (2683 voxels, 21.46 cm³, p = 0.0002), VMPFC (1245 voxels, 9.96 cm³, p = 0.0002), and PCC (369 voxels, 2.95 cm³, p = 0.0024; see Figure 3D and Table 1). Local maximum pseudo-t statistics were as follows: 7.11 in left striatum, 6.23 in right striatum, 5.28 in VMPFC, and 3.91 in PCC. No areas showed differences in the direction of denser clustering for negative effects than positive effects.

In summary, some brain regions showed both positively and negatively signed effects of SV on BOLD across studies, while other regions showed positive effects only. SV effects in VMPFC and PCC appear predominantly positive, whereas DMPFC and bilateral anterior insula showed a mixture of positive and negative effects. These two categories are not mutually exclusive: in striatum, negative effects occurred more densely than expected by chance, but still less densely than positive effects (see Figure 3E). Effects in striatum appeared spatially dissociable. Voxels in anterior VS showed only the difference (positive > negative), whereas voxels in dorsal and posterior striatum showed only the conjunction (positive & negative). ROI analyses evaluated within-region organization more directly.

3.1.2. ROI meta-analysis

Positive effects were more likely than negative effects to fall within our anatomically defined striatum ROI. Of 200 studies reporting positive effects, 145 (72.5%) had foci in striatum, compared to only 22 of the 77 studies reporting negative effects (28.6%). These rates differed significantly (Fisher p < 0.001). Followup ROI analyses separately examining the subregions of caudate, putamen, and VS showed that positive effects were significantly more frequent than negative effects in each subregion (caudate, 59/200 for positive vs. 9/77 for negative; putamen, 59/200 for positive vs. 7/77 for negative; VS, 61/200 for positive vs. 4/77 for negative; all Fisher ps < 0.002).

Spatial logistic regression, predicting whether striatum foci represented positive or negative effects on the basis of their spatial coordinates, achieved log likelihood (LL) = −57.45. This was significantly greater than for randomly permuted category labels (median null LL = −63.87; p = 0.002; see Figure 4B–C), indicating that the foci for positive and negative effects in striatum were, to some extent, spatially dissociable. Followup tests showed that the two categories did not differ in their absolute x coordinates (median |x| for positive foci = 14.67mm, IQR = 11.25–18; median |x| for negative foci = 16mm, IQR = 12–21; rank-sum p = 0.116), but did differ in their y (positive median = 9.89mm, IQR = 6–13.5; negative median = 4.25mm, IQR = −1–8; rank-sum p < 0.001) and z coordinates (positive median = −1mm, IQR = −5–2; negative median = 2mm, IQR = −2–5; rank-sum p = 0.039). In summary, within striatum, positive foci were centered approximately 5mm anterior and 3mm inferior to negative foci. Examination of Figure 4B suggests that dorsal and posterior striatum showed both positive and negative effects, whereas anterior VS showed positive effects predominantly. Signed x coordinates in the striatum ROI showed no evidence of lateralization for either positive or negative effects.

Figure 4.

Region-of-interest (ROI) analysis comparing positive and negative effects of SV on BOLD. A: Illustration of the two ROI masks. B: Scatterplot of foci for positive and negative effects in striatum. All foci are projected onto a single sagittal slice for visualization. Note that the five posterior/inferior foci fall in the putamen, lateral to the anatomical slice shown (|x|>=28). C: Permutation-based null distribution (gray histogram bars) and actual results (red line) for spatial logistic regression based on the data in Panel B.

Analyses of the VMPFC ROI similarly revealed a greater frequency of positive than negative effects: 112 of 200 studies with positive effects (56.0%), but only 12 of 77 studies with negative effects (15.6%), included foci in VMPFC (Fisher p < 0.001). The small number of foci (only 12 in the negative group) results in limited power to detect a spatial dissociation. Logistic regression revealed no significant spatial discriminability (LL = −39.23, median null LL = −38.20, p = 0.945).

Signed x coordinates in VMPFC were significantly lower than zero for positive effects (median = −1.00, IQR = −6.39–3.00, signed-rank p = 0.037), implying a small but reliable left lateralization. No lateralization was detected for negative effects, nor did positive and negative effects significantly differ.

3.2. Outcome valence

The co-occurrence of positive and negative effects in the same brain regions may initially appear counterintuitive. Since no individual result can be both positive and negative in the same location, this pattern necessarily reflects heterogeneity across the different studies or analyses aggregated together in the meta-analysis. A logical followup step is to attempt to identify the basis for this heterogeneity. What aspects of the experimental design determine whether signal in anterior insula, for example, responds as a positive or negative function of SV?

One possibility is that this variation reflects differences in the valence of the outcomes at stake. A neural structure with a linear SV response (see Figure 1, Pattern A) would show uniformly positive effects across studies. In contrast, a structure with a U-shaped response (Pattern B) would show positive effects in the domain of rewards but negative effects in the domain of penalties, leading to a mixture of findings across studies. Such a neural structure might be regarded as encoding not SV per se, but perhaps a related quantity such as salience (see, e.g., Litt et al., 2011).

To investigate the importance of outcome valence, we divided study results according to whether outcomes consisted of penalties or rewards. A statistical contrast was counted in the reward domain if it pitted positive outcomes (e.g., winning money) against smaller positive or neutral outcomes (e.g., winning nothing). A contrast was counted in the penalty domain if it pitted neutral or negative outcomes (e.g., winning nothing or losing money) against larger negative outcomes (e.g., losing more money). In the penalty domain, a positive effect of SV means a greater BOLD response for a smaller loss than a larger loss. A total of 127 studies contributed results in the reward domain and 37 in the penalty domain (with 35 studies contributing different results to each domain). We excluded direct contrasts of rewards against penalties, since these cannot be assigned to a single valence category (these contrasts are, however, included in the more comprehensive meta-analysis described in the previous section). Reward-vs.-penalty contrasts do not entail clear directional predictions if BOLD follows a U-shaped function of SV; instead, the sign of the effect would depend on the exact magnitudes of the positive and negative outcomes.

We classified outcomes as rewards or penalties using an absolute scheme, based on whether the outcome was preferable to receiving nothing. In this sense, our classification matches the ordinary meanings of “reward” and “penalty.” Pleasant experiences and monetary gains counted as rewards, while aversive experiences and monetary losses counted as penalties. An alternative might have been to use a relative scheme, taking participants’ expectations as a reference point and classifying valence according to the direction of the reward prediction error (Montague et al., 1996). An obstacle to applying such a scheme in the present context is that, for tasks not originally analyzed in this manner, identifying the applicable subjective reference point would often have required extensive additional assumptions. We discuss this issue further in Section 4 below.

We conducted four separate single-category analyses, examining the density of positive or negative effects within the domain of either rewards or penalties.

Of 127 studies in the reward domain, 126 reported positive effects and 20 reported negative effects (19 reported both). Results for positive effects in the reward domain were similar to the results described above for positive effects generally (these two meta-analyses are based largely on the same data). There was a large medial frontal and subcortical cluster (12,731 voxels, 101.85 cm³, p = 0.0002) and a cluster in PCC (374 voxels, 2.99 cm³, p = 0.0390; see Table 2 and Figure 5A). Local peak values of the meta-analysic statistic were as follows: 41.3 in left striatum, 40.5 in right striatum, 19.8 in VMPFC, 15.9 in left anterior insula, 19.8 in right anterior insula, 19.0 in brainstem, 15.9 in ACC, and 15.1 in PCC.

Table 2.

SV effects by outcome valence

Description	X	Y	Z	Peak meta- analytic statistic
Positive effects in the reward domain
L Striatum	−14	10	−6	41.3
R Striatum	12	6	−8	40.5
VMPFC	0	40	−12	19.8
L Anterior Insula	−32	26	0	15.9
R Anterior Insula	32	20	−6	19.8
Brainstem	0	−20	−10	19.0
ACC	−2	24	26	15.9
PCC	−4	−30	36	15.1
Negative effects in the penalty domain
L Striatum	−16	4	−4	25.0
R Striatum	12	6	4	31.3
L Anterior Insula	−36	22	−12	28.1
R Anterior Insula	46	22	−6	28.1
R Amygdala	24	−4	−18	21.9
Conjunction: Positive for rewards and negative for penalties
L Striatum	−16	4	−4	25.0
R Striatum	18	6	−6	28.1
L Anterior Insula	−32	26	0	15.9
R Anterior Insula	32	20	−6	19.8

Figure 5.

Whole-brain meta-analysis of positive and negative effects, accounting for valence. A: Significant clustering of positive effects in the domain of rewards. B: Significant clustering of negative effects in the domain of penalties. C: Overlap of the results in Panels A and B. This conjunction of effects would be expected in a region in which the BOLD response is a U-shaped function of SV (see Figure 1, Pattern B).

We observed no areas of significant clustering for negative effects in the reward domain. The largest subthreshold clusters occurred in left anterior insula (390 voxels, 3.12 cm³, p = 0.0832) and DMPFC (388 voxels, 3.10 cm³, p = 0.0972).

Next we turn to the domain of penalties. Of 37 publications reporting findings in the penalty domain, 10 reported positive effects and 32 reported negative effects (5 reported both). At the meta-analytic level, no clusters were significant for positive effects (i.e., greater BOLD response for smaller penalties), with the strongest finding being a 100-voxel (0.80 cm³) cluster in the vicinity of left anterior insula (p = 0.2610). For negative effects in the penalty domain (i.e., greater BOLD response for larger penalties), significant clustering occurred in left anterior insula (608 voxels, 4.86 cm³, p = 0.0002, peak = 28.1), right anterior insula (445 voxels, 3.56 cm³, p = 0.0006, peak = 28.1), and bilateral striatum extending to right amygdala (1512 voxels, 12.10 cm³, p = 0.0002, peak = 31.3; see Table 2 and Figure 5B).

A brain region with a nonlinear SV response (pattern B in Figure 1) would be expected to show both positive effects for rewards and negative effects for penalties. Consistent with this, regions of bilateral insula and striatum were significant in a conjunction test evaluating overlap between these two categories. Clusters passing the conjunction test occurred in bilateral striatum (1223 voxels, 9.78 cm³), left anterior insula (255 voxels, 2.04 cm³), and right anterior insula (273 voxels, 2.18 cm³; see Figure 5C and Table 2).

In principle, another meta-analytic strategy for disambiguating linear and nonlinear response profiles would be to compare positive versus negative effects solely within the domain of penalties. Pattern-A regions should show mostly positive effects, while Pattern-B regions should show mostly negative effects. An obstacle to this approach, however, is the small number of available data points: only 10 studies in our corpus reported coordinates for positive effects in the penalty domain. This compromises the power of a direct comparison between the two categories. Consistent with limited power, the comparison restricted to the penalty domain yielded no differences in either direction approaching statistical significance.

3.3. Decision time versus outcome receipt time

3.3.1. Whole-brain meta-analysis

The next theoretical question we address is whether different neural activity patterns are associated with SV at different stages of a decision process. In particular, we are interested in comparing the SV response when a decision is being evaluated to the response when an outcome is actually received.

To approach this question meta-analytically, we divided the findings in our corpus along a new dimension into two categories. In both cases we initially consider positive effects only. The first category involves positive effects restricted to the time period at which choice alternatives were being evaluated. For example, this set includes foci in which a greater BOLD response occurred for the presentation of more-valuable relative to less-valuable choice alternatives. The second category consists of positive effects at the time of outcome delivery. There were 27 studies contributing data at the decision stage and 140 studies contributing data at the outcome delivery stage (4 studies contributed data from different analyses to both categories). The present analysis excluded contrasts that did not clearly fall in either category, such as those focusing on the interval when a reward or penalty was being anticipated. In particular, contrasts involving the “cue” phase of the monetary-incentive-delay (MID) task (Knutson et al., 2001a) were categorized as neither “decision” nor “outcome receipt,” although these studies are examined further below. (Other recent reviews and meta-analyses have focused specifically on the issue of reward anticipation; e.g., Diekhof et al., 2012; Knutson and Greer, 2008).

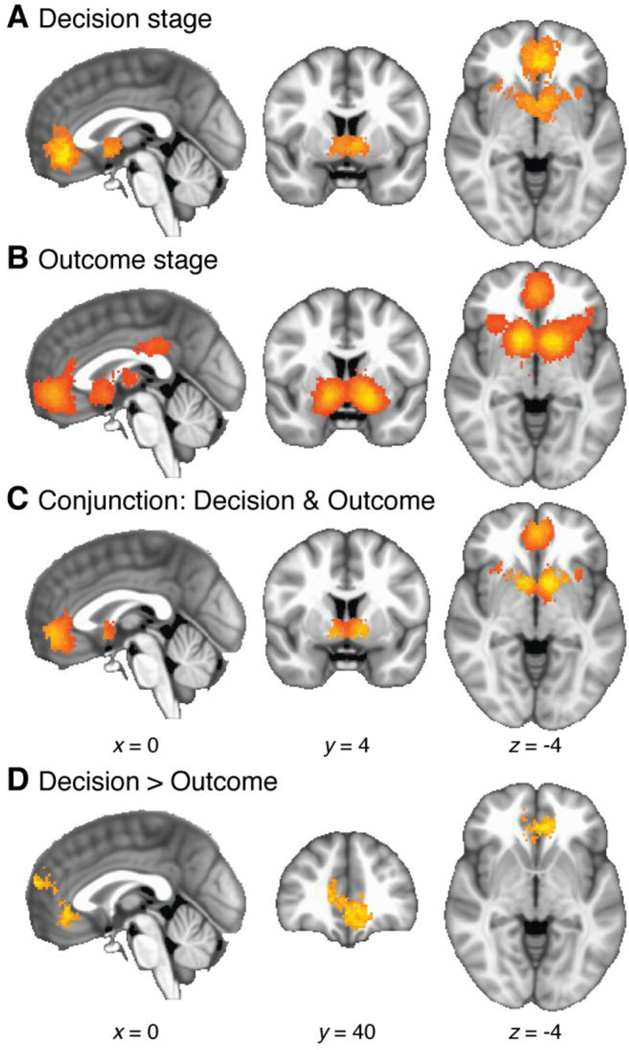
For positive effects at the decision stage, significant clustering occurred in a single connected region of bilateral striatum and VMPFC (3304 voxels, 26.43 cm³, p = 0.0002; see Table 3 and Figure 6A). Local maxima for the meta-analysis statistic were 48.1 in VMPFC, 37.0 in left striatum, and 29.6 in right striatum. A subthreshold cluster also appeared in PCC (309 voxels, 2.47 cm³, p = 0.0674).

Table 3.

SV effects by task stage

Description	X	Y	Z	Peak meta- analytic statistic
Decision stage
VMPFC	−2	40	−8	48.1
L Striatum	−6	8	−4	37.0
R Striatum	6	10	−8	29.6
Outcome receipt stage
L Striatum	−12	12	−6	37.9
R Striatum	12	10	−6	37.1
VMPFC	2	46	−8	24.3
L Anterior Insula	−30	22	−6	13.6
R Anterior Insula	28	26	−6	12.9
PCC	−4	−28	30	12.9
Conjunction: Decision stage and receipt stage
L Striatum	−8	8	−6	32.1
R Striatum	8	10	−6	29.6
VMPFC	2	46	−8	24.3
Comparison: Decision > receipt stage
R VMPFC	14	44	6	5.29

Figure 6.

Whole-brain meta-analysis of SV effects at either the time a decision is evaluated, or the time an outcome is received. These results consider positive effects only. A: SV effects at the decision stage. B: SV effects at the outcome receipt stage. C: Conjunction map, showing voxels with significant positive effects during both decision making and outcome receipt. An SV signal occurring in both these time periods is potentially positioned to guide value-based decision making. D: Regions showing significantly denser clustering of positive effects during the decision stage than during the outcome receipt stage.

Effects at the outcome receipt stage were clustered in bilateral striatum extending to bilateral anterior insula (6587 voxels, 52.70 cm³, p = 0.0002), VMPFC (1837 voxels, 14.70 cm³, p = 0.0002), and PCC (409 voxels, 3.27 cm³, p = 0.0142; see Table 3 and Figure 6B). Local peaks were 37.9 in left striatum, 37.1 in right striatum, 24.3 in VMPFC, 13.6 in left anterior insula, 12.9 in right anterior insula, and 12.9 in PCC.

For the conjunction of effects involving both time periods, clusters emerged in VMPFC (1107 voxels, 8.86 cm³) and bilateral striatum (1127 voxels, 9.02 cm³; see Table 3 and Figure 6C).

We next performed a direct contrast between effects at decision time and receipt time. Decision-stage effects were clustered more densely than receipt-stage effects in a 1580-voxel (12.64 cm³) region that included VMPFC and extended dorsally in rostral medial frontal cortex (p = 0.0058; see Figure 6D and Table 3). The peak pseudo-t statistic, located in right VMPFC, was 5.29. No areas showed significantly denser clustering of foci for the receipt stage than the decision stage.

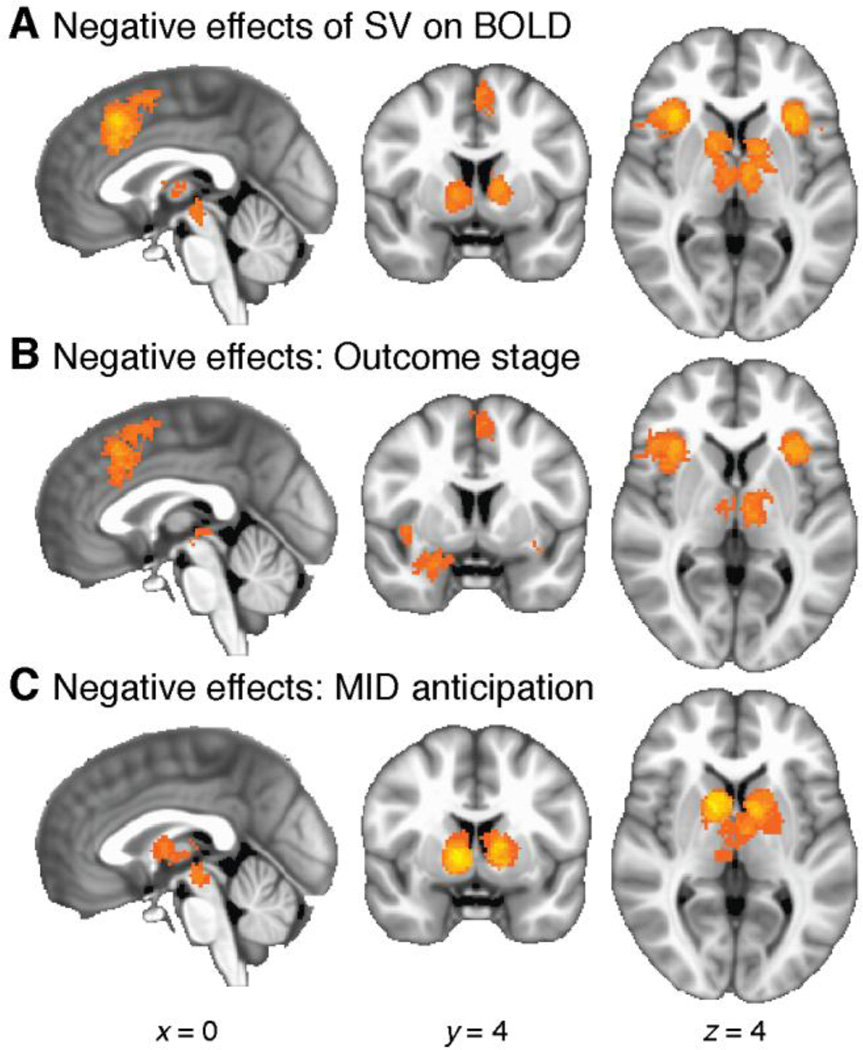
The above comparison of the decision and receipt stages only involves positive effects of SV on BOLD. There were too few data to run a full set of analogous meta-analyses for negative effects (only 7 studies in our corpus include negative effects at the decision stage anywhere in the brain). However, it is possible to examine negative effects restricting to the outcome receipt stage. We performed a single-group analysis of the 55 studies reporting negative effects at outcome receipt. Foci clustered significantly in left anterior insula (1039 voxels, 8.31 cm³, p = 0.0002), right anterior insula (1428 voxels, 11.42 cm³, p = 0.0002), DMPFC (1295 voxels, 10.36 cm³, p = 0.0002), bilateral thalamus (627 voxels, 5.02 cm³, p = 0.0104), and in the vicinity of right amygdala (560 voxels, 4.48 cm³, p = 0.0138). Local peaks were 25.5 in left insula, 27.3 in right insula, 20.0 in DMPFC, 16.4 in left thalamus, 10.9 in right thalamus, and 16.4 in right amygdala.

These results largely match the pattern of negative effects when data from all time periods are included (compare Figure 7A and 7B). There is one notable difference, however: the striatum showed significant negative effects in the overall analysis, but not in the analysis limited to the receipt stage. To examine why this might be, we reviewed the 23 studies that reported negative effects at times other than the outcome receipt stage. A subgroup stood out: 11 were studies that reported data for the anticipation stage of the MID (Knutson et al., 2001a) or a similarly structured task. In these tasks, participants view an incentive cue (indicating a monetary gain, loss, or neutral outcome), and subsequently make a speeded response to try to obtain the reward or avoid the penalty. We performed a single-category analysis of negative effects during the anticipation stage in these 11 studies. Despite the small sample, we observed significant clustering in bilateral striatum (2057 voxels, 16.46 cm³, p = 0.0002; see Figure 7C). The peak meta-analytic statistic was 81.8 in right striatum, reflecting that 9 of the 11 studies reported effects in the same location. To summarize, the striatum showed strong negative effects of SV on BOLD during anticipation, but we could not demonstrate negative effects in striatum during outcome receipt. In other regions, results limited to the receipt stage generally resembled the overall results reported above.

Figure 7.

Negative effects of SV on BOLD, broken down according to the time period at which effects are examined. A: Negative effects overall (identical to Figure 3B), reproduced here for reference. B: Negative effects limiting to the outcome receipt stage (55 studies). Results resemble those in Panel A except for the absence of effects in striatum. C: Significant clustering of negative effects in studies examining the anticipation stage of the MID task (11 studies); here, effects in striatum are strongly present.

3.3.2. ROI meta-analysis

Decision-stage and outcome-stage contrasts did not differ in the frequency with which they activated the striatum ROI. The rates were 15/27 (55.6%) for the decision stage and 97/140 (69.3%) for the outcome stage (Fisher p = 0.184). The frequency of outcome and decision-stage foci also did not differ in any striatal subregion (caudate, 4/27 for decision vs. 33/140 for outcome; putamen, 7/27 for decision vs. 36/140 for outcome; VS, 5/27 for decision vs. 38/140 for outcome; all Fisher ps > 0.44). However, the VMPFC ROI was significantly more likely to be activated at the decision stage (22 of 27 studies; 81.5%) than at the outcome stage (72 of 140 studies; 51.4%; Fisher p = 0.005). In this respect, ROI and whole-brain meta-analyses converge on the conclusion that VMPFC reflects SV especially reliably when a decision is being evaluated.

Spatial logistic regression showed no evidence that decision-stage and outcome-stage foci were spatially discriminable, either in striatum (LL = −43.30, median null LL = −42.86, p = 0.675), or in VMPFC (LL = −50.07, median null LL = −49.92, p = 0.559). Analysis of signed x coordinates showed a small degree of evidence for left lateralization in VMPFC at the decision stage (median = −2.67, IQR = −6.00–3.00, signed-rank p = 0.042) but not at the outcome stage. There was no evidence of lateralization in striatum, and no evidence in either ROI for differences in lateralization between the two time periods.

3.4. Monetary versus primary incentives

3.4.1. Whole-brain meta-analysis

The final theoretical question we address is whether different neural mechanisms are engaged during evaluation of primary rewards, such as food, and secondary rewards such as money. There are several reasons to hypothesize a neural dissociation between these categories. Primary rewards can be directly consumed as part of an experiment, whereas money is merely accumulated to support later consumption. Domain-specific appetitive mechanisms (whether anatomically overlapping or distinct) might conceivably have evolved to support the processing of certain primary rewards (Levy and Glimcher, 2011), but specific mechanisms for evaluating money are less plausible.

Conversely, there are also strong reasons to anticipate considerable similarity between the neural mechanisms involved in evaluating primary and secondary incentives. A utility-like signal should theoretically be amodal rather than category specific, given that its role is to facilitate comparisons across goods in different categories. Furthermore, a principal insight from research on classical conditioning is that a conditioned stimulus can come to influence behavior in the same manner as the primary reward with which it is associated. Money is presumably an especially well-learned secondary incentive.

To obtain meta-analytic evidence bearing on this question, we identified studies in our corpus involving either monetary or primary outcomes. The first category consisted of tasks with monetary outcomes; that is, a participant received a signal of real money to be paid after the experiment. The second category contained studies in which primary incentives were delivered during scanning. These included consumable liquids (e.g., water, juice, milkshakes, wine), odors, music, attractive faces, or arousing images. We limited both categories to findings of positive effects at the time of outcome delivery; that is, the monetary and primary categories are subdivisions of the “outcome stage” category examined above. The rationale is that primary and monetary outcomes are expected to be maximally different at the time when they are actually being received. Some studies were excluded from either category because their outcomes were non-monetary but also could not be unambiguously categorized as primary rewards. We excluded tasks in which the outcomes consisted of pictures of food, pictures of products, guided mental imagery, artwork, humor, signals of social approval, conditioned stimuli, or generic positive feedback messages.

In all, 82 studies contributed data to the monetary outcome category and 33 contributed to the primary outcome category, including 4 studies that contributed different analysis contrasts to both.

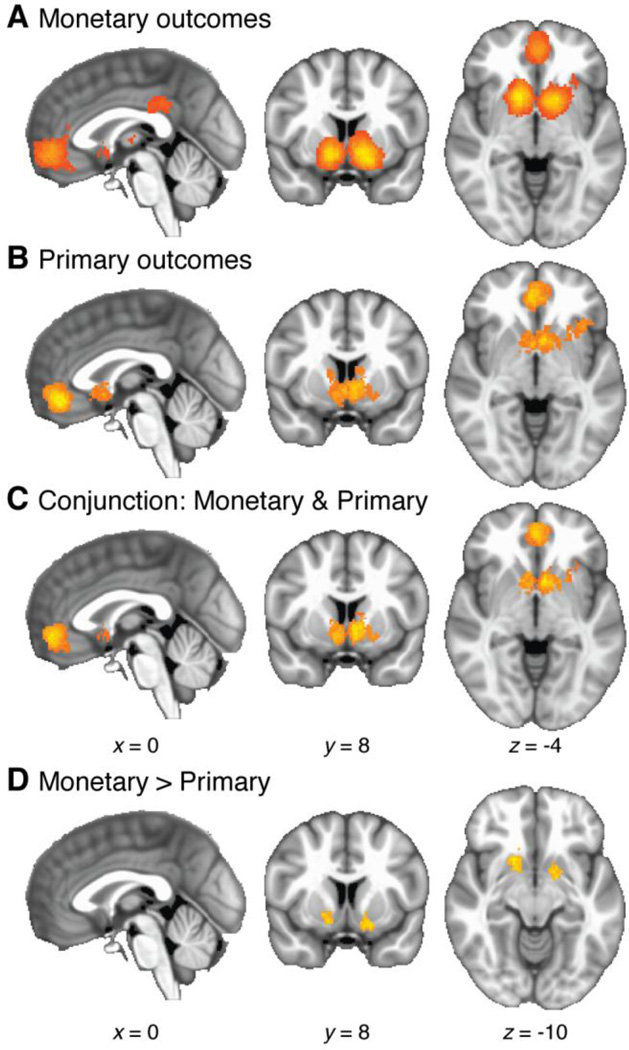
When monetary outcomes were considered in isolation, response foci were significantly clustered in bilateral striatum (3629 voxels, 29.03 cm³, p = 0.0002), VMPFC (1027 voxels, 8.22 cm³, p = 0.0002), and PCC (279 voxels, 2.23 cm³, p = 0.0010; see Table 4 and Figure 8A). Peak meta-analysis statistics were 43.9 in left striatum, 46.3 in right striatum, 26.8 in VMPFC, and 17.1 in PCC.

Table 4.

SV effects by outcome type

Description	X	Y	Z	Peak meta- analytic statistic
Monetary incentives
L Striatum	−12	12	−6	43.9
R Striatum	14	14	−6	46.3
VMPFC	0	52	−8	26.8
PCC	−2	−36	34	17.1
Primary incentives
VMPFC	2	46	−8	36.4
L Striatum	−4	10	−2	30.3
R Striatum	10	10	2	21.2
L Anterior Insula	−36	18	2	24.2
Conjunction: Monetary and primary incentives
L Striatum	−6	10	−6	30.3
R Striatum	10	12	−6	24.2
VMPFC	−2	50	−6	26.8
Comparison: Monetary > primary incentives
L Striatum	−14	2	−12	4.02
R Striatum	20	14	−8	4.48

Figure 8.

Whole-brain meta-analysis results for monetary vs. primary rewards and penalties. These analyses are limited to positive effects at the time of outcome receipt. A: SV effects for monetary outcomes. B: SV effects for primary outcomes (see text for details). C: Conjunction of SV effects for both categories of outcomes. D: Regions with more densely clustered SV effects for monetary than primary outcomes.

A similar pattern was found for primary outcomes alone. Significant clustering occurred in bilateral striatum extending to left anterior insula (1563 voxels, 12.50 cm³, p = 0.0002) and VMPFC (844 voxels, 6.75 cm³, p = 0.0002; see Table 4 and Figure 8B). Peak meta-analysis statistics were 30.3 in left striatum, 21.2 in right striatum, 24.2 in left anterior insula, and 36.4 in VMPFC. A subthreshold cluster occurred in right anterior insula (284 voxels, p = 0.0784).

We confirmed the overlap between the two categories by calculating the conjunction map. Clusters passed the conjunction in bilateral striatum (1008 voxels, 8.06 cm³) and VMPFC (547 voxels, 4.38 cm³; see Table 4 and Figure 8C).

To identify differential responses, we conducted a between-group comparison between the monetary and primary categories. Significantly denser clustering occurred for the monetary category in left striatum (161 voxels, 1.29 cm³, p = 0.0118) and right striatum (232 voxels, 1.86 cm³, p = 0.0030; see Figure 8D and Table 4). No significant differences in the opposite direction—denser clustering for primary than monetary rewards—were found in any location.

3.4.2. ROI meta-analysis

There was no difference in the frequency with which primary and monetary incentives activated the striatum ROI (19/33 for primary, 57.6%; 57/82 for monetary, 69.5%; Fisher p = 0.277). The frequencies did not differ for any striatal subregion (caudate, 6/33 for primary vs. 22/82 for monetary; putamen, 5/33 for primary vs. 21/82 for monetary; VS, 6/33 for primary vs. 23/82 for monetary; all Fisher ps > 0.32). Frequencies did not differ for the VMPFC ROI (17/33 for primary, 51.5%; 46/82 for monetary, 56.1%; Fisher p = 0.683). There was also no evidence that primary and monetary SV foci were spatially discriminable, either within striatum (LL = −40.84, median null LL = −41.48, p = 0.313) or within VMPFC (LL = −36.59, median null LL = − 35.48, p = 0.964). Analysis of signed x coordinates did not reveal significant lateralization for either category individually, in either ROI.

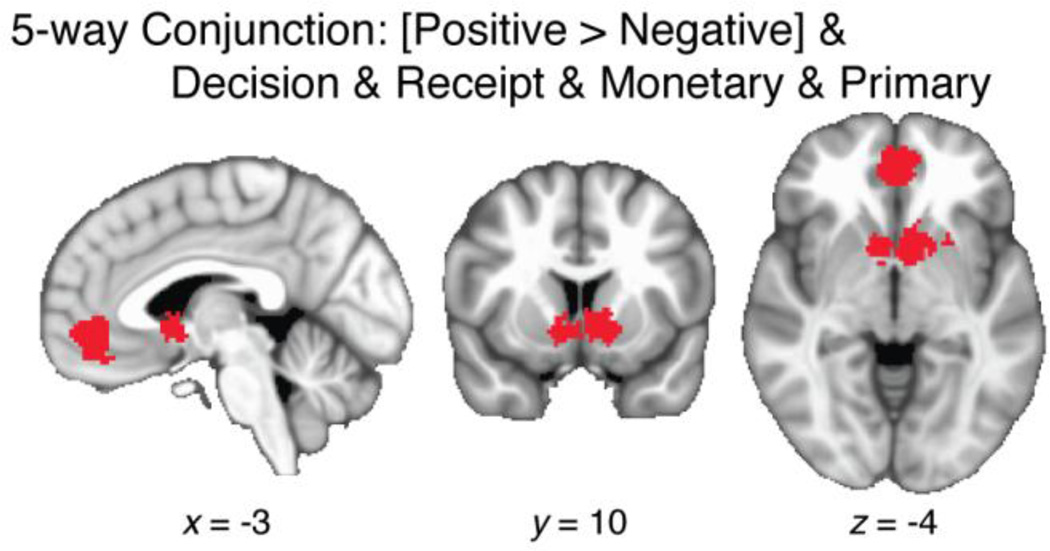
3.5. Five-way conjunction analysis

A recent theoretical review (Kable and Glimcher, 2009) proposed that VMPFC and VS function as a final common path in the computation of SV. Internal estimates of SV are theoretically capable of serving as a common currency, facilitating choices across time and across disparate domains. Regions that express the theoretically relevant neural signal would be expected to have several properties at the meta-analytic level: (1) they should show predominantly positive correlations with SV; (2) SV responses should occur both when outcomes are received and prospectively, during decision making; (3) SV responses should occur consistently across different modalities of outcomes.

To test for these properties, we applied a conjunction analysis identifying voxels that were significant in each of five tests: greater clustering of positive than negative effects (Figure 3D), positive effects at the time of both decision and receipt (Figure 6A–B), and positive effects for both monetary and primary outcomes at receipt time (Figure 8A–B). Two clusters of voxels met these criteria (see Figure 9): one in bilateral VS (500 voxels, 4.00cm³, center-of-mass x = −3, y = 10, z = −4), and the other in VMPFC (449 voxels, 3.59cm³, center-of-mass x = −1, y = 46, z = −7). Signal in these regions potentially qualifies as an index of SV, analogous in several key respects to economic utility (Kable and Glimcher, 2009).

Figure 9.

Results of a five-way conjunction analysis, designed to detect regions carrying a monotonic, modality-independent SV signal. Binary map indicates voxels that showed significantly greater density of foci for positive than negative effects (Fig. 3D), and showed above-chance clustering for positive effects at both the decision and receipt stages (Fig. 6C), as well as for both monetary and primary outcomes (Fig. 8C).

4. Discussion

4.1. Directionality and effect of valence

In the present paper we report a series of meta-analyses examining neural effects of SV as measured using fMRI. Our first step was to compare the locations of positive and negative effects of SV on BOLD. Positive effects consist of larger BOLD responses to more rewarding or less aversive outcomes; negative effects consist of larger BOLD responses to less rewarding or more aversive outcomes. We observed a greater density of positive than negative effects in the VMPFC, PCC, and striatum. We observed overlapping significant densities for both positive and negative effects in DMPFC, thalamus, striatum, and bilateral anterior insula. In the insula and striatum we could additionally demonstrate a conjunction of positive effects for rewards and negative effects for penalties. Several of the regions in which we observed negative effects also consistently respond to physical pain (Peyron et al., 2000).

Our results are consistent with the possibility that the response profile in VMPFC and PCC resembles Pattern A in Figure 1, while the response profile in anterior insula more closely resembles Pattern B. The striatum met criteria for both response profiles, a result that broadly agrees with the conclusions of several previous investigations (Bray et al., 2010; Plassmann et al., 2010; Seymour et al., 2007). This might signify that the true pattern in striatum is a hybrid of A and B, with a steeper positive slope for rewards than penalties. Alternatively, the response profile might differ across striatal subregions. In ROI meta-analyses, positive responses were clustered further anterior and ventrally within the striatum. More dorsal and caudal striatum showed a mixture of positive and negative responses, consistent with Pattern B. A similar functional subdivision has been observed in other contexts (Lohrenz et al., 2007). Our results differ in some respects from those of Litt and colleagues (2011), who observed a hybrid of Patterns A and B in VS and reported no voxels reflecting Pattern B in dorsal striatum. Our results agree with Litt and colleagues (2011) with respect to the response profiles found in VMPFC, PCC, and DMPFC.

The pattern of SV response in striatum may also depend on the task stage at which effects are examined. We were able to detect significant negative effects in striatum during anticipation, but could not detect these effects in an analysis restricted to the outcome receipt stage. Several individual studies focusing on outcome anticipation have directly plotted an apparent U-shaped SV response for striatal volumes of interest (e.g., Bjork et al., 2010; Knutson et al., 2001a; Samanez-Larkin et al., 2007). One possibility, therefore, is that the striatum shows a U-shaped SV response during active anticipation but a different response profile at other time periods. A firm conclusion on this point will require more data regarding negative effects of SV on BOLD during both anticipation and decision making.

Our findings are compatible with a distinction between two broad networks, one including VMPFC, PCC, and anterior VS, and the other including DMPFC, insula, and more dorsal and caudal striatum. Similar networks have been identified in previous work, but their interpretation remains a matter of debate. The former system has been implicated in the computation of SV (Kable and Glimcher, 2009), while the latter system has been implicated in assessments of risk (Christopoulos et al., 2009; Preuschoff et al., 2008) or salience and arousal (Litt et al., 2011; Zink et al., 2004). A somewhat different proposal associates VS and anterior insula with positive and negative affect, respectively (Knutson et al., 2007; Kuhnen and Knutson, 2005). The present findings suggest insula and associated structures resist characterization as solely representing costs or penalties.

Similarly, our findings imply that striatal BOLD signal cannot necessarily be interpreted as a monotonic proxy for SV unless great care is taken to identify a priori subregions in which positive responses predominate. This is especially true for tasks in which penalties are at stake (Carretié et al., 2009; Levita et al., 2009; Litt et al., 2011). It is generally recognized that reverse inference—inferring cognitive operations on the basis of an observed BOLD response—must be undertaken with extreme caution (Poldrack, 2006). At the same time, previous findings have suggested that the link between striatal activity and positive evaluation may be sufficiently exclusive to justify reasonably strong reverse inferences. Ariely and Berns (2010) found, based on a sample of 1,351 studies (68 of which involved reward), that the occurrence of activation in nucleus accumbens increased the odds that a study would involve reward by a factor of 9:1. Investigators routinely make inferences that a condition is more rewarding because it evinces greater striatal activity (e.g., de Quervain et al., 2004; Harbaugh et al., 2007; Satterthwaite et al., 2012). The present results suggest that such inferences may indeed be defensible provided they are carefully restricted to narrowly defined subregions in anterior VS.

We must acknowledge that our meta-analyses cannot confirm that regional BOLD responses are identical to the profiles illustrated in Figure 1. In particular, only very limited evidence is available regarding the behavior of putative Pattern-A regions for the domain of penalties, with only 10 studies reporting any positive effects of SV on BOLD in the penalty domain. One possibility is that the true response to SV in these structures is flat in the penalty domain and rising in the reward domain. To resolve this issue, further study is needed of SV responses in the domain of penalties (cf. Litt et al., 2011; Plassmann et al., 2010), including analyses specifically testing for the existence of positive effects in this domain (i.e., greater BOLD response to smaller penalties than larger penalties).

Practically speaking, testing the hypothesis of a U-shaped SV response requires an assumption about where the zero or neutral point falls. We have assumed for simplicity that zero corresponds to no outcome at all, but there is evidence that decision makers actually evaluate outcomes relative to a reference point based either on predictions (Montague et al., 1996) or concurrent context (Louie et al., 2011). The construction and representation of reference points is an important topic for future research.

Most SV effects were observed symmetrically in both hemispheres. Explicit ROI-based tests of lateralization showed no significant effects in striatum, but suggested a small tendency for positive responses in VMPFC to be left lateralized.

4.2. Task stage

Our meta-analyses identified areas of VMPFC and VS that independently responded to SV both when decisions were presented and when outcomes were delivered. SV is expected to be represented similarly at these two stages, as the predicted value of an action is required to compute a reward prediction error for learning, and the value of received outcomes can be used to learn SV estimates that guide future decisions (Kable and Glimcher, 2009).

Recent behavioral work has highlighted a phenomenon of hedonic misprediction, in which decision makers select alternatives that they ultimately fail to enjoy. This has been discussed in terms of a mismatch between "decision utility" and "experienced utility" (Kahneman et al., 1997), and potentially also relates to a distinction between "wanting" (i.e., incentive motivation) and "liking" (i.e., pleasure; Berridge, 1996). In our framework, hedonic misprediction would imply that SV estimates at the time of the decision fail to correspond to experienced SV. Our meta-analytic results provide no indication of qualitative differences in brain regions that encode SV during decision making and outcome receipt. Still, it remains possible that finer-grained anatomical or neurochemical distinctions exist (cf. Berridge, 1996), or that the same evaluative mechanism performs different computations (e.g., using different information) during decisions and during the receipt of outcomes.

Previous findings have pointed to a possible anterior/posterior gradient for value signals during receipt versus decision (Smith et al., 2010). In the present whole-brain meta-analyses, the peak for decision-time responses indeed lies posterior to the peak for receipt-time responses (see Figure 6A–B), which is qualitatively consistent with the proposed gradient. However, a direct comparison of foci locations within VMPFC failed to yield meta-analytic support for this hypothesis. In this respect our conclusions are similar to those of Peters and Büchel (2010), who observed no separation in orbitofrontal cortex between SV responses associated with 'outcome value,' 'decision value,' and 'goal value.'

The only difference we observed was that SV response foci clustered in VMPFC even more densely during the decision stage than during the receipt stage. This finding reinforces the widely emphasized role of VMPFC in value-based decision making (e.g., Rangel and Hare, 2010) and supports the importance of continued research to understand the computational functions supported by this cortical structure.

4.3. Incentive type

Both primary and monetary incentives elicited SV responses in the same brain regions. This aspect of our results aligns with an emerging consensus that a unitary neural system, including regions of striatum and VMPFC, represents SV across different categories of goods (Chib et al., 2009; Kim et al., 2011; Levy and Glimcher, 2011, 2012). We found no evidence for regions that encoded primary rewards exclusively.

The similarity of SV responses across monetary and primary-reward outcomes is important because it suggests that a reward that is merely signaled (e.g., money) is evaluated similarly to one that is actually consumed (e.g., juice). This equivalence would not necessarily have been expected under a literal interpretation of standard economic models (Camerer et al., 2005).

The only differences observed in our between-category comparisons were in the direction of a stronger response for money. Bilateral regions of striatum showed more densely clustered SV responses for monetary than primary incentives. An appealing interpretation of this finding is that monetary rewards are simply more valuable than the primary rewards used in these experiments, and therefore elicit striatal activation more reliably. Other investigators have commented on the difficulty of equating SV between primary and monetary rewards, noting that experimental primary rewards (e.g., squirts of juice) may have negligible monetary value from a research participant’s perspective (Kim et al., 2011).

While we reported primary-vs.-monetary comparisons for positive effects only, a similar analysis focusing on negative effects suggests qualitatively similar conclusions. Fewer studies report negative effects and the results are not statistically significant bilaterally, but differences trend in the direction of stronger negative effects in insula and striatum for monetary than primary outcomes, again consistent with the possibility that monetary incentives are simply more potent.

Our results do not rule out the possibility that domain-specific value representations might exist for narrower categories than those considered here, or at a finer spatial scale than is available to fMRI. While it remains possible that some carriers of value rely on anatomically segregated representations (e.g., Levy and Glimcher, 2011), our data offer no support for a large-scale functional distinction between primary and secondary rewards. In light of this result, which matches the conclusions of individual experiments that have targeted this question directly (Chib et al., 2009; Kim et al., 2011), we are inclined to treat proposals of domain-based functional segregation with caution pending replication.

4.4. Methodological considerations

One salient feature of our results is the overall low range of meta-analytic statistical values in single-group tests. Nearly all of our peak meta-analytic statistics are below 50; hardly ever did more than 50% of the studies in a meta-analysis report foci within 10mm of the same location. This state of affairs speaks to the heterogeneity of the fMRI literature, the limited detection power of fMRI experiments, and to the drawbacks of a peak-coordinate-based reporting convention. At the same time, it reinforces the importance of meta-analytically aggregating results across large numbers of experiments, and of quantifying the degree of cross-study overlap in a transparently interpretable manner (as we have attempted to do by using the unweighted MKDA statistic).

A methodological advance in the present investigation involves recognizing that the density of reported activation foci depends in a graded fashion on gray-matter probability. We have argued that the meta-analytic null hypothesis should account for this relationship, which implies that foci would have a nonuniform spatial distribution even under random conditions. This observation, and the methods developed here for addressing it, may prove useful in future location-based meta-analyses.

4.5. Automated approaches to meta-analysis

The present work is based on a hand-curated database of experimental results. Recently a new and exciting approach to coordinate-based synthesis of neuroimaging literature has been proposed, based on automated text mining and coordinate extraction (Yarkoni et al., 2011). The development of automated methods represents a significant advance, enabling large-scale databases of findings to be developed and continuously updated. In light of this, it is worth commenting on two particular challenges that an automated approach to the present investigation would face. (Related points have been noted previously; Yarkoni et al., 2011).

The first relates to the directions of effects, which automated techniques in their present form do not disambiguate. The present investigation relies heavily on discriminating positive and negative responses (see, e.g., Figure 3). While investigators predominantly report positive effects, nominally positive effects can correspond to negative effects of SV on BOLD. For example, a region with a negative response might be reported as responding positively in a “penalty minus neutral” contrast.

A second challenge for automated methods relates to experimenter-introduced bias in the anatomical locations at which effects are reported. A significant part of the labor in developing our database involved restricting the corpus to findings obtained using uniform whole-brain statistical thresholds. While it is entirely appropriate for an experimenter to adopt a less stringent threshold in a priori regions of interest, non-uniform sensitivity undermines the inferential logic of CBMA, which holds that findings are distributed randomly under the null hypothesis. This could lead to CBMA results that in part reflect researchers’ expectations. A related concern involves the need to distinguish studies that manipulated reward and observed striatum activity from studies that observed striatum activity and were therefore interpreted in terms of reward. Here again, an advantage of a manually curated database lies in our ability to reduce the influence of prevailing hypotheses on the input data to our meta-analyses.

To evaluate the similarities and differences between manual and automated approaches, we examined the Neurosynth meta-analysis for the term "reward" (using the "forward inference" test, which most closely resembles our own analyses). The method involves automatically identifying publications in which the word "reward" appears frequently and extracting reported coordinate foci from these papers. In each voxel, a chi-square test compares the observed frequency of nearby foci with the frequency expected if foci were spatially random in gray matter. Chi-square results are converted to z-scores and thresholded at a false discovery rate level of 0.05 to control for multiple comparisons (see Yarkoni et al., 2011 for full details). This procedure identified 203 studies (on 8/12/2012). For comparison, our corpus contained 200 studies reporting positive effects, but only 44 studies were in common between the two sets (21.7% of the Neurosynth sample). The low degree of overlap is not necessarily surprising given the very different inclusion criteria for the two methods. Of the 159 Neurosynth studies not in our corpus, 98 (61.6%) were papers we considered as candidates but determined did not meet our inclusion criteria. Even with different input data, Neurosynth results (see Figure 10A) are strikingly similar to ours (compare Figure 3A).

Figure 10.

Meta-analytic results obtained from the Neurosynth database at http://neurosynth.org/ (Yarkoni et al., 2011). Each map is based on foci reported in papers associated with a specific key term. A: Results for the term “reward.” B: Results for the term “punishment.” Despite using different methods and a largely non-overlapping sample of publications, these results resemble the analogous maps obtained in the present investigation (Figs. 3A and 3B, respectively).

We cannot explicitly test negative effects of SV on BOLD using Neurosynth, but we can obtain a preliminary picture by querying the term "punishment" (making the assumption that studies associated with this term focus predominantly on negative effects). This identifies 25 studies (compared to 77 studies with negative effects in our corpus), of which 6 overlap (24% of the Neurosynth sample). Of the 19 studies not in our corpus, we had considered and rejected 9 (47.4%). Again despite the low overlap, the results (Figure 10B) qualitatively resemble the corresponding results from our investigation (compare Figure 3B).

These results offer general support for the validity of automated meta-analytic methods, and provide convergent support for some of our basic findings in a largely independent sample of experimental data. At the same time, this exercise highlights some important strengths of the curated-database approach, including the ability to make more confident claims regarding the direction of effects, and to avoid bias in the anatomical locations that experimenters target for analysis. The manual approach also allows us to examine finer-grained, theoretically important distinctions (e.g., Figure 5 through Figure 9). We are optimistic that these challenges may be addressed as automated data synthesis methods continue to advance.

4.6. Future directions

An extremely worthwhile future direction would be to extend the present work from coordinate-based to image-based meta-analysis (IBMA; e.g., Salimi-Khorshidi et al., 2009). No amount of sophistication in CBMA methods can make amends for the loss of information that occurs when a statistical parametric map is reduced to a table of coordinates. IBMA permits meta-analytic investigation not only of effect locations but also effect sizes (cf. Fox et al., 1998), and holds greater potential to detect effects that may be weak but consistent across experiments. We echo other investigators (e.g., Yarkoni et al., 2010) in the hope that advances in data archival will smooth the way toward such endeavors.

Future meta-analytic work might examine contrasts and distinctions that we have not considered in the present paper. One possible target would be a contrast between “actively” and “passively” obtained outcomes (see also Diekhof et al., 2012). This is a less clear-cut distinction than it might first appear, since even relatively passive tasks usually still involve some type of response requirement. It would probably be necessary to examine multiple ways of delineating these categories, while taking measures to minimize other confounding differences. A second future direction would be to examine brain responses associated with different levels of risk or uncertainty. A meta-analysis of risk would require a somewhat different corpus of data from the one we have developed here. The most relevant type of experimental design for that purpose would be one that manipulated risk and SV orthogonally (e.g., Preuschoff et al., 2006). The present data set would exclude analysis contrasts that varied risk while holding SV constant.

In the long run it is necessary to aggregate findings not only within the domain of functional neuroimaging, but also across modalities. Conclusions derived using fMRI must be integrated with those from electrophysiology and other methods to arrive at a comprehensive perspective on the neural encoding and representation of SV (Kable, 2011). We view the present synthesis of the fMRI literature as one step on the road toward this eventual objective.

It remains entirely possible that methods with greater spatial resolution (e.g., electrophysiology, high-resolution fMRI, or IBMA) may yet identify functionally significant distinctions in brain regions that now appear homogeneous. In VMPFC, in particular, the present results suggest that SV representations are spatially indistinguishable during decision and receipt, as well as across different modalities of outcomes. While this conclusion is consistent with the theoretical concept of a domain-general SV signal, it is necessarily provisional given the low spatial resolution of the underlying data.

A pragmatic goal of the present work is to assist fMRI investigators in specifying a priori ROIs. Neuroimaging analyses can achieve substantially improved sensitivity through the use of ROIs or small-volume correction. However, current practice in this regard is less than optimal, with ROIs often derived from a single peak location in the previous literature. Meta-analysis offers a sounder and better-constrained approach to ROI specification. Our results will be made available in nifti format for this purpose. Our recommendation is to use the regions in Figure 9 for analyses targeting SV effects in general, and the regions in other figures when more specific hypotheses are merited (for example, Figure 6A when focusing on the decision stage alone).

4.7 Conclusions

Synthesizing results across 206 published fMRI experiments, we find meta-analytic evidence for two broad patterns of SV response in regional BOLD signal. One set of brain regions—including anterior insula, DMPFC, and much of the striatum—shows a heterogeneous pattern of SV effects across experiments, responding positively in some analysis contrasts and negatively in others. Such heterogeneity potentially emerges from a U-shaped SV response profile, which is sometimes interpreted as reflecting arousal or salience. A second set of regions, including VMPFC and anterior VS, consistently shows positively signed effects. SV responses in these areas occur both during decision making and outcome delivery, as well as for both monetary and primary-reward outcomes. Responses thus exhibit the basic properties expected of a general-purpose SV signal, implying that VMPFC and anterior VS may form the core of a 'valuation system.' Such a signal theoretically is positioned to underlie value-maximizing choice. Pressing goals for future work include specifying the details of how this signal is computed and utilized, and determining its relationship with other known functions of the same neural structures.

Highlights.

• Theories of decision making posit a domain-general subjective value signal.

• Numerous fMRI studies have tested for correlates of such a signal.

• We quantitatively meta-analyze findings from 206 studies.

• We identify a "valuation system" in ventromedial PFC and ventral striatum.

• Other regions show a mixture of positive and negative effects across experiments.

Abbreviations used

SV

Subjective value

fMRI

Functional magnetic resonance imaging

BOLD

Blood oxygen level dependent

VS

Ventral striatum

VMPFC

Ventromedial prefrontal cortex

PCC

Posterior cingulate cortex

DMPFC

Dorsomedial prefrontal cortex

MNI

Montreal Neurological Institute

CBMA

Coordinate-based meta-analysis

ALE

Activation likelihood estimation

MKDA

Multilevel kernel density analysis

ROI

Region of interest

SVC

Small-volume correction

IQR

Inter-quartile range

IM

Indicator map

FWE

Family-wise error

pGM

Gray-matter probability

LL

Log likelihood

ACC

Anterior cingulate cortex

pre-SMA

Pre-supplementary motor area

IBMA

Image-based meta-analysis