Memory and prediction in natural gaze control

Abstract

In addition to stimulus properties and task factors, memory is an important determinant of the allocation of attention and gaze in the natural world. One way that the role of memory is revealed is by predictive eye movements. Both smooth pursuit and saccadic eye movements demonstrate predictive effects based on previous experience. We have previously shown that unskilled subjects make highly accurate predictive saccades to the anticipated location of a ball prior to a bounce in a virtual racquetball setting. In this experiment, we examined this predictive behaviour. We asked whether the period after the bounce provides subjects with visual information about the ball trajectory that is used to programme the pursuit movement initiated when the ball passes through the fixation point. We occluded a 100 ms period of the ball's trajectory immediately after the bounce, and found very little effect on the subsequent pursuit movement. Subjects did not appear to modify their strategy to prolong the fixation. Neither were we able to find an effect on interception performance. Thus, it is possible that the occluded trajectory information is not critical for subsequent pursuit, and subjects may use an estimate of the ball's trajectory to programme pursuit. These results provide further support for the role of memory in eye movements.

1. Introduction

There are several factors that determine how visual attention is allocated in a scene. One that has been intensively studied is the local image features relative to the surrounding regions, commonly referred to as salience [1–3]. While these factors capture some of the variance in the distribution of attention, a stronger factor, in many circumstances, is the current cognitive goals [4–6]. Humans actively interrogate the image for the information required at the moment to satisfy some behavioural goal. A third factor that determines where attention, and consequently gaze, is allocated is visual memory. The information a subject gathers from a scene will depend on existing memory representations, or prior knowledge, of the scene. For example, familiarity with a scene speeds subsequent visual search [7]. Memory also influences saccadic targeting and eye–head coordination in natural task contexts [8]. Another way that the role of memory representations is manifest is in prediction, because the eye movements and associated attentional shifts that occur in advance of the stimulus must be based on stored knowledge of some kind. Both smooth pursuit and saccadic eye movements demonstrate predictive effects based on previous history of target movement [9–12]. For example, subjects attempting to pursue a target that is briefly occluded during movement in the fronto-parallel plane often make anticipatory movements to the expected point of target reappearance, and the gain of this anticipatory pursuit is scaled to the expected target velocity [13–16]. Evidence of prediction has also been found in the saccadic system. If a target is briefly occluded, then subjects make predictive saccades to the expected point of target reappearance [17,18]. This is also true even when the target moves along a curvilinear trajectory [19,20], or when it reflects off an angled barrier while it is occluded [21].

Recent evidence shows that predictive eye movements are robust and pervasive in natural behaviour. In addition to studies showing prediction along simple trajectories in the fronto-parallel plane, predictive eye movements are common in the natural world, where trajectories are more complex and prediction presumably more difficult. Athletes playing cricket, table tennis and squash make predictive eye movements to the ball's future location [22–24]. For example, Land et al. found that experienced cricket batsmen made a saccade to the anticipated bounce location of the ball, arriving 100–200 ms before the ball. Hayhoe et al. [22] also found predictive saccades to the anticipated location of the ball after it reflected off a wall in skilled squash players. More recently, Diaz et al. [25] investigated these predictive saccades in a more controlled setting using a virtual racquetball environment. Unskilled subjects intercepted a virtual ball that bounced once prior to interception. On almost every trial, subjects made a saccade ahead of the ball, just before it bounced, to a location that would intercept the future ball trajectory. Gaze was held in this location during the bounce, and until the ball passed within 1–2° of the fixated location after the bounce. The location of the predictive saccade was dependent on the ball's elasticity as well as its velocity. The accuracy of the predictions, both in time and space, despite variation in ball properties suggest that subjects use their history of experience with balls in order to target the eye movements to the ball's future location.

While it is clear that humans are very good at predicting ball trajectories following a bounce, it remains unclear precisely why they choose to do this. It may simply be that it is advantageous to avoid the trajectory discontinuity around the time of the bounce, and that nothing critical is gained by the behaviour. However, subjects’ predictions are very accurate, and this precision suggests a more specialized strategy than would be expected on the basis of simply avoiding the discontinuity. Furthermore, for more quickly moving or more elastic balls, subjects fixated at a location that was further away from the bounce point. This scaling of gaze-to-bounce distance with elasticity and velocity ensured that the ball passed through the fixation location at a constant time, approximately 170 ms after the ball bounced, despite wide variation in post-bounce ball speed and trajectory [25]. Note that if subjects had chosen to maintain a fixed gaze distance from the bounce point, then they could have been equally accurate, but the ball would have arrived at the gaze point at widely varying times after the bounce. This accurate placement in time suggests that subjects were actively attempting to position gaze so that they could view the trajectory for a fixed period after it bounced. One possible reason for this strategy is suggested by the fact that subjects invariably pursue the ball after it passes near the gaze point, until just prior to interception. Thus, the 170 ms period after the bounce may provide subjects with the necessary visual information to programme this pursuit movement. Pursuit of the target just prior to interception may, in turn, facilitate the interceptive movement. For example, it has been shown that pursuit movements facilitate prediction of future location, possibly though the contribution of efferent signals about gaze direction in space [26]. Thus, the saccade to position gaze on the predicted path may facilitate acquisition of trajectory information after the bounce, thereby facilitating the goal of tracking the ball after it bounces, which, in turn, may facilitate interception.

In the present experiment, we sought to better understand predictive gaze strategies during natural interception, under conditions where we could control the path of the ball. We tested whether the predictive fixation allows subjects to gather the necessary visual information required to programme the post-bounce pursuit. We tested the importance of the visual information in the post-bounce trajectory by making the ball invisible for 100 ms immediately after it bounced. For convenience, we refer to this as the ‘occlusion’ condition, even though the ball simply became invisible rather than passing behind a barrier. If the information from that portion of the ball's trajectory is critical for programming the subsequent pursuit movement, then we would expect to see some change in subjects' gaze patterns. Subjects might increase fixation distance and delay pursuit initiation in order to allow the ball to become visible for a longer portion of its post-bounce trajectory. Alternatively, if subjects do not compensate, then we might expect some impairment of subsequent pursuit. If neither of these effects are observed, then subjects may be able to ‘fill in’ the missing sensory data using memory representations.

2. Methods

(a). Participants

Fifteen subjects (10 males and five females) with normal or corrected-to-normal vision participated in the experiment. All subjects were unskilled at racquet sports, having either never played or played only an occasional game. Prior to participation, all subjects signed consent forms according to a protocol approved by the University of Texas Institutional Review Board.

(b). Apparatus

We used the same immersive virtual environment used in our previous study [25], which affords parametric manipulation of ball trajectories, without sacrificing the complexity of the natural world, or freedom of eye or body movements. The environment is illustrated in figure 1a. Subjects used a ping–pong paddle tracked by motion capture to hit virtual balls that were projected in an arc, and bounced once before their arrival, as shown in figure 1b.

Figure 1.

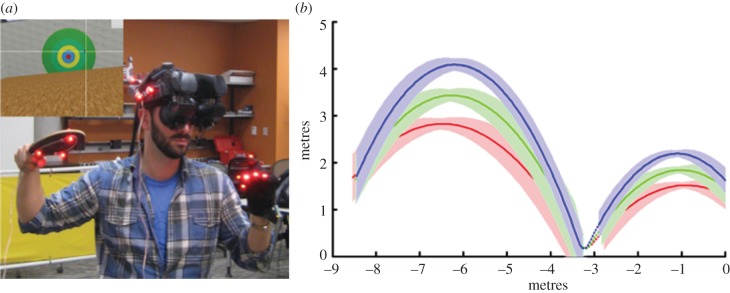
(a) Launched balls were hit with a ping–pong paddle that was tracked by a motion-capture system and represented visually in the virtual world. The inset shows the virtual court visible to the subjects inside the wide field-of-view head-mounted display. The image of the crosshair depicting gaze point, shown in the inset, was overlaid post hoc, and was not visible to the subject. (b) A side view depicting a possible set of distributions of ball trajectories for a single session. Group means are reflected by solid lines, and shaded areas span 1 s.d. from the mean in each direction. Three distributions of pre-bounce trajectories differ in the vertical component of the ball's speed upon bounce.

The stimulus was presented on an NVis SX111 head-mounted display (HMD) with a field of view that stretched 102° along the horizontal, and 64° along the vertical. The virtual environment was an enclosed court of 9 m in width, and 12 m from the back wall to the front wall. The position of a ping–pong paddle, the HMD and the subject's free hand were monitored using a 14 camera PhaseSpace motion-capture system running at 480 Hz. The total latency before the physical movement of the head or paddle was updated onscreen was between 33 and 50 ms or, at 60 Hz, between two and three visual frames. Subjects were instructed to use a virtual paddle to hit balls at a target of concentric circles drawn on the front wall of the court. The ball diameter was 5.7 cm, consistent with a regulation size racquetball. The dimensions of the virtual ping–pong paddle had a width, height and depth of 15, 28 and 10 cm, respectively. Although the height and width of the paddle reflected those of the real-world ping–pong paddle, the physical thickness of the virtual paddle was exaggerated to prevent the virtual ball from passing through the quickly moving paddle between frames.

(c). Procedure

The experiment began with a practice set of nine trials, which were followed by four experimental blocks. On each trial, the vertical component of the ball's velocity at the moment before the ball's collision with the ground, or, bounce speed, was one of three values (−7.5, −8.25 and −9 m s⁻¹). Subjects were presented with 15 repetitions of each bounce speed per block, presented in randomized order. This yielded a total of 45 trials per block, and 180 trials throughout the experiment. In the first group of eight subjects, the first two blocks of trials were normal, and in the third and fourth blocks, the ball was made invisible for approximately 100 ms (six frames) after the bounce. For convenience, we refer to these as ‘occlusion’ trials, although there was no visible occluder, and the ball simply disappeared. For the second group of seven subjects, the first two blocks of trials were occlusion trials, and the third and fourth blocks were normal.

Subjects could initiate a trial only when their head was inside a semi-opaque yellow column that extended from the floor to the ceiling, and that was of 0.5 m in width, and 0.25 m in depth. The box was centred 9 m from the front wall, and offset 0.45 m to the left of the room's midline for right-handed subjects, and 0.45 m to the right for left-handed subjects. Subjects held a motion-tracked ping–pong paddle in their dominant hand. To initiate the launch of a ball, subjects touched the thumb and middle finger on their non-dominant gloved hand together for a minimum duration of 500 ms. The column would disappear upon the gesture's initiation, and a ball would appear up-court at the location from which the ball's trajectory would begin. Once contact between the thumb and middle finger was broken, the ball would launch, and would be accompanied by an auditory signal (a popping noise). Subjects were informed that each ball would bounce once before its arrival, and instructed that their primary goal was to use the paddle to hit the ball as close as possible to the centre of a series of concentric circular targets visible on the far wall.

(d). Ball trajectories

Ball trajectories were consistent with the effects of −9.8 m s⁻² of acceleration owing to gravity, but did not account for drag owing to air resistance, Magnus forces or friction at the time of bounce. Because the floor was of infinite mass, the ball's coefficient of restitution was solely determined by the ball's elasticity of 0.73, meaning that the ball would retain 73% of its velocity in the vertical direction upon a bounce.

To prevent stereotyped strategies, several aspects of the balls’ initial conditions varied uniformly. The bounce point was drawn from a two-dimensional Gaussian distribution of (s.d. 0.25 m in width, and 0.1 m in depth) that was truncated at 2 s.d., and located 3.25 m from the front wall. The distance of the ball's initial position from the bounce point was randomly selected from a range of 5 to 5.5 m, so that the ball subtended approximately 0.38 visual degrees of the subject's visual field at the time of launch (s.d. = 0.01). The ball's approach angle was randomly selected from those approach angles that would bring the ball within 10 cm of the room's midline when the ball reached the subject's standing distance of 9 m from the front wall. This had the effect of ensuring that the ball would pass within a reasonable striking distance from the yellow column that defined the subject's initial standing location, and that was centred 0.45 m from the room's midline. Initial launch height varied from 1.5 to 2 m.

The vertical component of ball's velocity at launch was positive, so that all balls initially travelled along an upward arcing trajectory. The ball's initial height was selected from its uniform distribution prior to calculating the vertical component of the ball's velocity. Subsequently, the vertical velocity was selected so that, after the ball had accelerated with gravity, the vertical component of the ball's velocity was one of three bounce speeds at the moment before collision (−7.5, −8.25 or −9 m s⁻¹). This is shown by the different coloured trajectories in figure 1b. The mean trajectory in each condition is indicated by solid lines in figure 1b, and the standard deviation is indicated by pale-coloured bands. The variation in bounce speed was introduced in order to manipulate the range of trajectories in the experiment, and was not itself a focus of the investigation. The invisible part of the trajectory occurred in the 100 ms following the bounce, and is indicated by the dotted trajectory segments in the figure. After the ball's initial height, approach angle and vertical component of velocity had been selected, the resulting flight duration was used to calculate the X and Y components of the ball's initial velocity that would bring the ball from its randomly selected initial distance to the predetermined bounce point within the known flight duration. To provide an easier learning experience on practice trials, the ball was launched along a head-on trajectory from a starting height of 2 m, bounced 3.25 m in front of the subject with a bounce speed of −8.25 m s⁻¹.

(e). Gaze analysis

Prior to the practice trials, and between each experimental block, the Arrington infrared monocular eye-tracking system was calibrated using a nine-point calibration grid. Measurement involving the same equipment and calibration process with eight subjects that were not involved in this study suggests that the distance from the subject's fixation point to the calibration point after calibration when measured at each of the four corners of the calibration grid is approximately 1.11° (s.d. = 0.33°). The X/Y pixel coordinates of gaze position were recorded at 120 Hz, and subjected to a median filter with a width of four frames followed by a two frame moving average filter. Subsequently, each frame of the 60 Hz visual scene was paired with the first sample of gaze data to appear after the frame was presented to the subject. Subsequently, gaze data were combined with a measure of head orientation returned from the motion-capture system to calculate the unit ‘gaze vector’ that extended from the location of the subject's virtual left-eye through the virtual world. The gaze vector was defined within a world-centred reference frame, and will hereafter be referred to as gaze-in-world. Because tracking was monocular, vergence angle was not calculated. Fixations were defined as periods in which gaze velocity was below a threshold of 30° s⁻¹ for at least four frames (approx. 66 ms). Fixations that were separated temporally by less than three frames (approx. 50 ms) and spatially by less than 3° were grouped together as a single fixation, and isolated periods of fixation of less than 100 ms in duration were disregarded.

To produce a measure of gaze velocity, we calculated the angular change between frames as the inverse cosine of the dot product of subsequent frames of gaze in world vectors. A second-order finite impulse response filter (FIR) was used to identify saccades, consistent with the methods of Duchowski et al. [27], in which data were convolved with a kernel representative of a paradigmatic saccade (e.g. [0 1 2 3 2 1 0]). However, our use of a modified kernel [−1 0 1 2 3 2 1 0 −1] had the effect of producing exaggerated valleys in the gaze velocity signal just before and after the saccade, facilitating their subsequent identification. After application of the filter, we identified saccade peaks with gaze velocity greater than 40° s⁻¹. To identify saccade starts and stops, we differenced the filtered velocity to produce a measure of gaze acceleration. The start was defined as the first frame prior to peak saccade velocity in which the acceleration signal rose above 20° s⁻². The saccade end was defined as the first frame after the acceleration signal dropped below 20° s⁻².

Analysis of predictive saccades focused on trials in which a pre-bounce saccade was immediately followed by a fixation that ended after the bounce, with a maximum separation of 33 ms between the fixation and the end of the saccade. Restricting analysis to saccade/fixation pairs that extended across the time of bounce ensured that the saccadic endpoint and location of the subsequent fixation was not influenced by visual feedback about the post-bounce ball trajectory. These criteria were satisfied by 84.9% of all trials (s.d. = 8.7). On the remaining subset of trials, subjects often made an additional saccade just after the bounce, raising the possibility that the fixation location was influenced by visual information from the post-bounce portion of the ball's trajectory.

Periods of pursuit were classified as periods in which gaze velocity was above 30° s⁻¹, and in which the ratio of the velocity of the subject's gaze vector over the ball's retinal velocity (i.e. pursuit gain) fell between 0.3 and 1.2. Subsequently, mid-pursuit catch-up saccades were identified and removed from the gaze-velocity trace, and replaced with a linear interpolation from pre-saccadic and post-saccadic gaze velocity. The algorithm for identifying catch-up saccades was similar to the algorithm used to identify pre-bounce saccades, with a slight modification that improved robustness to differences in the values of the FIR-filtered gaze velocity before and after the saccade that were brought about by changes to the pursuit signal. Similar to the previous method, the classification algorithm was applied to the FIR-filtered velocity signal after differentiation, thus producing an FIR-filtered acceleration signal. The start of a catch-up saccade was defined as the first frame of the prior to peak saccade acceleration in which the acceleration signal rose above 20° s⁻². The peak of the catch-up saccade was identified as the first local maximum in the gaze velocity signal that surpassed a net increase of at least 5° s⁻¹ from velocity at the start of the catch-up saccade. The end of the catch-up saccade was defined as the first frame after the acceleration signal dropped below 20° s⁻².

3. Results

As we have observed previously, gaze patterns are very stable and consistent between subjects. An illustration of the typical sequence of movements is shown in figure 2. Subjects initially looked at the launch point, and then tracked the ball with a combination of pursuit and saccades before initiating a large saccade prior to the bounce. The subsequent fixation was maintained as the ball bounced and began its upward trajectory. The fixation ended shortly before the ball reached the gaze location, at which point subjects resumed tracking with a combination of smooth pursuit and catch-up saccades until shortly before contact with the paddle.

Figure 2.

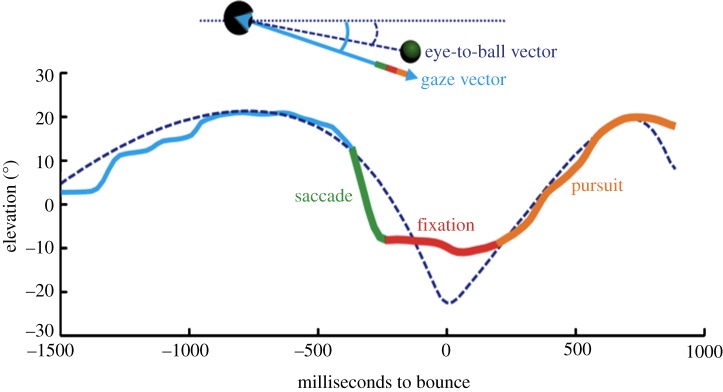
The time course of predictive gaze patterns on a representative trial from the time of launch, until the time of interception. The dashed blue line depicts the elevation of the ball from the plane that was located at eye-height, and parallel with the floor. The solid line depicts the elevation of the gaze-in-world vector extending from the eye, with the green segment reflecting a pre-bounce saccade, followed by a predictive fixation (red) and subsequent pursuit (orange).

Because we were interested in predictive eye movements, the analysis focuses on those trials in which a saccade was initiated prior to the bounce, with the subsequent fixation ending after the bounce. Such predictive saccades were observed in 87.5% of trials in the normal condition, and in 82.5% of trials in the occlusion condition. These values were not significantly different. (A repeated measures ANOVA found no significant differences by trial type, bounce speed, or group (α = 0.05).)

We first examined whether subjects adjusted the location of the predictive saccade to compensate for the reduced visual information in the occlusion condition. We examine angular distance of the gaze vector during fixation from the vector extending from the eye to the bounce location. Adjustment in this gaze-to-bounce distance would allow a longer period in which to gather information about the ball trajectory. Gaze-to-bounce distance is shown in figure 3 for both normal and occlusion trials. There were no significant effects of order in which the subjects did the conditions, so data have been averaged across the two groups. Consistent with Diaz et al. [25], fixations were distributed approximately 10° from the bounce point, and were slightly further away for greater bounce speeds (F_1.14,14.6 = 20.87; p ≤ 0.001, with Greenhouse–Geisser's methods used to correct for violations of sphericity). Contrary to expectations, there was no effect of occlusion on the location that subjects targeted for their predictive saccades. This saccade is programmed prior to the occluded segment. Our expectation was that subjects might adjust this location over trials, if the desired trajectory information was inadequate as a result of the occlusion. In particular, we expected that subjects might increase the fixation-to-bounce distance to allow for a longer period of observation following the bounce, to make up for the missing 100 ms segment. As we observed in our earlier study [25], subjects accurately targeted a point on the ball trajectory. This was measured by finding the minimum distance between the gaze location and the ball during the fixation. These minimum values are on average 1.2°. This means that the balls come very close to the gaze location targeted by the predictive saccade, for all conditions. That is, subjects were equally accurate in targeting a location on the ball's future trajectory. The time at which this minimum distance occurred was 156 ms on average and was unaffected by the occlusion manipulation. Thus, subjects do not appear to make a compensatory adjustment to the targeted location of the predictive saccade in response to reduction in trajectory information during subsequent fixation.

Figure 3.

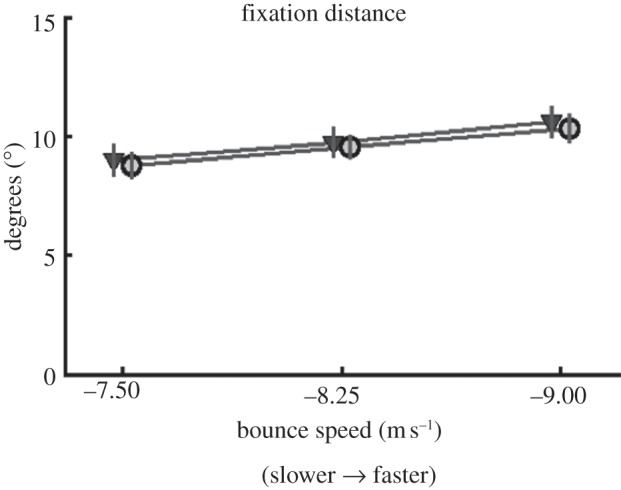
Average distance from the gaze vector to the ball at the time of bounce. Circles represent the occlusion condition, and triangles represent the normal condition. Data for group 1 and group 2, who performed the normal and occlusion conditions in counterbalanced order, were not significantly different and have been averaged. Individual subject data were averaged over trials, and these values were averaged across subjects. Error bars are ±1 s.e.m. between subjects. For clarity, the data points have been slightly offset along the abscissa. The abscissa shows the vertical component of the ball's speed at bounce, in metres per second.

As described above, subjects initiate pursuit of the ball just as the ball comes close to the predictive gaze location. Because we hypothesized that one function of the fixation might be to gather information used to programme this pursuit movement, we now turn to an examination of pursuit performance. Pursuit following the fixation was identified on 96.7% of normal trials with predictive saccades, and 98% of occlusion trials. There was no significant effect of occlusion on the number of trials where we could identify pursuit. Figure 4a shows the time at which pursuit was initiated relative to the bounce. There was no significant difference of pursuit initiation time between normal and occlusion conditions (F_1,13 = 2.7; p = 0.12). Thus, the occlusion did not appear to delay the onset of pursuit. We also calculated pursuit gain, interpolating across small catch-up saccades, as described in the Methods section, during the open-loop period 100–150 ms after pursuit onset. Pursuit gain did not differ significantly for the normal and occlusion conditions (F_1,13 = 2.9, p = 0.10). A final measure of pursuit performance was the number of catch-up saccades, during the pursuit phase. This is plotted in figure 4c. On average, there were between 0.3 and 1.4 catch-up saccades, with a greater probability of catch-up saccades at the higher ball speeds, as might be expected, but no difference between normal and occlusion conditions (F_1,13 = 1.6, p = 0.22).

Figure 4.

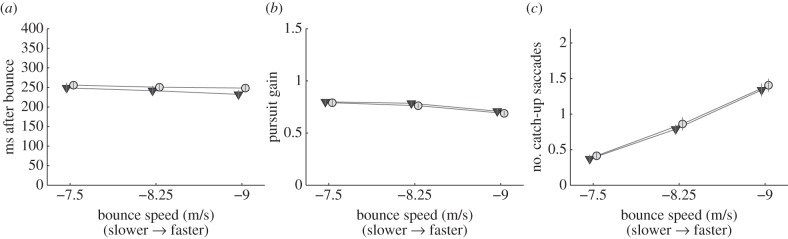
(a) Pursuit initiation time relative to the time of the bounce, as a function of ball speed. (b) Pursuit gain measured 100–150 ms after pursuit initiation. (c) Average number of catch-up saccades during the pursuit period. Circles indicate the occlusion condition, and triangles indicate normal trials. Data averaged across condition order. Error bars are ±1 s.e.m. between subjects. For clarity, the data points have been slightly offset along the abscissa.

One might be concerned that the null result reflects a lack of statistical power necessary to detect a difference between conditions. To address this issue, we calculated the power of the test against specific alternate hypotheses for the pursuit performance in figure 4. Thus, given the variability in the data, the power of the test would be 0.9 if the actual difference in latency was 20 ms, if the actual difference in pursuit gain were 0.03, and if the number of catch-up saccades was increased by 0.15. These numbers suggest that, although it is possible that differences smaller than these values exist and were not detected, these differences would be quite modest. We interpret our findings to mean that the occlusion had at most a small effect on pursuit performance, if any. Note that the observed mean differences in the normal and occlusion conditions were 16 ms for pursuit latency, a 0.02 change in gain, and a 0.06 increase in the number of catch-up saccades. These sample means are of course the best estimates of the true magnitude of the effect of occlusion, given the data.

One possible explanation for the robustness of the pursuit eye movements to the occlusion manipulation is that post-bounce pursuit involved a predictive component based on pre-bounce information. This is consistent with the observation that, on occlusion trials, a subset of pursuit eye movements were initiated after having viewed less than 75 ms of the ball's visible post-bounce ball trajectory. The number of trials where this occurred in the occlusion condition varied across subjects between 0% and 55%, with a median of 18%. In the normal trials, pursuit was only rarely initiated with less than 75 ms viewing time (average 3%). The presence of pursuit following less than 75 ms of post-bounce visual feedback is significant when one considers that the latency for feedback-driven pursuit has been well established to lie between 100 and 150 ms in the absence of an anticipatory component [28–33]. This is true across a wide variety of stimuli, as was demonstrated by Kimmig et al. [30], who tested smooth pursuit in the context of four commonly used paradigms. The reported distributions of subject pursuit latencies were consistently above those observed in our virtual racquetball task. Based on this observation that smooth pursuit latencies observed after the bounce of a ball were lower than those associated with purely feedback based pursuit, we can speculate that smooth pursuit following occlusion of the bounced ball involved a predictive component, similar to the saccadic eye movement initiated just prior to the bounce.

Although the null effect of occlusion on smooth pursuit might lead one to question the effectiveness of the pursuit manipulation, it is of note that the occlusion manipulation did have a reliable effect on gaze behaviour, as was evident in the time at which the pre-bounce predictive saccade was initiated. Pre-bounce saccade initiation time is depicted in figure 5. The difference between normal and occlusion conditions was statistically significant (F_1,13 = 7.7; p < 0.016), and the difference between the groups was marginally significant (F_1,13 = 4.6; p = 0.052). Finally, there was a significant interaction between bounce speed and group (F_2,26 = 4.94; p ≤ 0.016), as is indicated by the difference between filled and open symbols in figure 5. With respect to bounce speed, start times differed by −44.4, −41 and 15 ms, for group 1, and by −23.5, −30.5 and −42.1 ms for group 2. Thus, saccades were initiated later for group 2, where the occlusion condition was performed first. It is possible that having the occlusion strategy first led subjects to adopt a slightly different strategy, which was maintained through the second half of the trials, even though those trials were normal. One explanation is that delaying the anticipatory saccade allowed subjects to compensate for the post-bounce occlusion by gathering additional information from the pre-bounce trajectory. Our observation of this effect of occlusion on subjects’ strategy reveals that subjects are indeed sensitive to the experimental manipulation, despite the failure to find significant effects on pursuit performance.

Figure 5.

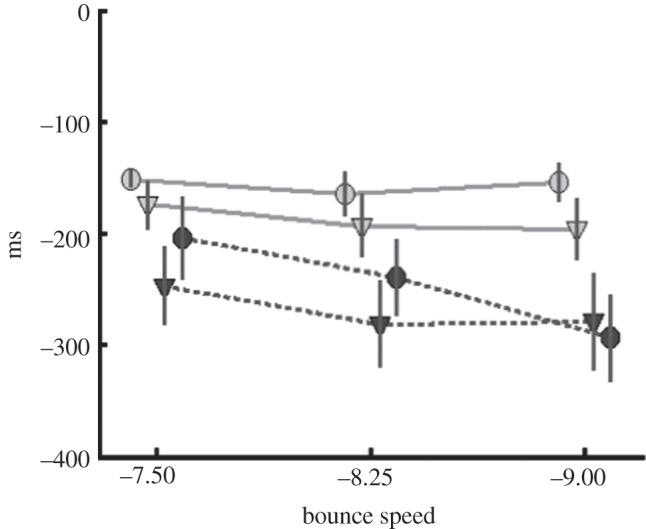
Saccade initiation time relative to the time of the bounce, as a function of ball speed. Negative values indicate the time before the bounce. Circles indicate the occlusion condition, and triangles indicate normal trials. Filled symbols indicate that normal trials were done first. Open symbols indicate that the occlusion trials were done first. Error bars are ±1 s.e.m. between subjects. For clarity, the data points have been slightly offset along the abscissa.

We also examined subjects’ interception performance. The probability of intercepting the ball was uniformly high (89.6% for all subjects, s.d. = 7.3%), and did not differ by condition or group. Nor was there an effect of condition or group on where the ball hit the front wall relative to the centre of the targets. Finally, although there was no effect of condition or group on the distance of the ball's contact point on the paddle to the nearest paddle edge, it should be noted that an interaction between bounce speed and trial type approached significance (F_1,13 = 4.52; p = 0.053). It is a surprise that there was no interaction of group and trial type in any of these measures, as this would have been consistent with learning effects as subjects familiarized themselves with the virtual reality environment. One possibility is that learning effects were obscured by noise inherent in the collision dynamics, which was apparent in the occasional observation of strange post-hit ball trajectories after the subject's strike. This probably arose from difficulty of the motion-capture system in accurately tracking the motion of the quickly moving racquet.

4. Discussion

This experiment was designed to better understand the role of prediction in interception. Naive subjects almost invariably make predictive saccades ahead of a bouncing ball in natural interception [25]. The pervasive nature of this behaviour and the accuracy with which unskilled subjects predict the future trajectory of the ball suggests that there is some particular advantage to the predictive movement, however, what this advantage is remains unclear. The experiment was intended to investigate potential benefits of this saccade for interception performance, and was motivated by the observation that subjects vary the location of the saccade endpoint to bring about a constant duration between the time of the bounce and the arrival of the ball at the fixated location. Note that, because of the variations in the ball's trajectories, this constant-duration strategy required subjects to vary the distance of the fixation depending on the speed of the ball after it bounced. In this experiment, we investigated whether this constant-duration strategy facilitated the subsequent pursuit of the ball, prior to interception. To test this, we made the ball invisible (‘occluded’ the ball) for the 100 ms period immediately after the bounce, with the expectation that, if this information were critical for pursuit, subjects would either show signs of impaired pursuit, or adjust gaze location to compensate for the missing information. For example, subjects might compensate for the occlusion by moving gaze further from the bounce point to increase the period when it was visible before initiating pursuit of the ball. However, we found no evidence of such a compensatory strategy. The gaze point was unaffected by the occlusion, and the ball passed through the gaze point at the same time, whether or not the post-bounce trajectory was occluded. Despite the lack of a compensatory strategy, pursuit of the ball following this fixation appeared unaffected or only weakly affected by the occlusion. Pursuit could be identified on over 96% of trials in both normal and occlusion conditions, pursuit was initiated at the same time in both conditions, and measures of pursuit quality, such as pursuit gain, or the number of mid-pursuit catch-up saccades, were unaffected. Thus, there was no indication that the pursuit was impaired, within the limits of the variability in our measures. The subject's ability to intercept the ball using a ping–pong paddle was similarly unaffected. The only indication that subjects were affected by the occlusion was the slight (27 ms) delay in initiating the predictive saccade. This strategy provides subjects with a slightly longer view of the trajectory while it is visible, just prior to the bounce, which may partly compensate for the loss of information after the bounce. In general, this minor adjustment suggests that the oculomotor system is, in fact, sensitive to the temporal evolution of visual information with a moving target, despite the absence of a detrimental effect on pursuit.

Subjects’ resilience to occlusion suggests that the missing trajectory information has at most a minor detrimental effect on subsequent pursuit, at least in the current context. This echoes the findings of López-Moliner et al. [34], who found that subjects’ catching accuracy was little affected by occlusion of the ball's trajectory as long as the ball was visible more than 200 ms before the catch, or if the throwing movement and the early part of the trajectory was visible. Thus, subjects can compensate for the effects of occlusion in a manner sufficient for interception. In our situation, similarly, subjects compensated for the lack of post-bounce visual feedback well enough to programme pursuit of the quickly moving ball. Given the important role of prediction in pursuit [29], this seems plausible. When the experiment begins with normal trials, subjects have time to become familiar with the set of trajectories. Although we might have expected that occlusion trials would be more difficult when they were performed first, essentially no effect of order of condition was observed, except the effect on saccade initiation, as depicted in figure 5.

Based upon the observation that pursuit was not affected by the occlusion manipulation, we speculate that post-bounce visual information was not critical for pursuit, and that pursuit may have included a predictive component. This speculation is consistent with the observation that a subset of pursuit movements were initiated with less than 75 ms of visible post-bounce trajectory, which is shorter than latencies previously observed in smooth pursuit in the absence of a predictive component [28–33]. The ability to use previously learnt information as a substitute for sensory data is often referred to as an internal model [35–39], which is to say that subjects demonstrate sensitivity to context-specific statistical regularities. Our findings are consistent with the fundamental role of such internal models for the guidance of eye movements [9,14,15]. They are also consistent with the more general observation that subjects were able to draw upon past experience to compensate for degraded visual information when performing a fast-paced, visually guided task [36,40,41]. However, it remains unclear what this implies about the mechanisms that allow us to compensate for these statistical regularities, or how internal models are combined with retinal information about the object's trajectory.

The fact that subjects initiate pursuit at the same time, despite occlusion of a 100 ms segment of the trajectory suggests that the important factor might simply be the pursuit movement itself. The length of the trajectory segment after pursuit begins is quite short, and delaying pursuit initiation may be more costly than less precise pursuit. Although pursuit is not always essential for interception it is a ubiquitous behaviour in interceptive contexts [4,22,24,25,42]. Peripherally guided pursuit behaviour while catching is even observed in subjects with foveal scotomas [43]. Interceptions are improved by pursuit, even if it is not essential [26,44]. This may be a consequence of the underlying neural machinery in posterior parietal areas, where the neural coding of reaches and eye movements are intimately linked.

Because subjects are so little affected by the occlusion of some of the trajectory information, the results provide further support for the important role of memory representations in oculomotor control, as discussed in the Introduction. In the present context, eye movements are based on some combination of the visual information specific to a particular trajectory together with a memory-based component. In reaching, there is evidence for the optimal Bayesian integration of current visual information with stored priors reflecting learnt statistics of the visual image [45,46]. The present results suggest it is likely that a similar combination of information sources occurs with pursuit movements. In the occlusion condition, the learnt statistics can substitute for visual information with no obvious cost. Because learnt information about the trajectory after the bounce is used for pursuit (this study) as well as saccades [25], our results are consistent with the suggestion that the locus of the information used to guide predictive pursuit and saccadic eye movements is shared. The frontal eye fields (FEFs) have been implicated in the guidance of both predictive saccades [17,21,47], and predictive smooth pursuit [48]. The supplementary eye fields (SEFs) are also thought to be involved with both predictive pursuit [49,50], and predictive saccades [51]. Based upon the involvement of both SEF and FEF in pursuit and saccadic eye movements, it has been suggested that the locus of prediction may exist at a higher, ‘supra-modal’ level [51], consistent with previous results on the role of cognitive factors in predictive pursuit [52,53]. Visual cortical areas might also encode predicted target location. For example, the parietal cortex shows activity corresponding to occluded target motion [54]. The transient shifting of receptive fields prior to a saccade [55,56] also reveals predictive effects in visual areas, and presumably reflects the expected visual consequences of an eye movement [57]. In the present context, the prediction cannot be based on efferent information, however, and must be based on an internal model or learned mapping that relates the current visual state of the moving object to a likely future visual state. It should also be noted that the existence of pervasive prediction in eye movement targeting is in marked contrast to image-based models of target selection, such as those based on image salience [1–3]. Although the current visual image has a critical role, predictive eye movements reveal the importance of learning the statistics of moving objects, allowing observers to direct gaze to the expected future location of a moving target.

This study was approved by the University of Texas Institutional Review Board.

Funding statement

This research benefitted from the programming support of John Stone, and diligent support of James Wyatt Ray III throughout the process of data collection. This research was supported by NIH grants EY 05729 and EY 019174, and NSF grant 0932277.