STATISTICAL GROWTH MODELING OF LONGITUDINAL DT-MRI FOR REGIONAL CHARACTERIZATION OF EARLY BRAIN DEVELOPMENT

Abstract

A population growth model that represents the growth trajectories of individual subjects is critical to study and understand neurodevelopment. This paper presents a framework for jointly estimating and modeling individual and population growth trajectories, and determining significant regional differences in growth pattern characteristics applied to longitudinal neuroimaging data. We use non-linear mixed effect modeling where temporal change is modeled by the Gompertz function. The Gompertz function uses intuitive parameters related to delay, rate of change, and expected asymptotic value; all descriptive measures which can answer clinical questions related to growth. Our proposed framework combines nonlinear modeling of individual trajectories, population analysis, and testing for regional differences. We apply this framework to the study of early maturation in white matter regions as measured with diffusion tensor imaging (DTI). Regional differences between anatomical regions of interest that are known to mature differently are analyzed and quantified. Experiments with image data from a large ongoing clinical study show that our framework provides descriptive, quantitative information on growth trajectories that can be directly interpreted by clinicians. To our knowledge, this is the first longitudinal analysis of growth functions to explain the trajectory of early brain maturation as it is represented in DTI.

1. INTRODUCTION

Longitudinal imaging studies with repeated scans per subjects require appropriate analysis procedures that take into account the special nature of such study designs. These include correlation due to repeated measures, often with unbalanced spacing due to acquisitions at different time points and missing data at certain time points. Early brain development is characterized by large initial growth that flattens off, which favors nonlinear growth modeling. Typical clinical questions are addressing growth trajectory characterizations such as delayed or advanced growth, accelerated or slowed growth, or the question if groups can reach the same level of maturation if they have a delayed start. Diffusion Tensor Imaging (DTI) provides a unique opportunity to assess the tissue structure of brain white matter in vivo, and has great potential to provide insight into early development. Previous studies have mostly focused on morphometry changes such as volume of gray and white matter, cortical thickness, and shape [1, 2, 3, 4]. Recent methods have also been developed to combine shape and appearance [5]. There is also considerable research on DTI, however these are cross sectional studies and/or studies on children older than 2 years [6, 7]. While longitudinal DTI of infants covering the few years of life are becoming available, analysis methodologies for assessing longitudinal changes of individuals and populations, to our knowledge, are limited.

In this study, we focus on developing longitudinal models for diffusion parameters which are obtained from repeated scans of children imaged at 2 weeks, 1 year and at 2 years of age. DTI indices have been shown to provide relevant information about brain maturation and the underlying tissue changes as they indicate water content and myelination [2]. Describing and analyzing the non-linear changes of white matter are difficult as regions in the brain begin to mature at different times, with different rates [6]. We quantify these differences using Gompertz functions that provide an intuitive parametrization representing delay, growth, and saturation rate in each region. In contrast to previous studies, we analyze growth trajectories based on an explicit growth function and a nonlinear mixed effect modeling scheme [8]. Diffusion changes are modeled in a hierarchical fashion, with the global population trend as a fixed effect and individual trends as random effects. Mixed effect models are well suited for longitudinal data, where each time series constitutes an individual curve. Classical statistical approaches assume each observation is independent and identically distributed (i.i.d.), which are not appropriate for repeated measures. We apply our framework to compare a set of white matter regions that are known to have different growth patterns and myelinate at different time periods. Quantitative analysis of these regions will provide further insight into brain maturation process and allow us to predict subject-specific growth trajectories with the potential of detecting pathological brain development related to brain disorders. We show that the statistical quantitative analysis results in parameters that use the clinician’s vocabulary for assessment of growth trajectories.

2. METHOD

Non-linear Mixed Effects Modeling

We use a non-linear mixed effects (NLME) model to analyze the longitudinal DTI data. Compared to cross-sectional regression analysis which uses least-squares fitting, this is a true longitudinal model where the average of all individual trajectories is the estimated population mean. As is shown in (Fig. 1) the cross-sectional model does not capture any individual trends and can give misleading estimates if interpreted as the “average” trend. The mixed effect model is also robust to outliers as it accounts for the variabilities within individuals. In this subsection, we present a review of the non-linear mixed effects model. We will present our approach for analyzing longitudinal DTI data using NLME in the next subsection. In the mixed effects model, the observed data is assumed to be a combination of both fixed effects, parameters associated with the entire population or at least within a sub-population, and random effects that are specific to an individual drawn at random. In non-linear mixed effects models, some or all of the fixed and random effects parameters present nonlinear responses. This makes nonlinear mixed effects model a natural and common choice for longitudinal data. We use the NLME model proposed by Lindstrom and Bates [8], where the jth observation on the ith individual is modeled as:

$$y_{ij}=f({\phi }_i,t_{ij})+e_{ij}i=1,\cdots ,M;j=1,\cdots ,n_i$$ (1)

where M is the number of individuals, n_i is the number of observations on the ith individual, f is a nonlinear function of the covariate vector t_ij and parameter vector φ_i, and e_ij ~ N(0, σ²) is an i.i.d. error term. The parameter vector can vary among individuals. This is incorporated into the model by writing φ_i as

Fig. 1.

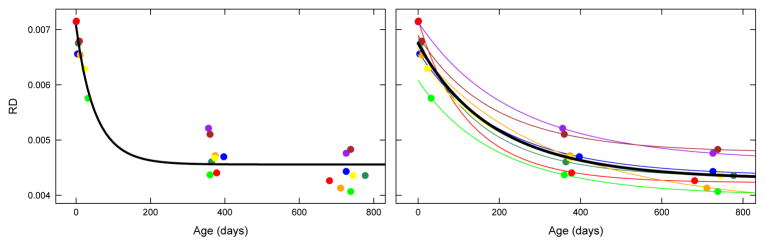
Population growth models, represented as black curves, obtained using nonlinear least squares (nls) on left and nonlinear mixed effect model (nlme) on right. Colored points represent data observations, and colored curves represent the individual growth trajectories.

$${\phi }_i=A_i\beta +B_i{b}_i{b}_i~N(0,\mathrm{\Psi })$$ (2)

β is a p-vector of fixed effects, and b_i is a q-vector of random effects associated with individual i with variance-covariance Ψ. A_i and B_i are design matrices.

Regional Analysis of Longitudinal DTI Patterns

We perform quantitative analysis on a population of longitudinal DTI data within anatomical regions. We model DTI features as non-linear mixed effects, which combines regional population trends and individual subject trends. For this section, we assume that DT MR images have been registered to a standard reference space. The primary goal for our analysis of growth trajectories is to determine whether patterns of growth are different among different regions, and if we can provide a descriptive, intuitive parametrization for each region that can be compared to other regions of brain. As the human brain undergoes rapid changes in the first year of development and slows considerably in later years, we model early development patterns in DTI using the Gompertz function. Specifically, we model temporal growth for an individual i, time points t_ij, and region r by nonlinear mixed effect model of the Gompertz function

$$y_{ij}^r=f({\phi }_i^r,t_{ij})+e_{ij}={\phi }_{1i}^{r}exp\{-{\phi }_{2i}^r{{\phi }_{3i}^r}^{t_{ij}}\}+e_{ij}$$ (3)

where the mixed effects are ${\phi }_i^r={[\begin{array}{ccc}{\phi }_{1i}^r& {\phi }_{2i}^r& {\phi }_{3i}^r\end{array}]}^T={\beta }^r+b_i^r$, the fixed effects, ${\beta }^r={[\begin{array}{ccc}{\beta }_1^r& {\beta }_2^r& {\beta }_3^r\end{array}]}^T$, for region r represent mean values of parameter ${\phi }_i^r$ in the population and the random effects for each subject i, $b_i^r={[\begin{array}{ccc}{b}_{1i}^r& b_{2i}^r& b_{3i}^r\end{array}]}^T$, explains individual variation from the mean. In this model, p and q are same size vectors, and the design matrices A and B are identity. We note that an alternative representation for Gompertz function is

$$y=\mathit{asymptote}\mathit{exp}(-\mathit{delay}\mathit{exp}(-\mathit{speed}t)).$$

This parametrization intuitively decomposes the mean of temporal changes of a population as saturation (β₁), delay (β₂), and speed (− log β₃) as shown in Fig. 2.

Fig. 2.

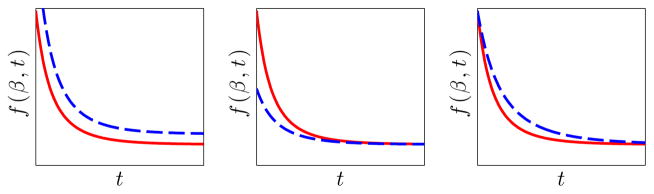
Effect of varying the parameters of the Gompertz functions. The red curve show the reference curve that is held fixed. Left to right: the dashed blue curves show the effect of increasing values of β₁, β₂, and β₃ respectively.

We obtain mixed effect model parameters using maximum likelihood estimation (MLE) on the marginal density of the response y: p(y|β, Ψ, σ²) = ∫ p(y|β, b, σ²)p(b|Ψ)db There is generally no closed form solution, so we use the approximation method proposed by Lindstrom and Bates [8], using the nlme function in R¹, to obtain model parameters, β, b, Ψ, σ. Once all the model parameters are estimated, we can conduct hypothesis testing and determine the significant modes of longitudinal changes in terms of asymptote, delay, and speed between regions. With N number of regions, we accomplish this through $\frac{N(N-1)}{2}$ pairwise fitting of nonlinear mixed effect model and test for fixed effect significance through t-test; corrected for multiple comparisons using Bonferroni correction. The parameters that are found to be significant can then be interpreted as the distinguishing feature between the longitudinal patterns of the two regions.

3. RESULTS AND CONCLUSIONS

Validation on Synthetic Data

We generated synthetic longitudinal data to ensure our analysis methodology can capture underlying differences as presented in the synthetic data. Random data representing two regions is generated, and we verify that the overall trend of the subjects and each subject’s specific growth trajectory matches the known ground truth. We also verify that the Gompertz parameters are significantly different between the two regions in a way that matches the synthetic model. Synthetic longitudinal data are generated following equation 3 where β^R₁ = [1, −2, .989], Ψ = diag(0.04², 0.02², .002²) and σ² = 0.001². Values for four time points of three subjects are generated while keeping some of the fixed parameters of β^R₂ the same as β^R₁. We then vary one of the fixed parameters of R₂ and perform three tests: β^R₂ = [1.1, −2, .989], β^R₂ = [1, −1, .989], β^R₂ = [1, −2, .992], and test for significant differences between two regions. Fig. 3 summarizes our experimental results. The results demonstrate that our approach can detect significant discriminatory features of growth patterns in a pair of regions in terms of Gompertz parameters.

Fig. 3.

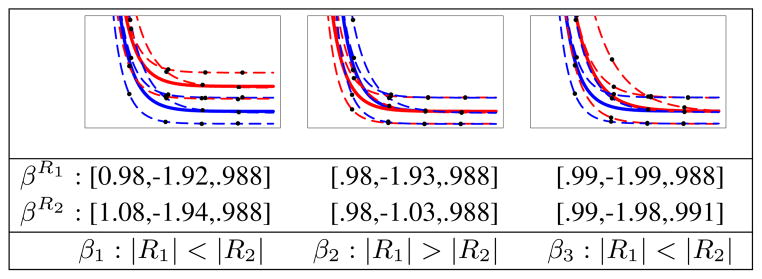
Example of randomly generated synthetic longitudinal data for two different regions colored blue (R₁) and red (R₂). Three different tests were performed. Left to right: varying β₁, β₂ and β₃ between two regions. Estimated β parameters for regions R₁ and R₂ along with Gompertz parameters with significant differences (p < 0.001) are shown.

Analysis of Clinical Data

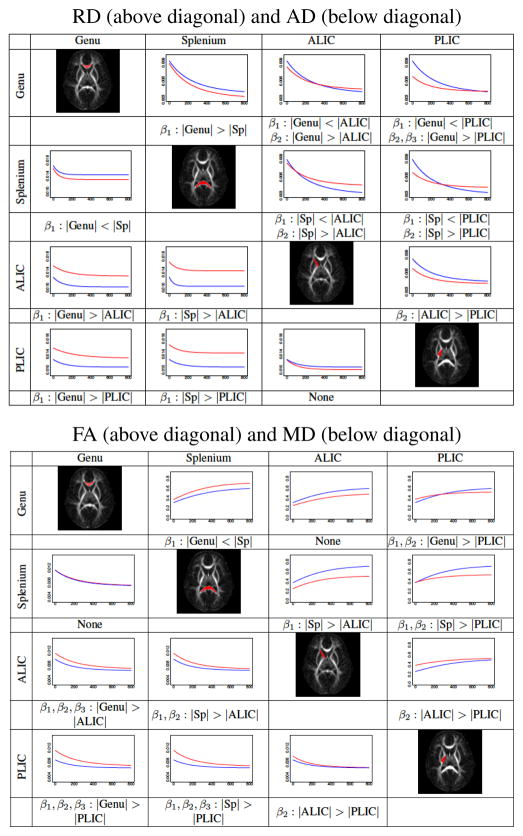
We perform analysis on a set of repeated scans of eight healthy subjects scanned at approximately 2 weeks, 1 year and 2 years of age. The images include T2W and DTI. We apply the unbiased atlas building framework [9] to the set of T2W images at 1 year to obtain spatial mappings between each subject through the estimated atlas. Scans of other time points of each subject are registered to this atlas via linear and nonlinear transformations ². Tensor maps are calculated for each DTI scan, and are registered to the atlas using transformations obtained by registering the DTI baseline (B0) images to T2W images. In this study, we extract the mean, axial, radial diffusivity, and fractional anisotropy features from the registered tensors, $MD=\frac{{\lambda }_1+{\lambda }_2+{\lambda }_3}{3}$, AD = λ₁, $RD=\frac{{\lambda }_2+{\lambda }_3}{2}$ and $FA=\sqrt{\frac{1}{2}}\frac{\sqrt{{({\lambda }_1-{\lambda }_2)}^2+{({\lambda }_1-{\lambda }_3)}^2+{({\lambda }_2-{\lambda }_3)}^2}}{\sqrt{{\lambda }_1^2+{\lambda }_2^2+{\lambda }_3^2}}$ where λ_i are the sorted eigenvalues of the tensor. For regional analysis, we select four anatomical regions in the unbiased atlas that are known to mature in distinctly different patterns and determine the characteristics of these differences. Since all DT images are registered to a common coordinate space, regions determined in this space can be automatically transferred to each individual image. We use regions defined by Mori et al. [10] that were registered to our unbiased atlas and modified through binary erosion for improved accuracy. The selection of regions in the atlas space allows automatic partitioning of the subjects’ scans into different anatomical regions. Fig. 4 show a summary of pairwise comparisons of estimated population means for Genu, Splenium, ALIC, and PLIC regions. We characterize the differences in an intuitive way using Gompertz asymptote, delay and speed parameters. When β₁: |R₁| > |R₂|, expected value of diffusion parameter for R₁ is higher than R₂ after early development. When β₂: |R₁| > |R₂|, region R₁ is delayed in maturation compared to R₂. β₃: |R₁| > |R₂| indicates accelerated growth for R₂ compared to R₁.

Fig. 4.

Pairwise testing of different white matter regions, shown in the diagonal. Gompertz parameters with significant differences (p < 0.001) are denoted. Curves represent the population trajectory of a region represented by the rows (blue), columns (red). The range of values are the following: x-axis: newborn to 2-years of age. y-axis: RD: [0.003,.009], AD: [0.01, .018], FA: [0, 0.8], and MD: [0.004, 0.012]

Conclusions

This paper presents a statistical methodology for characterizing longitudinal patterns of tissue properties in white matter regions. Our approach provides descriptions of the significant discriminating features of growth patterns, within a pair of regions or across patient groups, in terms of the Gompertz asymptote, delay, and speed parameters; a representation where maturation changes and differences can be interpreted in natural language terms. This provides an intuitive description of longitudinal trends, with potential for analyzing biological progression and change from normal in neurodevelopment, aging, disease progression or recovery. This is in contrast to current modeling and analysis of developmental and degenerative processes where testing for regional or group differences does not directly reveal the type, nature and time course of differences. The proposed analysis can be extended to arbitrary number of regions, performed on other measurements such as tissue property features extracted from structural MRI, and be extended to multivariate growth functions similar to a strategy described in [4]. Since the analysis is based on the regions of interest, we expect the method to be robust to misregistration, but future validation of the registration framework is needed. We also plan to estimate the p-value based on Markov chain Monte Carlo sampling from the posterior distribution of the parameters rather than t-test.

The experimental results from early development of white matter reveal developmental patterns of individual subjects, whole groups and differences across anatomical locations and across groups (not shown in this paper). E.g., FA of ALIC is delayed if compared to PLIC at birth, mostly explained by larger RD at birth but both converging at 2 years (Fig. 4). FA of splenium is higher than genu throughout the observed time interval, presenting same MD but explained by lower RD and higher AD. Delay parameter of RD best explains the temporal sequence of myelination in these selected regions and confirms previous histological findings [11]. Coupled with cognitive and behavioral scores, such quantitative analysis might give new insight into developmental processes in healthy and disease, and may even lead to prediction of onset of disease and eventual planning of early therapeutic intervention. Using the proposed framework, population models obtained from healthy subjects will serve as normative data for comparisons of developmental trajectories of at risk individuals.