Topology Preserving Atlas Construction from Shape Data without Correspondence using Sparse Parameters

Abstract

Statistical analysis of shapes, performed by constructing an atlas composed of an average model of shapes within a population and associated deformation maps, is a fundamental aspect of medical imaging studies. Usual methods for constructing a shape atlas require point correspondences across subjects, which are difficult in practice. By contrast, methods based on currents do not require correspondence. However, existing atlas construction methods using currents suffer from two limitations. First, the template current is not in the form of a topologically correct mesh, which makes direct analysis on shapes difficult. Second, the deformations are parametrized by vectors at the same location as the normals of the template current which often provides a parametrization that is more dense than required. In this paper, we propose a novel method for constructing shape atlases using currents where topology of the template is preserved and deformation parameters are optimized independently of the shape parameters. We use an L¹-type prior that enables us to adaptively compute sparse and low dimensional parameterization of deformations. We show an application of our method for comparing anatomical shapes of patients with Down’s syndrome and healthy controls, where the sparse parametrization of diffeomorphisms enables to decrease the parameter dimension by one order of magnitude.

1 Introduction

Shape statistics is fundamental to medical imaging studies, for instance to characterize normal versus pathological structures or to highlight the effect of treatments on anatomical structures. Usual methods build an average shape model, called template, that is representative of a shape ensemble, and correspondences between the template and each subject’s shape, altogether called an atlas. Differences appear in the shape model used and the way shapes are put into correspondence. Parametric models, such as medial axis representation [12], extract low-dimensional shape features, which are averaged and compared across subjects. Non parametric methods are often based on point correspondences across shapes with an either fixed or optimized parameterization of the curves or surfaces [2, 7, 9, 13]. Homologous point positions are averaged and 3D-deformations map the average model to the point configuration of each subject, such maps being used for deriving shape statistics [14, 11]. To alleviate the problem of finding point correspondences across shapes, which is not always possible in practice, one can compare shapes using the metric on currents [15]. In this framework, shape statistics are represented by a template current and diffeomorphic 3D mappings that map the template current to each subject’s shape.

Existing atlas construction approaches using the metric on currents [6, 4, 3] suffer from two main limitations. First, the template current is either the superimposition of warped surfaces [6] or a set of disconnected normals or tangents (Dirac currents) [4, 3] and therefore is not given as a mesh. It has never been shown that such templates could be the approximation of a continuous surface. In this sense, these approaches do not preserve the topology of the shapes, namely the continuity of the surfaces and the number of connected components of the shapes in the population, thus limiting its practical use for segmentation purposes, for instance. Second, the template-to-surface deformations are parameterized by momentum or speed vectors that are at the same location as the normal or tangent of the template current. However, there is no reason to link the parameterization of the template shape with the parameterization of the deformations. The most variable parts of the shape are not necessarily the parts that require the finest sampling, e.g. the most folded ones. Therefore, the template shape and the deformations should have independent parameterization.

In this paper, we propose to build a shape atlas using the metric on currents, but in a way which allow the user to fix the topology of the template mesh, namely the number of vertices and the edges connecting them, and to optimize their position in the 3D space. This will be possible due to an optimal control formulation of the diffeomorphic matching problem in the Large Deformation Diffeomorphic Metric Mapping paradigm [10, 5]. In this formulation, the three variables to optimize, namely the template shape, the control points positions and the momentum vectors attached to them that parameterize the deformations, are seen as the initial conditions of a dynamical system. We derive here the analytic expression of the gradient with respect to these variables. Additionally, we use a L¹ prior to select the most relevant subset of control points for the parameterization of the shape variability. Such a sparse and adaptive parameterization will be particularly well suited for statistical purposes. We show an application of our method to a study comparing anatomical features of patients with Down’s syndrome (DS) and healthy controls, where the sparse parametrization of shape variability enable statistical analysis in lower dimensional spaces.

2 Shape Atlas Construction

2.1 Joint Estimation of Template and Deformations

The purpose of the method is to estimate a template shape X₀ and template-to-subjects deformations φ_i from a set of shapes X₁, …, X_Nsu. Each X_i denotes a vector containing the positions of the vertices of the input shapes, which may be of different sizes. X₀ denotes the vertices of the template shape, whose number and connectivity is fixed by the user. Only the positions of the vertices of the template are optimized and not its connectivity, so that the topology of the template is preserved during optimization. In the framework of Fréchet means [11], we estimate one template and N_su deformations φ_i that minimize the following criterion:

$$E({\mathbf{X}}_0,\{{\phi }_1,\dots ,{\phi }_{N_{\text{su}}}\})=\sum _{i=1}^{N_{\text{su}}}D({\phi }_i({\mathbf{X}}_0),{\mathbf{X}}_i)+\text{Reg}({\phi }_i),$$ (1)

where D denotes the squared distance on currents, φ_i(X₀) the deformation of the template shape X₀ and Reg a measure of regularity of the deformations.

2.2 Parameterization of Deformations

We use a mechanical system of self-interacting particles, called control points, to build dense diffeomorphic deformations [5]. Let c₀ = {c_0,k} be a set of control points and α₀ = {α_0,k} a set of initial momenta of the particles, altogether called the initial state of the system S₀ = {c₀, α₀}. This set of particles moves from time t = 0 to t = 1 according to following equations of motion:

$$\{\begin{array}{l}{\stackrel{.}{c}}_k(t)=\sum _{p=1}^{N}K(c_k(t),c_p(t)){\alpha }_p(t)\hfill \\ {\stackrel{.}{\alpha }}_k(t)=-\sum _{p=1}^N{\alpha }_k{(t)}^t{\alpha }_p(t){\nabla }_{1}K(c_k(t),c_p(t))\hfill \end{array},$$ (2)

which are such that the energy of the system Σ_i,j α_i(t)^tK(c_i(t), c_j(t))α_j(t) is conserved in time. The kernel K models the interaction forces among the particles. These equations describe the evolution of the state of the system S(t) = {c_k(t), α_k(t)} and can be written in short: Ṡ(t) = F(S(t)) with the initial condition S(0) = S₀.

The motion of the control points defines a diffeomorphism of the whole 3D space [8]. The speed at position x₀ interpolates the speed of the control points:

$$\stackrel{.}{x}(t)=\sum _{k=1}^{N}K(x(t),c_k(t)){\alpha }_k(t).$$ (3)

This equation shows that the rate of decay of the kernel determines the size of the neighborhood that is “pulled” by each control point. It can be written in short as ẋ(t) = G(x(t), S(t)) with the initial condition x(0) = x₀. Using the vertices of the template shape x₀ as initial conditions, the integration of this equation computes the deformation of the template shape X₀ = X(0) to X(1) that is equal to φ(X₀) with φ is the diffeomorphism parameterized by S₀.

2.3 Atlas Estimation

The N_su template-to-subject deformations in the criterion (1) are parameterized by N_su vectors ${\mathbf{S}}_0^i$. Each of these vectors serves as the initial condition in (2). Then, the template deformation is obtained by integration of (2) followed by (3). We choose to use the same set of control points c₀ for all subjects, which defines a common basis for the deformations parameterization. By contrast, the set of initial momenta ${\mathit{\alpha }}_0^i$ are subject-specific. As a regularizer of the deformations, we P use the energy of the set of particles ${\sum }_{p,q}{{\alpha }_{0,p}^i}^{t}K(c_{0,p},c_{0,q}){\alpha }_{0,q}^i$, which is also the geodesic distance connecting the template to the the i^th shape [8]. In order to select the most relevant subset of control points, we add a L¹ penalty to (1), so that the criterion to minimize writes:

$$E({\mathbf{X}}_0,{\mathbf{c}}_0\{{\mathit{\alpha }}_0^i\})=\sum _{i=1}^{N_{\text{su}}}\left\{\frac{1}{2{\sigma }^2}D({\mathbf{X}}_0^i(1),{\mathbf{X}}_i)+\sum _{p,q}{{\alpha }_{0,p}^i}^{t}K(c_{0,p},c_{0,q}){\alpha }_{0,q}^i+\gamma \sum _p\left|\right|{\alpha }_{0,p}^i\left|\right|\right\}$$ (4)

subject to:

$$\{\begin{array}{ll}{\stackrel{.}{\mathbf{S}}}^i(t)=F({\mathbf{S}}^i(t))\hfill & \text{with}{\mathbf{S}}^i(0)=\{{\mathbf{c}}_0,{\mathit{\alpha }}_0^i\}\hfill \\ {\stackrel{.}{\mathbf{X}}}_0^i(t)=G({\mathbf{X}}_0^i(t),{\mathbf{S}}^i(t))\hfill & \text{with}{\mathbf{X}}_0^i(0)={\mathbf{X}}_0\hfill \end{array}$$ (5)

The first equation in (5) is the equations of motion of the particles, like in (2). The second equation is deformation of the template parameterized by the particles motion, like in (3). σ² and γ balance the data term against the regularization terms. The variables to be optimized are: (i) the position of the vertices of the template shape X₀, (ii) the position of the control points in the template domain c₀ and (iii) the N_su initial momenta ${\mathit{\alpha }}_0^i$ that parameterize each template-to-subject deformation. In practice, we also regularize the template shape defined by X₀ by applying a penalty on Gaussian curvature of the mesh.

Only the first two terms in (4) are differentiable. As shown in the supplementary material accessible at the first author’s webpage, the gradient of data term is given as:

$${\nabla }_{{\mathit{\alpha }}_0^i}D={\xi }^{\alpha ,i}(0){\nabla }_{\mathbf{c}}D=\sum _{i=1}^{N_{\text{su}}}{\xi }^{c,i}(0){\nabla }_{{\mathbf{X}}_0}D=\sum _{i=1}^{N_{\text{su}}}{\theta }^i(0)$$

where the auxiliary variables ξⁱ(t) = {ξ^c,i(t), ξ^α,i(t)} (of the same size as Sⁱ(t)) and θⁱ(t) (of the same size as X₀) satisfy the linear ODEs:

$$\begin{array}{l}{\stackrel{.}{\theta }}^i(t)=-{({\partial }_{1}G({\mathbf{X}}_0^i(t),{\mathbf{S}}^i(t)))}^t{\theta }^i(t)\text{with}{\theta }^i(1)=\frac{1}{2{\sigma }^2}{\nabla }_{{\mathbf{X}}_0^i(1)}D({\mathbf{X}}_0^i(1),{\mathbf{X}}_i)\\ {\stackrel{.}{\xi }}^i(t)=-\left({\partial }_{2}G{({\mathbf{X}}_0^i(t),{\mathbf{S}}^i(t))}^t{\theta }^i(t)+d_{{\mathbf{S}}^i(t)}F{({\mathbf{S}}^i(t))}^t{\xi }^i(t)\right)\text{with}{\xi }^i(1)=0\end{array}$$ (6)

To compute the gradient, one integrates the flow equations (5) forward in time to build the deformations of the template shape. Then, one computes the gradient of the residual data term ∇D, which serves as initial conditions in (6). The ODEs (6) transport this information from each subject’s space back to the template space, where the final value of the auxiliary variables θ(t) (resp. ξ(t)) is used to update the template (resp. the control point positions and momenta).

To optimize (4), which combines differentiable terms denoted E_L² with an L¹ penalty, we use an adapted gradient-descent scheme called Fast Iterative Shrinkage and Thresholding Algorithm [1]. The template and control points are not affected by the L¹ term and are updated using a gradient-descent step at each iteration. By contrast, the momenta ${\alpha }_{0,p}^i$ are updated according to:

$${\alpha }_{0,p}^i\leftarrow S_{\tau \gamma }\left(\Vert {\alpha }_{0,k}^i-\tau {\nabla }_{{\alpha }_{0,k}^i}{E}_{L^2}\Vert \right)\frac{{\alpha }_{0,k}^i-\tau {\nabla }_{{\alpha }_{0,k}^i}{E}_{L^2}}{\Vert {\alpha }_{0,k}^i-\tau {\nabla }_{{\alpha }_{0,k}^i}{E}_{L^2}\Vert },$$ (7)

where τ is the current step-size of the gradient descent and S the usual softthresholding function S_λ(x) = max(0, x − λ) + min(0, x + λ). This function zeroes out the momenta that are too small in magnitude, thus ensuring sparsity in the parametrization of deformations.

The parameters of the algorithm are the trade-offs σ and γ, the standard deviation of the Gaussian kernels for the momenta σ_V and the currents metric σ_W [15, 4]. We initialize the template shape with an ellipsoid for each connected component of the shapes, the control points with a regular lattice of step σ_V, and the initial momenta are set to zero.

3 Results

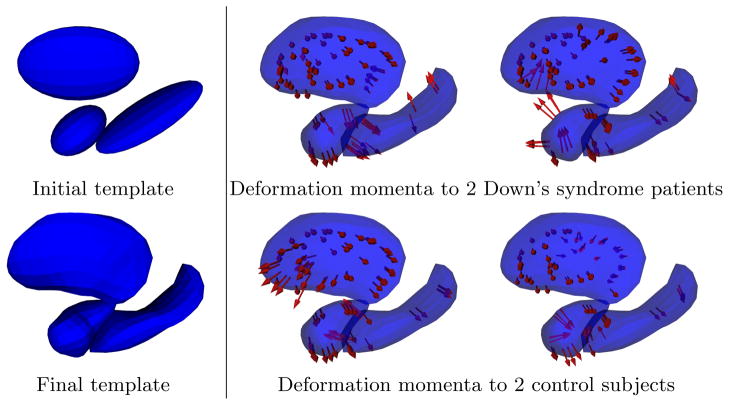
We apply our method to a study that seeks to compare neuroimaging, genetics, and neurotransmitter properties of patients with Down’s syndrome and healthy controls. We construct an atlas from surfaces of three different deep brain structures: amygdala, hippocampus, and putamen (Fig. 1). We initialize the atlas with one ellipsoid for each of the three anatomical structures, and we initialize the control points with a regular lattice of 650 points. After the optimization, the template shapes capture the common anatomical features across the populations (Fig. 2-left), and are given as meshes with the same topology as the initial set of ellipsoids. The parameterization of the template-to-subject deformations were also optimized: control points are moved toward the surfaces (where their theoretical optimal locations are, as shown in [15]) and the sparsity prior selects a subset of control points (99 out of 650) that carry a non-zero momentum vector. Results were generated using σ = 10⁻⁴, γ = 3 × 10⁶, σ_V = 5, and σ_W = 2.

Fig. 1.

Sample input shapes where hippocampus, amygdala, and putamen are shown in yellow, blue, and cyan respectively.

Fig. 2.

Atlas construction: template shape (left) and parameterization of the template-to-subject deformations (right). The template is initialized with an ellipsoid per connected components (top-left). After the optimization, the template shapes still have the same topology as the sample shapes. Simultaneously, template-to-subjects deformations are estimated, which are parameterized by the momentum vectors (red arrows). The vectors are located at the position of the control points, which are the same for all subjects. Control point positions were initialized as the nodes of a regular lattice, and our algorithm moves the control points to their optimal position near the surfaces and selects the most relevant ones according to the sparsity prior.

By comparison, we show the atlas built with the method of [4] in Fig. 3. The template shape is given as a set of disconnected normals: the continuity of the surfaces and the number of connected components of the input shapes have not been preserved. Moreover, the template-to-subjects deformations are parameterized with momenta located at the same place as the template normals. By contrast, our method optimized the position and the number of the control points independently of the vertices of the template shapes. Consequently, deformations are parameterized by more than 40 times fewer momenta. Constraining the template to remain a mesh has not introduced bias in the estimation: the norm of the difference between the templates generated by the two methods is 3.4 10⁻⁵, which is much smaller than the standard deviation and below the usual threshold of 3 times standard deviation to decide statistical significance.

Fig. 3.

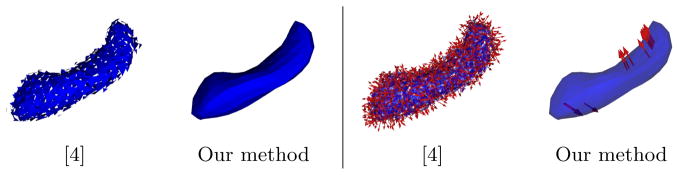
Comparison of hippocampus template generated using [4] and our method. Arrrows indicate the momenta driving the registration of the template to the first subject. Our method generates topologically correct mesh as opposed to triangle normals, and with deformations momenta that are not constructed to be located at the surface triangles.

We construct a common template for the combined DS and healthy populations, and perform a Principal Component Analysis (PCA) on the momentum vectors for each population separately. The results in Fig. 4 show that the two populations contain different variability at different objects and at different locations within each object. The sparse momentum vectors enable statistical analysis in lower dimensional space which has great potential for clinical studies.

Fig. 4.

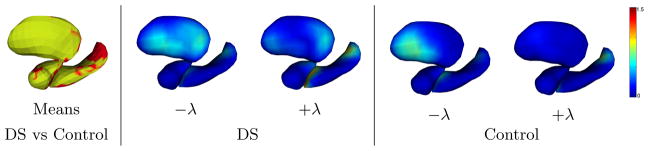
Statistical analysis of momentum vectors for Down’s syndrome (DS) and healthy control population. Left: template deformed according to the average momenta for DS (red) and control (yellow). Center and Right: Templates deformed according to the first mode of PCA on momentum vectors for DS and control population, demonstrating the different modes of variability. Colors indicate the magnitude of displacement from the population mean shape (in mm).

4 Conclusions

We propose a new method for estimating shape atlases using the currents metric. In contrast to [6, 4], the template shape is given as a mesh that has the same topology as the shapes in the population and the parameterization of the template-to-subject deformations were optimized independently of the template shape. We use a single gradient descent for estimating the template and the deformations, in contrast to the alternating minimization in [6, 4]. This scheme is much more efficient than using the matching pursuit technique and shows good convergence properties, even with the most naive initialization. Our non-parametric method makes use of the metric on currents, which enables the use of shapes without point correspondences, and therefore with minimal pre-processing.

The method also provides automatic parametrization of diffeomorphisms for mapping subjects within a population, where the parameters are constrained to lower dimensional spaces. We demonstrated the potential for these sparse parametrizations for performing statistical analysis on shapes from Down’s syndrome and healthy control population groups, which can enable future research correlating brain function, anatomy, and neurocircuitry.

In the future, we plan to analyze the robustness and statistical power of the parametrizations provided by our method, in particular in High Dimension Low Sample Size (HDLSS) settings that are typical in imaging studies of populations.