Effects of a Response-Based, Tiered Framework for Intervening With Struggling Readers in Middle School

Abstract

This study addressed the effects of multiyear, response-based, tiered intervention for struggling readers in grades 6–8. A sample of 768 sixth-grade students with reading difficulties was randomized to a response-based, tiered-intervention condition or “business as usual,” and initial treatment status was maintained over the three-year study. To estimate the effect of treatment and to address questions about the acceleration of learning, a multiple-indicator, multilevel growth model was fit, representing the likely trajectories of the group of students originally randomized (in the fall of sixth grade) to treatment. Three-year trajectories were fit, with the results representing likely multiyear trends for the three groups. Treatment students, on average, outperformed business-as-usual students. The effect size based on the multiple-indicator, multilevel model was .26. Treated students also outperformed the group of typical readers when achievement was characterized in terms of slope over time. However, a sizable gap remained between treated and typical students in the spring of eighth grade.

A compelling evidence base has developed for intervening with adolescent struggling readers (Biancarosa & Snow, 2006; Kamil et al., 2008). Multiple small-scale, investigator-led studies document strategies for improving older students' reading ability, and recent syntheses of this research base, including several meta-analyses (Edmonds et al., 2009; Scammacca et al., 2007), have reported mean treatment effects in the moderate-sized range. For example, Edmonds et al. calculated an average effect size of 0.89 for comprehension outcomes across 13 studies with students in grades 6–12, and word-level interventions were associated with an effect size of 0.34 on measures of comprehension. Scammacca et al. synthesized 23 studies that included one or more measures of reading comprehension, reporting an average effect size of 0.97. Among studies that used a standardized, norm-referenced measure of reading comprehension (n = 8), the treatment effect size was 0.35.

Attempts to combine and scale these strategies, however, have been less encouraging; a series of large-scale, randomized trials have reported null or, in some cases, very small-sized effects for multicomponent interventions comprising these research-based recommendations (Chamberlain, Daniels, Madden, & Slavin, 2007; Kim, Samson, Fitzgerald, & Hartry, 2010). Attenuation of this sort typifies the general relationship of effect and implementation scale, and factors that contribute to the generic case are likely to apply to the present situation as well. That is, differences in the average effect reported by small-scale, school-based studies and by large-scale trials may relate, in part, to factors inherent in scaling a new practice (e.g., logistics of implementation fidelity, mathematical realities of estimating treatment effects), suggesting a natural weakening of effect when implemented across multiple schools (James-Burdumy et al., 2012).

Response-based, tiered instructional models represent a means of regulating scale (in a sense) and potentially minimizing its diminishing effects by systematically refocusing instructional intensity according to identified need or risk. A more efficient and targeted allocation of available resources would, in theory, improve the average outcomes across a group of struggling students (Kim et al., 2010). The present study estimates the effect of a response-based, tiered model in the context of a series of reading interventions implemented across multiple school years and multiple middle schools.

Adolescent Struggling Readers

Findings from recent randomized studies of intensive programs implemented at scale have not been encouraging on the question of improving the reading ability or accelerating the reading achievement of older struggling students. For example, Chamberlain et al. (2007) found no statistically significant differences on the Gates–MacGinitie comprehension subtest in a sample of 405 sixth graders after a yearlong, randomized implementation of Reading Edge, a comprehensive, schoolwide literacy model developed for Title I middle schools and aligned with the Success for All program. Kim et al. (2010) found no differences in the posttest reading comprehension of struggling readers participating in an after-school program that provided 92 hours (60 minutes per day, four days per week, for 23 weeks) of evidence-based treatment to a randomized sample of students in grades 4–6.

An evaluation of the Enhanced Reading Opportunities Study found no statistically significant differences between two treatment groups and a business- as-usual (BaU) condition on oral language and vocabulary-related outcomes and very small differences on a measure of reading comprehension (Somers et al., 2010). Lang et al. (2009) provided 90 minutes of daily intensive reading instruction to older struggling readers over a nine-month period and found that low-performing readers made no statistically significant gains in reading comprehension. Finally, Denton, Wexler, Vaughn, and Bryan (2008) reported similar results in a sample of students in grades 6–8 provided with daily intensive instruction over an entire school year.

As suggested, these findings contrast with the more promising results of smaller-scaled studies on effective practices with older struggling readers, research that represents the evidence base for intervening with older struggling students, including programs used in many of the large-scale efforts described earlier. Adolescents with reading difficulties benefit from explicit and systematic intervention organized around their instructional needs (Edmonds et al., 2009), including support for morphological awareness (Nagy, Berninger, & Abbott, 2006) and opportunities to learn to read and understand complex, multisyllabic words (Bhattacharya & Ehri, 2004). These students need to understand the meanings of challenging words and be able to derive meaning for unfamiliar words encountered across multiple text types by applying knowledge of word roots and affixes (Baumann, Font, Edwards, & Boland, 2005).

For older struggling readers and for English learners, word-level instruction should be delivered as part of a comprehensive approach to teaching vocabulary (Kieffer & Lesaux, 2008). Oral reading fluency represents a useful indicator of student automaticity at the word level and is necessary, although not sufficient, for reading comprehension (RAND Reading Study Group, 2002). Older readers who are fluent but nonetheless struggle with comprehension may benefit from strategy instruction such as monitoring, summarization, and question generation, although strategy-related effects may be conditional on more substantive cognitive structures (Willingham, 2007) or on students' developmental status (Cantrell, Almasi, Carter, Rintamaa, & Madden, 2010).

Implementation Scale

The different patterns of findings across these two bodies of research may reflect a number of factors. The scale of a program's implementation and its relationship to fidelity generally influence an effect's magnitude; as scale increases, fidelity tends to diminish, downwardly biasing effect estimates for the normative model (i.e., the program as designed and implemented as intended). A larger-scale implementation increases the likelihood that individuals or groups in the BaU condition will be exposed to and begin to use elements of the intervention, threatening the study's internal validity and potentially compromising the estimate of treatment effect.

In smaller-scale implementations, investigators are better able to monitor program use and maximize or reliably measure fidelity and condition estimates of effect accordingly. Their greater involvement may also translate into increased opportunities to observe and perhaps influence aspects of the BaU condition, thus minimizing treatment implementation in nonexperimental classrooms, yielding a more reliable treatment effect, and diminishing threats to internal validity. Small-scale studies also tend to focus on a single instructional strategy or on a combination of two or three strategies (see Scammacca et al., 2007), further reducing the complexity of implementation compared with larger-scale trials, which generally feature a multifaceted intervention. This relative specificity (i.e., the evaluation of a single strategy) generally requires a comparably specific measure of outcome, often researcher developed and closely aligned to elements of the intervention. This specificity contrasts with large-scale trials of multifaceted programs, in which improved reading comprehension is the primary outcome and measurement relies on standardized, normed indexes, which tend to be relatively distal to a given intervention and less sensitive to treatment effects.

Features of the program, independent of the research design, the BaU, or measures of outcome, are considerations as well. A program's strength varies according to the quality of instructional tasks and the quantity of instructional time (e.g., number of days per year, number of minutes per day). The body of small-scale, investigator-led studies provides a compelling basis for identifying strong instructional tasks for older struggling readers. However, these studies are largely silent on strategies for delivering a multicomponent model as a coherent instructional whole or for regulating its delivery according to individual student need. The studies also fail to address questions about the amount of instructional intensity necessary for a collection of these validated strategies to yield a statistically meaningful effect in a large-scale randomized context.

Response-Based, Tiered Models and Treatment Intensity

Current research provides little evidence about the intensity necessary to accelerate the reading achievement of older struggling readers (Torgesen, 2005), except that the nine-month default may be inadequate, on average, to narrow the gap with typical readers (Kim et al., 2010). It is also apparent that the intensity needed to improve outcomes varies across individual students (Kamil et al., 2008). Some students may require a year of intervention, whereas others may need more intensive, longer-term intervention. Acknowledging this variation provides a mechanism for concentrating available supports on students who continue not to respond or who respond below an established standard (i.e., students with more entrenched reading deficits) while monitoring the ongoing achievement of students who do respond. Response-based, tiered models have become increasingly prevalent in schools, including middle schools (Ardoin, Witt, Connell, & Koenig, 2005), as a means of regulating the allocation of instructional intensity; identifying students requiring more intensive, specialized, or long-term support; and in terms used earlier, mitigating the attenuating effects of scale.

Models vary in their details, but all share core features, including efficient screening, evidence-based core instruction and intervention, progress monitoring, and well-articulated structures for identifying risk and for adjusting available levels of instructional intensity for individual students and for groups of students, based on risk status. In tiered models, all general education students (i.e., students who do not qualify for special education services) participate in the core instructional program (e.g., reading, English language arts), commonly referred to as Tier 1. Students identified as being at risk, based on screening results or low response to Tier 1 in struction, participate in additional intervention (Tier 2) that augments the core program. The additional time and/or smaller groups that characterize Tier 2 represent more intense instructional settings (Burns, Appleton, & Stehouwer, 2005). For students whose response continues to fall below an indicated standard, even greater intensity (i.e., tiers beyond Tier 2) can be achieved by adding instructional time during or outside of the school day and/or by further reducing group size.

One of the few randomized studies of a multiyear (i.e., more than nine months) reading treatment with middle school at-risk students (Vaughn et al., 2012) found that students receiving three years of intervention (grades 6–8) significantly outperformed a BaU group on the Woodcock–Johnson Passage Comprehension posttest (effect size [ES] = 1.20) at the end of eighth grade. This finding suggests that intensive, long-term intervention may benefit older students with significant reading problems. However, it applies only to students with persistent reading difficulties.

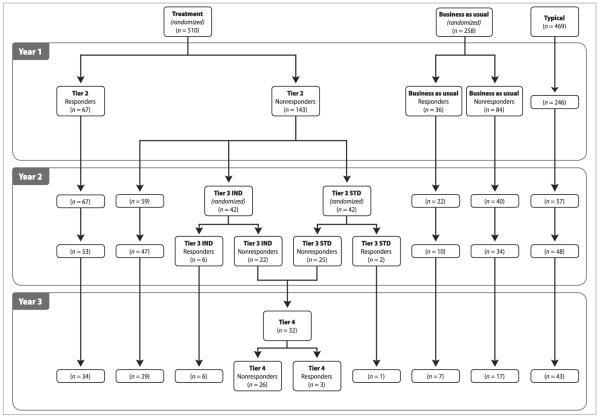
The eighth graders in that study were originally sampled and randomly assigned the summer before sixth grade, and they were included in the year 3 sample (as eighth graders) due to inadequate response to intervention in years 1 and 2 of the project. Thus, the large-sized effect (Hedges's g = 1.20) represents the impact of three years of treatment for the group of students most likely to be low responders. (Status as “low responder” was not knowable prior to treatment, so students' ongoing lack of response indicated the seriousness of their reading difficulties; see Figure 1.) Further, this earlier finding represents the impact of reading intervention because all students in the treatment sample received three years of intensive instruction; in other words, the reading intervention served as the independent variable.

FIGURE 1. Participant Movement Across Years per Initial Assignment.

Note. IND = individualized. STD = standardized.

The present study broadens this earlier work by considering the effect of a response-based, tiered model for allocating reading intervention across the middle school years (grades 6–8). Because the original experimental manipulation (prior to beginning the three-year program) was access to more intensive intervention (or BaU) and because initial assignment was maintained across the three-year project, the independent variable was the response-based, tiered model rather than the reading program per se; only the group of at-risk students assigned to treatment before sixth grade received intervention in year 1, and only those who did not respond adequately were eligible for ongoing support (see Figure 1).

This situation represents a departure from questions that are typical of intervention research. In this context, the reading program was a tool (previously validated, as described later) for improving students' reading; however, the causal agent, or independent variable, was the response-based model for allocating the evidence-based intervention, a design that allowed for a test of response to intervention, although our motivating purpose was more limited. Fully articulated Response to Intervention models, when implemented in general populations of students, generally address (a) prevention (e.g., preventing individuals or groups of students from falling behind established performance benchmarks), (b) remediation (Torgesen, 2005), and (c) identification (i.e., their utility in reliably identifying the specific learning disability). Given the population of interest in this study—older struggling readers—remediation was the primary focus.

Our goal was to estimate and compare likely three-year trends for students participating in the response-based, tiered model and for students participating in BaU. We also modeled three-year trajectories for a group of “typical” readers attending the participating schools. Specific research questions included the following:

• What is the effect of response-based, tiered model for delivering reading intervention to struggling students across grades 6–8 on overall reading achievement?

• To what extent does a sustained (over three years) response-based, tiered model for struggling students close the achievement gap with typically achieving peers?

Differences related to student attributes were evaluated through the following questions:

• Does primary language status in sixth grade influence the intervention's impact on overall reading achievement trajectories?

• Does special education status in sixth grade influence the intervention's impact on overall reading achievement trajectories?

Note that the questions focus on the impact of tiered models for instructional delivery. We do not propose tiered models as a substitute for high-quality instruction; having additional time or smaller groups (i.e., greater intensity) are meaningful only to the extent that such opportunities are well used (i.e., that quality instruction is provided).

Method

School Sites

This study was conducted with institutional review board approval in two large, urban cities (one large district, one medium district) in the southwestern United States, with approximately half the sample from each site. Students from seven middle schools (three from the first, larger site and four from the second site) participated in the study. The three schools from the first site were classified as urban, and the remaining four schools were classified as suburban and rural, with school populations ranging from 633 to 1,300 students. The rate of students qualifying for reduced or free lunch ranged from 56% to 86% across the schools in the larger site and from 40% to 85% in the smaller site.

Sampling and Assignment

The initial sampling frame included 2,034 fifth-grade students who had usable and eligible state test scores (Texas Assessment of Knowledge and Skills [TAKS]) and who were expected to attend one of seven middle schools that agreed to participate in the study. Students were excluded from participation if they (a) were enrolled in an alternative curriculum (e.g., life skills class), (b) read on a second-grade level or lower, (c) were identified as having a significant disability (e.g., blindness, deafness), or (d) had individualized education plans that prevented participation in a reading intervention. Of the initial sample, 768 students were identified as struggling readers, based on a scale score of 2,150 or below on the fifth-grade TAKS, a value that represents 0.5 of a standard measurement error (standard error of measurement is 100) above the Pearson-recommended cut score of 2,100.

The 768 at-risk students were randomized within schools to the response-based, tiered condition or to BaU, using a 2:1 assignment ratio, with 510 students assigned to treatment and 258 to BaU. The 2:1 ratio maximized potential benefits of program participation. Per the districts' request, randomization occurred in the spring and early summer of 2006 to accommodate the scheduling of classes in sixth grade (reading was scheduled during an elective period for students randomized to treatment). During the summer, the catchment areas for middle schools in one of the participating districts were realigned, diverting a subsample of the original 768 students to nonparticipating sites. Of the originally randomized students, 419 enrolled in one of the seven participating middle schools—278 students who were randomized to intervention and 141 students who were randomized to BaU, representing an approximate 40% loss of cases in both conditions.

These 419 students were administered the full assessment battery (only TAKS data were available for the 349 reassigned students). The proportion of students not available in the fall of sixth grade did not differ between the two groups (p > .05), and average TAKS scores at pretest did not differ (p > .05) between the group of students at participating schools in the fall of 2006 (i.e., the sample of 419) and the group of students reassigned to nonparticipating schools.

The groups of participating and reassigned students did not differ on key demographics, including race, gender, primary-language status, and free or reduced-price lunch status. Also, within the participating group, there were no differences in demographics across condition at pretest (p > .05). Of the total sample, 54% of the students were male (53% in treatment, 55% in BaU), 18% were limited-English proficient (LEP; 18% in treatment, 17% in BaU), and 85% received free or reduced-price lunch (82% in treatment, 85% in BaU). More than half of the students were African American (58% in treatment, 57% in BaU), 32% were Hispanic (32% in both treatment and BaU), 9% were white (9% in both treatment and BaU), and 1% were Asian (1% in treatment, 2% in BaU).

A group of typical readers from the same seven middle schools was followed over the three years. This population was defined as students in the participating schools who scored at least 1 standard error of measurement above the passing score (i.e., at or higher than 2,200 on the TAKS). Typical-reader data for this study were collected from a randomly drawn subsample (n = 469 in the spring of 2006). By design, the typical-reader sample size was constrained at approximately 0.60 the size of the struggling-reader sample. About 49% of the students in the typical-reader group were male, 7% were LEP, and 66% received free or reduced-price lunch. More than half (53%) of the students in the sample were African American, about 23% were Hispanic, 21% were white, and 3% were Asian.

The sample of typical readers was subject to the same district realignment in the summer of 2006 that affected the at-risk group, with a comparable loss (about 40%). A total of 281 typical readers enrolled in the expected middle school in the fall of 2006. This group and the group of reassigned students (n = 188) did not differ on key demographics, including race, gender, primary-language status, and free or reduced-price lunch status. This group of students represented normative reading performance in the local area.

Initial assignment (treatment or BaU) was maintained during the study. Only students assigned initially to the treatment condition were eligible for the reading intervention in years 2 and/or 3, and only if they continued to struggle, based on data from the annually administered TAKS. For example, treatment students who scored below the cut score on the TAKS (2,150) at the end of project year 1 (post–Tier 2 in Figure 1) were eligible for a second year of intensive reading instruction during project year 2 (i.e., Tier 3). Similarly, students with low or inadequate response at the end of project year 2 participated in a third year of more intense reading instruction during project year 3 (Tier 4).

The BaU and typical-reader samples were trimmed in the fall of seventh grade (prior to beginning project year 2) to accommodate budget constraints. The BaU sample size was reduced by 50% by using within-school random selection. The typical-reader group was reduced by 75% by using the same approach. The potential impact of these reductions was evaluated at the time by using power analysis. We also conducted a post hoc attrition analysis, which is described in the next section.

In summary, the following features in Figure 1 are worth highlighting. Treatment in the top row of three boxes refers to the group randomly assigned in the spring and early summer of 2006 to the response-based model. BaU refers to the group of students who were randomly assigned to the condition that did not participate in the response-based model. It also refers to usual practice within the schools for supporting struggling readers, whether core instruction, more intensive intervention, or some combination. Tier 2 is the intensive reading support provided in year 1 to students in the treatment group. Tier 3 is the intensive reading support provided to a randomly assigned subsample of treatment students in year 2. Tier 4 is the third year of intensive reading support provided to treatment students who did not respond adequately to intervention in years 1 and 2. The adequacy of student response was based on annual TAKS performance. For clarity, we use these labels throughout the remainder of this article to refer to the groups in question. The interventions provided in each tier are more fully described in a subsequent section.

Attrition

Overall attrition can bias a study's external validity to the extent that the initial sample represents a population of interest and the students who attrite differ from those who remain in the study (Valentine & McHugh, 2007). Differential attrition is evident when treatment and control groups differ (a) in the proportion of cases leaving prior to the study's terminal event or (b) in the average attributes (e.g., demographic characteristics) of noncontinuing participants. Although differential attrition can bias effect estimates and threaten a design's internal validity, its effect can be particularly profound when teamed with elevated levels of overall attrition (Miller & Hollist, 2007).

This study used the two-step method first described by Cook and Campbell (1979) to evaluate the effects of overall and differential attrition. Treatment condition, completer status (i.e., did or did not attrite), and the interaction of condition and completer status were regressed on the Woodcock–Johnson pretest measures and key demographic variables. Significant main effects for the group of completers were taken as an indication of significant overall attrition and a potential threat to the result's external validity. The treatment condition by completer status interaction provided an indicator of differential attrition. A significant interaction in this context signifies systematic group differences in the characteristics of dropped cases. Assumptions regarding missing data and causality were informed by Rubin's framework (e.g., Little & Rubin, 1987; Rubin, 1976).

We evaluated attrition in terms of the originally sampled group of 768 students because we randomized that sample to treatment and BaU. Differential attrition can result when randomized, and hypothetically non-different, groups vary in patterns of missingness at subsequent points in time. Our purpose was to evaluate the extent to which the randomized structure remained intact after the district-implemented changes in feeder patterns described earlier. Demographic data were available for the full sample of 768.

There were no significant main or interaction effects for the binomial logistic regression of gender on condition (p = .48), completer status (p = .10), or for the interaction term (p = .48). For the binomial logistic regression with LEP, there was no main effect. However, there was a statistically significant interaction of condition and completer status (p = .02), with a relatively higher percentage of completers in the BaU condition (33% LEP), although the low total number of cases in this group (n = 24) is a consideration. About 15% of the treatment students were LEP, in both the completer and noncompleter groups, as were about 13% of the non-completing BaU students.

A multinomial logistic regression with ethnicity as the dependent variable indicated differences in the group of African American students (with whites used as the reference group) on both completer status (p < .01) and the interaction terms (p = .01). As before, the source of the differences was the BaU condition in the group of completers, where 75% of the time four cases were not African American, compared with about 45% for the other groups. There were no differences for condition (p = .86) or the interaction term (p = .72) on free or reduced-price lunch status or on special education (p = .86 for condition; p = .63 for the interaction term).

When the three Woodcock–Johnson measures were regressed on completer status and the interaction of completer status and condition in the sample of 419 (pretest data were available for only the 419 students who enrolled in fifth grade at the participating middle schools), there were no significant main effects for completer status (p-values of .21–.72) or the interaction (p-values of .13–.70). Finally, in relation to the random sample reduction in year 2, there were no significant differences in demographics or test scores between the group of dropped cases and the group of retained cases, both in the BaU condition and in the typical group.

Teacher Participants

Experienced interventionists were hired by the research team and provided with ongoing training and supervision during each of the three project years. Intervention teachers varied across project years (see descriptions of teachers for year 1 in Vaughn et al., 2010; for year 2 in Vaughn et al., 2011; and for year 3 in Vaughn et al., 2012), depending on the nature of the reading intervention (i.e., Tier 2 intervention required a somewhat different skill set than Tier 3 intervention did, and we made decisions about interventionists accordingly), but all had high levels of knowledge, considerable experience in teaching students with reading disabilities, and valid teaching credentials. They were mostly female and either white or Hispanic, with about 10 years of prior teaching experience on average.

The research team provided approximately 60 hours of professional development each year prior to the start of treatment, fine-tuning teachers' knowledge about key elements of the treatment and practicing implementation. The professional development focused on the following instructional practices:

• Preteaching essential words to build vocabulary

• Teaching students to decode unknown words and derive their meanings, including multisyllabic words

• Promoting comprehension by teaching students to generate questions, identify the main idea, summarize, and apply related comprehension strategies

• Encouraging student engagement and motivation (e.g., choosing texts to read, establishing goals related to reading, working in student pairs and small groups, providing incentives to read).

The teachers participated in biweekly staff development meetings and received regular (once every one to two weeks) on-site feedback and coaching based on ongoing fidelity checks. Forms for monitoring fidelity were aligned with the normative program model and addressed program elements that were necessary and unique to the intervention (i.e., likely to not be part of BaU) and elements that were necessary but perhaps not unique (i.e., more likely to be part of BaU). We did not observe instruction in BaU classrooms because comparable opportunities were not available (i.e., a daily reading class was not offered to participants in BaU).

Program

As described in the introduction of this article and in the section on sampling and assignment, although the reading intervention did not represent the independent variable in the context of the three-year study because it was not manipulated as part of the initial assignment to condition (see Figure 1), the interventions used at each tier were subject to prior experimental investigation (Vaughn et al., 2010, 2011, 2012). We subsequently describe Tiers 2–4 and briefly summarize the evidence in support of the efficacy of each, after describing BaU.

BaU

BaU represents the typical school experience for at-risk readers. All students benefited from content area teachers' (e.g., social studies, science) participation in annual, six-hour, researcher-provided professional development sessions designed to better embed evidence-based vocabulary and reading comprehension instruction across the school day. Additionally, struggling readers attending the three schools in the larger of the two school districts received a daily, 45-minute reading class and an 85-minute English language arts class. Treatment students in the larger site participated in both the 45-minute, district-provided intervention and in the experimental intervention, offered during an elective period.

Treatment and BaU students attending the four schools in the smaller school district received a daily, 50-minute English language arts class. The schools in the smaller district did not offer additional reading classes to struggling readers, meaning that struggling students in the larger site received one additional daily reading-related class compared with struggling students in the smaller site (i.e., treatment students in the larger district received two reading classes, and treatment students in the smaller district received one). All students in both districts participated in rigorous test preparation training annually prior to the statewide administration of the high-stakes reading assessment.

Finally, we collected information on additional reading instruction (e.g., after-school tutoring) that BaU and treatment students may have received in addition to school-provided opportunities. About 25% of the initial BaU sample received out-of-school reading support. These students averaged about 30 hours total (SD = 15 hours) across the three years. A similar proportion of treatment students (about 25%) received outside reading support for a comparable number of hours on average (about 30 hours over the three years).

The Tiers 2–4 interventions were delivered during students' elective period. Students in the BaU condition participated in their usual electives, such as technology applications, fine arts, home economics, culinary arts, Web technologies, Advancement Via Individual Determination, content mastery, and career-related programs. BaU students also received supplemental reading instruction in the form of test preparation exercises provided to all students.

Tier 2

In Tier 2 (project year 1, secondary intervention), students in the treatment condition participated in classes of 10–12 students during their elective period (BaU students received usual school-provided services). Intervention was provided daily for 50 minutes over approximately 160 sessions per school year. A three-phase standardized treatment protocol was implemented sequentially during the first year, with each phase lasting several months.

Phase 1 focused initially on word study and fluency and increasingly on vocabulary, sentence and paragraph meaning, and overall comprehension. Fluency was supported though daily repeated reading practice for 10–15 minutes. Students tracked their progress via regularly administered assessments of oral reading fluency. The REWARDS program (Archer, Gleason, & Vachon, 2005) was used to teach advanced strategies for decoding multisyllabic words (word study). Progress in the program was dependent on individuals' mastery of sounds and word reading. Students received daily instruction and practice with individual letter sounds, letter combinations, and affixes. Students were taught a segmentation strategy for decoding and spelling multisyllabic words. Vocabulary was addressed daily by teaching the meanings of words in the texts used for instruction and practice. Student-friendly definitions were provided along with examples and nonexamples of the proper use of new words. Word knowledge was reinforced through reading, writing, and verbal use. Text comprehension was taught by asking students to answer questions of varying levels of difficulty (literal and inferential) during and after reading a passage. The purpose was to check for understanding and to model active thinking during reading. Students were taught to use text as a resource for answering questions and for justifying their responses.

Phase 2 focused on vocabulary and comprehension, with additional instruction and practice on the word study and fluency skills and strategies from phase I, as needed. In addition to previously described vocabulary work, students were introduced to word relatives and parts of speech (e.g., install, installation, installable) and reviewed the application of word study principles to spelling (encoding vs. decoding). Vocabulary words were selected from the texts read in class, including narrative (e.g., novels, chapter books) and expository sources (e.g., informational text). Teachers previewed vocabulary related to a given text, reviewed the spelling of new words, and then previewed the passage with students. Teachers guided students in the initial reading of the passage, asking questions to check for understanding and to model active thinking. While reading, students completed a graphic organizer as a means of processing and summarizing information. They also engaged in writing activities to summarize the newly covered content.

Phase 3 addressed the application of word-level and comprehension practices with expository texts that students encountered in school (i.e., topics and texts related to content area instruction in social studies and science). There was a particular emphasis on comprehension and critical thinking at the sentence, paragraph, and multiparagraph levels.

Vaughn et al. (2010) showed that participants in the Tier 2 intervention made statistically significant gains after nine months on measures of word attack, spelling, passage comprehension (TAKS), and phonemic decoding efficiency compared with students in BaU. Differences in decoding, fluency, and reading comprehension, as measured by the Woodcock–Johnson, favored the treatment group but did not differ statistically from gains in the BaU group. The median effect size across all reading outcome measures was 0.16 (Cohen's d). A complete description of the Tier 2 program, including sample lessons, is available on the Texas Center for Learning Disabilities website (www.texasldcenter.org).

Tiers 3 and 4

In project year 2 (Tier 3), a subsample of treatment students who did not meet the end-of-year criterion (passing the TAKS) was randomly assigned to either standardized treatment or the individualized treatment (see Figure 1). To provide a more intensive intervention for students in the two treatments, intervention was delivered in groups of five students per interventionist. For each student in the individualized treatment, teachers varied the instructional focus, time allocated daily to each instructional task, and instructional pacing over time, based on the results of weekly progress monitoring using curriculum-based measures developed for the intervention (for examples, see the Texas Center for Learning Disabilities website).

Additionally, a motivational plan built around students' interests and a goal-setting plan were implemented. In project year 3 (Tier 4), class size for the group of low responders was reduced further, from five students per group to two or three. Individualized instructional programs were developed for each student, according to the individualized protocol described earlier. BaU in years 2 and 3 was similar to that described for year 1.

In a nine-month efficacy trial of the Tier 3 reading interventions, students in both treatment groups (standardized and individualized) outperformed students in the BaU group (n = 59) in the fall of 2007 on assessments of decoding, fluency, and reading comprehension. The differences were statistically significant. Intervention type did not moderate the pattern of effects, although students in the standardized treatment had a small advantage over students in the individualized treatment on word attack. A complete description of the Tier 3 intervention is available in Vaughn et al.'s (2011) article, and sample lessons are posted on the Texas Center for Learning Disabilities website.

Prior research on the Tier 4 intervention (n = 22; Vaughn et al., 2012) was mentioned earlier. The small-group (two to four students), 50-minute daily intensive reading intervention for eighth-grade students with intractable reading problems was effective, as measured by the Woodcock–Johnson III Reading Comprehension (ES = 1.20) and Word Identification (ES = 0.49) subtests. However, students in the treatment condition continued to lack grade-level proficiency in reading despite three years of intervention.

Measures

The Woodcock–Johnson III Test of Achievement was administered as part of a larger assessment battery (Vaughn et al., 2010). Students were individually administered the Letter–Word Identification, Word Attack, and Passage Comprehension subtests in the spring and fall of the three project years. Scores from the fall of sixth grade and the spring of sixth, seventh, and eighth grades were used to estimate trends. The Letter–Word Identification subtest assesses the ability to read real words, with a median reliability of .91. The Word Attack subtest examines the ability to apply phonic and structural analysis skills to the reading of non-words, with a median reliability of .87. The Passage Comprehension subtest uses a cloze procedure to assess sentence-level comprehension by requiring the student to read a sentence or short passage and fill in missing words, based on the overall context. The Passage Comprehension subtest has a median reliability of .83.

Standard scores from these subtests were the dependent measures of interest. At pretest, coefficient αs in the entire sample of 486 struggling readers and 469 typical readers who contributed data throughout the year for the subtests were .98 for letter–word identification, .94 for word attack, and .96 for passage comprehension. At posttest, coefficient αs were .97 for letter–word identification, .99 for word attack, and .93 for passage comprehension.

The TAKS is a criterion-referenced assessment specific for each grade that aligns with state standards. Students read both expository and narrative passages and then answer several multiple-choice or short-answer questions designed to assess understanding of the literal meaning of the passages, vocabulary, and different aspects of critical reasoning about the passages. The internal consistency (coefficient α) of the grade 7 test is .89 (Texas Education Agency, Pearson Educational Measurement, Harcourt Educational Measurement, & Beck Evaluation and Testing Associates, 2004a, 2004b).

A variety of studies have found excellent construct validity comparing student performance on the TAKS with other assessments, such as the National Assessment of Educational Progress, the norm-referenced Iowa Tests of Basic Skills, college-readiness measures (Texas Education Agency et al., 2004a, 2004b), and individual norm-referenced assessments (Vaughn et al., 2010). We have used the TAKS in prior research with students in elementary grades (Vaughn, Linan-Thompson, & Hickman, 2003) and middle school. The TAKS represents a distal measure of comprehension. We include it in the battery because it typifies assessments used by educators and legislators, in Texas and other states, to make high-stakes decisions about educational funding and programming, and for a large segment of the educational community, treatment effects on such measures are of primary interest. As indicated elsewhere, this study used the TAKS to evaluate the adequacy of student response and to move students through the tiers.

Plan for Analysis

To estimate the effect of treatment and to address questions about the acceleration of learning, a multiple-indicator, multilevel growth model was fit. This type of model maximizes the advantages of structural equation modeling in a longitudinal context by explicitly modeling measurement error in observed variables and by constraining measurement variance across timepoints. It yields more precise trend estimates (Wu, Li, & Zumbo, 2007), provides a more rigorous basis for validity claims about the structure of a given data set (Valentine & McHugh, 2007), and offers a framework for evaluating measurement characteristics across time.

Level 1 was conceptualized as the measurement model, with reading ability estimated as a latent variable on each of four measurement occasions, using achieved w scores from three subtests of the Woodcock–Johnson as observed indicators. Reading ability was estimated as continuous, with a mean of 0 and freely estimated variances. Measurement error in structural models is specifically estimated so that for any given occasion (assuming a well-fit model), predicted values are more reliable estimates of students' reading ability than are the observed Woodcock-Johnson scores on which they are based.

Factor scores (i.e., reading ability at times 1–4) can be interpreted in terms of the growth model to which they are fit (level 2 in the multiple-indicator, multilevel model) and are particularly meaningful in the multi-group context, in which BaU groups provide points of reference for purposes of interpretation. Three parameters were estimated in the level 2 growth model: (a) intercept, (b) slope, and (c) shape or deceleration (a quadratic term was fit). These values provided the basis for addressing questions about overall reading ability and important conditional relationships. Level 3 of the model examined predictors of variation in different growth-related parameters. Treatment as an independent variable was of particular interest. Multigroup (n = 3; BaU students, treatment students, and typical readers) models were fit for purposes of estimating condition-related effects.

Temporal invariance is necessary for multiple-indicator, multilevel models because it eliminates the possibility that growth over time is due to variation in the measurement of latent constructs rather than or in addition to changes in the construct itself (Byrne, Shavelson, & Muthén, 1989). Invariance is indicated by constrained pathways (λ_y) between indicator variables (y_mt, where m represents the observed measure, and t represents measurement occasion) and the latent reading ability variables across the four timepoints. Strict invariance is indicated by (a) equality of factor indicator intercepts across time, (b) equality of factor indicator loadings across time, and (c) equality of residual variances over time (Meredith, 1993). However, in longitudinal designs where residuals accrue within students, the assumption of equal errors over time is generally untenable (Wu et al., 2007). Cross-group measurement invariance was assumed, given the randomized nature of the design and the imposition of temporal constraints in the measurement model.

Traditional fit criteria were used to evaluate models, with relative fit indexes of at least .95 and RMSEA of .05 or less as standards (Bovaird, 2007). Missing data were treated as missing at random, as described elsewhere, and a full information maximum likelihood estimator was used to fit models. Parameter differences were evaluated by constraining growth-related values (means and variance estimates for intercept, slope, and shape, e.g., quadratic) as equal across groups and comparing the relative fit (in terms of Δχ²) of nested models (Bovaird, 2007). Treatment effects were estimated in terms of differences between students in the BaU and treatment conditions (Feingold, 2009).

The extent to which treatment may have narrowed the achievement gap was evaluated in relation to the group of typical readers attending schools participating in the study and the group of initially struggling or at-risk students randomized into the treatment condition prior to time 1. Because this latter contrast (typical readers vs. treated students) was not subject to random assignment, results are presented descriptively. Effect sizes were calculated as the standardized difference (Hedges's g) in the groups' time 4 estimates for reading ability. Prior work with these data suggests minimal school-level variation; nonetheless, standard errors were adjusted for school-level clustering by using a sandwich estimator, as implemented in Mplus version 6.11 (Muthén & Muthén, 2010).

Finally, it is important to note again that the trajectories estimated by growth modeling and by the multiple-group, multilevel models reflect students' initial assignment to condition (i.e., the sample of 768). The objective was to represent the likely trajectories of the group of students originally randomized (in the summer before sixth grade) to treatment, requiring an assumption of data missing at random and the use of full information maximum likelihood. There was no attempt to model or control for dosage because the independent variable assumes variation depending on student need.

Results

The data were multivariate normal. Means and standard deviations are summarized for the sample available at each timepoint (see Table 1). Standard scores and w scores are provided. N differs across the three years (as indicated in Figure 1), depending on attrition and ongoing sampling. Differences in sample size are reflected in the Table 1 summaries.

TABLE 1.

Descriptive Statistics by Measure, Score Type, and Condition at the Four Timepoints

			Fall of grade 6			Spring of grade 6			Spring of grade 7			Spring of grade 8
Measure	Score type	Condition	Mean	SD	n	Mean	SD	n	Mean	SD	n	Mean	SD	n
Letter–Word Identification	Standard	Treatment	91.74	12.6	278	94.13	14.3	210	97.09	13.2	155	95.44	11.2	99
		BaU	91.59	12.4	141	93.07	13.4	120	95.63	14.2	44	90.36	13.8	24
		Typical	105.64	13.3	261	107.49	12.1	246	105.25	8.7	48	102.58	8.8	43
	Achieved w	Treatment	500.91	21.2	278	509.58	23.8	210	521.85	21.5	155	526.11	17.5	99
		BaU	501.60	21.9	141	508.60	22.8	120	519.70	22.4	44	518.72	22.9	24
		Typical	522.53	18.8	261	529.20	16.3	246	534.48	11.7	48	537.06	12.1	43
Word Attack	Standard	Treatment	95.18	11.0	278	96.53	12.1	210	98.59	11.9	155	95.98	11.9	99
		BaU	95.53	11.3	141	95.55	10.0	120	95.60	9.6	44	90.95	11.8	24
		Typical	103.43	11.2	261	105.66	11.4	246	105.15	10.1	48	103.19	10.7	43
	Achieved w	Treatment	498.04	17.6	278	502.30	18.7	210	508.90	16.8	155	509.17	16.1	99
		BaU	499.11	18.2	141	501.38	15.8	120	505.45	14.2	44	503.11	16.8	24
		Typical	510.41	16.0	261	515.00	15.6	246	518.08	12.7	48	518.57	13.4	43
Passage Comprehension	Standard	Treatment	86.57	11.1	278	87.87	11.5	210	90.85	11.6	155	90.54	10.6	99
		BaU	86.45	12.5	141	86.88	12.0	120	86.95	14.4	44	83.06	15.6	24
		Typical	98.61	11.0	261	100.27	9.8	246	100.52	10.0	48	99.70	11.0	43
	Achieved w	Treatment	492.29	13.3	278	496.35	13.5	210	503.59	12.9	155	506.58	10.4	99
		BaU	492.59	14.4	141	495.55	13.6	120	499.47	14.9	44	499.11	15.3	24
		Typical	505.84	11.2	261	509.64	9.9	246	513.54	10.0	48	515.50	10.7	43

Note. BaU = business as usual. Measures are subtests of the Woodcock-Johnson III Tests of Achievement.

Growth Trends in Overall Reading

An unconditional single-group growth model was fit to establish the basic structure of the data and to identify a baseline for comparing conditional models. With several modifications, this model (in Figure 1) fit the data very well: χ² = 78.28, df = 44, CFI = .99, TLI = .99, RMSEA = .033, RMSEA 90% CI = [.021, .045]. Intercepts for groups of indicator variables were constrained as invariant, although word attack at time 1 (y₂₁) and word attack at time 4 (y₂₄) were allowed to freely estimate for purposes of model identification (the freely estimated values did not differ statistically from the constrained estimates). Factor loadings across time were constrained, as described previously, and residuals for the observed variables were allowed to covary. The variance estimate for the quadratic term and for estimates of reading ability at times 2 and 4 were constrained as 0 (the estimated values for these parameters did not differ statistically from 0) for purposes of identification. Factor scores were 4.06 at time 2, 7.70 at time 3, and 10.92 at time 4. By default, the time 1 score (i.e., intercept) is 0. These values are model-predicted average scores based on estimates for the three growth parameters at each of the four measurement occasions. In the single-group model, the average slope estimate was 4.28 (p < .001), and the quadratic term was −.212 (p = .045).

The multigroup model also fit the data well: χ² = 255.00, df = 146, CFI = .98, TLI = .97, RMSEA = .056, RMSEA 90% CI = [.044, .067]. Temporal constraints in the single-group model were extended across the three conditions to establish group-level measurement invariance. Estimates of reading ability in the BaU group were 0 for time 1, 3.30 for time 2, 6.60 for time 3, and 9.91 for time 4 (see Figure 2). Reading ability estimates in the treatment and typical-reader groups should be interpreted in relation to BaU-group values. In the treatment groups, these estimates were −1.11 for time 1, 3.82 for time 2, 8.14 for time 3, and 11.84 for time 4. In the group of typical readers, the values were 9.67 for time 1, 13.21 for time 2, 16.25 for time 3, and 18.80 for time 4.

FIGURE 2. Reading Ability Factor Scores at Four Timepoints.

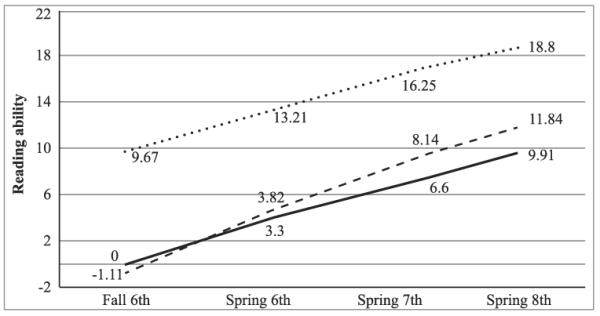
The solid line represents the BaU group, the dashed line represents the treatment group, and the dotted line represents the group of typical readers. The reading ability variable reflects the metric derived from the multiple-indicator, multilevel model.

Table 2 summarizes model fit and parameter estimates for the total group and for the treatment, BaU, and typical-reader groups. Statistically significant differences across the groups are indicated in Table 2 as well. The notable difference was in the means for slope: Δχ² = 8.87, Δdf = 2, p = .012. Follow-up pairwise contrasts indicated a statistically significant difference (Δχ² = 7.68, Δdf = 1, p = .006) between the treatment students (slope_mean = 5.24) and the combined group of BaU students (slope_mean = 3.30) and typical readers (slope_mean = 3.78). In head-to-head contrasts (i.e., separates of treatment to typical readers and treatment to BaU students), slope in the treatment group was greater than the average slope among typical readers (Δχ² = 5.04, Δdf = 1, p = .02) and the average slope of the BaU group (Δχ² = 6.47, Δdf = 1, p = .01). Overall differences in slope variance were not testable because variance in the group of typical readers was constrained at 0 for purposes of model identification (the estimated value for variance in the typical-reader group did not differ significantly from 0). There were no differences in slope variance between the treatment and BaU groups: Δχ² = 1.62, Δdf = 1, p = .203.

TABLE 2.

Model–Fit Indexes, Parameter Estimates, and Group Differences for Unconditional Single-Level and Multigroup Models

Measure	χ2 (df)	CFI	TLI	RMSEA [90% CI]	${\mathrm{I}}_{\widehat{y}}\left(p\right)$	${\mathrm{I}}_{\sigma }^2\left(p\right)$	${\mathrm{S}}_{\widehat{y}}\left(p\right)$	${\mathrm{S}}_{\sigma }^2\left(p\right)$	${\mathrm{Q}}_{\widehat{y}}\left(p\right)$	${\mathrm{Q}}_{\sigma }^2\left(p\right)$
Baseline	78.28 (44)	.99	.99	.033 [.021, .045]	.00 (.99)	118.90 (.00)	4.28 (.00)	1.11 (.04)	-.212 (.05)	—
Multigroup	255.0 (146)	.98	.97	.056 [.044, .067]
Treatment					-1.11a (.32)	127.33b (.00)	5.24c (.00)	1.25d (.12)	-.31e (.04)	—
Business as usual					.00a (.99)	104.67b (.00)	3.30f (.00)	3.64d (.01)	.001h (.99)	—
Typical					9.67i (.00)	50.79j (.00)	3.7j (.00)	—	-.25e (.16)	—

Note. CFI = comparative fit index. ${\mathrm{I}}_{\widehat{y}}$ = intercept mean. ${\mathrm{I}}_{\mathrm{s}}^2$ = intercept variance. ${\mathrm{Q}}_{\widehat{y}}$ = quadratic mean. ${\mathrm{Q}}_{\mathrm{s}}^2$ = quadratic variance. RMSEA = root mean square error of approximation. ${\mathrm{S}}_{\widehat{y}}$ = slope mean. ${\mathrm{S}}_{\mathrm{S}}^2$ = slope variance. TLI = Tucker–Lewis index. Estimates sharing a common superscript are not significantly different at p = .01. Estimates with different superscripts differ significantly at p < .01 or greater. Parameter estimates for intercept, slope, and the quadratic reflect the latently estimated scores for reading ability and can be evaluated in terms of the intercept estimate for the business-as-usual group.

Intercept means (with time 1 as intercept) differed statistically: Δχ² = 139.75, Δdf = 2, p < .001. As anticipated, the typical-reader group (intercept_mean = 9.67) scored significantly higher at time 1 than the treatment or BaU groups did. There were no significant differences in the mean intercept for the BaU group (intercept_mean = 0.00) and treatment group (intercept_mean = −1.11). The typical-reader group (intercept_variance = 50.79) also differed (Δχ² = 44.73, Δdf = 2, p < .001) from the BaU group (intercept_variance = 104.67) and treatment groups (intercept_variance = 127.33) in variance around the intercept. The mean value for the quadratic terms did not differ across groups (Δχ² = 0.81, Δdf = 2, p = .67) when slope was allowed to vary. The unbiased Hedges's g for the difference in the treatment group and BaU group was 0.26. This is based on a refit two-group model (χ² = 143.45, df = 95, CFI = .99, TLI = .98, RMSEA = .049, RMSEA 90% CI = [.031, .064]) with the time 1 average score for reading ability constrained as equal (i.e., 0) across the BaU and treatment conditions (note that the group-specific intercept for the treatment condition is −1.11; see Table 2). Time 4 means in this model were 9.97 for BaU and 12.31 for treatment. Variance estimates in time 4 scores were 59.30 in the BaU group and 93.84 in the treatment group. This difference was not statistically significant.

A relatively simple heuristic was used to compare the performance of treated students to that of typical readers (formal estimates of effect were not meaningful). The change from time 1 to time 4 in the treatment group was 12.95 units on the reading ability scale; the group of typical readers improved by an average of 9.13 points. The difference of 3.82 is about 42% of the score range in the typical-reader group, suggesting that changes in the treated group of students, on average, were about 40% greater than changes in the more skilled group of readers (alternatively, slope in the treatment group slope is about 40% greater than the slope for the typical-reader group). This finding does not represent a treatment effect because the group of typical readers was not subject to randomization, nor should it be interpreted as a proportion of a standard deviation, like standardized mean differences.

Finally, we evaluated the ongoing performance of students who initially responded to Tier 2 treatment. This group, indicated by the descending line along the far left-hand side of Figure 1 accounted for about a third of the end-of-year-1 sample assigned to treatment (67 of 210 students), and we reasoned that they would continue to represent the upper third of performers to the extent that they maintained their initial gains. The score that determines the upper third of a distribution is about midway along the first deviation above the mean (i.e., mean + 0.5, standard deviation). In the sample data described in Table 1, the cut score for year 2 is 96.65. The year 3 value is 95.84.

The average score in the spring of seventh grade for the group of responders (n = 53) was 96.63; in the spring of 8th grade, their (n = 34) mean score was 96.47. These values meet or exceed the cut scores in both year 2 and year 3, indicating that the group of responders continued to score better than about 67% of students in the sample on average. It also suggests that the group of initial responders maintained their end-of-year-1 status relative to others in the group of initially at-risk students. Although not a causal analysis, because we are considering data for cases within the treatment group, this finding supports the possibility that the group of initial responders outperformed other struggling students in years 2 and 3 even though they were no longer participating in the reading intervention. The initial responders continued to lag the group of typical readers by about one half of a sample standard deviation on average.

Student-Level Differences in Treatment Effect

The two-group multiple indicator, multilevel model provided a baseline for evaluating student-level differences in effect. For these comparisons, reading ability intercept was estimated at time 4 and regressed within treatment condition on targeted student-level variables, including English-proficiency status and special education status in the treatment and BaU conditions (i.e., typical readers were not included). Nested model comparisons indicated no differences in treatment effect for girls (Δχ² = 0.56, Δdf = 1, p = .45), for LEP students (Δχ² = 0.17, Δdf = 1, p = .68), or for students receiving special education services (Δχ² = 0.41, Δdf = 1, p = .52). The effect also did not differ statistically, depending on students' status at time 1: Δχ² = 0.71, Δdf = 1, p = .40.

Discussion

This study used data from a three-year randomized study to estimate the effects of a response-based, tiered intervention implemented over three years with middle school students. Participants were struggling readers, and the focus was on remediation of reading difficulties rather than prevention of risk or identification of learning disability. The study was conceptualized as a multi-tiered, sustained intervention, in which the amount of intervention varied by student, depending on prior response. We used a previously validated reading intervention as the instructional program.

The three-year trajectories were fit for the originally sampled group of students, based on their initial assignment in the summer before sixth grade, and for a group of typical readers who attended the same schools as the at-risk participants. The results represent likely multiyear trends for the three groups of students originally randomized in the spring and early summer of 2006. Treatment students, on average, outperformed students in the BaU condition. The effect size was .26, based on results of a multiple-indicator, multilevel model. Although the effects are in the small-to-medium range, they are practically and statistically significant and suggest that many struggling middle school students may require more than nine months of intervention to realize significant gains over comparable students.

Over a three-year period, students in the BaU lost ground to the group of struggling readers participating in the treatment, even though BaU included school-provided support designed to enhance performance on the state's high-stakes test (i.e., although it was a true BaU group, it was not a control condition of no additional reading instruction). The findings suggest that a response-based, tiered model may represent a vehicle for conditioning instructional intensity on prior response, at least when compared with BaU.

The treatment effect for overall reading represents roughly a threefold increase in the average estimates from the series of recent single-year randomized studies, as summarized in the introduction. Although it is tempting to conclude that the effect is additive in character (i.e., three years of treatment equals 3 times the effect), this conclusion may be overly simplistic, given the (intended) variation in instructional support. All treatment students received at least one year of intensive reading instruction (Tier 2 in year 1), but only a subsample received multiple years and only when such was warranted, based on prior response. This fact suggests that trends at the extremes of the distribution (the low extreme in this case, given the sample demographics) were constrained in the treatment condition by the tiered nature of the intervention and that this constraint may have a role in the treatment's effect.

Consistently low-achieving students received intensive intervention for the duration of the treatment period, and responding students who no longer required similar levels of support (i.e., after achieving response benchmarks) were routed into a BaU setting, freeing instructional capacity and allowing for its reallocation. Instructional support became increasingly focused over time as a function of student response, and treated students' instructional responses became less variable, given the need-based access to ongoing support.

Differences in the groups' average slope variances suggest a similar perspective. Although group means do not differ statistically, individual trend lines in the BaU condition may be relatively more variable (${\mathrm{S}}_{\sigma }^2$ = 3.64, p < .01) than trends in the treatment group (${\mathrm{S}}_{\sigma }^2$ = 1.25, p < .12) may be, given that the slope variance in the BaU group differs significantly from 0 and the value in the treatment group does not differ statistically from 0. Variation in intercept also is greater in the treatment condition (although not statistically so), suggesting that the treated group transitioned from a state of relative diversity (more variable than the BaU group at time 1) to an increasingly less disparate pattern. The BaU group, meanwhile, became increasingly diverse (relative to the treatment condition) in terms of achievement status at any given point, as indicated by individual trends in these data and consistent with normative patterns.

A systemic and long-term approach to instructional decision making and delivery appears to accompany an increasingly consolidated pattern of student achievement, in which rates of progress in the treatment group are more similar (i.e., less variable) across individuals than in BaU. A handful of students in the latter group made progress, but their success was the exception rather than the rule. This pattern might be less desirable in a group of typical readers, to the extent that it constrained the achievement of more capable students. However, in the group of low- and very low-performing older readers, a pattern in which most students make some progress seems preferable to only some students making some progress.

In sum, the treatment group outperformed a relatively robust BaU group. To the degree that the integrity of the original randomization was maintained across the three-year period and selection bias was minimized, participation in the treatment condition may be responsible for increases in average achievemen,; and there is a basis for suggesting that the tiered, response-based aspect of the intervention made a meaningful contribution to the overall effect.

Closing the Gap

Treated students also outperformed the group of typical readers when achievement was characterized in terms of slope over time; the average slope estimate for students originally randomized into treatment was statistically greater than slope in the group of typical readers. Average slope in the BaU group did not differ from the trend in the typical-reader group, which is unsurprising, given that typical and struggling students were from the same middle schools. The important point is that although the treatment group made progress in relation to both the randomized BaU group and the group of typical readers, a considerable gap remained at the end of eighth grade between typically achieving readers and the group of treatment condition students.

To sustain the middle school RTI model outlined in this article (a sustainability perspective as opposed to an implementation perspective), the following investments would be necessary: salary and benefits for instructional interventionists, budget to replenish consumable instructional materials, and time and staffing for ongoing professional development. Of these costs, those for instructional interventionists will represent the largest likely addition to typical middle school budgets (instructional materials and training and professional development are critical, but we assume that related costs are similar to existing expenditures and likely to be included in existing building- or district-level budgets).

About four interventionists per grade level (total of 12) would be needed to continue accommodating the number of students served in this study, bearing in mind that student numbers in any given school year depend on the effectiveness of prior instructional tiers and that the student numbers in this article were driven largely by prior response and partly by the need to control costs. This estimate assumes about 210 students in Tier 2 (grade 6), 85 in Tier 3 (grade 7), and 32 in Tier 4 (grade 8). Tier 2 has a 10:1 average student:teacher ratio, requiring 21 classes, or about five per day per interventionist. Tier 3 is 5:1 on average, meaning about 17 classes daily. Tier 4 is 3:1 and would involve 16 classes, or about four per interventionist. The cost per interventionist varies by school and could be assumed on an hourly basis. To provide this level of support across all three years would cost approximately the equivalent of 10 full-time teachers.

The findings do not rule out the possibility of the treatment group catching up to the group of typical readers by the end of 12th grade (if the lines in Figure 2 are extrapolated according to their current trajectories, the projected performance of treated students and typical readers is comparable by the end of 12th grade), although the likelihood of such is remote in normal high school settings, given challenges related to its reliable implementation, including the need for individualized intervention, frequent progress monitoring, and data-driven decision making. Even under very well-funded, highly structured circumstances, a scenario of closing the gap would require (at least) secondary-grade reading interventions as comprehensive as the program described earlier in this article, along with considerable professional development, ongoing coaching, and (possibly) a repurposing of some structures that typify U.S. high schools (i.e., scheduling, credits toward graduation, teacher training, etc.). A much more reasonable proposal is to intervene with at-risk students at points before grade 6. Although older struggling readers appear to benefit from response-based intensity compared with a group of comparably struggling peers, the gains represent only a narrowing of the gap with the group of typical readers rather than a closing of the gap.

Group Differences

There were virtually no differences in effects across subgroups, including girls, English learners, and students receiving special education services, nor were there achievement differences related to status at time 1. This finding is encouraging but subject to several caveats. First, the subgroups in question were not systematically randomized to treatment, so the absence of differences may be more reliably interpreted in a correlational, rather than a causal, context. Second, the sampled population is students at risk, suggesting less overall variability and fewer differences within and between subgroups, at least for students receiving special education and perhaps for the group of English learners (although the underlying relationship between general risk for reading failure and specific risk due to English learner or special education status is likely to differ for the two groups). The patterns reported in this study may not represent trends in more broadly drawn samples of middle school students.

Future Research

Group-randomized designs (vs. subject-randomized designs) may be a reasonable next step for considering the effects of tiered delivery models, particularly in a scaling-up context. Schools would be the appropriate level for randomization, to the extent that the school-level features that characterize similar models in elementary schools (e.g., universal screening, movement into and out of instructional groups based on need) also are present in middle schools (to the extent that the approach represents a schoolwide model). For studies using a within-school design, there may be interest in regression discontinuity methods, with measures of risk status serving as cut scores. Although recent research (Shadish, Galindo, Wong, Steiner, & Cook, 2011) suggests that randomized and cut score assignment may provide comparable estimates of effect, a regression discontinuity model may be an easier sell in schools when intervening with at-risk students.

The reading program used in this study was integral to the project; however, its unique effect, independent of the response-based, tiered model, could not be estimated (although we summarize earlier studies that document its efficacy). An alternative evidence-based program may have achieved similar or better results. Relatedly, although additional time and attention was the basis for increasing instructional intensity, simple attentional effects (i.e., benefits of additional time and attention independent of how the time is spent) are highly unlikely. Research clearly indicates that poor readers learn to read when taught to read and that some approaches to teaching reading are more efficacious than others. We stress this latter point, particularly as it relates to response-based models. Using smaller groups or providing additional instructional time improves student outcomes only to the extent that these more intense opportunities are used well. In the absence of evidence-based intervention, providing greater instructional intensity during the school day may be counterproductive and even wasteful.

Accordingly, greater insight is needed into the relative benefits of instructional intensity versus instructional programming. A good deal is known about the necessary features of effective reading instruction. An evidence base also supports the effects of increased intensity for struggling readers. However, this latter line of inquiry is confounded, necessarily, with the instructional program used to estimate the effects of greater intensity because the same reading program is used across different levels of intensity in the relevant studies. More instructional time and smaller instructional groups may affect students' reading achievement; alternatively, the instructional program used to examine the impact of increased time and smaller groups may be the more potent ingredient in such studies. Effects for increased instructional time may be better described as effects for increased instructional time when the added time is used effectively.

Future research can help untangle this confound by manipulating instructional components and features of instructional intensity (multiple experimental manipulations) to estimate the unique effects of each as well as the nature of their joint effect (e.g., additive, multiplicative). These conditional relationships (between intensity and instruction), assuming such, may further depend on learner differences. For example, older struggling readers may benefit from interventions with embedded motivational features delivered in medium-sized groups over multiple years, and younger struggling readers may require less lengthy interventions, benefit more from smaller group sizes, and benefit less from extrinsic sources of motivation. This conceptualization represents an aptitude–treatment interaction design.

Although the history of aptitude–treatment interaction designs is not encouraging, recent advances in statistical modeling suggest new possibilities. Latent class modeling, for instance, can empirically specify distinct subgroups within a larger sample, improving the precision with which aptitude groups are identified (vs. use of an arbitrary cut score) and increasing the likelihood that given treatments have a differential effect. On a related note, the Response to Intervention model described in this article is only one of several reasonable alternatives for use in the middle grades. For example, Fuchs, Fuchs, and Compton (2010) argue in favor of placing struggling middle school students in more intensive interventions sooner rather than later, based on the severity of the students' reading problems. Future work could address the relative merits of different normative program models.

Finally, there may be value in attempting to contrast the status of eighth-grade students who are similar in the fall of first grade but differ in the timing and pattern of reading intervention as a means of quantifying the benefits of early intervention (or prevention) compared with later-onset approaches (i.e., remediation). Although prospective randomized approaches may be untenable in this respect, the importance of the related questions and the potential consequences of their findings—to policymakers, funders, and practitioners—may warrant less rigorous approaches, including secondary analysis of high-quality extant databases.

Limitations

Accurately following samples across school years can be difficult, and maintaining the integrity of randomized groups across multiple years represents an even greater challenge. Overall attrition can compromise a study's external validity and erode the power to detect treatment effects, and in randomized designs, differential attrition can introduce bias and threaten the internal validity of parameter estimates. As a result, multiyear experimental studies in schools that preserve the integrity of an originally randomized structure are rare, and internally valid studies that consider the multiyear effects of interventions for middle school struggling readers are not available in the extant literature.

Overall attrition was considerable in the present study, although a sizable proportion was planned, as described elsewhere in this article. As a general evaluation of its effects, the model was refit, using list-wise deletion rather than a full information maximum likelihood (i.e., including only cases with data at all timepoints). Intercept in the treatment group (n = 90) was 2.02 (p > .05), and slope was 6.03 (p < .001). Slope in the BaU (n = 22) was 3.64 (p > .05). The quadratic in the treatment group was −.60 (p < .001). In the BaU, the estimate was −.27 (p > .05). When intercept was fixed at 0 across conditions, the slopes were 3.09 in the BaU group and 6.04 in treatment. The quadratic terms were −.17 (p > .05) in the BaU group and −.60 (p < .001) in the treatment group. These parameter estimates are very similar to the estimates in Table 2 and represent trajectories similar to the trends in Figure 2.

Differential attrition was also present, as outlined earlier. The potential source of bias in this case was the apparent difference in the percentage of African American completers in the BaU and treatment groups, with relatively more African American students in the BaU group completing the three-year study. To the extent that the reading achievement of struggling African American students differs generally from the achievement of struggling readers of other ethnicities, selection bias may be evident. It is worth noting, however, that more than half of the sample was African American, increasing the likelihood of detectable differences in attrition (i.e., greater power in the differential attrition analyses). Further, preliminary meta-analytic evidence suggests that the degree of overall or differential attrition may be less related to baseline comparability and to posttest effect size than previously suspected, findings that held under sensitivity analyses (Valentine & McHugh, 2007).

Conclusion

A response-based, tiered model for supporting the reading achievement of struggling and at-risk students appears to benefit participants when combined with evidence-based, efficacious reading interventions. Implementing such models is challenging, particularly in middle schools. Ongoing research should consider strategies for making implementation more feasible, supporting ongoing fidelity, and building and maintaining capacity for its effective use.