Abstract
Research on the development of reading skills through the primary school years has pointed to the importance of individual differences in initial ability as well as the growth of those skills. Additionally, it has been theorized that reading skills develop incrementally. The present study examined the genetic and environmental influences on two developmental models representing these parallel ideas, generalizing the findings to explore the processes of reading development. Participants were drawn from the Florida Twin Project on Reading, with a total of 2370 pairs of twins’ representative of the state of Florida. Twins’ oral reading fluency scores from school progress monitoring records collected in the fall of grades 1 through 5 were used to model development. Results suggested that genetic influences on the development of reading are general, shared across the early school years, as well as novel, with new genetic influences introduced at each of the first three years of school. The shared environment estimates suggest a pattern of general influences only, suggesting environmental effects which are moderate and stable across development.
Keywords: growth, simplex, oral reading fluency, early reading development, genetics, environments
Learning to read is a complex and cumulative process, beginning in early childhood and continuing through the school years. Reading skills in the early elementary years are commonly found to be significant predictors of later reading skill, even above other aspects of general cognition (Cunningham & Stanovich, 1997; Muter et al., 2004; Schatschneider et al., 2004). Normative patterns of development are commonly noted (e.g., Chall, 1983), however there is considerable variability in reading skill when children enter into formal education and in how they progress through school (Parrila et al., 2005; Storch & Whitehurst, 2002). Previous work has suggested that there are numerous potential sources of this variability in reading skills, including cognitive processes (Wagner & Torgesen, 1987), genetic influences (Harlaar et al., 2007; Petrill et al., 2012), and environmental sources such as socio-economic status (Sirin, 2005) and classroom effects (Taylor et al., 2010).
The development of reading is most commonly described using two types of developmentally sensitive longitudinal models: exploring individual differences in growth over time through latent growth curve modeling and exploring individual differences in occasion-to-occasion transmission through simplex modeling (e.g., Bast & Reitsma, 1997). These models are often used from an either/or perspective as they approach modeling development from different perspectives, although the findings from the models can be viewed as providing complementary information. Latent growth curve modeling views reading development as a continuous process that can be modeled throughout the range of time that is being examined. Once that process is adequately modeled, predictors (e.g., genetic and environmental influences) can be added to the model that attempt to explain the process as a whole (Francis, Schatschneider, & Carlson, 2000). This type of modeling can be used to describe potential cumulative development, or the extent to which initial ability in reading has a subsequent developmental effect on later years of reading performance (Aunola et al., 2002). Simplex modeling, in comparison, describes reading development as occurring in increments, where change relies on the relative position of each individual over an increment of time. It models this change based upon previous skill but has the potential for examining novel influences that may explain incremental change in reading that can occur from time-point to time-point (Jöreskog, 1979; Parrila et al., 2005). This potential for time-point to time-point change describes a more dynamic, or incremental, view of the development of reading.
Considerable work has explored these two developmental patterns in reading. It has been suggested that there is rank-order stability in mean growth based on initial status of reading skill but also individual differences in the rate of growth in children’s reading (Campbell et al., 2001; Foorman et al., 1998; McCoach, O’Connell, Reis, & Levitt, 2006). Individual differences in the growth pattern of reading through the school years indicate a slowing of annual gain through the early elementary to middle school years (Francis et al., 1996). Work has also suggested that there can be year-to-year specific effects on the individual differences of reading development (Bast & Reitsma, 1997; Leppanen et al., 2004; Stanovich, 1986; Wagner, et al., 1997). For instance, reciprocal development and mastery of component reading skills punctuating reading development (Leppanen, et al., 2004), the effect of reading education (Chall, 1983) or the effect of an individual teacher in a given school year (Connor et al., 2007; National Reading Panel, 2000), are all examples of potential sources of this dynamic relationship. Taken together this work suggests that there are individual differences in children’s reading growth through school, including both cumulative development and that which is more dynamic.
Twin studies have recently used quantitative genetic methodologies to further explore the etiology of individual differences on the development of reading. From an Ohio twin sample, Petrill et al. (2010), using latent growth curve modeling, suggested significant genetic and environmental influences shared within a twin pair (named the “shared environment”) affect initial reading status, and weak and mostly non-significant genetic and strong shared environmental influences affect the growth of reading. Logan et al. (in press) extended the linear model of Petrill et al. (2010) to examine the potential for curvilinear growth (e.g., Hill et al., 2008). Logan et al. found that change and deceleration of word reading skills were influenced by both genetic and environmental influences when accounting for curvilinear growth, slightly differing from Petrill et al. (2010). Recent work from a Colorado twin sample has also presented growth curve modeling results for word list reading fluency, reading comprehension and spelling (Christopher et al., in press). Using growth curve models with correlated residuals as the best fitting model, this work suggested genetic effects on the intercept and growth factors, with nonsignificant effects due to the shared environment. However, the authors also presented results more closely mapping onto the uncorrelated models presented by the Ohio project, and the results for word list reading fluency in this model also indicated shared environmental effects for the slope.
Also, initial quantitative genetic work has begun to explore the dynamic nature of reading using a Cholesky decomposition, a model which estimates all possible genetic and environmental relationships among time points (e.g., Harlaar, Dale, & Plomin, 2007). More specifically, a Cholesky decomposition is similar conceptually to a hierarchical multiple regression in a structural equation modeling framework. In a Cholesky decomposition with longitudinal data, for example, genetic and environmental relationships with the second time point are estimated after controlling for the first time point, and genetic and environmental relationships with the third time point are estimated after controlling for the previous two time points, and so on. Therefore, a longitudinal Cholesky decomposition serves as a starting point for understanding relationships across measurement time points. In general, the previous literature using longitudinal Cholesky decompositions has indicated a trend of genetic, and possibly to a lesser extent shared environmental effects, contributing to the stability of reading in both early and middle childhood (Byrne et al., 2007; Harlaar et al., 2007; Wadsworth, DeFries, Olson & Willcutt, 2007). Additionally, some of this previous work also suggested age-specific genetic influences outside of the general stable genetic influences (Byrne et al., 2007; Harlaar et al, 2007). Moving beyond the Cholesky, a simplex model allows for testing developmentally driven hypotheses based on the genetic and environmental influences on the stability and instability of reading development. The Cholesky and simplex models with two time points can be interpreted in the same way, but any additional time points separate the two models. With more than two time points, a Cholesky allows for all possible relationships between the time points to be estimated, which results in variance being attributed to relationships that are not as developmentally meaningful (e.g., the genetic effects of grade 1 on grade 5). Instead, the simplex model allows for a more meaningful interpretation of the data, estimating pathways that are developmentally relevant. Just as no child goes from grade 1 directly to grade 5, the simplex model replicates the trajectory of children through school, examining the genetic and environmental influences from each grade to the next. Despite this, no work using a genetically sensitive simplex model to explore the development of reading could be found, although it is commonly used in other areas of human development (e.g., Vasilopoulos, et al., 2010).
The primary goal of this study was to examine the genetic and environmental influences on the development of oral reading fluency from grades 1 through 5. Oral reading fluency, or rapid and accurate reading of connected text, requires both word-level reading as well as reading words in context (Jenkins, Fuchs, Van den Broek, Espin & Deno, 2003; Stanovich, 1980). Oral reading fluency has been highlighted as an efficient and reliable measure of reading skill in the primary grades (Roehrig et al., 2008), with indications of it having a high association with reading comprehension (e.g., Roberts, Good, & Corcoran, 2005). Given its importance as a measure of children’s progress through the education system (Fuchs, Fuchs, Hosp, & Jenkins, 2001), there has been considerable efforts made towards understanding the nature of the development of oral reading fluency (e.g., Kim et al., 2010). Behavioral genetics work examining the etiology of oral reading fluency is limited. One report on 10 year old twins in Ohio suggested that oral reading fluency is highly genetically influenced with no shared environmental effect (h2 = .82, c2 = .00; Hart et al., 2010). Work from the present sample examining oral reading fluency at the end of grade 1 indicated high genetic influences (h2 = .62), and low but significant shared environmental influences (c2 = .22; Taylor & Schatschneider, 2010). Overall, work using twin samples suggests that oral reading fluency is highly genetically influenced and to a lesser extent influenced by the shared environment.
This study will be the first to explore both genetically sensitive latent growth curve modeling and simplex modeling approaches to the development of reading, as previous work has been limited to latent growth curve modeling (Christopher et al., in press; Logan et al., in press; Petrill et al., 2010), and Cholesky decomposition modeling (e.g., Harlaar et al., 2007). This is important because even though previous work has highlighted the influence of genetics and environment on the mean growth of reading, there is only preliminary work exploring when novel genetic and environmental influences appear during the early school years. Importantly, there is a general shift in how reading is taught in elementary school, a move from “learning to read” (i.e., learning the key mechanics of reading) to “reading to learn” (i.e., using reading to learn other subjects with no explicit reading instruction) in third grade (Chall, 1983). For oral reading fluency, this shift may occur specifically as decoding becomes more automatic (e.g., Roberts, Good, & Corcoran, 2005). Previous work has indicated that it may be the case that there are stable genetic influences (Wadsworth et al., 2007) as well as unique genetic influences at age-specific time points through this shift (Byrne et al., 2007; Harlaar et al., 2007). However, this has yet to be explicitly tested using a simplex model, which specifically models developmental stability and time specific novel effects. Beyond this, the present sample is from a racially, ethnically and socioeconomically diverse twin project (see Taylor & Schatschneider, 2010, for an initial report from this project), allowing for greater generalizability from this study than previously available in the literature (e.g., Petrill et al., 2010).
We propose to use both a latent growth curve model and simplex model in concert, comparing and generalizing findings across both. This work will explore the genetic and environmental influences on the continuous growth of reading skill, as well as those which may contribute to the dynamic nature of reading development (Bast & Reitsma, 1997). Given methodological concerns and theoretical implications of using only a latent growth curve or simplex model (Bast & Reitsma, 1997; Kenny & Campbell, 1989; Stoolmiller & Bank, 1995), the use of both models in the present study offers a methodological improvement over prior designs. Finally, this work will be done in a twin sample which reflects the diversity of Florida. Given the previous literature, we hypothesize that there will be genetic and shared environmental influences on the intercept and growth terms of the latent growth curve model, and that these genetic and environmental influences will covary. Moreover, we hypothesize that the simplex model will suggest initial genetic and environmental effects which are transmitted across the grades with additional novel genetic influences seen in individual grades, most likely the earlier school years of active instruction in reading. Given the previous literature’s finding that the shared environment contributes primarily to the stability of reading (e.g., Harlaar et al., 2007), we do not expect to find novel shared environmental influences in individual grades.
Method
Participants
The Florida Twin Project on Reading is a cross-sequential study that ascertains progress monitoring and achievement data for reading via Florida’s Progress Monitoring and Reporting Network (PMRN), a statewide educational database (Taylor & Schatschneider, 2010). For the current report, reading data were collected over the 2003–2004 through 2008–2009 school years from 824 monozygotic (MZ; 419 female-female pairs, 405 male-male pairs) and 1546 dizygotic (DZ; 369 female-female pairs, 399 male-male pairs, 778 opposite-sex pairs) twin pairs. According to parent report, 19% of the twins were African American, 24% were Hispanic, 50% were White, and the remainder was mixed or other race/ethnicity. These percentages are very similar to those reported for the state of Florida by the U.S. Census Bureau. Consistent with data reported by the Florida Department of Education for the entire state of Florida, 53% of the present sample qualified for the U.S. Free or Reduced-Priced Lunch program. To maximize representativeness, no twin families are excluded from the project for any reason, including English as a second language status (approximately 20% of the total sample is identified as English as a second language status by the children’s school).
Due to the cross-sequential nature of the study and data collection procedures, data were not available for all twins at all time points. All available data for each grade were analyzed and the number of twins available for analyses at each grade level is presented in Table 1. Twins were approximately seven years old at the beginning of grade 1 (M=6.74, SD=.48).
Table 1.
Descriptive statistics, intraclass correlations, and biometric univariate estimates of genetic (h2), shared environmental (c2) and nonshared environmental (e2) components of variance, and confidence intervals [in brackets], for all grades of Oral Reading Fluency.
| Variable | Descriptive Statistics
|
Intraclass Correlations
|
Univariate Estimates
|
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | SD | Min. | Max. | n | MZ
|
DZ-S
|
DZ-OS
|
h2 | c2 | e2 | ||||
| r | n | r | n | r | n | |||||||||
| Whole Sample | ||||||||||||||
| ORF grade 1 | 26.94 | 27.55 | 0 | 182 | 1396 | 0.82 | 486 | 0.47 | 468 | 0.45 | 442 | .85* [.75–.94] | 0.01 [.00–.12] | .14* [.13–.16] |
| ORF grade 2 | 74.74 | 37.60 | 0 | 220 | 1269 | 0.85 | 447 | 0.59 | 416 | 0.48 | 406 | .63* [.54–.73] | .22* [.12–.32] | .15* [.13–.17] |
| ORF grade 3 | 91.10 | 37.10 | 0 | 239 | 896 | 0.85 | 303 | 0.60 | 295 | 0.51 | 298 | .56* [.45–.67] | .28* [.16–.40] | .16* [.13–.18] |
| ORF grade 4 | 101.68 | 33.78 | 0 | 196 | 287 | 0.82 | 108 | 0.52 | 83 | 0.45 | 96 | .65* [.42–.89] | 0.16 [.00–.39] | .19* [.14–.25] |
| ORF grade 5 | 122.32 | 38.93 | 27 | 248 | 134 | 0.73 | 48 | 0.30 | 42 | 0.48 | 44 | .71* [.35–1.01] | 0.09 [.00–.42] | .20* [.14–.33] |
| Selected Subsample | ||||||||||||||
| ORF grade 1 | 30.91 | 29.42 | 0 | 182 | 731 | 0.80 | 226 | 0.42 | 269 | 0.45 | 236 | 0.85* [.70–.94] | 0.00 [.00–.14] | 0.15* [.14–.20] |
| ORF grade 2 | 79.34 | 38.35 | 0 | 220 | 631 | 0.85 | 208 | 0.53 | 214 | 0.50 | 209 | 0.67* [.53–.82] | 0.19* [.04–.33] | 0.14* [.12–.18] |
| ORF grade 3 | 95.12 | 37.20 | 0 | 239 | 430 | 0.86 | 137 | 0.55 | 143 | 0.42 | 150 | 0.67* [.50–.85] | 0.17 [.00–.34] | 0.16* [.12–.19] |
| ORF grade 4 | 105.80 | 32.08 | 9 | 184 | 160 | 0.86 | 56 | 0.53 | 48 | 0.38 | 56 | 0.66* [.38–.95] | 0.17 [.00–.46] | 0.17* [.11–.24] |
| ORF grade 5 | 126.89 | 36.68 | 27 | 224 | 76 | 0.78 | 25 | 0.28 | 24 | 0.32 | 27 | 0.79* [.35–1.11] | 0.00 [.00–.00] | 0.21* [.13–.38] |
Note. Descriptive data represent the total number of words read correctly in a minute. The Selected Subsample are those self-identified as White. n’s refer to pairs of twins.
indicates significance as calculated through 95% confidence intervals which do not bound zero.
Procedure and Measures
Zygosity was determined via a parental five-item questionnaire on physical similarity obtained during intake of the twin families into the project (Lykken et al., 1990). Trained testers administered progress monitoring measures as part of normal school attendance and all scores were entered into the PMRN web-based data collection system. Scheduled administration of measures was determined by the Florida Department of Education and local school districts. In the present analyses, the first administration of oral reading fluency for each grade was used, typically given within a 45 day window beginning in September.
Oral Reading Fluency (ORF)
Dynamic Indicators of Basic Early Literacy Skills (DIBELS; Kaminski & Good, 2003) ORF was used to measure accuracy and fluency with connected text. Students read grade-level calibrated passages aloud for one minute. Fluency rate is assessed as the number of words read correctly in one minute. Reported parallel forms reliability (.94) and predictive criterion-related validity (.78; October to May) with the Woodcock-Johnson Basic Reading Skills Cluster score demonstrate the technical adequacy of the measure (Speece & Case, 2001).
Statistical Analyses
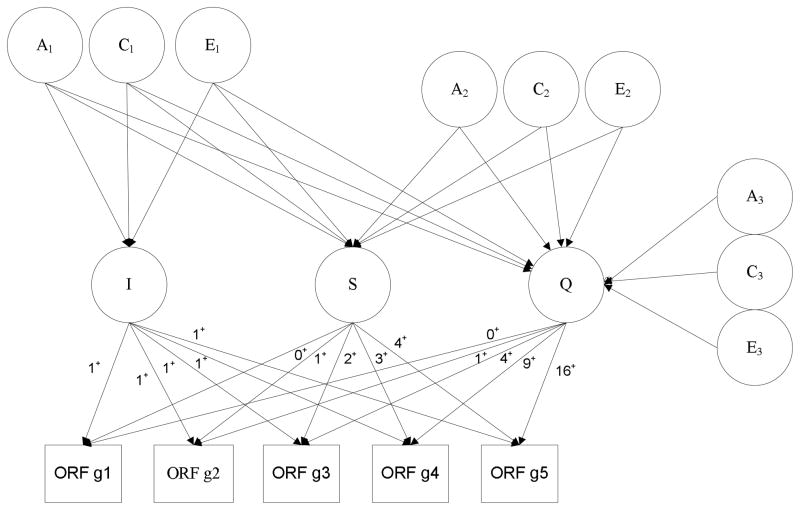
The primary goal of this study was to examine the development of reading during elementary school. To do so, three separate models were analyzed. Latent growth curve models were first fit to the phenotypic (non-genetic) data to determine the best fitting growth line to inform subsequent genetic analysis. Following the results from the phenotypic latent growth curve models, a quantitative genetic latent quadratic growth curve model was estimated. This allowed for an estimation of the additive genetic (A; genetic influences which are directly inherited from one’s parents), shared environmental (C; environmental influences which make siblings more similar to each other) and nonshared environment (E; environmental influences which make siblings unique) on where children start school (intercept), rate of growth through school (linear slope) and change in the rate of growth (quadratic slope; see Figure 1). This model also estimates the genetic and environmental influences on the covariance among the intercept, linear slope and quadratic slope terms. From the quadratic growth curve model, the effect of genetics and environments on the general growth pattern of individuals can be explored.
Figure 1.
Quantitative genetic latent quadratic growth model of five grades of Oral Reading Fluency. I = intercept, S = linear slope, Q = quadratic slope. A parameter value with a + sign indicates that the parameter was fixed at that value.
Finally, a quantitative genetic simplex model was applied to the data, allowing for an exploration of the stable and novel genetic and environmental influences across the early school years (Boomsma & Molenaar, 1987). More specifically, a simplex model estimates the influences on a given time point attributable to the previous time point (called “transmission”), as well as new influences unique to that time point (called “innovation”; see Figure 2). Using quantitative genetics methodology, the covariance between years as well as the unique variance within a year can be separated into genetic, shared environment and nonshared environment influences (Neale & Cardon, 1992).
Figure 2.
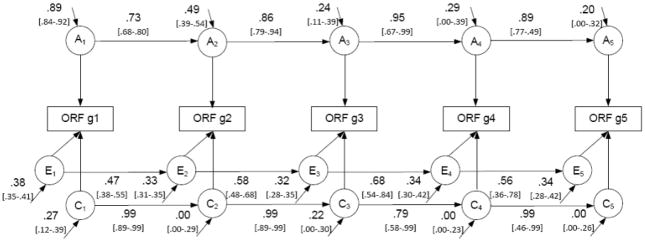
Quantitative genetic simplex model of five grades of Oral Reading Fluency (ORF), with path estimates and confidence intervals [in brackets]
The initial phenotypic growth model was conducted with all available raw data using Mplus software (Muthén & Muthén, 1998–2004). Model comparisons tests were used to determine the best fitting model (Hu & Bentler, 1999). Subsequent quantitative genetics modeling was done in Mx with all available raw data, with 95% confidence intervals to test for significance (i.e., confidence intervals which do not bound zero are significant; Neale et al., 2006). Raw data were used for the quantitative genetic quadratic growth curve modeling, with ORF scores from fall of first grade used to center the intercept. Z-scored data were used for simplex modeling. No mean or variance differences were found in ORF performance between boys and girls in the sample. Furthermore, a multigroup sex-limitation model of ORF scores testing gender effects was fit to the data at each grade and the variance across gender could be completely constrained for all grades, indicating that it was appropriate to combine male, female, and opposite-sex twins in analyses (results available from first author upon request).
Results
Phenotypic development of reading
Descriptive statistics for each grade of oral reading fluency (ORF) are presented in Table 11. Due to the uniqueness of this twin sample in its racial and ethnic diversity, to better facilitate comparison to other twin samples all data in Table 1 is also displayed on a subsample consisting of families self-reporting as “White” only. Twin intraclass correlations for each grade of ORF (monozygotic, dizygotic same-sex, and dizygotic oppostive-sex twin pairs), a descriptive method for estimating genetic and environmental influences, are also displayed in Table 1. In general, the extent to which monozygotic (MZ) twin intraclass correlations are greater than dizygotic (DZ) twin intraclass correlations (for both same-sex and opposite-sex pairs), additive genetic influences (or heritability; represented by h2) can be inferred. The extent to which the difference between MZ and DZ intraclass correlations is less than half indicates shared environmental influences (environmental effects which serve to make family members more similar; represented by c2). Finally, the extent to which MZ twin intraclass correlations are less than unity indicates nonshared environmental influences (environmental effects which serve to make family members less similar, including error; represented by e2). Additionally, Table 1 presents biometric univariate estimates of additive genetic, shared environmental, and nonshared environmental effects for each year of ORF scores, as calculated by structural equation modeling. In general, estimates across both intraclass correlations and structural equation modeling suggested a pattern of high and significant estimates of heritability and low estimates of the shared environment for the whole sample, with similar results for the selected subsample.
Pearson correlations of oral reading fluency (ORF) among the grades are presented in Table 2. In general, all correlations were moderate to high, and significant. There was a trend towards a decreasing magnitude of correlation for further apart testing periods.
Table 2.
Pearson correlations among all grades of Oral Reading Fluency (ORF).
| Variable | ORF grade 1 | ORF grade 2 | ORF grade 3 | ORF grade 4 | ORF grade 5 |
|---|---|---|---|---|---|
| ORF grade 1 | 1.00 | ||||
| ORF grade 2 | .76* | 1.00 | |||
| ORF grade 3 | .64* | .87* | 1.00 | ||
| ORF grade 4 | .52* | .81* | .88* | 1.00 | |
| ORF grade 5 | .57* | .77* | .86* | .88* | 1.00 |
Note.
p< .001
The phenotypic growth model indicated that randomly varying linear and quadratic growth was the best fit to the data (χ2(4)=267.21, p<.001; CFI .95; SRMR .03). Although, a non-significant chi-square value is preferred, this statisticis highly sensitive to large sample sizes and should be evaluated with caution. Investigation of alternative measures of model fit, specifically the comparative fit index (CFI) and the standardized root mean squared residual (SRMR) indicated adequate model fit (Hu & Bentler, 1999). The parameter estimates for the final model reported an intercept of 26.55, a linear slope of 54.10, and a quadratic slope term of −9.39. The positive linear growth term and negative quadratic growth term suggest that while the general trend of growth was positive across the five time points, there was also a significant deceleration effect as children advanced through school. More specifically, growth in oral reading fluency was the fastest in first grade, and decelerated as the students moved through elementary school.
Quantitative genetic development of reading
Latent growth curve modeling
For this model, latent factors of intercept, linear slope and quadratic slope were estimated, and the variance and covariance among the factors was decomposed into estimates of genetic (represented by A1, A2, and A3 in Figure 1), shared environmental (C1, C2, and C3), and nonshared environmental (E1, E2, and E3) effects. Age at grade 1 was modeled as a definition variable in Mx (Neale, et al., 2006). Using a definition variable in Mx allowed for initial age of assessment to be controlled for within assessment point while also accounting for the effect of age on the covariance among the assessment points. It is important to note that by allowing for randomly varying curvilinear growth, it implies that each individual’s instantaneous rate of change can vary throughout the developmental period under study. Therefore it is crucial to evaluate estimates of heritability, shared environmental, and nonshared environmental influences at specific points in time across the temporal range of the data. To that end, we examined the genetic and environmental influences on instantaneous change (the linear term) at each age point (by re-centering age at each time point). Because the estimates of heritability and environmental influences were relatively stable across each time point, we have chosen to present the results when age is centered at the first grade.
Estimates of genetic, shared environmental and nonshared environmental components of variance and covariance on and among the intercept, linear slope and quadratic slope factors are presented in Table 3, with confidence intervals indicating significance. Model fit parameters for the model were −2LL = 57479.19, AIC = 44747.19, df = 6366. Univariate estimates of heritability, shared environment and nonshared environment for each of the latent factors estimated are displayed on the diagonal. Results suggest that heritability for the intercept factor was high and significant (h2=.87), and the shared environmental estimate was non-significant (c2=.09). Heritability and shared environmental estimates for the linear slope factor were moderate and significant (h2=.42, c2=.53). Finally, heritability for the quadratic slope factor was low and significant (h2=.33), and the shared environmental effect was moderate and significant (c2=.66). For all factors, the estimates of nonshared environmental influences were small but significant (e2=.02–.05).
Table 3.
Estimates and confidence intervals [in brackets] for genetic and environmental components of variance from the quantitative genetic latent quadratic growth curve model.
| A1 | A2 | A3 | C1 | C2 | C3 | E1 | E2 | E3 | |
|---|---|---|---|---|---|---|---|---|---|
|
|
|||||||||
| Intercept | .87* [.76–.97] | .09 [.00–.20] | .04* [.02–.06] | ||||||
| Linear Slope | .21* [.07–.35] | .42* [.21–.65] | .08 [−.05–.20] | .53* [.31–.72] | .04* [.01–.31] | .05* [.02–.11] | |||
| Quadratic Slope | −.36* [−.48– −.19] | −.33* [−.60– −.13] | .33* [.12–.66] | −.10 [−.25–.05] | −.59* [−.77– −.32] | .66* [.32–.86] | −.02 [−.05–.00] | −.03 [−.09–.00] | .02* [.01–.10] |
Note.
indicates significance as calculated through 95% confidence intervals which do not bound zero.
Estimates displayed off the diagonal in Table 3 represent the components of covariance shared between the latent factors attributable to genetic and environmental influences. In general, there was significant covariance attributable to genetic influences among all the factors. For shared environmental influences, there was significant shared environmental covariance between the two slope factors only (−.59). Nonshared environmental covariance estimates between the intercept and linear slope only (.04) were small and significant.
Simplex modeling
Pathway estimates from the simplex model are displayed in Figure 2, with confidence intervals in brackets. Model fit parameters for the model were −2LL = 15794.56, AIC = −37.44, df = 7916. Genetic innovations were significant for the first three years of ORF testing, but non-significant for grades 4 and 5. Genetic transmission pathways were high and significant across all time points. For the shared environmental results, only the innovation at grade 1 was significant, but transmission path estimates were high and significant across the grades. Finally, all nonshared environmental innovation and transmission pathways were small to moderate and significant.
Discussion
The main goal of this study was to explore parallel developmental models to determine the pattern of growth and change in oral reading fluency through the early elementary school years when learning to read transitions into reading to learn. Genetically sensitive latent growth curve and simplex models were examined using oral reading fluency data from grades 1 through 5, with developmental models used to examine the genetic and environmental influences on the cumulative and dynamic change across the years.
Latent quadratic growth curve model
There are two aspects of the results from the latent growth curve analysis of particular interest: the univariate genetic and environmental influences in intercept, linear slope and quadratic slope, and the genetic and environmental covariance among these factors. In general, the univariate genetic influences on the intercept (.87, or 87% of the total variance) were higher than those on the linear and quadratic growth terms (42% & 33%, respectively). Shared environmental influences were only indicated on the growth parameters, whereas nonshared environmental influences were indicated for all three factors.
As for the covariance among the latent growth curve factors, there were common genetic influences between the intercept and linear slope terms, indicated by the estimate of .21. This suggests that of the total covariance between the intercept and linear slope terms estimated by the model (.33 = .21 + .08 + .04), 64% (.21/.33 * 100 = 64%) of the covariance between reading skills at the start of grade 1 and rate of growth in reading skills through grade 5 is attributable to common genetic influences. There was no significant shared environmental influence to the covariance between intercept and linear slope, but there was for nonshared environment (.04/.33 * 100 = 12%).
Common genetic influences were also indicated on the covariance between the linear and quadratic growth terms, represented by the covariance estimate of −.36. It should be noted that the estimate of the covariance is negative because faster growth was associated with more deceleration of growth (this finding was supported by the phenotypic growth curve modeling as well). Therefore, although the negative covariance infers a phenotypic relationship of interest, it is still interpreted the same way genetically, in that 35% [.33/(.33 + .59 + .03) * 100 = 35%] of the covariance between linear slope and quadratic slope is due to common genetic influences. As for the shared environment, the effect on the covariance between the linear and quadratic slope terms was significant (62%). The nonshared environmental influence was nonsignificant.
Finally, the covariance between the intercept and quadratic growth terms indicates that 75% is due to common genetic influences [.36/(.36 + .10 + .02) * 100 = 75%], and the negative direction of this relation indicates that children who started grade 1 with better oral reading fluency showed more deceleration of growth through the elementary school grades. Both environmental effects were nonsignificant.
In total, the latent growth curve results suggest that genetic effects strongly influence children’s reading skills prior to beginning formalized education in reading, as well children’s growth in reading through elementary school. Moreover, to a large part, the genetic influences on initial skill in oral reading fluency also influence growth in reading. These shared genetic influences may be in part indicative of variance associated with genes related to general cognitive processing or related to genes important for the development of reading performance specifically. In contrast, the shared environment only significantly influenced the differential growth rates of reading skills, and not the intercept. These shared environmental estimates on growth may be school related effects, as prior to grade 1 the primary source of shared environment is typically the family home environment. Given that the intercept did not reflect significant shared environmental influences, but the growth factors did, this could suggest that the variance across classrooms and schools is a significant contributor to growth in reading (e.g., Greenwald, Hedges, & Laine, 1996). However, this finding does not necessarily preclude family level influences on the growth of reading. For instance, home environment aspects related to academic achievement (e.g., homework environment; Xu & Corno, 2003) could be contributing novel variance towards the growth of reading, whereas, it could be considered that these influences may be less important to the individual differences in reading at the beginning of grade one. The small nonshared environmental influences are indicative of child-specific environmental influences only (i.e., less the error typically associated with this estimate due to the use of latent factors in this model; Gayan & Olson, 2003), suggesting that child characteristics influenced reading scores at entrance to first grade, as well as independent similar influences on the growth terms, with very little overlap among the factors.
These results are similar in some ways to the previous work done on the Ohio twin sample on the growth of reading (Petrill et al., 2010; Logan et al., in press), in that univariate genetic influences are statistically important for the intercept and growth terms while the shared environment influences growth. However, previous work from Ohio suggested shared environmental influences on the intercept factor as well, which were not indicated in the present work. These present results more closely mirror recent work from Colorado (Christopher et al., in press), which found high genetic effects but small and nonsignificant shared environmental influences on the intercept for growth of word list reading fluency. When using the same growth modeling procedure as the present, Colorado’s results from the growth factors are also similar these results, with genetic and shared environmental influences on the slope and quadratic terms. However, Christopher et al. (in press) presented as the best fitting model a growth curve model of correlated errors, a model with indicated nonsignificant effects due to shared environment on the slope factors. Turning towards the covariance among the growth curve parameters, the present results suggested no shared environmental overlap between the intercept and growth terms, which in previous studies from Ohio demonstrated substantial overlap between these constructs. Similar to the univariate estimates on the growth parameters, the present work more closely resembles the pattern of nonsignificant shared environmental correlations between the intercept and growth factors presented from the Colorado group (Christopher et al., in press).
In total, there are interesting similarities and differences between these results and the Ohio and Colorado samples. Examining grade-to-grade specific univariate genetic and environmental effects, the present sample more closely resembles the Ohio sample in that significant shared environmental influences are indicated over the first few years of formalized reading instruction. Indeed, word-level decoding in the Ohio sample indicates shared environmental influences through grade 3 (Logan et al., in press). Although the univariate shared environmental estimate in the present sample is nonsignificant for the beginning of grade 1, previous work from this project has suggested significant shared environmental influences at the end of grade 1 (Taylor & Schatschneider, 2010), and the present analyses indicates this pattern of significance extends through grade 3. Given this, the differences in the present growth curve modeling from the Ohio sample are most likely due to the lack of univariate shared environmental effects on the grade 1 fall time point in the present analyses. As for the Colorado sample, the grade-to-grade univariate estimates suggest for the most part significant genetic effects and little to no shared environmental effects at any grade (with an exception of post-kindergarten sight word reading). Despite this difference, interestingly the growth curve models from Colorado were more similar to the present work than Ohio was. This may in part be due to the similarity of the intercept time point between the two samples.
Additionally, the differences between the present results and the previous literature may also be due to different measures of reading being explored. Given the developmental pattern of shifting importance in reading skills (e.g., Chall, 1983), it is most likely not the case that the growth of fluent reading of connected text (i.e., oral reading fluency) would be the same as word-level decoding and other reading factors as measured by the Ohio and Colorado samples (Christopher et al., in press; Logan et al., in press). Beyond these measure differences, there are also likely sample differences that are leading to the differences in the results, particularly age differences at the first measurement occasion. This may especially be the case for comparing the Ohio sample, with a greater first time point age spread, to Colorado and the present work, each with a much more narrow age span.
Simplex modeling
With regard to the simplex modeling, results indicated that there were novel genetic influences at the beginning of grade 1 (.89), grade 2 (.49), and grade 3 (.24). The genetic innovations were non-significant for grades 4 and 5. Transmission of genetic influences from one grade to the next were significant and considerable across all the grades, suggesting that although there were new genetic influences on the first three grades of school, there was also a considerable overlap of genetic effects among the years. Interestingly, the magnitude of the innovations decreased from year to year, indicating a trend suggesting that new genetic influences become less important at each assessment point whereas transmitted genetic influences from previous years become more important.
One possible explanation for the large genetic transmission is that the genetic influences associated with the innovation at grade 1 (which represents the cumulative genetic effects on reading coming into grade 1) may have been directly associated with general cognitive processing, and so these genetic influences would continue to be important across the school years. In other words, this initial effect may represent genetic influences on general skills used for learning in school. On the other hand, the genetic innovation at grade 1 followed by the genetic transmission may also be linked with genes important in reading performance specifically. For example, early literacy skills such as phonological awareness may underlie the initial innovation, and the transmission may reflect the developmental importance of these skills to later reading performance, such as decoding followed by reading comprehension. The independent and smaller genetic influences appearing as new innovations in part in grade 1 and then in grades 2 and 3 may be measuring genetic influences associated with specific reading skills that develop incrementally during the early school years (e.g., Chall, 1983), or they may represent novel general processing skills (e.g., related to increased memory demands).
The results of the shared environmental influences from the simplex model indicate that there was only one significant innovation (at entrance to grade 1), with significant transmission of this effect across the years. This result would suggest that the shared environmental influences present at the entrance to formalized schooling, whether they represent home or school level influences, have a large and carrying effect on the development of reading skills, but this effect is singular. In other words, individual years seem to not contribute significant amounts of shared environmental variance above and beyond the general effect throughout school.
Nonshared environmental results in this model can capture any type of error (i.e., this model does not include latent factors) as well as child-specific environmental effects. These results would suggest that measurement and/or sampling error, and possibly child-specific environmental influences, are accounting for the significant innovations at each time point. A possible source of these child-specific environmental influences are classroom influences (e.g., Taylor et al., 2010), as approximately 60% of the twins in this sample are in separate classrooms at any given time point. The results also suggested that there are child-specific influences transmitted across the years. Aspects such as individual reading motivation or interest towards literacy may be associated with the stable nonshared environmental influences measured (Phillips & Lonigan, 2005).
Although no previous quantitative genetic work using a simplex model to explore the development of reading could be found, these results can be compared to similar literature using a Cholesky decomposition over longitudinal time points2. Harlaar et al. (2007) found significant general genetic overlap among teacher ratings of twins’ reading achievement at ages 7, 9 and 10 years, as well as evidence of age-specific genetic influences at each age. The shared environmental results indicated general overlap among the ages, as well as an additional age-specific effect at age 9. In general, the present simplex modeling results mirror the Harlaar et al. (2007) results, in that genetic influences affected the stability of reading, as shown by the genetic transmission across the grades, and that age-specific genetic influences are also important for the learning to read stage. The general shared environmental overlap among the ages in the Harlaar et al. (2007) paper was also similar to the significant shared environmental transmission in the present analyses.
General conclusions across models
Two models of development were explored to determine if the different modeling techniques would suggest similar results (i.e., Stoolmiller & Bank, 1995). The two models together allow for a description of development which encapsulates stable growth of skills that is sometimes interrupted with time-specific influences. The convergence of results across the models, coupled with the large available sample size, suggests that general conclusions concerning reading development may be indicated. Specifically, as we hypothesized, there are common genetic influences underlying initial skill at the beginning of grade 1 which are shared with the development of reading through the elementary years. This is represented by the significant genetic influence on the intercept which overlaps with the growth terms in the growth curve model, and the significant genetic innovation at grade 1 which is then transmitted across the years in the simplex model. This genetic transmission may represent genetic influences specific to reading performance or closely linked cognitive skills (e.g., phonological awareness), or possibly to other traits that are needed to participate in the learning environment in school (e.g., attention). Alternatively, it may be the case that the source of this genetic transference is genetic influences attributable to general cognitive ability, especially given the relative stability of genetic influences on general cognitive ability in childhood (Cardon et al., 1992). Moreover, there is a moderate to large phenotypic relationship between general cognitive ability and reading performance in childhood (r = .30–.70; Naglieri, 2001) as well as a moderate genetic correlation in 7 year olds (rg = .40; Harlaar, Hayiou-Thomas & Plomin, 2005). Determining the source of this variance has important implications, especially for educational researchers attempting to intervene with children who show poor growth in oral reading fluency. For example, if the source of the genetic stability of oral reading fluency is general cognitive ability, educational researchers would create a much different intervention plan that if the source of the genetic stability was reading specific.
Beyond these common genetic effects underlying the developmental process, there are also novel genetic influences which punctuate development in grades 1, 2 and 3 and then carry forward. We hypothesized this would be the case, drawing from previous work (e.g., Harlaar, et al., 2007). Although the simplex model is uniquely able to pick up these dynamic influences, the corresponding result in the growth curve model is the proportion of overlap in genetic influences between the intercept and the growth terms (i.e., 64% and 75% of the covariance). This result may be paralleling what is happening in the literacy classroom during these years, a period called “learning to read” where active instruction in more accurate and fluent word level reading processes is occurring (Chall, 1983). It may be the case that these genetic influences are associated with new specific reading skills (or beginning reading skills for some nonreaders entering into grade 1) that are developing as children matriculate through grades 1 through 3. After these years, active instruction shifts away from the process of reading towards using reading to understand content, called “reading to learn” (Chall, 1983). It may also be the case that these unique genetic innovations are related to general cognitive processing. Furthermore, it would seem that after this shift the genetic variance associated with any further development of oral reading fluency is specific to the accumulation of all previous genetic influences, with no novel effects. This is most likely due to most children becoming fluent word-level readers at this stage.
The shared environment also showed an interesting pattern across the two models. As we hypothesized, shared environmental influences were specific to the general development of reading through the school years, and not necessarily important in defining any specific grade level effects. This conclusion is represented by the univariate effect of the shared environment on the growth terms along with the common shared environmental influence on the covariance among them in the growth curve model, as well as the single innovation at grade 1 transmitting across the years in the simplex model. The two models suggest an overlapping general finding that the shared environment influences how children go through school, but does not seem to be influencing year to year deviations. This is specifically indicated by the lack of significant shared environmental innovations in the simplex model for grades 2 through 5, indicating that the environment does not appear to be as important to grade specific differences. The moderate and consistent shared environmental influence on the development of reading may be due to home environmental influences related to reading outcomes. It could be suggested that in general the home environment is more stable across time than the school environment, which changes year to year. Thus home environment could be reflected in the stable shared environmental transmission identified in the simplex modeling. Also, this shared environmental pattern may also be due to the general processes of being part of formalized education, more specifically with the specific instructional and classroom practices that influence the individual differences of how children interact with the broadly defined school environment. Some work has suggested that the year to year changes in schooling, such as changing classrooms, do not produce a large effect (e.g., Byrne et al., 2010). This suggests that there is little variance in reading development attributable to year to year changes in education, but instead the general influence of being in school on reading outcomes (Greenwald, et al., 1996).
There are three possible limitations to consider with this study. First, there was a reduction in available sample size in grades 4 and 5. This may be contributing to the lack of novel genetic influences on grades 4 and 5 in the simplex modeling. However, the sample available in grades 4 and 5 is approximately the same size as other published work using genetically sensitive designs exploring the development of reading (e.g., Petrill et al., 2010). Notably, the lower sample size available for grades 4 and 5 will not influence the power of the growth curve modeling, which uses all available data for modeling. Second, this study was limited to only one measure of reading due to the lack of other variables available longitudinally in the PMRN. Oral reading fluency represents one component of reading skill, and developmental results may be different for other component reading skills (e.g., reading comprehension; Petrill et al., 2012). However, understanding the developmental pattern of oral reading fluency has practical utility as it is a measure of reading skill that is commonly used in school standardized progress assessments (Fuchs, et al., 2001). Finally, DIBELS ORF passages, including those used in the present sample, have indicated possible form effects, in that difficulty is not uniform across all form administrations (Francis, Santi, Barr, Fletcher, Varisco, & Foorman, 2008; Petscher & Kim, 2011). The present results may be an artifact of individuals getting test passages of different difficulty across the testing cohorts, which if not random in this sample may undermine the conclusions.
This study is the first report on the dynamic development of reading using latent growth curve and simplex modeling from a large representative twin sample. Previous work has been limited to smaller, less-representative twin samples using latent growth curve modeling only, or large twin samples with fewer longitudinal time points and limited to a Cholesky decomposition. By generalizing across two developmental models and in concert with the previous literature, some general trends about the genetic and environmental influences on the developmental pattern of reading can be drawn. Genetic influences on the development of reading are both general, affecting the growth of skills, as well as novel, introduced through the first three years of school when word level reading skills are taught. The shared environment indicates general influences only, suggesting possible home- or school-level effects which are moderate and stable across development. Both of these results would suggest that environmental changes, such as a specific reading intervention, could change the dynamic genetic influences through a possible, unmeasured, gene-environmental interplay in the early school years, as well as affect the environmental influence on the general development of reading. More research is needed to identify the specific genetic and environmental influences underlying the developmental trends highlighted here.
Supplementary Material
Footnotes
A small amount of the sample scored a zero in grade 1 (3.97%), grade 2 (.75%), grade 3 (.39%) and grade 4 (.17%). All models were run with these children removed from the sample. In general, any estimate changed only slightly in magnitude, and the pattern of significance across the models remained the same. These results are available from the first author.
The results of a Cholesky decomposition of these data are available as online supplemental material for better comparison to the previous literature such as Harlaar et al., 2007. We note that a longitudinal Cholesky is not a developmentally motivated model, and the results from the model may not be directly interpretable to the results presented in the main manuscript.
References
- Aunola K, Leskinen E, Onatsu-Arvilommi T, Nurmi JE. Three methods for studying developmental change: A case of reading skills and self-concept. British Journal of Educational Psychology. 2002;72:343–364. doi: 10.1348/000709902320634447. [DOI] [PubMed] [Google Scholar]
- Bast J, Reitsma P. Mathew Effects in Reading: A Comparison of Latent Growth Curve Models and Simplex Models with Structured Means. Multivariate Behavioral Research. 1997;32(2):135–167. doi: 10.1207/s15327906mbr3202_3. [DOI] [PubMed] [Google Scholar]
- Boomsma DI, Molenaar PCM. The genetic analysis of repeated measures. I. Simplex models. Behavior Genetics. 1987;17(2):111–123. doi: 10.1007/BF01065991. [DOI] [PubMed] [Google Scholar]
- Byrne B, Samuelsson S, Wadsworth S, Hulslander J, Corley R, Defries JC, et al. Longitudinal twin study of early literacy development: Preschool through grade 1. Reading and Writing. 2007;20(1–2):77–102. [Google Scholar]
- Campbell FA, Pungello EP, Miller-Johnson S, Burchinal M, Ramey CT. The development of cognitive and academic abilities: Growth curves from an early childhood educational experiment. Developmental Psychology. 2001;37(2):231. doi: 10.1037/0012-1649.37.2.231. [DOI] [PubMed] [Google Scholar]
- Cardon LR, Fulker DW, DeFries JC, Plomin R. Continuity and change in general cognitive ability from 1 to 7 years of age. Developmental Psychology. 1992;28(1):64. [Google Scholar]
- Chall JS. Learning to read: The great debate. McGraw-Hill; New York: 1983. [Google Scholar]
- Christopher ME, Hulslander J, Byrne B, Samuelsson S, Keenan JM, Pennington B, DeFries JC, Wadsworth SJ, Willcutt E, Olson RK. Modeling the Etiology of Individual Differences in Early Reading Development: Evidence for Strong Genetic Influences. Scientific Studies of Reading. doi: 10.1080/10888438.2012.729119. (in press) NIHMSID402978. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Connor CM, Morrison FJ, Fishman BJ, Schatschneider C, Underwood P. Algorithm-guided individualized reading instruction. Science. 2007;315(5811):464. doi: 10.1126/science.1134513. [DOI] [PubMed] [Google Scholar]
- Cunningham AE, Stanovich KE. Early reading acquisition and its relation to reading experience and ability 10 years later. Developmental Psychology. 1997;33(6):934–945. doi: 10.1037//0012-1649.33.6.934. [DOI] [PubMed] [Google Scholar]
- Foorman BR, Francis DJ, Fletcher JM, Schatschneider C, Mehta P. The role of instruction in learning to read: Preventing reading failure in at-risk children. Journal of Educational Psychology. 1998;90(1):37. [Google Scholar]
- Francis DJ, Schatschneider C, Carlson CD. Introduction to individual growth curve analysis. Handbook of research in pediatric and clinical child psychology. 2000:51–73. [Google Scholar]
- Francis DJ, Santi KL, Barr C, Fletcher JM, Varisco A, Foorman BR. Form effects on the estimation of students’ oral reading fluency using DIBELS. Journal of School Psychology. 2008;46(3):315–342. doi: 10.1016/j.jsp.2007.06.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Francis DJ, Shaywitz SE, Stuebing KK, Shaywitz BA, Fletcher JM. Developmental lag versus deficit models of reading disability: A longitudinal, individual growth curves analysis. Journal of Educational Psychology. 1996;88(1):3. [Google Scholar]
- Fuchs LS, Fuchs D, Hosp MK, Jenkins JR. Oral reading fluency as an indicator of reading competence: A theoretical, empirical, and historical analysis. Scientific Studies of Reading. 2001;5(3):239–256. [Google Scholar]
- Gayan J, Olson RK. Genetic and environmental influences on individual differences in printed word recognition. Journal of Experimental Child Psychology. 2003;84(2):97–123. doi: 10.1016/s0022-0965(02)00181-9. [DOI] [PubMed] [Google Scholar]
- Greenwald R, Hedges LV, Laine RD. The effect of school resources on student achievement. Review of Educational Research. 1996;66(3):361. [Google Scholar]
- Harlaar N, Dale PS, Plomin R. From Learning to Read to Reading to Learn: Substantial and Stable Genetic Influence. Child Development. 2007;78(1):116–131. doi: 10.1111/j.1467-8624.2007.00988.x. [DOI] [PubMed] [Google Scholar]
- Harlaar N, Hayiou-Thomas ME, Plomin R. Reading and General Cognitive Ability: A Multivariate Analysis of 7-Year-Old Twins. Special Issue: Genes, Environment, and the Development of Reading Skills. 2005;9(3):197–218. [Google Scholar]
- Hart SA, Petrill SA, Thompson LA. A factorial analysis of timed and untimed measures of mathematics and reading abilities in school aged twins. Learning and Individual Differences. 2010;20(2):63–69. doi: 10.1016/j.lindif.2009.10.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hill CJ, Bloom HS, Black AR, Lipsey MW. Empirical benchmarks for interpreting effect sizes in research. Child Development Perspectives. 2008;2(3):172–177. [Google Scholar]
- Hu LT, Bentler PM. Cutoff Criteria for Fit Indexes in Covariance Structure Analysis: Conventional Criteria Versus New Alternatives. Structural Equation Modeling. 1999;6 (1):1–55. [Google Scholar]
- Jenkins JR, Fuchs LS, van den Broek P, Espin C. Sources of individual differences in reading comprehension and reading fluency. 2003;95(4):719–729. [Google Scholar]
- Jöreskog KG. Estimation and testing of simplex models. The British Journal of Mathematical and Statistical Psychology. 1970;23:121–145. [Google Scholar]
- Kaminski RA, Good RH. DIBELS: Dynamic Indicators of Basic Early Literacy Skills. Fredrick, CO: Sopris West; 2003. [Google Scholar]
- Kenny DA, Campbell DT. On the Measurement of Stability in Over Time Data. Journal of Personality. 1989;57(2):445–481. doi: 10.1111/j.1467-6494.1989.tb00489.x. [DOI] [PubMed] [Google Scholar]
- Kim YS, Petscher Y, Schatschneider C, Foorman B. Does growth rate in oral reading fluency matter in predicting reading comprehension achievement? Journal of Educational Psychology. 2010;102(3):652. [Google Scholar]
- Leppanen U, Niemi P, Aunola K, Nurmi JE. Development of reading skills among preschool and primary school pupils. Reading Research Quarterly. 2004;39(1):72–93. [Google Scholar]
- Logan JAR, Hart SA, Cutting L, Deater-Deckard K, Schatschneider C, Thompson LA, Petrill SA. Genetic and environmental etiology of latent quadratic growth in reading skills. Child Development (in press) [Google Scholar]
- Lykken DT, Bouchard TJ, Jr, McGue M, Tellegen A. The Minnesota twin registry: some initial findings. Acta Geneticae Medicate at Gemellologiae: Twin Research. 1990;39:35–70. doi: 10.1017/s0001566000005572. [DOI] [PubMed] [Google Scholar]
- McCoach DB, O’Connell AA, Reis SM, Levitt HA. Growing readers: A hierarchical linear model of children’s reading growth during the first 2 years of school. Journal of Educational Psychology. 2006;98(1):14. [Google Scholar]
- Muter V, Hulme C, Snowling MJ, Stevenson J. Phonemes, Rimes, Vocabulary, and Grammatical Skills as Foundations of Early Reading Development: Evidence From a Longitudinal Study. Developmental Psychology. 2004;40(5):665–681. doi: 10.1037/0012-1649.40.5.665. [DOI] [PubMed] [Google Scholar]
- Muthén LK, Muthén B. Mplus user’s guide. 3. Los Angeles: Muthén & Muthén; 1998–2004. [Google Scholar]
- Naglieri JA. Do ability and reading achievement correlate? Journal of Learning Disabilities. 2001;34(4):304–305. doi: 10.1177/002221940103400403. [DOI] [PubMed] [Google Scholar]
- National Reading Panel. NIH Pub No 00-4769. Washington, DC: 2000. National Reading Panel report: Teaching children to read: An evidence-based assessment of the scientific research literature on reading and its implications for reading instruction. [Google Scholar]
- Neale MC, Boker SM, Xie G, Maes HH. Mx: Statistical Modeling (Version 7th Edition) VCU Box 900126, Richmond, VA 23298: Department of Psychiatry; 2006. [Google Scholar]
- Neale MC, Cardon LR. Methodology for genetic studies of twins and families. Dordrecht, The Netherlands: Kluwer Academic Publishers; 1992. [Google Scholar]
- Parrila R, Aunola K, Leskinen E, Nurmi JE, Kirby JR. Development of Individual Differences in Reading: Results From Longitudinal Studies in English and Finnish. Journal of Educational Psychology. 2005;97(3):299. [Google Scholar]
- Petrill SA, Hart SA, Harlaar N, Logan J, Justice LM, Schatschneider C, et al. Genetic and environmental influences on the growth of early reading skills. Journal of Child Psychology and Psychiatry. 2010;51(6):660–667. doi: 10.1111/j.1469-7610.2009.02204.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petrill S, Logan J, Hart S, Vincent P, Thompson L, Kovas Y, et al. Math Fluency Is Etiologically Distinct From Untimed Math Performance, Decoding Fluency, and Untimed Reading Performance: Evidence From a Twin Study. Journal of Learning Disabilities. 2012;45(4):371–381. doi: 10.1177/0022219411407926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petscher Y, Kim YS. The utility and accuracy of oral reading fluency score types in predicting reading comprehension. Journal of School Psychology. 2011;49(1):107–129. doi: 10.1016/j.jsp.2010.09.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Phillips BM, Lonigan CJ. Social Correlates of Emergent Literacy. In: Snowling MJ, Hulme C, editors. The science of reading: A handbook. 2005. pp. 173–187. [Google Scholar]
- Reardon SF, Robinson J. Patterns and trends in racial/ethnic and socioeconomic academic achievement gaps. New York: Prentice Hall; 2007. [Google Scholar]
- Roberts G, Good R, Corcoran S. Story retell: A fluency-based indicator of reading comprehension. School Psychology Quarterly. 2005;20(3):304. [Google Scholar]
- Roehrig AD, Petscher Y, Nettles SM, Hudson RF, Torgesen JK. Accuracy of the DIBELS oral reading fluency measure for predicting third grade reading comprehension outcomes. Journal of School Psychology. 2008;46(3):343–366. doi: 10.1016/j.jsp.2007.06.006. [DOI] [PubMed] [Google Scholar]
- Schatschneider C, Fletcher JM, Francis DJ, Carlson CD, Foorman BR. Kindergarten Prediction of Reading Skills: A Longitudinal Comparative Analysis. Journal of Educational Psychology. 2004;96(2):265–282. [Google Scholar]
- Sirin SR. Socioeconomic status and academic achievement: A meta-analytic review of research. Review of Educational Research. 2005;75:417–453. [Google Scholar]
- Speece DL, Case LP. Classification in context: An alternative approach to identifying early reading disability. Journal of Educational Psychology. 2001;93(4):735–749. [Google Scholar]
- Stanovich KE. Toward an interactive-compensatory model of individual differences in the development of reading fluency. Reading Research Quarterly. 1980;16(1):32–71. [Google Scholar]
- Stoolmiller M, Bank L. Autoregressive effects in structural equation models: We see some problems. In: Gottman JM, editor. The analysis of change. Mahwah, NJ: Lawrence Earlbaum Associates; 1995. pp. 261–276. [Google Scholar]
- Storch SA, Whitehurst GJ. Oral language and code-related precursors to reading: Evidence from a longitudinal structural model. Developmental Psychology. 2002;38(6):934–947. [PubMed] [Google Scholar]
- Taylor J, Roehrig AD, Hensler BS, Connor CM, Schatschneider C. Teacher quality moderates the genetic effects on early reading. Science. 2010;328(5977):512. doi: 10.1126/science.1186149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor J, Schatschneider C. Genetic Influence on Literacy Constructs in Kindergarten and First Grade: Evidence from a Diverse Twin Sample. Behavior Genetics. 2010;40(5):591–602. doi: 10.1007/s10519-010-9368-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vasilopoulos T, Mack HA, McClearn GE, Berg S, Johansson B, Vogler GP. Stability of genetic influences on pulmonary function in a longitudinal study of octogenarian twins. American Journal of Human Biology. 2010;22(3):375–377. doi: 10.1002/ajhb.21003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wadsworth SJ, DeFries JC, Olson RK, Willcutt EG. Colorado Longitudinal Twin Study of Reading Disability. Annals of Dyslexia. 2007;57:137–160. doi: 10.1007/s11881-007-0009-7. [DOI] [PubMed] [Google Scholar]
- Wagner RK, Torgesen JK. The nature of phonological processing and its causal role in the acquisition of reading skills. Psychological Bulletin. 1987;101(2):192–212. [Google Scholar]
- Wagner RK, Torgesen JK, Rashotte CA, Hecht SA, Barker TA, Burgess SR, et al. Changing relations between phonological processing abilities and word-level reading as children develop from beginning to skilled readers: A 5-year longitudinal study. Developmental Psychology. 1997;33(3):468. doi: 10.1037//0012-1649.33.3.468. [DOI] [PubMed] [Google Scholar]
- Xu J, Corno L. Family help and homework management reported by middle school students. The Elementary School Journal. 2003:503–517. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.