Multi-task connectivity reveals flexible hubs for adaptive task control

Abstract

Extensive evidence suggests the human ability to adaptively implement a wide variety of tasks is preferentially due to the operation of a fronto-parietal brain network. We hypothesized that this network’s adaptability is made possible by ‘flexible hubs’ – brain regions that rapidly update their pattern of global functional connectivity according to task demands. We utilized recent advances in characterizing brain network organization and dynamics to identify mechanisms consistent with the flexible hub theory. We found that the fronto-parietal network’s brain-wide functional connectivity pattern shifted more than other networks’ across a variety of task states, and that these connectivity patterns could be used to identify the current task. Further, these patterns were consistent across practiced and novel tasks, suggesting reuse of flexible hub connectivity patterns facilitates adaptive (novel) task performance. Together, these findings support a central role for fronto-parietal flexible hubs in cognitive control and adaptive implementation of task demands generally.

INTRODUCTION

Following decades of research involving hundreds of human neuroimaging studies a consensus view has emerged suggesting that a core set of brain regions is centrally involved in implementing a wide variety of distinct task demands^1–3. This functional system includes portions of lateral prefrontal cortex (LPFC), posterior parietal cortex (PPC), anterior insula cortex, and medial prefrontal cortex, and has been variously termed the cognitive control network/system², the multiple-demand system¹, and the task-positive network⁴. Here we focus on a major component of this system (consisting primarily of LPFC and PPC) – the fronto-parietal control network (FPN) – for reasons described below. A fundamental mystery surrounding this system, and the FPN in particular, is how it can meaningfully contribute to such a wide variety of task demands. This computational mystery is compounded by the fact that the FPN is most active^1,5 during the implementation of novel/non-routine tasks that – by definition – the system could not have been shaped by practice or evolution to specifically implement.

Here we examine the hypothesis that the FPN is capable of such functional adaptation because it is composed of flexible hubs – brain regions that flexibly and rapidly shift their brain-wide functional connectivity patterns to implement cognitive control across a variety of tasks^5,6. We tested this hypothesis by combining recent methodological advances in human neuroimaging, involving multi-task cognitive testing⁷, task-state functional connectivity⁸, graph theory⁹, and machine learning¹⁰, that provide a means to test for flexible hub properties in the FPN. In particular, our central approach was to adapt functional MRI (fMRI) methods typically used to characterize functional connectivity during the resting state (i.e., patterns of inter-region temporal correlations) to determine whether such functional connectivity patterns are reliably modulated across a large set of cognitive task states.

The flexible hub account builds upon the earlier ‘guided activation’ framework¹¹ (which in turn was derived from the ‘biased competition’ account¹²). The guided activation framework describes how top-down signals originating in LPFC (representing current task goals) may implement cognitive control by biasing information flow across multiple large-scale functional networks. The guided activation framework was developed primarily to explain how current cognitive goals overcome conflict from previous habits. The flexible hub theory builds upon the guided activation theory by extending this mechanism to account specifically for novel task control, and also by broadening this mechanism to the entire FPN, rather than restricting it to the LPFC portion of the network.

We distinguish the FPN from other brain networks that may also be involved in cognitive control functions. This is based on recent analyses utilizing graph theory that suggest at least five distinct sub-networks are associated with cognitive control^9,13: the FPN, the cingulo-opercular control network (CON), the salience network (SAN), the ventral attention network (VAN), and the dorsal attention network (DAN). We focus specifically on the FPN for two reasons: First, because the FPN includes the LPFC (the focus of the guided activation theory) as a central component; and second, because the flexible hub theory predicts that most adaptive task-control flexible hubs likely exist within the FPN, based on evidence that the FPN is especially active (relative to other networks) during situations requiring highly adaptive task control^5,14.

Most importantly, the flexible hub theory expands on the guided activation framework by proposing two specific systems-level neural mechanisms that may enable adaptive task control: global variable connectivity and compositional coding (Fig. 1). Global variable connectivity refers to the possibility that some brain regions flexibly shift their functional connectivity patterns with multiple brain networks across a wide variety of tasks. Compositional coding refers to the possibility of a systematic relationship between connectivity patterns and task components (e.g., rules), allowing well-established representations to be recombined and thus reused in novel task states to enable transfer of knowledge/skill across tasks. Together, these two mechanisms describe a distributed coding system that provides for an efficient means of implementing a wide variety of task states, while also providing the means for novel task control – the remarkable ability for humans to quickly perform new tasks based only on instruction (which we have previously referred to as rapid instructed task learning, or RITL⁵).

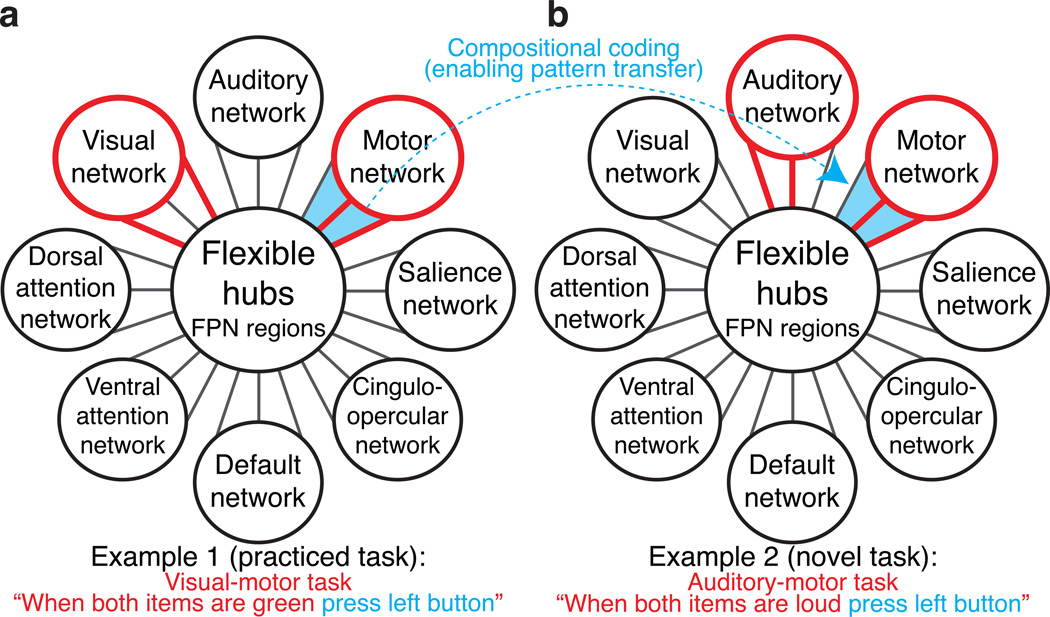
Figure 1.

Task-control flexible hubs are schematically illustrated as brain regions in the fronto-parietal control network (FPN) that exhibit a) global variable connectivity and b) compositional coding. These mechanisms may explain how the FPN contributes to a wide variety of tasks. Global variable connectivity is depicted by the shifting connectivity pattern (red lines connecting FPN to other brain networks) across multiple networks across the two example tasks. Compositional coding (enabling task skill transfer) is depicted by the reuse of a subset of the red connectivity pattern corresponding to the reuse of the ‘press left button’ task component. These mechanisms would likely allow the FPN to meaningfully contribute to a wide variety of task contexts by allowing rapid reconfiguration of information flow across multiple task-relevant networks via reuse of previously learned sets of connectivity patterns.

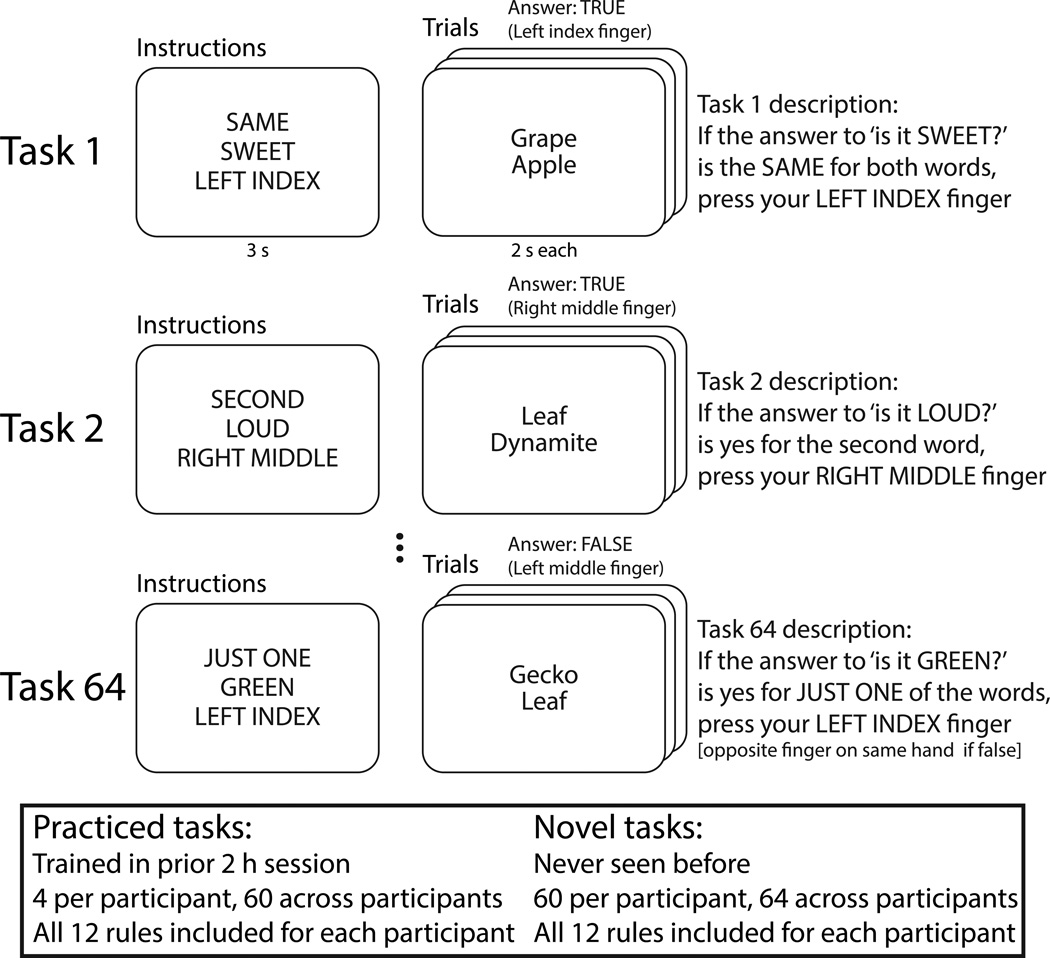
Existing evidence is consistent with the hypothesis that global variable connectivity and compositional coding are two prominent properties of the FPN. First, several studies have demonstrated that LPFC alters its functional connectivity according to the current task state^15,16. However, these findings were primarily limited to either within-FPN connectivity changes across a small number of tasks^17,18 or FPN connectivity changes with other networks as a function of working memory load or content (e.g., maintaining faces vs. scenes) rather than task rules^19–21. In contrast to these prior approaches, here we utilize a recently developed cognitive paradigm that permutes 12 task rules into 64 novel task states⁷ to test for FPN flexible connectivity across a large set of tasks (Fig. 2). To illustrate this paradigm, consider for example that one of the 64 tasks combines the ‘SAME’, ‘SWEET’, and ‘LEFT INDEX’ rules and can be described as: “If the answer to ‘is it SWEET?’ is the SAME for both words, press your LEFT INDEX finger”. For this task, the stimuli ‘grape’ (sweet) and ‘apple’ (sweet) would indicate a left index finger button press, since they are both sweet. In contrast, ‘leaf’ (not sweet) and ‘candy’ (sweet) would indicate a left middle finger button press (the other finger on the same hand), since they are not both sweet. With four rules for each of three types, 4 × 4 × 4 = 64 tasks are possible.

Figure 2.

The permuted rule operations behavioral paradigm – in combination with recent advances in task-state connectivity methods – allows detection of flexible connectivity across a wide variety of task states. The paradigm was designed to efficiently visit a variety of task states (60 novel & 4 practiced previously per subject) while controlling for extraneous factors across those task states (e.g., input and output modalities, task timing, stimuli). Tasks were defined as unique combinations of rules, such that the same stimuli would elicit a distinct set of cognitive operations across distinct tasks. Twelve rules were included across three qualitatively distinct domains, allowing for a well-controlled sampling of a moderately sized space of possible task states spanning multiple cognitive (logical decision rules), sensory (sensory semantic rules), and motor (motor response rules) processes. Participants were over 90% accurate for both novel and practiced tasks⁷.

The utilization of 64 tasks composed of a dozen rules across three qualitatively distinct domains (logical decision, sensory semantic, and motor response) allows for stronger inferences regarding the general properties of task implementation than has been possible in previous work. Further, the use of a large set of tasks now makes it possible to estimate the distribution of functional connectivity patterns across many task states. We utilized this approach to test whether global variable connectivity is a general (across many task contexts) and preferential (relative to other networks) property of the FPN – the first key prediction of the flexible hub theory.

The global variable connectivity mechanism suggests that FPN may exhibit functional connectivity with many brain networks as a means of facilitating the rapid coordination of information necessary for adaptive task control. Considered broadly, this hypothesis is consistent with a variety of findings suggesting the human brain exhibits ‘small-world’ properties due to the existence of hub regions with extensive connectivity²². Considered more specifically, the FPN has been shown to have among the highest global connectivity in the brain during resting state²³, suggesting the FPN contains hub regions. Supporting this conclusion, of all major brain networks the FPN was found to have the most broadly distributed across-network functional connectivity⁹. Further, it was recently found that individual differences in the global connectivity of a specific LPFC region in the FPN correlated with cognitive control abilities and intelligence⁶, suggesting that high global connectivity in the FPN is important for adaptive task control. Critically, however, these previous results were based on static resting-state functional connectivity estimates (i.e., inter-region correlations estimated as single values across a long time period, during which cognitive state was unconstrained by task demands). As such, it is not yet known whether the connectivity of the FPN varies systematically – and in a truly global manner (i.e., with all other brain networks) – across task states. We tested this prediction of the flexible hub theory using graph theoretical methods typically used to estimate functional connectivity of static networks, but here applying them instead to dynamic networks (i.e., taking into account shifts in connectivity across task states).

Compositional coding is proposed as a key flexible hub mechanism underlying the human ability to learn novel tasks extremely rapidly⁵, via reuse of task elements across task contexts^24–26. This mechanism is likely dependent on the simultaneous segregation (representing separate rules) and integration (representing task-relevant relations among the rules) of task information among brain regions²⁷. This would allow neural activity and connectivity patterns (representational components) that are refined and strengthened during practice to then be reused during novel task contexts (i.e., as a novel combination of components) to facilitate transfer of task knowledge/skill and thus performance in such contexts. Global variable connectivity in FPN may facilitate such transfer processes via integration of multiple practiced components (i.e., distributed task rule representations) that have never been used in combination before.

In prior work we have shown evidence of compositional coding within the FPN (specifically in LPFC), using multi-variate pattern analysis (MVPA) to confirm that activity patterns present during task rule performance can be used to accurately classify these rules, and that these activity patterns transfer from practiced to novel task contexts²⁴. However, these findings were limited to only one task rule domain (logical decision rules) and involved activity rather than connectivity patterns. Recent advances in the use of MVPA with task-state functional connectivity¹⁰ allowed us to more directly test the flexible hub theory here, by evaluating whether connectivity patterns map systematically to task states. Additionally, we tested whether the practiced-to-novel transfer of activity patterns in LPFC observed in our prior work could be extended more broadly to characterize task-state functional connectivity patterns across the full set of task rule domains (logical decision, sensory semantic, and motor response rules) and across the entire FPN as an integrated network.

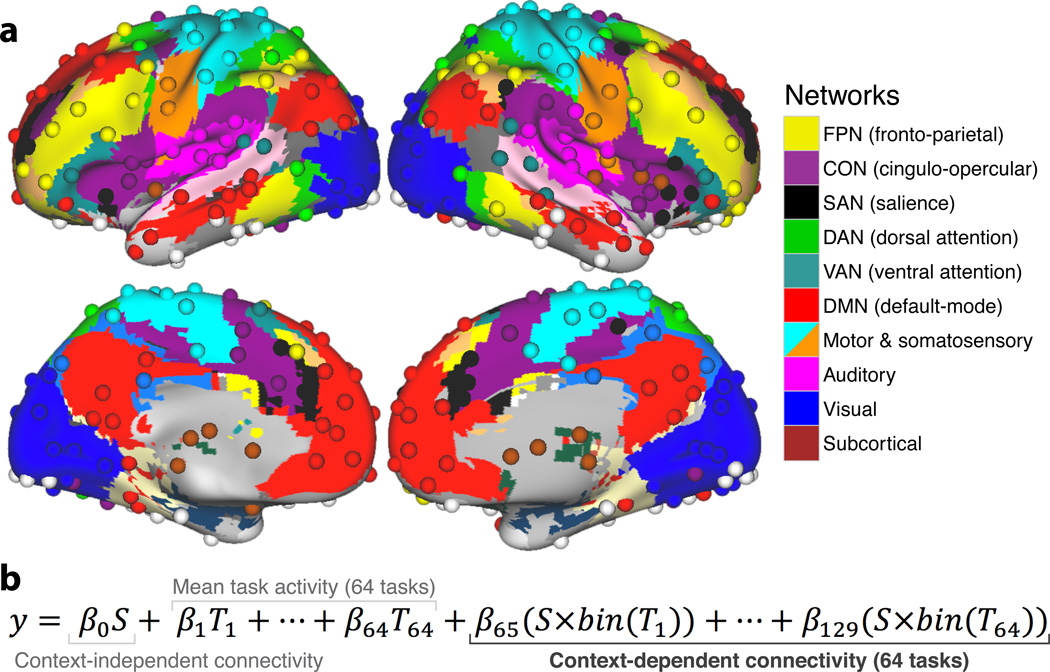
To carry out these investigations we relied upon advances in techniques for identifying the brain’s functional networks and the regions that comprise these networks. Specifically, it is now possible to partition the brain into a set of ‘intrinsic’ functional networks independent of any particular task state^9,28. Here we utilized the Power et al.⁹ network partitioning scheme, which identifies the FPN as one of 10 major functional networks in the human brain (Fig. 3a); independently of the current dataset and the 64 task states. We then estimated task-state functional connectivity patterns among the regions that comprise these networks (Fig. 3b) to test for the existence of flexible hubs in the FPN. Flexible hubs were identified as regions with functional connectivity patterns that met two key criteria: 1) consistent variability across many task states, and 2) consistent variability across many brain networks. This is in contrast to most previous definitions of hubs, which involve static/non-dynamic (resting-state functional or anatomical connectivity) estimates of global connectivity and therefore do not address the possible task-dependent dynamics of these highly connected regions^22,23 (though there has been some characterization of hub dynamics during resting state²⁹).

Figure 3.

Graph theoretical brain network partition and context-dependent functional connectivity estimation. (a) Network partition of 264 putative functional regions from Power et al.⁹. The 10 major networks (node communities) are labeled on the right. (b) The linear regression model equation (called generalized psycho-physiological interaction analysis; gPPI⁸) used to estimate context-dependent functional connectivity (between each pair of the 264 regions), while controlling for mean activation and context-independent functional connectivity. S is the ‘seed’ region’s time series and T is a given task’s timing (convolved with a hemodynamic response function). S×bin(T) is the seed time series multiplied by the binary version of a given task’s timing (all values above 0 set to 1), which results in the simple linear regression fitting of one region’s time series to another during each task context. Similar to the standard definition used for resting-state functional connectivity MRI⁴⁶, ‘functional connectivity’ is defined here as the linear association between two brain regions’ neural activity time series (likely reflecting direct or indirect communication), measured indirectly here using blood oxygen level dependent (BOLD) fMRI. See Online Methods for details.

In summary, we hypothesized that the FPN would involve greater variable connectivity across networks and across tasks than other networks. Further, we expected that these connectivity changes would map systematically to the currently implemented task components. We examined compositional coding by first testing whether connectivity patterns encoded the similarity relationships between tasks. Then we tested whether these distributed connectivity patterns could be used to reliably decode which task was being performed. Lastly, we examined whether such adaptive connectivity patterns could be used to implement practiced-to-novel transfer in task state classification. Confirmation of the presence of both global variable connectivity and compositional coding in the FPN would provide strong support for the idea that this brain network implements core flexible hub mechanisms. As such, we hoped to provide a more comprehensive account of how the human brain – via interactions between the FPN and other brain networks – may enable cognitive control across a wide variety of distinct task demands.

RESULTS

Global variable connectivity in the FPN

Previous research has shown that FPN regions have among the highest global connectivity of the entire brain^6,23. However, these studies were based on static resting-state functional connectivity estimates, such that it remains unknown whether this widespread connectivity is flexibly updated according to task demands. Other studies have shown that some FPN regions shift their functional connections across task conditions¹⁵. Importantly, these studies included only a small number of other regions and task conditions (typically two). Such analyses can be useful for demonstrating simple region-to-region correlation changes (see Supplementary Fig. 1 for such a ‘sanity check’ demonstration of connectivity shifts linked to changes in motor rules), but inferences are limited regarding the general flexible connectivity properties of the FPN. Our task paradigm visited 64 distinct task states, allowing us to estimate distributions of context-dependent functional connectivity to facilitate broader inferences. The flexible hub theory predicts that the FPN should involve extensive variable connectivity across: 1) a variety of task states and 2) a variety of networks. We tested this hypothesis by summarizing distributions of context-dependent functional connectivity across the 64 task states across the networks shown in Fig. 3a.

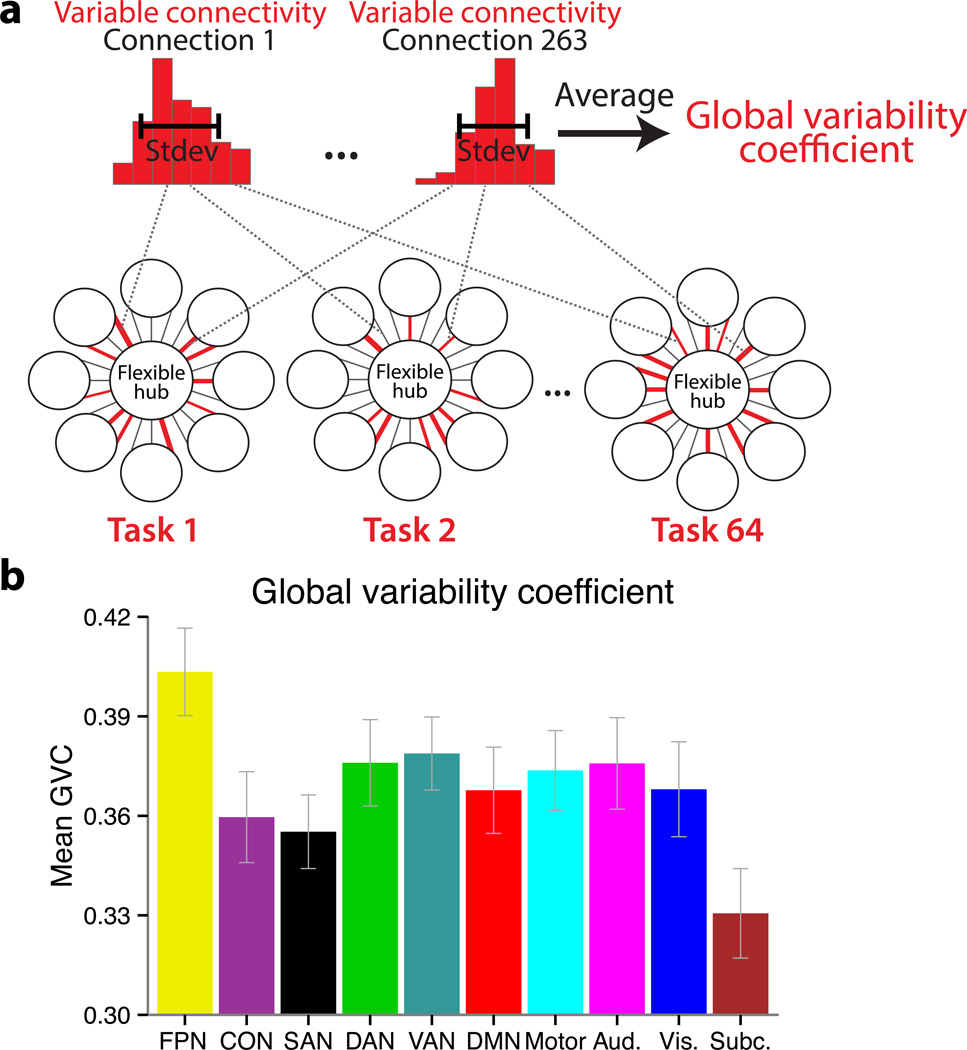
In order to summarize these distributions we created a new graph theoretical measure similar to global brain connectivity (i.e., normalized weighted degree centrality)²³, termed global variability coefficient (GVC), which summarizes the overall variability in connectivity patterns. The GVC is defined as the mean of the functional connectivity variability (across the 64 tasks) across all of a region’s connections (Fig. 4a). Specifically, for each subject, we computed a 264 × 264 × 64 matrix, representing between-region context-dependent connectivity for each of the 264 brain regions in each of the 64 task states. The standard deviation across the third dimension estimated the ‘variable connectivity’ for each connection. We then averaged this measure across all of each region’s 263 connections (the second dimension) to yield each region’s GVC. Finally, we averaged the GVC of the regions within a given network, to provide the network GVC, which summarizes that network’s connection strength changes with all other brain regions. Our specific goals were to develop a graph theoretical measure that: 1) quantifies a property highly related to the theoretical concept of global variable connectivity, and 2) is relatively simple (relative to alternative possibilities) in order to facilitate interpretation and communication of findings using the measure. In contrast to reporting many task-specific network configurations, the use of this measure facilitates identification of the general property of interest – global variable connectivity.

Figure 4.

Global variability coefficient (GVC) – a measure of global variable connectivity – is highest for the FPN. (a) We developed a measure to identify the highly global and flexible functional connectivity predicted by the flexible hub theory. A distribution of functional connection strengths across 64 task states was estimated for each region-to-region connection, and the variability (standard deviation) was then averaged across all of a given region’s connections. The distributions of an FPN region’s (LPFC region in Supplementary Fig. 1; Talairach coords: −45, 7, 24) connectivity with a visual network region (left) and a motor network region (right) for a single subject are shown as representative examples. The histograms summarize the spread of the 64 functional connectivity estimates in terms of connection strength (x-axis = 7 bins of connection strength, y-axis = count of task states with a given connection strength). (b) Each network’s GVC (mean of each network’s regions’ variable connectivity with all 264 regions). The error bars illustrate the inter-subject standard errors. The FPN had significantly (p<.05, FDR corrected) higher GVC than all other networks. Code for computing GVC is available at http://www.mwcole.net/cole-etal-2013/.

As predicted, the FPN had the highest GVC (Fig. 4b; Supplementary Table 1), with its GVC value being significantly higher (p<.05, false discovery rate [FDR] corrected for multiple comparisons) than each of the other brain networks. To further assess whether FPN had notably high GVC, we also calculated a kind of baseline GVC – the mean GVC across the entire brain (averaging over all 264 regions) – and found that the FPN’s GVC was significantly higher than this: whole-brain=.36, FPN=.40, t(14)=9.37, p=2.086e−07. Further, we found that these effects replicate across the three rule dimensions (Supplementary Table 2), demonstrating that no single rule type drove the observed effects. These results were also replicated when using a Pearson correlation method and a covariance method (computing inter-region Pearson correlations or covariances after regressing out mean task activity; see Supplementary Tables 3 and 4) instead of our primary methodological approach (which involved generalized psycho-physiological interaction; gPPI), suggesting these results are robust across functional connectivity methods. Importantly, the GVC results were also independent of mean task activation and stable (context-independent) functional connectivity, given that mean activity, context-independent connectivity, and context-dependent connectivity were modeled such that they were statistically independent components within the statistical model (see Online Methods; Fig. 3b). Further, FPN was not the only network showing high activity across the 64 tasks (e.g., DAN and CON were often engaged as well; Supplementary Fig. 2), demonstrating that GVC was not driven by activation or co-activation of regions. Together these results strongly support the hypothesis that the FPN consistently changes functional connectivity with a variety of regions across a variety of tasks.

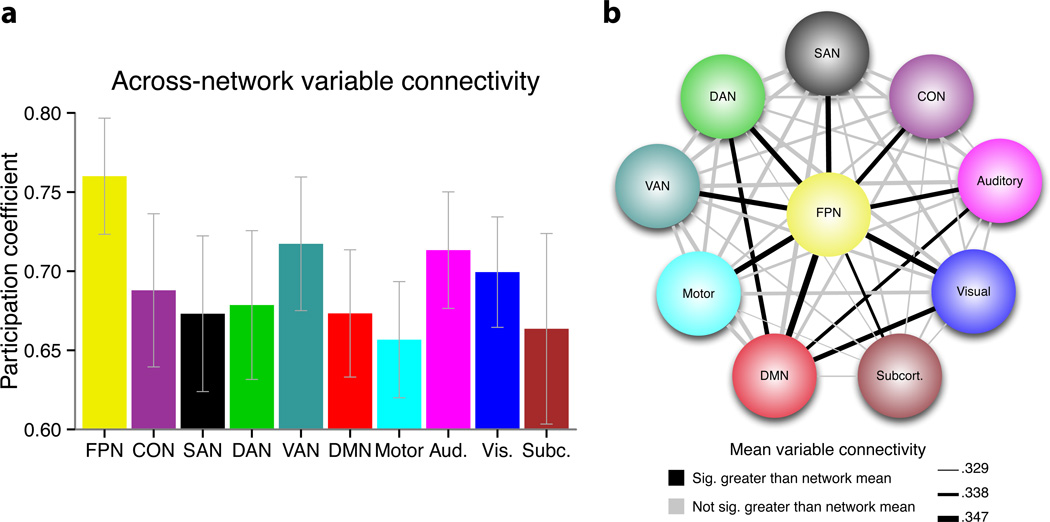
We next sought to provide more direct evidence that the variable connectivity patterns observed in the FPN were truly global in nature, rather than driven by very large changes in a small subset of FPN (e.g., within-network) connections. To examine this issue we used another graph theoretical measure, the participation coefficient³⁰, which estimates the uniformity of connections (or, in this case, connection variability) across all networks. Note that this measure is typically applied to static (resting-state functional or anatomical connectivity) networks, but here we applied it to dynamic (variable connectivity) networks. Consistent with the hypothesis that the FPN consists of flexible hubs (i.e., regions with variable connectivity patterns that are truly global), we found that this network had the highest mean participation coefficient of all examined brain networks (Fig. 5a). This finding was robust across various ways of calculating participation coefficient (i.e., across thresholds defining connections included in the calculation, Supplementary Table 5; and when using Pearson correlations or covariances to estimate the functional connections, Supplementary Tables 6 and 7).

Figure 5.

FPN’s variable connectivity is truly global. To rule out the possibility that FPN’s high GVC was driven by high variability of a small subset of connections: (a) Across-network variable connectivity (participation coefficient) was estimated for each network. Like GVC, FPN’s participation coefficient of variable connectivity was highest (p<.05, FDR corrected) across the 10 networks (the results for the top 2% variable connectivity are shown; see Supplementary Table 5 for results across all thresholds). This suggests FPN’s variable connectivity is truly global. The error bars illustrate the inter-subject standard errors. (b) Pairwise mean variable connectivity between networks was examined. Variable connections are highlighted that are significantly (p<.05, FDR corrected) greater for one of the networks included in a given link than the GVC of the other network included in that link. For example, the FPN-DMN link was highlighted because FPN’s mean variable connectivity with the DMN was significantly greater than the DMN’s mean variable connectivity with the entire brain (i.e., its GVC). Note that variable connectivity from the Pearson correlation analysis (see Supplementary Table 3) was used for illustration given that this method provides connectivity estimates that are identical in both directions (i.e., to/from seed and target regions). The three lines in the legend are the minimum, median, and maximum variable connectivity strengths. The FPN’s variable connectivity with each network was significantly greater than every network’s GVC (i.e., the mean over each network’s connections with all 264 regions), providing confirmation that this is truly a global effect.

To further test the robustness of this result we also analyzed FPN’s variable connectivity with each network separately (rather than summarize FPN’s variable connectivity across all networks in a single value). Specifically, we examined the pairwise variable connectivity between each of the 10 brain networks, to provide an index of the specific network-to-network variable connectivity. We then compared the network-to-network variable connectivity values that included the FPN with those involving other networks (Fig. 5b), using the mean network-to-network variable connectivity as a baseline. We found that variable connectivity between the FPN and each of the other 9 brain networks was significantly higher than this baseline value (p<.0001, FDR corrected). Moreover, it was the only network to show this effect. It is worth noting that these results also demonstrate that the 64 tasks were varied enough to drive the FPN to shift connectivity with every other brain network.

Lastly, we tested the hypothesis that individual FPN regions also have the flexible hub properties that were observed at the network level (Supplementary Fig. 3; Supplementary Table 8). Indeed, we found that 10 of the 25 FPN regions had significantly greater GVC than the whole-brain mean (p<.05, FDR corrected). Further, like the FPN as a whole, 9 of these regions had greater variable connectivity with every network relative to each network’s global/mean variable connectivity (p<.05, FDR corrected). Importantly, these 10 regions were in several major anatomical subdivisions of the FPN (anterior LPFC, dorsal LPFC, posterior LPFC, and PPC), supporting the existence of flexible hub regions throughout the FPN.

Compositional coding in the FPN’s functional connectivity patterns

The second mechanism proposed by the flexible hub theory is that the FPN’s functional connectivity patterns are systematic and structured, utilizing compositional coding to represent overlapping cognitive components. Compositional coding in connectivity patterns would allow for immediate transfer of knowledge/skills (represented in the connectivity patterns) into new task contexts⁵. As an initial test of such systematic connectivity, we examined whether the similarity among task states was reflected in similarity among FPN functional connectivity patterns. We examined this prediction using representational similarity analysis³¹ – a form of multivariate pattern analysis (MVPA). Representational similarity analysis has typically been applied to fMRI activity patterns, but here we applied it to functional connectivity patterns.

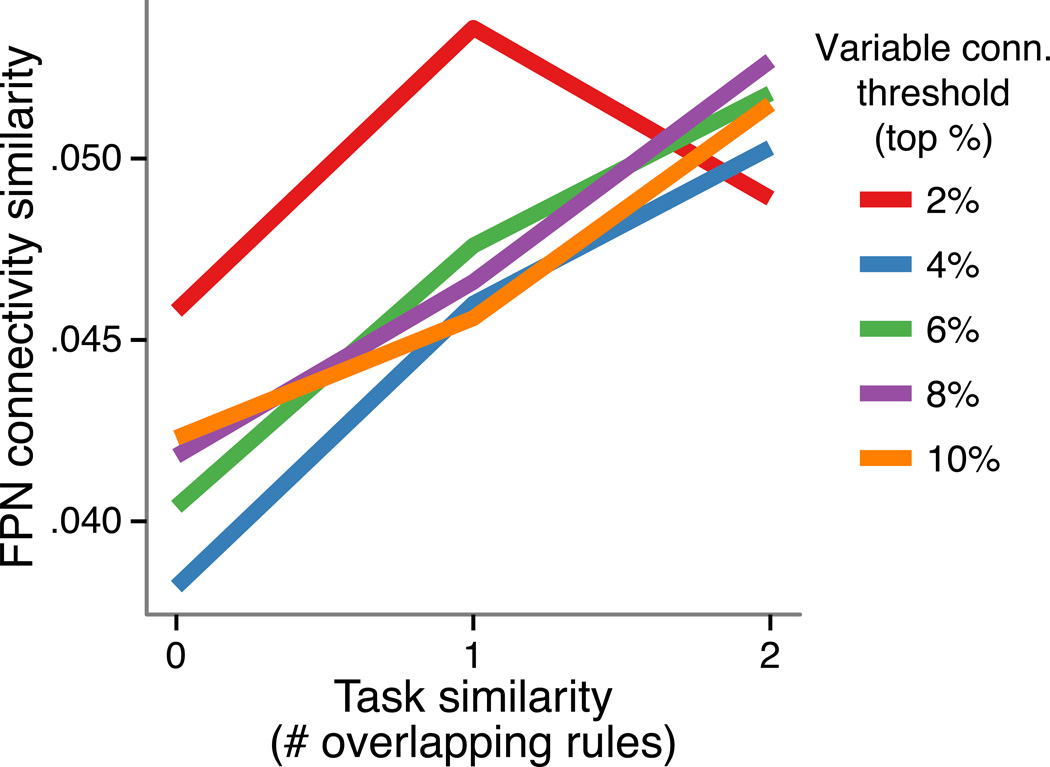
The current dataset is particularly well suited for representational similarity analysis given the innate similarity structure among the 64 tasks. Specifically, each task was related to each other task by two overlapping rules (e.g., SAME – SWEET – L.INDEX vs. SECOND – SWEET – L.INDEX), one overlapping rule, (e.g., SAME – SWEET – L.INDEX vs. SECOND – SWEET – R.MID), or no overlapping rules (e.g., SAME – SWEET – L.INDEX vs. SECOND – GREEN – R.MID). Thus, we could create a 64-by-64 matrix with a single number (0, 1, or 2) in each cell summarizing the pair-wise similarity among the 64 tasks. We could also create such a matrix summarizing the similarity among FPN connectivity patterns using a standard similarity/distance metric (Spearman’s rank correlation). Only the FPN connections with the highest variability (specifically, 25×263=6575 connections thresholded by top % of standard deviation across the 64 tasks) were analyzed in order to test if even highly variable connections contain systematic task information – a key assumption of the previous analyses. Consistent with this possibility, using a number of different variable connectivity thresholds (five thresholds: top 10% to 2%, in 2% increments) we observed that the effect was robust in all but the highest threshold (p = .006, .002, .001, .005, and .14; Spearman’s rank correlation, permutation tests; Fig. 6). Further, the relationship was consistently positive, suggesting that the FPN’s context-dependent connectivity throughout the brain – rather than varying solely as a function of noise – varied systematically as a function of the task being performed.

Figure 6.

The FPN’s connectivity varies systematically, suggesting the previous results were not simply due to network noise properties and that FPN connectivity likely represents task information. We assessed representational similarity between context-dependent connectivity patterns from FPN to the rest of the brain, revealing a relationship with the similarity between tasks.

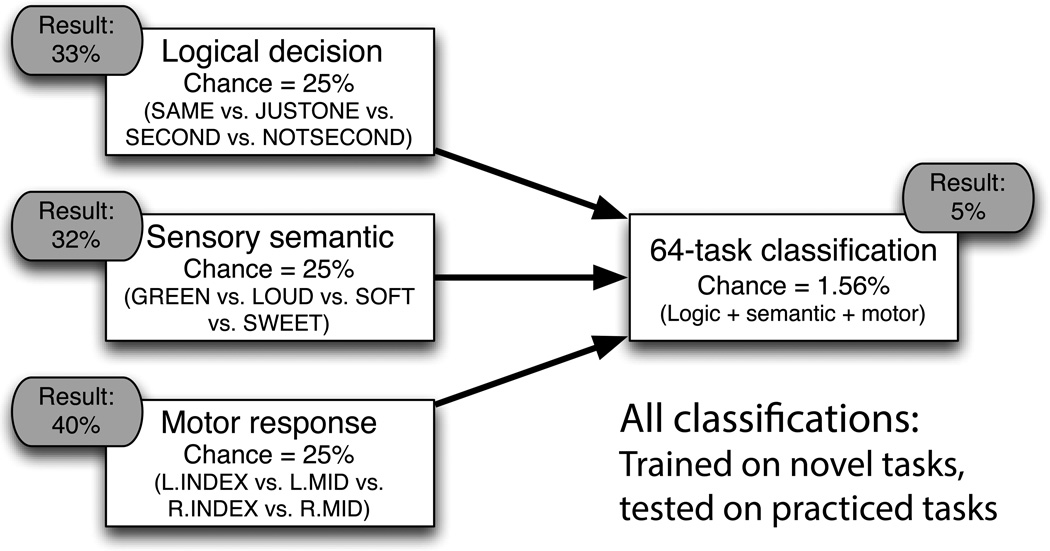
We next tested the compositional coding hypothesis more directly. We hypothesized that if FPN connectivity patterns were systematic and structured then they should provide information regarding the current cognitive task state. As such, we tested whether task state could be decoded using MVPA methods, based on the particular connectivity pattern instantiated during that state. Note that our paradigm provides a powerful test of this hypothesis, in that participants were engaged in a set of 64 distinct tasks, thus providing a large and challenging task space for classification. Indeed, prior MVPA approaches to fMRI cognitive task decoding have typically involved only 2-way classification problems, and even with this have typically achieved only modest accuracies relative to chance^10,24. In order to test for compositional coding of functional connectivity representations, we trained MVPA classifiers (linear support vector machines) in a hierarchical manner, with separate classifiers trained to do 4-way classification within each of the 3 task rule domains (logic, sensory, or motor). These classifiers were then combined to identify the individual task states (i.e., a 64-way classification).

To validate our approach, we began with a simple analysis. We examined the motor network (rather than FPN) with the expectation that this network could be used to successfully decode motor response rules, but not the other two task rule dimensions (chance = 25% in the 4-way classification of each task rule dimension). As expected, classification accuracy for the motor network was at or below chance for logic (26.7%) and sensory (23.3%) rule dimensions, but was significantly above chance for the motor rule dimension (41.7%, p=.001).

We repeated this analysis for the FPN, restricting its connections to the motor network for motor rules (given a priori expectations), but including the FPN’s whole-brain connectivity for logic and sensory rules (Fig. 7). As predicted, the FPN’s connectivity patterns could be used to decode all three rule dimensions: logic=33.3% (p=.040), sensory=31.7% (p=.077), and motor=40% (p=.003). We next combined these three FPN classifiers (logic, sensory, and motor) to predict which of the 64 tasks was being performed (64-way classification). This is a very difficult classification (as noted above, most classifications in neuroscience have been 2-way classifications), with chance accuracy being just 1.56%. The classification was successful with 5% accuracy (p=.013). While this accuracy is low, its statistical significance nonetheless demonstrates the ability to identify task information within FPN connectivity patterns. We conducted exploratory analyses to determine whether other brain networks showed decoding accuracy that was equal or higher than the FPN, and none did. Given our a priori hypotheses focusing on FPN and concerns about multiple comparisons testing (i.e., family-wise error inflation), we did not pursue classification based on full-brain connectivity patterns further.

Figure 7.

Decoding of task identity from FPN’s context-dependent connectivity patterns. Using MVPA methods applied to functional connectivity, three separate 4-way classifiers (logic, sensory, and motor) were trained with FPN connectivity patterns during novel tasks and tested with FPN connectivity from practiced tasks. All three classifiers were above chance. These classifiers were then combined to decode each of the 64 tasks (e.g., SAME + GREEN + L.INDEX). Classification was again above chance (p<.05) – a notable result giving the tremendously challenging nature of the 64-way classification (chance accuracy is 1/64 = 1.56%). The results support the second mechanism of the flexible hub theory – compositional connectivity – by suggesting that FPN connectivity patterns are transferred across practiced and novel task contexts.

Importantly, a particular aspect of the classification analysis supported the possibility that FPN connectivity patterns represent task information compositionally. Specifically, classification was achieved by training the classifier based on connectivity patterns present during novel task performance (i.e., the first time each participant had ever performed that task) but then testing it during performance of practiced tasks (i.e., a small set of tasks for which each participant was highly familiar). Because the classification was accomplished by training/testing on novel and practiced tasks separately, these results demonstrate transfer of compositional connectivity patterns across practiced and novel tasks.

Previous analyses of the present dataset indicated that there was a significant increase in the ability to learn the novel tasks relative to initial learning of the practiced tasks²⁴, suggesting there was transfer of task skill/knowledge from practiced to novel tasks. Further, these prior analyses established that there were only minimal differences in rule difficulty²⁴, such that difficulty differences were unlikely to drive the present effects. The present analysis also used an across-participant approach¹⁰ (one functional connection estimate per condition per participant) such that idiosyncratic differences in perceived difficulty³² were highly unlikely to have driven the results. Together these results suggest FPN’s global connectivity patterns 1) represent task information, 2) are compositional, and 3) transfer from practiced to novel task contexts.

DISCUSSION

Recent meta-analyses of functional neuroimaging results have revealed that certain distributed brain networks are consistently engaged across a wide variety of cognitively demanding task states¹. This suggests there may be a distributed cognitive control system (including the FPN) that implements domain-general functions, in addition to well-known specialized systems (e.g., sensory/motor and memory networks) for implementing relatively circumscribed functions. Recent evidence suggests that the FPN has extensive global connectivity (i.e., its regions are hubs)²³, suggesting it may gain its multi-function ability by flexibly interacting with a variety of functionally specialized networks throughout the brain. We tested this possibility – in the context of the flexible hub theory – using recent advances in human neuroimaging methodology.

Two specific mechanisms of the flexible hub theory were tested. First, the theory suggests FPN has highly flexible/variable connectivity throughout the brain, allowing the FPN to coordinate multiple networks during task performance. Confirming this hypothesis, we found that the FPN had the highest GVC – an index of global variable connectivity – of all the major brain networks. This pattern was robust: it was present in individual FPN regions, regardless of which functional connectivity measure was used to calculate GVC, and was also found using a different graph theoretical measure of global connectivity known as the participation coefficient. As a second mechanism, the flexible hub theory suggests that the FPN exhibits compositional coding in its connectivity patterns, such that these patterns are systematically related to cognitive task states and the relationships between states. Confirming this second hypothesis, we found that brain-wide FPN functional connectivity patterns across 64 task states: 1) encoded the similarity relationships between tasks; 2) could be used to identify task states; and 3) transferred from practiced to novel tasks.

The present findings have several limitations that will be important to address in future research. For instance, we used a necessarily imperfect set of putative functional regions, identified by a previous study using meta-analysis and functional connectivity⁹. We chose to use these regions given evidence that voxel-defined (i.e., using all voxels as nodes) and anatomy-defined (i.e., based on gyri/sulci) cortical regions do not align well with functional regions, which can inappropriately alter graph theoretical and functional connectivity MVPA findings^33,34. A related limitation is the inclusion of only the major brain networks, due to possibly imperfect graph theoretical community detection, such that regions from some potentially smaller networks (e.g., gustatory/olfactory networks, subcortical networks) were not included. Nonetheless, with 264 regions distributed throughout the brain this set is likely a sufficient approximation at this time, especially given that it approaches the number of distinct functional regions theoretically postulated to be present in the human brain (around 300)³⁵. Still, it will be important for future work to replicate these findings as the set of identified functional regions and networks becomes more accurate.

The relatively low (but statistically significant) classification accuracies identified in the decoding analyses are another potential limitation. However, support for the tested hypothesis – compositional coding of FPN functional connectivity – depends on the presence of information decodable across task contexts (as indicated by the statistical significance, rather than the absolute accuracies, of those classifications). Further, the classification results are consistent with the representational similarity analysis (Fig. 6), which also supports the compositional coding hypothesis. Finally, there are reasons to expect the classification accuracies to be relatively low. For instance, in contrast to the 4-way and 64-way classification results presented here, the majority of task rule classifications of fMRI activity and functional connectivity reported in prior studies have been easier two-way classification problems^10,36, and even these classifications have only performed modestly above chance. Indeed, to our knowledge, the present classification was the most difficult task rule classification of brain data to date, and the classification accuracy was proportionally higher than previous attempts (e.g., ~3× higher than chance for the 64-way classification). Increasing task rule classification accuracy is clearly an important challenge for near-term research. Future work may be able to increase connectivity-based classification accuracies of task rules by using, for instance, optimized classification algorithms or more distinct task states (here each classification discriminated among rules of the same task dimension).

The similarity among the 64 task states is another potential limitation, given that all 64 tasks involved some uniform attributes (e.g., task timing, input/output modality) that might have led to more across-task consistency in activation/connectivity patterns than a more distinct set of tasks would have. However, such uniform similarity was actually designed to control for things like task timing and input/output modality in order to isolate task states independently of brain state changes due to these lower-order properties. Further, the analyses tested for differences – rather than uniform similarity – in connectivity patterns across tasks, such that this uniform similarity could not have led to false positives. Though having some uniform similarity could have driven involvement of the FPN across all 64 tasks in theory, such widespread involvement of the FPN has been well documented across much more distinct tasks^14,37. Finally, involvement of regions across all 64 tasks – whether due to uniform task similarity or not – was not sufficient to lead to the observed flexible hub mechanisms given that the DAN, VAN, SAN, and CON networks exhibited activity levels comparable to the FPN across all or most of the 64 tasks (see Supplementary Fig. 2), but did not show the same level of connectivity pattern variability.

The involvement of five cognitive control-related networks across a wide variety of tasks begs the question of what each of these networks might contribute to task performance. We have provided a tentative answer to this question for the FPN by reporting evidence for two mechanisms of the flexible hub theory. It may be that the other cognitive control networks contribute to a variety of tasks by implementing a variety of distinct control processes, such as stable (rather than adaptive) task control/maintenance¹⁴, conflict detection³⁸, arousal/salience³⁹, or spatial attention⁴⁰. It will be important for future research to characterize both the integration and specialization of these networks in implementing different aspects of task control, in addition to testing for the existence of other kinds of flexible hubs (e.g., stable task control flexible hubs or attentional control flexible hubs).

Cognitive control permeates nearly every aspect of our lives and its disruption results in profound life-altering deficits^41,42. The present work extends several prominent theories of cognitive control^11,12 by testing their predictions in a more generalizable form, identifying FPN variable connectivity across a variety of tasks and across a variety of brain networks. Further, the flexible hub theory expands these frameworks to include flexible task control – including the highly adaptive behavior of first-trial task learning⁵ – in addition to expansion of flexible hub neural mechanisms to the entire FPN (rather than LPFC alone). These results are consistent with findings in the macaque suggesting individual FPN neurons are highly adaptive in their representations^43,44, as well as recent evidence that local functional connectivity is highly flexible within dorsal LPFC, shifting according to current task demands⁴⁵. Our findings suggest that an important way forward will be to identify correspondences between the present study’s systems-level flexible hub mechanisms and local neuronal mechanisms within flexible hubs (and among FPN regions) that may regulate switching of global connectivity patterns according to task demands. Such a multi-level theoretical framework would move us substantially closer to the ultimate goal of understanding how the brain implements the ability to adaptively control one’s own behavior.

ONLINE METHODS

Participants

15 right-handed participants (eight male, seven female), aged 19–29 (mean age 22) were included in this study. Note that this sample size is similar to those used in previous publications using within-subject experimental manipulations with fMRI. Results from highly distinct analyses of this dataset were reported in Cole et al.^7,24. The participants were recruited from the University of Pittsburgh (Pittsburgh, PA) and the surrounding area. Participants were excluded if they had any medical, neurological, or psychiatric illness, any contraindications for MRI scans, were non-native English speakers, or were left handed. All participants gave informed written consent.

Task paradigm

The fMRI experiments consisted of performing the permuted rule operations (PRO) cognitive paradigm⁷. The PRO paradigm combines a set of rule components in many different ways, creating dozens of complex task sets that are each novel to participants (Fig. 2). The paradigm was presented using E-Prime software⁴⁷.

Four logical decision, four sensory semantic, and four motor response rules were used in the paradigm. Each task consisted of one rule from each of these categories, allowing the creation of 4 × 4 × 4 = 64 distinct tasks by permuting the possible rules. Of these tasks, four (counterbalanced across participants) were practiced (30 blocks, 90 trials each) during a 2-h behavioral session 1–7 days before the neuroimaging session. These ‘practiced’ tasks were chosen for each subject such that each rule was included in exactly one of the four tasks, ensuring that all rules were equally practiced. This also ensured that rule identity was controlled for across novel and practiced tasks (i.e., only rule combinations differed across the conditions). During the neuroimaging session, half of the mini-blocks consisted of the practiced tasks and half of novel tasks, randomly interleaved. With 10 runs total per participant, each novel task was presented in one mini-block and each practiced task was presented in 15 mini-blocks.

The semantic rules consisted of sensory semantic decisions (e.g., “is it sweet?”). The logical decision rules specified how to respond based on the semantic decision outcome(s) for each trial (e.g., are the two items the same in sweetness?). The motor response rules specified which finger to use to respond, based on the logical decision outcome. The task instructions made explicit reference to the motor response for a “true” outcome (e.g., right index finger), while participants knew (from the practice session) to use the other finger on the same hand (e.g., right middle finger) for a “false” outcome.

Task mini-blocks included instruction encoding and three trials. Each mini-block began with a task type cue, indicating whether the upcoming task is novel (thin border) or practiced (thick border), followed by three instruction screens. The order of the instructions following the task type cue was consistent for each participant, but counterbalanced across participants. Asterisks filled in extra spaces in each instruction screen to control for differences in total visual stimulation across task rules. Each stimulus was presented for 800 ms with a 200 ms inter-stimulus interval. Inter-event intervals (i.e., between instructions and each of the three trials) were randomly varied between 2 and 6 seconds, while inter-mini-block intervals randomly varied between 12 and 16 seconds. There were 12 mini-blocks per run, with 6 novel task mini-blocks and 6 practiced task mini-blocks each.

All task mini-blocks were included in all analyses given that there was at least one accurate trial per mini-block for all participants.

MRI data collection

Image acquisition was performed on a 3T Siemens Trio MRI scanner. 39 transaxial slices were acquired every 2000 ms (field of view: 210 mm; echo time: 30 ms; flip angle: 90°; voxel dimensions: 3.2 mm³) with a total of 216 gradient echo-planar imaging volumes collected per run (across 10 runs). Siemens’ implementation of GRAPPA (generalized autocalibrating partially parallel acquisition) was used to double the image acquisition speed. Three-dimensional anatomical MP-RAGE (magnetization prepared rapid acquisition gradient echo) images and T2 structural in-plane images were collected for each subject before fMRI data collection.

fMRI preprocessing

Preprocessing was performed using AFNI⁴⁸ and Freesurfer⁴⁹. Preprocessing consisted of standard functional connectivity preprocessing (typically performed with resting-state data), with several modifications given that analyses were performed here on task-state data. Like standard functional connectivity preprocessing²³, we performed slice timing correction, motion correction, normalization to a Talairach template, removal of nuisance time series (motion, ventricle, and white matter signals, along with their derivatives) using linear regression, restriction of data to a gray matter mask (dilated by one voxel), and spatial smoothing within the gray matter mask (6 mm full width at half maximum). Unlike standard resting-state functional connectivity preprocessing, whole brain signal was not included as a nuisance covariate (given current controversy over this procedure⁵⁰), and a low-pass temporal filter was not applied (given the likely presence of task signals at higher frequencies than the relatively slow resting-state fluctuations). Freesurfer was used to identify ventricle, white matter, and gray matter anatomical structures for each participant.

Functional connectivity estimation

Task-state functional connectivity was estimated between each pair of the 264 functional brain regions of interest. Context-dependent connectivity was estimated using a linear model equivalent to the general linear model (GLM) typically used in fMRI analysis with several additional regressors. There were three kinds of regressors per linear model: 1) one task regressor per condition convolved with a subject-specific hemodynamic response function (equivalent to the regressors in a typical GLM), 2) a context-independent connectivity regressor consisting of the entire time series of the seed region across all task conditions and inter-block periods, and 3) a context-dependent connectivity regressor for each task condition, consisting of the seed region’s time series only during the time the subject was performing the task of interest (with a subject-specific hemodynamic lag included). Thus, the estimated functional connectivity during each task condition was statistically independent of mean activation during that task condition and overall context-independent functional connectivity (see Fig. 3b).

This approach was equivalent to a simplified version of the recently developed generalized psycho-physiological interaction (gPPI) approach⁸. We had four primary reasons for using gPPI: 1) the finding using a biologically realistic simulation that PPIs are more sensitive than Pearson correlations for detecting task-state connectivity changes⁵¹, 2) relative to Pearson correlation changes, PPI changes better reflect changes in linear association (rather than signal-to-noise, which can change due to changes in noise across conditions)⁵², 3) the inclusion of task regressors reduces the chance that the functional connectivity estimates were driven by simple co-activation (i.e., activation of multiple regions during a task without inter-regional communication), and 4) unlike the classic PPI implementation, gPPI allows for an unlimited number of task conditions to be modeled simultaneously. This was especially important here given the need to model 64 tasks and/or 12 rules (4 rules at a time) per subject. We used in-house software implemented in MATLAB 2008b (The Mathworks) to calculate the gPPIs. We simplified the gPPI procedure by eliminating the ‘deconvolution’ step⁸, given that it has not been empirically shown to improve PPI estimates and given that we used a mini-block design (the deconvolution step was primarily developed for event-related designs). This step is also not used in PPI analyses implemented with FSL software⁵³, making the current analysis approach quite similar to the standard FSL PPI method. One important improvement here, however, was the true zeroing-out of the non-current-task periods (by not mean-centering the task regressors) to ensure removal of non-current-task (e.g., rest) period fluctuations from the PPI regressors and thus improve sensitivity to true PPI effects.

The linear model equation used to simultaneously estimate task activity, context-independent connectivity, and context-dependent connectivity was:

$$y={\beta }_{0}S+{\beta }_1{T}_1+\cdots +{\beta }_{64}{T}_{64}+{\beta }_{65}(S\times \mathit{\text{bin}}(T_1))+\cdots +{\beta }_{129}(S\times \mathit{\text{bin}}(T_{64}))$$

Where y is the target region’s time series, S is the source region’s time series, β is the least-squares linear estimate, T is the task timing for a given task (convolved with a subject-specific hemodynamic response function), and bin(T) is a binarized version of the task timing (i.e., time points with values greater than 0 were set to a value of 1). Context-independent connectivity was estimated with the β₀ regressor while task activity was estimated with regressors β₁ – β₆₄; context-dependent connectivity was estimated with regressors β₆₅ – β₁₂₉. Note that an additional baseline regressor (all 1s) was also included, as is standard for linear modeling. Also note that the task activity regressors were constructed by modeling each event (within mini-blocks), with durations of 4 s (2 TRs) for instruction events and 2 s (1 TR) for trial events.

One potential limitation – which is an issue for all current task-state functional connectivity fMRI methods – is the possibility that some co-activation was falsely attributed to connectivity. The key problem is that simple activation of two non-interacting regions will lead to a linear association (i.e., a positive connectivity estimate) due to similarity of the hemodynamic response shape across regions. We used the standard PPI approach to dealing with this issue: including task condition timings (the same timing as would be included in a GLM) as covariates when estimating connectivity. Given that this approach requires highly accurate activity estimates, we obtained a separate hemodynamic response function for each individual (based on the average of the finite impulse response functions of 2 visual and 2 motor regions across all visual/motor task events) to more accurately estimate mean activity in each region and help rule out co-activation as a confound (Supplementary Fig. 4). Note that while regions differ in their hemodynamic responses, most hemodynamic variability is due to inter-subject differences⁵⁴, suggesting our approach likely accounted for much of the hemodynamic variability. Further, inter-region hemodynamic variability is unlikely to cause false positives given that co-activation leads to false positive connectivity only in so far as regions have similar hemodynamic response shapes. It will nonetheless be important for future studies to explore approaches for completely ruling out co-activation as a confound. See the Discussion section for more on this topic.

A simpler approach was also used for context-dependent connectivity analyses. This involved modeling mean activity for all 64 conditions in a GLM run on each of the 264 regions separately, then calculating pair-wise Pearson correlations (subsequently Fisher’s z-transformed) among the residual time series – separately for each task condition – from those GLMs. Finally, as an even simpler approach, we also computed connectivity estimates based on covariance alone (i.e., Pearson correlation without normalizing by each region’s time series standard deviation). Both of these alternative approaches resulted in similar results as the gPPI approach (see Supplementary Tables 3, 4, 6, and 7). The graph theoretical estimates for each of the 264 regions across the three ways of estimating functional connectivity are provided in Supplementary Table 9. The gPPI approach was used in the main analyses due to evidence that PPIs are more sensitive to functional connectivity changes than correlations⁵¹, and also because gPPIs include a context-independent covariate that may account for static/intrinsic connectivity (which was not of interest in the present study).

Graph theoretical analyses

We used MATLAB for graph theoretical analyses. This involved in-house software and the Brain Connectivity Toolbox⁵⁵. Code for computing GVC is available at http://www.mwcole.net/cole-etal-2013/. Analyses were run on the gPPI beta estimates (and, separately, using Pearson correlations or covariances). Unless stated otherwise, all null hypothesis statistical tests were conducted using paired (by subject) two-sided t-tests. We tested if the data were normally distributed using Q-Q plots prior to running t-tests. We sought to use a principled network partition based on an independent dataset using resting-state (i.e., task-independent) functional connectivity in order to use a network partition 1) unbiased by the current dataset, and 2) unbiased by the current or any other particular task states. Therefore, network identification was based on the regions and community detection reported by Power et al.⁹.

The 264 regions are 10 mm diameter spheres centered on the coordinates reported in Power et al.⁹. Those coordinates are the centers of putative functional areas (and subcortical and cerebellar nuclei), defined by multiple task fMRI meta-analyses⁵⁶ and by a resting state functional connectivity MRI parcellation technique⁵⁷.

In Power et al.⁹, several partitions of the 264 regions into highly correlated groups of nodes called communities were reported. The current report uses a summary set of node assignments based on the results of Power et al.⁹, using all of a node’s assignments into communities across two independent datasets and all thresholds reported in Power et al.⁹. A consensus assignment was made manually for each node based on the consistency of a nodes community assignment across groups and thresholds. Preference was given to assignments from the analyses on only the strongest correlations. These consensus assignments were made without knowledge of a node’s identity (location) or the identity of the assignment (the corresponding brain network). These consensus assignments are shown in Power & Petersen¹³ and are available at (http://sumsdb.wustl.edu/sums/directory.do?id=8293343&dir_name=power_Neuron11).

This consensus assignment resulted in 13 communities, with two communities (one exclusively in cerebellum and another with unknown functionality) excluded and two motor/somatosensory communities combined (the ‘hand’ and ‘face’ primary motor networks) based on strong consensus of a unified primary motor system. This resulted in 10 network communities. Note that all analyses involved functional connectivity between each of the 10 networks of interest and all 264 regions (i.e., all networks).

Multivariate pattern analyses

Representational similarity analyses were carried out using the methods described by Kriegeskorte et al.³¹. Specifically, Spearman’s rank correlation was used as a similarity/distance metric to identify similarity among task connectivity patterns (including thresholded sets of all FPN connections with all 264 regions). This same similarity metric was also used to compare the connectivity similarity matrix (averaged across subjects) with the task similarity matrix (quantifying the number of rules shared across tasks). Permutation tests were used (1000 permutations each; randomizing both matrices) to test for statistical significance of the relationship between the two similarity matrices across the variable connectivity density thresholds (top 10% to 2%, in 2% increments).

Linear support vector machines using LIBSVM⁵⁸ in MATLAB were used for the pattern classification analyses. Classifiers were trained and tested across subjects (one gPPI beta value per task rule per subject), given recent success with across-subject MVPA when classifying task-state connectivity¹⁰. Training and testing data were kept separate (to avoid circularity) by training on rules from novel tasks and testing on practiced tasks. Standard across-feature normalization (separately for each observation) was applied by subtracting the across-feature mean and dividing by the across-feature standard deviation. Classification significance was assessed using permutation tests (1000 permutations of random training & testing label orders). The 64-way task classification used the three rule classifiers (trained on novel tasks), with a correct task classification requiring that all three rule classifications were correct for a given practiced task.

Note that it was necessary to train with the novel tasks because (for each subject, counterbalanced across subjects) each rule was always confounded with two others for the practiced tasks, such that separate estimates were not possible. In other words, the variety of rule combinations across each subject’s 60 novel tasks allowed for separate estimates of each of the 12 rules (ideal for classification training), while the small number of rule combinations across each subject’s 4 practiced tasks only allowed for classification tests to determine the presence of a task rule among others. Note that the inference – that FPN functional connectivity patterns are consistent across practiced and novel tasks – would be the same had the classifiers been trained on practiced and tested with novel tasks.