Growth on demand: Reviewing the mechanobiology of stretched skin

Abstract

Skin is a highly dynamic, autoregulated, living system that responds to mechanical stretch through a net gain in skin surface area. Tissue expansion uses the concept of controlled overstretch to grow extra skin for defect repair in situ. While the short-term mechanics of stretched skin have been studied intensely by testing explanted tissue samples ex vivo, we know very little about the long-term biomechanics and mechanobiology of living skin in vivo. redHere we explore the long-term effects of mechanical stretch on the characteristics of living skin using a mathematical model for skin growth. We review the molecular mechanisms by which skin responds to mechanical loading and model their effects collectively in a single scalar-valued internal variable, the surface area growth. redThis allows us to adopt a continuum model for growing skin based on the multiplicative decomposition of the deformation gradient into a reversible elastic and an irreversible growth part.redTo demonstrate the inherent modularity of this approach, we implement growth as a user-defined constitutive subroutine into the general purpose implicit finite element program Abaqus/Standard. To illustrate the features of the model, we simulate the controlled area growth of skin in response to tissue expansion with multiple filling points in time. Our results demonstrate that the field theories of continuum mechanics can reliably predict the manipulation of thin biological membranes through mechanical overstretch. Our model could serve as a valuable tool to rationalize clinical process parameters such as expander geometry, expander size, filling volume, filling pressure, and inflation timing to minimize tissue necrosis and maximize patient comfort in plastic and reconstructive surgery. While initially developed for growing skin, our model can easily be generalized to arbitrary biological structures to explore the physiology and pathology of stretch-induced growth of other living systems such as hearts, arteries, bladders, intestines, ureters, muscles, and nerves.

1. MECHANOBIOLOGY OF GROWING SKIN

1.1. redAt the organ level, mechanical stretch induces skin growth

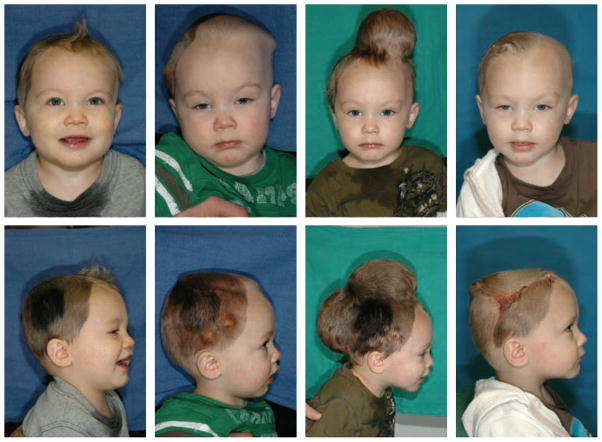
Skin is the largest mechanoreceptive interface of our body and protects our muscles, bones, ligaments, and all our internal organs from chemical, biological, thermal, and mechanical influences of our environment [43]. Remarkably, skin is highly responsive to mechanical loading and can easily double its initial area when subject to mechanical stretch [8]. Plastic and reconstructive surgery capitalize on this dynamic adaptation of skin through the concept of tissue expansion, a controlled application of overstretch to grow new skin in situ [59]. Figure 1 illustrates a clinical case of tissue expansion in pediatric scalp reconstruction. The patient, a one year-old boy, presented with a giant congenital nevus [5]. To grow extra skin for defect repair in situ, tissue expanders were implanted in the frontoparietal and occipital regions of his scalp. The expanders were gradually filled with saline solution to create mechanical overstretch and initiate controlled skin growth [23]. Four months post implantation, the tissue expanders were removed, the nevus was excised, and the defect area was covered by tissue flaps created from the newly grown skin [24]. When the concept of tissue expansion was first introduced, the stretched skin was believed to simply redistribute its mass by increasing its area while reducing its thickness [7]. We now know that skin actually grows in mass; it increases its area while its thickness remains virtually unchanged [54]. Macroscopically, the newly grown skin not only has the same thickness, but also the same mechanical properties as the native tissue [9]. Microscopically, it displays the same surface waviness and possesses a similar cell-to-matrix volume fraction as the original tissue [67]. While tissue expansion has become a widely used procedure in plastic and reconstructive surgery since it was first introduce more than half a century ago [46], there are still no quantitative, mechanistic criteria for the appropriate selection of the relevant clinical process parameters such as expander geometry, expander size, filling volume, filling pressure, and inflation timing [69]. The success of the procedure almost exclusively relies on the skills and experience of the surgeon and on his personal judgement [23]. A common complication associated with the lack of experience is overinflation, which causes skin thinning, necrosis, sloughing, and trauma through excessive tissue tension and compromised vascularization [40]. While it is virtually impossible to measure tissue tension in the living skin in vivo, mathematical modeling provides a safe and cheap alternative to estimate stress, strain, and area gain and avoid overstretch [11]. Personalized computational simulations have the potential to optimize the set of clinical process parameters with the ultimate goal of maximizing surface area gain while minimizing stress, tissue necrosis, inflation timing, and patient discomfort [72].

Figure 1.

Skin expansion in pediatric scalp reconstruction. The patient, a one year-old boy, presented with a giant congenital nevus, left. To grow extra skin for defect repair in situ, tissue expanders are implanted in the frontoparietal and occipital regions of his scalp, middle left. The expanders are gradually filled with saline solution to apply mechanical overstretch and trigger controlled skin growth, middle right. Four months post implantation, the tissue expanders are removed, the nevus is excised, and the defect area is covered by tissue flaps created from the newly grown skin, right.

1.2. redAt the tissue level, mechanical stretch initiates redcell-cell and cell-matrix signaling

Skin is a composite microstructural material consisting of two distinct layers, the epidermis and the dermis [14], see Figure 2. The epidermis, redshown in dark purple in Figure 2, is the 0.1–1.0 mm-thick, waterproof, protective, outer layer. It consists of an approximately four-cell-thick layer of densely packed keratinocytes, which constitute 95% of all cells in the epidermis [43]. Cells of the innermost epidermis, the basal keratinocytes, have a brick-type shape and are joined together tightly by desmosomal junctions. Basal keratinocytes are attached to the basement membrane, the 200 μm-thick divider between the epidermis and the dermis, via a complex network of proteins and glycoproteins including hemidesmosomes and integrin receptors [62]. Mechanical continuity at the basement membrane is key for appropriate force transfer between the epidermis and the dermis. The dermis, redshown in pink in Figure 2,, is the 0.5–5.0 mm-thick, load-bearing inner layer. In contrast to the epidermis, the dermis is largely acellular and consists of 60% water. Of its remaining dry weight, 80–85% consists of loosely interwoven, wavy, randomly oriented collagen fibers, supplemented by 2–4% of elastin [43]. At low mechanical strains, the elastin fibers are stretched out, while the wavy collagen fibers uncrimp and do not contribute markedly to the overall skin stiffness [37]. At higher strains, the stretched, crosslinked collagen network is the main load-carrying element responsible for the characteristic strain locking [32]. Fibroblasts, the major cell type in the dermis, are responsible for the synthesis of extracellular matrix proteins and regulate the collagen content. From below, the dermis is demarcated by the hypodermis, redshown in white in Figure 2, a subcutaneous fatty layer that connects skin to bone and muscle. The hypodermis consists primarily of adipocytes. Its major functions are to provide insulation, mechanical cushioning, and energy storage [43]. When exposed to tension, for example internally-generated during wound healing [13] or externally-applied during tissue expansion [16], forces need to be transferred between the different layers of skin [62]. In the epidermis, stretching of keratinocyte-keratinocyte junctions and of the keratinocyte-basement-membrane interface initiates active cell-cell crosstalk and cell-matrix interaction. In the dermis, stretching of fibroblast-fibroblast junctions and of the fibroblast-collagen interface triggers active cell-cell crosstalk and cell-matrix interaction. In the following two subsections, we review both the mechanisms and the associated mechanotransduction pathways in epidermal keratinocytes and dermal fibroblasts.

Figure 2.

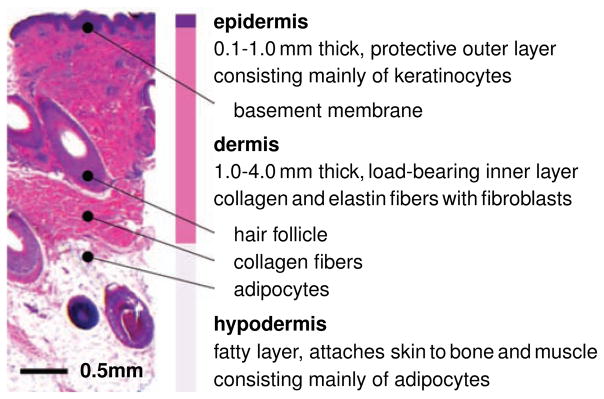
Histological cross section of human skin. Skin is a composite material of multiple layers: The epidermis, the thin outer layer, has a protective barrier function. It consists primarily of densely packed keratinocytes. The dermis, the inner layer, is the main load-bearing element of skin. Its extracellular matrix consists of loosely interwoven collagen and elastin fibers; its major cells are fibroblasts. The hypodermis, the subcutaneous layer, connects skin to bone and muscle. It consists primarily of adipocytes.

1.3. redAt the cellular level, epidermal tension upregulates keratinocyte mitosis

Epidermal tension initiates substantial changes in keratinocyte morphology [52], which manifest themselves in basal keratinocytes flattening [6], and in shape changes from columnar to cuboidal [29]. These configurational changes may directly impact the keratinocyte cytoskeleton and induce a reorientation of F-actin perpendicular to the direction of stretch [66]. These morphological alterations activate biochemical signaling cascades through the initiation of mitogen-activated protein kinase and extracellular signal-regulated kinase pathways [67]. Mitogen-associated protein kinase signaling pathways convey information to effectors, coordinate incoming information from other signaling cascades, amplify signals, and initiate a variety of response patterns [62]. In particular, they trigger the activation of growth factor pathways that affect gene expression and protein synthesis. These mechanisms jointly converge in an up-regulated mitotic activity [6, 52]. However, this increase is not associated with epidermal hyperplasia [18]. redUltimately, epidermal tension results in an increase in the total number of epidermal keratinocytes and a net gain in epidermal surface area. While epidermal stretch causes an acute thickening of the epidermal layer [52], after several months, the epidermal thickness chronically returns to its baseline value [54].

1.4. redAt the cellular level, dermal tension upregulates fibroblast mitosis and synthesis of extracellular matrix proteins

Dermal tension is sensed by dermal fibroblasts as a stretch in the extracellular matrix, see Figure 3. Transmembrane mechanosensors in the form of stretch-activated ion channels, integrins, growth factor receptors, and G-protein-coupled receptors translate these extracellular strains into intracellular signals [28, 71]. Stretch-activated ion channels, redshown in orange in Figure 3, open in response to elevated membrane strains, allowing positively charged calcium ions and other cations to enter the cell. Changes in the intracellular calcium concentration regulate intracellular signaling, alter actin polymerization, and trigger cytoskeletal remodeling [67]. Integrins are heterodimeric transmembrane receptors composed of a regulatory α-unit and a signal transducing β-unit, red-shown in pink and blue in Figure 3. They play a critical role in force transmission across the cell membrane by connecting extracellular collagen to intracellular actin filaments via focal adhesion complexes, talin, and vinculin [63]. Integrins initiate cytoskeletal rearrangement and trigger targets such as nitric oxide signaling, mitogen-associated protein kinases, Rho GTPases, and phosphoinositol-3-kinase. Fibroblast-collagen tension mediated by integrins is an important mechanism to maintain dermal structure and function [62]. Growth factor receptors, redshown in yellow in Figure 3, bind to growth factors outside the cell and turn on several receptor-mediated pathways inside the cell, such as nitric oxide signaling and mitogen-associated protein kinases [28]. G-protein-coupled receptors, redshown in blue in Figure 3,, are seven-transmembrane proteins, which can potentially be activated by mechanical stretch outside the cell to initiate mechanotransduction pathways inside the cell. Their stretch-induced conformational changes initiate second messenger cascades such as nitric oxide signaling and phosphoinositol-3-kinase [67]. Last, the cytoskeleton itself serves as an important internal signaling mechanism. It undergoes highly dynamic conformational changes induced by intracellular strain. These changes may affect the binding affinities to specific molecules and activate additional signaling pathways involving the protein kinase family, second messengers, and nuclear proteins [36]. In summary, dermal tension initiates multiple signaling pathways, which can have a substantial overlap and crosstalk. Since biomechanical signaling pathways are typically shared with biochemical receptor-mediated pathways, it is virtually impossible to study individual pathways in complete isolation. We know, however, that all these signaling pathways converge in the activation of transcription factors, which stimulate gene expression and other nuclear events [28, 71]. redUltimately, dermal tension causes an increase in extracellular matrix proteins and in the total number of dermal fibroblasts, which jointly result in a net gain in dermal surface area. While dermal stretch causes an acute thinning of the dermal layer [52], after several months, the dermal thickness chronically returns to its baseline value [54].

Figure 3.

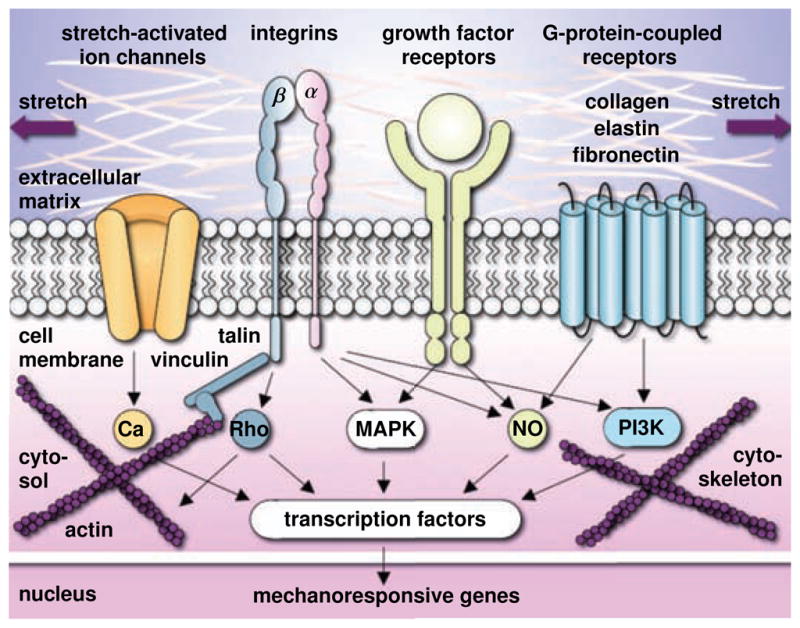
Mechanotransduction of growing skin. Transmembrane mechanosensors in the form of stretch-activated ion channels, integrins, growth factor receptors, and G-protein-coupled receptors translate extracellular signals into intracellular signaling pathways involving calcium (Ca), nitric oxide (NO), mitogen-associated protein kinases (MAPK), Rho GTPases (Rho) and phosphoinositol-3-kinase (PI3K). Biomechanical and biochemical signals converge in the activation of transcription factors that translocate the nucleus and activate mechanoresponsive genes. Increased mitotic activity and increased protein synthesis increase the skin surface area to restore the homeostatic equilibrium state.

2. HISTOLOGY OF GROWING SKIN

To explore structural changes upon tissue expansion, we collected skin samples from non-expanded and expanded regions of a pediatric human scalp. Figure 4 shows histological sections of a non-expanded control sample, left, an expanded normal skin sample, middle, and an expanded scar sample, right.

Figure 4.

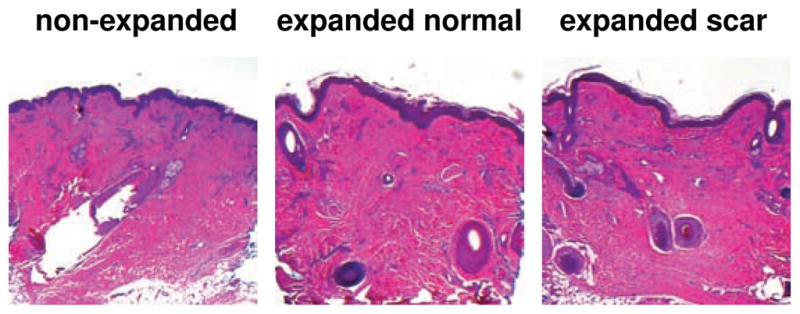
Histological sections of non-expanded control, left, expanded normal skin, middle, and expanded scar, left, from pediatric scalp. Skin expansion creates new skin with the same histological appearance as the native skin: The epidermis of the expanded skin displays a similar wrinkling pattern and thickness as the non-expanded skin. The dermis of the expanded skin displays the same thickness as the non-expanded skin. Expanded and non-expanded samples are histologically similar with similar cell-to-matrix volume ratios and a similar collagenous microstructure.

The epidermis, redstained in purple in Figure 4, does not change markedly upon expansion. It displays a similar wrinkling pattern in all three samples [38]. The thickness of the expanded epidermis is similar to the non-expanded epidermis. The expanded epidermis redshows no evidence of necrosis, inflammation, or epidermal hyperplasia. Overall, we conclude that tissue expansion initiates an increase in epidermal surface area at constant epidermal thickness through increased keratinocyte mitosis. These observations are in excellent agreement with findings reported in the literature [6, 18, 54]. Histological analyses in the literature report that, long-term, neither the epidermal thickness nor the number of epidermal layers redundergo statistically significant changes after tissue expansion [68, 70].

Similar to the epidermis, the dermis, redstained in pink in Figure 4, does not change noticeably upon tissue expansion. The average dermal thickness is 2.0 mm in the non-expanded sample and 2.05 mm in the expanded samples. However, the expanded dermal thickness varies locally depending on the presence of subcutaneous adipocytes. The expanded dermis is histologically similar to the non-expanded dermis with similar cell-to-matrix volume ratios and a similar loosely interwoven, wavy, randomly-oriented collagenous microstructure. It redshows no evidence of inflammation, no evidence of malignant degeneration, and no loss of microstructural organization. Overall, we conclude that tissue expansion initiates an increase in dermal surface area at constant dermal thickness through increased fibroblast mitosis and increased collagen synthesis. These observations are in agreement with findings reported in the literature both in animals [6, 52] and in humans [59].

Unlike the epidermis and the dermis, the subcutaneous hypodermis undergoes significant changes upon tissue expansion. Subcutaneous adipocytes are compressed and diminished in size. This results in a significant net thinning of the subcutaneous layer. The expanded region itself undergoes subcutaneous fibrosis with a host inflammatory response. Subcutaneous collagen fibers and fibroblasts reorient themselves parallel to the expander, which becomes surrounded by a thin layer of histiocytes. These observations agree nicely with findings in the literature [6, 18, 52]. Histological analyses in the literature report flattening, shrinkage, and atrophy of adipocytes as well as an acute thinning of the subcutaneous layer, which gradually returns to its baseline thickness within two years after completion of the procedure [53].

These histological observations have important consequences when modeling skin growth: First, we can confidently assume that the thickness of the epidermal and dermal layers does not change when skin is subjected to controlled chronic overstretch. Second, we can assume that the newly grown skin has the same microstructure and the same mechanical properties as the original native tissue. Third, since the skin area increases and the thickness remains constant, skin undergoes significant changes in mass and can be modeled thermodynamically as an open system.

3. CONTINUUM MODELING OF GROWING SKIN

Motivated by the mechanobiology of growing skin summarized in Section 1 and by our histological study in Section 2, we now formulate a continuum model for controlled stretch-induced skin growth. To characterize the large deformations when stretching skin, we introduce the deformation map ϕ, which maps points X from the undeformed configuration to their new positions x = ϕ (X, t) in the deformed configuration. We can then characterize changes of infinitesimal line elements through the deformation gradient,

$$\mathit{F}={\stackrel{\sim }{\mathit{N}}}_{\mathit{X}}\mathit{\phi }={\mathit{F}}^{\text{e}}·{\mathit{F}}^{\text{g}},$$ (1)

which we decompose multiplicatively into redan elastic part F^e and reda growth part F^g [19, 60]. Similarly, we can characterize changes in skin volume through the Jacobian,

$$J=det(\mathit{F})=J^{\text{e}}{J}^{\text{g}},$$ (2)

which we decompose into a reversibly elastic volume change J^e = det (F^e) and an irreversibly grown volume change J^g = det (F^g). redMotivated by our histological analysis in Section 2, we assume that the response in the thickness direction n₀ is purely reversible and elastic. In the skin plane, orthogonal to n₀, we characterize skin growth through a single scalar-valued variable, the surface area growth ϑ^g. This allows us to characterize changes in skin area through the area stretch,

$$\vartheta =\left|\right|J{\mathit{F}}^{-\text{t}}·{\mathit{n}}_0\left|\right|={\vartheta }^{\text{e}}{\vartheta }^{\text{g}},$$ (3)

which we decompose into a reversibly elastic area change ϑ^e and an irreversibly grown area change ϑ^g, where n₀ denotes the skin plane unit normal in the undeformed reference configuration [11]. With the assumptions above, the growth tensor F^g takes the following simple format [73],

$${\mathit{F}}^{\text{g}}=\sqrt{{\vartheta }^{\text{g}}}\mathit{I}+[1-\sqrt{{\vartheta }^{\text{g}}}]{\mathit{n}}_0\otimes {\mathit{n}}_0.$$ (4)

Since we assume that skin does not grow in the thickness direction, its area growth is identical to its volume growth, i.e., ϑ^g = ||J^g F^{g −t} · n₀|| = det(F^g) = J^g. Using the simple rank-one update structure of F^g, we can explicitly invert the growth tensor with the help of the Sherman-Morrison formula [45],

$${\mathit{F}}^{\text{g}-1}=\frac{1}{\sqrt{{\vartheta }^{\text{g}}}}\mathit{I}+\left[1-\frac{1}{\sqrt{{\vartheta }^{\text{g}}}}\right]{\mathit{n}}_0\otimes {\mathit{n}}_0.$$ (5)

From the multiplicative decomposition (1), we then obtain an explicit representation of the elastic tensor F^e = F · F^g−1,

$${\mathit{F}}^{\text{e}}=\frac{1}{\sqrt{{\vartheta }^{\text{g}}}}\mathit{F}+\left[1-\frac{1}{\sqrt{{\vartheta }^{\text{g}}}}\right]\mathit{n}\otimes {\mathit{n}}_0,$$ (6)

and of the elastic left Cauchy-Green tensor b^e = F^e · F^{e t},

$${\mathit{b}}^{\text{e}}=\frac{1}{{\vartheta }^{\text{g}}}\mathit{b}+\left[1-\frac{1}{{\vartheta }^{\text{g}}}\right]\mathit{n}\otimes \mathit{n}.$$ (7)

Here, b = F · F^t is the total left Cauchy-Green tensor and redn = F ·n₀ is the deformed skin normal, which is no longer a unit vector. redTo focus on the effect of growth, we neglect the skin’s collagenous microstructure and the associated anisotropy [12, 32]. Accordingly, we approximate its constitutive response as isotropically elastic, and characterize it through the following Helmholtz free energy function parameterized exclusively in terms of the reversible elastic part of the deformation,

$$\psi =\frac{1}{2}\lambda {ln}^2(J^{\text{e}})+\frac{1}{2}\mu [{\mathit{b}}^{\text{e}}:\mathit{i}-3-2ln(J^{\text{e}})].$$ (8)

Here, i denotes the spatial unit tensor. Motivated by our histological analysis in Section 2, we assume that the newly grown skin has the same microstructure, density, and stiffness, as the original native tissue [9, 11]. This implies that we can derive the Kirchhoff stress τ from the standard Colemann-Noll evaluation of the dissipation inequality for open systems [21, 31],

$$\tau =2\frac{\partial \psi }{\partial {\mathit{b}}^{\text{e}}}·{\mathit{b}}^{\text{e}}=[\lambda ln(J^{\text{e}})-\mu ]\mathit{i}+\mu {\mathit{b}}^{\text{e}}.$$ (9)

Next, we specify the evolution of area growth ϑ^g, which we model as a strain-driven process [24] using the following equation,

$${\stackrel{.}{\vartheta }}^{\text{g}}=k^{\text{g}}{\phi }^{\text{g}}.$$ (10)

Here we have introduced the weighting function

$$k^{\text{g}}=\frac{1}{\tau }{\left[\frac{{\vartheta }^{max}-{\vartheta }^{\text{g}}}{{\vartheta }^{max}-1}\right]}^{\gamma }$$ (11)

to control unbounded growth [20, 41]. It has three well-defined material parameters, the maximum possible area growth ϑ^max, the growth speed τ, and the nonlinearity parameter γ [25, 73]. In addition, we have introduced the growth criterion φ^g driven by the elastic area stretch ϑ^e,

$${\phi }^{\text{g}}=\langle {\vartheta }^{\text{e}}-{\vartheta }^{\text{crit}}\rangle =\langle \vartheta /{\vartheta }^{\text{g}}-{\vartheta }^{\text{crit}}\rangle .$$ (12)

The Macaulay brackets 〈 ○ 〉 ensure that growth is only activated if the elastic area stretch ϑ^e = ϑ/ϑ^g exceeds a critical physiological limit ϑ^crit. redHere we have adopted a phenomenological approach to introduce a stretch-driven evolution equation for the growth tensor F^g based on clinical observations [9]. Alternatively, we could have used thermodynamical considerations to formulate evolution equations for growth with the Mandel stress [17] or higher order gradients [15] as driving forces.

4. COMPUTATIONAL MODELING OF GROWING SKIN

To solve the nonlinear finite element equations for stretch-induced membrane growth, we implement the growth model as a user subroutine into the commercial implicit finite element solver Abaqus/Standard Version 6.12 [1]. We introduce the area growth ϑ^g as an internal variable, and solve its evolution equation (10) locally at the integration point level. We approximate the growth rate ϑ̇^g through a finite difference approximation,

$${\stackrel{.}{\vartheta }}^{\text{g}}=[{\vartheta }^{\text{g}}-{\vartheta }_{\text{n}}^{\text{g}}]/\mathrm{\Delta }t,$$ (13)

where Δt = t − t_n denotes the current time increment. We apply an implicit time integration scheme and reformulate the evolution equation (10) with the help of equation (13), introducing the discrete residual R^ϑ in terms of the unknown area growth ϑ^g,

$${\text{R}}^{\vartheta }={\vartheta }^{\text{g}}-{\vartheta }_{\text{n}}^{\text{g}}-k^{\text{g}}{\phi }^{\text{g}}\mathrm{\Delta }t\doteq 0.$$ (14)

To solve this nonlinear equation we apply a local Newton iteration. Within each iteration step, we calculate the linearization of the residual R^ϑ with respect to the current area growth ϑ^g,

$${\text{K}}^{\vartheta }=\frac{\partial {\text{R}}^{\vartheta }}{\partial {\vartheta }^g}=1-\left[\frac{\partial k^{\text{g}}}{\partial {\vartheta }^{\text{g}}}{\phi }^{\text{g}}+k^{\text{g}}\frac{\partial {\phi }^{\text{g}}}{\partial {\vartheta }^{\text{g}}}\right]\mathrm{\Delta }t.$$ (15)

Here, ∂k^g/∂ϑ^g = −γk^g/[ϑ^max − ϑ^g ] and ∂φ^g/∂ϑ^g = −ϑ/ϑ^g2 denote the linearizations of the weighting function and of the growth criterion introduced in equations (11) and (12). Within each Newton iteration, we update the unknown area growth

$${\vartheta }^{\text{g}}\leftarrow {\vartheta }^{\text{g}}-{\text{R}}^{\vartheta }/{\text{K}}^{\vartheta },$$ (16)

until we achieve local convergence, i.e., until the absolute value of the growth update Δϑ^g = −R^ϑ/K^ϑ reaches a user-defined threshold value. Once we have determined the current area growth ϑ^g from equation (16), we can successively determine the growth tensor F^g from equation (4), the elastic tensor F^e = F ·F^{g −1} from equation (6), the elastic left Cauchy-Green tensor b^e = F^e · F^{e t} from equation (7), the Kirchhoff stress τ from equation (9), and, finally, the fourth-order tensor of the Eulerian constitutive moduli [56],

$$\mathbf{c}=4{\mathit{b}}^{\text{e}}·\frac{{\partial }^2\psi }{\partial {\mathit{b}}^{\text{e}}\otimes {\mathit{b}}^{\text{e}}}·{\mathit{b}}^{\text{e}}={\mathbf{c}}^{\text{e}}+{\mathbf{c}}^{\text{g}}.$$ (17)

The first term, the Hessian of the free energy function at constant growth F^g, defines the standard elastic constitutive moduli,

$$\begin{array}{l}{\mathbf{c}}^{\text{e}}={4{\mathit{b}}^{\text{e}}·\frac{{\partial }^2\psi }{\partial {\mathit{b}}^{\text{e}}\otimes {\mathit{b}}^{\text{e}}}·{\mathit{b}}^{\text{e}}|}_{{\mathit{F}}^{\text{g}}=\text{const}}\\ =\lambda \mathit{i}\otimes \mathit{i}+[\mu -\lambda ln(J^{\text{e}})][\mathit{i}\overline{\otimes }\mathit{i}+\mathit{i}\underset{\_}{\otimes }\mathit{i}].\end{array}$$ (18)

Here we have used the common abbreviations, {●⊗̄○}_{i jkl} = {●}_ik {○}_jl and {●⊗○}_{i jkl} = {●}_il {○}_jk, for the non-standard fourth order products. The second term, the Hessian of the free energy function at constant deformation F, defines the correction of the constitutive moduli due to growth [72],

$$\begin{array}{l}{\mathbf{c}}^{\text{g}}={4{\mathit{b}}^{\text{e}}·\frac{{\partial }^2\psi }{\partial {\mathit{b}}^{\text{e}}\otimes {\mathit{b}}^{\text{e}}}·{\mathit{b}}^{\text{e}}|}_{\mathit{F}=\text{const}}\\ =-\frac{1}{{\vartheta }^{\text{g}3}}\frac{k^{\text{g}}}{{\text{K}}^{\text{g}}}\mathrm{\Delta }t[\lambda {\vartheta }^{\text{g}}\mathit{i}+\mu [\mathit{b}-\mathit{n}\otimes \mathit{n}]]\otimes [\vartheta \mathit{i}-J^2/\vartheta [{\mathit{F}}^{-\text{t}}·{\mathit{n}}_0]\otimes [{\mathit{F}}^{-\text{t}}·{\mathit{n}}_0]].\end{array}$$ (19)

Rather than working directly with the Kirchhoff stress (9) and with the constitutive moduli (17), the user-defined subroutine in Abaqus/Standard utilizes the Cauchy or true stress, σ = τ/J,

$${\sigma }^{\text{abaqus}}=[[\lambda ln(J^{\text{e}})-\mu ]\mathit{i}+\mu {\mathit{b}}^{\text{e}}]/J,$$ (20)

and the Jauman rate of the Kirchhoff stress divided by the Jacobian, which requires the following modification of the tangent moduli [1, 55],

$${\mathbf{c}}^{\text{abaqus}}=[\mathbf{c}+\frac{1}{2}[\mathit{\tau }\overline{\otimes }\mathit{i}+\mathit{i}\overline{\otimes }\mathit{\tau }+\mathit{\tau }\underset{\_}{\otimes }\mathit{i}+\mathit{i}\underset{\_}{\otimes }\mathit{\tau }]]/J.$$ (21)

The local stress σ^abaqus of equation (20) and the local tangent moduli c^abaqus of equation (21) enter the righthand side vector and the iteration matrix of the global Newton iteration. Upon its convergence, we store the current area growth ϑ^g locally at the integration point level.

5. SIMULATION OF GROWING SKIN

To explore the effects of skin growth, we simulate the process of controlled tissue expansion with multiple filling points in time, first in an idealized square skin sample and then in a patient-specific pediatric scalp.

5.1. Skin growth of an idealized square skin sample

For the first problem, we virtually implant expanders with four different shapes in the subcutaneous pocket underneath the dermis. We systematically increase the tissue stretch by gradually increasing the filling volume of all four expanders. To model the epidermis and the dermis, we discretize a 10 × 10 cm² flat sheet, 0.2 cm thick, with 33 × 33 × 2 = 2,178 C3D8 eight-noded linear brick elements, corresponding to a total of 3,468 nodes and 10,404 degrees of freedom. We model the elastic response as Neo-Hookean according to equations (8) and (9) with Lamé parameters redλ = 0.5440 MPa and redμ = 0.1785 MPa [48], and the growth response as transversely isotropic and strain driven according to equations (10), (11), and (12) with a maximum growth of ϑ^max = 2.4, a growth speed of τ = 10, a growth nonlinearity of γ = 2, and a critical growth threshold of ϑ^crit = 1.1 [72]. To model the tissue expander itself, we introduce a fluid-filled cavity with a base area of 36 cm², discretized with S3R and S4R shell elements. We model its elastic response using the material parameters of silicone [42] and discretize the fluid cavity with the same nodes and connectivity, but with F3D3 and F3D4 fluid elements. To allow the skin to slide freely along the expander we model their interaction as frictionless contact. We apply homogeneous Dirichlet boundary conditions to all neighboring nodes not involved in the expansion procedure.

Figure 5 displays the loading history for all four expanders: rectangular, crescent-shaped, square, and circular. We inflate each expander by gradually increasing its filling volume in three steps of 50 ml. After each filling step, we allow the skin to grow and establish a new equilibrium state before applying the next filling step. After three steps, we gradually release the entire filling volume to remove the expander.

Figure 5.

Skin growth upon tissue expansion. The filling volume of all four expanders, rectangular, crescent-shaped, square, and circular, is gradually increased by 150 ml in three steps of 50 ml each, and then gradually removed.

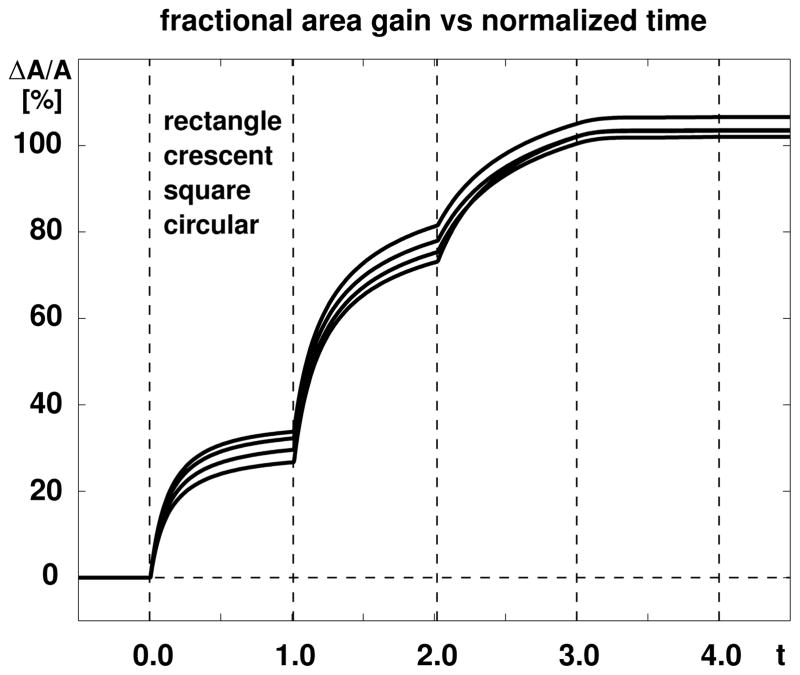
Figure 6 displays the evolution of the fractional area gain, i.e., the net integral of skin growth, scaled by the initial base surface area, for all four expanders. Upon increasing the expander volume, the skin stretch exceeds the critical physiological threshold ϑ^crit and triggers the skin area to grow. The area increases gradually until growth has converged towards the biological equilibrium state. At this point, the elastic area stretch ϑ^e = ϑ/ϑ^g has gradually returned to its physiological threshold value ϑ^crit. When subject to a new filling increment, the procedure repeats itself accordingly. The skin area above the four expanders increases on average by ~31% in the first step, ~46% in the second step, and ~25% in the third step. This illustrates the nonlinear nature of the growth process. When the filling volume is removed, the fractional area gain remains constant. This illustrates the irreversible nature of the growth process. At the end of the procedure, the rectangular expander has initiated the largest amount of fractional area growth with 1.0659, followed by the crescent-shaped expander with 1.0355, the square expander with 1.0201, and the circular expander with 1.0343. For all four expanders, skin has more than doubled its initial area, i.e., it has grown by more than 36 cm².

Figure 6.

Skin growth upon tissue expansion. The area above all four expanders increases by ~31% in the first step, by ~46% in the second step, by ~25% in the third step, and remains constant upon expander removal. The rectangular expander initiates the largest amount of growth, followed by the crescent-shaped, square, and circular expanders.

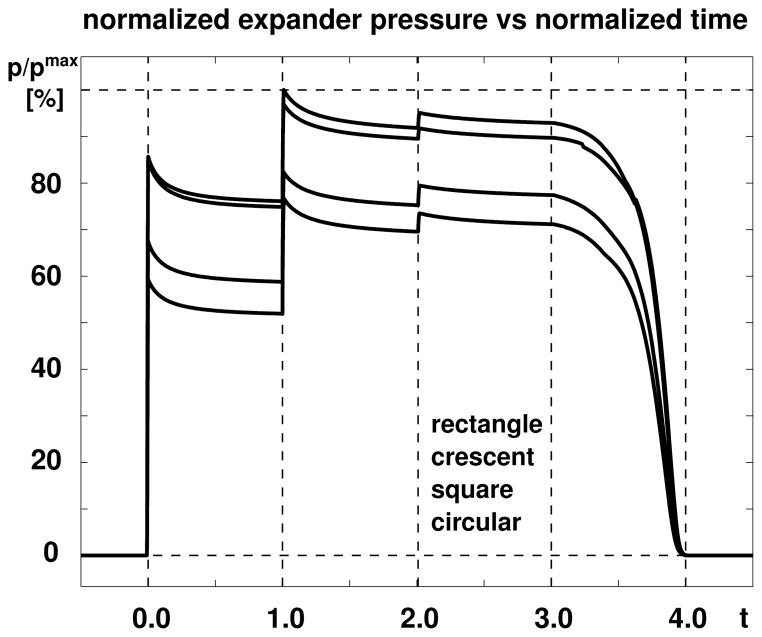
Figure 7 displays the evolution of the expander pressure for all four expanders. The increase in expander volume at the beginning of each filling step is associated with an instant increase in expander pressure and a gradual relaxation towards the homeostatic equilibrium state. Since we fill the expander with a constant volume, the total skin area stretch ϑ = ϑ^e ϑ^g remains constant within each step. As the skin flap grows, the area growth ϑ^g increases and the elastic area stretch ϑ^e decreases. Since the stresses in the growing skin are a function of the elastic strains alone, the skin stresses decrease accordingly. This implies that the pressure induced by a constant filling volume decreases over time converging towards an equilibrium state. This equilibrium pressure increases nonlinearly with the filling volume taking average values of 0.654 p^max in the first step, 0.816 p^max in the second step, and 0.828 p^max in the third step, before returning back to 0.000 p^max after expander removal. Because the filling pressure is not only equilibrated by the stresses in the skin, but also by the stresses in the expander, which increase with increased filling volume, the equilibrium pressure increases with volume. The rectangular expander is subject to the largest pressure with a maximum value of 0.3752 MPa, followed by the crescent-shaped expander with 0.3637 MPa, the square expander with 0.3087 MPa, and circular expander with 0.2879 MPa.

Figure 7.

Skin growth upon tissue expansion. The expander pressure of all four expanders increases instantly upon inflation and relaxes gradually as skin grows in area and the elastic strain decreases. The rectangular expander is subject to the largest pressured, followed by the crescent-shaped, square, and circular expanders.

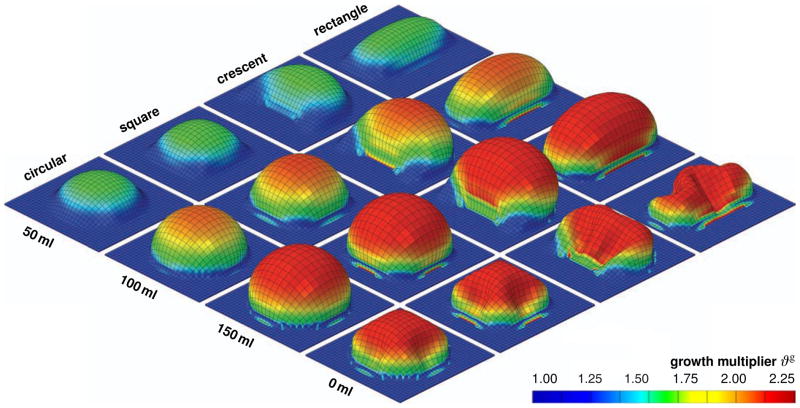
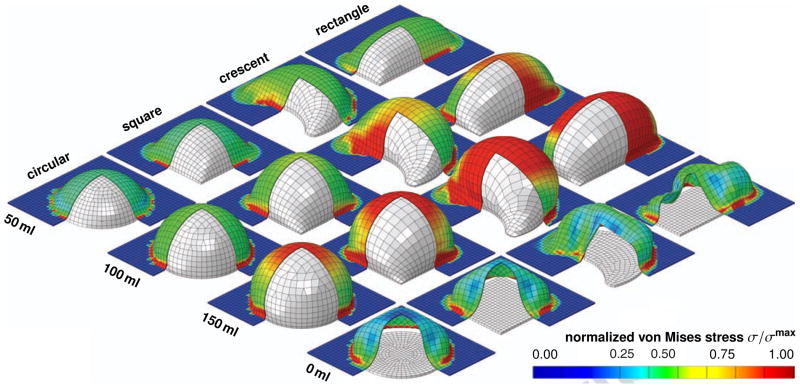
Figure 8 displays the spatio-temporal evolution of the growth multiplier ϑ^g for the rectangular, crescent-shaped, square, and circular expanders, from top to bottom. The individual snapshots correspond to the converged equilibrium states for filling volumes of 50 ml, 100 ml, and 150 ml, and to the deflated state with the filling volume reduced to 0 ml, from left to right. Skin growth displays significant regional variations. Largest growth takes place in the center region with values up to ϑ^g = 2.25, shown in red, indicating that the initial area has more than doubled in size. Smallest growth takes place along the expander edges with values of ϑ^g = 1.00, shown in blue, indicating that no growth has taken place at all.

Figure 8.

Skin growth upon tissue expansion. Spatio-temporal evolution of growth multiplier ϑ^g for rectangular, crescent-shaped, square, and circular expanders, from top to bottom. Snapshots correspond to converged equilibrium states for filling volumes of 50 ml, 100 ml, and 150 ml, and to deflated state with filling volume of 0 ml, from left to right. The color code illustrates the evolution of the growth multiplier ϑ^g, ranging from ϑ^g = 1.00 for the initial ungrown skin, shown in blue, to ϑ^g = 2.25 for the fully grown state, shown in red. Skin growth displays significant regional variations with largest values in the center region and smallest values along the expander edges.

Figure 9 displays the spatio-temporal evolution of the normalized von Mises stress σ/σ^max for the rectangular, crescent-shaped, square, and circular expanders, from top to bottom. The individual snapshots correspond to the converged equilibrium states for filling volumes of 50 ml, 100 ml, and 150 ml, and to the deflated state with the filling volume reduced to 0 ml, from left to right. To illustrate the individual skin expanders, we have virtually removed the lower corner of the skin patch. For the same filling volume and the same base surface area, the rectangular expander initiates the largest stresses, followed by the crescent-shaped, square, and circular expanders. Stresses display significant regional variations. Largest stresses are located in the center region and along the expander edges, shown in red. Moderate stresses are located at the expander sides, shown in green. No stresses occur in the unexpanded regions, shown in blue.

Figure 9.

Skin growth upon tissue expansion. Spatio-temporal evolution of normalized von Mises stress σ/σ^max for rectangular, crescent-shaped, square, and circular expanders, from top to bottom. Snapshots correspond to converged equilibrium states for filling volumes of 50 ml, 100 ml, and 150 ml, and to deflated state with filling volume of 0 ml, from left to right. Under the same filling volume and the same base surface area, the rectangular expander initiates the largest stresses, followed by the crescent-shaped, square, and circular expanders. The color code illustrates the evolution of the normalized stress σ/σ^max, ranging from σ/σ^max = 0.00 for the initial ungrown skin, shown in blue, to σ/σ^max = 1.00 for the fully grown state, shown in red.

5.2. Skin growth of a pediatric scalp

For the second problem, we closely follow a clinical tissue expansion protocol and simulate skin growth in the scalp of the pediatric patient shown in Figure 1. We virtually insert a rectangular expander with a base surface area of 14 × 10 cm² in a subcutaneous pocket of the frontoparietal scalp. The expander has a filling capacity of 450 ml, which we reach gradually by increasing the filling volume in three consecutive steps of 150 ml each. To model the epidermis and the dermis, we discretize the skin on top of the expander as a 14 × 10 cm² large, 0.2cm thick layer with 45 × 32 × 2 = 2,880 C3D8 eight-noded linear brick elements, corresponding to a total of 4,554 nodes and 13,662 degrees of freedom. Similar to the idealized square skin sample in Section 5.1, we model the elastic response as Neo-Hookean according to equations (8) and (9) with Lamé parameters redλ = 0.5440 MPa and redμ = 0.1785 MPa [48], and the growth response as transversely isotropic and strain driven according to equations (10), (11), and (12) with a maximum growth of ϑ^max = 2.4, a growth speed of τ = 10, a growth nonlinearity of γ = 2, and a critical growth threshold of ϑ^crit = 1.1 [72]. We model the skin expander as a fluid-filled cavity with a base area of 14 × 10 cm², discretized with 638 S4R shell elements, corresponding to a total of 640 nodes and 1,920 degrees of freedom. We model its elastic response using the material parameters of silicone [42] and discretize the fluid cavity with the same nodes and connectivity, but with F3D4 fluid elements. We allow the skin to slide freely along the expander and model the skin-expander interaction as frictionless contact. We fix all nodes that are not involved in the expansion procedure using homogeneous Dirichlet boundary conditions.

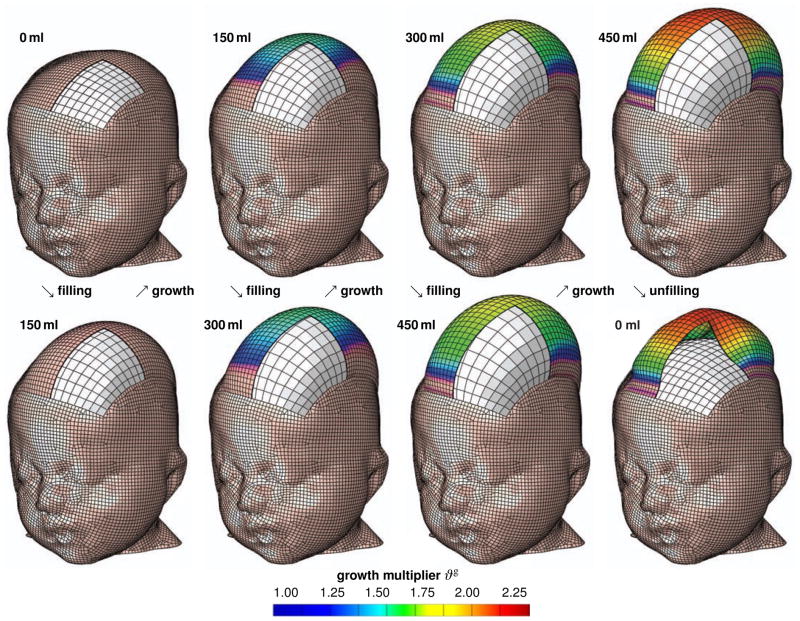
Figure 10 displays the spatio-temporal evolution of the growth multiplier ϑ^g immediately after filling, bottom row, and after converged growth, top row. The individual snapshots correspond to the initial filled states and the converged homeostatic equilibrium states for filling volumes of 150 ml, 300 ml, and 450 ml, and to deflated state with filling volume of 0 ml, from left to right. Similar to the idealized square skin sample in Section 5.1, skin growth displays regional variations in magnitude with largest values in the center region, shown in red, and smallest values along the expander edges, shown in blue.

Figure 10.

Skin growth upon tissue expansion in pediatric scalp reconstruction. Spatio-temporal evolution of growth multiplier ϑ^g immediately after filling, bottom row, and after converged growth, top row. Snapshots correspond to filling volumes of 150 ml, 300 ml, and 450 ml, and to deflated state with filling volume of 0 ml, from left to right. The color code illustrates the evolution of the growth multiplier ϑ^g, ranging from ϑ^g = 1.00 for the initial ungrown skin, shown in blue, to ϑ^g = 2.25 for the fully grown state, shown in red. Skin growth displays significant regional variations with largest values in the center region and smallest values along the expander edges.

6. DISCUSSION

6.1. Discussion of results

We have presented a constitutive model for overstretch-induced skin growth, which allows us to predict chronic changes in stress, strain, and area gain in thin biological membranes. Upon expander inflation, our model predicts an acute increase in the total area stretch ϑ = ϑ^eϑ^g, associated with an acute decrease in skin thickness. Inititally, in the absence of growth ϑ^g = 0, the total stretch is carried exclusively by the elastic stretch ϑ^e = ϑ, which increases acutely. Since the skin stress τ (b^e) is a function of the elastic part of the deformation only, the acute increase in elastic stretch induces an acute increase in tissue stress, and accordingly, an acute increase in the expander pressure, see Figure 7.

Over time, our model predicts a chronic increase in area growth ϑ^g, see Figures 6, 9, and 10. Since we drive expander inflation by controlling the filling volume, as shown in Figure 5, the total area stretch ϑ= ϑ^eϑ^g remains constant between two filling sessions. Accordingly, a chronic increase of the area growth ϑ^g ↑ implies a chronic decrease of the elastic area stretch ϑ^e ↓, which gradually returns to its homeostatic equilibrium value ϑ^e → ϑ^crit. Similarly, the model predicts a gradual return of the skin thickness to its initial baseline value. The chronic decrease of the elastic stretch induces a chronic decrease in the skin stress τ (b^e), which manifests itself in a decrease in expander pressure, see Figure 7. Rheologically, this chronic response resembles the phenomenon of relaxation. However, the expander pressure p/p^max never fully returns to zero because of the inherent resistance of the silicone expander itself.

Upon expander deflation, the elastic strain decreases below the critical threshold value ϑ^e < ϑ^crit associated with an acute arrest of further growth ϑ^g = const, see Figures 6 and 10, bottom right. Deflation is associated with an acute retraction of the reversible elastic area stretch back to its initial baseline value of ϑ^e → 1.0 and an acute release of the expander pressure p/p^max → 0, see Figure 7. Although the expander volume is fully released at the end of the procedure, the heterogeneity of the growth process leaves some residual elastic deformation, which manifests itself in residual stresses upon expander removal, see Figure 9, right, and Figure 10, bottom right.

redIn space, our model predicts regional variations in the amount of growth with larger values in the center region and smaller values in the periphery, see Figures 8 and 10. Expander inflation causes largest area strains in the center region. This triggers a heterogeneity of the growth process. In the center region, skin more than doubles its initial area with ϑ^g → ϑ^max, while the amount of growth gradually decays towards the expander edges.

6.2. Comparison with the literature

The characteristic features predicted by our model are in excellent agreement with the observed phenomena during tissue expansion in animals [9, 10] and in humans [24, 49]. In the tissue expansion literature, our decomposition of the deformation gradient into reversible and irreversible parts F = F^e · F^g is referred to as mechanical creep and biological creep [29] or, more illustratively, as loan and dividend [7]. What is referred to as stretch back in the tissue engineering literature [69] is associated with the reversible elastic part of the deformation, which is released upon expander removal. To account for this reversible deformation, empirical guidelines suggest to select an expander size with a base surface area which is 2.5 larger than the defect area to be closed [29]. A quantitative study of skin growth in pigs recommends to multiply the required surface area with an empirical correction factor. Recommended correction factors range from 6.00 to 4.50 and 3.75 for the circular, crescent shaped, and rectangular expanders, respectively [69]. In agreement with our findings in Figures 6 and 8, these correction factors suggest that the net area gain is greatest for the rectangular expander, followed by the crescent-shaped and circular expanders [10, 69]. A comparison of the fractional area gain ΔA/A revealed values ranging from 35% to 137% [29]. Our fractional area gain between 100% and 110% as displayed in Figure 6 is well within this range.

In one of the earliest quantitative studies of controlled tissue expansion in guinea pigs, it was argued that stretching skin stimulates cell proliferation just sufficient to relieve tension [18]. This is in agreement with the rheological analogy of stress relaxation [12], which we observed in Figure 7. In a chronic porcine model, the expander pressure was found to increase acutely, but returned to its homeostatic equilibrium state after a period of a few days [10]. The fact that this equilibrium state changes nonlinearly with the amount of filling was attributed to nonlinearities in the constitutive responses of both the expanded skin and the silicone expander itself [10]. This is in excellent agreement with our observations in Figure 7. Along the same lines, detailed thickness studies of expanded human skin revealed an initial epidermal thickening, dermal thinning, and and subcutaneous thinning five months after expansion. However, the thicknesses of all three layers returned to their pre-expansion baseline values two years after the procedure had been completed [53, 54]. This is in agreement with the acute and chronic features predicted by our model, see Figure 7.

redControlled tissue expansion studies in rodents revealed a regional variation of skin growth with largest growth in the center region and smallest growth in the periphery [9]. The authors hypothesized that larger strains in the center region would trigger larger growth. This feature is nicely reflected by our model, in which the evolution of area growth in equation (10) is directly correlated to the amount of overstretch through the growth criterion in equation (12). Figures 8 and 10 clearly support the experimental observations of a heterogeneous growth process with larger values in the center region and smaller values in the periphery [9].

red We have implemented our growth model as user-defined constitutive subroutine into the general purpose finite element program Abaqus/Standard Version 6.12 [1]. Instead of using the explicit version Abaqus/Explicit, as previously proposed for tissue expansion in breast reconstruction [47], we have used the implicit version of the program. To ensure optimal convergence of the global Newton iteration, our implicit user subroutine not only has to provide the constitutive equation for the Cauchy stress σ^abaqus from equation (20), but also the local tangent moduli c^abaqus from equation (21).

While the model for breast reconstruction can only account for mechanical creep in terms of the reversible deformation [47], our model is also capable of predicting biological creep in terms of irreversible deformation in the form of growth. The very first finite element model for biological creep, or rather skin growth, was also realized within Abaqus/Explicit, however only for axisymmetric circular expander geometries and restricted to an explicit time integration [64]. redWhile our first prototype finite element models for growth were fully three dimensional and implicit [11, 72], this manuscript documents our first implementation of the model into a commercially available finite element package. This allows us to use the entire infrastructure of a multi-purpose finite element program, including features such as the fluid filled cavity to model the expander [49], and frictionless sliding to model the expander-skin interface [1]. Our first prototype simulations did not discretize the expander explicitly, but were rather entirely pressure driven [12, 73]. The current model represents a significant advancement of our previous attempts to model skin expansion in a clinical setting, since it allows us to model expander inflation by precisely controlling filling volumes according to multi-step clinical filling protocols [61]. Driving tissue expansion through filling volume rather than filling pressure mimics the clinical procedure more closely [50, 51], and will eventually allow us to directly optimize clinical process parameters. Overall, our new model nicely captures the essential features of overstretch-induced area growth in skin, not only acutely but also chronically.

6.3. Future challenges

We believe that the proposed model is a successful first step towards studying the interaction of mechanics and biology during skin growth. Nevertheless, several open challenges need to be addressed in the future to turn this first prototype model into a reliable predictive tool for clinical research.

From reductionist to holistic

First and foremost, to gain a full understanding of the complex behavior skin as a living system, it is important to explore and characterize skin across different spatial and temporal scales [30]. We need to appreciate that skin, as a living system, is more than just the sum of its parts [49]. Throughout the past century, we have gained valuable insight from both biochemical assays and mechanical testing [27]. However, it has only been within the past decade that we have started to decipher the active crosstalk between biology and mechanics [71]. The biomechanics of skin, i.e., the ways in which biology influences mechanical characteristics such as stress, strain, or energy, seem relatively well understood by now. The mechanobiology of skin, i.e., the ways in which mechanical forces, stretch, or stretch rates can manipulate biological systems, are a lot less well characterized [16]. At this point, to gain a complete picture of the complex nature of skin as a living system, it seems that our efforts have to move from a classical reductionist to a more holistic approach. Computational modeling could be a valuable tool to integrate information across the scales and, more importantly, across individual disciplines [74]. Specifically, in terms of our growth model, a more holistic approach would imply tying the growth law in equation (4) more closely to the underlying mechanobiology described Section 1. Time sequences of gene expression assays and immunohistochemistry of growing tissue samples could help to identify the mechanisms that trigger skin growth redat the molecular and cellular levels [67]. Eventually, this information could help to replace the phenomenological evolution equation for the growth tensor (4) by a discrete network of mechanotransduction pathways of specific extracellular and intracellular events [62]. For example, a more mechanistic model could incorporate pathways from polymer synthesis to the deposition of large bundles of compacted immature collagen redat the microstructural level [8], which manifest themselves macrostructurally in the reorientation of the collagen network and through a realignment the direction of maximum principal strains [26, 34].

From qualitative to quantitative

Using mathematical modeling to better understand living systems emphasizes the need to move from qualitative to quantitative biochemical essays and biomechanics testing [3]. In this endeavor, mathematical modeling could help to specify and redesign biochemical assays with well-defined quantitative readouts. Ideally, a hybrid computational-experimental approach would help to identify quantitative biochemical metrics of growth, which could directly feed into discrete mechanotransduction network models of interconnected positive and negative feedback loops. These discrete network models would replace the phenomenological evolution equation for area growth (10) by a biochemically-motivated mechanistic evolution law with well-defined parameters with a clear physiological interpretation [45]. Specifically, in terms of our growth model, a more quantitative approach could allow us to correlate our phenomenological material parameters, for example the growth speed τ, to metabolic pathways and limit their range by metabolic constraints [73].

From ex vivo to in vivo

To better characterize the interaction of mechanics and biology, there is an ongoing need to move from the ex vivo characterization of explanted tissue samples to the in vivo characterization of skin as a living system [2]. redSpecifically, in terms of our growth model, an in vivo characterization would help us to refine the constitutive equations for the elastic baseline response [35], which we simplified to be isotropic Neo-Hookean. A better candidate might be a multiple-constituent anisotropic skin model [37], with in-plane anisotropy introduced through a pronounced stiffness along Langer’s lines [33, 39], which we have successfully combined with the proposed growth model in the past [12]. Calibrating our model with real in vivo data would allow us to include the effects of prestrain and residual stress [65]. Recent studies have shown that both play a critical role in collagenous thin biological membranes [4, 22]. To incorporate prestrain and residual stress within the context of finite deformations, we can introduce an additional mapping from a relaxed ex vivo to the prestrained in vivo configuration through another second-order tensor [44]. We have recently shown that incorporating pre-strain of only 20% to 30% can decrease the in vivo tissue stiffness by three to four orders of magnitude [58].

From acute to chronic

In the current model, the long-term response growing of skin is not yet calibrated in time. We have assumed that chronic growth between two filling increments takes place within a normalized time interval from zero to one. In reality, growth periods range from the order of days in rodents [9] to weeks in pigs [69] and humans [24]. In an ideal experimental setting, data would be acquired not only acutely but also chronically [57], and the relevant growth metrics would be quantified at multiple points in time [49]. Specifically, in terms of our growth model, quantitative chronic studies would allow us to calibrate the adaptation speed τ and the shape of the growth curve γ [72, 73], or the corresponding time parameters of more mechanistic biochemically driven evolution equations.

7. CONCLUSION

We have demonstrated the mathematical modeling and computational simulation of skin growth by mechanical overstretch. Previous models of skin growth have controlled overstretch by directly applying the expander pressure without discretizing the expander itself. Here, we have controlled the amount of overstretch by gradually filling a virtually implanted tissue expander. In contrast to previous models, this allows us now to predict the rheological effect of stress relaxation, i.e., a chronic increase in skin area at constant stretch, associated with a chronic decrease in elastic stretch, stress, and pressure. While it is virtually impossible to measure stresses in living biological membrane in vivo, the precise knowledge of skin stress and expander pressure is clinically critical to optimize capillary refill, minimize tissue necrosis, and maximize patient comfort. Once calibrated with long-term in vivo data, our model will be capable of predicting stress, pressure, strain, and area gain in thin biological membranes exposed to mechanical overstretch. It can serve as a valuable tool to rationalize clinical process parameters such as expander geometry, expander size, filling volume, filling pressure, and inflation timing. The proposed model for skin growth can easily be generalized to explore the physiology and pathology of stretch-induced growth in other living systems such as the bladder, intestine, ureter, blood vessels, muscles, and nerves, which display similar structural characteristics.

HIGHLIGHTS.

• Skin is a highly dynamic, autoregulated, living system.

• It responds to chronic mechanical overstretch through a gain in surface area.

• We model the effect of overstretch on skin growth using a mathematical model.

• Our model predicts the acute elastic response and the chronic growth response.

• It can be used to rationalize clinical process parameters in tissue expansion.