Envisioning migration: Mathematics in both experimental analysis and modeling of cell behavior

Abstract

The complex nature of cell migration highlights the power and challenges of applying mathematics to biological studies. Mathematics may be used to create model equations that recapitulate migration, which can predict phenomena not easily uncovered by experiments or intuition alone. Alternatively, mathematics may be applied to interpreting complex data sets with better resolution—potentially empowering scientists to discern subtle patterns amid the noise and heterogeneity typical of migrating cells. Iteration between these two methods is necessary in order to reveal connections within the cell migration signaling network, as well as to understand the behavior that arises from those connections. Here, we review recent quantitative analysis and mathematical modeling approaches to the cell migration problem.

In parallel rather than in series: mathematics in experimental biological methods

Complex biochemical networks responsible for the process of cell migration in different cell types have been identified through traditional biological assays, such as Western blots and morphological studies. From the vantage point of this tremendous body of work, a current challenge is to understand how these many signaling components receive and coordinate signals to produce productive migration. Mathematics has often been viewed as an endpoint for experimental studies: experimentally measured biochemical constants for known interactions are incorporated into equations, which can then be tested for their ability to recapitulate observed behavior. Recent advances have, however, allowed the emergence of a complementary approach: mathematics may be used to enhance experimental resolution and analysis (Figure 1). While traditional biological assays will continue to reveal important facets of cell migration, cell migration is also a particularly suitable subject for mathematically fine-tuned experimental methods, for reasons which we discuss below.

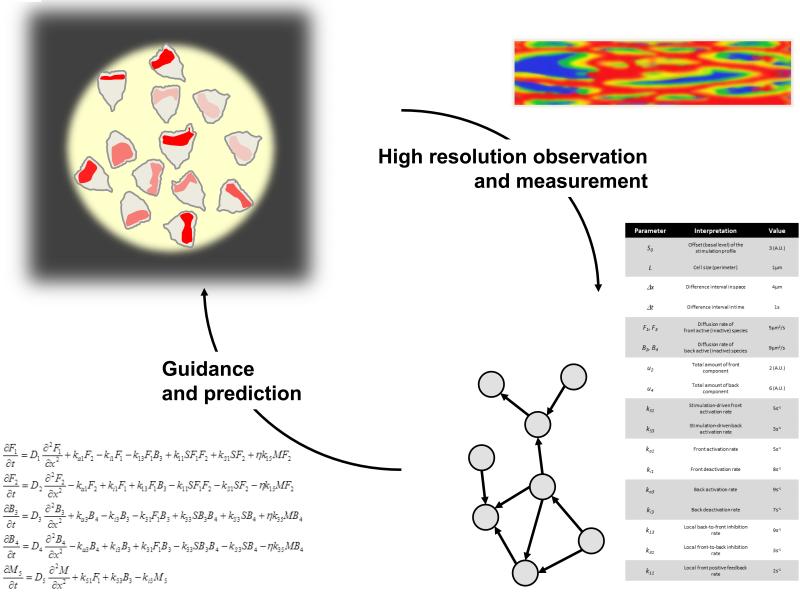
Figure 1.

Envisioning migration. Mathematically fine-tuned experimental analysis enhances the resolution with which behaviors can be observed, while mathematical models provide guidance and prediction of behaviors and networks.

Spatial coordination

The process of cell migration begins with polarization, in which cells generate a front and a back in order to achieve movement in one direction [1-4]. This spatial segregation of signaling components is critical for migration, but is difficult to analyze; traditional methods such as Western blots [5], light scattering [6], and standard flow cytometry cannot provide spatial information. Recent complementary approaches allow quantitative characterization of this spatial information. Machacek et al. performed cross-correlative analyses to track the activity of GTPases with respect to the protruding edge of a cell [7]; this allowed measurement of the distance from the cell edge at which GTPase activity peaked. Welf et al.’s cross-correlative analysis of PI3K signaling [8] showed that PI3K reinforces rather than produces protrusions in fibroblasts, while Galic et al. performed spatial cross-correlation analysis on cells adhered to surfaces patterned with nanocones to demonstrate that N-BAR proteins are directly recruited to the plasma membrane by membrane-curving forces [9]. Analysis of the spatial distributions of cytoskeletal readouts of polarizing primary neutrophils identified differential paths of information flow [10] and the insulation of the back signaling from the front signaling by the microtubules [11]. Quantifying spatial parameters allows trends in probe localization to be not only identified, but also tested for statistical significance, thus opening a new arena of study.

Meanwhile, clever image analysis has further been used to extract much more quantitative spatial information from the cell shape itself. Driscoll et al. used kymographs to study the evolution of cell shape, and found for Dictyostelium discoideum that cells change shape via traveling curvature waves, possibly due to actomyosin dynamics [12]. Barnhart et al. [13] tracked contours and created edge velocity maps of keratocytes on substrates of different adhesion strengths. They found that keratocyte speed and shape have a biphasic dependence on adhesion strength, and that adhesion strength (without long-term adaptation) is sufficient for switching the migration behavior of cells. These authors’ methods transform cell shape itself into a rich resource for the study of cell migration.

Timescales and cell-to-cell asynchrony

An additional difficulty in studying cell migration is achieving adequate temporal resolution, as the characteristic timescales of cell migration are very short. For example, neutrophils can rapidly transform extracellular cues into protrusive changes, creating actin ruffles within 20 seconds of initial chemoattractant exposure [14], and undergoing shape oscillations with a period of roughly 8 seconds [15]. This is in stark contrast to studies of other periodic behavior such as circadian clocks or stages of the cell cycle, where timescales may be on the order of hours to days. An offset of seconds between two migrating cells can be equivalent to a half-period shift. Readouts across a population of cells will thus be heterogeneous and hard to interpret in absolute time. Further, unlike cell cycle studies, in which cells may be synchronized with methods such as serum starvation, the protrusion-retraction cycles of separately migrating cells are not synchronized with one another. Traditional biochemical assays may demonstrate whether one protein activates, inhibits, or does not affect another protein. However, to further explore the signaling behavior and functional implications of a biochemical circuit, the temporal coordination of the components must be studied. The study of migrating cells thus requires high temporal resolution and resourceful computational methods that circumvent the difficulty of interpretation caused by cell-to-cell asynchrony within a population.

Recent studies have addressed the issue of asynchrony with an elegant computational multiplexing approach: the activity of a probe and the edge movement of the membrane are read out from the same cell, and the relative time and distance between probe activation and cell edge movement is recorded. This approach thus allows one readout from many individual cells to be pooled, and pools may be compared for multiple probes to uncover the coordination of the proteins represented by the probes. Using this approach, Machacek et al. uncovered the relative timing of GTPases within protrusions of fibroblasts [7], Tkachenko et al. demonstrated RhoGDI’s role in the temporal regulation of RhoA [16], and Ji et al. predicted intracellular forces from the F-actin network [17]. Meanwhile, Marco et al. [18] developed a math model to characterize the relations of several parameters of cell polarization, and then designed an experiment that tied in closely with their model. This model-directed experiment allowed extraction of different parameters, which are experimentally difficult to measure independently, and preserved context by allowing simultaneous measurement from the same timepoints and individual cells. Specialized application of mathematics can permit both computational alignment of asynchronous events and synchronous extraction of parameters, and is thus especially powerful for the study of cell migration.

Ab initio ad finem: the spectrum of uses for math modeling

Mathematical models vary widely in their levels of abstraction and biological detail [19]. At the one extreme are conceptual models, which may seek to identify minimal circuits and ab initio mechanisms underlying observed phenomena. At the other extreme are data-driven models, which incorporate experimental data in order to ask whether the resultant equations recapitulate, ad finem, experimentally observed behavior. What kind of models do we need to build to learn more about a behavior as complex as cell migration? Here, we argue that the path toward greater understanding of cell migration is not a straight shot through increasingly mechanistic territory.

Conceptual modeling is commonly used when a circuit is poorly characterized. However, conceptual models can also be applied to well characterized systems to replace the biological circuit’s details with simpler functional units–much like the creation of Thévenin equivalent circuits [20] for electronic circuits. Meanwhile, data-driven models are often applied to well-known systems to identify missing pieces. For example, in the case of bacterial chemotaxis, ultrasensitivity of the system could not be explained by known components, and data-driven modeling was used to demonstrate that the motor itself adapts at the level of switch component subunit clusters [21]. However, a data-driven approach may also be used to guide our knowledge of which pieces of a poorly-characterized system are most important to its operation. Iteration between conceptual and data-driven models can identify design principles and constraints which may guide future experimental and modeling endeavors in cell migration (Figure 1).

Bird’s eye view: conceptual modeling

Conceptual models can be used to capture the essence of what is currently known about a biological system. For instance, Ofer et al. [22] studied the simple migration system of keratocyte fragments, which lack cell bodies. The authors created force-balance equations to demonstrate the emergence of global shape and speed from underlying actin dynamics and membrane tension. This study elegantly highlighted the minimum requirements for coordinating retraction of the rear with protrusion at the front. Similarly, Neilson et al. [23] [24] studied pseudopod formation in Dictyostelium discoideum. The authors modified Meinhardt’s discrete model of chemotactic orientation [25] to demonstrate that a cyclical internal process can be used to recapitulate both pseudopod formation and orientation bias. This simple conceptual model suggested a pseudopod-centered mechanism of chemotaxis. Conceptual models can identify minimal circuits, and thus reveal general principles at the heart of more complex circuits.

Conceptual models for zooming out and narrowing in

Conceptual modeling can also be used to survey minimal circuits capable of creating observed phenomena, which in turn can guide future studies—that is, zooming out can allow the field to narrow in. For example, perfect or near-perfect adaptation enables cells to respond to the gradient, rather than the average value, of a signal [26]. Ma et al. explored this property not by modeling the known signaling components of these networks, but by generalizing chemotactic and other biological networks into abstract three-node networks, and performing a topology search over all of the possible relations of the three nodes [27]. This search revealed that only two network designs, the negative feedback loop and the incoherent feed forward loop, are capable of achieving perfect adaptation.

This general finding may then guide future mechanistic studies of cell migration. A recent cross-correlative study of GTPases, actin, phosphoinositides, and edge velocity by Kunida et al. indicated adaptation of Rac1 activity in response to PI3K inhibition [28]. To search for a source of this behavior, Kunida et al. looked to the abstract, conceptual search performed by Ma et al. for networks capable of adaptation. Of the two candidate topologies that Ma et al. identified, the negative feedback topology recapitulated Kunida et al.’s experimental findings. Kunida et al. thus searched for a negative regulator of actin and Rac1, and found that myosin light chain kinase acts as a node in the causative negative feedback loop for the observed adaptation. Although negative feedback between frontness signals such as Rac1 and backness signals such as myosin light chain kinase has long been established in migrating cells [5], the relevance of such feedback to adaptation is an unexplored area. Thus, mathematical modeling and constraints from an abstract topology search were used in this mechanistic study to find a new behavioral implication of a known biochemical link. More recent topology searches for networks capable of polarization [1] or for networks capable of front-back buffering [11] may provide similar guidance for future mechanistic efforts.

Data-driven models as predictors

Data-driven models may be used not only as final tests of understanding, but also as ways of picking up in silico where observation is limited in vitro. For instance, Shibata et al. [29] created kinetic equations to describe the reactions of phosphatidylinositol lipids in chemotactic cells. Their simulations and experiments both showed two types of behaviors for the localization of PtdIns(3,4,5)P3: traveling waves and the formation of transient domains. The authors explored ranges of variables in their simulations in a systematic manner that is not possible in vitro, and found that the traveling waves are induced by an instability of the stationary uniform state, while stochastic noise was important for transient domain-formation.

Similarly, Marée et al. [30] created a data-driven model to explore the effects of both biophysical and chemical feedback on cell polarization and motility. Their model suggested that cell shape is not just a downstream readout, but also feeds back by directly affecting the internal distribution of GTPases. Meanwhile, their model allowed them to test the effect of different values of phosphoinositide feedback; this allowed the authors to note that an intermediate level of phosphoinositide feedback creates normal migration. Lin et al. [31] expanded this model and predicted that a gradient of Rac activation can create a strong cell polarization response, that the timing of this polarization depended strongly on the gradient of Rac, and that antagonism between Rac and Rho could amplify polarization; in vitro creation of such a gradient with a rapamycin stimulation system confirmed their in silico prediction.

Finally, data-driven models have been used to predict not only outcomes, but also new hypotheses altogether. Wu et al. [32] created data-driven decision-tree models to analyze a ‘cue-signal-response’ data set from multipotent stromal cells. Similar to their work in fibroblasts [33, 34], the modeling classified responses to combinations of signals and conditions. Their decision trees revealed a non-intuitive prediction that decreasing ERK would promote cell migration, which they then confirmed in vitro.

Modeling new realms

How will we begin to combine the many models of different subprocesses of migration into a multiscale model? As the field progresses, previously coarse-grained models are becoming finer-grained as experimental findings provide more detailed metrics [4]. In addition, the field is growing wider with new models of subprocesses of migration that were not built in original models, including: social migration [35, 36], integrin-clustering [37], interactions with the extracellular matrix [38], haptotaxis [39, 40], and N-BAR domain proteins [41]. Iteration between conceptual and data-driven modeling will be required to navigate the future challenge of weaving together these subprocesses (some of which will be dependent on others).

Outlook

Cell migration is a multifaceted process, many pieces of which remain poorly elucidated. While the utility of mathematics in biology is often thought to be the creation of detailed models, the path to the elusive end-to-end, whole-cell model is not a straight line through increasingly mechanistic territory. Instead, the path to this distant goal requires feedback between experimental analysis, conceptual modeling, and data-driven modeling. Beyond the power of testing experimentally-derived models, mathematics may be incorporated throughout the iterative cycle of experiment and theory: to increase the resolution with which behaviors are observed and to predictively associate behaviors and networks. Importantly, these applications of mathematics may not only push the field closer to a whole-cell understanding of migration, but also reveal general principles utilized in cell migration and perhaps across many other cell signaling processes.