Abstract
In sign language research, we understand little about articulatory factors involved in shaping phonemic boundaries or the amount (and articulatory nature) of acceptable phonetic variation between handshapes. To date, there exists no comprehensive analysis of handshape based on the quantitative measurement of joint angles during sign production. The purpose of our work is to develop a methodology for collecting and visualizing quantitative handshape data in an attempt to better understand how handshapes are produced at a phonetic level. In this pursuit, we seek to quantify the flexion and abduction angles of the finger joints using a commercial data glove (CyberGlove; Immersion Inc.). We present calibration procedures used to convert raw glove signals into joint angles. We then implement those procedures and evaluate their ability to accurately predict joint angle. Finally, we provide examples of how our recording techniques might inform current research questions.
Keywords: sign language, phonetics, phonology, dataglove, articulation
1 Introduction
In sign language research, an understanding of the articulatory factors involved in shaping phonemic boundaries in handshape is still in its infancy. While there exists a small body of work comparing the anatomical structure of the hand with linguistic handshape distribution in sign languages (e.g. Mandel, 1979, 1981; Boyes Braem, 1990; Ann, 1993, 2006; Greftegreff, 1993), no comprehensive analysis of handshape thus far has been based on quantitative measurement of joint angles during sign production. Furthermore, very little is understood about the amount (and articulatory nature) of phonetic variation that exists in the production of visually similar handshapes, whether it be by a single signer, across signers, or cross-linguistically.
Although many researchers have discussed the phonological inventories of handshape in their respective sign languages, very few studies thus far have attempted to look at the different types of phonetic variation within or across phonemic categories. This dearth of phonetic research is partly due to limitations in the technology available to researchers for quantifying variation in handshape formation. Until recently, comparison of handshapes could only be done observationally using video images. Consequently, even in cases where phonetic analyses were attempted, variation was grouped into categories based on visual characteristics (e.g. position of the thumb relative to the fingers) rather than on quantitative measurements. For example, Klima & Bellugi (1979), in a cross-linguistic repetition study, noted subtle phonetic differences in the “closed fist handshape” ( ) between American Sign Language (ASL) and Chinese Sign Language users, but they could only express the differences qualitatively: “Whereas the ASL handshape…is relaxed, with fingers loosely curved as they close against the palm, in the CSL handshape…the fingers were folded over onto the palm and were rigid, not curved” (161–162). Similarly, Lucas, Bayley & Valli (2001) studied phonetic variation in ASL signs that used a ‘1’ (
) between American Sign Language (ASL) and Chinese Sign Language users, but they could only express the differences qualitatively: “Whereas the ASL handshape…is relaxed, with fingers loosely curved as they close against the palm, in the CSL handshape…the fingers were folded over onto the palm and were rigid, not curved” (161–162). Similarly, Lucas, Bayley & Valli (2001) studied phonetic variation in ASL signs that used a ‘1’ ( ) handshape across grammatical, phonological and social contexts. While this study was quantitative from a sociolinguistic perspective, the handshape variants themselves were coded (out of necessity) based on visually salient categories (e.g. thumb extended, unselected fingers relaxed) instead of being quantified using reproducible measurements of joint angle.
) handshape across grammatical, phonological and social contexts. While this study was quantitative from a sociolinguistic perspective, the handshape variants themselves were coded (out of necessity) based on visually salient categories (e.g. thumb extended, unselected fingers relaxed) instead of being quantified using reproducible measurements of joint angle.
Quantifiable information about the nature of these variations could help support (or refute) hypotheses, refine phonemic categories, and increase our understanding about the contexts in which variants occur. Most importantly, because quantitative measurements such as joint angle are reproducible, utilizing them in phonetic research allows for more accurate comparisons within and across subjects, as well as greater information-sharing (and testing of results) within the research community. While useful in a general sense, phonetic comparisons based on visual observation (no matter how detailed) unavoidably contain a certain degree of subjectivity on the part of the researchers/coders involved. In addition, coding methods tend to vary across projects reducing the reproducibility of results. The ability to use actual measurements while studying handshape variation would be a boon for the research community as a whole.
With recent advancements in motion capture technology, one might expect to see a steadily growing body of literature on the phonetic analysis of handshape; however, this is not yet the case. In fact, thus far we have found only one study (other than our own) that utilizes recent technological advances to collect quantitative handshape data in sign languages. Cheek (2001) used a 3-D camera system and infrared markers to study coarticulation between ASL signs using  or
or  . She did so via an examination of pinky extension, which was measured as the distance between markers placed at the fingertip and the wrist. Although this work did not look at joint angle, per se, it was (to our knowledge) the first attempt at quantitative—and therefore reproducible—measurement of handshape variation. While some sign language researchers have had success using camera systems like Cheek’s to collect detailed phonetic data involving kinematic movements and locations (e.g. Wilcox 1992, Cormier 2002, Tyrone & Mauk 2010, Grosvald & Corina and Mauk this issue), using them for a detailed study of handshape can be problematic due to the number of markers needed to measure each joint. Furthermore, there is a high likelihood that the markers will be occluded from the cameras’ view as the fingers overlap each other or as the hand is moved into different locations and orientations.
. She did so via an examination of pinky extension, which was measured as the distance between markers placed at the fingertip and the wrist. Although this work did not look at joint angle, per se, it was (to our knowledge) the first attempt at quantitative—and therefore reproducible—measurement of handshape variation. While some sign language researchers have had success using camera systems like Cheek’s to collect detailed phonetic data involving kinematic movements and locations (e.g. Wilcox 1992, Cormier 2002, Tyrone & Mauk 2010, Grosvald & Corina and Mauk this issue), using them for a detailed study of handshape can be problematic due to the number of markers needed to measure each joint. Furthermore, there is a high likelihood that the markers will be occluded from the cameras’ view as the fingers overlap each other or as the hand is moved into different locations and orientations.
It is for these reasons that we have chosen to utilize a different kind of technology in this pursuit. Unlike camera-based systems, glove-based data systems (such as the CyberGlove discussed in this work; CyberGlove Systems, formerly Virtual Technologies Inc.) allow one to collect data from all finger joints continuously, regardless of the position of the fingers in relation to each other or the hand in relation to the body. This freedom makes data glove systems useful in a wide range of applications, including information visualization/data manipulation, robotic control, arts and entertainment (e.g. computer animation, video games), medical applications (e.g. motor rehabilitation) and control for wearable/portable computers (see Dipietro, Sabatini & Dario 2008 for a review). Especially relevant for this work are the growing number of applications involving sign languages and those related to motor analysis (cf. Mosier et al. 2005; Liu & Scheidt 2008; Liu et al. 2011)
Since our ultimate goal is studying joint angle variation found in handshape data, we began by reviewing the literature for research that used data gloves (and more specifically the CyberGlove) as joint measuring devices. We found very few. The vast majority of data glove applications require only visual approximations of whole handshapes—not precise measurements of individual joint angles—to accomplish their goals. For example, in the existing sign language literature involving the CyberGlove (e.g. Vamplew 1996, Gao et al. 2000, Wang, Gao & Shan 2002, Huenerfauth & Lu 2010), gloves are most often used to either capture handshape data for animation, or build systems for automatic sign language recognition. To accomplish their goals, these projects only have to differentiate between broad phonemic distinctions. Handshape phonemes are typically quite distinct from each other visually, meaning that there is often a great deal of acceptable variation between them. As a consequence, these studies have not needed to calibrate their gloves to specific joint angles. Our ultimate goal, however, is to measure precisely the kind of variation these sign language reproduction and recognition projects are able to take advantage of—that is, we want to determine just how much variation is or is not acceptable between handshape phonemes—and for that we need a measurement technique that is both accurate and precise.
Other glove applications do exist for which precise information about hand movement is needed. For example, in research involving dexterous telemanipulation, the detailed finger motions (i.e. kinematics) captured by the glove must be mapped onto motions of a robotic tool (e.g. Fisher, van der Smagt & Hirzinger, 1998 Griffin, et al. 2000). Errors in this mapping process can result in a lack of dexterity and object collisions at the remote location. Unfortunately for us, because the geometry of the human hand is different from that of robot hands or other end effectors, telemanipulation studies often focus on details like fingertip position instead of joint angle.
In our search of the literature, we did find precedent for using data gloves for goniometric (i.e. joint measurement) purposes. Wise, et al. (1990) and Williams, et al. (2000) both evaluated data gloves as potential tools for automating joint angle measurement in clinical situations (e.g. physical therapy). Wise, et al. (1990) limited their investigation to finger and thumb flexion and focused mainly on within-subject repeatability rather than on the accuracy of their joint estimates across subjects. However, Williams, et al. (2000) evaluated a wide range of hand characteristics (including flexion and abduction across all joints) for both repeatability and accuracy as compared to known joint angles, attaining error rates comparable to those of traditional goniometry. Because both studies use types of gloves that are different than ours (Wise et al. used a fiber optic glove and Williams et al.’s glove was custom made), their work does not help us directly solve the problem of converting CyberGlove sensor data into joint angle estimates, but their success suggests that precise angle measurement using our glove is attainable.
After reviewing tphe relevant literature, we determined that the problem preventing researchers from doing phonetic research on handshape variation is no longer a lack of adequate technology; current glove systems like the CyberGlove are easily able to detect and record very small changes in hand configuration. What researchers lack now is a well developed methodology that allows them to translate the glove’s raw sensor data into useable joint angle measurements, thus enabling comparisons of variation across subjects. The goal of this work is to develop the mathematical models and calibration techniques needed to perform such translations for a subset of CyberGlove sensors. We then explore potential applications for the resulting quantitative handshape data, offering analysis options that we hope will ultimately afford sign language linguists a better understanding of how handshapes are produced at a phonetic level.
The remainder of this paper is organized as follows. Section 2 describes the CyberGlove, the scope of this paper with respect to the glove, and the tools we use in our calibration procedures. In Section 3, we explain both the mathematical models used to convert raw glove signals into joint measurements and the general calibration procedures used to inform those models. In Section 4, we implement the calibration procedures and evaluate their ability to accurately predict joint angle. Section 5 provides samples of possible data visualization and analysis techniques as well as example data demonstrating how this kind of methodology could inform current research questions. Finally, Section 6 concludes the paper and describes areas for future research.
2 Equipment
The first step in developing a measurement methodology adequate for the phonetic comparison of joint angles is to make sure that the equipment being used is sufficient for the task. In this section, we describe our choice in data glove, as well as the tools we designed to calibrate the glove to each wearer.
2.1 Data glove
For this research, we used a right-handed, 22-sensor CyberGlove (model CG2202; Virtual Technologies Inc.). One advantage of this model of CyberGlove is that it has more sensors than many other available data gloves, ultimately giving us the potential to capture more kinds of phonetic variation across handshapes. Specifically, this glove has the ability to measure the flexion of each finger at three joints–the metacarpophalangeal joint (MCP) and the proximal interphalangeal joint (PIP) and distal interphalangeal joint (DIP)–and the amount of abduction (spread) between the fingers, as well as the flexion, abduction and rotation of the thumb, the arching of the palm and a variety of wrist movements.
The glove sensors themselves are thin electrically resistive strips sewn into the glove above specific joint locations (see Figure 1). In most cases (see below), these strips are long enough to accommodate the inter-subject variations in glove positioning that results from differing hand sizes, but they are not so long that they overlap the adjacent joint. The sensors measure joint angle by measuring the electrical resistance, which varies as the strip is bent. This measurement is then converted into an 8-bit digital value between 0 and 255, which is then transmitted to a computer via serial port.1 For our project, this hand configuration data was collected at a rate of approximately 50 samples per second, and the programs used to collect and analyze the data were written using the MATLAB programming environment.
Figure 1.
The CyberGlove (Virtual Technologies Inc.) and the types of sensors calibrated in this study.
While the CyberGlove has the capability to measure positional changes at each of the 22 hand locations mentioned above, only a subset of these sensors will be discussed here, namely, the MCP flexion, PIP flexion and abduction (AB) sensors for the four fingers (see Figure 1). We do not focus our efforts on these sensors because we feel the remaining sensors will not provide important information—on the contrary, we are excited by the research possibilities these other sensors will eventually afford us. However, during our initial exploration into the glove’s capabilities, we discovered that determining the relationship between sensor reading and joint angle was more problematic for some of the glove sensors than for others. For example, due to their location at the ends of the fingers, the distal interphalangeal (DIP) joint sensor readings varied more or less during finger flexion depending on finger length, potentially complicating cross-subject comparisons.2 Calibration of the thumb sensors is also particularly challenging due to an additional degree of freedom for the thumb’s MCP joint (i.e. thumb rotation across the palm) that will require more elaborate tools than those designed for calibrating finger flexion and abduction in the current project (see next section).3 Finally, it is difficult to interpret readings from the palm arch and wrist position sensors because in each case, multiple joints contribute to variation in sensor values and as such, a description of data from any of these sensors is often omitted from the literature (e.g. Kessler, Hodges & Walker 1995; Wang & Dai 2009). By comparison, the MCP, PIP and AB sensors of the fingers are less problematic to work with. In addition, the data available from these sensors (i.e. the amount of flexion/extension and abduction in the four fingers) represents a large portion of the variation thought to be most useful in representing handshape phonemes (cf. Brentari 1998, Sandler 1996). For these reasons, we focused our initial attention on these 11 sensors, leaving investigations of the other sensors to subsequent work.
Although evaluations of the CyberGlove’s sensory characteristics are scarce, the literature that does exist—e.g. Kessler, Hodges & Walker 1995—indicates that CyberGloves in general should be sufficient for the task at hand. Following their lead, we began by performing a brief sensor noise evaluation to assess the fitness of our particular device for experimental use; i.e., we wanted to determine if the glove sensors or the signal amplifiers introduced unwanted variation that would affect the accuracy of our joint angle measurements. To do this, we sampled the raw sensor readings from the 11 sensors in question at 50 samples per second for a period of 4 s. During this time, a member of our research team donned the glove and held it still in one of two hand postures – a spread hand kept flat on a table or a closed fist (also resting on a table). We also performed a 4 s test while the glove lay empty on the table. The results agreed with the findings of Kessler’s group in that we observed very little signal noise while the glove was motionless—one sensor varied by two sensor-values for a single sample in the fist position, but no other sensor reading varied by more than a single sensor-value over any 4 s period. These results indicated that signal transduction noise (i.e. extra variation) from the glove itself was minimal, suggesting that our glove was fit to be used in our joint-measuring endeavors.
2.2 Calibration tools4
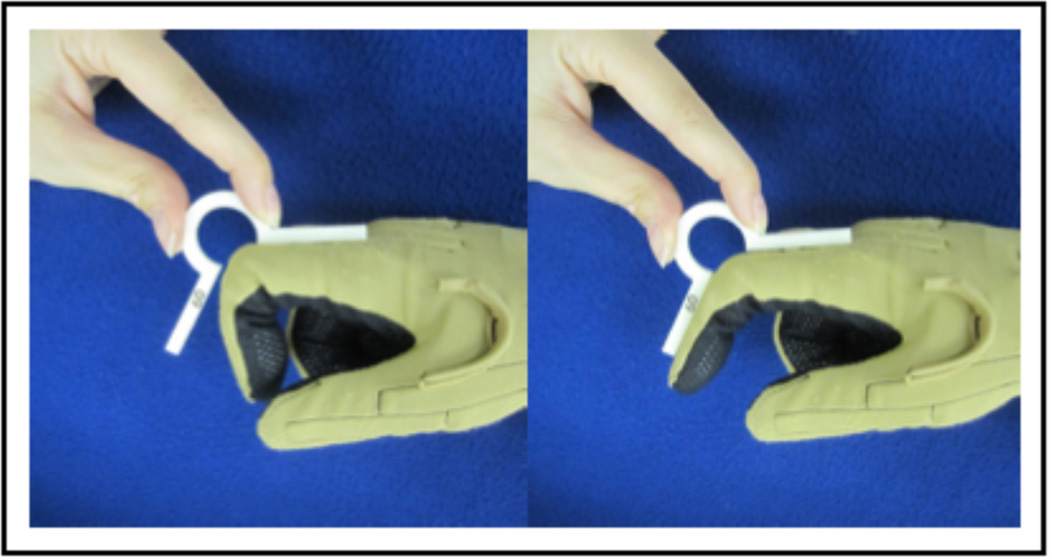
As previously mentioned, the majority of data glove applications require only visual approximations of whole handshapes and as a result, most existing approaches to data glove calibration require no special tools—they simply determine the range of useful data values by requiring subjects to form canonical hand postures (e.g. a closed fist or an extended hand with and without spread fingers). Because we wanted to use the glove to measure joint angles in a more precise manner, we needed calibration tools that could be used to position the fingers in specific flexion/extension and abduction angles spanning the entire range of motion. One option would be to use a goniometer (a hinged tool often used to measure joint angle and range of motion), however goniometers are imprecise joint-positioning devices because they are easily bumped away from their intended angle. We therefore designed a set of light-weight plastic calibration tools, examples of which can be seen in Figure 2. These tools are sufficiently rigid to constrain finger joint angles such that they do not exceed their designated value.
Figure 2.
Examples of calibration tools.
Our flexion/extension tools are similar in design to those described by Kessler, Hodges & Walker (1995) in that they constrain the finger to a specific angle when pressed against the dorsal aspect (back) of the finger (i.e. where the bend sensor is located on the glove). Unlike their tools, instead of having the two legs of each flexion tool meet at the vertex of the angle, we allowed room at the vertex for varying knuckle sizes to obtain a closer fit. The edges were also designed to be thin enough so as not to interfere with the abduction sensors. More importantly, we expanded the number of available angle measurements from Kessler, Hodges & Walker’s four (0°, 30°, 60° and 90°), to sixteen (10° increments from −40° to 110°), including tools allowing for hyper-extended positions (i.e. negative degrees of flexion).
Our abduction tools consist of plastic wedges whose long edges form the desired calibration angles, meeting at a rounded vertex that accommodates the webbing between fingers. These tools range from 10° to 90° in 10° increments.5 For situations where 0° abduction was to be measured, we used a thin – but rigid – plastic card similar to a credit card, since simply asking subjects to "close their fingers" without the card resulted in considerable trial-to-trial sensor variation.
Finally, to collect data comparing AB with MCP sensor readings (see Sections 3.1 and 3.2), we use a steeply angled ramp (~80°) with a thin, rigid, perpendicular constraint (used to define 0° abduction) to gather flexion and extension ranges at predetermined abduction angles (pictured in Section 3.2).
3 Data glove calibration
As discussed in Section 1, one problem that has prevented researchers from using data gloves in the study of phonetic handshape variation is that until now a means of translating the raw sensor readings into accurate joint angle estimates has not existed. Developing such a translation mechanism is not a straightforward endeavor due to complex relationships between glove sensor readings and differences in the glove’s fit across wearers. In other words, there is no “one-size-fits-all" signal-to-angle conversion chart that will work in all cases; instead, the glove must be calibrated to each signer individually, and that information must be fed into an empirical model (i.e. a series of equations) that accounts for the relationships between glove sensors. It is only after this translation mechanism is in place that we are able to use the glove as an angle measuring device in phonetic and phonological research.
Here, we describe one empirical model that translates the finger MCP, PIP and AB sensor readings into joint angle estimates, described generally in Section 3.1 with more technical detail in the Appendix. Section 3.2 then describes the calibration procedure we have developed to identify the parameters (i.e. set of variables) required by that model.
3.1 Data translation model
The data translation model that we defined (see Appendix) requires two different transformations. As we will show, a simpler one suffices for flexion/extension sensors while a more complex one is needed for abduction sensors. The flexion/extension model assumes linearity (i.e. simple proportionality) in the relationship between the raw MCP or PIP sensor data and joint angles (Kessler, Hodges & Walker 1995, Virtual Technologies 1998, Kahlesz, Zachmann & Klein 2004, Wang & Dai 2009). (Linear relationships are desirable in situations such as these because they greatly simplify the conversion process.) However, as we show in Section 4, the slopes of these linear relationships vary across individual sensors and across subjects, requiring calibration data from each person and for each sensor to acheive accurate joint angle estimates.
Unfortunately, the relationship between finger abduction angles and AB sensor readings is not as straightforward as the flexion/extension model. Due to the geometry of the AB sensors (see Figure 1) and the nature of the glove material, the raw AB sensor readings are influenced by the degree of flexion of neighboring MCP joints (Kahlesz, Zachmann & Klein 2004, Wang and Dai, 2009). Further complicating things, preliminary data analysis has found that while the relationship between abduction angle and AB sensor readings is reasonably linear when the hand is, for example, flat on the table, the relationship between these sensor readings and MCP joint motions curves dramatically. This requires an additional correction factor be added to the abduction sensor data translation model in order to account for the undesirable "cross-talk" between flexion/extension and abduction in any given pair of fingers. Again, the parameters used to define these complex relationships, as well as information about subject-specific variation is gleaned from the calibration procedure described below.
3.2 General calibration procedures
As already stated, the purpose of the calibration procedure we describe is to identify the parameters, or set of variables, for the model that converts raw glove data into joint angle estimates. Calibration must be performed for each individual separately, because differences in the size and shape of each person’s hand result in different amounts of bend in the sensors given the same change in angle. Our calibration procedure consists of two separate types of data collection. The first is used to identify the 16 model parameters associated with MCP and PIP finger flexion, and the second identifies the 12 parameters needed for finger abduction. (For more about these parameters, see Appendix.) During the first calibration we collect multiple data pairs for flexion/extension by using a set of "gold standard" calibration tools (Section 2.2) to place the finger joints in predetermined postures with known joint angles (e.g. 30°). During the second calibration procedure, we collect multiple calibration data sets for abduction by using the calibration tools to constrain finger abduction at particular angles (e.g. 10°) while the MCP joints on either side of the AB sensor are either kept flat or moved through their range of motion, thus providing us with important information about the interaction between MCP flexion and AB sensor readings. The whole calibration process takes approximately 20 minutes and is described in more detail below.
3.2.1 Flexion calibration
When calibrating MCP or PIP flexion, the subject is first asked to flex his or her finger at the joint of interest. The researcher then places one edge of a selected flexion tool on the dorsal (i.e. back) side of either the hand for the MCP, or the proximal finger segment for the PIP, centering the vertex of the tool over the joint. The researcher then extends the distal segment of the finger until it meets the other edge of the tool (Figure 3). The subject maintains this position while the glove sensors are sampled. Four flexion angle tools (10°, 30°, 50°, 70°) are used to calibrate each of the eight flexion/extension sensors. This set includes angles near the minimum and maximum of each joint’s typical range of motion as well as two internal sample points. The order of testing within and between joints is randomized to minimize any potentially-confounding order effects.
Figure 3.
Calibration tool placement for MCP or PIP flexion/extension
3.2.2 Abduction calibration
When calibrating abduction between pairs of fingers, we begin by collecting abduction data while the MCP joints are all in the same position, thus allowing us to gain an understanding of the underlying linear relationship between abduction angle and AB sensor readings. To collect this data, the hand rests flat on a table, and one (or more) wedge tools are inserted firmly between the fingers of interest. The subject is asked to apply pressure against the tool(s), such that the inner edges of the fingers firmly touch the sides of the tool(s). The researcher holds the tool(s) in place while the glove data is captured (Figure 4a). Three abduction angle tools (10°, 30°, 50°) are used to calibrate each of the three AB sensors. Again, the order of testing within and between joints is randomized to minimize any potentially-confounding order effects.
Figure 4.
a) Calibration tool placement for flat-hand abduction, and b) illustration of abduction curve data collection.
Next, we collect data that captures the complex relationship between abduction sensor readings and MCP joint motions. We used a "moving finger" approach to characterize this relationship, illustrated in Figure 4b. Specifically, we used a combination of abduction wedge tools and the ramp tool to keep the degree of abduction between the fingers constant while the MCP joints of each finger, in turn, are moved between the extremes of hyperextension and flexion (i.e. from about −30° to 60°). The point of this procedure is to gather the sensor data corresponding to a given angle of abduction as it combines with as many MCP positions as possible, thus aiding in our understanding of the AB-MCP coupling relationship.
The process begins with the subject placing his or her hand over the edge of the ramp tool (~80° flexion) with the vertical constraint between the fingers of interest. The researcher selects one finger to be the “moving finger” and the hand is adjusted so that this finger lies flush against the vertical constraint. A constant abduction angle between the fingers is enforced either by holding the other finger (the “stationary finger”) against the vertical constraint (representing 0° abduction) or by inserting one of two specific wedge tools (20° or 30°) between the stationary finger and the vertical constraint. The other finger is then moved throughout its range of motion three times as data is collected continuously from the glove. This sequence is performed for each MCP joint, at each of the three abduction angles. The entire sequence is then repeated with the stationary finger fixed at ~20° flexion (obtained by inserting another, wider wedge tool under the stationary finger and abduction tool).6 By including data collected from both ~20° and ~80° stationary finger flexion angles into each AB sensor calibration dataset, this calibration procedure admits a greater range of recorded values for the MCP flexion angle difference (θf1 – θf2,, see Appendix) and thus, a more accurate identification of the coupling relationship between the AB sensor readings and MCP joint motions.
4 Calibration results and validation testing
Of course, an empirical model and calibration procedure are only useful to phonetic research if we can demonstrate that they do what they were designed to do successfully. In this section, we describe an implementation of the procedures described in Section 3 to calibrate the data translation model to a cohort of human subjects. We then evaluate the ability of our procedures to accurately translate raw glove data into joint angle measurements.
4.1 Participants
Seven subjects (4 female, 3 male) each participated in a single experimental session in which we performed the calibration procedure described in Section 3.2 with extra data sets collected for assessment purposes (see below). Participants ranged in age between 22 and 45 and most were affiliated with Marquette University as students, staff or faculty.
4.2 Data collection and analysis
In testing our procedures, our goals were twofold. First, we wanted to test how good a fit our translation model was to the calibration data used to create it. For example, if the model assumes a linear relationship (e.g. Figure 5a), ideally, the calibration data whould not stray far from the line representing the model. To evaluate this fit, we computed the Variance Accounted For (VAF) by the model derived from the four calibration points. VAF is a measure of how well a model describes the variation in a set of data—in this case, how far the data points stray from the straight line predicted by the model—and it can range from 0–100% (100% being a perfect fit). VAF is calculated as:
where is the variance of the data, and is the variance of the residuals, i.e. the difference between the actual joint angle values (the angles prescribed by the tools) and the joint angle values predicted by the model (e.g. the points along the line).
Figure 5.
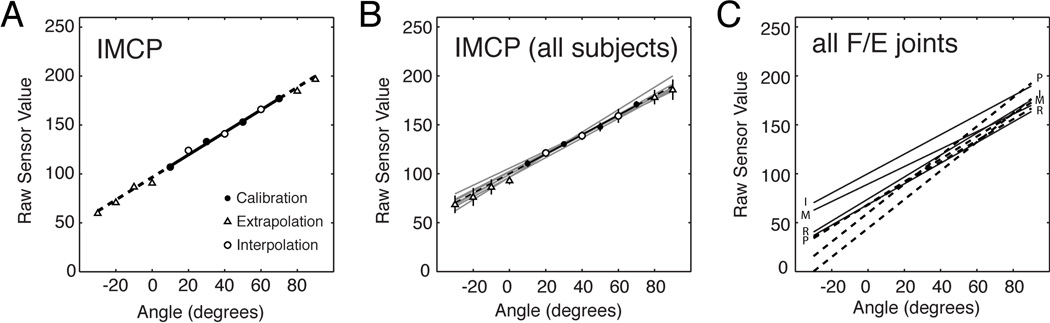
Flexion/extension sensor calibration. a) Index finger MCP joint (IMCP) sensor readings for fixed calibration (•), interpolation (◦) and extrapolation angles (△). The best-fit regression line is shown. b) IMCP calibration lines for each subject (gray) and the cohort average (black) are displayed along with the population mean ± 1 SD for each sample point. c) Cohort average calibration lines for the MCP and PIP joints for each finger.
Second, we wanted to assess the model's ability to generalize, that is, to interpolate (make predictions within the range of calibrated joint angles) and to extrapolate (make predictions beyond the calibration range). To accomplish this second goal, additional angles were added to the normal calibration procedure. In the case of flexion/extension, whereas the normal calibration procedure for the MCP and PIP sensors only includes four angles (10°, 30°, 50°, 70°), here we recorded sensor data using an expanded set of tools including 13 angles at the MCP joints (ranging from −30° to 90° in 10° increments) and 10 angles at the PIP joints (ranging from 0° to 90° in 10° increments). The sampling of flexion angle data was otherwise as described in Section 3.2 (Figure 3). We then assessed the model's ability to interpolate within the range of calibration by computing the model's VAF for the angles {20°, 40°, 60°}. Finally, we assessed the model's ability to extrapolate beyond the calibration range by computing VAF for {−30°, −20°, −10°, 0°, 80°, 90°} at the MCP joints and for {0°, 80°, 90°} at the PIP joints.
In the same way, we also expanded upon the flat-hand abduction calibration set (10°, 30°, 50°), additionally including {0°, 20°, 40°, 60°} abduction angles. Again, the data sampling was as described in Section 3.2 (Figure 4a). Next, we used the model (specifically Eqn 2, Appendix) to estimate the abduction model for the flat-hand data set. We then assessed the quality of the model’s fit to the calibration data using VAF computed over the {10°, 30°, 50°} abduction angles. Finally, we used VAF again with data from 20° and 40° abduction to assess the model's ability to interpolate and using data from 0° and 60° abduction to assess extrapolation.
Finally, we performed the "moving finger" analysis (Section 3.2, Figure 4b) for each pair of adjacent fingers with the stationary finger held at 10°, 30° and 50° abduction angles. All of the data from the moving finger datasets were used to correct for the MCP joints' influence on the AB sensors (see Eqns 3a and 3b, Appendix), and then those corrected values were compared to flat-hand abduction values to determine the validity of the correction calculations.
4.3 Results
4.3.1 Flexion/Extension model
As illustrated for a representative joint in a representative subject (Figure 5a), the assumption of linearity was valid for the calibration model translating raw flexion/extension sensor readings into joint angles (Eqn 1, Appendix). The across-subjects average VAF was high at the four calibration points for each joint (MCP: 98.9% ± 1.7%; PIP: 99.3% ± 0.89%). Moreover, the model performed exceedingly well in both interpolation (MCP VAF: 97.1% ± 3.9%; PIP VAF: 97.9% ± 2.4%) and extrapolation (MCP VAF: 99.0% ± 0.9%; PIP VAF: 99.2% ± 0.7%) and thus we are well-justified in using our calculations (specifically, Eqn 6, Appendix) to estimate flexion/extension angles from raw sensor values.
As shown for the index MCP joint (Figure 5b), the slope of the calibration curve varies somewhat across subjects, likely due to anatomical differneces between hands. This illustrates the need to perform separate calibrations for each subject. Using a single calibration for everyone would result in inaccurate estimates at high and low joint angles We also observed marked differences in the across-subject average models between the MCP and PIP joint, as shown in Figure 5c. This demonstrates the need to calibrate each sensor separately (as opposed to basing data translation on one or two representitive sensors). Not doing so could result in inaccurate estimations of flexion/extension angles as derived from raw sensor values.
4.3.2 Flat-hand Abduction Model
Like the flexion/extension model, the model for abduction when the hand rested on a flat surface was also shown to be highly linear (Figure 6a, black symbols). The across-subjects average VAF was high at the three calibration points (10°, 30°, and 50°) for each joint (IM: 99.9% ± 0.1%; MR: 99.8% ± 0.3%; RP: 99.9% ± 0.1%).7
Figure 6.
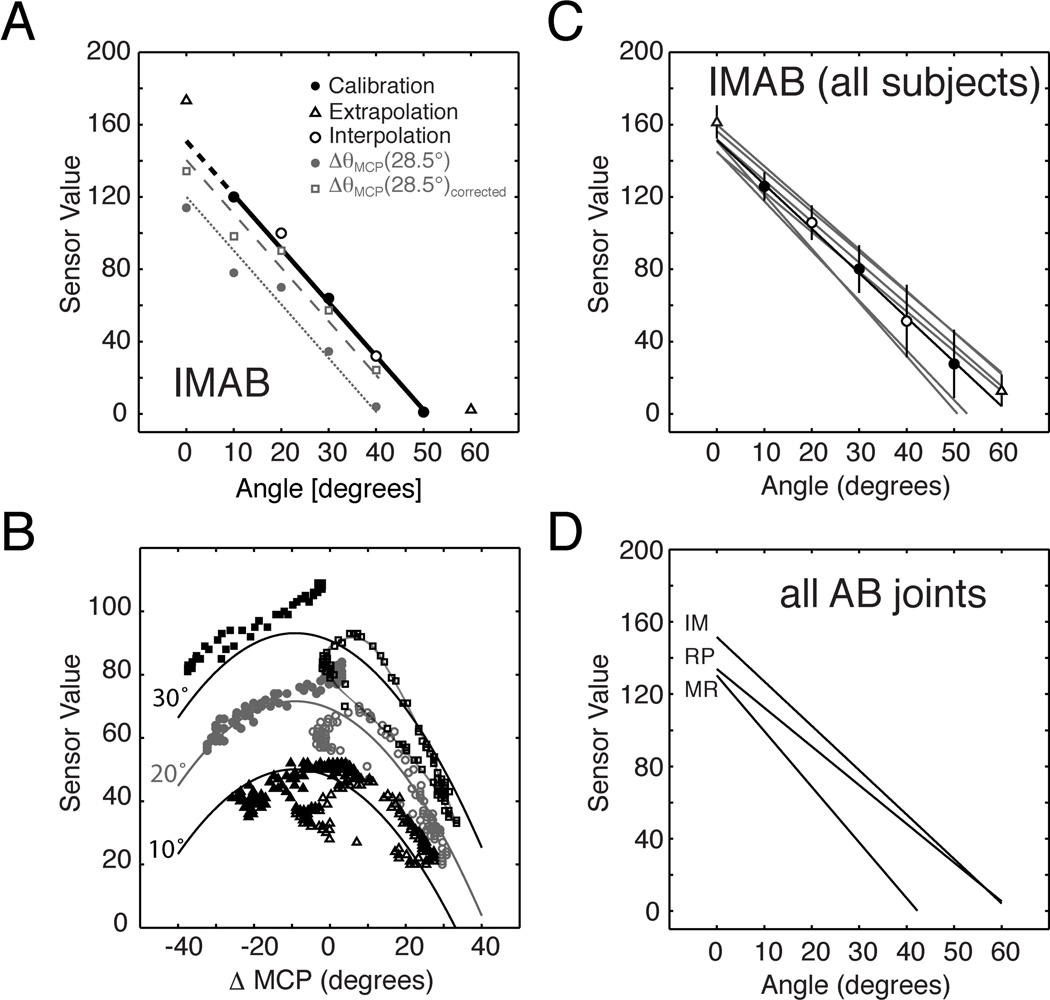
Abduction sensor calibration. a) Flat-hand IMAB readings for fixed calibration (•), interpolation (◦) and extrapolation angles (△), with calibration line are shown in black. Calibration data (•) collected with 28.5° differential in MCP (ΔθMCP) flexion are shown in gray with a solid calibration line. The 28.5° ΔθMCP data (□) corrected as per Eqn 3b are shown in gray with a dashed calibration line. b) IMAB sensor data collected using the moving finger approach. △: 10° abduction tool. • (gray): 20° abduction tool. □: 30° abduction tool. (The thin line for □ reveals hysteresis in the AB sensor recordings, not modeled using the correction model of Eqn 3b, Appendix.) c) IMAB calibration lines for each subject (gray) and the cohort average (black) with the population mean ± 1 SD for each sample point. d) Cohort average calibration lines for all AB joint sensors.
The linear model also performed exceedingly well in interpolation and extrapolation, except when the largest abduction tool, 60°, was inserted between adjacent fingers, in which case the AB sensor frequently reached the limit of the sensors’ dynamic range, thus yielding erroneous readings. When the 60° readings were excluded, VAF was quite high (IM: 99.8% ± 0.1%; MR: 97.2% ± 4.0%; RP: 99.7% ± 0.3%), and thus we are justified in estimating abduction angles from raw sensor values (Eqn 7, Appendix). However, when the 60° readings were included, accuracy of the model in interpolation and extrapolation was compromised at the widest abduction angles for the MRAB sensor (VAF for IM: 99.8% ± 0.2%; MR: 92.6% ± 0.2%; RP: 99.6% ± 0.3%), indicating that abduction angle estimates may not be as accurate at extremely large angles. (Fortunately, extreme angles such as this are likey to be rare in natural signing, and therefore the impact of this particular problem on sign language research should be minimal.)
As with flexion/extension, we observed variability in the abduction model both across subjects (Figure 6c) and across individual AB sensors (Figure 6d) suggesting again that each sensor must be calibrated separately for each subject in order that accurate estimations of abduction angles may be derived.
4.3.3 Abduction Model Corrected for MCP Flexion
When the flexion angles of the MCP joints surrounding a given AB sensor differed from each other, the AB sensor readings were different than those obtained for the same amount of abduction in a flat hand. For example, when the MCP joints at the two fingers differed by ~30° angle (i.e. 28.5° as measured by the flexion sensors) as shown in Figure 6a (gray filled circles and solid gray line), we obtained abduction sensor output values that were considerably less than those recorded when calibration was performed with the hand resting on a flat surface (black line). As previously stated, this difference was due to a mechanical influence of MCP flexion on the raw AB sensor readings (see Section 3.1). To correct for this influence, we first characterized the relationship between AB sensor readings and the difference between the MCP flexion for the two fingers surrounding the sensor using the “moving finger” procedure described in Section 3.2. Figure 6b shows six data sets collected for the IMAB sensor using this moving finger approach, (one for each finger moving with abduction of the stationary finger held at 10°, 20° and 30°). As shown, the relationship between AB sensor readings and MCP motion was reasonably approximated as a quadratic ("U"-shaped) function of the MCP flexion difference.8 As can be seen in Figure 6a (gray squares and dashed line), correcting the original raw sensor values using the quadratic function in the model (Eqn 3b, Appendix) yielded sensor values considerably closer to those obtained with a flat hand, thus demonstrating the validity of this approach.
4.4 Summary
This section showed that the mathematical translation model and the calibration procedures described in Section 3 perform very well in predicting joint angles from raw sensor readings. A linear (i.e. simple) relationship between sensor readings and joint angles for flexion and extension was not surprising given the success of others studies making similar measurements (e.g. Kessler, Hodges & Walker 1995, Kahlesz, Zachmann & Klein 2004, Wang & Dai 2009). However, our abduction model accounts for complex (non-linear) coupling between the MCP and AB sensors, more so than any previous attempt we have yet found (cf. Kahlesz et al. 2004, Wang & Dai 2009). Although our model is not perfect (e.g. it ignores effects such as degradation at the extremes of the abduction range), it provides a simple, systematic approach to data glove calibration, marking considerable progress towards solving this problem by providing a data translation model that performs well in both interpolation and extrapolation.
5 Example applications
We now describe potential applications of joint angle calibration for the study of handshape variation in sign languages. It should be noted that the data presented here is pilot data used only for demonstration purposes. Much more data is needed before we can begin to draw any meaningful conclusions in these areas.
5.1 Participants and brief methodology
Two signers, one hearing and one Deaf, participated in the set of sample data presented here. The hearing subject (‘Subject 1’) is a CODA (Child of Deaf Adults) from an extensive Deaf family, learned ASL from birth, and is employed as an ASL interpreter. The Deaf subject (‘Subject 2’) grew up signing Signed English and switched to ASL in adolescence. Both subjects are active members of Milwaukee’s Deaf Community and use ASL extensively in their everyday lives.
The two subjects were asked to provide ASL equivalents (using signs or classifier descriptions) for English words, letters, numbers, and pictures while wearing the CyberGlove.9 Stimulus items were shown on a laptop computer via presentation software. Further methodological descriptions are included in the sections below as necessary. Glove data was translated into angles using the methods described in Sections 3, and then plotted using MATLAB software. In the interest of clarity, only index finger data is presented in most of the illustrations below, but similar kinds of information were obtained for the other fingers as well.
5.2 Visualizations
Once we have quantitative data on joint angles in handshape, visualizing that data becomes a useful tool for analysis. By quantifying the data and plotting it in various ways, we are able to abstract the handshape information and distance ourselves from the linguistic biases often present when observing handshapes from live or video recorded signing. In this section, we provide examples of two of the many possible methods available for visualizing handshape data.
5.2.1 Joint changes over time
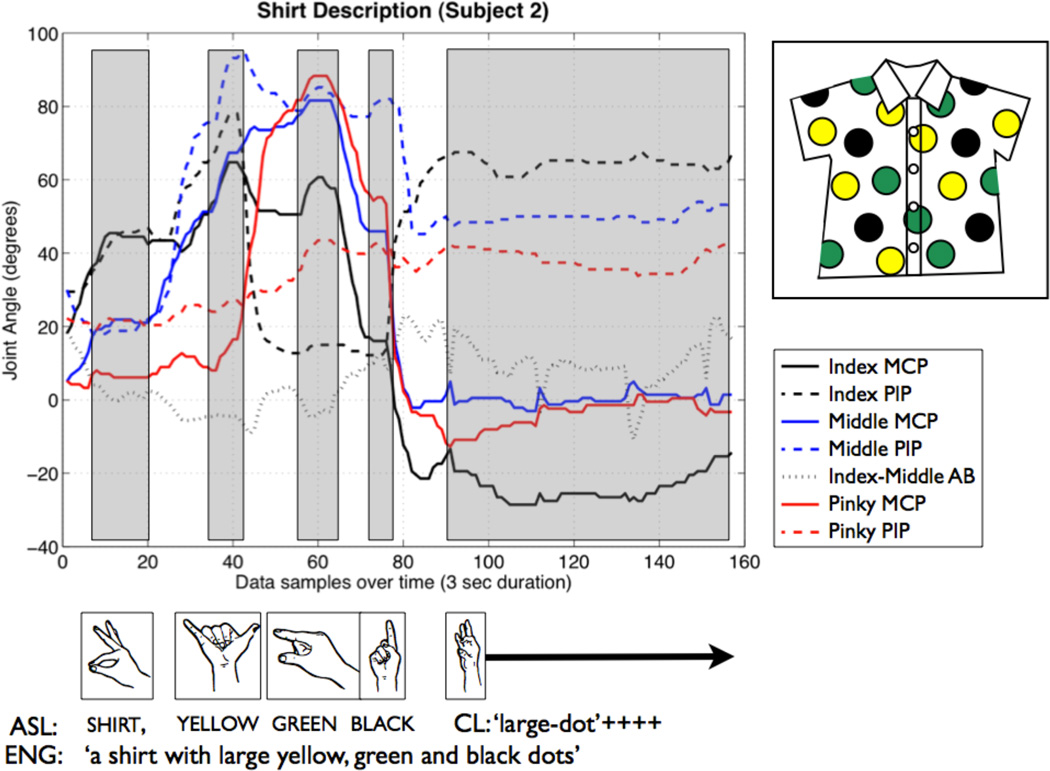
One way of visualizing handshape data involves plotting joint changes over time (cf. Cheek 2001). In this way, one can compare the joint angles for specific handshapes as well as examine the transitions between them. Figure 7 illustrates data from handshapes used in a description of a polka dotted shirt (pictured) by Subject 2. The figure shows the joint angle estimates calculated for seven glove sensors (IMCP, IPIP, MMCP, MPIP, IMAB, PMCP and PPIP, see Figure 1), chosen because they best exemplify the handshapes used in the signs of the description. The shaded areas in the plot indicate the approximate timing for each sign’s articulation, corresponding to the ASL glosses below, and the handshape pictures between the plot and the gloss represent the canonical handshapes for each sign in turn.
Figure 7.
Visualization of joint changes over time for the description of polka dotted shirt (pictured). Canonical handshapes for the signs used in the description are presented in line with both approximate duration boxes on the plot (above) and the glosses for their corresponding signs (below).
As an example of how this type of visualization represents the data, let us follow the progression of the IMCP joint (solid black line) throughout the utterance. In the sign for shirt, the index finger is selected with the MCP joint partially flexed (~40°) as it makes contact with the thumb in 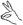 . For the
. For the  in yellow, the index finger flexes further to join the group of closed, non-selected fingers, such that its MCP joint angle measures between 50° and 60°. The index finger resumes its selected status for green and black, the MCP joint (after extending a bit during the transition) returning to ~60° to form the
in yellow, the index finger flexes further to join the group of closed, non-selected fingers, such that its MCP joint angle measures between 50° and 60°. The index finger resumes its selected status for green and black, the MCP joint (after extending a bit during the transition) returning to ~60° to form the  , and then extending to near 15° for the
, and then extending to near 15° for the 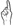 .10 Finally, this subject’s index MCP joint hyperextends (~ −20°) as it combines with a flexed PIP joint (dashed black line) to form the ‘large-dot’ classifier handshape that was repeated throughout the rest of the utterance.
.10 Finally, this subject’s index MCP joint hyperextends (~ −20°) as it combines with a flexed PIP joint (dashed black line) to form the ‘large-dot’ classifier handshape that was repeated throughout the rest of the utterance.
One potential benefit for this type of visualization is its usefulness in analyzing the phonetic influence of the surrounding joints (or surrounding handshapes) on phonologically equivalent joint configurations. For example, it is well known that the position of non-selected fingers in a handshape is either “extended” or “closed” (usually, but not always, in perceptual contrast to the position of the selected fingers), and that there is a great deal of acceptable phonetic variation that occurs within those two distinctions (Mandel 1981). However, very little is understood about the exact nature of this variation or when it occurs. Plots like the one in Figure 7 allow comparisons between numerous joint configurations at once—both across an utterance or at a given moment—which allows researchers to more easily identify or verify phonetic influences. For instance, in the sentence illustrated here, the middle finger is non-selected and extended in both the lexical sign shirt and the classifier handshape representing ‘large-dot’, but (at least in this particular utterance) the configuration of this finger is very different between the two handshapes. For shirt (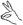 ), the MPIP (blue dashed line) and MMCP (blue solid line) are flexed approximately the same amount (~20°), indicating a slightly lax extension of the finger as a whole. In contrast, for the classifier handshape, the MPIP joint is flexed at ~50° while the MMCP is fully extended (~0°), likely echoing the more pronounced curved configuration of the selected index finger (PIP: ~60°, MCP: ~ −20°).
), the MPIP (blue dashed line) and MMCP (blue solid line) are flexed approximately the same amount (~20°), indicating a slightly lax extension of the finger as a whole. In contrast, for the classifier handshape, the MPIP joint is flexed at ~50° while the MMCP is fully extended (~0°), likely echoing the more pronounced curved configuration of the selected index finger (PIP: ~60°, MCP: ~ −20°).
Of course, more research is needed to discover how consistent such relationships are within and across signers, but the ability to measure multiple joint angles simultaneously across whole utterances using the data glove allows researchers to do this research much more quickly (and objectively) than they could by observation alone. Furthermore, while the number of glove sensors displayed in Figure 7 was limited for the sake of illustration, this type of plot could potentially represent data from all of the hand sensors, as well as motion capture data from other parts of the body (see Section 6), facilitating even more elaborate comparisons. With practice, researchers could even learn to read these more complex plots, much as a spectrogram is read for spoken language data.
5.2.2 Distribution in a “joint space”
Another potential visualization technique is plotting static handshape data within a biomechanically permissable “joint space”. Similar to the vowel space used for modeling some spoken languages phonemes (e.g. Lindblom & Sundberg 1971), a joint space describing handshapes would be based on the biomechanical (and ultimately, perceptual) characteristics of the articulators involved (in this case, the finger joints). From this information, we can draw boundaries based on the anatomical range of permissible joint configurations, and then handshape data can be plotted within those boundaries, facilitating the analysis of their respective distributions. By comparing the locations of contrastive segments within the vowel space, spoken language researchers have identified linguistic constraints based on notions of perceptual distance and relative articulatory ease (e.g. Flemming 2002). Here, by plotting sign language handshapes within the admissible joint space, we can gain a better understanding of the articulatory and perceptual distribution of sign language phonemes, as well as how they are situated relative to biomechanical boundaries. Defining a hand articulation space in this way facilitates a mathematically tractable definition of “distance” between handshapes as well as an intuitive means to visualize those differences.
Although much more research is necessary to truly understand the biomechanical limitations in handshape formation, Figure 8 illustrates what such a space might look like for handshapes given a single set of selected fingers—in this case, where all fingers are in the same joint configuration. This particular 3-D plot represents the joint configurations associated with the index finger: flexion of the MCP joint along the x-axis, abduction between the index and the middle fingers along the y-axis, and flexion at the PIP joint along the z-axis. The boundaries of this example space are based on the average dynamic flexion and abduction ranges of six non-signers, and the data within the space show the distribution of Battison’s (1978) basic handshapes utilizing only one set of selected fingers (i.e. 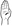

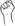

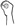
 ) as produced in core lexical items by Subject 1 in our sample data. At least for this sample, the plot shows that distribution of these basic unmarked handshapes is fairly spread out within the space, in many cases spreading towards the edges of the available space, much as vowels do in spoken languages.
) as produced in core lexical items by Subject 1 in our sample data. At least for this sample, the plot shows that distribution of these basic unmarked handshapes is fairly spread out within the space, in many cases spreading towards the edges of the available space, much as vowels do in spoken languages.
Figure 8.
Visualization of handshape distribution within a sample “joint space” for handshapes utilizing a single set of selected fingers. The handshapes plotted are from signs using Battison’s (1978) core set, as signed by Subject 1 in core lexical signs.
5.3 Handshape variation
However one chooses to visualize the data (we continue below by plotting handshapes in a 2-D space using IMCP vs. IPIP flexion), the type of data made available from these calibration procedures are invaluable to the study of handshape variation. As stated in the introduction, most work on handshape thus far has focused on phonemic distinctions. When researchers have examined phonetic variation, their results have typically been limited to visually salient categories of differences, (e.g. pinky extended or flexed). Precise quantitative production data could benefit both language internal and cross-linguistic research projects by providing more detailed information about the nature of the variations observed. In the sections that follow, we illustrate several ways that our methodology could be used to inform current research questions in the field of sign language phonology.
5.3.1 Comparisons across subjects
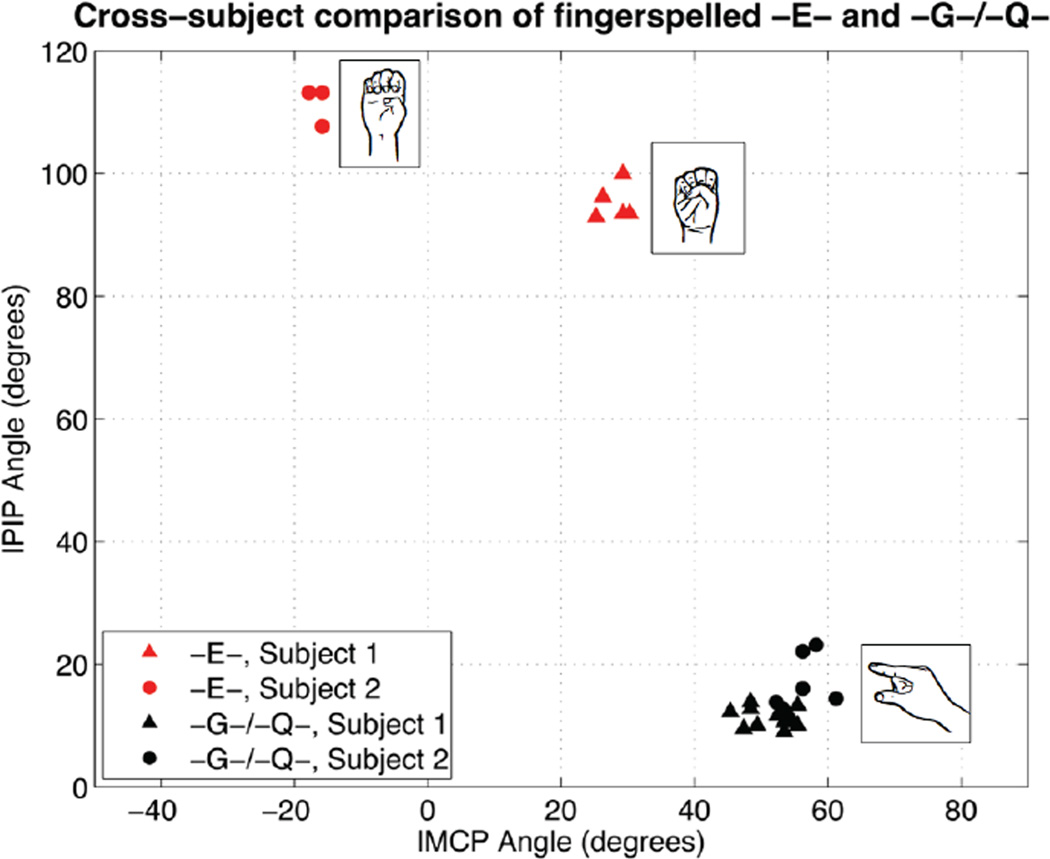
One way to examine variation is to simply compare handshape articulation across subjects. Our two pilot subjects were quite similar in their production of many of the handshapes we examined, especially for fingerspelling handshapes. One example of such similarity can be seen in the tightly clustered plot for all instances of fingerspelled -G- and -Q- handshapes (performed in isolation) by both subjects (Figure 9, black).11 Conversely, the plot of fingerspelled -E- (Figure 9, red) shows very different articulations between the two subjects; Subject 1 had a slightly flexed IMCP (indicative of the ‘closed E’ handshape variant), while Subject 2’s was slightly hyper-extended (indicative of the ‘open E’ variant).
Figure 9.
Comparison of fingerspelled -E- (red) and -G-/-Q- (black) across subjects.
Ultimately, of course, it will take data from large pools of subjects to make reliable claims about group differences, but one could easily imagine using this technique to identify and track regional variation, or even to identify historical processes like “handshape shifts”, i.e., subtle changes in joint position over time and across dialects of a language, similar to the vowel shifts studied in spoken languages. Also, by examining this type of handshape data across multiple signers for given phonological contexts (i.e. taking into consideration the surrounding handshapes and/or other phonological parameters, see Section 6), we can begin to identify which differences constitute allophonic variations across particular signing populations.
5.3.2 Cross-lexical comparisons
One can also use this methodology to look at how handshapes from specific ranges cluster depending on the type of sign in which they are used. Using observational evidence, Padden (1998) and Brentari & Padden (2001) first demonstrated that the morphological and phonological behavior of handshapes varies across different parts of sign language lexicons–specifically, between foreign borrowings (e.g. fingerspelling and initialized forms) and native signs from the core lexicon. Similar observations have also been made comparing handshape behavior between core forms, initialized forms and classifiers (Eccarius 2008, Brentari & Eccarius, 2010).
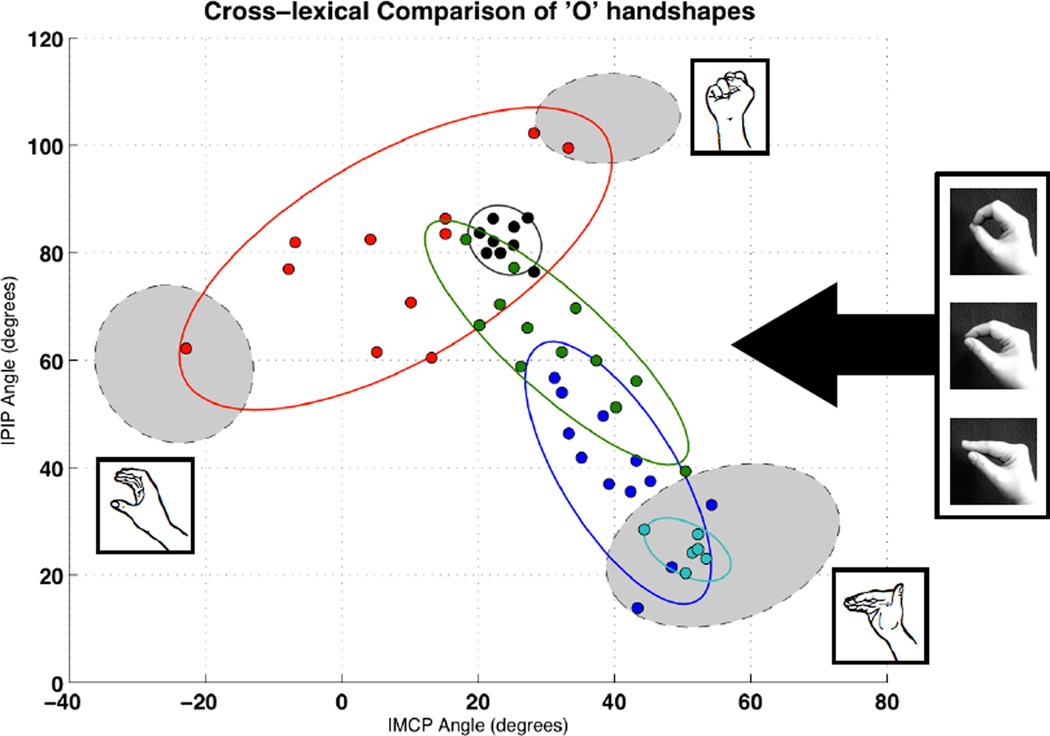
Eccarius (2008) expanded upon this literature by adding experimental evidence in support of such differences, using perceived stimuli.12 This experiment found different morphophonemic boundaries and (possibly) phonetic perceptual targets, within a particular handshape range (the “O” range depicted in Figure 10) depending on lexical category (core, initialized, or classifier). The results confirmed that there is a meaningful distinction between ‘round’ and ‘flat’ classifier forms at the extremes of the handshape range (something easily observed by language users), and also indicated that the mid-point handshape is ungrammatical as a shape classifier. In contrast, all three ‘O’ handshapes were deemed acceptable for core and initialized forms, although the results suggested that different phonetic preferences may exist between the lexical types; the results of a ‘goodness’ rating between the three handshapes in different lexical contexts showed that the flat handshape was less acceptable for initialized signs than for core forms, suggestingp a rounder phonetic target for initialized forms over core forms.
Figure 10.
Pilot data for “O” handshapes across lexical group with 95% confidence ellipses. Red = round classifiers, cyan = flat classifiers, black = fingerspelled -O-, green = initialized signs, and blue = core signs. Confidence ellipses for ‘S’, ‘C’ and ‘flatB’ handshapes are included for visual comparison.
The glove methodology we propose could be useful for confirming (or denying) such morphophonemic and phonetic differences across the lexicon by allowing researchers to examine the articulatory groupings of handshapes for signs from different parts of the lexicon. The results from our two pilot subjects illustrate how the glove data can capture articulatory variation across lexical categories. Figure 10 shows the handshape plots for the “O” handshapes in our sample data, as signed in core signs (teach, eat and home), initialized signs (opinion, office and organization), fingerspelling (-O-), and classifiers describing and/or manipulating round and flat objects (round: plumbing pipe, cardboard tube, telescope; flat: envelope). These plots are surrounded by 95% confidence ellipses for the data distribution from each lexical group. Confidence ellipses for nearby handshapes (also from the sample data) are included for the purposes of visual comparison. As shown in the figure, this data shows a clear distinction between round and flat classifier handshapes (red and cyan, respectively), as well as a tendency for initialized signs (green) to be rounder than core forms (blue), but not as round as fingerspelled -O- (black).13 These results support the earlier perceptual findings, although a larger data set is needed to verify that these articulatory tendencies are present for the greater signing population.
5.3.3 Categorical vs. gradient classifier comparisons
Another research question that could benefit from this methodology involves iconic representation in classifier forms–specifically, do the classifier handshapes used to depict different sized objects vary continuously or discretely? Emmorey and Herzig (2003) determined that size and shape classifier handshapes were categorical when produced by signers naïve to a specific range of sizes (e.g. different sized pendants seen in isolation). However, they also found that, at least perceptually, signers could be sensitive to gradient differences in handshape (analogous to changes in vowel length to indicate duration, e.g. ‘it was a looooong time’). Sevcikova (2010, forthcoming) found similar results for handling classifiers describing the manipulation of different sized objects (again, presented in isolation) in British Sign Language. The question now becomes, if asked to describe a series of objects with a range of sizes, will signers utilize information regarding scale in their production of classifier handshapes, or will their productions remain categorical in nature?
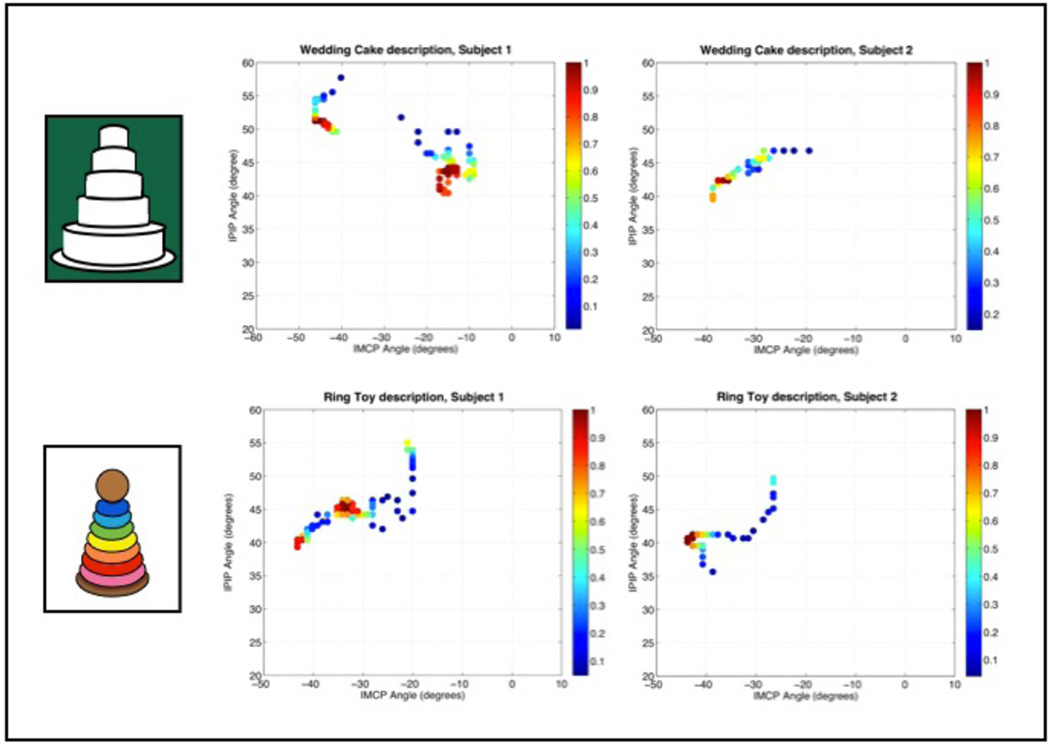
The plots in Figure 11 show examples of how this question might be explored using joint angle data from the CyberGlove. We showed both subjects pictures of a multi-tiered wedding cake and a toy with a range of ring sizes (pictured) and then plotted the classifier handshape data using a density plot.14 On this plot, the warmer the color (i.e. towards red on the accompanying color scale), the higher the frequency is for a given set of joint angles (in this case, for the index finger) over the course of the description. If each of the sizes were signed using a separate joint combination, we would expect a separate “hot spot” for the representation of each size (indicating a longer time spent at each configuration), interspersed with blue (brief) transitional configurations. However, Figure 11 demonstrates that at least in the cases shown here, not all of the possible size differences are being represented. For the wedding cake, each subject’s data shows only two handshape clusters, despite the fact that both descriptions contained representations for all five cake tiers. (Subject 1’s clusters are more distinct due to a quick transition between handshapes, but Subject 2’s are still apparent in the reddish and yellow clusters.) For the ring toy, both subjects represented at least six rings in their signing, but only two (by Subject 2) or three (by Subject 1) handshapes are apparent from the density plot clusters. As with the other examples presented here, a much larger pool of data is needed to draw conclusions on this issue, but we feel that the methodology presented provides an exciting opportunity for obtaining such data.
Figure 11.
Density plots for handshapes in descriptions of a 5-tier wedding cake (top) and a ring toy (bottom).
5.4 Additional applications
The example applications presented here are certainly not all-inclusive. For instance, it is our hope that the kinematic data ultimately collected using this type of methodology could be used to establish handshape “norms” for varying purposes. One important application for such norms would be in sign language therapy. Quantitative data describing the “normal” range of joint movements used for particular handshapes in a language could help clinicians set rehabilitation goals, either for Deaf patients after illness or stroke or for children with motoric sign language deficits (e.g. developmental apraxia).
Similar norms could also be used in second language/second modality acquisition research to improve teaching techniques. For example, Chen Pichler (2011) and her students looked at handshape variation in signs and gestures by new hearing learners of ASL via a sign repetition study in attempts to better understand what constituted “accented” versus “non-accented” signing. Unfortunately, without a clear understanding of the amount of variation deemed acceptable by the ASL community at large, it became difficult to differentiate “errors” from acceptable variation in the new signers. Indeed, Chen Pichler discusses in her conclusions “the need for more information on handshape variation in both conventional American gesture and signs in ASL” (115). The kind of information provided by the kinematic calibration and recording techniques we describe would not only allow acquisition researchers to better understand how handshapes are produced by adult learners of sign languages, but it would also inform researchers about the amount of variation that is or is not acceptable in these cases by the signing community.
Finally, it is worth mentioning that while we plan to use this methodology to analyze sign language variation, this methodology could also be used for non-linguistic purposes. Being able to precisely (and automatically) measure joint angle using a data glove would be useful in clinical or motor analysis applications (cf. Wise, et al. 1990, Williams et al. 2000) as well as in research studying non-linguistic types of hand movements such as gesture or grasp.
6 Conclusion
In the past, sign language researchers studying handshape variation have been limited to using visual observations of data from video images, but thanks to the commercial availability of data glove systems like the CyberGlove, this is no longer the case. Until now, however, no methodology has existed to translate raw glove sensor readings into the precise finger joint measurements needed for quantifiable comparisons of handshape across subjects. In this article, we have presented a methodology to do just that. We presented our empirical model and our calibration methods, as well as the results of data used to test the procedure. Finally, we demonstrated (via pilot data) potential applications for the resulting quantitative data, offering analysis options that we hope will ultimately aid sign language linguists as they seek to understand how handshapes are produced at a phonetic level.
The procedures presented here are incomplete. Future work will need to be done to improve the coupling equations – especially for data with extreme angular differences at the MCP joints (Section 4.3.2). There is also much progress yet to be made in the calibration procedures for the CyberGlove’s other sensors (e.g. thumb flexion, abduction and rotation).
We should also note that there are some inherent limitations involved with data glove use. For example, the gloves themselves are expensive, and not all researchers may have the financial resources to acquire them. Also, although our pilot subjects reported very little hinderance of movement, in cases where researchers desire more naturalistic signing from their subjects, the glove could prove unnecessarily cumbersome. Therefore, as useful as glove data will be for the study of handshape in sign language, using a dataglove to measure finger kinematics will never replace the need for observational data. Notation systems for handshapes (e.g. Prillwitz, et al. 1989, Eccarius & Brentari 2008b, Johnson & Liddell, 2011) will remain important for the analysis of signing in more naturalistic settings, or in situations where a glove is not available. Rather, the information gleaned from phonetic investigations involving the glove can be helpful in informing researchers about how narrow or broad their transcriptions should be in those situations based on the specific research questions being asked.
In addition, data from a data glove alone has its limits for more extensive phonological analyses. More specifically, in order to make extensive claims about, for example, allophonic variants or the relationship between handshape and place of articulation (i.e. orientation, see Brentari 1998), additional kinematic data is required. Fortunately, combining glove systems with other forms of motion capture technology is relatively easy to do, and once the glove data is combined with data about other parameters, the research potential is immense.
Despite these limitations, however, use of data glove systems like the CyberGlove as a measuring device for joint angle has amazing potential for the field of sign language phonology. Our goal for this project was to develop techniques to enable researchers to carry out such measurements, and we feel that this article describes significant progress toward that goal.
Acknowledgements
We would like to thank NIH grant R01NS053581, the Way-Klingler family foundation, the Birnschein Family Foundation and the Falk Foundation medical research trust for funding for this work. We would also like to thank Jon Wieser for his assistance, as well as all those who participated in our data collections.
Appendix
Here we present the technical details of our translation model. As explained in the text, the data translation model that we have defined uses different transformations for flexion/extension and abduction sensors. The flexion/extension model assumes linearity in the relationship between joint angle θ and "raw" data glove sensor values S:
| [1] |
at the two proximal joints (MCP and PIP) within each finger. In Eqn 1, subscript f can take on four values corresponding to each of the four fingers (hereafter, I: index; M: middle; R: ring; P: pinky) whereas subscript j takes on two values corresponding to the two joints of interest within each finger. Model coefficients af,j and bf,j are parameters to be identified during the calibration process.
Ideally, we also would want to characterize a similar relationship for the AB sensors, which are sensitive to the angular spread ϕ between pairs of adjacent fingers:
| [2] |
Here, S is a time series of AB sensor readings and the subscript p can take on three values corresponding to the three pairs of adjacent fingers (IM: index-middle; MR: middle-ring; RP: ring-pinky).
Unfortunately, the neighboring MCP joints influence the raw AB sensor readings (see Section 3.1) resulting in a highly nonlinear relationship. Therefore, instead of including a constant offset dp as in Eqn 2, the abduction model must instead include a correction factor g(·) that accounts for "cross-talk" between flexion/extension and abduction at the two fingers of interest:
| [3a] |
As shown in Section 4, the AB sensor readings vary as a quadratic function of the difference between MCP flexion angles for the two fingers of interest:
| [3b] |
where the α, β and χ are additional model parameters to be identified during calibration. Eqns 1 and 3 may both be rewritten succinctly in vector-matrix form as:
| [4a] |
where S is a column vector of N sensor readings, Θ is a regressor matrix arranged as column vectors and M is a column vector of parameters to be identified. For flexion/extension (Eqn 1):
| [4b] |
where T indicates the matrix transpose. For abduction (Eqns 3a and 3b,):
| [4c] |
During calibration (Section 3.2), we collect multiple data pairs {θf,j, Sf,j} for flexion/extension by using a set of "gold standard" calibration tools to place the finger joints in a predetermined posture with known joint angle θf,j. During a second calibration procedure, we collect multiple calibration data sets {ϕp, θf1, θf2, Sp} for abduction by using the calibration tools to constrain finger abduction while the MCP joint on either side of the AB sensor are moved through their range of motion.
To form the data vectors required to compute the model coefficients for flexion/extension (Eqn 4b), we concatenate each of the calibration angles into a column vector θf,j and the raw data glove sensor values into a second column vector Sf,j. To form the data vector Sp for a given pair of adjacent fingers, we concatenate the raw AB sensor readings at each sample instant from each of 6 abduction motion trials (3 abduction angles × 2 fixed MCP flexion angles; see Section 3.2) into a single, large column vector. To form the regressor matrix, we similarly concatenate the calibration angles ϕp, the computed values [(θf1 −θf2)2, (θf1 −θf2)] and the scalar constant 1 at each sample instant into separate column vectors organized side-by-side into a 4×R matrix, where R equals the grand total of all sampling instants across all 6 trials for sensor p.
For both sets of sensor reading vectors S and regressor matrices Θ, the data translation model's parameters can be identified by inverting Eqn 4a using least mean squares (LMS) regression:
| [5] |
Note that the flexion/extension model is used for 8 sensors (2 joints × 4 fingers) and has 2 parameters per sensor. The abduction model is used for 3 sensors and has 4 parameters per sensor. The data translation model thus includes 28 parameters.
Once all of the model parameters have been identified by the calibration process (Section 3.2), joint angles θf,j and ϕp can be estimated directly from raw glove sensor readings Sf,j. For flexion/extension measurements:
| [6] |
where the asterisk indicates an estimated value. For the abduction angles:
| [7] |
where g(·) can be calculated from the MCP flexion angles computed using Eqn 6.
Footnotes
Because of system software constraints, a reading of ‘0’ never occurs, making the glove's actual "raw data" output range 1 – 255. Furthermore, "typical" hands only utilize a range of 40 – 220, thus allowing for hand sizes outside the norm (Virtual Technologies 1998). For “atypical” subjects whose hands are able to reach or exceed the upper and/or lower limits of the range, the offset and gain values for each sensor can be adjusted using software from the manufacturer, however they were not adjusted during our data collections so that comparisons could be made across subjects (cf. Kessler, Hodges & Walker 1995).
Virtual technologies (1998) acknowledges the logistical difficulty of DIP measurement, and suggests that anyone who does not explicitly need to know DIP angles should use instead the 18-sensor CyberGlove, which has no DIP sensors. Such a glove was used in Kessler, Hodges & Walker (1995).
Special thumb tools are currently under development.
For more information about these tools, please contact the authors.
70°, 80° and 90° are too large to be used between fingers but were included in the set for use with the thumb in future work.
Use of calibration wedges underneath the finger is not recommended for calibrating finger flexion due to inaccuracies arising from tool placement difficulties and finger geometry, and should only be done in cases such as the “moving finger” procedure where MCP flexion is calculated later from actual sensor readings.
From this point forward, I = index; M = middle; R = ring; P = pinky.
We do note substantial deviation from the quadratic form, especially in the form of "hysteresis" that was sometimes observed (e.g. the thin loop traced out for one of the two 30° trials using open symbols in Figure 6b) when one or the other of the moving joints was cycled through its range of motion. A signal has hysteresis when its value depends on its own recent history. For example, the IMAB sensor values in Fig 6c appear to take on markedly different values when the middle finger MCP joint is flexing vs. when it is extending. We ignored this complication in the current calibration procedure and approximated the relationship between AB sensor readings and MCP motion as a quadratic ("U"-shaped) function of the MCP flexion difference.
Because of differing time constraints for the collection sessions of each subject, the numbers of data points for some stimulus items may vary.
See Crasborn (2001) for discussion of why the MCP joint for 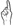 is not fully extended in this context.
is not fully extended in this context.
Both used the  handshape for -G- and -Q-, differentiating between them using orientation.
handshape for -G- and -Q-, differentiating between them using orientation.
Various aspects of this experiment are also reported in Eccarius & Brentari (2008a) and Brentari & Eccarius (2011).
Because of the free nature of the picture description task (i.e. there was no guidance about which handshape to use), the classifiers representing round objects ranged from ‘C’-type handshapes (no contact between thumb and finger tips) through ‘O’ (contact), to handshapes nearing ‘S’ (fingers tucked to some degree under the thumb). Because we currently lack a way of detecting or measuring contact with the thumb, we included all variants in the figure.
In all descriptions, each representation of tier/ring size was visually identifiable by an altered spacing between the hands and a slight pause.
References
- Ann Jean. A linguistic investigation of the relationship between physiology and handshape. Tucson, AZ: University of Arizona dissertation; 1993. [Google Scholar]
- Ann Jean. Frequency of occurrence and ease of articulation of sign language handshapes: The Taiwanese example. Washington, D.C.: Gallaudet University Press; 2006. [Google Scholar]
- Battison Robbin. Lexical borrowing in American Sign Language. Silver Spring, MD: Linstok Press; 1978. [Google Scholar]
- Boyes Braem Penny. Acquisition of the handshape in American Sign Language: A preliminary analysis. In: Volterra V, Erting C, editors. From gesture to language in hearing and deaf children. New York: Springer; 1990. pp. 107–127. [Google Scholar]
- Brentari Diane. A Prosodic Model of Sign Language Phonology. Cambridge, MA: MIT Press; 1998. [Google Scholar]
- Brentari Diane, Padden Carol. A language with multiple origins: Native and foreign vocabulary in American Sign Language. In: Brentari Diane., editor. Foreign vocabulary in sign language: A cross-linguistic investigation of word formation. Mahwah, NJ: Lawrence Erlbaum; 2001. pp. 87–119. [Google Scholar]
- Brentari Diane, Eccarius Petra. Handshape constrasts in sign language phonology. In: Brentari Diane., editor. Sign Languages: A Cambridge Language Survey. Cambridge: Cambridge University Press; 2010. pp. 284–311. [Google Scholar]
- Brentari Diane, Eccarius Petra. In: Formational units in sign languages. Rachel Channon, van der Hulst Harry., editors. Boston, MA: De Gruyter; 2011. pp. 125–150. [Google Scholar]
- Cheek Davina Adrianne. The phonetics and phonology of handshape in American Sign Language. Austin, TX: University of Texas dissertation; 2001. [Google Scholar]
- Chen Pichler Deborah. Sources of handshape error in first-time signers of ASL. In: Donna Jo Napoli, Mathur Gaurav., editors. Deaf around the world. Oxford: Oxford University Press; 2011. pp. 96–121. [Google Scholar]
- Cormier Kearsy. Grammaticization of indexic signs: How American Sign Language expresses numerosity. Austin, TX: University of Texas dissertation; 2002. [Google Scholar]
- Crasborn Onno. Phonetic implementation of phonological categories in Sign Language of the Netherlands. Leiden University dissertation; 2001. [Google Scholar]
- Dipietro Laura, Sabatini Angelo, Dario Paolo. A survey of glove-based systems and their applications. IEEE Transactions on Systems, Man, and Cybernetics–Part C: Applications and Reviews. 2008;38:463–482. [Google Scholar]
- Eccarius Petra. A constraint-based account of handshape contrast in sign languages. West Lafayette, IN: Purdue University dissertation; 2008. [Google Scholar]
- Eccarius Petra, Brentari Diane. Proceedings from the Annual Meeting of the Chicago Linguistic Society. Vol. 44. University of Chicago: Chicago Linguistic Society; 2008a. Contrast differences across lexical stubstrata: Evidence from ASL handshapes; pp. 187–201. [Google Scholar]
- Eccarius Petra, Brentari Diane. Handshape coding made easier: A theoretically based notation for phonological transcription. Sign Language & Linguistics. 2008b;11:69–101. [Google Scholar]
- Emmorey Karen, Herzig Melissa. Categorical versus gradient properties of classifier constructions in ASL. In: Karen Emmorey., editor. Perspectives on classifier constructions in sign languages. Mahwah, NJ: Lawrence Erlbaum; 2003. pp. 221–246. [Google Scholar]
- Fisher M, van der Smagt P, Hirzinger G. Learning techniques in a dataglove based telemanipulation system for the DLR hand. Proceedings of the IEEE International Conference on Robotics & Automation; Leuven, Belgium. 1998. pp. 1603–1608. [Google Scholar]
- Flemming Edward. Auditory representations in phonology. New York: Routledge; 2002. [Google Scholar]
- Gao Wen, Ma Jiyong, Wu Jiangqin, Wang Chunli. Sign language recognition based on HMM/ANN/DP. International Journal of Pattern Recognition and Artificial Intelligence. 2000;14:587–602. [Google Scholar]
- Greftegreff Irene. A few notes on anatomy and distinctive features in NTS handshapes. University of Trondheim, Working Papers in Linguistics. 1993;17:48–68. [Google Scholar]
- Griffin Weston, Findley Ryan, Turner Michael, Cutkosky Mark. Calibration and mapping of a human hand for dexterous telemanipulation. Proceedings ASME IMECE, Dynamic Systems and Controls Division. 2000;69:1145–1152. [Google Scholar]
- Huenerfauth Matt, Lu Pengfei. Accurate and accessible motion-capture glove calibration for sign language data collection. ACM Transactions on Accessible Computing. 2010;3(2):1–32. [Google Scholar]
- Johnson Robert, Liddell Scott. Toward a phonetic representation of hand configuration: The fingers. Sign Language Studies. 2011;12:5–45. [Google Scholar]
- Kahlesz Ferenc, Zachmann Gabriel, Klein Reinhard. ‘Visual-fidelity’ dataglove calibration. Proceedings of the Computer Graphics International. 2004:403–410. [Google Scholar]
- Kessler G Drew, Hodges Larry, Walker Neff. Evaluation of the CyberGlove as a whole-hand input device. ACM Transactions on Computer-Human Interaction. 1995;2:263–283. [Google Scholar]
- Klima Edward, Bellugi Ursula. The Signs of language. Cambridge, MA: Harvard University Press; 1979. [Google Scholar]
- Lindblom Björn, Sundberg Johan. Acoustical consequences of lip, tongue, jaw, and larynx movement. Journal of the Acoustical Society of America. 1971;50:1166–1179. doi: 10.1121/1.1912750. [DOI] [PubMed] [Google Scholar]
- Liu Xiaolin, Mosier Kristine, Mussa-Ivaldi Ferdinando, Casadio Maura, Scheidt Robert. Reorganization of finger coordination patterns during adaptation to rotation and scaling of a newly-learned sensorimotor transformation. Journal of Neurophysiology. 2011;105:454–473. doi: 10.1152/jn.00247.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Xiaolin, Scheidt Robert. Contributions of online visual feedback to the learning and generalization of novel finger coordination patterns. Journal of Neurophysiology. 2008;99:2546–2557. doi: 10.1152/jn.01044.2007. [DOI] [PubMed] [Google Scholar]
- Lucas Ceil, Bayley Robert, Valli Clayton. Sociolinguistic variation in American Sign Language. Washington, DC: Gallaudet University Press; 2001. [Google Scholar]
- Mandel Mark A. Natural constraints in sign language phonology: Data from anatomy. Sign Language Studies. 1979;24:215–229. [Google Scholar]
- Mandel Mark A. Phonotactics and morphophonology in American Sign Language. Berkeley, CA: University of California dissertation; 1981. [Google Scholar]
- Mosier Kristine, Scheidt Robert, Acosta Santiago, Mussa-Ivaldi Ferdinando. Remapping hand movements in a novel geometrical environment. Journal of Neurophysiology. 2005;94:4362–4372. doi: 10.1152/jn.00380.2005. [DOI] [PubMed] [Google Scholar]
- Padden Carol. The ASL lexicon. Sign Language & Linguistics. 1998;1:39–60. [Google Scholar]
- Prillwitz Siegmund, Leven Regina, Zienert Heiko, Hanke Thomas, Henning Jan. HamNoSys. Version 2.0; Hamburg Notation System for sign languages. An introductory guide. Hamburg: Signum Verlag; 1989. [Google Scholar]
- Sandler Wendy. Representing handshapes. In: William Edmondson, Wilbur Ronnie., editors. International review of sign linguistics. Volume 1. Mahwah, NJ: Lawrence Erlbaum Associates; 1996. pp. 115–158. [Google Scholar]
- Sevcikova Zed. Categorical vs. gradient properties of handling handshapes in British Sign Language. Poster presented at the tenth Theoretical Issues in Sign Language, Purdue University; West Lafayette, IN. 2010. [Google Scholar]
- Sevcikova Zed. Categorical versus gradient properties of handling handshapes in British Sign Language (BSL): Evidence from handling handshape perception and production by deaf BSL signers and hearing speakers. London: University College London dissertation; (forthcoming). [Google Scholar]
- Tyrone Martha, Mauk Claude. Sign lowering and phonetic reduction in American Sign Language. Journal of Phonetics. 2010;38:317–328. doi: 10.1016/j.wocn.2010.02.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vamplew Peter. Proceedings of the First European Conference on Disability, Virtual Reality and Associated Technologies. Maidenhead, UK: 1996. Recognition of sign language gestures using neural networks; pp. 27–33. [Google Scholar]
- Virtual Technologies, Inc. CyberGlove reference manual. Palo Alto, CA: 1998. [Google Scholar]
- Wang Bin, Dai Shuling. Dataglove calibration with constructed grasping gesture database; Proceedings of the International Conference on Virtual Environments, Human-Computer Interfaces and Measurements Systems; 2009. [Google Scholar]
- Wang Chunli, Gao Wen, Shan Shiguang. An approach based on phonemes to large vocabulary Chinese Sign Language recognition; Proceedings of the Fifth IEEE International Conference on Automatic Face and Gesture Recognition; 2002. [Google Scholar]
- Wilcox Sherman. The phonetics of fingerspelling. Philadelphia, PA: John Benjamins; 1992. [Google Scholar]
- Williams NW, Penrose JMT, Caddy CM, Barnes E, Hose DR, Harley P. A goniometric glove for clinical hand assessment. Journal of Hand Surgery. 2000;25B:200–207. doi: 10.1054/jhsb.1999.0360. [DOI] [PubMed] [Google Scholar]
- Wise Sam, Gardner William, Sabelman Eric, Valainis Erik, Wong Yuriko, Glass Karen, Drace John, Rosen Joseph M. Evaluation of a fiber optic glove for semi-automated goniometric measurements. Journal of Rehabilitation Research and Development. 1990;27:411–424. doi: 10.1682/jrrd.1990.10.0411. [DOI] [PubMed] [Google Scholar]