Video Time Encoding Machines

Abstract

We investigate architectures for time encoding and time decoding of visual stimuli such as natural and synthetic video streams (movies, animation). The architecture for time encoding is akin to models of the early visual system. It consists of a bank of filters in cascade with single-input multi-output neural circuits. Neuron firing is based on either a threshold-and-fire or an integrate-and-fire spiking mechanism with feedback. We show that analog information is represented by the neural circuits as projections on a set of band-limited functions determined by the spike sequence. Under Nyquist-type and frame conditions, the encoded signal can be recovered from these projections with arbitrary precision. For the video time encoding machine architecture, we demonstrate that band-limited video streams of finite energy can be faithfully recovered from the spike trains and provide a stable algorithm for perfect recovery. The key condition for recovery calls for the number of neurons in the population to be above a threshold value.

I. INTRODUCTION

TIME encoding machines (TEMs) [1] are asynchronous signal processors that encode analog information in the time domain. TEMs play a key role in the representation of analog waveforms by silicon-based information systems and in sensing the natural world by biological sensory systems. There is also substantial amount of interest in TEMs as front ends of brain-machine interfaces, i.e., as building blocks connecting biological and silicon-based information systems.

Intuitively, TEMs encode a (input) band-limited time signal into a multidimensional time sequence. For applications in the visual space, however, the input is a space-time function. TEMs encoding space-time analog waveforms that are of interest in silicon-based information systems and in early biological vision systems are discussed below.

Early hardware implementations of space-time encoding mechanisms include silicon retinas for spike-based vision systems [2], [3]. Applications of silicon retinas include, among others, spatial-contrast image encoding [4], motion detection [5], and real-time 2-D convolutions [6]. The question of implementing silicon retinas that faithfully represent video streams in the time domain and the associated design of perfect recovery algorithms has not been addressed in the literature. In neuromorphic engineering practice, the recovery of real-time video streams has shown substantial aliasing effects [7].

Decoding of stimuli encoded by early biological visual systems is a grand challenge in neuroengineering. A number of encoding models exist in the literature including computational models for the retina, lateral geniculate nucleus (LGN), and V1 of mammals. However, the representation power of these circuits in unknown. In [8], we initially addressed the use of neurons modeled akin to simple V1 cells having Gabor-like spatial receptive fields and a non-leaky integrate-and-fire (IAF) spiking mechanism. However, a general methodology for building arbitrary neural circuits with feedback and arbitrary receptive fields is not available.

In this paper, we introduce for the first time a general architecture of space-time video TEMs. The architecture is inspired by models of the early visual system; it applies as a template architecture for silicon-based TEMs. The basic TEM architecture is based on a flexible set of interconnected building blocks. The key building blocks are filters modeling receptive fields and single-input multiple-output (SIMO) neural circuits with feedback representing analog information akin to neuronal circuits in the early visual system.

For each SIMO neural circuit, neuron spike generation is based on a threshold-and-fire (TAF) or an IAF mechanism. The circuit models employed here include general feedback connections within and in-between neurons. For each of the encoding neural circuits, we study the representation of the input analog signal and its recovery from the output spike train. As we shall demonstrate, these circuits project the input signal on a set of functions determined by the spike sequence. Under appropriate conditions, these functions span the space of band-limited signals, and, consequently, the encoded stimulus can be recovered from these projections. We devise algorithms that faithfully recover the stimulus and investigate changes in encoding due to feedback. We also demonstrate that encoding circuits based on TAF and IAF mechanisms can be operationally treated in a similar manner.

For the overall video TEM architecture, we derive conditions for the faithful representation of the analog input stream as a multidimensional time (spike train) sequence. We also provide a stable algorithm for recovery of the video input from spike times. The key condition for recovery comes from the mathematical theory of frames [9] and requires that the population spike density as well as the number of neurons is above the Nyquist rate.

This paper is organized as follows. In Section II, we present SIMO neural circuits that map an analog signal into a multidimensional time sequence. We show how these circuits encode information and establish invertibility conditions. In Section III, the problem of time encoding of analog video streams is posed in a general setting. We shall derive a time decoding algorithm that faithfully recovers the video signal from the multidimensional spike train in Section IV. Detailed examples are given in Section V. Finally, Section VI concludes our work and discusses future directions.

II. Time Encoding with Neural Circuits with Feedback

In this section, we analyze the representation power of a number of encoding circuits based on models of neurons of the early visual system as well as models of neurons arising in silicon retina and related neuromorphic hardware. The basic encoding circuit investigated here is a SIMO neural circuit with feedback that maps an analog input signal into a multidimensional time sequence (see Fig. 1).

Fig. 1.

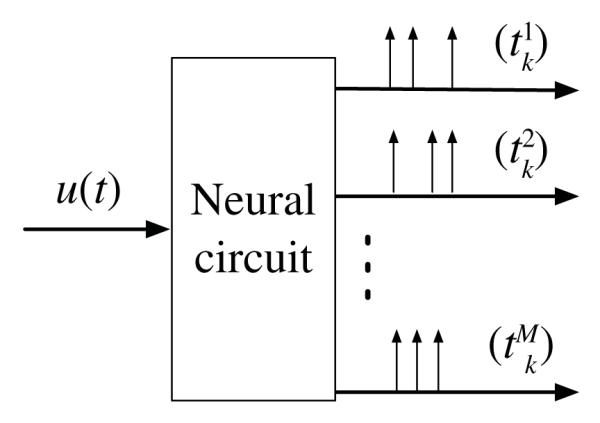
SIMO neural circuit with feedback.

All analog input signals of interest u = u(t), t ∈ ℝ, in this section live in the space of band-limited functions with finite energy and with spectral support in, the [−Ω, Ω]. We denote this space with letter Ξ. In Section II-A, single-input single-output (SISO) neural circuits are investigated, in Section II-B and II-C single-input two-output neural circuits are considered. We shall show that existing models of retinal ganglion cells (RGCs) and LGN neurons [10] and simple neural circuits arising in frame-free cameras [5] have the same representation properties. They are simple instantiations of the neural circuit model with feedback (see Fig. 1).

We demonstrate that information contained at the input of the neural encoding circuit can be recovered by a decoder provided the average number of spikes is above the Nyquist rate. For each TEM, we will show how to build a time decoding machine (TDM) that perfectly recovers the encoded signal. The structure of the decoders is the same and consists of a low-pass filter (LPF) whose input is a train of weighted spikes derived from those generated by the neural circuit.

The theoretical framework presented in this section was first developed in [11]. It has only been formally applied, however, to the decoding of stimuli encoded with a population of unconnected IAF neurons without feedback. Here we show how to apply it to stimuli encoded with fully pulse-connected neural circuits and extend it to circuits with neurons with TAF with feedback. Moreover, by explicitly calculating the spike density of all the neural circuits of interest, we greatly improve on the bounds presented in [11]. Examples are given in Section II-D.

A. Time Encoding with a Single Neuron

The object of this section is the analysis of SISO TEMs with feedback (see Fig. 2). We will refer to these circuits as single neuron TEMs. Fig. 2(a) shows the spiking mechanism of a time encoding neural circuit consisting of a single neuron with feedback. The structure of the circuit is inspired by a neuron model that was first proposed in [10]. The neuron fires whenever its membrane potential reaches a fixed threshold value δ. After a spike is generated, the membrane potential is reset through a negative feedback mechanism that gets triggered by the just emitted spike. The feedback mechanism is modeled by a filter with impulse response h(t).

Fig. 2.

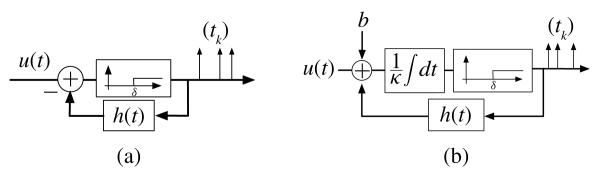
Single neuron TEMs with feedback. (a) TAF with feedback. (b) IAF with feedback.

The encoding is quantified with the t-transform [1] that, given the input stimulus, describes in mathematical language the sampling process. Let (t_k), k ∈ ℤ, be the set of spike times at the output of the neuron. Then the t-transform of the TEM depicted in Fig. 2(a) can be written for all k, k ∈ ℤ, as

$$u\left(t_k\right)=\delta +\sum _{l<k}h(t_k-t_l).$$ (1)

Equation (1) can be written in inner product form as

$$\langle u,{\chi }_k\rangle =q_k$$ (2)

where q_k = δ + Σ_l<k h(t_k−t_l), χ_k(t) = g(t−t_k), k ∈ ℤ, and g(t) = sin(Ωt)/πt, t ∈ ℤ, is the impulse response of a LPF with cutoff frequency Ω. The impulse response of the filter in the feedback loop is causal, and in widely adopted models it is decreasing with time (e.g., exponential decay) [10].

Fig. 2(b) depicts a time encoding neural circuit consisting of an IAF neuron with feedback. IAF neurons have been used to model RGCs and LGN neurons in [12]. The t-transform of the encoding circuit can be written as

$${\int }_{t_k}^{t_{k+1}}u\left(s\right)ds=k\delta -b(t_{k+1}-t_k)-\sum _{l\le k}{\int }_{t_k}^{t_{k+1}}h(s-t_l)ds$$ (3)

or in inner product form as

$$\langle u,{\chi }_k\rangle =q_k$$ (4)

where $q_k=\kappa \delta -b(t_{k+1}-t_k)-{\sum }_{l\le k}{\int }_{t_k}^{t_{k+1}}h(s-t_l)ds$ and χ_k = g *1_{[tk, tk+1]}, for all k, k ∈ ℤ (* denotes the convolution).

It is easy to see that both encoding circuits described above have a similar operational structure. Both encode the signal u by projecting it on a set of sampling functions (χ_k), k ∈ ℤ. A decoder with observations (t_k), k ∈ ℤ, can readily evaluate the inner product (projection) sequence (q_k), k ∈ ℤ. Assuming that the spike density of the observations is above a threshold value, the following proposition provides a representation of the stimulus that is stable. The spike density intuitively formalizes the notion of average number of spikes in an arbitrarily large time interval. Appendix A provides a detailed methodology for computing the spike density of the simple neurons models employed in this paper.

Proposition 1: The band-limited input stimulus u, encoded with a single neuron TEM (Fig. 2), can be recovered as

$$u\left(t\right)=\sum _{k\in \mathbb{Z}}{c}_k{\eta }_k\left(t\right)$$ (5)

where η_k (t) = g(t−t_k), provided that the spike density of the single neuron TEM is above the Nyquist rate Ω/π. Moreover, with [c]_k = c_k, the vector of coefficients c is given by

$$\mathbf{c}={\mathbf{G}}^{+}\mathbf{q}$$ (6)

where G⁺ denotes the pseudoinverse of G, [q]_k = q_k and [G]_kl = 〈χ_k, η_l〉, for all k, l ∈ ℤ.

Proof: The representation result (5) holds and it is stable if the sequences of sampling functions χ = (χ_k), k ∈ ℤ, and representation functions η = (η_k), k ∈ ℤ, form frames for the space of band-limited functions Ξ. From the theory of frames for complex exponentials [13], the sequence η is a frame if the spike density is above the Nyquist rate. For the TAF with feedback TEM of Fig. 2(a), χ_k = η_k, for all k ∈ ℤ, and therefore, the sequence χ is a frame. For the IAF with feedback TEM of Fig. 2(b), the sequence η can be mapped to χ by a bounded operator with closed range, and thus, the frame property is preserved [9]. The interested reader can find a more detailed technical discussion in [11] and [14].

Equation (6) can be obtained by substituting the representation of u in (5) into the equation of the t-transform in (2) or (4), respectively. Since the sequence η, is a frame for Ξ, (5) and (6) are guaranteed to give a stable reconstruction [15].

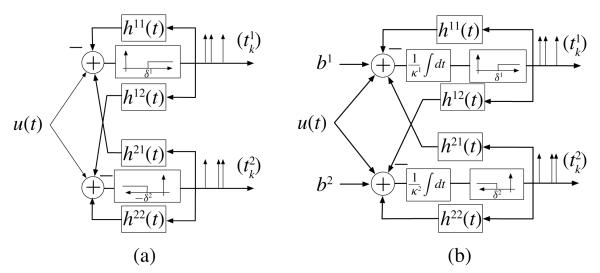
B. Time Encoding with ON-OFF Neurons

In this section, we analyze single-input two-output TEMs with feedback (see Fig. 3). Two different circuits are shown. Each circuit consists of two neurons with the same spike triggering mechanism and feedback. We will refer to these circuits as ON-OFF TEMs.

Fig. 3.

ON-OFF TEMs with feedback. (a) TAF with feedback. (b) IAF with feedback.

Fig. 3(a) shows a circuit consisting of two interconnected ON-OFF neurons each with its own feedback. Each neuron is endowed with a level crossing detection mechanism with a threshold that takes a positive value δ¹ and a negative value −δ², respectively. Whenever a spike is generated, the feedback mechanism resets the corresponding membrane potential. In addition, the firing of each spike is communicated to the other neuron through cross-feedback. In general, the cross-feedback brings the other neuron closer to its firing threshold and thereby increases its spike density. The two neurons in Fig. 3(a) arise as models of ON and OFF bipolar cells in the retina and their connections through the non-spiking horizontal cells [16].

With ($t_k^j$), k ∈ ℤ, the set of spike times of the neuron j, j = 1, 2, the t-transform of the ON-OFF TEM amounts to

$$\begin{array}{cc}\hfill u\left(t_k^1\right)& =+{\delta }^1+\sum _{l<k}{h}^{11}(t_k^1-t_l^1)-\sum _l{h}^{21}(t_k^1-t_l^2)1_{\{t_l^2<t_k^1\}}\hfill \\ \hfill u\left(t_k^2\right)& =-{\delta }^2-\sum _{l<k}{h}^{22}(t_k^2-t_l^2)+\sum _l{h}^{12}(t_k^2-t_l^1)1_{\{t_l^1<t_k^2\}}\hfill \end{array}$$ (7)

for all k, k ∈ ℤ. Equation (7) can be written in inner product form $\langle u,{\chi }_k^j\rangle =q_k^j$, where $q_k^j$ is the right side of (7) and ${\chi }_k^j\left(t\right)=g(t-t_k^j)$, k ∈ ℤ, j = 1, 2, are the sampling functions.

Fig. 3(b) shows a circuit consisting of two interconnected ON-OFF neurons each with its own feedback. The neurons are IAF. The t-transform of the neural circuit can be written as

$$\begin{array}{cc}\hfill {\int }_{t_k^1}^{t_{k+1}^1}u\left(s\right)ds& =-b^1(t_{k+1}^1-t_k^1)+\sum _{l\le k}{\int }_{t_k^1}^{t_{k+1}^1}{h}^{11}(s-t_l^1)ds-\sum _{l:\{t_l^2<t_{k+1}^1\}}{\int }_{t_k^1}^{t_{k+1}^1}{h}^{21}(s-t_l^2)ds+{\kappa }^1{\delta }^1\hfill \\ \hfill {\int }_{t_k^2}^{t_{k+1}^2}u\left(s\right)ds& =-b^2(t_{k+1}^2-t_k^2)-\sum _{l\le k}{\int }_{t_k^2}^{t_{k+1}^2}{h}^{22}(s-t_l^2)ds+\sum _{l:\{t_l^1<t_{k+1}^2\}}{\int }_{t_k^2}^{t_{k+1}^2}{h}^{12}(s-t_l^1)ds+{\kappa }^2{\delta }^2\hfill \end{array}$$ (8)

or in inner product form $\langle u,{\chi }_k^j\rangle =q_k^j$, with $q_k^j$ the right side of (8), and the sampling functions are ${\chi }_k^j=g\ast 1_{[t_j^k,t_{k+1}^j]}$, for k ∈ ℤ, and j = 1, 2.

Proposition 2: The input stimulus u, encoded with an ON-OFF TEM (Fig. 3), can be recovered as

$$u\left(t\right)=\sum _{k\in \mathbb{Z}}{c}_k^1{\eta }_k^1\left(t\right)+\sum _{k\in \mathbb{Z}}{c}_k^2{\eta }_k^2\left(t\right)$$ (9)

where the representation functions are given by ${\eta }_k^j\left(t\right)=g(t-t_k^j)$, j = 1, 2, provided that the spike density of the ON-OFF TEM is above the Nyquist rate Ω/π. Moreover, with c = [c¹; c²] and ${\left[{\mathbf{c}}^j\right]}_k=c_k^j$, the vector of coefficients c can be computed as

$$\mathbf{c}={\mathbf{G}}^{+}\mathbf{q}$$ (10)

where q = [q¹; q²] with ${\left[{\mathbf{q}}^j\right]}_k=q_k^j$, and

$$\mathbf{G}=\left[\begin{array}{cc}\hfill {\mathbf{G}}^{11}\hfill & \hfill {\mathbf{G}}^{12}\hfill \\ \hfill {\mathbf{G}}^{21}\hfill & \hfill {\mathbf{G}}^{22}\hfill \end{array}\right],{\left[{\mathbf{G}}^{ij}\right]}_{kl}=\langle {\chi }_k^i,{\eta }_l^i\rangle$$

for all i, j = 1, 2, and k, l ∈ ℤ.

Proof: It is similar to the proof of Proposition 1.

C. Time Encoding with Silicon ON-OFF TEMs

ON-OFF spiking mechanisms have been used in various neuromorphic hardware applications [2], [5]. In this section, we present simplified versions of the ON-OFF neurons presented in Section II-B that have been implemented in silicon. We will refer to these circuits as silicon ON-OFF TEMs.

Fig. 4(a) depicts the silicon neuron implemented in [5]. A spike is generated whenever a positive or negative change of magnitude δ is detected. Immediately thereafter, the input to the thresholding blocks is reset to zero through a simple feedback mechanism. The encoding circuit in Fig. 4(a) can be obtained from the ON-OFF TEM depicted in Fig. 3(a) by setting δ¹ = δ² = δ and h¹¹(t) = h²²(t) = h¹²(t) = h²¹(t) = δ · 1_[t>0]. The input to both the ON and OFF branch is

$$v\left(t\right)=u\left(t\right)-u\left(\tau \right(t\left)\right)$$

where τ(t) is the last spike before time t.

Fig. 4.

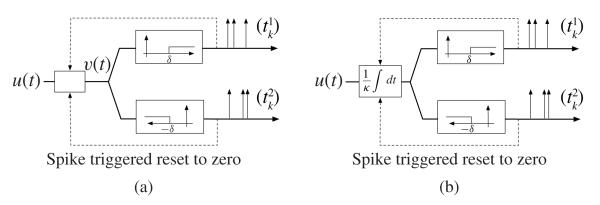
Encoding with a silicon ON-OFF TEM. (a) TAF with feedback. (b) IAF with feedback.

For arbitrary n ∈ ℤ and k ∈ ℕ, the t-transform of the silicon TEM amounts to

$$\begin{array}{cc}\hfill u\left(t_{n+k}^1\right)& =u\left(t_n^1\right)+\delta \left(k-\sum _{l\in \mathbb{Z}}{1}_{[t_n^1<t_l^2<t_{n+k}^1]}\right)\hfill \\ \hfill u\left(t_{n+k}^2\right)& =u\left(t_n^2\right)-\delta \left(k-\sum _{l\in \mathbb{Z}}{1}_{[t_n^2<t_l^1<t_{n+k}^2]}\right).\hfill \end{array}$$ (11)

As in the previous examples, the above equalities can also be expressed in inner product form.

The circuit in [17, Fig. 4(b)] can be obtained by simplifying the ON-OFF TEM shown in Fig. 3(b) with δ¹ = δ² = δ, κ¹ = κ² = κ and h¹¹(t) = h²²(t) = h¹²(t) = h²¹(t) = κδ · 1_[t>0]. We finally note that Proposition 2 holds for the silicon ON-OFF TEMs briefly sketched above, thus establishing conditions for perfect recovery.

D. Example

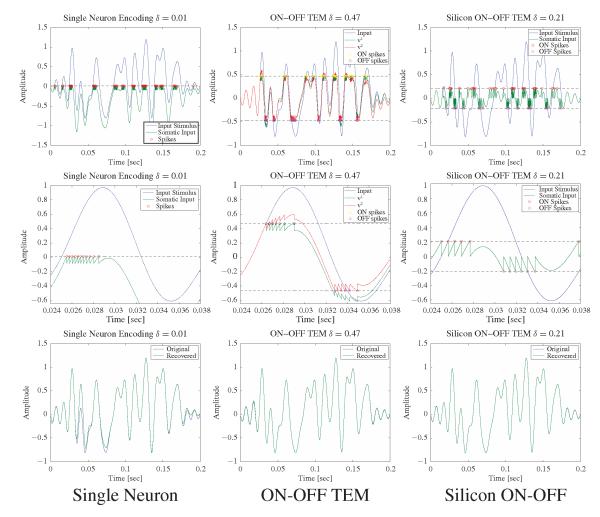
We illustrate the recovery algorithms for the TEMs presented above with an example using a band-limited function with Ω = 2π · 100 rad/s on the time interval [0, 0.2] s. For simplicity in presentation, we restrict ourselves to neuron models based on TAF spiking mechanism. In order to simplify the comparison of the performance of recovery algorithms for signals encoded with different neural circuits, the circuit parameters were chosen so that all TEMs approximately generated the same number of spikes.

For the single neuron TEM, the threshold was δ = 0.01 and the feedback filter h(t) = 0.1 exp(−100t)1_[t>0] For the ON-OFF TEM, δ¹ = δ² = 0.47, h¹¹(t) = h²²(t) = 0.1 exp(−100t)1_[t>0], and h¹²(t) = h²¹(t) = 0.075 exp(−t/0.015)1_[t>0]. For the silicon ON-OFF TEM δ = 0.21. The results are shown in Fig. 5.

Fig. 5.

Recovery of signals encoded with TAF with feedback TEMs. Top row: Encoding mechanisms. Single neuron TEM (left), ON-OFF TEM (middle), and silicon ON-OFF TEM (right). Middle row: Encoding mechanisms zoomed in, in the time interval [0.024, 0.038 s. Bottom row: Comparison between the encoded and the recovered signals.]

The single neuron TEM fired a total of 87 spikes, fired in clusters when the input signal is greater than the threshold and the stimulus is increasing. The neuron does not fire any spikes when the input is negative. In theory, this does not create problems as long as the spike density is above the Nyquist rate. In practice, however, signals have finite time support. As a result, in negative signal regions the recovery might be poor.

The situation improves with the ON-OFF TEM which also fired a total of 87 spikes (51 for the ON part and 36 for the OFF part). Trigger times occur again in clusters but sample the stimulus at both positive and negative values. Note that the signal entering the thresholding block has a reduced range when compared to the encoded stimulus. In general, for the same number of trigger times, the ON-OFF TDM tends to lead to better recovery results than the single neuron TDM. For example, in the time interval [0.025, 0.175] s the single neuron TDM had a signal-to-noise ratio (SNR) = 13.87 [dB] whereas the ON-OFF TDM recovered the stimulus with SNR = 54.04 [dB].

Finally, the silicon ON-OFF TEM produced a similar number of spikes (84 spikes, 42 for each branch). The spikes were more uniformly distributed when compared to the spikes of the single neuron TEM and the ON-OFF TEM, both of which occur in clusters. This resulted in a better stimulus recovery with SNR = 64.2 [dB] in the time interval [0.025, 0.175] s. The improved performance is primarily due to the precision in representing the signal samples as integer multiples of the threshold value. In the case of the ON-OFF TEM, numerical errors are introduced through the feedback current. The latter is dependent on the previous spike times that are measured with a finite temporal resolution.

III. Architecture of Video TEMs

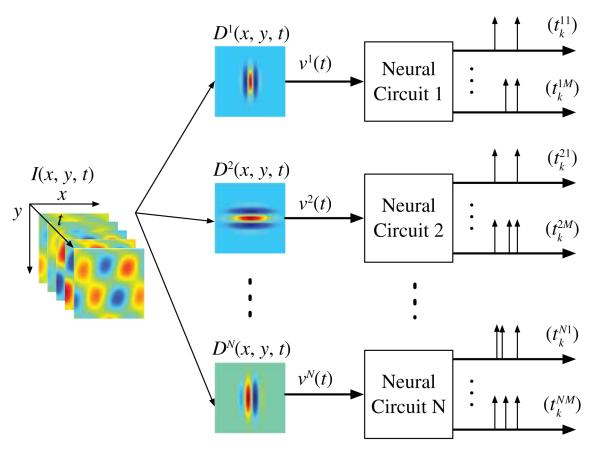
In this section, we introduce a model architecture for video TEMs (see Fig. 6). The architecture consists of a bank of N spatiotemporal filters and N neural circuits. The neural circuits are SIMO TEMs. Each filter is connected to a single neural circuit and represents its spatiotemporal receptive field (STRF). The input video stream is considered to be band-limited in time and continuous in space.

Fig. 6.

Architecture of the video TEM.

By establishing the t-transform of the video TEM, we show how an analog video stream is represented in the time domain. In Section IV, we shall prove that under mild conditions the video stream can be perfectly recovered by only knowing the encoder parameters and the spike times and derive perfect recovery algorithms.

Let $\mathcal{H}$ denote the space of (real) analog video streams I = I (x, y, t), (x, y, t) ∈ ℝ³, that are band-limited in time and continuous in space, and have finite energy. It is clear that the space $\mathcal{H}$ is a Hilbert space, when endowed with the inner product $\langle \cdot ,\cdot \rangle :\mathcal{H}\times \mathcal{H}\mapsto ℝ$ defined by

$$\langle I_1,I_2\rangle ={\int }_{{ℝ}^3}{I}_1(x,y,t)I_2(x,y,t)dxdydt.$$

In full generality, we assume that each neural circuit j has an STRF described by the function D^j = D^j (x, y, t), (x, y, t) ∈ ℝ³, j = 1, 2, …, N. In what follows, we assume that the filters describing the STRFs are bounded-input bounded-output stable. Filtering the video stream with the receptive field of the neural circuit j gives the receptive field output v^j(t). The latter serves as the main input to neural circuit j and amounts to

$$v_j\left(t\right)={\int }_{ℝ}\left({\int }_{{ℝ}^2}{D}^j(x,y,s)I(x,y,t-s)dxdy\right)ds.$$ (12)

Following the discussion of Section II, the t-transform of ith branch of the jth neural circuit is described by

$${\langle v^j,{\chi }_k^{ji}\rangle }_{\Xi }=q_k^{ji}$$ (13)

where the sampling functions ${\chi }_k^{ji}\in \Xi$ and the inner products $q_k^{ji}\in ℝ$, for all k ∈ ℤ, i = 1, 2, …, M, and all j = 1, 2, …, N. Depending on the spiking mechanism of the neural circuit, the sampling functions are of the form ${\chi }_k^{ji}\left(t\right)=g(t-t_k^{ji})$ or ${\chi }_k^{ji}\left(t\right)=(g\ast 1_{[t_k^{ji},k_{k+1}^{ji}]})\left(t\right)$, t ∈ ℤ, where ($t_k^{ji}$), k ∈ ℤ, i = 1, 2, …, M, and j = 1, 2, …, N, is the spike sequence generated by the video TEM. Therefore, the t-transform of the video TEM is given by

$${\langle I,{\varphi }_k^{ji}\rangle }_{\mathcal{H}}=q_k^{ji}$$ (14)

where ${\varphi }_k^{ji}(x,y,t)=\left({\tilde{D}}_j\right(x,y,\cdot )\ast {\chi }_k^{ji}(\cdot \left)\right)\left(t\right)$ for all k ∈ ℤ, i = 1, 2, …, M, and j = 1, 2, …, N (D̃^j(x, y, t) = D^j (x, y, −t)).

The t-transform in (14) quantifies the projection of the video stream I onto the sequence of sampling functions $\varphi =\left({\varphi }_k^{ji}\right)$, j = 1, 2, …, N, i = 1, 2, …, M, k ∈ ℤ. If the sequence ϕ is a frame for $\mathcal{H}$, then I can be perfectly recovered from this set of projections. Furthermore, the recovery is stable. Our goal in the next section is to find sufficient conditions on the sequence ϕ to be a frame for $\mathcal{H}$ and to provide a recovery algorithm.

IV. Time Decoding and Perfect Recovery

In this section, we present the conditions on the set of receptive fields that guarantee a faithful representation of video stimuli and provide an algorithm for perfect signal recovery.

A. Conditions for Perfect Stimulus Recovery

Theorem 1: The input video stream I can be perfectly recovered from the set of spike times ($t_k^{ji}$), j = 1, 2, …, N, i = 1, 2, …, M, k ∈ ℤ, provided that the spike density of the neural circuits is sufficiently large, and for every ω_t ∈ [−Ω_t, Ω_t]

$$\left({\mathcal{F}}_{2D}^{-1}\left\{\left({\mathcal{F}}_{3D}{D}^j\right)(\cdot ,\cdot ,{\omega }_t)\right\}\right),j=1,\dots ,N$$ (15)

is a frame for the space of spatially band-limited images. Here, ${\mathcal{F}}_{2D}$ and ${\mathcal{F}}_{3D}$ denote the 2-D and 3-D Fourier transforms, respectively.

Proof: The proof is presented in Appendix B. Note that an explicit sufficient density condition is to have the spike density of every neural circuit above the temporal Nyquist rate Ω_t/π. Note also that a necessary condition for (15) to hold is to have the number of neurons at least equal to the number of independent spatial components of the input video stimulus. The latter is in full generality equal to Ω_x · Ω_y/π² per unit area, where Ω_x and Ω_y denote the spatial bandwidth along the x and y directions, respectively. In practice, although the video streams are defined on a finite spatial aperture, the spatial bandwidths are assumed to be finite.

Remark 1: The assumption of finite spatial bandwidth is supported in practice. In the visual system, the maximum spatial resolution is finite and depends (among others) on the density of the photoreceptor rods and cones [18].

Remark 2: Space-time separable receptive fields of the form

$$D^j(x,y,t)=D_s^j(x,y)D_{\tau }^j\left(t\right)$$ (16)

are of particular interest in systems neuroscience. For such receptive fields, the frame condition for perfect recovery becomes

$${\mathcal{F}}_{2D}^{-1}\left\{\right({\mathcal{F}}_{3D}{D}^j\left)\right(\cdot ,\cdot ,{\omega }_t\left)\right\}(x,y)=D_s^j(x,y){\widehat{D}}_{\tau }^j\left({\omega }_t\right)$$

where ${\widehat{D}}_{\tau }^j$ denotes the (1-D) Fourier transform of $D_{\tau }^j$. This holds, for example, when the temporal components of the receptive fields have full frequency support, i.e., $\mathrm{supp}\left({\widehat{D}}_{\tau }^j\right)\supseteq [-{\Omega }_t,{\Omega }_t]$, and the spatial receptive fields form an overcomplete wavelet filterbank. Such filterbanks arise as a model of receptive fields in the primate retina [19]. For more information, see the examples in Section V or [8].

The required conditions of Theorem 1 are rather abstract. These conditions are satisfied, however, for a number of practical applications with STRFs that:

1. are space-time separable and the spatial components form an overcomplete spatial filterbank (see Remark 2);

2. form an overcomplete space-time wavelet filterbank. Such a case can be useful for tracking applications [20];

3. are chosen randomly according to a known distribution (e.g., Gaussian). The latter case, briefly explored in example V-C, arises in analog-to-information conversion for compressed sensing [21].

Remark 3: The result of Theorem 1 along with the above discussion has a simple evolutionary interpretation. If every neuron responds to the stimulus with a positive, nonvanishing, spike rate, then visual stimuli can be faithfully represented in the spike domain using a finite number of neurons.

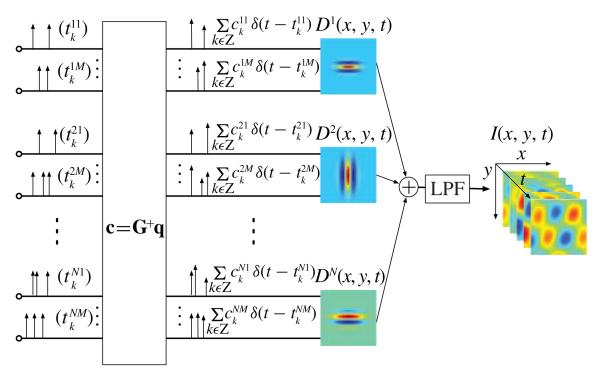
B. Perfect Recovery Algorithm

In order to devise a general recovery algorithm for the infinite dimensional case, we use the sequence of representation functions k ∈ ℤ, j = 1, 2, …, N, i = 1, 2, …, M, k ∈ ℤ, with

$${\psi }_k^{ji}(x,y,t)=\left(D^j(x,y,\cdot )\ast {\eta }_k^{ji}(\cdot )\right)\left(t\right)$$ (17)

where ${\eta }_k^{ji}\left(t\right)=g(t-t_k^{ji})$, t ∈ ℤ. We have the following.

Algorithm 1: If the assumptions of Theorem 1 hold, then for a sufficiently large N, the video stream I, encoded with a video TEM (Fig. 6), can be recovered as

$$I(x,y,t)=\sum _{j=1}^N\sum _{i=1}^M\sum _{k\in \mathbb{Z}}{c}_k^{ji}{\psi }_k^{ji}(x,y,t)$$ (18)

where $c_k^{ji}$, j = 1, 2, …, N, i = 1, 2, …, M, k ∈ ℤ, are suitable coefficients. With c = [c¹, c², …, c^N]^T, c^j = [c^j1, c^j2, …, c^jM]^T and ${\left[{\mathbf{c}}^{ji}\right]}_k=c_k^{ji}$, the coefficients c can be computed as

$$\mathbf{c}={\mathbf{G}}^{+}\mathbf{q}$$ (19)

where T denotes the transpose, q is a vector with entries ${\left[{\mathbf{q}}^{ji}\right]}_k=q_k^{ji}$, and G⁺ denotes the pseudoinverse of G. G is a N × N block matrix. Each block G^ij is in turn a M × M block matrix with entries given by

$${\left[{\mathbf{G}}_{mn}^{ij}\right]}_{kl}=\langle {\varphi }_k^{im},{\psi }_l^{jn}\rangle$$ (20)

for all i, j = 1, 2, …, N; k, l ∈ ℤ and m, n = 1, 2, …, M.

Proof: Equation (19) can be obtained by substituting the representation of I in (18) into thet-transform equation (14).

The video TDM pertaining to Algorithm 1 is depicted in Fig. 7.

Fig. 7.

Architecture of the video TDM.

V. Examples

In this section, we present examples of encoding of synthetic and natural video scenes with various video TEM architectures and analyze the performance of the associated decoding algorithms. The examples highlight the versatility of video TEMs for modeling purposes and the generality of their underlying structure. A note of caution, the video TEMs are clockless. In order to simulate them on Turing machines, however, only frame-based digital video sequences can be used. Consequently, in all our examples we employed natural scenes with a high frame rate. The high frame rate allowed us to load an approximation of the analog waveforms into our computation platform.

In Section V-A and V-B, we consider video TEMs with receptive fields used in models of RGCs and simple cells in V1. In Section V-C, the STRFs are randomly drawn and are space-time nonseparable. An encoding example of natural video scenes is presented in Section V-D.

A. Video TEM with Spatial Gabor Filterbank

The video TEM in this section consists of a spatial Gabor filter bank and neural circuits using four different firing mechanisms. Such encoding circuits are encountered in modeling simple cells and their receptive fields in the area V1 of the visual cortex in mammals [22].

The signal at the input of the video TEM is a synthetically generated space-time separable video stream of the form I (x, y, t) = S(x, y)u(t). The stream has the following characteristics. The temporal component has an equivalent bandwidth of 20 Hz in the time interval 𝕋 = [0, 250] ms. A temporal bandwidth of 20 Hz (Ω = 2π · 20 rad/s) has been reported to contain almost all the information for natural video streams [23]. The spatial component is defined on the domain (aperture) ⅅ = [−4, 4] × [−4, 4]. One hundred and twenty-eight pixels were used for the spatial discretization in each direction. This spatial resolution supports stimuli with spatial bandwidth of up to 8 Hz in each direction. In our case, the spatial bandwidth was 2.5 Hz in each spatial direction (2π · 2.5 rad/degree).

The architecture of the video TEM consists of a spatial Gabor filterbank in cascade with a population of neural circuits. The (Gabor) mother wavelet employed here was originally proposed by Lee [24] based on a number of mathematical and biological constraints. It is given by

$$\gamma (x,y)=\frac{1}{\sqrt{2\pi }}\exp \left(-\frac{1}{8}(4x^2+y^2)\right)(e^{i\kappa x}-e^{-{\kappa }^2∕2})$$

with κ/2π = 0.75 Hz. For (real) video streams, the mother wavelet decomposes into two wavelets corresponding to its real and imaginary part, respectively. To construct a spatial filterbank, one performs the operations of rotations, dilations, and translations on the mother wavelet. More information can be found in [8]. On both wavelet components, operations on three scales, three rotations, and 5 × 5 translations along both dimensions were used to generate a spatial Gabor filterbank consisting of a total of N = 2 × 3 × 3 × 5 × 5 = 450 filters.

Four different firing mechanisms for the neural circuits were considered, single neuron TEMs (with TAF, IAF with bias and feedback, and IAF with feedback without bias) and ON-OFF TAF TEM. In each case, the 450 SIMO TEMs were chosen to be the same. By appropriately choosing certain parameters, the four different video TEMs realizations approximately generated the same number of spikes. More specifically, the parameters of the neurons were chosen as follows. For every single neuron TEM with TAF, δ = 0.06 and h(t) = 0.055 exp(−t/0.03) · 1(t ≥ 0). For every single neuron TEM with IAF with bias, b = 1.1, δ = 2.7, κ = 0.01, and h(t) = 0.055 exp(−t/0.03) · 1(t ≥ 0), and finally, for the IAF without bias, b = 0, δ = 0.068, κ = 0.01, and h(t) = 0.055 exp(−t/0.03) · 1(t ≥ 0). For every ON-OFF TEM δ1 = −δ2 = 0.085, h¹¹(t) = h²²(t) = 0.08 exp(−t/0.06) · 1(t ≥ 0) and h¹²(t) = h²¹(t) = 0 (time in seconds).

To quantify the quality of the recovery, we used the peak-SNR (PSNR) for the spatial component (PSNR[S]) and for the entire video stream (PSNR[I]) and, SNR for the temporal component (SNR[u]). The performance of the various architectures under these metrics is summarized in Table I, where we also provide the total number of spikes for each architecture and the number of neurons that fired spikes out of the total 450. All the quality metrics are measured in dB.

TABLE I.

Performance of the Various Video TEM Realizations

	PSNR[S]	SNR[u]	PSNR[I]	Spikes	# fired
TAF	26.67	28.21	29.25	4667	259
IAF w bias	44.36	44.44	40.90	4409	450
IAF w/o bias	20.17	28.83	25.69	4543	215
ON-OFF TAF	32.63	42.3	35.11	4258	239

From Table I, we conclude that the best results were achieved by the video TEM realized with IAF neurons with bias, followed by the video TEM realized with ON-OFF TAF TEMs. The bias term in the former TEM forces every neuron to fire and, thereby, provides a “more uniform” sampling of the video stream. Consequently, information about all the projections of the video stream onto the elements of the filterbank is obtained. This leads to improved performance in recovery.

For the remaining cases, it is clear that the video TEM built with ON-OFF TAF TEMs significantly outperforms the other two. The reasons are similar to the ones mentioned in the example of Section II. It is important to note that for the spatial component, the largest errors appear at the spatial boundaries of the video stream. This is of course expected since the finite aperture stream fails to be spatially band-limited. By excluding the boundaries (5 pixels on each side), the spatial component PSNR[S] and of the video stream PSNR[I] significantly increases in all four cases (2–3.5 [dB]).

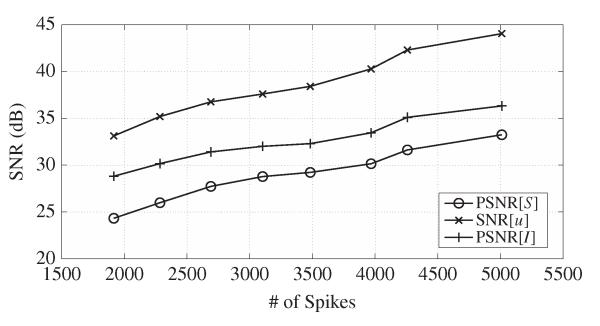
For the ON-OFF TAF-based video TEM, we also examined the quality of signal recovery as a function of the number of spikes that the neurons produced. In order to do so, we changed the feedback parameters of the ON-OFF TEMs while leaving the rest of the parameters (receptive fields, thresholds) unchanged. The plot of the three quality measures (PSNR[S], SNR[u], and PSNR[I]) as a function of the number of spikes is shown in Fig. 8. As shown, with an increase in the number of spikes, the quality of the recovery also increases.

Fig. 8.

Performance of the video TEM as a function of the number of spikes. Each neuron is realized as an ON-OFF TEM.

B. Video TEM with Spatial Isotropic Wavelet Filterbank

The methodology presented in the previous example can also be applied to video TEMs with spatial receptive fields constructed from other mother wavelets. For example, a filter bank with a difference-of-Gaussians (DoG) mother wavelet has been used to model the spatial receptive fields of RGCs [25], [26].

As above, we used a space-time separable video stream with the same bandwidth, duration of 200 ms, spatial domain ⅅ = [−2, 2] × [−2, 2], and 128 pixels in each direction. To eliminate the boundary effects, the spatial domain was extrapolated to [−2.5, 2.5] × [−2.5, 2.5] (with 160 pixels per direction). The spatial filterbank had a wavelet structure generated from an isotropic wavelet given by a DoG

$$\gamma (x,y)=\frac{1}{4{\alpha }_1^2}\exp \left(-\frac{x^2+y^2}{2{\alpha }_1^2}\right)-\frac{1}{4{\alpha }_2^2}\exp \left(-\frac{x^2+y^2}{2{\alpha }_2^2}\right)$$

with α₂ = 0.5, α₁ = α₂/1.6. Since the DoG wavelet is isotropic, the filterbank was constructed by performing only dilations and translations. Six different scales were used, m = −2, −1, …, 3, and $a_0=\sqrt{2}$, and a different number of translations was performed for each scale. For each scale $a_0^m$, the number of translations in each direction was given by $2\cdot \mathrm{nint}(2.25∕b_0{a}_0^m)+1$, with resolution $b_0{a}_0^m$, where b₀ = 0.55. Here nint(x) denotes the nearest integer of x. In total, 622 filters were constructed. The ON-OFF TEM had a TAF with feedback spiking mechanism and parameters δ¹ = −δ² = 0.7, h¹²(t) = h²¹(t) = 0.01 exp(−t/0.01)1_[t>0] and h¹¹(t) = h²²(t) = 0.65 exp(−t/0.015)1_[t>0]. Overall, 554 neuron pairs fired at least one spike amounting to a total of 5660 spikes. The input and the recovered components of the stimuli are shown in Fig. 9. The performance of the stimulus recovery was PSNR[S] = 34.57 dB, PSNR[I] = 30.26 dB, and SNR[u] = 39.37 dB.

Fig. 9.

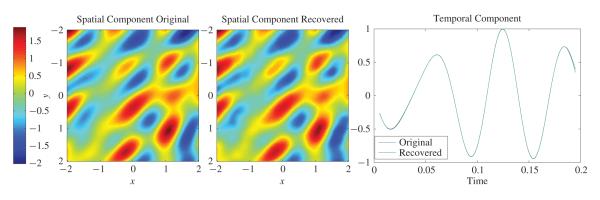
Performance of a video TEM based on a DoG wavelet. Each neuron is realized as an ON-OFF TEM.

The results of Fig. 9 suggest that any possible mother wavelet (or in general x-let structure) can be used as long as the set of wavelets is “dense enough” so that it can faithfully represent the required spatial characteristics of the input video stream. Consequently, the optimal choice of the mother wavelet largely depends on the desired application.

C. Video TEM with Nonseparable STRFs

In this section, we highlight the versatility of the theoretical framework and the generality of the decoding algorithms presented in this paper. From a technical standpoint, both the input video stimulus I and the set of STRFs are nonseparable.

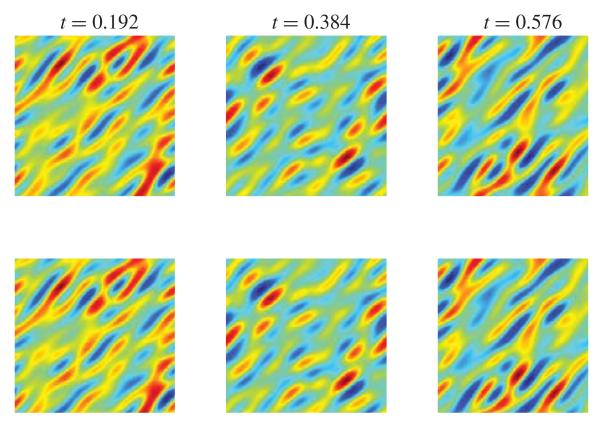
The input video stream belongs to a discretized version of $\mathcal{H}$, the space of trigonometric polynomials (see Appendix B) with M_x = M_y = 3, M_t = 5, and bandwidth Ω_x = Ω_y = 2π · 2 rad/degree, Ω_t = 2π · 7.5 rad/s. The STRFs also belong to the same space of trigonometric polynomials. Their line frequency response was randomly chosen, for each frequency, from a standard normal distribution. One hundred STRFs were constructed in this way. Since the frequency responses were picked randomly, all the necessary rank conditions (required rank = 49) were satisfied with high probability. The neural circuits consisted of ON-OFF neuron pairs with TAF with feedback spiking mechanism. These neurons produced a total of 1150 spikes.

The video synthetic stream was reconstructed using Algorithm 2 (see Appendix C). The encoded and recovered synthetic video stream are shown for three different time instances in Fig. 10. The embedding of the videos and the STRFs into the finite-dimensional space of trigonometric polynomials enables the closed form evaluation of the dendritic outputs v^j [see (30)] as well as the entries of the matrix F. As such, there are no numerical errors introduced during the encoding and reconstruction phase beyond finite precision considerations of the spike times. This leads to a practically perfect reconstruction of the input stimulus. The performance of the reconstruction algorithms speaks for itself: SNR [I] = 74.78 [dB] and PSNR 86.96 [I] = [dB]. Note that random filters have been used as analog-to-information converters for compressed sensing applications [21].

Fig. 10.

Performance of a video TEM based on filters with random STRFs. The upper row shows three of the encoded frames and the lower one the corresponding recovered ones.

D. Natural Video Scene Example

The most experimentally demanding case pertains to the encoding and decoding of natural scenes. As already mentioned, we used high-frame-rate video sequences captured with special cameras. The high computational demands were met by employing a computational platform based on GPUs.

The video TEM architecture consisted of 2744 neurons with spatial receptive fields drawn from a Gabor filterbank. Seven different scales and four different orientations were used. On average, for each pair of orientation/scale 49 different translations along the both axes were employed, more translations were used for finer scales and less for coarser ones. For m = 0 and m = −1, three translations were used in each direction, for m = −2 five, for m = −3 and m = −4 seven, for m = −5 nine and finally for m = −6 eleven translations were used.

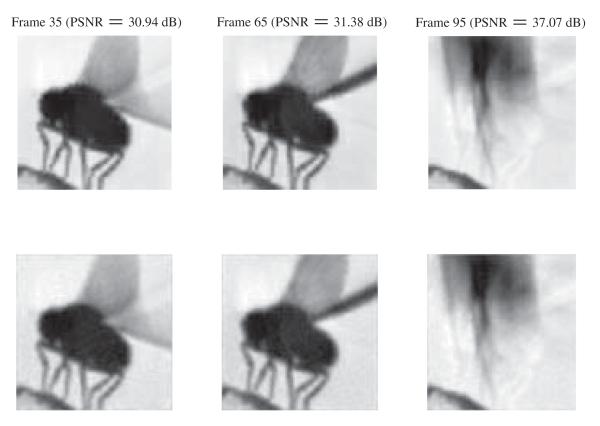
All the neurons had an IAF spiking mechanism with bias b = 0.25, threshold δ = 0.04, and integration constant κ = 0.01. The input video, showing a fly taking off, had a duration 20 ms with a frame rate of 6000 frames/s, resulting in an effective temporal bandwidth of 3 kHz. Ninety-six pixels were used in each direction giving a total of 9216 pixels. The neurons fired a total of 33 713 spikes, giving an average of 12.3 spikes per neuron, and 615 spikes per neuron per second. Note that this number is one order of magnitude less than the 6-kHz frame rate of the video stream. The recovered video had PSNR[I] = 31.28 [dB].

Three of the recovered video, along with the corresponding encoded ones, are shown in Fig. 11. Note that the number of neurons used to encode the video is significantly lower than the number of pixels that are used to display the video stream. This highlights one of the potential advantages of the video TEMs when compared to past silicon retina implementations.

Fig. 11.

Encoding of a natural video scene with a video TEM. The upper row shows three of the encoded frames and the lower one the corresponding recovered frames. The PSNR for each of these three frames is also displayed.

VI. Discussion and Conclusion

Stringent requirements for extremely low-power information processing systems are one of the main drivers for information representation in the time domain. Due to the ever-decreasing size of integrated circuits and the attendant low voltage, in traditional silicon-based information systems amplitude-domain high precision quantizers are more and more difficult to implement. By representing information in the time domain, SISO TEMs leverage the phenomenal device speeds that a temporal code can take advantage of [27]. Consequently, next-generation encoders in silicon are expected to represent information in the time domain [28]. Widely used modulation circuits such as asynchronous sigma/delta modulators and FM modulators in cascade with zero-crossing detectors have been shown to be instances of TEMs [1]. These advances served as a basis for (1-D) TEM implementations in hardware [29]-[35]. These implementations exhibit extremely low power requirements, see [34] for an extensive discussion on SISO TEMs meeting these power requirements.

Video TEMs realized in silicon are a natural extension of SISO information systems that represent analog waveforms in the time domain. They are highly versatile for modeling purposes, since they enable different combinations of filters/receptive fields and spiking mechanisms. Unlike asynchronous silicon retina implementations, which assign to every pixel a neuron, video TEMs use a bank of STRFs to map the incoming video streams into a train of spikes. Thus, video TEMs provide a more compact representation of information in the time domain and can serve as templates for future neuromorphic hardware applications. In quantized form, the spike sequence generated by video TEMs can be used for transmission and for further processing with any digital communications and/or signal processing system.

The interest in temporal encoding in systems neuroscience is closely linked with the natural representation of sensory stimuli (signals) as a sequence of action potentials (spikes) in early olfaction, audition, and vision. TEMs based on single-neuron models such as IAF neurons [36] and more general Hodgkin–Huxley neurons with multiplicative coupling, feedforward, and feedback have also been investigated [37]. Video TEMs can be used to represent analog information residing in the visual world as a multidimensional time (spike) sequence. They are versatile encoding circuits for modeling information representation in the early visual system.

From a theoretical point of view, video TEMs realize two operators in cascade. The first, which is a filter bank or receptive field, is a vector linear operator. The second, which is population of neural circuits, is a vector nonlinear operator. The task of decoding, which is a key challenge both in silicon-based information systems and in systems neuroscience, calls for finding the inverse of the composition of these two operators. We formally investigated conditions for the existence of the inverse, i.e., for the faithful representation of analog band-limited video streams using the sequence of spikes. We examined a variety of neuron spiking mechanisms, such as level-crossing detection and IAF with feedback, and combined these with models of receptive fields that arise in the early visual system. Our investigations demonstrated that the visual world can be faithfully represented with a population of neurons, provided that the size of the population is beyond a critical value. Based on the characteristics of the input signal, we showed that this estimate is substantially smaller than the total number of pixels.

Finally, we note that the formal representation of spatiotemporal information as a set of projections in the Hilbert space of band-limited functions may serve as a theoretical foundation for future asynchronous stimulus encoding algorithms. The work presented here raises a number of issues regarding the encoding efficiency of video TEMs. These and other issues will be investigated elsewhere.

Biography

Aurel A. Lazar (S’77–M’80–SM’90-F’93) is a Professor of electrical engineering at Columbia University, New York, NY. In the mid-1980s and 1990s, he pioneered investigations into networking games and programmable networks (www.ee.columbia.edu/~aurel/networking.html). His current research interests (www.bionet.ee.columbia.edu) are at the intersection of computational, systems and theoretical neuroscience. In silico, his focus is on neural encoding, systems identification of sensory systems, and spike processing and neural computation in the cortex. In this work, he pioneered rigorous methods of encoding information in the time domain, functional identification of spiking neural circuits, and massively parallel neural computation algorithms in the spike domain. In vivo, his focus is on the olfactory system of the Drosophila. His current work primarily addresses the nature of odor signal processing in the antennal lobe of the fruit fly.

Eftychios A. Pnevmatikakis (S’08-M’11) received the Diploma degree in engineering from the School of Electrical and Computer Engineering, National Technical University of Athens, Athens, Greece, in 2004. He received the M.Sc. and Ph.D. degrees from Columbia University, New York, NY, both in electrical engineering, in 2006 and 2010, respectively. He was an Adjunct Assistant Professor with the Department of Electrical Engineering, Columbia University, in 2010. Since May 2010, he has been a Post-Doctoral Researcher with the Department of Statistics and the Center for Theoretical Neuroscience, Columbia University. His current research interests include theoretical neuroscience, signal processing, brain inspired computation, and methods for statistical analysis of neural data. Dr. Pnevmatikakis received the Jury Award from the Department of Electrical Engineering, Columbia University, in 2010, for outstanding achievement by a graduate student in the area of systems, communications, and signal processing.

appendix A

Spike Density of Spiking Neural Circuits

In this section, we present a formal definition of the notion of spike density and a general methodology for its computation for spiking neural circuits. The methodology to evaluate the spike density for spiking neurons was first developed in [38] for the case of a single IAF neuron without feedback.

Definition 1: A real sequence $\Lambda ={\left({\lambda }_k\right)}_{k\in \mathcal{I}}$ is called separated if inf_k≠l |λ_k − λ_l| > 0 and relatively separated if it is a finite union of separated sequences.

Definition 2: Let $\Lambda ={\left({\lambda }_k\right)}_{k\in \mathcal{I}}$ be a sequence of real numbers that is relatively separated. Let N(a, b) the number of elements of Λ that are contained in the interval (a, b). The upper and lower (Beurling) densities of Λ are defined as

$$\begin{array}{cc}\hfill D^{-}\left(\Lambda \right)& =\underset{t\to \infty }{\lim \inf }\underset{t_0\in ℝ}{\inf }\frac{1}{t}N(t_0,t_0+t)\hfill \\ \hfill D^{+}\left(\Lambda \right)& =\underset{t\to \infty }{\lim \sup }\underset{t_0\in ℝ}{\sup }\frac{1}{t}N(t_0,t_0+t).\hfill \end{array}$$ (21)

A. Spike Density of Ideal IAF Neural Circuits

Lemma 1: The interspike time interval generated by an IAF neuron (wlog without feedback) with input $u\in \Xi$ and bias b > 0 is bounded.

Proof: Let t₁ be a spike time and assume that the neuron did not fire another spike until time t₂, (t₂ > t₁). Then

$$-\parallel u\parallel \sqrt{t_2-t_1}\le {\int }_{t_1}^{t_2}u\left(s\right)ds<\kappa \delta -b(t_2-t_1)$$

where the first inequality follows from the Cauchy–Schwartz inequality. Solving for t₂ − t₁ we obtain the bound

$$t_2-t_1\le \frac{{\parallel u\parallel }^2}{2b^2}\left(1+\sqrt{1+4b\kappa \delta ∕{\parallel u\parallel }^2}\right)+\frac{\kappa \delta }{b}.$$ (22)

Note that this bound is presented here for the first time.

Let [a₁, a₂] be an arbitrary time interval and let t₁ denote the first spike time immediately after a₁ and t₂ denote the last spike time just before a₂. The average number of spikes in the interval [a₁, a₂], D(a₁, a₂), of the IAF neuron is given by

$$D(a_1,a_2)=\frac{1}{a_2-a_1}\left(\frac{{\int }_{t_1}^{t_2}\left(u\right(s)+)ds}{\kappa \delta }\right).$$ (23)

Assume that |a₂ − a₁| → ∞. From Lemma 1, we have (t₁−α₁)/(α₂−α₁) → 0(t₂−α₂)/(α₂−α₁) → 0 and therefore the integration interval [t₁, t₂] in (23) can be replaced with [a₁, a₂].

Proposition 3: For all inputs u, u ∈ Ξ, the spike density of an ideal IAF neuron with feedback is equal to

$$D=\{\begin{array}{cc}\frac{b}{\kappa \delta -{\int }_{ℝ}h\left(s\right)ds},\hfill & \mathrm{if}{\int }_{ℝ}h\left(s\right)ds<\kappa \delta \hfill \\ +\infty ,\hfill & \mathrm{if}{\int }_{ℝ}h\left(s\right)ds\ge \kappa \delta .\hfill \end{array}\phantom{\}}$$ (24)

Proof: We will compute the lower and upper densities D⁻, D⁺ defined above. Let I denote the whole current due to feedback. Proceeding as above

$$\begin{array}{cc}\hfill D^{-}& =\underset{t\to \infty }{\lim \inf }\underset{t_0\in ℝ}{\inf }\frac{1}{t}\left(\frac{{\int }_{t_0}^{t_0+t}(b+u(s)+I(s\left)\right)ds}{\kappa \delta }\right)\hfill \\ \hfill & \ge \frac{b}{\kappa \delta }+\frac{1}{\kappa \delta }\underset{t\to \infty }{\lim \inf }\underset{t_0\in ℝ}{\inf }\frac{1}{t}{\int }_{t_0}^{t_0+t}u\left(s\right)ds+\frac{1}{\kappa \delta }\underset{t\to \infty }{\lim \inf }\underset{t_0\in ℝ}{\inf }\frac{1}{t}{\int }_{t_0}^{t_0+t}I\left(s\right)ds.\hfill \end{array}$$

Using again the Cauchy-Schwarz inequality, we get

$$\underset{t\to \infty }{\lim \inf }\underset{t_0\in ℝ}{\inf }\mid \frac{1}{t}{\int }_{t_0}^{t+t_0}u\left(s\right)ds\mid \le \underset{t\to \infty }{\lim \inf }\underset{t_0\in ℝ}{\inf }\frac{1}{\sqrt{t}}\parallel u\parallel =0.$$ (25)

For the feedback current we have

$$\underset{t\to \infty }{\lim \inf }\underset{t_0\in ℝ}{\inf }\frac{1}{t}{\int }_{t_0}^{t+t_0}\frac{I\left(s\right)}{\kappa \delta }ds=+\infty$$

provided that ${\int }_{-\infty }^{\infty }h\left(s\right)ds\ge \kappa \delta$ since each spike produces enough feedback current to elicit another spike with a continuously increasing frequency. Otherwise

$$\underset{t\to \infty }{\lim \inf }\underset{t_0\in ℝ}{\inf }\frac{1}{t}{\int }_{t_0}^{t+t_0}\frac{I\left(s\right)}{\kappa \delta }ds=\frac{D^{-}}{\kappa \delta }{\int }_{ℝ}h\left(s\right)ds$$

and the result of (24) is a lower bound for D⁻. Repeating the procedure for the upper density D⁺ we can show that the right side of (24) is an upper bound and the general result follows.

Remark 4: Note that the result of (24) is asymptotic in the sense that the instantaneous firing rate of the neuron converges to the value of the density.

Using similar arguments, one can also derive the spike density of the IAF ON-OFF TEM as follows.

Proposition 4: Consider the IAF ON-OFF TEM of Fig. 3(b) and let $H^{ij}={\int }_{ℝ}{h}^{ij}\left(s\right)$, i, j = 1, 2. Assume that H^ij > −κⁱδⁱ, i = 1,2 and that

$$({\kappa }^1{\delta }^1+H^{11})({\kappa }^2{\delta }^2+H^{22})-H^{12}{H}^{21}>0.$$

The spike density of the IAF ON-OFF TEM is given by

$$\begin{array}{cc}\hfill D& =D^1+D^2\hfill \\ \hfill D^1& =\frac{({\kappa }^2{\delta }^2+H^{22})b^1+H^{21}{b}^2}{({\kappa }^1{\delta }^1+H^{11})({\kappa }^2{\delta }^2+H^{22})-H^{12}{H}^{21}}\hfill \\ \hfill D^2& =\frac{H^{12}{b}^1+({\kappa }^1{\delta }^1+H^{11})b^2}{({\kappa }^1{\delta }^1+H^{11})({\kappa }^1{\delta }^2+H^{22})-H^{12}{H}^{21}}.\hfill \end{array}$$ (26)

If one of the inequality conditions is not satisfied, then the spike density is infinite.

Proof: Similar to the proof of Proposition 3.

B. Spike Density of TAF Neural Circuits

For completeness, we present the evaluation of the spike density of neurons with TAF with feedback spiking mechanism. We assume that the neuron exhibits a bias b. This bias was absent in our analysis in Section II since in applications stimuli have finite time support and therefore the neural circuits do not fire infinitely often.

Proposition 5: The spike density D of the single neuron TEM with TAF with feedback spiking mechanism and external bias b is 0 for b ≤ δ. For b > δ, the spike density is the solution of the equation

$$b-\sum _{k\in \mathbb{N}}h\left(\frac{k}{D}\right)=\delta$$ (27)

where ℕ is the set of positive integers.

Proof: In the absence of a time-varying external input, the neuron will not fire at all if b < δ. If b > δ, then the neuron will fire periodically with period T at times t_k = kT, k ∈ ℤ. From (1), we have that

$$u\left(t_k\right)+b=\delta +\sum _{l<k}h\left(\right(k-l\left)T\right).$$

Since u = 0, the result follows. If the feedback mechanism is of the form h(t) = h(0) exp(−t/τ) · 1_[t≥0], with h(0) > 0, then the spike density becomes

$$D=\{\begin{array}{cc}{\left(\tau \ln \left(1+\frac{h\left(0\right)}{b-\delta }\right)\right)}^{-1},\hfill & b>\delta \hfill \\ 0,\hfill & \text{otherwise}.\hfill \end{array}\phantom{\}}$$ (28)

Appendix B

Proof of Theorem 1

In this section, we first present the proof of Theorem 1 for band-limited video streams that belong to the finite-dimensional space of trigonometric polynomials. Subsequently we shall extend these results to the infinite-dimensional case.

Let the set of functions (e_{mx, my, mt} (x, y, t)) for all m_x = −M_x, …, M_x, m_y = −M_y, …, M_y, and m_t = −M_t, …, M_t, be defined as

$$e_{m_x,m_y,m_t}(x,y,t)=e_{m_x}\left(x\right)e_{m_y}\left(y\right)e_{m_t}\left(t\right)$$

with $e_{m_x}\left(x\right)=\sqrt{(1∕2\pi )({\Omega }_x∕M_x)}\exp \left(j{m}_x\right({\Omega }_x∕M_x\left)x\right)$ and e_my, e_mt similarly defined. The space spanned by this set consists of the band-limited and periodic video streams, with space-time bandwidth (Ω_x, Ω_y, Ω_t) and period (2πM_x/Ω_x, 2πM_y/Ω_y, 2πM_t/Ω_t), respectively. The band-limited and periodic video streams are elements of a Hilbert space endowed with the usual (sesquilinear) inner product and with (e_{mx, my, mt} (x, y, t)) as its orthonormal basis.

The elements of the space represent a natural discretization of band-limited functions in the frequency domain. The functions in the Hilbert space have a discrete spectrum at frequencies (m_y(Ω_x/M_x), m_y(Ω_y/M_y), m_t(Ω_t/M_t). By letting M_x, M_y, M_t → ∞, the spectrum becomes dense in [−Ω_x, Ω_x] × [−Ω_y, Ω_y] × [−Ω_t, Ω_t] and these functions converge to band-limited functions.

Let the input video I and the STRFs D^j be expressed by

$$\begin{array}{cc}\hfill I(x,y,t)& =\sum _{m_x,m_y,m_t}{a}_{m_x,m_y,m_t}{e}_{m_x,m_y,m_t}(x,y,t)\hfill \\ \hfill D^j(x,y,t)& =\sum _{m_x,m_y,m_t}{d}_{m_x,m_y,m_t}^j{e}_{m_x,m_y,m_t}(x,y,t).\hfill \end{array}$$ (29)

Let a = [a₁; … ; a_mt], denote the column vector of coefficients, with

$${\mathbf{a}}_{m_t}=[a_{-M_x,-M_y,m_t},\dots ,a_{M_x,M_y,m_t}].$$

Similarly, let ${\mathbf{d}}_j=[{\mathbf{d}}_j^j;\dots ;{\mathbf{d}}_{m_t}^j]$ for all j, j = 1, 2, …, N, denote the set of coefficients for every STRF. To simplify the notation we assume that i = 1, i.e., all neurons have a single component (this can easily be generalized). The problem is to recover the vector a.

We assume here that the spike density of every neural circuit j, j = 1, 2, …, N, is above the temporal Nyquist rate Ω_t/π. Based on Propositions 1 and 2, for each j, j = 1, 2 …, N, the set of sampling functions (${\chi }_k^j$), forms a frame for Ξ. Therefore, all the dendritic outputs (v^j), j = 1, 2, …, N, can be perfectly recovered. Equation (12) can be rewritten as

$$v^j\left(t\right)=\sum _{m_t}{v}_{m_t}^j{e}_{m_t}\left(t\right)$$

where the coefficients are given by

$$v_{m_t}^j=\sum _{m_x,m_y}{a}_{m_x,m_y,m_t}{d}_{m_x,m_y,m_t}^j={\left({\mathbf{a}}_{m_t}\right)}^T{\mathbf{d}}_{m_t}^j.$$ (30)

For a fixed m_t ∈ [−M_t, …, M_t] we can write (30) for all neurons in the matrix form

$${\left({\mathbf{D}}_{m_t}\right)}^T{\mathbf{a}}_{m_t}={\mathbf{v}}_{m_t}$$ (31)

where ${\mathbf{D}}_{m_t}=[{\mathbf{d}}_{m_t}^1,\dots ,{\mathbf{d}}_{m_t}^N]$, ${\mathbf{v}}_{m_t}={[v_{m_t}^1,\dots ,v_{m_t}^N]}^T$, for each m_t, m_t = −M_t, …, M_t. For these equations to be solvable, we need the matrices D_mt to have full row rank (2M_x + 1)(2M_y + 1) for all m_t. A necessary condition to achieve full row rank is to have the number of neurons N at least equal to the number of independent spatial components (2M_x + 1)(2M_y + 1). Note that this full row rank condition is equivalent with having the columns of the matrix form a frame for the space of images spanned by the set of basis functions (e_{mx, my}) [9]. Moreover, each vector ${\mathbf{d}}_{m_t}^j$ represents the Fourier transform of the receptive field D^j at the temporal frequency m_tΩ_t/M_t. Therefore, the rank condition on the matrices D_mt calls for the set of STRFs to form a frame for the space of spatial images when restricted to each and every temporal frequency m_tΩ_t/M_t, m_t = −M_t, …, M_t.

In order to extend the above results to the infinite dimensional case, let M_x, M_y, M_t → ∞. Then the set {m_xΩ_x/M_x}, m_x = −M_x, …, M_x becomes dense in the interval [−Ω_x, Ω_x], and

$$a_{m_x,m_y,m_t}=\left({\mathcal{F}}_{3D}I\right)(m_x{\Omega }_x∕M_x,m_y{\Omega }_y∕M_y,m_t{\Omega }_t∕M_t)$$

where ${\mathcal{F}}_{3D}$ denotes the 3-D Fourier transform. Let also ${\mathcal{F}}_{2D}$ denote the 2-D (spatial) Fourier transform. In the limit, the rank condition becomes a frame condition for every ω_t ∈ [−Ω_t, ω_t], the set of spatial receptive fields (${\mathcal{F}}_{2D}^{-1}\left\{\right({\mathcal{F}}_{3D}{D}^j\left)\right(\cdot ,\cdot ,{\omega }_t\left)\right\}$), j = 1, …, N, is a frame for the set of spatially band-limited images.

Appendix C

Finite-Dimensional Recovery Algorithm

We now present an algorithm that faithfully recovers a video stimulus with a finite-dimensional representation in the space of trigonometric polynomials.

Algorithm 2: If the assumptions of Theorem 1 hold, then for a sufficiently large N, the finite dimensional video stream I, encoded with a video TEM (Fig. 6), can be recovered as

$$I(x,y,t)=\sum _{m_x,m_y,m_t}{c}_{m_x,m_y,m_t}{e}_{m_x,m_y,m_t}(x,y,t)$$ (32)

where the vector of coefficients c is given by

$$\mathbf{c}={\mathbf{F}}^{+}\mathbf{q}$$ (33)

with q = [q¹; q²; … q^N]^T, q^j = [q^j1, q^j2, …, q^jM]^T and ${\left[{\mathbf{q}}^{ji}\right]}_k=q_k^{ji}$ and F⁺ denotes the pseudoinverse of F. The matrix F has dimensions N_T × (2M_x + 1)(2M_y + 1)(2M_t + 1), where N_T is the total number of spikes (measurements). If the lth entry of the vector q corresponds to the spike at time $t_k^{ji}$, then the lth row of F is given by

$${\left[\mathbf{F}\right]}_l=[\langle {\varphi }_k^{ji},e_{m_x,m_y,m_t}\rangle ]$$

with m_x = −M_x, ’, M_x, m_y = −M_y, …, M_y, m_t = −M_t, …, M_t.

Proof: By considering (14) for all spike times and substituting the finite-dimensional representations of the sampling functions and of the input video stream, we obtain

$$\mathbf{Fc}=\mathbf{q}.$$

If the rows of F form a frame for the finite-dimensional video space, then the inversion is stable. A necessary condition is to have F of rank (2M_x + 1)(2M_y + 1)(2M_t + 1). This can be guaranteed by increasing the number of neurons and appropriately chosing their receptive fields (e.g., randomly).

Algorithm 2 assumes that the input stimulus belongs to a known space of trigonometric polynomials, i.e., has a discrete spectrum with a known structure. This assumption leads to an algorithm that can be fully discretized and implemented without numerical errors, thereby exhibiting very high accuracy (see for example, V-C). In practice, however, this information may not be available.