Incorporating prey refuge in a prey–predator model with a Holling type I functional response: random dynamics and population outbreaks

Abstract

A prey–predator discrete-time model with a Holling type I functional response is investigated by incorporating a prey refuge. It is shown that a refuge does not always stabilize prey–predator interactions. A prey refuge in some cases produces even more chaotic, random-like dynamics than without a refuge and prey population outbreaks appear. Stability analysis was performed in order to investigate the local stability of fixed points as well as the several local bifurcations they undergo. Numerical simulations such as parametric basins of attraction, bifurcation diagrams, phase plots and largest Lyapunov exponent diagrams are executed in order to illustrate the complex dynamical behavior of the system.

Introduction

The simplest population model in continuous time was first introduced by Verhulst [1] and describes the growth rate of the population of a single species. This model is known as the logistic differential equation. Lotka [2] and Volterra [3] were the first who described predator-prey interaction by introducing the known Lotka–Volterra predator–prey continuous-time model. A drawback of the Lotka–Volterra model, which makes this model unrealistic, is that the predator never becomes saturated. This problem was solved by Holling [4, 5], who suggested three kinds of functional responses for different species of predator, which are called Holling type I, II, and III. The function indicates the number of prey killed by one predator at various prey densities. Thus, Rosenzweig and MacArthur [6] later studied the Lotka–Volterra model with a logistic growth rate of prey, while the saturation of the predator was taken into account by a Holling type II functional response. The Rosenzweig–MacArthur model is one of the basic models since prey–predator coexistence is not limited to a stable equilibrium; a limit cycle appears when the stable equilibrium undergoes the Hopf bifurcation. For many years, the studies of prey–predator interactions focused mainly on continuous-time models, where the dynamics could produce only a stable equilibrium or limit cycles. However, in recent years the research has turned to discrete-time prey–predator models, as it seems their dynamics may include a much richer set of patterns. Maynard Smith [7] first studied the Lotka–Volterra prey–predator model with a logistic growth rate of prey in discrete time. Hadeler and Gerstmann [8] studied the discrete-time version of the Rosenzweig–MacArthur model. Later, Danca et al. [9] studied a simple discrete-time prey–predator model with Holling type I taking place and showed that such a simple discrete model can exhibit chaotic dynamics. Liu and Xiao [10] studied the Rosenzweig–MacArthur prey–predator model with Holling type I, proving once again that the discrete system exhibits far richer dynamics compared to the continuous model. However, since many prey populations incorporate some form of refuge available, a prey refuge provides a more realistic prey–predator model. Maynard Smith [11] showed that a constant proportion of refuge did not alter the dynamics of the neutrally stable Lotka–Volterra model, while a constant number of refuge of any size replaced the neutrally stable behavior with a stable equilibrium. Also, Hassel [12] showed that a large refuge in a model, which in the absence of a refuge exhibits divergent oscillations, replaces the oscillatory behavior with a stable equilibrium. Thus, we observe that many studies have shown that refugia have a stabilizing effect on predator–prey interactions. However, as Taylor [13] mentioned, it would be an oversimplification to assume this is always the case.

In the present paper, we extend Danca et al.’s [9] Lotka–Volterra model with a Holling type I functional response incorporating prey refuge. The Holling type I functional response mainly refers to passive predators like spiders, which wait for their prey to come close in order to capture them [4]. The spiders are the main predators of insects. A single spider eats at least 100 insects in a year and therefore it is estimated that in temperate countries, the annual total weight of insects the spiders eat is larger than the weight of the human population [14]. However, a huge number of many infectious diseases are usually transmitted into human blood by insects (vectors), which feed on blood such as biting flies, mosquitoes, ticks, and other pests, which spiders also eat [15]. For instance, the infectious disease tularemia, which can be transmitted by deer flies and ticks [16], sleeping sickness, which can be transmitted by the tsetse fly [17], the viral disease yellow fever, which is a mosquito-borne disease [18], or the parasitic disease malaria, which can be transmitted by mosquitoes of the genus Anopheles, which has also been associated with causing brain tumors [19]. So from this perspective, spiders in the role of predators, which prey on vectors, can be really useful to humans.

However, by incorporating a prey refuge into Danca et al.’s [9] model, we assume that pests are able to protect themselves from spiders and escape from predation in some way, but in the real world pest insects are one of those insects that may show population outbreaks [14]. So, if a prey refuge leads to population outbreaks, then serious infectious diseases, which pests may carry, could spread through human populations across a large region and a pandemic could be possible. Does a prey refuge stabilize the prey–predator interactions as many studies have shown or leads eventually to population outbreaks? This is the main question we try to answer in this study.

The model system

Danca et al. [9] studied the following discrete prey–predator model with a Holling type I1 functional response taking place:

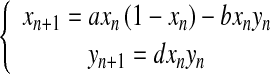1

They showed that as the growth rate of the prey increases, chaotic dynamics appear in the system and the prey–predator interactions become irregular. Particularly, they showed that for the parameter values b = 0.2, d = 3.5, as parameter a varies in the interval 0 < a < 4, the dynamical system (1) exhibits a strange attractor (Fig. 1).

Fig. 1.

The strange attractor without a prey refuge (m = 0) for a = 3.99654

Extending Danca et al.’s [9] Lotka–Volterra model by incorporating a prey refuge, we take the following prey–predator system:

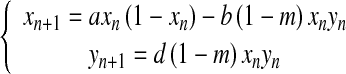2

where,

x_n:

the prey population after n generations with 0 < x_n < 1; y_n: the predator population after n generations. Thus we extend the basic model (1) by adding the new terms (+bmx_ny_n) and (−dmx_ny_n) associated with a refuge protecting the prey from the predator.

a > 0:

the growth rate of the prey in the absence of predators, in the presence of sufficient food and all other requirements.

b > 0:

the foraging efficiency of the predator; it measures the intensity of the predator’s negative impact on the prey population’s growth.

d > 0:

the growth rate of the predator.

mx:

a refuge protecting the prey from the predator; (1 − m)x: the prey available to the predator, where m ∈ [0, 1).

Analytical stability analysis

The dynamical system (2) has the following three fixed points: the origin (E₁), a boundary fixed point (E₂) and a fixed point for which both populations survive (E₃):

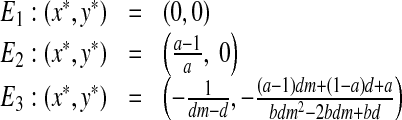The Jacobian matrix at any point (x, y) is:

The determinant of the Jacobian matrix is:

If 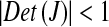the system is dissipative, while if the system is conservative.

In order to study2 the local behavior around each of the three fixed points, we calculate the Jacobian matrix at E₁, E₂, E₃. If λ₁, λ₂ are the eigenvalues of the Jacobian matrix at each fixed point, then the fixed point is stable, if ∣ λ₁ ∣ < 1 and ∣ λ₂ ∣ < 1. By using Vieta’s equations 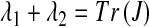, and applying Jury’s conditions [20] the fixed point is linearly asymptotically stable if and only if:

3

Local stability of the fixed point E₁

The Jacobian matrix at E₁:(x^∗, y^∗) = (0, 0) is:

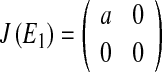with eigenvalues λ₁ = a, λ₂ = 0, determinant DetJ(E₁) = 0 and trace TrJ(E₁) = a. For a < 1 the origin is a stable node (λ₁, λ₂ < 1), while for a > 1 the origin is a saddle (λ₁ > 1, λ₂ < 1). For a = 1 the fixed point is non-hyperbolic (λ₁ = 1, λ₂ < 1); this parameter value is associated with the stability condition TrJ = 1 + DetJ (3) and a real eigenvalue crossing the unit circle at +1. So a = 1 is a bifurcation point at which a fold bifurcation occurs.

Local stability of the fixed point E₂

The Jacobian matrix at is:

The eigenvalues of the Jacobian matrix at E₂ are given by and λ₂ = 2 − a.

The determinant and the trace are .

Using stability conditions (3), we obtain the following:

1. If and a < 1 then E₂: unstable node (∣λ₁ ∣, ∣λ₂ ∣ >1)

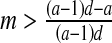2. If and then E₂: saddle

3. If 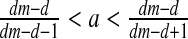then E₂: stable node (∣λ₁ ∣, ∣λ₂ ∣ <1)

4. If 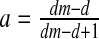then E₂: non-hyperbolic (λ₁ = 1); this parameter value is associated with the stability condition TrJ = 1 + DetJ (3) and a real eigenvalue crossing the unit circle at +1. So this is another bifurcation point at which a fold bifurcation occurs in the system.

Local stability of the fixed point E₃

The Jacobian matrix at 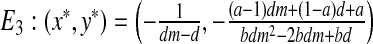is:

with eigenvalues

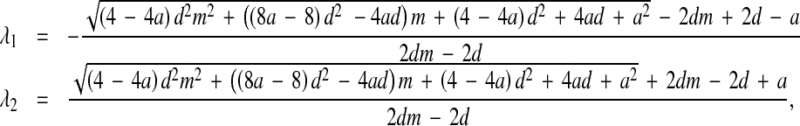determinant 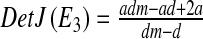and trace .

Using stability conditions (3) we obtain the following:

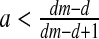1. If and 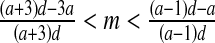then E₃: saddle (∣λ₁ ∣ <1, ∣λ₂ ∣ >1)

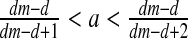2. If and then E₃: stable focus (complex eigenvalues with DetJ(E₃) < 1) or stable node (∣λ₁ ∣, ∣λ₂ ∣ <1).

3. If and 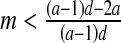then E₃: unstable focus (complex eigenvalues with DetJ(E₃) >1).

4. If then E₃: unstable node (∣λ₁ ∣, ∣λ₂ ∣ >1).

5. If then E₃: non-hyperbolic (λ₂ = 1); this parameter value is associated with the stability condition TrJ = 1 + DetJ (3) and a real eigenvalue crossing the unit circle at +1. So this is a bifurcation point at which a fold bifurcation occurs in the system.

6. If and 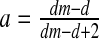then E₃: center (complex eigenvalues with DetJ(E₃) = 1 and −2 < TrJ(E₃) < +2); this parameter value is associated with the stability condition DetJ = 1 (3) and two complex eigenvalues crossing the unit circle simultaneously. So this is a bifurcation point at which a Neimark–Sacker bifurcation occurs in the system.

7. If 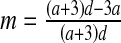then E₃: non-hyperbolic (λ₁ = −1); this parameter value is associated with the first stability condition −TrJ = 1 + DetJ (3) and one real eigenvalue crossing the unit circle at −1. Hence, this parameter value corresponds to a bifurcation point at which a flip bifurcation occurs in the system.

Numerical simulations

We use various numerical simulation3 tools (parametric basins of attraction, bifurcation diagrams, phase plots and largest Lyapunov exponent diagrams) to study the complex dynamics of the dynamical system (2). In order to see the effect of a refuge on prey–predator interactions, we choose the initial conditions x₀ = 0.83 and y₀ = 0.55. We also assume b < d since observational studies of spiders have shown that while many species have very low capture rates of prey (parameter b) [22, 23], they produce many offspring (parameter d) (i.e., female spiders lay up to 3,000 eggs in one or more silk egg sacks [24]). This paradox of “low foraging efficiency–high offspring production” is likely related to the fact that spiders have very low metabolic rates compared to other animals. On average, the resting metabolic rate of spiders is 70% of that of comparable ectothermic arthropods [25].4 This is ecologically an important factor that allows spiders to survive extended periods of time (which are sometimes in excess of 200 or 300 days) without food [27].5 Furthermore, even when spiders elevate their metabolic rate during activities (such as searching for food,6 producing webs,7 producing eggs,8 courtship9), the increase in respiration and metabolic rates is relatively low compared to other animals; two to six times resting rates [32]. Hence, the general low metabolic rates make them very efficient in their use of energy, so that despite their low foraging efficiency, they have high reproduction rates. Thus, the parameters b = 0.2 and d = 3.5 [9] are fixed10 and we vary the parameters of the growth rate of prey a and refuge m.

Parametric basins of attractions

This plot is a numerical analysis tool that matches different colors to periodic cycles of different periods in a two-dimensional parameter space [21]. So, we plot the parametric basins of attraction for the parameter values a ∈ [0, 4.35] and m ∈ [0, 1] to see how the dynamics of the system change as the refuge increases (Fig. 2).

Fig. 2.

The parametric basins of attraction (a, m)

The different colors in the parametric plane (a, m) correspond to the following stable states: light blue for an attracting fixed point, dark blue for a stable two-period cycle, yellow for a three-period cycle, pink for a four-period cycle, orange for a five-period cycle, red for a six-period cycle, light green for a seven-period cycle, dark green for an eight-period cycle, grey for a nine-period cycle and purple for a ten-period cycle. The white area corresponds to those values of parameters for which the behavior of solutions may be quasi-periodic (invariant curves) or non-periodic (chaos; strange attractors). The black area is the set of parameters for which every orbit diverges to infinity.

Observing the 2D parameter space we point out the following:

• For small values of prey refuge, 0 < m < 0.254, as the growth rate of prey a increases, the stable fixed point (light blue area) is giving rise to non-periodic behavior (white area). So, adding a small refuge does not seem to alter significantly the dynamics of the basic model (1).

• For slightly higher values of refuge, 0.254 < m < 0.467, we see that as a increases, the aperiodic dynamics is being replaced by a stable equilibrium. So, by adding more prey refuge, the refuge stabilizes the prey–predator interactions.

• However, for even higher values of prey refuge, 0.467 < m < 1, the stabilizing effect of refuge is not the case anymore. Now, as a takes higher values, the stable fixed point, through successive period-doubling bifurcations; two-period cycle (dark blue area), four-period cycle (pink area) and eight-period cycle (dark green area), is giving rise to non-periodic behavior (white area). So, adding a large refuge makes the system unstable once again.

• Higher values of the refuge parameter, m > 1, do not correspond to a positive equilibrium and therefore it has no realistic ecological significance.

Bifurcation diagrams

In order to see in detail what happens in both populations’ species, as the refuge parameter increases, we use bifurcation diagrams. The bifurcation diagram is another useful numerical analysis tool that illustrates how the characteristics of a fixed point change as the varying parameter increases in a specific interval [33]. We plot the bifurcation diagram as the system’s parameter increases in the interval m ∈ [0, 1] for various values of parameter a and we distinguish the following cases (Fig. 3):

1. For a low-growth rate of prey, 0 < a < 1.45, as refuge increases in m ∈ [0, 1], the prey population survives in a small quantity, because of the low reproduction rate, while the predators cannot survive because of refuge. As we see in Fig. 3a, with such a low birth rate of prey, a = 1.1, all preys are able to find refuge and the food is enough to feed them all, while predators cannot find food at all and become extinct immediately. So in this case the system has a stable boundary equilibrium point, 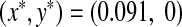, where both populations are fixed in time.

2. For an average birth rate of prey, 1.45 < a < 2.3 and a small prey refuge, m < 0.45, both populations survive (x^∗ > 0, y^∗ > 0) temporarily (Fig. 3b). This happens because for such a growth rate, a = 2, the prey density is larger than the amount of refuge. Therefore, the predators are able to find preys to eat and since their population increases faster than the prey population, d = 3.5 > a = 2, the predator population survives in a higher quantity than the prey population (y^∗ > x^∗) temporarily. As the prey refuge increases, more and more preys find refuge and therefore the prey population increases, while the predator population decreases. When the amount of refuge is m > 0.45, all preys are able to find refuge and since the food is enough to feed them all, they survive in larger density (x^∗ = 0.514) due to their higher birth rate. On the other hand, predators cannot find food anymore and become extinct (y^∗ = 0). Moreover, this qualitative change in the behavior of solutions, as the refuge parameter increases, is associated with a local bifurcation. For a = 2 (Fig. 3b) in particular and m < 0.4286, the fixed point E₃:(x^∗ > 0, y^∗ > 0) is a stable node and the boundary fixed point E₂:(x^∗, y^∗) = (0.5, 0) is a saddle (the origin E₁:(x^∗, y^∗) = (0, 0) is always a saddle since a = 2 > 1). For m = 0.4286, both fixed points become non-hyperbolic; the eigenvalues of the Jacobian matrix at E₃ are (λ₁ = −0.0001, λ₂ = 1) and the eigenvalues at E₂ are (λ₁ = 1, λ₂ = 0). For m > 0.4286, E₃ becomes a saddle and E₂ becomes a stable node. Hence, as the varying parameter passes through the critical value m = 0.4286, both fixed points undergo a fold bifurcation.

3. For a high birth rate of prey, 2.3 < a < 3 and exceptionally small values of refuge, m < 0.11, we observe aperiodic dynamics in both populations’ species (Fig. 3c). This happens because the high reproduction rate of prey, a = 2.8, combined with the exceptionally small amount of refuge results in a large number of preys not being able to find refuge and to protect themselves from predators. The high birth rate of predators results in both populations appearing as irregular oscillations. However, for m > 0.11, refuge stabilizes the system to a positive fixed point (x^∗, y^∗ > 0), while the predator population is temporarily higher than the prey population (y^∗ > x^∗) again. For even higher values of prey refuge, m > 0.56, all preys are able to find refuge and food and because of their higher birth rate, they survive in an even larger density (x^∗ = 0.67). The predators cannot find preys; they do not have food and become extinct (y^∗ = 0) once again.

4. However, for a higher growth rate of prey, 3 < a < 3.57, the increase of the amount of refuge does not always stabilize the system. As we see in Fig. 3d for m < 0.53, refuge replaces the chaotic regimes with a stable positive equilibrium in both populations (y^∗ > x^∗ > 0). However, once the prey refuge exceeds the threshold m ≈ 0.53, the system loses stability and all orbits in the prey population lie on an attracting four-period cycle x^∗:(0.387, 0.507, 0.83, 0.88). At the same time, the predator population decreases up to extinction (y^∗ = 0), once again. Particularly, as parameter a increases in the interval (3, 3.57) and for an amount of refuge m > 0.5, successive period-doubling bifurcations appear in the prey population; two-period cycle (Fig. 3e), four-period cycle (Fig. 3d) and eight-period cycle (Fig. 3f). This is because once predators become extinct and the birth rate of preys is significantly high, the available food is not enough to feed the large prey density. Therefore, the prey population becomes slowly unstable, as their birth rate increases continuously.

5. Finally, for an even higher birth rate of prey, a > 3.57, as the refuge takes higher values, m > 0.523, the successive cycles of higher periodsin the prey’s population lead to chaotic behavior; period-doubling route to chaos (Fig. 3g). Thus, once predators become extinct, the exceptionally high reproduction rate of the prey and the resource limitation compete with each other, leading the prey population sometimes to extinction (x^∗ = 0.01) and sometimes to excessive growth (x^∗ = 1) once again (Fig. 3h). However, now, the chaotic dynamics in the prey population looks random. Particularly, observing both chaotic regimes in Fig. 3h, we see that for a small prey refuge, m < 0.237, the system alternates between chaotic behavior and periodic behavior, while for higher values of the prey refuge, m < 0.372, the system produces dynamics, which seems to have lost almost all its determinism. So, we observe that for such a high reproduction rate, a = 3.983, the refuge not only destabilizes the system but moreover makes the prey’s population behavior almost random.

6. Furthermore, observing the behavior of the predator’s population for a = 3.7, just before the predators become extinct (Fig. 3g), we see a small chaotic region. This chaotic regime could also be a result of the competition between the reproduction rate of the prey and their resource limitation. Particularly, because of the resource limitation, many preys are not able to find food and therefore die, but the piles of dead preys are food for the predators. While due to the high growth rate of prey, preys die in irregular frequencies, so maybe these two facts lead eventually to the appearance of chaotic behavior in the predator’s population as well.

Fig. 3.

Bifurcation diagrams (m, x^∗) and (m, y^∗) as m varies in the interval [0, 1] for the parameter values: aa = 1.1, ba = 2, ca = 2.8, da = 3.5, ea = 3.2, fa = 3.56, ga = 3.7 and ha = 3.983

Phase plots

Another numerical tool in investigating prey–predator interactions is the phase diagram (x, y). The strange attractor (Fig. 1) appears in the system for a high-growth rate of prey. In order to see how the refuge replaces the chaotic strange attractor with a stable equilibrium point (i.e., stabilizes the prey–predator interactions), we plot phase diagrams for the parameter value a = 3.986, as the refuge varies in the interval m ∈ [0, 0.24] (Fig. 4).

• For m = 0 the origin E₁:(x^∗, y^∗) = (0, 0) is a saddle (with eigenvalues (λ₁ = 3.986, λ₂ = 0); it remains a saddle for every value of the varying parameter m since a = 3.986 > 1), the boundary fixed point E₂:(x^∗, y^∗) = (0.7491, 0) is an unstable node (with eigenvalues (λ₁ = 2.6219, λ₂ = −1.986) it remains an unstable node as m increases), the fixed point E₃:(x^∗, y^∗) = (0.2857, 9.2357) is an unstable focus (with eigenvalues λ_1,2 = 0.4306 ± 1.2341i, determinant DetJ(E₃) = 1.7083 > 1 and trace TrJ(E₃) = 0.8611) and all solutions converge to the strange attractor (Fig. 4a).

• As the refuge parameter increases in the range 0 < m < 0.0286, the strange attractor deforms and becomes less complicated. The strange attractor splits, locks into a stable four-period cycle and near the value m ≈ 0.02868 reappears more deformed (Fig. 4b).

• For the refuge parameter values 0.029 < m < 0.092, the strange attractor becomes less and less complicated. Particularly, near the value m ≈ 0.065, the strange attractor evolves into a strange contiguous band (Fig. 4c).

• The contiguous strange band breaks apart into a motion of period 5 near the value m ≈ 0.0926 (Fig. 4d) and then it splits again into a motion of period 10 at m ≈ 0.1067 (Fig. 4e).

• For higher values of the parameter, 0.11 < m < 0.1777, a series of period-halving bifurcations takes place in both populations (twenty-period cycle at m ≈ 0.112, ten-period cycle at m ≈ 0.1164, and a five-period cycle at m ≈ 0.133). The system has an ordered behavior (Fig. 4f).

• For even higher values of the refuge parameter, 0.1777 < m < 0.235, the locally stable orbit of period 5 gives rise to a kinked curve at m ≈ 0.179 (Fig. 4g). The kinked curve loses and gains stability consecutively, deforms and becomes an invariant circle near the value m ≈ 0.22 (Fig. 4h). At this point, the prey coexists with the predator population and both oscillate among all the states of the invariant circle.

• Eventually, the invariant circle diminishes in size and near the value m ≈ 0.2372 the fixed point E₃:(x^∗, y^∗) = (0.3746, 9.7863) undergoes a subcritical Neimark–Sacker bifurcation becoming a center (DetJ(E₃) = 1 & TrJ(E₃) = 0.507 < +2). For 0.2372 < m < 0.443, E₃ becomes a stable focus fixed point (with complex eigenvalues and DetJ(E₃) < 1), where both populations settle down (Fig. 4i).

In Fig. 5 we plot the phase diagram for the growth rate of prey a = 3.7 as the refuge parameter increases in the interval m ∈ [0.515, 0.55]—the small chaotic region (Fig. 3g). We can observe the fountain phenomenon [8] just before the predators become extinct.

• For the parameter value m = 0.515, the origin E₁:(x^∗, y^∗) = (0, 0) is a saddle fixed point (a = 3.7 > 1), the boundary fixed point E₂:(x^∗, y^∗) = (0.7297, 0) is an unstable node (with eigenvalues (λ₁ = 1.2387, λ₂ = −1.7); it remains an unstable node as m increases) and all solutions converge to the fixed point E₃:(x^∗, y^∗) = (0.5891, 5.3642), which is a stable node (with eigenvalues λ₁ = −0.9068, λ₂ = 0.7271).

• As the refuge parameter increases in the range 0.515 < m < 0.522, the attracting fixed point E₃:(y^∗ > x^∗ > 0) near the value m ≈ 0.52 undergoes a flip bifurcation (λ₁ = −1), becomes a saddle and a two-period cycle appears surrounding it. The attracting cycle of period 2 loses stability via another period-doubling bifurcation giving rise to a stable orbit of period 4 at m ≈ 0.522 (Fig. 5a).

• Close to the value m ≈ 0.5224, we observe a period-doubling route to chaos and the trajectory mimics the Feigenbaum bifurcation diagram (Fig. 5b).

• Chaos appears in both populations and as the refuge increases in the interval 0.5224 < m < 0.5364, the trajectory is pushing upward (Fig. 5c).

• Near the value m ≈ 0.53647, the chaotic motion is being replaced by a six-period cycle (Fig. 5d).

• For higher values of the refuge parameter 0.5365 < m < 0.55, chaos reappears in the system (Fig. 5e) and the predator population decreases continuously until, finally, it becomes extinct (Fig. 5f).

Fig. 4.

Phase plots (x, y) for a growth rate of prey a = 3.986 and refuge parameter values: am = 0, bm = 0.0267, cm = 0.0848, dm = 0.097, em = 0.1067, fm = 0.1791, gm = 0.1794, hm = 0.2351 and im = 0.24

Fig. 5.

Phase plots (x, y) for a growth rate of prey a = 3.7 and refuge parameter values: am = 0.52278, b m = 0.52282, cm = 0.53266, dm = 0.536003, em = 0.54436 and fm = 0.54696

Lyapunov exponent diagrams

A Lyapunov exponent diagram illustrates for which values of a varying parameter two orbits, with neighboring initial conditions, converge or diverge from each other exponentially, depending on the sign11 of the Lyapunov exponents. Moreover, the largest value of the Lyapunov exponents indicates whether the system is chaotic or non-chaotic. The higher the maximum Lyapunov exponent (MLE), the more chaotic the system is and the lower the possibility of predictability [34]. So, we plot the Lyapunov exponent diagram (a, ℓ) as the growth rate of the prey increases in the interval a ∈ [2.2, 4.1] for three cases of the refuge parameter: (a) if there is no prey refuge (m = 0) (Fig. 6), (b) if we have a small refuge (m = 0.1) (Fig. 7) and (c) if we have a large refuge (m = 0.783) (Fig. 8).

Fig. 6.

Lyapunov exponent diagram (a, ℓ) without a refuge m = 0

Fig. 7.

Lyapunov exponent diagram (a, ℓ) along with the bifurcation diagram (a, x^∗) with a small refuge m = 0.1

Fig. 8.

Lyapunov exponent diagram (a, ℓ) along with the bifurcation diagram (a, x^∗) with a large refuge m = 0.783

If there is no prey refuge (m = 0), for a low birth rate of prey 2.329 < a < 3.195, the populations oscillate between quasi-periodic and periodic behavior and the Lyapunov exponents vary among negative and exceptionally small positive values ℓ_i ≤ 0.001. For an average to high birth rate of prey, 3.195 < a < 3.578, the system alternates between chaotic and high-periodical behavior and the Lyapunov exponents vary among negative and rather higher positive values, ℓ_i ≤ 0.086, in comparison to the previous interval of the birth rate of prey. For an exceptionally high birth rate of prey, 3.578 < a < 4, chaotic dynamics appear in both populations and the Lyapunov exponent reaches its maximum value, ℓ _max  ≈ 0.296364, for a growth rate of prey, a ≈ 4.002179.

For a small prey refuge (m = 0.1), periodic and quasi-periodic dynamics along with exceptionally small Lyapunov exponent values ℓ_i ≤ 0.002 appear for an average to high birth rate of prey, 2.738 < a < 3.67. For a high birth rate of prey, 3.67 < a < 3.77, the populations oscillate among chaotic and periodic behavior, while the Lyapunov exponents vary among negative and small positive values, ℓ_i ≤ 0.037. For a higher birth rate of prey, 3.77 < a < 4.047, the period-doubling route to an order of chaotic bands and the largest value of the Lyapunov exponent, which corresponds to a growth rate of prey a ≈ 4.043010, is remarkably low ℓ _max  ≈ 0.096923.

For a large prey refuge (m = 0.783), for which predators inevitably become extinct, dynamical system (2) becomes the well-known discrete-time logistic map. For an average to high birth rate of prey, 3 < a < 3.57, the system goes through successive period-doubling bifurcations and the Lyapunov exponents take only negative values ℓ_i < 0. For a high birth rate of prey, 3.57 < a < 3.83, the period-doubling route to chaos and the Lyapunov exponents vary among negative and significantly high positive values, ℓ_i ≤ 0.4434. For an exceptionally high birth rate of prey, 3.83 < a < 4.002, another series of period-doubling (3 · 2ⁿ) routes to chaos and the largest Lyapunov exponent reaches the remarkably high value ℓ _max  ≈ 0.673651, for a growth rate of prey a ≈ 3.998271.

Comparing the Lyapunov exponent diagrams without a prey refuge to those with small and large refuges, we point out the following:

• iThe minimal addition of a small refuge gives rise to periodic and quasi-periodic dynamics, even for a high birth rate of prey a ≈ 3.67, while chaotic dynamics appears only for exceptionally higher birth rates. Moreover, the maximum value of the Lyapunov exponent is considerably lower than the corresponding one without a prey refuge ℓ _max  ≈ 0.0969 < 0.2964 (Figs. 6 and 7). Thus, a small prey refuge stabilizes the system for high birth rates of prey, while for exceptionally even higher birth rates, the prey–predator interactions become much less chaotic. Consequently, the oscillations of the prey’s population are much smaller x^∗ ∈ (0.14, 0.65) and preys do not tend anymore to extinction or to overgrowth (Fig. 7).
• iiHowever, by adding a large refuge the system has a lot of similarities with having only a single species with limited resources, while the situation changes drastically for a high birth rate of prey a > 3.57. For such a high birth rate, the dynamics of the system looks random and therefore the prey population tends to extinction or to overgrowth x^∗ ∈ (0, 1) with almost random changes (Fig. 3h). The maximum Lyapunov exponent is higher than in the corresponding case without refuge ℓ _max  ≈ 0.6737 > 0.2964 (Figs. 6 and 8), the system is extremely chaotic and because of its dependence on initial conditions, it is almost impossible to predict the behavior of the prey’s population.

Concluding remarks

We have shown that although the addition of a small prey refuge stabilizes prey–predator interactions, the addition of a large refuge makes the prey population to behave even more chaotic than without a refuge. While a small refuge could control the prey population, a large refuge leads to almost unpredictability (i.e., random-like prey population outbreaks). Therefore, taking into consideration that the prey population could be insects, which feed off of human blood like any kind of biting flies and that they are able to protect themselves effectively from passive predators like spiders, we may conclude that a pandemic could be a possible scenario.

Of course this is just a simple mathematical prey–predator model and in the real world there are other predators, which also prey on insects like biting flies. So, even if spiders would become extinct, other predators could control the biting flies’ population (biological control) [14]. Moreover, humans have developed various chemical methods in order to control pest populations. However, history has shown that despite any kind of pest control, significant pandemics have been recorded such as the medieval Black Death pandemic, which was transmitted by fleas living on rats [14]. So, considering the usually devastating cost of treatment and the high growth rate of the human population, even infectious diseases, which can be cured, could be extremely dangerous for humanity.