Spatially constrained hierarchical parcellation of the brain with resting-state fMRI

Abstract

We propose a novel computational strategy to partition the cerebral cortex into disjoint, spatially contiguous and functionally homogeneous parcels. The approach exploits spatial dependency in the fluctuations observed with functional Magnetic Resonance Imaging (fMRI) during rest. Single subject parcellations are derived in a two stage procedure in which a set of (~1000 to 5000) stable seeds is grown into an initial detailed parcellation. This parcellation is then further clustered using a hierarchical approach that enforces spatial contiguity of the parcels.

A major challenge is the objective evaluation and comparison of different parcellation strategies; here, we use a range of different measures. Our single subject approach allows a subject-specific parcellation of the cortex, which shows high scan-to-scan reproducibility and whose borders delineate clear changes in functional connectivity. Another important measure, on which our approach performs well, is the overlap of parcels with task fMRI derived clusters. Connectivity-derived parcellation borders are less well matched to borders derived from cortical myelination and from cytoarchitectonic atlases, but this may reflect inherent differences in the data.

Introduction

A cortical parcellation is a subdivision of the cerebral cortex into a set of areas that share certain neurobiological properties. They thus provide fundamental maps for functional neuroimaging and provide the first abstractions on which many models of brain function are based. Parcellations in which each region specifies a functionally distinct area are of particular interest, as these encapsulate the fundamental neurobiological principles of functional specialisation and segregation, and thus form a basis for connectomics (Sporns et al., 2005). A reliable parcellation is especially important, because errors in the specification of the “network node” regions can significantly confound the quality of brain network estimates (Smith et al., 2011).

Several neurobiological properties can be used to derive parcellations, including cytoarchitecture, sensory topography, functional homogeneity and connectivity. Cortical areas delineated by architectonic and/or topographic (e.g., retinotopic or somatotopic) criteria show several within-area commonalities, including their connectivity. However, in the macaque, many cytoarchitectonically well-defined cortical areas also show within-area heterogeneity. As this can exceed the connectivity differences between topographically corresponding locations in neighbouring areas, parcels based on internal homogeneity of functional connectivity can reveal organisational principles different from those captured by anatomically delineated cortical areas (Van Essen and Glasser, submitted for publication).

Properties of fMRI data acquired during “rest” (rs-fMRI) can provide evidence of both functional homogeneity and functional connectivity (Biswal et al., 1995). There is now an extensive literature on rs-fMRI based parcellation (recent examples include Bellec et al., 2010; Craddock et al., 2011; Kim et al., 2010; Lashkari et al., 2010; Mumford et al., 2010; Power et al., 2011; Shen et al., 2010; Yeo et al., 2011; Zhang et al., 2011; a longer list can be found in the Supplementary material.). As these approaches are able to reveal organisational principles not captured by other modalities, they now complement traditional parcellation approaches such as postmortem studies of cytoarchitecture (Zilles and Amunts, 2010), in vivo studies of myelin content (Glasser and Van Essen, 2011) or methods that look at brain connections using diffusion MRI and tractography (Behrens et al., 2003).

Our aim here is to develop a robust and fully automated technique that uses rs-fMRI data to produce reliable parcellations of the entire human cerebral cortex, ideally on a single subject basis. These parcellations are envisaged to delineate fundamental functional subdivisions of the brain and thus better reflect subject-specific brain organisation. Such parcellations would thus provide more appropriate models of brain organisation for further connectivity analysis, which are currently often defined using cytoarchitectonic atlases or gross anatomical landmarks, and thus fail to accurately reflect a subject's functional anatomy.

After an extensive survey, we found that current methodologies do not yet satisfy the above requirements. Whilst many algorithms are able to reliably parcellate several relatively small cortical regions, even for single subjects, parcellation of the entire cortex is a much more complex task. We found that the methods that worked well on small regions did not provide the same robustness and reproducibility when applied to the entire cortex.

One reason for this failure is likely to be found in the high inter-subject variability in functional brain organisation in many brain regions, which prevents larger multi-subject data-sets to be leveraged effectively to enhance parcellation accuracy. These problems are further exacerbated by the fundamental difficulties inherent in the lack of a ground truth that would provide a reliable and clear-cut basis on which to evaluate different methods.

We therefore set out to (i) design a parcellation approach that could be applied robustly across the whole cerebral cortex, and could be applied to individual datasets, and (ii) design a set of measures that could be used to evaluate the success of this parcellation scheme and compare it with alternative approaches.

We address (i) through an approach based on region-growing and spatially constrained hierarchical clustering. This method forces parcels to be spatially homogeneous, a requirement that has been found to be advantageous in cortical parcellation before (Craddock et al., 2011; Lu et al., 2003; Bellec et al., 2006; Heller et al., 2006).

An initial outline of the approach presented here has been previously presented at MICCAI (Blumensath et al., 2012). The current paper provides a more detailed description of the approach and a larger body of evidence to demonstrate its performance.

Methodology

Subjects and data acquisition

To evaluate our approach, we used two different data sets, both generated at the University of Minnesota as part of the initial stages of the NIH-funded Human Connectome Project.

The first data set was originally used in Smith et al. (2012). The data-set was acquired in six sessions from 5 different subjects (ages 18–25, 3 males, one subject was scanned twice, i.e. in two different sessions). During each session, six 10-min fMRI datasets were acquired from each subject using the accelerated protocol described in Feinberg et al. (2010), providing whole brain coverage at a TR of 0.8 s and with an isotropic spatial resolution of 3 mm. Data was acquired on a 3 T scanner (Siemens Trio). In each scanning session, a single EPI reference image was acquired between each of the 10 min blocks. A1 × 1 × 1 mm resolution structural image (T1-weighted) was acquired.

The second data set consisted of 14 scanning sessions acquired from 10 different subjects (4 subjects being scanned twice) (ages 20–49, 6 females). Each scan consisted of a 23 min eyes-open resting state fMRI scan using a 4-fold Multi-band accelerated EPI protocol as described in Feinberg et al. (2010). The scan parameters were as follows: 2 mm isotropic resolution, TR = 1370 ms, TE = 36 ms, flip angle = 68°, echo spacing = 0.55 ms. We also acquired B0 field-map images and an additional fully-relaxed “single-band” reference EPI. Data was acquired on the HCP's customised 3 T scanner (Siemens Skyra) using a 32-channel head coil. For each subject two 0.8 mm resolution structural images (T1-weighted, MPRAGE) and two 0.8 mm resolution structural images (T2-weighted) were acquired to aid registration. Each of the sessions also included a set of task fMRI scans acquired using the same EPI sequence as the rs-fMRI acquisition. The tasks included four 6 min working memory paradigms, one 5 min motor task, one 6 min biomotion task, two 6 min language tasks and two 6.5 min social cognition tasks.

Preprocessing

Data set 1 was preprocessed as follows. FSL (FMRIB's Software Library) (Smith et al., 2004) was used for 1) head motion correction and 2) full width 200 s temporal high-pass filtering and 3) T1 images were segmented using FreeSurfer (Dale et al., 1999) and the functional data was projected onto the cortical surface using FreeSurfer's mri_vol2surf functionality.

Data set 2 was preprocessed using a preliminary version of the Human Connectome Project's structural and functional minimal preprocessing pipelines, final versions to be published separately (Glasser et al. unpublished). Briefly, this involved 1) brain extraction based on FNIRT registration and registration of T2w to T1w image using FLIRT, bias field correction using the square root (T1w × T2w) (Rilling et al., 2012), and final registration to MNI152 space with FNIRT. Then data were fed into FreeSurfer cortical surface modelling, with final surface placement adjustment using the full high resolution T1w image, and dura and blood vessels removed using the high resolution T2w image. Surfaces were transformed nonlinearly into MNI space, registered to the 164 k vertex fs_LR atlas (Van Essen et al., 2011) and downsampled to 32 k vertices. Myelin maps were generated as presented previously (Glasser and Van Essen, 2011). Functional (R-fMRI and T-fMRI) data were motion corrected, distortion corrected and EPI to T1w registration with FLIRT + BBR (Greve and Fischl, 2009) applied, mean normalised and resampled in a single spline interpolation into 2 mm MNI152 space. fMRI data were mapped onto the cortical surface using a cortical-ribbon-based volume to surface mapping method (that excludes voxels with locally high temporal coefficient of variance) and transformed from the native mesh to the 32 k registered mesh. Surface smoothing of 2 mm FWHM was applied.

All fMRI data-sets were de-noised using FSL's spatial-ICA tool MELODIC (Multivariate Exploratory Linear Optimised Decomposition of Independent Components) (Beckmann and Smith, 2004) as described in Smith et al. (2012). In short, spatial-ICA with automatic dimensionality estimation was run on each data-set. Using two heuristics (fraction of power above 0.2 Hz and extent of a component's spatial map overlapping low-intensity voxels in the original raw data), each ICA component was automatically classified into “definitely-artefact” vs. “signal-or-artefact”. The full space of all “definitely-artefact” time-series was then regressed out of the pre-processed fMRI data.

All of our processing was carried out on the cortical surface. For the work presented here, we discarded the data associated with subcortical structures, though our approach does not rely on this and could utilise this data in addition to cortical data.¹ Data-set 1 included the data from the “medial wall” (i.e. the data on the FreeSurfer surface that is not within the cortical mask), whilst this data was masked out when processing data-set 2. Our processing pipeline thus starts with a cortical mesh representation, which specifies the spatial location for each vertex and also defines its neighbourhood structure. Our approach is not specific to surface representations and can be used for volumetric processing and even for joint surface and volume based data representations (Marcus et al., 2011). All that is required is that for each BOLD time-series, there be an associated spatial location and a structure that defines the neighbourhood.

After preprocessing and de-noising, each BOLD time-series was normalised by (1) subtracting its temporal mean and (2) re-scaling to unit variance.

Single subject parcellation

Our single-subject algorithm attempts to improve on previous approaches in several ways.

1. We grow the regions from a large (~1000 to ~5000) number of seed locations, each of which is selected based on two criteria, (a) a seed location is centred within a small functionally homogeneous region and (b) a seed has a representative time-courses for its region.

2. Initial regions are further clustered using a hierarchical approach that again enforces spatial cluster contiguity. This hierarchical framework not only produces a final parcellation, but an entire parcellation tree, reflecting our perspective that there is no single “correct” resolution, but a spectrum of meaningful parcellations.

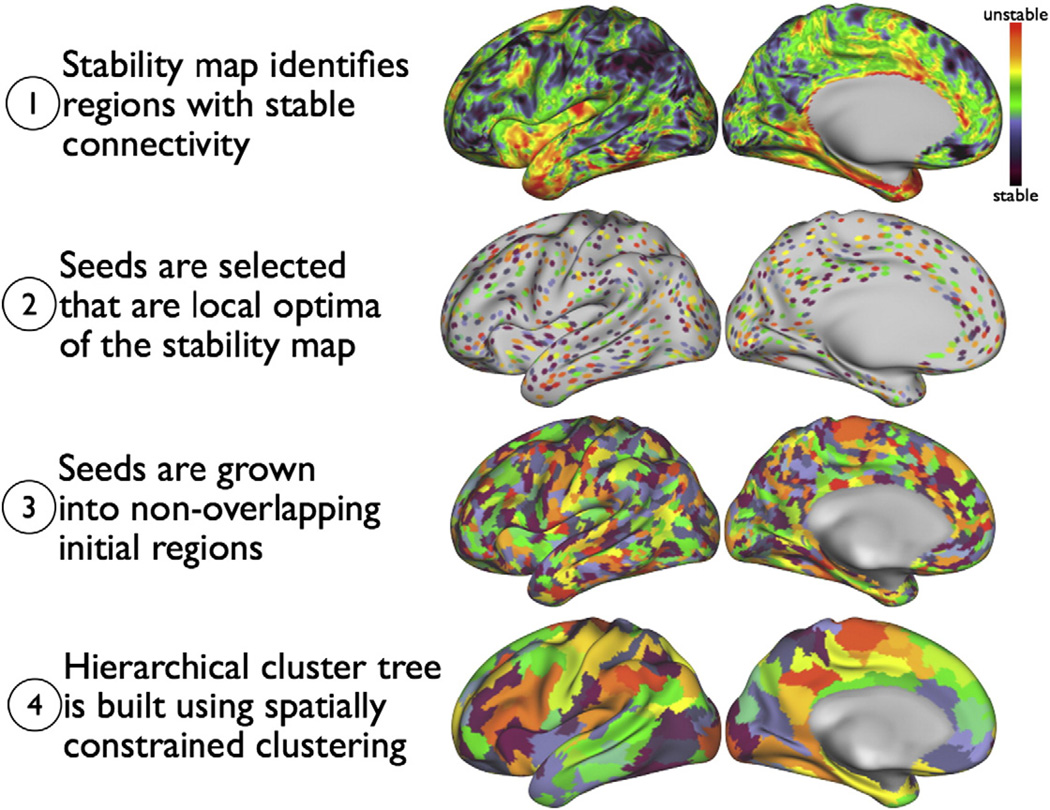
The main steps in the clustering approach are visualised in Fig. 1 and described in more detail below.

Fig. 1.

After preprocessing, clustering proceeds in four steps. In step (1) a slightly smoothed stability map is computed (black: more stable, red: less stable). Local optima are identified in step (2). The locations of these optima will be the seed regions used in the next step. In step (3) the seeds are grown into disjoint clusters, giving the finest clustering. Finally, in step (4), a spatially constrained hierarchical clustering method builds a cluster tree, giving not only a single parcellation, but an entire spectrum of parcellations at different resolutions (we here only show one of these).

Defining locally stable seeds

We propose an approach that tries to estimate cortical locations that lie inside functionally homogeneous brain regions and whose BOLD time-series are representative of local BOLD activity. This is done through the estimation of a stability map, whose local minima encode these two properties. There are several methods available to estimate local regional homogeneity in functional MRI data and a recent review can be found in Zuo et al. (2013). We here use an approach that calculates stability maps as the root mean square error between all time-series in an ROI and the ROI's mean time-series. The ROI's radius then influences the smoothness of the resulting stability map.² Due to the normalisation of the fMRI time-series, our approach produces similar results to those achieved using correlation based regional homogeneity measures.

A surface-based Gaussian kernel smoother with a full width half maximum of 2.35 mm (σ = 1 mm) was used to further smooth the stability maps. Seed locations were then identified as the local minima of the stability map.³ An evaluation of the influence of the reliable identification of initial seed locations is presented in the Supplementary material.

Growing the seeds

Each seed is grown into an initial cluster by an iterative process in which neighbouring vertices are attached to a cluster if the correlation between their time-courses and the region's time-course⁴ exceeds 0.9 times the maximal correlation between all region time-courses and associated neighbourhood vertex time-courses.⁵ If a vertex neighbours more than one region, then it is assigned to the region to which it is most correlated.

Clustering the seed regions using a spatial constraint

The initial region-growing step produces a single parcel for each seed. These are then clustered further using a hierarchical clustering algorithm that ensures spatial contiguity of clusters. The hierarchical algorithm builds up an entire cluster tree in which neighbouring regions are joined if their similarity is maximal among all pairs of neighbouring regions.

We calculated initial cluster similarity using the correlation between the mean time-courses extracted from a 3 mm radius ROI centred on the region's seed vertex. When joining neighbouring clusters, the similarity matrix is updated using Ward's linkage rule (Ward, 1963), even though Ward's method was developed under the assumption of Euclidean distances instead of correlations. Different similarity measures and hierarchical clustering rules were explored and the results are presented in the Supplementary material.

Parcellations of different granularities can then be derived by cutting the tree at different levels.

Performance measures

Cortical parcellations are difficult to evaluate given the lack of ground truth data. The relationship between anatomical atlases and functional specialisation is one of the questions we would like such an approach to elucidate, so the use of cytoarchitectonic atlases for the verification of a functional parcellation might potentially lead to circular arguments.

To measure the quality of a parcellation, we instead resorted to a range of different measures, each of which can shed light on a different aspect of the approach. Of particular interest are measures that allow us to quantify the reproducibility of a parcellation. However, when looking at reproducibility alone, care must be taken. Any fMRI driven parcellation will be a compromise between fMRI data dependent constraints and algorithmic specific constraints. For example, a parcellation algorithm that returns the Brodmann atlas (i.e., ignores the fMRI data) will obviously give highly reproducible parcellations, yet these are not driven by the fMRI data at all. This is obviously an extreme example; however, the same can happen to a lesser extent with other methods. Many methods include explicit or implicit constraints that can have a large influence on the parcellation found. When using explicit constraints care has to be taken to ensure that these are sensible. Implicit constraints are even more difficult to deal with, as these might not be apparent a priori and only a careful analysis of the results might reveal inherent bias.

Given these difficulties, it is desirable to find measures that are less sensitive to biases introduced by the clustering approach itself. We therefore generated subject-specific functional clusters from task fMRI studies. As these came from the same subjects, they should reflect the same functional brain architecture, but, as they were derived from a different modality using well established analytical tools, they are not liable to be affected by biases in the same way that parcellation reproducibility is.

As different parcels are presumed to represent distinct functional areas which are assumed to exhibit a different functional activation pattern and different functional connectivity, we expect that parcellation borders should align well with changes in functional connectivity. Whilst this is difficult to quantify, visual inspection of the change in correlation across borders was found to be a useful indicator.

Dice similarity (parcellation overlap)

To measure parcellation reproducibility we use Dice similarity (Dice, 1945)

$$\text{Dice}=\frac{2|X\cap Y|}{|X|+|Y|},$$ (1)

where X is the index set of the vertices in one parcel and Y is the vertex set in the other parcel. X ∩ Y is the set of all vertices that are in both parcels and | • | indicates the size of this set.

Two parcellations can then be compared by (1) matching parcels in different parcellations based on their Dice similarity and (2) averaging the Dice similarity between all matched parcels. Parcel matching is done iteratively. The two parcels with the largest overlap are matched in each iteration (where already matched parcels are no longer considered in subsequent iterations). If two parcellations have different numbers of parcels, the remaining parcels after matching count as zero in the dice averaging.

Our parcellations are hierarchical; hence a common parcellation resolution must be set to allow fair comparisons between methods. Consider two random spatially contiguous parcellations. In this scenario, parcellations with few larger parcels will have a smaller similarity measure than parcellations with many smaller clusters. Dice similarity is thus easiest to interpret if different methods use a comparable number of parcels.

It can happen that individual parcels are split into two or more parcels in one parcellation whilst they form a single cluster in another parcellation. In order to take this effect into account, when reporting Dice similarity in this paper, we not only report the parcellation similarity at one resolution, but also report similarity results after a “joining” step. The joining step we use is again iterative. Given two parcellations, we calculate the Dice overlap between each parcel in one parcellation and each parcel in the other parcellation. Any parcel that overlaps with a parcel in another parcellation by more than 50% is matched to that parcel. If there is more than one parcel in one parcellation that is matched in this way to the same parcel in the other parcellation, then all of these matched parcels are combined into one larger parcel.

Comparison to task activation clusters

The task fMRI data of data-set two was analysed using two alternative approaches. After temporally concatenating the data of the ten different task-paradigm scans for each subject, we used the MELODIC ICA tool (Beckmann and Smith, 2004) to extract 20, 30, 40 and 50 spatially independent components respectively. Activation clusters were identified using MELODIC's mixture model and a threshold of p = 0.5 (Beckmann and Smith, 2004).⁶ The thresholded ICA maps were then sub-split into distinct spatially contiguous clusters, and only the largest 3 * d clusters were kept (where d is the number of ICA components extracted).

We also analysed the t-fMRI data using a general linear model (GLM) using FSL's FEAT analysis tool (Smith et al., 2004). For each task, the GLM included the task timing and its temporal derivative. As we are not interested in a traditional statistical analysis of the task-data and are thus not unduly concerned about proper control of false positives, we used a threshold of p = 0.05 (uncorrected for multiple comparisons) to derive thresholded activation maps. The thresholded statistical maps were again split into contiguous clusters from which only the largest clusters were retained.

Each t-fMRI cluster was then matched to a cluster in each of the rs-fMRI parcellations using Dice similarity. For each parcellation, a measure of overlap between task clusters and rs-fMRI parcellation could then be calculated by averaging over all Dice similarities between matched clusters.

Results

Scan-to-scan repeatability

We evaluate the region growing approach in terms of its single-subject reproducibility and compare the results to those achievable with several other approaches. This was done using a subset of data-set 1. Data-set 1 contained data from one subject which was scanned twice (on different days) and it was this subject's data that was used here. In each of the scanning sessions, six 10-min rs-fMRI scans were performed as outlined in the Methodology. This provided a total of twelve 10-min rs-fMRI scans, which were partitioned into two different sets. For each set, data was temporally concatenated before parcellation. To reduce potential variability in the results due to scanning day or order effects, we used the first, third and fifth scans from session one together with the second, fourth and sixth scans from session two to generate the first parcellation. The second parcellation was derived from the remaining six scans.

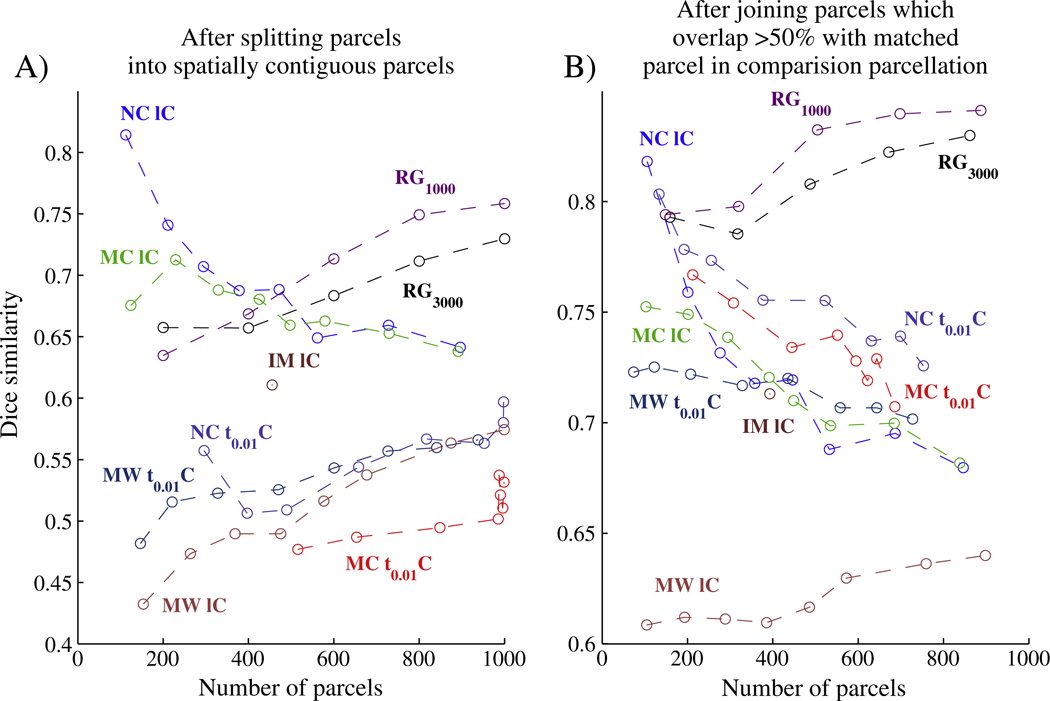
Fig. 2A plots the Dice similarity (y-axis) for different parcellation resolutions (x-axis) whilst Fig. 2B shows similarity after parcel joining (The standard deviation of dice similarity over different parcels is shown in Fig. 11 in the Supplementary material.). We here compare the region growing approach based on two different levels of the initial stability map smoothness, leading to ~1000 and ~3000 seeds (no additional smoothing). Fig. 3A demonstrates visually the high reproducibility of our approach. A visual comparison between the results for 9 different subjects can be found in Fig. 12 in the Supplementary material and a more detailed evaluation of the influence on parcellation results due to scan day and scan length effects is provided in Fig. 10 in the Supplementary material.

Fig. 2.

Average Dice similarity between matched parcellations vs. parcellation level, calculated for parcellations from different datasets of the same subject before (A) and after (B) joining split clusters. Reproducibility results are shown for the data-set one subject which was scanned twice for 60 min. The number of parcels is the total across both hemispheres. Region growing approach with ~1000 (RG₁₀₀₀) and ~3000 (RG₃₀₀₀) seeds outperforms all other tested approaches over a range of parcellation resolutions, especially after parcel joining (B). Also shown is a small subset of the results obtained with other methods (including the next best performing method, NCUTS (NC IC) (Shi et al., 2000) used in Craddock et al. (2011), a spectral clustering approach to optimise network modularity (MC IC, black) (Newman, 2006), a hierarchical clustering approach using Ward's linkage rule (HW1C) (Ward, 1963) and the infomap algorithm (IM IC) (Ward, 1963) as used in Power et al., 2011, all with the same locally restricted correlation similarity measure. For comparison, the results obtained by the same approaches with a sparser similarity matrix (a correlation matrix in which values were thresholded so that only 1% of the entries in each column/row were non-zero (Power et al., 2011)) are also shown ({NC, MC, HW} t_0.01C).).

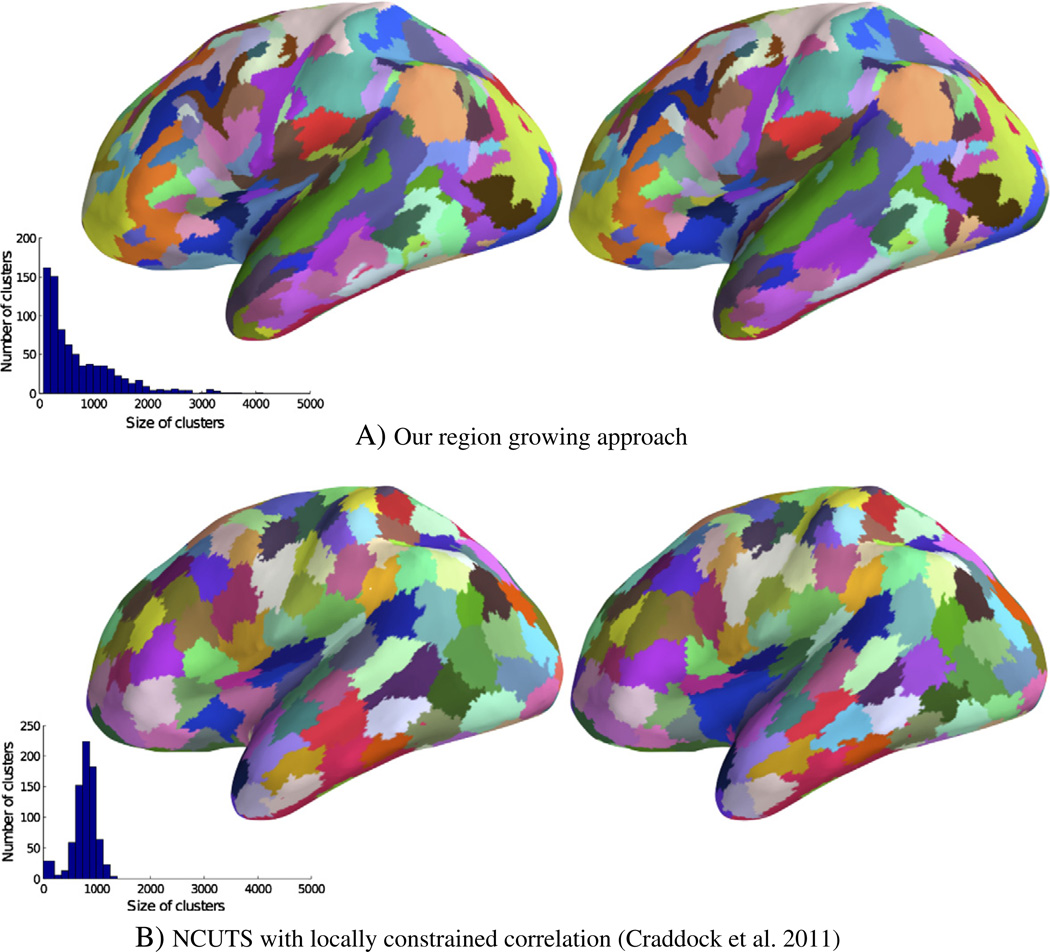
Fig. 3.

Split-half parcellation reproducibility for the one subject from data-set one which was scanned twice. Shown are joined clusters derived from six 10 min rs-fMRI scans (left) and those derived from a different set of six 10 min rs-fMRI scans of the same subject (right). (The original parcellation had a resolution of 400 clusters (~200 per hemisphere)). Histogram inlays show the distribution of parcel sizes. Parcel colours have been matched to ease comparison.

We also tried many other parcellation approaches and found that the region growing approach outperformed most of these over the entire range of parcellation resolutions and all of them over a wide range of resolutions, especially after parcel joining (red and orange curves in Fig. 2B). We show a subset of these results here. The next best performing method was based on normalised CUTS clustering using a locally constrained similarity measure (Craddock et al., 2011). We also show results for a spectral clustering approach to optimise network modularity (Newman, 2006) and a hierarchical clustering approach based on Ward's linkage rule (Ward, 1963), both again with a locally restricted correlation similarity measure. The results obtained by the same approaches with a sparser version of the similarity matrix (a correlation matrix in which values were thresholded so that only 1% of the entries in each column/row were non-zero (Power et al., 2011)) are also shown.

The only other approach that performed as well as our method in terms of DICE similarity was the locally constrained normalised cuts (NCUTS) spectral clustering method when a spatially constrained similarity matrix was used. Looking at these results, it is apparent that NCUTS produced parcels that were all of comparable shape and size, something that was not observed for the parcels derived with our approach (compare the histogram inlays in Fig. 3). The stark difference seems to be mainly due to NCUTS being strongly biased towards a parcellation with uniformly sized clusters. For example, even when we run NCUTS on random data (see the supplementary material), similar parcellations emerged that remained highly reproducible. We also note from the left panel in Fig. 2 that Dice reproducibility increases with increasing parcellation resolution for most approaches, whilst it decreases with increased resolution for the NCUTS algorithm with spatial constraint. This is likely due to the fact that NCUTS reproducibility is driven to a large extent by the spatial constraint and the restriction on cluster size. These constraints have a decreasing influence on reproducibility when the size of the parcels is reduced. We also observed this phenomenon when using NCUTS with random data, a case in which reproducibility is entirely driven by the reduction in the degrees of freedom. For the other approaches we observed the expected behaviour of Dice similarity increasing with an increase in the number of parcels.

When comparing results before and after joining, cluster similarity improves significantly for our approach whilst the same increase is not observed for the NCUTS algorithm. This suggests that some of the parcellation mismatch observed for our approach is due to inconsistent cluster splitting at different granularities.

Borders represent changes in the connectivity profile

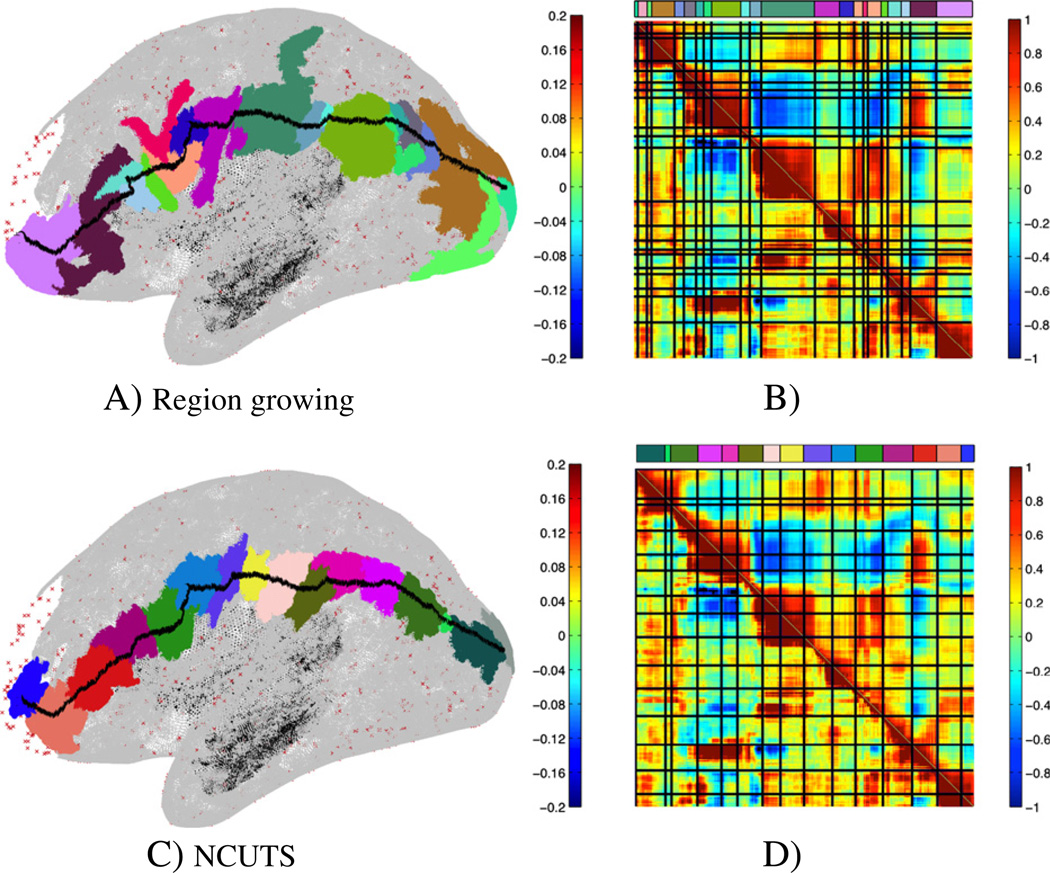
To test whether the borders of the derived parcellations indicate changes in functional connectivity, we drew a path along the cortical surface (shown for the same subject used above in Fig. 4A and C). We drew this path such that it crossed parcellation borders at roughly a right angle. We here show a path that was optimised to some extent for the NCUTS parcellation (i.e., we tried to ensure that the path crosses from one parcel into the other at roughly a right angle in the NCUTS based parcellation). However, we also tried to keep this requirement consistent with the same requirement in the region growing parcellation. We then calculated correlations between the time-series of the vertices along this path (the correlation matrix (thresholded at ±0.4) is shown in the lower left corner of the matrix in Fig. 4B and D). In addition to direct correlation, we also compared correlation between connectivity fingerprints along the path. Correlation fingerprints were calculated as vectors of r-to-z transformed correlations between the vertex time-series and the time-series of 1000 randomly chosen but fixed target vertices on the cortical surface (shown in red in the figures). The correlation between these connectivity feature vectors is shown as the upper triangular part of the matrix. The parcellation borders are indicated by black lines. The correlation and connectivity profiles shown here were calculated from a different data-set (but from the same subject) to that used to derive the parcellation itself. Parcel borders derived with our approach (Fig. 4A and B) align significantly better with significant changes in connectivity than those derived with NCUTS (Fig. 4C and D).

Fig. 4.

Region growing results (A, B) and NCUTS results with locally constrained correlation (Craddock et al., 2011) (C, D). Path drawn on the cortical surface together with the parcels the path crosses (A, C) and the correlation (lower left part of the matrix) and connectivity (upper right part of the matrix, where connectivity is measured to the vertices marked in red in the figure) profiles along the path with parcel borders shown as blue lines (B, D). The colour bar above the similarity matrix matches the parcel colour for each location along the path. Shown are results for a typical subject.

To quantify these results, we measured similarity in connectivity within the parcels. This was done by averaging the connectivity fingerprints along the path within each parcel (after a Fisher r to z transform) and then calculating the root mean square error between a parcel's mean connectivity and the connectivity at each vertex on the path. To compare different parcellations, we also need to account for the overall number of parcels along the path. This is done using the Akaike Information Criterion (AIC) which modifies the root mean square error with a model complexity term. For the path in Fig. 4 we observed a 9% improvement in AIC for our region growing method over the NCUTS parcellation. Similar improvements were observed over 8 other paths, 4 of which were optimised to go through parcel centres in the NCUTS parcellation whilst the other 4 where optimised for our approach. Mean improvement was 4.5% (std. 3%).

Parcellation borders align with task activations

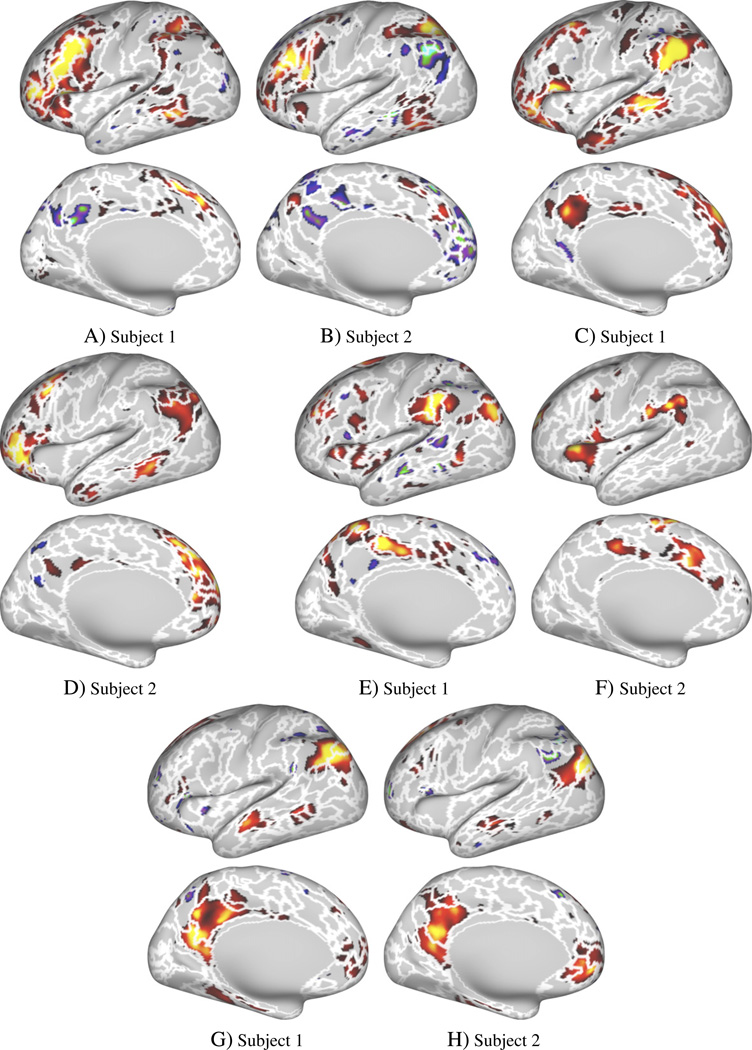
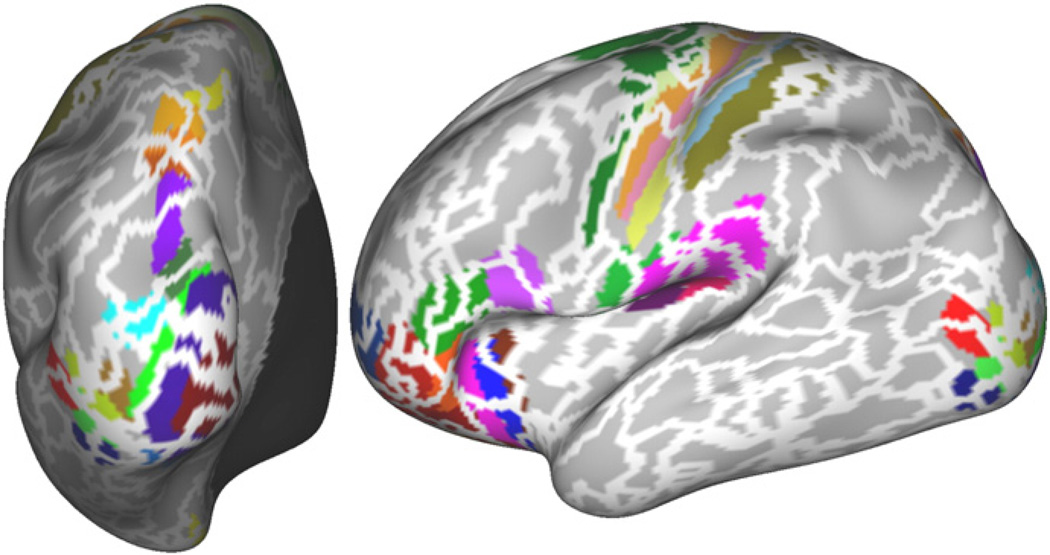
Data-set 2 also allowed us to compare individual parcellations to clusters derived from task-data. Example task activation maps are shown in Fig. 5 (p < 0.05, uncorrected), and Fig. 6 shows four maps derived using spatial ICA analysis of the task data. The white borders in Figs. 5 and Fig. 6 show the parcellation borders derived with the region growing method (at a resolution of 400 clusters).

Fig. 5.

Comparison of rs-fMRI parcellation borders and four t-fMRI activation maps for two different subjects. Region growing borders (at a resolution of 400 parcels) overlaid over four example task contrasts (p ≤ 0.05, uncorrected).

Fig. 6.

Comparison of rs-fMRI parcellation borders and t-fMRI ICA maps for two different subjects. Region growing method borders (at a resolution of 400 parcels) overlaid over example t-fMRI ICA maps derived from the same subject (ICA dimension = 20). ICA maps were matched visually for comparison.

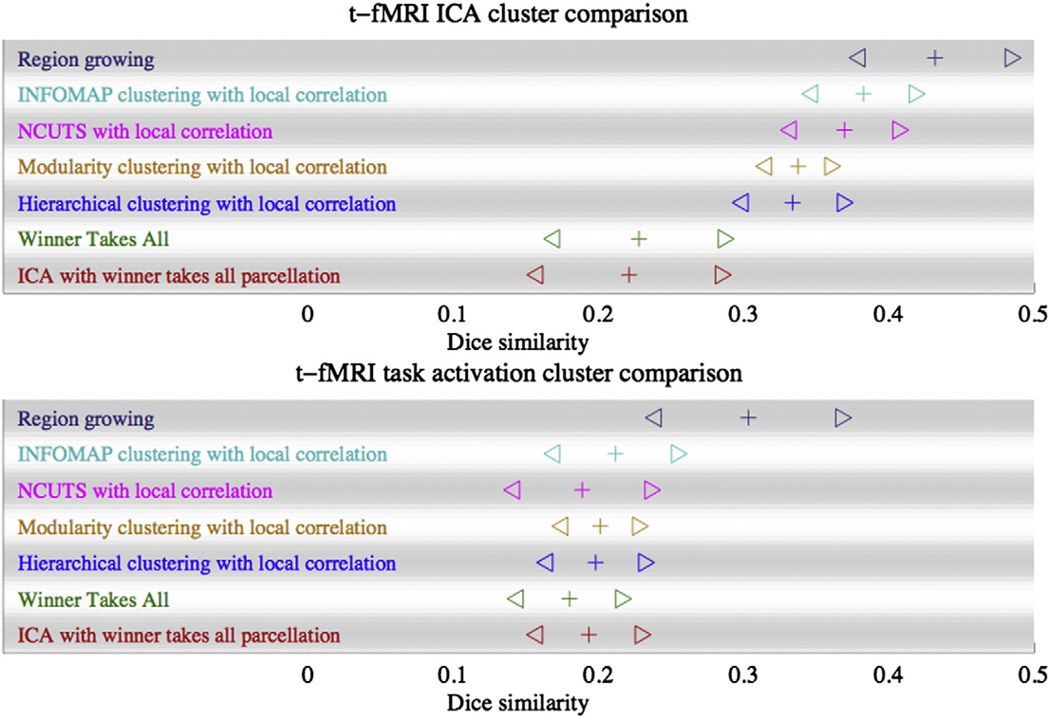
The numerical cluster overlap results are shown in Fig. 7, where the crosses are the average Dice similarity (averaged over all matched parcels and all subjects) and where the triangles are the mean Dice ± three standard deviations. In addition to the results for the region growing method, we also show the results derived using several other methods. More detailed results for the comparison to both GLM and ICA analysis for different thresholds and ICA dimensionality can be found in Fig. 13 in the Supplementary material.

Fig. 7.

Comparison of different methods. rs-fMRI cluster similarity to clusters derived from tfMRI data for the same subject. Top: Dice similarity between rs-fMRI clusters and clusters found with ICA applied to t-fMRI data. Bottom: Dice similarity between clusters from rfMRI to clusters found with GLM from t-fMRI data. The plus symbol (+) indicates the Dice mean (averaged over all parcels and over all subjects), whilst the triangles (⊳ and ⊲) indicate the mean plus and minus 3 standard deviations across parcels. The results shown here are for the region growing method, the infomap algorithm (Rosvall and Bergstrom, 2008) as used in Power et al. (2011) but with the local correlation similarity measure of Craddock et al. (2011), the NCUTS algorithm with a local correlation similarity measure (Craddock et al., 2011), a spectral clustering approach to optimise network modularity (again with a local correlation similarity measure) (Newman, 2006), a hierarchical clustering approach using Ward's linkage rule and the local correlation similarity measure (Ward, 1963). Also shown are results obtained by using spatial ICA followed by a winner takes all clustering in which each vertex is assigned to that cluster for which its normalised ICA map had the largest value and an iterative winner takes all algorithm, where a low-rank matrix decomposition is constructed by iterating two steps, a winner takes all cluster assignment and a reduction in approximation error.

Parcellation borders align with cytoarchitectonic boundaries and anatomical atlases

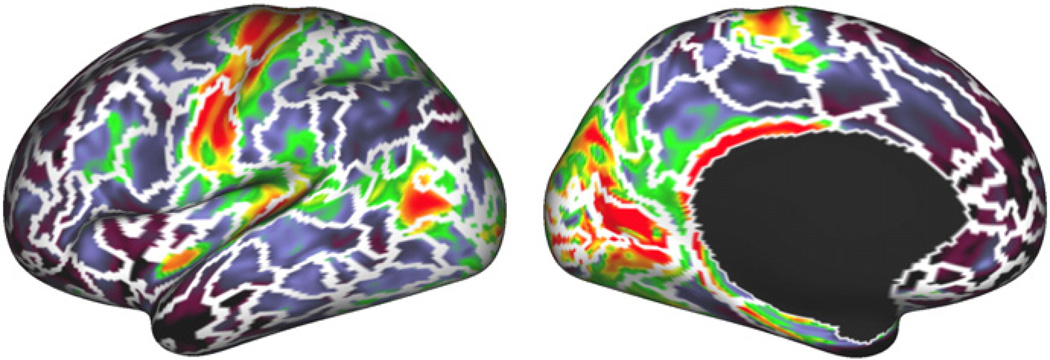
To compare parcellation borders to cytoarchitectonic properties, we use data-set 2. For this data-set, we also had cortical myelin maps generated as described in Glasser and Van Essen (2011). Fig. 8 shows the borders of our parcellation at a resolution of 400 parcels overlaid over the myelin map of the same subject. Numerical results at several resolutions are provided in Figs. 14 and 15 in the Supplementary material, though due to the high variability in the measures used, these results are less instructive. Nevertheless, many of the borders found in the sensory-motor cortex, in the primary visual cortex, in the cingulate cortex and around area MT align well with significant changes in cortical myelination. These are areas in which similar alignment between myelination and rs-fMRI or task fMRI derived parcellations have been reported previously (Glasser et al., 2011, 2012).

Fig. 8.

Visual comparison of parcellation borders derived from one subject's data with myelin maps (Glasser and Van Essen, 2011) of the same subject. Solid white borders are borders at a resolution of 400 parcels for both hemispheres.

The same borders are also shown on the composite atlas of Van Essen et al. (2011) in Fig. 9. Again we observe the generally good correspondence between many borders in the sensory-motor cortex to the borders found with our approach. However, there are some discrepancies within somato-motor and visual cortex, similar to those reported by Yeo et al. (2011) and Power et al. (2011), and in other regions as well (see Discussion).

Fig. 9.

Region growing method borders (at a resolution of 400 parcels) overlaid over the composite atlas from Van Essen et al. (2011), registered to the individual subject.

Discussion

A subject-specific cortical parcellation based on resting state functional MRI data has many applications in the study of neuroanatomy and functional brain connectivity. We have proposed a new approach based on region growing and spatially constrained hierarchical clustering. When applied to individual subjects, our approach shows high scan-to-scan reproducibility and was able to derive parcellation borders that clearly follow changes in the functional connectivity profile. Comparison of the parcellations to clusters derived from task data also demonstrated a high overlap. In particular, we have compared our approach to a range of other approaches suggested in the literature and found our method to outperform other approaches on almost all measures we have used.

Another advantage of our approach is that it not only produces a single parcellation, but an entire tree. This encodes rich information regarding the hierarchical structure of functional organisation and can thus lead to more powerful tools to study functional brain anatomy. However, this is at an early stage in the development and there are as yet no appropriate tools available that would allow us to fully exploit this tree structure in further analysis.

One of the major challenges in the development of cortical parcellation methods remains the difficulty of assessing and comparing the results. Several methods incorporate a range of implicit or explicit constraints that effectively reduce the degrees of freedom, which in turn will influence measures such as parcellation reproducibility. On the other hand, when comparing rs-fMRI parcellations to neuro-anatomical atlases or task activation clusters, the size of parcels does not always match cortical areas delineated in the atlas or task fMRI derived regions, so overlap is generally lower and a direct comparison is more difficult to interpret. Importantly, heterogeneity of connectivity within well-defined cortical areas is to be expected, based on anatomical tracer studies in monkeys, so it is not surprising to encounter such mismatches when analyzing human functional connectivity data (Van Essen and Glasser, submitted for publication). Furthermore, comparisons with anatomically derived atlases, whilst giving additional confidence in a method's ability to delineate meaningful neuro-anatomical regions, are not able to capture a method's ability to capture subject-specific variability.

In order to produce reliable single subject parcellations and to overcome the poor signal-to-noise ratio in single subject data, prior constraints have to be exploited. We thus here enforced spatial contiguity, a constraint explicitly enforced only in a small number of other methods (Bellec et al., 2006; Craddock et al., 2011; Heller et al., 2006; Lu et al., 2003). We found that our approach led to more reliable and interpretable parcellations compared to these other approaches. For example, the approach of Craddock et al. (2011) restricts the original similarity matrix to only include similarity measures for neighbouring vertices or voxels. The similarity between non-neighbouring vertices can then only be assessed indirectly though a chain of similarities of neighbouring vertices. Our spatially constrained hierarchical approach does not suffer from this problem and calculates similarity between distant vertices more directly. The approaches in Lu et al. (2003), Bellec et al. (2006), and Heller et al. (2006) are more similar to our method. The main difference is that we use an additional step in which stable seeds are identified. This step was found to further increase robustness to noise and improve computational speed.

An alternative to the hard constraint on spatial contiguity of clusters is the use of softer constraints. Many other methods, whilst not doing so explicitly, still tend to encourage spatial contiguity. However, this is typically achieved through extensive spatial smoothing (see for example Goulas et al., 2012), which has the undesired side effect that the locations of the boundaries between parcels become less well defined.

Single subject parcellations are useful for the study of between-subject variability in functional anatomy and we have here concentrated on the derivation of single subject results. Whilst our approach demonstrates high within-subject reproducibility, comparing parcellations across subjects (compare for example cross-subject reproducibility in Fig. 12 in the Supplementary material to Fig. 3) does not yet seem to indicate the same level of inter-subject alignment. It remains to be seen if this is an artefact of the algorithm or whether this is an inherent property of subject-to-subject variability in functional brain organisation. Nevertheless, our method outperforms other methods in terms of within-subject reproducibility and thus seems to be a step in the right direction also for group studies. We here deliberately choose to avoid excessive smoothing of data so that the results are not influenced by the biases introduced through this. However, between subject reproducibility is likely to improve with increased smoothing, though at the cost of increased bias and a reduction in neuroanatomical detail and interpretability.

There are several ways in which our single subject approach could be extended to group data. A common approach to group analysis is based on averaging (or concatenating) of single subject data or connectivity information. Whilst such approaches will improve the signal-to-noise ratio, subject-to-subject variability will also blur fine spatial detail. This is further compounded through the use of spatial smoothing applied normally in this setting. For example, Yeo et al. (2011), who based their analysis on average connectivity information, were only able to reliably estimate a maximum of 17 networks (~50 separate parcels), even though they used 500 subjects. To overcome this limit, group approaches need to be able to better capture and exploit single subject characteristics. For example, our subject-specific parcellations could be used as a starting point in an inter-subject registration process that is driven by functional rather than gross anatomical similarity. Such a registration approach could not only improve the derivation of more accurate group parcellations, but could also improve the analysis of task data, as functional areas would be better aligned across subjects than is currently possible with traditional registration algorithms. Using such a group approach, it would then be desirable to be able to go back to the subject level to generate subject level parcellations. A potential advantage of such an approach would be that it would allow the subject-level parcellations to exhibit a correspondence inherited from the group parcellation, so that the approach would become more easily applicable to the study of brain network variation across groups of subjects. We have not explored this aspect here in any detail; however several standard approaches could be used in conjunction with our method. For example, a group parcellation could be derived which could then either be matched to single subject parcels or mapped back to the individual subjects using methods such as dual regression. We are currently looking into the adaptation of these standard approaches to also take into account the tree structures of our approach.