Skip to main content
PMC home page
Nature Portfolio logoLink to Nature Portfolio
. 2013 Jul 23;4:2202. doi: 10.1038/ncomms3202

One hundred fold increase in current carrying capacity in a carbon nanotube–copper composite

Chandramouli Subramaniam 1, Takeo Yamada 1,2, Kazufumi Kobashi 1,2, Atsuko Sekiguchi 2, Don N Futaba 1,2, Motoo Yumura 1,2, Kenji Hata 1,2,3,a
PMCID: PMC3759037  PMID: 23877359

Abstract

Increased portability, versatility and ubiquity of electronics devices are a result of their progressive miniaturization, requiring current flow through narrow channels. Present-day devices operate close to the maximum current-carrying-capacity (that is, ampacity) of conductors (such as copper and gold), leading to decreased lifetime and performance, creating demand for new conductors with higher ampacity. Ampacity represents the maximum current-carrying capacity of the object that depends both on the structure and material. Here we report a carbon nanotube–copper composite exhibiting similar conductivity (2.3–4.7 × 105 S cm−1) as copper (5.8 × 105 S cm−1), but with a 100-times higher ampacity (6 × 108 A cm−2). Vacuum experiments demonstrate that carbon nanotubes suppress the primary failure pathways in copper as observed by the increased copper diffusion activation energy (∼2.0 eV) in carbon nanotube–copper composite, explaining its higher ampacity. This is the only material with both high conductivity and high ampacity, making it uniquely suited for applications in microscale electronics and inverters.

Inline graphicHigh electrical conductivity and ampacity are usually mutually exclusive properties. Here, in a carbon nanotube–copper composite, Subramaniam et al. achieve a similar conductivity to copper, but with a hundred fold increase in current carrying capacity.

Development of electronic devices is undergoing a paradigm shift with their continued miniaturization1. Such miniaturization provides greater portability and versatility to the devices, leading to their ubiquity. Simultaneously, the functionality and performance of these devices have been increasing. Although single-atom transistors2 and few-atom memory devices3 have been demonstrated to keep pace with the progressive miniaturization, there has been very little progress in conductors (such as Cu and Au), which supply power to these components within devices. With shrinking size of devices, pathways for carrying current to operate these components have significantly reduced. This has resulted in higher current density being carried by the conductors, reaching the limit of conventional conductors (such as Cu and Au) in present-day devices. In fact, the International Technology Roadmap for Semiconductors (ITRS) predicts4 that the current density in these devices is expected to exceed the breakdown limit of Cu and Au in 2015. Therefore, new conductors with higher ampacity are in great demand1. Ampacity represents the maximum current-carrying capacity of the object that depends both on the structure and material. However, high ampacity and high conductivity are mutually exclusive properties. This is because the former requires a strongly bonded system, whereas the latter requires the free electrons from a weakly bonded system5. Therefore, achieving high electrical conductivity and ampacity in the same material has been impossible.

Here we report a carbon nanotube–copper (CNT–Cu) composite that overcomes this mutual exclusivity to achieve an ampacity (630 × 106 A cm−2) 100 times higher than common electrical conductors, such as Cu6,7,8,9 and Au9,10 (∼106 A cm−2), approaching the theoretical limit for CNTs11,12,13,14,15,16 (1000 × 106 A cm−2). Compared with copper, the macroscopic CNT–Cu conductivity (4.7 × 105 S cm−1) rivaled, exceeded and doubled at 23 °C, above 80 °C and 227 °C, respectively from a one-order-of-magnitude lower temperature coefficient of resistivity. To understand the high ampacity of CNT–Cu composite, we performed activation energy (Ea) analysis to evaluate the energy required for Cu diffusion in CNT–Cu composite. Our analysis demonstrated that the Ea for Cu diffusion in the composite was ∼2.0 eV. In comparison, the primary electromigration failure pathways in pure Cu have much lower Ea, with surface and grain-boundary Cu diffusion requiring ∼0.6 eV and ∼1.0 eV, respectively17. Thus, the primary electromigration failure pathways (surface and grain-boundary diffusion) are suppressed by the presence of CNTs. Further, Cu diffusion is thus smaller (104 times) in our composite compared with bulk Cu, explaining its high ampacity.

Results

Conductivity of CNT–Cu composite

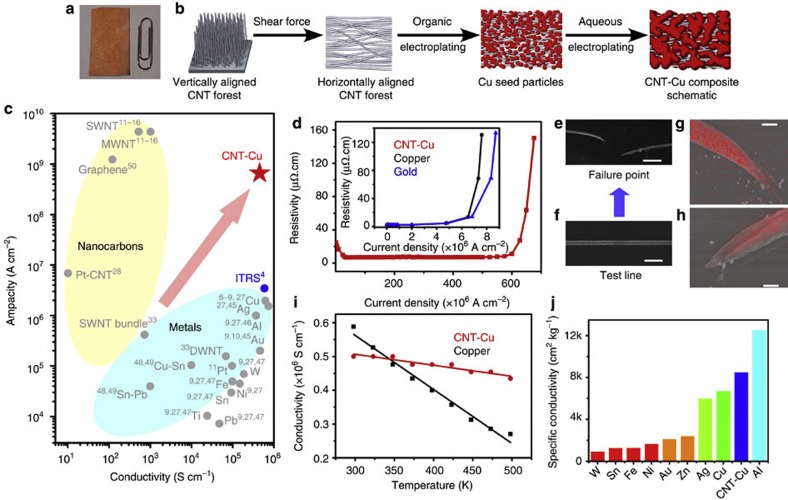
Significantly, a macroscopic (2.5 × 3.5 cm; Fig. 1a) CNT–Cu composite solid exhibited a room temperature conductivity of 4.7±0.3 × 105 S cm−1, as measured by the four-probe method, comparable to that of Cu18 (5.8 × 105 S cm−1), three orders higher than pristine CNT19,20 (∼102 S cm−1) and an order higher than pure CNT fibre21 (104 S cm−1). A microscopic CNT–Cu composite fabricated in an identical protocol (Fig. 1b) exhibited a room temperature conductivity of 2.1±0.3 × 105 S cm−1. High CNT volume fraction (45 vol%) resulted in a 42% density reduction (5.2 g cm−3) compared with Cu18 (8.9 g cm−3). Therefore, the specific conductivity for our CNT–Cu composite was 26% higher than Cu and exceeded most materials (Au, Ag and Cu) with the exception of Al (Fig. 1j). The temperature dependence of the conductivity, that is, temperature coefficient of resistivity, of the CNT–Cu composite (7.5 × 10−4 K−1) was one order of magnitude lower than that of Cu22 (6.8 × 10−3 K−1) (Fig. 1i), highlighting one benefit of our CNT–Cu composite. Consequently, the decrease in conductivity with temperature for the CNT–Cu was far less than Cu, and the conductivity was on par at room temperature, exceeded above 80 °C, and was double at 227 °C. This feature is important for heavy load applications, because the operating temperature is often higher than 80 °C.

Figure 1. Fabrication and ampacity of CNT–Cu composite.

Figure 1

Open in a new tab

(a) Picture of CNT–Cu composite alongside a paperclip for size reference. (b) Schematic representation of various steps for CNT–Cu composite fabrication. Cu seeds nucleate on the CNT surface during the organic electrodeposition and subsequently grow during the aqueous electrodeposition to yield the CNT–Cu composite. (c) Ashby plot of ampacity versus conductivity for various relevant materials, including metals (such as Cu, Au, Ag, Al, etc), alloys (such as Sn-Pb), nanocarbons (such as SWNT, graphene) and composites (such as Pt–CNT). The ITRS recommended level of current density is also shown for comparison, with the performance of CNT–Cu exceeding it. (d) Variation of resistivity with current density for CNT–Cu composite. The electrical conductivity of the wire was 2 × 105 S cm−1. Similar traces for Cu and Au lines are shown in inset for comparison. (e) SEM image of CNT–Cu test structure after failure. Scale bar, 4 μm. (f) SEM image of the same CNT–Cu composite test line before failure. Scale bar, 4 μm. (g,h) EDX mapping (based on Cu) of the failure points of CNT–Cu composite line presented in Fig. 1e. Scale bar, 500 nm. (i) Variation of conductivity with temperature for CNT–Cu (red) and Cu (black), showing the largely invariant conductivity of CNT–Cu composite with temperature. In comparison, Cu shows a decreasing conductivity with temperature, as expected for metals. (j) Comparison of conductivity per unit weight (specific conductivity) of CNT–Cu with different metals.

Ampacity of CNT–Cu composite

Central to this report, we found that our CNT–Cu exhibited a 100 times higher ampacity than Cu6,7,8,9. For this measurement, a CNT–Cu composite line structure (width=800 nm, height=900 nm, length=50 μm) was fabricated by electrodepositing Cu into a CNT line fabricated with conventional electron-beam lithography and reactive ion etching from a thin, closely packed and aligned CNT film23,24, that is, ‘CNT wafer'. Similar structures with Cu and Au were used for comparison. The current was increased while monitoring the resistivity (Fig. 1d). Initially, the resistivity unexpectedly decreased with current. Scanning electron microscopy (SEM) images revealed a smoothening of the initially rough CNT–Cu surface, indicating reorganization of the deposited Cu (Supplementary Fig. S1). We believe that this phenomenon is similar to filament aging to increase lifetime, which contributed to the higher ampacity. The resistivity remained unchanged up to 600 × 106 A cm−2 (600 MA cm−2), after which the resistivity exponentially increased leading to failure at ∼690 MA cm−2 at the central region of the test structure (Fig. 1e). The ampacity is defined as the maximum current density where the resistivity remains constant and thus was estimated to be 600 MA cm−2 from an average of five measurements. For comparison, we measured the ampacity of Cu and Au (both wire and sputter-deposited) test structures, which showed ampacities of 6.1 MA cm−2 and 6.3 MA cm−2, respectively, close to literature values6,7,8,9,10 (∼1 MA cm−2) ∼100 times smaller than that of the CNT–Cu composite (inset, Fig. 1d). Not only was the ampacity of CNT–Cu composite 100 times higher than conventional conductors, such as Cu, Al, Au and Ag6,7,8,9,10,25 (∼1 MA cm−2) and reports using Pt decorated CNTs26 (7.5 MA cm−2), it approached the highest value (1,000 MA cm−2) reported from individual CNTs11,12,13,14,15,16. Further, the composite was stable at a DC current density of 100 MA cm−2 for over 1200, h (50 days) with less than 10% variation in resistivity (Supplementary Fig. S2). SEM observation of the failure point revealed thinning at both ends of the rupture (Fig. 1e). Energy dispersive X-ray microscopy (EDX) detected only carbon at the ruptured surfaces (Fig. 1g). These results demonstrate that Cu had diffused away from this region and that the failure mechanism of the CNT–Cu composite was Cu electromigration27,28,29.

The CNT–Cu composite was plotted onto a conductivity-ampacity Ashby map for comparison with other high-performance materials (Fig. 1c). An inverse trend between conductivity and ampacity was clearly apparent with metals possessing higher conductivities and nanocarbons possessing higher ampacities. The CNT–Cu composite did not follow this trend creating a distinct and isolated point in the high-ampacity and high-conductivity domain with conductivity 1,000 times higher than nanocarbons and ampacity 100 times higher than metals. Although having been proposed theoretically30, no methods, to date, have achieved simultaneous increase in both properties. For example, alloying of copper decreases conductivity and doping or bundling of CNTs decreases ampacity31. For example, Xu et al.32 have demonstrated a similar conductivity (no estimation on ampacity) for CNT fibre–Cu composite, but the Cu deposition was limited to the outer surface of the CNT fibre. In this case, the high conductivity is derived from the surface Cu, but we expect that it will fail to exhibit high ampacity. Furthermore, Behabtu et al.21 reported high conductivity of 2.9 × 104 S cm−1 in pure CNT fibre; however, this report also did not characterize the ampacity.

Fabrication and characterization of CNT–Cu composite

To fabricate a CNT–Cu composite (Fig. 1a) that synergistically combines the strengths of both materials, we developed a unique fabrication process. In contrast to conventional approaches that use CNT–Cu ion dispersions, we electrodeposited Cu into the pores of premade, macroscopic CNT structures, for example, buckypaper, and CNT solids (bulk, packed, aligned CNT material33). Long, vertically aligned single-wall CNT forests (diameter=3 nm, height=500–700 μm, density=0.04 g cm−3) were synthesized on a substrate by the water-assisted method34. The sparse forests were densified (∼0.5 g cm−3) into closely packed and aligned CNT structure by the liquid densification technique33 with Cu ions. Then, this CNT structure was transformed into CNT–Cu composite by two-stage nucleation-growth electrodeposition processes (Fig. 1b), as described below.

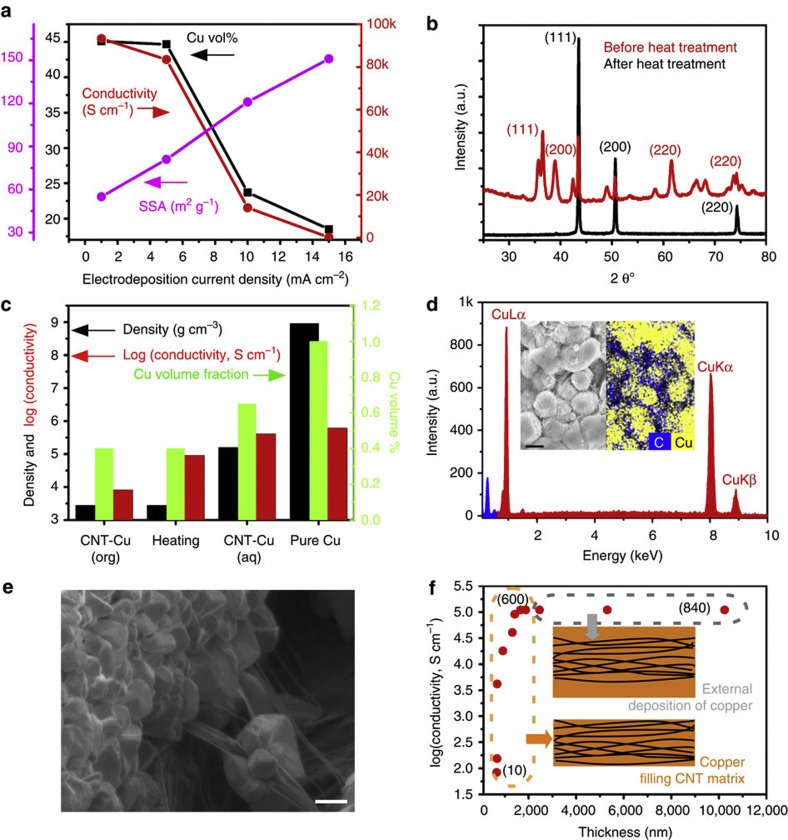
Several key processes were developed to achieve this CNT–Cu composite. First, the electrodeposition was separated into two phases: (1) wetting the hydrophobic CNTs with Cu ions in an organic solution to nucleate Cu seeds on CNT surface and (2) grow the Cu seeds in an aqueous solution until all the mesopores were filled. Second, in the organic electrodeposition phase, homogeneous seeding required that the rate-limiting step be the Cu nucleation on the CNTs rather than the Cu ion diffusion through the CNT structure. Therefore, slow deposition rates (1–5 mA cm−2 versus conventional rates35 of 50–100 mA cm−2) were required to electrodeposit Cu throughout the dense CNT matrix, not only on the surface. At low current densities (1–5 mA cm−2), Cu homogeneously nucleated throughout the CNT matrix, resulting in high conductivity, high Cu filling-ratio and low specific surface area (an indicator of accessible CNT surface area; Fig. 2a). In contrast, at high current densities (5–15 mA cm−2) Cu deposited only at the outer surfaces of the CNT matrix, resulting in exactly the opposite effect (Fig. 2a). Third, annealing in hydrogen ambient reduced the (111), (200) and (220) CuxOy phases to a pure (111), (200) and (220) Cu phase as seen from X-ray diffraction (Fig. 2b). In addition, the Cu particles sintered resulting in an improvement in electrical conductivity from 8.2 × 103 to 9.1 × 104 S cm−1 (Fig. 2c). Finally, through aqueous electrodeposition, the Cu volume fraction was increased, as seen by the steep density increase (Fig. 2c).

Figure 2. Characterization of CNT–Cu composite.

Figure 2

Open in a new tab

(a) Variation of CNT–Cu composite properties as a function of organic electrodeposition current density. The direct correlation between conductivity and volume occupancy of Cu is observed. (b) XRD traces of CNT–Cu composite before (red) and after (black) heat treatment. (c) Evolution of the CNT–Cu composite properties (conductivity, density and Cu volume occupancy) with every advancing step in the fabrication process. Similar properties of bulk Cu are also given alongside for comparison. (d) EDX spectrum of CNT–Cu composite showing the absence of any other impurities with the cross-sectional SEM and EDX mapping images. Scale bar, 2 μm. (e) Cross-sectional SEM images showing the polycrystalline Cu tightly bound with long, intertwined, well-dispersed CNTs. Scale bar, 6 μm. (f) Evolution of CNT–Cu conductivity with thickness and electrodeposition time for a current density of 5 mA cm−2. Values given in brackets pertain to electrodeposition time in minutes.

Through this scheme, we succeeded in making a CNT–Cu composite with the CNT covering the surfaces and grain boundaries of Cu (inset, Fig. 2d). No contamination by oxygen was observed by EDX (Fig. 2d). Thermo-gravimetry showed that the composite was composed of ∼55 vol% Cu and 45% CNT (Supplementary Figs S3 and S4) (total density=5.2 g cm−3), indicating a 42% density reduction from pure Cu18 (8.9 g cm−3). A control experiment was carried out to verify that the observed conductivity arose from the CNT–Cu bulk as opposed to its outer surface. Hence, the thickness and conductivity were plotted as a function of electrodeposition time (10–840 min; Fig. 2f). Initially (up to 600 min), the electrical conductivity monotonically increased and saturated at 105 S cm−1 while the thickness remained unchanged. This meant that the Cu deposited within the CNT matrix. Further electrodeposition (beyond 600 min) led to a thickness increase, which indicated deposition on the outer surfaces. Importantly, the conductivity did not increase during this phase, meaning that the measured conductivity did not stem from the surface deposition of Cu.

Discussion

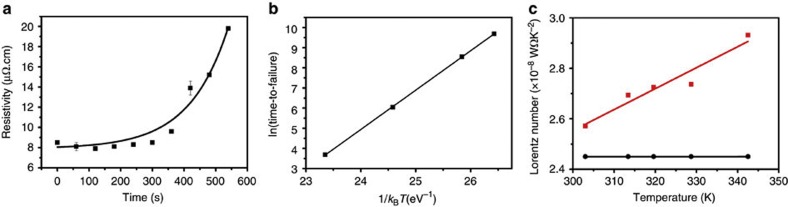
As experimental results demonstrate, electromigration of Cu atoms is also the failure mechanism of the CNT–Cu composite (like pure Cu). Within this framework, several experiments and analyses were carried out to understand the mechanism of high ampacity of the CNT–Cu composite. The activation energy for Cu diffusion in CNT–Cu composite was estimated by failure kinetics tests carried out at different temperatures (440 K, 450 K, 473 K and 498 K). Applying a current density (720 MA cm−2) higher than the ampacity (600 MA cm−2) of CNT–Cu results in accelerated failure (Fig. 3a). The ‘time of failure,' t, was estimated from the point of 40% resistivity increase. The results of several such experiments carried out at different temperatures (constant current density) were assembled into an Arrhenius plot of ln(t) versus 1/kT (Fig. 3b). Therefore, the activation energy for Cu diffusion in CNT–Cu composite was estimated from the slope of this plot, based on Black's equation36,

Figure 3. Mechanistic analysis of CNT–Cu composite.

Figure 3

Open in a new tab

(a) Variation of resistivity with time for CNT–Cu composite at a current density of 720 MA cm−2 at 473 K. (b) Experiment in a repeated at different temperatures to give an Arrhenius plot of ln(time-to-failure) versus 1/kBT. The activation energy for Cu diffusion in CNT–Cu is determined from the slope of this graph. (c) Comparison of Lorentz number for CNT–Cu (red) with Cu (black) as a function of temperature, indicating an increasing phonon contribution of CNT with temperature in CNT–Cu composite.

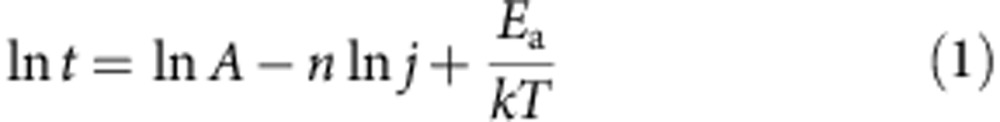graphic file with name ncomms3202-m1.jpg

where j is the current density, Ea is the activation energy, k is the Boltzmann constant, T is the mean temperature of the test structure, n is the current-density exponent and A is the pre-exponential factor. The activation energy for Cu diffusion in CNT–Cu composite was estimated, from slope of Fig. 3b to be 2.03 eV. We wish to note that our choice of the current-density exponent (n) and pre-exponential factor (A) were taken from similar electromigration studies on Cu under identical measurement conditions, namely in vacuum and with the test structure not surrounded by any dielectric27,37,38. Further, we note that this estimation of the activation energy (Ea) is independent of the choice of pre-exponential factor (A) and current-density exponent (n). The value of 2.03 eV was identical to that of Cu lattice diffusion17,28,29 (∼2.0–2.3 eV), which means that the Cu diffusion follows the most difficult pathway. For bulk Cu, diffusion occurs at the surfaces and grain boundaries that possess much lower activation energies17,28,29 (∼0.7 eV and ∼1.0 eV, respectively). Our results showed that for the CNT–Cu composite, the Cu diffusion pathways through surface and grain boundaries were greatly suppressed. The Cu diffusion coefficient (D*, related the ease of electromigration) was calculated from the activation energy by:

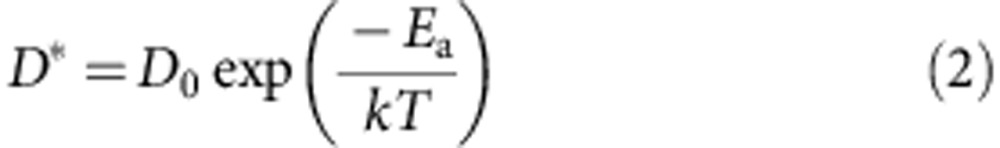graphic file with name ncomms3202-m2.jpg

where D0 is the diffusion coefficient at infinity17. As a result, the estimated diffusion coefficient of Cu in the CNT–Cu composite by bulk diffusion was 104 times lower than that of copper, which should significantly contribute to the observed high ampacity. Internal structure observations the CNT–Cu composites by SEM and EDX revealed a fine, continuous, mesh-like CNT network covering the surfaces and grain boundaries of Cu (inset, Fig. 2d). Theoretical studies have proposed that the activation energy for carbon-doped Cu diffusion increased by suppressing surface and grain boundary pathways39. Although lowering of Cu electromigration by CNT has been reported, the exact mechanism and the 100 times ampacity increase, without compromising on electrical conductivity, reported here have never been achieved40. We draw a distant parallel of this effect with the well-known practice of alloying steel with carbon for strengthening. We believe that the CNT in CNT–Cu composite has a similar role in suppressing Cu diffusion39.

We numerically estimated the ampacity of the CNT–Cu composite by assuming that the material ruptured by current-induced Joule heating, leading to melting. The temperature increase by current is described by41,

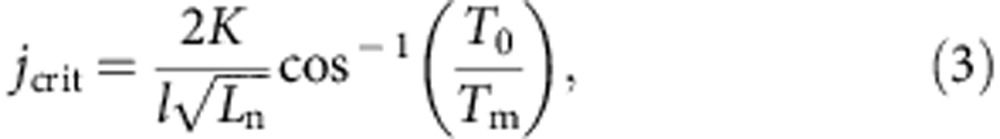graphic file with name ncomms3202-m3.jpg

where jcrit is the ampacity, K is the thermal conductivity (∼800 Wm−1 K−1), l is the length of the test structure (50 × 10−6 m), and Ln is the Lorentz number (∼3.44 × 10−8WΩ K−2). The melting point of the composite was taken as that of Cu18 (as 1357 K), because the CNT melting point is significantly higher in an inert ambient. The Lorentz number (ratio of thermal and electrical conductivities) was calculated from the experimentally measured temperature-dependent thermal conductivity and were plotted versus temperature (Fig. 3c). Interestingly, the Lorentz number for the CNT–Cu composite linearly increased while remaining constant for Cu. Increasing Lorentz number indicates phonon contribution to the thermal conductivity, unlike a constant Lorentz number for a free electron system42. We extrapolated the Lorentz number at higher temperatures from the slope. The theoretically estimated ampacity was thus estimated as ∼1,200 MA cm−2, which agrees with our measured ampacity of 600 MA cm−2. These analyses and experimental results demonstrate the significant role of the CNT phonons in achieving high thermal conductivity and Lorentz number at elevated temperatures for the CNT–Cu composite. This phenomenon was vital for the high ampacity.

Furthermore, we quantitatively evaluated the electromigration by estimating the Cu atomic fluxes in bulk Cu and CNT–Cu due to current (mass flux) described by the Nernst–Einstein equation43:

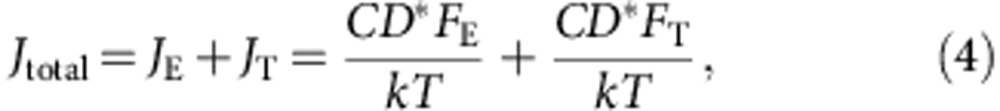graphic file with name ncomms3202-m4.jpg

where C is the concentration of atoms, k is the Boltzmann constant, T is the temperature, D* is the diffusion coefficient, FE and FT are the respective driving forces due to electron wind and temperature gradient. Electromigration consists of two components: the mass flux from electron wind (electron-Cu atom collisions, JE) and from thermal gradient (diffusion caused by Joule heating, JT). For Cu, the electron wind is known to be one order larger than that of the thermal gradient44; thus, thermal gradient was neglected in the following discussion.

We calculated the electron wind driving force by, 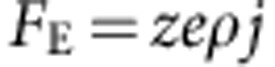Inline graphic where, z is the effective charge number38 (=10), e the electronic charge (1.6 × 10−19 C), ρ the material resistivity (4.3 × 10−6 Ω cm), and j the current density (600 MA cm−2). By using experimentally obtained data, the electron-driving force was estimated to be (2,083 eV cm−1), two orders higher than that of Cu44 (40 eV cm−1); accordingly, the electron wind mass flux was ∼100 times smaller than that of pure Cu. We think that this 100 times difference agrees well with the observed 100 times difference in ampacity.

In summary, we developed a high-performance electrical conductor (CNT–Cu composite) that combines the best electrical properties of CNT (high ampacity) and Cu (high conductivity). Moreover, the CNT–Cu composite is the only material satisfying the ampacity and conductivity levels stipulated by ITRS4 for 2015.

Methods

Materials

Single-walled CNTs were synthesized through the water-assisted supergrowth technique34. All chemicals were purchased from Wako and used without further purification, unless specified otherwise.

Prefilling of CNT matrix with Cu electrolyte

A free-standing CNT forest was obtained by carefully removing it from the growth substrate. This was subjected to a shear force between two glass slides to change the alignment direct of the CNT forest from vertical to horizontal (with reference to the glass slides). The arrangement, held in place using clips, was immersed into a densification solution of Copper acetate dissolved in acetonitrile (2.75 mM) and left undisturbed was 20 min. The densified solid was carefully removed and assembled into the electroplating setup.

Electroplating setup

The electroplating setup consists of a cathode of densified, prefilled CNT solid backed onto an stainless steel mesh for providing an equipotential surface for electroplating. The cathode was sandwiched between thin strips of pure Cu which served as anodes. Filter paper from Advantech acted as insulating separators between the anodes and cathode. The whole assembly was held in place using a specially designed polyether ether ketone cell. For the organic electroplating, the electrolyte consists of the same liquid, which was used during forest densification. In case of the second step aqueous electrodeposition, the electrolyte used was a commercially available electroplating solution (ATMI, without accelerators or suppressors). Trapped air and dissolved gases was removed from the setup before electrodeposition. Electrodeposition of Cu was carried out under galvanostatic conditions using a VMP3 Electrochemical workstation (Princeton Applied Research).

Reductive annealing

The composite after each electrodeposition was washed with pure acetonitrile and dried using a vacuum desiccator at 60 °C for 30 min. This was followed by heating at 250 °C for 3 h in a tube furnace. The heating and subsequent cooling was carried out under a controlled flow of H2 gas at 150 sccm.

Conductivity measurement

The electrical conductivity measurements were carried out in two different geometries. The four-probe conductivity was measured using a hand-held four-probe conductivity meter fitted with Au-coated electrodes. For the two-probe measurement, the edges of the composite were cut using a CO2 laser to remove the Cu deposited on the edges first removed to force the electrical path through the thickness (bulk) of the composite. Thin Cu strips were attached to either faces of the composite and were in turn connected to a digital multimeter. Plastic clips were used to hold the setup in place and ensure good, stable electrical contact between the electrodes and samples. Thus, the resistance measured was from the bulk of the composite, in a direction perpendicular to the thickness of the composite. The resistance of the composite was normalized to the thickness and cross-sectional area of the composite to arrive at its two-probe resistivity. The two-probe and four-probe conductivity values presented here are an average of five such measurements at different places of the composite across three composites.

Microfabrication of CNT–Cu composite

For microfabrication, vertically aligned CNT thin films were grown from patterned catalyst using water-assisted supergrowth chemical vapor deposition method. The average size of the films used here was 700 μm × 700 μm with an as-grown thickness of 8 μm. This was transferred to the desired substrate in the desired orientation using an liquid-induced densification approach23,24. Thickness of the CNT films after transfer was measured to be around 700 nm.

Patterning of CNT film

Ti-Au (3/100 nm) electrode lines, required during electrodeposition, were defined using conventional E-beam lithography followed by sputtering and lift-off. We used a TiN-coated Si3N4 substrate to prevent Cu diffusion into the substrate, and large Ti/Au bottom contacts that ensured breakdown at the centre of the line. After CNT thin-film transfer, the substrate was vacuum baked at 180 °C for 15 min before resist coating. Positive tone PMMA-495 was spin-coated at 4,700 r.p.m. for 60 s on the substrate followed by baking at 180 °C for 60 s. This was followed by spin coating a negative tone FOX 16 resist at 4,500 r.p.m. for 60 s. The substrate was baked at 120 °C for 8 min for slow curing of the resist. E-beam lithography was used to define the required areas of CNT. The sample was developed using tetramethylammonium hydroxide, rinsed with water and dried under a dry N2 flow. Reactive-ion etching using a mixture of O2/Ar /CHF3 was carried out to remove the unwanted CNT areas. The negative resist was stripped by immersing in buffered hydrogen fluoride for ∼10 s followed by thorough rinsing and drying. The positive resist was removed using 1:1 micture of methylisobutyl ketone/isopropyl alcohol followed by rinsing in isopropyl alcohol and drying under N2 stream.

Current density testing of CNT–Cu composite

A home-built setup was used to perform the current density testing on CNT–Cu composite. It consists of a T-joint fitted with electrical feedthrough on one side. The other two openings were connected to a vacuum pump and a vacuum gauge, respectively. All experiments were carried out at the pressure of 1.3 × 10−4 Pa. The electrical feedthrough was connected to an Agilent U3606A DC power supply-Digital multimeter system capable of supplying up to 3 A. For higher currents, a Kikusui 10–105 DC power supply was used. The experiments were carried out by sequentially stepping up the voltage and simultaneously recording the current flowing through the system. Resistance at every voltage step, computed from the I–V correlation, was translated to resistivity with knowledge of length and cross-sectional area of the test structure. The cross-sectional area was also used to compute the applied current density at every stage of experiment. The testing was carried out on five devices with identical results. Sputtered and electroplated Cu films, Cu and Au wires (25 μm diameter), which are conventionally used in wire-bonding were also tested under identical conditions using the same setup.

Activation energy analysis

Accelerated lifetime tests were carried out at different temperatures using a modified setup consisting of a test chamber with temperature control. Electrical feedthrough in the test chamber enabled a constant current density to be applied while the temperature of the experiment could be modified. The time-to-failure of the sample at each temperature was recorded at a constant current density, providing an Arrhenius plot of ln(time-to-failure) versus 1/kT. Activation energy for Cu diffusion in CNT–Cu composite was estimate from the slope of this graph.

Lorentz number estimation

Thermal diffusivity (α) of CNT–Cu composite was measured at various temperatures with a Bethel Thermowave Analyser system fitted with a temperature controller. Differential scanning calorimetry was used to estimate the specific heat capacity (Cp) of the material in the same temperature range. Thermal conductivity (κ) of the sample at various temperatures was estimated using the relation

graphic file with name ncomms3202-m6.jpg

where ρ is the density of the material (5.2 g cm−3). From the knowledge of electrical conductivity (σ) at various temperatures (Fig. 1i), the Lorentz number (L) was estimated using Wiedmann–Franz law as

graphic file with name ncomms3202-m7.jpg

The Lorentz number estimated for Cu and CNT–Cu composite is plotted in Fig. 3c.

Author contributions

C.S., T.Y. and K.H. devised the experiments, C.S. performed the experiments, K.K. and A.S. provided assistance for process development, D.N. provided instrumental assistance, M.Y. was in-charge of project management, C.S. and K.H. cowrote the paper, K.H. designed and supervised the project.

Additional information

How to cite this article: Subramaniam et al. One hundred fold increase in current carrying capacity in a carbon nanotube–copper composite. Nat. Commun. 4:2202 doi: 10.1038/ncomms3202 (2013).

Supplementary Material

Supplementary Information

Supplementary Figures S1-S4

ncomms3202-s1.pdf (276.7KB, pdf)

Acknowledgments

We thank Tatsuo Toida for assistance in making the figures. Financial assistance from New Energy and Industrial Technology Development Organization (NEDO) is gratefully acknowledged.

References

  1. U.S. Congress, Office of Technology Assessment. Miniaturization Technologies OTA-TCT-514 (U.S. Government Printing Office: Washington, DC, (1991). [Google Scholar]
  2. Fuechsle M. et al. A single atom transistor. Nat. Nanotech. 7, 242–246 (2012). [DOI] [PubMed] [Google Scholar]
  3. Loth S., Baumann S., Lutz C. P., Eigler D. M. & Heinrich A. J. Bistability in atomic-scale antiferromagnets. Science 335, 196–199 (2012). [DOI] [PubMed] [Google Scholar]
  4. ITRS International Technology Working Groups. International Technology Roadmap for Semiconductors (http://www.itrs.net ) (2010). [Google Scholar]
  5. Pauling L. The Nature Of The Chemical Bond 3rd edn (Cornell University Press: USA, (1960). [Google Scholar]
  6. Li P.-C. & Young T. K. Electromigration: the time bomb in deep-submicron ICs. IEEE Spectrum 33, 75–78 (1996). [Google Scholar]
  7. Lloyd J. R. & Clement J. J. Electromigration in copper conductors. Thin Solid Films 262, 135–141 (1996). [Google Scholar]
  8. Tao J. & Cheung N. W. Electromigration characteristics of copper interconnects. IEEE Electr. Device L. 14, 249–251 (1993). [Google Scholar]
  9. Preece W. H. On the heating effects of electric current. P. R. Soc. London 464–471 (1884). [Google Scholar]
  10. Huntington H. B. & Grone A. R. Current induced marker motion in gold wires. J. Phys. Chem. Solids 20, 76–87 (1961). [Google Scholar]
  11. Yao Z., Kane C. L. & Dekker C. High-field electrical transport in single-wall carbon nanotubes. Phys. Rev. Lett. 84, 2941–2944 (2000). [DOI] [PubMed] [Google Scholar]
  12. Wei B. Q., Vajtai R. & Ajayan P. M. Reliability and current carrying capacity of carbon nanotubes. Appl. Phys. Lett. 79, 1172–1174 (2001). [Google Scholar]
  13. Collins P. G., Hersam M., Arnold M., Martel R. & Avouris P. h. Current saturation and electrical breakdown in multiwalled carbon nanotubes. Phys. Rev. Lett. 86, 3128–3131 (2001). [DOI] [PubMed] [Google Scholar]
  14. Frank S., Poncharal P., Wang Z. L. & de Heer W. A. Carbon nanotube quantum resistors. Science 280, 1744–1746 (1998). [DOI] [PubMed] [Google Scholar]
  15. Park et al. Electron-phonon scattering in metallic single-walled carbon nanotubes. Nano. Lett. 4, 517–520 (2004). [Google Scholar]
  16. Naeemi A. & Meindl J. D. Compact physical models for multiwall carbon-nanotube interconnects. IEEE Electr. Device L. 27, 338–341 (2006). [Google Scholar]
  17. Butrymowicz D. B., Manning J. R. & Read M. E. Diffusion in copper and copper alloys: Part 1. Volume and surface self-diffusion in copper. J. Phys. Chem. Ref. Data 2, 643–657 (1973). [Google Scholar]
  18. Lide D. R. CRC Handbook of Chemistry and Physics 54 edn (CRC Press: USA, (1973). [Google Scholar]
  19. Lee R. S., Kim H. J., Fischer J. E., Thess A. & Smalley R. E. Conductivity enhancement in single-walled carbon nanotube bundles doped with K and Br. Nature 388, 255–257 (1997). [Google Scholar]
  20. Dai H., Wong E. W. & Lieber C. M. Probing electrical transport in nanomaterials: conductivity of individual carbon nanotubes. Science 272, 523–526 (1996). [Google Scholar]
  21. Behabtu N. et al. Strong, light, multifunctional fibers of carbon nanotubes with ultrahigh conductivity. Science 339, 182–186 (2013). [DOI] [PubMed] [Google Scholar]
  22. US Government Printing Office. Copper wire tablesNational Bureau of Standards Handbook 100 US Government Printing Office: Washington DC, (1966). [Google Scholar]
  23. Hayamizu Y. et al. Integrated three-dimensional microelectromechanical devices from processable carbon nanotube wafers. Nat. Nanotech. 3, 289–294 (2008). [DOI] [PubMed] [Google Scholar]
  24. Yamada T. et al. A stretchable carbon nanotube strain sensor for human-motion detection. Nat. Nanotech. 6, 296–301 (2011). [DOI] [PubMed] [Google Scholar]
  25. Ho P. S. & Kwok T. Electromigration in metals. Rep. Prog. Phys. 52, 301–348 (1989). [Google Scholar]
  26. Kim Y. L. et al. Highly aligned scalable platinum decorated single-wall carbon nanotube arrays for nanoscale electrical interconnects. ACS Nano. 3, 2818–2826 (2009). [DOI] [PubMed] [Google Scholar]
  27. Lloyd J. R. Electromigration failure. J. Appl. Phys. 69, 7601–7604 (1991). [Google Scholar]
  28. Lloyd J. R., Clemens J. & Snede R. Copper metallization reliability. Microelectron. Reliab. 39, 1595–1602 (1999). [Google Scholar]
  29. Huang Q., Lilley C. M. & Divan R. An in-situ investigation of electromigration in Cu nanowires. Nanotechnology 20, 075706 (2009). [DOI] [PubMed] [Google Scholar]
  30. Hjortstam O., Isberg P., Soderholm S. & Dai H. Can we achieve ultra-low resistivity in carbon nanotube-based metal composites? Appl. Phys. A. 78, 1175–1179 (2004). [Google Scholar]
  31. Zhao Y., Wei J., Vajtai R., Ajayan P. M. & Barrera E. V. Iodine doped carbon nanotube cables exceeding specific electrical conductivity of metals. Sci. Rep. 1, 83 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Xu et al. Continuous electrodeposition for lightweight, highly conducting and strong carbon nanotube-copper composite fibers. Nanoscale 3, 4215–4219 (2011). [DOI] [PubMed] [Google Scholar]
  33. Futaba D. N. et al. Shape-engineerable and highly densely packed single-walled carbon nanotubes and their application as super-capacitor electrodes. Nat. Mater. 5, 987–994 (2006). [DOI] [PubMed] [Google Scholar]
  34. Hata K. et al. Water-assisted highly efficient synthesis of impurity-free single-walled carbon nanotubes. Science 306, 1362–1364 (2004). [DOI] [PubMed] [Google Scholar]
  35. Schlesinger M., Paunovic M. (eds) Modern Electroplating 5th ednJohn Wiley& Sons, Inc., Ed5, (2010). [Google Scholar]
  36. Black J. R. Electromigration - A brief survey and recent results. IEEE Trans. Electron. Dev. 16, 338–347 (1969). [Google Scholar]
  37. Lloyd J. R. Electromigration for Designers: An Introduction for the Non-Specialist http://www.eet.bme.hu/~benedek/CAD_Methodology/Cadence_Papers/electromigration.pdf (2013). [Google Scholar]
  38. Shatzkes M. & Lloyd J. R. A model for conductor failure considering diffusion concurrently with electromigration resulting in a current exponent of 2. J. Appl. Phys. 59, 3890–3893 (1986). [Google Scholar]
  39. Liu C.-L. Screening beneficial dopant to Cu interconnects by modeling. Appl. Phys. Lett. 80, 763–765 (2002). [Google Scholar]
  40. Chai Y. Copper/carbon nanotubes composite interconnect for enhanced electromigration resistance. 58th Electronic Components and Technology Conference, Florida, USA 412–420 (2008). [Google Scholar]
  41. Ohring M. Reliability And Failure Of Electronic Materials And Devices Ch. 5 (Academic Press Limited: London, (1998). [Google Scholar]
  42. Hone J., Whitney M., Piskoti C. & Zettl A. Thermal conductivity of single-walled carbon nanotubes. Phys. Rev. B 59, R2514 (1999). [Google Scholar]
  43. Nguyen H. V. et al. Electrothermomigration-induced failure in power IC metallization. 6th Annual Workshop on Semiconductor Advances for Future Electronics and Sensors 622, (2003). [Google Scholar]
  44. Nguyen H. V. et al. Effect of thermal gradients on the electromigration lifetime in power electronics. 42nd Annual International Reliability Physics Symposium Proceedings 25–29 (2004). [Google Scholar]
  45. Hummel R. E. & Geier H. J. Activation energy for electrotransport in thin silver and gold films. Thin Solid Films 25, 335–342 (1975). [Google Scholar]
  46. Black J. R. Electromigration failure modes in aluminum metallization for semiconductor devices. P. IEEE 57, 1587–1594 (1969). [Google Scholar]
  47. Oliver K. G. Basic Industrial Electricity: A Training and Maintenance Manual Ch. 3, (Industrial Press Inc.: New York, (1990). [Google Scholar]
  48. Abdulhamid M. F., Basaran C. & Lai Y. S. Thermomigration versus electromigration in microelectronics solder joints. IEEE Trans. Adv. Pack 32, 627–635 (2009). [Google Scholar]
  49. Yoon M. S. et al. In-situ observation of electromigration in eutectic SnPb solder lines: atomic migration and hillock formation. J. Electron. Mater 36, 562–567 (2007). [Google Scholar]
  50. Murali R., Yang Y., Brenner K., Beck T. & Meindl J. D. Breakdown current density of graphene nanoribbons. Appl. Phys. Lett. 94, 2431143 (2009). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Figures S1-S4

ncomms3202-s1.pdf (276.7KB, pdf)

Articles from Nature Communications are provided here courtesy of Nature Publishing Group

RESOURCES