Automatic functional analysis of left ventricle in cardiac cine MRI

Abstract

Rationale and objectives

A fully automated left ventricle segmentation method for the functional analysis of cine short axis (SAX) magnetic resonance (MR) images was developed, and its performance evaluated with 133 studies of subjects with diverse pathology: ischemic heart failure (n=34), non-ischemic heart failure (n=30), hypertrophy (n=32), and healthy (n=37).

Materials and methods

The proposed automatic method locates the left ventricle (LV), then for each image detects the contours of the endocardium, epicardium, papillary muscles and trabeculations. Manually and automatically determined contours and functional parameters were compared quantitatively.

Results

There was no significant difference between automatically and manually determined end systolic volume (ESV), end diastolic volume (EDV), ejection fraction (EF) and left ventricular mass (LVM) for each of the four groups (paired sample t-test, α=0.05). The automatically determined functional parameters showed high correlations with those derived from manual contours, and the Bland-Altman analysis biases were small (1.51 mL, 1.69 mL, –0.02%, –0.66 g for ESV, EDV, EF and LVM, respectively).

Conclusions

The proposed technique automatically and rapidly detects endocardial, epicardial, papillary muscles’ and trabeculations’ contours providing accurate and reproducible quantitative MRI parameters, including LV mass and EF.

Introduction

To quantitatively analyze global and regional cardiac function of the left ventricle (LV) from cine magnetic resonance (MR) images, clinical parameters such as ejection fraction (EF), systolic and diastolic volumes, and myocardial mass are required (1,2). Calculation of these parameters depends upon accurate delineation of endocardial, epicardial, papillary and trabecular muscles’ contours. Manual delineation is time-consuming and has high interobserver variability. Moreover, in clinical practice the manual delineation is typically limited to the end diastolic (ED) and end systolic (ES) phases due to time constraints, which is insufficient to fully analyze wall motion or compute the peak ejection and filling rates. As a result, an accurate, rapid, fully automatic LV contour detection (segmentation) algorithm analyzing all phases of the cardiac cycle is highly desirable.

A number of methods have been proposed for (semi-) automatic LV segmentation including: probability atlas (3), dynamic programming (4), fuzzy clustering (5), deformable model (6,7), active appearance model (8), active shape model (9), variational and level sets (10,11), graph cuts (12), and image-driven approaches (13,14). For a complete review of recent literatures describing cardiac segmentation techniques see (15). Despite recent advances, accurate LV segmentation is still acknowledged as a difficult problem, and typically faces three main challenges: (I) the difficulty in localizing the LV and distinguishing it from other features and artifacts; (II) the lack of edge information where contours are required; and (III) the shape variability of the endocardial and epicardial contours across slices, phases, and subjects.

In this work, we describe our method for the fast, robust, and fully automatic LV segmentation from short axis (SAX) cine MR images. The method localizes the LV and segments its major features including the endocardial and epicardial contours, and papillary and trabecular muscles in all phases. The segmentation algorithm was evaluated with a database of clinical cardiac MR studies with diverse pathology.

Materials and methods

Study population and imaging

For this study, data from two scanners were analyzed: GE (1.5 T, CV/i Excite, GE Healthcare, Milwaukee, WI), Philips (1.5 T, Achieva, Philips Medical Systems, Best, Netherlands). Cine steady state free precession (SSFP) MR-SAX images were obtained with imaging during 10-15 s breath-holds, with coverage from the atrioventricular ring to the apex. Patients with motion artifact, banding artifact or gross abnormality (e.g., due to a tumor) were excluded from the study.

GE scanner

Data from 133 patients were retrospectively analyzed (35 female, 98 male; age: 59.4±16.1 yrs). Imaging parameters were as follows: repetition/echo times, 3.7/1.6 ms; flip angle, 45º; matrix size, 256×256; field of view, 320 mm × 320 mm; contiguous sections, 10-14; section thickness were 8-10 mm; slice gap, 0 mm; and number of phases, 20. The patient datasets were classified into four groups representing diverse morphologies, based on the following clinical criteria: (I) heart failure with infarction (HFI) group had EF <40% and evidence of late gadolinium (Gd) enhancement; (II) heart failure with no infarction (HFNI) group had EF <40% and no late Gd enhancement; (III) LV hypertrophy (HYP) group had normal LV EF (>55%) and a ratio of LV mass/body surface area >83 g/m² (16); and (IV) healthy (HEA) group had EF >55% and no hypertrophy. Patient selection ensured the group sizes were approximately equal (HFI N =34, HFNI N =30, HYP N =32, HEA N =37).

Philips scanner

Six datasets were analyzed (6 male; age: 61.5±12.4 yrs). Imaging parameters were as follows: repetition/echo times, 3.9/1.9 ms; flip angle, 60º; matrix size, 320×320; field of view, 330 mm × 330 mm; contiguous sections, 15-20; section thickness, 8 mm; slice gap, 0 mm; and number of phases, 25.

Manual contours

The endocardial and epicardial contours were drawn by three well-trained readers for all slices at the ED and ES phases, and confirmed by a cardiologist with 10 years of experience in cardiac imaging, and these manual contours were the evaluation reference standard. The inter- and intra-observer variability has been previously reported (17). The convention of including papillary muscles and trabeculations within the endocardial contour was followed (16). The most basal LV slice was defined as the one preceding the atrium having the ED blood pool ≥50% encircled by myocardium, and included the LV outflow tract (LVOT). The apical slice was defined as the ones that beyond the papillary muscles to the apex. The patients consented to research use of their imaging data, with approval by our institutional ethics review board.

Segmentation algorithm

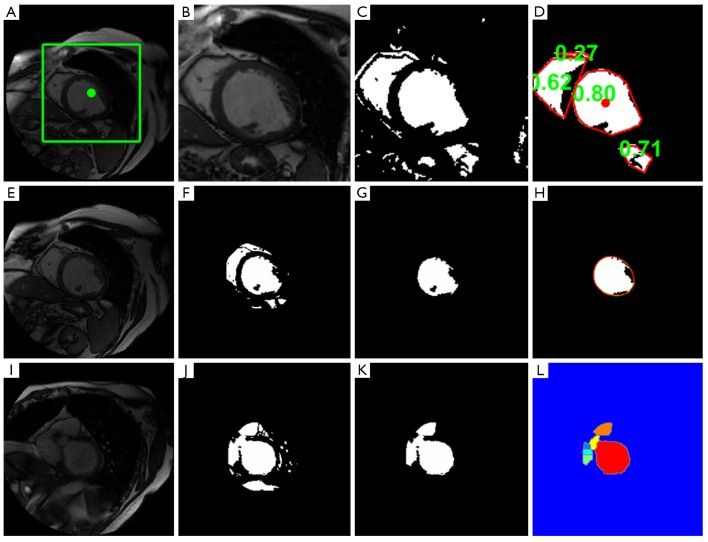
The calculation starts from the middle slice, and each image is processed sequentially in the basal direction, followed by sequential processing from the middle slice to the apex (18). The images for each cardiac phase are calculated independently. First, the myocardium is located by calculating the centroid of the LV blood pool on the middle slice at the specified phase based on a roundness metric technique (Figure 1A-D). Second, the endocardial and papillary muscles’ and trabeculations’ contours are detected by applying the optimal threshold method of Otsu (19) watershed, and 1D fast Fourier transform (FFT) (20) method (Figure 1E-I). Finally, the epicardial contour is calculated by mapping the pixels from Cartesian to polar coordinates, and using a multiple seed, region-growing method (Figure 2). Refer to the Supplementary Material for a detailed description of the image processing.

Figure 1.

Left ventricle (LV) localization, endocardial contour detection and outflow tract segmentation. A-D. LV localization procedure; E-H. LV endocardial contour detection; I-L. Identify and segment basal slice with LV outflow tract. A. Target image with rectangular region-of-interest (ROI) and image center, (green square and point); B. ROI image; C. Binary image; D. Surviving objects’ convex hulls (red), the corresponding roundness metrics (green), and the detected LV blood pool centroid (red point); E. Target image; F. Binary image masked by ROI. G. Located LV blood pool; H. Smoothed endocardial contour (red), and papillary muscles and trabeculations (black regions in the smoothed endocardial contour); I. Basal slice image with LV outflow tract (LVOT); J. Binary image masked by ROI; K. Blood pool including LV; L. Watershed results, Watershed results, with detected LV blood pool (red), LVOT (yellow), right ventricle outflow tract (orange). Other colored objects indicate regions from right ventricle and atrium

Figure 2.

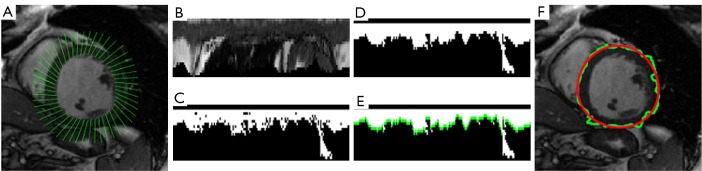
LV segmentation of epicardial contour. A. Scan lines (green) for mapping the pixels from Cartesian to polar coordinates; B. Result of image transform; C. Region growing binary image; D. Image after filling holes; E. Edge points (green); F. Epicardial contour before (green) and after fast Fourier transform smoothing (red)

Evaluation and statistical analysis

In order to quantitatively evaluate the automatically detected endocardial and epicardial contours of the ED and ES phases of all slices, four quantitative measures were assessed (17). Average perpendicular distance (APD) is the distance from the automatic contour to the corresponding manually drawn expert contour, averaged over all contour points. Dice metric (DM) (21) is a measure of contour overlap utilizing the area of automatically (A) and manually segmented (M) contours, and their intersection area (I) with formula DM = I/[0.5× (A+M)]. In addition, the percentage of patients where the blood pool is correctly localized and distinguished from other features was calculated (LV located).

Paired sample, two-tailed Student’s t-test statistics (α=0.05) were computed to determine if the functional values calculated were significantly different when using automatic contours instead of manual contours. The end systolic volume (ESV), end diastolic volume (EDV), EF and left ventricular mass (LVM) were evaluated. The manually and automatically determined ESV, EDV, EF and LVM were also compared by means of linear regression to determine the correlations. Bland-Altman plots were calculated to assess the bias and limits of agreement between manual and automatic contours.

To investigate the impact of methodological difference on clinical care, EF used for patient classification in this study (HFNI: EF <40%, HFI: EF <40%, HYP: EF >55%, HEA: EF >55%) were applied to the corresponding patient group to evaluate whether clinical classification would differ based on manual and automated results. The categorical variable of agreement between the manual and automated results was assessed with Cohen’s Kappa statistics.

The computation time was tested on consumer hardware (2×2.8 GHz Quad-core Intel Xeon Mac Pro, Apple) with a non-optimized Matlab code (Mathworks) implementation.

To provide a direct basis of comparison for our results, the APD, DM and EF were calculated with commercial, automatic segmentation software [QMass® MR 7.5, Medis Medical Imaging Systems (22), Leiden] using our GE data. We adopted a threshold of APD >10 mm to eliminate clearly erroneous contours detected by QMass. For these cases, the automatic contour was replaced by the corresponding manual contour to simulate the expected usage of the automatic contours and subsequent calculation of APD, DM and EF.

Results

The contour evaluation results averaged across all subjects, for all slices at the ED and ES phases of each group, are shown in Table 1. Representative segmentation contours for one dataset are shown in Figure 3. For three of the 133 datasets, the segmentation algorithm failed to locate the LV automatically, thus manual corrections were applied. The HYP group had the largest APD for both endo- and epicardial contours, and the smallest DM for the endocardial contours. The APD was small indicating good agreement between individual contours. The APD for GE data was 2.08 and 1.92 mm (1.7 and 1.6 pixels) for endo- and epi-cardial contours, and the APD for Philips data was 1.9 and 2.14 mm (1.5 and 1.8 pixels), respectively.

Table 1. Evaluation of contours calculated with the proposed method.

Scanner vendor	Patient group	LV located (%)	APD (mm)			DM
			endo	epi		endo	epi
GE	HFI	100 (34/34)	1.86	1.90		0.92	0.94
	HFNI	96.7 (29/30)	1.89	1.88		0.92	0.94
	HYP	93.8 (30/32)	2.67	2.08		0.85	0.93
	HEA	100 (37/37)	1.89	1.81		0.89	0.93
	Mean	97.7 (130/133)	2.08	1.92		0.90	0.94
Philips		100 (6/6)	1.90	2.14		0.91	0.93

APD, Average perpendicular difference; DM, Dice metric; endo, endocardial contour; epi, epicardial contour; LV, left ventricle. Patients were grouped according to pathology: HEA, healthy; HFI, heart failure with ischemia; HFNI, heart failure with no ischemia; HYP, hypertrophy

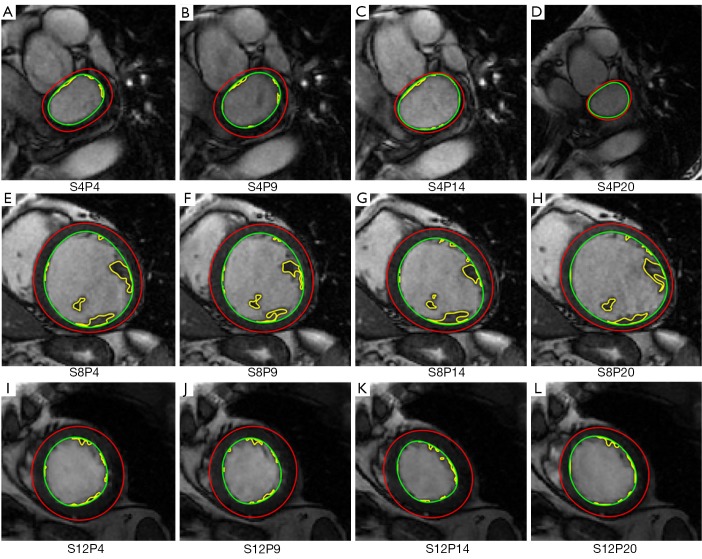
Figure 3.

Representative segmentation results. SxPy indicates the image for slice x and cardiac phase y. The contours of the endocardium (green), papillary muscles and trabeculations (yellow), and epicardium (red) are shown.

The paired sample t-test and linear regression results for ESV, EDV, EF and LVM between manual and the automatic methods are shown in Table 2. There were no significant differences found between automatically and manually determined ESV, EDV, EF and LVM. The automatically determined ESV and EDV for individual patient groups showed excellent correlations (R≥0.89) with those derived from manual contours. The EF and LVM of the automatically and manually analyzed studies correlated very well generally, with lower correlations evident for the HYP and HEA groups. Grouping together all subjects and pathological categories, the coefficient of determination (R²) between the manual and automatic methods was high for all functional parameters (ESV: 0.98, EDV: 0.98, EF: 0.90, and LVM: 0.88).

Table 2. Evaluation of functional parameters.

Patient group	ESV (mL)				EDV (mL)				EF (%)				LVM (g)
	Difference	P	R2		Difference	P	R2		Difference	P	R2		Difference	P	R2
HFI	2.72±13.77	0.26	0.98		1.47±17.11	0.62	0.96		–0.43±4.36	0.57	0.77		5.34±16.56	0.07	0.78
HFNI	3.19±12.51	0.17	0.97		2.47±13.18	0.31	0.97		–0.51±4.33	0.53	0.90		2.20±15.32	0.44	0.90
HYP	–0.41±12.59	0.86	0.80		1.73±13.87	0.49	0.91		1.01±9.45	0.55	0.51		–3.22±11.80	0.13	0.95
HEA	0.71±4.99	0.39	0.94		1.21±4.75	0.13	0.98		–0.15±4.28	0.84	0.73		–1.51±13.89	0.51	0.71
Overall	1.51±11.30	0.13	0.98		1.69±12.76	0.13	0.98		–0.02±5.93	0.97	0.90		0.66±14.72	0.60	0.88

Difference: mean ± standard deviation of paired difference (manual measurement minus automated measurement). Probabilities (P) were obtained by paired sample t-test. For linear regression the automatically obtained values (y) were plotted as a function of the manual values (x) to calculate the fits and coefficients of determination (R²). EDV, end diastolic volume; EF, ejection fraction; ESV, end systolic volume; LVM, left ventricular mass; HEA, healthy; HFI, heart failure with ischemia; HFNI, heart failure with no ischemia; HYP, hypertrophy

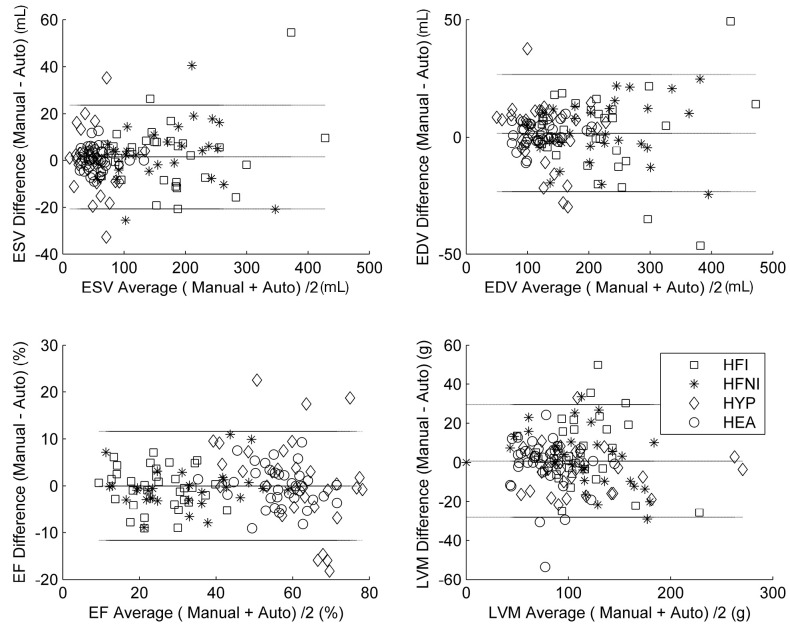
The Bland-Altman analysis (Figure 4) confirmed the good agreement between the automatic and manual contours with negligible biases (1.51 mL, 1.69 mL, –0.02%, –0.66 g for ESV, EDV, EF and LVM, respectively). The limits of agreement (±1.96 SD) were as follows: ±22.1 mL (ESV), ±11.6% (EF), ±25.0 mL (EDV), and ±28.8 g (LVM).

Figure 4.

Bland-Altman plots for functional parameters. The horizontal lines show the mean ±1.96 SD of the paired sample differences. Symbol shapes indicate the groups: heart failure with ischemia (square), heart failure with no ischemia (star), hypertrophy (diamond), and healthy (circle). ESV, end systolic volume; EDV, end diastolic volume; EF, ejection fraction; LVM, left ventricular mass

The patient classification agreement between automated and manual contours were good (HFNI: Kappa statistic 0.84, P-value <0.001, HFNI: Kappa statistic 1, P-value 0, HYP: Kappa statistic 0.57, P-value 0.004, HEA: Kappa statistic 0.51, P-value 0.002). The agreement is highly significant.

The average computation time of LV location was 0.096 s per subject. The average computation time for segmentation was 0.8 s per image. Moreover, the algorithm segmented the basal slice with LVOT by a fast watershed technique (0.027 s per image). Manual analysis for EF calculation (ES and ED phases) required 10-15 min per subject.

The QMass contour evaluation results were calculated for comparison and shown in Table 3. All contours were detected. The average APD for endocardial and epicardial contours was higher (3.30, 3.99 mm) than for the proposed algorithm. The EF difference (QMass EF- manual EF) shows that QMass overestimated the EF (except for the hypertrophy patient group), although this was statistically insignificant for all groups.

Table 3. Evaluation of contours calculated with QMass.

Patient group	APD (mm)			DM			EF
	endo	epi		endo	epi		Difference	P
HFI	2.83	3.73		0.87	0.89		4.00±3.83	0.08
HFNI	3.15	5.18		0.86	0.85		1.73±6.09	0.62
HYP	4.09	4.24		0.76	0.86		–3.21±13.08	0.23
HEA	3.40	3.16		0.80	0.89		0.28±8.94	0.89
Overall	3.30	3.99		0.83	0.88		0.75±8.93	0.74

APD, Average perpendicular difference; DM, Dice metric; EF, ejection fraction; endo, endocardial contour; epi, epicardial contour; HEA, healthy; HFI, heart failure with ischemia; HFNI, heart failure with no ischemia; HYP, hypertrophy

Discussion

This study demonstrates that the proposed image driven segmentation algorithm rapidly and accurately quantifies clinically relevant parameters with minimal user input. This method is based on the assumptions that (I) the heart is approximately in the centre of the original image, and (II) the left ventricular blood pool is approximately circular. These assumptions are routinely satisfied in cine SSFP MR imaging, and therefore the method should be suitable for datasets with a wide range of anatomy, function, and image contrast as required for clinical use.

Novel aspects of this algorithm include that it obviates initialization by manually drawn contours, prior statistical shape model, or gray-level appearance model. In addition, the algorithm locates the LV automatically by utilizing a roundness metric that is fast (0.096 s per subject) and robust (97.7% located), which compares favorably to another automatic LV location technique (23).

The algorithm detects not only endocardial contours and epicardial contours, but also the papillary muscles’ and trabeculations’ contours. Clinical studies have employed different quantification methods for calculation of LV volume, mass, and EF by including or excluding papillary muscles and trabeculations’ in the ventricular cavity. Recent studies have shown that the papillary muscles and trabeculations’ have a significant impact on calculation of LV volume, mass (24) and EF (25). Therefore the proposed method provides additional important options for daily clinical application.

A difficult challenge of LV segmentation is the accurate delineation of the epicardial contours. The typical problem is the ballooning of epicardial contours at the junction between myocardium and lung parenchyma and subdiaphragmatic tissues, due to the small intensity differences between these tissues. Following transformation from Cartesian to polar coordinates, the multiple-seed region-growing method was found to provide a robust solution that accounted for intensity gradients at edges that differed around the myocardium

Accurate assessment of quantitative LV parameters is essential for all imaging techniques. For instance, current guidelines for the implantation of cardioverter defibrillators use a selection criterion based upon EF, mandating that an accurate quantitative method be used to determine EF (26). Furthermore, reducing the quantity of patients required for clinical research studies depends upon increasing the interstudy reproducibility. CMR currently has the best interstudy reproducibility of any imaging technique for both mass and volume in the left and right ventricles, and is considered superior to that of two dimensional echocardiography (1). Interstudy reproducibility, determined from the standard deviation of the differences in two measurements of a parameter over a reasonable time period wherein no clinical change is expected, is currently influenced by inter- and intra-observer variability (27,28). Automatic segmentation algorithms will further reduce interstudy variability, therefore reducing patient numbers required. This advantage together with the time efficiency for quantitation by study readers will reduce the costs of clinical trials while improving data quality (2).

Among the four groups, the results of the hypertrophy group were least successful for both the endocardial and epicardial contours because the concomitant hypertrophy of the papillary muscles obscured the target contours. Table 2 shows that there were good correlations for all of the four groups between automatically and manually determined clinical parameters, as expected from the small APD and large DM. These results compare favorably to recent literature describing automatic or semi-automatic segmentation methods (Table 4). Although dataset specifics are not uniform and thus hinder direct comparison, this meta-analysis provides additional confidence in our method.

Table 4. Literature values of left ventricle contour errors.

Method	Distance (mm)*		Number of subjects
	endo	epi
Lorenzo-Valdes 2004 (3)	2.21	2.99	12
Kaus 2004 (6)	2.28 (ES), 2.76 (ED)	2.62 (ES), 2.92 (ED)	169
Lötjönen 2004 (29)	2.01	2.77	25
Van Assen 2005 (30)	2.24	2.83	14
Uzümcü 2006 (31)	1.86	1.77	20
Fradkin 2008 (32)	1.27	1.56	35
van Assen 2008 (33)	1.34	1.27	15
Jolly 2009 (34)	2.48	2.91	19
Peter 2009 (35)	0.69	0.83	42†
Grosgeorge 2010 (36)	3.24 (ES), 2.92 (ED)	N/A	59
Sun 2010 (37)	0.87	N/A	40

*, Different distance measures were utilized, with similarity to APD; ^†, Image volumes. Subject number unknown. ED, end diastolic; ES, end systolic; endo, endocardial contour; epi, epicardial contour

The mean difference shown in Table 2 compares well to interobserver variation of manually drawn contours in previous reports (17,38). The Bland-Altman plots demonstrate negligible biases for ESV, EDV, EF and LVM, and the limits of agreements were reasonable considering the image quality heterogeneity of the datasets. While the proposed method is fully automatic, setting and adjusting the parameters interactively by checking the contours visually could further improve results.

In conclusion, the proposed fully automated segmentation technique is fast, robust and effective for the quantification of cine cardiac MR in clinical practice.

Supplementary Material

LV location

This section presents a method based on a roundness metric to automatically locate the LV blood pool’s centroid on the middle slice at the specified phase. This procedure consists of five steps (refer to Figure 1A-D):

1. Choose the middle (normally in the mid-cavity level) slice image in a given phase (e.g., ED) as the target image;

2. Specify a centered, fixed rectangular region of interest (ROI) on the target image. The size of the rectangular is 110×110 pixels (Figure 1A);

3. Apply the optimal threshold method of Otsu (19) to convert the ROI to a binary image (Figure 1C);

4. Remove all objects smaller than a predefined threshold (40 pixels) and compute the convex hull of the surviving objects;

5. Compute the roundness metric of each surviving convex-hulled object, where A is area and P is perimeter length. R =1 for a circle. The object with the largest roundness metric is recognized as the LV blood pool (Figure 1D), and a 11×11 mask is defined centered on the centroid of the LV blood pool for the subsequent segmentation.

LV endocardial contour detection

The endocardial contour is detected by the following steps (refer to Figure 1E-L):

1. Specify a ROI dilated from the previously identified LV blood pool;

2. Apply the optimal threshold method of Otsu to convert the ROI to a binary image (Figure 1F);

3. The LV blood pool object is identified by choosing the object that has maximum overlap with the predefined mask centered on the LV blood pool centroid (Figure 1G);

4. Compute the convex hull of the refined blood pool (Figure 1H);

5. Smooth the convex hull’s contour by applying the 1D fast Fourier transform (FFT) (20). We first compute the FFT of the x coordinate of the contour point index, multiply the result by a low pass filter transfer function (retaining the four lowest frequency components), then take the inverse transform to produce the smoothed x coordinate. Repeat for y coordinates (Figure 1H);

6. Identify and segment basal slice with LVOT. If the ratio of current contour’s major axis length (L) to preceding contour’s L is larger than a prede□ned threshold (1.2, in this work), basal slice with LVOT is identi□ed. Then, the blood pool is separated from the LVOT by the following steps: Calculate the Euclidean distance transform of the binary object, i.e., compute the distance between each object pixel and its nearest background pixel. Then calculate the watershed regions of the distance image (Figure 1I-L). Then compute the smoothed contour (as in step V).

Detection of contour delineating LV papillary muscles and trabeculations

Black pixels in the smoothed LV blood pool (Figure 1H) are detected as papillary muscles and trabeculations.

Epicardial contour detection

The epicardial contour is calculated by the following steps (refer to Figure 2A-F):

1. Map the pixels from Cartesian to approximately polar coordinates, as suggested previously (18). An outer boundary is calculated by dilation of the endocardial contour. The two contours are interpolated to the same number of points, and paired to derive scan lines, each of a predefined length (20 pixels) (Figure 2A). The result is a rectangular image that extends from the endocardial contour (top row) outward (bottom row) (Figure 2B);

2. Use each top-row pixel as a region growing seed, with all grown regions summed and converted to a binary image (Figure 2C). For region growing, intensities are normalized by the original image’s maximum;

3. Fill image holes by morphological operations (Figure 2D);

4. The end point of each column’s grown region determines an edge point (Figure 2E);

5. Inverse transform the edge point coordinates to the original (Cartesian) coordinate space to determine the epicardial contour (Figure 2F);

6. Smooth the contour by applying the 1D fast Fourier transform (Figure 2F).