A Mechanistic Model for Amorphous Protein Aggregation of Immunoglobulin-like Domains

Abstract

Protein aggregation is associated with many debilitating diseases including Alzheimer’s, Parkinson’s, and light-chain amyloidosis (AL). Additionally, such aggregation is a major problem in an industrial setting where antibody therapeutics often require high local concentrations of protein domains to be stable for substantial periods of time. However, despite a plethora of research in this field, dating back over 50 years, there is still no consensus on the mechanistic basis for protein aggregation. Here we use experimental data to derive a mechanistic model that well describes the aggregation of Titin I27, an immunoglobulin-like domain. Importantly, we find that models that are suitable for nucleated fibril formation do not fit our aggregation data. Instead, we show that aggregation proceeds via the addition of activated dimers, and that the rate of aggregation is dependent on the surface area of the aggregate. Moreover, we suggest that the “lag time” seen in these studies is not the time needed for a nucleation event to occur, but rather it is the time taken for the concentration of activated dimers to cross a particular solubility limit. These findings are reminiscent of the Finke–Watzky aggregation mechanism, originally based on nanocluster formation and suggest that amorphous aggregation processes may require mechanistic schemes that are substantially different from those of linear fibril formation.

Introduction

Protein aggregation is at the root of a number of costly, debilitating diseases.^1,2 It is also a major concern during purification, formulation, and manufacture of therapeutic protein products where high protein concentrations are required to be stable for substantial periods of time (see ref (3) and references therein). Although the first kinetic studies of protein aggregation occurred over 50 years ago, there is still no consensus as to the underlying mechanisms that control these aggregation processes. Indeed, a recent review of the literature suggests that there are at least five fundamentally different classes of proposed mechanism, each comprising several variants.⁴ Most of these mechanisms are based on fiber formation (natural or amyloid) and thus focus on the addition of monomers to the ends of a growing linear polymer.⁵⁻⁹ However, it is becoming increasingly apparent that it may be the prefibrillar, often amorphous, aggregates that are the most toxic species in vivo.¹⁰⁻¹³ Any rational intervention in the accumulation of these amorphous species will require a detailed understanding of their pathways of formation (and degradation), which are likely to be fundamentally different to the mechanisms of fibril growth.¹⁴ Recently, Stranks et al. considered amorphous aggregate growth in three dimensions, limited by aggregate surface area.¹⁵ This is similar to an approach by Finke and Watzky, who considered a two-step mechanism of slow continuous nucleation followed by typically fast, autocatalytic surface growth.¹⁶ Both methods were very successful at fitting the data; however, in each case the results were largely empirical and gave no mechanistic insight into the underlying physical processes.

In this paper, we use experimental data to derive a mechanistic model, from first principles, that well describes the aggregation kinetics of the 27th immunoglobulin-like domain from human cardiac titin (I27); i.e., we identify the kinetically relevant species and reactions necessary to describe this aggregating system. The importance of such an analysis is that it enables us, for the first time, to present a model for amorphous aggregation comprising a number of components, each of which may be explicitly challenged by mutation, solvent conditions, or chemical additives. We show that aggregation proceeds via the addition of activated dimers, and that the rate of aggregation is dependent on the surface area of the aggregate, as seen previously for nanocluster formation.¹⁷ Moreover, we suggest that the “lag time” seen in these studies is not the time needed for a nucleation event to occur, but rather it is the time taken for the concentration of activated dimers to cross a particular solubility limit.

Surprisingly, our studies also brought to light some concerns about standard methods for collection and presentation of aggregation data. We show that, with correct experimental procedures, turbidity measurements can be an accurate measure of the concentration of aggregate present. In the literature, however, raw aggregation data are often normalized to an extrapolated end-point, which we show could be entirely misleading and can mask the fact that the aggregation process is reversible and operates over a very broad range of time scales.

Results

We chose to study the aggregation of the 27th immunoglobulin-like domain from human cardiac titin, which rapidly forms aggregates in 28% trifluoroethanol (TFE).¹⁸ These aggregates show extensive beta-sheet formation, as determined by far-ultraviolet circular dichroism spectroscopy (Figure S6, Supporting Information), and produce an X-ray diffraction pattern that is consistent with a cross-beta structure. They also bind Thioflavin T and show red/green birefringence upon staining with Congo Red.¹⁸ The TFE-induced aggregates thus show “characteristics of amyloid fibrils and their precursors”, as mentioned previously.¹⁸ However, the samples lack the long straight character of mature amyloid fibres, as judged by TEM experiments (Figure S1, Supporting Information), and are more similar in morphology to the previously described p53 “amorphous” aggregates observed by Fersht and co-workers.¹⁹ As we show later, the kinetics of aggregate formation also indicate a mechanism controlled by surface area, and are inconsistent with a linear polymerization model. The I27 aggregates remain amorphous over long time scales and exhibit no evidence of rearrangement to mature fibrils, even after four months, (CF Wright, PhD Thesis, University of Cambridge, 2004), which contrasts with observations of other amorphous protein aggregates such as protein L and prion protein H1.^12,20 In keeping with previous experiments, we use turbidity at 400 nm as a measure of the degree of protein aggregation because this is compatible with the fast mixing times and rapid data collection of standard stopped-flow instruments. Although several papers have questioned the accuracy of such data,²¹⁻²³ turbidity measurements have proven to be reproducible, have given much insight into many aggregation processes,^15,24−26 and usually coincide with data from intrinsic tryptophan fluorescence, thioflavin T binding, and light scattering.²⁷ Moreover, kinetic studies on the Sup35 prion protein have shown that simple spectroscopic techniques, such as light scattering and circular dichroism, (CD), give aggregation rates that are in excellent agreement with end-point analyses such as sedimentation and dye binding.²⁸ Nevertheless, we recognize that turbidity is not linear with aggregate concentration (Figure S2, Supporting Information) and thus, rather than using the scaling method of Flyvbjerg et al.,²⁵ we produced detailed calibration curves to directly relate the turbidity measurements to the quantity of aggregate in the sample.

I27 protein was produced as described elsewhere¹⁸ and, after purification, was used to calibrate the stopped-flow machine, as described in Materials and Methods. As expected, there was significant nonlinearity between turbidity measurements and aggregate concentration (Figure 1). We considered the fact that this nonlinearity may be due to changes in aggregate size and/or morphology as a function of initial protein concentration. To address this point, we aggregated three different protein stocks at 1, 4, and 8 mg mL^–1. Each stock was then quickly concentrated and diluted to create a range of protein solutions from 0.1 to 8 mg mL^–1. All three stock solutions showed identical calibration curves (Figure S3, Supporting Information, performed on a plate reader for speed), indicating that there is no discernible difference in aggregate size and/or morphology between the samples. We thus attribute the nonlinearity in both machines (stopped-flow and plate reader) to the instrumental setup and not to the aggregation conditions.

Figure 1.

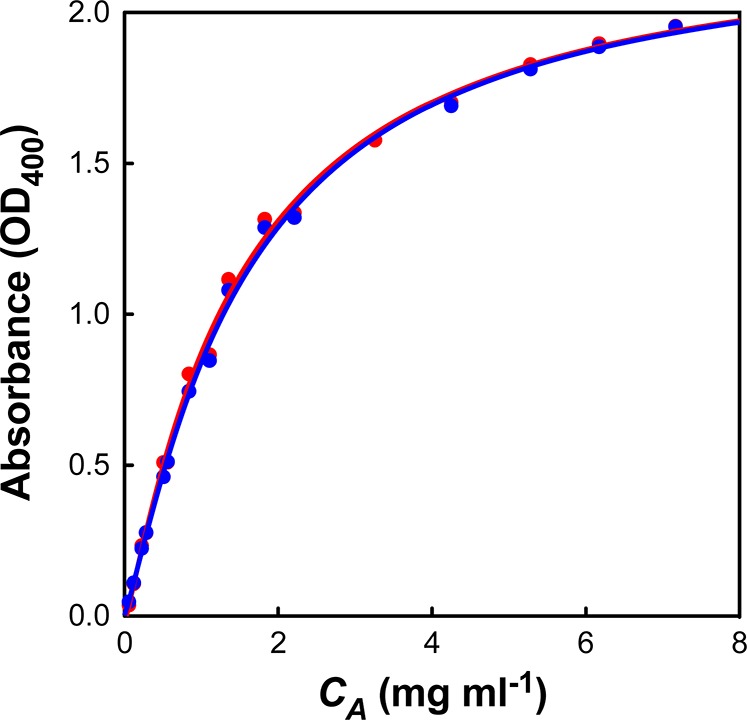
Calibration curve of turbidity (OD₄₀₀) versus aggregate concentration (C_A) derived from the stopped-flow instrument. Red and blue points represent two separate data sets. The curves were fit with the equation C_A = a × OD₄₀₀ + b × (OD₄₀₀)^c giving the parameters a = 1.047, b = 0.126, and c = 5.523. This equation was then used to convert all subsequent turbidity measurements into aggregate concentrations.

We repeated the measurements described by Wright et al.¹⁸ under the same solution conditions but using a stopped-flow instrument rather than a plate reader to allow for an accurate determination of the lag times. I27 aggregation was followed at nine different concentrations, ranging from 0.48 mg mL^–1 to 7.59 mg mL^–1 (Figure 2). As expected, there is a linear correlation between the initial protein concentration and the final concentration of aggregate (data not shown). We then examined the aggregation traces for any mechanistic insights and discovered three interesting features:

Figure 2.

Aggregation kinetics of I27 in 28% TFE. The aggregate concentration (C_A) was measured over time for nine initial concentrations (C₀) of I27: 0.48 mg mL^–1 (purple), 0.68 mg mL^–1 (magenta), 0.94 mg mL^–1 (blue), 1.34 mg mL^–1 (cyan), 1.89 mg mL^–1 (green), 2.69 mg mL^–1 (yellow), 3.66 mg mL^–1 (beige), 5.25 mg mL^–1 (orange), 7.59 mg mL^–1 (red). Raw absorbance data were converted to C_A using the calibration curve as described in Figure 1.

1. At Short Time Scales, the Concentration of Aggregate (C_A) Scales with Time Cubed

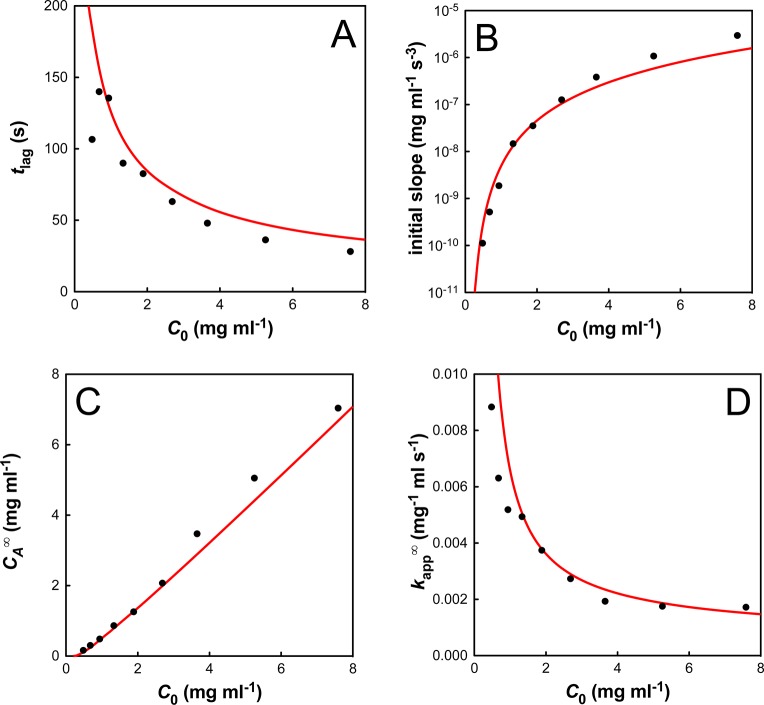
In contrast to previous findings, which suggest that aggregate concentration should scale with time squared,^5,8,20 we find that C_A ∝ t³ at short time scales (Figure 3A). A linear fit to these data gives two parameters: the initial slope (gradient) and the lag time (t_lag, x-intercept). The initial slope is strongly dependent on the initial protein concentration (C₀), but the lag time varies significantly less (Figure S4, Supporting Information). This behavior is reminiscent of a batch crystallization regime, where the initial rate of growth scales with the surface area (SA) of the solid (dC_A/dt ∝ SA ∝ C_A^2/3).

Figure 3.

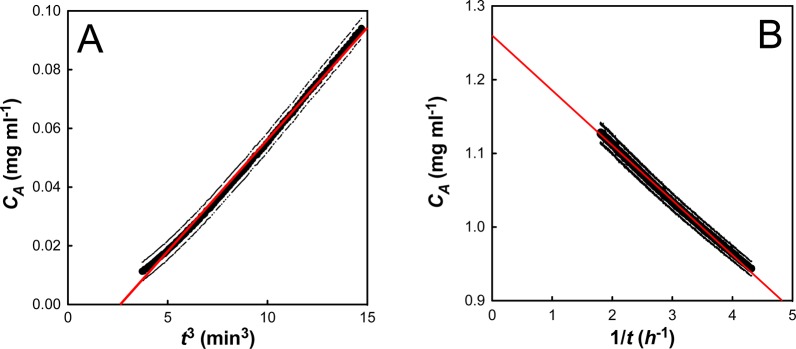
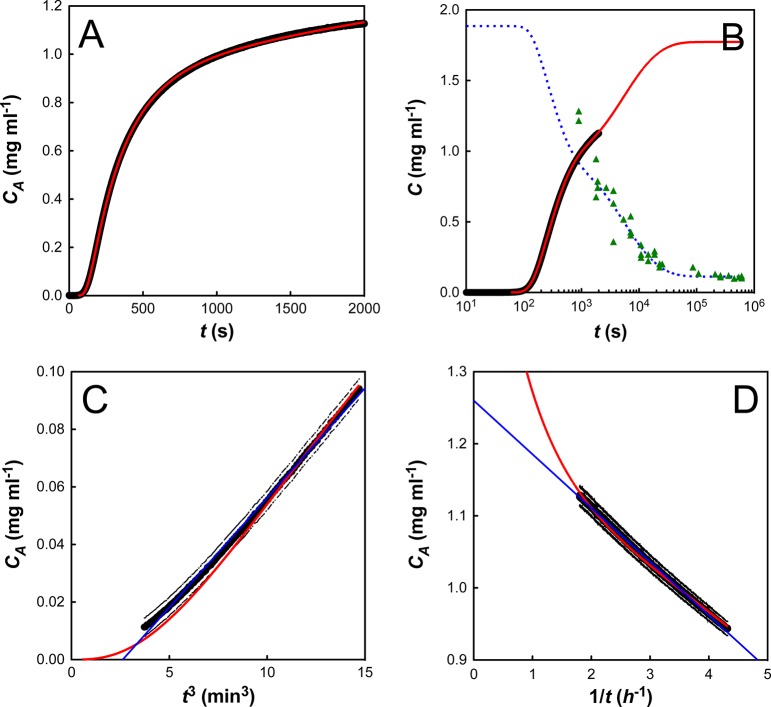
I27 aggregation at an initial protein concentration (C₀) of 1.89 mg mL^–1. (A) A plot of aggregate concentration (C_A) against t³ demonstrates a linear relationship at short time scales (less than 10% aggregate). The linear fit determines the initial slope and the lag time, t_lag. (B) A plot of aggregate concentration (C_A) against 1/t demonstrates a linear relationship at long time scales (greater than 50% aggregate). The linear fit determines the apparent second-order rate constant (k_app^∞) and the apparent equilibrium concentration of aggregate (C_A^∞). The error bars denote the errors on both the initial turbidity measurement and the conversion of the raw data to C_A.

2. At Long Time Scales, the Rate of Aggregation Is Hyperbolic

Once the aggregation data has been appropriately scaled, it is clear that the long-time stopped flow data do not follow single exponential kinetics. Indeed, a plot of aggregate concentration (C_A) against 1/t gives a straight line, suggesting hyperbolic behavior (Figure 3B). Mechanistically, this hyperbolic behavior suggests a second-order process, such as dimerization, as being rate limiting. A linear fit to these data gives two parameters: the apparent second-order rate constant (k_app^∞, gradient) and the apparent equilibrium concentration of aggregate (C_A^∞, y-intercept). It is interesting (and initially puzzling) to note that this apparent second-order rate constant (k_app^∞) varies with initial protein concentration (Figure S5, Supporting Information).

3. The Apparent Equilibrium Concentration of Aggregate, C_A^∞, Is Consistently Lower Than C₀

It is well-known that many aggregation reactions are reversible, and that a constant amount of soluble protein often remains after aggregation has gone to completion.²⁹⁻³¹ However, for all I27 aggregation traces, the extrapolated end-point from the stopped flow data (C_A^∞) indicates the presence of substantially more soluble protein than is expected from long-term equilibrium measurements. To address this discrepancy, we followed the aggregation of a 2.0 mg mL^–1 solution of I27 over a one-week period. Because very long time scale turbidity measurements are hampered by the settling of aggregate, the measurements quantified the concentration of soluble protein remaining, rather than the concentration of aggregated protein. These experiments revealed that the I27 aggregation took days to reach equilibrium, but that a constant concentration of protein remained soluble at the end of the experiment (Figure 4). Interestingly, this decay also showed hyperbolic behavior, indicating that a second-order process may be rate limiting in the very long time scale regime. This “double decay” in soluble protein has been seen previously,^12,20,32 and in each case it was shown to be due to the presence of an off-pathway species that slowly converted back to on-pathway aggregates.

Figure 4.

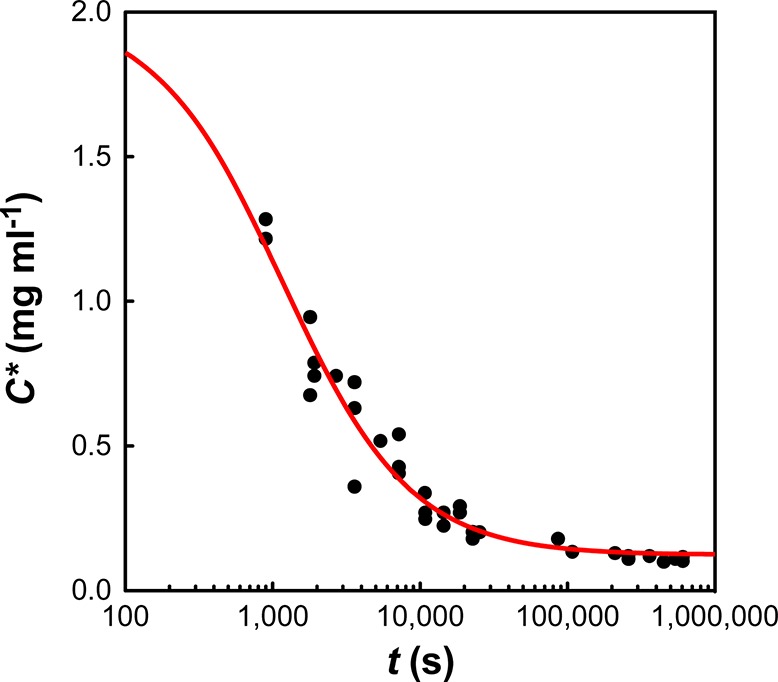
The concentration of soluble protein (C) remaining over an extended aggregation time course (1 week) for C₀ = 2 mg mL^–1. The red line shows a hyperbolic fit to the data with an apparent rate constant of 4.8 × 10^–4 mg^–1 mL s^–1.

On the basis of these observations, we devised the reaction scheme as described in Figure 5. The important features of this model are that (i) aggregates do not form until the concentration of activated dimer reaches a saturation concentration, (ii) aggregates grow by incorporation of dimer (not monomer) at a rate proportional to the aggregate surface area, (iii) the protein aggregate behaves as a soluble solid so that at very long times a constant concentration of soluble protein is found, and (iv) there are two non-native monomeric species, only one of which is aggregation competent. The rate laws resulting from this model are described in Table S1, Supporting Information. We note that our model requires a simple lumping approximation to relate aggregate mass and surface area, which states that the number of aggregates does not change significantly with time: the consequence of this assumption is discussed below. It is also important to note that this scheme contains no explicit nucleation event. The lag time is simply a consequence of the time required for the protein to unfold and form sufficient activated dimer to reach its solubility level.

Figure 5.

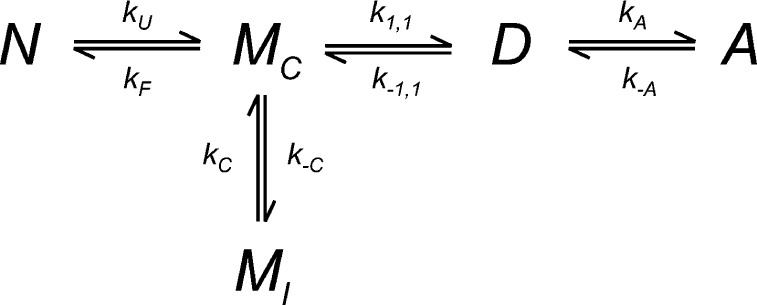
The proposed reaction mechanism for amorphous aggregation of I27 in 28% TFE. N is the natively folded protein, M_C is the aggregation-competent unfolded monomer, and M_I is an unfolded state, which is not aggregation-competent (incompetent). D is a dimer, formed from two units of M_C, and A is aggregate. k_U and k_F are the rate constants for unfolding and folding of N; k_1,1 and k_–1,1 are the forward and reverse rate constants for dimerization of M_C to D; k_A and k_–A are the forward and reverse rate constants for aggregation (of D); and k_C and k_–C are the forward and reverse rate constants for the conversion of M_I to M_C.

To fit the data, the protein folding rate constant in 28% TFE (k_F) was set as zero, and the remaining seven rate constants were reconfigured to give the following variables: k_U, the protein unfolding rate constant in 28% TFE; k_1,1, the dimerization rate constant; K_1,1, the equilibrium constant for dimerization; k_–C, the conversion rate constant for M_I to M_C; k_C, the conversion rate constant for M_C to M_I; k_A,L, the “lumped” aggregation rate constant, and C_S, the saturation concentration of dimer (for further details, see Table S2, Supporting Information).

The rate constant for I27 unfolding in 28% TFE was measured using circular dichroism (Figure S6, Supporting Information) and was found to be in excellent agreement with that found from tryptophan florescence (data not shown). In addition, the very long time scale solubility results were used to fix the final concentration of soluble protein (C* = M_I + M_C+ D) at 0.113 mg mL^–1. This left five independent variables, which were fit to the experimental data using a chi-square minimization approach with a purpose-built Mathematica package, ODEFit. Chi-square was estimated from the residual square error and the observed uncertainty in the measured data. ODEFit adjusts the parameters to be estimated using a Levenberg–Marquardt approach until the chi-square is at a minimum.^33,34 The uncertainty in the parameters was estimated from the computed covariance matrix using the method described by Press et al.³⁵ This method of analysis is very similar to the dynamic simulation approach used by programs such as Global Kinetic Explorer.³⁶

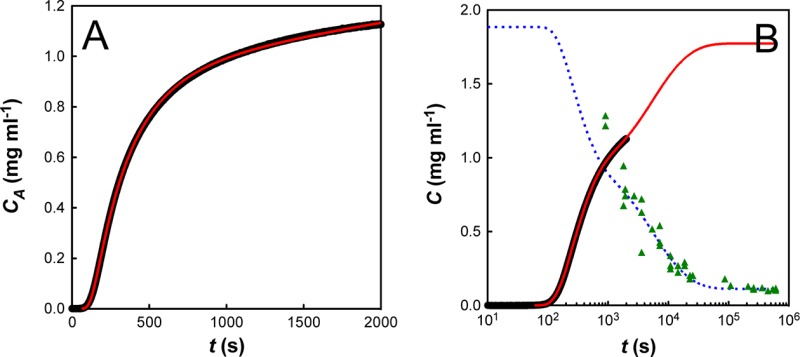
We started with a fit of the C₀ = 1.89 mg mL^–1 data set, because it closely matched our 2 mg mL^–1 long-time solubility data. We note that our model describes the experimental data very well (Figure 6A): it captures the initial linear dependence of aggregate concentration with t³ (Figure 6C), the later second-order behavior (Figure 6D), and the very slow final approach to equilibrium (Figure 6B). The kinetic parameters for this fit are summarized in Table 1. We next used these kinetic parameters to simulate I27 aggregation at all other initial protein concentrations. The emergent behavior from the simulated fits was compared to that from the experimental data and was found to be in excellent agreement (Figure 7).

Figure 6.

Fit of the model for C₀ = 1.89 mg mL^–1. The concentration of aggregate (C_A) is plotted in black (for clarity error bars are not plotted for every point), with model fits displayed in red. (A) Fit of stopped-flow data. (B) Concurrent fit of the stopped-flow data and the long time scale solubility results (data: green triangles; fit: blue dashed line). (C) Plot of C_A vs t³. (D) Plot of C_A vs 1/t. In C and D, thin blue lines are linear fits to the data (as described in the text).

Table 1. Kinetic Parameters from a Fit of the Model to Data Where C₀ = 1.89 mg/mL.

parameter	value	source
kU (s–1)	4.0 ± 0.4 × 10–3	a
k–C (s–1)	3.83 ± 0.04 × 10–3	b
kC (s–1)	6 ± 4 × 10–4	c
k1,1 (mg–1 mL s–1)	1.73 ± 0.04 × 10–2	b
kA,L (mg–2/3 mL2/3 s–1)	0.82 ± 0.05 × 10–2	b
CS (mg mL–1)	2.7 ± 0.2 × 10–5	b
C* (mg mL–1)	0.113 ± 0.001	c
K1,1 (mg mL–1)	0.115	d
k–1,1 (s–1)	0.150	d

^aObtained from fits of fluorescence unfolding.

^bObtained from a fit to the stopped-flow data where C₀ = 1.89 mg mL^–1 (Figure 6B).

^cObtained from a fit to the solubility data where C₀ = 2.0 mg mL^–1 (Figure 4).

^dDerived from the other kinetic parameters using eq 1: K_1,1 = [C_S(k_–C² + 2k_–Ck_C + k_C)]/[(C_S – C*)²k_C²].

Figure 7.

Initial concentration (C₀) dependence of the four emergent characteristics of the aggregation data: (A) the lag time, t_lag; (B) the initial slope; (C) the apparent equilibrium aggregate concentration, C_A^∞; (D) the apparent second-order rate constant, k_app^∞. The simulations (red lines) are in excellent agreement with the experimental data (black circles).

Although this model produced an excellent fit to all data sets, it was not possible to obtain a single set of kinetic parameters that described all protein concentrations; however, each parameter was of a constant order of magnitude (Table S3, Supporting Information). The probable reason for this discrepancy is the use of the simple “lumping” assumption, which states that the number of aggregates does not change significantly with time and is independent of the initial protein concentration. The lumped aggregation rate constant, k_A,L, is therefore not a true molecular rate constant because it depends on the concentration of nuclei, which may change with both initial protein concentration and with time. To avoid this lumping assumption, it would be necessary to model kinetics and rate laws for the growth of each oligomer as a series of polymerization reactions. This necessitates the inclusion of literally thousands of extraordinary differential equations (ODEs) which, in the absence of information on the molecular weight distribution of the aggregates, resulted in untestable complexity. Nevertheless, it is important to stress that our model is able to accurately predict the trends in the aggregation profiles (Figure 7), even if the absolute numbers show a slight discrepancy.

To check whether our model was the best solution for I27 aggregation, we also tested two alternate reaction schemes. First, several papers on the aggregation of immunoglobulin-like domains have suggested that the off-pathway species may be dimeric³⁷ or octameric.³⁸ We thus modified the model (Figure 5) so that the nucleation incompetent species (M_I) was dimeric. In this case, the model was discounted because the resulting kinetic parameters varied by several orders of magnitude between each experimental data set, although the errors of the fit were comparable (data not shown). Second, we also tested a linear polymerization model as described by Powers and Powers,⁸ because this represents one of the most commonly proposed schemes for fibrillar protein aggregation.⁴ In this case, the fits were comparable to our surface-area controlled model, with fairly robust kinetic parameters between data sets. Thus, to distinguish between these two models, we used speciation data provided by earlier TEM experiments.¹⁸ A standard aggregation experiment at 2 mg mL^–1 produced aggregates with a typical raidus of about 1 μM. Assuming spherical aggregates (as with our proposed model), this predicts around 290 million aggregates per milliliter of solution. If this number does not vary during the course of the experiment (a valid assumption, because aggregation is much faster than nucleation), then the aggregates would be approximately 150 nm radium (300 nm diameter) at the end of the observable lag phase. This number is determined from the calculated amount of aggregate at 90 s (Figure S7A, Supporting Information) and is entirely consistent with the stopped-flow data. In contrast, a fit of the linear polymerization model to the 1.89 mg mL^–1 data set (Figure S7B) would predict a final average aggregate size of around 25 monomers, or 75 nm, which is far short of the 1–2 μM aggregates seen by TEM. Moreover, almost 100% of the aggregate is predicted to exist as nuclei (tetramers) until about 200 s (Figure S7B). Such species (∼12 nm) are far too small to significantly absorb light at 400 nm, and therefore the linear polymerization model was discounted because it is incompatible with the turbidity response from the stopped-flow machine. These inconsistencies could potentially be addressed by separating the nucleation and aggregation rate constants, but this extra variable makes the linear polymerization model more complex than our proposed model and the overparameterization does not allow Mathematica to converge to a robust solution.

Our simulations predict that the major component of the lag time is the time taken for the protein to unfold and to develop a saturation concentration of activated dimer. To verify this hypothesis, we conducted experiments where the I27 protein was incubated in 56% TFE, prior to 1:1 mixing in the stopped-flow (giving “standard” aggregation conditions of 28% TFE, 1xPBS). In 56% TFE the protein is ‘unfolded’ (as judged by fluorescence and CD), but remains monomeric and does not associate (as judged by analytical size exclusion chromatography). These experiments showed no discernible lag phase for aggregation (Figure S8A, Supporting Information), suggesting that it is indeed protein unfolding that limits aggregation initiation. This finding agrees with previous assertions that true nucleation events should be stochastic in nature,^23,27 and provides a contrasting explanation for the physical basis of the aggregation lag time. As a final check of the mechanism, we sought to elucidate whether the disappearance of the lag phase was simply due to the fast reconfiguration times of unfolded protein, or whether aggregation proceeded from a specific monomeric TFE unfolded state. We started with alkali-unfolded protein, and neutralized it 1:1 with acidic TFE to give the standard reaction conditions (28% TFE, 1X PBS). In these experiments, there is a short lag phase (Figure S8B), although it is substantially shorter than for the “native” experiments (∼5 s versus ∼80 s at C₀ = 2 mg mL^–1). This suggests a necessary fast transition from the alkali unfolded state to a more structured (helical) TFE state, which is required for dimerization and hence aggregation to occur.

Discussion

The aggregation data were used directly to build the model as shown in Figure 5: the hyperbolic behavior at long and very long time scales indicated a rate limited by dimerization, the t³ dependence at short time scales indicated a reaction controlled by surface area, and the very long time scale data indicated the presence of an off-pathway, aggregation-incompetent species. We built the simplest mechanistic scheme possible that contained these features, and note that the deviation of the fit from the experimental results is exceptionally low (Figure 6B). Moreover, the kinetic parameters of this model are capable of predicting how the emergent trends, such as lag time, vary with the initial concentration of protein (C₀, Figure 7).

From our results, it is clear that the I27 domains must unfold before they can aggregate. The model also illustrates that, because the amorphous aggregates behave as soluble solids, the aggregation is reversible and will only occur above a critical threshold of activated soluble species. Thermodynamically stable proteins are thus unlikely to aggregate in vivo, as they maintain a very low concentration of unfolded forms. Importantly, we observe that the rate constant for unfolding is a key component of the lag time, which cannot be ignored in the analysis of aggregation kinetics. Here the unfolding half-time of I27 is ∼180 s, leading to a short but discernible lag time. However, slower unfolding rate constants should correlate with substantially longer lag times.

We have also used the model to investigate the evolution of each molecular species with time (Figure S7). This reveals that the concentration of activated dimer is always extremely low, because it converts rapidly to aggregate or dissociates to monomer, which explains why this species cannot be directly observed in any experiment. Importantly, it is the activated dimer (and not the monomer) that adds to the aggregate’s surface. This clearly distinguishes this amorphous aggregation from fibril formation, which apparently proceeds by the addition of monomers to fibril ends. Aggregation via the addition of activated oligomers has already been shown for the yeast prion protein, in a mechanism called nucleated conformational conversion.²⁸ Interestingly, of the two different monomeric, non-native forms, only one is aggregation competent. This has been seen several times before, especially for the amorphous aggregation of immunoglobulin-like domains.^12,20,32,39 The fact that I27 aggregation occurs from a specific, TFE-induced structure is reminiscent of recent work on the p53 core domain, which demonstrated that aggregation from the apoprotein is substantially faster than aggregation from the holo-protein.⁴⁰ It also agrees with observations that the stabilization of partly folded intermediate states causes increased aggregation in proteins such as transthyretin (TTR) and lysozyme.^41,42 Here, the sequestering of non-native protein into an aggregation-incompetent species (M_I) is a kinetic effect, and over long time scales the population of this species decreases as it rearranges, dimerizes, and aggregates (Figure S7). Because the very long time scale solubility results show a hyperbolic decrease, it can be assumed that the dimerization step is still rate limiting in this regime. Assuming a fast pre-equilibrium between M_I and M_C, and fast postequilibrium between D and A, this long-term rate constant simplifies to k_obs ≈ k₁₁ × (k_C/k_–C)². The value obtained from a direct hyperbolic fit (4.8 × 10^–4 mg^–1 mL s^–1, Figure 4) is extremely close to the calculated value from the kinetic parameters (4.7 × 10^–4 mg^–1 mL s^–1, Table 1), lending further credibility to our model. It is interesting to note that the initial fraction of soluble protein found as M_I increases as the concentration decreases and, at equilibrium, over 90% is found in this form.

The largest variation between the model and the experimental data is in the behavior of the initial slope obtained from the C₀ vs t³ plots (Figure 7B). We attribute this discrepancy to the use of a “lumped” aggregation rate constant, which does not account for a variation in the number of aggregation nuclei, n, with increasing initial concentration, C₀. The discrepancy can be accounted for by observing that the model fits if n ∝ C₀^2.6±0.4. This relationship suggests that aggregation does not occur via external nucleation (e.g., nucleation by dust particles), because this would be independent of the initial protein concentration giving an index of 0. Nor does aggregation occur via preformed I27 nuclei, where n should be directly proportional to C₀. Instead, the observed index is most consistent with a series of sequential chemical reactions, such as two activated dimers associating to form a stable nucleus, as we propose.

As mentioned previously, the initial stages of the amorphous aggregation are reminiscent of batch crystallization regimes where the rate is dominated by the aggregate surface area. This idea has been explored thoroughly by Finke and co-workers^16,17,43 who propose a mechanistic scheme whereby “continuous nucleation is followed by typically fast, autocatalytic surface growth”. They have used this scheme to successfully fit over 40 different sets of aggregation data, from many different proteins and from several different research groups. Although highly successful, the authors themselves admit that “the [Finke–Watzky] two-step mechanism is obviously a highly condensed, oversimplified, phenomenological model of the real protein agglomeration that often consists of probably hundreds if not thousands of steps”. In this paper, we have independently derived a mechanistic scheme that both agrees with, and enhances, this simple model. Both models are based on the idea that the surface area of the aggregate determines the aggregation rate; however, where the Finke–Watzky mechanism makes no predictions about how this value relates to the quantity of aggregate, we are able to show that the surface area is proportional to the mass-concentration of aggregate to the power 2/3 (C_A^2/3). In addition, a fit to the Finke–Watzky mechanism would not have deduced the presence of the activated dimer (D) nor the aggregation incompetent monomer (M_I). It would also have been unable to account for the soluble protein remaining at the end of each aggregation reaction (which is explained in our model by the dimer solubility, C_S).

Amorphous aggregates have been reported to play a role in the formation of amyloid fibres from the prion protein,¹² and conversion between amorphous and amyloid aggregate morphologies has been previously been suggested for the similarly structured immunoglobulin domains.^44,45 It is therefore reasonable to question whether the TFE-induced aggregates of I27 are the thermodynamically most stable species, or whether they may be on-pathway intermediates for amyloid formation. While I27 has been observed to form amyloid fibrils under alternative reaction conditions, (CF Wright, PhD Thesis, University of Cambridge, 2004), we can state categorically that under the conditions used within this study, (28% TFE, 1x PBS), we saw no evidence of conversion from amorphous aggregate to a typical fibrillar amyloid within a timescale of at least 4 months. The mechanistic model that we have derived is thus applicable to the amorphous protein aggregation of immunoglobulin-like domains. We make no assumptions about what may or may not happen over very long timescales.

Conclusion

Although our exact mechanistic scheme is unlikely to be applicable to all aggregating protein systems, it is likely that other proteins share some of the features of aggregation observed in this immunoglobulin domain, such as the presence of aggregation-incompetent species and/or a surface area rather than a linear polymerization dependence. Moreover, the methods of data collection, instrument calibration, and analysis that we have used should be generally applicable to all aggregating protein systems. It is important to note that, had we used and presented normalized aggregation data (which is unfortunately common practice), we would not have deduced the existence of the nucleation incompetent (misfolded) species. We would have missed the hyperbolic behavior of the aggregation traces and would have reported inaccurate kinetic rate constants for the amorphous aggregation of I27 domains. This work also highlights the importance of studying aggregation profiles at a range of different protein concentrations to distinguish between similar mechanisms that that are equally good at fitting individual data sets, a point that has been experimentally demonstrated more than once.^19,27

Finally, we would like to stress that although turbidity is not linearly proportional to aggregate concentration, by careful calibration of the optical instruments it is possible to collect highly quantitative, concentration-dependent kinetic data for the process of amorphous aggregation. Our model succeeds in capturing all of the features of the aggregation data and describes the amorphous aggregation in as yet unmatched detail. The significance of such a model is that we are now in a position to ask which steps of the mechanism are affected by changes in the system (such as point mutations and solvent conditions). A full mutagenic study will be able to separate the residues responsible for unfolding, misfolding, dimerization, and aggregation. Furthermore, it should be possible to interrogate the model to uncover the modes of action of small molecule inhibitors of I27 aggregation.

Materials and Methods

Protein was produced as described previously.⁴⁶ Buffering was achieved using phosphate-buffered saline (PBS) pH 7.4 in all experiments. Protein unfolding data were analyzed with KaleidaGraph software (Synergy Software, Reading, PA). CD spectra of I27 aggregating at 0.3 mg mL^–1 in buffered 28% TFE were recorded on a Jasco J-810 spectropolarimiter (scan from 280 to 200 at 0.5 nm s^–1, 25 °C, 1 mm path length). Unfolding of I27 (<0.1 mg mL^–1) in buffered 28% TFE was monitored by following the loss of fluorescence at 320 nm with excitation at 280 nm on a Perkin-Elmer LS-55 luminescence spectrophotometer (25 °C, 1 cm path length, 5 mm slit widths). Unfolding was initiated by manually mixing one volume of protein with 10 volumes of buffered 28% TFE, with an average dead time from mixing to data acquisition of 5 s. Traces were averaged and fit with a single exponential to give an unfolding rate of 4.0 × 10^–3 s^–1.

Aggregation profiles were collected by measurement of absorbance at 400 nm (turbidity) on an Applied Photophysics stopped-flow spectrophotometer at 25 °C. Native protein in 1X PBS was mixed rapidly in a 1:1 ratio with buffered 56% TFE solution, achieving aggregation conditions of PBS-buffered 28% TFE. Measurements were performed for 2000 s. The absorbance signal was blanked before each experiment with all components except the protein. The machine was thoroughly cleaned between each run with 2% Hellmanex II solution (Hellma Gmbh, Germany) followed by copious amounts of Milli-Q water. Data were collected for nine different initial concentrations of protein, with three repeats at each concentration. The raw data traces were averaged and then converted from raw signal into concentration of aggregate using eq 2, which was obtained from the instrument calibration curve (see below).

2

The very long time scale measurements were performed for aggregation reactions of I27 at 2 and 4 mg mL^–1 in buffered 28% TFE at 25 °C. A 100 μL aliquot was removed periodically, the aggregate was pelleted by centrifugation at 17 000g for 35 min, and the concentration of protein in the soluble fraction was determined by absorbance at 280 nm.

Instrument Calibration

A calibration curve of the stopped-flow instrument was produced to allow for accurate conversion of the OD₄₀₀ absorbance signal into a quantitative concentration of aggregated I27. Two concentrated solutions of I27 in buffered 28% TFE (15.96 mg mL^–1 and 16.4 mg mL^–1) were left to aggregate for 24 h at 25 °C. The concentration of aggregated protein was then calculated from the known solubility in the long time scale measurements. A series of dilutions was made from each concentrated stock by dilution with buffered 28% TFE, and the OD₄₀₀ readings of these solutions were measured in the stopped-flow spectrophotometer after 1:1 rapid mixing with buffered 28% TFE. Every solution was measured twice, and the experiments were performed quickly (control experiments at all I27 concentrations used herein show no significant re-equilibration of the aggregate with the solvent within 2 h). The resulting data were fit to the equation C_A = a × OD₄₀₀ + b × (OD₄₀₀)^c to obtain the parameters a, b, and c (see eq 2).

Fitting of Data to the Model

The model was fitted to the data using a weighted least–squares (chi-square) method. The weights were calculated from the estimated errors in each data point which in turn were calculated from the measured errors in absorbance modified by the nonlinearity of eq 2. The least-squares fit was performed in Mathematica 7.0 (Wolfram, Champaign, IL) using an in-house package ODEFit which searches over the parameter space using the in-built function FindMinimum. For each set of parameters, the inbuilt function NDSolve is used to integrate the ordinary differential equations (ODEs) in Table S2, Supporting Information, allowing chi-square to be calculated.

Supporting Information Available

Additional information as noted in the text. Raw data from this work can be downloaded from http://www-clarke.ch.cam.ac.uk/JACS.php. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Author Present Address

^∥ Biochemisches Institut, Universität Zürich, Winterthurerstrasse 190, 8057 Zürich, Switzerland.

Author Contributions

^§ These authors contributed equally to this work.