Groupwise whole-brain parcellation from resting-state fMRI data for network node identification

Abstract

In this paper, we present a groupwise graph-theory-based parcellation approach to define nodes for network analysis. The application of network-theory-based analysis to extend the utility of functional MRI has recently received increased attention. Such analyses require first and foremost a reasonable definition of a set of nodes as input to the network analysis. To date many applications have used existing atlases based on cytoarchitecture, task-based fMRI activations, or anatomic delineations. A potential pitfall in using such atlases is that the mean timecourse of a node may not represent any of the constituent timecourses if different functional areas are included within a single node. The proposed approach involves a groupwise optimization that ensures functional homogeneity within each subunit and that these definitions are consistent at the group level. Parcellation reproducibility of each subunit is computed across multiple groups of healthy volunteers and is demonstrated to be high. Issues related to the selection of appropriate number of nodes in the brain are considered. Within typical parameters of fMRI resolution, parcellation results are shown for a total of 100, 200, and 300 subunits. Such parcellations may ultimately serve as a functional atlas for fMRI and as such three atlases at the 100-, 200- and 300-parcellation levels derived from 79 healthy normal volunteers are made freely available online along with tools to interface this atlas with SPM, BioImageSuite and other analysis packages.

1. Introduction

Since the first demonstration of functional connectivity mapping through the analysis of resting-state fMRI data (Biswal et al., 1995), neuroscientists have been investigating the relationship between resting-state connectivity and functional organization of the brain. A number of functional networks have been identified associated with the motor system, language, and memory, in addition to numerous studies highlighting the default mode network (Greicius et al., 2003; van den Heuvel et al., 2008; Smith et al., 2009; Salvador et al., 2005). These networks have been shown to be reproducible under different conditions and in various brain states including different levels of consciousness (Vincent et al., 2007; Greicius et al., 2008; Martuzzi et al., 2011). Together the previous work suggests that resting-state connectivity reflects the underlying functional architecture of the brain.

More recently there has been an explosion of interest in applying network theory methods to the analysis of functional connectivity data in order to characterize the connectivity between nodes at the brain systems level (Rubinov and Sporns, 2009; Hagmann et al., 2010; Achard et al., 2006; Bullmore and Sporns, 2009; Bressler and Menon, 2010). Voxel-level network analyses have been developed that can provide insight into the functional connectivity of individual tissue elements, and a number of important works have been published using such approaches (Buckner et al., 2009; Martuzzi et al., 2011; Scheinost et al., 2012; Stufflebeam et al., 2011). The voxel-level analyses have the benefit of not requiring a priori seed region of interest (ROI) definitions but suffer from the need for arbitrary thresholds to define network properties (although a recent solution to this problem has been presented in mapping the intrinsic connectivity distribution (Scheinost et al., 2012)).

While voxel-based connectivity analyses are highly promising, there remains a need for node-based approaches to allow studies of the brain’s basic functional organization. The study of how different functional regions interact in complex tasks represents the next phase in understanding how the brain works. Investigating the network level organization of the brain may also provide important information in understanding a wide range of clinical disorders and diseases (Buckner et al., 2009; Auer, 2008; Supekar et al., 2008; Brown et al., 2011; Cao et al., 2011; Yao et al., 2010; Sanz-Arigita et al., 2010; Wang et al., 2012; Anticevic et al., 2012; Venkataram et al., 2012). A significant challenge in applying nodal connectivity analysis and network theory analyses to the whole brain is how to define nodes. If a node contains a mixture of independent timecourses, then the net timecourse of that node may not be representative of any of the individual timecourses and the resultant connectivity or network results could be erroneous. Nodes have been defined using task-based fMRI studies (Biswal et al., 1995; Cordes et al., 2000; Arfanakis et al., 2000; Hoffman et al., 2011; Stevens et al., 2012; Fair et al., 2007) but these activate only a very limited fraction of the brain and thus this approach is not appropriate for whole-brain network analyses.

Many authors have used atlas-based definitions such as Brodmann areas (Brodmann, 1909; Baria et al., 2011), or the Brodmann-based automatic anatomic labeling atlas (AAL) (Tzourio-Mazoyer et al., 2002; Achard et al., 2006). This atlas results in a parcellation on the order of 90 regions but different investigators have used different numbers of regions (van den Heuvel et al. 2010, 108 regions; Lynall et al. 2010, 72 regions; Liu et al. 2008, 90 regions; Supekar et al. 2008, 90 regions). Others have used arbitrary spheres (Margulies et al., 2007; Salvador et al., 2005) or arbitrary parcellation of the cortex into x number of nodes (Hagmann et al., 2008). Finally, other studies have relied on parcellation algorithms independent of anatomy or function that divide the brain into regions according to a set of basic parameters–i.e., that nodes do not span hemispheres, and that there is no more than a twofold difference in size between any two nodes (Alexander-Bloch et al. 2012, 278 regions). While apparently meaningful results have been obtained with such approaches, they are not ideal because of the aforementioned risk of mixing different timecourses within a single node, with the consequence that the resultant mean timecourse may not accurately represent of any of the contributing timecourses. Thus there is a clear need for a method to identify functional subunits throughout the brain in order to provide meaningful nodes (with uniform temporal resting-state fluctuations within them) to facilitate whole-brain connectivity and network analysis in both healthy and diseased brains. This work could ultimately lead to a functional-connectivity-based atlas which could then be useful not only in connectivity studies but for framing task-based activation studies as well. There are atlases based on anatomy (MNI (Evans et al., 1992), Talairach (Talairach and Tournoux, 1988)) and cytoarchitecture (Brodmann (Brodmann, 1909)) but to date there is no atlas based on functional connectivity.

In this study, we present a novel approach to brain parcellation that is optimized to yield nodes containing voxels with similar timecourses. This approach builds on our previous work (Shen et al., 2010) to develop a brain atlas composed of minimal functional subunits based on correlated BOLD signal, rather than cytoarchitecture or other anatomic distinctions.

A number of approaches have been introduced for parcellating the cortex. Independent component analysis (ICA) is the most popular of many data-driven analyses for delineating resting-state brain functional networks (Damoiseaux et al., 2006; Luca et al., 2006; Smith et al., 2009; Beckmann et al., 2005; Chen et al., 2008). A group level ICA is usually performed by concatenating the temporal courses from each subject and applying the ICA algorithm to the group data. ICA does not rely on a priori definitions of regions of interest (ROI) and decomposes the data into a set of statistically independent components, which are interpreted as brain networks. The number of components found using the ICA approach is typically less than a hundred for a whole-brain analysis. This represents a similar coarseness to the Brodmann atlas, which is insufficient for comprehensive nodal analyses.

Graph-theory-based approaches offer another option for whole-brain functional parcellation without the need for a priori information. Van den Heuvel et al (van den Heuvel et al., 2008) showed that the normalized cut algorithm (Shi and Malik, 2000) was capable of identifying seven consistent functionally connected networks across a group of subjects. This gross-level network identification represents a promising start for this approach but is also still too coarse for many applications.

There are also a great variety of other algorithms available for functional brain parcellation. Some of the approaches require an initial data reduction. For example, hierarchical clustering (Salvador et al., 2005) can be performed on a set of mean timecourses generated initially from a 90-region anatomical template. Yeo et al (Yeo et al., 2011) applied a clustering algorithm based on a mixture model (Lashkari et al., 2010) to a whole-brain correlation matrix yielding both a seven-node network and a 17-node network parcellation. The correlation was computed from every individual voxel to a set of ROIs obtained by uniformly sampling the cortex. Other clustering approaches have limited the size of the data by focusing on a particular anatomical structure or a region of interest. In our previous work (Shen et al., 2010) we applied the normalized cut algorithm to segment the visual cortex and the intraparietal sulcus. Kim et al (Kim et al., 2010) applied the k-means clustering algorithm to delineate the medial frontal cortex into SMA and pre-SMA subregions. Cohen et al (Cohen et al., 2008) presented a correlation pattern-classification approach and applied it to a region near the left cingulate sulcus and adjacent medial cortex. More recently, Ryali et al (Ryali et al., 2013) proposed a parcellation scheme based on von Mises-Fisher distributions and Markov random fields and applied it to segment artificially combined data drawn from a number of regions including primary auditory, primary motor, primary visual, superior parietal lobule, inferior frontal gyrus, etc. All of these voxel based approaches have the potential to be extended to whole-brain parcellation. However, the ability to extend such approaches could be limited by the increase in computational complexity caused by the increase of data size or the increase in the number of parameters to be estimated.

The most related work was by Craddock et al (Craddock et al., 2012), where a series of whole-brain functional parcellations were generated based on resting-state data. It was shown that ROIs extracted from these parcellations had higher functional homogeneity and thus were more relevant for fMRI analysis. However, the group parcellation approaches used in their work suffered from two shortcomings. First, the approaches relied on the use of a spatial constraint to obtain spatially coherent segments. Second, the averaging and hard thresholding used in the computation of the group parcellation discarded the original connectivity information from individual subjects and as such, individual connectivity information was lost. The two parcellation approaches used by Craddock et al are described in section 3.5. We demonstrate that the groupwise clustering approach proposed in this work does not require the use of spatial constraint, yet it outperforms these two approaches in terms of both classification accuracy and spatial continuity.

The work presented here is focused on whole-brain parcellation using a data-driven approach. We introduce a new groupwise clustering algorithm that jointly optimizes the group and the individual parcellation. The group constraint is imposed implicitly in the formulation of the optimization problem, and it drives the clustering of each individual subject toward a common configuration while allowing individual differences. Additionally there is no need to add a spatial constraint to the model. Group results obtained by the new algorithm are shown to have high spatial coherence. Another important contribution of this work is the proposed use of reproducibility as a measure to evaluate the reliability of each parcellated functional subunit and the parcellation as a whole. Due to high individual functional and anatomic variability in the organization of the brain, it is unrealistic to assume uniform functional homogeneity at all scales across a population. Therefore it is crucial to be able to differentiate subunits or regions of high reproducibility from subunits or regions of low reproducibility for both interpretation and ROI selection.

The paper is organized as follows. In the algorithm section, we outline the derivation of the proposed groupwise multigraph K-way spectral clustering algorithm. The generation of synthetic data and the acquisition of the resting-state fMRI data are described in the Material and Methods section. Also in the Methods section, we define the measure of reproducibility that is used to evaluate parcellations based on resting-state fMRI data. We also include a description of the two competing whole-brain parcellation approaches used in Craddock et al. 2012 and van den Heuvel et al. 2008 in the Methods section. The results, evaluation and interpretation are presented in the Results and Discussion sections respectively.

2. Groupwise Clustering

2.1. Normalized Cut

In a previous study (Shen et al., 2010) we showed that the normalized cut, a graph-based partitioning algorithm, had the best performance in subdividing the cortex using resting-state fMRI data. This new approach begins with the same basic graph structure. Given a resting-state fMRI dataset, we construct a graph G = {V, E}, where the vertex set V = {v₁, v₂, …, v_N} corresponds to all selected voxels in the brain (e.g. within the gray matter), and the edge set E = {e(i, j)|v_i, v_j ∈ V} represents the connections between pairs of voxels. The strength of the connections are characterized by the weight w(i, j), which is usually a function of the Pearson’s correlation coefficient between the two resting-state timecourses at voxel i and voxel j. A two-way normalized cut divides the set V into two disjoint sets A₁ and A₂ (A₁ ∪ A₂ = V) through simultaneously maximizing the similarity within each of the two sets and minimizing the similarity between the two sets. The objective function for the optimization is given by

$$N\mathit{cut}(\{A_1,A_2\},W)=\frac{{\sum }_{i\in A_1,j\in A_2}w(i,j)}{{\sum }_{i\in A_1,j\in V}w(i,j)}+\frac{{\sum }_{i\in A_1,j\in A_2}w(i,j)}{{\sum }_{i\in A_2,j\in V}w(i,j)}.$$ (1)

The normalized cut criteria can be extended to a K-way partition of a graph. Yu and Shi (Yu and Shi, 2003) proposed an iterative algorithm called the multiclass spectral clustering to solve the K-way normalized cut. For derivation and discussion, we refer the readers to the original paper.

2.2. Multigraph K-way clustering

The proposed multigraph K-way spectral clustering algorithm jointly segments a set of graphs, under the assumption that the connectivity of the graphs should exhibit similar patterns across subjects. In other words, the functional brain networks obtained from different healthy individuals should have similar connectivity patterns. The algorithm we present here is closely related to the K-way normalized cut algorithm developed by Yu et al (Yu and Shi, 2003).

Let S = {1, 2, …, M} denote the set of graphs to be partitioned. We first obtain a new set of coordinates X_s for each graph. The matrix X_s is of size N by K, the columns of X_s are the first K eigenvectors of the normalized weight matrix W̃_s ranked by the eigenvalues (1 = λ₀ > λ₁ > ··· > λ_K), ${\stackrel{\sim }{W}}_s=D_s^{-\frac{1}{2}}{W}_s{D}_s^{-\frac{1}{2}}$, where D_s is the diagonal matrix of degrees D_s(i, i) = Σ_j w_s(i, j). Each row of the input data X_s is normalized to have unit norm, thus X_s represents a set of points projected to the unit sphere. These points on the unit sphere are rotation invariant, meaning that the absolute position of any point is irrelevant, the relevant information is encoded in the relative positions of the individual points, hence we can rotate the sphere arbitrarily with no effect on the clustering. The multigraph clustering approach is formulated as follows,

$$\begin{array}{ll}\hfill \text{minimize}& \phi (Y,\{R_s\})=\sum _s{\Vert Y-X_s{R}_s\Vert }^2\hfill \\ \hfill \text{subject}\text{to}& Y\in {\{0,1\}}^{N\times K},Y{1}_K=1_N,R_s^T{R}_s=I_K.\hfill \end{array}$$ (2)

where ||·|| denotes the Frobenius norm of matrix, and $1_N={[\underset{N}{\underbrace{11\dots 11}}]}^T$. The solution Y to the optimization problem defined in (2) is a binary matrix of K columns, where each column is an indicator vector that defines the membership to the kth cluster. The matrix R_s is a generalized rotation matrix in this high-dimensional space (similar to the hyperalignment approach of Haxby et al. 2011). By definition, $R_x^T{R}_s=I_K$, where I_K is the identity matrix. The goal of the groupwise optimization is to rotate the individual point sets so that corresponding points from each graph (subject) align with the same axes (in the K-dimensional space) thus resulting in a groupwise parcellation. The multigraph clustering approach includes all graphs in a single optimization and solves for one groupwise parcellation. The advantage of this formulation is that the groupwise parcellation Y acts like an implicit constraint that directs the parcellation of each graph toward a common configuration. However, in the meantime, each graph is still kept as a separate entity through the individual rotation matrix R_s, which allows us the flexibility of creating “groupwise influenced” individual parcellations. The objective function in Eq. 2 can be further simplified,

$$\begin{array}{l}\phi (Y,\{R_s\})=\sum _s{\Vert Y\Vert }^2+\sum _s{\Vert X_s{R}_s\Vert }^2-\sum _{s}2\ast \text{tr}(Y{(X_s{R}_s)}^T)\\ =2NM-2\ast \text{tr}\left(Y\sum _s{(X_s{R}_s)}^T\right),\end{array}$$

where tr(·) denotes the trace of a matrix, and $\Vert X_s{R}_s\Vert =\sqrt{\text{tr}(X_s{R}_s{R}_s^T{X}_s^T)}=\sqrt{\text{tr}(X_s{X}_s^T)}=\sqrt{N}$.

The solution to the discretization problem (2) can be found iteratively using the following two steps.

• Step 1: given {R_s}, Eq. 2 is reduced to,

  $$\begin{array}{ll}\hfill \text{minimize}& \phi (Y)=\sum _s{\Vert Y-X_s{R}_s\Vert }^2\hfill \\ \hfill \text{subject}\text{to}& Y\in {\{0,1\}}^{N\times K},Y{1}_K=1_N.\hfill \end{array}$$

Let Z = Σ_s X_sR_s, each row of Y is given by,

$$Y(i,t)=\{\begin{array}{ll}1,\hfill & \text{if}t={\text{argmax}}_{l}Z(i,l),\hfill \\ 0,\hfill & \text{elsewhere}.\hfill \end{array}$$ (3)

• Step 2: given Y, Eq. 2 is reduced to,

  $$\begin{array}{ll}\hfill \text{minimize}& \phi (\{R_s\})=\sum _s{\Vert Y-X_s{R}_s\Vert }^2\hfill \\ \hfill \text{subject}\text{to}& R_s^T{R}_s=I_K,\hfill \end{array}$$
  and the optimal solution of R_s is given by,

  $$Y^T{X}_s=U\mathrm{\sum }{V}^T,R_s={VU}^T.$$ (4)
  Note that after convergence, we not only obtain the group parcellation Y, but we also obtain the individual parcellation Y_s through Z_s = X_sR_s,

  $$Y_s(i,t)=\{\begin{array}{ll}1,\hfill & \text{if}t={\text{argmax}}_l{Z}_s(i,l),\hfill \\ 0,\hfill & \text{elsewhere}.\hfill \end{array}$$ (5)

Because the whole parcellation is performed simultaneously, the correspondence between all individual and group results is straightforward. Note also that the normalized cut problem is NP-complete even in the case of K = 2 for one graph. The multigraph K-way clustering algorithm does not solve for a global minimum, but is aimed at finding a close enough solution that is computationally efficient.

2.3. Algorithm

The multigraph K-way clustering algorithm is summarized in Figure. 1.

Figure 1.

Multigraph (groupwise) K-way Clustering Algorithm

3. Material and Methods

In order to investigate the performance of the proposed groupwise multigraph clustering algorithm, we generated a set of synthetic data and compared the parcellation results to those obtained using the two competing approaches described later in this section (3.5). The evaluation and comparison were based on three measures: the Hausdorff distance, the Dice’s coefficient and the median minimal distance (MMD), each of which is defined below. In addition, resting-state fMRI data from 79 healthy subjects was collected to measure the performance of this approach with real data. The groupwise clustering algorithm was applied to a series of whole-brain parcellations at a number of different scales.

3.1. Synthetic data

In generating the synthetic data, we created 10 virtual subjects to form a group. For each subject, a single slice of fMRI data was simulated. The simulated fMRI data was divided into six regions. The actual partitioning of the six regions was a randomly varied version of the base template shown in Figure 2. The variation was mainly from the four boundary lines and the size of the inner circle, which can be clearly seen from the probability map in Figure 2. The probability map shows the maximal probability that a voxel belongs to one of the six regions. Note that among all six regions, region three has bilateral components that are spatially disconnected. It was created in this way to mimic certain parts of the human brain.

Figure 2.

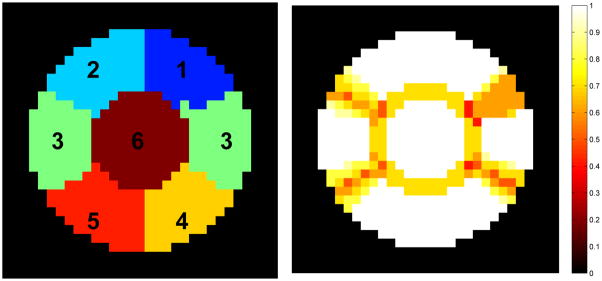
Simulated data includes six regions in a single slice. The boundaries between the six regions are set to change randomly for each virtual subject. The image on the right shows the maximal probability that a voxel belongs to one of the six regions.

Timecourses of the synthetic data were generated using real resting-state fMRI time series. We manually selected six regions from the group parcellation results of the in vivo data using the proposed clustering approach (see Fig. 3). The regions were chosen based on their high reproducibility and spatial locations. The mean timecourses from the six regions were computed and used as the signal timecourses s_i(t) for the synthetic data. The noise-corrupted time series f(t) is given by,

Figure 3.

Mean timecourses from 10 subjects for the above six regions were used to generate the synthetic data. These six regions were obtained from a group parcellation using the groupwise multigraph clustering approach.

$$f(t)=s_i(t)+\alpha n(t),i\in \{1,2,3,4,5,6\},$$ (6)

where n(t) is white Gaussian noise with mean 0 and standard deviation 1. α is the parameter we used to control the signal to noise ratio (SNR). It was tested at levels of 0.2, 0.3 and 0.4, representing low, medium and high SNR. At a given SNR, 10 sets of simulated data were created for each of the 10 virtual subjects, thereby providing 10 group parcellation results which were used for statistical comparison of the different parcellation approaches. The synthetic data matrix was of size 31 × 31 × 212.

3.2. Resting-state fMRI

Imaging was performed on two 3T Siemens Trio scanners at Yale University School of Medicine in the Yale Magnetic Resonance Research Center. A T1-weighted 3-plane localizer was used to localize the slices to be obtained and T1 anatomic scans were collected in the axial-oblique orientation parallel to the AC-PC line. Resting-state fMRI data was obtained using a gradient echo T2*-weighted echo planar imaging sequence, flip angle alpha= 80 degrees, echo time TE = 30ms, repetition time TR = 1550ms, 64 × 64 matrix, with 25 slices 6mm thick, skip 0mm, 22 × 22cm² FOV, providing whole-brain coverage with voxel size of 3.4mm × 3.4mm × 6mm. Eight six-minute runs of resting-state data were collected for each subject. A total of 100 healthy right-handed subjects participated in the study after giving informed written consent and from this data a subset of 79 subjects with the requisite number of complete runs and minimal motion were retained for the parcellation. This study was approved by the Human Investigation Committee of the Yale University School of Medicine.

Functional data was motion corrected and slice-time corrected using SPM5. The data was then mapped to a common space of size 3mm × 3mm × 3mm using BioImage Suite software (BioImage-Suite.org). Masks of white matter, gray matter and the cerebrospinal fluid (CSF) were created in the common space. The mean timecourses from the white matter and CSF were calculated. Time-courses from the gray matter were orthogonalized with respect to the white matter and CSF mean timecourses and to the six motion-related signals estimated by SPM5. The timecourses were filtered using a bandpass Butterworth filter with passing band 0.02 – 0.1Hz. A Gaussian kernel of FWHM 6mm was applied for spatial smoothing and the linear trend was removed from all signals.

3.3. Quantitative Evaluation of Parcellation Accuracy

We evaluated the performance of all three parcellation approaches using the synthetic dataset. The evaluation was based on measuring the accuracy of the groupwise parcellation against the ground truth. Note that the cluster labels of the ground truth and the resulting parcellations may be different, therefore we matched each cluster to the most overlapped cluster in the ground truth.

There are a number of measures available for the evaluation purpose: for this work we used the Dice’s coefficient, the Hausdorff distance, and the median minimal distance (MMD). Each of these measures is described below.

3.3.1. Dice’s coefficient

Dice’s coefficient is a measure of parcellation overlap. Given two sets A and B, the Dice’s coefficient measures the ratio of the number of voxels that belong to both sets to the total number of voxels in A and B,

$$\text{Dice}=\frac{2·\mid A\cap B\mid }{\mid A\mid +\mid B\mid }$$ (7)

When two sets are perfectly aligned, the Dice’s coefficient is one and if there is no overlap between the two sets, the Dice’s coefficient is zero.

3.3.2. Hausdorff distance

The Hausdorff distance between two sets A and B is the maximal distance one needs to travel if starting from a point in A and trying to reach any point in B or vice versa,

$$\text{Hausdorff}=\text{Max}\{{max}_{i\in A}{min}_{j\in B}d(i,j),{max}_{j\in B}{min}_{i\in A}d(i,j)\},$$ (8)

where d(i, j) is the Euclidean distance. If the two sets are close in Hausdorff distance, then points in either set must be close to some points in the other set. The Hausdorff distance is more sensitive to outliers than the Dice’s coefficient in measuring closeness of two sets. For example, if there are a few points in one parcellated region that are far away from all points in the other region, then the Hausdorff distance would be large, while the Dice’s coefficient would remain close to one.

3.3.3. Median minimal distance

To compensate for the fact that a few misclassified points could dramatically increase the Hausdorff distance, we designed another measure, the median minimal distance (MMD), as an additional way to characterize the distance between two sets. Instead of finding the maximal distance, the MMD finds the median of the minimal distances from any point in set A to set B and the minimal distances from any point in set B to set A,

$$(\mathit{MMD})=\text{Median}\{{min}_{i\in A}d(i,j),{min}_{j\in B}d(i,j)\}$$ (9)

A zero MMD does not guarantee an exact match of two sets, but they should be very similar.

In the results that follow, all three of these measures are used to evaluate the accuracy of the parcellation. Moreover, visual inspection of the parcellation results was also used to ensure each segment was spatially coherent.

3.4. Reproducibility

To investigate the extent to which functionally homogeneous subunits are stable and invariant across a healthy population, we measure the extent to which similar parcellation results are obtained in different groups of healthy subjects. Reproducibility is an important measure to assess the reliability of the delineation of each parcellated subunit. It could well be the case that some brain regions have higher reproducibility due to their highly focused functionality and high anatomic reproducibility, while other regions have relatively low reproducibility due to their functional diversity and/or anatomic variability. Reproducibility of functional subunits is inherently affected by how well anatomic variations line up across subjects. In this work, reproducibility was obtained at both whole-brain level and individual subunit level. At the whole-brain level, the reproducibility was obtained by comparing parcellation results obtained from mutually exclusive groups of subjects. Given the 79 healthy subjects used in this work, we divided them into two groups, one containing 40 subjects and the other containing the rest. We performed the division 20 times with a random permutation of subjects, thus obtained 20 pairs of mutually exclusive groups of subjects. We applied the groupwise clustering algorithm on the mutually exclusive groups and obtained 20 pairs of parcellation results. We denote one pair of parcellation results as A₁ and A₂. For each subunit in A₁, we found the best matching subunit in A₂ with the highest Dice’s coefficient and saved the coefficient as the reproducibility score for that subunit, and repeatd this same calculation for all subunits in A₂. Then the reproducibility score from each individual subunit was weighted by the ratio between the size of the subunit and the total number of voxels within the gray matter mask and summed over the whole brain. The whole-brain reproducibilities of A₁ and A₂ were then averaged to yield the reproducibility of that particular pair.

To further evaluate the reproducibility of an individual subunit, we extended the comparison to groups of overlapping subjects. Basically, we included all 40 parcellations from the pairwise comparison described above. Denote the whole set of parcellation results as {A^(r), r = 1, 2, …, 40}, with each individual parcellation A^(r) composed of K subunits, $A^{(r)}={\cup }_{k=1}^K{A}^{(r)}(k)$. The reproducibility of an individual subunit in a single parcellation was computed as follows. Given the kth subunit in the rth parcellation, denoted as A^(r)(k), we first found its best matching subunit in each of the remaining 39 parcellations. For example, to find the best matching subunit in parcellation A^(q), q ≠ r, we computed the Dice’s coefficient between the target subunit A^(r)(k) and all subunits in A^(q), and we selected the one subunit in A^(q) with the highest Dice’s coefficient as the best matching subunit. The highest Dice’s coefficient was saved as the matching score M((r, k), q) for subunit A^(r)(k) and parcellation A^(q). The matching scores for all 39 parcellations across subjects were computed and the reproducibility Rep(r, k) of subunit A^(r)(k) was defined to be the average of the 39 matching scores, $\mathit{Rep}(r,k)=\frac{1}{39}{\sum }_{q=1,q\ne r}^{40}M((r,k),q)$.

3.5. Competing Groupwise Approaches

In addition to the proposed groupwise multigraph clustering algorithm introduced in section 2.2, there are two other approaches that have been used to obtain whole-brain groupwise parcellation based on the graph-theory-based normalized cut algorithm. In the first approach (used by Craddock et al. 2012), which we will label GP1, the correlation matrix is computed for every subject, a threshold is applied to each of the matrices to eliminate weak and negative coefficients (the correlation threshold is typically chosen to be between 0.25 and 0.5 for most applications), and the group mean correlation matrix is computed. The multi-class normalized cut algorithm is then applied to the mean matrix in order to obtain the group parcellation. The second approach (used by both van den Heuvel et al. 2008 and Craddock et al. 2012), which we label GP2, first applies the normalized cut to each subject’s correlation matrix after thresholding. The partitioning results from each individual are then used to generate a second-level weight matrix as follows. For any entry w(i, j) of the second-level weight matrix, the number of subjects where voxel i and voxel j have the same partitioning label is counted, and this number is divided by the total number of subjects, and this ratio is used as the value for w(i, j). Therefore the second level weight matrix is a groupwise estimate of the probability that any pair of voxels are classified into a single region. The normalized cut is applied to this weight matrix to obtain a final groupwise parcellation. We explicitly compared the performance of these two existing approaches with our proposed groupwise clustering algorithm using synthetic data in the results section, and demonstrated that our approach outperformed the other two in both classification accuracy and spatial continuity.

We were also aware that group ICA would be another option to obtain a groupwise parcellation using resting-state fMRI data. However substantial data reduction needs to be performed at both the individual and the group level before the group ICA can be applied. Because of the issue of model order selection and the fact that not all ICA components are meaningful (manual selection of components are always needed), we chose not to apply group ICA for the task of whole-brain parcellation and we did not include the comparison for the synthetic datasets either.

4. Results

In this section, we first show a comparison between the proposed algorithm and two other group parcellation approaches based on the synthetic data. The proposed approach outperformed the other two approaches. The proposed approach was then applied to real resting-state fMRI data and the whole-brain parcellation results are shown along with reproducibility maps.

4.1. Results from synthetic data

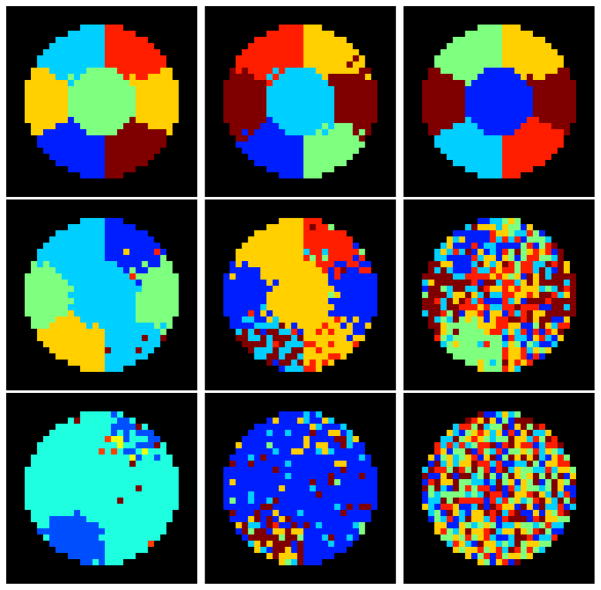
The multigraph clustering algorithm and the GP1 and GP2 methods were run on the synthetic data, using a correlation threshold of 0.2 for GP1 and GP2 approaches. Figure 4 shows examples of the parcellation results from the three approaches at different SNRs. These examples are included for visual inspection purposes. The results of the quantitative evaluation are summarized in Figure 5. The evaluation was performed separately for each region, because the parcellation accuracy varied region by region. The spatial variation in the results arises because the baseline effective SNRs were different for each region, thus some regions were easier to parcellate than others.

Figure 4.

Examples of parcellation results at different signal to noise level with increasing noise added as α = 0.2 (top row), α =0.3(middle row) and α =0.4 (bottom row). Our proposed multigraph clustering algorithm and two other parcellation approaches were applied to obtain the results. Left: the proposed multigraph clustering parcellation; Middle: GP1; Right: GP2. By visual inspection, the multigraph clustering parcellation approach shows the best performance at all three noise levels in term of the classification accuracy and regional homogeneity.

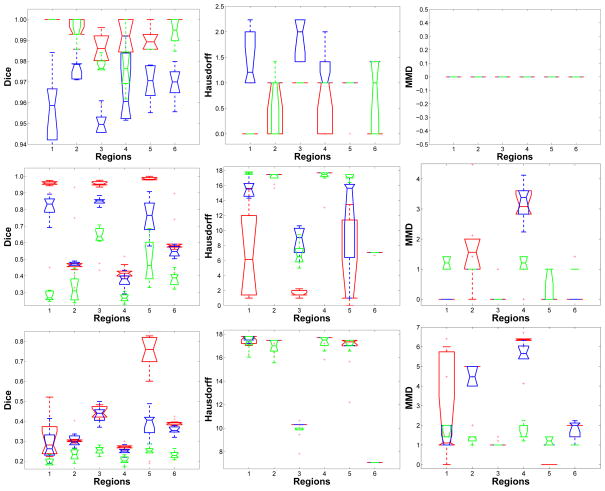
Figure 5.

Quantitative evaluation using the Dice’s coefficient, the Hausdorff distance and the median minimal distance. The colors indicate different approaches: our multigraph clustering parcellation (red), GP1 (blue), GP2 (green). α = 0.2, 0.3 and 0.4 from top row to bottom row respectively. The quantitative analysis confirms the visual inspection that the proposed multigraph clustering approach outperformed both the GP1 and GP2 approaches. At the lowest noise level α =0.2, all three approaches were successful at identifying the six regions. At an increased noise level α =0.3, the multigraph approach was still good at identifying regions 1, 3 and 5 with high accuracy (mean Dice’s coefficients being above 0.9). At this noise level, GP1 was able to identify regions 1, 3 and 5 with lower accuracy and GP2 basically failed the classification task. At the highest noise level α =0.4, only the proposed multigraph approach was able to identify region 5 with good accuracy. The other two approaches both failed.

All three approaches performed well when the SNR scale factor was high (α = 0.2). The top row in Figure 4 shows the group parcellation results from a set of 10 subjects and indicates that all six regions were well separated. There were only a few voxels that were misidentified using the GP1 approach. Quantitatively the results of the analysis shown in Figure 5 demonstrate that the average Dice’s coefficients for all regions and for all approaches were above 0.95, indicating a very good match with the ground truth. The Hausdorff distance and the MMD were also small. As the noise is amplified with α = 0.3, the three approaches begin to fail, but in different ways. From the middle row in Figure 4 we see that none of the approaches were able to correctly identify all six regions. However, the multigraph clustering algorithm performed the best by identifying three of the six correctly, namely region one, three and five, and each of these correctly identified regions were spatially contiguous and connected. In Figure 5 the red boxes had Dice’s coefficients above 0.9 for regions 1, 3 and 5, confirming the visual inspection. There were also a few outliers in regions 2 and 6 that had Dice’s coefficients above 0.9, but in general the statistics at regions 2, 4, and 6 indicated failure of the parcellation for these regions. At α = 0.3, GP1 performed worse than the multigraph clustering approach but better than the GP2 approach. The middle image of the second row in Figure 4 shows that the GP1 approach was able to identify region 1 and 3 with compromised spatial continuity. It can also be seen from Figure 5 that the GP1 approach was able to identify region 1, 3 and 5, with Dice’s coefficients of approximately 0.8 for those regions. The GP1 approach was not able to correctly segment regions 2, 4 and 6. The GP2 approach failed the group parcellation at this SNR level. At the lowest SNR level (α = 0.4), the multigraph clustering method was still able to parcellate region 5 with relatively good accuracy–the Dice’s coefficients were between 0.6 and 0.8–while the other two approaches failed to segment any of the six regions. These results were for a correlation threshold of 0.2. We also tested different values of correlation thresholds (at higher noise level α =0.3 and 0.4, we tested the thresholds of 0.3 and 0.4) for the GP1 and the GP2 approaches, but we found that using higher correlation thresholds did not improve the parcellation results.

4.2. Resting-state fMRI data

The comparison in the previous section demonstrated that as expected, the proposed multigraph clustering algorithm is capable of producing more accurate and more spatially homogeneous parcellation results than the other approaches.

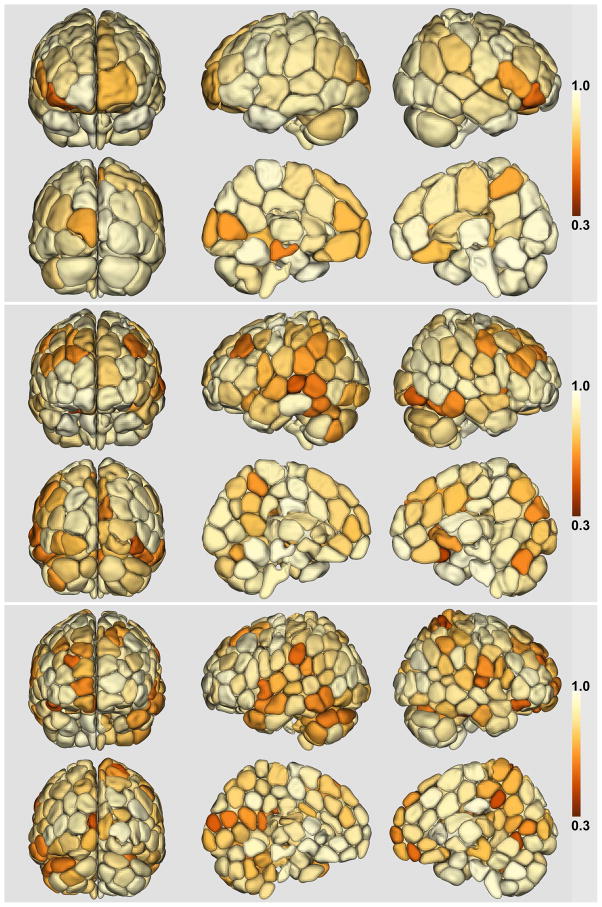
The whole-brain parcellation was performed separately for each hemisphere, and the results are shown in Figure 6. The number of regions K for each hemisphere was initially set to be 50, 100, and 150 respectively, resulting in whole-brain parcellations of approximately 100, 200 and 300 regions. The results shown in Figure 6 are for the groupwise parcellation Y obtained from one group of 40 randomly selected subjects. The colormap on the partitioning shows the reproducibility of each subunit with hotter colors indicating higher reproducibility.

Figure 6.

Whole-brain parcellation using the multigraph K-way clustering method. The number of regions K are 50, 100, 150 for each hemisphere yielding total nodes of 94, 189 and 281 (for the three parcellations shown in this figure). The cross-subject reproducibility is indicated by the shading of each subunit in the parcellation. The same heat colormap and reproducibility scale was used for all levels of parcellation.

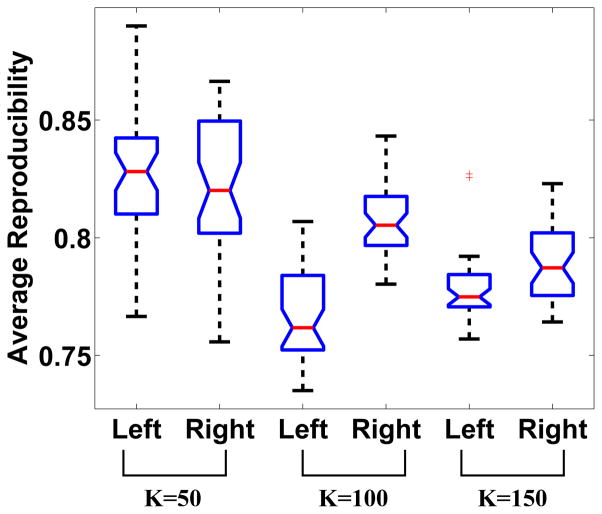
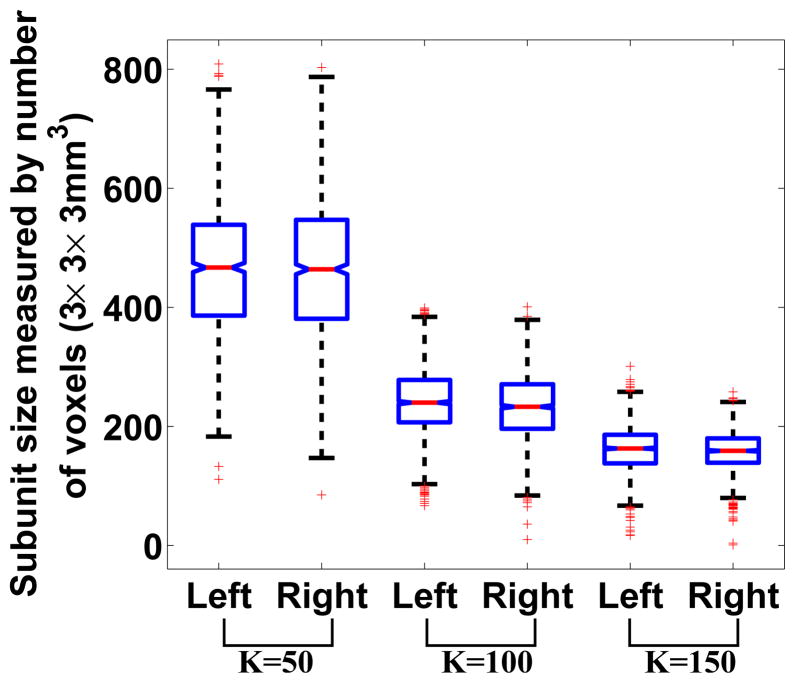
Figure 7 presents the whole-brain averaged reproducibility for different numbers of initial target region K’s. The boxplot at each K was generated based on group parcellation results obtained from 20 pairs of mutually exclusive groups of subjects. The right hemisphere showed higher reproducibility at K = 100 and K = 150, but the reproducibility at K = 50 was approximately the same for both hemispheres. The mean reproducibilities for all K’s were above 0.75. As K increased, the reproducibility decreased, with the exception that at K = 100, the reproducibility of the left hemisphere was lower than the reproducibility at K = 150. The whole-brain reproducibility dropped below 0.5 when K was set to 400, indicating that this level of parcellation is too high. Table 1 lists the median number of regions in the left and right hemisphere for different starting numbers of initial K values. Additionally, Figure 8 shows that at every given K value, the average size of the subunits was approximately the same in each hemisphere. There is some variation in the size of the subunits, and for example at K = 50, there is a subunit that contains less than 200 voxels while there are other subunits that contain approximately 800 voxels. However, there are only a few such cases and the overall variation is relatively small. We also examined the hemispheric symmetry of the parcellations by comparing the centers of mass of the subunits. To do this we computed the (x,y,z) coordinates of the center of mass for each subunit in the left hemisphere, flipped each of these to the right hemisphere and measured the Euclidean distance to the nearest center of mass of the corresponding subunit in the right hemisphere. The mean distance and standard deviation across all regions were 2.76/1.336 at K = 50, 2.564/0.948 at K = 100 and 2.38/0.891 at K = 150. The calculation was performed in the common space with voxel size of 3 × 3 × 3mm³. This distance measure provides a quantitative assessment of the hemispheric symmetry of the parcellations.

Figure 7.

Whole-brain reproducibility distribution at different number of K’s. Each boxplot was generated based on parcellations from 20 pairs of mutually exclusive groups of subjects.

Table 1.

Median of number of regions in each hemisphere

No of regions (K)	Left Hemisphere	Right Hemisphere
50	47	47
100	92.5	93
150	139	138

Figure 8.

Sizes of subunits of the groupwise parcellation at different number of K’s. Each boxplot was generated based on parcellations from 40 groups of randomly selected subjects. The sizes were measured by the number of voxels of dimension 3 × 3 × 3mm³. The boxplot shows that the variation of the sizes of the subunits is relative small across the whole brain.

4.3. Subunit homogeneity evaluation

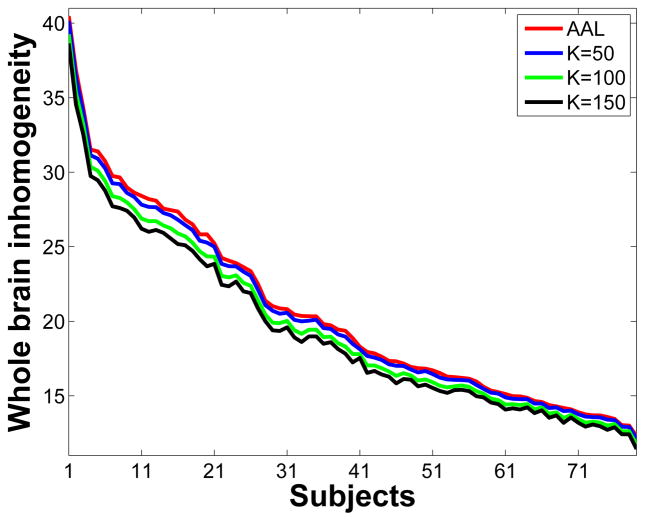
The groupwise multigraph clustering algorithm was designed to produce subunits with homogeneous temporal patterns. In the ideal parcellation the mean timecourse of each subunit should be a good representative of all of the timecourses within the subunit. In order to quantitatively evaluate this property, we computed the Euclidean distance between individual timecourses to the mean timecourse for every subunit in the parcellated brain (shown in Fig. 6). We used data without the Gaussian spatial smoothing for this computation. The voxel-wise Euclidean distance is a measure of the variation within each subunit, such that larger distances indicated less homogeneity within the parcellated functional subunit. The whole-brain inhomogeneity index was calculated by summing up all voxel-wise Euclidean distances for all 79 subjects. The same computation was performed for the AAL atlas which contains 114 regions. Figure 9 shows the curves of the whole-brain inhomogeneity indices. The x-axis is the subject index, with subjects ordered according to their whole-brain inhomogeneity indices based on the AAL atlas. The four curves have no crossover and the AAL atlas has the highest inhomogeneity scores among all four parcellations. A paired t-test between the AAL curve and the K = 50 parcellation curve (K = 50), which contained 96 regions, indicated significant differences in homogeneity of the two approaches with p less than 10⁻¹⁰. Even higher homogeneity was achieved with the higher order parcellations (K = 100 and 150), as could be expected in part because these are smaller regions.

Figure 9.

Curves of whole-brain inhomogeneity indices for 79 subjects from four parcellations, namely the AAL atlas (red), groupwise parcellation using the multigraph clustering algorithm with 50 regions for each hemisphere (blue K = 50), groupwise parcellation using the multigraph clustering algorithm with 100 regions for each hemisphere (green K = 100), groupwise parcellation using the multigraph clustering algorithm with 150 regions for each hemisphere (black K = 150). The x-axis is the subject index. The subjects were ordered according to their whole-brain inhomogeneity indices based on the AAL atlas. The calculation of the inhomogeneity indices used data without the Gaussian spatial smoothing.

4.4. Computation

The multigraph clustering algorithm code was written in Matlab. The part of the algorithm where Eq. 2 was solved iteratively used the Matlab GPU computing utilities. The graphics card installed was an NVIDIA Quadro 6000 with CUDA version 4.2. The use of Maltab GPU functions increases the computational efficiency by at least a factor of 10. The running time for the groupwise clustering is a function of the size of the input data, the number of clusters, the size of the group and the number of initializations. In the experiments reported in Table 2, we included 45 randomly selected subjects in a groupwise parcellation. Additionally we ran the groupwise parcellation 10 times with different initializations and chose the one parcellation that had the best optimization score. Table 2 lists the mean running time of one groupwise parcellation using whole-brain data (both hemispheres) at different numbers of K. The running times reported in Table 2 are total running times of 10 different initializations but they do not include the time for fMRI preprocessing and Eigen decomposition of the weight matrix for each subject. Eigen decomposition of the weight matrix W̃_s (of size N × N) was performed once for each subject to prepare the input data X_s. The weight matrices were sparse and we used the Matlab built in function “eigs” for the Eigen decomposition.

Table 2.

Computing time of the multigraph clustering algorithm

K	50	100	150	200	250	400
Time in seconds	877	1945	2353	3632	7484	20663

5. Discussion

5.1. Spatial constraint and spatial smoothing

In our experiments using both the synthetic and the real fMRI data, the weight matrices were constructed without any spatial constraints. The entries in W were only based on the Euclidean distance between any pair of timecourses. The computation of the weights and the selection of parameters was the same as described in (Shen et al., 2010). There are at least two reasons to avoid adding a spatial constraint. First, the acquisition and preprocessing of fMRI data, especially the spatial smoothing, has already directly introduced substantial spatial correlation into the dataset. While adding a spatial constraint could improve the spatial coherence in the results, it could also serve to make the functional boundaries less distinct, making the parcellation more difficult. Secondly adding a spatial constraint means adding additional parameters to the model. It is very hard to estimate to what extent a particular spatial constraint would affect the parcellation result. Excessive use of spatial constraints could lead to parcellations that are based more on anatomy rather than functional connectivity. Admittedly, if appropriate anatomic spatial constraints could be derived then this could potentially improve the parcellation results. Parcellating the two hemispheres separately imposes a very clear anatomic constraint, but other anatomic constraints are not so easily defined.

To further investigate how the groupwise parcellation was affected by the Gaussian kernel smoothing, we used the unsmoothed data and applied the groupwise parcellation. We observed that the parcellation results were largely the same in terms of subunit location, shape, size and spatial continuity comparing to results obtained using the smoothed data. In other words, the groupwise parcellation is not sensitive to the effect of spatial smoothing introduced by the Gaussian kernel in addition to the other existing smoothing in the data. In fact, the resampling from the fMRI resolution of 3.4375 × 3.4375 × 6 to the MNI resolution of 3 × 3 × 3 indirectly introduces spatial smoothing to the data. Therefore the spatial continuity of the parcellated subunits we observe is not only a result of the functional coherence of the brain, but also reflects the smoothness of the data to some extent. With the unsmoothed data, we did observe one outlier subunit that had spatially disconnected components, which included a fully connected region of the brain stem, part of the cerebellum and a few voxels located along the boundaries between the gray and white matter. This can be explained by the relative small magnitude of the timecourses from these regions. Because we used the Euclidean distance as the similarity measure to construct the weight matrix W, these timecourses of small magnitude are close in the functional space, thus the corresponding voxels were clustered to one subunit in the groupwise parcellation. There were no spatially disconnected subunits in the parcellation using the smoothed data.

The groupwise clustering approach introduced here has a built-in mechanism that enforces spatial coherence in the parcellation results by examining all the subjects simultaneously. For any individual subject, a few mislabeled voxels could easily lead to spatial discontinuity within a certain region. However, it is very unlikely that the same set of voxels would be mislabeled in the same way across multiple subjects. Therefore the optimization defined in Eq. 2 is capable of eliminating such errors because it takes into account the clustering of all individuals. Results from both the synthetic and the in vivo resting-state fMRI data suggest that the multigraph clustering algorithm produces results with excellent spatial continuity.

5.2. Number of regions

The groupwise parcellation approach requires as input the approximate number of regions to solve for in advance. For the synthetic data, the number of regions was known exactly and this number was used when testing the algorithm. However when working with in vivo fMRI data, there is little a priori information as to the appropriate K–value to use. In the brain network analysis and whole-brain parcellation literature, the number of regions varies from less than 10 to 1000. The Brodmann atlas has 52 regions in each hemisphere covering the cerebral cortex defined based on the cytoarchitectural organization of the neurons. The whole-brain atlas of Harvard Medical School has defined approximately 70 anatomical structures including the ventricular system and the subcortex (www.med.harvard.edu/aanlib/home.html).

The correct number of regions for a functional atlas at the group level ultimately will depend on a number of factors including the acquisition resolution, the consistency across subjects of functional organization within regions, the consistency of network organization between regions, and the consistency of anatomic organization. An analysis of the inter-individual variability in cytoarchitecture, for example, has shown significant differences in the location of even primary sensory cortical areas as well as heteromodal association areas even after correction for differences in brain size (Ulyings et al., 2005). Analysis of a wide range of anatomic registration methods has also shown significant spatial mismatch (of the order of 1cm) between subjects in many brain regions (Hellier et al., 2003; Thirion et al., 2007). Even if anatomical variations could be taken into account, differences in functional organization are also important (Brett et al., 2002). It is also likely the case that such functional parcellations will need to be defined for each stage of development and aging as functional organization is known to change throughout the life span (Hampson et al., 2012; Power et al., 2010).

It is known that many levels of functional organization exist in the cortex. Above the neuronal level are cortical columns and other organizational modes, suggesting the need for multi-scale analysis. In this work, the goal was to obtain a groupwise functional parcellation at the level of resolution typically encountered in fMRI studies and thus we tested a range of K values yielding final parcellations of 100, 200 and 300 functional subunits or nodes. Here our focus was not on a particular number but on the operating scale. It should also be note that with the groupwise clustering algorithm, the number of regions in the final parcellation may be less than or equal to the input K (see Table 1). We stopped at K = 150 (300 nodes) because of the observation that the average whole-brain cross-subject reproducibility dropped below 0.5 when a parcellation of 400 regions was targeted. The significant decrease in the reproducibility indicates that subunits obtained at K = 400 are no longer consistent across subjects. In addition to the aforementioned limits attributed to acquisition resolution, anatomic and functional organization matching across subjects, it is also possible that at higher K values, the iterative approach proposed in Section 2 to achieve the optimization may not be sufficient. We are currently in the process of collecting higher resolution resting-state data to further investigate the limits of coherent functional organization across subjects.

5.3. Parcellation by hemisphere

The parcellation presented in Figure 6 was obtained by applying the groupwise multigraph clustering algorithm to each hemisphere separately, directly invoking the constraint that functional subunits do not span hemispheres. We also parcellated the whole brain without this constraint and the results were similar in terms of average whole-brain reproducibility. However, using the latter approach, we observed that there were regions containing components located in both the left and right hemispheres. Some of these regions were spatially connected directly across the interhemispheric fissure, e.g. regions along the cingular cortex, but some included more distal components, for example a region that contained both left and right insula in a parcellation at K = 50. To eliminate the possibility of a single parcellated subunit spanning both hemispheres we chose to parcellate each hemisphere separately. It should be noted that the fact that the multigraph clustering approach generates regions with disconnected but spatially symmetric components further supports the notion that these parcellations are truly based on function rather than anatomy.

5.4. Reproducibility

As the number of regions increased, we were able to identify functionally homogeneous regions on finer scales. For network analyses there is a need to delineate functional regions that represent the minimal functional subunit that can be identified in typical fMRI studies. In this work, reproducibility was computed and interpreted at both the local and whole-brain levels. At the local level, regions with high reproducibility were repeatedly parcellated from different groups of healthy subjects, suggesting that these regions are more likely to be functionally meaningful and salient in group studies. Some anatomically well-defined structures such as the caudate and putamen showed very high reproducibility scores and functional parcellations that coincided with their anatomic boundaries. In general, though, we did not observe obvious patterns in location-dependent reproducibility. Reproducibility did vary within brain lobes and from left hemisphere to right hemisphere, with the right hemisphere generally showing slightly higher reproducibility (Fig. 7). At a whole-brain level, a satisfactory parcellation must have a relatively high overall reproducibility. Figure 7 shows that the mean overall reproducibility across all K’s was above 0.75. Such high values of reproducibility not only add confidence to these findings, but the relative consistency of the reproducibility curve (across the range of K-values) supports the hypothesis that the brain indeed operates at multiple scales (Gonzalez-Castilloa et al., 2012). Minimal functional subunits are thus achievable using the proposed clustering approach as long as good whole-brain reproducibility is maintained and we do not approach the acquisition resolution limit (as we discussed in the previous section). The minimal functionally homogeneous subunits we present in this paper were obtained at K = 150 for a total whole-brain parcellation of approximately 300 functional subunits.

6. Conclusions

We have presented an approach to whole-brain parcellation based on resting-state fMRI data that yields nodes with coherent internal timecourses, making such nodes optimal for subsequent network analysis. The cross-subject reproducibility was measured at different levels of parcellations and, with consideration to acquisition resolution and anatomic variance across subjects, a whole-brain parcellation of approximately 300 functional subunits appears reasonable. We demonstrate that this parcellation has more coherent resting-state timecourses within nodes compared to anatomic atlases such as the AAL atlas. While future work will investigate whether these nodes rearrange under different conditions and if so the extent to which this occurs, the parcellations presented here represent the first attempt at a whole-brain functional subunit atlas of the healthy human brain at the level of typical fMRI acquisition resolutions. Previous work by Vincent et al. (Vincent et al., 2007) has shown that the connections measured by resting-state fMRI are intrinsic and present even under deep levels of anesthesia. However it is likely that just as the high baseline activity in fMRI can be modulated slightly by task, so too can connections between nodes. What is unclear at this point is the extent to which the nodes may rearrange with task or the extent to which it is simply the connection strengths between nodes that change. Nevertheless these parcellations provide a template for defining nodes for subsequent network analyses of the brain.

To use such a tool to examine the network level organization of a patient population versus a control group, one could apply the presented approach to the control group (or use our online parcellation from 79 healthy control subjects) and then use the resulting parcellation on both populations in order to contrast network properties for the entire set of nodes. A wide range of conditions can be contrasted in this manner; for example, in drug studies, the parcellation could be applied to the baseline data on the subjects prior to drug administration and then the network properties on and off the drug could be compared. In patient versus control studies it may also be interesting to obtain parcellations for each groups and directly compare them to determine the extent to which diseases or disorders are associated with differential organization in the brain at the level of these functional subunits.

In summary, a novel approach to parcellate the whole brain into functionally homogeneous subunits based on resting-state fMRI data is presented. The functional subunits obtained are from groupwise optimization and each subunit is assigned a reproducibility score, which shows the extent of agreement between different group selections using data from healthy control subjects. The proposed approach was validated using synthetic datasets and was shown to outperform other approaches in terms of the parcellation accuracy and spatial coherence. The ability to derive a whole-brain delineation of subunits solely based on function has great importance for fMRI in general and especially for network connectivity analyses. Using the proposed approach, the homogeneity of temporal signals from a subunit is assured by the algorithm, such that the mean timecourse from any given node is an accurate representation of activity from that part of the brain, and this is achieved without the need for a priori assumptions or hypotheses. Such a data-driven parcellation improves in the input to network analyses and will prevent the erroneous results that can arise if multiple timecourses are mixed within the same node. This approach should therefore improve the reliability and sensitivity of network analyses.

Highlights.

• Resting-state connectivity data parcellated using graph theory approach

• Yields groupwise whole-brain parcellation of the order of 300 nodes

• Uniform timecourses within nodes

• Ideal for network analysis of functional connectivity

• Functional atlas available online