Abstract
Intrinsic functional connectivity analysis using resting-state functional magnetic resonance imaging (rsfMRI) has become a powerful tool for examining brain functional organization. Global artifacts such as physiological noise pose a significant problem in estimation of intrinsic functional connectivity. Here we develop and test a novel random subspace method for functional connectivity (RSMFC) that effectively removes global artifacts in rsfMRI data. RSMFC estimates the partial correlation between a seed region and each target brain voxel using multiple subsets of voxels sampled randomly across the whole brain. We evaluated RSMFC on both simulated and experimental rsfMRI data and compared its performance with standard methods that rely on global mean regression (GSReg) which are widely used to remove global artifacts. Using extensive simulations we demonstrate that RSMFC is effective in removing global artifacts in rsfMRI data. Critically, using a novel simulated dataset we demonstrate that, unlike GSReg, RSMFC does not artificially introduce anti-correlations between inherently uncorrelated networks, a result of paramount importance for reliably estimating functional connectivity. Furthermore, we show that the overall sensitivity, specificity and accuracy of RSMFC are superior to GSReg. Analysis of posterior cingulate cortex connectivity in experimental rsfMRI data from 22 healthy adults revealed strong functional connectivity in the default mode network, including more reliable identification of connectivity with left and right medial temporal lobe regions that were missed by GSReg. Notably, compared to GSReg, negative correlations with lateral fronto-parietal regions were significantly weaker in RSMFC. Our results suggest that RSMFC is an effective method for minimizing the effects of global artifacts and artificial negative correlations, while accurately recovering intrinsic functional brain networks.
Keywords: fMRI, resting state, functional connectivity, random subspace, partial correlation, global artifacts
Introduction
Resting-state functional magnetic resonance imaging (rsfMRI) has emerged as a powerful technique for characterizing brain networks and functional connectivity (Beckmann et al., 2005; Biswal et al., 1995; Fox and Raichle, 2007; Fox et al., 2005; Greicius et al., 2003; Supekar et al., 2008; Van Dijk et al., 2010). One commonly used method for functional connectivity analysis is a seed-based investigation in which time series from a seed region of interest (ROI) is used as a covariate in a regression analysis with all other voxels in the brain. This approach has led to a number of important discoveries including the default mode network (DMN) (Greicius et al., 2003). Despite its widespread application to the characterization of intrinsic functional brain circuits in health and disease, the question of how global noise processes should be removed represents a significant and vexing problem (Birn, 2012; Weissenbacher et al., 2009).
Spontaneous fluctuations of rsfMRI signals contain multiple sources of noise that are, in general, hard to estimate and remove. For example, cardiac pulsation induces signal fluctuations in large vessels which then cause widespread BOLD signals changes in the brain (Dagli et al., 1999). Global noise also arises from respiration cycles that can cause head movements and variations in the static magnetic field, which subsequently impact signals across the entire brain (Raj et al., 2001). Additionally, variations in both respiration and heart rate can cause correlated signal changes throughout gray matter (Birn et al., 2006; Chang et al., 2009; Shmueli et al., 2007; Wise et al., 2004). Critically, due to the aliasing effects from long sampling times typically used in rsfMRI scanning, such physiological noise cannot be removed by filtering in the frequency domain (Lowe et al., 1998). Consequently, rsfMRI signal fluctuations arising from neurophysiological activity are confounded by multiple global noise processes, thereby leading to overestimation of intrinsic functional connectivity. Removal of these global artifacts from rsfMRI signals is therefore of paramount importance for accurate measurement of intrinsic functional connectivity.
In recent years, several methods have been developed to remove different components of these global artifacts. RETROICOR (Glover et al., 2000) removes time-locked cardiac and respiratory artifacts, and RVHRCOR (Chang et al., 2009) regresses out signal changes related to respiration and heart rate variations. Both methods require independent and accurate external measurements of heart rate and respiration; data that is often difficult to acquire in pediatric and clinical participants. Furthermore, most public domain rsfMRI datasets from sources such as the 1000 Functional Connectomes Project and Autism Brain Imaging Data Exchange (ABIDE) do not contain measures of heart rate and respiration thereby precluding the use of existing global artifact removal methods for these important publically available datasets. Thus, alternate and accurate methods are needed for global artifact removal in rsfMRI data. Most commonly used methods to achieve this goal are based on estimation and removal of global noise derived from the rsfMRI data itself. These approaches are much more flexible and researchers have used a variety of methods to estimate non-neurophysiological noise in the data. For example, some studies have used principal components from white matter and cerebrospinal fluid (CSF) fMRI signals as nuisance regressors that presumably do not contain signals from neurophysiological sources (Behzadi et al., 2007; Chai et al., 2012). However, because respiration also impacts gray matter (Birn et al., 2006; Wise et al., 2004), signals from white matter alone do not fully represent global artifacts, and consequently functional connectivity between brain regions may still be overestimated. To overcome this issue researchers have used various types of global signal regression (GSReg) procedures based on either the global mean signal computed across the whole brain (Desjardins et al., 2001; Greicius et al., 2003; Macey et al., 2004) or a linear combination of signals computed from voxels in grey matter, white matter and CSF (Fox et al., 2005). GSReg has been the most widely used approach because early studies revealed a more consistent and focal pattern of functional brain connectivity (Fox et al., 2005; Fox et al., 2009; Greicius et al., 2003). For example, analysis of PCC connectivity using GSReg has consistently identified major nodes of the DMN consistent with other approaches such as ICA (Seeley et al., 2007). One problem with GSReg is that it also identifies strong negative correlations. The validity of GSReg has recently been questioned because it introduces artificial anti-correlations in ways that can be unambiguously demonstrated mathematically (Murphy et al., 2009; Weissenbacher et al., 2009). Thus, observed anti-correlation between brain systems in experimental data might arise as an artifact of the procedures currently used to estimate and remove the global artifacts. It currently remains unclear how to derive optimal nuisance regressors that can produce the most robust and accurate functional connectivity map.
A different approach is to use partial correlation based methods that can remove the effects of global artifacts by measuring the connectivity between the seed region and every voxel in the brain after removing the (linear) dependence of other voxels. Partial correlations between the seed region and all brain voxels can be computed by inverting and appropriately scaling the sample covariance matrix (Edwards, 2000) based on the time series of the seed region and all brain voxels. Unfortunately, since the number of features (p, number of voxels) is larger than the number of samples (N, number of time points or scans), the sample covariance matrix is singular and is not invertible (Ryali et al., 2012). In such cases, pseudo-inverse methods are often used. The pseudo-inverse is constructed from nonzero eigenvalues of the sample covariance matrix and corresponding eigenvectors. However, pseudo-inverse solutions suffer from significant estimation error when p valli N because components corresponding to nonzero eigenvalues of the sample covariance matrix may be eliminated even though they contain useful information (Hoyle, 2010). To overcome this problem, Hoyle (2010) proposed a random subspace method (RSM) to reduce estimation errors of standard pseudo-inverse methods. In RSM, multiple subsets of features are randomly sampled from the feature space, and partial correlations between features within each subset are computed using a pseudo-inverse. RSM provides a more accurate estimate of the partial correlation matrix because the sample-to-feature ratio is higher in each random subspace compared to the original feature space, thus shifting the estimation error curve towards the direction of a larger effective sample size.
Here, we develop a novel RSM-based method to remove global artifacts and estimate whole-brain functional connectivity in rsfMRI data – an approach we refer to as RSM functional connectivity or RSMFC. We first evaluate our methods on a carefully constructed simulated dataset in which there are no inherent negative correlations. We then use this dataset to examine the performance of RSMFC and compare its performance with results from GSReg. Critically, we demonstrate that unlike GSReg, RSMFC does not artificially introduce negative correlations in data in which there are no inherent negative correlations. Finally, we examine functional connectivity of the posterior medial cortex based on experimental rsfMRI data from 22 healthy adults and show that our method effectively removes global artifacts and recovers the DMN with better anatomical specificity than GSReg.
Methods
Estimation of partial correlations in seed-based functional connectivity analysis
Let YN×p be BOLD fMRI time series of p voxels. Observations (rows of Y) are sampled from a multivariate normal distribution N(µ1 ×p,Σp×p). A partial correlation value Πi j is a measure of the direct linear interaction between brain voxels i and j that cannot be explained by influence of the remaining (p – 2) voxels. It can be shown that the partial correlation matrix Π can be computed from the covariance matrix Σ of p voxels by using the following relations (Edwards, 2000)
| (1) |
| (2) |
Typically, Σ is estimated by the sample covariance matrix
| (3) |
and Π is estimated by using the sample estimate of (Σ̂−1). However, the inversion of Σ in Equation (1) is problematic for high-dimensional fMRI data because when the number of time points (N) is less than the number of voxels (p), Σ̂ becomes singular and is not invertible. To circumvent this issue, Moore-Penrose pseudo-inverse (here, referred to pseudo-inverse) is commonly used, which is constructed from the eigenvectors of corresponding nonzero eigenvalues of the sample covariance matrix Σ̂. In Equations (1) and (2), Θ and Π are now estimated as
| (4) |
| (5) |
where Σ̂+ denotes the pseudo-inverse of Σ̂.
For the whole brain seed-based functional connectivity analysis, Y is augmented to include the mean time course of the seed brain region as well as the time course of every voxel in the brain, and now Y has (p + 1) columns in total. Assuming that the first column of Y stores the time course of the seed region, values in the first column of Π̂ are the partial correlation coefficients between the seed region and every voxel in the brain. However, it is undesirable to directly use the pseudo-inverse to estimate Π̂. Even though zero eigenvalues and corresponding eigenvectors of the sample covariance matrix are discarded to construct the pseudo-inverse, precision of the pseudo-inverse still depends on those small, but nonzero, eigenvalues. When p ≫ N, which is typical for a whole-brain functional connectivity analysis, nonzero eigenvalues may become small enough to result in an unreliable estimate of the partial correlation matrix. Thus, additional thresholding is applied to remove small nonzero eigenvalues. However, arbitrary thresholding inevitably discards small eigenvalues that may be large in the population covariance matrix (Σ), thus resulting in significant bias (Hoyle, 2010). This is because as N/p becomes smaller, the sample eigenvalues become more spread out than population eigenvalues. One consequence is that sample eigenvalues for noise processes can become larger than the largest population eigenvalue.
Hoyle (2010) proposed an elegant random subspace method (RSM) to address this issue. In RSM, a subset of features are randomly sampled without replacement from the entire feature space, and a pseudo-inverse is applied to compute partial correlations between features within the subspace. Since each subspace only provides an estimate of a subset of the partial correlation matrix (Π̂) multiple random subsets are sampled to cover the entire Π̂. for RSM to be accurate, the partial correlation matrix computed from each subspace needs to be a good estimate of the corresponding sub-matrix of Π̂. In other words, it requires weak dependence between the selected subset of features and subsets chosen from omitted features. Even for data for which this assumption is not met, Hoyle (2010) showed that RSM can greatly improve accuracy in estimating the pseudo-inverse for a wide range of population covariance structures. Moreover, for its application to functional connectivity analysis, we are only interested in regressing out global artifacts, which are expected to be well captured by confounds contained in randomly selected subsets of voxels. Therefore, the influence to be regressed out is similar within each subspace, which is equivalent to removing global artifacts from each subspace.
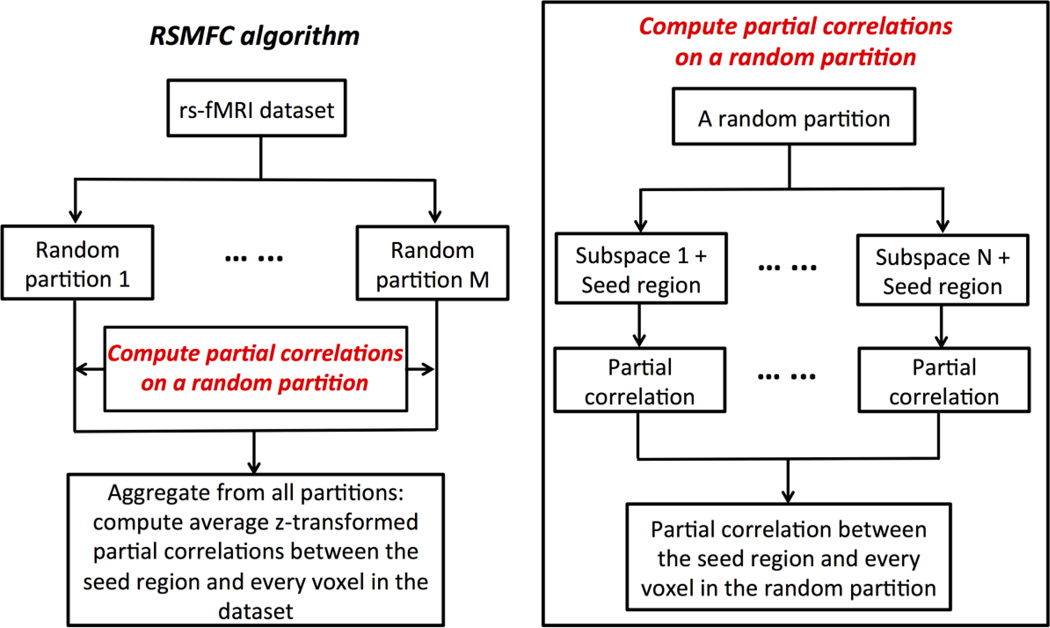
Here, we employ RSM to estimate functional connectivity between the seed region and every voxel in the brain conditional upon randomly selected subsets of voxels. Figure 1 shows the schematic flow of our RSMFC algorithm. In RSMFC a subset of p0 voxels is randomly selected without replacement and put together with the seed region. The data in the lth subspace is denoted as , assuming the first column is always the signal of the seed region. Thus, the first column of the partial correlation matrix of represents correlation strength between seed region and each voxel in the subset, which is conditional on influence of the remaining (p0 – 1) voxels. Multiple subsets need to be sampled in order to (1) compute a complete set of partial correlations between the seed region and every voxel in the brain, and (2) reduce sampling variance by taking into account spatially heterogeneous global artifacts (e.g. physiological noises in white matter versus gray matter). To sample multiple subsets, we first randomly permute the original voxel indices and note the correspondence between the permuted and the actual voxel indices for the subsequent aggregation of the computed partial correlations in each partition. In the permuted voxel sequence, we take a specific number of voxels (p1) from the beginning of the permuted voxel sequence and append them to the end of the permuted voxel sequence such that the total number of voxels (p + p1) is a multiple of p0 (p1 ≤ p0). Then, we perform a partitioning on the newly created voxel sequence (i.e., the first p0 voxels is the first subset, the second p0 voxels is the second subset, etc.). With this approach, for a single partitioning on the voxel sequence, no voxel is represented twice in a same subset. We repeat the previous steps to create multiple partitions. Pseudo-codes of the sampling procedure are provided in the Supplementary Materials (Appendix A.1). The proposed sampling scheme guarantees that each single partition provides a complete set of partial correlations between the seed region and every voxel in the brain. Finally, each subject’s partial correlations from all partitions are first z-transformed and then averaged for group level analysis. The final output is a vector of group-level t-statistics for voxels in the brain, with each t-statistic representing the functional connectivity strength between the seed region and a voxel in the brain.
Figure 1.
Random subspace method functional connectivity (RSMFC) algorithm.
Tuning parameters in RSMFC
There are two tuning parameters that determine the efficacy of RSMFC. They are: (1) the number of voxels in a subset (subspace size), and (2) the number of random partitions on the voxel sequence. If the number of voxels in a subset is too large, it is more likely that the randomly sampled voxels in a subspace may include those that have inherent functional correlations with the seed region. Therefore using partial correlations may obscure true functional correlations when influence of those voxels is regressed out. Additionally, a larger subspace results in a loss of degrees of freedom, thus decreasing power for the detection of the true functional connectivity. On the other hand, if a subset is too small, it may not accurately capture global artifacts, leading to a significant overestimation of functional correlations. However, in practice, the true underlying connectivity pattern is unknown, and it is hard to determine the optimal subspace size.
To address these issues, we develop a novel approach to select the optimal subspace size for removing global artifacts. Described below are the procedures we use to select the optimal subspace size. Before removing any global artifacts, a simple full correlation is computed between the seed region and every other voxel in the brain. For simplicity, we denote this scenario as a subspace size of zero to imply no application of RSMFC. The resulting distribution of voxel-wise group-level t-statistics is significantly shifted away from zero (e.g. mode of the distribution), representing an overestimation of functional connectivity (Chai et al., 2012; Murphy et al., 2009; Weissenbacher et al., 2009). When the subspace size increases, the distribution is expected to shift closer to zero because global artifacts are increasingly regressed out. However, after removal of global artifacts, additional shift of the distribution due to suppression of global artifacts becomes slower, and the shift is likely caused by loss of degrees of freedom. One intuitive approach to quantify this behavior is to compute changes in Euclidian distance between zero and vectors of voxel-wise group-level t-statistics associated with different subspace sizes,
| (6) |
where ti,S is the t-statistic for the ith voxel corresponding to the sth subspace size. We vary the subspace size from 10 to 100 voxels in increments of 10 voxels. We select the optimal subspace size as the one at which the percentage change in Euclidean distance defined in Equation (6) between two successive subspace sizes is less than or equal to 10%.
The second tuning parameter is the number of partitions for RSMFC to converge on a stable connectivity pattern given a specific subspace size. Similar to the approach in selecting the optimal subspace size, we monitor changes in Euclidean distances between zero and vectors of voxel-wise group-level t-statistics associated with an increasing number of partitions. If the connectivity pattern is stable beyond a certain number of partitions, little change in each voxel’s t-statistic is expected when one additional partition is performed, and the slope of Euclidean distance becomes zero. Here, RSMFC is determined to converge if the percentage change (ΔD) in Euclidean distances between two consecutive number of partitions is less than or equal to 1%
| (7) |
where ti,m is the t-statistic for the ith voxel associated with m partitions. We choose a stricter criterion for convergence to promote stability of the functional connectivity map.
Implementation details
Since it is computationally infeasible to tune RSMFC on the whole brain dataset, we first generate a subset from the original whole brain dataset solely for the purpose of parameter tuning. Specifically, we randomly sample a subset of voxels (10,000 voxels). Their time courses across all subjects comprise the subset. In order to keep optimizing subspace size independent from estimating seed-based functional connectivity, the seed of interest for the original dataset is not used here. Instead the first voxel is taken as the seed for the subset, and we confirm that the selected seed voxel is in gray matter. Its partial correlations with the rest of voxels in the subset are computed using the RSMFC algorithm. Another advantage of using an independent seed in the subset is that the selected optimal subspace size can be applied to the original dataset for different seeds of interest that do not contain the independent seed used for parameter tuning. To select the optimal subspace size, we first fix the number of partitions at 200 because it is usually large enough. For example, in the Results section, we show that convergence within 200 partitions is robust across various subspace sizes. Finally, we apply RSMFC to the original whole-brain dataset with the selected optimal subspace size and 200 partitions using the same algorithm (Figure 1).
Experimental rsfMRI data
Data Acquisition
rsfMRI data were acquired from 22 adult participants (Supekar and Menon, 2012). The Stanford University Institutional Review Board approved the study protocol. The subjects (11 males, 11 females) ranged in age from 19 to 22 yrs (mean age 20.4 yrs) with an IQ range of 97 to 137 (mean IQ: 112). The subjects were recruited locally from Stanford University and neighboring community colleges.
For the rsfMRI scan, participants were instructed to keep their eyes closed and their bodies still for the duration of the 8-min scan. Functional Images were acquired on a 3 T GE Signa scanner (General Electric) using a custom-built head coil. Head movement was minimized during scanning by a comfortable custom-built restraint. A total of 29 axial slices (4.0 mm thickness, 0.5 mm skip) parallel to the AC-PC line and covering the whole brain were imaged with a temporal resolution of 2 s using a T2* weighted gradient echo spiral in-out pulse sequence (Glover and Law, 2001) with the following parameters: TR = 2,000 ms, TE = 30 ms, flip angle = 80°, interleave. The field of view was 20 cm, and the matrix size was 64×64, providing an in-plane spatial resolution of 3.125 mm. To reduce blurring and signal loss arising from field inhomogeneity, an automated high-order shimming method based on spiral acquisitions was used before acquiring functional MRI scans. A high-resolution T1-weighted spoiled grass gradient recalled (SPGR) inversion recovery 3D MRI sequence was acquired to facilitate anatomical localization of functional data. The following parameters were used: Tl = 300 ms, TR = 8.4 ms; TE = 1.8 ms; flip angle = 15°; 22 cm field of view; 132 slices in coronal plane; 256 × 192 matrix; 2 NEX, acquired resolution = 1.5×0.9×1.1 mm. Structural and functional images were acquired in the same scan session.
Data Preprocessing and Analysis
Data were preprocessed using SPM8. For each subject, the first eight image acquisitions of the rsfMRI time series were discarded to allow for stabilization of the MR signal. The remaining 232 volumes were preprocessed by the following steps: realignment, slice-timing, normalization to the MNI template, and smoothing carried out using a 6-mm full-width half maximum Gaussian kernel to decrease spatial noise. Excessive motion, defined as greater than 3.5 mm of translation or 3.5° of rotation in any plane, was not present in any of the resting state scans.
Nuisance effects from motion (six regressors generated by SPM8 realignment procedure, three in translation and three in rotation) were regressed out from the preprocessed data for each subject. Data was further filtered using a band-pass filter (0.008 Hz < f < 0.1 Hz). For GSReg, the mean time course of voxels within the brain was additionally regressed out of the band-pass filtered data before computing the seed based functional connectivity map. For RSMFC, we perform functional connectivity analysis only on the band-pass filtered data in which the global mean signal is not regressed out. Both GSReg and RSMFC were first applied at the individual subject level. For the group-level analysis, we performed voxel-wise one-sample t-tests across z-transformed correlation coefficients of 22 subjects (a random effects analysis). On the experimental dataset, we thresholded the group-level connectivity t-map using a combination of a voxel-wise height threshold of p < 0.001 and a spatial extent threshold of 42 voxels using a Monte Carlo simulation approach similar to AFNI’s AlphaSim program (Forman et al., 1995; Ward, 2000). The overall p-value corresponds to p < 0.01 for a family-wise error correction.
The seed region used to generate a whole brain connectivity map is a 6-mm sphere ROI located in posterior cingulate cortex (PCC). The center of our ROI was the same as seed number 4 (PCC: MNI coordinates: X = −2, Y = −36, Z = 35) used by Margulies et al. (2009) located in one of the core nodes of default mode network (DMN) (Greicius et al., 2003)
To compare spatial connectivity patterns estimated by GSReg and RSMFC, we created two sets of 6-mm sphere ROIs. The first set consists of major nodes in DMN, including bilateral medial prefrontal cortex (mPFC), angular gyrus regions (AG), and medial temporal lobes (MTL). The second set consists of lateral fronto-parietal regions for which GSReg revealed significant negative correlations with the PCC. These ROIs are in bilateral frontal eye field (FEF), intraparietal sulcus (left IPS and right IPS) and middle temporal complex (left and right MT+). Centers of all ROIs except the ones in MTL were taken from local peaks in the connectivity map from GSReg, while centers of ROIs in MTL were taken as local peaks identified by RSMFC.
Additional analysis compared our results with those obtained using aCompCor (Behzadi et al., 2007; Chai et al., 2012) a method that uses principal component analysis to identify and remove global artifacts. Detailed description of this method is in the Supplementary Materials (Appendix A.2).
Simulated rsfMRI data
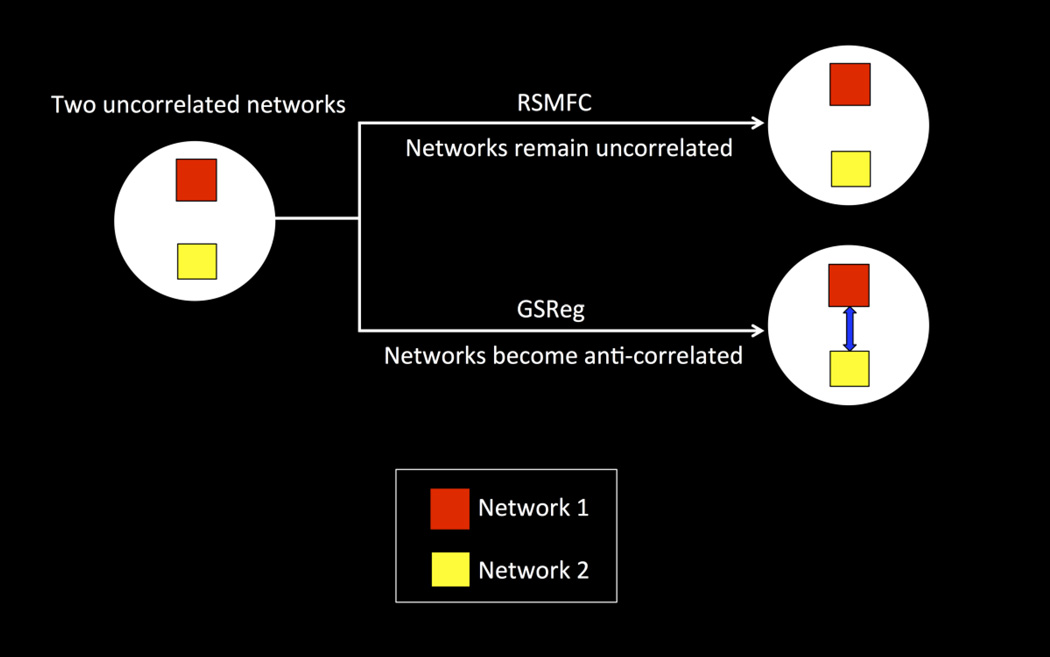
We generated a simulated dataset to demonstrate that (1) RSMFC is able to successfully suppress global artifacts and (2) RSMFC does not artificially introduce anti-correlations between uncorrelated networks. Specifically, we expect uncorrelated networks to become anti-correlated under GSReg but remain uncorrelated under RSMFC (see the illustrative model in Figure 2).
Figure 2. Model illustrating advantages of RSMFC.
Network 1 (denoted as the red square) and network 2 (denoted as the yellow square) are two uncorrelated networks. Using RSMFC, the two networks remain uncorrelated while GSReg introduces strong anti-correlations (represented by blue arrow) between the two uncorrelated networks. RSMFC = random subspace method functional connectivity. GSReg = global signal regression method.
We created two uncorrelated networks in the simulated dataset. Each voxel’s signal was modulated by two linearly additive sources
| (8) |
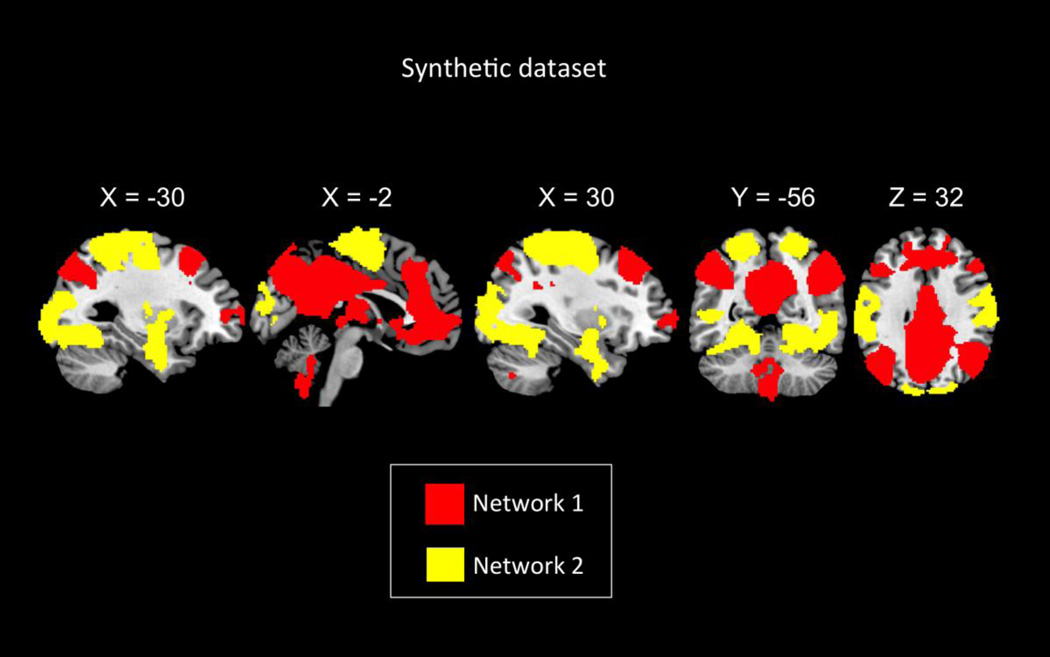
where fi is the network specific signal, g is the global artifact and ci is the strength or influence of global artifacts at the ith voxel. We used the following procedure to synthesize two networks from rsfMRI data. We used the selected PCC seed region to find functional connectivity between PCC and rest of the brain’s voxels using GSReg. Figure 3 shows spatial boundaries of the two networks created by thresholding the group-level whole brain connectivity map of the PCC seed after applying GSReg on the 22-subject experimental rsfMRI dataset described in the previous section (FDR < 0.001). Voxels that were positively correlated (12.33% of the whole brain voxels) with the PCC seed comprised the network 1. Voxels that had negative correlations (22.51% of the whole brain voxels) are part of network 2. Since voxels were highly correlated both within and between networks in the original band-pass filtered rsfMRI dataset, we destroyed the between-network correlation by randomizing the phase between the time courses of the two networks. This manipulation has the advantage of keeping the spectral information of the original time courses. Specifically, to destroy the correlation between networks, we added a randomly generated common phase to all time courses within network 1, and similarly another random common phase to time courses in network 2. We also added a different random phase to each voxel-wise time course outside the two networks such that voxels outside the two networks were uncorrelated with each other as well as with voxels in either network. As a result, correlations between voxels within each network still remained high and were spatially varied, thereby providing a more realistic model of brain activity. Finally, a global artifact signal was added to all voxels in the brain. The confound signal at each voxel was generated as the original global mean signal weighted by its correlation with each voxel’s original time course. The scaling was used to introduce regional difference in the global artifact. We used the same PCC seed region to compute the whole-brain functional connectivity map in both GSReg and RSMFS.
Figure 3. Spatial maps of the two simulated uncorrelated networks.
Network 1 consists of voxels colored in red while network 2 consists of voxels colored in yellow.
The performance of RSMFC and GSReg were assessed using ROC curves. The false positive rate (FPR) and true positive rate (TPR) used in ROC curves are defined as:
| (9) |
| (10) |
where FP is the number of false positives, TN is the number of true negative, TP is the number of true positives and FN is the number of false negatives. Specifically, we varied thresholds on the absolute t-statistics and computed FPR and TPR under each threshold. Thus both false anti-correlations and false positive correlations are counted as false positives. The resulting FPR-TPR pairs were used to plot ROC curves for both RSMFC and GSReg.
Results
Performance on the simulated fMRI dataset
Selection of the optimal subspace size and convergence of RSMFC
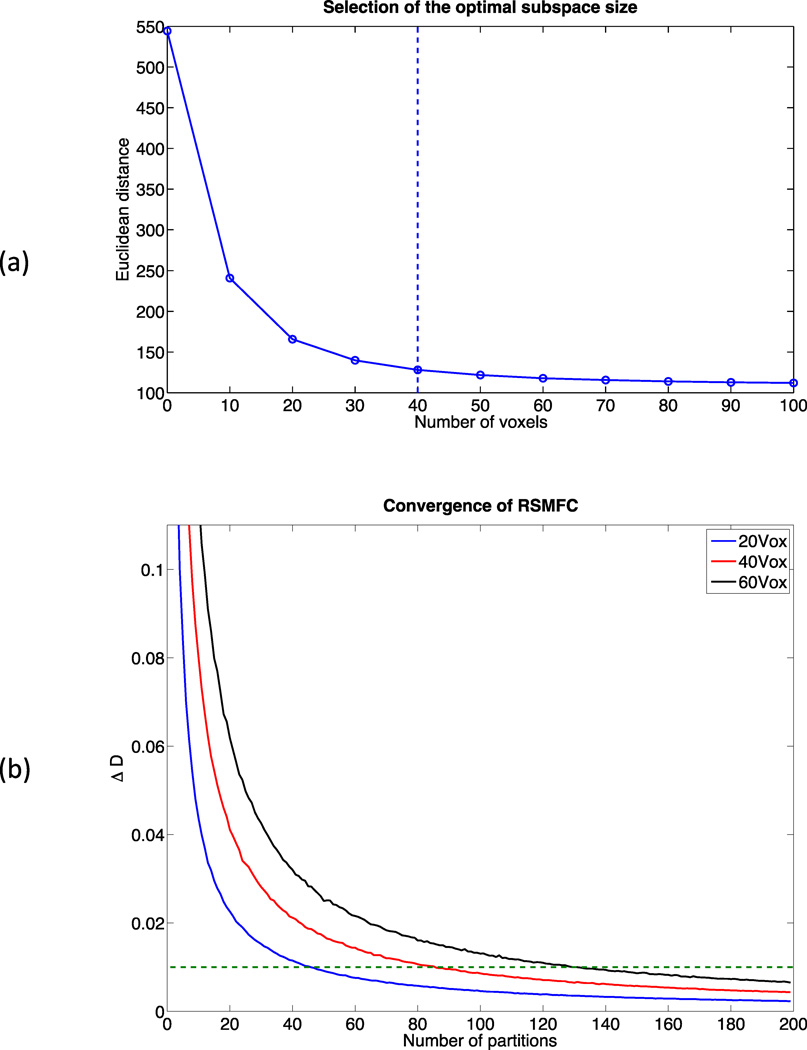
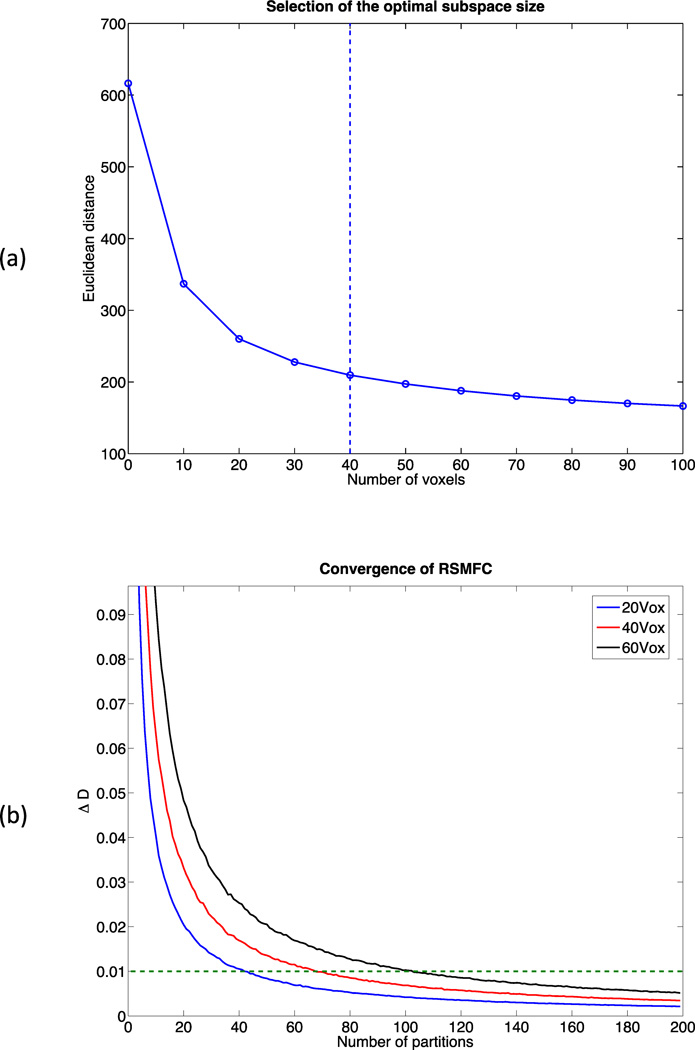
Parameter tuning was performed on a sub-dataset consisting of 10,000 randomly selected voxels. Figure 4 (a) shows changes in distance between zero and the vector of t-statistics of 10,000 voxels. Based on the criteria of percentage change in distance less than or equal to 10%, 40 voxels were selected as the optimal subspace size. For subspace sizes smaller than 40 voxels, distance dropped significantly, indicating a large shift of the distribution of voxel-wise t-statistics towards zero. For subspace sizes greater than 40 voxels, the change rate was relatively constant, likely representing the relatively stable adjustment from loss of degrees of freedom. Additionally, based on the criteria of less than or equal to 1% change rate, we found 200 partitions were large enough for RSMFC to converge. Figure 4 (b) shows convergence curves for RSMFC under subspace sizes of 20, 40 and 60 voxels, and we observed robust convergence. Therefore, we applied RSMFC to the simulated dataset with 200 partitions and a subspace size of 40 voxels.
Figure 4. Parameter tuning of RSMFC on the simulated dataset.
(a) Changes in Euclidean distance between zero and the vector of group-level voxel-wise t-statistics with respect to the subspace size. The optimal subspace size is selected as the percentage change in distance less than or equal to 10%, which is indicated by the dashed line. The optimal subspace size is chosen as 40 voxels for the simulated data. (b) Percentage change in distance with various subspace sizes. The dashed line marks the convergence criterion of 1%. RSMFC converges robustly within 200 partitions. RSMFC = random subspace method functional connectivity. GSReg = global signal regression method.
Comparison of RSMFC and GSReg on the simulated dataset
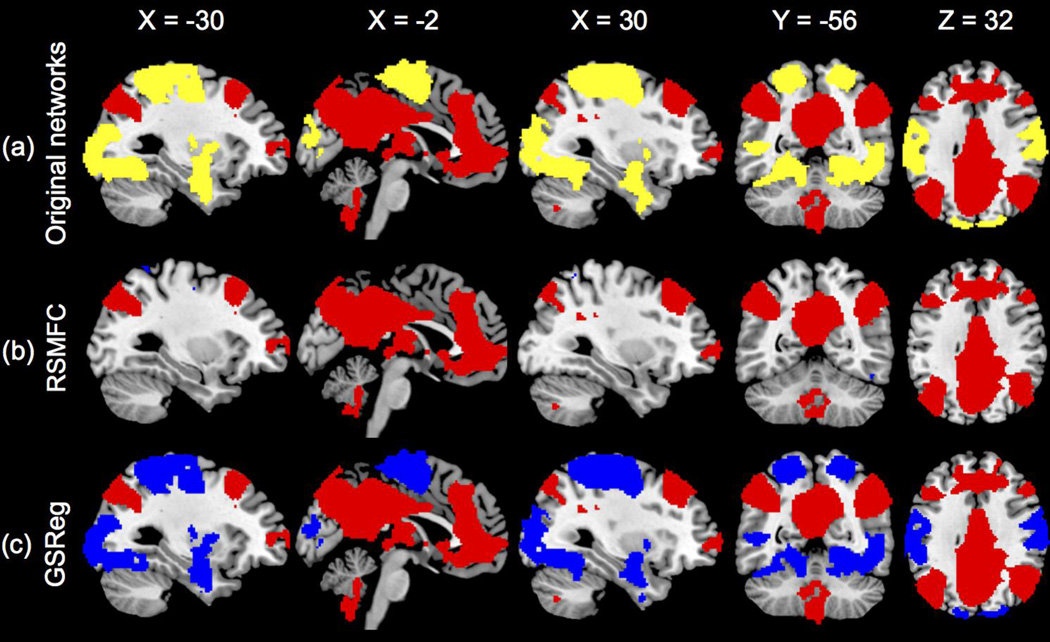
Figure 5 shows the functional connectivity maps estimated by both GSReg and RSMFC with the selected optimal subspace size of 40 voxels. Both maps were thresholded with FPR < 0.001 and further masked by the two predetermined networks because we were primarily interested in the relation change between the two originally uncorrelated networks. RSMFC successfully removed the added global artifacts because it spatially uncovered network 1 in which voxels were highly positively correlated with the seed ROI, and network 2 remained uncorrelated with network 1. In contrast, the two inherently uncorrelated networks became strongly anti-correlated using GSReg method.
Figure 5. Identification of networks by RSMFC and GSReg on the simulated dataset.
(a) Original uncorrelated simulated networks. (b) RSMFC accurately identifies the positively correlated network and correctly excludes the uncorrelated network. The two networks remain uncorrelated in RSMFC. (c) In GSReg, the two originally uncorrelated networks become anti-correlated. Voxels that have positive correlations with the ROI seed are colored red and voxels in the other uncorrelated network are colored yellow. Voxels that have negative correlations are colored blue. Both connectivity maps are thresholded under FDR < 0.001 and then masked by the two preset networks. RSMFC = random subspace method functional connectivity. GSReg = global signal regression method.
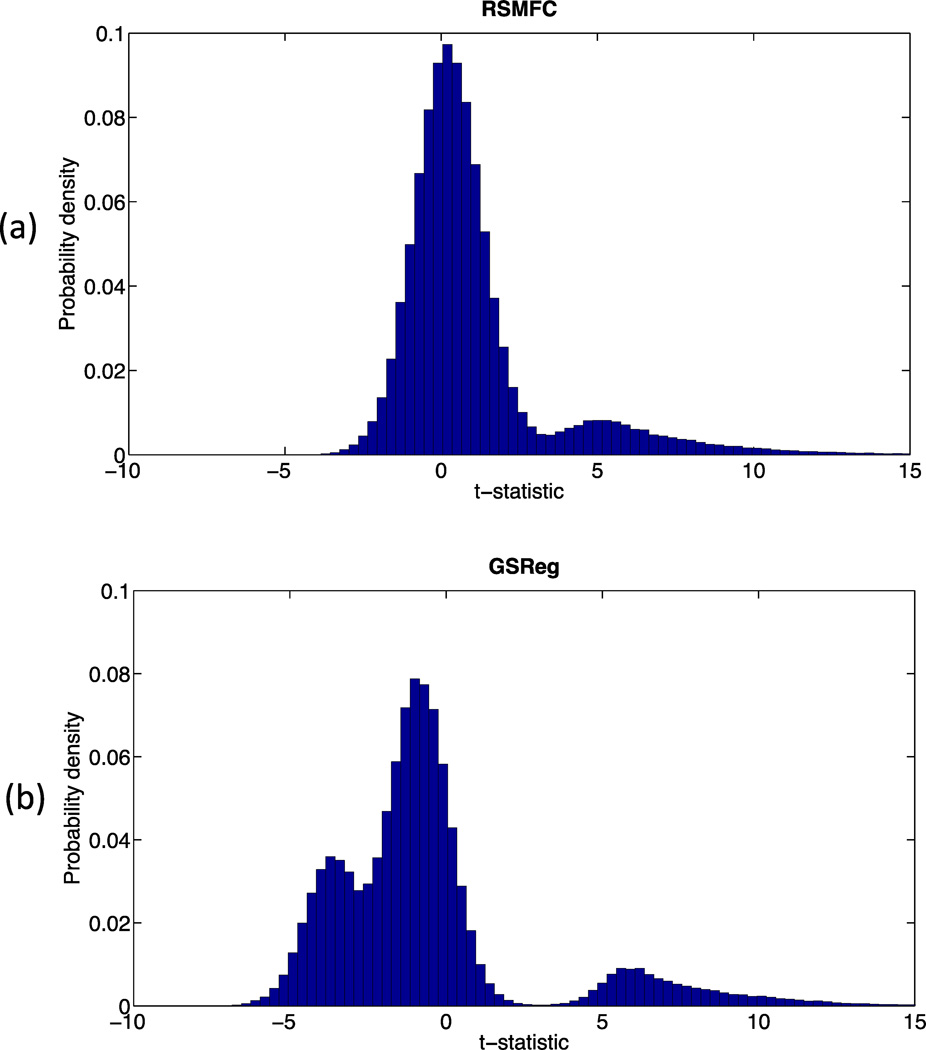
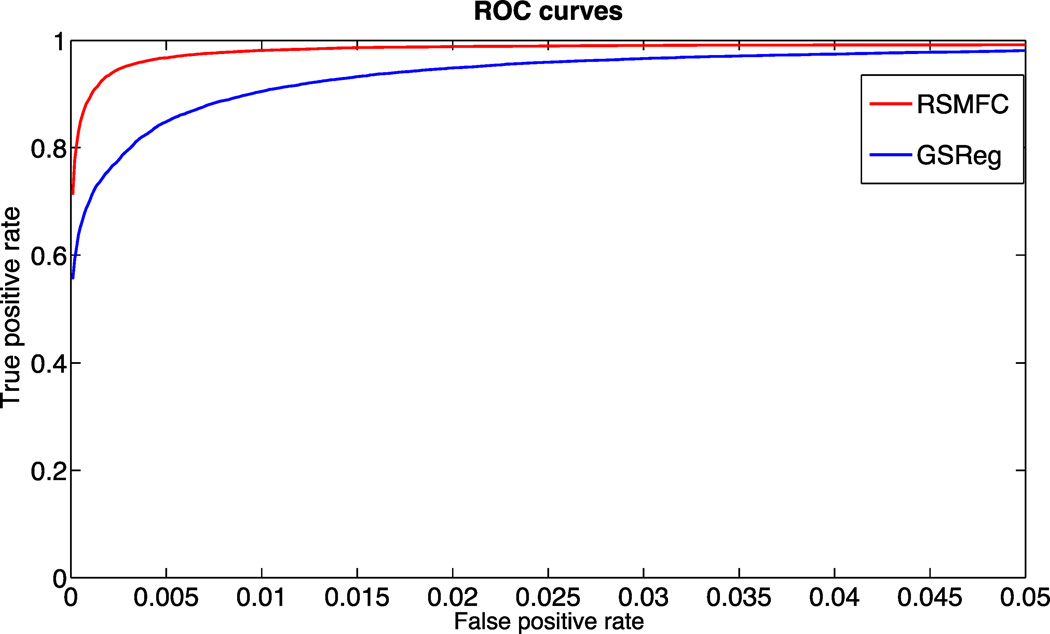
Table 1 shows the percentages of voxels in network 2 that are anti-correlated with the seed region under various commonly used voxel-wise height thresholds (p < 0.05, 0.01 and 0.001). In contrast to GSReg that consistently resulted in large numbers of negative correlations, the percentage of negative correlations using RSMFC were well controlled and were close to the preset voxel-wise height threshold. Figure 6 further illustrates this phenomenon by comparing distributions of voxel-wise t-statistics from both methods. The t-statistics of the majority of voxels (i.e., voxels uncorrelated with the seed ROI) were negative for GSReg, however RSMFC centered t-statistics of uncorrelated voxels around zero and those of voxels in the same network of the seed region around the t-statistic of 5. Overall, by considering both false positive and true positive measures using ROC curves, performance of RSMFC was shown to be superior to GSReg on the simulated dataset (Figure 7).
Table 1. Percentages of voxels in network 2 that are anti-correlated with the seed ROI on the simulated dataset.
Percentages are shown for both RSMFC and GSReg under 3 different commonly used voxel-wise height thresholds of p < 0.05, 0.01 and 0.001.
| p < 0.05 | p < 0.01 | p < 0.001 | |
|---|---|---|---|
| RSMFC | 6.74% | 1.29% | 0.07% |
| GSReg | 99.30% | 92.86% | 55.86% |
Figure 6. Comparison of normalized histograms of group-level whole-brain t-statistics on the simulated dataset.
Distribution of voxel-wise t-statistics with (a) RSMFC and (b) GSReg. Unlike GSReg in which a major portion of the distribution had negative values, RSMFC has a distribution centered at zero. This indicates successful suppression of the added global artifacts and no significant negative correlations. RSMFC = random subspace method functional connectivity. GSReg = global signal regression method.
Figure 7. ROC curves for RSMFC and GSReg on the simulated dataset.
RSMFC performs significantly better than GSReg in terms of area under the curve. Red line shows ROC curve for RSMFC; blue line shows ROC curve for GSReg. ROC = Receiver Operating Characteristic. RSMFC = random subspace method functional connectivity. GSReg = global signal regression method.
Performance on the experimental rsfMRI dataset
Selection of the optimal subspace size and convergence of RSMFC
Figure 8(a) shows changes in distance between zero and the vector of t-statistics of a subset of 10,000 voxels, and Figure 8(b) shows convergence curves of RSMFC with various subspace sizes of 20, 40 and 60 voxels. Based on the same criteria used on the simulated sub-dataset, the optimal subspace size was 40 voxels, which happened to be the same subspace size determined for the simulated data set. Therefore, we applied RSMFC to the experimental rsfMRI dataset with 200 partitions and an optimal subspace size of 40 voxels.
Figure 8. Parameter tuning for RSMFC on the experimental rsfMRI dataset.
(a) Change in Euclidean distance between zero and the vector of group-level voxel-wise t-statistics with respect to the subspace size. The optimal subspace size is selected as the percentage change in distance less than or equal to 10%, as indicated by the dashed line. The optimal subspace size is chosen as 40 voxels for the experimental rs-fMRI dataset. (b) Percentage change in distance with respect to the number partitions for various subspace sizes. The dashed line indicates the convergence criterion of 1%. RSMFC robustly converges within 200 partitions. RSMFC = random subspace method functional connectivity. GSReg = global signal regression method.
Comparison of RSMFC and GSReg on the experimental rsfMRI dataset
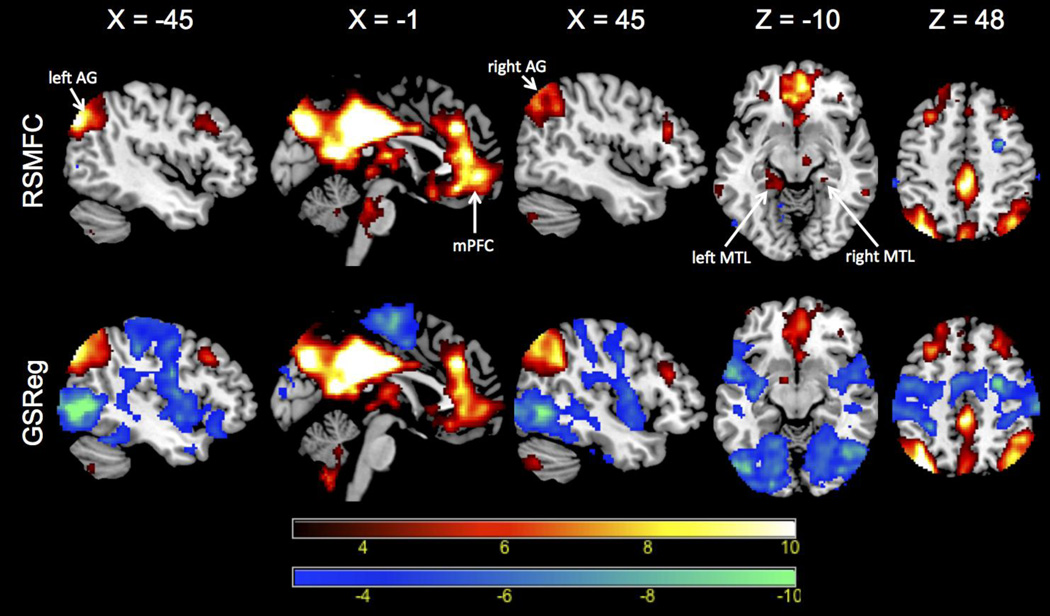
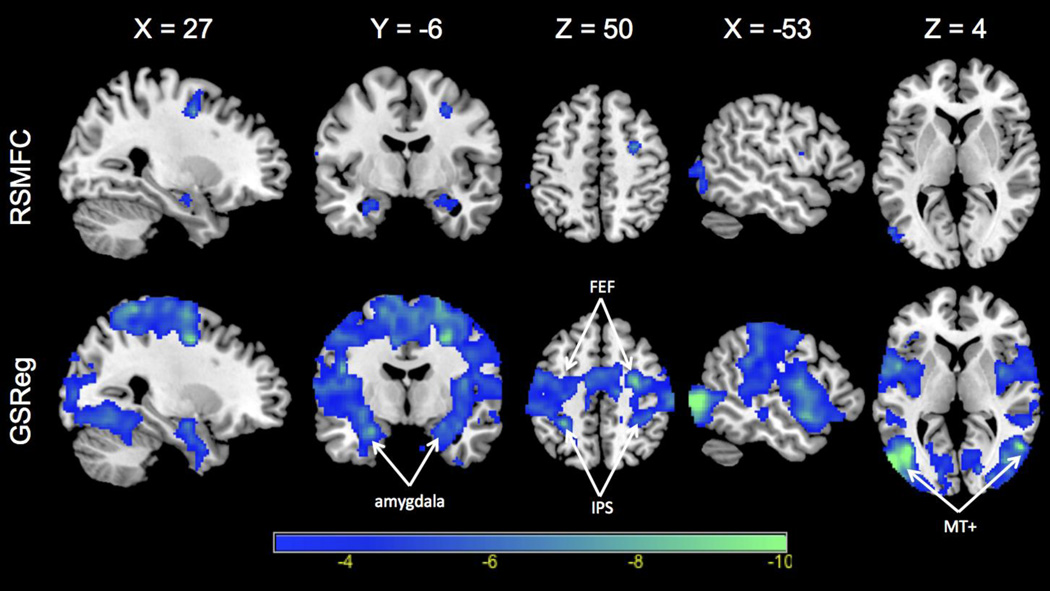
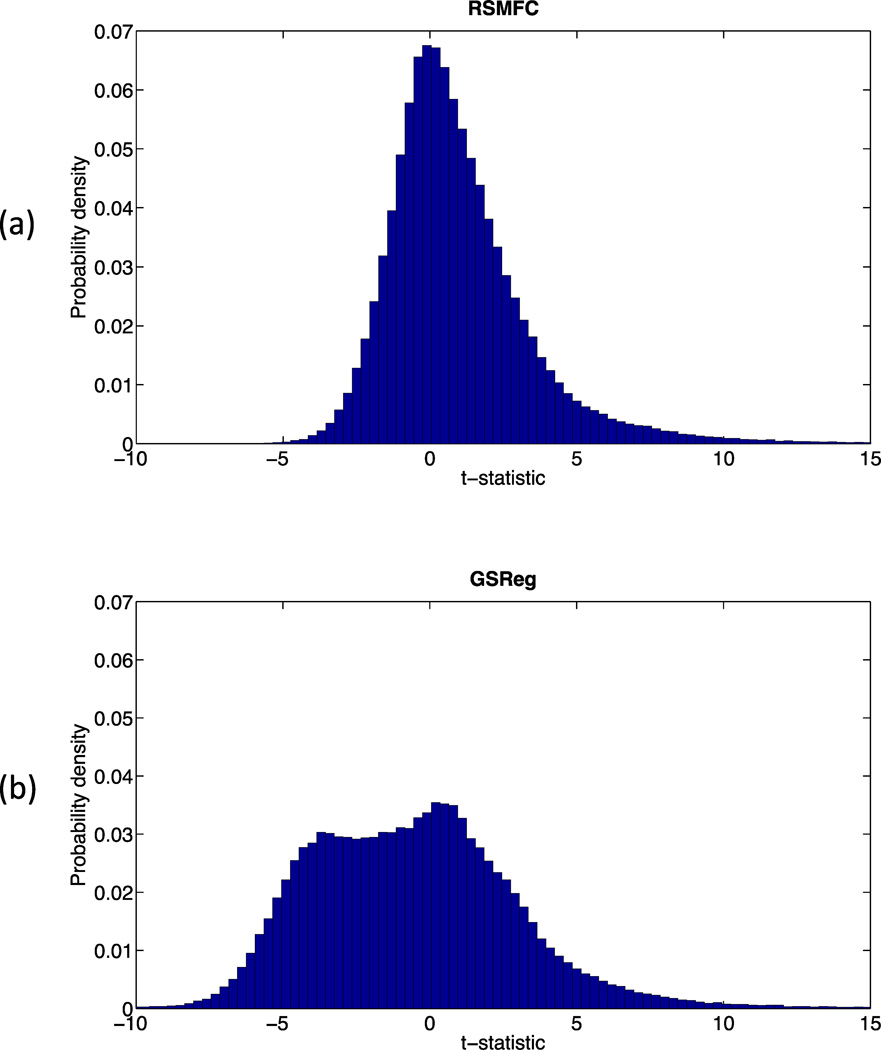
Figure 9 shows brain regions that had significant correlations (both positive and negative) with the PCC seed region under GSReg and RSMFC (with a voxel-wise height threshold of p < 0.001 and spatial extent threshold of 42 voxels). For positive correlations, RSMFC and GSReg identified the same target regions. Both methods revealed most of the core nodes in the DMN, including the mPFC and bilateral AG. However, RSMFC was able to uncover additional connections between PCC and both left and right medial temporal lobe (MTL) while GSReg did not uncover these connections (Figure 9, axial slice with Z = −10). With regards to negative correlations, RSMFC revealed three major focal regions, including left and right amygdala and right FEF. In contrast, results from GSReg revealed widespread negative correlations across the brain (Figure 10). Figure 11 furthers illustrates this difference by contrasting the two distributions of t-statistics of whole-brain voxels generated by the two methods. The distribution under GSReg was shifted to negative values (e.g. the wide plateau between t-statistics of −5 and 0). In contrast, in RSMFC, the mode of the distribution was centered around zero.
Figure 9. PCC functional connectivity determined by RSMFC and GSReg.
Voxels that have positive correlation with the PCC are colored red and voxels that have negative correlations are colored blue. For positive correlations, both methods yield similar spatial patterns in DMN networks, except that RSMFC reveals left and right MTL nodes missed by GSReg (slice at Z = −10). Critically, negative correlations identified by GSReg (shown in blue) are much more widespread than in RSMFC. Both connectivity maps are thresholded using a voxel-wise height threshold of p < 0.001 and a spatial extent threshold of 42 voxels, corresponding to an overall p < 0.01 for a family-wise error correction. PCC = posterior cingulate cortex. DMN = default mode network. AG = angular gyrus. mPFC = medial prefrontal cortex. MTL = medial temporal lobe. RSMFC = random subspace method functional connectivity. GSReg = global signal regression method.
Figure 10. Negative connectivity with PCC identified by RSMFC and GSReg.
Negative correlations are widespread in GSReg and significantly weaker in RSMFC. RSMFC identifies focal areas in right FEF (frontal eye field), left and right amygdala. PCC = posterior cingulate cortex. FEF = frontal eye field. IPS = intraparietal sulcus. MT+ = middle temporal complex. RSMFC = random subspace method functional connectivity. GSReg = global signal regression method.
Figure 11. Histogram of group-level whole-brain t-statistics on the experimental rsfMRI dataset.
Distribution of voxel-wise t-statistics using (a) RSMFC and (b) GSReg. In GSReg, the distribution shifts towards negative values, e.g. the wide plateau between t-statistics of −5 and 0. In contrast, the mode of the distribution is centered at zero in RSMFC. RSMFC = random subspace method functional connectivity. GSReg = global signal regression method.
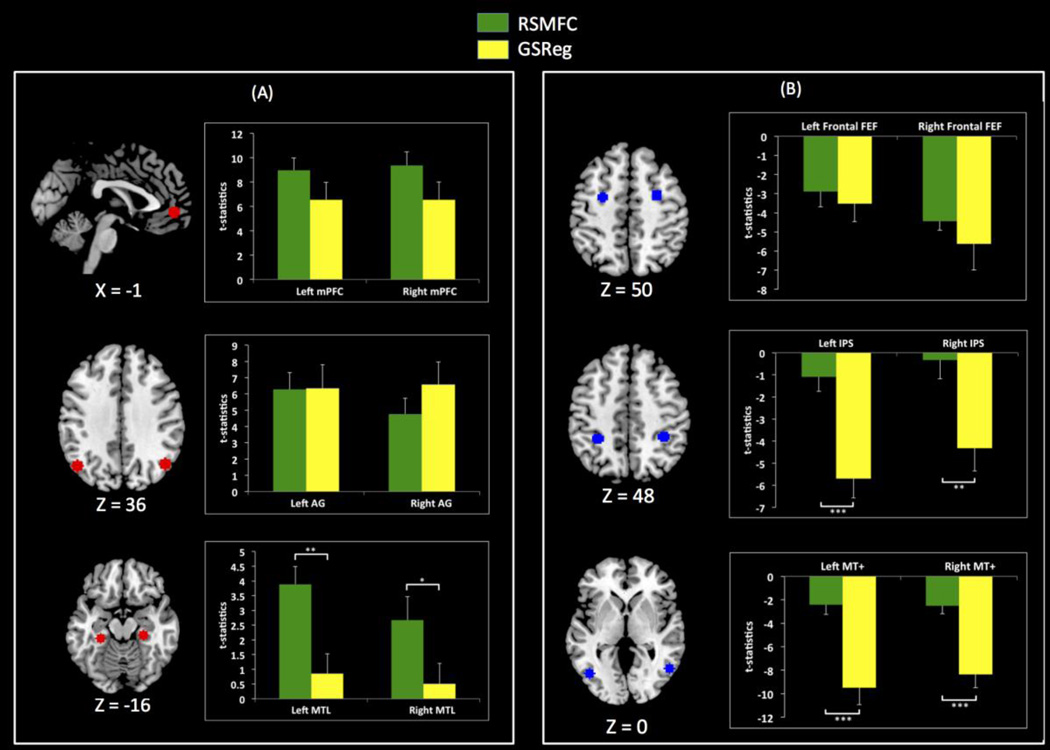
Figure 12 shows the strength of PCC connectivity with ROIs in both the DMN and anti-correlated regions. Average t-statistics within the DMN ROIs were comparable between GSReg and RSMFC except for bilateral MTL ROIs, where RSMFC yielded significantly higher mean t-statistics compared to GSReg. The average t-statistics within anti-correlated ROIs were smaller in RSMFC than in GSReg. Anti-correlations in the bilateral IPS and bilateral MT+ were significantly stronger in GSReg when compared to RSMFC. Detailed comparisons with aCompCor are described in the Supplementary Materials (Appendix A.2) as well as in the discussion section.
Figure 12. Comparison of PCC connectivity with target ROIs.
(a) Average t-statistics for PCC connectivity with DMN ROIs. For most DMN ROIs, GSReg and RSMFC yield comparable connectivity strength. However, compared to GSReg, RSMFC reveals that PCC is more tightly connected to bilateral left and right MTL. (b) Average t-statistics for ROIs that are negatively correlated with PCC. Anti-correlations are significantly weaker in RSMFC, compared to GSReg (*** p < 0.001, ** p < 0.01, * p < 0.05). PCC = posterior cingulate cortex. mPFC = medial prefrontal cortex. AG = angular gyrus. MTL = medial temporal lobe. FEF = frontal eye field. IPS = intraparietal sulcus. MT+ = middle temporal complex. RSMFC = random subspace method functional connectivity. GSReg = global signal regression method. DMN = default mode network.
Discussion
We developed RSMFC, a novel method based on partial correlations, to overcome weaknesses in global signal regression methods that can heavily bias estimates of functional connectivity. Previous studies have successfully used partial correlations to examine functional connectivity patterns based on a number of preselected ROIs (Huang et al., 2010; Lee et al., 2011; Marrelec et al., 2007; Marrelec et al., 2006; Ryali et al., 2012). However, to our knowledge, no previous study has applied partial correlation methods in extremely high-dimensional settings where connectivity of a seed region must be examined with respect to every other voxel in the brain. In such situations it is difficult to accurately estimate partial correlations using conventional approaches that compute the pseudo-inverse of the sample covariance matrix.
Specifically, in the case of very high dimensions, it has been shown that pseudo-inverse solutions suffer from significant estimation errors because they may both retain noise signals and discard informative signals (Hoyle, 2010; Xu et al., 2012). Here we overcome difficulties associated with estimating partial correlations on high dimensional rsfMRI data using a novel random subspace method (Hoyle, 2010). The premise for this method is that by sampling a relatively small subset of voxels, the sample-to-feature ratio in subspaces becomes higher, and the pseudo-inverse in each subspace incurs reduced estimation errors compared to the original dataset. In fact, random subspace methods have been successfully applied in other domains to construct more accurate classifiers, which similarly benefit from higher sample-to-feature ratios in subspaces (Kuncheva et al., 2010; Skurichina and Duin, 2002; Tin Kam, 1998).
Using extensive simulations we showed that RSMFC effectively removes global artifacts in rsfMRI data while at the same time accurately estimating whole-brain functional connectivity pattern. As demonstrated by our simulations, a critical advantage of RSMFC is that it does not erroneously introduce anti-correlations between uncorrelated networks, which is one of the main drawbacks of the widely used GSReg method. On the experimental dataset, we found that our method was able to identify strong functional connectivity in the default mode network, including more reliable identification of connectivity with left and right medial temporal lobe regions that were missed by GSReg. Below, we first discuss how to select tuning parameters in RSMFC, then results from both simulated and experimental fMRI data, and finally the advantages of our method over existing data-driven methods for removal of global artifacts.
Implementation of RSMFC
To implement RSMFC, two data-dependent parameter values need to be selected beforehand: the number of partitions and the number of voxels contained in a subspace. Since it is computationally not feasible to tune these parameters on a whole-brain level, we first constructed a sub-dataset by randomly selecting a relatively smaller number of voxels (10,000 voxels in this study). We assume that the global artifacts contained in the sub-dataset can accurately represent those in the original dataset. The sub-dataset is used for the sole purpose of selecting appropriate tuning parameter values. Next, in this sub-dataset, we randomly selected a seed voxel in the gray matter, applied RSMFC and determined the optimal tuning parameter values. In addition, because of the independence in constructing the sub-dataset, the optimal tuning parameter values are applicable to different seed ROIs in the original whole-brain dataset. It is possible that the randomly selected seed used for parameter tuning may fall in other seeds of interests for functional connectivity analysis. One strategy to overcome this is to randomly select several independent seeds and performed parameter selection based on the average performance across seeds. The advantage of this approach is that by examining several independently selected seeds together, the optimal tuning parameters are more likely to be suitable for a majority of potential seeds of interest. On both simulated and real experimental fMRI sub-datasets, we used 200 partitions and found that RSMFC consistently converged for various subspace sizes ranging from 10 to 100 voxels. Our analyses suggest that 200 partitions are sufficient for rsfMRI application. RSMFC with an optimal subspace size of 40 voxels was found to converge around 100 partitions on both simulated and experimental data. We also performed additional analysis using RSMFC with 100 partitions, and found that RSMFC with 200 and 100 partitions yielded similar results (Figure S1 – Figure S3 in the Supplementary Materials). Since each partition is independent from the other, researchers only need to run additional partitions if the algorithm does not converge based on the same criterion proposed in this paper (1% change rate of Euclidean distance between two consecutive partitions, Equation 7) And previous partitions can be reused to compute functional connectivity.
To select the optimal subspace size, we started by computing full correlations between time-series of the seed voxel and those of every other voxel in the sub-dataset. In this case, no global artifacts are removed, and the histogram of group-level voxel-wise t-statistics is expected to deviate from zero. We quantified the deviation as a l2-norm of the vector of voxel-wise t-statistics (i.e., vector length in Euclidean distance, Equation 6) because global artifacts lead to overestimation of functional connectivity on a whole-brain scale (Murphy et al., 2009; Weissenbacher et al., 2009). With increasing subspace size, more global artifacts are sampled and subsequently removed using partial correlations. Since global artifacts are increasingly removed, overestimation is mitigated and the distribution of voxel-wise t-statistics shifts to zero, resulting in decreased l2-norm. The l2-norm change rate between two consecutive subspace sizes becomes smaller if sufficient number of voxels are sampled (i.e. major global artifacts are sampled and removed). As a rule of thumb, we selected the optimal subspace size at which the relative l2-norm change rate is equal to or less than 10%. The success of our heuristic approach was clearly demonstrated on the simulated dataset. As predicted, with RSMFC, voxels that are uncorrelated with the seed ROI had t-statistics centered around zero (Figure 6), resulting in a distinct mode around zero. Additionally, there is also a distinct mode around a t-value of 5, consisting mainly of voxels in the same network as the seed region. This clearly indicates that the optimal subspace size chosen is indeed able to effectively remove global artifacts and recover the true functional network.
Performance of RSMFC on simulated fMRI data
We first evaluated RSMFC on simulated fMRI data with two networks that were known to be uncorrelated. RSMFC successfully removed the influence of global artifacts and correctly identified the network associated with the seed ROI. For example, at a height threshold of p < 0.01, only 1.29% of the voxels showed false negative correlations (Table 1). In sharp contrast, in GSReg nearly the entire network which was supposed to uncorrelated became anti-correlated with the seed region. At a height threshold of p < 0.01, 92.86% of the voxels showed false negative correlations. This is consistent with previous critiques that GSReg induces strong negative correlations in the data (Murphy et al., 2009; Weissenbacher et al., 2009). In fact, it has been mathematically proven that in GSReg the sum of voxel-wise correlation coefficients with a seed voxel is less than or equal to zero (Murphy et al., 2009). Thus, in seed-based functional connectivity analysis, GSReg will generate negative correlations to counterbalance positive correlations with the seed ROI. Consistent with this argument, the distribution of whole-brain voxel-wise t-statistics clearly demonstrate this effect in our simulations (Figure 6). The histogram of correlations from GSReg showed a distribution that was significantly shifted to negative values. Specifically, our simulations identified two modes, or patterns of connectivity, in the negative part of the distribution. The mode closer to zero has voxels outside the two simulated networks, and the mode further away from zero has voxels in the network originally uncorrelated with the seed ROI. This observation further suggests that multiple types of errors contribute to incorrect functional networks in GSReg. Our simulations suggest that this is due to the fact that once a voxel within a network captures an artificial negative correlation the entire network suffers. Consistent with these observations, Anderson and colleagues showed that larger networks are more prone to stronger artificial negative correlations caused by GSReg (Anderson et al., 2011). In contrast, the distribution of correlations estimated by RSMFC is bimodal with one distinct mode centered around zero, indicating successful removal of global artifacts and strong protection from false negative correlations. Furthermore, as demonstrated by our ROC analysis on the simulated dataset, performance of RSMFC was consistently superior to GSReg, and RSMFC is able to recover more true connections compared to GSReg under the same rate of false detections.
Performance of RSMFC on the experimental fMRI data
We then examined the performance of RSMFC on an rsfMRI dataset of 22 healthy adult participants. We estimated the functional connectivity of each voxel in the brain using a seed ROI in the posterior cingulate cortex. As expected, RSMFC recovered positive correlations with all major nodes of the DMN including the ventromedial prefrontal cortex, posterior medial cortex, angular gyrus and the MTL (Greicius et al., 2003). The spatial extent and connection strengths were comparable between RSMFC and GSReg in many, but not all, brain regions. Specifically, RSMFC revealed additional connections between PCC and both left and right MTL that were significantly underestimated by using GSReg. Our findings of MTL connectivity using RSMFC are consistent with DTI studies demonstrating white matter fiber tracts between the PCC and the MTL (Greicius et al., 2009; Supekar et al., 2010). The inability of GSReg to consistently identify the MTL nodes of the DMN is particularly problematic because of the hypothesized role of this region in autobiographical and other mnemonic functions of the DMN (Buckner et al., 2008; Greicius and Menon, 2004).
Critically, unlike RSMFC, GSReg revealed widespread anti-correlations throughout the brain including large areas of lateral frontal and parietal cortices (Fox et al., 2005). This was also clearly demonstrated by the distribution of voxel-wise t-statistics (Figure 11). The distribution of voxel-wise t-statistics from GSReg suggested two modes in the negative part, one close to zero and the other far away from zero, similar to the histogram on the simulated data. Based on these similarities with simulated data, it is reasonable to assume that the extensive anti-correlations in the frontal-parietaI networks identified by GSReg are artificially overestimated to some degree. In sharp contrast, the single mode of the distribution of voxel-wise t-statistics from RSMFC was centered around zero. Indeed, negative correlations detected by RSMFC were limited to only a few focal areas in the right FEF, and bilateral amygdala. Negative correlations in bilateral IPS and MT+ regions were significantly weaker than those detected by GSReg (Figure 12). The existence of strong anti-correlations in rsfMRI, such as those identified by GSReg, is hotly debated in the cognitive neuroimaging community. For example, fMRI studies using GSReg have consistently reported strong anti-correlations between DMN and lateral fronto-parietal cortex (Chai et al., 2012; Fox et al., 2005; Fox et al., 2009). However, Chang and Glover (2009) found much weaker anti-correlations between DMN and lateral frontal and parietal cortices after applying RETROICOR and RVHRCOR. For example, inferior parietal, inferior and middle frontal regions were found to be negatively correlated with the precuneus/PCC seed only at an uncorrected threshold of p < 0.05 but no regions were significant at FDR corrected thresholds of p < 0.05. Similarly, Anderson et al. (2011) used nuisance regressors constructed from soft tissues of the face and calvarium (regions without neural signals) and found no significant anti-correlations between DMN and lateral frontal and parietal cortices. Consistent with these findings, de Pasquale et al. (2010) observed no negative correlations between the dorsal attention network and the DMN in MEG signals. Critically, more precise electrophysiological studies in cats found that anti-correlated power fluctuations between homologs of DMN and task-activated regions occurred at most 20% of the time (Popa et al., 2009). Furthermore, resting state functional connectivity between brain regions have also been shown to be highly non-stationary (Chang and Glover, 2010), and are also modulated by subjects’ state of vigilance (Chang et al., 2013; Horovitz et al., 2009; Samann et al., 2011) and whether the data are acquired under eyes-open or eyes-closed conditions (Wong et al., 2012). Anti-correlations in lateral fronto-parietal regions are generally very weak or non-existent during eyes-closed recording conditions in these and other related studies, consistent with our findings using RSMFC.
Comparison between RSMFC and aCompCor
Chai et al. (2012) proposed aCompCor to identify and remove global artifacts based on a component based noise reduction method (Behzadi et al., 2007) and estimate functional connectivity Specifically, in their method, the first 5 principal components were extracted as nuisance covariates from areas such as the white matter and cerebral spinal fluid (CSF) regions, where BOLD signals are unlikely to be related to neural activity. Nuisance covariates were then regressed out from each voxel’s time course, and functional connectivity was computed based on residual signals between the seed region and every voxel in brain. To compare RSMFC with aCompCor, we applied aCompCor on the same experimental fMRI dataset (Appendix A.2). Supplementary Figure S4 (b) shows the functional connectivity map of the PCC using aCompCor, with the first 5 principal components from the white matter and CSF images eroded by 2 voxels in each direction. Compared to the results of RSMFC (Figure S4 (a)), there were much more widespread positive correlations with PCC across the whole brain (e.g. sagittal slice X = −1). Critically, RSMFC not only captured the local peaks detected by aCompCor but also yielded much better anatomical specificity than aCompCor. For example, in the functional connectivity map generated by RSMFC, we can clearly see three separate local peaks in regions of vmPFC, anterior cingulate cortex and paracingulate gyrus (sagittal slice X = −1). In contrast, there was no such clear distinction in the map from aCompCor. Moreover, the distribution of voxel-wise t-statistics from aCompCor had a mode around t-statistic of 2.3, rather than 0 (Supplementary Figure S5 (a)). These results suggest that aCompCor significantly overestimated functional connectivity; consequently it is not surprising that virtually no brain regions were negatively correlated with the PCC. Previous studies have shown that physiological noise (e.g. respiration) impacts grey matter more than white matter and CSF (Birn et al., 2006; Wise et al., 2004). Our results suggest that it may not be sufficient to take nuisance signals only from white matter and CSF. To further illustrate this, we performed two additional analyses. First, we expanded the white matter and CSF mask to capture some gray matter by eroding 1 voxel instead of 2 voxels in each direction, and extracted the first 5 principal components. The resulting functional connectivity map of PCC seed became much clearer (Figure S4 (c)) and more comparable to results from RSMFC (Figure S4 (a)). Moreover, the mode for the distribution of voxel-wise t-statistics became more centered around zero (Figure S5 (b)), indicating a more effective removal of global artifacts. Second, we used the same initial mask (2-voxel erosion) but extracted the first 50 principal components instead of 5 (50 was chosen to be arbitrary large to include some gray matter signals). Similarly, compared to the map from using the same mask but with only 5 principal components (Figure S4 (b)), the resulting functional connectivity map (Figure S4 (d)) became clearer and closer to the map obtained using RSMFC (Figure S4 (a)). The mode for the distribution of voxel-wise t-statistics shifted towards zero, centering on a t-statistic of 0.9 instead of 2.3 if the first 5 principal components were used (Figure S5 (c)). These two additional analyses suggest that in order to remove global artifacts, some nuisance signals from gray matter need to be regressed out. Further research is necessary to address these issues with aCompCor.
Comparison between full correlation and partial correlation
There are important differences between full correlation and partial correlation models for estimating functional connectivity. On the one hand, both full correlation and partial correlation measure linear dependence between brain regions. However, the two methods differ in how linear dependence is measured. Full correlation estimates marginal linear dependence between a pair of brain regions without considering the influence of other regions as well as common driving influences. For example, physiological processes induce widespread consistent BOLD signal fluctuations across the brain. Without removing these global signals, full correlation tends to overestimate functional correlations between brain regions. Therefore, all possible sources of global artifacts need to be first removed in order to use full correlation methods for accurately inferring function connectivity between brain regions. In contrast, our partial correlation based methods estimate linear dependence between brain regions conditional on removing influence from multiple other regions and any common input signals. Thus, partial correlation measures more direct interaction between a pair of brain regions and our current study shows that it is a promising tool for estimating functional connectivity between brain regions.
Extensions and limitations of RSMFC
In the present study we have mainly focused on inferring functional connectivity pattern at the group level. Although the same approach can be used for individual subjects, it is non-trivial to threshold individual subject connectivity maps because (1) the distribution of sample partial correlations is not straightforward to compute and the distribution of average z-transformed partial correlations is only approximately normal, (2) for each voxel, it’s z-transformed partial correlations from 200 partitions need to be averaged. The variance of the distribution of average z-transformed partial correlation is much smaller than the variance of the z-transformed partial correlation from a single partition. A better approach to infer individual functional connectivity patterns would be to use the approach described by Schwartzman et al. (2009), where the empirical null distribution of average z-transformed partial correlations is inferred from the data itself. This will help to address the issues of inappropriate null distribution as well as the variance change associated with averaging z-transformed partial correlations from multiple partitions.
Our study has focused on the application of RSMFC for seed-based whole brain functional connectivity analysis. However, RSMFC can be extended to other types of functional connectivity analysis as well. For example, it can also accommodate voxel-to-voxel connectivity analysis by calculating partial correlations between randomly sampled voxels. Instead of taking the first column of the partial correlation matrix, the whole matrix is retained to store partial correlations between voxels. Additionally, RSMFC can also be extended to a large-scale ROI-to-ROI network analysis using partial correlations (e.g. when the number of ROIs is greater than or equal to 1000) (Huang et al., 2010; Lee et al., 2011; Marrelec et al., 2007; Marrelec et al., 2006; Ryali et al., 2012). In this case, instead of sampling subsets of voxels, subset of ROIs could be sampled. Future research will examine performance of RSMFC in these types of applications. Future work will also investigate how effectively RSMFC can mitigate the head motion related artifacts on estimates of functional brain connectivity.
RSMFC uses a pseudo-inverse based approach for computing partial correlations. An alternative approach is to use shrinkage-based methods for estimating partial correlations for a large number of brain regions (Huang et al., 2010; Ryali et al., 2012). Unlike RSMFC, shrinkage-based approaches are able to reduce partial correlations between the seed region and noisy voxels to exactly zero. This approach yields a sparse functional connectivity pattern that is easier to interpret. However, it requires separate tuning on the amount of shrinkage for every different seed region, and no studies have applied shrinkage-based approaches to seed-based whole-brain functional connectivity analysis. Further research is needed to examine applications of shrinkage-based methods and compare their performance with the pseudo-inverse approach used here.
One limitation is that RSMFC is a computationally intensive method requiring sampling multiple subsets and computing multiple partitions. For example, on a 2.26 GHz CPU, it took 1.5 hours to run a seed-based whole brain analysis with a subspace of 40 voxels and 200 partitions for a single subject. However, the computation cost can be greatly reduced by utilizing faster CPUs and parallel computing which is readily available as a MATLAB toolbox and easy to implement.
Conclusions
We have developed a novel random subspace based partial correlation method to remove global artifacts and reliably estimate whole brain functional networks. Using simulated data, we showed that our method is able to accurately remove global artifacts and, unlike global signal regression, it does not introduce erroneous negative correlations. Analysis of PCC connectivity on experimental rsfMRI data showed that our method recovers the DMN with better anatomical specificity and significantly fewer negative correlations compared to GSReg. Taken together, these findings suggest that RSMFC is an effective method for minimizing the effects of global artifacts and artificial negative correlations, while accurately recovering intrinsic functional networks.
Supplementary Material
Highlights.
We develop novel random subspace method for functional connectivity (RSMFC)
RSFMC effectively removes global artifacts in resting-state fMRI
RSMFC validated using extensive computer simulations
RSMFC does not artificially introduce negative correlations
RSMFC improves anatomical specificity of functional brain networks
Acknowledgement
This research was supported by grants from the National Institutes of Health (HD047520, HD059205, HD057610, NS071221), the Child Health Research Institute (CHRI) at Stanford University and Lucile Packard Foundation for Children’s Health and the Stanford CTAS (UL1RR025744). We thank Drs. Kaustubh Supekar, Daniel A. Abrams and Arron Metcalfe for helpful comments.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Anderson JS, Druzgal TJ, Lopez-Larson M, Jeong EK, Desai K, Yurgelun-Todd D. Network anticorrelations, global regression, and phase-shifted soft tissue correction. Hum Brain Mapp. 2011;32:919–934. doi: 10.1002/hbm.21079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beckmann CF, DeLuca M, Devlin JT, Smith SM. Investigations into resting-state connectivity using independent component analysis. Philos Trans R Soc Lond B Biol Sci. 2005;360:1001–1013. doi: 10.1098/rstb.2005.1634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Behzadi Y, Restom K, Liau J, Liu TT. A component based noise correction method (CompCor) for BOLD and perfusion based fMRI. Neuroimage. 2007;37:90–101. doi: 10.1016/j.neuroimage.2007.04.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Birn RM. The role of physiological noise in resting-state functional connectivity. Neuroimage. 2012;62:864–870. doi: 10.1016/j.neuroimage.2012.01.016. [DOI] [PubMed] [Google Scholar]
- Birn RM, Diamond JB, Smith MA, Bandettini PA. Separating respiratory-variation-related fluctuations from neuronal-activity-related fluctuations in fMRI. Neuroimage. 2006;31:1536–1548. doi: 10.1016/j.neuroimage.2006.02.048. [DOI] [PubMed] [Google Scholar]
- Biswal B, Yetkin FZ, Haughton VM, Hyde JS. Functional connectivity in the motor cortex of resting human brain using echo-planar MRI. Magn Reson Med. 1995;34:537–541 . doi: 10.1002/mrm.1910340409. [DOI] [PubMed] [Google Scholar]
- Buckner RL, Andrews-Hanna JR, Schacter DL. The brain's default network: anatomy, function, and relevance to disease. Ann N Y Acad Sci. 2008;1124:1–38. doi: 10.1196/annals.1440.011. [DOI] [PubMed] [Google Scholar]
- Chai XJ, Castanon AN, Ongur D, Whitfield-Gabrieli S. Anticorrelations in resting state networks without global signal regression. Neuroimage. 2012;59:1420–1428. doi: 10.1016/j.neuroimage.2011.08.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang C, Cunningham JP, Glover GH. Influence of heart rate on the BOLD signal: the cardiac response function. Neuroimage. 2009;44:857–869. doi: 10.1016/j.neuroimage.2008.09.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang C, Glover GH. Effects of model-based physiological noise correction on default mode network anti-correlations and correlations. Neuroimage. 2009;47:1448–1459. doi: 10.1016/j.neuroimage.2009.05.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang C, Glover GH. Time-frequency dynamics of resting-state brain connectivity measured with fMRI. Neuroimage. 2010;50:81–98. doi: 10.1016/j.neuroimage.2009.12.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang C, Liu Z, Chen MC, Liu X, Duyn JH. EEG correlates of time-varying BOLD functional connectivity. Neuroimage. 2013;72:227–236. doi: 10.1016/j.neuroimage.2013.01.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dagli MS, Ingeholm JE, Haxby JV. Localization of cardiac-induced signal change in fMRI. Neuroimage. 1999;9:407–415. doi: 10.1006/nimg.1998.0424. [DOI] [PubMed] [Google Scholar]
- de Pasquale F, Della Penna S, Snyder AZ, Lewis C, Mantini D, Marzetti L, Belardinelli P, Ciancetta L, Pizzella V, Romani GL, Corbetta M. Temporal dynamics of spontaneous MEG activity in brain networks. Proc Natl Acad Sci U S A. 2010;107:6040–6045. doi: 10.1073/pnas.0913863107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Desjardins AE, Kiehl KA, Liddle PF. Removal of confounding effects of global signal in functional MRI analyses. Neuroimage. 2001;13:751–758. doi: 10.1006/nimg.2000.0719. [DOI] [PubMed] [Google Scholar]
- Edwards D. Introduction to graphical modelling. 2nd ed. New York: Springer; 2000. [Google Scholar]
- Forman SD, Cohen JD, Fitzgerald M, Eddy WF, Mintun MA, Noll DC. Improved assessment of significant activation in functional magnetic resonance imaging (fMRI): use of a cluster-size threshold. Magn Reson Med. 1995;33:636–647. doi: 10.1002/mrm.1910330508. [DOI] [PubMed] [Google Scholar]
- Fox MD, Raichle ME. Spontaneous fluctuations in brain activity observed with functional magnetic resonance imaging. Nat Rev Neurosci. 2007;8:700–711. doi: 10.1038/nrn2201. [DOI] [PubMed] [Google Scholar]
- Fox MD, Snyder AZ, Vincent JL, Corbetta M, Van Essen DC, Raichle ME. The human brain is intrinsically organized into dynamic, anticorrelated functional networks. Proc Natl Acad Sci U S. 2005;A102:9673–9678. doi: 10.1073/pnas.0504136102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox MD, Zhang D, Snyder AZ, Raichle ME. The global signal and observed anticorrelated resting state brain networks. J Neurophysiol. 2009;101:3270–3283. doi: 10.1152/jn.90777.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glover GH, Law CS. Spiral-in/out BOLD fMRI for increased SNR and reduced susceptibility artifacts. Magn Reson Med. 2001;46:515–522. doi: 10.1002/mrm.1222. [DOI] [PubMed] [Google Scholar]
- Glover GH, Li TQ, Ress D. Image-based method for retrospective correction of physiological motion effects in fMRI: RETROICOR. Magn Reson Med. 2000;44:162–167. doi: 10.1002/1522-2594(200007)44:1<162::aid-mrm23>3.0.co;2-e. [DOI] [PubMed] [Google Scholar]
- Greicius MD, Krasnow B, Reiss AL, Menon V. Functional connectivity in the resting brain: a network analysis of the default mode hypothesis. Proc Natl Acad Sci U S A. 2003;100:253–258. doi: 10.1073/pnas.0135058100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greicius MD, Menon V. Default-mode activity during a passive sensory task: uncoupled from deactivation but impacting activation. J Cogn Neurosci. 2004;16:1484–1492. doi: 10.1162/0898929042568532. [DOI] [PubMed] [Google Scholar]
- Greicius MD, Supekar K, Menon V, Dougherty RF. Resting-state functional connectivity reflects structural connectivity in the default mode network. Cereb Cortex. 2009;19:72–78. doi: 10.1093/cercor/bhn059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horovitz SG, Braun AR, Carr WS, Picchioni D, Balkin TJ, Fukunaga M, Duyn JH. Decoupling of the brain's default mode network during deep sleep. Proc Natl Acad Sci U S A. 2009;106:11376–11381. doi: 10.1073/pnas.0901435106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoyle DC. Accuracy of Pseudo-Inverse Covariance Learning - A Random Matrix Theory Analysis. IEEE Trans Pattern Anal Mach Intell. 2010 doi: 10.1109/TPAMI.2010.186. [DOI] [PubMed] [Google Scholar]
- Huang S, Li J, Sun L, Ye J, Fleisher A, Wu T, Chen K, Reiman E. Learning brain connectivity of Alzheimer's disease by sparse inverse covariance estimation. Neuroimage. 2010;50:935–949. doi: 10.1016/j.neuroimage.2009.12.120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuncheva LI, Rodriguez JJ, Plumpton CO, Linden DE, Johnston SJ. Random subspace ensembles for FMRI classification. IEEE Trans Med Imaging. 2010;29:531–542. doi: 10.1109/TMI.2009.2037756. [DOI] [PubMed] [Google Scholar]
- Lee H, Lee DS, Kang H, Kim BN, Chung MK. Sparse brain network recovery under compressed sensing. IEEE Trans Med Imaging. 2011;30:1154–1165. doi: 10.1109/TMI.2011.2140380. [DOI] [PubMed] [Google Scholar]
- Lowe MJ, Mock BJ, Sorenson JA. Functional connectivity in single and multislice echoplanar imaging using resting-state fluctuations. Neuroimage. 1998;7:119–132. doi: 10.1006/nimg.1997.0315. [DOI] [PubMed] [Google Scholar]
- Macey PM, Macey KE, Kumar R, Harper RM. A method for removal of global effects from fMRI time series. Neuroimage. 2004;22:360–366. doi: 10.1016/j.neuroimage.2003.12.042. [DOI] [PubMed] [Google Scholar]
- Margulies DS, Vincent JL, Kelly C, Lohmann G, Uddin LQ, Biswal BB, Villringer A, Castellanos FX, Milham MP, Petrides M. Precuneus shares intrinsic functional architecture in humans and monkeys. Proc Natl Acad Sci U S A. 2009;106:20069–20074. doi: 10.1073/pnas.0905314106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marrelec G, Horwitz B, Kim J, Pelegrini-Issac M, Benali H, Doyon J. Using partial correlation to enhance structural equation modeling of functional MRI data. Magn Reson Imaging. 2007;25:1181–1189. doi: 10.1016/j.mri.2007.02.012. [DOI] [PubMed] [Google Scholar]
- Marrelec G, Krainik A, Duffau H, Pelegrini-Issac M, Lehericy S, Doyon J, Benali H. Partial correlation for functional brain interactivity investigation in functional MRI. Neuroimage. 2006;32:228–237. doi: 10.1016/j.neuroimage.2005.12.057. [DOI] [PubMed] [Google Scholar]
- Murphy K, Birn RM, Handwerker DA, Jones TB, Bandettini PA. The impact of global signal regression on resting state correlations: are anti-correlated networks introduced? Neuroimage. 2009;44:893–905. doi: 10.1016/j.neuroimage.2008.09.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Popa D, Popescu AT, Pare D. Contrasting activity profile of two distributed cortical networks as a function of attentional demands. J Neurosci. 2009;29:1191–1201. doi: 10.1523/JNEUROSCI.4867-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raj D, Anderson AW, Gore JC. Respiratory effects in human functional magnetic resonance imaging due to bulk susceptibility changes. Phys Med Biol. 2001;46:3331–3340. doi: 10.1088/0031-9155/46/12/318. [DOI] [PubMed] [Google Scholar]
- Ryali S, Chen T, Supekar K, Menon V. Estimation of functional connectivity in fMRI data using stability selection-based sparse partial correlation with elastic net penalty. Neuroimage. 2012;59:3rcp3861. doi: 10.1016/j.neuroimage.2011.11.054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Samann PG, Wehrle R, Hoehn D, Spoormaker VI, Peters H, Tully C, Holsboer F, Czisch M. Development of the brain's default mode network from wakefulness to slow wave sleep. Cereb Cortex. 2011;21:2082–2093. doi: 10.1093/cercor/bhq295. [DOI] [PubMed] [Google Scholar]
- Schwartzman A, Dougherty RF, Lee J, Ghahremani D, Taylor JE. Empirical null and false discovery rate analysis in neuroimaging. Neuroimage. 2009;44:71–82. doi: 10.1016/j.neuroimage.2008.04.182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seeley WW, Menon V, Schatzberg AF, Keller J, Glover GH, Kenna H, Reiss AL, Greicius MD. Dissociable intrinsic connectivity networks for salience processing and executive control. J Neurosci. 2007;27:2349–2356. doi: 10.1523/JNEUROSCI.5587-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shmueli K, van Gelderen P, de Zwart JA, Horovitz SG, Fukunaga M, Jansma JM, Duyn JH. Low-frequency fluctuations in the cardiac rate as a source of variance in the resting-state fMRI BOLD signal. Neuroimage. 2007;38:306–320. doi: 10.1016/j.neuroimage.2007.07.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Skurichina M, Duin RPW. Bagging, Boosting and the Random Subspace Method for Linear Classifiers. Pattern Analysis & Applications. 2002;5:121–135. [Google Scholar]
- Supekar K, Menon V. Developmental maturation of dynamic causal control signals in higher-order cognition: a neurocognitive network model. PLoS Comput Biol. 2012;8:el002374. doi: 10.1371/journal.pcbi.1002374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Supekar K, Menon V, Rubin D, Musen M, Greicius MD. Network analysis of intrinsic functional brain connectivity in Alzheimer's disease. PLoS Comput Biol. 2008;4:el000l00. doi: 10.1371/journal.pcbi.1000100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Supekar K, Uddin LQ, Prater K, Amin H, Greicius MD, Menon V. Development of functional and structural connectivity within the default mode network in young children. Neuroimage. 2010;52:290–301. doi: 10.1016/j.neuroimage.2010.04.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tin Kam H. The random subspace method for constructing decision forests. Pattern Analysis and Machine Intelligence, IEEE Transactions on. 1998;20:832–844. [Google Scholar]
- Van Dijk KR, Hedden T, Venkataraman A, Evans KC, Lazar SW, Buckner RL. Intrinsic functional connectivity as a tool for human connectomics: theory, properties, and optimization. J Neurophysiol. 2010;103:297–321. doi: 10.1152/jn.00783.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ward BD. Simultaneous Inference for FMRI Data. AFNI 3dDeconvolve Documentation. Medical College of Wisconsin; 2000. [Google Scholar]
- Weissenbacher A, Kasess C, Gerstl F, Lanzenberger R, Moser E, Windischberger C. Correlations and anticorrelations in resting-state functional connectivity MRI: a quantitative comparison of preprocessing strategies. Neuroimage. 2009;47:1408–1416. doi: 10.1016/j.neuroimage.2009.05.005. [DOI] [PubMed] [Google Scholar]
- Wise RG, Ide K, Poulin MJ, Tracey I. Resting fluctuations in arterial carbon dioxide induce significant low frequency variations in BOLD signal. Neuroimage. 2004;21:1652–1664. doi: 10.1016/j.neuroimage.2003.11.025. [DOI] [PubMed] [Google Scholar]
- Wong CW, Olafsson V, Tal O, Liu TT. Anti-correlated networks, global signal regression, and the effects of caffeine in resting-state functional MRI. Neuroimage. 2012;63:356–364. doi: 10.1016/j.neuroimage.2012.06.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu H, Caramanis C, Mannor S. Outlier-Robust PCA: The High-Dimensional Case. Information Theory, IEEE Transactions on. 2012;PP:1–1. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.