Estimating and interpreting F_ST: The impact of rare variants

Abstract

In a pair of seminal papers, Sewall Wright and Gustave Malécot introduced F_ST as a measure of structure in natural populations. In the decades that followed, a number of papers provided differing definitions, estimation methods, and interpretations beyond Wright's. While this diversity in methods has enabled many studies in genetics, it has also introduced confusion regarding how to estimate F_ST from available data. Considering this confusion, wide variation in published estimates of F_ST for pairs of HapMap populations is a cause for concern. These estimates changed—in some cases more than twofold—when comparing estimates from genotyping arrays to those from sequence data. Indeed, changes in F_ST from sequencing data might be expected due to population genetic factors affecting rare variants. While rare variants do influence the result, we show that this is largely through differences in estimation methods. Correcting for this yields estimates of F_ST that are much more concordant between sequence and genotype data. These differences relate to three specific issues: (1) estimating F_ST for a single SNP, (2) combining estimates of F_ST across multiple SNPs, and (3) selecting the set of SNPs used in the computation. Changes in each of these aspects of estimation may result in F_ST estimates that are highly divergent from one another. Here, we clarify these issues and propose solutions.

Since its introduction by Sewall Wright (1949) and Gustave Malécot (1948), F_ST estimation (Weir and Cockerham 1984; Holsinger and Weir 2009) has become a key component of studies of population structure in humans (International HapMap Consortium 2007; Li et al. 2008; The 1000 Genomes Project Consortium 2010; International HapMap 3 Consortium 2010) and other species (Malécot 1948; Wright 1949; Selander and Hudson 1976; Guries and Ledig 1982; Ellstrand and Elam 1993; Palumbi and Baker 1994). Though the utility of F_ST and related measures has been subject to recent debate (Jost 2008; Ryman and Leimar 2009), F_ST continues to be widely used by population geneticists (Xu et al. 2009; Edelaar et al. 2012; Hangartner et al. 2012).

Despite this widespread use in genetic studies, confusion remains about what F_ST is and how to estimate it. Beyond Wright's original description of F_ST as a ratio of variances, F_ST has been conceptually defined in many ways (Wright 1949; Cockerham 1969; Cavalli-Sforza and Bodmer 1971; Nei 1973; Slatkin 1991; Hudson et al. 1992). Additionally, multiple estimators for F_ST have been described in the literature (Nei 1973, 1986; Weir and Cockerham 1984; Hudson et al. 1992; Holsinger 1999; Weir and Hill 2002), often making the correct choice of estimator unclear.

With this diversity of definition and estimation in mind, we consider estimates of F_ST published by The 1000 Genomes Project Consortium (2010) of 0.052 for European and East Asian populations and 0.071 for European and West African populations. These are less than half of the published estimates, 0.111 and 0.156, from HapMap3 data (International HapMap 3 Consortium 2010) and may be the result of demography that differentially impacts F_ST at rare variants. These estimates have subsequently been used to simulate properties of recent rare variants (Mathieson and McVean 2012), making it imperative to know whether this reduction in F_ST is a meaningful result of the inclusion of rare variants or merely an artifact of estimation.

To answer these questions, we examine the issues surrounding F_ST estimated on data containing rare variants. We focus our attention on F_ST estimation in the context of comparing two populations—potentially with differing amounts of drift since the populations split—using a series of bi-allelic SNPs. We use the definition of Weir and Hill (2002), which allows for population-specific F_ST. Using this definition, we divide the issues surrounding estimation into three categories and examine them using both simulated and 1000 Genomes data:

1. Choice of F_ST estimator.

2. Combining estimates of F_ST across multiple SNPs.

3. Dependence of F_ST on the set of SNPs analyzed.

We conclude that the lower F_ST estimates reported by The 1000 Genomes Project Consortium (2010) are a consequence of the estimation method that was applied and are not informative for human demographic history. Correcting for differences in estimation method yields F_ST estimates of 0.106 for Europeans and East Asians and 0.139 for Europeans and West Africans—much closer to HapMap3 estimates. Overall, our results contradict a recent statement “among human populations, F_ST is typically estimated to be <0.1” by Mathieson and McVean (2012), which was based on results from The 1000 Genomes Project Consortium (2010).

Altogether, in the setting of rare variants, a careful protocol for producing F_ST estimates is warranted. We provide such a protocol.

Results

Theory

Defining F_ST

We use the definition of Weir and Hill (2002) (WH) throughout our manuscript to analyze estimators in the context of comparing two populations at a series of bi-allelic SNPs. In this context, WH define F_ST as the correlation between randomly drawn alleles from a single population relative to the most recent common ancestral population:

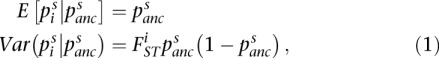where 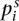is the allele frequency of the derived allele in population i, at SNP s, 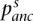is the allele frequency of the derived allele in the ancestral population at SNP s, and 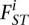is the population-specific F_ST for population i. For a pair of populations, F_ST is

Although we use the WH definition of F_ST to compare estimation methods, numerous alternate definitions exist in the literature (see Supplemental Material), in part because of confusion regarding Wright's original description of F_ST.

Wright (1949) defined F_ST as the correlation of randomly drawn gametes from the same population, relative to the total population. However, he did not clearly specify the “total population,” leaving subsequent investigators to interpret its meaning. For Nei (1973) the “total population” is the combination of the two population samples. This means that F_ST quantifies drift relative to an average of the two population samples. For Cockerham (1969) and WH, the “total” population is the most recent common ancestral population to the two populations being considered. Consistent with those investigators, we view F_ST as a parameter of the evolutionary process and not a statistic from observed samples as Nei has described.

To view F_ST as a parameter of the evolutionary process, the Cockerham and WH definitions assume that studied SNPs were polymorphic in the ancestral population. This is clear from Equation 1 as 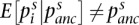for SNPs arising from recent mutations. While this assumption does not always hold, we believe that the WH definition provides a valid basis for comparing estimation methods, and also assesses the performance of estimators when this assumption is violated.

By defining only one F_ST for both populations in a comparison, Cockerham (1969) and Weir and Cockerham (1984) also assumed that the two populations have experienced identical amounts of drift since splitting. This assumption, which may be unrealistic in many real data sets, was generalized by WH, and motivates our use of the WH definition. In this study, we focus on cases without migration and admixture, though these cases were considered in WH and are the subject of future work (B Weir, pers. comm.).

In addition to the definitions described above, F_ST has been related to divergence time, coalescent times, and migration rates. Additionally, likelihood-based definitions view F_ST as a parameter of the distribution of allele frequencies in current populations (Balding and Nichols 1995; Nicholson et al. 2002; Balding 2003). Further details are provided in the Supplemental Material.

Choice of F_ST estimator

While estimators of F_ST handle issues related to finite sample size, we are interested in their behavior in the limit of large sample sizes, or the “quantity being estimated.” Most published estimates of F_ST are produced using the Weir and Cockerham (WC) (Weir and Cockerham 1984) (>8000 citations) or Nei (Nei 1973) (>5500 citations) estimators. However, we recommend a different estimator motivated by Hudson et al. (1992).

The WC estimator was developed for the case of populations with identical F_ST, and if it is used when F_ST is not identical for both populations, we demonstrate that the WC quantity being estimated becomes dependent on the ratio of sample sizes M according to (see Methods):

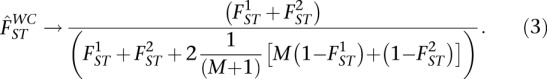We note that this variation with sample size is not due to any flaw in the WC estimator, but rather due to the use of the WC estimator for a purpose different from what was intended. We also note that the WC estimator is often used to produce single SNP estimates of F_ST to detect selection. We caution that when sample sizes are very different, the WC estimator can give inflated single SNP estimates of F_ST, resulting in false-positive signals of selection (see Supplemental Material).

In the context of the WH definition, the Nei estimator will consistently overestimate F_ST, and the degree of overestimation will depend upon the magnitude of F_ST values (see Methods):

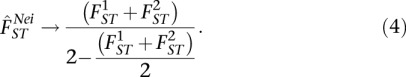We note that this result, with a maximum value of 2, makes it impossible to view F_ST as a correlation.

The Hudson estimator (Hudson et al. 1992; Keinan et al. 2007) produces estimates that are the simple average of F_ST according to the WH definition. These estimates are independent of sample sizes even when F_ST is not identical across populations. We note that while Hudson did not explicitly provide an estimator of F_ST, he did describe a method of estimation that corresponds to the estimator that we explicitly provide here (see Supplemental Material). Thus, we refer to this estimator as the Hudson estimator. Hudson estimates correspond to a simple average of the population specific F_ST estimates as given by (see Methods):

We note that the Hudson estimator is a simple average of the population-specific estimators proposed by Weir and Hill (2002). We provide comparisons of this estimator to the WC and Nei estimators when applied to simulated data (see Supplemental Material) and empirical data (see below).

Combining estimates of F_ST across multiple SNPs

We investigate two approaches for combining estimates of F_ST across multiple SNPs. In the first approach, variance components—the numerator and denominator—are averaged separately and the genome-wide estimate of F_ST is a “ratio of averages” (Weir and Cockerham 1984; International HapMap 3 Consortium 2010). In the second approach, single SNP estimates of F_ST are averaged across SNPs. The resulting “average of ratios” is reported as the genome-wide estimate (The 1000 Genomes Project Consortium 2010) (see Methods).

In the context of the WH definition, the numerator of the Hudson F_ST estimator (see Methods) is an unbiased estimator of the variance between populations. The denominator is an unbiased estimator of the total variance in the ancestral population. However, this does not mean that the ratio of the estimators is itself an unbiased estimator of F_ST. We are not aware of any unbiased estimator.

While an unbiased estimator is not available, F_ST estimates produced using a ratio of these two unbiased estimates will be asymptotically consistent, in the sense that they will converge to the correct underlying value as the number of independent SNPs increases. This is the basis of our recommendation that F_ST be estimated as a ratio of averages.

We analyze the effects of choosing an average of ratios in coalescent simulations detailed in the Supplemental Material.

Dependence of F_ST on the set of SNPs analyzed

It is well known that population genetic factors can cause variation in F_ST estimates, and that ascertainment schemes can alter the properties of studied SNPs (Ramírez-Soriano and Calafell 2008; Albrechtsen et al. 2010). For example, selection can result in differences between F_ST estimated on genic and nongenic SNPs (Clark et al. 2005; Barreiro et al. 2008; Hernandez et al. 2011); complex demography can cause F_ST to vary with SNP allele frequency (Schaffner et al. 2005) (see below). Indeed, variation in F_ST estimates between ascertained classes of SNPs can be used to test a variety of hypotheses about population history (Weir et al. 2005; McVicker et al. 2009). This usage of F_ST demonstrates that there is no single correct ascertainment scheme, as F_ST is a parameter of both the populations and the set of SNPs that are used in the computation.

Though there is no single correct ascertainment scheme, ascertainment in an outgroup may have desirable properties. Outgroup ascertainment guarantees that studied SNPs were polymorphic in the most recent common ancestral population (ignoring recurrent mutation), satisfying an assumption made in the Weir and Hill definition. This leads estimates of F_ST to be independent of allele frequency and depend upon time since divergence according to a simple equation (see Supplemental Material, Equation s1).

While we view these as desirable properties, if no reasonable outgroup sample is available, it may become necessary to choose SNPs that are polymorphic in one, both, or either of the populations studied. These choices will affect the estimate of F_ST produced and may explain discrepancies in F_ST estimates across studies of the same populations.

We explore the effects of various ascertainment schemes on F_ST estimates across the allele frequency spectrum in a variety of simulated demographic scenarios (see Supplemental Material).

Other F_ST estimators

In addition to the WC, Nei, and Hudson estimators that we analyzed above, we have also analyzed several additional estimators. Our results on each of these estimators are described in detail in the Supplemental Material.

The moment-based estimator of Weir and Hill (2002) (WH) introduced population-specific estimates of F_ST. Weir and Hill recommend a sample size weighted average of these estimates, which may result in a wide variation with sample size. However, one could also report these estimates independently or perform a simple average of these estimates.

A separate maximum-likelihood estimator of Weir and Hill (2002) (WH-ML) is based upon a normal approximation to genetic drift. However, the equations provided for the WH-ML estimator are not applicable to the general case of unequal sample size, and the investigators recommend that estimates be “simply averaged across loci,” causing WH-ML estimates to vary widely with the inclusion of rare variants.

We evaluated two max-likelihood estimators based on the beta-binomial likelihood using point estimates for the allele frequency in the ancestral population (D Balding, pers. comm.). These estimates perform well for small values of F_ST, but do poorly as F_ST increases. It may be possible to improve on these methods by integrating over the distribution of ancestral allele frequencies, an interesting direction for future research.

We also considered the beta-binomial MCMC method of Holsinger (1999). However, our simulations suggest that Holsinger estimates increase dramatically if rare SNPs are analyzed. Additionally, the MCMC-based approach imposes a significant computational burden, making the method difficult to apply to modern data sets.

Analysis of 1000 Genomes data

We analyzed data from 1000 Genomes populations (The 1000 Genomes Project Consortium 2010) to illustrate the effects of changes in each of the aspects of estimation described above. We focus largely on the comparison of Utah residents of European ancestry (CEU) and Chinese individuals from Beijing (CHB), as the Yoruba in Ibadan, Nigeria (YRI) sample functions as a natural outgroup for ascertainment of SNPs. This ascertainment has desirable properties (see above).

Choice of F_ST estimator

Estimates of F_ST for CEU and CHB are 0.106 (s.e. 0.0006), 0.112 (s.e. 0.0006), and 0.107 (s.e. 0.0006) for the WC, Nei, and Hudson estimators, respectively. These estimates were produced over SNPs ascertained as polymorphic in YRI. The higher Nei estimate is expected. In addition, sample sizes for CEU (85 individuals) and CHB (97 individuals) are similar, so we do not expect WC and Hudson estimates to differ.

In order to investigate the effects of sample size variation we selected 14 individuals—the size of the smallest sample (Iberian populations in Spain; IBS) in the 1000 Genomes Consortium data—from both CEU and CHB to produce populations CEU14 and CHB14. Hudson F_ST estimates for CEU14 and CHB are similar to those for CHB14 and CEU (see Table 1). However, WC estimates are 0.114 (s.e. 0.0006) and 0.107 (s.e. 0.0006) for CEU14 vs. CHB and CHB14 vs. CEU, respectively. The difference between these estimates is statistically significant (greater than eight standard errors). To verify that this difference is not due to different sets of polymorphic SNPs, we re-estimated F_ST restricting to SNPs that were polymorphic in YRI and at least one of CEU14 or CHB14. Re-estimated values of F_ST were similar to those above and WC estimates remained discordant (data not shown).

Table 1.

F_ST estimates for pairs of populations in 1000 Genomes

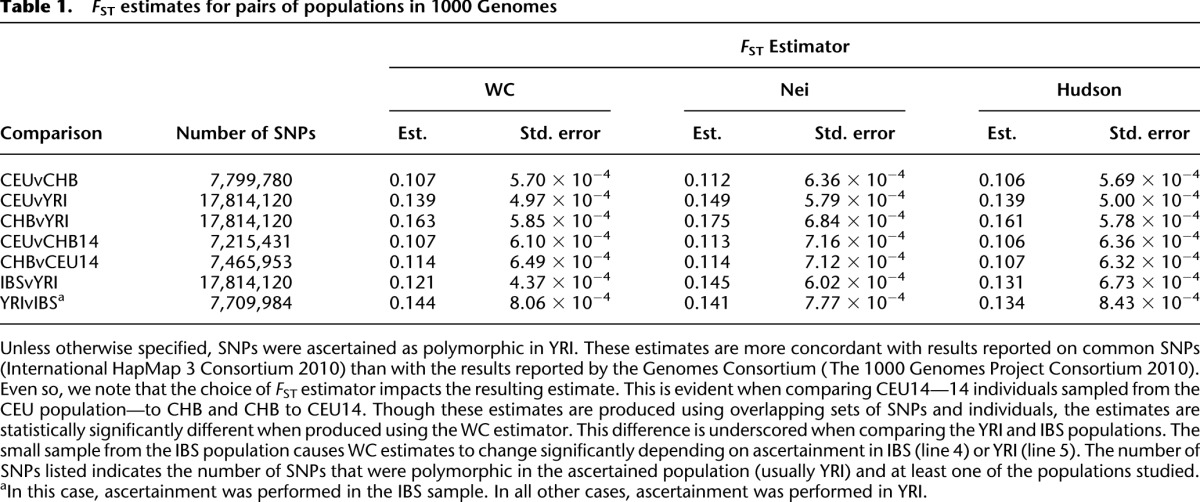
The effect of sample size variation is further exacerbated when ascertainment is performed within the populations studied. For example, in comparing IBS—with a sample size of only 14 individuals—to YRI, no reasonable outgroup population exists in the 1000 Genomes data. If we ascertain within one of these populations, WC estimates are 0.121 and 0.144 for ascertainment in YRI and IBS, respectively. These estimates—computed using identical populations and even identical individuals—are highly divergent at >25 standard errors apart, whereas Hudson estimates are much more stable (see Table 1). This underscores that F_ST estimates can vary substantially based on the choice of estimator.

Regardless of choice of estimator, our estimates of F_ST from 1000 Genomes data are relatively close to previously reported values of F_ST (see Supplemental Table S1 for all populations). This suggests that while the choice of estimator can impact the resulting value of F_ST, it does not explain the disparate results reported by the 1000 Genomes Consortium, and other aspects of estimation may be involved. We consider these in the sections below.

Combining estimates of F_ST across multiple SNPs

From 1000 Genomes data, we estimated F_ST for CEU and CHB as 0.106 (s.e. 0.0006) and 0.072 (s.e. 0.0003) for the ratio of averages and average of ratios, respectively. These estimates were produced over SNPs ascertained as polymorphic in YRI. This suggests that the result reported by the 1000 Genomes Consortium (0.052) may be partially explained by the large reduction in F_ST obtained by use of an average of ratios. These results are replicated for several comparisons of populations included in the 1000 Genomes data (see Table 2).

Table 2.

A comparison of the F_ST estimated using 1000 Genomes and HapMap data by either using a ratio of averages or an average of ratios

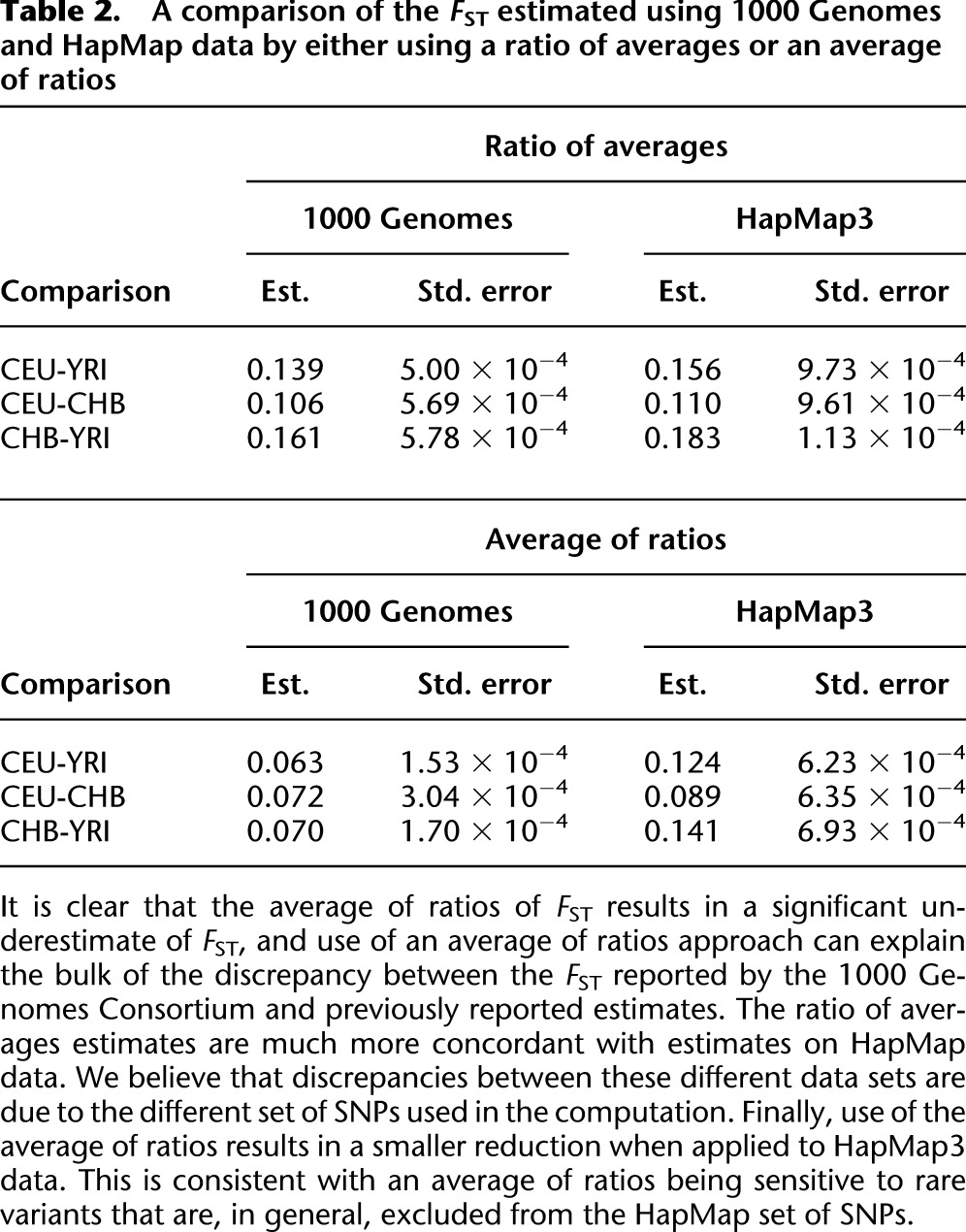
To explore the effect of the rare variants included in sequence data, we compared our results to those obtained using HapMap3 genotypes. We obtain F_ST estimates for CEU and CHB of 0.110 (s.e. 0.0010) and 0.089 (s.e. 0.0006) using the ratio of averages and average of ratios, respectively. This suggests that the inclusion of rare variants with low single-SNP F_ST estimates in the 1000 Genomes data tends to exacerbate the discrepancy produced by the average of ratios. We expect that this discrepancy will grow with sample sizes and sequencing depth (see Supplemental Fig. S2). Ultimately, using the average of ratios may make estimates incomparable across studies and unrelated to population demographic history.

While the use of the average of ratios clearly results in lower estimates of F_ST, these estimates are not as low as those published by the 1000 Genomes Consortium. Below, we explore the possibility that the remaining discrepancy can be accounted for by differences in the set of SNPs analyzed.

Dependence of F_ST on the set of SNPs analyzed

When estimating F_ST for CEU and CHB, we compared the effects of ascertaining in YRI (YRI ascertainment) versus ascertaining SNPs that were polymorphic in CEU, CHB, both populations, or either population (see Table 3). When using an average of ratios, our estimates of F_ST were ∼0.103 for all of these modified ascertainment schemes. These can be compared to an F_ST of 0.106 produced from YRI ascertainment in 1000 Genomes data or 0.110 in HapMap3 data. Though statistically significant, these results suggest that the effects of modified ascertainment are not very large when analyzing human populations using a ratio of averages. This indicates that reasonable estimates of F_ST may be produced when comparing populations without access to an outgroup.

Table 3.

Assessing the effect of ascertainment schemes and combination methods on the resulting F_ST estimate for CEU and CHB

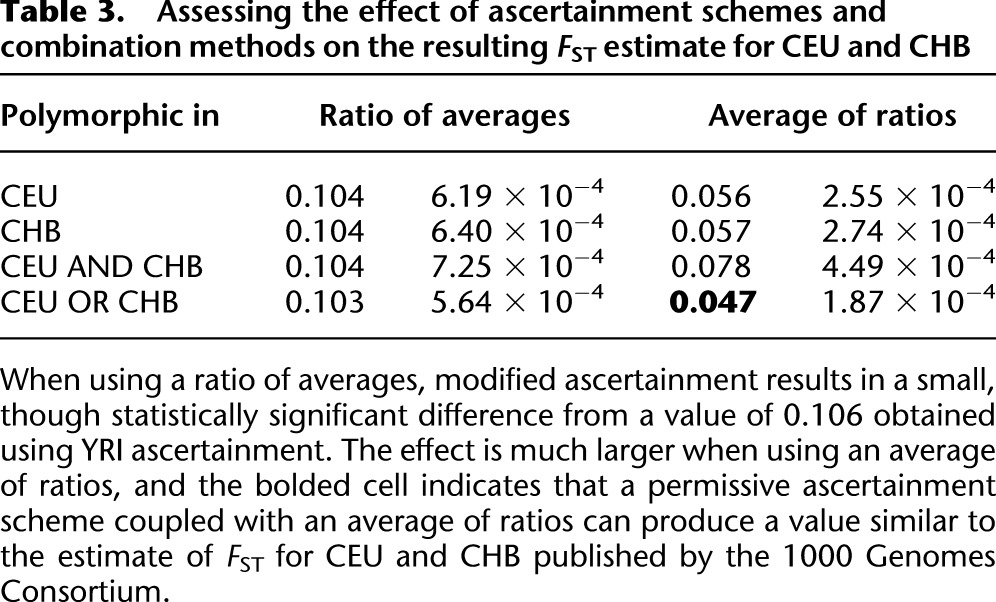
However, when using an average of ratios and including all SNPs polymorphic in either CEU or CHB, our estimate changed from 0.072 to 0.047 (s.e. 0.0002), which is similar to the result reported by the 1000 Genomes Consortium. This suggests that much of the discrepancy between previously published estimates of F_ST for CEU and CHB and the published 1000 Genomes estimate is explained by using the average of ratios and an ascertainment scheme that includes all SNPs that are polymorphic in either of the two populations. These results are replicated for comparisons of continental populations included in the 1000 Genomes data as we obtained values of 0.056 and 0.063 for comparisons of CEU-YRI and CHB-YRI, respectively.

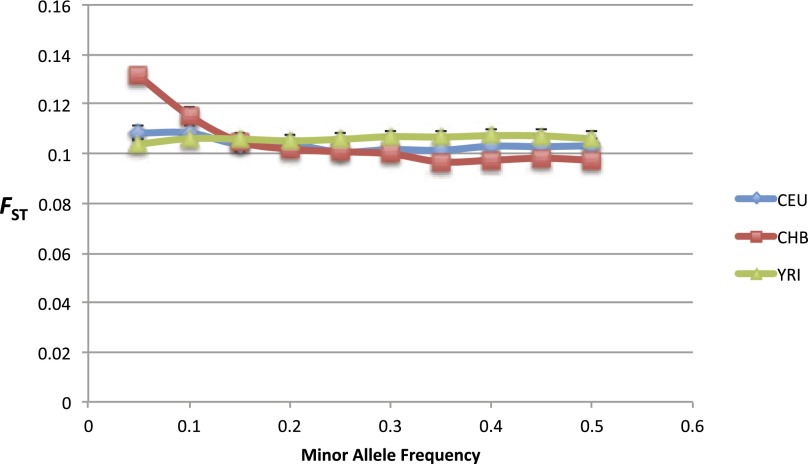
Separately, we note that when comparing CEU to CHB on the 1000 Genomes data we observed larger F_ST estimates of 0.108 for the lowest frequency SNPs (0.0 < MAF ≤ 0.05) versus estimates of 0.103 for the most common SNPs (0.45 < MAF < 0.5) when ascertaining in CEU. These estimates were 0.131 and 0.097 when ascertaining in CHB (see Fig. 1). Increased F_ST for rare variants suggests that bottlenecks are likely to be a stronger influence on F_ST estimates for CEU and CHB than recent expansions. Our results also indicate that bottlenecks in the population history of CHB are likely to be stronger than those in the population history of CEU, consistent with the findings of Keinan et al. (2007). This is in contrast to the much lower F_ST estimates reported on sequence data by the 1000 Genomes Consortium, which might suggest that expansions are a stronger influence on F_ST at rare SNPs.

Figure 1.

Allele frequency dependence of F_ST under different ascertainment schemes. This shows F_ST for CEU and CHB as a function of allele frequency when ascertaining in either CEU, CHB, or YRI. The increased F_ST for rare variants is consistent with bottlenecks being a stronger force on F_ST for CEU and CHB than recent expansion. In fact, this is consistent with a stronger bottleneck in the population history of CHB. We note that this frequency dependence disappears when ascertaining in YRI, suggesting that YRI is a reasonable outgroup for the comparison of CEU and CHB.

Under a simple demographic history (i.e., without migration or admixture), this dependence on minor allele frequency is expected to disappear when ascertaining SNPs in an outgroup. When ascertaining in YRI we do not observe any significant dependence on frequency, which suggests that YRI is a reasonable outgroup for the comparison for CEU and CHB.

We note that when ascertaining in YRI, our genome-wide estimate of F_ST (0.106) is lower than estimated from HapMap3 (0.110). To investigate whether this difference is due to non-random ascertainment of HapMap3 SNPs, we sampled 10 subsets of SNPs from the 1000 Genomes data that matched the allele frequency spectrum of HapMap3 SNPs (see Supplemental Material). We estimated F_ST for CEU and CHB in each of these subsets ranging from 0.106 to 0.107 (s.e. 0.0010). This suggests that HapMap3 SNPs are more highly differentiated than random SNPs, consistent with previous findings on the effects of ascertainment on genotyping arrays (Clark et al. 2005; Albrechtsen et al. 2010).

Recommendations

Choice of F_ST estimator

Because the Hudson estimator is not sensitive to the ratio of sample sizes and does not systematically overestimate F_ST, we recommend that it be used to estimate F_ST for pairs of populations. The Hudson estimator for F_ST and a corresponding block-jackknife estimator for the standard error of F_ST are implemented in the EIGENSOFT software package (EIGENSOFT 4.2 http://www.hsph.harvard.edu/faculty/alkes-price/software/).

Combining estimates of F_ST across multiple SNPs

Using an average of ratios will result in large reductions in F_ST estimates. This effect will be exacerbated when estimating F_ST from sequence data. Therefore, we recommend using a ratio of averages.

Dependence of F_ST on the set of SNPs analyzed

Estimating F_ST from SNPs ascertained in an outgroup has the following valuable properties: (1) F_ST estimates are expected to be independent of allele frequency in the outgroup, and (2) F_ST estimates will relate to divergence time according to Supplemental Equation s1 if there has been no migration or admixture. However, data from a reasonable outgroup is not always available. Additionally, comparison of F_ST between ascertained classes of SNPs (e.g., genic vs. nongenic) can be used to test a variety of hypotheses regarding population history. Thus, we recommend that future publications of F_ST estimates include details of the ascertainment scheme used, including the proportion of SNPs that are polymorphic in each sample.

Discussion

The use of F_ST to quantify the genetic distance between populations and to assess differentiation at individual SNPs is widespread. Here, we point out several challenges surrounding F_ST and provide a protocol for its robust estimation in the case of two populations and bi-allelic SNPs. We show that the estimator of F_ST, the method of combining estimates across SNPs, and the scheme for SNP ascertainment can impact the resulting estimate of F_ST. An inappropriate choice for any of these aspects of estimation can lead to widely disparate estimates of F_ST, especially in a setting of large numbers of rare variants.

Indeed, the F_ST estimate 0.052 for CEU and CHB reported by The 1000 Genomes Project Consortium (2010) underscores the need for a careful analysis. Utilizing the careful protocol set out here, we provide an estimate of 0.106 for CEU and CHB on 1000 Genomes data, which is close to our estimate of 0.110 on HapMap3 (International HapMap 3 Consortium 2010) data. Additionally, we show that when ascertaining for SNPs in one of the two populations studied, rare variants have higher F_ST estimates than common variants. This is the exact opposite of the results suggested by the 1000 Genomes data. The difference between these two results changes the conclusions that are drawn about the role of demography in shaping the patterns of differentiation between human populations. In addition to altering genome-wide estimates of F_ST, the choice of estimator can introduce inflation at the level of single SNP estimates, potentially making it difficult to interpret high F_ST estimates as signals of selection (see Supplemental Material).

Another concern about F_ST was considered by Jost (2008), who showed that as heterozygosity becomes large, F_ST will naturally approach 0—indicating low differentiation—even if all alleles at a locus are population private. In an effort to avoid this problem, Jost introduced D as an alternate measure of differentiation. However, it has been suggested that Jost's D shares the same problems as F_ST, and that these problems are sometimes even more pronounced for Jost's D (Ryman and Leimar 2009). In any case, F_ST and related measures “unquestionably provide important insights into population structure” (Jost 2008), particularly for species such as humans, in which heterozygosity is relatively low.

In conclusion, we recommend the use of the Hudson estimator (Hudson et al. 1992; Keinan et al. 2007) of F_ST that is independent of sample size. We demonstrate that a ratio of averages is an appropriate method for combining these estimates across multiple SNPs. We also show the value of estimating F_ST from SNPs ascertained in an outgroup, though we do not view this as a necessity. We do recommend, however, that future publications of F_ST estimates include details of the ascertainment of SNPs.

Methods

Weir and Cockerham's F_ST (WC)

Definition

Weir and Cockerham (1984) used the definition provided by Cockerham (1969) of F_ST as a ratio of the variance between populations to the total variance in the ancestral population. We analyze this definition in the Supplemental Material.

Estimator

In the setting of population-specific F_ST, described by the WH definition, the WC estimator will result in estimates that vary with the ratio of sample sizes (see Supplemental Material for details). In the case of two populations and biallelic SNPs, the WC estimator is

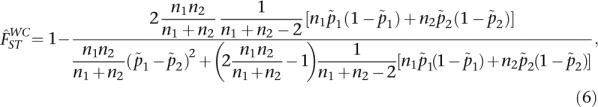where n_i is the sample size and 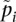is the sample allele frequency in population i for i ∈ {1, 2}. Then, in the limit of large sample sizes (n_i − 1 ≈ n_i), we can assume that sample allele frequencies become close to population allele frequencies 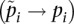. We analyze the estimator as the sample sizes increase, but their ratio goes to a constant M (see Supplemental Material for a derivation). In this case, we show (see Supplemental Material) that the estimate tends toward Equation 1 (see Results).

If the sample sizes are equal, M = 1, then the estimate becomes

Also, when F_ST is identical for both populations, i.e., 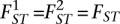, it is straightforward to see that 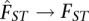, i.e., the estimate will not depend upon the ratio of sample sizes (M). We note that if F_ST is identical across populations, weighting by sample sizes will reduce the variance of the estimator. This was the intent of Weir and Cockerham. If the sample sizes are unequal or this assumption does not hold, however, the estimate will depend upon the ratio of sample sizes underlying the limit. Given the complexity of human population history, it is unlikely that this assumption will hold in general. This means that even if large numbers of samples and SNPs are used to estimate F_ST for a pair of populations, this estimate may not be comparable across studies with different sample sizes.

We note that when F_ST is not identical for both populations, it is possible to estimate F_ST separately for each population (i.e., 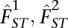) (Weir and Hill 2002). Estimates for those produced according to the method given in Weir and Hill (2002) will not depend on sample size. We focus here on estimating F_ST for a pair of populations, as this is a very common use when analyzing human genetic data.

Nei's F_ST

Definition

Nei (1986) defined F_ST (he used the term G_ST) based upon the sample gene diversity between and within populations as

where 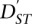is the average gene diversity between populations and H_T is the diversity in the average of the two population samples. We consider this definition in detail in the Supplemental Material.

Estimator

In the case of two populations and bi-allelic SNPs, Nei's estimator is

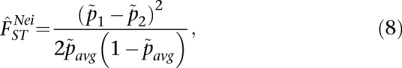where

and 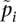is the sample allele frequency in population i for i ∈ {1, 2}. We note that this is Nei's updated estimator and, in the case of two populations, differs from the estimator given in Nei (1973) and Nei and Chesser (1983) by a factor of 2. We use the estimator given in Nei (1986), as it is most closely related to the other estimators considered.

Using the definition of Weir and Hill (2002) we show (see Supplemental Material) that estimates made using Nei's estimator will tend toward Equation 2 (see Results), with a maximum value of 2 as 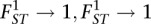. This overestimates the average of population-specific F_ST values and alters the relation from this average of F_ST values to divergence time (see Supplemental Material). Estimates of F_ST given for the Nei estimator were generated using the proposed estimator for the numerator (see Supplemental Material) and a simple estimator for the denominator.

Hudson's F_ST

Definition

Hudson et al. (1992) defined F_ST in terms of heterozygosity. The fundamental difference between these estimators is that for Hudson, the total variance is based upon the ancestral population and not the current sample.

Estimator

Hudson's estimator for F_ST is given by

where H_w is the mean number of differences within populations, and H_b is the mean number of differences between populations. While Hudson did not give explicit equations for H_w and H_b, we cast his description into an explicit estimator (see Supplemental Material for a derivation). The estimator that we analyze is

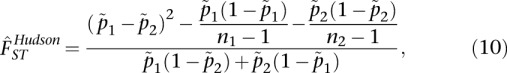where n_i is the sample size and 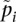is the sample allele frequency in population i for i ∈ {1, 2}. Analyzing this estimator using the definition of Weir and Hill (2002), we show (see Supplemental Material) that F_ST estimated using Hudson's estimator will tend toward Equation 3 (see Results), which is exactly the average of population-specific F_ST values that we seek to estimate. This emerges naturally, as the proposed estimator is the simple average of the population-specific estimators given in Weir and Hill (2002). This estimator has the desirable properties that it is (1) independent of sample composition, and (2) does not overestimate F_ST (it has a maximum value of 1). We recommend its use to produce estimates of F_ST for two populations.

Combining estimates of F_ST across multiple SNPs

The Hudson estimator is asymptotically consistent, as the estimators of the variance components involved in the computation of F_ST are unbiased in the context of the WH definition. However, as their quotient is not an unbiased estimator of F_ST, use of an average of ratios will, in general, result in a biased estimate.

As many rare variants discovered by deep sequencing are population specific, we analyze the effect of this approach in the presence of many such variants. Consider a rare SNP with p₁ = ɛ, p₂ = 0. This yields a single SNP F_ST = ɛ. An estimate produced using an average of ratios will be highly sensitive to rare SNPs of this type and is likely to exhibit dependence on both the sequencing depth and sample size used in the analysis (see Supplemental Fig. S2).

Previous works have examined this choice and advocated for the use of a ratio of averages (Reynolds et al. 1983; Weir and Cockerham 1984). However, in describing the WH-ML method, Weir and Hill recommend that estimates be “simply averaged over loci.” We believe that use of an average of ratios can account for the bulk of the discrepancy between the estimates of F_ST from The 1000 Genomes Project Consortium (2010) and previously published estimates (International HapMap 3 Consortium 2010) (see Results).

Dependence of F_ST on the set of SNPs analyzed

In relating quantities being estimated from current populations to parameters of the evolutionary model, we have calculated expected values given the allele frequency in the ancestral population. This implicitly performs an ascertainment of SNPs that are polymorphic in the ancestral population or, equivalently, in an outgroup population. Provided there is no migration or admixture between populations, the relationship between F_ST and divergence time is given in Supplemental Equation s12.

This relationship accounts for changes in effective population size (i.e., bottlenecks or expansions) in the demographic history of the populations being compared. Additionally, ascertainment in an outgroup renders the estimate independent of the allele frequency spectrum in the outgroup. Therefore, with this type of ascertainment scheme, estimates should be concordant regardless of whether they are produced from rare or common SNPs.

While ascertainment in an outgroup has several helpful properties, in many practical circumstances no data from a reasonable outgroup is available. In these instances, F_ST can be estimated using SNPs ascertained in either one of the populations under study. However, in these instances estimates are not expected to be independent of allele frequency spectrum or complex demographic scenarios.