Effects of fatigue on synergies in a hierarchical system

Abstract

We investigated the effect of fatigue produced by timed maximal voluntary contraction (MVC) of the index finger of one of the hands on performance in MVC and accurate cyclic force production tasks in right-handed subjects. Based on earlier studies, we hypothesized that fatigue would produce an increase in the indices of force-stabilizing synergies in both hands as well as between the hands in two-hand tasks. Synergies were defined as co-varied adjustments of commands to fingers (modes) across cycles that stabilized total force. Fatigue caused a significant reduction in the MVC of the exercised as well as the non-exercised hand. Indices of finger enslaving (lack of individuation) increased with fatigue in both hands, although the increase was significant in the exercised hand only. In contrast to the significant effects of fatigue on MVC forces performed by the non-exercised hand, there were no comparable transfer effects on the root mean square errors during accurate force production. During one-hand tasks, both hands showed high indices of force-stabilizing synergies. These indices were larger in the left hand. Fatigue led to a general increase in synergy indices. Exercise by the left hand had stronger effects on synergy indices seen in both hands. Exercise by the right hand showed ipsilateral effects only. Smaller effects of fatigue were observed on accuracy of performance of the force-down segments of the force cycles compared to the force-up segments. For the bimanual tasks, synergies were analyzed at two hierarchical levels, two-hand (four-finger) and within-a-hand (two-finger). An increase in the synergy index with fatigue was observed at the lower (two-finger) level of the hierarchy only. We interpret the lack of effects of fatigue at the upper (two-hand) level as a consequence of a trade-off between synergies at different levels of the hierarchy. The differences between the hands are discussed within the dynamic dominance hypothesis.

1. Introduction

Exercise-induced fatigue impairs the motor function and has detrimental effects on contractile muscle properties (reviewed in Barry & Enoka, 2007; Gandevia, 2001; Gandevia, Allen, Butler, & Taylor, 1996). Despite the changes in the neuromotor apparatus, goal-relevant features of performance by redundant motor systems are relatively preserved during fatigue of one (or a few) of the elements involved in the task (Forestier & Nougier, 1998; Fuller, Lomond, Fung, & Côté, 2009; Gates & Dingwell, 2010; Huffenus, Amarantini, & Forestier, 2006; Missenard, Mottet, & Perrey, 2009; Rodacki, Fowler, & Bennett, 2001). Large sets of elements (multiple muscles crossing a joint, multiple joints within an extremity, or multiple extremities) are traditionally viewed as redundant (Bernstein, 1967; Latash, 1996; Turvey, 1990) and posing computational problems for the central nervous system (CNS). Alternatively, they may be viewed as abundant (Gelfand & Latash, 1998) and organized by the neural controller into synergies that ensure stable performance in a variety of motor tasks.

By the term “synergy” we imply neural organizations that ensure co-varied (across trials) adjustments of elemental variables (output variables of individual elements) that reduce variance of an important performance variable produced by all the elements together (reviewed in Latash, 2008; Latash, Scholz, & Schöner, 2007). The framework of the uncontrolled manifold hypothesis (Scholz & Schöner, 1999) has been used to quantify synergies. The UCM hypothesis implies that the central nervous system (CNS) acts in a space of elemental variables, creates in this space a subspace (UCM) corresponding to a desired value of a performance variable, and then limits variance of the elemental variables to that subspace. Variance of elemental variables may be viewed as the sum of two components, “good variance” along the UCM (V_UCM) that does not affect performance, and “bad variance” orthogonal to the UCM (V_ORT) that does. If V_UCM > V_ORT (both variance indices quantified per degree-of-freedom), a conclusion is drawn that a synergy stabilizes the performance variable. If V_UCM ≤ V_ORT, we conclude that there is no synergy stabilizing the performance variable. The relative difference (ΔV) between V_UCM and V_ORT has been used as a quantitative index of synergy. Our previous studies of exercise-induced fatigue have shown an increase in the index of synergy for accurate multi-digit force production tasks as well as in multi-muscle postural tasks (Park, Singh, Zatsiorsky, & Latash, 2012; Singh & Latash, 2011; Singh, SKM, Zatsiorsky, & Latash, 2010a, 2010b).

Our earlier studies of the effects of fatigue on multi-finger synergies were limited to performance by the dominant arm. It has been shown, however, that the two arms are specialized for different aspects of coordinated behavior (Sainburg, 2002; Wang & Sainburg, 2007). The dynamic dominance hypothesis (Sainburg, 2005) states that the dominant arm is specialized for trajectory control while the non-dominant hand is better for the control of postural states. In the current study, the main task involved sinusoidal rhythmic force production and, hence, our first hypothesis was that, in the right-handers, the right hand would have higher indices of force stabilizing synergy than the left hand.

The previous studies have shown an increase in the index of force-stabilizing synergy for the exercised limb (Singh et al., 2010a, 2010b) but whether these effects transfer to the non-exercised limb is unknown. Several studies have documented fatigue-induced decline in the maximal voluntary contraction force (MVC) (Martin & Rattey, 2007; Rattey, Martin, Kay, Cannon, & Marino, 2006; Todd, Petersen, Taylor, & Gandevia, 2003; Zijdewind, Zwarts, & Kernell, 1998) and increased motor-unit synchronization (Boonstra, Daffertshofer, As, Vlugt, & Beek, 2007; Boonstra et al., 2008) not only within the exercised limb but also in the non-exercised limb. Thus, our second hypothesis was that the non-exercised hand would show effects on the two variance components (V_UCM and V_ORT) and synergy index (ΔV) similar to those in the exercised hand, but possibly of smaller magnitude.

Bimanual tasks have been viewed as being controlled in a hierarchical fashion (Dounskaia et al., 2005; Gorniak, Zatsiorsky, & Latash, 2007a, 2007b; Tseng, Scholz, & Galloway, 2009). At the upper level of the hierarchy the task is distributed between the two arms, while at the lower level the action of each arm is distributed amongst the elements (joints or digits). A trade-off between synergy indices at different levels within a hierarchically organized system has been demonstrated (Gorniak et al., 2007a; Gorniak, Zatsiorsky, & Latash, 2009): There were strong force-stabilizing synergies at the higher level of the hierarchy (between-hands) but not at the lower level (within-a-hand). Hence, we expected to see force-stabilizing synergies between the hands (ΔV > 0) but not within-a-hand (ΔV < 0) in two-hand tasks. We also investigated whether adjustments of multi-digit synergies to fatigue of a single finger were seen at both within-a-hand and between-hands levels. We hypothesized that during fatigue synergy indices would show an increase at both levels of the hierarchy.

2. Experimental procedure

2.1. Participants

Thirteen right-hand dominant participants (seven males) [age: 26.0 ± 5.3 (SD) years, mass: 74.5 ± 19.97 kg, height: 1.69 ± 0.08 m, left hand width: 7.9 ± 0.48 cm, left hand length: 18.25 ± 1.20 cm, right hand width: 7.92 ± 0.536 cm right hand length: 18.26 ± 1.19 cm] participated in the experiment. All the participants were healthy with no known history of neurological or motor disorders. Hand length was measured as the distance from the tip of the distal phalanx of digit three to the distal crease of the wrist with the hand in a neutral flexion extension pose. Hand width was measured between the lateral aspects of the index and little finger metacarpophalangeal (MCP) joints. None of the participants had a history of long-term involvement in hand or finger activities such as typing or playing musical instruments. All participants gave informed consent according to the procedures approved by the Office for the Research Protections of the University.

2.2. Apparatus

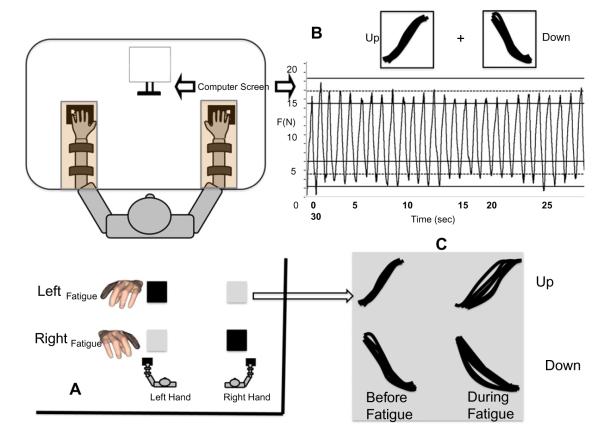
This study involved force production with the index and middle fingers of the left and right hands. Four six-component force sensors (Nano-17, ATI Industrial Automation, Garner, NC) were used to measure the normal forces generated by individual digits. Two force sensors (for the index and middle fingers) were attached to two customized flat panels for each of the hands (see panel A, Fig. 1). Only the normal forces were collected from the sensors. The ring and little fingers rested on cylindrical supports that were similar to the geometrical shapes of the sensors. Each sensor was covered with sand-paper (300 grit) to increase friction and prevent temperature effects on the sensors. All the sensors were placed within slots in the panel that allowed the movement of the sensors in the sagittal plane of the participant. The participants determined the most comfortable location for each sensor and the sensors were placed accordingly. The fixed distance between the centers of the sensors along the medial–lateral direction was 3.0 cm.

Fig. 1.

(A) The block experimental design (inset). The rows show the factor exercised-hand and the columns show tested-hand. The index fingers of the exercised-hands have been darkened to show that it was the exercised finger. When the exercised-hand and tested-hand were the same, the tested-hand was also the fatigued-hand (black boxes) and when they were not the same, the tested-hand was the non-fatigued hand (grey boxes). (B) A schematic of the experimental setup; the bottom right part shows the feedback shown to the participants on the computer screen. The cycles were separated into force up and down half-cycles. (C) The up and down cycles were analyzed separately within each block of the experimental design.

The analog signals of the normal force from the four force sensors were collected and digitized with a 12-bit analog–digital converters (PCI-6031 and PCI-6033,National Instrument, Austin, TX) with the help of a customized LabVIEW program (LabVIEW 9.0, National Instruments, Austin, TX). The sampling frequency was set at 200 Hz. Before each trial, all signals from the sensors were set to zero.

During the experiment, the participants sat in a chair facing the test table with both their upper arms at ~45° of abduction in the coronal plane and ~45° of flexion in the sagittal plane. The elbow was flexed at ~135°. Both forearms rested on two wooden boards that housed the sensors (see panel A, Fig. 1). Each forearm was strapped to the wooden board with two sets of Velcro straps. A custom-fit support object was placed underneath both palms to help maintain a constant configuration of the hand and fingers while the participants performed the experiment. The participant’s hands formed a dome-like structure with the MCP joint flexed at 20° and all interphalangeal joints slightly flexed as well. Participants were asked to select comfortable thumb positions during the experiment. A computer monitor was located 0.65 m away from the participant. The monitor displayed the task (described in Section 2.3).

2.3. Procedures

The participants performed unimanual and bimanual rhythmic accurate force production tasks (see a representative performance in panel A of Fig. 1). The participants were given feedback on the force produced by the instructed finger(s), by a real-time plot of the force magnitude (y-axis) against time (x-axis). Each participant made three visits to the laboratory. The first visit was a practice session without a fatiguing exercise. The second and third sessions were separated exactly by one week. Within the second and third sessions, participants exercised the index finger of the left hand (Left_Fatigue) or the index finger of the right hand (Right_Fatigue). The participants also performed control trials in both sessions both before and after the fatiguing exercise. We employed a randomized block design for the study with three fixed factors. The first factor was fatigue and it had two levels – before-fatigue and during-fatigue. The second factor in our design was exercised-hand and it also had two levels – Left_Fatigue and Right_Fatigue. Tested-hand was the third factor (exercised and non-exercised hand as levels). The experimental design is illustrated in panel B of Fig. 1. When the tested-hand was the same as the exercised-hand, we refer to the effects of fatigue as ipsilateral effects (e.g., blacksquares in panel B of Fig. 1) and when the tested hand was the non-exercised hand, we addressed the effects of fatigue as contralateral effects (e.g., grey squares in panel B of Fig. 1).

2.3.1. Session 1

During this session, the participants were familiarized with the experimental protocol. The familiarization exercise was done to minimize learning during and between the second and third sessions. The participants completed all the trials involved in the experimental protocol that they were going to perform during Sessions 2 and 3.

2.3.2. Sessions 2 and 3; before-fatigue trials

Sessions 2 and 3 were the main experimental sessions when data were recorded. In each session, an index finger either of the left hand (Left_Fatigue) or of the right hand was exercised (Right_Fatigue). The order of the exercised hand was randomized across participants. There were three tests: MVC trials, one-finger ramp trials, and rhythmic force production trials.

2.3.3. MVC trials

The participants were required to produce MVCs by each of the four fingers (I_L, M_L, I_R and M_R), two finger combinations (IM_L and IM_R) and a four-finger combination (IM_L + IM_R). Initially (for the first 5 s) the participants rested their fingers on the sensors. Then after the cursor passed a vertical line (at 5 s), they were instructed to press in a self-paced manner as hard as they could with the instructed finger(s) without lifting any of the other fingers off the sensors. The participants were told that after they reached their maximum force, they could relax. The participants got visual feedback on the amount of force they produced on the computer screen. The total duration of each MVC trial was 30 s. The order of the seven MVC trials was randomized across participants. Only one MVC trial for each finger combination was collected during each session. If the MVC for a finger combination during Session 3 was less than that of Session 2 by more than 15%, then the participant was asked to repeat the MVC trial. This was found to be the case in less than 3% of the MVC trials.

2.3.4. One-finger ramp trials

In these trials, the participants were shown a template on the screen that had zero force for the first 5 s and then a slanted line from 0% to 40% MVC over the next 10 s. The total trial duration was 20 s. In each trial, the participants were asked to produce a force profile matching the template on the screen by pressing with one of the fingers. Feedback on the force produced by that finger was shown on the screen. The participants were instructed to keep the other fingers on the sensors and were instructed not to pay attention to any force production by the other fingers. No feedback on forces produced by these fingers was provided. The data from these trials were used to compute the enslaving matrix E (described in Data Processing). One trial for each finger, as the instructed finger, was recorded. There was a 15-s interval between ramp trials.

2.3.5. Rhythmic force production trials

Participants produced rhythmic, sine-like force profiles with five different finger combinations (I_L, IM_L, I_R, IM_R and IM_L-IM_R) between two horizontal targets placed at 10% and 30% of MVC for that finger combination. The task was to change force in a smooth, sine-like fashion in such a way that the crests and troughs lied within the target range of ±3% MVC specified by two horizontal lines. The participants were required to do this at a pace set by a metronome that produced audible “ticks” at a frequency of 0.9 Hz. This frequency was set based on earlier studies as comfortable for most participants (Friedman, SKM, Zatsiorsky, & Latash, 2009). The order of the finger combinations (I_L, IM_L, I_R, IM_R and IM_L + IM_R) was randomized across participants. Participants completed two 30-s trials for each finger combination. There were 15-s intervals between the two trials within a finger combination and a 30-s interval between finger combinations.

2.3.6. Sessions-2 and -3; fatigue exercise and during-fatigue trials

The participants were given a 3–4 minute break after the completion of the before-fatigue trials. Participants performed a 1-min fatiguing exercise with the index finger at MVC followed by a 20 s re-fatiguing exercises after each trial to avoid recovery. At all times, the participants were verbally encouraged to produce as high forces as possible. This protocol was used in our previous studies (Danion, Latash, Li, & Zatsiorsky, 2001; Danion, Li, Zatsiorsky, & Latash, 2000; Singh et al., 2010a, 2010b). During the fatiguing exercise, the participants were reminded to try not to involve other fingers of the hand and to avoid excessive muscle co-contraction (stiffening the hand). For each participant, the during-fatigue trials within a condition were conducted in the same order as the before-fatigue trials but the order of the trials was changed between Sessions 2 and 3.

2.4. Data processing

MATLAB (MATLAB 7.12.0, Mathworks Inc., Natick, MA) programs were written for data processing and analysis. The data were filtered using a fourth-order zero-lag Butterworth low-pass filter with a cutoff frequency of 12 Hz. MVC of a particular finger combination was measured at the time when the force produced by the task finger(s) peaked. For the two- and four-finger tasks, MVC was computed at the instant when the total force peaked.

Finger forces show enslaving (addressed also as “lack of individuation”), i.e., unintended force production by non-task fingers (Keen & Fuglevand, 2004; Kilbreath & Gandevia, 1994; Ohtsuki, 1981; Zatsiorsky, Li, & Latash, 1998). Therefore, we first converted the force data matrix into elemental variables, force modes. Force modes are hypothetical variables that can be modified by the controller one at a time. We first computed the enslaving matrices (E) for each participant by using the single-finger ramp trials. For each trial, a linear regression of the forces produced by individual fingers against the total force produced by the two fingers of the same hand over the 10-s ramp time interval was computed. The entries of the enslaving matrices (E_L and E_R, 2 × 2) were computed as the regression coefficients of the individual finger forces vs. the total force of the hand over the ramp duration: F_i,j = a_i,j + b_i,j •F_TOT, where F_i,j is the force produced by finger i in the j finger task, a and b are constants, and F_TOT is the total force produced by both fingers. Enslaving matrix, E, was block-diagonal because one-finger ramp tasks did not lead to visible force production by the fingers of the other hand:

$$E=\left[\begin{array}{cccc}\hfill b_{I_L,I_L}\hfill & \hfill b_{I_L,M_L}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill b_{M_L,I_L}\hfill & \hfill b_{M_L,M_L}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill b_{I_R,I_R}\hfill & \hfill b_{I_R,M_R}\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill b_{M_R,I_R}\hfill & \hfill b_{M_R,M_R}\hfill \end{array}\right]$$ (1)

The index of enslaving [E_L] or [E_R], was computed for each hand separately as the sum of the off-diagonal entries of E_L and E_R respectively.

E was used to compute the time changes in the vector of hypothetical commands to fingers (force modes, m) based on force changes:

$${\mathbf{m}}_{\mathit{ij}}={\mathbf{E}}^{-1}{\mathbf{f}}_{\mathit{ij}}$$ (2)

where m and f are force mode and force matrices respectively. Subscript ‘i’ denotes a finger (I_L, M_L, I_R or M_R), and ‘j’ denotes a time-point.

For the rhythmic trials, we rejected data from the first and last three seconds of each trial to remove end effects within a trial. To compute the root mean square error (RMSE) for the rhythmic task, the quasi-sinusoidal force profiles were aligned and averaged. The total force data (F_TOT) were segmented into the periods of force increase (force-up) and force decrease (force-down). The accepted segments were then resampled into 100 points using cubic spline interpolation. RMSE and variance of force was computed about the mean at each of the resampled points and then averaged separately for both the force-up and force-down half-cycles. The RMSE was computed for the total force whereas the variance of force was computed for the forces produced by each finger. For across-participants comparisons, RMSE was normalized by 20% MVC (mean value of the sinusoidal cycle) and variance was normalized by the square of 20% MVC. For the IM_L, IM_R, and IM_L + IM_R trials, the variance of the forces produced by the I_L, M_L, I_R, and M_R fingers was computed at each of the 100 resampled points and then averaged across the points. The force variance indices were normalized to the squared MVC of that particular finger.

2.4.1. Analysis of multi-finger synergies

The analysis of multi-finger synergies stabilizing the total force in the unimanual (IM_L, IM_R) and bimanual (IM_L + IM_R) tasks was performed in the framework of the UCM hypothesis (Scholz & Schöner, 1999; Schöner & Scholz, 2007). The hypothesis assumes that the controller organizes co-variation amongst elemental variables to stabilize a performance variable. We used force modes, m, as elemental variables computed as described in Equation 2. Further, two components of variance were computed, within the UCM (V_UCM) and orthogonal to it (V_ORT). A synergy index was computed as the normalized difference between V_UCM and V_ORT: ΔV = (V_UCM − V_ORT)/V_TOT, where V_TOT is total variance, and all the variance indices are normalized by degrees-of-freedom in the corresponding sub-spaces. For more details on the computations see Latash, Scholz, Danion, and Schöner (2001) and Singh et al. (2010a). For two-element tasks ΔV varies between −2 and 2; and for four-element tasks ΔV varies between −4 and 1.33.

2.5. Statistics

Standard descriptive statistics were used (means ± SE). Repeated-measures ANOVAs were used to test hypotheses on the effects of fatigue on outcome variables such as V_UCM, V_ORT and MVC. A linear-mixed model for repeated measures (RM) was fit to the data. For multiple comparisons, Bonferroni’s correction was used. The level of significance was chosen as α = .05. We analyzed the unimanual and bimanual tasks separately. The unimanual tasks had three fixed factors, fatigue (before- and during-fatigue as levels), tested-hand (fatigued and non-fatigued as levels), and exercised-hand (Left_Fatigue and Right_Fatigue). The bimanual tasks had only two fixed factors, fatigue, and exercised-hand. For both the unimanual and bimanual rhythmic tasks, we separated the force-up and force-down parts of the cycles and analyzed the two separately.

The following steps were involved:

1. We first checked if the before-fatigue differences for any variable of interest between Sessions 2 and 3 were significant. This wasn’t found to be the case for any of the variables.

2. We analyzed the main effect of factor hand (left and right hand as levels) on the before-fatigue data to compare the differences in the performance of the two hands.

3. Our main hypotheses were tested using a three-way RM ANOVA with fatigue, tested-hand and exercised-hand as factors.

4. If there was a main effect of fatigue and an interaction of fatigue with either exercised-hand or tested-hand, then we eliminated fatigue as a factor by computing the change in the dependent variable. For example, ΔV_UCM was computed as the change between the before-fatigue V_UCM and during fatigue V_UCM. The following hypotheses were tested in separate t-tests (appropriate Bonferroni corrections were used):

   1. H_A: No effect of fatigue on the exercised hand.
   2. H_B: If we rejected H_A, then the effects of Left_Fatigue and Right_Fatigue on the exercised hands were equal.
   3. H_C: No effect of fatigue on the non-exercised hand.
   4. H_D: If we rejected H_C, then the effects of Left_Fatigue and Right_Fatigue on the non-exercised hands were equal.

3. Results

3.1. Effects of fatigue on MVC

Before fatigue, the right hand was stronger than the left hand by ~15% (Table 1). Fatigue led to a significant reduction in the MVC produced by the I and IM finger combinations. During fatigue, on average, the MVC of the I finger dropped by 23.4% and that of the IM combination dropped by 20.4%. The MVC of the exercised hand (ipsilateral fatigue) dropped more than the MVC of the non-exercised hand (contralateral fatigue) (Table 1). Fatigue led to a ~20% drop in MVC of the IM_L + IM_R combination. A two-way RM ANOVA with fatigue and exercised-hand as factors showed a main effect of fatigue (p < 0.001). There were no other significant effects.

Table 1.

Changes in MVC and index of enslaving for the exercised and non-exercised hands.

Variable	Left Hand			Right Hand
	Before Exercise	Non-Exercised	Exercised	Before Exercise	Non-Exercised	Exercised
MVC Index (N)	33.1 ± 1.28	30.1 ± 2.23*,**	21.32 ± 1.21*	37.76 ± 1.27	33.35 ± 1.47*,**	23.84 ± 1.67*
MVC (IM) (N)	51.07 ± 2.35	47.79 ± 2.98**	35.16 ± 2.82*	58.71 ± 2.77	52.68 ± 4.22*,**	39.04 ± 2.58*
Enslaving	0.21 ± 0.02	0.26 ± 0.04	0.31 ± 0.04*	0.18 ± 0.02	0.22 ± 0.03	0.29 ± 0.05*

^*Denotes significant difference from the before exercise values (p < .05).

^**Denotes significant difference between the non-exercised and exercised values for each hand.

3.2. Effects of fatigue on enslaving

Before fatigue, enslaving in the left hand, [E_L], was larger than in the right hand, [E_R], by ~15% (Table 1). Fatigue led to a large ( ~38%) increase in enslaving. The enslaving in the exercised hand increased more than in the non-exercised hand by about 100%.

3.3. Effects of fatigue on accuracy of task performance

There were no differences between the hands in the RMSE index prior to the fatiguing exercise. RMSE in the force-up direction was larger than in the force-down direction (by ~5%, p < 0.05).

3.3.1. Unimanual accurate force production tasks

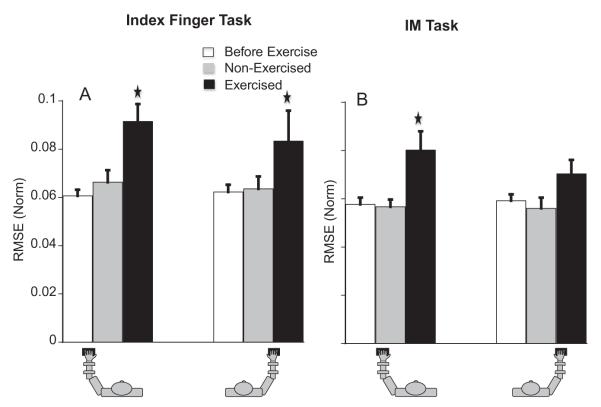
Fatigue did not have a significant effect on RMSE in the force-down direction and therefore, these data were not analyzed further. For the force-up direction, fatigue led to an increase in RMSE by about 16.7% for the I-finger task (see panel A of Fig. 2). The three-way RM ANOVA on RMSE of I showed effects of fatigue, F(1,36.82) = 6.7, p < .05, tested-hand, F(1,32.37) = 6.57, p < .05, and fatigue × tested-hand (p < .05). The ipsilateral effects of exercise were strong; the RMSE of the left hand increased by ~27% and that of the right hand by ~22% (both p < .01). There were no changes in the RMSE of the non-exercised hand. Fatigue increased the RMSE for the IM combination in the force-up direction for the exercised hand but had no effect on the non-exercised hand. Overall, RMSE increased by about 12% (see panel B of Fig. 2). Statistically, the only significant increase in RMSE was for the left hand under Left_Fatigue (a 31% increase, p < .01).

Fig. 2.

(A) Average normalized RMSE (normalized by MVC) in the up direction for the I combination before-fatigue, during contralateral, and ipsilateral fatigue. The bars show the means over 13 participants of RMSE for the before-fatigue (white), non-fatigued (grey, contralateral fatigue), and fatigued (black, ipsilateral fatigue) condition. The left three bars show the means for the left hand. The right three bars show the means for the right hand. (⁥) Represents significant difference from the before-fatigue condition. (B) Average RMSE in the up direction for the IM combination before-fatigue, during contralateral, and ipsilateral fatigue.

3.3.2. Bimanual accurate force production tasks

For the bimanual task, the RMSE were similar for both force-up and force-down directions before fatigue. Fatigue increased the RMSE for the force-up direction by about ~14% (main effect of fatigue; F(1,46.02) = 4.35, p < .05). There were no effects of fatigue on the RMSE for the force-down direction.

3.4. Effects of fatigue on finger force variance

3.4.1. Unimanual accurate force production tasks

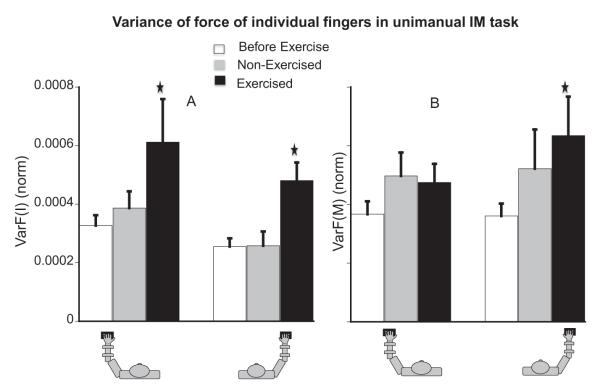
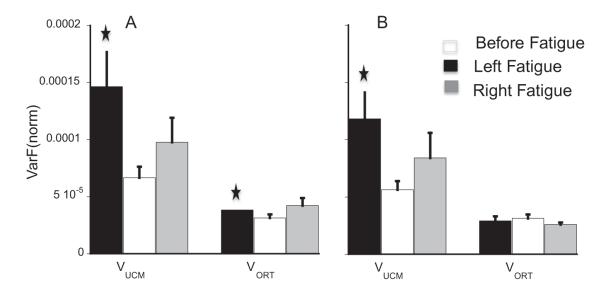
We also looked at the variance of force of each finger in the unimanual two finger pressing tasks. Fatigue increased VarF(I) (both left and right), on average, by about 54% (see panel A of Fig. 3). A three-way RM ANOVA on VarF(I) with the factors fatigue, exercised-hand and tested-hand showed effects of fatigue, F(1,44.80) = 4.05, p < .05 and fatigue × Exercised-hand (p < .05). The variance of force for the exercised hand increased significantly: During Left_Fatigue, VarF(I_L, IM_L) increased by ~60% (p < .05) and during Right_Fatigue, VarF(I_R, IM_R) increased by ~90% (p < .01). Fatigue also increased VarF(M) by about 49% (see panel B of Fig. 3), effects of fatigue, F(1,43.6) = 6.01, p < .05 and fatigue × tested-hand (p < .05). During Right_Fatigue, VarF(M_R, IM_R), increased by ~60%, (p < .01). Left_Fatigue did not have a significant effect on VarF(M_L, IM_L ). For the force-down direction, fatigue increased VarF(I) by ~30% (effect of fatigue, F(1,42.83) = 4.84, p < .05) and most of the increase was in the exercised hand. Contralateral fatigue did not increase the variance of the index or the middle finger.

Fig. 3.

(A) Average normalized VarF(I) (normalized by square of MVC) in the up half-cycle before-fatigue, during contralateral, and ipsilateral fatigue. The left three bars are for I_L when the left hand was the tested-hand and the right three bars are for I_R when the right hand was the tested-hand. (B) Average VarF(M) (norm) in the up half-cycle before-fatigue, during contralateral, and ipsilateral fatigue. The left three bars are for M_L when the left hand was the tested-hand and the right three bars are for M_R when the right hand was the tested-hand. (⁥) Represents significant difference from the before-fatigue condition.

3.4.2. Bimanual accurate force production tasks

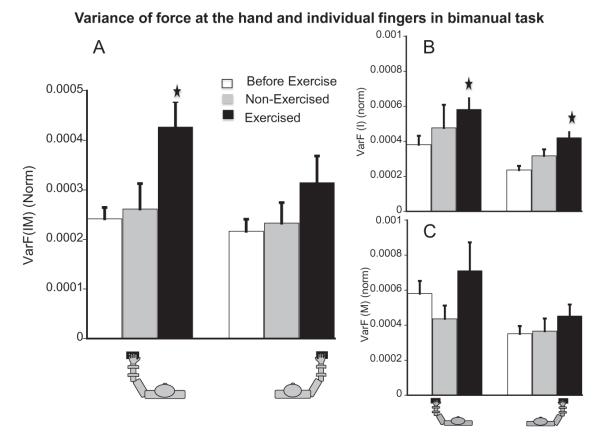
First, we computed the variance of the total force produced by the left hand, VarF(IM_L), and the right hand, VarF(IM_R) (upper level of hierarchy). Fatigue had no effect on these indices for the force-down direction, while it led to an increase in VarF(IM) for the force-up direction by about 38% (see panel A of Fig. 4). There was a main effect of fatigue, F(1,19.51) = 5.21, p < .05, tested-hand, F(1,49.26) = 5.68, p < .05, and fatigue × tested-hand (p < .001). Pairwise comparisons showed only a strong ipsilateral effect of Left_Fatigue on VarF(IM_L) (increase of 86%, p < .01).

Fig. 4.

(A) Variance (normalized by square of MVC) of the total force (index + middle fingers) produced by each hand in the bimanual task in the up half-cycle. (B) Top panel- Average VarF(I) (norm) in the up direction for the bimanual task before-fatigue, during contralateral, and ipsilateral fatigue. Bottom panel- Average VarF(M) (norm) in the up half-cycle for the bimanual task before-fatigue, during contralateral, and ipsilateral fatigue. (⁥) Represents significant difference from the before-fatigue condition.

We also analyzed the variance of force of the individual fingers (lower level of hierarchy). Fatigue increased VarF(I) for the force-up direction (see panel B of Fig. 4). There was a main effect of fatigue, F(1,41.67) = 7.71, p < .01, and Exercised-hand × Tested-hand, F(1,84.44) = 6.22, p < .05. Both the ipsilateral effects were strong (p < .05). For the force-down direction, fatigueled to an increase in VarF(I) (main effect of fatigue, F(1,42.11) = 5.35, p < .05. There were no significant effects of fatigue on VarF(M) (panel C of Fig. 4).

3.5. Effects of fatigue on multi-finger synergies

3.5.1. Unimanual accurate force production tasks

We analyzed the two components of variance, V_UCM and V_ORT, each one quantified per degree-of-freedom in the corresponding sub-space, and the index of force-stabilizing synergy, ΔV in the finger mode space (for details see Methods and cf. Singh et al., 2010a). Both exercises (Left_Fatigue and Right_Fatigue) had strong ipsilateral effects on V_UCM. Ipsilateral fatigue also increased V_ORT but the increase in V_ORT was not as large as that of V_UCM. There were no contralateral effects of fatigue on V_ORT.

On average, before fatigue, V_UCM was greater than V_ORT by about 115%. For the force-up direction, before-fatigue there were no significant differences in any of the variance indices between the left and right hand (white bars in panels A and B of Fig. 5). The results were similar for force-down direction.

Fig. 5.

A and B: Average normalized V_UCM (panel A) and V_ORT (panel B) for the up half-cycle. The bars show the means over 13 participants for the before-fatigue (white), non-fatigued (grey, contralateral fatigue), and fatigued (black, ipsilateral fatigue) condition. The left three bars show the means for the left hand. The right three bars show the means for the right hand. C and D: average V_UCM (panel C) and V_ORT (panel D) in the down half-cycle. Notice that contralateral fatigue has no effect on V_ORT but V_UCM increases for both the up and down half-cycles. (⁥) Represents significant difference from the before-fatigue condition.

Fatigue led to an increase in V_UCM in both exercised and non-exercised hands (the black and gray columns in panels A and C of Fig. 5) for both force-up and force-down segments, although only the increase in the exercised hand reached significance [effects of fatigue, F(1,45.27) = 11.25, p < .01; tested-hand, F(1,59.06) = 4.51, p < .05; fatigue × tested-hand, p < .001; fatigue, F(1,48.82) = 10.91, p < .01; tested-hand, F(1,67.68) = 5.16, p < .05; fatigue × tested-hand, p < .01) in ANOVAs for the force-up and force-down segments respectively]. On average V_UCM increased by 160% in the exercised hand and by 35% in the non-exercised hand. V_ORT showed an increase in the exercised hand only, and this increase was significant for the force-up segments (on average, by ~100%) but not in the force-down segments.

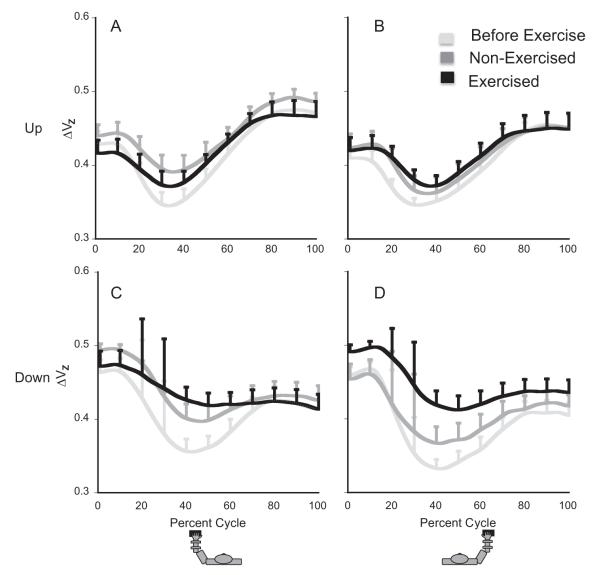
Fatigue resulted in an overall increase in the synergy index ΔV (averaged across subjects z-transformed values, ΔV_Z are shown in Fig. 6). These effects of fatigue were significant for the force-down segments (bottom panels in Fig. 6; effect of fatigue, p < .05), but were under the significance level for the force-up segments (top panels in Fig. 6). For the force-down segments, the effects were similar in the exercised and non-exercised hands (no Fatigue × Tested-Hand interaction).

Fig. 6.

A and B: ΔV_Z over the up half-cycle (normalized to 100 time points) for the left (panel A) and right hand (panel B). Each curve is the average ΔV_Z for 13 participants. C and D: ΔV_Z over the down half-cycle for the left (panel C) and right hand (panel D). Notice that fatigue induces a substantial change in ΔV_Z in the down but not the up direction.

3.5.2. Bimanual accurate force production tasks, upper level of the hierarchy

We performed the analysis in a four-dimensional mode space for I_L, M_L, I_R, and M_R (see Eq. (2)) and also in a two-dimensional space (I_L + M_L, I_R + M_R) where we combined the total force of the fingers of the left hand (and multiplied it by the appropriate enslaving matrix) into one mode and that of the right into another mode. The results were qualitatively and statistically almost identical. Therefore, we present the results only for the four-dimensional analysis.

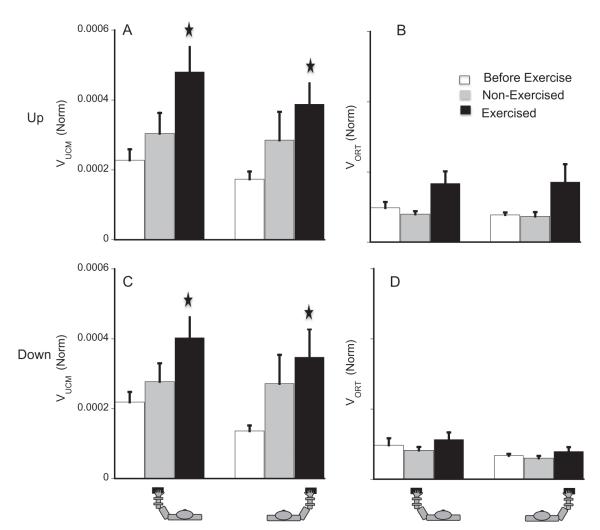
Fatigue increased V_UCM by about 80% on average (see left columns in the panels A and B of Fig. 7). Left_Fatigue increased V_UCM more than Right_Fatigue by about 35%. A two-way RM ANOVA on V_UCM with fatigue and exercised-hand as factors showed a main effect of fatigue for both force-up and force-down directions, F(1,47.64) > 4.90, p < .05. Fatigue also increased V_ORT for the force-up direction by about 28% (see right columns in the panels A and B of Fig. 7). The effect of fatigue approached significance (p = .06). Pairwise comparisons for V_UCM (p < .05) and V_ORT (p < .05) show a significant effect of Left_Fatigue only. The increase in V_UCM and V_ORT during Right_Fatigue approached significance. For the force-down direction, Left_Fatigue significantly increased V_UCM (p < .05). V_UCM and V_ORT changed in a way that resulted in no significant effect on ΔV.

Fig. 7.

A and B: Average V_UCM and V_ORT at the upper level of the hierarchy for the bimanual task for the force-up (panel A) and force-down (panel B) directions. (⁥) Represents significant difference from the before-fatigue condition.

3.5.3. Bimanual accurate force production tasks, lower level of the hierarchy

Before fatigue, V_UCM was larger for the left hand than for the right hand by about 72% (see the white bars in panel A of Fig. 8, effect of hand, F(1,21.61) > 9.4, p < .01 for both force-up and force-down directions. Fatigue significantly increased V_UCM for the force-up direction (see grey and black bars in panel A of Fig. 8). There were significant effects of fatigue, F(1,46.51) = 3.90, p < .05, and Exercised-hand × Tested-hand, p < .05. Left_Fatigue increased V_UCM for both the exercised and non-exercised hands, but the effect was significant for the non-exercised hand only (p < .01). Right_Fatigue caused a significant increase in V_UCM for the exercised-hand (p < .05). Fatigue increased V_ORT significantly, and the exercised-hand showed significantly higher V_ORT than the non-exercised hand (see panel B of Fig. 8). A three-way RM ANOVA on V_ORT showed main effects of fatigue, F(1,45.11) = 4.12, p < .05), tested-hand, F(1,62.84) = 6.08, p < .05, and Fatigue × Tested-hand, p < .001. In the force-down direction, fatigue had no effect on either V_UCM or V_ORT.

Fig. 8.

V_UCM (panel A) and V_ORT (panel B) for the force-up direction at the lower level of the hierarchy for the bimanual task. (⁥) Represents significant difference from the before-fatigue condition.

4. Discussion

Two of the three specific hypotheses could not be confirmed in the experiments, while the third one received partial support. Our first hypothesis was that the right hand would have higher indices of force stabilizing synergy than the left hand (cf. Zhang, Sainburg, Zatsiorsky, & Latash, 2006). This hypothesis could not be confirmed. Indeed, there was an opposite trend for the synergy indices to be higher in the left hand, although the trend did not reach statistical significance.

The second hypothesis was that in the two-finger (IM) tasks the effects of fatigue on the two variance components (V_UCM and V_ORT) and synergy index (ΔV) in the non-exercised hand would be similar to those in the exercised hand, but possibly of smaller magnitude. We expected the variance components and ΔV to increase for the non-exercised hand during fatigue. This hypothesis received partial support. The results confirmed the hypothesis for the exercised hand only, while no significant changes in the variance indices were seen in the non-exercised hand. So, we failed to demonstrate transfer of the fatigue-induced adaptation of the two-finger synergy (as in Singh et al., 2010a) to the non-exercised hand. This result stands in stark contrast to the significant transfer effects of fatigue observed in the MVC tests.

The third hypothesis addressed fatigue-induced changes in the synergy indices at the two levels of the assumed hierarchy (cf. Gorniak et al., 2007a). We expected adaptive changes to fatigue at both levels. This hypothesis has been falsified: adaptive changes to fatigue were seen at the lower level of the hierarchy but not at the higher level.

In addition to testing the specific hypotheses, we discovered different effects of fatigue on task segments that required force increase (force-up) as compared to those on task segments that required force decrease (force-down). Besides, fatiguing exercise by the left hand showed significantly stronger effects on synergy indices as compared to the exercise by the right hand. Further, we discuss implications of the study for the effects of fatigue on multi-digit coordination and associated neurophysiological mechanisms.

4.1. Transfer effects of fatigue: facts and possible mechanisms

Fatigue leads to changes at virtually all the levels of the neuromotor hierarchy that participates in the production of voluntary actions, from contractile muscle properties to cortical mechanisms (reviewed in Enoka & Duchateau, 2008; Gandevia, 2001; Maluf, Barry, Riley, & Enoka, 2007; Maluf & Enoka, 2005). When a single effector (joint, limb, digit, etc.) performs a fatiguing exercise, effects of fatigue are not limited to performance of that effector. Changes in the MVC force and muscle activation patterns in non-exercised effectors have been attributed to changes in neural factors (Hortobágyi, Taylor, Petersen, Russell, & Gandevia, 2003; Howatson et al., 2011; Post, Bayrak, Kernell, & Zijdewind, 2007; Rattey et al., 2006; Todd et al., 2003).

In our study, the fatiguing exercise was performed by the index finger of one of the hands. The exercise required high levels of activation of the extrinsic hand muscle, flexor digitorum profundus (FDP), which is the focal agonist during fingertip force production, as well as other muscles serving the finger. FDP is a multi-tendon, multi-digit muscle. It was, therefore, natural to expect effects of its activation on force producing capabilities of the other fingers of the hand. In earlier studies, the exercise-induced drop in the I-finger MVC was accompanied by smaller but significant changes in the MVC of non-exercised fingers (Singh et al., 2010a). These effects of fatigue transfer can be naturally attributed to the multi-digit design of the extrinsic hand muscles, although a degree of independence of muscle compartments serving individual digits has been emphasized (Danion, Latash, & Li, 2003a).

The drop in the MVC of the contralateral finger cannot be explained by peripheral effects alone and suggests an important role of mechanisms within the central nervous system. Transcranial magnetic stimulation (TMS) studies have shown that during a fatiguing contraction of the first dorsal interosseous there is a decline in the intracortical facilitation (ICF) of cortical areas serving the homologous contralateral hand muscle (Bäumer, Münchau, Weiller, & Liepert, 2002; Tergau et al., 2000). This decline in ICF has been viewed as reflecting fatigue-induced cortical changes (Brasil-Neto et al., 1993; Tergau et al., 2000). This mechanism could be responsible for the MVC reduction in the non-exercised hand in our study. Additionally, muscle vibration has been shown to cause a decline in the MVC of the ipsilateral as well as contralateral leg (Jackson & Turner, 2003). This could be due to the prolonged effect of vibration on intracortical inhibition or because of increased motoneuron excitability (tested with the H-reflex) in the contralateral limb following prolonged afferent stimulation (Robinson, McIlwain, & Hayes, 1979). Therefore, it is also possible that changes in motoneuron excitability during fatigue may be due to spinal mechanisms (Wolpaw, 1994) leading to a decline in MVC of the contralateral hand.

The drop in MVC was the only significant transfer effect of fatigue, although several outcome variables showed trends in the non-exercised hand that were similar to the changes in the exercised hand. However, all these effects were under the level of statistical significance. We would like to emphasize the change in the index of finger non-independence (Danion et al., 2003b; Zatsiorsky et al., 1998), which showed a significant increase in the exercised hand with a smaller, non-significant, increase in the non-exercised hand. Earlier reports on changes in enslaving with fatigue have been controversial. Danion and colleagues (Danion et al., 2001) reported a drop in enslaving with fatigue. These observations fit the general rule of higher enslaving in persons with higher MVC force confirmed over male–female and young-elderly comparisons (Shinohara, Latash, & Zatsiorsky, 2003a, 2003b). On the other hand, Singh and colleagues (Singh et al., 2010a, 2010b) observed no changes or an increase in the enslaving index, which is similar to our current observations. The differences between the findings of Danion et al. and Singh et al. may be due to the differences in the methods used to quantify enslaving. Danion and colleagues used single-finger MVC production tasks, while our studies used single-finger accurate force production within a much smaller force range. Although enslaving has traditionally been viewed as a linear interdependence among finger forces over the whole force range (Li, Danion, Latash, Li, & Zatsiorsky, 2000; Zatsiorsky et al., 1998), it is possible that the linearity is violated under fatigue leading to indices that are force-range specific.

Fatiguing exercise in our study led to significant changes in accuracy of performance only in tasks performed by the exercised hand (see Fig. 2). The drop in accuracy of force production could get contribution from the fatigue-induced increase in motor unit synchronization (Bigland & Lippold, 1954; Semmler & Nordstrom, 1998). The increase in motor unit synchronization during fatigue has also been linked to an increase in correlated tremor between fingers (Hwang, Yang, Huang, & Guo, 2009), possibly due to enhanced central oscillation at 8–12 Hz during fatigue (Boonstra et al., 2008; Dartnall, Nordstrom, & Semmler, 2008; Kattla & Lowery, 2010). The lack of fatigue effects on accuracy of performance by the non-exercised hand suggests that these factors do not spread to the ipsilateral (to the exercise site) hemisphere. Note, however, that fatigue has been reported to cause an increase in tremor in the exercised as well as the non-exercised limb (Boonstra et al., 2008; Chen, Yang, & Hwang, 2011). The contrast between this report and our results suggests that factors other than tremor may define errors in performance of accurate force production tasks.

4.2. Adaptive change in synergies within a hierarchical system

In this study, we accepted the principle of abundance and the idea of synergies as neural organizations that ensure stability of performance by co-varied adjustments of elemental variables (reviewed in Latash et al., 2007). Earlier studies documented co-varied adjustments of commands to fingers (modes, see Danion et al., 2003b) stabilizing the total force in multi-finger pressing tasks (Kang, Shinohara, Zatsiorsky, & Latash, 2004; Latash et al., 2001). We observed similar results: The amount of “good “variance (V_UCM) was consistently larger than that of the “bad” variance (V_ORT) confirming the hypothesis that across all tasks and conditions commands to individual finger modes co-varied to reduce variance (stabilize) the total force time profile.

Non-trivial relations between synergies at different levels within a hierarchical system have been shown in both pressing (Gorniak et al., 2007a, 2007b) and prehensile tasks (Gorniak et al., 2009). In particular, large synergy indices at the higher level of a hierarchy were typically associated with low (frequently not different from zero) indices at the lower level. In certain situations, however, this trade-off could be overcome. This was seen for some of the variables in prehensile tasks such as the tangential force during holding an object with a prismatic grip (Shim, Latash, & Zatsiorsky, 2003) as well as during manipulation of a fragile object (Gorniak, Zatsiorsky, & Latash, 2010). In this study, we expected fatigue to lead to an increase in the synergy indices at both levels.

Overall, fatigue led to a predictable increase in the force variance indices (Singh et al., 2010a; Singh & Latash, 2011). As in earlier studies (Singh et al., 2010a; Singh & Latash, 2011), we observed disproportionate changes in the two variance components, “good “ (V_UCM) and “bad” (V_ORT) with a larger increase in V_UCM. Hence, the adaptive increase in the synergy index to fatigue has been confirmed. During the two-hand, four-finger tasks, however, these effects were limited to the lower level of the hierarchy, that is, to variance indices computed for the system of two fingers within the exercised hand. There were no comparable effects on the synergy index computed for the two-hand system although accurate performance of the two-hand system was dictated by the task, not accurate performance by individual hands.

This result is unexpected. Indeed, if the increase in the synergy index to fatigue is functionally important, it was expected at the task-specific, higher level of the hierarchy. The current findings suggest that adaptive effects of synergies to fatigue are limited to tasks controlled by one hemisphere. Indeed, earlier studies that reported effects of fatigue of an element on performance of a redundant multi-element system were all limited to actions performed by a single extremity (Singh et al., 2010a, 2010b). It is possible that the effects within-a-hand (at the lower level of the hierarchy) prevented similar results to occur at the higher level because of the mentioned trade-off between the two levels. The current results are highly non-trivial, the offered interpretation is speculative, and both require confirmation in other two-limb tasks.

4.3. Synergic control of force during contraction and relaxation

In natural movements, phases of muscle contraction and relaxation naturally interweave without a clear separation. In laboratory tasks, however, these phases may be separated by asking the subjects to perform accurate alternating phases of force increase and decrease that require agonist muscle contraction and relaxation respectively. A few studies explored the control of accurate muscle relaxation tasks at various rates (Häkkinen & Komi, 1986; Ruiter, Jones, Sargeant, & Haan, 1999; Schieppati & Crenna, 1984; Shim, Olafsdottir, Zatsiorsky, & Latash, 2005b). In the study by Shim and colleagues, accuracy of performance during accurate ramp-like force decrease was worse than during force increase for slow tasks and better than during force increase with very short ramp times. In our study, RMSE was significantly smaller for the force-down segments similar to the mentioned results with shorter times of force change.

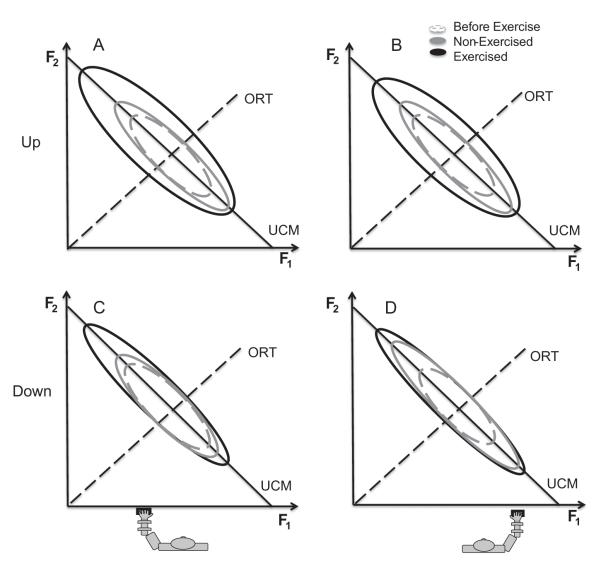
The most striking difference between the force-up and force-down segments was in the effects of fatigue. These results were consistent with our results in an earlier study (Singh et al. 2010b). This difference is illustrated in Fig. 9, which shows hypothetical data distributions for a two-finger task with ellipses. Data before fatigue are shown with dashed ellipses, while data after fatigue are shown with solid ellipses (black for the exercised hand, and grey for the non-exercised hand). Fig. 9 illustrates that fatigue had strong effects on V_UCM for both force-up and force-down segments, whereas only for the force-up segments there was also a significant increase in V_ORT (reflected in higher RMSE).

Fig. 9.

An illustration of hypothetical data point distributions for the task of accurate total force production with 2 fingers. A and B: In the force-up direction, for both the left (panel A) and the right hand (panel B), notice a larger increase in V_UCM than V_ORT during fatigue for the exercised hand. For the non-exercised hand, there is no change in V_ORT but V_UCM increases. The center of the during-fatigue ellipses has been shifted to account for the changes in the force sharing. C and D: In the force-down direction, for both the left (panel C) and the right hand (panel D), notice that there is no change in V_ORT for both the exercised hand as well as the non-exercised hand. V_UCM increases for the exercised as well as the non-exercised hand.

Why are force-down segments immune to effects of fatigue on accuracy of performance? We suggest that this result was a consequence of selecting frequency of force production close to preferred frequency by the subjects. Preferred frequency has been shown to be close to the natural frequency in several studies of movements of body segments (Latash, 1992; Singh & Latash, 2011; Treffner & Turvey, 1993). In isometric force production tasks, the notion of natural frequency is poorly defined. Nevertheless, all subjects prefer to perform accurate finger force production tasks at about the same frequency (similar to the one used in our study). We suggest that comfortable frequency is the one, which requires minimal involvement of the antagonist muscle (and, hence, minimal co-contraction) and which corresponds to the half-period equal to the natural time of relaxation of the prime agonist. Such performance requires control of accurate force time profile only during force increase, while force decrease happens with minimal involvement of the hypothetical controller, as a result of natural relaxation of the FDP muscle. As a result, relaxation phases at such frequencies are highly reproducible and lead to small RMSE indices.

4.4. Implications for the dynamic dominance hypothesis

The dynamic dominance hypothesis (Sainburg, 2005) suggests that the dominant and non–dominant limbs are specialized for different aspects of performance. Namely, it is assumed that the dominant arm is specialized for time-varying features of performance such as endpoint trajectory. In contrast, the non-dominant arm is specialized for steady-state performance. Applied to isometric force production, the hypothesis predicts that the dominant hand will show better performance and possibly stronger synergies during quick force changes, while the non-dominant hand will be more accurate (and show stronger synergies) during steady-state tasks. This prediction has been partly confirmed in an experiment with quick force production from a steady-state (Zhang et al., 2006). Since the current task required quick accurate force changes, we expected the dominant (right) hand to show better performance and stronger synergies.

The results did not confirm this hypothesis. Indeed, the left hand, on average, showed higher indices of force-stabilizing synergy. In addition, performance of both hands was more sensitive to exercise performed by the left hand. In fact, only this exercise led to higher synergy indices in the contralateral hand, while exercise by the right hand failed to show such an effect. To reconcile these observations with the dynamic dominance hypothesis, one has to assume that performance of the accurate force production task in our study qualifies as a steady-state task. This assumption sounds not unreasonable if one considers that we selected the frequency of force production that was close to the self-selected frequency in such tasks. Natural cyclic force production at the self-selected frequency may be viewed as an example of steady-state performance, that is, performance of a system close to its natural frequency (cf. Sternad, Turvey, & Saltzman, 1999; Treffner & Turvey, 1993).

4.5. Concluding comments

Our results confirmed the changes in multi-finger synergies stabilizing total force under fatigue and extended these observations to performance of the non-exercised hand. One of the most unexpected results is the strong change at the one-hand level, which was seen in two-hand tasks. These findings ask for confirmation using a more natural task controlled in a hierarchical manner. We plan to use a static prehensile task (Shim, Latash, & Zatsiorsky, 2005a; Zatsiorsky & Latash, 2004) to confirm or disprove the offered interpretation. We would also like to emphasize the asymmetry of the effects seen in the right and left hands and also of the effects seen during force-up and force-down segments. Although we offered explanations for these effects, we are still far from complete understanding on the effects of fatigue on the different levels of control within redundant neuromotor systems.

The current experimental design can be criticized for using a relatively unnatural pressing task and for not including a number of potentially helpful conditions, such as different frequencies of force production and tasks performed by all four fingers of each hand. The design was a consequence of a compromise as we tried to limit each session to 1.5 h and avoid loss of concentration by the subjects.

Abbreviations

UCM

uncontrolled manifold

MVC

maximal voluntary contraction

CNS

central nervous system

I

index

M

middle