Limited-information Goodness-of-fit Testing of Hierarchical Item Factor Models

Abstract

In applications of item response theory, assessment of model fit is a critical issue. Recently, limited-information goodness-of-fit testing has received increased attention in the psychometrics literature. In contrast to full-information test statistics such as Pearson’s X² or the likelihood ratio G², these limited-information tests utilise lower order marginal tables rather than the full contingency table. A notable example is Maydeu-Olivares and colleagues’ M₂ family of statistics based on univariate and bivariate margins. When the contingency table is sparse, tests based on M₂ retain better Type I error rate control than the full-information tests and can be more powerful. While in principle the M₂ statistic can be extended to test hierarchical multidimensional item factor models (e.g., bifactor and testlet models), the computation is non-trivial. To obtain M₂, a researcher often has to obtain (many thousands of) marginal probabilities, derivatives, and weights. Each of these must be approximated with high-dimensional numerical integration. We propose a dimension reduction method that can take advantage of the hierarchical factor structure so that the integrals can be approximated far more efficiently. We also propose a new test statistic that can be substantially better calibrated and more powerful than the original M₂ statistic when the test is long and the items are polytomous. We use simulations to demonstrate the performance of our new methods and illustrate their effectiveness with applications to real data.

1 Introduction

In this paper we consider the application of limited-information tests (e.g., Bartholomew & Leung, 2002, Cai, Maydeu-Olivares, Coffman, & Thissen, 2006; Maydeu-Olivares & Joe, 2005) to the case of hierarchical multidimensional item response theory (IRT) models (e.g., Cai, 2010b; Cai, Yang, & Hansen, 2011; Gibbons & Hedeker, 1992; Wainer, Bradlow, & Wang, 2007). In the context of IRT, limited-information goodness-of-fit test statistics have been suggested as a potential solution to the problem of extreme sparseness of the underlying multinominal table upon which the IRT model is defined (see, e.g., Bartholomew & Tzamourani, 1999). In contrast to the usual full-information test statistics (e.g., Pearson’s statistic) that depend on probabilities of the full set of cells in the table (hence full-information), the limited-information statistics use only the lower-order marginal probabilities. While the idea of limited-information estimation is not new (e.g., Christoffersson, 1975; Muthén, 1978; Jöreskog & Moustaki, 2001) and the seeds of limited-information testing have been planted earlier in the psychometric literature (e.g., Reiser, 1996), the theory of limited-information goodness-of-fit tests has seen major new development in recent years largely thanks to a theoretical breakthrough made by Maydeu-Olivares and Joe (2005). We now have a comprehensive set of test statistics that have far better calibrated Type I error rates than their full-information counterparts under sparseness. We also understand that limited-information tests can be more powerful than full-information tests. They work for a variety of IRT models, full- and sub-tables alike (Maydeu-Olivares & Joe, 2006), and statistics not restricted to marginal tables have also been developed (Joe & Maydeu-Olivares, 2010).

At the same time, large-scale data collection efforts in both health outcomes research (e.g., PROMIS; Reeve et al., 2007) and educational surveys (e.g., PISA; Adams & Wu, 2002) have resulted in item response data for which hierarchical item factor models prove to be natural. In these contexts, unidimensionality is often violated either because of the complexity of the domain under consideration or because of the assembly of the measurement instruments. A prime example of the former is described in detail by Gibbons et al. (2007), who considered a quality-of-life scale for mental health patients that is made up of questions from a multitude of subdomains, such as family, health, finance, social, leisure, etc. These subdomains contribute to the measurement of quality-of-life, but they also introduce additional nuisance dimensions above and beyond the general quality-of-life dimension. Gibbons et al. (2007) fitted a bifactor model to the data to not only account for the local dependence due to the subdomains but also to reflect the essential goal of the measurement endeavour, which is to derive an estimate of the patient’s quality-of-life. In educational testing, it is routine to organise several test items around a common stimulus, such as the questions following a passage in a reading comprehension test. The existence of these so-called “testlets” significantly alters the latent dimensionality of the tests. To obtain correct estimates of ability as well as standard errors of measurement, testlet response theory models have been proposed (Wainer et al., 2007). As an alternative, Cai, Yang, and Hansen (2011) also considered bifactor models for large-scale educational survey data.

In both bifactor and testlet response theory models, there is a general dimension on which all items load. In addition, there may be S group-specific dimensions that are mutually orthogonal, and orthogonal to the general dimension. As a critical feature, an item is allowed to load on at most one group-specific dimension. This is in contrast to standard item factor models (e.g., Reckase, 2009) wherein the factors may be correlated and items may load on more than two factors. Historically, Holzinger and Swineford’s (1937) bifactor analysis and Thurstone’s (1947) multiple factor analysis reflect two somewhat different intellectual leanings in factor analysis, with the former being a derivative of Spearman’s (1904) one-factor model. In an attempt to merge the two types of multidimensional IRT models, Cai (2010b) proposed a two-tier model in which an item can load on P potentially correlated primary dimensions, as in Reckase’s (2009) models, and at the same time, is only permitted to load on a single group-specific dimension, as in the bifactor model.

From a computational perspective, these hierarchical item factor models are highly attractive because maximum marginal likelihood estimation for these models requires at most P + 1 dimensional numerical integration as opposed to the full P + S dimensional integration (Cai, 2010b; Gibbons & Hedeker, 1992; Rijmen, 2009). When P is (most often) equal to 1, the computational burden of obtaining the maximum likelihood solution does not increase exponentially as the number of group-specific dimensions increases. The standard (correlated factors) multidimensional models do not enjoy such freedom from the “curse of dimensionality.” In some applications, the number of group-specific dimensions in the model may be quite large (Cai, 2010b, for example, presented an analysis of educational test data in which the fitted model included 12 group-specific factors), but dimension reduction guarantees that the item parameters can still be estimated efficiently using maximum likelihood.

It would seem from the growing awareness and importance of limited-information goodness-of-fit testing and hierarchical item factor models that it is only natural to assess the fit of bifactor or testlet or two-tier models using limited-information test statistics – the best of both worlds. Yet to our knowledge, no researcher has attempted the limited-information testing of hierarchical item factor models.

Theoretically, existing results on limited-information goodness-of-fit testing can be straightforwardly extended to the case of multidimensional IRT. However, a major computational stumbling block remains. The limited-information statistics for a realistic psychological or educational test depend on the calculation of hundreds or sometimes thousands of model-implied probabilities and derivatives, all of which must be approximated by numerical integration. If P + S dimensional integration is required, when S is 10 or more, the computation burden may render limited-information goodness-of-fit testing practically useless for hierarchical item factor models. This dilemma is similar to the state of affairs in IRT parameter estimation prior to Gibbons and Hedeker’s (1992) discovery of the bifactor dimension reduction method.

Our main purpose in this paper is to extend the dimension reduction technique, already used in parameter estimation, to limited-information goodness-of-fit testing. We show that the dimensionality of integration problem can be directly tackled in the same manner as in item parameter estimation. For example, for a bifactor model, where P is equal to 1, the probabilities and derivatives involved in limited-information goodness-of-fit test statistics require at most 2 dimensional numerical integration, regardless of the number of factors in the model. As such, we are now able to test much larger models with much larger latent dimensionality than what was practically available previously.

As a secondary goal, we consider a new quadratic form test statistic, which we call $M_2^{\ast }$, that is based on the general limited-information testing principles proposed by Joe and Maydeu-Olivares (2010). The statistic is best understood as a further reduction (or concentration) of the univariate and bivariate marginal tables. The residuals used in the quadratic form are linear functions of the multinomial cell residuals, but they are are not marginal moments. Maydeu-Olivares, Cai, and Hernandez (2011) proposed a similar (but not identical) statistic in the context of unidimensional graded IRT models.

We propose this new test statistic in response to a phenomenon well-known in limited-information estimation, but relatively obscure in limited-information goodness-of-fit testing. That is, when the items are polytomous, even the bivariate marginal tables can become too sparse. Consider the following example. For the quality-of-life of life scale analysed by Gibbons et al. (2007) and described above, respondents rate their satisfaction with respect to various aspects of their lives using a seven-point scale. Accordingly, each bivariate marginal table has 49 cells. Because all the items are intended to measure the same primary construct, we expect that the responses for any two items would generally have a positive relationship. Moreover, some response combinations (e.g., a high rating for one item, low for the other) would be rather uncommon or unexpected, especially for items belonging to the same subdomain.

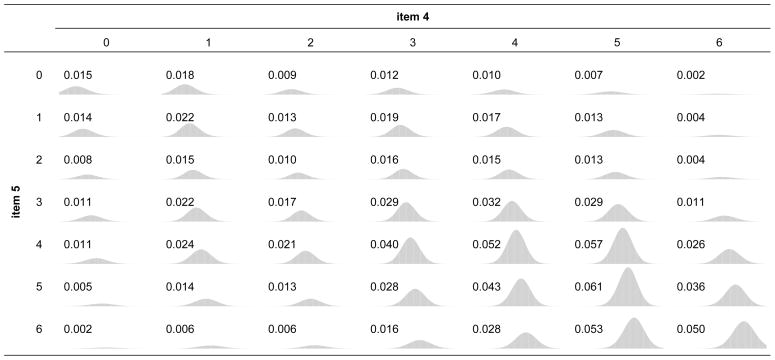
To illustrate the situation, we fit a unidimensional logistic graded IRT model to data from 586 respondents to the quality-of-life scale and obtained marginal maximum likelihood item parameter estimates. We focus our attention on items 4 and 5, which belong to the “family” subdomain and are fairly strongly related to the underlying dimension (with standardised factor loadings of .65 and .68, respectively). The parameter estimates for each item were used to generate univariate category response curves. For each of the 49 possible rating combinations, we took the product of the category response curve for item 4, the response curve for item 5, and the assumed (standard normal, in this example) population distribution. These distributions were then appropriately normalised to obtain the posterior of the particular rating combination. The posteriors of all combinations (i.e., all cells in the bivariate marginal table for this item pair) and the corresponding model-implied cell probabilities are shown in Figure 1. Not surprisingly, the cells with the highest model-implied probabilities and greatest posterior densities are along the main diagonal, where ratings for the two items are the same or within one or two points of each other. Cells in the bottom-left and upper-right corners, where the differences between the two ratings are most different, have rather low expected probabilities. In other words, we observe sparseness even in the second order marginal table.

Figure 1.

Bivariate posterior distributions and expected cell probabilities for items 4 and 5 of a quality-of-life scale.

Recall that the primary reason why limited-information test statistics have better chi-square approximations than the full-information test statistics is that the lower-order marginal tables are better filled. However, as we have seen, this central tenet in support of limited-information goodness-of-fit testing can be invalid when models for polytomous items are used. Again, as in full-information testing, the sparseness in the marginal tables leads to inadequate chi-square approximations. We will subsequently show that the distribution of limited-information test statistics as originally described by Maydeu-Olivares and Joe (2006) are often stochastically smaller than their theoretical limiting chi-square distributions for tests made up of polytomous items. This leads to severely mis-calibrated Type I error rates and significant loss of power to detect misspecification. On the other hand, by further condensing the marginal tables, the new test statistic has a much improved chi-square approximation and higher power than the original M₂. The new test statistic reduces to the original M₂ when all items are dichotomous.

The remainder of this paper will be organised in the following manner. In Section 2, we present some technical details related to the computation of the original M₂ statistic and the proposed alternative. We describe in detail the dimension reduction strategy that may be utilised in the case of hierarchical item factor models to improve the efficiency of computing M₂. In Section 3, we apply the limited-information test statistics to simulated data. First, we illustrate the improvement in computational efficiency achieved through dimension reduction. Then, we examine the distribution of the two M₂ statistics across a wide range of conditions, with and without model misspecification. Section 4 presents an analysis of an empirical dataset. We conclude in Section 5 with a brief discussion of this work, summarising our findings and highlighting directions for further research.

2 Technical Details

2.1 An Item Bifactor Analysis Model

Let there be n polytomously scored items so that the dichotomous responses become a special case. Let the ith response pattern be y_i = (y_i1, …, y_in), where y_ij = 0, …, K_j − 1, where the number of categories K_j for item j can vary. The total number of possible response patterns is $C={\mathrm{\Pi }}_{j=1}^n{K}_j$. Let there be a simple random (calibration) sample of size N. Without loss of generality, let us consider the logistic version of the graded item bifactor model (Cai, Yang, & Hansen, 2011) as a representative hierarchical item factor analysis model. Other models such as the two-tier model (Cai, 2010b) follow the derivations naturally, but we do not address them here due to space constraints. In the graded bifactor model, the cumulative response probabilities (i.e., the probability of a response in category k and above) are expressed as

$$\begin{array}{lll}\hfill \underset{j}{\overset{+}{Pr}}(0\mid {\eta }_0,\dots ,{\eta }_s,\mathit{\theta })& =\hfill & 1,\hfill \\ \hfill \underset{j}{\overset{+}{Pr}}(1\mid {\eta }_0,\dots ,{\eta }_s,\mathit{\theta })& =\hfill & \frac{1}{1+exp(-{\alpha }_{j,1}-{\beta }_{j0}{\eta }_0-{\beta }_{js}{\eta }_s)},\hfill \\ \hfill & \hfill ⋮\hfill & \hfill \\ \hfill \underset{j}{\overset{+}{Pr}}(k\mid {\eta }_0,\dots ,{\eta }_s,\mathit{\theta })& =\hfill & \frac{1}{1+exp(-{\alpha }_{j,k}-{\beta }_{j0}{\eta }_0-{\beta }_{js}{\eta }_s)},\hfill \\ \hfill & \hfill ⋮\hfill & \hfill \\ \hfill \underset{j}{\overset{+}{Pr}}(K_j-1\mid {\eta }_0,\dots ,{\eta }_s,\mathit{\theta })& =\hfill & \frac{1}{1+exp(-{\alpha }_{j,K_j-1}-{\beta }_{j0}{\eta }_0-{\beta }_{js}{\eta }_s)},\hfill \end{array}$$

where the latent variable η₀ is the general dimension with slope β_j0, and η_s is the sth group-specific dimension with slope β_js. Note that item j is permitted to load on at most one group-specific dimension s. For an item with K_j categories, there are also K_j − 1 intercepts (the α’s). The item parameters are components of the parameter vector θ ∈ Θ, where Θ is the parameter space. Denote the dimensionality of Θ as ν. This is equal to the number of unconstrained parameters in the model.

Taken together, the category response probability can be written as the difference:

$$\underset{j}{Pr}(k\mid \mathit{\eta },\mathit{\theta })=\underset{j}{\overset{+}{Pr}}(k\mid {\eta }_0,\dots ,{\eta }_s,\mathit{\theta })-\underset{j}{\overset{+}{Pr}}(k+1\mid {\eta }_0,\dots ,{\eta }_s,\mathit{\theta }),$$ (1)

where η = (η₀, η₁, …, η_s, …, η_S)′. For any generic item j, we may use

$$\pi (y_{ij}\mid \mathit{\eta },\mathit{\theta })=\prod _{k=0}^{K_j-1}{[\underset{j}{Pr}(k\mid \mathit{\eta },\mathit{\theta })]}^{{\chi }_k(y_{ij})}$$ (2)

to denote the conditional density of the observed item response y_ij on the latent variables η, where χ_k(y_ij) is an indicator function that takes on a value of 1 if and only if y_ij = k, and 0 otherwise. The formulation in Equation (2) is especially flexible because if y_ij is not among the legitimate response categories (e.g., missing data), it does not affect the estimation of θ.

The item bifactor model has S + 1 latent variables. As with any IRT model, the response pattern probability π_i(θ) = π(θ|y_i) is obtained by integrating over the latent variables,

$${\pi }_i(\mathit{\theta })=\int \prod _{j=1}^n\pi (y_{ij}\mid \mathit{\eta },\mathit{\theta })h(\mathit{\eta })d\mathit{\eta },$$ (3)

where h(η) is the assumed (prior) distribution of the latent variables, typically taken as standard multivariate normal (see Cai, Yang, & Hansen, 2011).

2.2 Some Asymptotic Distribution Theory

As with any other IRT model, the item bifactor model is defined on an underlying n-way contingency table made up of the full list of C cross-classifications of the response patterns. Let the C (unstructured) multinomial cell probabilities be π = (π₁, …, π_i, …, π_C)′. The corresponding observed cell proportions based on a sample of size N are p = (p₁, …, p_i, …, p_C)′. The restrictions ${\mathrm{\sum }}_{i=1}^C{\pi }_i=1$ and ${\mathrm{\sum }}_{i=1}^C{p}_i=1$ are implicit. Following standard results in Bishop, Fienberg, and Holland (1975), the asymptotic distribution of p − π is C-variate normal with zero means and limiting covariance matrix Ξ = diag(π) − ππ′, i.e.,

$$\sqrt{N}(\mathbf{p}-\mathit{\pi })\stackrel{D}{\to }{\mathcal{N}}_C(\mathbf{0},\mathbf{\Xi }).$$ (4)

The bifactor model imposes the following structure on the multinomial cell probabilities: π(θ) = [π₁(θ), …, π_i(θ), …, π_C(θ)]′. The log-likelihood is

$$logL(\mathit{\theta })\propto \sum _{i=1}^C{p}_{i}log{\pi }_i(\mathit{\theta }).$$ (5)

Fitting this model to the observed proportions by maximum likelihood yields the solution θ̂. Standard estimation algorithms such as the Bock-Aitkin EM algorithm (Bock & Aitkin, 1981) can be used to optimise the log-likelihood.

It is once again a standard discrete multivariate analysis result (see, e.g., Maydeu-Olivares & Joe, 2005 for a derivation) that the cell residual vector e = p − π(θ̂) is also asymptotically normally distributed with zero means and limiting covariance matrix Ω(θ) = Ξ(θ) − Δ(θ)[ (θ)]⁻¹Δ(θ)′, i.e.,

$$\sqrt{N}[\mathbf{p}-\mathit{\pi }(\widehat{\mathit{\theta }})]\stackrel{D}{\to }{\mathcal{N}}_C[\mathbf{0},\mathbf{\Omega }(\mathit{\theta })],$$ (6)

where Δ(θ) = ∂π(θ)/∂θ is the C × ν Jacobian matrix containing all first order partial derivatives of the model-implied probabilities with respect to the parameters, and (θ) is the Fisher information matrix (θ) = Δ(θ)′diag[π(θ)]⁻¹Δ(θ).

Testing the goodness-of-fit of the model under maximum likelihood estimation involves the following composite hypothesis H₀ : there exists some θ ∈ Θ such that π = π(θ). The null is tested against the alternative H_A : π ≠ π(θ) for any θ ∈ Θ. While algorithms developed by Gibbons and Hedeker (1992) and extended by Cai, Yang, and Hansen (2011) have made parameter estimation for item bifactor analysis practical in routine applications, testing the goodness-of-fit of the models is not straightforward when n is relatively large. This issue is well-known in categorical data analysis. The number of cells increases exponentially as the number of items increases, which will quickly exceed any conceivable sample size in psychological and educational measurement. For more than a dozen or so items, the underlying contingency table is extremely sparse, with many cells having near zero expected probabilities. Under sparseness, the Pearson test statistic $X^2=N{\mathrm{\sum }}_{i=1}^C{[p_i-{\pi }_i(\widehat{\mathit{\theta }})]}^2/{\pi }_i(\widehat{\mathit{\theta }})$, or its large-sample equivalent, the likelihood ratio test statistic $G^2=2N{\mathrm{\sum }}_i^C{p}_{i}log[p_i/{\pi }_i(\widehat{\mathit{\theta }})]$, can no long achieve the limiting central chi-square distribution with C − ν − 1 degrees-of-freedom under the null hypothesis. As documented extensively in the literature, both Type I error rates and power are adversely affected when the contingency table is sparse (see, e.g., Bartholomew & Leung, 2002).

2.3 Limited-information Goodness-of-fit Testing

To resolve the sparseness issue, limited-information tests have been suggested, most notably by Maydeu-Olivares and Joe (2005). In limited-information goodness-of-fit tests, marginal sub-tables are used. A number of authors, including Maydeu-Olivares and Joe (2005) and Cai et al. (2006), consider marginal residuals up to order 2, i.e., first and second order margins. The marginal residuals are obtained via operator matrices, e.g.,

$${\mathbf{e}}_2={\mathbf{L}}_2\mathbf{e}={\mathbf{L}}_2\mathbf{p}-{\mathbf{L}}_2\mathit{\pi }(\widehat{\mathit{\theta }})={\mathbf{p}}_2-{\mathit{\pi }}_2(\widehat{\mathit{\theta }}),$$ (7)

where L₂ is a particular d × C fixed matrix of 0s and 1s that can collapse the cell residuals into first and second order marginal residuals (see, e.g., Maydeu-Olivares & Joe, 2006). Let us elaborate a little more on the dimensionality of the various matrices.

As Maydeu-Olivares and Joe (2006) explained, the number of linearly independent first order marginal residuals is equal to $d_1={\mathrm{\sum }}_{j=}^n(K_j-1)$. The number of linearly independent second order marginal residuals is equal to $d_2={\mathrm{\sum }}_{l=2}^n{\mathrm{\sum }}_{m=1}^{l-1}(K_l-1)(K_m-1)$. Thus, taken together, d = d₁ + d₂. In partitioned form, we may also write

$${\mathbf{e}}_2=\left(\begin{array}{c}{\stackrel{.}{\mathbf{e}}}_1\\ {\stackrel{.}{\mathbf{e}}}_2\end{array}\right)=\left(\begin{array}{c}{\stackrel{.}{\mathbf{L}}}_1\\ {\stackrel{.}{\mathbf{L}}}_2\end{array}\right)\mathbf{e}=\left(\begin{array}{c}{\stackrel{.}{\mathbf{L}}}_1\\ {\stackrel{.}{\mathbf{L}}}_2\end{array}\right)\mathbf{p}-\left(\begin{array}{c}{\stackrel{.}{\mathbf{L}}}_1\\ {\stackrel{.}{\mathbf{L}}}_2\end{array}\right)\mathit{\pi }(\widehat{\mathit{\theta }})=\left(\begin{array}{c}{\stackrel{.}{\mathbf{p}}}_1-{\stackrel{.}{\mathit{\pi }}}_1(\widehat{\mathit{\theta }})\\ {\stackrel{.}{\mathbf{p}}}_2-{\stackrel{.}{\mathit{\pi }}}_2(\widehat{\mathit{\theta }})\end{array}\right),$$ (8)

where L̇₁ is a d₁ × C operator matrix that collapses the cell proportions and model-implied cell probabilities into d₁ first order marginal proportions ṗ₁ = L̇₁p and marginal probabilities π̇₁(θ̂) = L̇₁π(θ̂), and L̇₂ is a d₂ × C operator matrix that collapses the cell proportions and probabilities into d₂ second order marginal proportions ṗ₂ = L̇₂p and marginal probabilities π̇₂(θ̂) = L̇₂π(θ̂). It is also clear that e₂ is made up of the first and second order marginal residuals ė₁ and ė₂.

For convenience, let us order the first order marginal probabilities by item number, i.e., j = 1, …, n. Similarly, let us order the second order marginal probabilities by unique item pairs, i.e., (l, m) = (2, 1), (3, 1), (3, 2), …, (n, n − 1). There are n(n − 1)/2 such unique pairs. As mentioned above, for any item j, there are K_j cells in the first order marginal table, but there are only K_j − 1 linearly independent marginal probabilities because the K_j cells must sum to 1. These can be conveniently obtained by removing cells that correspond to the first category, the 0 category. By similar reasoning, while there are K_lK_m cells in each bivariate table, there are only (K_l − 1)(K_m − 1) linearly independent marginal probabilities. Removing the cells that correspond to the 0 category for both item l and item m would leave the linearly independent probabilities. Let us denote a generic first order marginal probability as π̇_1,j,k(θ̂). It can be interpreted as the model-implied probability of responses in category k for item j. Let a generic second order marginal probability be π̇_2,l,m,klkm (θ̂). It is interpreted as the model-implied joint probability of responses in category k_l for item l, and in category k_m for item m.

The following is an example of obtaining first order marginal probabilities for a test with 3 items. The first two items have 3 categories, and the 3rd one has 2 categories:

$$\begin{array}{l}{\stackrel{.}{\mathit{\pi }}}_1(\widehat{\mathit{\theta }})=\left(\begin{array}{c}{\stackrel{.}{\pi }}_{1,1,1}(\widehat{\mathit{\theta }})\\ {\stackrel{.}{\pi }}_{1,1,2}(\widehat{\mathit{\theta }})\\ {\stackrel{.}{\pi }}_{1,2,1}(\widehat{\mathit{\theta }})\\ {\stackrel{.}{\pi }}_{1,2,2}(\widehat{\mathit{\theta }})\\ {\stackrel{.}{\pi }}_{1,3,1}(\widehat{\mathit{\theta }})\end{array}\right)={\stackrel{.}{\mathbf{L}}}_1\mathit{\pi }(\widehat{\mathit{\theta }})\\ =\left(\begin{array}{cccccccccccccccccc}0& 0& 0& 0& 0& 0& 1& 1& 1& 1& 1& 1& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 1& 1& 1& 1& 1& 1\\ 0& 0& 1& 1& 0& 0& 0& 0& 1& 1& 0& 0& 0& 0& 1& 1& 0& 0\\ 0& 0& 0& 0& 1& 1& 0& 0& 0& 0& 1& 1& 0& 0& 0& 0& 1& 1\\ 0& 1& 0& 1& 0& 1& 0& 1& 0& 1& 0& 1& 0& 1& 0& 1& 0& 1\end{array}\right)\left(\begin{array}{c}{\pi }_{(000)}(\widehat{\mathit{\theta }})\\ {\pi }_{(001)}(\widehat{\mathit{\theta }})\\ {\pi }_{(010)}(\widehat{\mathit{\theta }})\\ {\pi }_{(011)}(\widehat{\mathit{\theta }})\\ {\pi }_{(020)}(\widehat{\mathit{\theta }})\\ {\pi }_{(021)}(\widehat{\mathit{\theta }})\\ {\pi }_{(100)}(\widehat{\mathit{\theta }})\\ {\pi }_{(101)}(\widehat{\mathit{\theta }})\\ {\pi }_{(110)}(\widehat{\mathit{\theta }})\\ {\pi }_{(111)}(\widehat{\mathit{\theta }})\\ {\pi }_{(120)}(\widehat{\mathit{\theta }})\\ {\pi }_{(121)}(\widehat{\mathit{\theta }})\\ {\pi }_{(200)}(\widehat{\mathit{\theta }})\\ {\pi }_{(201)}(\widehat{\mathit{\theta }})\\ {\pi }_{(210)}(\widehat{\mathit{\theta }})\\ {\pi }_{(211)}(\widehat{\mathit{\theta }})\\ {\pi }_{(220)}(\widehat{\mathit{\theta }})\\ {\pi }_{(221)}(\widehat{\mathit{\theta }})\end{array}\right),\end{array}$$ (9)

where the subscripts in parentheses for the 18 × 1 vector above indicate a particular (reverse lexicographical) ordering of the C = 18 response patterns created by the 3 items. There are 2 + 2 + 1 = 5 linearly independent first order marginal probabilities. In particular, this may be verified from the fact that L̇₁ has full row rank. To obtain the (3 − 1)(3 − 1) + (3 − 1)(2 − 1) + (3 − 1)(2 − 1) = 8 second order marginal probabilities, consider the following:

$$\begin{array}{l}{\stackrel{.}{\mathit{\pi }}}_2(\widehat{\mathit{\theta }})=\left(\begin{array}{c}{\stackrel{.}{\pi }}_{2,2,1,1,1}(\widehat{\mathit{\theta }})\\ {\stackrel{.}{\pi }}_{2,2,1,1,2}(\widehat{\mathit{\theta }})\\ {\stackrel{.}{\pi }}_{2,2,1,2,1}(\widehat{\mathit{\theta }})\\ {\stackrel{.}{\pi }}_{2,2,1,2,2}(\widehat{\mathit{\theta }})\\ {\stackrel{.}{\pi }}_{2,3,1,1,1}(\widehat{\mathit{\theta }})\\ {\stackrel{.}{\pi }}_{2,3,1,1,2}(\widehat{\mathit{\theta }})\\ {\stackrel{.}{\pi }}_{2,3,2,1,1}(\widehat{\mathit{\theta }})\\ {\stackrel{.}{\pi }}_{2,3,2,1,2}(\widehat{\mathit{\theta }})\end{array}\right)={\stackrel{.}{\mathbf{L}}}_2\mathit{\pi }(\widehat{\mathit{\theta }})\\ =\left(\begin{array}{cccccccccccccccccc}0& 0& 0& 0& 0& 0& 0& 0& 1& 1& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 1& 1& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 1& 1& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 1& 1\\ 0& 0& 0& 0& 0& 0& 0& 1& 0& 1& 0& 1& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 1& 0& 1& 0& 1\\ 0& 0& 0& 1& 0& 0& 0& 0& 0& 1& 0& 0& 0& 0& 0& 1& 0& 0\\ 0& 0& 0& 0& 0& 1& 0& 0& 0& 0& 0& 1& 0& 0& 0& 0& 0& 1\end{array}\right)=\left(\begin{array}{c}{\pi }_{(000)}(\widehat{\mathit{\theta }})\\ {\pi }_{(001)}(\widehat{\mathit{\theta }})\\ {\pi }_{(010)}(\widehat{\mathit{\theta }})\\ {\pi }_{(011)}(\widehat{\mathit{\theta }})\\ {\pi }_{(020)}(\widehat{\mathit{\theta }})\\ {\pi }_{(021)}(\widehat{\mathit{\theta }})\\ {\pi }_{(100)}(\widehat{\mathit{\theta }})\\ {\pi }_{(101)}(\widehat{\mathit{\theta }})\\ {\pi }_{(110)}(\widehat{\mathit{\theta }})\\ {\pi }_{(111)}(\widehat{\mathit{\theta }})\\ {\pi }_{(120)}(\widehat{\mathit{\theta }})\\ {\pi }_{(121)}(\widehat{\mathit{\theta }})\\ {\pi }_{(200)}(\widehat{\mathit{\theta }})\\ {\pi }_{(201)}(\widehat{\mathit{\theta }})\\ {\pi }_{(210)}(\widehat{\mathit{\theta }})\\ {\pi }_{(211)}(\widehat{\mathit{\theta }})\\ {\pi }_{(220)}(\widehat{\mathit{\theta }})\\ {\pi }_{(221)}(\widehat{\mathit{\theta }})\end{array}\right).\end{array}$$ (10)

The observed marginal proportions can be obtained similarly. We shall denote ṗ_1,j,k as the observed first order marginal proportion for item j in category k. The observed second order marginal proportion for item l in category k_l and item m in category k_m is ṗ_2,l,m,klkm.

From the above derivations, it is clear that e₂ = p₂ − π₂(θ̂) is a linear combination of e. The rank of L₂ is equal to d. As such, the marginal residual moments are asymptotically d-variate normally distributed with zero means and limiting covariance matrix Ω₂(θ) = Ξ₂(θ) − Δ₂(θ)[ (θ)]⁻¹Δ₂(θ)′,

$$\sqrt{N}[{\mathbf{p}}_2-{\mathit{\pi }}_2(\widehat{\mathit{\theta }})]\stackrel{D}{\to }{\mathcal{N}}_d[\mathbf{0},{\mathbf{\Omega }}_2(\mathit{\theta })],$$ (11)

where ${\mathbf{\Xi }}_2(\mathit{\theta })={\mathbf{L}}_2\mathbf{\Xi }(\mathit{\theta }){\mathbf{L}}_2^{\prime }$ is d × d, and the Jacobian Δ₂(θ) = L₂Δ(θ) = ∂π₂(θ)/∂θ is d × ν containing all first order partial derivatives of the marginal probabilities with respect to the parameters of the model.

Maydeu-Olivares and Joe (2005) noted that if the model is locally identified from the marginal moments, i.e., when Δ₂(θ) has full column rank, then there exists a d × (d − ν) orthogonal complement Δ̄₂(θ) such that Δ̄₂(θ)′Δ₂(θ) is zero. By implication, Δ̄₂(θ̂)′e₂ is (d − ν)-variate normal with zero means and limiting covariance matrix Δ̄₂(θ)′Ξ₂(θ)Δ̄₂(θ), i.e.,

$$\sqrt{N}{\overline{\mathbf{\Delta }}}_2{(\widehat{\mathit{\theta }})}^{\prime }{\mathbf{e}}_2={\overline{\mathbf{\Delta }}}_2{(\widehat{\mathit{\theta }})}^{\prime }\sqrt{N}[{\mathbf{p}}_2-{\mathit{\pi }}_2(\widehat{\mathit{\theta }})]\stackrel{D}{\to }{\mathcal{N}}_{d-\nu }(\mathbf{0},{\overline{\mathbf{\Delta }}}_2{(\mathit{\theta })}^{\prime }{\mathbf{\Xi }}_2(\mathit{\theta }){\overline{\mathbf{\Delta }}}_2(\mathit{\theta })).$$ (12)

Consequently, by arguments in Maydeu-Olivares and Joe (2005), the statistic

$$M_2=N{\mathbf{e}}_2^{\prime }{\overline{\mathbf{\Delta }}}_2(\widehat{\mathit{\theta }}){[{\overline{\mathbf{\Delta }}}_2{(\widehat{\mathit{\theta }})}^{\prime }{\mathbf{\Xi }}_2(\widehat{\mathit{\theta }}){\overline{\mathbf{\Delta }}}_2(\widehat{\mathit{\theta }})]}^{-1}{\overline{\mathbf{\Delta }}}_2{(\widehat{\mathit{\theta }})}^{\prime }{\mathbf{e}}_2$$ (13)

is asymptotically chi-square distributed with d − ν degrees-of-freedom under the null hypothesis that the model fits exactly.

2.4 A New Test Statistic

As discussed in Section 1, a potential problem with the original M₂ statistic as given in Equation (13) when the test items are polytomous is the sparseness of the bivariate marginal tables. We adopt the strategies endorsed by Joe and Maydeu-Olivares (2010) and Maydeu-Olivares et al. (2011) in a new test statistic that is based on a further reduction or concentration of the cells in the marginal tables. Specifically, let ė_1,j,k = ṗ_1,j,k − π̇_1,j,k(θ̂) denote a first order marginal residual for item j in category k. We sum across the categories such that

$${\stackrel{.}{\epsilon }}_{1,j}=\sum _{k=1}^{K_j=1}k{\stackrel{.}{e}}_{1,j,k}=\sum _{k=1}^{K_j-1}k[{\stackrel{.}{p}}_{1,j,k}-{\stackrel{.}{\pi }}_{1,j,k}(\widehat{\mathit{\theta }})]=\left(\begin{array}{ccc}1& \cdots & K_j-1\end{array}\right)\left(\begin{array}{c}{\stackrel{.}{e}}_{1,j,1}\\ ⋮\\ {\stackrel{.}{e}}_{1,j,K_j-1}\end{array}\right)={\stackrel{.}{\mathbf{T}}}_{1,j}{\stackrel{.}{\mathbf{e}}}_{1,j}$$ (14)

is the reduced first order marginal residual for item j, where Ṫ_1,j is a 1 × (K_j − 1) vector and ė_1,j = (e_1,j,1, …, e_1,j,Kj−1)′ is the vector of all linearly independent first order marginal residuals for item j. Let ε̇₁ = (ε̇_1,1, …, ε̇_1,n)′ be the n × 1 vector of reduced first order marginal residuals for all n items. We may represent ε̇₁ using matrices

$${\stackrel{.}{\mathit{\epsilon }}}_1=\left(\begin{array}{c}{\stackrel{.}{\epsilon }}_{1,1}\\ ⋮\\ {\stackrel{.}{\epsilon }}_{1,j}\\ ⋮\\ {\stackrel{.}{\epsilon }}_{1,n}\end{array}\right)=\left(\begin{array}{ccccc}{\stackrel{.}{\mathbf{T}}}_{1,1}& \mathbf{0}& \cdots & \cdots & \mathbf{0}\\ \mathbf{0}& \ddots & & & ⋮\\ ⋮& & {\stackrel{.}{\mathbf{T}}}_{1,j}& & ⋮\\ ⋮& & & \ddots & \mathbf{0}\\ \mathbf{0}& \cdots & \cdots & \mathbf{0}& {\stackrel{.}{\mathbf{T}}}_{1,n}\end{array}\right)\left(\begin{array}{c}{\stackrel{.}{\mathbf{e}}}_{1,1}\\ ⋮\\ {\stackrel{.}{\mathbf{e}}}_{1,j}\\ ⋮\\ {\stackrel{.}{\mathbf{e}}}_{1,n}\end{array}\right)={\stackrel{.}{\mathbf{T}}}_1{\stackrel{.}{\mathbf{e}}}_1.$$ (15)

From Equation (15) and Equation (8), it is clear that ε̇₁ = Ṫ₁ė₁ = Ṫ₁L̇₁e, which shows that the reduced first order marginal residual vector ε ₁ is a linear function of the multinomial cell residuals. Furthermore, it is clear that Ṫ₁ is an n × d₁ matrix that has full row rank. Therefore, the product Ṫ₁L̇₁ has full row rank.

Moving on to the second order residuals. Let ė_2,l,m,klkm = ṗ_2,l,m,klkm − π_2,l,m,kl,km (θ̂) be a second order marginal residual for item pair l and m in categories k_l and k_m, respectively. We define the reduced marginal residual for item pair l and m as a product moment:

$$\begin{array}{l}{\stackrel{.}{\epsilon }}_{2,l,m}=\sum _{k_l=1}^{K_l-1}\sum _{k_m=1}^{K_m=1}{k}_l{k}_m{\stackrel{.}{e}}_{2,l,m,k_l,k_m}=\sum _{k_l=1}^{K_l=1}\sum _{k_m=1}^{K_m=1}{k}_l{k}_m[{\stackrel{.}{p}}_{2,l,m,k_l,k_m}-{\stackrel{.}{\pi }}_{2,l,m,k_l,k_m}(\widehat{\mathit{\theta }})]\\ =({\stackrel{.}{\mathbf{T}}}_{1,l}\otimes {\stackrel{.}{\mathbf{T}}}_{1,m})\left(\begin{array}{c}{\stackrel{.}{e}}_{2,l,m,1,1}\\ ⋮\\ {\stackrel{.}{e}}_{2,l,m,1,K_m-1}\\ {\stackrel{.}{e}}_{2,l,m,2,1}\\ ⋮\\ {\stackrel{.}{e}}_{2,l,m,2,K_m-1}\\ ⋮\\ {\stackrel{.}{e}}_{2,l,m,K_l-1,1}\\ ⋮\\ {\stackrel{.}{e}}_{2,l,m,K_l-1,K_m-1}\end{array}\right)={\stackrel{.}{\mathbf{T}}}_{2,l,m}{\stackrel{.}{\mathbf{e}}}_{2,l,m},\end{array}$$ (16)

where Ṫ_2,l,m is 1 × (K_l − 1)(K_m − 1), formed by a direct product of Ṫ_1,l with Ṫ_1,m, and ė_2,l,m is the vector of all linearly independent second order marginal residuals for item pair (l, m). Let ε̇₂ = (ε̇_2,2,1, …, ε̇_2,n,n−1)′ be the n(n − 1)/2 × 1 vector of reduced second order marginal residuals for all n(n − 1)/2 unique item pairs. We may represent ε̇₂ using matrices

$${\stackrel{.}{\mathit{\epsilon }}}_2=\left(\begin{array}{c}{\stackrel{.}{\epsilon }}_{2,2,1}\\ ⋮\\ {\stackrel{.}{\epsilon }}_{2,i,m}\\ ⋮\\ {\stackrel{.}{\epsilon }}_{2,n,n-1}\end{array}\right)=\left(\begin{array}{ccccc}{\stackrel{.}{\mathbf{T}}}_{2,2,1}& \mathbf{0}& \cdots & \cdots & \mathbf{0}\\ \mathbf{0}& \ddots & & & ⋮\\ ⋮& & {\stackrel{.}{\mathbf{T}}}_{2,i,m}& & ⋮\\ ⋮& & & \ddots & \mathbf{0}\\ \mathbf{0}& \cdots & \cdots & \mathbf{0}& {\stackrel{.}{\mathbf{T}}}_{2,n,n-1}\end{array}\right)\left(\begin{array}{c}{\stackrel{.}{\mathbf{e}}}_{2,2,1}\\ ⋮\\ {\stackrel{.}{\mathbf{e}}}_{2,i,m}\\ ⋮\\ {\stackrel{.}{\mathbf{e}}}_{2,n,n-1}\end{array}\right)={\stackrel{.}{\mathbf{T}}}_2{\stackrel{.}{\mathbf{e}}}_2={\stackrel{.}{\mathbf{T}}}_2{\stackrel{.}{\mathbf{L}}}_2\mathbf{e}.$$ (17)

It is clear that the reduced second order marginal residual vector ε̇₂ is a linear function of the multinomial cell residuals. Again, because Ṫ₂ is an n(n − 1)/2 × d₂ matrix that has full row rank, Ṫ₂L̇₂ has full row rank as well.

Given the foregoing development, let the n + n(n − 1)/2 = n(n + 1)/2 = κ reduced first and second order marginal residuals be

$${\mathit{\epsilon }}_2=\left(\begin{array}{c}{\stackrel{.}{\mathit{\epsilon }}}_1\\ {\stackrel{.}{\mathit{\epsilon }}}_2\end{array}\right)=\left(\begin{array}{cc}{\stackrel{.}{\mathbf{T}}}_1& \mathbf{0}\\ \mathbf{0}& {\stackrel{.}{\mathbf{T}}}_2\end{array}\right)\left(\begin{array}{c}{\stackrel{.}{\mathbf{L}}}_1\\ {\stackrel{.}{\mathbf{L}}}_2\end{array}\right)\mathbf{e}={\mathbf{T}}_2{\mathbf{e}}_2.$$ (18)

From Equation (18), we have

$$\sqrt{N}{\mathit{\epsilon }}_2=\sqrt{N}{\mathbf{T}}_2{\mathbf{e}}_2\stackrel{D}{\to }{\mathcal{N}}_{\kappa }[\mathbf{0},\mathbf{\Phi }(\mathit{\theta })],$$ (19)

where $\mathbf{\Phi }(\mathit{\theta })={\mathbf{T}}_2{\mathbf{\Xi }}_2(\mathit{\theta }){\mathbf{T}}_2^{\prime }={\mathbf{T}}_2{\mathbf{\Omega }}_2(\mathit{\theta }){\mathbf{T}}_2^{\prime }-{\mathbf{T}}_2{\mathbf{\Delta }}_2(\mathit{\theta }){[ℱ(\mathit{\theta })]}^{-1}{\mathbf{\Delta }}_2^{\prime }(\mathit{\theta }){\mathbf{T}}_2^{\prime }$. Rewrite ${\mathbf{T}}_2{\mathbf{\Omega }}_2(\mathit{\theta }){\mathbf{T}}_2^{\prime }$ as Ψ₂(θ) and T₂Δ₂(θ) as Γ₂(θ). We see that Φ(θ) = Ψ₂(θ) − Γ₂(θ)[ (θ)]⁻¹Γ₂(θ)′ has a similar structure as Ω₂(θ) in Equation (19). In particular, if the κ × ν reduced marginal Jacobian Γ₂(θ) has full column rank, i.e., when the model is locally identified from the reduced first and second order marginal residuals, there exists a κ × (κ − ν) orthogonal complement Γ̄₂(θ) such that Γ̄₂(θ)′Γ₂(θ) is zero. Therefore, Γ̄₂(θ̂)′ε₂ is (κ − ν)-variate normal with zero means and limiting covariance matrix Γ̄₂(θ)′Ψ₂(θ)Γ̄₂(θ), i.e.,

$$\sqrt{N}{\overline{\mathbf{\Gamma }}}_2{(\widehat{\mathit{\theta }})}^{\prime }{\mathit{\epsilon }}_2\stackrel{D}{\to }{\mathcal{N}}_{k-\nu }(\mathbf{0},{\overline{\mathbf{\Gamma }}}_2{(\mathit{\theta })}^{\prime }{\mathbf{\Psi }}_2(\mathit{\theta }){\overline{\mathbf{\Gamma }}}_2(\mathit{\theta })),$$ (20)

and we now present the new test statistic:

$$M_2^{\ast }=N{\mathit{\epsilon }}_2^{\prime }{\overline{\mathbf{\Gamma }}}_2(\widehat{\mathit{\theta }})[{\overline{\mathbf{\Gamma }}}_2{(\mathit{\theta })}^{\prime }]{\mathbf{\Psi }}_2(\mathit{\theta }){\overline{\mathbf{\Gamma }}}_2{(\mathit{\theta })}^{-1}{\overline{\mathbf{\Gamma }}}_2{(\widehat{\mathit{\theta }})}^{\prime }{\mathit{\epsilon }}_2,$$ (21)

which is asymptotically chi-square distributed with κ − ν degrees-of-freedom under the null hypothesis that the model fits exactly. Again, M₂ and $M_2^{\ast }$ are numerically equivalent when all items are dichotomous because then the matrix T₂ is going to be an identity matrix.

The further reduction in $M_2^{\ast }$ is akin to using means and product moments for model fit testing. We will show using simulations that the new statistic has well calibrated Type I error rates and significantly higher power than the original M₂ when the test is made up of polytomous items. When the test items are dichotomous, T₂ becomes an identity matrix, implying that $M_2^{\ast }$ is equivalent to M₂. A critical requirement of $M_2^{\ast }$ is that the model must be locally identified from the set of reduced marginals so that the degrees-of-freedom is positive. For graded response bifactor models, the minimum number of items to achieve local identification is typically not excessive. If all test items are dichotomous, at least 6 items are needed. If the number of categories is equal to 5 for all items, the minimum is 12 items.

2.5 Computing the Marginals with Dimension Reduction

The observed marginal proportions are easy to tabulate from the observed data univariate and bivariate frequencies. On the other hand, while the model-implied marginal probabilities and elements of Δ₂ are defined as linear combinations of elements of π and Δ, their computation need not involve the L matrices at all. The L matrices are mostly useful as theoretical devices for studying the asymptotic distributions of the marginal residuals. The number of columns in L is same as C, the total number of response patterns. Multiplications of dense matrices with dimension C quickly become infeasible as the number of items n increases.

2.5.1 The First and Second Order Marginal Probabilities

In reality, the marginal probabilities are computed directly, as integrals over the latent variable distribution. The integrals nominally have dimensionality equal to S + 1, and they must be numerically approximated using quadrature. For instance, the first order marginal probability π̇_1,j,k(θ̂) can be computed as

$$\begin{array}{l}{\stackrel{.}{\pi }}_{1,j,k}(\widehat{\mathit{\theta }})=\int \underset{j}{Pr}(k\mid \mathit{\eta },\widehat{\mathit{\theta }})h(\mathit{\eta })d\mathit{\eta }\\ \approx \underset{(S+1)\text{fold}}{\underbrace{\sum _{q_S=1}^Q\cdots \sum _{q_0=1}^Q}}\underset{j}{Pr}(k\mid X_{q_0},\dots ,X_{q_S},\widehat{\mathit{\theta }})W(X_{q_0})\cdots W(X_{q_S}),\end{array}$$ (22)

where X_q0, …, X_qS denotes a set of (direct product) quadrature nodes, with Q points per dimension, and W(·) denotes the corresponding quadrature weights, e.g., Gauss-Hermite nodes and weights (Abramowitz & Stegun, 1964). Similarly the second order marginal probability π̇_2,l,m,klkm (θ̂) is equal to

$$\begin{array}{l}{\stackrel{.}{\pi }}_{2,l,m,k_l,k_m}(\widehat{\mathit{\theta }})=\int \underset{l}{Pr}(k_l\mid \mathit{\eta },\widehat{\mathit{\theta }})\underset{m}{Pr}(k_m\mid \mathit{\eta },\widehat{\mathit{\theta }})h(\mathit{\eta })d\mathit{\eta }\\ \approx \underset{(S+1)\text{fold}}{\underbrace{\sum _{q_S=1}^Q\cdots \sum _{q_0=1}^Q}}\underset{l}{Pr}(k_l\mid X_{q_0},\dots ,X_{q_S},\widehat{\mathit{\theta }})\underset{m}{Pr}(k_m\mid X_{q_0},\dots ,X_{q_S},\widehat{\mathit{\theta }})W(X_{q_0})\cdots W(X_{q_S}).\end{array}$$ (23)

Clearly, when S is large, numerical approximation suffers from the curse of dimensionality since there must be Q^S+1 function evaluations per marginal probability.

Just as in parameter estimation, we may use the item bifactor model’s special feature (that each item loads on at most one group-specific dimension) to analytically reduce the dimensionality of the integrals. For the first order marginal probability, this is simple to accomplish. Assume for the moment that item j loads on group-specific dimension s. We have:

$$\begin{array}{l}{\stackrel{.}{\pi }}_{1,j,k}(\widehat{\mathit{\theta }})=\int \underset{j}{Pr}(k\mid \mathit{\eta },\widehat{\mathit{\theta }})h(\mathit{\eta })d\mathit{\eta }\\ =\int \int \underset{j}{Pr}(k\mid {\eta }_0,{\eta }_s,\widehat{\mathit{\theta }})h({\eta }_s)h({\eta }_0)d{\eta }_{s}d{\eta }_0\\ =\int \left[\int \underset{j}{Pr}(k\mid {\eta }_0,{\eta }_s,\widehat{\mathit{\theta }})h({\eta }_s)d{\eta }_s\right]h({\eta }_0)d{\eta }_0\\ \approx \sum _{q_0=1}^Q\left[\sum _{q_s=1}^Q\underset{j}{Pr}(k\mid X_{q_0},X_{q_s},\widehat{\mathit{\theta }})W(X_{q_s})\right]W(X_{q_0}).\end{array}$$ (24)

To go from the first to the second line in (24), we simply need to realise that besides the general dimension η₀, out of all the group-specific dimensions η₁, …, η_s, …, η_S, item j is only influenced by η_s. For the second order marginal probability, we have to consider two distinct possibilities. When items l and m both load on the same group-specific dimension s, we have:

$$\begin{array}{l}{\stackrel{.}{\pi }}_{2,l,m,k_l,k_m}(\widehat{\mathit{\theta }})=\int \underset{l}{Pr}(k_l\mid \mathit{\eta },\widehat{\mathit{\theta }})\underset{m}{Pr}(k_m\mid \mathit{\eta },\widehat{\mathit{\theta }})h(\mathit{\eta })d\mathit{\eta }\\ =\int \int \underset{l}{Pr}(k_l\mid {\eta }_0,{\eta }_s,\widehat{\mathit{\theta }})\underset{m}{Pr}(k_m\mid {\eta }_0,{\eta }_s,\widehat{\mathit{\theta }})h({\eta }_s)h({\eta }_0)d{\eta }_{s}d{\eta }_0\\ =\int \left[\int \underset{l}{Pr}(k_l\mid {\eta }_0,{\eta }_s,\widehat{\mathit{\theta }})\underset{m}{Pr}(k_m\mid {\eta }_0,{\eta }_s,\widehat{\mathit{\theta }})h({\eta }_s)d{\eta }_s\right]h({\eta }_0)d{\eta }_0\\ \approx \sum _{q_0=1}^Q\left[\sum _{q_s=1}^Q\underset{l}{Pr}(k_l\mid X_{q_0},X_{q_s},\widehat{\mathit{\theta }})\underset{m}{Pr}(k_m\mid X_{q_0},X_{q_s},\widehat{\mathit{\theta }})W(X_{q_s})\right]W(X_{q_0}).\end{array}$$ (25)

When item l loads on group-specific dimension s and item m loads on group-specific dimension t, we have instead of Equation (25):

$$\begin{array}{l}{\stackrel{.}{\pi }}_{2,l,m,k_l,k_m}(\widehat{\mathit{\theta }})=\int \underset{l}{Pr}(k_l\mid \mathit{\eta },\widehat{\mathit{\theta }})\underset{m}{Pr}(k_m\mid \mathit{\eta },\widehat{\mathit{\theta }})h(\mathit{\eta })d\mathit{\eta }\\ =\int \int \int \underset{l}{Pr}(k_l\mid {\eta }_0,{\eta }_s,\widehat{\mathit{\theta }})\underset{m}{Pr}(k_m\mid {\eta }_0,{\eta }_t,\widehat{\mathit{\theta }})h({\eta }_s)h({\eta }_t)h({\eta }_0)d{\eta }_{s}d{\eta }_{t}d{\eta }_0\\ =\int \left[\int \underset{l}{Pr}(k_l\mid {\eta }_0,{\eta }_s,\widehat{\mathit{\theta }})h({\eta }_s)d{\eta }_s\right]\left[\int \underset{m}{Pr}(k_m\mid {\eta }_0,{\eta }_t,\widehat{\mathit{\theta }})h({\eta }_t)d{\eta }_t\right]h({\eta }_0)d{\eta }_0\\ \approx \sum _{q_0=1}^Q\left[\sum _{q_s=1}^Q\underset{l}{Pr}(k_l\mid X_{q_0},X_{q_s},\widehat{\mathit{\theta }})W(X_{q_s})\right]\left[\sum _{q_t=1}^Q\underset{m}{Pr}(k_m\mid X_{q_0},X_{q_t},\widehat{\mathit{\theta }})W(X_{q_t})\right]W(X_{q_0}).\end{array}$$ (26)

In either case, the dimensionality of integration is equal to 2. More generally, regardless of the number of factors in the model, we can compute the marginal probabilities with (P + 1)-dimensional quadrature, as long as the model is a bifactor (P = 1), testlet (P = 1), or two-tier (P ≥1) type of hierarchical item factor model. The resulting computational savings in the calculation of goodness-of-fit has been previously unavailable to researchers.

2.5.2 The Elements of the Jacobian

As to the elements of the Jacobian, they are also integrals that can be approximated by the same quadrature rule as for the marginal probabilities. The dimensionality of integration can be reduced by the same line of reasoning. Consider a generic element θ in θ. Assuming that item j loads on group-specific dimension s, the derivative of the first order marginal probability π̇_1,j,k(θ) with respect to θ, when evaluated at θ̂, can be numerically approximated as the following 2-dimensional integral:

$$\begin{array}{l}\frac{\partial {\stackrel{.}{\pi }}_{1,j,k}(\widehat{\mathit{\theta }})}{\partial \theta }=\int \underset{j}{Pr}(k\mid \mathit{\eta },\widehat{\mathit{\theta }})\frac{\partial log{Pr}_j(k\mid \mathit{\eta },\widehat{\mathit{\theta }})}{\partial \theta }h(\mathit{\eta })d\mathit{\eta }\\ =\int \left[\int \underset{j}{Pr}(k\mid {\eta }_0,{\eta }_s,\widehat{\mathit{\theta }})\frac{\partial log{Pr}_j(k\mid {\eta }_0,{\eta }_s,\widehat{\mathit{\theta }})}{\partial \theta }h({\eta }_s)d{\eta }_s\right]h({\eta }_0)d{\eta }_0\\ \approx \sum _{q_0=1}^Q\left[\sum _{q_s=1}^Q\underset{j}{Pr}(k\mid X_{q_0},X_{q_s},\widehat{\mathit{\theta }})\frac{\partial log{Pr}_j(k\mid X_{q_0},X_{q_s},\widehat{\mathit{\theta }})}{\partial \theta }W(X_{q_s})\right]W(X_{q_0}).\end{array}$$ (27)

For the derivative of second order marginal probabilities, we find after some algebra

$$\begin{array}{l}\frac{\partial {\stackrel{.}{\pi }}_{2,l,m,k_l,k_m}(\widehat{\mathit{\theta }})}{\partial \theta }=\int \underset{l}{Pr}(k_l\mid \mathit{\eta },\widehat{\mathit{\theta }})\underset{m}{Pr}(k_m\mid \mathit{\eta },\widehat{\mathit{\theta }})\left[\frac{\partial log{Pr}_l(k_l\mid \mathit{\eta },\widehat{\mathit{\theta }})}{\partial \theta }+\frac{\partial log{Pr}_m(k_m\mid \mathit{\eta },\widehat{\mathit{\theta }})}{\partial \theta }\right]h(\mathit{\eta })d\mathit{\eta }\\ \approx \sum _{q_0=1}^Q\left[\sum _{q_s=1}^Q\underset{l}{Pr}(k_l\mid X_{q_0},X_{q_s},\widehat{\mathit{\theta }})\underset{m}{Pr}(k_m\mid X_{q_0},X_{q_s},\widehat{\mathit{\theta }})\frac{\partial log{Pr}_l(k_l\mid X_{q_0},X_{q_s},\widehat{\mathit{\theta }})}{\partial \theta }W(X_{q_s})\right]+\\ \left[\sum _{q_s=1}^Q\underset{l}{Pr}(k_l\mid X_{q_0},X_{q_s},\widehat{\mathit{\theta }})\underset{m}{Pr}(k_m\mid X_{q_0},X_{q_s},\widehat{\mathit{\theta }})\frac{\partial log{Pr}_m(k_m\mid X_{q_0},X_{q_s},\widehat{\mathit{\theta }})}{\partial \theta }W(X_{q_s})\right]W(X_{q_0}),\end{array}$$

provided that both item l and item m load on the same group-specific dimension s. As as the case in Equation (26), when item l loads on group-specific dimension s and item m loads on group-specific dimension t, the derivative can be numerically approximated as:

$$\begin{array}{l}\frac{\partial {\stackrel{.}{\pi }}_{2,l,m,k_l,k_m}(\widehat{\mathit{\theta }})}{\partial \theta }=\int \underset{l}{Pr}(k_l\mid \mathit{\eta },\widehat{\mathit{\theta }})\underset{m}{Pr}(k_m\mid \mathit{\eta },\widehat{\mathit{\theta }})\left[\frac{\partial log{Pr}_l(k_l\mid \mathit{\eta },\widehat{\mathit{\theta }})}{\partial \theta }+\frac{\partial log{Pr}_m(k_m\mid \mathit{\eta },\widehat{\mathit{\theta }})}{\partial \theta }\right]h(\mathit{\eta })d\mathit{\eta }\\ =\int \left[\int \underset{l}{Pr}(k_l\mid {\eta }_0,{\eta }_s,\widehat{\mathit{\theta }})\frac{\partial log{Pr}_l(k_l\mid {\eta }_0,{\eta }_s,\widehat{\mathit{\theta }})}{\partial \theta }h({\eta }_s)d{\eta }_s\right]\left[\int \underset{m}{Pr}(k_m\mid {\eta }_0,{\eta }_t,\widehat{\mathit{\theta }})h({\eta }_t)d{\eta }_t\right]+\\ \left[\int \underset{l}{Pr}(k_l\mid {\eta }_0,{\eta }_s,\widehat{\mathit{\theta }})h({\eta }_s)d{\eta }_s\right]\left[\int \underset{m}{Pr}(k_m\mid {\eta }_0,{\eta }_t,\widehat{\mathit{\theta }})\frac{\partial log{Pr}_m(k_m\mid {\eta }_0,{\eta }_t,\widehat{\mathit{\theta }})}{\partial \theta }h({\eta }_t)d{\eta }_t\right]h({\eta }_0)d{\eta }_0\\ \approx \sum _{q_0=1}^Q\left[\sum _{q_s=1}^Q\underset{l}{Pr}(k_l\mid X_{q_0},X_{q_s},\widehat{\mathit{\theta }})\frac{\partial log{Pr}_l(k_l\mid X_{q_0},X_{q_s},\widehat{\mathit{\theta }})}{\partial \theta }W(X_{q_s})\right]\left[\sum _{q_t=1}^Q\underset{m}{Pr}(k_m\mid X_{q_0},X_{q_t},\widehat{\mathit{\theta }})W(X_{q_t})\right]+\\ \left[\sum _{q_s=1}^Q\underset{l}{Pr}(k_l\mid X_{q_0},X_{q_s},\widehat{\mathit{\theta }})W(X_{q_s})\right]\left[\sum _{q_t=1}^Q\underset{m}{Pr}(k_m\mid X_{q_0},X_{q_t},\widehat{\mathit{\theta }})\frac{\partial log{Pr}_m(k_m\mid X_{q_0},X_{q_t},\widehat{\mathit{\theta }})}{\partial \theta }W(X_{q_t})\right]W(X_{q_0}).\end{array}$$

We can see that the amount of computation required for the Jacobian elements is equal to a constant multiple of Q² function evaluations, after dimension reduction. For two-tier models, the number of function evaluations is equal to Q^P+1, when P is relatively small, as opposed to the full Q^P+S function evaluations without dimension reduction.

2.5.3 The Elements of the Weight Matrix

Dropping reference to θ for the moment, the weight matrix Ξ₂ can be written as

$${\mathbf{\Xi }}_2={\mathbf{L}}_2\mathbf{\Xi }{\mathbf{L}}_2^{\prime }={\mathbf{L}}_2\text{diag}(\mathit{\pi }){\mathbf{L}}_2^{\prime }-{\mathbf{L}}_2\mathit{\pi }{\mathit{\pi }}^{\prime }{\mathbf{L}}_2^{\prime }={\mathbf{L}}_2\text{diag}(\mathit{\pi }){\mathbf{L}}_2^{\prime }-{\mathit{\pi }}_2{\mathit{\pi }}_2^{\prime }=\mathbf{\sum }-{\mathit{\pi }}_2{\mathit{\pi }}_2^{\prime }.$$ (28)

In the last expression, the second part involves the first and second order marginal probabilities in π₂, which are already computed following results in Section 2.5.1. The first part $\mathbf{\sum }={\mathbf{L}}_2\text{diag}(\mathit{\pi }){\mathbf{L}}_2^{\prime }$ involves second, third, and fourth order marginal probabilities. We may gain a clearer understanding of what it takes to compute the elements of Σ from a partitioning of L₂, as in Equation (8):

$$\mathbf{\sum }={\mathbf{L}}_2\text{diag}(\mathit{\pi }){\mathbf{L}}_2^{\prime }=\left(\begin{array}{cc}{\stackrel{.}{\mathbf{L}}}_1\text{diag}(\mathit{\pi }){\stackrel{.}{\mathbf{L}}}_1^{\prime }& \\ {\stackrel{.}{\mathbf{L}}}_2\text{diag}(\mathit{\pi }){\stackrel{.}{\mathbf{L}}}_1^{\prime }& {\stackrel{.}{\mathbf{L}}}_2\text{diag}(\mathit{\pi }){\stackrel{.}{\mathbf{L}}}_2^{\prime }\end{array}\right)=\left(\begin{array}{cc}{\mathbf{\sum }}_{11}& \\ {\mathbf{\sum }}_{21}& {\mathbf{\sum }}_{22}\end{array}\right).$$

Consider the upper-left block ${\mathbf{\sum }}_{11}={\stackrel{.}{\mathbf{L}}}_1\text{diag}(\mathit{\pi }){\stackrel{.}{\mathbf{L}}}_1^{\prime }$. As is clear from Equation (9), each row of L̇₁ can be understood as a set of binary logical conditions that whether each of the C response patterns contributes to a particular first order marginal. Suppose row r of L̇₁ corresponds to the first-order marginal for item l in category k_l. And further let row c of L̇₁ corresponds to the first-order marginal for item m in category k_m. We realise that the (r, c) element of Σ₁₁ is equal to the second order marginal probability π_2,l,m,klkm, if l ≠ m. If l = m, the entry is zero.

Now consider the lower-left block ${\mathbf{\sum }}_{21}={\stackrel{.}{\mathbf{L}}}_2\text{diag}(\mathit{\pi }){\stackrel{.}{\mathbf{L}}}_1^{\prime }$. Suppose row r of L̇₂ corresponds to the second-order marginal wherein item l is in category k_l and item m is in category k_m. Let row c of L̇₁ correspond to the first-order marginal for item l′ in category $k_l^{\prime }$. Then the (r, c) element of Σ₂₁ is equal to a third order marginal probability ${\stackrel{.}{\pi }}_{3,l,m,l^{\prime },k_l,k_m,k_l^{\prime }}$, i.e., indicating the joint probability of item l in category k_l, item m in category k_m, and item l′ in category $k_l^{\prime }$, if l, m, and l′ are distinct. Recall that l and m are always distinct due to the construction of L̇₂ (see Equation 10). If l′ is equal to either l or m and at the same time if $k_l^{\prime }$ is equal to either k_l or k_m, then the (r, c) element of Σ₂₁ is equal to the second order marginal probability π̇_2,l,m,klkm. Otherwise the (r, c) element of Σ₂₁ is equal to zero. Thus, we must be able to compute π̇_{3,l,m,j,klkm,kj}, in addition to the pre-computed second order marginals.

Finally, consider the lower-right block ${\mathbf{\sum }}_{22}={\stackrel{.}{\mathbf{L}}}_2\text{diag}(\mathit{\pi }){\stackrel{.}{\mathbf{L}}}_2^{\prime }$. Let row r of L̇₂ correspond to the second-order marginal wherein item l is in category k_l and item m is in category k_m. And let row c of L̇₂ correspond to the second-order marginal wherein item l′ is in category $k_l^{\prime }$ and item m′ is in category $k_m^{\prime }$. If l, m, l′, and k′ are distinct, the (r, c) element of Σ₂₂ is equal to the fourth order marginal ${\stackrel{.}{\pi }}_{4,l,m,l^{\prime },m^{\prime },k_l,k_m,k_l^{\prime },k_m^{\prime }}$. If l′ is equal to either l or m and at the same time if $k_l^{\prime }$ is equal to either k_l or k_m, the (r, c) element of Σ₂₂ is equal to the third order marginal ${\stackrel{.}{\pi }}_{3,l,m,m^{\prime },k_l,k_m,k_m^{\prime }}$, or zero otherwise. If m′ is equal to either l or m and at the same time if $k_m^{\prime }$ is equal to either k_l or k_m, the (r, c) element of Σ₂₂ is equal to the third order marginal ${\stackrel{.}{\pi }}_{3,l,m,l^{\prime },k_l,k_m,k_l^{\prime }}$, or zero otherwise. If l = l′ and m = m′ and at the same time $k_l=k_l^{\prime }$ and $k_m=k_m^{\prime }$, the (r, c) element of Σ₂₂ is equal to the second order marginal π̇_2,l,m,klkm, or zero otherwise.

We note here that the third and fourth order marginal probabilities can be computed with dimension reduction as well, so that the actual dimension of integration is equal to 2 for bifactor/testlet models and P + 1 for two-tier models with P primary dimensions. The computational details are lengthy and are relegated to the Appendix. The numeric engine of IRTPRO (Cai, Thissen, & du Toit, 2011) contains an implementation of M₂ and $M_2^{\ast }$ used in the remainder of this paper.

3 Applications to Simulated Data

3.1 The Efficiency of Dimension Reduction

In order illustrate the computational efficiency achieved through the strategy described above, we conducted a simple timing experiment. Data were simulated from a graded item bifactor model with 15 items in 2, 3, 4, or 5 categories. Three items loaded on each group-specific factor (in addition to the general dimension), and the number of group-specific factors (S) ranged from 2 to 5. The total number of dimensions (S + 1) thus ranged from 3 to 6. For each condition, the generating model was fit to the simulated data, and we recorded the time (in seconds) required to calculate M₂ with and without dimension reduction. Nine quadrature points spread evenly from −4 to 4 standard deviation units were used in approximating the marginal probabilities. This relatively small number is necessary to allow us to obtain results in the high-dimensional cases where we do not utilise dimension reduction. However, with dimension reduction, a larger number of quadrature points can and should be used, in order to obtain the best possible approximations of the marginal probabilities. The results for Maydeu-Olivares and Joe’s (2005) M₂ test statistic based on the full first- and second-order marginal tables (Equation 13) are presented in Table 1. Without implementing dimension reduction, the time required to obtain the test statistic increases with both the number of categories and the number of dimensions. In contrast, when dimension reduction is used, the computing time remains relatively constant for models with a given number of response categories, regardless of the number of group-specific dimensions. Though not presented here, a similar pattern of results was observed for the alternative $M_2^{\ast }$ statistic based on further reduced residuals.

Table 1.

Timing Comparison Results

#Group-Specific Dimensions	Number of Response Categories
	2	3	4	5
	without dimension reduction
2	0.4	3.1	26.5	147.0
3	3.5	16.7	70.8	262.4
4	32.3	145.3	489.4	1369.5
5	335.2	1459.8	5305.7	13437.5
	with dimension reduction
2	0.2	2.0	22.4	141.4
3	0.2	2.2	22.8	145.3
4	0.2	2.2	23.7	146.7
5	0.2	2.2	22.4	142.9

Notes. The entries are time (in seconds) required to compute M₂ for a graded item bifactor model with 15 items.

3.2 Monte Carlo Simulations

A second simulation study was conducted to evaluate the performance of the test statistics under repeated sampling. Both Maydeu-Olivares and Joe’s (2005) M₂ statistic based on the full first- and second-order marginal tables (Equation 13) and the alternative version $M_2^{\ast }$ (Equation 21) were considered. We generated data in two sample sizes (N = 750 or 1500) for 15 items from models that varied in their factor structure and the number of response categories (K = 2, 3, 4, or 5).

The factor structures of the generating models in this study can be broadly characterised according to their “major” and “minor” factor domains (see, e.g., Tucker, Koopman, & Linn, 1969; MacCallum & Tucker, 1991). For each condition, the major domain consisted of either a single dimension or 4 dimensions with a bifactor structure (1 general dimension and 3 orthogonal group-specific dimensions). In some conditions, a minor factor domain was added to the generating model, utilizing a variation of the Tucker, Koopman, and Linn (1969) procedure (TKL). This minor domain consisted of 50 additional common factors that (1) were orthogonal to one another and to the dimension(s) in the major domain and (2) collectively accounted for some fixed proportion of variance not accounted for by the common factor(s) in the major domain.

The TKL procedure has been utilised in numerous simulation studies of principal components and factor analytic methods (see, e.g., MacCallum & Tucker, 1991; Hong, 1999; Briggs & MacCallum, 2003; Timmerman & Lorenzo-Seva, 2011). To our knowledge, this may be the first application to simulation studies in IRT, though Davey, Nering, and Thompson (1997) implemented an approach based on Tucker et al.’s (1969) logic. The key benefit of the TKL procedure, as articulated by Tucker et al. (1969), lies in its realism. The minor factors cannot, in principle, be represented parsimoniously in any item factor model. As such, the minor dimensions result in a kind of model misspecification that is likely to be quite pervasive in analyses of real data. Such misspecification is not tied to the omission of just one or a few parameters from the generating model to the fitted model, as in most other simulation studies.

In all, there were 6 different factor structures obtained by crossing the major and minor domain structures. Specifically, the generating models consisted of, first, either a unidimensional or 4-dimensional bifactor structure as the major domain and, second, additional minor common factors accounting for 0% (i.e., no additional minor factors), 10% (TKL10), or 30% (TKL30) of variance. For the conditions with no minor factors, an exactly correctly specified model does exist; it is either the unidimensional model or the bifactor model (depending on the major domain factor structure). These represent the null conditions. For TKL10 and TKL30, the unidimensional or bifactor models will be mildly misspecified (accounting for most influential dimensions while ignoring the minor ones).

The simulation procedure started with the major domain. The generating item slope parameters for the major domain factors were randomly drawn from a log-normal distribution with a mean of 0 and standard deviation of 0.2. A total of 30 slope parameters were drawn, 15 for the general dimension (also used in the unidimensional conditions) and 15 for the group-specific factors. Threshold values were randomly drawn from uniform distributions with ranges that varied according to the number of response categories. For each item, these values were then multiplied by the negative of the corresponding general dimension slope parameters; these products were used as intercept parameters. For simplicity, the same intercepts were used for all conditions with a given number of response categories, regardless of the factor structure. The generating item parameters for the unidimensional and bifactor model conditions (with no additional minor domain factors) are summarised in Table 2.

Table 2.

Generating Item Parameters with No Additional Minor Domain Factors

Item	General	Group-Specific			K = 2	K = 3		K = 4			K = 5
	βj0	βj1	βj2	βj3	αj,1	αj,1	αj,2	αj,1	αj,2	αj,3	αj,1	αj,2	αj,3	αj,4
1	0.65	0.99			1.44	0.83	−0.98	1.46	0.49	−1.68	1.48	0.71	−0.84	−1.59
2	0.87	2.16			0.21	1.82	−0.25	1.10	0.71	−2.23	1.80	0.16	−0.38	−2.30
3	0.84	0.70			2.45	2.51	−0.22	1.18	0.21	−1.95	1.66	0.15	−0.32	−1.43
4	1.13	1.76			−1.53	2.45	−1.09	1.95	1.05	−2.13	2.13	0.57	−1.50	−3.02
5	0.57	0.97			1.58	0.01	−1.04	1.53	0.00	−0.82	1.65	0.78	−0.21	−1.26
6	1.41		1.47		−2.13	3.21	−2.45	1.84	−0.82	−1.95	2.72	0.98	−1.85	−2.87
7	0.78		2.00		2.06	2.07	−2.10	1.02	−0.57	−1.34	1.49	1.16	−0.51	−1.81
8	0.73		1.18		−1.03	1.59	−1.09	1.32	0.61	−1.34	2.09	0.69	−0.22	−1.59
9	1.03		0.91		−1.00	2.95	−1.71	1.88	−0.62	−1.69	2.07	1.16	−1.33	−2.08
10	0.47		0.61		−0.62	0.48	−0.10	0.56	0.04	−0.98	1.15	0.29	−0.16	−0.91
11	1.00			0.82	−2.26	2.91	−1.30	1.82	0.99	−2.07	2.26	1.27	−0.36	−1.82
12	0.38			1.41	0.64	1.03	−0.89	0.89	−0.02	−0.57	0.87	0.30	−0.04	−0.71
13	1.07			1.59	2.41	1.01	−0.48	1.66	0.86	−2.24	2.86	1.40	−1.50	−3.20
14	1.36			1.86	−1.58	0.56	−1.90	2.63	−0.23	−3.36	2.10	0.15	−0.75	−2.75
15	0.77			0.29	−1.53	0.09	−2.17	1.86	−0.19	−0.82	2.24	0.75	−0.14	−1.90

In order to obtain slopes for the minor domain factors, the slope parameters for the major domain factors in Table 2 were first transformed to standardised factor loadings. Next, factor loadings were randomly drawn using the TKL procedure for the 50 minor factors such that (1) successive minor factors would have diminishing influence on the item responses, and (2) the total variance explained by the minor factors would equal the intended value (either 10% or 30%). The loadings were then transformed back to the metric of logistic slopes. The item response data for the TKL10 and TKL30 conditions were then simulated from this (highly) multidimensional IRT model, with 51 total factors when the major domain consisted of a single factor and 54 total factors when the major domain had a bifactor structure.

For each condition, 1000 datasets were generated. After generating data, item parameters were estimated by fitting either a unidimensional or bifactor model using the Bock-Aitkin EM algorithm (Bock & Aitkin, 1981). Details concerning item bifactor model estimation are provided in Cai, Yang, and Hansen (2011). The number of quadrature points was Q = 19, and convergence was declared if maximum absolute inter-cycle parameter change dropped below 10⁻⁴. In all cases, the fitted model corresponded to the structure of the “major” factor domain of the data generating model; minor domain factors were ignored, if present. This allowed us to test goodness-of-fit in both the null case and under what we consider to be rather mild model misspecification. Given the data and item parameter estimates, we computed both M₂ and $M_2^{\ast }$ test statistics for each replication. The dimension reduction strategy described in Section 2.5 was used for all bifactor conditions. Results from unconverged replications or in cases where numerical instability was evident were identified and omitted from subsequent analyses. Across all conditions, the minimum number of replications reported is 922.

3.2.1 Type I Error Rates

In Tables 3 and 4, we present simulation study results for the unidimensional and item bi-factor models, respectively, under the null condition, in which the fitted and generating models were the same. Here, we are concerned with whether the test statistics follow their asymptotic distribution and the extent to which the empirical model rejection rates match their nominal alpha levels. The results for the unidimensional and bifactor models are quite similar. For both models, it appears that the original M₂ test statistic is well-calibrated for dichotomous (K = 2) response data. However, as the number of response categories increases (K > 2), it appears that this M₂ statistic becomes stochastically smaller than the expected chi-square distribution. This is seen in the smaller mean value and in the empirical rejection rates, which fall well below the corresponding alpha levels, starting with 3 categories for the unidimensional model and 4 categories for the item bifactor model. In contrast, the $M_2^{\ast }$ statistic based on the reduced marginal tables appears to be fairly well-calibrated for the conditions we tested. As Maydeu-Olivares et al. (2011), we calculated Root Mean Square Error of Approximation (RM-SEA; Browne & Cudeck, 1993) values from the M₂ and $M_2^{\ast }$ statistics. Mean RMSEA and a 90% confidence interval (based on the the observed 5th and 95th percentiles across replications) are reported. The means ranged from .001 to .007. For all conditions, the lower limit of the 90% confidence interval was 0; the highest upper limit was .024.

Table 3.

Simulation Results: Unidimensional Model, Null Condition

K	N	reps	M2			RMSEA		rejection rates
			df	Mean	Var	Mean	(90% CI)	.150	.100	.050	.010
test statistic based on full one- and two-way marginal tables (M2)
2	750	1000	90	90.9	183.4	.006	(.000,.019)	.164	.104	.053	.016
	1500	1000	90	89.9	162.0	.004	(.000,.013)	.133	.075	.044	.008
3	750	1000	405	399.8	781.8	.003	(.000,.011)	.099	.062	.032	.009
	1500	1000	405	396.2	794.8	.002	(.000,.008)	.082	.063	.031	.005
4	750	1000	930	904.8	1857.9	.002	(.000,.008)	.055	.033	.010	.002
	1500	1000	930	903.5	1716.1	.001	(.000,.006)	.054	.034	.015	.001
5	750	1000	1665	1622.1	3380.4	.001	(.000,.007)	.042	.020	.010	.001
	1500	1000	1665	1619.6	3320.3	.001	(.000,.004)	.033	.022	.008	.000
test statistic based on reduced one- and two-way marginal tables( $M_2^{\ast }$)
3	750	1000	75	75.7	158.5	.006	(.000,.020)	.160	.106	.061	.020
	1500	1000	75	75.5	149.8	.004	(.000,.014)	.155	.103	.053	.012
4	750	1000	60	60.2	120.2	.006	(.000,.021)	.159	.106	.056	.010
	1500	1000	60	60.4	129.4	.005	(.000,.015)	.165	.117	.056	.012
5	750	1000	45	45.0	95.5	.007	(.000,.023)	.150	.105	.057	.019
	1500	1000	45	45.1	91.7	.005	(.000,.016)	.158	.106	.052	.012

Notes. K is the number of categories. N is the sample size. The number of valid (converged and stable) solutions are reported under the column heading “reps.” The reference distribution of M₂ and $M_2^{\ast }$ statistics is central chi-square with df degrees of freedom. Note that M₂ is equivalent to $M_2^{\ast }$ when K is 2.

Table 4.

Simulation Results: Bifactor model, Null Condition

K	N	reps	M2			RMSEA		rejection rates
			df	Mean	Var	Mean	(90% CI)	.150	.100	.050	.010
test statistic based on full one- and two-way marginal tables (M2)
2	750	935	75	74.4	147.1	.006	(.000,.019)	.144	.106	.049	.006
	1500	922	75	74.7	147.8	.004	(.000,.013)	.153	.104	.044	.007
3	750	995	390	390.1	754.1	.004	(.000,.012)	.153	.098	.047	.009
	1500	998	390	389.8	706.4	.003	(.000,.009)	.140	.093	.039	.007
4	750	998	915	888.7	1838.3	.002	(.000,.008)	.057	.030	.009	.002
	1500	1000	915	891.2	1703.6	.001	(.000,.006)	.059	.035	.010	.003
5	750	989	1650	1601.5	3149.9	.001	(.000,.006)	.029	.015	.008	.001
	1500	989	1650	1604.8	3318.4	.001	(.000,.004)	.033	.014	.007	.001
test statistic based on reduced one- and two-way marginal tables ( $M_2^{\ast }$)
3	750	995	60	59.4	133.5	.006	(.000,.021)	.140	.096	.052	.014
	1500	998	60	59.4	116.5	.004	(.000,.014)	.128	.091	.042	.009
4	750	998	45	45.2	96.6	.007	(.000,.023)	.154	.106	.059	.017
	1500	1000	45	45.1	86.3	.005	(.000,.015)	.157	.097	.042	.007
5	750	989	30	29.8	62.3	.006	(.000,.024)	.140	.092	.055	.017
	1500	989	30	30.1	60.2	.004	(.000,.017)	.151	.095	.047	.013

Notes. K is the number of categories. N is the sample size. The number of valid (converged and stable) solutions are reported under the column heading “reps.” The reference distribution of M₂ and $M_2^{\ast }$ statistics is central chi-square with df degrees of freedom. Note that M₂ is equivalent to $M_2^{\ast }$ when K is 2.

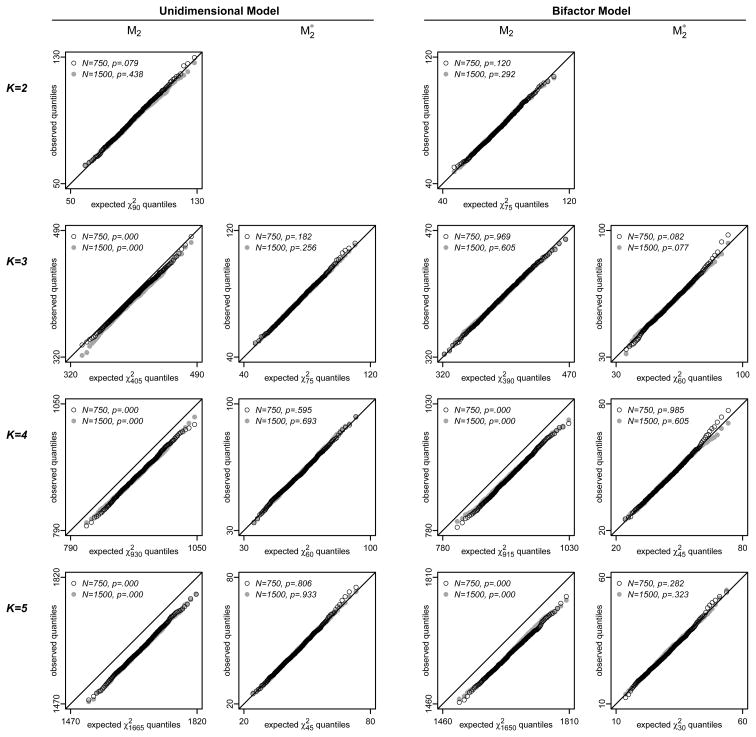
Observed and expected quantiles of the M₂ and $M_2^{\ast }$ statistics are presented in Figure 2. Two-sided Kolmogorov-Smirnov tests were performed to compare the observed and expected distributions; the resulting p-values are shown within each panel of Figure 2. Consistent with the results in Tables 3 and 4, the observed statistics are smaller than expected for the original M₂ statistic for items with 4 or more categories (3 or more for the unidimensional model), while the alternative $M_2^{\ast }$ statistic seems to better follow the expected distribution.

Figure 2.

Q-Q plots of observed M₂ and $M_2^{\ast }$ values and their reference chi-square distributions (degrees-of-freedom shown in the subscripts of the x-axis labels). Closed grey circles indicate conditions with sample size N = 1500; open black circles indicate N = 750. Reported p-values are for a two-tailed Komogorov-Smirnov test.

3.2.2 Power to Detect Misspecification

We examined the sensitivity of the test statistics to model misspecification by fitting models which ignored the common factors in the minor domain of the data generating model. As described above, those minor domain factors collectively accounted for 10 or 30% of unique item variance in the TKL10 and TKL30 conditions, respectively. Table 5 presents results for the unidimensional model; results for the item bifactor model are shown in Table 6. Null condition results are included for comparison. The empirical rejection rates for all conditions are presented in a set of power curves in Figure 3.

Table 5.

Simulation Results: Unidimensional model, Power at .05 Alpha Level

K	N	df	null model			TKL10			TKL30
			M	RMSEA (90% CI)	rej	M	RMSEA (90% CI)	rej	M	RMSEA (90% CI)	rej
test statistic based on full one- and two-way marginal tables (M2)
2	750	90	90.9	.006 (.000,.019)	.053	100.1	.011 (.000,.023)	.186	180.7	.036 (.028,.044)	.997
	1500	90	89.9	.004 (.000,.013)	.044	100.2	.008 (.000,.016)	.189	180.1	.026 (.019,.032)	.998
3	750	405	399.8	.003 (.000,.011)	.032	425.5	.007 (.000,.015)	.194	620.1	.026 (.022,.031)	1.000
	1500	405	396.2	.002 (.000,.008)	.031	451.4	.008 (.000,.013)	.483	841.5	.027 (.024,.030)	1.000
4	750	930	904.8	.002 (.000,.008)	.010	937.2	.004 (.000,.011)	.077	1180.6	.019 (.015,.022)	.999
	1500	930	903.5	.001 (.000,.006)	.015	973.1	.005 (.000,.009)	.259	1462.2	.019 (.017,.022)	1.000
5	750	1665	1622.1	.001 (.000,.007)	.010	1663.9	.003 (.000,.009)	.047	1933.1	.015 (.011,.018)	.997
	1500	1665	1619.6	.001 (.000,.004)	.008	1699.9	.003 (.000,.007)	.159	2246.4	.015 (.013,.017)	1.000
test statistic based on reduced one- and two-way marginal tables ( $M_2^{\ast }$)
3	750	75	75.7	.006 (.000,.020)	.061	98.3	.019 (.000,.030)	.538	246.0	.055 (.046,.064)	1.000
	1500	75	75.5	.004 (.000,.014)	.053	119.4	.019 (.011,.026)	.886	413.0	.055 (.049,.061)	1.000
4	750	60	60.2	.006 (.000,.021)	.056	87.0	.023 (.007,.035)	.670	206.2	.057 (.045,.070)	1.000
	1500	60	60.4	.005 (.000,.015)	.056	113.9	.024 (.016,.031)	.971	337.8	.055 (.047,.064)	1.000
5	750	45	45.0	.007 (.000,.023)	.057	59.2	.018 (.000,.033)	.376	138.7	.052 (.041,.064)	1.000
	1500	45	45.1	.005 (.000,.016)	.052	73.8	.020 (.010,.028)	.799	232.7	.053 (.045,.060)	1.000

Notes. K is the number of categories. N is the sample size. The reference distribution of M₂ and $M_2^{\ast }$ statistics is central chi-square with df degrees of freedom. Note that M₂ is equivalent to $M_2^{\ast }$ when K is 2. Means are reported under M and the empirical rejection rates at alpha level of .05 are shown under column heading “rej.”

Table 6.

Simulation Results: Bifactor model, Power at .05 Alpha Level

K	N	df	null model			TKL10			TKL30
			M	RMSEA (90% CI)	rej	M	RMSEA (90% CI)	rej	M	RMSEA (90% CI)	rej
test statistic based on full one- and two-way marginal tables (M2)
2	750	75	74.4	.006 (.000,.019)	.049	77.6	.007 (.000,.020)	.070	104.6	.022 (.010,.032)	.694
	1500	75	74.7	.004 (.000,.013)	.044	77.7	.005 (.000,.015)	.087	105.1	.016 (.007,.023)	.695
3	750	390	390.1	.004 (.000,.012)	.047	397.5	.005 (.000,.014)	.082	458.1	.015 (.007,.021)	.734
	1500	390	389.8	.003 (.000,.009)	.039	406.5	.005 (.000,.011)	.133	529.0	.015 (.012,.019)	.996
4	750	915	888.7	.002 (.000,.008)	.009	901.1	.002 (.000,.009)	.020	974.0	.009 (.000,.014)	.383
	1500	915	891.2	.001 (.000,.006)	.010	908.6	.002 (.000,.007)	.046	1061.2	.010 (.007,.013)	.938
5	750	1650	1601.5	.001 (.000,.006)	.008	1614.3	.001 (.000,.007)	.008	1698.1	.006 (.000,.011)	.203
	1500	1650	1604.8	.001 (.000,.004)	.007	1625.1	.001 (.000,.006)	.018	1796.8	.007 (.004,.010)	.783
test statistic based on reduced one- and two-way marginal tables ( $M_2^{\ast }$)
3	750	60	59.4	.006 (.000,.021)	.052	64.3	.009 (.000,.024)	.111	106.8	.032 (.020,.042)	.941
	1500	60	59.4	.004 (.000,.014)	.042	70.3	.009 (.000,.019)	.220	153.8	.032 (.025,.038)	.999
4	750	45	45.2	.007 (.000,.023)	.059	50.2	.011 (.000,.026)	.129	84.3	.033 (.020,.045)	.925
	1500	45	45.1	.005 (.000,.015)	.042	56.2	.011 (.000,.022)	.303	121.6	.033 (.025,.041)	.996
5	750	30	29.8	.006 (.000,.024)	.055	33.3	.011 (.000,.030)	.125	60.4	.035 (.018,.050)	.872
	1500	30	30.1	.004 (.000,.017)	.047	37.1	.011 (.000,.024)	.237	93.0	.037 (.027,.047)	.997

Notes. K is the number of categories. N is the sample size. The reference distribution of M₂ and $M_2^{\ast }$ statistics is central chi-square with df degrees of freedom. Note that M₂ is equivalent to $M_2^{\ast }$ when K is 2. Means are reported under M and the empirical rejection rates at alpha level of .05 are shown under column heading “rej.”

Figure 3.

Empirical rejection rates at α = .05 for M₂ and $M_2^{\ast }$ across all simulated conditions. K is the number of categories.

Consistent with the results for the null case, the original M₂ statistic appears to have less power than the statistic based on the reduced marginal tables. These differences are most evident for the TKL10 conditions. It is interesting to note that the RMSEA values are generally quite small for the conditions examined in the study. The mean RMSEA based on the alternative $M_2^{\ast }$ statistic was roughly .02 for TKL10 conditions and .05–.06 for TKL30; for the bifactor model, the corresponding means were .01 and .03–.04. These relatively small values are consistent with our intention of simulating data with rather mild misspecification.

4 An Application to Empirical Data

Having examined the performance of the test statistics in a range of simulated conditions, we now present an analysis of real data. A sample of 1042 daily cigarette smokers responded to 18 items regarding possible consequences of quitting smoking. Each item was rated on a 5-point ordinal scale. The items were administered within a larger questionnaire dealing with various attitudes, beliefs, and behaviors related to smoking (see Shadel, Edelen, & Tucker, 2011). The study was itself part of the development of the National Institute of Health’s Patient Reported Outcomes Measurement Information System (PROMIS; see, e.g., Reeve et al., 2007).

All 18 items dealt with negative consequences of quitting, and it seems plausible that the items would be influenced by a common dimension. At the same time, there were small groups of items that dealt with rather similar consequences. Two items asked about potential difficulty concentrating, three items related to weight control, two items dealt with stress management, and so on. In total, we identified 7 possible groups among the 18 items. In similar testing contexts, such item groups with shared content create dependencies that cannot be fully accounted for by a single common dimension. The bifactor model provides a way to explicitly model these dependencies, while still assuming a common dimension. Thus, we consider the unidimensional and bifactor models as competing alternatives. We fit these models to the data and then used the M₂ and M₂ − statistics, as well as likelihood-based criteria, to compare them. The bifactor model used here allows all items to load on a general dimension. In addition, groups of two or three items load onto one of 7 group-specific factors, based on shared content. Thus, this model has a total of 8 dimensions. The results of this model comparison are presented in Table 7.

Table 7.

Application to Empirical Data

	Unidimensional Model	Bifactor Model
number of free parameters, ν	90	103
−2 x log-likelihood	47374.5	44361.0
Akaike Information Criterion (AIC)	47554.5	44567.0
Bayesian Information Criterion (BIC)	47999.9	45076.7
test statistic based on full one- and two-way marginal tables (M2)
M2	8489.4	6541.6
degrees-of-freedom	2430	2417
p	0.0001	0.0001
RMSEA (90% Confidence Interval)	0.049 (0.048,0.050)	0.032 (0.031,0.034)
test statistic based on reduced one- and two-way marginal tables ( $M_2^{\ast }$)
M2	2131.8	199.3
degrees-of-freedom	81	68
p	0.0001	0.0001
RMSEA (90% Confidence Interval)	0.156 (0.150,0.162)	0.043 (0.036,0.050)

Based on the log-likelihood and information criteria, it appears that the bifactor model should be preferred. Because the unidimensional model is nested within the bifactor model, a likelihood ratio test may be performed. Under appropriate conditions, −2 times the difference in the log-likelihoods is asymptotically distributed as a central chi-square variable and provides a test of whether the constraints imposed in the nested model are correct (Haberman, 1977). In this case, the value of the likelihood ratio test statistic is over 3000, while the degrees of freedom (equal to the difference in the number of parameters estimated) is 13. The implication is that the restrictions imposed in going from the bifactor to the unidimensional model (which amount to fixing all group-specific factor slopes to 0) are not plausible. Such an assessment of relative fit has been a common approach to IRT model selection. Among the “appropriate conditions” for using the likelihood ratio test, however, is that the less constrained model be correctly specified (Maydeu-Olivares & Cai, 2006), which is a matter of absolute model fit. Here, we use the fit statistics to evaluate how well this condition is met (i.e., the extent to which the bifactor model fits the data).

We present results for both the original M₂ and alternative $M_2^{\ast }$ statistics. Both the unidimensional and bifactor models are rejected by either statistic. This is not surprising, given the sensitivity of these statistics demonstrated in the simulation study. The RMSEA values provide an assessment of the severity of the model misspecification. Using the RMSEA computed from the original M₂ statistic, both the unidimensional and bifactor model appear to provide reasonably good fit, at least by standards suggested for linear factor analysis and structural equation models (e.g., Browne & Cudeck, 1993). Of course, the applicability of such suggestions to IRT models has not been fully investigated. Perhaps more importantly, however, we observed in the simulation studies that for polytomous data, the original M₂ statistic was often stochastically smaller than its expected distribution, and the discrepancy between the observed and expected distributions increased as the number of response categories increased. For data scored in 5 categories, as we have in this analysis, the alternative $M_2^{\ast }$ statistic, based on the reduction of the marginal tables, was found to have much better calibration. The RMSEA values based on $M_2^{\ast }$ – in contrast to the original M₂ – reveal a substantial difference between the fit of the uni-dimensional and bifactor models. The RMSEA for the unidimensional model is .156 – a value that we consider to be indicative of rather poor fit (unlike the value of .049 obtained from the original M₂). Meanwhile, the RMSEA for the bifactor model is about .043, which is similar to the values observed in the simulation study for the TKL30 bifactor model conditions. We conclude that the 8-dimensional bifactor model fits the smoking data reasonably well. Had we used the original M₂ statistic and the associated RMSEA, we would have perhaps come to the wrong conclusion that the unidimensional model is reasonable for this data set.

5 Discussion

It is a well-known problem in IRT modelling that full-information tests such as the likelihood ratio G² and Pearson’s X² do not follow their asymptotic distributions due to spareness in the full contingency table. As a consequence, tests of absolute model fit based on these statistics may not be trustworthy. Work by Maydeu-Olivares and colleagues has demonstrated that limited-information statistics based on lower-order margins are a promising alternative to full-information statistics. The M₂ family of statistics is a notable example. M₂ is based on the one- and two-way margins of the contingency table, thus less susceptible to sparseness. In previous studies (see, e.g., Maydeu-Olivares & Joe, 2006), M₂ has been shown to have better calibration than the full-information tests. Moreover, it can be more powerful to detect model misspecification.

In this research, we considered the application of limited-information goodness-of-fit testing to hierarchical multidimensional models, which include item bifactor models (Gibbons et al., 2007; Cai, Yang, & Hansen, 2011), testlet response models (Wainer et al., 2007), and two-tier models (Cai, 2010b). Extension of M₂ to these conditions is non-trivial; approximating marginal response pattern probabilities, derivatives, and weights can involve high-dimensional integration. However, for hierarchical IRT models, some of this complexity can be alleviated. We presented an approach to computing M₂ that takes advantage of the constraints that characterise these models in order to greatly improve the computational efficiency. This analytical dimension reduction is closely related to the strategies for estimating hierarchical models (e.g., Gibbons & Hedeker, 1992) that have contributed to the popularity of these models. After deriving the strategy, we demonstrated the improved efficiency through a timing experiment with simulated data.

We have also considered the use of M₂ with polytomous data. Although limited-information testing is based on the premise that lower-order margins are better filled than the full contingency table, we showed that there are circumstances in which even the lower-order margins can become sparse. This is not to suggest that the limited-information statistics would be inferior to the full-information statistics in such cases. After all, sparseness at the lower-order margins guarantees sparseness in higher-order margins and in the full contingency table. However, the sparseness undermines the ability of the limited-information statistics to overcome the very problem they were intended to address. This problem was anticipated by Joe and Maydeu-Olivares (2010) and Maydeu-Olivares et al. (2011), who suggested that the lower-order margins might be further reduced or summarised. Following this suggestion, we have proposed a new $M_2^{\ast }$ statistic for polytomous data and hierarchical item factor models that is based on a collapsing of the first- and second-order marginal tables.

In simulation studies, we demonstrated that the original M₂ statistic performs well with dichotomous data for both the unidimensional and bifactor models. However, as the number of categories increased, it was shown that the original test statistic was stochastically smaller than expected, resulting in Type I error rates that were well below the nominal alpha levels. In contrast, the alternative $M_2^{\ast }$ demonstrated rejection rates very close to the alpha level, even as the number of response categories (and, thus, the size of each marginal contingency table) increases. In addition, the proposed $M_2^{\ast }$ statistic was more sensitive to model misspecification, demonstrating higher empirical rejection rates for the conditions of model misspecification tested. We used the M₂ and $M_2^{\ast }$ statistics to evaluate the fit of two models to an empirical data set, showing how the ability to assess absolute model fit provides a useful complement to tests of relative fit.

In both simulation study and our empirical example, RMSEA values were calculated. In the simulation study, these were found to be rather small by traditional standards (e.g., Browne & Cudeck, 1993) for the conditions tested. This may be indicative of the fact that ignoring “minor” factors (present in the data generating models but absent from the fitted models) constituted only a rather mild level of model misspecification. On the other hand, it is possible that the suggested guidelines for interpreting RMSEA, based on experience fitting models for continuous data, may not apply to IRT models. Given the apparent power of the test statistics to reject misspecified models, further research will be needed in order to develop guidelines for interpreting RMSEA values (and any other indices we might derive from the M₂ statistics). Such guidelines could suggest what RMSEA values might be expected for a “good”-fitting model, as well as the values that would suggest only “acceptable” or even “poor” fit. The analogous guidelines for factor analysis and structural equation models were based largely on experience – developed over time – of fitting many models and observing the values of the fit indices. Our hope is that by developing test statistics for IRT models and by making them available in software, practitioners may begin to accumulate that sort of experience.

Although we have demonstrated the computation of M₂ for hierarchical IRT models, we have not addressed the challenge of obtaining the test statistic for high-dimensional models that do not conform to this structure. The strategy we implemented (analytical dimension reduction) to achieve improved efficiency followed an approach already applied in model estimation. Accordingly, methods for obtaining fit statistics for general multidimensional IRT models could perhaps draw upon the strategies developed for estimating those models (e.g., Cai, 2010a).

Appendix: Computation of Elements of the Weight Matrix

The computation of third and fourth order moments continues to benefit from dimension reduction. Let us consider the third order moment π̇_{3,l,m,j,kl,km,kj} as a case in point. When items l, m, and j all load on the same group-specific dimension s, the marginal probability is simply

$$\begin{array}{l}{\stackrel{.}{\pi }}_{3,l,m,j,k_l,k_m,k_j}=\int \int \underset{l}{Pr}(k_l\mid {\eta }_0,{\eta }_s,\widehat{\mathit{\theta }})\underset{m}{Pr}(k_m\mid {\eta }_0,{\eta }_s,\widehat{\mathit{\theta }})\underset{j}{Pr}(k_j\mid {\eta }_0,{\eta }_s,\widehat{\mathit{\theta }})h({\eta }_s)h({\eta }_0)d{\eta }_{s}d{\eta }_0\\ =\int \left[\int \underset{l}{Pr}(k_l\mid {\eta }_0,{\eta }_s,\widehat{\mathit{\theta }})\underset{m}{Pr}(k_m\mid {\eta }_0,{\eta }_s,\widehat{\mathit{\theta }})\underset{j}{Pr}(k_j\mid {\eta }_0,{\eta }_s,\widehat{\mathit{\theta }})h({\eta }_s)d{\eta }_s\right]h({\eta }_0)d{\eta }_0\\ \approx \sum _{q_0=1}^Q\left[\sum _{q_s=1}^Q\underset{l}{Pr}(k_l\mid X_{q_0},X_{q_s},\widehat{\mathit{\theta }})\underset{m}{Pr}(k_m\mid X_{q_0},X_{q_s},\widehat{\mathit{\theta }})\underset{l}{Pr}(K_j\mid X_{q_0},X_{q_s},\widehat{\mathit{\theta }})W(X_{q_s})\right]W(X_{q_0}).\end{array}$$

When items l, m load on group-specific dimension s and j on group-specific dimension t, the marginal probability becomes

$$\begin{array}{l}{\stackrel{.}{\pi }}_{3,l,m,j,k_l,k_m,k_j}=\int \int \int \underset{l}{Pr}(k_l\mid {\eta }_0,{\eta }_s,\widehat{\mathit{\theta }})\underset{m}{Pr}(k_m\mid {\eta }_0,{\eta }_s,\widehat{\mathit{\theta }})\underset{j}{Pr}(k_j\mid {\eta }_0,{\eta }_t,\widehat{\mathit{\theta }})h({\eta }_s)h({\eta }_t)h({\eta }_0)d{\eta }_{s}d{\eta }_{t}d{\eta }_0\\ =\int \left[\int \underset{l}{Pr}(k_l\mid {\eta }_0,{\eta }_s,\widehat{\mathit{\theta }})\underset{m}{Pr}(k_m\mid {\eta }_0,{\eta }_s,\widehat{\mathit{\theta }})h({\eta }_s)d{\eta }_s\right]\left[\int \underset{j}{Pr}(k_j\mid {\eta }_0,{\eta }_t,\widehat{\mathit{\theta }})h({\eta }_t)d{\eta }_t\right]h({\eta }_0)d{\eta }_0\\ \approx \sum _{q_0=1}^Q\left[\sum _{q_s=1}^Q\underset{l}{Pr}(k_l\mid X_{q_0},X_{q_s},\widehat{\mathit{\theta }})\underset{m}{Pr}(k_m\mid X_{q_0},X_{q_s},\widehat{\mathit{\theta }})W(X_{q_s})\right]\left[\sum _{q_s=1}^Q\underset{j}{Pr}(k_j\mid X_{q_0},X_{q_t},\widehat{\mathit{\theta }})W(X_{q_t})\right]W(X_{q_0}).\end{array}$$

Finally, when items l, m, and j each loads on a different group-specific dimension, say, s, t, and u, the marginal probability π̇_{3,l,m,j,kl,km,kj} becomes

$$\begin{array}{l}\int \left[\int \underset{l}{Pr}(k_l\mid {\eta }_0,{\eta }_s,\widehat{\mathit{\theta }})h({\eta }_s)d{\eta }_s\right]\left[\int \underset{m}{Pr}(k_m\mid {\eta }_0,{\eta }_t,\widehat{\mathit{\theta }})h({\eta }_t)d{\eta }_t\right]\left[\int \underset{j}{Pr}(k_j\mid {\eta }_0,{\eta }_u,\widehat{\mathit{\theta }})h({\eta }_u)d{\eta }_u\right]h({\eta }_0)d{\eta }_0\\ \approx \sum _{q_0=1}^Q\left[\sum _{q_s=1}^Q\underset{l}{Pr}(k_l\mid X_{q_0},X_{q_s},\widehat{\mathit{\theta }})W(X_{q_s})\right]\left[\sum _{q_t=1}^Q\underset{m}{Pr}(k_m\mid X_{q_0},X_{q_t},\widehat{\mathit{\theta }})W(X_{q_t})\right]\times \\ \left[\sum _{q_u=1}^Q\underset{j}{Pr}(k_j\mid X_{q_0},X_{q_u},\widehat{\mathit{\theta }})W(X_{q_u})\right]W(X_{q_0}).\end{array}$$

The case of fourth order moment is completely analogous.