Predicting Glaucomatous Progression in Glaucoma Suspect Eyes Using Relevance Vector Machine Classifiers for Combined Structural and Functional Measurements

Abstract

Purpose.

The goal of this study was to determine if glaucomatous progression in suspect eyes can be predicted from baseline confocal scanning laser ophthalmoscope (CSLO) and standard automated perimetry (SAP) measurements analyzed with relevance vector machine (RVM) classifiers.

Methods.

Two hundred sixty-four eyes of 193 participants were included. All eyes had normal SAP results at baseline with five or more SAP tests over time. Eyes were labeled progressed (n = 47) or stable (n = 217) during follow-up based on SAP Guided Progression Analysis or serial stereophotograph assessment. Baseline CSLO-measured topographic parameters (n = 117) and baseline total deviation values from the 24-2 SAP test-grid (n = 52) were selected from each eye. Ten-fold cross-validation was used to train and test RVMs using the CSLO and SAP features. Receiver operating characteristic (ROC) curve areas were calculated using full and optimized feature sets. ROC curve results from RVM analyses of CSLO, SAP, and CSLO and SAP combined were compared to CSLO and SAP global indices (Glaucoma Probability Score, mean deviation and pattern standard deviation).

Results.

The areas under the ROC curves (AUROCs) for RVMs trained on optimized feature sets of CSLO parameters, SAP parameters, and CSLO and SAP parameters combined were 0.640, 0.762, and 0.805, respectively. AUROCs for CSLO Glaucoma Probability Score, SAP mean deviation (MD), and SAP pattern standard deviation (PSD) were 0.517, 0.513, and 0.620, respectively. No CSLO or SAP global indices discriminated between baseline measurements from progressed and stable eyes better than chance.

Conclusions.

In our sample, RVM analyses of baseline CSLO and SAP measurements could identify eyes that showed future glaucomatous progression with a higher accuracy than the CSLO and SAP global indices. (ClinicalTrials.gov numbers, NCT00221897, NCT00221923.)

Results indicate that relevance vector machine classifiers, trained and tested on baseline HRT and SAP data from glaucoma suspect eyes followed longitudinally, could discriminate between progressing and stable eyes, while baseline HRT and SAP global indices could not.

Introduction

To successfully manage disease in glaucoma patients, the ability to identify patients who are at the greatest risk of progression is desirable. One way to determine this is by studying baseline measurements and demographics from patients that have been followed longitudinally and have either progressed or remained stable over time. This may enable the identification of factors that are the most significant predictors of glaucomatous change.

The recent Ocular Hypertension Treatment Study¹ and the European Glaucoma Prevention Study² have shown that certain risk factors are predictive of the development of glaucoma. In addition, several studies have indicated that optical imaging measurements or visual field measurements are predictive of the development of glaucoma in glaucoma suspect eyes or the progression of glaucoma in glaucomatous eyes.^3–11 Therefore, it is likely that baseline imaging and/or visual field measurements contain information that can increase the accuracy of predicting glaucomatous progression in glaucoma suspect eyes. It can be difficult, however, to combine the large amount of data provided by currently available glaucoma detection techniques in a meaningful way. Machine learning classifiers (MLCs) can accomplish this objectively, without the classification constraints required by many statistical techniques (e.g., linear or hyperbolic decision surfaces).

MLCs have equaled or exceeded the performance of statistical classifiers to discriminate between healthy and glaucomatous eyes using optical imaging (confocal scanning laser ophthalmoscopy [CSLO], scanning laser polarimetry [SLP], optical coherence tomography [OCT])^12–20 and psychophysical techniques (standard automated perimetry [SAP]; short-wavelength automated perimetry [SWAP])^21–31 (see Bowd and Goldbaum³² for a review). In two recent studies, we trained and tested support vector machines (SVMs) and other MLCs on SAP²⁶ and CSLO¹³ data individually and described the ability of the trained MLCs to discriminate glaucomatous from healthy eyes. In a follow-up study, we applied SVM-derived cut-offs for discriminating between healthy and glaucomatous eyes (derived from the prior study) to baseline CSLO measurements from glaucoma suspect (ocular hypertensive or glaucomatous appearing disc with normal SAP results) eyes and determined that when suspect eyes were classified based on glaucoma/no glaucoma cut-offs, results were predictive of the future development of repeatable glaucomatous SAP defects.⁴

Recent methodological advances in MLCs suggest that more accurate prediction of glaucomatous progression likely is possible. Relevance vector machine^33,34 (RVM) is a relatively new MLC that uses Bayesian strategies to provide a probability of group membership during training based on the characteristics of a training set (e.g., of healthy and glaucomatous eyes or progressed and stable eyes). Studies have shown that RVM is able to classify glaucoma eyes as well as or better than other techniques.^35–38

In a previous study, we demonstrated that RVM analysis of structural measurements could predict which glaucoma suspect eyes would develop glaucomatous visual field defects. In the current study, we determine whether RVMs trained and tested on baseline CSLO and/or SAP measurements from known progressed and stable eyes can identify eyes most likely to progress. We predicted that RVMs trained and tested on baseline CSLO and SAP measurements (and combinations of these measurements) would better separate stable eyes from eyes that showed future glaucomatous progression than baseline global indices provided by both technologies.

Methods

Subjects

Subjects included in the current study were participants in the University of California, San Diego (UCSD)-based Diagnostic Innovations in Glaucoma Study (DIGS) and African Descent and Glaucoma Evaluation Study (ADAGES, which also includes participants from University of Alabama, Birmingham [UAB] and New York Eye and Ear Infirmary [NYEE]). Two hundred sixty-four eyes from 193 individuals were studied based on the inclusion criteria that all eyes have five or more reliable SAP 24-2 Swedish Interactive Threshold Algorithm (SITA) tests and be glaucoma suspects at the time of the baseline examination. That is, they were under the care of a glaucoma specialist and had some combination of a suspicious looking optic nerve/retinal nerve fiber layer by photography or examination, suspicious or abnormal visual field (not repeatable and defined as pattern standard deviation or Glaucoma Hemifield Test outside normal limits), or a history of elevated intraocular pressure in one or both eyes.

Each study participant underwent a comprehensive ophthalmologic evaluation including review of medical history, best-corrected visual acuity testing, slit-lamp biomicroscopy, intraocular pressure measurement with Goldmann applanation tonometry, gonioscopy, dilated fundus examination with a 78 diopter (D) lens, simultaneous stereoscopic optic disc photography (TRC-SS, Topcon Instruments Corp. of America, Paramus, NJ), and SAP using the 24-2 SITA test strategy (Humphrey Field Analyzer II, Carl Zeiss Meditec, Dublin, CA). To be included in the study, participants had to have a best-corrected acuity better than or equal to 20/40, spherical refraction within ±5.0 D and cylinder correction within ±3.0 D at baseline, and open angles on gonioscopy. Eyes with nonglaucomatous optic neuropathy, uveitis, or coexisting retinal disease that could affect visual fields were excluded.

For labeling eyes during classifier training, eyes were divided into two groups: progressed and nonprogressed (i.e., stable). Eyes were defined as progressed (n = 47) if they showed likely visual field progression in sequential fields based on the SAP Guided Progression Analysis (GPA) or had progressive GON (PGON) based on assessment of serial stereoscopic optic disc photographs, during follow-up. GPA indicates change from baseline by evaluating all test points and indicates “likely” progression for the full field if change (greater than the variability observed in two baseline measurements) in three of the same points, is repeatable in three consecutive exams.³⁹ For our purposes, PGON was defined as increased neuroretinal rim thinning or RNFL defect size, or the appearance of a new RNFL defect. Photographic evidence of PGON was based on masked (patient name, diagnosis, and temporal order of photographs) comparison between baseline and follow-up photographs by two UCSD Hamilton Glaucoma Center-based Imaging Data Evaluation and Analysis (IDEA) Center certified observers. In the case of a disagreement, a third observer served as an adjudicator. Of the 47 progressed eyes, 18 had PGON only, 23 progressed by GPA only, and 6 progressed by both assessment techniques. This level of agreement between progression detection techniques is similar to that observed in other studies (e.g., Kishor K, et al. IOVS 2009; 50: ARVO E-Abstract 2241). Stable eyes (n = 217) were stable by both assessment methods for a minimum of 4 years.

This research followed the tenets of the Declaration of Helsinki, Health Insurance Portability and Accountability Act guidelines, and the UCSD, UAB, and NYEE Human Research Protection Programs approved all methodology.

Confocal Scanning Laser Ophthalmoscopy

Study participants underwent ocular imaging with the commercially available HRT II (software version 3.0, Heidelberg Engineering, Heidelberg, Germany). The HRT is a confocal scanning laser ophthalmoscope that provides software-generated measurements describing the topography of the surface of the optic disc and adjacent parapapillary retina. One hundred seventeen software-generated parameters were used in the current analysis. These included global and sectoral (superior temporal, temporal, inferior temporal, inferior nasal, nasal, and superior nasal) measurements of all available parameters as well as global measurements of Mean Depth of Reference, Vertical CDR, Horizontal CDR, Linear CDR, and Reference Height. We decided not to limit this large number of parameters in order to permit the MLCs to empirically select the most relevant parameters, rather than to preselect them based on presumptions regarding independence.

For HRT, good quality images were those with mean pixel height standard deviation (MPHSD) <50 μm and with even image exposure and good centering as determined by UCSD IDEA Center personnel. Seven of 271 (2.6%) images included had a MPHSD between 40 and 50 μm and approximately 75% of images had an image MPHSD ≤18 μm.

Standard Automated Perimetry

Reliable SAP (using SITA) total deviation (TD) values at each of the 52 test points (excluding those representing the blind spot) that compose the 24-2 test pattern were obtained from each participant within 6 months of HRT II imaging. Reliability was defined as false positives, fixation losses, and false negatives ≤ 25%. Visual fields had no observable testing artifacts as determined by UCSD Hamilton Glaucoma Center-based Visual Field Assessment Center (VisFACT) personnel. TD values were used because pilot analyses suggested superior performance of TD compared to thresholds and pattern deviation results.

Relevance Vector Machine

The RVM learning classifier is a Bayesian model which provides probabilistic predictions (e.g., probability of future progression based on the training examples) through Bayesian inference during the training process.^33,34 RVM is considered a sparse classifier because its decision function depends on fewer input data (i.e., is more sparse) than SVM classifiers, which minimize the training error under the constraint of maximum smoothness, requiring more decision points.³³ A sparser classifier decreases data-specific over-fitting, permitting the classifier's results to be more generalizable to other independent data sets. Because RVM analysis incorporates probability, its output is the probability of class membership. This provides a conditional distribution of input parameters that accounts for uncertainty in the prediction.⁴⁰

The RVM was implemented using the SparseBayes V1.0 algorithm (Microsoft Research, Cambridge, UK) for MATLAB (The Mathworks, Natick, MA). The kernel width was optimized by a grid search with width = 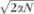, where α = 0.4, 0.5, 0.6, 0.8, 1.0, 1.5, 2.0, 2.5, and 3.0; N is the number of input parameters (i.e., variables). The α that yielded the largest areas under the Receiver operating characteristic (ROC) curve (AUROC) was chosen for final analysis. We applied feature selection by backward elimination (see section on data optimization) to rank the parameters by their contribution to the classification decision and to improve classifier performance by eliminating the least useful parameters.

Analyses

First, the RVM classifiers were trained and tested separately on the 117-dimension HRT data and the 52-dimension SAP TD data from progressed and stable eyes. Next, RVMs were trained and tested on HRT data and SAP TD data combined, resulting in 169 input dimensions (117 HRT inputs + 52 SAP inputs). Performance of the RVM classifiers trained on HRT data, SAP data, and combined data were compared to the HRT Glaucoma Probability Score (GPS) and to SAP mean deviation (MD) and pattern standard deviation (PSD) values, in order to compare RVM performance to the performance of currently available (i.e., standard) global indices from HRT and SAP. Finally, these results were compared to RVM results based on optimized (by backward elimination) HRT, SAP, and combined data sets.

For each eye, RVM provided a conditional probability of progression as output, p(progression | HRT and/or SAP parameters), which was used for estimating the diagnostic accuracy of the RVM for identifying future glaucomatous progression. AUROCs for classifying eyes as progressed or stable from baseline measurements were determined for each RVM classifier and each global index from HRT and SAP using a nonparametric technique for clustered data (because both eyes of some participants were included).^41,42 This technique also was used to identify significant differences in AUROCs. Significant differences between AUROCs and chance discrimination (i.e., AUROC = 0.50) were indicated when the 95% confidence interval (CI) of an AUROC did not include 0.50.⁴³

Training and Testing Machine Learning Classifiers

Tenfold cross-validation was used to train and test RVM classifiers to avoid training and testing on the same data. First, the full complement of progressed (n = 47) and stable (n = 217) eyes was randomly divided into 10 approximately equal, exhaustive, and mutually exclusive subsets (subsets of 26 or 27 eyes). Next, classifiers were trained on nine subsets and subsequently tested on the 10th subset. This sequence was repeated 10 times, with each subset serving as the test set one time, so that each tested eye was never part of its training set and was tested only once. The test results from all eyes were then used to plot the bias-corrected ROC curves. Sensitivities for detecting progressors from baseline examinations at 75% and 85% specificities, arbitrarily chosen to represent moderate and high specificity, respectively, also were reported.

Data Set Optimization

Because the dimensionality of the data sets (number of parameters) is large relative to the size of the data sets (number of study eyes), we used backward elimination to reduce the data dimension to minimize the inclusion of irrelevant parameters in the solution set⁴⁰ for all RVM analyses. We have found backward elimination to be a slight but consistent improvement over forward selection for optimal feature selection.^13,26,35 Backward elimination started with the full-dimensional feature set and iteratively deleted the least contributing parameter until performance peaked and began to decline (i.e., the number of features that resulted in the maximum AUROC before additional features resulted in AUROC decline were included).

Similar to using 10-fold cross-validation to minimize bias in the testing and training of the full-dimension RVM, we used fivefold cross-validation to minimize bias in the test sets used during the process of optimizing the RVM feature sets. This technique for optimization has been discussed in greater detail previously.²⁰

Several optimized feature sets were investigated for RVM using each data set tested (HRT only, SAP only, and HRT+SAP combined). We report here results from the optimized feature set for each data set that resulted in the largest AUROC only, although differences in AUROC were not always significant among sets.

Results

Demographic descriptors of study participants and baseline global HRT (i.e., GPS) and SAP (i.e., MD and PSD) indices are shown in Table 1. Only baseline age and SAP PSD were significantly different (with α = 0.05) between progressed and stable groups. Reported P values are for two-tailed tests. Baseline RVM outputs for all RVMs investigated are shown in Table 2. There was a significant difference in output between progressed and stable eyes for all RVMs (all P ≤ 0.002) except HRT trained and tested on the full-dimensional (117 features) data (P = 0.157). Because we expected baseline values to be higher in progressed eyes, reported P values are for one-tailed tests.

Table 1.

Demographic Data and HRT and SAP Global Indices at Baseline and Average Follow-Up Duration for Progressed and Stable Eyes

	Progressed Eyes (SD) (n = 47)	Stable Eyes (SD) (n = 217)	P
Age at baseline (y)	60.23 (10.9)	56.2 (13.0)	0.028
Percent female	69	58	0.272*
HRT GPS at baseline	0.508 (0.321)	0.470 (0.304)	0.462
SAP MD at baseline (dB)	−0.62 (1.30)	−0.58 (1.39)	0.850
SAP PSD at baseline (dB)	1.80 (0.57)	1.61 (0.48)	0.031
Average follow-up duration (y)	5.35 (1.90)	5.10 (1.09)	0.378

^* Fisher's Exact Test.

Table 2.

RVM Output (i.e., Probability of Progression) Measured at Baseline between Progressed and Stable Eyes. RVM Classifier Output Indicates Assigned Probability of Progression

Input Parameters	Progressed Eyes (SD) (n = 47)	Stable Eyes (SD) (n = 217)	P
HRT (117 features)	0.187 (0.078)	0.174 (0.070)	0.157
Optimized HRT (8 features)	0.214 (0.092)	0.169 (0.083)	0.001
SAP TD (52 features)	0.230 (0.166)	0.150 (0.153)	0.002
Optimized SAP TD (23 features)	0.328 (0.242)	0.141 (0.164)	<0.0001
HRT and SAP TD (169 features)	0.150 (0.166)	0.244 (0.209)	0.002
Optimized HRT and SAP TD (28 features)	0.372 (0.249)	0.130 (0.164)	<0.0001

Classification Results

AUROCs (95% CI) for discriminating between progressed and stable eyes for baseline HRT GPS, SAP MD, and SAP PSD values were 0.517 (0.349, 0.685), 0.513 (0.359, 0.668), and 0.620 (0.475, 0.766), respectively. None of these AUROCs were significantly different from 0.5 (i.e., none of these parameters discriminated between baseline measurements from progressed and stable eyes any better than chance).

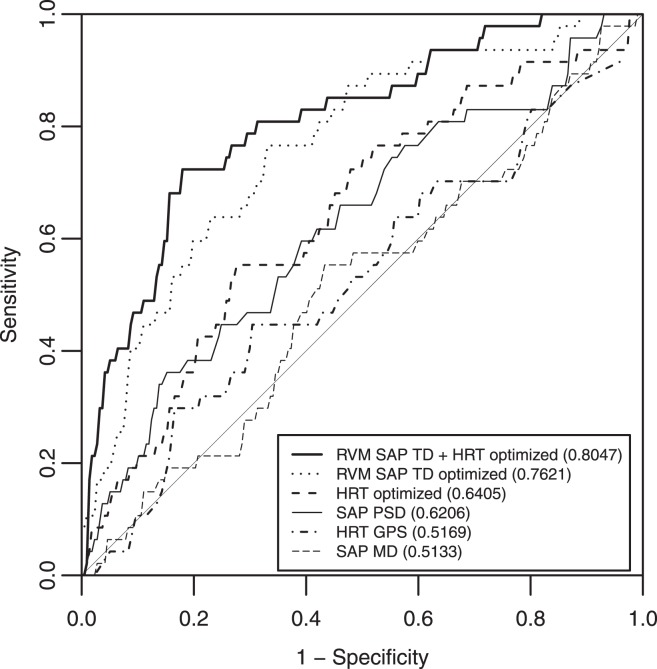
Because AUROCs for RVMs using optimized HRT/SAP data tend to be higher than nonoptimized AUROCs (if not always significantly so),^13,20,26,35 nonoptimized results are shown in Table 3 only, while optimized results are reported both in the table and in the following text. The AUROC for RVM using optimized HRT data alone (8 features) was 0.640 (0.524, 0.757). The AUROC for RVMs using optimized SAP TD alone (23 features) and optimized HRT and SAP TD combined (28 features; 15 HRT features and 13 VF features) were 0.762 (0.646, 0.878) and 0.805 (0.696, 0.913), respectively. Both of these values were significantly larger than the AUROCs for HRT GPS and SAP MD. In addition, the AUROC for RVM using optimized HRT and SAP TD combined was greater than that for RVM using optimized HRT data alone (all P < 0.05). AUROCs for all of the RVM results described above were significantly larger than 0.5 (i.e., were significantly better than chance) and are shown in Figure 1. Sensitivities at fixed specificities of 0.75 and 0.85 are shown in Table 3 and are somewhat higher when HRT and SAP data are combined and optimized.

Table 3.

AUROCs and Sensitivities at fixed Specificities for Classifying Eyes as Progressed or Stable at Baseline for All Techniques/Parameters

Technique	AUROC (95% CI)	Sensitivity at ≈0.75 Specificity	Sensitivity at ≈0.85 Specificity
HRT GPS	0.517 (0.349–0.685)	0.319	0.213
SAP MD	0.513 (0.359–0.668)	0.213	0.192
SAP PSD	0.620 (0.475–0.766)	0.447	0.340
RVM using all HRT parameters (117 features)	0.544 (0.395–0.694)	0.383	0.255
RVM using optimized set of HRT parameters (8 features)	0.640 (0.524–0.757)	0.447	0.255
RVM using all SAP TD parameters (52 features)	0.669 (0.528–0.808)	0.489	0.277
RVM using optimized set of SAP TD parameters (23 features)	0.762 (0.646–0.878)	0.638	0.468
RVM using all HRT and SAP TD parameters (169 features)	0.644 (0.528–0.761)	0.404	0.362
RVM using optimized set of HRT and SAP TD parameters (28 features)	0.805 (0.696–0.913)	0.723	0.596

Figure 1.

ROC curves for global HRT and SAP parameters and optimized RVM results. AUROCs are provided in the Legend.

Because the probability of progression in glaucoma is generally quite low, we also reported and compared the partial AUROCs (pAUROCs) for moderate to high specificities greater than 0.75 and 0.85 (i.e., from 0.75 to 1.0 specificity and from 0.85 to 1.0 specificity). It should be noted that the maximum possible areas for these two curves are 0.25 and 0.15, respectively. No significant differences among pAUROCs were observed with α = 0.05,⁴⁴ likely because of the limited range of AUROC values in these small segments of the curves. However, pAUROCs for both RVM using optimized SAP TD values and RVM using optimized HRT and SAP TD parameters combined performed better than chance when specificity was >0.75 (pAUROC for chance = 0.03125, in this case). No SAP or HRT global indices or RVM models performed better than chance when specificity was > 0.85 (pAUROC for chance = 0.01125). These results are shown in Table 4.

Table 4.

pAUROCs for Classifying Eyes as Progressed or Stable at Baseline for All Techniques/Parameters when pAUROC > 0.75 Specificity and pAUROC > 0.85 Specificity

Technique	pAUROC > 0.75 Specificity (95% CI)	pAUROC > 0.85 Specificity (95% CI)
HRT GPS	0.033 (0.000–0.091)	0.014 (0.000–0.045)
SAP MD	0.031 (0.000–0.084)	0.009 (0.000–0.036)
SAP PSD	0.062 (0.001–0.124)	0.025 (0.000–0.064)
RVM using all HRT parameters (117 features)	0.048 (0.001–0.106)	0.013 (0.000–0.049)
RVM using optimized set of HRT parameters (8 features)	0.060 (0.001–0.125)	0.022 (0.000–0.059)
RVM using all SAP TD parameters (52 features)	0.062 (0.000–0.127)	0.020 (0.000–0.060)
RVM using optimized set of SAP TD parameters (23 features)	0.101 (0.033–0.169)	0.044 (0.000–0.091)
RVM using all HRT and SAP TD parameters (169 features)	0.065 (0.003–0.125)	0.026 (0.000–0.062)
RVM using optimized set of HRT and SAP TD parameters (28 features)	0.126 (0.056–0.196)	0.055 (0.003–0.108)

Probabilistic Results

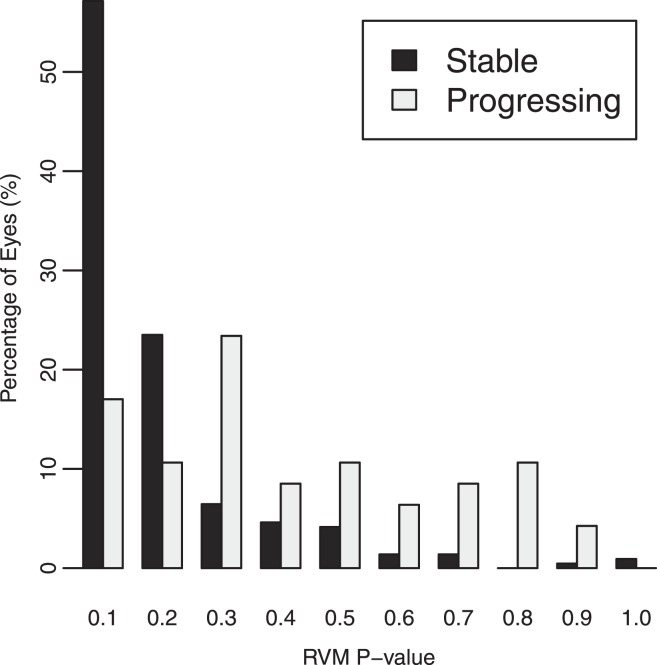
RVM output is in the form of a probability of an eye belonging to the progressing group of the training set. The nominally best-performing (by largest AUROC area) RVM, an optimized combination of HRT and SAP measurements, provided a mean probability of progression of 0.369 (SD = 0.251) for progressing eyes and 0.132 (SD = 0.165) for stable eyes (P < 0.001). Figure 2 shows the number of progressed and stable eyes that fell into each 10% probability-of-progression bin based on RVM output. Using a probability-of-progression cut-off of 0.50 (selected arbitrarily), baseline measurements from 14 of 47 progressing eyes were correctly assigned a probability of progressing (sensitivity = 0.30) and baseline measurements from 9 of 217 stable eyes were incorrectly assigned a probability of progressing (specificity = 0.96). Although the AUROC for this analysis was 0.805, there was a considerable overlap in RVM output between progressing and stable eyes. In particular, 70% of progressed eyes were classified as stable at baseline, when using a cut-off of 0.50. An RVM progression/stable cut-off of 0.50 is not necessarily ideal because the criterion for a meaningful cut-off is dependent on the desired sensitivity and specificity pairing. When we set the specificity to an acceptable 0.85 in stable eyes (RVM cut-off = 0.274) the sensitivity of RVM output increased to 0.58, resulting in a positive likelihood ratio of 3.66 (95% CI = 2.45 to 5.73).

Figure 2.

Percentage of progressed or stable eyes assigned by relevance vector machine classifier (RVM) to each 10% probability bin. Thirty percent of progressed eyes and 4% of stable eyes were assigned a probability at or over 0.50 (sensitivity was 0.30 and specificity was 0.96). When the RVM cut-off P value was set to result in a specificity of 0.85 (RVM P value cut-off = 0.274), sensitivity increased to 0.58.

Discussion

Results from the current study indicate that RVM analysis of baseline HRT and SAP measurements from glaucoma suspect eyes can predict which eyes will and will not show glaucomatous progression in the future, while baseline global indices from HRT and SAP cannot. Combining HRT and SAP measurements improved the discrimination somewhat. These results indicate that there is valuable information available in baseline HRT and SAP output that is not apparent to current algorithms.

A previous study suggested that MLC-based analyses of HRT data could discriminate between baseline measurements from progressing and stable eyes.⁴ This earlier study applied MLC cut-offs that were most effective at classifying healthy and glaucoma eyes (i.e., eyes with repeatable SAP defects) to the baseline measurements from longitudinal series. We believe the current study provides stronger evidence of the ability of MLCs to predict progression because cut-offs were derived from baseline measurements in glaucoma suspect eyes.

In the current study, combining HRT and SAP information resulted in a general trend of increased performance for discriminating between progressed and stable eyes. However, significant improvements over the best results using HRT or SAP data alone were not always observed. For instance, the AUROC for optimized RVM for HRT and SAP TD combined was not significantly greater than the AUROC for optimized RVM for SAP TD alone (P > 0.10). Accuracy of MLC analyses of HRT and SAP parameters improved upon standard parameters for each technique. These results agree with those of studies using OCT,¹⁵ SAP,²⁶ CSLO,¹³ and SLP³⁵ to discriminate between healthy and glaucomatous eyes and indicate that RVM analyses show promise for predicting progression from complex imaging and visual field data.

RVM techniques provide intuitive probability of group membership as output. Output from RVMs indicated that the majority of progressed eyes were assigned a higher probability of belonging to the progressed training-group. However, the RVM probabilities derived for progressed and stable eyes were not maximally different. This likely is because baseline HRT and SAP measurements from progressed and stable eyes were not dramatically different (evidenced by similar HRT GPS and SAP MD between groups, Table 1). We examined the baseline HRT and SAP printouts from two outlier eyes with a high probability of progression (≥90%, see Fig. 2) that remained stable during follow-up. In both cases HRT and SAP measurements were unremarkable. It is possible, if not likely, that the RVM is detecting complex combinations of parameters that suggest progression in other eyes (i.e., in the training set of progressing eyes) that did not apply to these particular test eyes.

Other classification techniques have successfully found information in baseline examinations that enables the identification of eyes that are likely to progress. Recently, Demirel and colleagues⁵ used classification and regression tree analysis (CART, a form of machine learning classification) to determine if baseline visual fields were predictive of future glaucomatous progression (defined based on assessment of serial optic disc stereophotographs) in high-risk ocular hypertensives and early glaucoma patients. Input to the training and test data sets included age-corrected SAP thresholds measured at the test points described in the current study, baseline age, baseline intraocular pressure, and central corneal thickness. Measurements from the worst eye of 168 individuals was used for CART modeling (CART cannot control for the correlated data from both eyes of an individual, inputs must be independent). Of these 168 eyes, 67 showed progression and 101 remained stable. Results from the two groups of eyes indicated that CART models could be predictive of glaucomatous progression with a sensitivity of 65% and a specificity of 87%. Only thresholds at SAP test points were included as branches in the best models (i.e., other risk factors were not as predictive), and the model presented had only six branches (indicating significant optimization of the number of test-points used for classification). The same models tested on measurements from 100 healthy eyes showed a highest specificity of 69%. Our best RVM model, using an optimized combination of HRT and SAP parameters, showed a sensitivity of 51% at a specificity of 87%. In order to reach a sensitivity of 65%, an additional 6 of 47 progressed eyes would have needed to be identified. Of the six SAP test points included in the best performing CART models described by Demirel et al.,⁵ three were include in both our optimized SAP TD and optimized HRT and SAP TD feature sets.

In a somewhat related study because it used a machine-learning classifier-like dimension reduction technique, Essock and colleagues⁶ showed that wavelet-Fourier analysis (WFA) of preconversion, baseline SLP (fixed corneal-compensator GDx) RNFL thickness measurements in ocular hypertensive eyes can detect abnormalities that predict conversion to glaucoma. Briefly, first WFA extracts features that describe the shape of the RNFL thickness profile in terms of scaled components. Next, principal component analysis is employed to reduce the dimensionality of the data by isolating and/or combining components. Finally, linear discriminant functions are created that best separate the resulting components into two categories (in this case, convert and stable eyes from the measurements obtained before conversion). In the described study, AUROCS for detecting future conversion from preconversion data were 0.73 at an average of 2 years prior to conversion and 0.77 at approximately 6 months prior to conversion. In the current study, optimized RVM analyses of combined HRT and SAP TD results obtained at baseline resulted in an AUROC of 0.805 at an average of 5 years prior to progression.

Other recent studies have assessed the ability of baseline imaging and visual field testing to predict future glaucomatous change. In general, results indicate that standard imaging parameters and stereophotograph assessment^2,3,10,45,46 and psychophysical tests^8,47 are predictive of the conversion to, or the progression of, primary open angle glaucoma. The results of the current study, therefore, are not surprising. However, in our sample, HRT GPS, SAP MD, and SAP PSD at baseline were not predictive of progression (but see Alencar et al.³), while RVM analyses of full-dimensional HRT and SAP measurements generally were. We believe this is evidence for the usefulness of MLC analyses as techniques for combining complex data to predict (and likely identify) glaucomatous change.

The present study has possible limitations. First, AUROC results from our MLC techniques might be somewhat overestimated because we used cross-validation instead of truly independent training and test sets. Although RVMs were trained and tested on different data, each data set was generated from the same pool. This fact might exaggerate somewhat the differences in classification ability between MLCs and global HRT and SAP indices. In addition, we did not consider differences in IOP lowering treatments during follow-up between the progressed and stable groups. This analysis would be difficult to complete because progressed and stable groups were eye specific, rather than participant specific. Because of this, it is likely that in some cases, both a progressed and a stable eye from the same individual received the same treatment. Next, studies have suggested limited agreement between observers when detecting glaucomatous progression by stereophotograph assessment,^48,49 possibly resulting in an over- or under-estimation of the number of progressors identified using this technique. Recently we have reported moderate agreement among our trained observers (κ = 0.57),⁵⁰ and in the current study, stereophotographs that lacked agreement between the initial two observers required adjudication by a third, likely decreasing the uncertainty of the technique. Further, uncertainty is minimized in SAP-defined progression by using GPA software that requires consecutive change compared to baseline.

Finally, it is possible that baseline SAP measurements might provide better predictions of SAP-detected progression, while baseline HRT measurements might provide better predictions of stereophotograph-detected progression. To investigate this possibility, we conducted post hoc analyses in which AUROCs were calculated independently for eyes progressed by SAP GPA only (n = 23) and eyes progressed by stereophotograph assessment only (n = 18). In both cases, the stable group remained the same. For eyes progressed by SAP only; RVM trained on optimized SAP TD data resulted in an AUROC of 0.777 (0.649, 0.904), RVM trained on optimized HRT data resulted in an AUROC of 0.594 (0.462, 0.725), and RVM trained on optimized HRT and SAP TD data combined resulted in an AUROC of 0.789 (0.681, 0.897). For eyes progressed by stereophotograph assessment, these values were 0.701 (0.548, 0.864) for optimized SAP TD, 0.630 (0.470, 0.790) for optimized HRT and 0.755 (0.608, 0.91) for optimized combined data. It appears then, that RVM trained on SAP data is a slightly better predictor of progression defined by SAP GPA as well as progression defined by stereophotograph assessment, although pairs of AUROCs were not significantly different in any case (all P ≥ 0.05). An optimized RVM combining both SAP TD and HRT measurements was slightly (although not significantly) better at predicting progression defined using both progression detection criteria. It is interesting that eyes that progressed by photograph assessment only were somewhat better identified by RVM analysis of baseline SAP TD values than by RVM analysis of baseline HRT parameters. It is possible that this represents a greater variability in baseline HRT measurements compared to SAP measurements. Alternately, it is possible that the variability of both measurements was similar, but there was a greater overlap of HRT measurements between nonprogressing eyes and eyes progressing by both SAP GPA and/or stereophotograph assessment.

To date, methods for predicting glaucomatous progression from baseline visual field and optic disc topography generally have relied on the isolated assessment of individual software generated-parameters from each technique independently. Results from the current study suggest that assessing baseline structural and functional measurements combined, using MLC analyses, can identify more informative parameters to successfully predict future progression. Combining known risk factors and information from additional tests may improve this prediction.