Effects of sutures and fontanels on MEG and EEG source analysis in a realistic infant head model

Abstract

In infants, the fontanels and sutures as well as conductivity of the skull influence the volume currents accompanying primary currents generated by active neurons and thus the associated electroencephalography (EEG) and magnetoencephalography (MEG) signals. We used a finite element method (FEM) to construct a realistic model of the head of an infant based on MRI images. Using this model, we investigated the effects of the fontanels, sutures and skull conductivity on forward and inverse EEG and MEG source analysis. Simulation results show that MEG is better suited than EEG to study early brain development because it is much less sensitive than EEG to distortions of the volume current caused by the fontanels and sutures and to inaccurate estimates of skull conductivity. Best results will be achieved when MEG and EEG are used in combination.

Introduction

We now have sophisticated approaches for estimating the location of active tissues in the brain and temporal course of activity at the source level in each active region on the basis of extracranial MEG and EEG measurements (Baillet et al., 2001; Dale and Sereno, 1993; Dale et al., 2000; Hämäläinen, 1995; Hämäläinen and Ilmoniemi, 1994; Lucka et al., 2012; Ou et al., 2009a; Uutela et al., 1998, 1999). Due to the ill-posed nature of the electromagnetic source estimation problem, each of these methods constrains the current sources using anatomical and physiological information and regularizes the solution to mitigate the effects of measurement noise. However, in all of these inverse approaches, a biophysical forward model is needed to relate the neural current sources to the MEG/EEG measurements. The overall task is then to search for the best estimates for the neural currents given the measurements of signals of interest, estimates of noise, selected source constraints, regularization, and the forward model. The accuracy of the solution, therefore, depends on an accurate forward model.

The required forward model accuracy can be achieved by using individual anatomical information based on MRI to define the actual conductivity geometry of the head, combined with numerical solvers which allow the use of these data in the computation of the MEG/EEG forward solutions (Dale et al., 1999; Fischl et al., 1999a,b, 2001a,b, 2002; Hämäläinen and Hari, 2002; Hämäläinen and Sarvas, 1987, 1989; Hämäläinen et al., 1993; Wolters et al., 2006, 2007a,b). The most advanced inverse models for interpreting MEG and EEG from the neo-cortex incorporate the exact geometry of the scalp, skull, CSF, and brain into the forward model and constrain the sources to lie in the gray matter, perpendicular to the cortical surface. It is furthermore possible to functionally constrain the inverse solutions by incorporating the map of active brain regions estimated from fMRI (Dale and Sereno, 1993; Dale et al., 2000; Ou et al., 2009b). These models have been used to identify multiple active regions in the brain, to estimate the time course of activity in each region, and to assess functional connectivity between the regions.

An accurate forward model is important for interpreting MEG/EEG signals not only from adults, but also from infants and children as the interest in human brain development continues to grow. Somatosensory activity at the early age has been investigated with ERP (EEG) methods (Karniski, 1992; Karniski et al., 1992; Taylor et al., 1996; Xiang et al., 2003). Infant language development has also been studied with ERPs (Buiatti et al., 2009; Cohen et al., 2000; Dehaene-Lambertz et al., 2006). MEG has become a new modality of studying infant brain activity in infant speech perception (Imada et al., 2006; Kujala et al., 2004), sensory perception during sleep (Kakigi et al., 2003), somatosensory development (Pihko et al., 2009), vision (Haddad et al., 2006), and auditory response as an immature brain marker (Wakai et al., 2007). MEG instruments optimized for the pediatric population are beginning to be developed (e.g. Okada et al., 2006).

The models for the newborns, infants and preschool children are not simple extensions of the models for adults because of the characteristic features of the human skull and brain during the early development. The cranial bones of the human skull are unfused and separated by fontanels and sutures for at least several months after full-term birth to accommodate birth and the growth of the brain. The fontanels are present at the midline junctions of the bregma and lambda. They are small during the delivery, but become larger in the first several months, up to even 3–4 cm along the coronal suture, and then eventually close. The unclosed sutures can be quite wide near the fontanels. The mean width of the coronal and lambdoidal sutures at their midpositions is 3–4 mm for infants between 0 and 60 days after birth (Erasmie and Ringertz, 1976). The sutures may not close for several years in healthy children (Hansman, 1966). In children with CNS pathology, there is a wide variation in size of the fontanels, width of the sutures, and thickness of the skull. In patients with craniostenosis (also called craniosynostosis), the cranial bones fuse prematurely. In the opposite extreme, for example in children with hydrocephalus, the width of the sutures may change during the development of the disease and become as wide as 10 mm or more (Erasmie and Ringertz, 1976). Recently, the effect of the fontanel on EEG source analysis was investigated using a three-compartment (the scalp, the skull, and the brain) volume-conductor model (Roche-Labarbe et al., 2008). The numerical solution was computed with the boundary element method (BEM). The fontanel was modeled with a thinner zone in the skull and it was found that the fontanel causes a dipole shift towards the modeled skull defect. Experimental studies show that holes in the skull, mimicking the fontanel, do not significantly affect MEG signals when they are small (Barth et al., 1986; Okada et al., 1999). However, the effect may depend on the size of the fontanel. The inverse solutions for MEG are only weakly affected by inaccurate modeling of these layers (Hämäläinen and Sarvas, 1987, 1988, 1989). However, we still do not have realistic head models of infants to assess the skull effect on MEG in human infants.

The conductivity of the skull also decreases and its thickness increases with age (Gibson et al., 2000). The thickness of the skull increases from 1 to 2 mm on the dorsal surface at term to several millimeters during the early adulthood (Hansman, 1966). The skull conductivity decreases as the external and internal hard layers become thicker and the more conductive middle layer becomes relatively thin with age. In adults the conductivity can be estimated with electrical impedance tomography (Goncalves et al., 2003). The measurements show a large variability in conductivity with a standard deviation of 48% of the mean. Therefore, it is likely that the skull conductivity is also highly variable in infants. Modeling studies have shown that the skull thickness and conductivity are quite important for correctly predicting EEG signals (Dannhauer et al., 2011; Hallez et al., 2005; Hämäläinen and Sarvas, 1987; Hämäläinen et al., 1993; Marin et al., 1998; Vallaghe and Clerc, 2009; van den Broek et al., 1998; Wolters et al., 2006). Distortion of EEG signals by a hole in the skull has been also demonstrated experimentally in the swine with a large brain (Flemming et al., 2005).

To the best of our knowledge, the effects of the infant skull on both MEG and EEG have not yet been investigated with identical realistic forward models. There are several advanced numerical methods to model the head of an infant, i.e., the finite difference method (FDM) (Hallez et al., 2005), the finite volume method (FVM) (Cook and Koles, 2006), and the finite element method (FEM) (Awada et al., 1997; Buchner et al., 1997; Lew et al., 2009; Marin et al., 1998; Thevenet et al., 1991; van den Broek et al., 1998; Wolters et al., 2007a,b). In this study, we used a high-resolution geometry-adapted five-compartment FEM model of the head of an infant, since it achieves high accuracies in multicompartment head volume conductor modeling studies (Lew et al., 2009; Vorwerk, 2011; Wolters et al., 2007a,b). Employing an isoparametric FEM in this geometry, the influences of the fontanels and sutures in the infant skull as well as its conductivity on the MEG and EEG source analysis were characterized using forward and inverse simulations.

Materials and methods

MRI acquisition

A female neonate with uneventful pre- and perinatal circumstances was imaged at 3 days of life on a Siemens Trio-Tim 1.5 T MRI scanner using a standard 8-channel head coil. T1 weighted MPRAGE images (Fig. 1a) were collected with the following parameters: Field of view = 200.000, TR/TE = 2530.00/3.39 ms, flip angle = 7.00°, matrix size = 200 × 200, slice thickness = 1.0 mm, number of slices = 176, and in sagittal orientation. The brain of the infant was found clinically normal by a pediatric neuroradiologist and the patient showed no persistent neurological symptoms upon discharge. In addition, a large subcutaneous fluid collection containing a small amount of blood product was observed at the vertex, most prominently in the left parietal region.

Fig. 1.

(a). MR images of the infant in sagittal, coronal, and axial slices. (b) Segmentation of different tissue types featuring sutures and fontanels (in blue) on the same cross sections as in (a). (c) The skull compartment with sutures and fontanels viewed from the front, right, and back. Skull is shown in red, sutures and fontanels in white.

Segmentation

When the MRIs of neonates are processed, manual segmentation is usually employed because automated segmentation often cannot detect accurate structural borders in the neonatal brain due to incomplete myelination, low contrast, low signal to noise ratio, motion effects, etc. Therefore, we segmented the skull, scalp, cerebrospinal fluid, and gray and white matter manually in Freeview, a volume and surface visualization tool within the FreeSurfer software application (Dale et al., 1999). The segmentation was carried out in the coronal, axial, and sagittal planes concurrently, based on detailed neuroanatomical knowledge. The anterior fontanel was identified from a visible discontinuation of the skull in the coronal, sagittal, and axial planes. The accuracy of the segmentation was confirmed by expert review of every segmented image. Other fontanels were not easily identifiable, and were, therefore, not taken into account in the MRI based segmentation of the skull. Instead, the posterior fontanel, the sphenoidal fontanel, and the mastoid fontanel were segmented based on the knowledge of skull geometry from an infant skull atlas. In addition, the sagittal suture, the coronal suture, the lambdoidal suture, and the squamosal suture were also manually segmented based on the segmented fontanels and the atlas (Fig. 1b). The fontanels and sutures divide the skull into the frontal bone, the parietal bone, and the occipital bone (Fig. 1c).

As described above, it is, indeed, difficult to identify the fontanels in T1-weighted MRIs. We did our best to segment the anterior fontanel, which is the largest among the fontanels. All other fontanels and sutures were segmented based on an atlas because they were not clearly visible enough in the MR images. Thus, the fontanel and suture segmentation might not be exact, but this is not a critical issue in this study.

FEM mesh

A FEM volume conductor model was created based on the segmentation described above. A finite element hexahedral mesh with boundary nodes shifted was created from the segmented volume, including the fontanels and the sutures. The voxels could be used as hexahedral elements directly. However, in order to increase conformance to the real geometry and to mitigate the stair-case effects in a voxel-based mesh, Camacho et al. (1997) proposed a technique to shift nodes on material interfaces, resulting in smoother and more accurate boundaries. This approach was evaluated and validated for EEG source analysis in a multi-layer spherically symmetric conductor, where the errors reduced significantly compared to regular hexahedral approaches (Wolters et al., 2007a,b), leading to high numerical accuracies especially for 1 mm resolution meshes (Vorwerk, 2011). We therefore created a geometry-adapted hexahedral finite element mesh from the segmentation volume including the fontanels and the sutures.

Each finite element was assigned to one of five tissues (scalp, skull, CSF, GM and WM) based on the segmentation. The fontanels and sutures were labeled as scalp. The resulting numbers of FEM nodes and hexahedral elements were 718,974 and 688,663, respectively. We will refer to this model as the fs⁺ model. The software SimBio-VGRID was used for mesh generation. As a simplified model for our study, we created a FEM model with the fontanels and sutures manually filled as skull. We call this simplified model the fs⁻ model. Fig. 1c shows the FEM mesh of the skull with the fontanels and sutures. The brain dimensions are approximately 108 mm from the anterior to posterior, 87 mm from the right to left, and 78 mm from the superior to inferior.

Cortical surface

Given the T1 MRI and the manual segmentation, we extracted a gray and white matter boundary of both hemispheres as a cortical source space using the FreeSurfer brain imaging reconstruction software (Dale et al., 1999). Surface normal vectors at the vertices of the triangulation were defined as the average of the normals of the triangles neighboring a vertex to be able to constrain the sources to the cortical normal direction in the simulations.

EEG/MEG sensors

In the simulations, we used a grid of evenly distributed 277 EEG electrodes on the infant’s scalp. We also simulated a whole-head infant MEG system with magnetometers measuring the magnetic field component normal to the scalp at a distance of 5 mm. The diameter of the coils of the magnetometers was assumed to be 6 mm. The average distance between adjacent EEG electrodes was ~11 mm and that of adjacent MEG sensors ~12 mm, see Fig. 2.

Fig. 2.

Positions of the 277 EEG electrodes (left) on the scalp and the same number of MEG sensors (right) over the head.

Forward simulation

Using SimBio-NeuroFEM (SimBio, 2012), EEG/MEG forward simulations were carried out with the fs⁺ and the fs⁻ model. We used an isoparametric FE approach for the geometry-adapted hexahedral meshes (Wolters et al., 2007a) and the Venant direct method (Buchner et al., 1997; Wolters et al., 2007a) for modeling a dipole source, because it yielded suitable accuracy across all realistic source locations in multilayer sphere model validation studies (Lew et al., 2009; Vorwerk, 2011; Wolters et al., 2007a,b). Electric tissue conductivity values of the scalp, CSF, GM, and WM were selected as 0.33, 1.8, 0.33, and 0.14 S/m, respectively (Baumann et al., 1997; Ramon et al., 2004). The conductivity of the fontanels and sutures was chosen to be 0.3 S/m, which is almost the same value as the one for the scalp. We chose a skull conductivity value of 0.04 S/m. This value was inferred from an experimental measurement of a neonatal piglet skull, which indicated 0.03 S/m (23 °C) (Pant et al., 2011). Considering the higher body temperature of human neonate and a 2% increase of conductivity per one degree Celsius, we chose 0.04 S/m as the neonatal skull conductivity. Two other skull conductivity values of 0.03 and 0.05 S/m (±25% variation from 0.04 S/m) were also used as lower and upper limits in order to explore the effect of the skull conductivity in the simulations.

At each source node in the cortical source space, we defined a “tangential” and a “radial” source direction. Since the tangential and radial directions are strictly speaking defined only in the sphere model, we defined these directions for the realistic head model with help of the SVD of B = (b_xb_yb_z ) = USV^T, where b_x, b_y, and b_z are the MEG field patterns of three dipoles at one location, pointing to the x, y, and z directions, respectively. We defined the “tangential” and “radial” dipole orientations as the first and last columns of V, corresponding to the largest and smallest singular values in S, respectively (Huang et al., 2007). In addition to these two source orientations we also studied sources constrained to be normal to the cortical mantle, see section Cortical surface above.

Source estimation

Using the inverse toolbox of Simbio, SimBio-IPM (SimBio, 2012), we carried out inverse single dipole fits in the fs⁻ model, given the simulated reference EEG and MEG signals computed using the fs⁺ model. A Nelder–Mead simplex optimizer was used to find the optimal source parameters. The initial guess was set to the position of each source in the cortical source space. In this way, possible entrapment to local minima could be avoided and as a result the estimated parameters did not suffer from the local optimizer error. The estimated sources were then compared with the true sources and the errors were characterized by differences in dipole location, orientation and magnitude. The skull conductivity was an adjustable parameter in the source estimation, and the influences of both the inexact skull conductivity and the suture–fontanel effect were investigated. The conductivity of the fontanels and sutures was also adjusted to 0.2 and 0.4 instead of 0.3 S/m to see how much misspecification of the suture–fontanel conductivity affects the accuracy of source estimation.

Figures of merit

In order to quantify the difference of forward simulations between the fontanel and no fontanel models, we used the relative difference measure (RDM) and the magnification factor (MAG), similar to the definition in Meijs et al. (1989), as

$$\text{RDM}(\%):=100\times {\Vert {\mathrm{\Phi }}_{{fs}^{+}}/{\Vert {\mathrm{\Phi }}_{{fs}^{+}}\Vert }_2-{\mathrm{\Phi }}_{{fs}^{-}}/{\Vert {\mathrm{\Phi }}_{{fs}^{-}}\Vert }_2\Vert }_2/2$$ (1)

$$\text{MAG}(\%):=100\times \left|1-{\Vert {\mathrm{\Phi }}_{{fs}^{-}}\Vert }_2/{\mathrm{\Phi }}_{{fs}^{+}}{\Vert }_2\right|,$$ (2)

where Φ_{f s⁺} is the forward solution computed with the fs⁺ model, and Φ_{f s⁻} is the forward solution computed with the fs⁻ model. RDM (Eq. (1)) measures topographic differences driven primarily by changes in dipole location and orientation, and MAG (Eq. (2)) measures magnitude differences associated with changes in apparent source strengths (Marin et al., 1998; Schimpf et al., 2002).

Other figures of merit are the effects of conductivity model misspecification on the errors of inverse modeling. Therefore we calculated the dipole location, orientation, and magnitude errors corresponding to several types of errors in the volume conductor model. The location error was calculated as the Euclidean distance between the true and the estimated dipole locations. The orientation error was calculated from the angle between true and estimated source vectors. A magnitude error is the ratio of dipole strength difference between the true and the estimate to the true strength.

Results

Forward model comparison

In order to quantify how much the sutures and fontanels in the skull affect the measured MEG/EEG signals, forward solutions were simulated in the fs⁺ model (σ_suture = 0.3 S/m) and the fs⁻ model. RDM and MAG were computed for current dipoles oriented tangentially and radially to the skull layer, and normally to the cortical surface at each location in the cortical source space. Averaged RDM and MAG over the source space for the fs⁻ model with the three different skull conductivity values (σ_skull = 0.03, 0.04 or 0.05 S/m) were calculated and plotted in Fig. 3 with maximum values indicated. The prevailing skull conductivity values of 0.005 and 0.01 S/m found in the literature (see, e.g., Dannhauer et al., 2011) are appropriate only for adults. Instead, those of 0.03, 0.04, and 0.05 S/m are evaluated to reflect the fact that an infant skull has higher conductivity than that of an adult (Gibson et al., 2000; Pant et al., 2011). Maps of RDM and MAG on the cortical surface are presented in Fig. 4.

Fig. 3.

Average RDM and MAG over the cortical source space as a function of skull conductivity for tangential, normal, and radial dipoles. The number above each bar indicates the maximum value.

Fig. 4.

RDM and MAG mapped on the inflated cortical surface. RDM and MAG are computed between the fs⁺ model and the fs⁻ model for tangentially, radially, and normally oriented sources (σ_suture = 0.3 S/m, σ_skull = 0.04 S/m). The color map is scaled nonlinearly. RDM scales are 0–2–15% (Gray–Red–Yellow) for tangential and normal sources, and 0–2–63% for radial sources. MAG scales are 0–3–38% for tangential and normal sources, and 0–6–94% for radial sources.

For tangential dipoles in MEG, modeling the sutures and fontanels in the conductor model resulted in a 0.2% difference in the average RDM and MAG over the three skull conductivity values, while in EEG the corresponding effect was 0.5%. The spatial distributions of RDM and MAG shown in Fig. 4 for σ_skull = 0.04 S/m confirm that, in overall, these error measures are smaller for MEG than for EEG. A similar pattern was found for the other skull conductivity values tested (not shown).

In MEG, tangential dipoles have the smallest errors, which grow larger for normal and radial sources. On average, radial dipoles produced around 11 times larger RDM and around 4 times larger MAG than tangential dipoles (Fig. 3). In contrast to MEG, in EEG the dipole orientation has a negligible influence on the RDM error metric.

It is interesting to see that the ratio of averaged MEG RDM for normal dipoles to the tangential dipoles was 1.5, while that of maximum RDM was 7.6. MAG behaved in a similar way, with the ratio of averaged MAG of 1.4 and the ratio of maximum MAG of 4.9. This means that there were regions of very high RDM and MAG peaks for normal sources. In the spatial RDM and MAG maps in Fig. 4, we can identify these regions (yellow) that fall into the gyri, where normal dipoles are oriented most radially relative to the inner skull boundary.

MEG RDM and MAG show only a small variation over the three skull conductivity values. In EEG the corresponding measures show a stronger dependency on the skull conductivity for all dipole orientations. The RDM and MAG decrease as the skull conductivity increases. This is because the conductivity contrast between the suture–fontanel and the skull become smaller as the skull conductivity increases, resulting in a decrease of both RDM and MAG.

Inverse localization comparison

The RDM and MAG measures quantify the errors resulting from a simplified fs⁻ forward model in the measured signals. More importantly, however, the misspecification of the forward model can be critical to the accuracy of the inverse solutions. To see the effects of the sutures and fontanels on the accuracy of source localization, we generated forward solutions from current dipoles using the fs⁺ model including the fontanels and sutures and computed inverse dipole solutions using the fs⁻ models.

In the following subsections, we discuss four cases to elucidate the effects of the sutures, fontanels, and skull. Case 1 was designed to see the effect of exclusion of the sutures and fontanels in the inverse head model. Case 2 was designed to investigate the effect of exclusion of both the sutures and fontanels and incorrect skull conductivity in the inverse model. Case 3 was designed to find the effect of incorrect skull conductivity in the inverse model. Finally, Case 4 was designed to see the effect of the suture–fontanel conductivity in the inverse model. In addition, we studied the effect of the number of EEG channels on source estimation as Case 5.

Case 1: effect of the suture–fontanel conductivity

Simulated EEG and MEG were computed in the fs⁺ forward head model with σ_skull = 0.03, 0.04 and 0.05 S/m and σ_suture = 0.3 S/m for tangential, radial, and normal sources. The inverse fs⁻ head models with the same σ_skull = 0.03, 0.04, and 0.05 S/m were used for dipole fit. This is a case where a head model used in the inverse dipole fit does not consider the sutures and the fontanels in the skull, but the skull conductivity is assumed to be correct. The errors in dipole location, orientation, and magnitude were evaluated using the measures in the Figures of merit section.

When averaged over the three skull conductivity values for tangential sources, the maximum position error was 6 times larger in EEG (3.6 mm) than in MEG (0.6 mm). Therefore, the exclusion of the sutures and fontanels in the inverse head model has more impact on EEG than on MEG source localization. The variation of skull conductivity changes the errors in EEG, where the highest skull conductivity causes the smallest position errors. This is because the conductivity difference between the skull and the suture–fontanel (0.3 S/m) becomes smaller and thus the importance of the skull defects is reduced. The MEG results were largely independent of the skull conductivity.

Compared to the tangential sources, the maximum position error in MEG (6.2 mm) for normal sources was 10.3 times larger than that (0.6 mm) of tangential sources when averaged over the three skull conductivity values. This increase in MEG errors stems from the radially oriented dipoles present in the ensemble of the normal sources. Due to the radially oriented dipoles, the maximum errors in MEG (6.2 mm) were 2.1 times larger than those of EEG (2.9 mm) when averaged over the skull conductivity values, while the overall error distribution in MEG is below that of EEG. EEG errors for normal sources were close to those for tangential sources, implying that the effects of the forward model on EEG source localization accuracy are independent of the source orientation.

As an illustrative example of the above, Fig. 5 shows the spatial distribution of dipole position, orientation, and magnitude errors for normal dipole sources when σ_skull = 0.04 S/m is used in the dipole fit. Overall, the spatial distribution shows that MEG has less error than EEG, but there is a distinctive region of higher errors in MEG than in EEG. This is generally a region at the crests of the gyri where dipoles normal to the cortical mantle are likely to be oriented radially with respect to the nearby inner skull surface. For these normal sources on the gyri, EEG may have a better accuracy than MEG. For the maximum position errors, MEG error is 6.5 mm and EEG is 2.4 mm and for the maximum orientation errors, maximum MEG error is 174° and EEG is 42°.

Fig. 5.

Position, orientation, and magnitude errors mapped on the inflated cortical surface for normal sources when a fs⁻ model with σ_skull = 0.04 S/m is used for dipole fit. Simulated MEG and EEG were computed with the fs⁺ model with σ_suture = 0.3 S/m and σ_skull = 0.04 S/m. The scales of position error, orientation error, and magnitude error are 0–1–6.5 mm, 0–10–170°, and 0–20–140% (G–R–Y), respectively.

The detailed effects of the skull conductivity on MEG and EEG are shown in Fig. 6, which displays the spatial distribution of dipole position errors for tangential sources for the three skull conductivity values. The EEG errors become smaller as skull conductivity increases, while MEG errors show almost no difference among them. The reason for the reduction of errors in EEG is that the conductivity difference between the suture–fontanel (0.3 S/m) and the skull gets smaller and, accordingly, the effect of the suture–fontanel becomes less prominent. This result also confirms that MEG is less influenced by skull conductivity than EEG.

Fig. 6.

Position estimation error mapped on the inflated cortical surface of lateral right hand side for tangential sources when a fs⁻ model with σ_skull = 0.03, 0.04, and 0.05 S/m (Case 1) is used for dipole fit. Simulated MEG and EEG were computed with the fs⁺ model with σ_suture = 0.3 S/m, σ_skull = 0.03, 0.04, 0.05 S/m correspondingly. The position error scale is 0–1–4 mm (G–R–Y).

The ratios of maximal EEG position and orientation errors to MEG were 6.3 and 1.4 for tangential sources, 0.4 and 0.2 for normal sources, and 0.2 and 0.3 for radial sources, respectively, see Case 1 with σ_skull = 0.04 S/m in Fig. 7. Except for the tangential case, EEG has smaller maximum position and orientation errors than MEG. The ratio of maximum EEG magnitude error to MEG was 3.5 for tangential sources, 1.4 for normal sources, and 1.2 for radial sources. The magnitude errors of MEG were smaller than those of EEG for all three dipole orientations.

Fig. 7.

Maximum estimation errors when inverse models of Case 1 (fs⁻ model with correct σ_skull = 0.04 S/m), Case 2 (fs⁻ model with incorrect σ_skull = 0.03 and 0.05 S/m), and Case 3 (fs⁺ model with incorrect σ_skull = 0.03 and 0.05 S/m) are used for dipole fit. Simulated MEG and EEG were computed with the fs⁺ model with σ_suture = 0.3 S/m, σ_skull = 0.04 S/m.

Case 2: combined effect of the suture–fontanel and skull conductivity

Simulated EEG and MEG were computed in the fs⁺ head model with σ_skull = 0.04 S/m and σ_suture = 0.3 S/m for tangential, normal, and radial sources. The inverse fs⁻ head models with σ_skull = 0.03 and 0.05 S/m were used for dipole fit. This is a likely case in practice where a head model used in the inverse dipole fit does not consider the sutures and the fontanels and the skull conductivity is either under- or overestimated.

Fig. 8 shows the distributions of position, orientation, and magnitude errors for tangential sources. The overall MEG and EEG errors for under- and over-approximated skull conductivity values are higher than in Case 1. The averaged EEG errors over position, orientation, and magnitude for underestimated σ_skull = 0.03 S/m and overestimated σ_skull = 0.05 S/m are 3.0 and 1.5 times larger than in Case 1 with σ_skull = 0.04 S/m, respectively. The averaged MEG error is 1.9 times larger for both under- and overestimated skull conductivity values. However, MEG has very little difference between the different skull conductivity values.

Fig. 8.

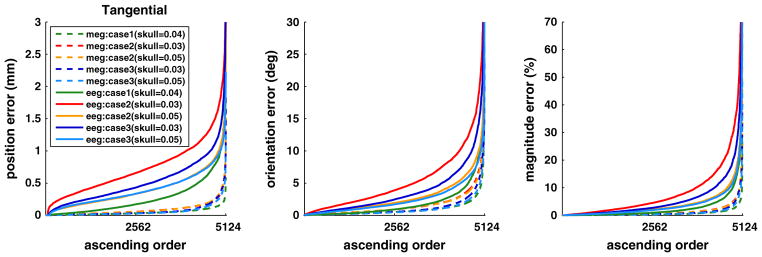
Distribution of position, orientation and magnitude errors for dipole fit with MEG and EEG, when the inverse models of Case 1 (fs⁻ model with correct σ_skull = 0.04 S/m), Case 2 (fs⁻ model with incorrect σ_skull = 0.03 and 0.05 S/m), and Case 3 (fs⁺ model with incorrect σ_skull = 0.03 and 0.05 S/m) are used for dipole fit. Plotted in ascending order for tangentially oriented dipoles. Simulated MEG and EEG were computed with the fs⁺ model with σ_suture = 0.3 S/m, σ_skull = 0.04 S/m. The curves are clipped to show the majority of distribution. The maximum value for each curve is in Fig. 7.

Compared to Case 1, these increases in localization error indicate that, in addition to the omission of the fontanel and sutures, the inexact skull conductivity in the inverse head model contributes adversely to dipole estimation error in MEG and EEG. It is noteworthy that the underestimated skull conductivity affects more negatively on EEG than the overestimated one (Fig. 9). The reason is that the conductivity difference between the fontanel (0.3 S/m) and the skull becomes larger when σ_skull = 0.03 S/m is used in the inverse than when σ_skull = 0.05 S/m is employed.

Fig. 9.

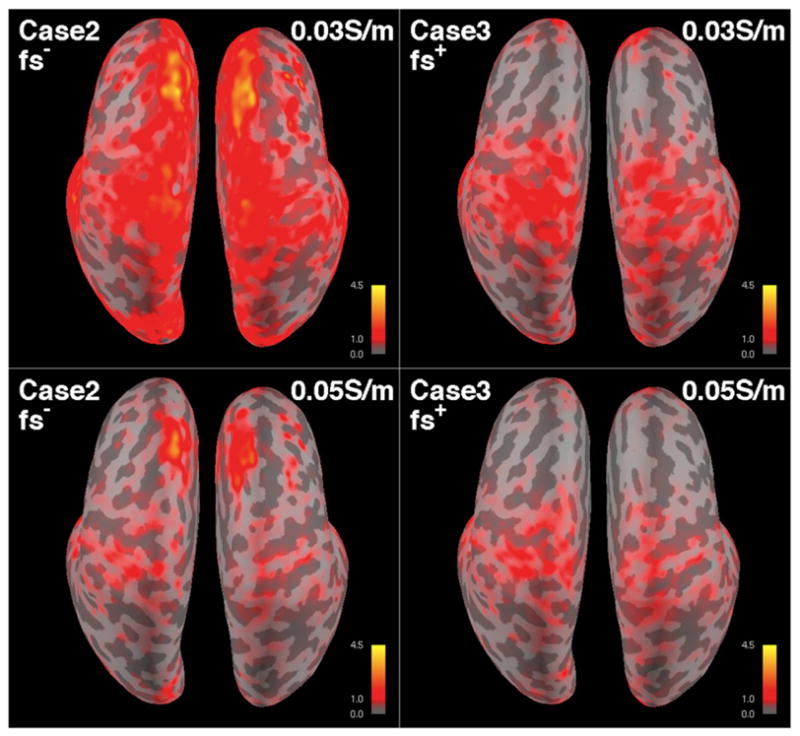
EEG position errors on the inflated cortical surface for two inverse models of Case 2 (fs⁻ model with incorrect σ_skull = 0.03 and 0.05 S/m), and Case 3 (fs⁺ model with incorrect σ_skull = 0.03 and 0.05 S/m). Sources are oriented tangentially. Skull conductivity used in the inverse model is indicated in each map. Simulated EEG was computed with the fs⁺ model with σ_suture = 0.3 S/m and σ_skull = 0.04 S/m. The scale is 0–1–4.5 mm (G–R–Y).

Case 2 represents very well the present practice of using a model where the sutures and fontanels are absent and the skull conductivity is incorrect: both MEG and EEG have errors and EEG errors are larger than those in MEG. Furthermore, an underestimated skull conductivity inverse model has a more adverse effect than an overestimated one.

Case 3: effect of skull conductivity

In this case, EEG and MEG were simulated with the fs⁺ model with σ_suture = 0.3 S/m and σ_skull = 0.04 S/m for tangential and normal sources. The fs⁺ head models with σ_suture = 0.3 S/m and with σ_skull = 0.03 and 0.05 S/m were used for dipole fit. Therefore, as in Case 2, the skull conductivity was either under- or over-estimated in the inverse model to quantify the effect of inaccurate skull conductivity alone with the fontanels and sutures present in both the forward simulation and inverse modeling.

The overall MEG and EEG errors for under- and overestimated skull conductivity values were higher than those in Case 1, but smaller than those in Case 2 (Fig. 8). The average dipole position, orientation, and magnitude errors in EEG for underestimated σ_skull = 0.03 S/m and overestimated σ_skull = 0.05 S/m are 2.0 and 1.4 times larger than those in Case 1, respectively. The averaged MEG errors were 1.4 (σ_skull = 0.03 S/m) and 1.2 times (σ_skull = 0.05 S/m) larger than that of Case 1. These results indicate that the skull conductivity mismatch could cause more dipole estimation errors than the exclusion of the sutures and fontanels from the model, given the size of the sutures and fontanels and its ratio to the skull size in the head model of the subject. Similar to Case 2, the dipole localization accuracy is affected more when the skull conductivity is underestimated than when it is overestimated (Fig. 9).

It is interesting to see that for the overestimated σ_skull = 0.05 S/m, the EEG error distribution of Case 3 is similar to Case 2 in Fig. 8. However, we could see a clear difference in the spatial error mapped on cortical surface in Fig. 9, where the spatial EEG error distributions are different. It is noteworthy that the higher error in the superior-anterior region for Case 2 is absent in Case 3. Therefore, this is a consequence of excluding the sutures and fontanels from the inverse model.

Case 4: effect of the suture–fontanel conductivity

In the previous simulations, the sutures and the fontanels, when present, are modeled as a tissue with conductivity of 0.3 S/m. In this section we simulate the effects when the conductivity values of the sutures and fontanels in the forward fs⁺ model were either 0.2 or 0.4 S/m, deviating from 0.3 S/m by 33%.

For MEG and EEG, the errors increase as the suture conductivity increases. The difference between the suture and the skull conductivity (0.04 S/m) becomes smaller as the suture conductivity decreases, resulting in a smaller error. The EEG maximum errors of assuming σ_suture = 0.2 and 0.4 S/m for tangential sources in the forward model were 3.1 mm and 4.0 mm, 43° and 48°, and 72% and 108%, respectively, while those with σ_suture = 0.3 S/m are 3.8 mm, 50°, and 97%. The maximum position, orientation, and magnitude errors in MEG, averaged over the three suture conductivity values, are 17%, 62%, and 27% of EEG errors, respectively. It is thus expected that as the fontanels and sutures ossify until turning into skull, their effect becomes smaller and smaller.

Case 5: effect of number of EEG channels

In practice, an EEG array usually has a smaller number of channels than the 277 used in the previous simulations. Therefore, we also simulated a case with only 74 EEG channels for the Case 1 with σ_skull = 0.04 S/m and normal sources. The result shows that the averaged position, orientation, and magnitude errors are about 1.2 times larger with the smaller number of EEG channels. From the result, we can see that the number of EEG channels has some effects on the localization errors, and the EEG errors presented in the paper could be adjusted accordingly when the smaller number of EEG channels is used.

Discussion

Overall, our results show that spatial distributions of the MEG signals outside the head are less affected by the presence of the sutures and fontanels and by variations in skull conductivity than those measured by EEG when the dipoles are oriented tangentially with respect to the inner surface of the skull. Moreover, MEG leads to more accurate source localization than EEG when the fs⁻ forward model was used in source estimation. This finding provides a legitimate ground to use the simplified fs⁻ conductor model, which ignores the details of the skull geometry, for MEG source localization, when an exact model is not practical. On the other hand, such a model may not be acceptable in EEG source localization. Instead the sutures and fontanels should be included in the model and the conductivity of the suture should be estimated as accurately as possible.

The EEG localization accuracy suffers not only from the use of the fs⁻ model, but also from the inexact skull conductivity used in the dipole fit. This represents a practical situation. It is interesting to see that for EEG, the skull conductivity mismatch contributed more negatively to the localization accuracy than the exclusion of the sutures and fontanels. This means that mere addition of the sutures and fontanels to the model does not necessarily improve the accuracy when the skull conductivity is not exact. It is also likely that having skull conductivity close to the exact value may improve the overall localization accuracy more than having the sutures and fontanels present in the conductor model.

In case of sources oriented perpendicularly to the cortex, MEG localization accuracy with the simplified fs⁻ inverse head model is slightly deteriorated from tangential sources. This is obviously due to radially oriented sources being present in the ensemble of sources oriented normally to the cortical mantle. The radially oriented sources produce very weak MEG signals and thus even small modeling errors may lead to relatively large localization errors. In spite of this negative effect, the inverse fs⁻ head model is effective for MEG source localization with normal sources. It is also noteworthy that MEG maintains higher localization accuracy over EEG, in normal sources, despite the presence of radially oriented sources.

In Fig. 5, the largest error in MEG occurs at the crest of a gyrus on the medial surface of the left hemisphere, which is due to a dipole fit that terminated in a local minimum. Nevertheless, the second maximum on the frontal lobe in Fig. 5 and other high error regions in red appear at the crests of the gyri, where normally constraint dipoles are close to be radial to the skull layer.

Although the maximum EEG position error reaches almost 5 mm, the majority of errors remain below 1 mm. It is important to identify the most affected sources spatially in order to justify the use of the fs⁺ model for the EEG source estimation. It is also important to evaluate how the changes of fontanel size, skull thickness, suture, and skull conductivity impact the EEG localization accuracy over the first few years of infant brain development, since EEG depends heavily on these factors.

The accuracy of the skull conductivity estimate has an influence on the localization errors as well. The conductivity difference between the skull and the suture–fontanel plays an important role in the localization error. The underestimated skull conductivity causes higher errors (especially, magnitude errors) than the overestimated, which is closer to the suture conductivity than the underestimated one.

The conductivity of the sutures and fontanels decreases due to ossification as an infant grows and eventually matches that of the skull. For both MEG and EEG, the errors become smaller when the conductivity of the sutures and fontanels is decreased because the reference model (fs⁺) is then closer to the simplified model (fs⁻), where the sutures and fontanels assume the conductivity of the skull. Regardless of the conductivity value used for the suture and fontanel for the localization, the errors are smaller for MEG than for EEG.

The impact of the sutures and fontanels is not evenly distributed throughout the cortex, but selective to the locations and the orientations of the sources. MEG has a limited sensitivity to some of the normal sources when the inexact inverse model is used. In this case, EEG shows a better accuracy than MEG. Therefore, best results will be obtained by using MEG and EEG in combination.

It is also important to point out that the infant head is very small such that 1 mm in infant could be equivalent of a few millimeters in adult, so that the relatively small errors reported could be more significant than similar errors in an adult. For an accurate source analysis for infants, a high-quality inverse model should be considered along with a higher-resolution MRI.

In this manuscript, we focused on the effect of the fontanels and sutures in an infant head on EEG and MEG, while we otherwise modeled the skull as homogeneous and isotropic, as is also currently the standard not only for infant (Roche-Labarbe et al., 2008), but also for adult source analysis studies (see, e.g., Hämäläinen et al., 1993; Michel et al., 2004). Our available information of the infant skull compartment, extracted from a T1w-MRI, did not offer us the possibility to distinguish skull compacta from spongiosa. In the case of adults, it was reported that skull spongiosa have on average a 3.6 times higher conductivity than skull compacta (Akhtari et al., 2002) and it was recently found that this skull-layeredness leads to skull conductivity inhomogeneity which has important implications on EEG source analysis (Dannhauer et al., 2011; Sadleir and Argibay, 2007). For adults, it was shown that an additional T2w-MRI with minimal water-fat-shift could be exploited for successfully (and non-invasively) distinguishing skull spongiosa and compacta (Dannhauer et al., 2011; Pursiainen et al., 2012, 2013). However, in infants this separation of the skull layers may not yet be present and, therefore, in young infants detailed modeling of the skull may not be as important as in adults.

A second simplification in our infant skull model is the simplification of the inferior skull and the inferior tissues. It was recently shown in an adult study that such simplifications lead to significant errors in EEG source analysis for sources from especially the lower parts of the source space and it was concluded that a downward extension of the model is one of the most important points in the guidelines for accurately modeling the lower model geometry in EEG source analysis (Lanfer et al., 2012). Future studies thus have to show if these influences are also significant in infant studies for both EEG and MEG and how they relate to the effect studied here. We do not, however, expect that those additional volume conduction aspects have a significant effect on the statements made in the study at hand.

In addition to the changes in the skull, the conductivity of the brain undergoes dramatic changes during the first year of life. Conductivity changes in the brain can affect both EEG and MEG source estimates as well (Güllmar et al., 2010; Wolters et al., 2006). Thus, more studies are needed to evaluate the effects of rapidly changing infant brain conductivity and anisotropy to MEG/EEG source estimation.

Finally, in this paper, only single source scenarios have been investigated. The effect to the reconstruction in case of multiple sources might be higher and remains to be investigated in future studies. In addition, the size of the sutures and fontanels as well as the head volume were fixed to correspond to an early stage of development in the volume conductor model we used for this study. Therefore, it is important to further investigate the effect in the changes of the skull imperfections and the head volume as the brain develops.

In summary, the infant brain changes rapidly over the first few years. During this period, the skull and the brain undergo major restructuring including fusing of the sutures and fontanels and development of neuronal myelination (Bystron et al., 2008; Rakic, 2006). The volume conductor model of an infant head should accommodate this development to accurately infer the sources of the non-invasive MEG and EEG measurements. The relative ease of accurate MEG forward modeling gives MEG an advantage over EEG, especially in longitudinal studies of the developing brain. This advantage is present when the sources are oriented tangentially to the skull layer and normally to the cortical mantle. With radial sources, EEG is more appropriate, as long as the EEG source localization uses an accurate inverse head model that includes the sutures and fontanels and skull conductivity. Therefore, MEG and EEG need to be ultimately combined to extract complete and accurate information of the neurophysiology of the infant brain.

Conclusion

Forward modeling and inverse source estimation of MEG are less affected by the presence of the sutures and fontanels than those of EEG when sources are oriented tangentially to the skull or normally to the cortex. Especially for tangentially oriented sources MEG is not significantly disturbed by the presence of the sutures and fontanels and by the uncertainty of skull conductivity. For sources oriented normally to the cortex, the location of the source on the cortical mantle is important for MEG source localization. Since some of these sources have a dominant radial component, localization errors can be higher than in EEG when an inexact model is used. Therefore, best results will be achieved when MEG and EEG are used in combination. Overall, however, our simulations show that MEG has clear benefits over EEG in studies of infants who have structural irregularity not present in older subjects and undergo fast changes during maturation such as the closure of the fontanels and sutures.