Skip to main content
PMC home page
OMICS : a Journal of Integrative Biology logoLink to OMICS : a Journal of Integrative Biology
. 2013 Sep;17(9):473–485. doi: 10.1089/omi.2013.0010

Evaluation of Normalization Methods to Pave the Way Towards Large-Scale LC-MS-Based Metabolomics Profiling Experiments

Bedilu Alamirie Ejigu 1,2,✉, Dirk Valkenborg 1,2,3, Geert Baggerman 2,3, Manu Vanaerschot 4, Erwin Witters 2,3, Jean-Claude Dujardin 4,5, Tomasz Burzykowski 1, Maya Berg 4
PMCID: PMC3760460  PMID: 23808607

Abstract

Combining liquid chromatography-mass spectrometry (LC-MS)-based metabolomics experiments that were collected over a long period of time remains problematic due to systematic variability between LC-MS measurements. Until now, most normalization methods for LC-MS data are model-driven, based on internal standards or intermediate quality control runs, where an external model is extrapolated to the dataset of interest. In the first part of this article, we evaluate several existing data-driven normalization approaches on LC-MS metabolomics experiments, which do not require the use of internal standards. According to variability measures, each normalization method performs relatively well, showing that the use of any normalization method will greatly improve data-analysis originating from multiple experimental runs. In the second part, we apply cyclic-Loess normalization to a Leishmania sample. This normalization method allows the removal of systematic variability between two measurement blocks over time and maintains the differential metabolites. In conclusion, normalization allows for pooling datasets from different measurement blocks over time and increases the statistical power of the analysis, hence paving the way to increase the scale of LC-MS metabolomics experiments. From our investigation, we recommend data-driven normalization methods over model-driven normalization methods, if only a few internal standards were used. Moreover, data-driven normalization methods are the best option to normalize datasets from untargeted LC-MS experiments.

Introduction

Large-scale liquid chromatography and mass spectrometry-based (LC-MS) metabolomics studies are often hampered by the fact that samples need to be collected over a long period of time. For such studies, it is often inevitable to measure samples in different batches, and to combine them into one large dataset for data-processing and statistical analysis. However, pooling these datasets may result in biased results due to the systematic variation of LC-MS platforms that occurs over time. Variation in LC-sampling, pH shift of the mobile phase, unstable ionization and electrospray fluctuations, variations in stationary phase conditions, inter-column variations, suboptimal calibration of the MS, state of the detectors, noncontinuous gas supply, temperature shifts, and maintenance events can significantly affect the reproducibility of retention time, mass accuracy, and ion intensity—factors important for an accurate identification and quantification of metabolites (Berg et al., 2012, Sysi-Aho et al., 2007). A quantitative comparison across samples of different LC-MS batches thus remains controversial at present.

To correct for retention time drift, bioinformatics solutions such as OBI-Warp (Prince et al., 2006) allow the alignment of LC-MS signals for both LC-MS proteomics and metabolomics datasets. To handle drift in mass calibration, internal mass calibration or alignment of the spectra can be achieved through the mass deviation present in certain prevalent contaminants, since they are shared by all or most spectra in a dataset (Breitling et al., 2012). Another possibility is to include replicate measurements of a series of authentic standards covering the whole mass range of interest, which allows for recalibration during data-processing (Valkenborg et al., 2009). However, correcting for the drift in signal intensities proves more challenging. Procedures to handle drift in signal intensities can be divided into method-driven and data-driven approaches.

Method-driven approaches extrapolate an external model that is based upon quality control samples or internal standards to the dataset of interest. Especially the latter are often used to normalize data, with or without the combination with pooled calibration samples (Bijlsma et al., 2006; Gullberg et al., 2004; Redestig et al., 2009; Sysi-Aho et al., 2007; van der Kloet et al., 2009). However, spiking standard reference material into the samples of interest is not practical due to several reasons. First, standard reference materials are either stable isotopes or structural analogues that do not occur naturally, so they are very expensive to produce and whose availability is often very limited. Second, correction of intensity level fluctuations based on a small set of internal standards is not recommended because the selected internal standards only represent a limited number of metabolite classes, and intensity level fluctuations may differ between various classes. Third, this strategy is not achievable for untargeted metabolomics studies since it is by definition not known beforehand which metabolites will be of interest, and spiking each sample with hundreds of internal standards would be too expensive and labor-intensive (Sysi-Aho et al., 2007; Wang et al., 2003). The use of ‘housekeeping metabolites’ to normalize data from different runs, similar to what has proven successful in gene expression studies (Vandesompele et al., 2002), is also not self-evident: metabolites in blood, urine, or cell samples are highly susceptible to environmental changes (Sysi-Aho et al., 2007). Interestingly, Dunn et al. (2011) included a commercially available serum sample to allow for quality control-based local regression (Loess) signal correction of serum and plasma samples, and thus pooling of data from multiple analytical batches. Unfortunately, such commercially available quality control samples are not available for all types of samples that are analyzed in various metabolomics studies.

Data-driven methods, on the other hand, normalize data by assuming that a large amount of the metabolites stay constant without the necessity of knowing the identity of these specific metabolites. In 2003, Wang and co-authors suggested a normalization approach based on the linearity of signal versus molecular concentration without using internal standards, even though serious concerns are expressed regarding the nonlinearity and ion suppression effects of complex biological samples, especially in the case of LC-MS (Berg et al., 2012). In 2006, van den Berg et al. tested the effect of six linear scaling and two heteroscedasticity methods on a gas chromatography-mass spectrometry (GC-MS) metabolomics dataset to reduce the systematic variability. They emphasized that the choice of a normalization method depends on the biological question, the properties of the dataset, and the selected data analysis method.

In a recent communication by Kohl et al. (2011), an analogy was made between DNA microarray data normalization and normalization for nuclear magnetic resonance (NMR) datasets showing that the quantile- and cubic spline normalization methods performed best for NMR metabolomics data. These conclusions can, however, not be readily extrapolated to LC-MS metabolomics. In contrast to NMR data, LC-MS data are two-dimensional, and hence even more prone to systematic variability. In addition, LC-MS signal intensities do not always scale linearly with metabolite concentrations as shown by dilution series (Jankevics et al., 2011): this strongly depends on specific characteristics of the column that is used and the concentration of the metabolite (ion suppression occurs more frequently with higher concentrations). A rigorous evaluation of intensity normalization techniques to complete the data processing pipeline in order to unambiguously pinpoint statistical and biological significant changes is thus currently unavailable in the context of LC-MS metabolomics data analysis.

Thus, in this study we aim to evaluate the performance of a series of data-driven normalization methods that are often used in microarray analysis to allow reliable analysis of pooled datasets of LC-MS metabolomics experiments (without spiked standards) executed across different time blocks. Importantly, we do not intend to provide an exhaustive comparison of the state-of-the-art literature on normalization, but we chose to compare classical normalization methods that are embedded in many standard software packages. The better normalization method was then validated on a previously published L. donovani dataset (t'Kindt et al., 2010b) to show that it succeeds in removing systematic difference between samples but still accurately reproduces fold changes.

Materials and Methods

Data

Background of the datasets

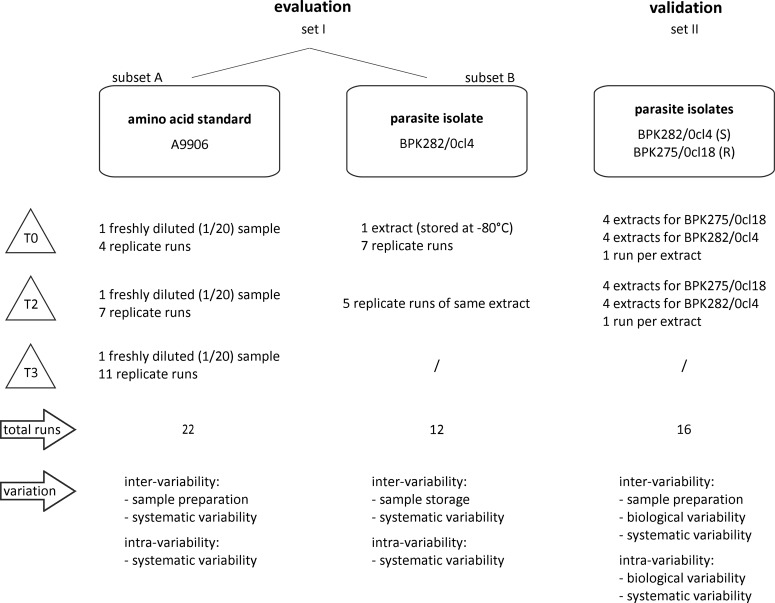
Two different datasets were included in this study. Set I was used to evaluate the different normalization methods, and Set II was used to validate the best performing normalization method (Fig. 1). Set I itself was composed of two subsets: (i) Subset A was obtained from LC-MS experiments on a freshly diluted mixture of 38 physiological amino acid standards [Product No. A9906, Sigma; preparation of this mixture is described elsewhere (Jankevics et al., 2012)], which were performed at three different time points, hereafter called time blocks: four LC-MS runs in time block 0 (T0), seven runs 2 months later (T2), and 11 runs 3 months later (T3), while (ii) Subset B was obtained from LC-MS experiments on a single, at −80°C stored, extract of Leishmania donovani (MHOM/NP/03/BPK282/0cl4), which was measured at two different time points: seven LC-MS runs at T0, and five runs at T2. It is important to note that biological variability is not present in Set I because it involves replicate measures of (i) a freshly diluted standard (Subset A) and (ii) one single parasite extract (Subset B). Set II consists of data acquired from LC-MS experiments on extracts of two clinical strains of Leishmania donovani with a different drug susceptibility towards antimonials: MHOM/NP/03/BPK282/0cl4 (sensitive) and MHOM/NP/03/BPK275/0cl18 (resistant) (Fig.1: Set II). Four extracts per strain per time block (T0 and T2) were prepared from independent cultures and measured soon after preparation. In this case, biological variability might be responsible for both intra- and inter-batch variability, as the data include biological replicates of the same strain (intra-batch) and freshly prepared extracts per time block (inter-batch). Methods for phenotyping and according metabolic differences related to antimonial-resistance for these strains have been reported elsewhere (t'Kindt et al., 2010b). Metabolite changes are regarded as biologically and significantly different if the average signal intensity differs at least a two-fold (e.g., fold change BPK275/BPK282 >2 or <0.5) and if the calculated p value of the t-test is smaller than 0.05. Set II will serve as a benchmark dataset with negative and positive controls used in the validation part of the manuscript.

FIG. 1.

FIG. 1.

Open in a new tab

Experimental design. Description of sample preparation, number of runs and source of possible batch variability for each experiment (T0, timeblock 0; T2, timeblock 2; T3, timeblock 3).

LC-MS measurements

The analytical samples were measured on a liquid chromatography instrument (Waters Acquity UPLC system) using a HILIC column (ZIC-HILIC 3.5 μm 100Å 150×2.1 mm from Sequant, Merck) coupled to a high-accuracy mass spectrometer (LTQ Orbitrap Velos, Thermo Fisher Scientific Inc.). Specifications on the LC part can be found in t'Kindt et al. (2010a). The mass spectrometer was operated in positive ion electrospray mode. ESI source voltage was optimized to 4.5 kV and capillary voltage was set to 30 V. The source temperature was set to 380°C and the sheath gas and auxiliary gas flow rates were set respectively to 45 and 20 (arbitrary units). The S-lens RF level was set to 59%. Full-scan spectra were obtained over an m/z range of 100–1000 Da, with the mass resolution set to 30,000 at 400 m/z. FT ions gain was set to 500,000 ions, maximum injection time was 100 micro seconds, three micro scans were summed. All spectra were collected in continuous single MS mode. The LC-MS systems were controlled by Xcalibur version 2.0 (Thermo Fisher Scientific Inc.). With every fifth analysis, a standard mixture containing fixed concentration of amino acids (Product No. A9906, Sigma) was injected to check the performance of the instrumental set-up.

Data processing

Raw data files acquired from analyzed samples were converted to mzXML format by the msconvert.exe tool of ProteoWizard (http://proteowizard.sourceforge.net). The CentWave (Tautenhahn et al., 2008) feature detection algorithm from the XCMS package (Smith et al., 2006) was applied to each individual data file. Further processing was handled by the flexible data processing pipeline mzMatch (Scheltema et al., 2011) integrated in R (http://www.R-project.org) and involved (i) aligning of the chromatographic features between replicates of a specific time block (i.e., all samples of one time block are combined in one file); (ii) retention time alignment to correct for drift between time blocks (inter-batch); (iii) combining all measurements (i.e., time blocks) in a single file; (iv) filtering on peak shape and intensity; (v) automatic annotating of derivative signals (isotopes, adducts, dimers, and fragments) by correlation analysis on both signal shape and intensity pattern as described by Scheltema et al. (2011). Putative identification was made against an in-house database of amino acids or a Leishmania database [based on LeishCyc which was further completed with identifications from Lipid MAPS (Fahy et al., 2007)]. If a metabolite was detected only once in a time block, it was discarded from further analysis. If a metabolite was missing in only one replicate, the average of the other values was imputed. Feature selection resulted in 28 identified amino acids and derivatives for the amino acid standard (six standard amino acids were not detected because they had a molecular weight lower than 100 Da, four compounds were undistinguishable isomers, for example, leucine and isoleucine), 189 metabolites for the Leishmania extract (MHOM/NP/03/BPK282/0cl4) (Fig. 1S; Supplementary material is available online at www.liebertpub.com/omi), and 135 metabolites for the validation dataset (MHOM/NP/03/BPK282/0cl4 combined with MHOM/NP/03/BPK275/0cl18). Table 1S with identifications is provided as supplementary material for this study. The R code is available from the first author upon request. Statistical analysis and data visualization were handled in R. Unsupervised hierarchical clustering analysis (HCA) and principal component analysis (PCA) were used to identify groups of samples that show similar characteristics. For more background on both HCA and PCA, refer to t'Kindt et al. (2010b).

Employed normalization methods

Systematic changes in the average intensity levels across different experimental runs/timeblocks can obscure the biological information. As a consequence, the conclusions drawn from the non-normalized data may be incorrect. To remove the systematic variation across different experimental blocks observed in the original data, we have applied seven different data-driven normalization methods, which are commonly used for large-scale microarray datasets: (1) linear baseline normalization, (2) normalization by sum (analogous to total ion count normalization), (3) median normalization, (4) cyclic-Loess normalization, (5) quantile normalization, (6) probabilistic quotient normalization, and (7) cubic-spline normalization. These normalization methods were applied to both Subsets A and B of dataset I. More information about each of these normalization methods is available in the Supplementary Material. R scripts allowing applications of the described normalization methods to other data sources are also provided in the Supplementary Material (Supplementary Material is available online at www.liebertpub.com/omi).

Evaluation of normalization methods

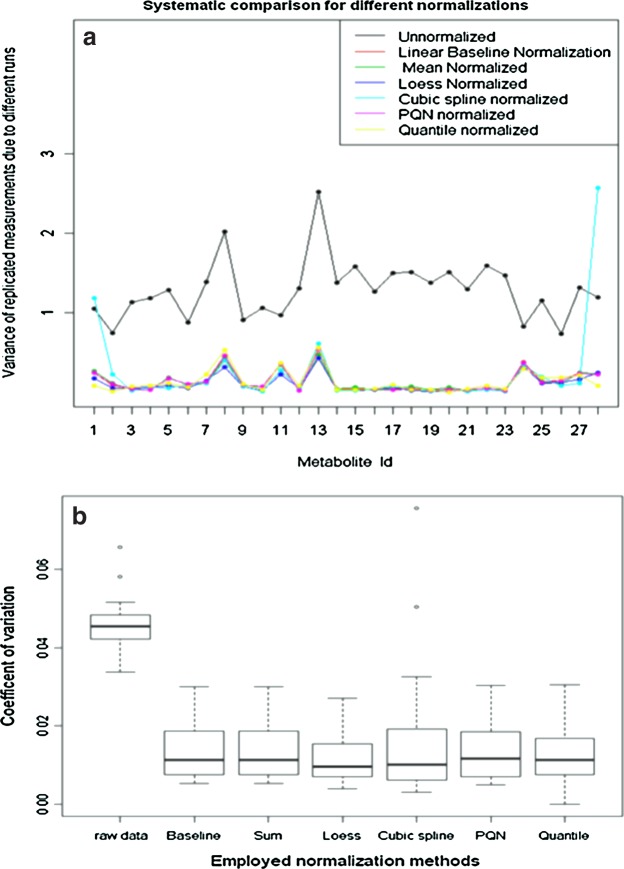
In order to assess the performance of the different normalization methods, we assume that the majority of the metabolites are approximately similarly expressed across different experimental runs. As a result, the observed intensity measures for all metabolites are adjusted to satisfy this assumption. As described by Mar et al. (2009), Schmid et al. (2010), and Hill et al. (2001), this is a well-known assumption in gene-expression data normalization. Since the observed intensities are influenced by different factors, it is hard to predict the effect of this assumption on the assessment of normalization methods. By adopting the assumption is satisfied, the performance of the applied normalization methods was assessed using the variance and coefficient of variation between replicated measurements or time blocks. Both metrics are common statistical measures reflecting the spread (variation) of measurements across different experimental runs. Accordingly, the better the normalization method, the lower the coefficient of variation and the lower the variance between replicated measurements will be. More details on the calculation of these variability measures are given below.

Variance between replicated measurements

Let yij be the log intensity value for metabolite i (I=1,2,3..a) at run time j (j=1,2,3,…k), using the replicated observations due to different experimental runs. Our goal is to derive the variability measures of yij. It is expected that successful normalization should reduce the between-experimental run variability for each metabolite, as compared to the original data. A line plot for the variance was constructed to inspect visually which normalization method consistently reduces the variability across all the considered metabolites, as depicted in Figure 2 (top panel). The variance for the ith metabolite 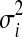Inline graphic is computed as:

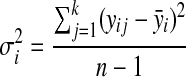graphic file with name M2.gif (1)

FIG. 2.

FIG. 2.

Open in a new tab

Line plots for the log-intensity variance for different metabolites of the amino acid standard across runs before and after normalization (a), and box-whisker plots for the coefficients of variation (b).

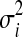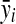where Inline graphic and Inline graphic are the variance and the mean of the ith metabolite across different experimental runs, respectively; k represents the number of runs.

Coefficient of variation

The coefficient of variation (CV) is a measure that allows us to assess the degree of spread in a given data set relative to its mean value. It represents the ratio of the standard deviation to the mean. Since it is a unitless measure of variation, it is a useful statistic for comparing the degree of variation from one data series to another, even if the means are drastically different from each other. As a result, we used the CV (2) as an extra criterion to discriminate between different normalization methods. The better the normalization method, the lower the average metabolite specific coefficient of variation. The coefficient of variation for the ith metabolite is defined as

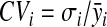graphic file with name M5.gif (2)

where CVi, σi, and 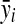Inline graphic are the coefficient of variation, standard deviation (square root of (1)), and mean for the ith metabolite, respectively.

It is important to stress that, when the logarithmized data contains negative values, the CV is meaningless. Thus, for logarithmized data, the application of CV should be handled with caution. Since the log transformed data contains only positive values larger than 10 before (Fig. 3, lower channel) and after normalization (Fig. 4), we used equation (2) to compute CV.

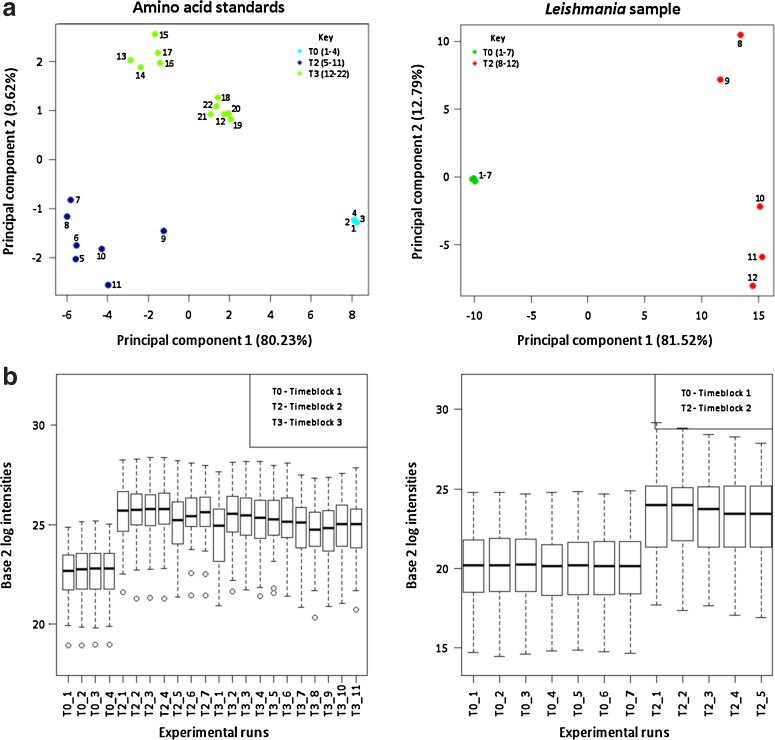
FIG. 3.

FIG. 3.

Open in a new tab

(a) Principal component analyses (PCA) distinguishes replicate runs between timeblocks (T0, T2, and T3) for both amino acid standard (left, T0 with runs 1–4, T2 with runs 5–11, and T3 with runs 12–22) and Leishmania sample (right, T0 with runs 1–7 and T2 with runs 8–12). PCA is an unsupervised cluster method based on quantitative measurement of 28 amino acids and derivatives (left) and 189 metabolites (right). (b) Box-whisker plots for both amino acid standard (left) and Leishmania sample (right) before normalization.

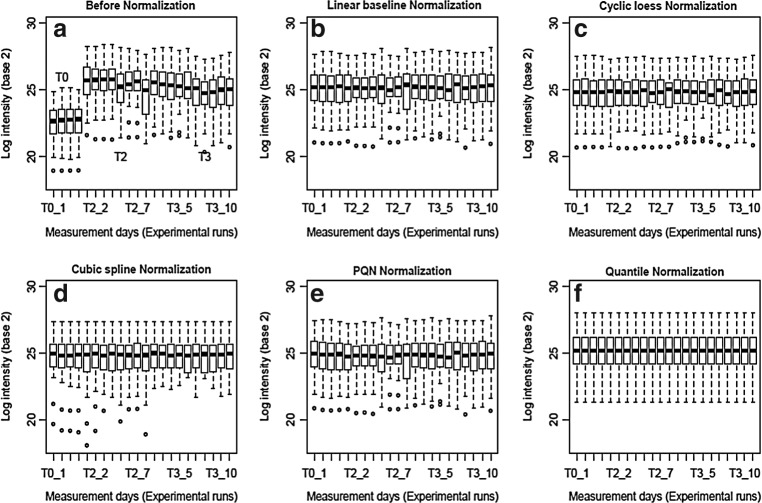
FIG. 4.

FIG. 4.

Open in a new tab

Box-whisker plots for the log-intensity data (a) before and (b—f) after different normalization methods for the amino acid standard (Subset A). The top and bottom of the box represents the 75th and 25th percentiles of the distribution, respectively. The line inside the box represents the median value, and the dots indicate data points on the extreme of the distribution.

In addition to the numerical variability measures, box-plots and heat maps were prepared to visualize the effect of the employed normalization techniques. For the heat maps (Fig. 5), the intensities of each metabolite were rescaled between 0 and 100 to improve graphical interpretation. Moreover, an ANOVA model (3) was fitted to the data before and after normalization in order to test whether the batch effect was successfully removed from the data after normalization. ANOVA is a special case of regression model when all the explanatory variables are categorical/class variables (factors). The model was formulated as follows:

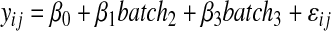graphic file with name M7.gif (3)

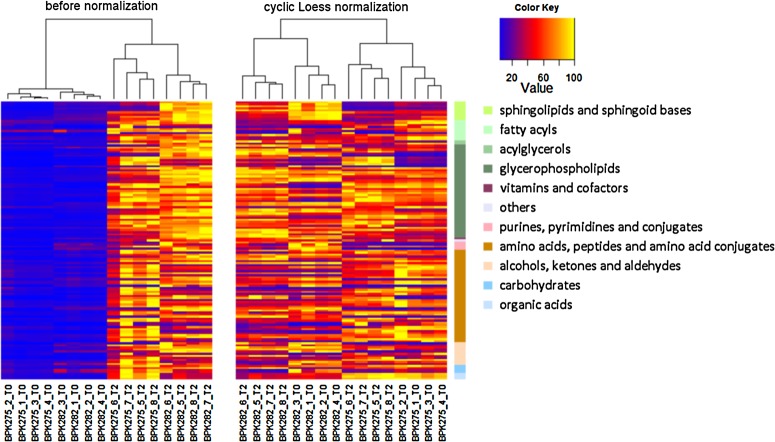
FIG. 5.

FIG. 5.

Open in a new tab

Metabolic profiles of the 135 metabolites detected in dataset II in heat map format with hierarchical clustering before normalization (left) and after cyclic-Loess normalization (right). The samples are presented along the x-axis, the 135 detected metabolites are presented along the y-axis; the major classes of metabolites are color coded on the right. The intensity of each metabolite was rescaled between 0 (blue) and 100 (yellow). Before normalization, the clustering algorithm detects the measurement period as group. After normalization, the sensitive and resistant strains are properly separated by the clustering.

where yij is the log intensity value for metabolite i at run time j, and batch2 and batch3 are indicator variables for measurement taken from T2 and T3, respectively, for dataset I Subset A, and for Subset B only batch2 kept in the model.

If the batch effects (time block) are successfully removed, their effects should become equal (β1=β2). This ANOVA model was also used to find differentially abundant metabolites for the validation data set.

Results

To find the optimal normalization method, we used two different datasets that both have been measured at different time blocks: (i) a commercially available amino acid standard mixture, and (ii) an extract of the protozoan parasite Leishmania donovani. The most optimal normalization method was selected and validated on a previously published L. donovani dataset (t'Kindt et al., 2010b) to show that it succeeds in removing systematic difference between samples but still accurately reproduces fold changes. A. fortiori, pooling the normalized data from multiple measurement campaigns lead to an increased sample size that enables a more powerful detection of differences in the metabolomics profile.

Observed variation in the original dataset

Both principal component analysis and box-whisker plots (Fig. 3) distinguish a clear clustering per time block for the replicate runs of both the amino acid standard (Set I Subset A) and the Leishmania sample (Set I Subset B). While systematic variation between time blocks is present in all data (Sub-)sets, it is important to note that in each (Sub-)set, other plausible sources of variation inherent to the origin of the extracts or standards, can be present. As such, Subset A of dataset I likely also contains variation induced by random errors in sample dilution, while Subset B of Set I might contain variation induced by storage of the extract at −80°C between T0 and T2. Supplementary Figure 2S shows how the experiment-oriented biases influence the measured intensity for four randomly selected compounds from dataset I Subset A. Besides systematic LC-MS difference, Set II contains additional biological and technical components in its total variation induced by the independent cultures at the two different time blocks and the preparation of the extracts from these cultures at those time blocks, respectively.

For both subsets, the largest variability (presented by principal component 1 which shows the greatest variability in the dataset: PC1>80%) is observed between samples measured on T0 and T2 (Fig. 3a). The box-plots in Figure 3b further clarify that the signal intensity of the T0 dataset is much lower compared to the other time blocks (total ion count of T0 dataset is 7-fold lower). The second principal component presents the second largest variability in the dataset and shows the separation between T2 and T3 in the amino acid standard dataset (PC2=9.62%). An ‘intra-batch variability’ is observed for both datasets. For example, PC2=12.8% illustrates this variability for the Leishmania sample. It is unlikely that storage of the Leishmania sample at −80°C is responsible for the large ‘inter-batch variability’ because a similar variability (PC2=9.62%) is observed for the amino acid standard replicates that were freshly made for each time block, suggesting that the variability induced by storage is equivalent to the variability of pipetting out a fresh standard.

Variation after applying normalization techniques

To evaluate the performance of the different normalization methods, normalized data were presented in a box-plot (Fig. 4 and Supplementary Fig. 3S) and heat map format (Supplementary Figs. 4S and 5S). The variance and the coefficient of variation were calculated and presented in Table 1 and the line plot in Figure 2. For the purpose of direct visual comparison, only results from the normalization methods which have the same scale as the original data are presented. Figure 4 presents the box-whisker plots for the log-intensity of amino acid standard before (Fig. 4a) and after different normalization methods (Fig. 4b–4f). The same plots have been constructed for the Leishmania sample of Subset B of dataset I and can be found in the Supplementary Material (Supplementary Fig. 3S). Supplementary Figure 4S shows the heat map of the amino acid standard data before and after normalization. In the plotted heat map, the 22 LC-MS experiments are presented along the x-axis, and the 28 identified amino acids (and derivatives) are depicted along the y-axis. The original intensity of each metabolite in the sample set was rescaled to a range between 0 (blue) and 100 (yellow). A similar heat map was provided for the Leishmania sample (Subset B of dataset I, Supplementary Fig. 5S). In addition, Figure 2 (top panel) shows the variance of the replicated measurements for a given metabolite across the experimental runs, whereas Figure 2 (lower panel) shows the box-whisker plots for the coefficients of variation. Normalization by using a reference metabolite (i.e., an amino acid standard that remained constant across different runs) does not perform well as compared to the data-driven methods (Supplementary Fig. 6S). Thus, normalization on a limited set of internal standards is not easily extrapolated to the entire set of analytes in the data.

Table 1.

Summary Statistics for Variance and Coefficient of Variation Based on Replicate Measurements Before and After Normalization of Amino Acid Standard and Leishmania Sample

 
 Amino acid standard
 Leishmania sample
 
 Variance
 Coefficient of variation
 Variance
 Coefficient of variation
Normalization method mean St. Dev Mean St. Dev Mean St. Dev Mean St. Dev
Original data 1.2904 0.3767 0.0456 0.0064 3.4320 2.1241 0.0845 0.0283
Baseline 0.1363 0.1422 0.0133 0.0074 0.3995 0.8494 0.0254 0.0240
Loess 0.1060 0.1101 0.0119 0.0066 0.4364 0.9204 0.0252 0.0232
Cubic 0.2405 0.5187 0.0154 0.0157 0.3954 0.7832 0.0241 0.0216
PQN 0.1344 0.1430 0.01333 0.0077 0.4104 0.9166 0.0251 0.0252
Quantile 0.1302 0.1468 0.01268 0.0074 0.3903 0.7753 0.0255 0.0233
Open in a new tab

St. Dev, standard deviation.

It becomes clear that all the employed normalization methods considerably reduce the variability observed in the original data (Fig. 3, Table 1, Supplementary Fig. 7S). First, Figure 4 clearly shows that normalization removes the block effects seen in the original data. After normalization, the mean intensities are similar across different experimental runs. For quantile normalization, the distribution of the normalized intensity is identical across experimental runs as expected for any type of datasets (Fig. 4f). According to the ANOVA model results (Supplementary Table 1S), and the box-plot of the CVs, showed a significant difference between normalized and non-normalized data [Fig. 2 (lower panel)]. The whiskers of the box-plots ARE lie on the same interval for the different normalization methods (Fig. 2b). Hence, there is no statistically significant difference between the different normalization methods (Fig. 2). These findings are also reflected in the heat maps of the data shown in Supplementary Figures 4S and 5S.

Nevertheless, the CV shows that the cyclic-Loess and cubic-spline normalization methods performed slightly better for the amino acid standards and the Leishmania sample, respectively, (Table 1) in terms of variance reduction. Hence, the cyclic-Loess normalization method was selected for the validation section, although, in general, all normalization methods performed well.

Validation of the selected normalization technique

In this Section, we evaluate the performance of the cyclic-Loess normalization on an additional dataset (Set II in Fig.1). In ideal circumstances, this dataset would be the result of a designed experiment, which contains positive and negative controls. The positive controls could be spiked-in metabolites with known differential concentrations, which could show that a given normalization removes unwanted variation while retaining the biologically interesting effects. In such a case, normalization should not attenuate nor amplify the measurements of the spiked-in concentration differences of the positive controls. The negative controls could be standards that are present at a constant concentration in all the samples of the experiment (cfr., Subset I of dataset I). In that case, normalization should not change the intensity measurements of the internal standards. For the purpose of the validation, we used the dataset described in the Material and Methods Section (Fig.1, Set II), which does not contain aforementioned controls. However, it should be pointed out that experiments similar to the one described above have been conducted in the past by t'Kindt et al. (2010b). In the experiment, metabolic differences correlated to antimonial-resistance have been reported and validated through biological assays for the Leishmania strains under scrutiny. The outcome of the previous study can serve as the set of positive and negative controls in order to evaluate to which extent the normalization influences the reported statistics or fold changes and whether the findings are reproducible. It should be mentioned that the dataset of t'Kindt et al. (2010b) was recorded in a different laboratory by using a different technology.

The distribution of the logarithmically transformed intensities of the 135 identified metabolites is visualized by the box-plots in Supplementary Figure 8S for the non-normalized and cyclic-Loess normalized data. The mean intensity level of the 135 metabolites measured on time block T2 are higher as compared to the measurements of T0 (Fig. 8bS). We can already state that the cyclic-Loess normalization was able to remove the systematic effect in a similar fashion as indicated by previous data sets (Fig. 8cS). Furthermore, it can be noted that, within a measurement period, the metabolite intensity distributions between the sensitive (BPK282) and resistant (BPK275) parasite isolates are comparable (Supplementary Fig. 8bS). The absence of such a pronounced systematic effect within a measurement period makes the data especially suited to study the impact of normalization on a downstream statistical analysis. In other words, by conducting the statistical analysis within the time block before and after normalization, we can evaluate if the number of differential findings and their consistency is influenced, since, in this case, there is no apparent need for data normalization.

A straightforward method to assess the quality of the normalization can be achieved by a hierarchical clustering approach (HCA) on the metabolite intensities (constructed with heat map.2 function from gplots package in R). The clustering algorithm looks for correlations between the metabolomics profiles and aims to group similar data together. The heat map in Figure 5 illustrates this principle. Clearly, the intensity differences between the measurement blocks are large, as indicated by the color code. These obvious differences are captured by the hierarchical clustering. As a result, metabolomics profiles within a time block are recognized as similar and consequently, are grouped together. The grouping is illustrated by the tree-like structure at the top of the figure. On the other hand, after normalization, the heat map seems more uniform and therefore the clustering algorithm groups the data according to other metabolite features. In this case, it can be seen that the resistant and sensitive strains are grouped together. Note that the grouping at the lower hierarchical levels in the treelike structure still reveals the time block structure, which can be due to technical differences in the preparation of the samples. This preliminary and simple analysis already indicates that normalization removes the unwanted systematic block effects while retaining the valuable metabolite information. In the next analysis, we evaluate the effect of normalization on the results of a statistical analysis.

A simple statistical analysis by means of volcano plots (Cui et al, 2003) (Fig. 6) is proposed. Metabolites are considered to be statistically and biologically significant when they have a p value below a 5% significance level based on a two-sample t-test and an average fold change larger than 2.

FIG. 6.

FIG. 6.

Open in a new tab

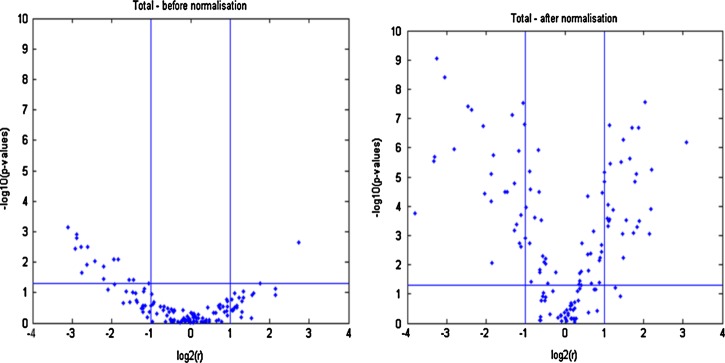
Volcano plot of the pooled data (a) before and (b) after normalization. The plots indicate that the systematic effect results in an increased variability, which yields lower −log10 (p values) (plot a).

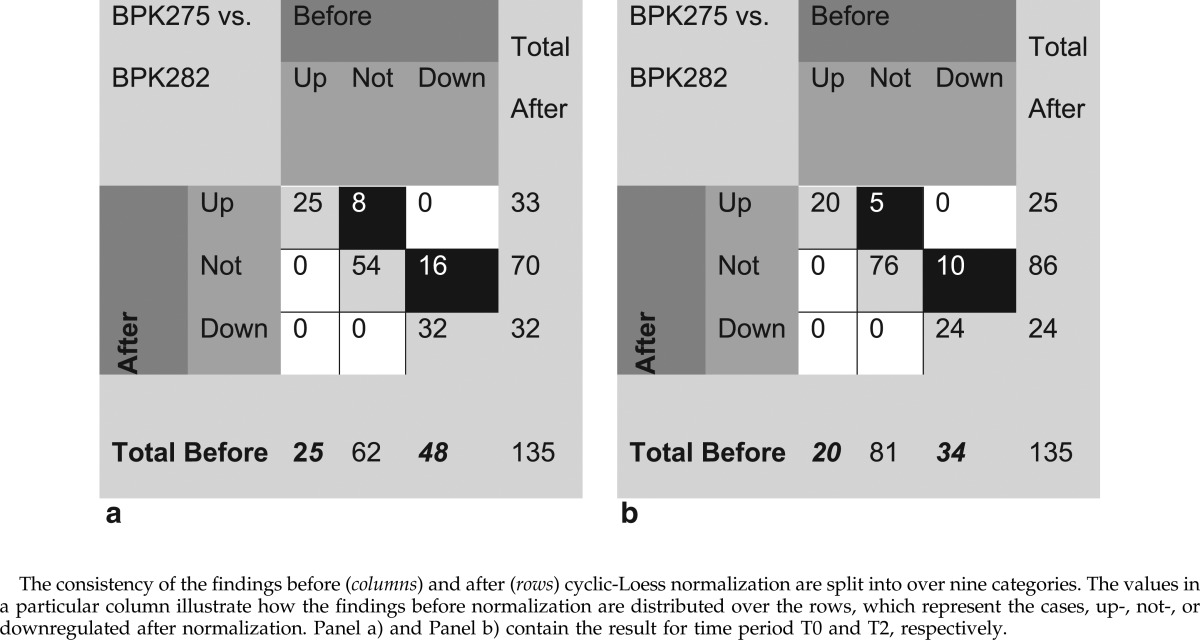
In a first step, a Volcano plot analysis is conducted for each time period T0 and T2 separately using aforementioned thresholds. The number of differential findings, comparing the analysis before and after normalization, when comparing parasite isolate BPK275 with BPK282 in time period T0, is reported in Table 2a. Before normalization, 25 metabolites were upregulated, 48 metabolites were downregulated, and 62 metabolites were not differentially regulated. This information can be read from Table 2a in the row indicated with the label ‘Total Before’. The column with the label ‘Total After’ in Table 2a, illustrates the results after data normalization (i.e., 33, 32, and 70 metabolites found to be up-, down, and non-differentially-regulated, respectively). Because the aim of the study is to evaluate the effect of data normalization, the results are split into nine categories to illustrate the consistency of the differential findings before and after normalization. In ideal circumstances, when normalization would not influence the results of a statistical analysis at all, a complete agreement of the differential findings would be achieved. In such a situation, only the diagonal cells (highlighted in light gray) that indicate the number of metabolites which are found to be up-, not- or downregulated in the analysis before and after normalization, should contain values. However, in this study, 8 metabolites (highlighted in black in Table 2a) that were not differentially expressed using the data before normalization, were found to be upregulated after the normalization. Similarly, there are 16 metabolites (highlighted in black in Table 2a) that were downregulated before normalization, and were not differentially expressed after normalization. The same trend is also present in Table 2b (highlighted in black). A possible explanation is the presence of a slight systematic bias between the parasite isolates BPK275 and BPK282, as can be observed in Figure 8S. The figure illustrates that the log-intensity distribution of the BPK282 isolates are slightly higher than BPK275 when comparing within the time periods. Nevertheless, it is reassuring that the majority of the findings for the 135 metabolites are in the diagonal cells, highlighted by light gray in Table 2 (i.e., are consistently found before and after normalization). This result indicates indeed that within a time period, a good reproducibility of the measurements was achieved with negligible systematic effects. The effect of an unnecessary normalization does not alter the outcome of a statistical analysis severely. A similar observation can be made when looking at the findings in time period T2 displayed in Table 2b.

Table 2.

Result of Statistical Analysis Between BPK275 and BPK282 on 135 Metabolites with p<0.05 and Fold Change of >2, Before and After Normalization

graphic file with name fig-7.jpg
Open in a new tab

Second, in a statistical analysis it is good practice to include all available data because a larger sample size enables a more powerful test to discern differential metabolites. Instead of performing an analysis for each time period separately, it is preferable to pool the collected data. Therefore, the same statistical test, as described earlier, was applied on the pooled data set, before and after normalization. Panel a of Table 3 contains the results of the analysis before data normalization and compares them with our benchmark dataset published by t'Kindt et al. (2010) and described in Materials and Methods. The table should be interpreted similarly as the consistency matrix presented in Table 2. It can be noted that pooling the data without accounting for systematic variation is undesirable, as only 1 out of the 31 upregulated metabolites from t'Kindt et al., is found to be upregulated in dataset II. Furthermore, 11 out of 19 downregulated metabolites from t'Kindt et al. are downregulated in dataset II. A possible explanation for this poor agreement is that, in this case, pooling the data sets increases the variability present in the data and makes it more difficult to detect statistically significant differences regardless the higher number of data points in the pooled analysis. In fact, there seems also to be a bias towards finding mostly downregulated metabolites. For these reasons, it is mandatory to remove the systematic bias from the data prior to a statistical analysis. Panel b of Table 3 contains the result of the statistical analysis after applying normalization. It can be observed that the agreement between the differential findings of t'Kindt et al. (2010b) and dataset II is improved (i.e., 16 out of 31 and 15 out of 19 are consistently found up- and downregulated, respectively). However, the agreement between both studies is still poor, regardless which normalization strategy is used. The cells highlighted in black from Panel b of Table 3 illustrate the disagreement. For example, in dataset II, there are 13 additional upregulated metabolites that could not be found by t'Kindt et al. However, it is reassuring that 9 of the 13 additional metabolites were below the limit of quantification in the study of t'Kindt et al. and consequentially were classified as not regulated. A similar conclusion can be drawn for the 12 downregulated metabolites. Closer inspection of the results confirm that, although the metabolites are not found differential according to the volcano plots, the same trends with respect to up- and downregulation were observed (Fig. 6). As depicted in Supplementary Figure 9S (Supplementary material are available online at www.liebertpub.com/omi), two-fold change increases or decreases are indicated by blue and red dots for each identified analyte. A possible reason for these inconsistent findings is due to inter-laboratory variation. It is worth keeping in mind that the results of t'Kindt et al. were obtained one year earlier (2010) on another LC-MS platform (2.1 mm HILIC column coupled to a Finnigan LTQ-Orbitrap XL mass spectrometer) and that the biological samples, although originating from the same Leishmania clone and prepared by the same protocol in the same laboratory settings, might be slightly different. A possible conclusion from these observations could be a more optimal validation data set is required.

Table 3.

Result of Statistical Analysis Between BPK275 and BPK282 on 135 Metabolites with p<0.05 and Fold Change of >2 for Dataset II and Findings of t'Kindt et al.

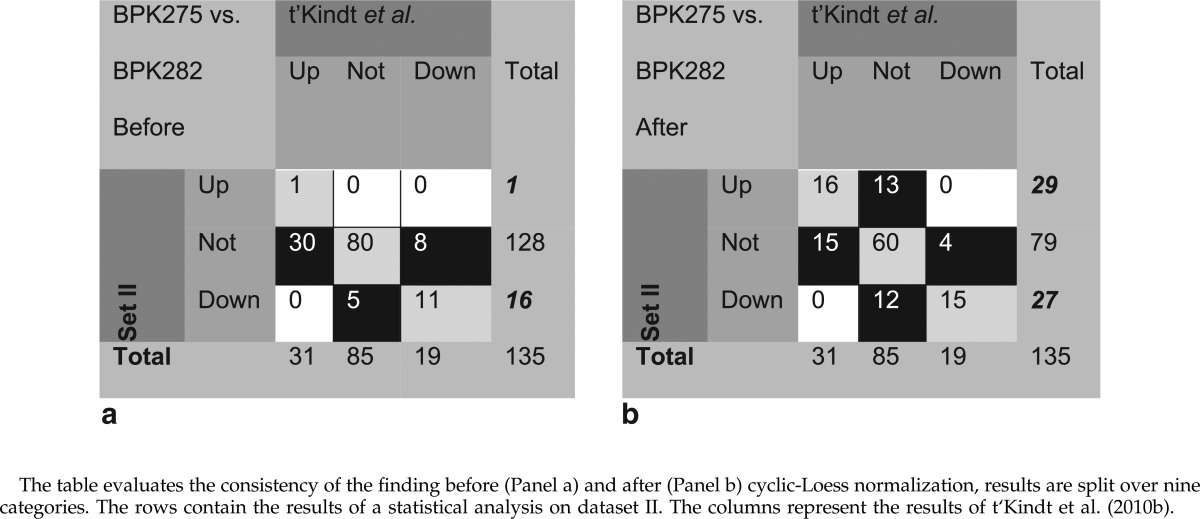graphic file with name fig-8.jpg
Open in a new tab

However, when comparing the differential findings on dataset II before and after normalization across Panels a and b of Table 3, as highlighted by bold and italic numbers in the columns indicated by ‘Total’, one can conclude that pooling without taking into consideration the systematic effects is unfavorable for a downstream analysis: after normalization, 29 and 27 differential metabolites could be found opposed to the 17 differential findings before normalization. The numbers indicated by bold and italic in Panel b of Table 3 could be contrasted with the bold and italic numbers of the two panels in Table 2. Indeed the number of differential metabolites found when analyzing the separate time blocks before normalization corresponds to the findings presented in Panel b of Table 3.

Third, to put previous results in a better perspective and to illustrate that the inconsistent findings are not an artifact of the data normalization, we compared the statistical analysis on the time blocks T0 and T2 before normalization separately with the findings of t'Kindt et al. (2010b). Such a comparison is valid because only a slight systematic bias was present in the time blocks, as indicated by Table 2. The results of the comparison are displayed by the consistency matrix of Supplementary Table 2S (Supplementary Data are available online at www.liebertpub.com/omi) for time period T0 (Panel a) and T2 (Panel b). The cells highlighted in black indicate inconsistent findings across the comparison and confirms our hypothesis that these changes are primarily caused by inter-laboratory variation. More information on the consistency of findings is provided in Supplementary Figure 9S (Supplementary Material is available online at www.liebertpub.com/omi), which illustrates that in this example downregulated metabolites are consistently found disregarding the normalization.

Another way of illustrating the consequences of not properly accounting for the systematic effects is provided by the volcano plot presented in Figure 6. The plots indicate that the systematic variation results in an increased variability, which yield lower −log10 (p values). In addition, there seems to be a linear trend in the averaged ratios (resistant/sensitive strain) when compared to the normalized data, where the ratios are more scattered in the plot.

Discussion

A majority of metabolomics publications address the issue of normalization by using internal standards (Bijlsma et al., 2006, Gullberg et al., 2004, Redestig et al., 2009; Sysi-Aho et al., 2007). However, in the case of metabolomics studies, spiking of a standard reference material into the sample of interest is often not practical due to the high cost, the limited availability, and the correct choice (in the case of an untargeted approach the metabolites of interest are not known beforehand). In order to illustrate the performance of a normalization approach based on an internal standard, dataset I Subset A was normalized by using serine as a reference metabolite. The result shows that this normalization technique does not perform as well as data-driven normalization techniques (Fig. 7S). Ridder and coauthors (2002) also showed that the improvement in normalization factor increases proportionally to the square root of the number of internal standards. Hence, correction of the systematic variability based on only a small subset of internal standards is not recommended. In this article, we have evaluated the performance of several data-driven normalization techniques that were developed for microarray data when applied to LC-MS data without spiked standards. A comparison between normalization methods was based on the extent of the removal of the systematic variability observed between replicate runs of an amino acid standard and a Leishmania sample (Fig. 1, Set I). Successful normalization should reduce the inter- and intra-batch variability, as compared with original (non-normalized) data. The employed normalization methods significantly reduce the variability between the measured intensity levels that were observed in the original (non-normalized) datasets. According to the ANOVA model (Supplementary Table 1S) and variability measures, significant differences between the variance for the different normalization methods were absent (Fig. 2 and Supplementary Fig. 7S). Each of the employed normalization methods performed relatively well. Thus, using any of the normalization methods will greatly improve data analysis. Based on the coefficient of variation, cyclic-Loess normalization performed slightly better than the other methods, and was used for a validation experiment on a biologically relevant Leishmania dataset (Fig. 1, Set II). Normalization of this dataset succeeded in the removal of the systematic variability and maintained the majority of the differential metabolites. Moreover, it allowed pooling datasets from different time blocks and increased the number of metabolites found to be differentially regulated as compared to the non-normalized pooled datasets, allowing increase of the power of the statistical analysis and the scale of the LC-MS metabolomics experiments.

Different publications including this one, describe normalization as an independent step in the data processing workflow. However, data normalization cannot be seen as disconnected from the statistical analysis. However, by disconnecting the normalization from the statistical analysis, information about uncertainty concerning the normalization factors is lost. As pointed out by Haldermans et al. (2007) and Hill et al. (2008), following a good statistical practice, we should think about data analysis and normalization as one comprehensive model. In addition to the employed normalization methods mentioned in this study, more modern, but less accessible normalization methods aimed at removing batch effects in microarray data were mentioned by Johnson et al. (2007) and Redestig et al. (2009), respectively. An elaborate study of these new generation algorithm will be part of future research.

Conclusion

The employed data-driven normalization methods succeeded in the removal of systematic variability, and allowed pooling datasets from different experimental runs to increase the power of the statistical analysis. It is important to indicate that data normalization should not be expected to correct for all sources of variability introduced by different source of biases (i.e., extract preparation and sample storage). Normalization should be regarded more as a remedial measure to combine data obtained from different experimental runs. From our investigation, we recommend data-driven normalization methods over model-driven normalization methods, if only a few internal standards were used. Thus, data normalization on a limited set of internal standards is not easily extrapolated to the entire set of analytes in the data. But, even though it is impractical for untargeted experiments, if every analyte had its own label, we would prefer an internal standard-based normalization. In our discovery study, since the number of analytes of interest is unknown, internal standards cannot be obtained even if the cost and scarcity did not play any role. Therefore, data-driven normalization methods are the only options to normalize the entire dataset collected from untargeted LC-MS experiments.

Supplementary Material

Supplemental data
supp_data.zip (1.1MB, zip)

Acknowledgments

The authors would like to thank Andris Jankevics (University of Manchester, University of Glasgow, University of Groningen), Prof. Dr. Frank Sobott (Centre for Proteomics, University of Antwerp), and Ilse Maes for helpful discussions and technical support. We also would like to thank Prof. Dr. Bert Maes for the use of the Waters Acquity UPLC system. This research was funded by the GeMInI consortia (grant ITMA SOFI-B), the Research Foundation Flanders (FWO project G.0B81.12 ), the Inbev-Baillet Latour Fund (grant for M.B.), and the EC-FP7 project Kaladrug-R (contract 222895). Support from the IAP Research Network P7/06 of the Belgian State (Belgian Science Policy) is gratefully acknowledged.

Author Disclosure Statement

The authors declare that no competing financial interests exist.

References

  1. Amaratunga D. Cabrera J. New York: John Wiley & Sons, Inc; 2004. Exploration and Analysis of DNA Microarray and Protein Array Data. [Google Scholar]
  2. Astrand M. Contrast normalization of oligonucleotide arrays. J Comput Biol. 2003;10:95–102. doi: 10.1089/106652703763255697. [DOI] [PubMed] [Google Scholar]
  3. Baggerly KA. Coombes KR. Morris JS. Bias, randomization, and ovarian proteomic data: A reply to “Producers and Consumers”. Cancer Informatics. 2005;1:9–14. [PMC free article] [PubMed] [Google Scholar]
  4. Bijlsma S. Bobeldijk I. Verheij ER, et al. Large-scale human metabolomics studies: A strategy for data (pre-) processing and validation. Anal Chem. 2006;78:567–574. doi: 10.1021/ac051495j. [DOI] [PubMed] [Google Scholar]
  5. Berg M. Vanaerschot M. Jankevics A. Cuypers B. Breitling R. Dujardin JC. LC-MS metabolomics from study design to data-analysis: Using a versatile pathogen as a test case. Comput Struct Biotechnol J. 2013;4/5 doi: 10.5936/csbj.201301002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Bilban M. Buehler LK. Head S. Desoye G. Quaranta V. Normalizing DNA microarray data. Curr Issues Mol Biol. 2002;4:57–64. [PubMed] [Google Scholar]
  7. Breitling R. Bakker BM. Barret MP. Decuypere S. Dujardin JC. Metabolomic systems biology of protozoan parasites. In: Suhre K., editor. Chapter 6. Genetics Meets Metabolomics: From Dxperiment to Systems Biology; 2012. [DOI] [Google Scholar]
  8. Cui X. Churchill GA. Statistical tests for differential expression in cDNA microarray experiments. Genome Biol. 2003;4:210. doi: 10.1186/gb-2003-4-4-210. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Dillies MA. Rau A. Aubert J, et al. A comprehensive evaluation of normalization methods for Illumina high-throughput RNA sequencing data analysis. Brief Bioinform. 2012 doi: 10.1093/bib/bbs046. [DOI] [PubMed] [Google Scholar]
  10. Dunn WB. Broadhurst D. Begley P, et al. Procedures for large-scale metabolic profiling of serum and plasma using gas chromatography and liquid chromatography coupled to mass spectrometry. Nature Protocols. 2011;6:1060–1083. doi: 10.1038/nprot.2011.335. [DOI] [PubMed] [Google Scholar]
  11. Fahy E. Sud M. Cotter D. Subramaniam S. LIPID MAPS online tools for lipid research. Nucleic Acids Res. 2007;35:W606–W612. doi: 10.1093/nar/gkm324. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Gullberg J. Jonsson P. Nordström A. Sjöström M. Moritz T. Design of experiments: An efficient strategy to identify factors influencing extraction and derivatization of Arabidopsis thaliana samples in metabolomic studies with gas chromatography/mass spectrometry. Anal Biochem. 2004;331:283–295. doi: 10.1016/j.ab.2004.04.037. [DOI] [PubMed] [Google Scholar]
  13. Haldermans P. Shkedy Z. Van Sanden S. Burzykowski T. Aerts M. Using linear mixed models for normalization of cDNA microarrays. Stat Appl Genet Mol Biol. 2007;6 doi: 10.2202/1544-6115.1249. Article 19. [DOI] [PubMed] [Google Scholar]
  14. Hill AA. Brown EL. Whitley MZ. Tucker-Kellogg G. Hunter CP. Slonim DK. Evaluation of normalization procedures for oligonucleotide array data based on spiked cRNA controls. Genome Biol. 2001;2:RESEARCH0055. doi: 10.1186/gb-2001-2-12-research0055. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Hill EG. Schwacke JH. Comte-Walters S, et al. A statistical model for iTRAQ data analysis. J Proteome Res. 2008;7:3091–3101. doi: 10.1021/pr070520u. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Jankevics A. Merlo ME. de Vries M. Vonk RJ. Takano E. Breitling R. Separating the wheat from the chaff: A prioritisation pipeline for the analysis of metabolomics datasets. Metabolomics. 2012;8:29–36. doi: 10.1007/s11306-011-0341-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Johnson WE. Li C. Rabinovic A. Adjusting batch effects in microarray expression data using empirical Bayes methods. Biostatistics. 2007;8:118. doi: 10.1093/biostatistics/kxj037. [DOI] [PubMed] [Google Scholar]
  18. Kohl SM. Klein MS. Hochrein J. Oefner PJ. Spang R. Gronwald W. State-of-the-art data normalisation methods improve NMR-based metabolomic analysis. Metabolomics. 2011;8:146–160. doi: 10.1007/s11306-011-0350-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Leek JT. Storey JD. Capturing heterogeneity in gene expression studies by surrogate variable analysis. PLoS Genetics. 2007;3:e161. doi: 10.1371/journal.pgen.0030161. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Mar J. Kimura Y. Schroder K, et al. Data-driven normalization strategies for high-throughput quantitative RT-PCR. BMC Bioinformat. 2009;10:110. doi: 10.1186/1471-2105-10-110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Prince JT. Marcotte EM. Chromatographic alignment of ESI-LC-MS proteomics data sets by ordered bijective interpolated warping. Anal Chem. 2006;78:6140–6152. doi: 10.1021/ac0605344. [DOI] [PubMed] [Google Scholar]
  22. R Development Core Team. R Foundation for Statistical Computing; Vienna, Austria: 2011. [Aug;2012 ]. R: A language and environment for statistical computing. ISBN 3-900051-07-0, URL. [Google Scholar]
  23. Redestig H. Fukushima A. Stenlund H, et al. Compensation for systematic cross-contribution improves normalization of mass spectrometry based metabolomics data. Anal Chem. 2009;81:7974–7980. doi: 10.1021/ac901143w. [DOI] [PubMed] [Google Scholar]
  24. Ridder FD. Pintelon R. Schoukens J. Navez J. Andre L. Dehairs F. An improved multiple internal standard normalisation for drift in LA-ICP-MS measurements. JAAS. 2002;17:1461–1470. [Google Scholar]
  25. Scheltema RA. Decuypere S. Dujardin JC. Watson DG. Jansen RC. Breitling R. Simple data reduction method for high-resolution LC-MS data in metabolomics. Bioanalysis. 2009;1:1551–1557. doi: 10.4155/bio.09.146. [DOI] [PubMed] [Google Scholar]
  26. Scheltema R. Jankevics A. Jansen RC. Swertz MA. Breitling R. PeakML/mzMatch: A file format, Java library, R library, and tool-chain for mass spectrometry data analysis. Anal Chem. 2011;83:2786–2793. doi: 10.1021/ac2000994. [DOI] [PubMed] [Google Scholar]
  27. Schmid R. Baum P. Ittrich C, et al. Comparison of normalization methods for Illumina BeadChip HumanHT-12 v3. BMC Genomics. 2010;11:349. doi: 10.1186/1471-2164-11-349. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Sysi-Aho M. Katajamaa M. Yetukuri L. Oresic M. Normalization method for metabolomics data using optimal selection of multiple internal standards. BMC Bioinformat. 2007;8:93. doi: 10.1186/1471-2105-8-93. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Tautenhahn R. Böttcher C. Neumann S. Highly sensitive feature detection for high resolution LC/MS. BMC Bioinformat. 2008;9:504. doi: 10.1186/1471-2105-9-504. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. t'Kindt R. Jankevics A. Scheltema RA, et al. Towards an unbiased metabolic profiling of protozoan parasites: Optimization of a Leishmania sampling protocol for HILIC-orbitrap analysis. Analyt Bioanal Chem. 2010a;398:2059–2069. doi: 10.1007/s00216-010-4139-0. [DOI] [PubMed] [Google Scholar]
  31. t'Kindt R. Scheltema RA. Jankevics A, et al. Metabolomics to unveil and understand phenotypic diversity between pathogen populations. Plos Neg Tropic Dis. 2010b;4:e904. doi: 10.1371/journal.pntd.0000904. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Valkenborg D. Thomas G. Krols L. Kas K. Burzykowski T. A strategy for the prior processing of high-resolution mass spectral data obtained from high-dimensional combined fractional diagonal chromatography. J Mass Spectrom. 2009;44:516–529. doi: 10.1002/jms.1527. [DOI] [PubMed] [Google Scholar]
  33. van den Berg RA. Hoefsloot HCJ. Westerhuis JA. Smilde AK. van der werf MJ. Centering, scaling, and transformations: Improving the biological information content of metabolomics data. BMC Genom. 2006;7:142. doi: 10.1186/1471-2164-7-142. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. van der Kloet FM. Bobeldijk I. Verheij ER. Jellema RH. Analytical error reduction using single point calibration for accurate and precise metabolomic phenotyping. J Proteome Res. 2009;8:5132–5141. doi: 10.1021/pr900499r. [DOI] [PubMed] [Google Scholar]
  35. Vandesompele J. De Preter K. Pattyn F, et al. Accurate normalization of real-time quantitative RT-PCR data by geometric averaging of multiple internal control genes. Genome Biol. 2002;3 doi: 10.1186/gb-2002-3-7-research0034. RESEARCH0034. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Wang W. Zhou H. Lin H, et al. Quantification of proteins and metabolites by mass spectrometry without isotopic labeling or spiked standards. Anal Chem. 2003;75:4818–4826. doi: 10.1021/ac026468x. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplemental data
supp_data.zip (1.1MB, zip)

Articles from OMICS : a Journal of Integrative Biology are provided here courtesy of Mary Ann Liebert, Inc.

RESOURCES