Abstract
We present a new model of airway smooth muscle (ASM), which surrounds and constricts every airway in the lung and thus plays a central role in the airway constriction associated with asthma. This new model of ASM is based on an extension of sliding filament/crossbridge theory, which explicitly incorporates the length distribution of thick sliding filaments to account for a phenomenon known as dynamic passive length adaptation; the model exhibits good agreement with experimental data for ASM force–length behaviour across multiple scales. Principally these are (nonlinear) force–length loops at short timescales (seconds), parabolic force–length curves at medium timescales (minutes) and length adaptation at longer timescales. This represents a significant improvement on the widely-used cross-bridge models which work so well in or near the isometric regime, and may have significant implications for studies which rely on crossbridge or other dynamic airway smooth muscle models, and thus both airway and lung dynamics.
Keywords: Crossbridge model, Myosin filament length distribution, Airway constriction, Asthma
1. Introduction
Understanding the behaviour of airway smooth muscle (ASM) is crucial to understanding the reversible airway obstruction central to asthma. A layer of ASM surrounds each airway in the lung, and ASM activation thus leads to airway narrowing (and, potentially, closure). Similarly the relaxation of ASM may reverse airway narrowing or closure; mechanisms which limit the ability of ASM to exert force are especially important.
The relationship between airway calibre and force is thus central to understanding the dynamic processes associated with asthma, and ASM exhibits a rich series of behaviours in this regard. These are often termed force–length relationships, where of course the length of the ASM wrapped around the airway is connected with airway calibre.
There are three characteristic behaviours widely seen in active ASM, each occurring at a different scale. It is important to note that in what follows we consider only the active component of ASM, with the passive component excluded.
Force–length loops: At the shortest timescale, with length oscillations measured in seconds, ASM exhibits a characteristic, nonlinear, hysteretic force–length ‘loop’ where the degree of hysteresis and nonlinearity are dependent on the amplitude and frequency of the length oscillations (Mijailovich et al., 2000; Bates et al., 2009). These are sometimes referred to as ‘banana-shaped’ and a typical example is reproduced in the left panel of Fig. 1.
Force–length curves: At an intermediate timescale, measured in minutes, changes in the length of ASM affect a change in the ability of the muscle to exert force. Typically the peak of this force–length curve, where maximal force is exerted, is at what is called the adapted length. Increases or decreases away from this adapted length result in reductions in exerted force, and the typical shape might be roughly characterised by an inverted quadratic (Wang et al., 2001; Gunst and Stropp, 1988). Typical data are reproduced in the right panels of Fig. 1, where one should consider for now only a single curve. The peak of any single curve is the adapted length; if the muscle is shortened or lengthened away from this value the exerted force will be decreased as shown after 5 min.
Length adaptation: If left at a new length for a suf ficiently long time, ASM will adapt to its new length, now exerting peak force at this new length (Wang et al., 2001; Bossé et al., 2008)—thus ASM can exert maximal force at any length. Moreover, if the force–length curve protocol is repeated at this new adapted length, the same characteristic shape is observed, which can be seen in the experimental data reproduced in the right panels of Fig. 1, where the two panels illustrate passive shortening and lengthening, from top to bottom.
Fig. 1.
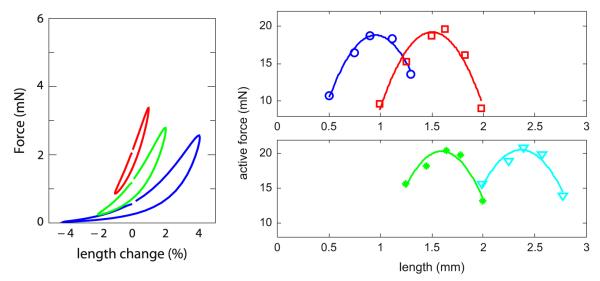
Characteristic ASM behaviours. Left panel: Force–length loops, data from Bates et al. (2009). These force measurements are taken with length oscillations imposed with amplitude 1, 2 and 4% of reference length and frequency 2 Hz. Right panels: Force–length curves and adaptation, data from Wang et al. (2001) with best-fit quadratics. Here in the top (bottom) panels the muscle is passively shortened (lengthened) to a new adapted length and allowed to re-equilibrate over 24 h. At each adapted reference length, the characteristic (1−L2) shape is observed, with adaptation simply shifting this shape left and right along the length axis. Peak force for each adapted length is roughly constant.
Because of the importance of ASM force–length dynamics to understanding airway and asthma dynamics, it is thus important to understand the origins of each of these representative behaviours. In this manuscript a new mathematical model of ASM is presented which accounts for all three via the explicit inclusion of thick filament length distributions. While existing models may account for one or more, none reproduce all; this is discussed in more detail below.
A number of models of ASM exist in the literature, and these can primarily be classified into two groups: viscoelastic models, and crossbridge models. The former category describes the muscle behaviour empirically using mechanical analogues (i.e. springs and dashpots) and is able, depending on the construction, to reproduce at least some of the characteristic force–length behaviours (i.e. Bates et al., 2009). The latter group is based on the sliding-filament model of Huxley (1957), which has been extended by several groups to incorporate important phenomena specific to smooth muscle (i.e. Hai and Murphy, 1988; Mijailovich et al., 2000; Wang et al., 2008). Later models of this type are capable of predicting reasonable force–length loops on the shortest timescale, but the combination of force–length curves and length adaptation remains unexplained with this family of models. In general, for existing crossbridge models the force–length curve is a length-independent constant rather than the desired parabolic shape, and thus the concept of adaptation is moot as the muscle already exerts equal force at all lengths.1 It is possible to impose, empirically, a force–length relationship which approximates the experimental data merely by a multiplicative scaling factor (i.e. Politi et al., 2010); however this approach has neither a biophysical basis, nor does it allow for adaptation.
Recently, the hypothesis that the force exerted by ASM is controlled by the ASM length-dependent overlap between adjacent thin filaments has gained traction (Seow, 2005; Ali et al., 2007; Seow and Fredberg, 2011; Syyong et al., 2011; Brook and Jensen, in press), and thus that changes in muscle length lead to changes in filament overlap and thus altered ASM force. Combined with the quantitative measurement of the distribution of thick filament lengths found in ASM, this allows the construction of a crossbridge-type model in which crossbridge binding sites are preferentially available within and near the thin filament overlap region, and dependent on the thick filament length distribution. The distribution of thick filament lengths provides a stochastic component, which determines the availability of binding sites. Away from the filament overlap region, then, binding sites are increasingly unavailable and thus exerted muscle force is reduced. This is the central hypothesis on which this model is based, and it provides a simple and elegant explanation for the characteristic force–length behaviours at all three scales. This has potentially important implications for understanding airway and asthma dynamics, and for other models which depend upon crossbridge or ASM dynamics as one of their constituent parts (i.e. Anafi and Wilson, 2001; Venegas et al., 2005; Politi et al., 2010; Amin et al., 2010).
There are other models in the literature which address length adaptation, including the empirical and viscoelastic type approaches of Ijpma et al. (2011) and Lambert et al. (2004), as well as the 2D cytoskeletal network model of Silveira et al. (2005). Here instead this phenomenon is incorporated into the well-known framework of the crossbridge model, obtaining appropriate force–length behaviours across the three scales discussed above.
2. Model
2.1. The crossbridge model
In order to understand the theoretical framework of the model presented in this manuscript, it is useful to outline briefly the basic precepts of crossbridge theory (see, i.e. Keener and Sneyd, 2008).
Based on the sliding filament theory of Huxley (1957) for striated muscle and extended to smooth muscle by Hai and Murphy (1988) and others (i.e. Mijailovich et al., 2000; Wang et al., 2008), the central concept is the binding of actin filaments to myosin filaments, and the asymmetric cycling of the so-called crossbridges. Actin and myosin are also referred to as the thin and thick filaments, respectively. The thick filament contains heads, known as crossbridges, which bind to the thin filament. It is the ratchet-like interaction of these crossbridge heads, which occurs asymmetrically, that generates muscle force. The relative sliding of these filaments along their length is then directly connected with the muscle length. This theory has been widely, and successfully deployed to account for a number of important aspects of smooth muscle behaviour. The typical model for ASM thus consists of four populations: unphosphorylated, unbound myosin (M); phosphorylated, unbound myosin (Mp); bound, phosphorylated (AMp); bound, dephosphorylated (AM). Transitions between these states are governed by (spatially-independent) phosphorylation and dephosphorylation rates, and spatially-dependent binding and unbinding. The model is illustrated schematically in Fig. 2, specifically the gray portion (the black is part of the new model, to be discussed). The relative sliding velocity of the filaments is connected with the ASM length, and thus one arrives at a coupled set of hyperbolic partial differential equations governing the evolution of the populations. The force exerted is then given by the moment integral
| (1) |
under the assumption that both bound species exert equal force.
Fig. 2.

Model schematic illustrating population states and transition rates. The new treatment of unavailable sites is in black, while the standard 4-state crossbridge model is in grey. The new state A for unavailable binding sites is populated from unbound myosin, phosphorylated or not, by the spatially-dependent transition rate fE(x) (see text). Re-equilibration occurs via the slow recovery rate gE. The other populations are governed by traditional crossbridge mechanics (i.e. Mijailovich et al., 2000; Wang et al., 2008).
2.2. Unavailable sites and partial length adaptation
The model of partial length adaptation presented in this manuscript is formulated according to the following principles:
Traditional crossbridge models work well in isometric conditions, and near adapted length.
Availability of crossbridge binding sites is determined by the thin filament overlap region and thick filament length distribution—there is high binding site availability in and near the overlap region at steady state.
Away from the overlap region, binding sites are increasingly unavailable, leading to a reduction in exerted force.
Once disrupted, re-formation of the thick filament within the myofilament lattice (i.e. Seow, 2005) is a slow process.
These ideas are illustrated schematically in Fig. 3. Here we see two thin filaments at top and bottom, each attached to a dense body at the left and right, respectively. The thick filament is formed by a combination of myosin monomers and polymers, according to a length distribution to be discussed, and interspersed with unavailable sites (denoted ‘X’). The central idea is that within and near the filament overlap region, the density of available myosin binding sites is near to 1 and traditional crossbridge theory applies; while away from the overlap region sites are increasingly unavailable (according to the myosin length distribution). From this arrangement, we define several values which lie outside the typical crossbridge model: (1) The width of the thin filament overlap region, δ; (2) the length of a single thick filament dimer ε; (3) the transition rate from available, unbound sites to unavailable sites fE(x), and (4) the return rate from unavailable sites to available sites gE. The structure of the model is then as given in Fig. 2, which contains the four traditional crossbridge populations along with the new state A(x, t) containing the unavailable The new treatment of unavailable sites is in black, while the standard 4-state crossbridge model is in grey.
Fig. 3.
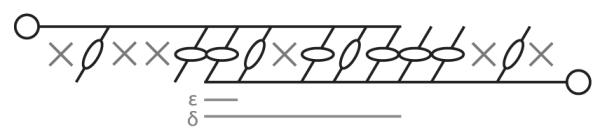
Schematic illustration of sliding filament and binding site arrangement. Two thin filaments, attached at each end to dense bodies, may be bound preferentially to the thick filament within the binding region, due to binding site availability. Thick filaments are illustrated in various lengths, with unavailable sites denoted ‘X’.
The governing equations are then given by the following set of hyperbolic PDEs:
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
subject to the conservation equation
with exerted ASM force given by Eq. (1) as before. The rates k1, k2, k3, k4, g(x), fp(x), gp(x) are identical to those used in Wang et al. (2008). The relative motion of the ASM filaments is governed by what is termed the crossbridge velocity, denoted v(t), which is the derivative with respect to time of the relative crossbridge filament positions. Thus crossbridge velocity and tissue length are related by
following the convention that velocity is positive during shortening.
2.3. Modelling the site loss rate using the thick filament length distribution
Assuming initially alignment between the crossbridge displacement and the discrete filament lengths, as illustrated in Fig. 3, for ∣x∣ > δh define
as the required discrete thick filament length to extend from site x to the overlap region. Then given a (discrete) thick filament length distribution with probability mass function z(m), the probability that the thick filament at x does not reach the overlap region is
By taking z(m) to be a geometric distribution z(m) = (1−p)(m−1)p, with p=0.45 as an approximation to the experimental data (see Section 4), can be expressed in terms of the cumulative distribution function as
However, this still assumes alignment between the crossbridge binding site and the discrete lengths of the thick filament; accounting for binding site alignment offset gives
where Δ is a uniform random variable on [−ε/2, ε/2]. The site loss function, averaged over all alignment offsets, can be computed directly by Monte Carlo simulation, or easily approximated by a moving average. For details of the alignment concept and the moving average approximation, see Appendix B.
Now the overall site loss function can be constructed. Away from the overlap region the loss rate increases according to the probability that thick filaments of the required length exist in the muscle; within the overlap region there is a small loss rate proportional to the mean thick filament length (thick filaments with more binding sites are more likely to remain, even within the overlap region). Thus we have
Intuitively, one may think of fE1 as the maximal rate of site loss far from the thin filament overlap region, and fE2 as the (lower) rate of basal loss which occurs within the overlap region. The function FE, based on the distribution of thick filament lengths, provides the transition between these rates in the area adjacent to the overlap region.
Binding sites are re-established at a constant, slow rate all along the thin filament according to
We maintain the approximation that δ is constant for simplicity because both fE and gE are slow processes; this could of course be relaxed to the natural assumption that δ’(t)∝v(t), though this introduces an additional degree of computational complexity via the dynamic recalculation of FE; for more on this point see Section 4.
Steady state solutions of the governing equations are obtained by setting the left hand side of Eqs. ((2)–(6)) to zero and solving the resulting system of 5 equations for the 5 unknowns, which is then used as the initial condition for all simulations. These equations are reduced to systems of ordinary differential equations via the method of characteristics (Gockenbach, 2011) which are then solved numerically by high-order variable stepsize routine (i.e. by MATLAB’s ODE45() routine). Parameter values and fitting are discussed in Appendix A.
3. Results
The model as described accounts for the characteristic force–length behaviours at each scale, as outlined in Section 1.
3.1. Force–length loops
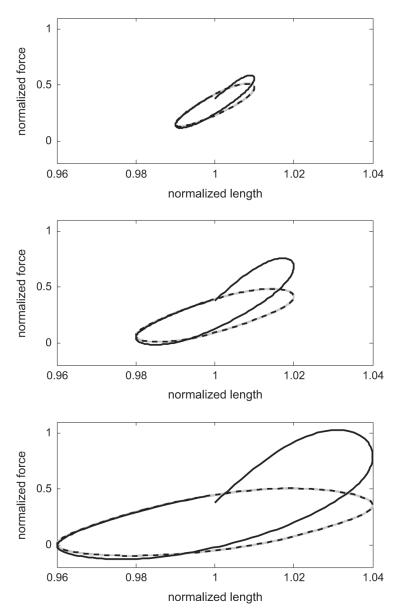
At the shortest timescale, length oscillations with amplitudes of 1%, 2% and 4% of the adapted length (2, 4 and 8% peak-to-trough, respectively) are imposed at 2 Hz, and the ASM force is tracked over 20 s. The resulting force–length loops are given in Fig. 4, where the first loop is coloured solid black and the last loop is the dashed black curve. These loops demonstrate the typical increasing hysteresis and nonlinearity, increasing with oscillation amplitude (i.e. Bates et al., 2009; Mijailovich et al., 2000). These results are largely unchanged from existing crossbridge models, by design as the protocol is confined to near the adapted length. The precise ‘banana-shaped’ loops seen experimentally are instead more elliptical in the model and this remains a point of discrepancy between experiment and theory (either this model, or previous crossbridge type models). Recent work has shed some light on this matter (Brook and Jensen, in press).
Fig. 4.
Force–length loops: short timescale. Model simulations of force–length loops at 2 Hz, with amplitudes 1%, 2% and 4% of reference length from top to bottom. The first loop is given in solid black, subsequent loops in grey, and the 40th loop in dashed black. The loops illustrate the typical hysteresis seen experimentally (see, i.e. Fig. 1 or Bates et al., 2009) and in crossbridge models (Mijailovich et al., 2000).
3.2. Force–length curves
On the medium timescale, to produce force length curves the tissue begins at the adapted length (at steady state) before being passively lengthened over the course of 10 s to the target length. The muscle is then activated by the increase of intracellular calcium to 1:3 μM and agonist dose to 1 (a.u., see Wang et al., 2008), and held at the target length for 5 m. The exerted force is then measured, and this value is recorded in Fig. 5. A total of seven target values are taken between 0.6 and 1.4 times reference length, and a best-fit quadratic is given for comparison. Here the model reproduces very well the characteristic shape observed with this protocol experimentally (i.e. Wang et al., 2001).
Fig. 5.

Force–length curve: medium timescale. Here the model is passively shortened or lengthened over 10 s, and then activated by the elevation of intracellular calcium (see text). After 5 min, the resulting force is measured and the data plotted in the black dots. The grey curve is a best-fit quadratic.
3.3. Length adaptation
For the longer timescale, we examine adaptation by passively shortening or lengthening the tissue by one third of the adapted length and allowing equilibration for 24 h, mimicking the protocol of Wang et al. (2001). After this, the force–length curve protocol (see Section 3.2) is repeated around the new adapted length. The results of these measurements are given in Fig. 6, showing that the muscle re-equilibrates fully to the new length and exhibits identical force–length curves at each new adapted length, and thus the model accounts well for passive length adaptation. This is of course the expected result, as over the long re-equilibration period the model returns to (length independent) steady state. The slow recovery timescale was chosen from the data for passive length adaptation, and may vary with activation or other factors—see Section 4.
Fig. 6.
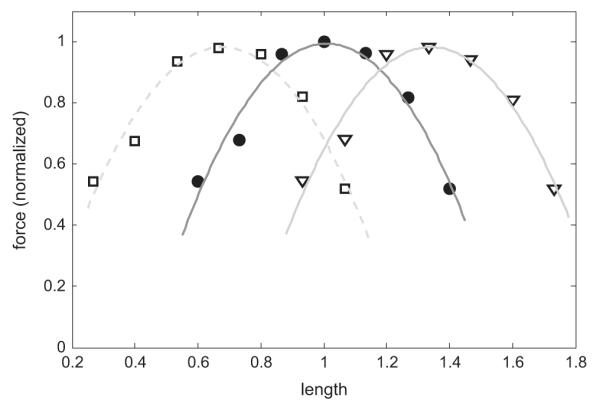
Length adaptation: long timescale. Here the model is allowed to re-equilibrate to a new length over a period of 24 h; after this, the protocol in Fig. 5 is repeated about this new length. The solid dots are as in Fig. 5; measurements relative to the shortened length are given in the unfilled squares; measurements relative to the lengthened tissue are the inverted triangles. In each case a best fit quadratic is given in grey. The model illustrates the characteristic parabolic shape at each new length, and the peak force of each curve is roughly constant.
4. Discussion
By incorporating explicitly the availability of actin-myosin binding sites, based on the distribution of thick filament lengths of ASM, we have shown that this new model reproduces well the force–length behaviours seen across multiple scales. Moreover, this is based on the widely-used crossbridge model which reproduces well many behaviours near the isometric regime. By retaining these near-isometric behaviours and extending to capture new features away from the equilibrated length, we greatly extended the viable range of the model.
While the model does accurately reproduce many key results, there are several limitations. For instance, force–length loops measured experimentally (i.e. Mijailovich et al., 2000; Bates et al., 2009) typically exhibit a so-called ‘banana-shaped’ character (see Fig. 1, left panel.) Crossbridge models, on the other hand, have force–length loops which are closer to elliptical, especially in equilibrated loops. By construction this model has similar behaviour, and hence elliptical loops, rather than truly banana-shaped. Recent work has suggested that this discrepancy may lie with the passive component (Brook and Jensen, in press), which we have excluded here.
While the thick filament length distribution is assumed to be a geometric distribution with parameter p=0.45 from experimental data,2 several other parameters pertaining to the site loss rate (FE) are fit parameters (see Appendix A).
It is also important always to be aware of the distinction between passive and active tissue, and to be aware that here we have not considered all possible combinations of passive/active mechanics and passive/active protocols. We have considered active mechanics in the sense that the ASM model does not generate force without activation, as opposed to passive mechanics (i.e. Donovan et al., 2010) where unactivated muscle responds to stretch with force. Similarly, we consider only passive length adaptation, wherein the muscle is adjusted to its new length without stimulation. This combination leaves several important caveats: (1) ASM activation affects the adaptation timescale (i.e. Wang et al., 2001), with a much faster recovery timecourse when the muscle is periodically stimulated. This is easily accommodated by making gE activation dependent, however, the data currently available make such a crude empirical adjustment undesirable. In particular, while it is clear that activation accelerates the adaptation timescale, the dependence upon strength and frequency of stimulation is unclear. Thus we have opted to treat only the passive adaptation case for now, and thus the adaptation timescale is set to fall within the observed 3–24 h range for passive recovery; (2) Passive force also exhibits length adaptation, and without the inclusion of a passive mechanics model this cannot be considered at all. Both of these points remain important areas for future work.
By construction, this new model preserves the behaviours seen in crossbridge models near to the adapted length, while extending to incorporate non-equilibrium force–length curves as well as length adaptation. We have shown that certain characteristic behaviours are retained, though there are other important behaviours as well. For example, the characteristic, hyperbolic shortening velocity-load curves originally due to Hill (1938) remain intact (data not shown); it remains an area of future work to explore if other important crossbridge model results are retained as well. Nonetheless, we have demonstrated that accounting for thick filament length distributions and binding site availability allows sliding filament theory to match experimental data in this set of data at multiple time scales, and far from the equilibrated length.
HIGHLIGHTS.
Airway smooth muscle (ASM) is implicated in asthma and airway constriction.
Relationship between exerted force and ASM length is critical for airway behaviour.
Long-term changes in force–length relationship are governed by length adaptation.
New model of ASM with length adaption, based on Huxley’s sliding filament theory.
Critical role for the distribution of filament lengths, based on recent data.
Acknowledgements
The author gratefully recognises the helpful comments of James Sneyd and the support of the NIH via NHLBI HL103405.
Appendix A. Parameter fitting
The modified model introduces a minimal number of free parameters, with gE1, fE2, and ε chosen from data as described below. This leaves δ and fE1 as fit parameters, obtained as follows. Because of the computational complexity of solving the governing equations with high resolution over long times, we appeal to a reduced problem to obtain an initial, approximate fit. To do so, we observe that the force exerted after a length change at the intermediate timescale will be limited by unavailable sites, and because fE and gE are slow we can approximate A(x, t) by a translation of the steady state distribution A0(x, t) by
for a length change corresponding to the crossbridge displacement Δx. Then for equivalent muscle activation conditions, the force exerted by the muscle is proportional to the available sites determined by (1–A) as
Then by normalising to F(0) we eliminate the unknown α, and fit a quadratic approximation to the experimental data. The error in this fit is then minimised by Markov Chain Monte Carlo (MCMC) parameter estimation (Robert et al., 1999).
Having obtained an approximate fit as above, a smaller number of MCMC simulations are used from this starting point using full dynamic simulations. The resulting parameter values are δ = 11:84, fE1 = 4:32 × 10−5(1/s), fE2 = 1:5 × 10−5(1/s), ε = 4, gE1 = 3 × 10−5(1/s), p=0.45. All other parameters are as in Wang et al. (2008).
Appendix B. Approximation of site loss function FE
The site loss function FE can be computed directly by Monte Carlo simulation; however, as a computational convenience it can also be approximated by a moving average with window width ξ = 3.5; see Fig. B1, left panel. The right panel illustrates two configurations with identical overlap regions, but differing binding site alignments. The site loss function is averaged over all possible alignments.
Fig. B1.
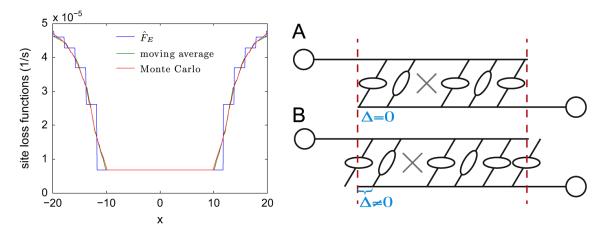
Left panel: The site loss function FE, directly calculated by Monte Carlo simulation and approximated by a moving average. Right panel: Illustration of alignment between filament overlap region and binding sites. Here configurations A and B have identical overlap regions, but different alignments (Δ = 0 in A, and Δ≠0 in B). The site loss function is computed as an average over all possible alignments.
Footnotes
This is true for the model of Wang et al. (2008) and a 5 min re-equilibration period: by the measurement time the muscle has already re-equilibrated. Strictly speaking the result depends upon the model recovery timescale and the recovery time allowed by the protocol, but no such combination exists which simultaneously yields appropriate force–length curves and adaptation in a traditional crossbridge model.
Approximate fit to unpublished, submitted data from Chun Seow’s lab, University of British Columbia. The model results presented here are qualitatively robust to a reasonable range of thick filament length distribution assumptions. Specifically, any monotonically decreasing probability mass function will broadly match the results shown here; that is, that shorter filaments are more likely than longer filaments at any point on the curve.
References
- Ali F, Chin L, Paré P, Seow C. Mechanism of partial adaptation in airway smooth muscle after a step change in length. J. Appl. Physiol. 2007;103:569–577. doi: 10.1152/japplphysiol.00216.2007. [DOI] [PubMed] [Google Scholar]
- Amin S, Majumdar A, Frey U, Suki B. Modeling the dynamics of airway constriction: effects of agonist transport and binding. J. Appl. Physiol. 2010;109:553–563. doi: 10.1152/japplphysiol.01111.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anafi R, Wilson T. Airway stability and heterogeneity in the constricted lung. J. Appl. Physiol. 2001;91:1185–1192. doi: 10.1152/jappl.2001.91.3.1185. [DOI] [PubMed] [Google Scholar]
- Bates J, Bullimore S, Politi A, Sneyd J, Anafi R, Lauzon A. Transient oscillatory force–length behavior of activated airway smooth muscle. Am. J. Physiol. Lung Cell. Mol. Physiol. 2009;297:L362–L372. doi: 10.1152/ajplung.00095.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bossé Y, Sobieszek A, Paré P, Seow C. Length adaptation of airway smooth muscle. Proc. Am. Thorac. Soc. 2008;5:62–67. doi: 10.1513/pats.200705-056VS. [DOI] [PubMed] [Google Scholar]
- Brook B, Jensen O. The role of contractile unit reorganization in force generation in airway smooth muscle Math. Med. Biol. doi: 10.1093/imammb/dqs031. http://dx.doi.org/10.1093/imammb/dqs031, in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Donovan G, Bullimore S, Elvin A, Tawhai M, Bates J, Lauzon A, Sneyd J. A continuous-binding cross-linker model for passive airway smooth muscle. Biophys. J. 2010;99:3164–3171. doi: 10.1016/j.bpj.2010.09.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gockenbach M. Partial differential equations: analytical and numerical methods. Second Edition Society for Industrial and Applied Mathematics; Philadelphia, PA, USA: 2012. [Google Scholar]
- Gunst S, Stropp J. Pressure-volume and length-stress relationships in canine bronchi in vitro. J. Appl. Physiol. 1988;64:2522–2531. doi: 10.1152/jappl.1988.64.6.2522. [DOI] [PubMed] [Google Scholar]
- Hai C, Murphy R. Cross-bridge phosphorylation and regulation of latch state in smooth muscle. Am. J. Physiol. Cell Physiol. 1988;254:C99. doi: 10.1152/ajpcell.1988.254.1.C99. [DOI] [PubMed] [Google Scholar]
- Hill A. The heat of shortening and the dynamic constants of muscle. Proc. R Soc. London Ser. B Biol. Sci. 1938;126:136–195. [Google Scholar]
- Huxley A. Muscle structure and theories of contraction. Prog. Biophys. Biophys. Chem. 1957;7:255–318. [PubMed] [Google Scholar]
- Ijpma G, Al-Jumaily A, Cairns S, Sieck G. Myosin filament polymerization and depolymerization in a model of partial length adaptation in airway smooth muscle. J. Appl. Physiol. 2011;111:735–742. doi: 10.1152/japplphysiol.00114.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keener J, Sneyd J. Mathematical Physiology: Systems Physiology. vol. 2. Springer Verlag; 2008. [Google Scholar]
- Lambert R, Pare P, Seow C. Mathematical description of geometric and kinematic aspects of smooth muscle plasticity and some related morphometrics. J. Appl. Physiol. 2004;96:469–476. doi: 10.1152/japplphysiol.00736.2003. [DOI] [PubMed] [Google Scholar]
- Mijailovich S, Butler J, Fredberg J. Perturbed equilibria of myosin binding in airway smooth muscle: bond-length distributions, mechanics, and ATP metabolism. Biophys. J. 2000;79:2667–2681. doi: 10.1016/S0006-3495(00)76505-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Politi A, Donovan G, Tawhai M, Sanderson M, Lauzon A, Bates J, Sneyd J. A multiscale, spatially distributed model of asthmatic airway hyper-responsiveness. J. Theor. Biol. 2010;266:614–624. doi: 10.1016/j.jtbi.2010.07.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robert C, Casella G, Robert C. Monte Carlo Statistical Methods. vol. 2. Springer; New York: 1999. [Google Scholar]
- Seow C. Myosin filament assembly in an ever-changing myofilament lattice of smooth muscle. Am. J. Physiol. Cell Physiol. 2005;289:C1363–C1368. doi: 10.1152/ajpcell.00329.2005. [DOI] [PubMed] [Google Scholar]
- Seow C, Fredberg J. Emergence of airway smooth muscle functions related to structural malleability. J. Appl. Physiol. 2011;110:1130–1135. doi: 10.1152/japplphysiol.01192.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Silveira P, Butler J, Fredberg J. Length adaptation of airway smooth muscle: a stochastic model of cytoskeletal dynamics. J. Appl. Physiol. 2005;99:2087–2098. doi: 10.1152/japplphysiol.00159.2005. [DOI] [PubMed] [Google Scholar]
- Syyong H, Raqeeb A, Paré P, Seow C. Time course of isotonic shortening and the underlying contraction mechanism in airway smooth muscle. J. Appl. Physiol. 2011;111:642–656. doi: 10.1152/japplphysiol.00085.2011. [DOI] [PubMed] [Google Scholar]
- Venegas J, Winkler T, Musch G, Melo M, Layfield D, Tgavalekos N, Fischman A, Callahan R, Bellani G, Harris R. Self-organized patchiness in asthma as a prelude to catastrophic shifts. Nature. 2005;434:777–782. doi: 10.1038/nature03490. [DOI] [PubMed] [Google Scholar]
- Wang I, Politi A, Tania N, Bai Y, Sanderson M, Sneyd J. A mathematical model of airway and pulmonary arteriole smooth muscle. Biophys. J. 2008;94:2053–2064. doi: 10.1529/biophysj.107.113977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang L, Paré P, Seow C. Selected contribution: effect of chronic passive length change on airway smooth muscle length-tension relationship. J. Appl. Physiol. 2001;90:734–740. doi: 10.1152/jappl.2001.90.2.734. [DOI] [PubMed] [Google Scholar]