Abstract
Purpose
To assess the effect of echo-sampling strategy on the accuracy of out-of-phase (OP) and in-phase (IP) multi-echo gradient-echo magnetic resonance imaging (MRI) hepatic fat fraction (FF) estimation, using MR spectroscopy (MRS) proton density FF (PDFF) as a reference standard.
Materials and Methods
In this IRB-approved, HIPAA-compliant prospective study, 84 subjects underwent proton MRS and non-T1-weighted gradient-echo imaging of the liver at 3T. Imaging data were collected at 16 nominally OP and IP echo times (TEs). MRI-FF was estimated while varying two echo-sampling parameters (number of consecutive echoes, starting echo number). For each combination of these parameters, MRI-FF estimation accuracy was assessed with slope, intercept, average bias and R2 from a linear regression of MRS-PDFF on MRI-FF. The relationship between accuracy metrics and echo-sampling parameters was assessed by Spearman rank correlation.
Results
For FF calculations using 3-16 echoes and a starting echo number of 1, the intercept ranged from 0.0046 to 0.0124, slope from 0.941 to 0.96, average bias from 0.0034 to 0.0078, and R2 from 0.968 to 0.976. All four accuracy metrics were the best with the 3- and 4- echo calculations and worsened progressively with increasing number of echoes. For a given number of echoes, there was an overall trend toward decreasing accuracy as starting echo number increased. Spearman correlation coefficients between starting echo number and intercept, slope, average bias and R2 were 0.911, -.64, -.889 and -.954, respectively, indicating progressive loss of accuracy in each case.
Conclusion
Multi-echo OP and IP imaging provided high FF estimation accuracy. Accuracy was highest using the earliest 3 or 4 echoes. Incorporation of additional echoes or delaying the starting echo number progressively reduced accuracy.
Keywords: Fatty liver disease, hepatic steatosis, magnetic resonance, fat quantification, multiecho
INTRODUCTION
A magnitude-data chemical shift-based multi-echo out-of-phase (OP) and in-phase (IP) gradient echo magnetic resonance imaging (MRI) technique (1) has previously been demonstrated to estimate proton density fat fraction (PDFF) of human liver at 1.5T(2) and at 3.0T(3). The technique uses low flip angle (FA) to minimize T1 effects and acquires multiple echoes at echo times (TE) at which fat methylene and water signals are nominally OP or IP relative to each other. Signal intensity values acquired at each TE are passed to a nonlinear least-squares fitting algorithm that models the water signal as a single frequency component and the fat signal as a superposition of multiple frequency components, estimates and corrects T2* effects and estimates the relative fat and water proton densities. The PDFF is calculated from the relative fat and water proton density values. The accuracy of MRI for estimating PDFF with this technique has previously been shown in vivo (2,3) using the PDFF measured by magnetic resonance spectroscopy (MRS) as a reference standard.
Prior studies on the diagnostic accuracy of this technique used a six-echo acquisition, with the first echo acquired at the first OP TE. However, the effect on estimation accuracy of the number of echoes or the time to first echo used in the computation has not yet been systematically studied, and it is conceivable that six echoes beginning with the first OP TE is not the best sampling strategy.
The purpose of this study was to assess systematically the effect of echo-sampling strategy on hepatic fat fraction (FF) estimation accuracy by MRI (MRI-FF), using MRS-PDFF as the reference standard. Images were acquired in human subjects using a total of 16 echoes. The effect of echo sampling strategy was analyzed by varying the number of echoes used by the MRI-FF estimation algorithm and by varying starting echo number.
MATERIALS AND METHODS
Study Design and Subjects
This prospective, cross-sectional, single-site observational clinical study was approved by an Investigational Review Board (IRB) and was compliant with the Health Insurance Portability and Accountability Act (HIPAA). Between March 2009 and September 2009, subjects were recruited from the institutional hepatology and obesity clinics, as well as from the general public, and were enrolled consecutively. Adults and pediatric subjects with known steatosis were included in the study, as well as normal healthy adults with no known steatosis. Exclusion criteria were contraindication for MR, known extreme claustrophobia, weight exceeding 250 lbs, and pregnancy. These eligibility criteria were used to enroll subjects with a broad range of liver fat fraction. No a-priori sample size calculation was performed. Adult subjects gave informed consent, while pediatric subjects (age 10-18) gave assent with parental informed consent. Subject age, sex and etiology of liver disease (if any) were recorded.
Magnetic Resonance Examinations
Subjects were examined supine using an 8-channel torso phased array receive coil at 3T (GE Signal EXCITE HD, GE Medical Systems, Milwaukee, WI, USA). A three-plane localization imaging sequence was performed at the beginning of the exam. An experienced MR technologist performed the MRS and MRI acquisitions.
Magnetic Resonance Spectroscopy
Avoiding major blood vessels, bile ducts, or liver edges seen on the localization images, a single 20 × 20 × 20 mm3 voxel was placed in the right hepatic lobe (segment V-VIII) and shimmed automatically. A reference image was created by overlaying the voxel on the corresponding axial localization image, and the reference image was transferred offline for future reference. Stimulated echo acquisition mode (STEAM) proton MRS was performed using long TR (3500 ms) to minimize T1-weighting. After a single pre-acquisition excitation pulse to balance T1 saturation on subsequent excitations, five STEAM spectra were acquired at TEs of 10, 15, 20, 25 and 30 ms in a single 21-second breath-hold. This TE range enabled reproducible T2 estimation while minimizing the confounding effects of fat-peak J coupling (4). The shortest possible mixing time (TM, 5 ms) was used to minimize both J coupling and T1 weighting. No water, fat, or spatial saturation was applied. Signals recorded at eight array elements were combined into a single spectrum per TE using singular-value-decomposition (5), and saved as text files for off-line analysis.
Magnetic Resonance Imaging
Multislice axial magnitude images were acquired through the liver (including the location of the MRS voxel) using a 2D spoiled gradient recalled echo (SGRE) sequence using all coil elements without parallel imaging. To minimize T1-weighting, low FA (10°) was used with repetition time (TR) >= 100 ms (100-225 ms, adjusted by the technologist to accommodate each subject's breathhold capacity. Sixteen magnitude images were obtained at TEs of 1.15, 2.30, 3.45, 4.60, 5.75, 6.90, 8.05, 9.20, 10.35, 11.50, 12.65, 13.80, 14.95, 16.10, 17.25, and 18.50 ms in a single 18-30 second breath-hold. Other imaging parameters were 8-mm slice thickness, 0% interslice gap, ± 142 kHz receiver bandwidth, 0.8 fractional echo sampling, 192×192 base matrix, one signal average, and rectangular field-of-view (FOV) adjusted to body habitus and breath-hold capacity. Number of slices varied from 14 to 26 depending on TR and phase FOV. Images were transferred offline (Osirix, Pixmeo, Geneva, Switzerland) for storage, analysis and postprocessing.
Data Analysis
Magnetic Resonance Spectroscopy
The spectroscopy data were analyzed off-line by a MR physicist (GH, 8 years of experience) in the time-domain using Advanced Method for Accurate, Robust and Efficient Spectral fitting algorithm (AMARES) in the Java-based Magnetic Resonance User Interface software (http://sermn02.uab.es/mrui) (6). T1 weighting was assumed negligible at 3500 ms TR and 5 ms TM. At each TE, the areas of the water (4.7 ppm) and three major fat spectral peaks (0.9, 1.3, 2.1 ppm) were measured. For each frequency, the peak area was corrected for T2 exponential decay using nonlinear least-square fitting to determine its relative proton density. Based on prior knowledge of the triglyceride molecular structure, the relative proton densities of the two non-measurable minor fat peaks (4.2, 5.3 ppm) were determined from those of the measurable three major fat peaks (7). The smallest spectral component (2.75 ppm) was not considered because it is not consistently or reliably measurable at clinical field strengths in vivo (3). Spectral peaks other than water and fat were not measured. The MRS-PDFF, was calculated by dividing the fat proton density (sum of all fat peaks) by the sum of the fat and water proton densities.
Magnetic Resonance Imaging
A trained image analyst (JC, 2 year-experience) independently reviewed and analyzed the MR images on an image processing workstation. Using the saved reference image as a guide, a circular region of interest (ROI) of 20 mm diameter was manually placed on one of the multi-echo images at the spectroscopic voxel location. The ROI was automatically propagated with the same spatial coordinates to the other multi-echo images. The average ROI value at each TE was entered into a fitting routine in MATLAB (MathWorks, Natick, MA) using a multi-interference spectral model described previously (2), from which the MRI-FF and T2* were calculated, assuming the T2* of the fat and water components are the same. This method models water as a single frequency signal at 4.7 ppm, and the total fat signal as a weighted sum of five individual fat signals at 0.9, 1.3, 2.1, 4.2, and 5.3 ppm with normalized weights of 0.09, 0.70, 0.12, 0.04, and 0.05, respectively. These weights were derived from human subjects with fatty liver disease (8). The smallest 2.75 ppm spectral component was not included, to maintain consistency with the spectroscopy analysis described above.
The 16-echo acquisition protocol used in this study allowed the MRI-FF calculation to be repeated systematically from the same set of acquired images by varying two key echo sampling parameters:
Number of echoes (n) included in the calculation: n was allowed to vary from n=3, the minimum number of echoes required for T2*-corrected MRI-FF estimation, to n=16, the maximum number of echoes available for analysis from a 16-echo acquisition.
Starting echo number (m) of the data points included in the calculation. m was allowed to vary from m=1, the first acquired echo, to m=16-(n-1), the maximum starting echo number possible for a dataset with n echoes.
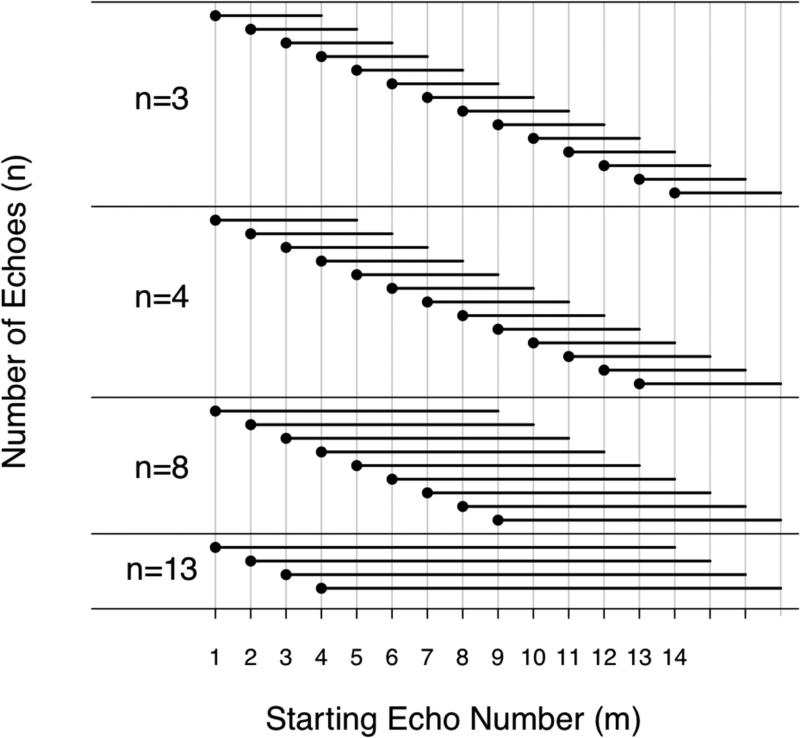
For each number of echoes (n=3,4,...,16) and starting echo number (m=1,...16-(n-1)), MRI-FF(n,m), was calculated using the consecutive n echoes beginning with the m-th echo. For example, for a 3-echo calculation (n=3) with starting echo 1 (m=1), MRI-FF(3,1) was calculated from echo set [1 2 3]. Similarly, for a 4-echo calculation (n=4) with starting echo 3 (m=3), MRI-FF(4,3) was calculated from echo set [3 4 5 6]. This MRI-FF calculation design with variable number of echoes, n, and starting echo number, m, is illustrated in Figure 1. For illustrative purposes, MRI-FF maps were generated for select values of n and m by applying the model pixel by pixel to the source data.
Figure 1.
Illustration of MRI-FF estimation with the number of echoes, n = 3, 4, 8, and 13 echoes. The total number of echoes, n, is represented by the length of the black bars. Each bar starts at the at the starting echo number, m. m of 1 to 14 is possible for n=3; 1 to 13 for n=4, 1 to 9 for n=9; 1 to 3 for n=13: the number of possible starting echo numbers decreases as the total number of echoes increases.
Statistical Analysis
Statistical analyses were performed by a team of two biostatisticians (AG and TW, both at 15+ year-experience) using R statistical software (R Foundation for Statistical Computing, Vienna, Austria). Demographic summaries of study subjects were computed.
Accuracy Metrics
MRS-PDFF was the reference standard for MRI-FF(n,m), in this study. For each number of echoes (n=3,4,...16) with starting echo number (m=1,...16-(n-1)), MRS-PDFF was modeled as a function of MRI-FF(n,m) in a separate univariate linear regression. From each regression, four accuracy metrics were identified: the intercept of the regression line; the slope of the regression line; the average bias of the fitted regression, defined as the square root of the average squared difference between the regression line and the MRS = MRI line (a line with intercept of 0 and slope of 1); and the coefficient of determination R2, which is the proportion of variance explained by the model. Nonparametric bootstrap (9) was used to build bias-corrected, accelerated (BCA) confidence intervals around all four accuracy metrics.
Accuracy and Number of Echoes
For this part of the analysis, the starting echo number was fixed at m=1. Bland-Altman plots of MRS and MRI-FF(n,1) were generated for all each number of echoes, n. Slope, intercept, bias and R2 were plotted as a function of n. To formally test the difference in accuracy between different numbers of echoes, each of the four accuracy metrics were compared between pairs of calculations selected a-priori: (a) 3- vs. 4-echo, (b) 3- vs. 6-echo, (c) 3- vs. 16-echo, (d) 4- vs. 6-echo, (e) 4- vs. 16-echo, and (f) 6- vs. 16-echo. The statistical significance of these differences in accuracy metrics were assessed using the BCA confidence intervals. Bonferroni adjustment for multiple testing at the 0.05 significance level was applied to each set of six comparisons. The relationship between the accuracy metrics and number of echoes was assessed by Spearman rank correlation analysis; confidence intervals around the correlation values were computed.
Accuracy and Starting Echo Number
The analysis in the previous section fixed the starting echo number at m=1. In a separate analysis we systematically varied m from m=1 to m=16-(n-1) for all n from 3 to 16. Slope, intercept, bias and R2 estimates were plotted as a function of starting echo number, m, for MRI-FF(m,n) calculations using different n's. Formal pairwise comparisons were not done. The relationship between accuracy metrics and starting echo number, m, was assessed by Spearman rank correlation analysis. In determining the Spearman rank correlation, all data points for a given starting echo number m were included. Thus, for m = 1, there were 14 data points, corresponding to n = 3, 4, ...,16. For m = 10, there were 5 data points, corresponding to n = 3, 4, ..., 7.
Secondary Analysis
To better understand the results of the primary analyses, we conducted a secondary analysis of the effect of n (setting m = 1) on T2* estimated by our signal model, using linear mixed-effects regression. Estimated T2* was log-transformed to stabilize the variance of the residuals and to enforce the T2* non-negativity constraint. The observed relationship between log-transformed T2* and n were plotted for each subject and qualitatively reviewed. Then, log-transformed T2* was modeled as a function of the fixed effects of n and n2, with a random (subject-specific) intercept fitted to the data. In addition to subject-specific trajectories, this model estimates and assesses the significance of the fixed (averaged over all subjects) trajectory of T2* as n increases. Additionally, we qualitatively reviewed, in all 84 subjects, the plots showing the fits of the signal model to the measured signal intensities at increasing echo numbers n while keeping the starting echo number m fixed at 1.
RESULTS
Subjects
During the study period, 84 subjects were enrolled (45 male, 39 female, age range 10-74 years, mean±standard deviation (SD) of 35.9 ± 22.2). MRS-PDFF range was 0.006-0.326 with mean±SD of 0.115 ± 0.083. TR ranged from 100 to 225 ms. In 80 of the 84 subjects, TR was greater than 125 ms.
Accuracy and number of echoes
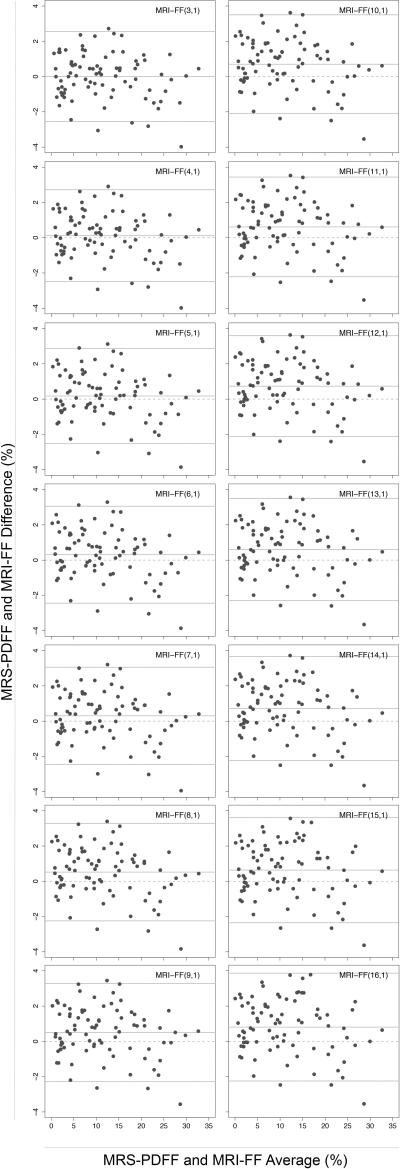
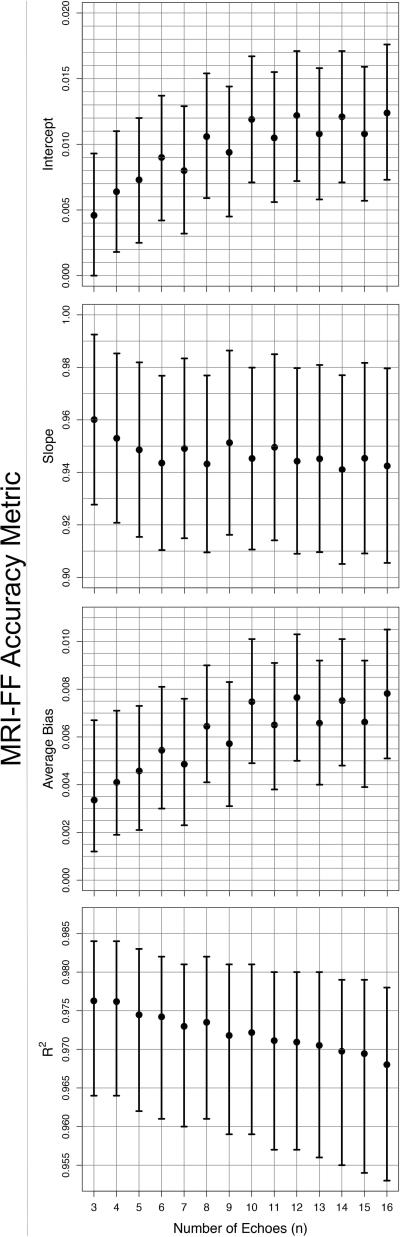
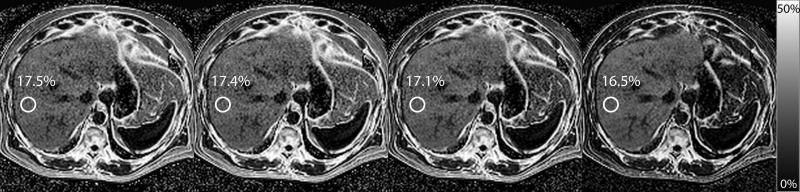
Bland-Altman plots are presented in Figure 2. Figure 3 shows the accuracy of MRI-FF(n,1) relative to MRS-PDFF for each n, as assessed by the four regression accuracy metrics: slope, intercept, average bias and R2. All n provided accurate MRI-FF estimation with intercept ranging from 0.0046 to 0.0124, slope ranging from 0.941 to 0.960, average bias ranging from 0.0034 to 0.0078, and R2 ranging from 0.968 to 0.976. The intercept was closest to 0 for MRI-FF(3,1) and MRI-FF(4,1) calculations (intercept = 0.0046, 95%CI [0, 0.0093] for MRI-FF(3,1) and 0.0064, 95% CI [0.0018, 0.0110] for MRI-FF(4,1)) and then increased steadily with increasing n. Slope was closest to 1 for MRI-FF(3,1) and MRI-FF(4,1) calculations and then generally decreased with increasing n (slope = 0.960, 95% CI [0.928, 0.992] for MRI-FF(3,1) and 0.953, 95% CI [0.921, 0.985] for MRI-FF(4,1)). Average bias was lowest for MRI-FF(3,1) and MRI-FF(4,1) calculations and then increased with increasing n (average bias = 0.0034, 95% CI [0.0012, 0.0067] for MRI-FF(3,1) and 0.0041, 95% CI [0.0019, 0.0071] for MRI-FF(4,1)). R2 was highest for MRI-FF(3,1) and MRI-FF(4,1) calculations (R2 = 0.976 and 95% CIs [0.964, 0.984] for both) and then decreased almost monotonically with increasing number of echoes. Spearman's correlation between accuracy metrics and n was 0.904 [0.854, 0.938] for both intercept and bias, -0.604 [-0.728, -0.443] for slope and -0.991 [-0.994, -0.986] for R2, confirming progressive loss of accuracy with increasing n. Bootstrap-based Bonferroni-corrected pairwise comparisons indicated that MRI-FF(3,1) and MRI-FF(4,1) were significantly more accurate than MRI-FF(16,1) on slope, average bias and R2, although neither was significantly more accurate than MRI-FF(6,1) or than each other. In all pairwise comparisons of the intercept, the calculation with lower n has significantly higher accuracy than the calculation with the higher n. Figure 4 illustrates in one research subject the loss of accuracy (relative to MRS) with higher n.
Figure 2.
Bland-Altman plots of MRS-PDFF and MRI-FF(n,1) for all n from 3 to 16. Each plot shows the limits of agreement: average difference +/- 1.96 standard deviation of the differences. The average difference summarizes the size and overall direction of the raw differences between MRS-PDFF and MRI-FF.
Figure 3.
Accuracy metrics: intercept (a), slope (b), average bias (c) and R2 (d) as a function of n used in MRI-FF(n,1) estimation. Means and bootstrap-based BCA confidence intervals are shown on the plot.
Figure 4.
MRI-FF(n,1) for n = 3, 4, 6, and 16 is depicted for a subject whose MRS-PDFF was found to be 18.3%. MRI-FF(3,1) is 17.5% for an absolute error of 0.8%. For n = 4,6, and 16, MRI-FF(n,1) was 17.4%, 17.1% and 16.5%, with absolute error of 0.9%, 1.2%, and 1.8%, respectively.
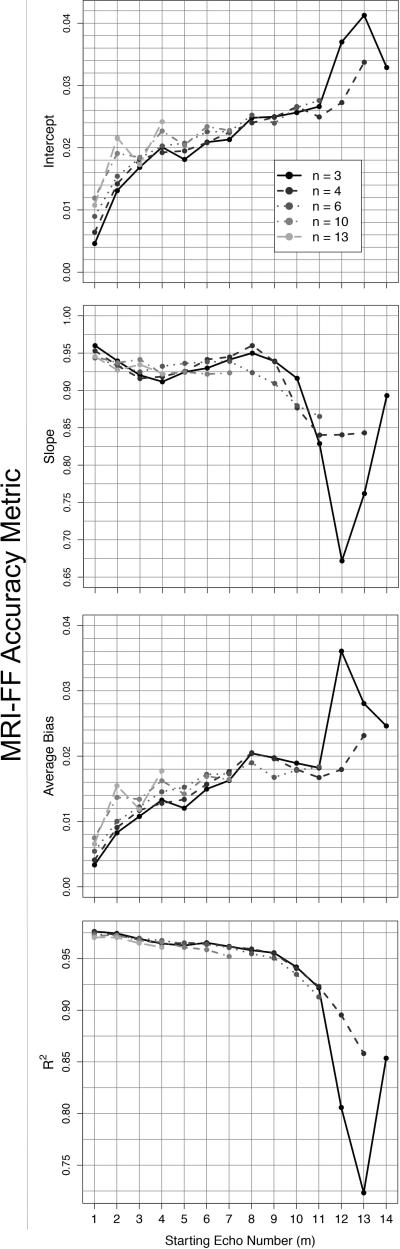
Accuracy and Starting Echo Number
Figure 5 shows the accuracy of MRI-FF(n,m) as a function of the starting echo number, m, assessed by the four accuracy metrics (intercept, slope, average bias and R2), using MRS-FF as the reference standard. In each graph of the figure one of the metrics is plotted against m. Each separate curve in the graphs represents the MRI-FF(n,m) estimates derived from the same number of echoes, n, and variable starting echo number, m. For clarity, each plot shows only five curves (with n= 3, 4, 6, 10, or 16), rather than the complete set of 14 curves, with m varying (as appropriate) from 1 to 14. Depending on m and n, intercept ranged from 0.0046 to 0.041, slope from 0.671 to 0.960, bias from 0.0033 to 0.0360, and R2 from 0.723 to 0.976. In general, for a given n, R2 and slope decreased while intercept and average bias increased as m increased, suggesting progressive loss of accuracy. Spearman correlation coefficients between accuracy metrics and m were 0.911 [0.908, 0.914] for intercept, -0.640 [-0.651, -0.629] for slope, 0.889 [0.885, 0.893] for average bias and -0.954 [-0.956, -0.952] for R2, suggesting an overall trend of decreasing accuracy with increasing starting echo. The tendency for loss of accuracy with increasing m is illustrated in Figure 6 on the same subject as in Figure 4.
Figure 5.
Accuracy metrics: intercept (a), slope (b), average bias (c) and R2 (d) as a function of starting echo number for the cases in which n = 3, 4, 6, 10, and 13 were used for MRI-FF estimation. In each panel, each curve corresponds to a specific n, as indicated in the figure legend. Each point on a curve corresponds to a different m. For example, the first point on the interval curve MRI-FF(3,m) corresponds to MRI-FF(3,1), the MRI-FF calculation for echoes (1,2,3). The second point corresponds to MRI-FF(3,2): the MRI-FF calculation for echoes (2,3,4). The number of points in each curve depends on n: there are 14 possible estimates in the MRI-FF(3, m) curve, but only 4 possible estimates in the MRI-FF(13, m) curve.
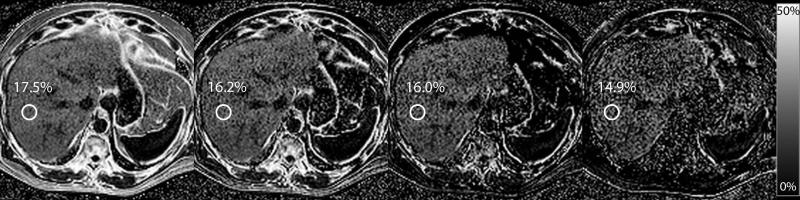
Figure 6.
MRI-FF(3,m) is depicted for m = 1, 3, 6, and 13 for the same subject as in Figure 3, with MRS-PDFF of 18.3%. MRI-FF(3,1) is 17.5% for an absolute error of 0.8%. For m = 3,6, and 13, MRI-FF(3,m) was 16.2%, 16.0%, and 14.9%, for absolute errors of 2.1%, 2.3% and 3.4%, respectively.
Secondary Analysis
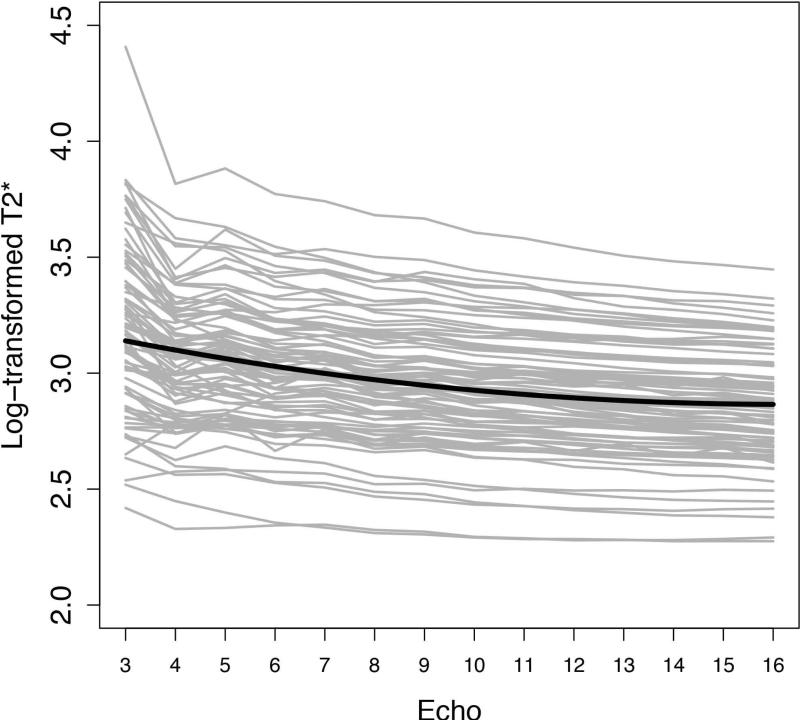
The relationship between n and estimated T2*, for m = 1, is shown in Figure 7. As shown in the figure, the T2* for almost all individual subjects and for the study sample as a whole decreased with increasing n. The coefficients of both the linear and the quadratic components of the fixed T2* trajectory were statistically significant (p < 0.0001 in both cases), i.e. overall T2* decreases significantly as n increases, with a non-linear component to the decline.
Figure 7.
Log-transformed T2* as a function of echo number. Gray lines represent individual subjects’ log-transformed T2* values, connected across echoes. The superimposed black curve represents the fixed (common to all subjects) fitted trajectory of the linear mixed effects regression model.
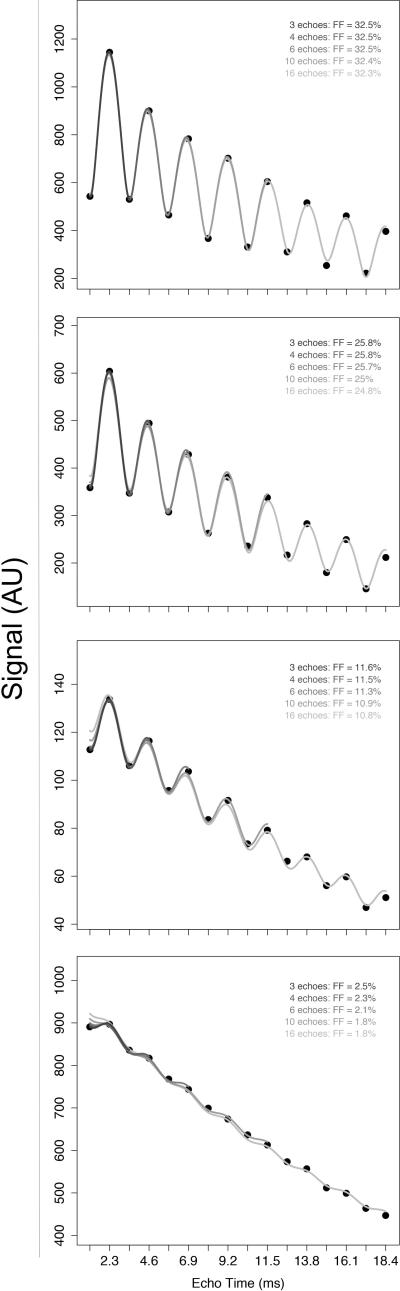
Four representative plots of individual subjects’ signal data and the fitted curves from the multi-interference spectral model for n=3, 4, 6, 10 and 16 are shown in Figure 8. As shown in this figure, as the echo number n was increased, the fit of the model to the measured signal became progressively flatter, resulting in progressive underestimation of the observed signal oscillation between nominal OP and IP echoes, especially for the first echo, and hence progressive underestimation of the FF. The only exceptions were in occasional subjects at the very high FF end, in whom the observed fits qualitatively were excellent for all echo numbers and in whom the FF estimates remained stable with increasing n.
Figure 8.
Four representative plots of individual subjects’ signal data and the fitted curves from the multi-interference spectral model for n=3, 4,6,10 and 16. FF ranges from high (top panel) to low (bottom panel). With occasional exceptions at the very high FF range (top panel), all individual plots exhibit a progressive underestimation of the observed signal oscillation between nominal OP and IP echoes as n increases, especially for the first echo, and hence progressive underestimation of the FF.
DISCUSSION
This prospective clinical study assessed the effects of number of echoes and starting echo number in liver FF estimation accuracy at 3T by a magnitude-data chemical shift-based multi-echo OP and IP gradient echo MR imaging technique in human subjects, using proton spectroscopy as the reference technique. 84 human subjects underwent proton MR spectroscopy and 16-echo MR imaging of the liver. Using the multi-echo imaging data, MRI-FF was calculated with variable number of echoes and starting echo number and, for each combination of these echo-sampling parameters, the accuracy of the MRI-FF estimation by imaging was assessed with respect to MRS-PDFF at a co-registered location in the liver.
We selected spectroscopy, rather than histology, as the reference technique for the following reasons. First, FF calculated from spectroscopy-determined proton densities has been shown to be directly related to the molecular triglyceride content (10-12). Second, spectroscopy and imaging both are used to measure fat content volumetrically by the relative number of fat protons and therefore are directly comparable with each other. Histologic examination assesses the number of fat-containing cells and does not measure volumetric fat content. Additionally, spectroscopy can be performed contemporaneously with imaging, the sampling volumes are similar, and reasonable spatial co-localization is achievable. By comparison, core biopsy is two orders of magnitude smaller in volume, prone to sampling error, difficult to co-localize spatially with imaging, and more difficult to perform contemporaneously with imaging.
Four accuracy metrics were utilized: slope, intercept, average bias and R2. High levels of accuracy were achieved with all numbers of echoes from 3 to 16. For all four metrics, we observed that accuracy declined with increasing number of echoes and that the highest accuracy was achieved with 3 or 4 echoes. Furthermore, regardless of the number of echoes, accuracy was highest when the earliest echoes were used for estimation. (The n = 3 curves in figures 4 and 7 deviate from the overall trend in the specific cases of m = 12 and 13, as intercept and bias were significantly higher while slope and R2 was significantly lower than for m = 14. Our study did not elucidate this unusual behavior and further investigation is necessary. Nonetheless, the overall conclusion is unchanged.)
In general, signal modeling algorithms perform better as the number of data points is increased, but only if the data points are acquired within the range over which the model fits the data. The following observations suggest that signals acquired at echoes after the fourth echo begin to diverge meaningfully from the model as implemented in this study: (1) both the estimated FF and the estimated T2* became progressively lower with increasing echo number (with a perfect model, the parameter estimates would remain stable) and (2) qualitatively the fits of the model to the measured data became flatter with increasing n, resulting in progressive mis-fitting of the peaks and the troughs (with a perfect model, the fits would consistently fit the oscillation). While our study was not designed to determine the causes of signal model divergence, several possible causes can be considered. Firstly, there may be chemical shift errors from modeling the peak at 2.1 ppm as a single peak rather than as two closely associated peaks, modeling the chemical shift between the water peak and the dominant fat methylene peak as exactly 4.7 ppm, or using a fat spectrum derived from the average over a reference population. Any divergence of the actual fat spectrum for an individual subject from the spectrum based on the above assumptions will lead to errors in phase, which can accrue with increasing TE. Another possible cause is the assumption that all fat peaks and the water peak have identical T2*. This assumption is correct only if intravoxel field inhomogeneity (often denoted T2’) is the dominant source of transverse relaxation. Another assumption is that the signal decay follows a purely exponential form, whereas Gaussian or sinc-like variations can be obtained in some situations. Finally noise bias from using magnitude data may become relevant when the signal is low, e.g. on later echoes.
Other authors have evaluated the impact of number of echoes on MRI-FF estimation. Yu et al (13) used 3-echo, 4-echo, 6-echo, and 16-echo acquisitions to measure fat using an investigational complex-data chemical shift-based technique. Rather than using a composite multifrequency fat spectral model derived from a reference population, the authors used the information provided by the additional echoes to derive a tailored fat spectral model for individual phantoms and clinical subjects. The authors demonstrated that this information could be used to provide better water-fat separation than an algorithm that models fat using a single frequency corresponding to the methylene component of fat. However, the study of Yu et al did not use a reference standard such as MRS for fat quantitation and did not assess the robustness of the technique in a large patient cohort. Moreover, as the technique is complex-data based and the fat spectrum is adipose tissue- rather than liver fat-based, results may not be generalizable to the approach described here. Yokoo et al (3) compared the estimation accuracy of MRI-FF using 3, 4 and 6 echoes using a magnitude-based technique with the same multifrequency interference model implemented in this paper and found no significant differences. However, that study did not systematically assess the effect of additional echoes beyond 6 or the effect of starting echo number. Our study was the first to systematically analyze the effect of number of echoes and starting echo number on MRI-FF estimation.
Other fat-water separation and FF quantification approaches have been proposed for MR imaging. These are based on fat-suppression techniques via: frequency-selective saturation or excitation, inversion-recovery, or composite RF-pulses. The goal is to obtain two sets of images, water-only and fat-only, to calculate FF. In general these methods require two separate acquisitions, for example, with and without chemical-shift selective (CHESS) fat saturation method, which generate fat-only and water+fat images, respectively. These methods are also subject to biases due to relaxation effects, and may require additional image acquisitions with different imaging parameters to correct for the relaxation effects. The multi-echo GRE method is more efficient because it is capable of acquiring all necessary imaging data for fat-water separation and relaxation correction using a single pulse-sequence in a single breath-hold. Therefore multi-echo GRE is more practical for routine clinical applications.
Our study was limited to subjects who had nonalcoholic fatty liver disease (NAFLD) or who served as normal controls. A further limitation is that only a small volume of the liver was assessed in each subject; imaging ROI was compared to one spectroscopic voxel. Perfect co-localization of the imaging ROI with the spectroscopic voxel cannot be achieved, due to differences in shape and slice thickness, and due to possible changes in patient position or inspiratory effort between the spectroscopic and imaging acquisitions. We did not analyze nonconsecutive subsets of echoes; only consecutive echo intervals were considered. Four of the 84 subjects were imaged using a TR ≥100 ms and < 125 ms. It has previously been demonstrated (3) that for TR 125 ms, a small flip angle of 10o results in negligible effects on FF estimation. Thus, for the four subjects with TR < 125 ms, the MRI sequence had slight T1 weighting with consequent T1-related FF overestimation. It is unlikely, however, that this meaningfully affected our results, which focused on the effect of echo sampling strategy on estimation accuracy, rather than estimation accuracy per se. Finally, although the study suggested that the signal model may be imperfect at later TEs, the study was not designed to delineate the causes or to optimize the model. Systematic evaluation and refinement of the model, including the spectral peak correction, T2* estimation, non-exponential decay and noise bias, were outside the scope of the present study and require further investigation.
In conclusion, we find that in a multi-echo magnitude-based MR imaging for liver fat quantification at 3T, fat estimation accuracy does not improve with acquisition of additional echoes. Acquisition of the earliest few echoes (3 or 4) may suffice for accurate proton-density FF estimation by magnitude-based MR imaging.
Acknowledgments
Grant support:
This research was supported by the National Institutes of Health (grants NIDDK R01 DK075128, NCMHD EXPORT P60 MD00220, NIH T32 EB005970)
REFERENCES
- 1.Bydder M, Yokoo T, Hamilton G, et al. Relaxation effects in the quantification of fat using gradient echo imaging. Magnetic resonance imaging. 2008;26(3):347–359. doi: 10.1016/j.mri.2007.08.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Yokoo T, Bydder M, Hamilton G, et al. Nonalcoholic fatty liver disease: diagnostic and fat-grading accuracy of low-flip-angle multiecho gradient-recalled-echo MR imaging at 1.5 T. Radiology. 2009;251(1):67–76. doi: 10.1148/radiol.2511080666. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Yokoo T, Shiehmorteza M, Hamilton G, et al. Estimation of hepatic proton-density fat fraction by using MR imaging at 3.0 T. Radiology. 2011;258(3):749–759. doi: 10.1148/radiol.10100659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.DeGraff R, Rothman D. In vivo detection and quantification of scalar coupled 1H NMR resonances. Concepts in Magnetic Resonance. 2001;13:32–76. [Google Scholar]
- 5.Bydder M, Hamilton G, Yokoo T, Sirlin CB. Optimal phased-array combination for spectroscopy. Magnetic resonance imaging. 2008;26(6):847–850. doi: 10.1016/j.mri.2008.01.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Naressi A, Couturier C, Castang I, de Beer R, Graveron-Demilly D. Java-based graphical user interface for MRUI, a software package for quantitation of in vivo/medical magnetic resonance spectroscopy signals. Computers in biology and medicine. 2001;31(4):269–286. doi: 10.1016/s0010-4825(01)00006-3. [DOI] [PubMed] [Google Scholar]
- 7.Hamilton G, Middleton MS, Bydder M, et al. Effect of PRESS and STEAM sequences on magnetic resonance spectroscopic liver fat quantification. Journal of magnetic resonance imaging : JMRI. 2009;30(1):145–152. doi: 10.1002/jmri.21809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Hamilton G, Yokoo T, Bydder M, et al. In vivo characterization of the liver fat (1)H MR spectrum. NMR in biomedicine. 2011;24(7):784–790. doi: 10.1002/nbm.1622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Efron B. Better bootstrap confidence intervals (with discussion). Journal of the American Statistical Association. 1987;82:171–200. [Google Scholar]
- 10.Reeder S, Hines C, Yu H, McKenzie C, Brittain J. On the definitino of fat-fraction for in vivo fat quantification with magnetic resonance imaging. ISMRM 17th annual meeting and exhibition. Honolulu. 2009:211. [Google Scholar]
- 11.Szczepaniak LS, Babcock EE, Schick F, et al. Measurement of intracellular triglyceride stores by H spectroscopy: validation in vivo. The American journal of physiology. 1999;276(5 Pt 1):E977–989. doi: 10.1152/ajpendo.1999.276.5.E977. [DOI] [PubMed] [Google Scholar]
- 12.Thomsen C, Becker U, Winkler K, Christoffersen P, Jensen M, Henriksen O. Quantification of liver fat using magnetic resonance spectroscopy. Magnetic resonance imaging. 1994;12(3):487–495. doi: 10.1016/0730-725x(94)92543-7. [DOI] [PubMed] [Google Scholar]
- 13.Yu H, Shimakawa A, McKenzie CA, Brodsky E, Brittain JH, Reeder SB. Multiecho water-fat separation and simultaneous R2* estimation with multifrequency fat spectrum modeling. Magnetic resonance in medicine : official journal of the Society of Magnetic Resonance in Medicine / Society of Magnetic Resonance in Medicine. 2008;60(5):1122–1134. doi: 10.1002/mrm.21737. [DOI] [PMC free article] [PubMed] [Google Scholar]