Dynamic model for the tissue concentration and oxygen saturation of hemoglobin in relation to blood volume, flow velocity, and oxygen consumption: Implications for functional neuroimaging and coherent hemodynamics spectroscopy (CHS)

Abstract

This article presents a dynamic model that quantifies the temporal evolution of the concentration and oxygen saturation of hemoglobin in tissue, as determined by time-varying hemodynamic and metabolic parameters: blood volume, flow velocity, and oxygen consumption. This multi-compartment model determines separate contributions from arterioles, capillaries, and venules that comprise the tissue microvasculature, and treats them as a complete network, without making assumptions on the details of the architecture and morphology of the microvascular bed. A key parameter in the model is the effective blood transit time through the capillaries and its associated probability of oxygen release from hemoglobin to tissue, as described by a rate constant for oxygen diffusion. The solution of the model in the time domain predicts the signals measured by hemodynamic-based neuroimaging techniques such as functional near-infrared spectroscopy (fNIRS) and functional magnetic resonance imaging (fMRI) in response to brain activation. In the frequency domain, the model yields an analytical solution based on a phasor representation that provides a framework for quantitative spectroscopy of coherent hemodynamic oscillations. I term this novel technique coherent hemodynamics spectroscopy (CHS), and this article describes how it can be used for the assessment of cerebral autoregulation and the study of hemodynamic oscillations resulting from a variety of periodic physiological challenges, brain activation protocols, or physical maneuvers.

1. Introduction

Models for hemodynamic-based neuroimaging studies fall under either one or both of two categories. The first category includes models that characterize the features and physiological relationships among the hemodynamic and metabolic perturbations associated with brain activation [namely cerebral blood flow (CBF), cerebral blood volume (CBV), and metabolic rate of oxygen (CMRO₂)] as well as the pathways linking them to neural activity. The second category includes models that specify and quantify the relationship between a given set of activation-induced perturbations in CBF, CBV, and CMRO₂, and the quantities or signals measured by a particular neuroimaging technique (for example, the tissue concentrations of oxy-hemoglobin and deoxy-hemoglobin measured with functional near-infrared spectroscopy (fNIRS), or the blood oxygenation level dependent (BOLD) signal measured with fMRI). The dynamic model presented in this article falls under the second category.

Modeling cerebral hemodynamics and tissue oxygenation is a challenging task because of the various interconnected contributions from blood flow velocity distributions and oxygen transport within the vasculature, oxygen diffusion between the microvascular space and tissue, cerebral autoregulation, active and passive vascular compliance effects, individual contributions from multiple vascular compartments, etc. Successful approaches should identify a set of key parameters that reproduce the salient features of signals measured with neuroimaging techniques, while providing a necessarily simplified description of the dynamic features of the brain vasculature, blood flow, and oxygen delivery to tissue. An example of such a successful approach is the dynamic balloon model [Buxton et al., 1998], a pioneering model based on just three parameters: the oxygen extraction factor (and its dependence on flow based on the oxygen limitation model [Buxton and Frank, 1997]), the mean blood transit time through the venous compartment, and the exponent in the power law relationship between volume and flow (with some flexibility to account for a slow volume recovery after activation). The balloon model predicts the BOLD response on the basis of the activation-induced perturbation in CBF, it is consistent with experimental results [Buxton et al., 1998; Mildner et al., 2001; Toronov et al., 2003], and accounts for nonlinear features of evoked brain responses [Friston et al., 2000]. Another pioneering contribution is a windkessel model based on similar ideas (delayed venous compliance) built on a biophysical model of blood flow driven by arterial blood pressure through a resistive and compliant vasculature [Mandeville et al., 1999a]. A steady state deoxy-hemoglobin dilution model was also proposed in the late 1990’s to derive a relationship between the BOLD signal, CBF and CMRO₂ [Hoge et al., 1999]. A series of refined, modified, and extended models have been developed over the past decade with growing levels of complexity and sophistication, in an attempt to better describe the complicated underlying physiology of brain activation, and to quantify the effects of physiological and metabolic parameters on the signals measured with neuroimaging techniques. For example, multi-compartment versions of the balloon and windkessel models have been developed to include contributions from the arterial compartment [Blockley et al., 2009], from a serial [Zheng et al., 2005; Payne, 2006; Huppert et al., 2007] or network [Boas et al., 2008] combination of arterial, capillary and venous compartments, and to account for cerebral autoregulation [Payne, 2006; Payne et al., 2009; Diamond et al., 2009]. Quasi-static models for the tissue concentration and saturation of hemoglobin have been developed on the basis of blood flow velocity and the rate of oxygen diffusion from blood vessels [Fantini, 2002; Kocsis et al., 2006]. While many of these models, at least initially, were specifically aimed at predicting/interpreting fMRI data, and therefore focused on deoxy-hemoglobin and blood volume with a special emphasis on the venous compartment, any approach aimed at modeling the tissue concentration and oxygen saturation of hemoglobin is directly relevant to both fMRI and fNIRS. Major differences between the two techniques are the voxel size (linear dimensions: 1–4 mm for fMRI, 10–30 mm for fNIRS) and the fact that fNIRS is highly sensitive to both oxygenated and deoxygenated hemoglobin (since they both feature significant absorption in the near-infrared) while fMRI is sensitive only to the paramagnetic deoxygenated form of hemoglobin. However, both techniques are sensitive to changes in cerebral blood volume and hemoglobin saturation, and the model presented here is therefore relevant to both fNIRS and fMRI.

Near-infrared spectroscopy (NIRS) affords non-invasive measurements of the concentrations of deoxy-hemoglobin and oxy-hemoglobin in macroscopic (~1–10 cm³) tissue volumes, and can be applied to functional studies of the human brain (fNIRS) [Wolf et al., 2008; Lloyd-Fox et al., 2010; Ferrari and Quaresima, 2012]. Translating diffuse optical intensity measurements into hemoglobin concentrations is typically based on the assumption of a spatially uniform hemoglobin distribution within the optically probed tissue volume, so that optical measurements of hemoglobin concentration and saturation reflect some weighted average of the contributions from various vascular compartments in tissues. In functional magnetic resonance imaging (fMRI), the BOLD signal is a weighted average of extravascular signals (resulting from susceptibility differences between blood vessels and surrounding tissue) and intravascular signals (resulting from the concentration of deoxy-hemoglobin in blood), and depends on the blood volume and blood oxygenation in the tissue considered [Obata et al., 2004].

A first issue to consider is the impact on NIRS measurements of hemoglobin localization in blood vessels. It was proposed that an empirical volume-weighted sum of contributions from multiple blood vessels can account for measured optical signals in tissues [Liu et al., 1995]. Diffusion theory and Monte Carlo simulations have shown that for smaller blood vessels ($d<0.06/{\mu }_a^{(\text{small vessel})}$, where d is the blood vessel diameter and ${\mu }_a^{(\text{small vessel})}$ is the absorption coefficient of blood in small blood vessels) the assumption of a homogeneous distribution of hemoglobin in tissue is valid [Firbank et al., 1997]. The near-infrared absorption of blood in the microvasculature results from: the blood hemoglobin concentration (~2.3 mM), the molar extinction coefficient of hemoglobin (~2 cm⁻¹/mM at the isosbestic point of 800 nm [Matcher et al., 1995]), and the reduced hematocrit in arterioles and capillaries (by as much as 30% in the cerebral vasculature [Lammertsma et al., 1984]) per the Fårhaeus effect. As a result, ${\mu }_a^{(\text{small vessel})}~3.2{\text{cm}}^{-1}$ and the assumed homogeneous distribution of hemoglobin holds for blood vessels that are smaller than ~200 µm in diameter. The contribution of larger blood vessels to the overall blood volume in tissue tends to be underestimated by diffuse optical measurements in tissue [Firbank et al., 1997]. However, it was reported that the oscillatory displacement and pulsation of blood vessels as large as 1 mm in diameter result in optical spectra that reflect the optical properties of blood within the oscillating blood vessels rather than the background tissue [Chen et al., 2010]. As a result, dynamic diffuse optical measurements can be quantitatively associated with the optical properties of blood in larger vessels (this latter result accounts for the feasibility of pulse oximetry for arterial saturation measurements). One can therefore assume that individual vascular compartments contribute to the NIRS signals proportionally to their volume fraction, in general for the microvasculature (d ≾ 200 µm) and for larger blood vessels (d ≾ 1 mm) in the case of dynamic perturbations (vascular dilation, contraction, displacement, etc.).

A second issue to consider is associated with the longitudinal variation of hemoglobin saturation and hematocrit in the microvasculature. In fact, oxygen diffusion from arterioles and capillaries to parenchymal tissue accounts for a longitudinal oxygen gradient in the microvasculature, while the network Fårhaeus effect results in a reduced hematocrit in the microvascular network compared to the hematocrit of the incoming blood [Pries et al., 1986]. Since the lengths of arteriolar and capillary branches (typically 300–1,000 µm [Guyton and Hall, 2011 (Ch. 14)], ~400 µm in the rat mesentery [Pries et al., 1995]) are shorter than the linear size of the optically probed volume (~cm) and fMRI voxels (~mm), it is appropriate to consider average levels of longitudinal oxygenation, hematocrit, and oxygen delivery to tissue when modeling NIRS and fMRI measurements. These average levels are more appropriately termed effective values since they reflect further complex processes such as uneven partitions of erythrocytes and plasma at bifurcations (resulting in heterogeneous vessel hematocrit), arteriovenous shunting, cross-diffusion of oxygen between adjacent microvessels, greater velocity of red blood cells than plasma in the microvasculature etc. One must also consider contributions from larger arterioles and venules, where blood flow has different properties than in capillaries, for example because of pulsatile effects (in arterioles) and faster flow velocity.

A quantitative summary of morphological (diameter, length) and functional (flow velocity, tube hematocrit) properties of rat mesentery microvasculature is reported in Table I [Pries and Secomb, 2008]. The tube hematocrit represents the volume concentration of red blood cells within small blood vessels, which is lower than the hematocrit of blood entering or leaving the microvascular network (discharge hematocrit) because of the Fåhraeus effect. The size and morphology of cortical arteries (40–280 µm in diameter) and veins (30–380 µm in diameter) in the human brain have been studied postmortem by intravascular injection of India ink [Duvernoy et al., 1981]. A similar method, refined by the introduction of confocal microscopy and 3D digital morphometry, has led to statistical distributions of diameter and length of vascular segments in the human cerebral cortex, resulting in capillary diameters of 6.5 ± 1.7 µm and capillary lengths of 53 ± 50 µm [Lauwers et al., 2008]. A number of animal studies on the cat and rat brain have reported capillary diameters of 2.5–8.8 µm [Pawlik et al, 1981; Motti et al., 1986; Hudetz et al., 1993; Schlageter et al., 1999], and segment lengths of 10–300 µm [Motti et al., 1986; Hudetz et al., 1993]. Capillary flow velocity was found to be highly variable among capillaries within the range 0.4–3.9 mm/s (median: 1.5 mm/s) in the cat cortex [Pawlik et al, 1981], and 0.77–2.22 mm/s (mean: 1.56 mm/s) in the rat cortex [Hudetz et al., 1993]. Therefore, the reference values reported in Table I, which are based on a systematic study on a large number of vascular segments on multiple microvascular networks in the rat mesentery, appear to be representative also of the cerebral microvasculature, with the possible exception of the shorter capillary lengths observed in the brain cortex. However, given the net-like structure of capillaries [Cassot et al., 2006], one needs to consider the total capillary length over which oxygen diffusion from blood to tissue occurs, which is longer than the individual capillary segment length of 53 µm reported in [Lauwers et al., 2008]. Finally, the blood volume fraction in brain tissue was found to be ~1–1.5% for capillaries and ~2–4% for the entire vasculature, depending on cortical depth [Cassot et al., 2006], so that it is reasonable to assume volume fractions in the order of 0.015 for capillaries and 0.005 for both arterioles and venules.

Table I.

Length, diameter, flow velocity, and tube hematocrit measured in microvessel networks of the rat mesentery [Pries and Secomb, 2008].

Blood vessel	Length (mm)	Diameter (µm)	Velocity (mm/s)	Tube hematocrit
Arterioles	0.337	13.2	2.03	0.29
Capillaries	0.424	8.7	0.85	0.23
Venules	0.334	20.6	1.07	0.31

This article presents a dynamic model that builds on my previous quasi-static model [Fantini, 2002] to relate tissue concentration and saturation of hemoglobin to hemodynamic (i.e. blood volume, flow velocity) and metabolic (i.e. oxygen consumption) processes involving different vascular compartments. Rather than applying a mass conservation equation to relate blood inflow, outflow, and volume as done in the balloon and windkessel models [Buxton et al., 1998; Mandeville et al., 1999a], I have considered blood volume, flow velocity, and rate of oxygen extraction as independent variables, and I have developed a dynamic model that specifies the hemoglobin saturation as a function of time and longitudinal coordinate along a blood vessel. This approach does not attempt to specify the relationship between CBF, CBV, and CMRO₂, which is left to physiological models (for example, I use here the high-pass model that relates flow velocity changes to blood pressure changes in cerebral autoregulation), but it affords a dynamic analysis of the tissue concentration and saturation of hemoglobin in response to given perturbations in CBF, CBV, and CMRO₂. In particular, I have introduced a phasor representation that allows for the quantitative analysis of periodic hemodynamic oscillations (ideally sinusoidal) that may arise from the heart beat, respiration, spontaneous low-frequency oscillations, or from a variety of periodic stimulation protocols, physiological challenges, or physical maneuvers. Such quantitative analysis leads to a novel approach to the study of tissue hemodynamics that I name coherent hemodynamics spectroscopy (CHS). This model also yields a time-domain solution that allows for the derivation of tissue concentration and saturation of hemoglobin in response to arbitrary perturbations in blood volume (independently in the arterial, capillary, and venous compartments), capillary flow velocity, and oxygen consumption. The multi-compartment analysis presented here treats the arterial, capillary, and venous compartments as a complete vascular network without the need to define morphological and functional details beyond the effective blood transit times in capillaries and venules, and the rate constant of oxygen extraction from the blood in the capillaries.

2. Hemodynamic model

2.1. Nomenclature

The relevant hemoglobin-related quantities modeled here are the average volume concentrations of deoxy-hemoglobin, oxy-hemoglobin, and total (oxy+deoxy) hemoglobin in tissue, and the average oxygen saturation of hemoglobin in tissue. These four quantities are indicated with D, O, T, and S, respectively. Superscripts in parenthesis indicate partial contributions from a specific vascular compartment, namely (a) arterial, (c) capillary, and (v) venous. Note that a lack of superscript indicates average tissue concentrations or saturation. Here, the arterial compartment includes arteries and larger arterioles (diameter >40 µm) that are characterized by pulsatile blood flow and negligible oxygen diffusion to tissue [Tsai et al., 2003]; the capillary compartment refers to the microvasculature involved in oxygen diffusion to tissue, which in addition to the capillaries also includes smaller arterioles (diameter <40 µm) [Tsai et al., 2003]; the venous compartment includes venules and veins which are not involved with oxygen diffusion to tissue. A schematic representation of the blood vasculature and its decomposition into arterial, capillary, and venous compartments is presented in Fig. 1.

• D: average concentration of deoxy-hemoglobin in tissue (mol_Hb/l_tissue);

• O: average concentration of oxy-hemoglobin in tissue (mol_HbO/l_tissue);

• T: average concentration of total hemoglobin in tissue (mol_HbT/l_tissue);

• D^(a), D^(c), D^(v): contributions to D from the arterial, capillary, venous compartments (mol_Hb/l_tissue);

• O^(a), O^(c), O^(v): contributions to O from the arterial, capillary, venous compartments (mol_HbO/l_tissue);

• T^(a), T^(c), T^(v): contributions to T from the arterial, capillary, venous compartments (mol_HbT/l_tissue);

• S = O/T: average tissue saturation;

• S^(a) = O^(a)/T^(a): average arterial saturation;

• 〈S^(c)〉 = 〈O^(c)〉/T^(c): average capillary saturation;

• S^(v) = O^(v)/T^(v): average venous saturation;

• ctHb: concentration of total hemoglobin in blood (mol_HbT/l_blood);

• ϕ^(a), ϕ^(c), ϕ^(v): volume fractions of arterial, capillary, and venous blood in tissue (ml_blood/ml_tissue);

• Ƒ^(c): Fåhraeus factor (ratio of capillary to large vessel hematocrit).

Figure 1.

Schematic representation of the blood vasculature, including its decomposition into arterial (arteries, larger arterioles), capillary (smaller arterioles, capillaries), and venous (venules, veins) compartments. Small arterioles (<40 µm) are included within the capillary compartment because they are involved together with capillaries with oxygen out-diffusion to tissue. The topological structure of capillaries is net-like, while that of cerebral arterioles and venules is tree-like [Cassot et al., 2006].

It must be noted that D^{( )}, O^{( )}, and T^{( )} (where the empty parentheses in the superscripts refer to any vascular compartment) represent concentrations in tissue, so that they are given by the corresponding concentrations in blood (ctHb for total hemoglobin) multiplied by the volume fraction ϕ^{( )} (or ^(c)ϕ^(c) for capillaries) of the corresponding vascular compartment over the tissue volume of interest V. Here, ϕ^(a), ϕ^(c), and ϕ^(v) are considered as steady state, constant volume fractions (i.e. baseline, initial, or average values). From these definitions, it follows that:

$$O^{()}+D^{()}=T^{()}=\{\begin{array}{cc}\mathrm{c}\mathrm{t}\mathrm{H}\mathrm{b}{\varphi }^{()}\hfill & \hfill \text{for arterial and venous compartments}\\ \mathrm{c}\mathrm{t}\mathrm{H}\mathrm{b}{}^{(c)}{\varphi }^{(c)}\hfill & \hfill \text{for the capillary compartment}\end{array},$$ (1)

and that the tissue saturation S is a weighted average of S^(a), 〈S^(c)〉, and S^(v), with weights of ϕ^(a), ^(c)ϕ^(c), and ϕ^(v), respectively.

• c^(c): average blood flow velocity in the capillary compartment (mm/s);

• c^(v): average blood flow velocity in the venous compartment (mm/s);

• L^(c): effective combined length of small arterioles and capillaries (mm);

• L^(v): effective combined length of venules (mm);

• t^(c) = L^(c)/c^(c): blood transit time in capillaries (s);

• t^(v) = L^(v)/c^(v): blood transit time in venules (s);

• α_ȯ: rate constant of oxygen diffusion from blood to tissue (s⁻¹).

The rate constant of oxygen diffusion to tissue α_ȯ is proportional to the metabolic rate of oxygen (Ȯ) through the oxygen solubility in tissue and the microvascular partial pressure of oxygen [Secomb et al., 1993]. The time dependence of blood volume, flow velocity, and oxygen consumption is described by the temporal changes in these quantities normalized to their baseline values (i.e. (x − x₀)/x₀ where x represents volume, flow velocity, or oxygen consumption, and x₀ represent the baseline value).

• v^(a)(t): arterial blood volume change normalized to baseline value $V_0^{(a)}$;

• v^(c)(t): capillary blood volume change normalized to baseline value $V_0^{(c)}$;

• v^(v)(t): venous blood volume change normalized to baseline value $V_0^{(v)}$;

• f^(c)(t): capillary flow velocity change normalized to baseline value $c_0^{(c)}$;

• ȯ(t): oxygen consumption change normalized to baseline value α_ȯ0.

Arterial (v^(a)), capillary (v^(c)), and venous (v^(v)) volume changes are considered separately. The model shows that changes in the arterial and venous flow velocities do not affect the tissue concentration and saturation of hemoglobin, so that only f^(c) is considered. Oxygen consumption changes are directly associated solely with the capillary compartment, so that no superscripts in ȯ are introduced.

With these notations, denoting the tissue volume of interest with V, the time dependent blood volume fractions for the arterial, capillary, and venous compartment are:

• V^(a)(t)/V = ϕ^(a)[1 + v^(a)(t)]: time varying arterial blood volume fraction;

• V^(c)(t)/V = ϕ^(c)[1 + v^(c)(t)]: time varying capillary blood volume fraction;

• V^(v)(t)/V = ϕ^(v)[1 + v^(c)(t)]: time varying venous blood volume fraction.

We have recently introduced phasor notation to describe sinusoidal oscillations of the tissue hemoglobin concentration at angular frequency ω [Zheng et al., 2010]. Consistent with the above notation, a lack of superscript indicates average tissue quantities that comprise all contributions within the volume of interest, whereas superscripts are used to indicate partial contributions from the arterial [superscript (a)], capillary [superscript (c)], or venous [superscript (v)] compartment. Furthermore, subscripts are introduced to indicate partial contributions originating from blood volume (subscript V), flow velocity (subscript F), or oxygen consumption (subscript Ȯ) oscillations. In other words, superscripts specify the vascular compartment and subscripts specify the physiological source of oscillations. The following phasors can all have (a), (c), or (v) superscripts to indicate their components associated with arterial, capillary, or venous compartments.

• D, O, T: Phasors of D, O, T (mol_Hb/HbO/HbT/l_tissue);

• D_V, D_F, D_ȯ: Phasor components of D associated with blood volume, flow velocity, oxygen consumption oscillations (D = D_V + D_F + D_ȯ) (mol_Hb/l_tissue);

• O_V, O_F, O_ȯ: Phasor components of O associated with blood volume, flow velocity, oxygen consumption oscillations (O = O_V + O_F + O_ȯ) (mol_HbO/l_tissue);

• T_V, T_F, T_ȯ: Phasor components of T associated with blood volume, flow velocity, oxygen consumption oscillations (T = T_V + T_F + T_ȯ) (mol_HbT/l_Tissue);

• S: Phasor of tissue saturation;

• S_V, S_F, S_ȯ: Phasor components of S associated with blood volume, flow velocity, oxygen consumption oscillations (S = S_V + S_F + S_ȯ);

• 〈S〉_V = |O_V|/|T_V|: Average saturation of volume-oscillating vascular compartment(s).

From the definition of 〈S〉_V (which, for in-phase volume oscillations of arterial, capillary, and venous compartments, is a weighted average of S^(a), 〈S^(c)〉, and S^(v), with respective weights given by $|{\mathbf{T}}_{\mathbf{V}}^{(a)}|/|\mathbf{T}|,|{\mathbf{T}}_{\mathbf{V}}^{(c)}|/|\mathbf{T}|$, and $|{\mathbf{T}}_{\mathbf{V}}^{(v)}|/|\mathbf{T}|$) and considering that, in general, flow velocity and oxygen consumption changes are not associated with changes in the total hemoglobin concentration [Fantini, 2002], it follows that:

$${\langle S\rangle }_{\mathrm{V}}{\mathbf{D}}_{\mathrm{V}}=(1-{\langle S\rangle }_{\mathrm{V}}){\mathbf{O}}_{\mathrm{V}},$$ (2)

$${\mathbf{O}}_{\mathrm{F}}=-{\mathbf{D}}_{\mathbf{F}},$$ (3)

$${\mathbf{O}}_{\mathbf{ȯ}}=-{\mathbf{D}}_{\mathbf{ȯ}},$$ (4)

$${\mathbf{T}}_{\mathrm{F}}={\mathbf{T}}_{\mathbf{ȯ}}=0,$$ (5)

For small oscillations, which are often associated with periodic physiological perturbations of interest, it is shown in Appendix A that:

$$\mathbf{S}=\frac{1}{T}(\mathbf{O}-S\mathbf{T}).$$ (6)

I also introduce phasors that describe the sinusoidal oscillations of blood volume, flow velocity, and oxygen consumption at a given angular frequency ω. Their direction indicates the phase of the associated oscillations, and their magnitude is the amplitude of the oscillations normalized to the average value. Consequently, the blood volume, flow velocity, and oxygen consumption phasors are all dimensionless.

• v^(a): Arterial blood volume phasor;

• v^(c): Capillary blood volume phasor;

• v^(v): Venous blood volume phasor;

• f^(c): Capillary flow velocity phasor;

• ȯ: Oxygen consumption phasor.

Table II reports the set of representative values of key parameters that have been used to obtain quantitative predictions of the model. Throughout the manuscript, the values of Table II are used to estimate predictions of the model unless otherwise specified.

Table II.

Numerical values of key parameters used to derive quantitative predictions of the model presented. The last seven parameters in the Table (〈S(c)〉, S(ν), ${\omega }_c^{(c)},{\omega }_c^{(v)}$, T, O, D) are not independent, as they are derived from the other parameters according to the model.

Parameter	Symbol	Value	Units
Hemoglobin concentration in blood	ctHB	2.3	mM
Rate constant of oxygen diffusion	αȯ	0.8	s−1
Capillary length	L (c)	0.6	mm
Venule length	L(v)	1.0	mm
Flow velocity in capillaries	c(c)	0.8	mm/s
Flow velocity in venules	c(v)	1.0	mm/s
Arterial volume fraction	ϕ(a)	0.005	-
Capillary volume fraction	ϕ(c)	0.015	-
Venous volume fraction	ϕ(v)	0.005	-
Fåhraeus factor	Ƒ(c)	0.8	-
Relative arterial blood volume phasor	v(a)	0.02∠0°	-
Relative capillary blood volume phasor	v(c)	0.02∠0°	-
Relative venous blood volume phasor	v(v)	0.02∠0°	-
High-pass autoregulation cutoff frequency	$\frac{{\omega }_c^{(\text{AutoReg})}}{2\pi }$	0.15	Hz
Asymptotic flow/volume amplitude ratio	k	5	-
Relative oxygen consumption phasor	ȯ	0	-
Arterial saturation	S(a)	0.98	-
Average capillary saturation	〈S(c)〉	0.74	-
Venous saturation	S(v)	0.54	-
Low-pass capillary cutoff frequency	$\frac{{\omega }_c^{(c)}}{2\pi }$	0.58	Hz
Low-pass venous cutoff frequency	$\frac{{\omega }_c^{(v)}}{2\pi }$	0.32	Hz
Tissue concentration of total hemoglobin	T	50.6	µM
Tissue concentration of oxy	O	37.8	µM
Tissue concentration of deoxy	D	12.8	µM

2.2. Arterial compartment

Because the arterial compartment is not involved in the diffusion of oxygen to tissue, it does not feature a longitudinal oxygen gradient and it is unaffected by changes in flow velocity and oxygen consumption (i.e. ${\mathbf{O}}_{\mathrm{F}}^{(a)}={\mathbf{O}}_{\mathbf{ȯ}}^{(a)}=0$). Consequently:

$${\mathbf{D}}^{(a)}={\mathbf{D}}_{\mathbf{V}}^{(a)}=(1-S^{(a)}){\mathbf{T}}_{\mathbf{V}}^{(a)}=(1-S^{(a)})T^{(a)}{\mathbf{v}}^{(a)},$$ (7)

$${\mathbf{O}}^{(a)}={\mathbf{O}}_{\mathbf{V}}^{(a)}=S^{(a)}{\mathbf{T}}_{\mathbf{V}}^{(a)}=S^{(a)}{T}^{(a)}{\mathbf{v}}^{(a)},$$ (8)

$${\mathbf{T}}^{(a)}={\mathbf{T}}_{\mathbf{V}}^{(a)}=T^{(a)}{\mathbf{v}}^{(a)},$$ (9)

$${\mathbf{S}}^{(a)}=\frac{1}{T}({\mathbf{O}}^{(a)}-S{\mathbf{T}}^{(a)})=\frac{S^{(a)}-S}{T}{\mathbf{T}}^{(a)}=(S^{(a)}-S)\frac{T^{(a)}}{T}{\mathbf{v}}^{(a)},$$ (10)

where Eq. (6) has been used to derive Eq. (10). Equations (7) and (8) reflect the approach to arterial saturation measurements by pulse oximetry [Wukitsch et al., 1988].

2.3. Capillary compartment

The vascular compartment from which the diffusion of oxygen to tissue occurs (small arterioles and capillaries) is the one in which the interplay between blood flow velocity and oxygen consumption induces changes in the blood concentrations of oxy-hemoglobin and deoxy-hemoglobin. The total concentration of hemoglobin, according to Eq. (5), is only affected by volume changes, so that:

$${\mathbf{T}}^{(c)}={\mathbf{T}}_{\mathbf{V}}^{(c)}=T^{(c)}{\mathbf{v}}^{(c)}.$$ (11)

Changes in the capillary blood volume can be associated with dilation/contraction of the microvasculature, and/or by capillary recruitment/derecruitment. However, capillary recruitment may not play a significant role in the brain [Gobel et al., 1989].

Delivery of oxygen to the tissue involves convective transport through blood flow in the vasculature, release of oxygen from hemoglobin to the plasma, and diffusion down an oxygen tension gradient from the plasma to the tissue. If we indicate with [O₂]_in and [O₂]_out the upstream and downstream concentrations of oxygen in the blood, the rate of oxygen extraction (Ȯ₂) from a capillary can be expressed as the product of the convective inflow of oxygen (σc^(c)[O₂]_in, where σ is the cross sectional area of the blood vessel and c^(c) is the speed of blood flow in the capillary) times the oxygen extraction factor {([O₂]_in − [O₂]_out)/[O₂]_in}. Because 97–98% of the oxygen in blood is bound to hemoglobin [McLellan and Walsh, 2004; Guyton and Hall, 2011 (Ch. 40)], [O₂]_in ~ 4S_inctHb, where S_in is the saturation of incoming blood, ctHb is the total hemoglobin concentration in blood, and the factor 4 takes into account the four binding sites for oxygen of hemoglobin. By introducing a probability of oxygen extraction from blood per unit time (κ), which depends on the capillary wall permeability [Buxton and Frank, 1997] and the oxygen tension gradient across the capillary wall [Hyder et al., 1998], one can define a rate constant for oxygen diffusion to tissue α_ȯ = κr, where r is the ratio of plasma-to-blood oxygen content [Buxton and Frank, 1997; Hyder et al., 1998; Zheng et al., 2002]. Even though r is not strictly constant along the capillary length, its variability can be neglected in the evaluation of the profile of the oxygen concentration in blood along the capillary length [Zheng et al., 2002]. Therefore, the oxygen saturation of hemoglobin, which is equal to the arterial saturation S^(a) as blood enters the capillary compartment, decays exponentially over the capillary length ℓ [Fantini, 2002]:

$$S^{(c)}=S^{(a)}{e}^{-{\alpha }_{\mathrm{ȯ}}\ell /c^{(c)}},$$ (12)

and the average capillary saturation over the total capillary length L^(c) is given by [Fantini, 2002]:

$$\langle S^{(c)}\rangle =S^{(a)}\frac{c^{(c)}}{{\alpha }_{\mathrm{ȯ}}{L}^{(c)}}(1-e^{-{\alpha }_{\mathrm{ȯ}}{L}^{(c)}/c^{(c)}}),$$ (13)

so that:

$${\mathbf{O}}_{\mathbf{V}}^{(c)}=\langle S^{(c)}\rangle {\mathbf{T}}_{\mathbf{V}}^{(c)}=\frac{S^{(a)}}{{\alpha }_{\mathrm{ȯ}}{t}^{(c)}}(1-e^{-{\alpha }_{\mathrm{ȯ}}{t}^{(c)}})T^{(c)}{\mathbf{v}}^{(c)},$$ (14)

where I have introduced the blood transit time in capillaries t^(c) = L^(c)/c^(c). Equation (14) takes into account the fact that there is no delay or phase difference between changes in blood volume and changes in the tissue concentration of oxy-hemoglobin (because they are just proportional to each other).

The situation is different for changes in blood flow velocity and oxygen consumption, since they induce delayed changes in the tissue concentration of oxy-hemoglobin due to the blood transit time in the capillaries. By considering the vascular network as a linear and time-invariant system, which may be justified for relatively small hemodynamic perturbations and for measurements over relatively short periods of time, one can model the frequency dependence of the hemodynamic phasors defined above by means of transfer functions.

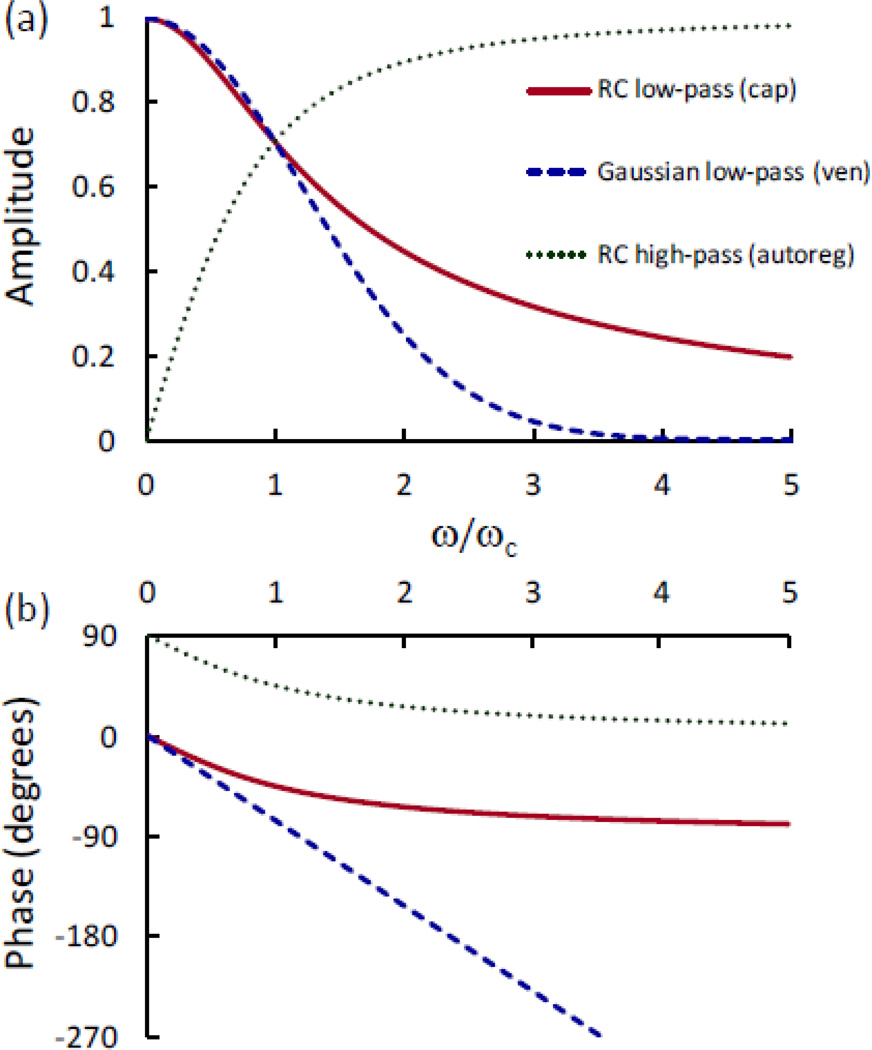
The response of the average capillary saturation to a step change in the capillary blood flow velocity is derived in Appendix B and results in an RC-like low-pass response with time constant τ^(c) = t^(c)/e (where t^(c) is the blood transit time in the capillaries). The complex transfer function vs. angular frequency (ω) for the capillary RC low-pass filter $[{\mathscr{H}}_{RC-LP}^{(c)}(\omega )]$ and the time constant indicated above is as follows and is shown in Fig. 2 (solid line):

$${\mathscr{H}}_{RC-LP}^{(c)}(\omega )=\frac{1}{\sqrt{1+{(\omega {\tau }^{(c)})}^2}}{e}^{-i{\text{tan}}^{-1}(\omega {\tau }^{(c)})}=\frac{1}{\sqrt{1+{\left(\frac{\omega t^{(c)}}{e}\right)}^2}}{e}^{-i{\text{tan}}^{-1}\left(\frac{\omega t^{(c)}}{e}\right)}.$$ (15)

As discussed in Appendix D, the transfer function of Eq. (15) also applies to a saturation response to oscillations in the oxygen consumption rate. For small flow velocity oscillations, one can use this transfer function, together with the steady state capillary saturation changes resulting from relative changes in capillary flow velocity (Δc^(c)/c^(c)) and oxygen consumption rate (Δα_ȯ/α_ȯ) [Fantini 2002], to obtain the frequency dependence of capillary saturation phasors associated with flow velocity and oxygen consumption oscillations:

$${\mathbf{S}}_{\mathrm{F}}^{(c)}=\frac{S^{(a)}}{{\alpha }_{\mathrm{ȯ}}{t}^{(c)}}[1-e^{-{\alpha }_{\mathrm{ȯ}}{t}^{(c)}}({\alpha }_{\mathrm{ȯ}}{t}^{(c)}+1)]{\mathscr{H}}_{RC}^{(c)}(\omega ){\mathbf{f}}^{(\mathit{c})}=(\langle S^{(c)}\rangle -S^{(v)}){\mathscr{H}}_{RC-LP}^{(c)}(\omega ){\mathbf{f}}^{(\mathit{c})},$$ (16)

$${\mathbf{S}}_{\mathbf{ȯ}}^{(c)}=-\frac{S^{(a)}}{{\alpha }_{\mathrm{ȯ}}{t}^{(c)}}[1-e^{-{\alpha }_{\mathrm{ȯ}}{t}^{(c)}}({\alpha }_{\mathrm{ȯ}}{t}^{(c)}+1)]{\mathscr{H}}_{RC}^{(c)}(\omega )\mathbf{ȯ}=-(\langle S^{(c)}\rangle -S^{(v)}){\mathscr{H}}_{RC-LP}^{(c)}(\omega )\mathbf{ȯ}.$$ (17)

The oxy-hemoglobin and deoxy-hemoglobin phasor components due to flow velocity and oxygen consumption rate oscillations are therefore given by:

$${\mathbf{O}}_{\mathbf{F}}^{(c)}=-{\mathbf{D}}_{\mathbf{F}}^{(c)}=T^{(c)}{\mathbf{S}}_{\mathrm{F}}^{(c)}=(\langle S^{(c)}\rangle -S^{(v)})T^{(c)}{\mathscr{H}}_{RC-LP}^{(c)}(\omega ){\mathbf{f}}^{(\mathit{c})},$$ (18)

$${\mathbf{O}}_{\mathbf{ȯ}}^{(c)}=-{\mathbf{D}}_{\mathbf{ȯ}}^{(c)}=T^{(c)}{\mathbf{S}}_{\mathbf{ȯ}}^{(c)}=-(\langle S^{(c)}\rangle -S^{(v)})T^{(c)}{\mathscr{H}}_{RC-LP}^{(c)}(\omega )\mathbf{ȯ}.$$ (19)

The phasors of tissue concentrations of oxy-hemoglobin and deoxy-hemoglobin result from the superposition of contributions from volume, flow velocity, and oxygen consumption oscillations, while the hemoglobin saturation phasor can be obtained by using Eq. (6):

$${\mathbf{O}}^{(c)}={\mathbf{O}}_{\mathbf{V}}^{(c)}+{\mathbf{O}}_{\mathbf{F}}^{(c)}+{\mathbf{O}}_{\mathbf{ȯ}}^{(c)}=\langle S^{(c)}\rangle {\mathbf{T}}_{\mathbf{V}}^{(c)}+T^{(c)}({\mathbf{S}}_{\mathbf{F}}^{(c)}+{\mathbf{S}}_{\mathbf{ȯ}}^{(c)})=\langle S^{(c)}\rangle T^{(c)}{\mathbf{v}}^{(c)}+(\langle S^{(c)}\rangle -S^{(v)})T^{(c)}{\mathscr{H}}_{RC-LP}^{(c)}(\omega )({\mathbf{f}}^{(c)}-\mathbf{ȯ}),$$ (20)

$${\mathbf{D}}^{(c)}={\mathbf{D}}_{\mathbf{V}}^{(c)}+{\mathbf{D}}_{\mathbf{F}}^{(c)}+{\mathbf{D}}_{\mathbf{ȯ}}^{(c)}=(1-\langle S^{(c)}\rangle ){\mathbf{T}}_{\mathbf{V}}^{(c)}-T^{(c)}({\mathbf{S}}_{\mathbf{F}}^{(c)}+{\mathbf{S}}_{\mathbf{ȯ}}^{(c)})=(1-\langle S^{(c)}\rangle )T^{(c)}{\mathbf{v}}^{(c)}-(\langle S^{(c)}\rangle -S^{(v)})T^{(c)}{\mathscr{H}}_{RC-LP}^{(c)}(\omega )({\mathbf{f}}^{(\mathit{c})}-\mathbf{ȯ}),$$ (21)

$${\mathbf{S}}^{(c)}=\frac{1}{T}({\mathbf{O}}^{(c)}-S{\mathbf{T}}^{(c)})=\frac{T^{(c)}}{T}[(\langle S^{(c)}\rangle -S){\mathbf{v}}^{(c)}+(\langle S^{(c)}\rangle -S^{(v)}){\mathscr{H}}_{RC-LP}^{(c)}(\omega )({\mathbf{f}}^{(\mathit{c})}-\mathbf{ȯ})].$$ (22)

Fig. 2.

Frequency dependence of the (a) amplitude and (b) phase of the complex transfer functions that describe the low-pass response of the average capillary (cap) and venule (ven) saturation in response to sinusoidal changes in blood flow velocity and oxygen consumption rate. The capillary network is approximated by an RC low-pass filter, while the venous compartment is approximated by a time-shifted Gaussian low-pass filter. Recalling that t^(c) and t^(v) are the blood transit time in capillaries and venules, respectively, the cutoff angular frequency (ω_c) is given by ~e/t^(c) for the capillary network and ~1[0.281(t^(c) + t^(v))] for the venous compartment. Therefore, for these low-pass responses, the x axis (ω/ω_c) is proportional to the ratio between the blood transit time and the period of oscillations. This figure also shows the (a) amplitude and (b) phase of the high-pass response of blood flow velocity to blood volume changes as a result of cerebral autoregulation (autoreg). In the case of this high-pass response, ω_c represents the cutoff angular frequency for autoregulation.

2.4. Venous compartment

The total concentration of hemoglobin is only affected by volume changes [see Eq. (5)], so that:

$${\mathbf{T}}^{(v)}={\mathbf{T}}_{\mathbf{V}}^{(v)}={\mathbf{T}}^{(v)}{\mathbf{v}}^{(v)}.$$ (23)

Changes in the venous blood volume can be associated with dilation/contraction of the venules and veins.

The oxygen saturation of hemoglobin, which is equal to the arterial saturation S^(a) at the entrance of the capillary and decays exponentially along the capillary, takes the following value at the end of the capillary length L^(c), which is the venous saturation S^(v) [Fantini, 2002]:

$$S^{(v)}=S^{(a)}{e}^{-{\alpha }_{\mathrm{ȯ}}{L}^{(c)}/c^{(c)}}.$$ (24)

Consequently:

$${\mathbf{O}}_{\mathbf{V}}^{(v)}=S^{(v)}{\mathbf{T}}_{\mathbf{V}}^{(v)}=S^{(a)}{e}^{-{\alpha }_{\mathrm{ȯ}}{t}^{(c)}}{T}^{(v)}{\mathbf{v}}^{(v)},$$ (25)

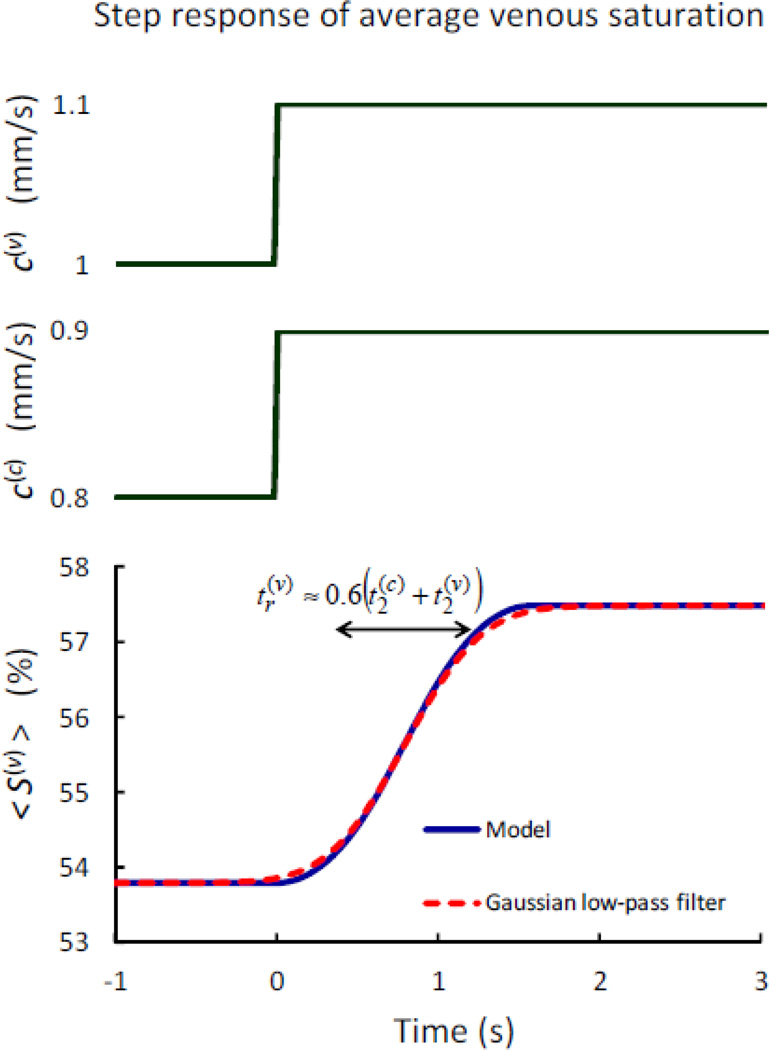
where t^(c) = L^(c)/c^(c) is the blood transit time in capillaries. The response of the average venous saturation to step changes in the capillary and venule blood flow velocities is derived in Appendix C, and results in a time-shifted Gaussian low-pass response with rise time $t_r^{(v)}~0.6(t^{(c)}+t^{(v)})$ and temporal shift $t_{0.5}^{(v)}=0.5(t^{(c)}+t^{(v)})$. Here, t^(c) and t^(v) are the blood transit times in capillaries and venules, respectively. The complex transfer function vs. frequency for the venule Gaussian low-pass filter $[{\mathscr{H}}_{G-LP}^{(v)}(\omega )]$ and the time constants indicated above is given by the following expression and is shown in Fig. 2 (dashed line):

$${\mathscr{H}}_{G-LP}^{(v)}(\omega )=e^{-\frac{\text{ln}2}{2}{\left(\frac{\omega }{{\omega }_c}\right)}^2}{e}^{-i\omega t_{0.5}^{(v)}}=e^{-\frac{\text{ln}2}{2}{[\omega 0.281(t^{(c)}+t^{(v)})]}^2}{e}^{-i\omega 0.5(t^{(c)}+t^{(v)})},$$ (26)

where the factor 0.281 in Eq. (26) results from the fact that the cutoff angular frequency of the Gaussian low-pass filter is given by ${\omega }_c^{(v)}=2\pi 0.34/t_r^{(v)}\approx 2\pi 0.34/[0.6(t^{(c)}+t^{(v)})]\approx 1/[0.281(t^{(c)}+t^{(v)})]$. As discussed in Appendix D, the transfer function of Eq. (26) also applies to a saturation response to oscillations in the oxygen consumption rate. For small flow velocity oscillations, one can use this transfer function, together with the steady state venous saturation changes resulting from relative changes in capillary flow velocity (Δc^(c)/c^(c)) and oxygen consumption rate (Δα_ȯ/α_ȯ) [Fantini, 2002], to obtain the frequency dependence of the venous saturation phasors associated with flow velocity and oxygen consumption oscillations:

$${\mathbf{S}}_{\mathbf{F}}^{(v)}=S^{(a)}{\alpha }_{\mathrm{ȯ}}{t}^{(c)}{e}^{-{\alpha }_{\mathrm{ȯ}}{t}^{(c)}}{\mathscr{H}}_{G-LP}^{(v)}(\omega ){\mathbf{f}}^{(\mathit{c})},$$ (27)

$${\mathbf{S}}_{\mathbf{ȯ}}^{(v)}=-S^{(a)}{\alpha }_{\mathrm{ȯ}}{t}^{(c)}{e}^{-{\alpha }_{\mathrm{ȯ}}{t}^{(c)}}{\mathscr{H}}_{G-LP}^{(v)}(\omega )\mathbf{ȯ},$$ (28)

where ±S^(a)α_ȯt^(c)e^−α_ȯt(c) is the steady state change in venous saturation due to capillary flow velocity (+ sign) and oxygen consumption (− sign) changes. The phasor components of tissue concentrations of oxy-hemoglobin and deoxy-hemoglobin due to flow velocity and oxygen consumption oscillations are therefore given by:

$${\mathbf{O}}_{\mathbf{F}}^{(v)}=-{\mathbf{D}}_{\mathbf{F}}^{(v)}=T^{(v)}{\mathbf{S}}_{\mathbf{F}}^{(v)}={\alpha }_{\mathrm{ȯ}}{t}^{(c)}{S}^{(v)}{T}^{(v)}{\mathscr{H}}_{G-LP}^{(v)}(\omega ){\mathbf{f}}^{(\mathit{c})},$$ (29)

$${\mathbf{O}}_{\mathbf{ȯ}}^{(v)}=-{\mathbf{D}}_{\mathbf{ȯ}}^{(v)}=T^{(v)}{\mathbf{S}}_{\mathbf{ȯ}}^{(c)}=-{\alpha }_{\mathrm{ȯ}}{t}^{(c)}{S}^{(v)}{T}^{(v)}{\mathscr{H}}_{G-LP}^{(v)}(\omega )\mathbf{ȯ}.$$ (30)

The phasors of tissue concentrations of oxy-hemoglobin and deoxy-hemoglobin result from the superposition of contributions from blood volume, flow velocity, and oxygen consumption oscillations, whereas the hemoglobin saturation phasor can be obtained by using Eq. (6):

$${\mathbf{O}}^{(v)}={\mathbf{O}}_{\mathbf{V}}^{(v)}+{\mathbf{O}}_{\mathbf{F}}^{(v)}+{\mathbf{O}}_{\mathbf{ȯ}}^{(v)}=S^{(v)}{\mathbf{T}}_{\mathbf{V}}^{(v)}+T^{(v)}({\mathbf{S}}_{\mathrm{F}}^{(v)}+{\mathbf{S}}_{\mathbf{ȯ}}^{(v)})=S^{(v)}{T}^{(v)}{\mathbf{v}}^{(v)}+{\alpha }_{\mathrm{ȯ}}{t}^{(c)}{S}^{(v)}{T}^{(v)}{\mathscr{H}}_{G-LP}^{(v)}(\omega )({\mathbf{f}}^{(\mathit{c})}-\mathbf{ȯ}),$$ (31)

$${\mathbf{D}}^{(v)}={\mathbf{D}}_{\mathbf{V}}^{(v)}+{\mathbf{D}}_{\mathbf{F}}^{(v)}+{\mathbf{D}}_{\mathbf{ȯ}}^{(v)}=(1-S^{(v)}){\mathbf{T}}_{\mathbf{V}}^{(v)}-T^{(v)}({\mathbf{S}}_{\mathbf{F}}^{(c)}+{\mathbf{S}}_{\mathbf{ȯ}}^{(c)})=(1-S^{(v)})T^{(v)}{\mathbf{v}}^{(v)}-{\alpha }_{\mathrm{ȯ}}{t}^{(c)}{S}^{(v)}{T}^{(v)}{\mathscr{H}}_{G-LP}^{(v)}(\omega )({\mathbf{f}}^{(\mathit{c})}-\mathbf{ȯ}),$$ (32)

$${\mathbf{S}}^{(v)}=\frac{1}{T}({\mathbf{O}}^{(v)}-S{\mathbf{T}}^{(v)})=\frac{T^{(v)}}{T}[(S^{(v)}-S){\mathbf{v}}^{(v)}+{\alpha }_{\mathrm{ȯ}}{t}^{(c)}{S}^{(v)}{\mathscr{H}}_{G-LP}^{(v)}(\omega )({\mathbf{f}}^{(\mathit{c})}-\mathbf{ȯ})].$$ (33)

2.5. Combination of contributions from arterial, capillary, and venous compartments

By recalling that the concentration of hemoglobin in tissue is given by the concentration of hemoglobin in blood times the volume fraction of the vascular compartment of interest, with the additional Fåhraeus factor for the capillary compartment [see Eq. (1)], one can write the following expressions for the tissue concentrations and saturation phasors:

$$\mathbf{D}={\mathbf{D}}^{(a)}+{\mathbf{D}}^{(c)}+{\mathbf{D}}^{(v)}==\mathrm{c}\mathrm{t}\mathrm{H}\mathrm{b}\left\{\begin{array}{c}\hfill {\varphi }^{(a)}(1-S^{(a)}){\mathbf{v}}^{(a)}+{}^{(c)}{\varphi }^{(c)}(1-\langle S^{(c)}\rangle ){\mathbf{v}}^{(c)}+{\varphi }^{(v)}(1-S^{(v)}){\mathbf{v}}^{(v)}+\hfill \\ \hfill -[{}^{(c)}{\varphi }^{(c)}(\langle S^{(c)}\rangle -S^{(v)}){\mathscr{H}}_{RC-LP}^{(c)}(\omega )+{\varphi }^{(v)}{S}^{(v)}{\alpha }_{\mathrm{ȯ}}{t}^{(c)}{\mathscr{H}}_{G-LP}^{(v)}(\omega )]({\mathbf{f}}^{(\mathit{c})}-\mathbf{ȯ})\hfill \end{array}\right\},$$ (34)

$$\begin{gathered} \mathbf{O}={\mathbf{O}}^{(a)}+{\mathbf{O}}^{(c)}+{\mathbf{O}}^{(v)}= \\ =\mathrm{c}\mathrm{t}\mathrm{H}\mathrm{b}\left\{\begin{array}{c}\hfill {\varphi }^{(a)}{S}^{(a)}{\mathbf{v}}^{(a)}+{}^{(c)}{\varphi }^{(c)}{S}^{(c)}{\mathbf{v}}^{(c)}+{\varphi }^{(v)}{S}^{(v)}{\mathbf{v}}^{(v)}+\hfill \\ \hfill +[{}^{(c)}{\varphi }^{(c)}(\langle S^{(c)}\rangle -S^{(v)}){\mathscr{H}}_{RC-LP}^{(c)}(\omega )+{\varphi }^{(v)}{S}^{(v)}{\alpha }_{\mathrm{ȯ}}{t}^{(c)}{\mathscr{H}}_{G-LP}^{(v)}(\omega )]({\mathbf{f}}^{(c)}-\mathbf{ȯ})\hfill \end{array}\right\}, \end{gathered}$$ (35)

$$\begin{gathered} \mathbf{T}={\mathbf{T}}^{(a)}+{\mathbf{T}}^{(c)}+{\mathbf{T}}^{(v)}=T^{(a)}{\mathbf{v}}^{(a)}+T^{(c)}{\mathbf{v}}^{(c)}+T^{(\mathbf{v})}{\mathbf{v}}^{(v)}= \\ =\mathrm{c}\mathrm{t}\mathrm{H}\mathrm{b}({\varphi }^{(a)}{\mathbf{v}}^{(a)}+{}^{(c)}{\varphi }^{(c)}{\mathbf{v}}^{(c)}+{\varphi }^{(v)}{\mathbf{v}}^{(v)}), \end{gathered}$$ (36)

$$\mathbf{S}=\frac{1}{T}(\mathbf{O}-S\mathbf{T})=\frac{1}{{\varphi }^{(a)}+{\varphi }^{(c)}+{\varphi }^{(v)}}\times \left\{\begin{array}{c}\hfill {\varphi }^{(a)}(S^{(a)}-S){\mathbf{v}}^{(a)}+{}^{(c)}{\varphi }^{(c)}(S^{(c)}-S){\mathbf{v}}^{(c)}+{\varphi }^{(v)}(S^{(v)}-S){\mathbf{v}}^{(v)}+\hfill \\ \hfill +[{}^{(c)}{\varphi }^{(c)}(\langle S^{(c)}\rangle -S^{(v)}){\mathscr{H}}_{RC-LP}^{(c)}(\omega )+{\varphi }^{(v)}{S}^{(v)}{\alpha }_{\mathrm{ȯ}}{t}^{(c)}{\mathscr{H}}_{G-LP}^{(v)}(\omega )]({\mathbf{f}}^{(\mathit{c})}-\mathbf{ȯ})\hfill \end{array}\right\}.$$ (37)

It is worth observing that the partial volumes ϕ^(a), ϕ^(c), and ϕ^(v) in Eqs. (34)–(37) act as the relative weights of the contributions of the arterial, capillary, and venous compartments to the tissue concentration and saturation of hemoglobin. If a measurement of tissue concentration and saturation of hemoglobin features an inhomogeneous spatial sensitivity and/or a selective sensitivity to the different vascular compartments or to blood vessels of different sizes (as is the case of NIRS) then corrective factors may have to be incorporated into the weights ϕ^(a), ϕ^(c), and ϕ^(v) to take this into account.

3. Implications of the model

The dynamic model presented here provides a quantitative description of the changes in the concentrations of deoxy-hemoglobin, oxy-hemoglobin, total hemoglobin, and hemoglobin saturation (hemoglobin-related parameters) within a tissue volume that is affected by changes in blood volume, flow velocity, and metabolic rate of oxygen (physiological parameters). For sinusoidal oscillatory changes, the phasor equations of the model provide the frequency dependence of the phase and amplitude of the phasors associated with hemoglobin-related parameters (D, O, T, S) for a set of given phasors associated with the physiological parameters (ȯ, v, f^(c)) [Eqs. (34)–(37)]. This model does not attempt to derive expressions for the physiological parameters and their relationships under specific physiological/functional/pathologic conditions, but either takes them as known quantities on the basis of previous studies, or treats them as variables to identify their set of values that are consistent with experimental results for hemoglobin-related parameters. I now consider some relevant scenarios where the quantitative features of the model can help to investigate the underlying physiological processes and perform dedicated analyses of some of their features.

3.1. Pulse oximetry and spiroximetry

If the blood volume oscillations of either the arterial compartment (|v^(a)|) or the venous compartment (|v^(v)|) are the dominant source of changes in the tissue concentrations of oxy- and deoxy-hemoglobin, then:

1. contributions from f^(c) and ȯ in Eq. (34)–(37) can be neglected (provided that |f^(c)| does not increase proportionally to the dominant volume oscillations);

2. the phasors D, O, and T, are all in phase with each other;

3. the ratio between the amplitudes of O and T provides a measure of the hemoglobin saturation of the volume-oscillating vascular compartment.

This is the basis for measurements of arterial saturation by pulse oximetry at the heart-beat frequency (ω_H) [Wukitsch et al., 1988; Wolf et al., 1997; Franceschini et al., 1999], and venous saturation by so-called spiroximetry at the respiratory frequency (ω_R) [Wolf et al., 1997; Franceschini et al., 2002]. In fact, according to point (3) above, for dominant contributions from arterial or venous volume oscillations, Eqs. (34) and (35) yield the following results, respectively:

$$S^{(a)}=\frac{|\mathbf{O}({\omega }_H)|}{|\mathbf{T}({\omega }_H)|},$$ (38)

$$S^{(v)}=\frac{|\mathbf{O}({\omega }_R)|}{|\mathbf{T}({\omega }_R)|}.$$ (39)

3.2. Frequency-resolved spectral measurements of hemodynamic oscillations: coherent hemodynamics spectroscopy (CHS)

The model presented here provides a theoretical framework for a novel kind of frequency-resolved, spectral studies of cerebral hemodynamics and oxygenation. By properly designing protocols involving periodic brain stimulation, physiological challenges, or other kinds of active or passive physical maneuvers, one can measure the amplitude and phase of associated hemodynamic oscillations as a function of frequency. Furthermore, protocols designed to induce or enhance hemodynamic oscillations at a particular frequency can achieve a high level of coherence between the oscillations of physiological properties and the oscillations of hemoglobin concentration and saturation in tissue, for which the proposed approach based on transfer function analysis is especially suited. In fact, besides indicating a lack of correlation, low coherence values between physiological perturbations and observed hemoglobin-related tissue responses may reflect (1) a non-linear relationship, (2) a further dependence of the observed quantities on input variables not considered in the model, and/or (3) a significant contribution from observational or extraneous noise [Timmer et al., 1998]. All three of these conditions would negatively impact the accuracy of the model [points (1) and (2)] or the precision of the amplitude and phase measurements [point (3)]. Because of the relevance of a high level of coherence between physiological perturbations and the observed tissue hemoglobin concentration and saturation, I term this novel approach coherent hemodynamics spectroscopy (CHS), for which Eqs. (34)–(37) provide a quantitative and analytical description. The critical coherence value to reject the null hypothesis of zero coherence (which depends on the significance level of the statistical test and the equivalent number of degrees of freedom associated with the data acquisition and analysis procedure) typically assumes values between 0.1 and 0.3 [Halliday et al., 1995; Timmer et al., 1998; Winterhalder et al., 2006]. The requirement of a high level of coherence, as opposed to that of a non-zero coherence, translates into more stringent conditions associated with greater threshold coherence values. The role of high coherence levels in the analysis of hemodynamic oscillations in the low-frequency range (≾ 0.1 Hz) has been pointed out in studies of cerebral autoregulation (Zhang et al., 1998; Hahn et al., 2011) and functional brain activation (Obrig et al., 2000), where coherence threshold values of ~0.5 were considered.

Near-infrared spectroscopy affords separate measurements of the tissue concentration phasors of deoxy-hemoglobin (D) and oxy-hemoglobin (O), which combine into the phasors of total hemoglobin concentration (T) and tissue hemoglobin saturation (S). Figure 3 shows the frequency spectra predicted by the model for the phase difference and amplitude ratio of D and O, and for the phase difference and amplitude ratio of O and T (as obtained by using the numerical values of Table II). I observe that the stronger spectral variability of the amplitude ratio of O and T with respect to D and O [Fig. 3(a)] is mirrored by the weaker spectral variability of the phase difference of O and T with respect to D and O [Fig. 3(b)]. These spectral features carry information about systemic vs. local, static vs. dynamic, and anatomical/functional/metabolic parameters that affect tissue hemodynamics as described in the model. A number of relevant features of CHS spectra are further described in the companion article, which also reports experimental CHS spectra (and associated fits using the model presented here) collected with NIRS on the brain and calf muscle of human subjects [Pierro et al., 2013, this issue].

Fig. 3.

Representative spectra of coherent hemodynamics spectroscopy (CHS). (a) Frequency dependence of the amplitude ratio of phasors O and T (solid line), and D and O (dashed line). (b) Frequency dependence of the phase difference of phasors O and T (solid line), and D and O (dashed line). Note the negative phase of D vs. O (i.e. deoxy-hemoglobin oscillations lag oxy-hemoglobin oscillations in tissue), and the positive phase of O vs. T at low frequencies that becomes negative at higher frequencies (>0.2 Hz in this case). These spectra correspond to the model parameter values of Table II.

By taking into account the dependence of the fMRI BOLD signal (𝒮_BOLD) on the deoxy-hemoglobin content and the venous blood volume [Buxton et al., 1998; Obata et al., 2004], one can also introduce a BOLD signal phasor (𝒮_BOLD) in terms of the deoxy-hemoglobin concentration phasor D [Eq. (36)], and the partially deoxygenated blood volume represented by arterial, capillary, and venous volume phasors v^(a), v^(c), and v^(v):

$${\mathbf{𝒮}}_{\mathbf{\text{Bold}}}=({\varphi }^{(a)}+{\varphi }^{(c)}+{\varphi }^{(v)})[3.4(1-\frac{\mathbf{D}}{D_0})-\frac{(1-S^{(a)}){\mathbf{v}}^{(a)}+(1-\langle S^{(c)}\rangle ){\mathbf{v}}^{(c)}+(1-S^{(v)}){\mathbf{v}}^{(v)}}{3-S^{(a)}-\langle S^{(c)}\rangle -S^{(v)}}],$$ (40)

where I have introduced a combination of the contributions from arterial, capillary, and venous blood volumes (v^(a), v^(c), and v^(v)), weighted by the respective deoxy-hemoglobin contents (which are proportional to 1 − S^(a), 1 − 〈S^(c)〉, and 1 − S^(v), respectively). Equation (40) shows that the fMRI BOLD signal can also be used to perform coherent hemodynamics spectroscopy (CHS), possibly in combination with measurements of cerebral blood flow [by perfusion MRI or arterial spin labeling (ASL)] or arterial blood pressure oscillations (by finger plethysmography).

3.3. Measurements of cerebral autoregulation

Cerebral autoregulation is the process that maintains a relatively constant cerebral blood flow over a range of cerebral perfusion pressures. It has been shown that cerebral autoregulation behaves as a high-pass filter for regulating cerebral blood flow velocity in response to changes in arterial blood pressure [Diehl et al., 1995; Zhang et al., 1998] with a high-pass cutoff frequency of ~0.15 Hz [Blaber et al., 1997]. Consistent with such high-pass behavior, oscillations at ~0.1 Hz in blood flow velocity (measured by transcranial Doppler ultrasound in the middle cerebral artery) lead oscillations in arterial blood pressure (measured by beat-to-beat finger plethysmography), with a phase angle that is reduced in the case of impaired autoregulation [Reinhard et al., 2006]. Pressure and flow velocity oscillations at a frequency of ~0.1 Hz occur spontaneously [Panerai et al., 1998, Cheng et al., 2012], but they can also be induced at a controlled frequency by paced breathing [Reinhard et al., 2006], head-up-tilting [Hughson et al., 2001], squat-stand maneuvers [Claassen et al., 2009], or pneumatic thigh-cuff inflation [Aaslid et al., 2007].

The magnitude of the relative changes in arterial blood pressure are comparable to those of the associated blood flow velocity changes [Panerai et al., 2001; Reinhard et al., 2006; Zhang et al., 2009]. By contrast, the relative changes in flow velocity are about 5 times greater than the relative changes in blood volume, as estimated by the relative changes in tissue hemoglobin concentration on the basis of the data presented in [Reinhard et al., 2006; Rowley et al., 2007] after considering that the total hemoglobin concentration in the adult human brain is ~60 µM [Hallacoglu et al., 2012]. Since the oscillations reported in [Reinhard et al., 2006; Rowley et al., 2007] are at a frequency of ~0.1 Hz, which is in the order of the cutoff frequency for autoregulation, the amplitude of flow velocity oscillations at high frequencies may be even greater than ~5 times the amplitude of blood volume oscillations. It must be noted that the Grubb’s exponent, which is the ratio between relative changes in cerebral blood volume and blood flow, has been found to assume a broad range of values from 0.38–0.40 [Grubb et al., 1974, Lee et al., 2001] to 0.23 [Cheung et al., 2001]. These steady state Grubb’s exponent values have been found to not necessarily represent transient conditions involving autoregulation or brain activation. For example, a value of 0.27 has been reported over a time window of 10–30 s post stimulus in the rat somatosensory cortex, with lower values approaching 0.2 at ~10 s post stimulus [Mandeville et al., 1999b] and getting as low as 0.1–0.2 after stimulation onset [Kida et al., 2007]. Furthermore, rather than considering cerebral blood flow, the present article considers blood flow velocity, which is associated with a modified Grubb’s exponent that has been reported to be lower (0.13 vs. 0.30) than the standard Grubb’s exponent [Leung et al., 2009]. While, strictly speaking, the ratio between relative changes in flow and volume is not exactly given by the inverse of the Grubb’s exponent [Leung et al., 2009], the inverse of the modified (~0.13) and dynamic (~0.2) Grubb’s exponents is consistent with the reported factor of ≿5 between flow velocity and blood volume changes associated with autoregulation. Therefore, one can write the following relationship between the blood volume phasor (v), which is directly linked to arterial blood pressure oscillations, and the corresponding flow velocity phasor (f^(c)) that results from cerebral autoregulation:

$${\mathbf{f}}^{(\mathit{c})}=k{\mathscr{H}}_{RC-HP}^{(\text{AutoReg})}(\omega )\mathbf{v},$$ (41)

where ${\mathscr{H}}_{RC-HP}^{(\text{AutoReg})}(\omega )$ is the RC high-pass transfer function with cutoff frequency ${\omega }_c^{(\text{AutoReg})}/(2\pi )~0.15\mathrm{H}\mathrm{z}$, and k ≈ 5. The blood volume phasor v in Eq. (41) represents, in general, a weighted average of the arterial, capillary, and venous volume phasors (v^(a), v^(c), v^(v)) to take into account their individual relationships to the flow velocity phasor (f^(c)) associated with autoregulation. In fact, autoregulation typically occurs at the level of arterioles, which actively dilate or constrict to modulate cerebral vascular resistance through myogenic, shear-dependent, and metabolic responses [Carlson et al., 2008; Gabrielli et al., 2009 (Ch. 43)]. However, capillaries and venules also exhibit passive cross-sectional changes in response to arterial pressure changes, even though these effects on autoregulation are typically neglected because of the small contributions of capillaries and venules to the total flow resistance [Carlson et al., 2008]. For simplicity, here I have considered v to be the average of the arterial, capillary, and venous volume phasors, i.e. v = (v^(a) + v^(c) + v^(v))/3, but unequal weights can of course be introduced for the three vascular compartments. The complex transfer function vs. frequency for the autoregulation RC high-pass filter $[{\mathscr{H}}_{RC-HP}^{(\text{AutoReg})}(\omega )]$ is shown in Fig. 2 (dotted line). The model allows one to compute phasor diagrams for f^(c), D, and O (using Eqs. (41), (34), and (35), respectively) for any given phasor v as a function of frequency, so that one can visualize the frequency evolution of the phase and amplitude relationship among the various oscillatory quantities. Such phasor diagrams are shown in Fig. 4(a) for four different frequencies [ω/(2π) = 0.05, 0.15, 0.30, and 0.50 Hz], by using the above values for ${\omega }_c^{(\text{AutoReg})}/(2\pi )$ (i.e. 0.15 Hz), k (i.e. 5), and the values in Table II for the other relevant model parameters. Figure 4(b) shows the corresponding phasor diagrams in the absence of autoregulation [i.e. by setting ${\mathscr{H}}_{RC-HP}^{(\text{AutoReg})}(\omega )=1$]. Figure 4(a) shows that, in the presence of autoregulation, phasor O (tissue concentration of oxy-hemoglobin) leads phasor v (blood volume) at low frequencies, while O lags v at higher frequencies. A comparison of Figs 4(a) and 4(b) shows that, at low frequencies, a lack of autoregulation causes a significant increase in the phase lag of D (tissue concentration of deoxy-hemoglobin) with respect to O (tissue concentration of oxyhemoglobin). At angular frequencies greater than ${\omega }_c^{(\text{AutoReg})}$, for which autoregulation is less effective, the effect of autoregulation on the phase lag of D vs. O becomes less and less pronounced. These results can be used to measure the effectiveness of autoregulation as illustrated in Fig. 5(a), which shows the phase difference between D and O as a function of frequency for three different values of ${\omega }_c^{(\text{AutoReg})}/(2\pi )$. The effectiveness of autoregulation can be expressed in terms of ${\omega }_c^{(\text{AutoReg})}$, with higher values of ${\omega }_c^{(\text{AutoReg})}$ representing a more effective autoregulation (i.e. effective regulation of blood flow over a broader range of frequencies of blood pressure fluctuations). Figure 5(b) shows that the effect of autoregulation is to decrease the phase lag of tissue concentrations of deoxy-hemoglobin vs. oxy-hemoglobin, i.e. the negative phase difference between D and O becomes smaller in absolute value. This result is true regardless of the cutoff frequencies of the low-pass responses associated with blood transit times in capillaries and venules, as shown by the three curves in Fig. 5(b) and associated blood transit times reported in the figure caption. In a study of the effect of hemodynamic impairment of autoregulation, Reinhard et al. found that autoregulation impairment was associated with a decrease (by ~40°) in the phase lag of 0.1 Hz oscillations of deoxy-hemoglobin vs. oxy-hemoglobin concentrations in tissue [Reinhard et al., 2006], which is consistent with the results of Fig. 5(b).

Fig. 4.

Phasor diagrams representing oscillations of blood volume (v), capillary flow velocity (f^(c)), tissue concentration of oxy-hemoglobin (O) and tissue concentration of deoxy-hemoglobin (D) at the four frequencies indicated. (a) Phasor diagrams in the presence of cerebral autoregulation $[{\omega }_c^{(\text{AutoReg})}/(2\pi )=0.15\mathrm{H}\mathrm{z}]$. (b) Phasor diagrams in the absence of autoregulation $({\omega }_c^{(\text{AutoReg})}=0)$. These phasor diagrams have been generated using the numerical values listed in Table II for the model parameters.

Fig. 5.

(a) Frequency dependence of the difference between the phase of tissue concentration of deoxy-hemoglobin [Arg(D)] and that of oxy-hemoglobin [Arg(O)]. The three lines in panel (a) correspond to different values of the cutoff frequency of the high-pass autoregulatory response $[{\omega }_c^{(\text{AutoReg})}/(2\pi )]$. (b) Phase difference between 0.1 Hz oscillations in deoxy-hemoglobin and oxy-hemoglobin concentrations as a function of autoregulation effectiveness [as identified by ${\omega }_c^{(\text{AutoReg})}/(2\pi )$]. The three lines of panel (b) correspond to different sets of values for the blood transit times in the capillaries and venules, resulting in the indicated values for the cutoff frequencies of the capillary $[{\omega }_c^{(c)}/(2\pi )]$ and venous $[{\omega }_c^{(v)}/(2\pi )]$ low-pass responses. Specifically, for the solid line: t^(c) = 0.75 s, t^(v) = 1 s; for the long-dashed line: t^(c) = 0.13 s, t^(v) = 0.2 s; for the short-dashed line: t^(c) = 1.2 s, t^(v) = 4.3 s.

Figure 5(b) shows how the phase difference between oscillations of tissue concentrations of deoxy-hemoglobin and oxy-hemoglobin is sensitive to cerebral autoregulation, and how the quantitative framework of the model presented here can be used to quantitatively analyze and interpret experimental data. This result is confirmed in the inline supplementary Fig. S4(a) and is complemented by the results of inline supplementary Figs. S4(b)–(d), which show the dependence on autoregulation of the |D|/|O| ratio [Fig. S4(b)], |O|/|T| ratio [Fig. S4(d)], and the zero-crossing frequency at which O transitions from leading to lagging T [Fig. S4(c)].

3.4. Functional brain studies

The model presented here approximates the low-pass effects associated with capillaries and venules using a first-order RC low-pass response [Eq. (B.3)] and a time-shifted Gaussian response [Eq. (C.3)], respectively. The associated transfer functions are given in Eq. (15) and (26), and their inverse Fourier transforms provide the following impulse responses for the RC low-pass filter:

$$h_{Rc-LP}^{(c)}(t)=H(t)\frac{1}{{\tau }^{(c)}}{e}^{-t/{\tau }^{(c)}},$$ (42)

[where H(t) is the Heaviside unit step function (H(t) = 0 for t < 0; H(t) = 1 for t ≥ 0)], and for the time-shifted Gaussian low-pass filter:

$$h_{G-LP}^{(v)}(t)=\frac{1}{t_r^{(v)}}{e}^{-\pi {(t-t_{0.5}^{(v)})}^2/{(t_r^{(v)})}^2},$$ (43)

where I recall from Appendices B and C that τ^(c) = t^(c)/e, $t_r^{(v)}~0.6(t^{(c)}+t^{(v)})$, and $t_{0.5}^{(v)}=(5/6)t_r^{(v)}$. For any given temporal shape of blood volume [v^(a)(t), v^(c)(t), v^(v)(t)], flow velocity [f^(c)(t)], and oxygen consumption [ȯ(t)] perturbations (such as those associated with functional brain activation), one can determine the corresponding responses in the measured hemoglobin-related parameters by means of convolution integrals as follows:

$$\begin{gathered} D(t)=D^{(a)}(t)+D^{(c)}(t)+D^{(v)}(t)= \\ \mathrm{c}\mathrm{t}\mathrm{H}\mathrm{b}\left\{\begin{array}{c}\hfill {\varphi }^{(a)}(1-S^{(a)})[1+v^{(a)}(t)]+{}^{(c)}{\varphi }^{(c)}(1-\langle S^{(c)}\rangle )[1+v^{(c)}(t)]+{\varphi }^{(v)}(1-S^{(v)})[1+v^{(v)}(t)]+\hfill \\ \hfill -\left[\begin{array}{c}\hfill {}^{(c)}{\varphi }^{(c)}(\langle S^{(c)}\rangle -S^{(v)}){\int }_0^t{h}_{RC-LP}^{(c)}(t-\tau )[f^{(\mathit{c})}(\tau )-ȯ(\tau )]d\tau +\hfill \\ \hfill +{\varphi }^{(v)}{S}^{(v)}{\alpha }_{\mathrm{ȯ}}{t}^{(c)}{\int }_0^t{h}_{G-LP}^{(v)}(t-\tau )[f^{(\mathit{c})}(\tau )-ȯ(\tau )]d\tau \hfill \end{array}\right]\hfill \end{array}\right\}. \end{gathered}$$ (44)

$$\begin{gathered} O(t)=O^{(a)}(t)+O^{(c)}(t)+O^{(v)}(t)= \\ =\mathrm{c}\mathrm{t}\mathrm{H}\mathrm{b}\left\{\begin{array}{c}\hfill {\varphi }^{(a)}{S}^{(a)}[1+v^{(a)}(t)]+{}^{(c)}{\varphi }^{(c)}\langle S^{(c)}\rangle [1+v^{(c)}(t)]+{\varphi }^{(v)}{S}^{(v)}[1+v^{(v)}(t)]+\hfill \\ \hfill +\left[\begin{array}{c}\hfill {}^{(c)}{\varphi }^{(c)}(\langle S^{(c)}\rangle -S^{(v)}){\int }_0^t{h}_{RC-LP}^{(c)}(t-\tau )[f^{(\mathit{c})}(\tau )-ȯ(\tau )]d\tau +\hfill \\ \hfill +{\varphi }^{(v)}{S}^{(v)}{\alpha }_{\mathrm{ȯ}}{t}^{(c)}{\int }_0^t{h}_{G-LP}^{(v)}(t-\tau )[f^{(\mathit{c})}(\tau )-ȯ(\tau )]d\tau \hfill \end{array}\right]\hfill \end{array}\right\}, \end{gathered}$$ (45)

$$\begin{gathered} T(t)=T^{(a)}(t)+T^{(c)}(t)+T^{(v)}(t)=T^{(a)}[1+v^{(a)}(t)]+T^{(c)}[1+v^{(c)}(t)]+T^{(v)}[1+v^{(v)}(t)]= \\ =\mathrm{c}\mathrm{t}\mathrm{H}\mathrm{b}\{{\varphi }^{(a)}[1+v^{(a)}(t)]+{}^{(c)}{\varphi }^{(c)}[1+v^{(c)}(t)]+{\varphi }^{(v)}[1+v^{(v)}(t)]\}, \end{gathered}$$ (46)

Furthermore, this model can also be used to predict the fMRI BOLD response, i.e. the blood oxygenation level dependent signal (𝒮_BOLD) measured in functional magnetic resonance imaging. In fact, 𝒮_BOLD can be expressed in terms of the normalized voxel content of deoxyhemoglobin [D(t)/D₀, where D₀ is the tissue concentration of deoxy-hemoglobin at rest] and the normalized venous blood volume [1 + v^(venous)(t)] [Buxton et al., 1998; Obata et al., 2004] that is considered here to include all partially deoxygenated blood in the arterial, capillary, and venous compartments as in Eq. (40):

$${𝒮}_{\text{Bold}}(t)=({\varphi }^{(a)}+{\varphi }^{(c)}+{\varphi }^{(v)})[3.4(1-\frac{D(t)}{D_0})-\frac{(1-S^{(a)})v^{(a)}(t)+(1-\langle S^{(c)}\rangle )v^{(c)}(t)+(1-S^{(v)})v^{(v)}(t)}{3-S^{(a)}-\langle S^{(c)}\rangle -S^{(v)}}].$$ (47)

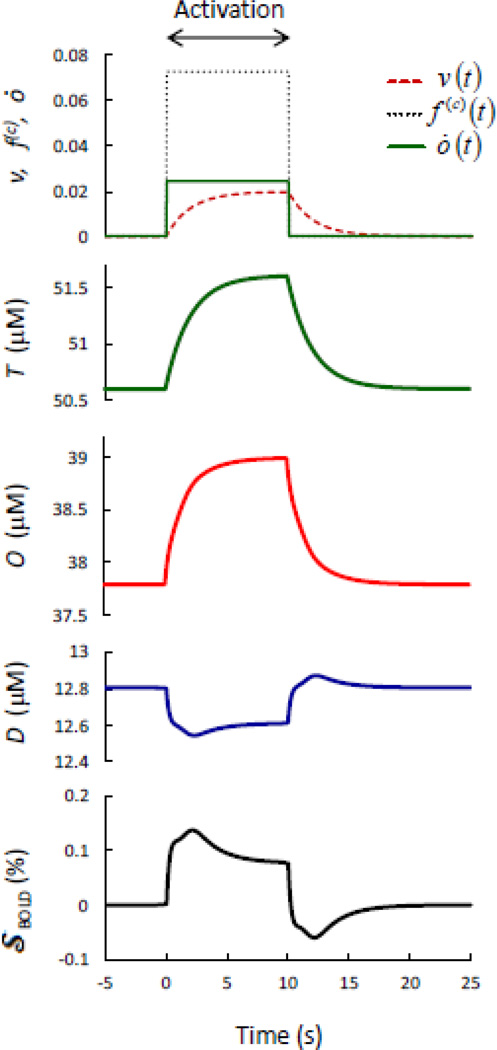
Figure 6 shows the tissue concentrations of deoxy-hemoglobin [Eq. (44)], oxy-hemoglobin [Eq. (45)], and total-hemoglobin [Eq. (46)] (measurable with fNIRS), and the blood oxygenation level dependent (BOLD) signal [Eq. (47)] (measurable with fMRI) in response to ideal blood volume, flow velocity, and oxygen consumption perturbations induced by brain activation. Such ideal perturbations are based on the reported single exponential rise (after the onset of stimulation) and decay (following stimulation) of the cerebral blood volume [Mandeville et al., 1998] (to generate Fig. 6, I have used v^(a)(t) = v^(c)(t) = v^(v)(t) and a time constant of 2 s), and ideal square waves of flow velocity [f^(c)(t)] and oxygen consumption [ȯ(t)] perturbations coinciding with the stimulation time block (10 s in Fig. 6). The amplitudes of the perturbations in blood volume (2.0%), flow velocity (7.3%), and oxygen consumption (2.4%) in Fig. 6 are such that their relative amplitudes match those reported in [Mandeville et al., 1999b], and correspond to a modified Grubb’s exponent of 0.27. Figure 6, in conjunction with Eqs. (44)–(47), demonstrates how this model can predict fNIRS and fMRI signals in response to any given combination of physiological perturbations in blood volume, flow velocity, and oxygen consumption. Of course, while the simplistic choice for the physiological perturbations of Fig. 6 only allows for a qualitative interpretation of the results, some typical results of fNIRS and fMRI are reproduced. For example, reproduced results include the increase in T as a result of an increase in blood volume, the concurrent increase in O and decrease in D as a result of a dominant increase in blood flow velocity, and the initial overshoot [Krüger et al., 1996] and post-stimulus undershoot in the BOLD signal as a result of the delayed blood volume recovery [Mandeville et al., 1998], even though other metabolic or activity-related factors not modeled here likely play a role in the post-stimulus undershoot [Buxton, 2012]. By contrast, it has been reported that a decrease in blood flow induced by either hypoxia [Cohen et al., 2002] or caffeine administration [Liu et al., 2004] speeds up the BOLD signal, as opposed to the prediction of this model for which a decrease in flow velocity results in an increase in the low-pass time constant associated with blood transit time and thereby in a slower hemodynamics response. The vascular constriction associated with hypoxia and caffeine may, however, also increase the effectiveness of neurovascular coupling and speed-up the hemodynamic perturbations [Behzadi and Liu, 2005], and these factors are not considered in the simple application of this model using ideal square perturbations for flow velocity and oxygen consumption.

Fig. 6.

Model predictions for the time responses of the fMRI BOLD signal (𝒮_BOLD) and the tissue concentrations of deoxy-hemoglobin (D), oxy-hemoglobin (O), and total hemoglobin (T) to ideal brain-activation-induced perturbations to the blood volume (v), capillary blood flow velocity (f^(c)), and metabolic rate of oxygen (ȯ).

By using Eqs. (44)–(47), one can predict fNIRS and fMRI BOLD signals resulting from general brain-activation-induced perturbations in blood volume, flow velocity, and oxygen consumption, so that exponential flow velocity transients [Mandeville et al., 1999b], or any other temporal shape of blood volume perturbations (independently in arterioles, capillaries, and venules), capillary flow velocity perturbations, and oxygen consumption perturbations can be considered. The companion article reports a comparison between the model predictions, and fNIRS and BOLD fMRI measurements reported in the literature for a given set of measured perturbations in blood volume, flow velocity, and oxygen consumption (Pierro et al., 2013, this issue).

4. Discussion

4.1. Input and output parameters for the model

The model presented here requires the specification of 14 parameters as input, plus any additional physiological or functional relationship among them. A first set of seven parameters is related to steady state, baseline quantities, namely the hemoglobin concentration in blood, the Fåhraeus factor, the arterial saturation, the oxygen diffusion rate from microvasculature to tissue, and the blood volume fractions [(1) ctHb, (2) Ƒ^(c), (3) S^(a), (4) α_ȯ, (5) ϕ^(a), (6) ϕ^(c), (7) ϕ^(v)]. A second set of two parameters is related to the low-pass frequency response associated with the blood transit times in the microvasculature [(8) t^(c) = L^(c)/c^(c), (9) t^(v) = L^(v)/c^(v)]. A third set of five parameters is related to dynamic changes in blood volume, blood flow velocity, and metabolic rate of oxygen [(10) v^(a)(t), (11) v^(c)(t), (12) v^(v)(t), (13) f^(c)(t), (14) ȯ(t)]. In this work, two further parameters have been introduced to describe the high-pass autoregulation response of flow velocity changes to blood volume changes, namely ${\omega }_c^{(\text{AutoReg})}$ (cutoff angular frequency) and k (asymptotic amplitude ratio of flow to volume oscillations). The outputs of the model are the time resolved, absolute tissue concentrations of deoxy-hemoglobin [D(t), or phasor D] and oxy-hemoglobin [O(t), or phasor O], that combine into the total tissue concentration of hemoglobin [T(t), or phasor T], tissue saturation [S(t), or phasor S], and fMRI BOLD signal [𝒮_Bold, or phasor 𝒮_Bold]. The complete set of the input and output parameters (and their distribution among arterial, capillary, venous, and tissue compartments) is shown in Fig. 7, which is a comprehensive block diagram of the hemodynamic model presented here.

Fig. 7.

Block diagram of the presented hemodynamic model showing the input dynamic parameters (oxygen consumption, blood volume, flow velocity) and the output dynamic parameters predicted by the model (tissue concentrations of deoxy-, oxy-, and total hemoglobin, tissue saturation, and fMRI BOLD signal). The baseline, steady state model parameters are the concentration of hemoglobin in blood (ctHb), the arterial saturation (S^(a)), the arterial, capillary, and venous volume fractions (ϕ^(a), ϕ^(c), ϕ^(v)), the Fåhraeus factor (Ƒ^(c)), the capillary and venous blood transit times (t^(c), t^(v)), and the rate constant of oxygen diffusion to tissue (α_ȯ). Further inputs include any physiological/functional relationships between blood volume, flow velocity, and oxygen consumption perturbations (such as the high-pass relationship between flow velocity and blood volume that has been considered in this work). The basic input-output parameters of the model may be used to label it as ȯvf-DOTS (or simply DOTS) model.

We observe that the results of the model are weakly sensitive to the blood concentration in tissue and the arterial saturation, at least within ranges of normal physiological values. There is also a weak sensitivity to α_ȯ, for which even a large change from 0.4 to 1.2 s⁻¹ results in negligible effects on the phase difference between D and O [see inline supplementary Fig. S1(a)], and some effects on the spectra of the phase difference between O and T [see inline supplementary Fig. S1(c)], and of the amplitude ratios |D|/|O| and |O|/|T| [see inline supplementary Figs. S1(b),(d)], which however all retain their qualitative features. A collection of phase and amplitude spectra for twenty-two different sets of values of the model parameters (reported in the inline supplementary Table S1 and Figs. S1–S6) illustrates the sensitivity of the various spectra to the model parameters, as well as the robustness of some key features of the various spectra. The phase difference between D and O is a robust and consistent parameter, mostly affected by the capillary and venous partial volumes [Fig. S2(a)], the blood transit times in the microcirculation [Fig. S3(a)], autoregulation effectiveness [Figs. S4(a), S5(a)], and the relative contributions of arterial, capillary, and venous volume oscillations [Fig. S6(a)]. The spectrum of the amplitude ratio |D|/|O| is typically relatively flat and featureless, except for the case of comparable capillary and venous volume fractions [Fig. S2(b)] and a large modified Grubb’s exponent (or low k) [Fig. S5(b)]. The phase difference between O and T features a typical bimodal behavior, with positive values at low frequencies (O leading T) and negative values at high frequencies (O lagging T), with capillary/venous volume fractions [Fig. S2(c)] and autoregulation efficiency [Fig. S4(c)] having the strongest effect on the zero-crossing frequency at which O and T are in phase. Finally, the spectra of the amplitude ratio |O|/|T| consistently feature a broad peak reaching a maximum value greater than one (which is not inconsistent with the phasor relationship T = O + D). The peak frequency is mostly sensitive to the venule blood transit time [Fig. S3(d)] and to autoregulation cutoff frequency [Fig. S4(d)], whereas the peak value is mostly sensitive to autoregulation [Fig. S4(d)] and the volume-to-flow amplitude ratio [Fig. S5(d)]. The companion article reports a comprehensive summary (in its Table I) of the major spectral features discussed above, as well as their dependence on the hemodynamic model parameters (Pierro et al., 2013, this issue).

In summary, the dynamic model presented here allows one to quantitatively determine the dynamic features of the concentration and oxygen saturation of hemoglobin in tissue, in response to perturbations in blood volume (with separate contributions from arterial, capillary, and venous compartments), capillary flow velocity, and metabolic rate of oxygen, under given baseline conditions for the blood transit time in the microvasculature, oxygen consumption, and relative partial volumes of arterial, capillary, and venous blood.

4.2. Collective treatment of the microvasculature as a microvascular network

This model treats the arterioles, capillaries, and venules that comprise the tissue microvasculature as a complete network, without a need for any assumptions on the details of the architecture and morphology of such vascular network. In fact, the only premise of the model is that red blood cells, in their convective motion through the vasculature sequentially travel through an arterial, a capillary, and a venous compartment, and that oxygen exchange with the tissue occurs only in the capillary compartment. What matters for the model is the effective time that red blood cells spend in the capillary compartment, regardless of the details of the statistical distribution of such transit time over the red blood cell population as determined by narrowing, bifurcations, and merging of capillaries, non-laminar flow, etc. At the heart of the model lies this effective blood transit time through capillaries (t^(c) = L^(c)/c^(c)) and its associated probability of oxygen release to tissue of (1 − e^−α_ȯt(c)) via the rate constant α_ȯ of oxygen diffusion to tissue. In the spirit of this observation, it is important to note that even though the derivations of Eqs. (B.1) and (C.1) in Appendices B and C are based on the ideal blood vessels illustrated in Figs. B.1 and C.1, one may see the linear coordinates ℓ′ and ℓ″ as the curvilinear coordinates of the path of red blood cells in the microvasculature regardless of whether they undergo turbulent flow, tortuous paths, etc. This also implies that the total length of their paths in the capillary (L^(c)) and venous (L^(v)) compartments may be longer than the physical length of the corresponding combined vascular segments. The role of the average blood transit time through the venous compartment (t^(v) = L^(v)/c^(v)) is to introduce a delay, or phase lag, to the tissue saturation changes associated with a change in the oxygen extraction factor (as determined by a change in either or both of t^(c) and α_ȯ). Such a phase lag is limited to ~180° because of the strong amplitude attenuation of the associated Gaussian low-pass transfer function for greater phase delays (see Fig. 2). This approach results in a robust treatment of the complexity of the tissue microvasculature by the identification of the key issues of blood and oxygen transport through the vasculature that affect the overall tissue concentration and oxygen saturation of hemoglobin, which are the focus of this dynamic model.

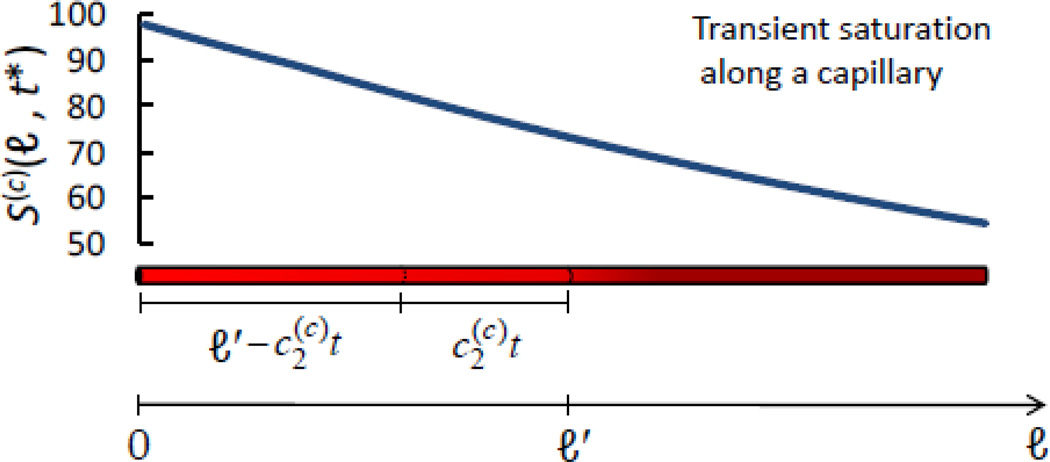
Figure B.1.

Snapshot of transient hemoglobin saturation along a capillary, S^(c) (ℓ, t* = 0.122 s), in response to a step change in blood flow velocity. ℓ is the linear coordinate along the blood vessel, and its generic value along the capillary is indicated with ℓ′. S^(c) (ℓ, t*) has been computed from Eq. (B.1) using the following set of values for the parameters: S^(a) = 0.98, α_ȯ = 0.8 s⁻¹, $c_1^{(c)}=0.8\mathrm{m}\mathrm{m}/\mathrm{s},c_2^{(c)}=0.9\mathrm{m}\mathrm{m}/\mathrm{s}$. The length of the capillary in the figure corresponds to the entire capillary length L^(c) = 0.6 mm, and $c_2^{(c)}{t}^{*}=0.11\mathrm{m}\mathrm{m}$.

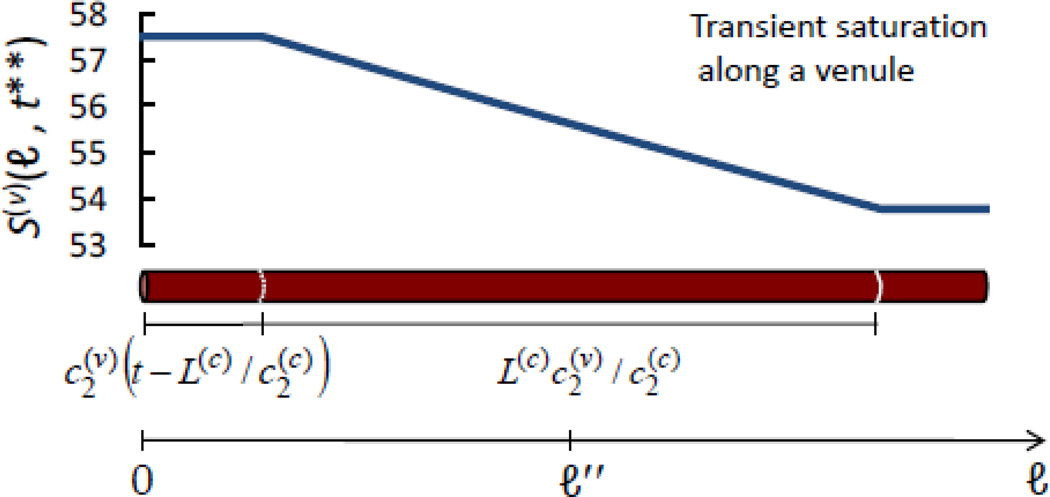
Figure C.1.

Snapshot of transient hemoglobin saturation along a venule, S^(v) (ℓ, t** = 0.8 s), in response to a step change in blood flow velocity. ℓ is the linear coordinate along the blood vessel, and its generic value along the venule is indicated with ℓ″. S^(v) (ℓ, t**) has been computed from Eq. (C.1) using the following set of values for the parameters: S^(a) = 0.98, α_ȯ = 0.8 s⁻¹, L^(c) = 0.6 mm, $c_1^{(c)}=0.8\mathrm{m}\mathrm{m}/\mathrm{s},c_2^{(c)}=0.9\mathrm{m}\mathrm{m}/\mathrm{s},c_1^{(v)}=1.0\mathrm{m}\mathrm{m}/\mathrm{s},c_2^{(v)}=1.1\mathrm{m}\mathrm{m}/\mathrm{s}$. The length of the venule in the figure is 1 mm, and the length of the venule segment featuring a linearly decaying saturation is $L^{(c)}{c}_2^{(v)}/c_2^{(c)}=0.733\mathrm{m}\mathrm{m}$.

4.3. Assumptions of the model

The low-pass effects associated with the blood transit time in the microvasculature, and the high-pass effects associated with autoregulation are treated here within the framework of transfer function analysis, which relies on the linearity and time-invariance between the input (perturbations in blood volume, flow-velocity, and oxygen-consumption) and the output (changes in tissue concentration and oxygen saturation of hemoglobin). In the case of small hemodynamic perturbations associated with brain activation or minor physiological challenges, the assumption of linearity is reasonable and typically satisfied. For example, total hemoglobin changes associated with brain activation (0.5–5%) [Wolf et al., 2008; Lloyd-Fox et al., 2010; Ferrari and Quaresima, 2012], paced breathing (~3%) [Reinhard et al., 2006], or spontaneous low-frequency oscillations (~3%) [Rowley et al., 2007] are small enough to justify a linear approximation. However, strong physiological perturbations or extreme conditions that are potentially associated with pathological states, may invalidate the linearity assumption and require the introduction of non-linear models. Even strong physiological perturbations such as the large changes in cerebral blood flow associated with brain activation (80–100% in the rat somatosensory cortex [Mandeville et al., 1999b; Kida et al., 2007] may be treated within the framework of linear models provided that the resulting perturbations in the measured signals (fMRI BOLD, NIRS intensity) are small and feature a monotonic dependence on them. While linear models were found to be sufficient to describe brain activation maps [Deneux and Faugeras, 2006] and are applicable to small physiological perturbations, one should consider steps to validate the assumption of linearity in the particular application considered. Time invariance is likely fulfilled when considering measurements over times that are short compared to the time scale of changes for underlying physiological conditions. Phase and amplitude measurements of hemodynamic oscillations require a good signal-to-noise ratio that, together with the linearity between input and output signals, results in a high coherence between the perturbations in physiological quantities and the changes in tissue concentration/saturation of hemoglobin. The requirement of a high coherence between the input and output signals may not be fulfilled in the presence of weak and highly variable oscillations (as may be the case of spontaneous low-frequency oscillations) or in the case of non-linear regimes, but it is usually fulfilled by regular oscillations induced by periodic maneuvers such as paced breathing [Reinhard et al., 2006], head-up-tilting [Hughson et al., 2001], squat-stand maneuvers [Claassen et al., 2009], or pneumatic thigh-cuff inflation [Aaslid et al., 2007]. In the case of cerebral autoregulation, several groups have proposed nonlinear analysis [Mitsis et al., 2002] and wavelet transforms [Latka et al., 2005; Peng et al., 2010] to refine the predictions of linear transfer function analysis, and these approaches may also benefit the model presented here, especially when considering low-coherence hemodynamic fluctuations. In addition to the above considerations, the phasor representation of Eqs. (34)–(37), (40) requires that the oscillations under consideration have a well-defined frequency and a sinusoidal shape. This condition may be attained by proper band-pass filtering of the data or by proper experimental design in the case of protocols involving periodic stimulation, physiological challenges, or other kinds of physical maneuvers, but it is nevertheless an approximation in the study of biological tissue in vivo.

4.4. Deoxy-hemoglobin oscillations lag oxy-hemoglobin oscillations at low frequencies (~0.1 Hz)

The model provides a quantitative description for the phase lag of deoxy-hemoglobin concentration oscillations (described by the phasor D) with respect to oxy-hemoglobin concentration oscillations (described by the phasor O) that have been reported in NIRS studies of spontaneous low frequency oscillations [Taga et al., 2000; Obrig et al., 2000; Lee et al., 2010; Tian et al., 2011; Pierro et al., 2012] and paced-breathing-induced oscillations [Obrig et al., 2000; Reinhard et al., 2006] at frequencies of ~0.1 Hz. From the model, it follows that at these low frequencies of oscillation deoxy-hemoglobin always lags oxy-hemoglobin, so that an apparent phase lead of D vs. O by a certain angle θ should really be interpreted as a phase lag by 2π−θ. The reason can be seen by inspection of Eqs. (35) and (36), and by considering that the low-pass effect of the blood transit time in the vasculature on the hemoglobin saturation [Eqs. (16), (17), (27), (28)] and the high-pass effect of autoregulation for the blood flow velocity [Eq. (41)] both result in a decrease with frequency of the phase of the second term in the bracket of Eqs. (35) and (36) (see Fig. 2(b) for the frequency dependence of the phase of the RC low-pass, RC high-pass, and Gaussian transfer functions). As a result, D and O are in phase at zero frequency (because f^(c) = 0 at zero frequency) and grow out of phase as frequency increases. Because the second phasor in the bracket has the same magnitude in Eq. (35) for O and in Eq. (36) for D, and the first phasor in the bracket (the blood volume phasor) has a greater magnitude in Eq. (35) for O than in Eq. (36) for D, it follows that the phase of D decreases with frequency at a faster rate than the phase of O (the phase of O may even increase with frequency at very low frequencies as a result of the high-pass, positive phase contribution of autoregulation), with the net result that the difference between the phase of D and the phase of O becomes more and more negative as frequency increases (this is generally true as long as relative changes in flow velocity are larger than relative changes in blood volume as observed in response to hypoxia/hyperoxia [Grubb et al., 1974] and brain activation [Mandeville et al., 1999b]).

The result that deoxy-hemoglobin oscillations lag oxy-hemoglobin oscillations in the low-requency band stems from the fact the flow-induced oxy-hemoglobin oscillations (O_F) lag the flow velocity oscillations (f^(c)) that cause them [see Eqs. (18) and (29)]). This means that even in the complete absence of autoregulation (i.e. in-phase blood volume and flow velocity oscillations), one would expect a phase lag of D with respect to O at frequencies in the order of the low-pass cutoff frequencies associated with the blood transit time in the microvasculature (~0.3–0.6 Hz for the model parameters reported in Table II). This result leads to a refinement of our approach to the study of the oscillatory components of deoxy- and oxy-hemoglobin concentration in tissue. In fact, while the combination of different physiological processes that are out-of-phase with respect to each other would certainly result in out-of-phase oscillations of deoxy- and oxy-hemoglobin oscillations [Zheng et al., 2010], this model shows that even in-phase physiological processes may lead to phase-shifted measurements of deoxy- and oxy-hemoglobin phasors at relatively low frequencies. Furthermore, our previous assumption [Pierro et al., 2012] that the flow-velocity-induced oxy-hemoglobin phasor (O_F) is in phase with the flow velocity phasor (f^(c)) is not in general correct, as this model shows that there is a phase delay of O_F with respect to f^(c) [see Eqs. (18) and (29)].

5. Conclusions

The study of the spatial and temporal features of the effects of brain activation on cerebral hemodynamics and oxygenation is a primary focus of hemodynamic-based neuroimaging techniques such as fNIRS and fMRI. The dynamic model presented here provides a tool to translate a given set of activation-induced perturbations in the cerebral blood volume, flow velocity, and metabolic rate of oxygen into the concentration and oxygen saturation of hemoglobin in cerebral tissue. Such a tool can be used in the framework of two different scenarios. Firstly, it can be used to predict the cerebral hemodynamic and oxygenation response to given perturbations in the blood volume, flow velocity, and metabolic rate of oxygen. Secondly, it can be used to identify a set of perturbations in the blood volume, flow velocity, and metabolic rate of oxygen that is consistent with observed experimental results of hemodynamic-based neuroimaging techniques. The fact that hemodynamic-based neuroimaging techniques are indirectly sensitive to neural activation through its associated hemodynamic effects poses an intrinsic limitation to their spatial [Turner, 2002] and temporal [de Zwart et al., 2005] resolution, and this work quantifies the latter effect through the time constants t^(c) and t^(v) for blood transit in the capillary and venous vascular compartments, respectively.

Spontaneous hemodynamic oscillations in the low frequency spectral band (≾ 0.1 Hz) have been extensively investigated to assess cerebral functional connectivity using fMRI [Biswal et al., 1995; Greicius et al., 2003; Fox and Raichle, 2007], NIRS [White et al., 2009; Lu et al., 2010; Sasai et al., 2011; Sassaroli et al., 2012], and both techniques combined [Duan et al., 2012]. The hemodynamic model presented here provides a novel tool for the quantitative study of periodic hemodynamic oscillations, provided that they exhibit a high level of coherence, which may or may not be the case for spontaneous hemodynamic oscillations. Furthermore, the presented hemodynamic model provides a theoretical framework for a novel technique to investigate a number of anatomical, functional, metabolic, and physiological quantities by inducing coherent hemodynamic oscillations at controlled frequencies. This novel technique, coherent hemodynamics spectroscopy (CHS), is based on measurements of the frequency spectra of the phase difference and amplitude ratio of oscillatory concentrations of oxy-hemoglobin and deoxy-hemoglobin in tissue, and the quantitative assessment of their relevant spectral features.

Supplementary Material

01. Fig. S1.

Frequency spectra of (a) the phase difference between D and O, (b) the amplitude ratio |D|/|O|, (c) the phase difference between O and T, and (d) the amplitude ratio |O|/|T|. The solid lines are the reference spectra obtained using the parameter values of Table II. The dotted lines correspond to a lower rate constant for oxygen diffusion from blood to tissue (α_ȯ = 0.4 s⁻¹) with respect to the reference value of 0.8 s⁻¹, whereas the dashed lines correspond to a greater rate constant of 1.2 s⁻¹. The parameter values for the reference set (Ref. Set) and for Sets 1a and 1b are listed in Table S1. Note the counterintuitive result that a higher oxygen consumption may result in a greater |O|/|T| ratio [over the band 0.1–0.5 Hz in panel (d)] due to the opposition of phase of the deoxy-hemoglobin and oxy-hemoglobin oscillations [phase difference of 180° at a frequency of ~0.2 Hz in panel (a)].

02. Fig. S2.

Frequency spectra of (a) the phase difference between D and O, (b) the amplitude ratio |D|/|O|, (c) the phase difference between O and T, and (d) the amplitude ratio |O|/|T|. The solid lines are the reference spectra obtained using the parameter values of Table II. The various spectra correspond to different combinations of the partial volumes of the arterial (ϕ^(a)), capillary (ϕ^(c)), and venous (ϕ^(v)) compartments, resulting in tissue concentrations of total hemoglobin within the range 40–80 µM. The parameter values for the reference set (Ref. Set) and for Sets 2a, 2b, 3a, 3b, 4a, and 4b are listed in Table S1.

03. Fig. S3.

Frequency spectra of (a) the phase difference between D and O, (b) the amplitude ratio |D|/|O|, (c) the phase difference between O and T, and (d) the amplitude ratio |O|/|T|. The solid lines are the reference spectra obtained using the parameter values of Table II. The various spectra correspond to different combinations of the blood transit time in the capillary (t^(c)), and venous (t^(v)) compartments. The range of t^(c) values considered here (0.3–1.0 s) results in venous saturation values within the range 44–77%. The parameter values for the reference set (Ref. Set) and for Sets 5a, 5b, 6a, and 6b are listed in Table S1.

04. Fig. S4.

Frequency spectra of (a) the phase difference between D and O, (b) the amplitude ratio |D|/|O|, (c) the phase difference between O and T, and (d) the amplitude ratio |O|/|T|. The solid lines are the reference spectra obtained using the parameter values of Table II. The dotted and dashed spectra correspond to two different cutoff frequencies for autoregulation, ${\omega }_c^{(\text{AutoReg})}/(2\pi )=0.03\mathrm{H}\mathrm{z}$ for the dotted spectra, and ${\omega }_c^{(\text{AutoReg})}/(2\pi )=0.30\mathrm{H}\mathrm{z}$ for the dashed spectra. A higher cutoff frequency corresponds to more effective autoregulation. Consequently, these figures indicate that more effective autoregulation results in a reduced phase lag of deoxy-hemoglobin vs. oxy-hemoglobin oscillations, and in a higher zero-crossing frequency for the phase of oxy-hemoglobin vs. total hemoglobin oscillations. The parameter values for the reference set (Ref. Set) and for Sets 7a and 7b are listed in Table S1.

05. Fig. S5.

Frequency spectra of (a) the phase difference between D and O, (b) the amplitude ratio |D|/|O|, (c) the phase difference between O and T, and (d) the amplitude ratio |O|/|T|. The solid lines are the reference spectra obtained using the parameter values of Table II. The dotted and dashed spectra correspond to two different values of the maximum flow-to-volume amplitude ratio (~inverse of the modified Grubb’s exponent); k = 2.5 for the dotted spectra, and k = 10 for the dashed spectra. A smaller k value corresponds to a smaller flow velocity change in response to a given blood volume change. The parameter values for the reference set (Ref. Set) and for Sets 8a and 8b are listed in Table S1.

06. Fig. S6.

Frequency spectra of (a) the phase difference between D and O, (b) the amplitude ratio |D|/|O|, (c) the phase difference between O and T, and (d) the amplitude ratio |O|/|T|. The solid lines are the reference spectra obtained using the parameter values of Table II. The various spectra correspond to different combinations of arterial (|v^(a)|), capillary (|v^(c)|), and venous (|v^(v)|) blood volume oscillation amplitudes. Amplitudes of 0 and 10% have been considered for |v^(a)| (Sets 9a and 9b), |v^(c)| (Sets 10a and 10b), and |v^(v)| (Sets 11a and 11b). The parameter values for the reference set (Ref. Set) and for Sets 9a, 9b, 10a, 10b, 11a, and 11b are listed in Table S1.

Highlights.

• A dynamic model quantifies tissue concentration and saturation of hemoglobin.

• Inputs are perturbations in oxygen consumption, blood volume, and flow velocity.

• The model yields analytical solutions in the time domain and frequency domain.

• Multi-compartment vasculature, autoregulation, fNIRS/fMRI signals are addressed.

• A novel technique called coherent hemodynamics spectroscopy (CHS) is proposed.

Appendix A

Phasor of tissue saturation

Phasor analysis requires that all of the oscillating quantities are linearly related to each other. Such a requirement is typically fulfilled by small oscillations, for which even non-linear relationships (such as the one between tissue saturation and the concentrations of oxy-hemoglobin and deoxy-hemoglobin) can be linearized. By differentiating the expression for the average tissue saturation [S = O/(O + D)], and by considering that T = O + D and dD = dT − dO, one can write:

$$dS=\frac{1}{T^2}(DdO-OdD)=\frac{1}{T}(dO-SdT).$$ (A.1)

By introducing phasor notation for the oscillations described by differentials, Eq. (A.1) becomes:

$$\mathbf{S}=\frac{1}{T}(\mathbf{O}-S\mathbf{T}).$$ (A.2)

Appendix B

Transient capillary saturation for a step change in blood flow velocity

Oxygen exchange from blood to tissue occurs in the smaller arterioles and capillaries, and is described by a rate constant α_ȯ of oxygen diffusion to tissue. A change in blood flow velocity corresponds to a change in the oxygen flow, resulting in a change in blood saturation for a given oxygen diffusion rate α_ȯ to tissue. This is a key point, which results from the fact that the oxygen extraction per unit length traveled by blood is given by α_ȯ/c^(c). With reference to Fig. B.1, one can introduce a linear coordinate ℓ (0 ≤ ℓ ≤ L^(c)) along the capillary, and consider the distribution of blood saturation along ℓ in response to a step change of capillary flow velocity from $c_1^{(c)}$ to $c_2^{(c)}$ at time t = 0. Of course, at times t < 0 and $t>L^{(c)}/c_2^{(c)}$, the capillary saturation along ℓ assumes the steady state values of $S^{(a)}{e}^{-{\alpha }_{\mathrm{ȯ}}\ell /c_1^{(c)}}$ and $S^{(a)}{e}^{-{\alpha }_{\mathrm{ȯ}}\ell /c_2^{(c)}}$, respectively (see Eq. (12)) [Fantini 2002]. For a given coordinate ℓ′, one needs to consider that at times $t>\ell \prime /c_2^{(c)}$ the steady state condition $(S^{(a)}{e}^{-{\alpha }_{\mathrm{ȯ}}\ell \prime /c_2^{(c)}})$ has already been reached, so that one needs only to consider times $0\le t\le \ell \prime /c_2^{(c)}$. Within this time window, the blood element at coordinate ℓ′ was located at position $\ell =\ell \prime -c_2^{(c)}t$ at the time when the blood velocity was switched, so that its saturation was $S^{(a)}{e}^{-{\alpha }_{\mathrm{ȯ}}(\ell \prime -c_2^{(c)}t)/c_1^{(c)}}$ at time t = 0 and it has been deoxygenating at a constant rate α_ȯ since then. Consequently, the time dependence of the saturation of blood element at coordinate ℓ′ is as follows:

$$S^{(c)}(\ell \prime ,t)=\{\begin{array}{cc}\hfill S^{(a)}{e}^{-\frac{{\alpha }_{\mathrm{ȯ}}\ell \prime }{c_1^{(c)}}},\hfill & \hfill t<0\hfill \\ S^{(a)}{e}^{-\frac{{\alpha }_{\mathrm{ȯ}}(\ell \prime -c_2^{(c)}t)}{c_1^{(c)}}}{e}^{-{\alpha }_{\mathrm{ȯ}}t},\hfill & \hfill 0\le t<\frac{\ell \prime }{c_2^{(c)}}\\ S^{(a)}{e}^{-\frac{{\alpha }_{\mathrm{ȯ}}\ell \prime }{c_2^{(c)}}},\hfill & \hfill t\ge \frac{\ell \prime }{c_2^{(c)}}\end{array}$$ (B.1)

The decay of hemoglobin saturation as a function of ℓ in a capillary is shown in Fig. B.1(a) at a time t* = 0.122 s (i.e. 0.122 s after the capillary velocity has changed from $c_1^{(c)}$ to $c_2^{(c)}$) for the set of parameter values given in the caption of Fig. B.1. In Fig. B.1, $c_2^{(c)}{t}^{*}=0.11\mathrm{m}\mathrm{m}$.

The time dependence of the average capillary saturation for $0\le t\le L^{(c)}/c_2^{(c)}$ can be obtained by integration of S^(c) over ℓ′:

$$\langle S^{(c)}\rangle (t)=\frac{1}{L^{(c)}}[{\int }_0^{t{c}_2^{(c)}}{S}^{(a)}{e}^{-\frac{{\alpha }_{\mathrm{ȯ}}\ell \prime }{c_2^{(C)}}}d\ell \prime +{\int }_{t{c}_2^{(c)}}^{L^{(c)}}{S}^{(a)}{e}^{-\frac{{\alpha }_{\mathrm{ȯ}}(\ell \prime -c_2^{(c)}t)}{c_1^{(c)}}}{e}^{-{\alpha }_{\mathrm{ȯ}}t}d\ell \prime ]=S^{(a)}\frac{c_1^{(c)}}{{\alpha }_{\mathrm{ȯ}}{L}^{(c)}}(1-e^{-\frac{{\alpha }_{\mathrm{ȯ}}(L^{(c)}-c_2^{(c)}t)}{c_1^{(c)}}})e^{-{\alpha }_{\mathrm{ȯ}}t}+S^{(a)}\frac{c_2^{(c)}}{{\alpha }_{\mathrm{ȯ}}{L}^{(c)}}(1-e^{-{\alpha }_{\mathrm{ȯ}}t}).$$ (B.2)

Equation (B.2) indicates a low-pass response of the average capillary saturation to a change in blood flow velocity. It can be shown that under the conditions ${\alpha }_{\mathrm{ȯ}}{L}^{(c)}/c_1^{(c)}\precsim 1$ and ${\alpha }_{\mathrm{ȯ}}{L}^{(c)}/c_2^{(c)}\precsim 1$, the right hand side of Eq. (B.2) can be closely approximated by the following RC low-pass filter response:

$$\langle S^{(c)}\rangle (t)\approx \langle S^{(c)}\rangle (t=0)+[\langle S^{(c)}\rangle (t=t_2^{(c)})-\langle S^{(c)}\rangle (t=0)](1-e^{-\frac{e{c}_2^{(c)}}{L^{(c)}}t}),$$ (B.3)

where the steady state capillary saturation values at t = 0 and $t=t_2^{(c)}=L^{(c)}/c_2^{(c)}$ are given by Eq. (13) with $c^{(c)}=c_1^{(c)}$ and $c^{(c)}=c_2^{(c)}$, respectively. Equation (B.3) shows that the time constant (τ^(c)) for the low pass response of the average capillary saturation to a change in blood flow velocity is ${\tau }^{(c)}=L^{(c)}/(e{c}_2^{(c)})=t_2^{(c)}/e$, which is equal to 1/e times the transit time of blood in the capillary $(t_2^{(c)})$. The step response of average capillary saturation predicted by this model [Eq. (B.2)] is shown in Fig. B.2 together with the RC low-pass filter approximation of Eq. (B.3). By considering typical values of α_ȯ, L^(c), and c^(c), one can verify that the condition for the validity of Eq. (B.3), namely α_ȯL^(c)/c^(c) ≾ 1 is satisfied. In fact, the diffusion time of oxygen from capillaries to brain tissue (τ_O2) can be estimated by the square of the intercapillary distance (~50 µm [Masamoto et al., 2004]) divided by the diffusion coefficient of oxygen in brain tissue (~2×10⁻⁵ cm²/s [Baumgärtl and Lübbers, 1983]), resulting in τ_O2 ~ 1.25 s [Masamoto et al., 2007] and α_ȯ = 1/τ_O2 ~0.8 s⁻¹. The combined typical length of arteriolar and capillary branches is ~600–1,000 µm [Guyton and Hall, 2011 (Ch. 14); Pries et al., 1995], and the blood velocity in arterioles and capillaries is typically 2 mm/s and 0.8 mm/s [Pries et al., 1995], respectively. As a result, it is indeed the case that α_ȯ, L^(c)/c^(c) ≾ 1. The cutoff angular frequency of the RC low-pass response is given by ${\omega }_c^{(c)}=1/{\tau }^{(c)}\approx e\mathrm{/}{t}_2^{(c)}$.

Fig. B.2.

Step response to a change in blood flow velocity for the average capillary saturation as predicted by the model [solid line, Eq. (B.2)]. The numerical values for the various parameters are the same as in Fig. B.1. The step response of the average capillary saturation can be approximated by a first-order RC low-pass filter (dashed line). The time constant τ of this RC low-pass filter corresponds to a cutoff angular frequency $({\omega }_c^{(c)})$ that is ~e times the inverse of the blood transit time in the capillaries, namely: ${\omega }_c^{(c)}\cong e\mathrm{/}{t}_2^{(c)}$.

Appendix C

Transient venous saturation for a step change in blood flow velocity

Since there is no oxygen exchange from blood in venules/veins to tissue, one can simply consider the hemoglobin saturation at the end of the capillary (i.e. ℓ′ = L^(c)), and consider that it travels at velocity $c_2^{(v)}$ along the venule. By considering that the saturation at any time t > 0 and location ℓ″ along the venule is equal to the saturation that occurred at the end of the capillary at a previous time $t-\ell ″/c_2^{(v)}$, one can write the hemoglobin saturation along the venule as follows:

$$S^{(v)}(\ell ″,t)=\{\begin{array}{cc}{S}^{(a)}{e}^{-\frac{{\alpha }_{\mathrm{ȯ}}{L}^{(c)}}{c_1^{(c)}}},\hfill & \hfill t<0\\ S^{(a)}{e}^{-\frac{{\alpha }_{\mathrm{ȯ}}[L^{(c)}-c_2^{(c)}(t-\frac{\ell ″}{c_2^{(v)}}\left)\right]}{c_1^{(c)}}}{e}^{-{\alpha }_{\mathrm{ȯ}}(t-\frac{\ell ″}{c_2^{(v)}})}H[c_2^{(v)}t-\ell ″]++S^{(a)}{e}^{-\frac{{\alpha }_{\mathrm{ȯ}}{L}^{(c)}}{c_1^{(c)}}}H[\ell ″-c_2^{(v)}t],\hfill & \hfill 0\le t<\frac{L^{(c)}}{c_2^{(c)}}\\ S^{(a)}{e}^{-\frac{{\alpha }_{\mathrm{ȯ}}{L}^{(c)}}{c_2^{(c)}}}H\left[c_2^{(v)}\right(t-\frac{L^{(c)}}{c_2^{(c)}})-\ell ″]++S^{(a)}{e}^{-\frac{{\alpha }_{\mathrm{ȯ}}(L^{(c)}-c_2^{(c)}(t-\frac{\ell ″}{c_2^{(v)}}\left)\right)}{c_1^{(c)}}}{e}^{-{\alpha }_{\mathrm{ȯ}}(t-\frac{\ell ″}{c_2^{(v)}})}\times \times \left\{H\right[\ell ″-c_2^{(v)}(t-\frac{L^{(c)}}{c_2^{(c)}})]-H[\ell ″-c_2^{(v)}t\left]\right\}++S^{(a)}{e}^{-\frac{{\alpha }_{\mathrm{ȯ}}{L}^{(c)}}{c_1^{(c)}}}H[\ell ″-c_2^{(v)}t],\hfill & \hfill \frac{L^{(c)}}{c_2^{(c)}}\le t<\frac{L^{(v)}}{c_2^{(v)}}\\ S^{(a)}{e}^{-\frac{{\alpha }_{\mathrm{ȯ}}{L}^{(c)}}{c_2^{(c)}}}H\left[c_2^{(v)}\right(t-\frac{L^{(c)}}{c_2^{(c)}})-\ell ″]+S^{(a)}{e}^{-\frac{{\alpha }_{\mathrm{ȯ}}(L^{(c)}-c_2^{(c)}(t-\frac{\ell ″}{c_2^{(v)}}\left)\right)}{c_1^{(c)}}}{e}^{-{\alpha }_{\mathrm{ȯ}}(t-\frac{\ell ″}{c_2^{(v)}})}H[\ell ″-c_2^{(v)}(t-\frac{L^{(c)}}{c_2^{(c)}}\left)\right],\hfill & \hfill \frac{L^{(v)}}{c_2^{(v)}}\le t<\frac{L^{(v)}}{c_2^{(v)}}+\frac{L^{(c)}}{c_2^{(c)}}\\ S^{(a)}{e}^{-\frac{{\alpha }_{\mathrm{ȯ}}{L}^{(c)}}{c_2^{(c)}}},\hfill & \hfill t\ge \frac{L^{(v)}}{c_2^{(v)}}+\frac{L^{(c)}}{c_2^{(c)}}\end{array}$$ (C.1)

where H(x) is the Heaviside unit step function [H(x) = 0 for x < 0; H(x) = 1 for x ≥ 0]. On the basis of typically longer venule branches with respect to capillary segments, it is assumed that $L^{(v)}/c_2^{(v)}>L^{(c)}/c_2^{(c)}$. The decay of hemoglobin saturation as a function of ℓ in a venule is shown in Fig. C.1 at a time t** = 0.8 s (i.e. 0.8 s after the venule blood velocity has changed from $c_1^{(v)}$ to $c_2^{(v)}$) for the set of parameter values given in the caption of Fig. C.1. In Fig. C.1, $c_2^{(v)}{t}^{**}=0.88\mathrm{m}\mathrm{m}$.

By taking an integral over ℓ″, namely $1/L^{(v)}{\int }_0^{L^{(v)}}{S}^{(v)}(\ell ″,\mathrm{t})\mathrm{d}\ell ″$, one can find the time dependence of the transient average venous saturation for $0\le t<L^{(v)}/c_2^{(v)}+L^{(c)}/c_2^{(c)}$:

$$\langle S^{(v)}\rangle (t)=\{\begin{array}{cc}\hfill S^{(a)}{e}^{-\frac{{\alpha }_{\mathrm{ȯ}}{L}^{(c)}}{c_1^{(c)}}}[1-\frac{c_2^{(v)}}{L^{(v)}}t+\frac{c_2^{(v)}}{{\alpha }_{\mathrm{ȯ}}{L}^{(v)}}(\frac{c_1^{(c)}}{c_2^{(c)}-c_1^{(c)}}\left)\right(e^{{\alpha }_{\mathrm{ȯ}}(\frac{c_2^{(c)}-c_1^{(c)}}{c_1^{(c)}})t}-1\left)\right],\hfill & \hfill 0\le t<\frac{L^{(c)}}{c_2^{(c)}}\hfill \\ \hfill S^{(a)}{e}^{-\frac{{\alpha }_{\mathrm{ȯ}}{L}^{(c)}}{c_1^{(c)}}}[1+\frac{c_2^{(v)}}{{\alpha }_{\mathrm{ȯ}}{L}^{(v)}}(e^{\frac{{\alpha }_{\mathrm{ȯ}}{L}^{(c)}}{c_2^{(c)}}\left(\frac{c_2^{(c)}-c_1^{(c)}}{c_1^{(c)}}\right)}-1\left)\right({\alpha }_{\mathrm{ȯ}}t+\frac{c_1^{(c)}}{c_2^{(c)}-c_1^{(c)}})-\frac{c_2^{(v)}{L}^{(c)}}{c_2^{(c)}{L}^{(v)}}{e}^{\frac{{\alpha }_{\mathrm{ȯ}}{L}^{(c)}}{c_2^{(c)}}\left(\frac{c_2^{(c)}-c_1^{(c)}}{c_1^{(c)}}\right)}],\hfill & \hfill \frac{L^{(c)}}{c_2^{(c)}}\le t<\frac{L^{(v)}}{c_2^{(v)}}\hfill \\ \hfill S^{(a)}{e}^{-\frac{{\alpha }_{\mathrm{ȯ}}{L}^{(c)}}{c_1^{(c)}}}\left\{\begin{array}{c}\hfill \frac{c_2^{(v)}}{{\alpha }_{\mathrm{ȯ}}{L}^{(v)}}\left(\frac{c_1^{(c)}}{c_2^{(c)}-c_1^{(c)}}\right)[e^{{\alpha }_{\mathrm{ȯ}}\left(\frac{c_2^{(c)}-c_1^{(c)}}{c_1^{(c)}}\right)\frac{L^{(c)}}{c_2^{(c)}}}-e^{{\alpha }_{\mathrm{ȯ}}\left(\frac{c_2^{(c)}-c_1^{(c)}}{c_1^{(c)}}\right)(t-\frac{L^{(v)}}{c_2^{(v)}})}]+\hfill \\ \hfill \frac{c_2^{(v)}}{{\alpha }_{\mathrm{ȯ}}{L}^{(v)}}{e}^{\frac{{\alpha }_{\mathrm{ȯ}}{L}^{(c)}}{c_2^{(c)}}\left(\frac{c_2^{(c)}-c_1^{(c)}}{c_1^{(c)}}\right)}({\alpha }_{\mathrm{ȯ}}t-\frac{{\alpha }_{\mathrm{ȯ}}{L}^{(c)}}{c_2^{(c)}})\hfill \end{array}\right\},\hfill & \hfill \frac{L^{(v)}}{c_2^{(v)}}\le t<\frac{L^{(v)}}{c_2^{(v)}}+\frac{L^{(c)}}{c_2^{(c)}}\hfill \end{array}$$ (C.2)

We observe that $c_1^{(v)}$ does not appear in Eq. (C.2) and that 〈S^(v)〉 is a constant unless there is a change in capillary flow velocity (i.e $c_1^{(c)}\ne c_2^{(c)}$). This means that while a change in the capillary flow velocity affects 〈S^(v)〉, a change in the venous flow velocity (by itself) does not. The only role of the venous flow velocity is to propagate the saturation perturbation along the venous compartment with a speed $c_2^{(v)}$, which is the venous flow velocity after the step change in flow velocity. Equation (C.2) indicates that during the transient time interval $(0,L^{(c)}/c_2^{(c)}+L^{(v)}/c_2^{(v)})$, whose duration equals the total blood transit time through capillaries and venules $(t_2^{(c)}+t_2^{(v)})$, there is an exponential response of the average venule saturation during the initial and final time intervals of duration $t_2^{(c)}$, and a linear temporal response in between. As a result, the rise time (defined as the time from 10% to 90% of the step height) of the average venule saturation is shorter than 0.8 times the transient time interval of $(t_2^{(c)}+t_2^{(v)})$ (which would be the case of a perfectly linear transient) and I found that it can be closely approximated by $t_r^{(v)}~0.6(t_2^{(c)}+t_2^{(v)})$. Using this rise time one can approximate the venule saturation step response with the following Gaussian low-pass filter response that is time-shifted by the time-to-half of the step height $(t_{0.5}^{(v)})$:

$$\langle S^{(v)}\rangle (t)\approx \langle S^{(v)}\rangle (t=0)+\frac{1}{2}[\langle S^{(v)}\rangle (t=t_2^{(c)}+t_2^{(v)})-\langle S^{(v)}\rangle (t=0)][1+\mathrm{e}\mathrm{r}\mathrm{f}(\sqrt{\pi }\frac{t-t_{0.5}^{(v)}}{t_r^{(v)}}\left)\right],$$ (C.3)

where erf indicates the error function, and $t_{0.5}^{(v)}$ is given by $t_{0.5}^{(v)}=(1/2)(t_2^{(c)}+t_2^{(v)})=(5/6)t_r^{(v)}$. The steady state venous saturation values at t = 0 and $t=t_2^{(c)}+t_2^{(v)}$ are the saturation values at the end of the capillary segment as given by Eq. (12) with ℓ = L^(c). The step response of the average venule saturation predicted by the model [Eq. (C.2)] is shown in Fig. C.2 together with the Gaussian low-pass filter approximation of Eq. (C.3). The cutoff angular frequency of the Gaussian low-pass response is given by ${\omega }_c^{(v)}=2\pi 0.34/t_r^{(v)}\approx 2\pi 0.34/[0.6(t_2^{(c)}+t_2^{(v)})]\approx 3.56/(t_2^{(c)}+t_2^{(v)})$.

Fig. C.2.

Step response to a change in blood flow velocity for the average venule saturation as predicted by the model [solid line, Eq. (C.2)]. The numerical values for the various parameters are the same as in Fig. B.2, and L^(v) = 1 mm. The step response of the average venule saturation can be approximated by a first-order low-pass Gaussian filter (dashed line). The rise time t_r of this Gaussian low-pass filter corresponds to a cutoff angular frequency $({\omega }_c^{(v)})$ that is ~3.56 times the inverse of the combined blood transit time in the capillaries and venules, namely: ${\omega }_c^{(v)}\cong 3.56/(t_2^{(c)}+t_2^{(v)})$.

Appendix D

Transient capillary and venous saturation for a step change in oxygen consumption rate

Because blood flow velocity (c) and oxygen consumption rate (α_ȯ) do not appear independently but are coupled in the ratio α_ȯ/c, the expressions for the transient saturation changes in response to a step change in oxygen consumption are formally the same as those for the step change in flow velocity, at least in the case of small perturbations The asymptotic saturation step responses to velocity and oxygen consumption rate changes have the same magnitude and opposite signs [Fantini, 2002]. In other words, a 1% increase in c and a 1% decrease in α_ȯ result in steady-state average capillary and venous saturations that are higher than the corresponding initial values by the same amount. As a result, Eq. (B.3) also describes the average capillary saturation response to a step change in oxygen consumption rate (with the replacement of $c_2^{(c)}$ with c^(c)), and Eq. (C.3) also describes the average venous saturation response to a step change in oxygen consumption rate.