Stochastic Properties of Neurotransmitter Release Expand the Dynamic Range of Synapses

Abstract

Release of neurotransmitter is an inherently random process, which could degrade the reliability of postsynaptic spiking, even at relatively large synapses. This is particularly important at auditory synapses, where the rate and precise timing of spikes carry information about sounds. However, the functional consequences of the stochastic properties of release are unknown. We addressed this issue at the mouse endbulb of Held synapse, which is formed by auditory nerve fibers onto bushy cells (BCs) in the anteroventral cochlear nucleus. We used voltage clamp to characterize synaptic variability. Dynamic clamp was used to compare BC spiking with stochastic or deterministic synaptic input. The stochastic component increased the responsiveness of the BC to conductances that were on average subthreshold, thereby increasing the dynamic range of the synapse. This had the benefit that BCs relayed auditory nerve activity even when synapses showed significant depression during rapid activity. However, the precision of spike timing decreased with stochastic conductances, suggesting a trade-off between encoding information in spike timing versus probability. These effects were confirmed in fiber stimulation experiments, indicating that they are physiologically relevant, and that synaptic randomness, dynamic range, and jitter are causally related.

Introduction

The probabilistic nature of neurotransmitter release has been clear since early recordings of synaptic potentials (Fatt and Katz, 1952), but the functional implications are poorly understood. Most importantly, when the average size of synaptic potentials is near threshold, the randomness of release potentially introduces noise and unreliability. This could have a major impact in the auditory system, where the rate and precise timing of spikes carry information about the nature and location of sound sources, so the loss or mistiming of spikes will degrade auditory processing.

This is a particular issue for relay neurons in the auditory pathway, such as bushy cells (BCs) in the anteroventral cochlear nucleus. BCs receive excitatory input from auditory nerve fibers (ANFs) at synapses called “endbulbs of Held” (Lorente de Nó, 1981; Ryugo and Fekete, 1982; Limb and Ryugo, 2000). BCs relay ANF activity to brain areas involved in sound localization. Endbulbs are among the largest and fastest synapses and, at low frequencies of activation (<100 Hz), show near-perfect fidelity in triggering action potentials in BCs. However, ANFs are capable of firing at up to 300 Hz in vivo (Johnson, 1980; Joris et al., 1994; Taberner and Liberman, 2005). At these rates, endbulb EPSCs can depress below spike threshold (Wang and Manis, 2006; Strenzke et al., 2009; Yang and Xu-Friedman, 2009; Chanda and Xu-Friedman, 2010a). Furthermore, single quanta at the endbulb are particularly large (mEPSCs ∼100 pA, mEPSPs 1–2 mV) (Oleskevich et al., 2004; Chanda and Xu-Friedman, 2010b). Thus, variability in EPSP amplitude could have a large impact on spiking during ongoing activity when endbulbs are depressed.

The stochastic properties of release have been used to elucidate fundamental mechanisms of synaptic transmission (Scheuss and Neher, 2001; Silver, 2003) but have not been addressed in their own right. Average EPSCs typically measured in vitro do not reflect the moment-by-moment variation that the nervous system normally encounters in vivo. Recently, considerable variability has been found in EPSP amplitude in vivo (Lorteije et al., 2009; Künzel et al., 2011). Although it is not yet clear how much of that variability results from deterministic versus stochastic processes, it seems likely that the fidelity of postsynaptic spiking is influenced by the stochastic nature of neurotransmitter release. Furthermore, the persistence of synaptic variability in vivo raises the question whether there may be unrecognized benefits of stochastic release.

We addressed these issues by quantifying the variability of release at the endbulb and assessing its impact experimentally using dynamic clamp. Variability in BC spiking is almost entirely accounted for by variability in synaptic conductance, whereas spike threshold remains highly stable. This reduces reliability for EPSPs that are on average just over threshold, but it also increases spiking for EPSPs that are on average below threshold. The overall effect of the stochastic properties of release is therefore that postsynaptic spike probability encodes information about average EPSP amplitude, which increases the dynamic range of synapses. However, it does so at a cost to precise timing, as latency is closely tied to EPSP amplitude.

Materials and Methods

Electrophysiology.

Brain slices were prepared from the cochlear nucleus of CBA/CaJ mice of either sex 15–21 days of age according to procedures described previously (Yang and Xu-Friedman, 2008), and approved by the Institutional Animal Care and Use Committee at the University at Buffalo. Recordings were performed at 32°C in external solution containing the following (in mm): 125 NaCl, 26 NaHCO₃, 1.25 NaH₂PO₄, 2.5 KCl, 1 MgCl₂, 1.5 CaCl₂, 20 glucose, 4 Na L-lactate, 2 Na pyruvate, 0.4 Na L-ascorbate, and 10 μm strychnine. For ANF stimulation experiments, in current-clamp, 5 μm CPP was also included. Patch electrodes contained the following (in mm): (voltage clamp) 35 CsF, 100 CsCl, 10 EGTA, 10 HEPES, 1 QX-314, pH 7.3, 311 mOsm, or (current/dynamic clamp) 130 KMeSO₃, 10 NaCl, 2 MgCl₂, 0.16 CaCl₂, 0.5 EGTA, 10 HEPES, 4 Na₂ATP, 0.4 NaGTP, 14 phosphocreatine di(tris), pH 7.3, 305 mOsm. Recordings were made using a Multiclamp 700B controlled by an Instrutech ITC-18 digital interface through Wavemetrics Igor running custom-written routines. Patch electrodes had resistances of 1.5–2.5 MΩ, yielding series resistances of 5–10 MΩ, which were compensated to 70%. Individual ANFs were stimulated in the neuropil using a 3–5 μm electrode connected to a stimulus isolator (WPI, A365), passing 14 μA of current for 0.2 ms. Dynamic clamp was performed using the ITC-18 interface at 50 kHz (for more details, see Xu-Friedman and Regehr, 2005a). Conductance threshold (see Figs. 3 and 5) was measured with 0.5 nS resolution by applying AMPA-like conductances of different amplitudes, and finding the minimum conductance that drove spiking with an adaptive procedure. The conductance of dynamic clamp trains was scaled to 5–6 times this value. In most cases, the value of the first pulse was changed to a more moderate suprathreshold value (e.g., 30 nS) to avoid recording artifacts caused by the very large conductances that rested endbulbs are capable of (≫100 nS). This was in keeping with our focus on later pulses in the train when synaptic depression has set in.

Figure 3.

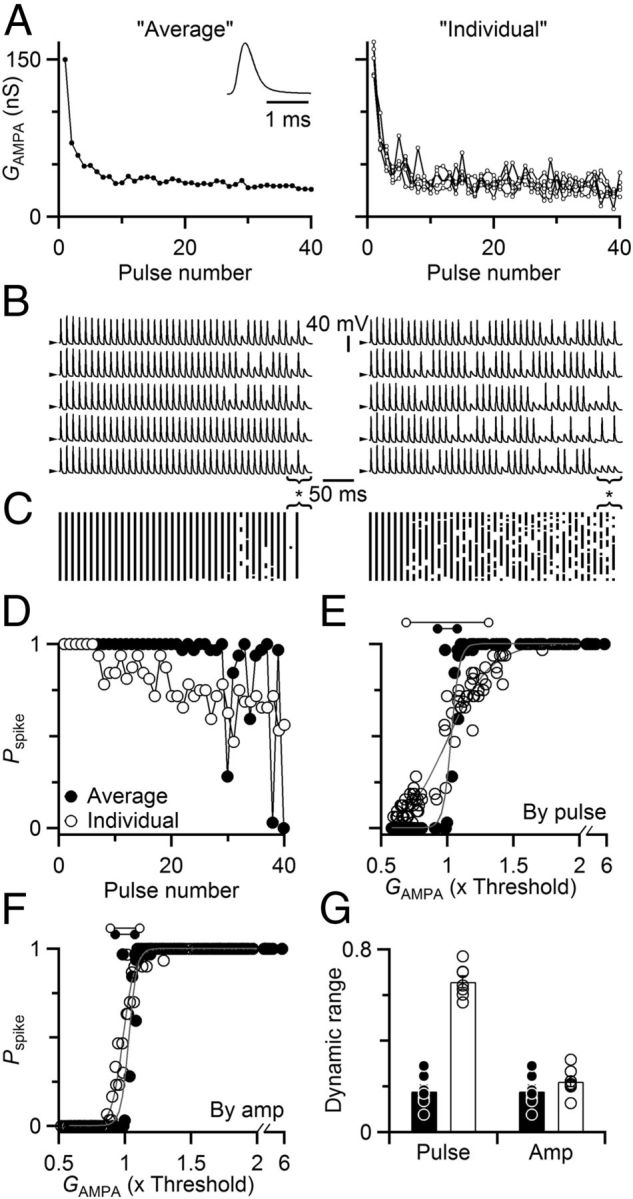
Stochastic EPSC amplitude increases the dynamic range of synaptic transmission. A–D, Representative dynamic-clamp recording. A, Synaptic conductances used to drive dynamic-clamp experiments. Synaptic conductances were based on EPSCs measured in separate voltage-clamp experiments shown in Figure 2A–C. On different dynamic clamp trials, either the overall average amplitude (left, average of 20 trials) or amplitudes measured on individual trials (right shows five examples) were convolved with a unitary EPSC (left, inset). B, Sample dynamic clamp trials, with conductances drawn from the overall average EPSC on each trial (left), or the EPSC amplitudes measured in individual trials (right, each trace uses a unique set of conductances, shown in A). Spiking was highly repeatable using the average conductance compared with the individual conductances. For the average conductance (left), the 39th pulse in the 100 Hz train showed nearly 100% reliable spiking (asterisk below traces), whereas the 38th and 40th failed to elicit spikes, even though differences in the average conductance are imperceptible over this range (A). Spiking was much more variable when using the conductances from individual trials (right). Arrowheads to the left of traces indicate −60 mV. C, Raster diagram of spike times from 32 trials using the average (left) or individual (right) conductances. Continuous vertical lines indicate highly regular firing. D, P_spike for dynamic clamp trials driven with average versus individual conductance for 100 Hz trains, calculated from the rasters in C. The average conductance led to sharp oscillations in P_spike (closed circles) compared with the individual conductances (open circles), which showed a gradual decline. E, Relationship between P_spike and average pulse conductance G_AMPA. G_AMPA was the same for dynamic clamp conductances based on either individual voltage-clamp trials (A–C, right) or the overall average (A–C, left) for trains of 50, 100, and 200 Hz. P_spike values are derived from the same analysis as in D but are plotted against the average conductance for that pulse. Lines are sigmoidal fits to the data using Equation 1, and the derived measure of dynamic range is indicated by the dumbbells above the graph. F, P_spike as a function of conductance amplitude, regardless of position in the train. Synaptic conductances from the experiments of A and B were sorted by amplitude across all trials, then binned to calculate P_spike. Data from average trials are shown with solid symbols, and from individual trials are shown with open symbols. Lines are sigmoidal fits to the data as in E, with dynamic ranges indicated by the dumbbells above the graph. The average difference in dynamic range was 0.32 ± 0.10, which was not significant (p = 0.12, N = 7 cells). G, Dynamic range increased when stochastic properties of neurotransmitter release were included in dynamic-clamp trials. We fit sigmoidal curves (Eq. 1) to measure the dynamic range for individually variable trials (open circles, open bars) and the average trials (closed circles, solid bars). The dynamic range increased significantly when considering P_spike as a function of average conductance amplitude for individual pulses (p < 0.001), but not when considering P_spike as a function of conductance amplitude regardless of train position (p = 0.12). Data are averages from seven cells.

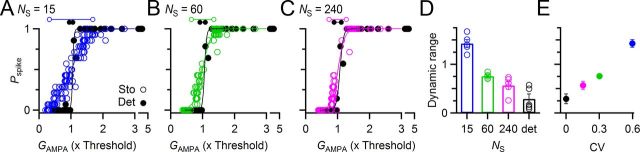
Figure 5.

Dynamic range increases with synaptic variance. Data are results of dynamic-clamp experiments run using the deterministic (solid symbols) and stochastic (open symbols) models of neurotransmitter release, with model parameters held constant, except for the number of release sites (N_S). As N_S increased, the conductance variability decreased. A–C, Spike probability for each pulse (P_spike) as a function of the pulse's average synaptic conductance (G_AMPA) in a representative experiment. For the deterministic model (solid symbols), dynamic range was uniformly narrow. For the stochastic model, the dynamic range was greater for low N_S. Dynamic ranges for the different conditions are indicated using the dumbbells above each plot. D, Dynamic range as a function of N_S for five experiments. Dynamic range was widest for the smallest number of release sites and narrowed with increasing N_S. Dynamic range was most narrow with the deterministic model. E, Dynamic range as a function of synaptic variance. Dynamic ranges from D are plotted against the CV of the steady-state synaptic conductances for different N_S (mean ± SEM of five experiments).

Stochastic model of release.

This model is modified from an earlier, deterministic model (Yang and Xu-Friedman, 2008, 2009), that added receptor desensitization to the release and recovery model of Dittman et al. (2000). These models share many features in common with a number of existing models of neurotransmitter release. This model is mechanistically based, but it is not claimed to be complete. For example, the model does not take into account delayed release, receptor saturation, or variability in quantal size (Chanda and Xu-Friedman, 2010a; Yang and Xu-Friedman, 2010). Phenomenologically, it yields EPSCs with mean and SDs that match voltage-clamp data of trains of activity reasonably well.

The deterministic model used analytical solutions for each release and recovery process. The stochastic model was implemented using an Euler integration approach, with time step dt = 0.5 ms. The model tracked a number of independent release sites (N_S). Each release site, equivalent to one active zone, contained its own pool of releasable vesicles of maximum size N_V, and an unlimited reserve pool. The vesicle pool was initialized with N_V vesicles, which was depleted with activity. When a stimulus occurred, the number of vesicles released by one release site, r_i, followed a binomial distribution, with parameter N equal to the number of available vesicles at site i (N_i), and parameter P equal to the probability that each releases, which we held fixed in this model with a value of P₀. The vesicle pool recovered according to two processes: a slow recovery with rate k₀, and a fast recovery with rate k_max. The balance of these was determined by accumulation of an activity sensor D, which incremented with each pulse, and decayed back to rest with time constant τ_D. The activity sensor was modeled as driving fast recovery according to a simple binding reaction with dissociation constant K_D.

The decay of D was implemented deterministically as follows:

The value of D was used to determine the instantaneous recovery rate:

The actual number of vesicles that recovered during each interval dt was probabilistic, drawn from a binomial distribution, with parameter N equal to the number of open slots in the site's releasable pool (i.e., N_V − N_i), and parameter P dependent on the rate of recovery (i.e., k_recov dt). On average, this produced exponential recovery.

To drive the desensitization part of the model, cleft glutamate at each site, S_i, was incremented according to the number of vesicles released at that site. Cleft glutamate decayed deterministically back to 0 with time constant τ_S. This was implemented for each time step as follows:

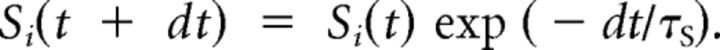Receptor desensitization was modeled as an instantaneous binding reaction with cleft glutamate, using dissociation constant K_S. Early versions of the model calculated the synaptic current contributed by each site, EPSC_i, as follows:

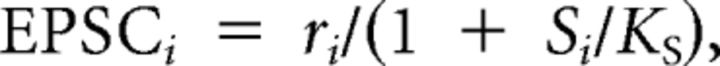where r_i was the number of vesicles released from site i after the stimulus. However, this led to the problem that adjustments in the parameter N_V, to tune the stochastic properties of release, had the side effect of changing the depth of desensitization, which was a deterministic aspect of synaptic plasticity that it was preferable to hold constant. To break this interaction, we revised this to:

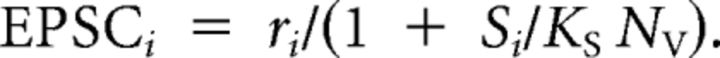The overall EPSC was the sum of every site's EPSC_i.

We found that including a facilitation component in the model was not necessary to fit our experimental data, but for completeness we describe it here. Following Dittman et al. (2000), a facilitation sensor F would be incremented after each stimulus, which decays exponentially with time constant τ_F:

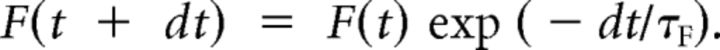The probability of release at any moment, P(t), would be influenced by the facilitation sensor according to a simple binding reaction with dissociation constant K_F:

Model validation.

We validated the conversion of the model from deterministic to stochastic by comparing the output of both types of model. We ran the stochastic model either with thousands of release sites, or by running the model thousands of times, and comparing the average against the output of the deterministic model. These were always essentially identical. Once it was clear that the model was well behaved, we selected a representative voltage-clamp experiment and adjusted the parameters of the model to match both the average EPSC amplitude and the SD (see Fig. 4). To improve similarity, we fit parameters iteratively by hand to minimize a χ² statistic.

Figure 4.

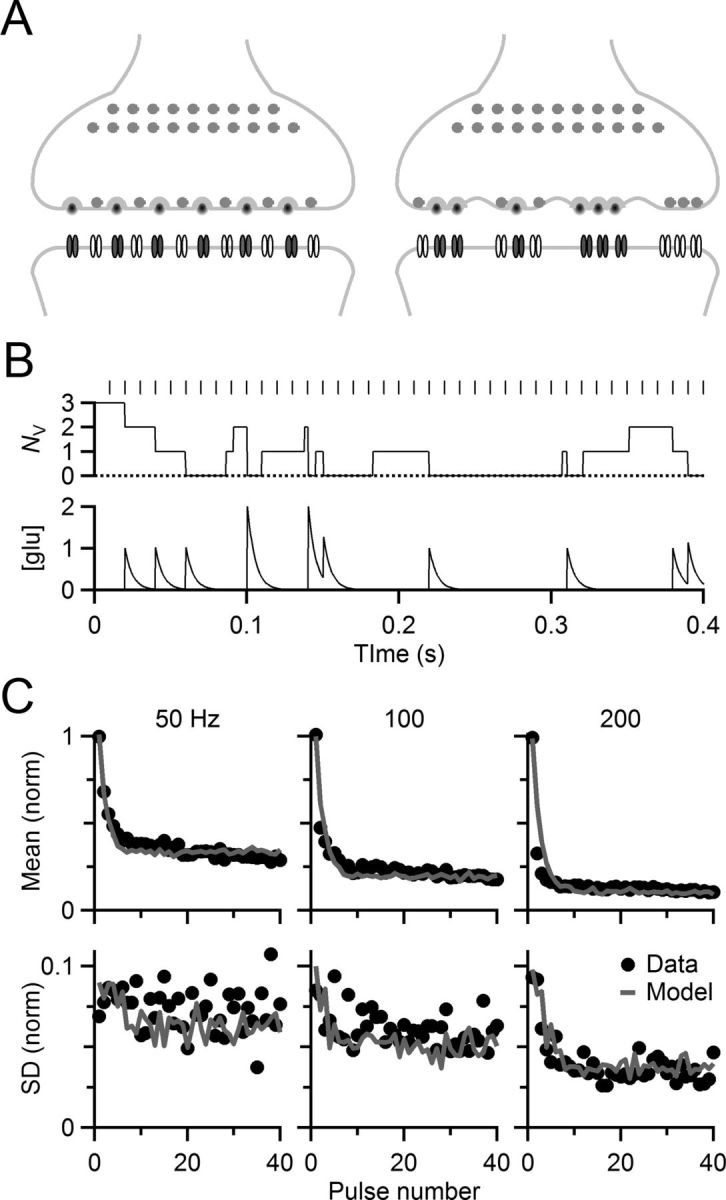
Stochastic model of neurotransmitter release. A, Diagrammatic view of deterministic (left) and stochastic (right) models of release. The deterministic model tracked the average behavior of a synapse, using fixed rates of release and recovery of a pool of vesicles, as well as desensitization and recovery of postsynaptic receptors (see Materials and Methods). The stochastic model tracked multiple sites, each with its own pool of vesicles and receptors. Release and recovery were governed by binomially distributed random processes. The deterministic model used seven parameters, and two parameters were added for the stochastic model. B, Activity of a single release site, showing fluctuations in vesicle pool size (N_V) and extracellular glutamate concentration during a train of activity. C, The stochastic model captured both mean and variance of synaptic transmission. Symbols show mean (top) and SD (bottom) of voltage-clamp data from the cell depicted in Figure 2A–C. Solid lines show mean and SD of conductances given by the stochastic model.

The parameters for the model used to derive conductances in Figures 4 and 6 were P₀ = 0.4, k₀ = 0.5/s, k_max = 7/s, τ_D = 10 ms, K_D = 0.05, τ_S = 5 ms, K_S = 1 N_V, N_S = 60, N_V = 3, and facilitation was not included. Figure 5 used identical parameters, except that the number of sites (N_S) was varied.

Figure 6.

Stochastic properties of release uncover high-frequency activity. A–D, Data from a representative dynamic-clamp experiment using a 75 Hz Poisson-distributed train of activity to drive the conductance model. A, B, Responses of a BC driven by deterministic (A) or stochastic (B) model conductances. The actual (A) or average (B) conductances are shown above the rasters. For scale, the final conductance in the train was 20 nS. With the deterministic model (A), responses were highly bimodal, either reliably firing or reliably failing to fire on nearly every trial. By contrast, responses to the stochastic model (B) were much more variable. Many pulses produced spikes in B that failed to do so in A. Responses are shown at steady state, beginning with the 10th pulse. C, Conductances at short intervals tended to be smaller. Conductance amplitudes were from the deterministic model. D, P_spike as a function of preceding interval, revealing a wider dynamic range for trials using the stochastic model (open circles) compared with the deterministic model (closed circles). Lines are sigmoid fits to the data to quantify the dynamic range, which is indicated using dumbbells above the graph. E, Average dynamic ranges from five experiments using deterministic (closed circles, solid bar) and stochastic models (open circles, open bar). The increase is statistically significant (p = 0.003, t test).

Results

Probabilistic effects in current clamp

Synaptic variability is evident in current-clamp recordings. We made whole-cell recordings of BCs in slices from the anteroventral cochlear nucleus of P15–P21 mice and activated individual ANFs using a small stimulating electrode in long trains of different frequencies. Spiking was initially highly reliable, but this reliability dropped off as activity continued, particularly at high frequencies of activation (Fig. 1A–C). Notably, even though spiking became less reliable, it did not vanish. As the train of activity continued, spiking decreased to 75% (at 100 Hz) to as little as 25% (at 333 Hz) for prolonged periods on average. Different synapses appeared to cut out at different frequencies (Fig. 1D), presumably reflecting different degrees of synaptic depression (Yang and Xu-Friedman, 2009).

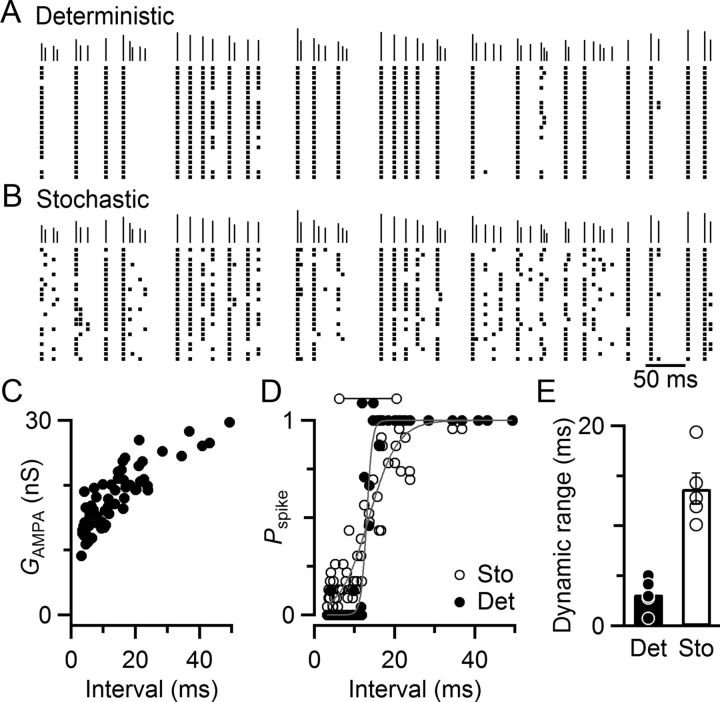
Figure 1.

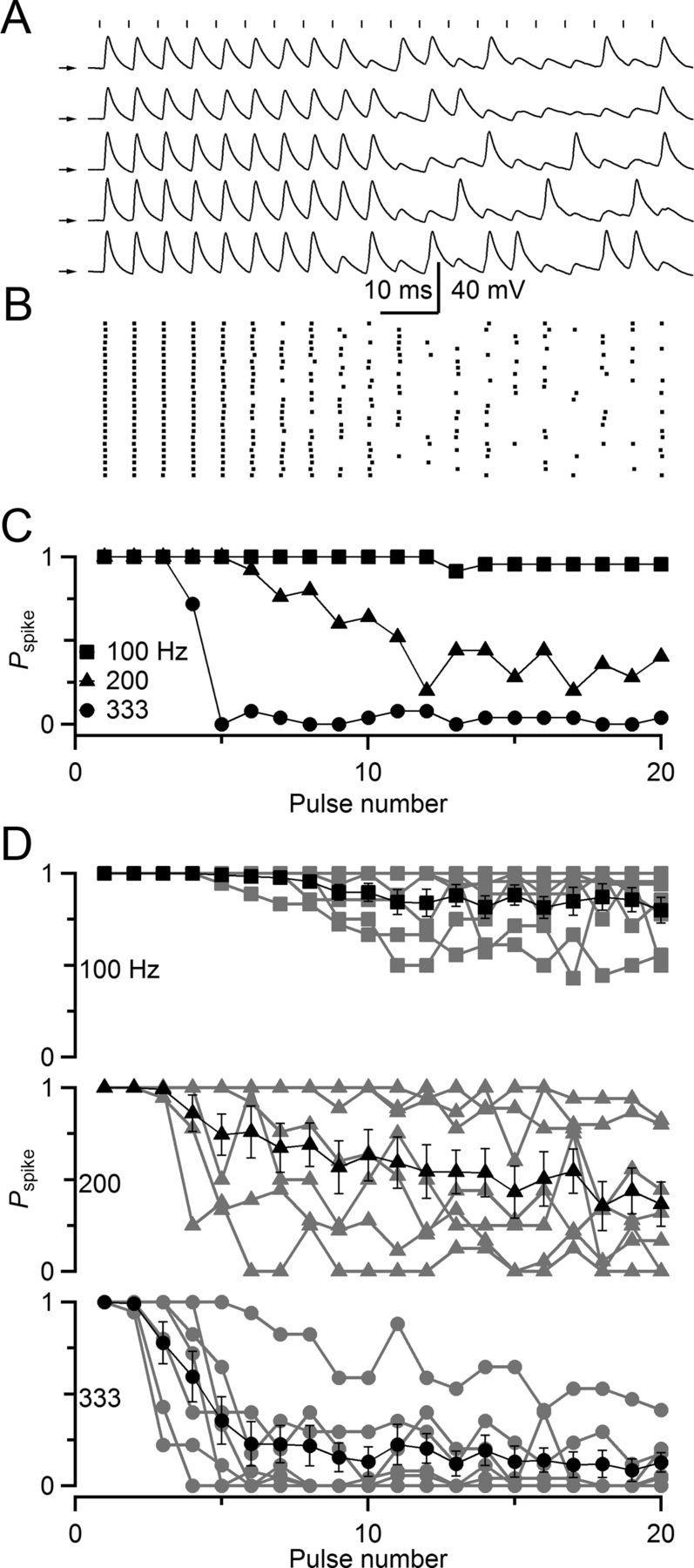
Stochastic firing properties of BCs in the cochlear nucleus. A–C, Representative current-clamp recording from a BC in response to ANF stimulation. A, ANF stimulation (vertical markers) at 200 Hz triggers BC spikes or EPSPs. Arrows indicate −60 mV for each trace. B, Raster plot of spike times over 25 trials, showing a sustained, but irregular, response. C, Probability of spiking for stimulation trains of different frequency. At 100 Hz, the probability of spiking (P_spike) was nearly 100% after stimulation, whereas at 333 Hz, P_spike was nearly 0%. At intermediate stimulation rates, P_spike took on intermediate values. D, Average P_spike for six experiments similar to A. On average, P_spike decreased gradually over the course of a train at all frequencies.

The question is why spiking reached intermediate values, rather than 100% when the EPSP was above threshold or 0% when it was below. This indicates that spiking is influenced by a stochastic process. The stochastic process could be presynaptic, such as through variability in the amount of neurotransmitter release, or postsynaptic through fluctuations in resting membrane potential or spike threshold. Shifts in resting membrane potential of <5 mV have measurable effects on spike probability in BCs (Pliss et al., 2009; Chanda and Xu-Friedman, 2011), and spike threshold can be affected by activity (Xu-Friedman and Regehr, 2005a).

Contribution of synaptic variability

We wanted to determine which factors contributed to the persistence of spiking, so as to understand their implications for neuronal computation. We first quantified the variability in neurotransmitter release at the endbulb using voltage-clamp recordings and activating single ANFs over 40 stimuli. EPSCs show substantial variability from one pulse to the next (Fig. 2A). We recorded EPSCs over many trials and found substantial variability in EPSCs at all frequencies of stimulation (Fig. 2B,C). We observed similar effects in six cells. We quantified the average EPSC during trains (Fig. 2D), as well as the SD (σ). The coefficient of variation (CV = σ/mean) rose during the train, until variability represented a large percentage of the total amplitude (∼30%, Fig. 2E).

Figure 2.

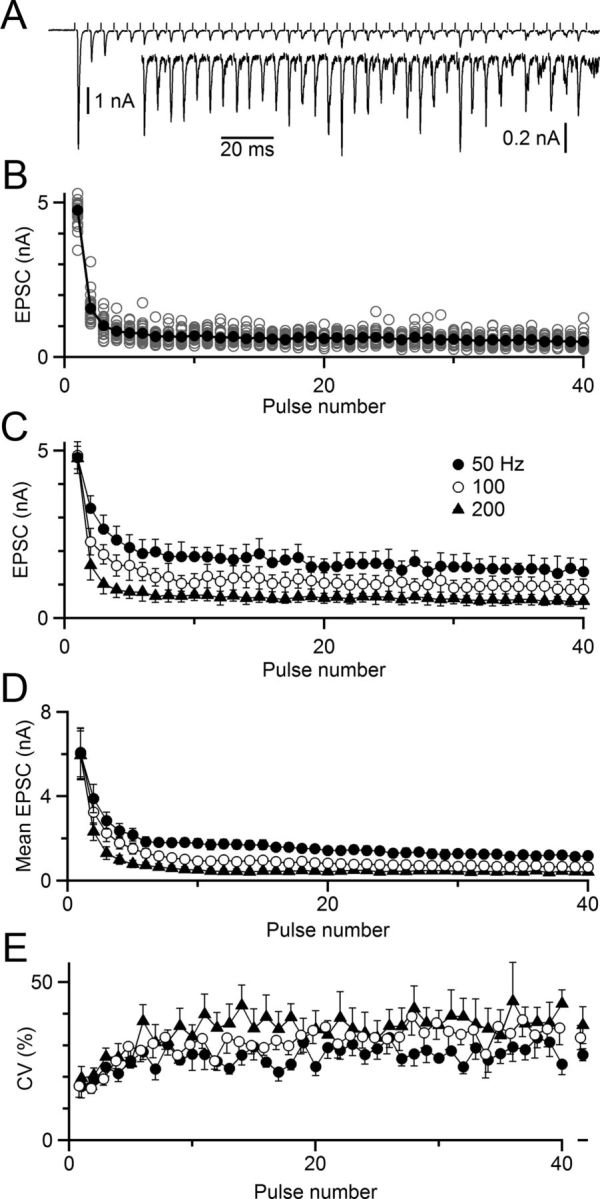
Variability in EPSCs during trains of activity. A–C, Representative voltage-clamp recording. A, Single trial of a 40-pulse, 200 Hz train. Inset, Magnified view of the same trace. EPSC amplitude is quite variable from pulse to pulse, even at steady state. B, EPSC amplitudes from 24 trials similar to A. Open circles represent EPSCs on single trials, and closed circles represent the overall average. C, EPSC mean ± SD for trains of multiple frequencies. These amplitudes were used to drive dynamic-clamp experiments in Figure 3 and were fit using the model of stochastic release in Figure 4. D, EPSC mean ± SEM for 6 cells recorded in voltage clamp. E, Variability in EPSC represents a large fraction of the EPSC amplitude at steady state. Mean CV (SD/mean) is plotted over the train for 6 cells recorded in voltage clamp. The steady-state CV for pulses 11–40 is shown at right.

To determine whether the variability evident in voltage-clamp recordings might account for the variability in spiking seen in Figure 1, we used the dynamic-clamp technique. Dynamic clamp is a powerful tool (Robinson and Kawai, 1993; Sharp et al., 1993; Prinz et al., 2004) that is particularly appropriate for these experiments. First, endbulbs are axosomatic terminals, so currents passed by the dynamic clamp setup at the soma are naturalistic (Xu-Friedman and Regehr, 2005a). Second, we want to understand the effect of synaptic variability, but it is very difficult and perhaps impossible to control the variability of synapses in isolation from other synaptic properties, such as overall amplitude and short-term plasticity. We avoided that problem by using dynamic clamp to mimic synaptic conductances with and without variability. We applied synaptic conductances based on two different sources: (1) the EPSC amplitudes we measured in individual voltage-clamp trials (Fig. 3A, right) or (2) the average EPSC amplitude across all trials (Fig. 3A, left). Each conductance amplitude was convolved with a constant unitary EPSC (Fig. 3A, left, inset). Over the course of the experiment, the BC received the same average synaptic conductance under both stimulus regimes, but one was variable across trials and the other fixed. When we applied the conductance based on the average EPSC amplitude in dynamic clamp, the BC spiked with high regularity from trial to trial (Fig. 3B,C, left). In many cases, even imperceptible fluctuations in the amplitudes of synaptic conductance were reflected in consistent failure or success of firing (Fig. 3B,C, left, bracketed pulses).

We quantified the probability of spiking (P_spike) during the train, which oscillated sharply between near 100% reliability and lower probability (Fig. 3D, closed symbols). We have observed similar regularity in other dynamic-clamp studies using fixed conductances that addressed entirely different issues (Pliss et al., 2009; Chanda and Xu-Friedman, 2010a). This behavior contrasts strongly against the gradual changes in P_spike with ANF stimulation (Fig. 1), suggesting that spike generation itself contributes very little to the observed variability in P_spike.

We tested whether the stochastic properties of release might contribute to the variability observed during ANF stimulation, by applying dynamic-clamp stimuli that were based on individual voltage-clamp records (Fig. 3A, right). Spiking was much more variable (Fig. 3B,C, right), and P_spike changed gradually during the train, showing no sharp oscillations (Fig. 3D, open symbols).

To understand how the stochastic properties of release affect the transmission of information across the synapse, we consider a stimulus, which is encoded into a temporal pattern of auditory nerve spiking activity. For a given temporal pattern of presynaptic activity, such as a train, an individual EPSP would fluctuate around an average conductance on repeated presentation. The average conductance amplitude is influenced by both tonic levels of presynaptic activity as well as the temporal fine structure of activity. A great number of studies emphasize how presynaptic activity is transformed into postsynaptic conductances and spiking (Zucker, 1989; Abbott and Regehr, 2004), but it is also important to consider this from the opposite viewpoint. Does a pattern of activity in a postsynaptic cell reveal the activity presynaptic to it? For a reliable relay, the answer is obviously yes. However, for an unreliable relay, such as an endbulb driven at high frequency, the absence of spiking is quite ambiguous. Was there no spike because there was no presynaptic activity or because presynaptic activity failed to trigger a spike? Can P_spike reveal more information about presynaptic activity than just presence or absence?

We addressed these questions by considering the relationship between P_spike and the average conductance for individual pulses (G_AMPA), which gives us a dramatically different view of threshold and synaptic function. For dynamic-clamp trials using the average EPSC conductance, there was a sharp transition from nonresponsive to 100% spiking over a short range of EPSC amplitudes (Fig. 3E, closed symbols). However, when P_spike for the variable trials was plotted against the average pulse amplitude, the relationship shows a much more shallow dependence (Fig. 3E, open symbols). When the conductance reflected natural variability (Fig. 3E, open symbols), there was a significant chance for conductances that were on average below threshold to drive spikes as much as 20% of the time. However, when only the average conductance was applied, these largely failed to drive any spiking at all (Fig. 3E, closed symbols).

We view the relationship in Figure 3E as an important way to describe the dynamic range of the synapse. From this perspective, the average synaptic conductance is the input to the synapse, and P_spike is the output. The range over which the synapse shows a graded change in P_spike carries information about the size of the synaptic conductance. When that range is narrow, P_spike reports little about the amplitude of the synaptic conductance, and downstream elements would lose access to activity that failed to trigger spikes at the relay synapse. When the range is wide, then P_spike carries more nuanced information about the amplitude of synaptic conductances, thereby reflecting more about presynaptic activity levels and fine structure of sensory information.

To quantify the dynamic range, we fit the data of Figure 3E to a sigmoidal function as follows:

where G_AMPA is the average conductance amplitude for a specific pulse, G_1/2 is the half-maximal conductance, and r reflects the steepness of the transition from nonfiring to firing. We define the dynamic range d ≡ 4r, which is the inverse of the maximal slope (when G_AMPA = G_½). This value marks the range of conductances over which P_spike changes from 0.1 to 0.9, which is an appropriately intuitive measure of dynamic range. In the experiment of Figure 3E, the dynamic range was 0.15 for dynamic-clamp trials using synaptic conductances based on the overall average and 0.63 using synaptic conductances based on individual voltage-clamp trials (Fig. 3E, top horizontal lines; i.e., a fourfold difference). These dynamic ranges are scaled relative to the conductance threshold because the conductances were normalized in Figure 3E to that threshold.

We did the same experiment in seven cells and quantified the dynamic range for trials driven with variable conductances compared with average conductances. The dynamic range increased significantly from 0.18 ± 0.03 for average conductances to 0.66 ± 0.03 for variable conductances (p < 0.001, t test, Fig. 3G). This was an average increase of 333 ± 85%.

We verified that this difference in response was not a result of differences in spike threshold between average and stochastic conditions. We reanalyzed the data of Figure 3 to consider P_spike as a function of individual conductance amplitude, not average pulse amplitude. To do this, we grouped synaptic conductances of similar amplitude, regardless of their timing in the train, and calculated P_spike for the group. In the example of Figure 3F, each point represents P_spike across 30 conductances of similar amplitude. When we did this more conventional analysis, we found that spike threshold was identical for both conditions, with a sharp cutoff between amplitudes that triggered versus those that did not trigger a spike (Fig. 3F). Similar results were found for multiple cells, and there was only a small difference in dynamic range (0.22 ± 0.02 for stochastic vs 0.18 ± 0.03 for average conductances, N = 7, Fig. 3G), representing an increase of 32 ± 10%. Thus, the moment-by-moment synaptic conductance predicts with high success whether or not a spike is triggered, and variation in spike threshold plays no obvious role under our experimental conditions. Furthermore, the stochastic properties of release generate a large increase in the dynamic range of the synapse.

Synaptic variability and dynamic range

We wanted to probe the effects of the stochastic properties of release further, but the experimental approach of Figure 3 was constrained to specific patterns of activity with EPSCs quantified in voltage clamp. To go further, we wanted to set the amplitudes of conductances in dynamic clamp using a model. We began with a deterministic model of synaptic plasticity that was developed to capture the average effects of depletion, desensitization, and recovery (Yang and Xu-Friedman, 2008, 2009), but in the absence of synaptic variability. To implement stochastic release, release and recovery were modeled as binomial random processes involving a finite pool of vesicles, which was spread across multiple release sites (N_S), each with its own, limited pool of releasable vesicles (N_V) (Fig. 4A,B; see Materials and Methods). The model tracked the local glutamate concentration in each release site's synaptic cleft to drive desensitization with a simplified first-order binding reaction (Fig. 4B; see Materials and Methods). On average, deterministic and stochastic models had the same behavior. From our voltage-clamp studies, we selected one cell with average levels of depression and determined model parameters that would mimic both the average and stochastic behavior of this representative cell (see Materials and Methods). The model matched this representative cell reasonably well over a wide range of activity levels (Fig. 4C, compare lines and symbols). For our purposes, it was not necessary that the model duplicate the true mechanisms underlying either deterministic or stochastic properties of release, as long as it yielded synaptic conductances with reasonably similar average and SD. There are many additional contributions to variability in real synapses that we did not incorporate in the model, including quantal variability and variability in P between release sites. We only used two model parameters to introduce variability, N_S and N_V, so to match the variance of experimental data, these parameters had to take on unrealistically low values to compensate for missing sources of variability (see Materials and Methods).

We first considered the relationship between the dynamic range and the variance of the EPSC. We varied the SD of the synaptic conductance by changing the number of release sites, N_S, and leaving all other parameters unchanged. Our starting value for N_S was 60. When N_S was quadrupled (240), the conductance SD produced by the model dropped in half; and when N_S was reduced to one-fourth (15), the SD approximately doubled. We performed dynamic-clamp experiments similar to Figure 3, but using the model synaptic conductances in place of measured ones and assaying spiking in real BCs. In half the trials, we used the deterministic model of release; and in half the trials, we used the stochastic model with different values of N_S. Trains of 50, 100, and 200 Hz were applied. The deterministic conductances showed a sharp transition between 0% and 100% reliability (Fig. 5A, closed symbols), similar to the “average” stimulus used in Figure 3. The stochastic conductances showed a graded relationship between G_AMPA and P_spike (Fig. 5A, open symbols), similar to the “individual” stimulus used in Figure 3.

The dynamic range depended heavily on the number of release sites in the stochastic model. With 15 release sites (Fig. 5A), the dynamic range was greatest, decreased with 60 release sites (Fig. 5B), and the dynamic range was narrowest with 240 release sites (Fig. 5C). Similar effects were found in five cells, where the dynamic range increased over the deterministic model by 830 ± 320% for N_S = 15 (Fig. 5D, p = 0.001, paired t test). Smaller, but still significant, increases in dynamic range were found with more release sites (p = 0.003 for N_S = 60; p = 0.01 for N_S = 240), and effects were significantly different between all conditions (p < 0.05 for all pairwise comparisons). Thus, a greater variance in synaptic conductance led to an increase in the dynamic range of the synapse (Fig. 5E).

Irregular activity

We investigated the impact of stochastic properties of release for more naturalistic activity patterns. We used dynamic clamp to apply an irregular, Poisson-distributed, pulse train at 100 Hz, with a 3 ms refractory period imposed. Synaptic conductances were set using the deterministic and stochastic models on alternate trials. BC spiking was regular and repeatable with the deterministic model, particularly when the interval between conductances was >15 ms (Fig. 6A). However, many of the synaptic conductances failed to elicit any response at all, trial after trial. This primarily occurred when the interval between pulses was short and synaptic depression was strong (Fig. 6C). In this representative experiment, nearly complete failure was observed for intervals <10 ms (Fig. 6D, closed symbols).

The consistent failures represent an inability to relay information at short intervals. Close spiking can reflect fine temporal detail in a stimulus, so a complete lack of spiking would mean the loss of potentially important stimulus information. For auditory activity, this seems particularly important, as natural sounds can contain high temporal complexity, particularly in a natural environment. Thus, with a deterministic synapse, important information could be masked by being in the shadow of a highly effective synaptic conductance.

For the stochastic synaptic conductances, the situation was quite different. Under these conditions, P_spike remained >0% even for the briefest intervals (Fig. 6B), so that stimulus information encoded in brief, high-frequency activity could be relayed on to higher centers. We modified our measure of dynamic range to consider the pulse interval as the “input” to the synapse. In this case, the dynamic range was greater for the stochastic model of release (Fig. 6D, open symbols). We saw similar effects in five cells, with a significant increase in dynamic range from 3.2 ± 0.7 ms with deterministic release to 13.7 ± 1.6 ms with stochastic release (p < 0.003) and an average relative increase of 540 ± 250% (Fig. 6E).

Thus, the stochastic properties of release enhance the dynamic range of synapses and could reveal stimulus features that fall in temporal shadows. The results of Figure 5 indicate that these effects are greater with increased synaptic variability, which we accomplished in our model using fewer release sites. It is therefore a question of why endbulbs do not show greater variance naturally. Real endbulbs have a large number of release sites. Serial EM reconstructions of rat endbulbs had an average of 155 release sites (Nicol and Walmsley, 2002), and some endbulbs in cats are estimated to have up to 10 times as many (Ryugo et al., 1996). The dynamic range could be increased if endbulbs had fewer release sites. To maintain the same overall amplitude, each release site would need to contribute a higher current. Average mEPSC amplitudes are ∼100 pA, and individual mEPSCs up to 300 pA are commonly observed (Oleskevich et al., 2004; Chanda and Xu-Friedman, 2010b; Yang and Xu-Friedman, 2010), so it would be possible to increase the contribution of individual release sites. So the question becomes: why did the advantages of a wide dynamic range not drive endbulbs to have fewer release sites and larger quantal size?

Spike timing variability

To address this question, we investigated other consequences of synaptic variance. The endbulb of Held is notable for preserving highly precise temporal information about sounds (Carr, 1993; Oertel, 1999). We tested whether synaptic variance interferes with temporal precision by measuring the spike latency for experiments similar to Figure 5 using trains of model conductances for a different number of release sites. We measured spike latency after the start of the most recent conductance (Fig. 7A). Variability in spike timing (“jitter”) was strongly affected by the number of release sites. When the number of release sites was low, jitter was high. As the number of release sites increased, jitter decreased. With the deterministic model, jitter was very low indeed, near the level of detectability for the recording setup. Histograms of spike latencies showed that the variance of spike times was highly dependent on the number of release sites, but also that the overall mean latency remained constant (Fig. 7B). The amount of jitter likely relates to the effect of conductance amplitude on the rate of depolarization (Cao et al., 2007) and subsequent spike latency (Xu-Friedman and Regehr, 2005a, b). There was a strong inverse relationship between the amplitude of individual conductances and spike latency (Fig. 7C).

Figure 7.

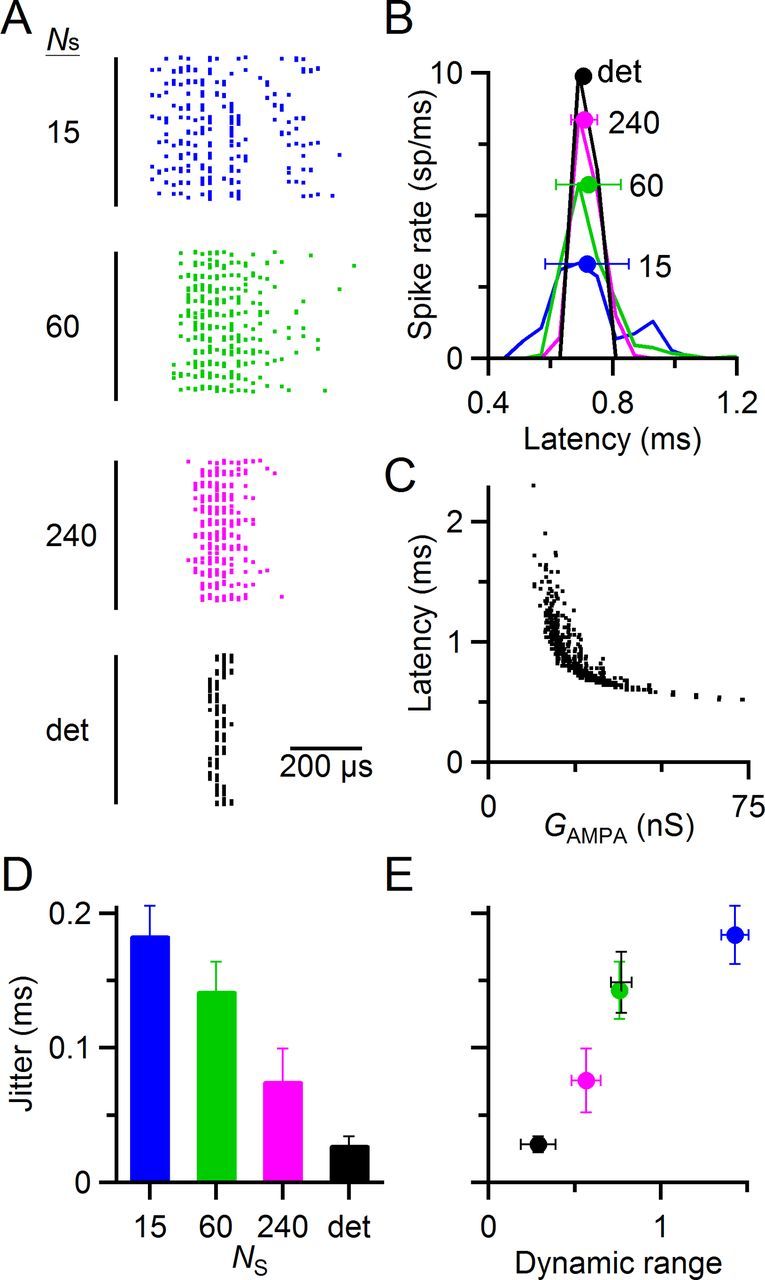
Increased variability also drives an increase in jitter, causing a trade-off. A–C, Data from a representative dynamic-clamp experiment illustrating the effects of synaptic variability on jitter. A, Spike latency after synaptic conductances in regular, 50 Hz trains (similar to the experiments of Fig. 5). Each horizontal line shows the spike latencies from steady-state pulses 11–40 of a single trial all overlaid, with a small vertical displacement to avoid perfect overlap. Spike latencies have a resolution of 20 μs. The black line at left indicates the time of the peak of the synaptic conductance (Fig. 3A, left, inset). The variability of synaptic conductances was controlled by changing the number of release sites (N_S). Spike latencies were more variable for smaller N_S (i.e., more variable conductance amplitude). The deterministic model had the least jitter. B, Latency histogram of spikes from A. Markers indicate overall mean and SD of the latency. The mean was unaffected by the variability of synaptic conductance, but the SD (i.e., the jitter) increased with decreasing N_S. C, Effect of individual synaptic conductance G_AMPA on spike latency. Spike latency is inversely related to G_AMPA. Thus, variability in synaptic conductance results in variability in spike latency. D, Spike jitter as a function of the number of release sites, from five experiments similar to A–C. E, Trade-off in spike jitter and dynamic range. As dynamic range increases, so does jitter. Jitter data are from D, and dynamic range data are from Figure 5D. The measurements of dynamic range and jitter from current-clamp experiments in Figure 8 are also included for comparison (black +).

We found similar effects in five cells. As the number of release sites in the model increased, spike jitter decreased from 180 ± 20 μs with 15 release sites to just 28 ± 6 μs with the deterministic model (Fig. 7D, p < 0.001 for all pairwise comparisons, F test). Thus, there appear to be two functional effects of changing the number of release sites that counter each other. When the number of release sites decreases, both dynamic range and jitter increase (Fig. 7E). This suggests that there may be a trade-off in these two possible optimizations of synaptic function.

Dynamic range during fiber stimulation

We wanted to verify whether real synapses showed a large dynamic range and whether this might increase jitter, so we also conducted current-clamp experiments using ANF stimulation. We measured EPSP amplitude after ANF stimulation using the first derivative of membrane potential (V′, in V/s; Fig. 8A). Our strategy was to identify spikes by thresholding V′. When there was no spike (e.g., Fig. 8A, stimulation 4), then the EPSP amplitude was taken as the peak in V′. When there was a spike, we tried to isolate a second earlier peak in the second derivative (V″), reflecting the EPSP. It was common to find no second peak, particularly early in stimulus trains when the EPSP is extremely large and merges with the spike (e.g., Fig. 8A, stimulation 1). These stimuli were excluded from further analysis. After depression set in, EPSPs were often clearly distinct from the resulting spike (e.g., Fig. 8A, stimulation 3), and the EPSP amplitude could be unambiguously measured from V′. Sometimes, there was only a partial separation between EPSP and spike in V″, so EPSP amplitude was taken at the time V″ reached a minimum (e.g., Fig. 8A, stimulation 2).

Figure 8.

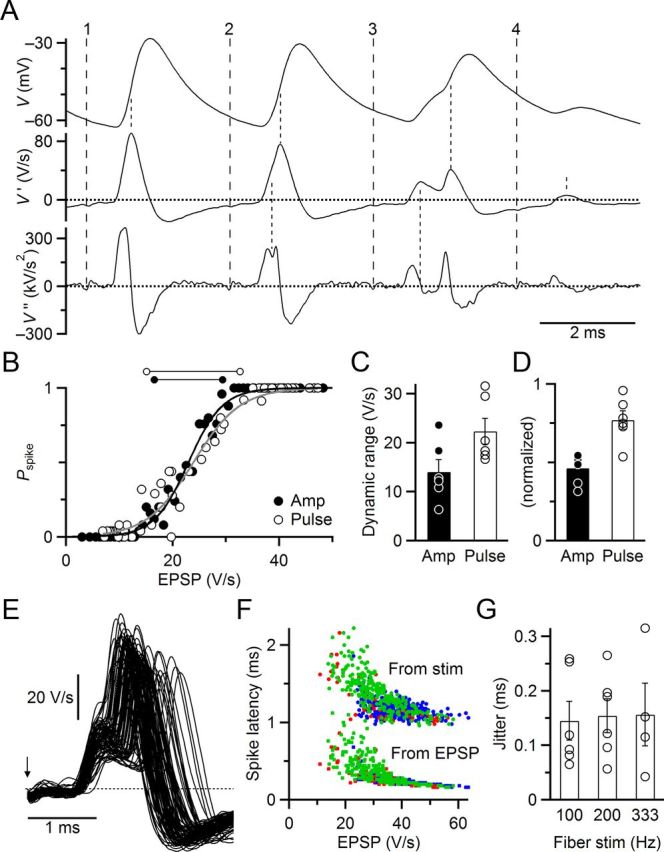
Dynamic range and jitter for real fiber stimulation match dynamic-clamp experiments. A, Measuring EPSP amplitudes. Traces are raw membrane potential (V, top) and first (V′, middle) and second (V″, bottom) derivatives. Broad-dashed lines indicate fiber stimulation times (stimulus artifact was small in this example). Fine-dashed lines indicate times of EPSPs and spikes as used for subsequent analyses. All traces are filtered at 5 kHz. B, Dynamic range. Average P_spike was calculated for individual pulses in trains of 100, 200, and 333 Hz stimulation rates and plotted against the average EPSP amplitude (open circles). This relationship was fit to Equation 1 to estimate the dynamic range (open dumbbells above the plot). To estimate the deterministic dynamic range, we sorted EPSPs by amplitude before calculating P_spike and average EPSP (closed circles). C, Average dynamic ranges from six similar experiments averaging by EPSP amplitude (closed circles, solid bar) or train pulse (open circles, open bar). The increase is statistically significant (p < 0.001, t test). D, Same data as C, but normalized to spike threshold (EPSP_1/2), to facilitate comparison with dynamic-clamp experiments. E, BC spike jitter in the same cell as A and B. All successful spikes are overlaid for pulses 11–20 in 200 Hz trains (86), which cover a wide range of EPSP amplitudes. The EPSP latency is quite constant, whereas spikes are extremely variable. The arrow indicates the stimulus time. F, Spike latency for the same cell as A, B, and E. Latency was measured from the stimulus (upper circles) or the EPSP (lower squares). All spike times are shown for 100 (blue), 200 (green), and 333 (red) Hz stimulation. Both methods indicate that latency is highly inversely dependent on EPSP amplitude. G, Average spike jitter in six experiments for pulses 11–20 of 100, 200, and 333 Hz trains. In two cells, spike probability was too low to measure jitter at 333 Hz stimulation.

We were able to apply this algorithm to 6 of the 7 experiments of Figure 1. We measured the average EPSP as well as P_spike for each pulse in trains of 100, 200, and 333 Hz (Fig. 8B, open circles) and fit to the sigmoidal curve of Equation 1 (substituting EPSP amplitude and EPSP_1/2 in place of G_AMPA and G_1/2), to yield the dynamic range (Fig. 8B, horizontal lines), which was 17.5 V/s in this example. In other words, there was a large change in spike rate as average EPSP varied over a range of 17.5 V/s. This curve was analogous to the “individual” and “stochastic” curves of Figures 3 and 5. We wanted to compare this against the nonrandom case, in essence, to determine how “hard” threshold is. However, with ANF stimulation, we could not control the randomness of neurotransmitter release. Instead, we estimated the dynamic range for nonrandom release using the same approach as in Figure 3F. We sorted all EPSPs by amplitude and binned a number of them together to calculate P_spike (Fig. 8B, closed circles). We fit this relationship using Equation 1 to obtain the dynamic range, which was narrower, 12.8 V/s in this example (horizontal lines in Fig. 8B).

We found similar effects in multiple cells. The dynamic range was wider when considering P_spike for individual pulses in trains (22.3 ± 2.7 V/s, N = 6 cells; Fig. 8C), whereas the dynamic range was significantly narrower when considering simply the efficacy of EPSPs at driving spikes (14.0 ± 2.5 V/s; p < 0.001; Fig. 8C, left). This represents an increase in dynamic range of 71.6 ± 19.0%. We scaled the dynamic range for each cell by the threshold EPSP (EPSP_1/2), which yielded a normalized dynamic range of 0.77 ± 0.6 (Fig. 8D), which is very similar to the dynamic-clamp experiments of Figures 3G (0.66 ± 0.03) and 5B (0.76 ± 0.03). This validates that our dynamic-clamp experiments accurately captured the effects of the randomness of neurotransmitter release. However, the estimate of the nonrandom dynamic range in current-clamp experiments (0.46 ± 0.04) was somewhat larger than in dynamic-clamp experiments (0.2 in Fig. 3G). We attribute this to the fact that conductance amplitudes were specified in the dynamic-clamp experiments, whereas EPSP amplitudes had to be measured in current clamp. Noise in current-clamp recordings would cause errors in measurement of EPSP amplitude, so they would be sorted incorrectly by amplitude, and the binned values of P_spike would tend to be drawn toward 0.5, yielding an overestimate of dynamic range. By contrast, such errors would cancel out when the average amplitude was calculated for individual pulses, and not have any systematic influence on dynamic range. Despite this quantitative difference, it is clear that our current-clamp experiments show the same trend as the dynamic-clamp experiments, that the randomness of neurotransmitter release increases the dynamic range of synapses.

We examined whether the randomness of neurotransmitter release had the same consequences on BC spike latency in current clamp as it did in dynamic clamp (Fig. 7). EPSP latency was very stable during trains of ANF stimulation, but spike latency was quite variable (Fig. 8E). Spike latency showed a strong inverse dependence on EPSP amplitude, whether latency was measured relative to the stimulus (Fig. 8F, circles) or the EPSP (Fig. 8F, squares), similar to dynamic clamp (Fig. 7C). We quantified spike timing jitter during trains of ANF stimulation at 100, 200, and 333 Hz. The jitter in spike timing across all stimuli was considerable, ∼150 μs regardless of stimulation frequency (Fig. 8G). This value was close to the spike jitter in response to physiologically based dynamic clamp stimuli using N_S = 60 (143 ± 21 μs; Fig. 7D,E).

Discussion

We have studied functional implications of the stochastic properties of neurotransmitter release using dynamic and current clamp. Our data strongly suggest that the randomness of EPSP amplitude has implications beyond just revealing the mechanisms underlying neurotransmitter release. This randomness also can play an important role in transmitting information. Our key approach was to apply synaptic conductances using dynamic clamp so that we could precisely control the stochastic and deterministic components independently. We did this using both recorded and modeled synaptic conductances. Both approaches indicated that the stochastic properties of release increase the dynamic range of synapses, when we consider the average synaptic conductance as the input and the probability of spiking as the output. We validated these effects in current-clamp experiments using fiber stimulation, producing an extremely close match with our physiologically based dynamic-clamp experiments (Fig. 7E, compare green, closed symbol and black cross), indicating that this wider dynamic range occurs with real synapses. Our experiments emphasize that it is important to take synaptic variance into account when considering synaptic function. This is particularly true in dynamic-clamp experiments, where using a fixed set of conductances could exaggerate spike reliability.

Spike probability (P_spike) can in principle be used downstream of the synapse to reconstruct more fully the structure of auditory nerve activity. However, this computational benefit comes at a cost because the stochastic properties of presynaptic release also introduce jitter into postsynaptic spike timing, seen in both dynamic clamp and with fiber stimulation. Jitter would be expected to compromise BC function, by degrading precise timing information, and rendering BC spike timing more variable than incoming ANF spikes. Our modeling work suggests that synapses can potentially emphasize dynamic range or timing, by controlling the number of release sites. The dynamic range and jitter shown by BC responses to real ANF activation suggest that endbulbs compromise between these two computational imperatives.

Dynamic range

Our data indicate that spike threshold in BCs is highly stable, with a sharp cutoff for individual EPSPs (Fig. 3F,G). That is, for these cells, fluctuations in resting membrane potential or spike threshold contribute very little to spike variability seen with fiber stimulation (Fig. 1). However, this mechanistic reliability poses a significant problem. For features of complex auditory stimuli that are encoded in closely spaced spikes, this would lead to depressed EPSPs. Depressed EPSPs would reliably fail to drive spiking, thus losing representation of these features in higher stages of the auditory pathway.

The stochastic properties of release provide a solution to this problem. Even EPSPs that are highly depressed on average may randomly score extra quanta on a given stimulus presentation that drive them over threshold, triggering spikes. This allows those stimulus features to be passed along the auditory pathway. A second consequence is that spike probability also decreases for EPSPs that are on average just above threshold. Both effects contribute to an increase in the dynamic range.

We have made two assumptions in our treatment of the dynamic range of the endbulb. The first is that there is information to be gleaned from the average EPSP amplitude that is valuable to sensory processing. We have already considered the value of preserving the presence of subthreshold EPSPs, but it also seems likely that the amplitude of individual EPSPs carries information. In in vitro experiments, EPSP amplitude is robustly influenced by presynaptic spike rate over short and long time-scales, through the various mechanisms of short-term plasticity (Regehr and Stevens, 2001). Thus, EPSP amplitude may carry information about long- and short-term sensory features. Recently, it has been questioned whether this extends to the situation in vivo (Lorteije et al., 2009), where it is difficult to distinguish deterministic from stochastic contributions to EPSP amplitude. These issues deserve further investigation.

The second assumption is that there is a way for spike probability to be read out downstream. For simple, repetitive stimuli, such as long tones, this could be done by downstream neurons integrating over long time periods. For fast, nonrepeating sensory features, it would be necessary for multiple cells to react probabilistically to the same presynaptic activity, and then these cells converge at other sites downstream. This may be occurring in the auditory pathway. Individual ANFs can contact multiple BCs, and BCs receive input from multiple ANFs (Ryugo and Fekete, 1982; Liberman, 1991; Spirou et al., 2005; Cao and Oertel, 2010). The probabilistic responses of BCs may then be integrated at targets, such as neurons in the medial superior olive, which integrate multiple BC inputs (Couchman et al., 2010). The randomness of neurotransmitter release would ensure that some response is preserved at the population level, even during stimuli that cause high depression.

The effects we observe are distinct from stochastic resonance. In stochastic resonance, noise added to a signal leads to improved detectability for small stimuli (Douglass et al., 1993). By contrast, the stochastic properties of neurotransmitter release led to increased spiking for small EPSPs, but also decreased spiking for large EPSPs. Thus, there is no net change in BC spiking over the full range of EPSP amplitude, so EPSPs are not more “detectable” with the addition of the stochastic component.

Timing versus rate codes

We have found an explicit trade-off between timing and rate codes. These codes are often posed as theoretical extremes, but in the auditory system, they both play a role. Precise spike timing carries important information related to the spatial origin of a sound, and spike rate carries information about sound intensity. Our study suggests that synapses could specialize to support the dominant coding strategy. Spike timing is favored by less randomness, whereas spike probability is favored by more randomness. We predict that the degree of randomness at a synapse would provide insight into how information is represented.

Specifically, our model indicates that the degree of randomness at a synapse is greatly affected by the number of release sites or releasable vesicles. Other synaptic properties not incorporated in our model would also contribute to synaptic variability, including calcium channel activity, vesicle glutamate content, and postsynaptic receptor density. Our model did not include these, so the values for numbers of release sites and releasable vesicles are unrealistically low (60 and 3, respectively). If randomness were a problem by generating too much spike jitter, one would predict endbulbs to have many release sites and small mEPSCs. The endbulb has particularly great flexibility in this regard because it is an axosomatic synapse with large surface area. Endbulbs do form many release sites (100–1000) (Ryugo et al., 1996; Nicol and Walmsley, 2002), but they also have relatively large mEPSCs (∼100 pA), which are a significant percentage of EPSC amplitude at steady state (Fig. 2). Thus, endbulbs do not appear to be simply designed to eliminate the effects of randomness for the sake of enhanced spike timing. Rather, the endbulb appears to strike a compromise between precise spike timing and spike probability.

The situation in vivo is likely somewhat more complex because each BC receives multiple converging ANFs (Liberman, 1978; Sento and Ryugo, 1989; Spirou et al., 2005; Cao and Oertel, 2010). Synaptic variability would be expected to increase as EPSPs from different ANFs do or do not overlap at different times during a sound stimulus, potentially increasing jitter yet further. However, the interaction of these multiple inputs is also thought to contribute to reduced jitter in some BCs (Joris et al., 1994; Xu-Friedman and Regehr, 2005a, b; Yang and Xu-Friedman, 2009). Future experiments will be needed to address the full complexity of this situation.