Abstract
Genome sizes and mutation rates covary across all domains of life. In unicellular organisms and DNA viruses, they show an inverse relationship known as Drake’s rule. However, it is still unclear whether a similar relationship exists between genome sizes and mutation rates in RNA genomes. Coronaviruses, the RNA viruses with the largest genomes (∼30 kb), encode a proofreading 3′ exonuclease that allows them to increase replication fidelity. However, it is unknown whether, conversely, the RNA viruses with the smallest genomes tend to show particularly high mutation rates. To test this, we measured the mutation rate of bacteriophage Qβ, a 4.2-kb levivirus. Amber reversion-based Luria–Delbrück fluctuation tests combined with mutant sequencing gave an estimate of 1.4 × 10−4 substitutions per nucleotide per round of copying, the highest mutation rate reported for any virus using this method. This estimate was confirmed using a direct plaque sequencing approach and after reanalysis of previously published estimates for this phage. Comparison with other riboviruses (all RNA viruses except retroviruses) provided statistical support for a negative correlation between mutation rates and genome sizes. We suggest that the mutation rates of RNA viruses might be optimized for maximal adaptability and that the value of this optimum may in turn depend inversely on genome size.
RNA viruses are among the fastest mutating and evolving entities in nature (Domingo 2006; Holmes 2009). However, their mutation rates vary substantially, from 10−6 to 10−4 substitutions per nucleotide per cell infection (s/n/c) (Sanjuán et al. 2010), and little is known about the mechanistic and evolutionary causes of this variability. Among DNA viruses and unicellular organisms, mutation rates vary inversely with genome size, as first noted by Drake (Drake 1991; Drake et al. 1998; Lynch 2010; Sanjuán et al. 2010; Sung et al. 2012). However, evidence supporting a similar relationship for RNA genomes has remained elusive. This may be due to error and bias in mutation rate estimates, use of different estimation methods, or the relatively narrow range of variation in RNA virus genome sizes. Despite this, some indirect observations support this correlation. First, coronaviruses have the largest RNA genomes and are the only RNA virus family for which a 3′-exonuclease proofreading activity has been demonstrated (Minskaia et al. 2006; Eckerle et al. 2007, 2010; Denison et al. 2011; Ulferts and Ziebuhr 2011). Second, there is a weak but significant negative association between genome size and the rate of molecular evolution among RNA viruses (Sanjuán 2012) and, since evolution rates are partly determined by mutation rates, this suggests that the latter may correlate negatively with genome sizes.
Analysis of published mutation rates for 11 different riboviruses (i.e., all RNA viruses except reverse-transcribing viruses) suggested a negative correlation with genome size (Sanjuán et al. 2010). However, this finding has to be taken carefully because its significance depended critically on inclusion of bacteriophage Qβ, the virus with the smallest genome in this data set (4217 bases). The estimate for this phage was based on pioneer work from Domingo et al., who scored a single G → A substitution at position 40 from the 3′ end of the genome, using T1 RNase digestion (Batschelet et al. 1976; Domingo et al. 1976). The calculated mutation rate, 1.1 × 10−3 s/n/c, is the highest reported for an RNA virus (Sanjuán et al. 2010). Extrapolating from a single-nucleotide site, though, can lead to large errors, and the fact that transitions are generally more frequent than transversions makes this value a likely overestimation. Recently, the mutational properties of bacteriophage Qβ were further characterized (García-Villada and Drake 2012). In that study, the read-through gene was redundantly expressed from a plasmid to suppress selection against loss-of-function mutations in this gene. Mutations were first scored phenotypically by plating the virus in bacteria lacking the plasmid and then confirmed by sequencing, giving a mutation rate of 1.8 × 10−5 s/n/c. However, the estimated rate increased by nearly 10-fold when mutations were scored directly by sequencing instead of using a phenotypic screen first.
Therefore, current mutation rate estimates for bacteriophage Qβ range across two orders of magnitude. Use of different estimation methods probably contributes to explaining this high level of uncertainty. For instance, in trans-complementation studies, selection may not be fully removed if the expression level or timing of the plasmid gene copy does not match the wild-type expression profile or if this region of the viral genome contains functional RNA structures or other cis-acting elements. Here, we measured the mutation rate of bacteriophage Qβ as substitutions per nucleotide per round of copying (s/n/r), using the Luria–Delbrück fluctuation test, a standard estimation method that has been used previously for at least six other RNA viruses (Sedivy et al. 1987; Suárez et al. 1992; Schrag et al. 1999; Chao et al. 2002; Furió et al. 2005; de La Iglesia et al. 2012). To do so, we engineered amber mutant viruses that could grow only on an Escherichia coli amber suppressor strain and then scored revertants to a functional codon by assaying for viral growth in nonsuppressor cells. This yielded an estimate of 1.4 × 10−4 s/n/r, the mutation rate per cell (s/n/c) being probably very similar because the phage undergoes approximately one replication cycle per cell. This value was confirmed by a direct plaque sequencing approach in which a larger genome region was analyzed. Careful analysis of potential sources of error or bias in our data and in previously published estimates strongly suggests that the average mutation rate of bacteriophage Qβ is probably close to 10−4 s/n/c, and comparison with other riboviruses supports the existence of a negative correlation between mutation rates and genome sizes.
Materials and Methods
Creation of amber mutants
The infectious clone pBRT7Qβ, originally provided by René C. Olsthoorn (Leiden University), was used as a template for introducing UAG codons by site-directed mutagenesis. To do so, full-length PCR amplicons were obtained from 500 pg of template, using Phusion high-fidelity DNA polymerase (New England Biolabs, Beverly, MA) and a pair of adjacent, divergent, 5′-phosphorylated primers, one of which carried the desired nucleotide substitution. PCR products were circularized with Quick T4 ligase (New England Biolabs) and used to electro-transfect E. coli K12 F– competent cells (TOPO cloning kit; Invitrogen, Carlsbad, CA). Transformant colonies were grown in liquid cultures and used for purifying the mutant pBRT7Qβ by standard miniprep. Then, χ225 cells (Coli Genetic Stock Center strain 6529) expressing an amber suppressor Gln tRNA were electro-transfected, plated on top agar, and incubated at 37° overnight. Plaques were resuspendend in LB, and the presence of the UAG codon was verified by plating in χ225 vs. nonsuppressor E. coli F+ cells obtained from J. J. Bull [strain IJ1862 (Bull et al. 2004)]. Only plaques showing a titer ratio <1/1000 in nonsuppressor/suppressor cells were used for fluctuation tests. This ensured that the initial frequency of UAG revertants was < 1/1000.
Luria–Delbrück fluctuation tests
The titer of each amber mutant phage was adjusted to 105 plaque-forming units (pfu)/ml and 15 ml of χ225 cells was inoculated with 103 pfu. Cultures were thoroughly mixed, immediately split into 24 aliquots of 0.5 ml containing on average = 33 pfu each, and incubated for 2 hr in a Thermomix (Eppendorf) shaker at 37° at 650 rpm. To check , the inoculum was diluted 1/10 and plated on χ225 cells. Since < 1/1000, we expected <33 × 24/1000 = 0.8 initial revertants in each entire fluctuation test. To also check this, 10 µl of the undiluted inoculum (103 pfu) was plated on IJ1862 cells in triplicate. The 24 parallel cultures were placed on ice after the 2-hr incubation time to stop viral growth and centrifuged twice to remove cells. Then, 6/24 randomly chosen supernatants were used to estimate the final total number of pfu () by plating on χ225 cells, and 400 µl of each of the 24 cultures (80% of total supernatant volume) was plated on IJ1862 cells. In 4/216 cultures, there were >100 revertants, and these were excluded from mutation rate calculations because we could not rule out that revertants were already present in the inoculum. However, their inclusion had a minimal impact on the results. Since mutation is a rare and random event, the number of mutational events per culture was assumed to follow a Poisson distribution, such that the probability of observing no mutants is , where P denotes the Poisson distribution and m is the reversion rate. The fraction of cultures containing no mutants was determined for each test and the reversion rate was calculated as , where is the average of the six values (null-class method).
Correction for incomplete plating in fluctuation tests
The null-class method assumes that all the culture is tested on the selective medium (IJ1862 cells). When only a fraction z is plated, the probability of not observing mutants can be written as , where is the probability of k actual mutants in the culture. Here, we plated only 80% of the supernatant volume, and cell-bound particles were removed by centrifugation. In a pilot experiment, we determined that centrifugation reduced the viral titer by a factor of 0.78, which means that the estimated fraction of the total culture being actually plated is z = 0.8 × 0.78 = 0.62. In our tests, we had typically , implying that viral growth was essentially restricted to one cell infection cycle, because the burst size of bacteriophage Qβ and other leviviruses is on the order of ≥103 pfu (De Paepe and Taddei 2006; García-Villada and Drake 2012). Also, the replication of Qβ conforms to a stamping-machine model (García-Villada and Drake 2012) such that there is essentially only one replication cycle per cell. Therefore, the number of mutants should be approximately equal to the number of mutation events, and we thus assumed , where z′ is a correction factor for incomplete plating in the determination. Here, z′ = 0.78 because this titration was affected by centrifugation only. We numerically solved m given , , , z, and z′. After implementing this correction m-values increased only very slightly and, even assuming a plating fraction as low as z = 0.05, estimates changed less than twofold (not shown).
Correction for selection bias in fluctuation tests
If amber suppression was not fully efficient, revertant viruses would have higher fitness than amber mutants in χ225 cells, thus inflating revertant counts and mutation rate estimates. However, this bias should be small for two reasons: first, as indicated above, viral growth was essentially restricted to one cell infection cycle and, in this first cycle, viral RNA genomes carrying reversions in the amber codon genomes should share proteins with nonrevertant RNAs from the same cell and thus should have no fitness advantage. Second, the null-class method is in principle insensitive to fitness differences because it scores the probability of no reversion and, obviously, selection cannot act until revertants appear. However, since plating was not fully efficient (see above), some cultures may have contained undetected revertants. The probability of detecting one or more mutants depends on actual revertant counts, which in turn depend on their relative fitness. Hence, selection may affect the null-class estimate when there is incomplete plating. If progeny sizes are assumed to be Poisson distributed and the revertant has an excess progeny R (assumed integer) over the amber mutant, then for k > 0 we have . To quantify R, we performed competition assays between one of the amber mutants (am1067) and its revertants. Exponentially growing χ225 cells were inoculated with 104 pfu of each virus and after 2 hr 45 min of incubation, cells were removed by centrifugation and supernatants were plated on χ225 and IJ1862 cells. The former plating indicated the total viral titer, whereas the latter indicated the revertant titer. Fitness was calculated as the growth rate difference; i.e., , where and are the revertant to amber mutant titer ratios at inoculation and harvesting, respectively. Based on eight independent fitness assays, revertants were found to be fitter than the amber mutant, the growth rate difference being w = (0.34 ± 0.18) hr–1. Therefore, after the 2-hr incubation time used in fluctuation tests, the excess progeny of revertants should be = 3.72 ± 1.54. We assumed R = 4 and numerically solved m given , , , z, z′, and R.
Plaque sequencing
Plaques were picked from independent cultures, resuspended in 50 µl of LB, and used for RT-PCR and sequencing. The RT was carried out with MMLV reverse transcriptase directly from 2 µl of plaque suspension, and 2.5 µl of cDNA was then used for PCR amplification with Phusion DNA polymerase. PCR products were sequenced by the Sanger method and analyzed with the Staden package (http://staden.sourceforge.net).
Correction for selection in plaque sequences
As shown in previous work (Sanjuán et al. 2010), observed mutation frequencies f can be transformed into mutation rates µ (s/n/c), using the empirically characterized distribution of mutational fitness effects of random single-nucleotide substitutions. We did so by simulating the effects of mutation and selection. For simplicity, we modeled mutational fitness effects, s, using an exponential distribution truncated at plus a class of lethal mutations occurring with probability pL; that is, if 0 < s < 1, if s = 1, and otherwise. In previous work, mutational fitness effects in bacteriophage Qβ were measured as growth rate ratios, , where r is the exponential growth rate and subscripts i and 0 refer to the mutant and wild type, respectively (Domingo-Calap et al. 2009). These s-values can be transformed to fitness effects s′ per cell infection (our unit of interest) as , where B is the burst size. After simulating fitness effects using the truncated exponential plus lethal model and converting them to per cell infection units, selection was applied by picking individuals for the next cell infection cycle with weighted probability 1 – s′. Genetic drift was ignored since it should not modify the expected value of f. Also, for simplicity, mutations were assumed to have independent fitness effects (no epistasis) and back mutations were ignored, which seems reasonable in the short term, when single forward mutations will greatly outnumber secondary and back mutations. This simulation was performed with Wolfram Mathematica. A graphical representation is shown in Figure 1 of Sanjuán et al. (2010).
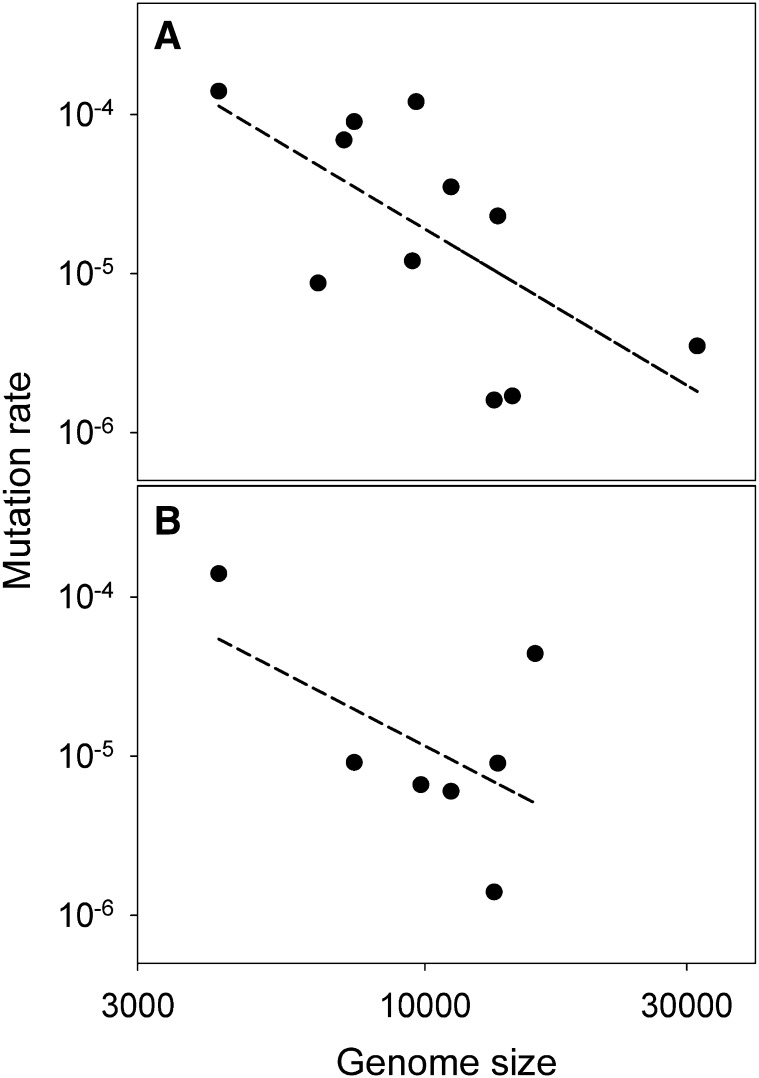
Figure 1.
(A) Mutation rate (s/n/c) vs. genome size in riboviruses. From left to right, data points correspond to bacteriophage Qβ (this study), tobacco mosaic virus, human rhinovirus 14, poliovirus 1, tobacco etch virus, hepatitis C virus, vesicular stomatitis virus, bacteriophage φ6, influenza A virus, influenza B virus, and murine hepatitis coronavirus (reviewed in Sanjuán et al. 2010). The dashed least-squares regression line has slope –2.06 ± 0.79. (B) Mutation rates (s/n/r) from Luria–Delbrück tests vs. genome size in riboviruses. From left to right, data points correspond to bacteriophage Qβ (this study), poliovirus 1, turnip mosaic virus, vesicular stomatitis virus, bacteriophage φ6, influenza A virus, and measles virus (reviewed in Sanjuán et al. 2010). For turnip mosaic virus, it was estimated that the rate of appearance of mutants escaping an artificial microRNA was 5.55 × 10−5 s/r (de La Iglesia et al. 2012). Assuming that escape was conferred by every single substitution in the 21-nucleotide micro RNA target, and assuming that ∼40% of such substitutions are lethal to the virus as in other plant viruses (Carrasco et al. 2007), = 21 × 3 × 0.4 = 25.2 and the per-nucleotide mutation rate is µ = 5.55 × 10−5 × 3 / 25.2 = 6.6 × 10−6 s/n/r. The dashed least-squares regression line is shown and has slope –1.79 ± 1.23.
Results
Fluctuation tests
We used site-directed mutagenesis to engineer three different mutants, each carrying a single CAG → UAG substitution, which converts Gln into an amber (am) stop codon. The mutated genome positions (432, 696, and 1067) mapped to the A2 maturation protein. For each mutant, we performed three independent Luria–Delbrück fluctuation tests to determine the rate at which the UAG codon reverted to other, viable, codons. For each test, 24 parallel cultures of E. coli cells encoding a Gln amber suppressor tRNA (χ225 cells) were inoculated with a small number () of pfu each, incubated until pfu were produced (2 hr incubation), and assayed for revertants by plating on nonsuppressor cells. The results are shown in Table 1. The average rates of reversion estimated by the null-class (P0) method were m = (8.1 ± 2.9) × 10−5, m = (9.3 ± 1.5) × 10−5, and m = (9.4 ± 2.6) × 10−5 for sites 432, 696, and 1067, respectively. The per-nucleotide mutation rate expressed as s/n/r can be obtained as (Sanjuán et al. 2010), where the factor 3 stands for the number of possible nucleotide substitutions per site and is the mutational target size (total number of viable substitutions leading to the revertant phenotype). To determine we sequenced >20 independent revertant plaques for each of the amber mutants (Table 2). This revealed that, in addition to the UAG → CAG reversion, there were other codons restoring the ability to grow in nonsuppressor cells. In total, six of the eight possible nucleotide substitutions transforming UAG into a sense codon were observed, although the UAG → CAG reversion was the most abundant. The numbers of different substitutions observed at sites 432, 696, and 1067 were 5, 3, and 1. Using these Ts-values, the mutation rate estimates are μ = 4.9 × 10−5, μ = 9.3 × 10−5, and μ = 2.8 × 10−4 s/n/r for each of the three sites, respectively. The mutation rate, averaged across the three sites, is thus μ = (1.4 ± 0.7) × 10−4 s/n/r.
Table 1. Results from Luria–Delbrück fluctuation tests.
| am432 | am696 | am1067 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Fluctuation testa | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 |
| (pfu)b | 24.1 | 24.7 | 24.9 | 13.0 | 63.3 | 12.0 | 34.6 | 17.1 | 39.0 |
| Initial revertants (pfu)c | 0.00 | 0.27 | 0.53 | 0.00 | 0.27 | 0.00 | 7.2 | 0.40 | 0.80 |
| × 10−3 (pfu)d | 8.39 | 5.69 | 6.47 | 14.3 | 11.6 | 3.19 | 11.4 | 1.63 | 6.21 |
| × 10−3 (pfu)e | 2.18 | 2.25 | 4.28 | 4.85 | 6.15 | 2.67 | 4.69 | 1.18 | 4.07 |
| Cultures with no revertants | 9 | 21 | 12 | 9 | 6 | 18 | 13 | 20 | 11 |
| Cultures with 1 revertant | 7 | 3 | 6 | 5 | 6 | 4 | 6 | 3 | 7 |
| Cultures with 2 revertants | 3 | 0 | 3 | 4 | 6 | 2 | 1 | 1 | 4 |
| Cultures with 3 revertants | 1 | 0 | 2 | 2 | 1 | 0 | 0 | 0 | 0 |
| Cultures with 4–100 revertants | 3 | 0 | 1 | 4 | 5 | 0 | 1 | 0 | 2 |
| Cultures with >100 revertants | 1 | 0 | 0 | 0 | 0 | 0 | 3 | 0 | 0 |
| P0f | 9/23 | 21/24 | 12/24 | 9/24 | 6/24 | 18/24 | 13/21 | 20/24 | 11/24 |
| Reversion rateg m × 104 | 1.1 | 0.24 | 1.1 | 0.69 | 1.2 | 0.90 | 0.42 | 1.1 | 1.3 |
| Reversion rateh × 104 | 4.4 | 0.60 | 1.6 | 2.0 | 2.3 | 1.1 | 1.0 | 1.6 | 1.9 |
| Reversion ratei m(z) × 104 | 1.4 | 0.29 | 1.3 | 0.86 | 1.5 | 1.1 | 0.53 | 1.4 | 1.6 |
| Reversion ratej m(z, R) × 104 | — | — | — | — | — | — | 0.34 | 0.91 | 1.0 |
Each test consisted of 24 parallel cultures.
As determined from three independent titrations of the inoculum.
Expected initial number of revertants in 24 cultures as determined from three independent titrations of the inoculum.
Arithmetic mean of obtained from 6/24 random cultures.
Harmonic mean of obtained from the same random cultures.
Fraction of cultures showing no revertants, excluding cultures with >100 revertants from the total.
.
.
Correction for incomplete plating using a numerically estimated , where .
Correction for incomplete plating and selection, using a numerically estimated , where . R was quantified only for am1067 and its CAG revertant by fitness assays. For am432 and am696 selection bias should be lower, because probably the fittest revertants were those carrying the wild-type CAG codon.
Table 2. Genetic changes found in revertant plaques for each of the three amber mutants studied.
| Mutation | am432 | am696 | am1067 |
|---|---|---|---|
| UAG → CAG (Gln) | 16 | 14 | 20 |
| UAG → AAG (Lys) | 1 | 0 | 0 |
| UAG → GAG (Glu) | 1 | 0 | 0 |
| UAG → UGG (Trp) | 3 | 0 | 0 |
| UAG → UCG (Ser) | 0 | 9 | 0 |
| UAG → UUG (Leu) | 0 | 0 | 0 |
| UAG → UAC (Tyr) | 1 | 0 | 0 |
| UAG → UAU (Tyr) | 0 | 2 | 0 |
| Observed Ts | 5 | 3 | 1 |
To ascertain the reliability of our estimate, we considered several sources of error and bias. First, differences in titer among cultures introduce variance in . For each culture j, we have because . Thus, we recalculated the average reversion rate as , where subindex H denotes the harmonic mean. Second, incomplete plating of total and/or revertant viruses should reduce the probability of detecting revertants and thus lead us to underestimate the mutation rate. This was dealt with by calculating the probability of observing no mutants (P0) given that only a fraction z was plated (see Materials and Methods for details). Third, inefficient suppression of amber mutants could confer a fitness advantage to revertants in χ225 cells and therefore lead us to overestimate the mutation rate. To quantify this effect, we performed competition assays between am1067 and its CAG revertant, estimated the expected excess progeny of revertants produced by selection, and recalculated reversion rates accordingly (see Materials and Methods for details). The m-values after correcting for each of the above sources of error or bias are shown in Table 1. Additionally, our results may be affected by uncertainties in . If some substitutions were selectively neutral but occurred at very low rates, they may not be observed in plaque sequences but should be included in anyway. In the most extreme case, we should use if all substitutions at each of the three UAG sites except UAG → UAA were neutral. However, this is an unlikely scenario, because most single-point mutations are deleterious or lethal in bacteriophage Qβ (Domingo-Calap et al. 2009). Therefore, most of the unobserved substitutions were probably selected against rather than occurring at low rates, as also supported by the fact that the most frequent substitution was always the reversion to the wild-type CAG codon.
Direct sequencing
The above mutation rate estimate was based on analysis of three codons only, making extrapolation to other genome sites risky. To obtain an independent estimate based on more sites, we used a direct sequencing approach. We infected 48 E. coli χ225 cultures with the am1067 mutant, setting = 30 and = 3.1 × 104 pfu; plated each culture in nonsuppressor cells; picked one plaque per culture; and sequenced genome positions 890–1489 (reference GenBank accession no. GQ153931). As expected, the UAG → CAG reversion was present in 47/48 plaques (the plaque with no reversion was discarded), and 1/47 plaques had an additional synonymous substitution, U1024C. It has been previously suggested that mutations in RNA viruses tend to be clustered in hypermutated genomes and that, as a result, plaques already showing one mutation (UAG → CAG) should be enriched in additional mutations (Drake et al. 2005; García-Villada and Drake 2012). To test whether this may affect our results, we also plated each of the 48 cultures in χ225 amber suppressor cells and picked one plaque per culture. After sequencing the same region as above, we found that none of the 48 plaques showed any mutation in the UAG codon and 2/48 plaques showed mutations at other sites (T1431C and C1213T, both synonymous). Therefore, mutation frequency does not seem to depend on whether amber mutants or revertants were scored. Pooling all data and dividing the number of mutations by the size of the sequenced fragment and the number of plaques sequenced yields a mutation frequency f = 3/600/95 = 5.26 × 10−5. Since , viral growth was limited to approximately one cell infection cycle. However, this f-value should be lower than the per-cell-infection mutation rate, because selection acts against deleterious mutations, as strongly suggested by the fact that all three substitutions were synonymous.
Since we have previously characterized the distribution of mutational fitness effects in this same phage (Domingo-Calap et al. 2009), it is possible to correct the effect of selection. In this previous study, of 42 random single-nucleotide substitutions obtained by site-directed mutagenesis, 29% were lethal, viable mutations reduced fitness (defined as the growth rate ratio) by 10.3% on average, and the distribution of mutational fitness effects for nonlethals was reasonably well described by an exponential model. Simulation of a mutation–selection process based on these values and for a burst size of 103 pfu indicates that ∼40% of spontaneous mutations produced should be observed after one generation (see Materials and Methods for details). Therefore, the estimated mutation rate after correcting for selection is f /0.4, or μ = 1.3 × 10−4 s/n/c.
Discussion
Mutation rate of bacteriophage Qβ
Our fluctuation tests based on scoring amber revertants yielded a mutation rate of 1.4 × 10−4 s/n/r with a reasonable confidence interval of less than twofold. The mutation rate per cell infection cycle (s/n/c) should be similar because the replication mode of this phage is essentially stamping machine-like (García-Villada and Drake 2012), and thus there should be only one replication cycle per cell. We also obtained an independent mutation rate estimate by direct plaque sequencing, which gave μ = 1.3 × 10−4 s/n/c after correcting for selection, in full agreement with the fluctuation test results.
Recently, García-Villada and Drake (2012) reported several mutation rate estimates for bacteriophage Qβ. First, after growing the virus in cells that expressed the read-through gene from a plasmid (RTH cells) and scoring for mutants with nonsense mutations in the viral gene copy, the authors obtained μ = 1.8 × 10−5 s/n/c. An important assumption behind this estimate is that it was possible to efficiently suppress selection against premature stop codons by trans-complementation. However, in that same study, it was shown that a mutant carrying a nonfunctional read-through gene produced 2.9 times fewer progeny per infection cycle than the wild-type phage in RTH cells, contradicting the above assumption. Second, the intraplaque variability of the isolated mutants was analyzed by direct sequencing of the read-through gene. This yielded a mutation frequency f = 6.80 × 10−5, which is very similar to our estimate also obtained by plaque sequencing (f = 5.26 × 10−5). Applying the same selection correction as above, we would have μ = f/0.4 = 1.7 × 10−4 s/n/c, a value nearly 10 times higher than the one obtained by scoring stop codons in RTH cells. According to García-Villada and Drake, the direct-sequencing estimate was inflated by transitory bouts of hypermutation. Because sequences were obtained from plaques that already contained at least one mutation (loss-of-function of the read-through gene), they would be more likely to belong to hypermutated genomes and thus carry additional mutations. However, the authors found no genetic changes in the polymerase of the phage that may explain hypermutation. Also, our plaque sequencing experiments were not consistent with this claim, since amber revertants and nonrevertants showed similar frequencies of additional mutations (1/47 and 2/48, respectively). We conclude that the simplest explanation for the discrepancy between the two estimates obtained by García-Villada and Drake is that selection against stop codons in the viral read-through gene was not fully supressed by trans-complementation. Finally, these authors also performed a third set of experiments in which, similar to our fluctuation tests, a read-through nonsense mutant was grown in trans-complementing (RTH) cells and scored for revertants. This gave a reversion rate of m = 2.5 × 10−5 but, since the mutational target size Ts was not determined, the corresponding per-nucleotide mutation rate is uncertain.
Taking into account the above considerations, the most likely mutation rate for bacteriophage Qβ should be on the order of 10−4 s/n/c. Alternatively, instead of focusing on our own preferred value, we may just consider all estimates available for this phage (s/n/c): 1.1 × 10−3 (Batschelet et al. 1976; Domingo et al. 1976), 1.8 × 10−5 (García-Villada and Drake 2012), 1.7 × 10−4 (García-Villada and Drake 2012) (with a correction for selection), 1.4 × 10−4 (this study), and 1.3 × 10−4 (this study). Giving all of them equal weight, the geometric mean is 1.4 × 10−4. Therefore, we again reach the conclusion that the mutation rate of Qβ is on the order of 10−4 s/n/c. Furthermore, pooling different estimates each based on a few genome sites overcomes problems associated with mutation rate site and base dependency.
Correlation between mutation rate and genome size among riboviruses
Using µ = 1.4 × 10−4 s/n/c and the rates reported in Sanjuán et al. (2010) for 10 other riboviruses, there is a negative correlation between genome size and mutation rate that is statistically significant in log-scale (Figure 1A; Pearson r = –0.655, P = 0.029). Another way to test for this correlation is to consider only estimates that were obtained using Luria–Delbrück fluctuation tests (expressed as s/n/r). This increases methodological consistency but reduces the data set to six riboviruses only, in addition to the estimate for bacteriophage Qβ. In this case, the correlation with genome size is again negative, but not significant (Figure 1B; r = –0.546, P = 0.205). However, the statistical power is lower due to the smaller size of the data set and to the narrower range of variation in genome size. Alternatively, some viruses may truly deviate from the correlation. For instance, measles virus shows an estimated mutation rate higher than expected from its genome size, and after removal of this single data point the correlation becomes significant again (r = –0.882, P = 0.020). It is also important to note that the above correlation is strongly determined by the bacteriophage Qβ single data point. Estimates for other RNA viruses of similarly small genome size, such as phages MS2 and NL95, would be required for concluding generality. On the other hand, the correlation is also supported by the presence of 3′-exonuclease activity in coronaviruses (Minskaia et al. 2006; Eckerle et al. 2010; Denison et al. 2011; Ulferts and Ziebuhr 2011) and the negative association between genome size and the rate of evolution in RNA viruses (Sanjuán 2012). Therefore, different lines of evidence support mutation rate dependency on genome size, extending Drake’s rule to riboviruses.
However, there appear to be some differences between riboviruses and DNA viruses or microorganisms. First, the correlation is noisier for riboviruses. As mentioned above, this could be due to the smaller range of variation in ribovirus genome sizes or to measurement error, but it also may indicate that there are additional factors determining mutation rates. For instance, in single-stranded (ss)(+)RNA viruses, the genomic RNA is used directly as mRNA whereas in ss(–)RNA and double-stranded (ds)RNA viruses it needs to be transcribed first and is generally tightly bound by nucleoproteins. As a result, ss(+)RNA might be more exposed to RNA damage or host-mediated editing. Although there is at present no empirical evidence supporting an effect of genome polarity on mutation rate, it is notable that the lowest rate among riboviruses corresponds to the dsRNA bacteriophage φ6, despite its genome size being less than half of those of coronaviruses. Another potentially interesting difference between riboviruses and DNA viruses or microorganisms is in the slope of the log-log linear regression relating mutation rates and genome sizes. The latter show an inverse relationship with slope –1 in log-log scale, such that the genomic mutation rate remains approximately constant (Drake 1991; Drake et al. 1998; Lynch 2010; Sung et al. 2012). In contrast, in riboviruses, the log-log slope is more negative (Figure 1).
Mutation rate evolution
How the evolutionary factors acting on mutation rates may produce a correlation with genome size remains to be elucidated, and the answer may depend on the group of organisms considered. Since new mutations are more likely to be deleterious than beneficial, increasing the mutation rate tends to reduce the average fitness of the population in the short term and, therefore, natural selection should favor the lowest possible mutation rate (Kimura 1967; Johnson 1999; Sniegowski et al. 2000; André and Godelle 2006). However, there are several factors that may contribute to elevating the mutation rate: first, genotypes with high mutation rates are more likely to produce beneficial mutations and, thus, mutator alleles may be indirectly selected (Sniegowski et al. 1997; Giraud et al. 2001; de Visser 2002). Assuming that only genotypes free of deleterious mutations can reach fixation, infinite asexual populations should maximize their adaptability for a genomic mutation rate U* = sH, where is the harmonic mean of selection coefficients against deleterious mutations (Orr 2000). However, if beneficial mutations are sufficiently strong to offset the effect of deleterious mutations, then U* = sb, where sb is the selection coefficient favoring beneficial mutations (Johnson and Barton 2002). Simulation studies have shown that natural selection can favor higher U when the strength, proportion relative to deleterious mutations, or supply (through changes in population size) of beneficial mutations increases, although this result is dependent on population structure (Jiang et al. 2010) and the topology of the fitness landscape (Clune et al. 2008). Other studies have shown that selection may favor the maintenance of some level of genetic variability in the population such that long-term evolvability is ensured (Barton 1995; Hayden et al. 2011; Wagner 2011). A second factor that may prevent mutation rates from plummeting is the cost of maintaining replication fidelity mechanisms (Dawson 1998; Sniegowski et al. 2000). For instance, it has been suggested that intrinsic fidelity or proofreading may negatively affect fitness in very small genomes such as those of some viruses by reducing replication speed (Furió et al. 2005, 2007). Third, genetic drift sets a limit on the ability of natural selection to minimize mutation rates. This is because, as the mutational load becomes smaller, the fixation probability of changes leading to further increases in fidelity becomes comparable to that of other, random changes. This “drift barrier” is determined by the inverse effective population size, 1/Ne (Lynch 2011; Sung et al. 2012).
How mutational load, beneficial mutations, the cost of fidelity, and the drift barrier combine to produce an evolutionarily stable mutation rate in each organism remains to be investigated. Several hints, however, suggest that riboviruses replicate close to the optimal mutation rate defined by the balance between deleterious and beneficial mutational fitness effects (U*). First, slightly elevating the mutation rate with chemical mutagens produces drastic fitness losses in a wide variety of RNA viruses, indicating that these viruses replicate close to the maximum allowable mutational load (Anderson et al. 2004; Domingo 2006) and suggesting that such high mutation rates should be maintained by some selective pressure or functional constraints. Second, the rate of molecular evolution in nature increases less than linearly with the mutation rate and appears to stagnate in ssRNA viruses and reverse-transcribing viruses, suggesting that their mutation rates are close to maximizing evolvability (Sanjuán 2012). Third, it has been shown that polymerase variants producing slight replication fidelity increments or reductions have lower fitness or virulence than the wild type in polioviruses (Pfeiffer and Kirkegaard 2005; Vignuzzi et al. 2006; Gnadig et al. 2012) and alphaviruses (Coffey et al. 2011). If mutation rates were determined by the balance between deleterious mutation and adaptability, riboviruses may satisfy U = sH or U = sb and per-site mutation rates would then show an inverse relationship with genome sizes, provided that sH or sb varies little among riboviruses. It is also possible that the smallest ribovirus genomes may be mutationally less robust because of their small genetic redundancy and frequent multifunctional or overlapping genes. Therefore, sH and sb would increase in smaller genomes, potentially explaining why mutation rates disproportionately decrease with increasing genome size in riboviruses.
The factors determining mutation rate evolution in DNA viruses and, thus, Drake’s rule, may differ from those acting on riboviruses. DNA viruses show lower per-nucleotide and per-genome mutation rates (Sanjuán et al. 2010), slower adaptation and molecular evolution (Duffy et al. 2008), and better tolerance to chemical mutagenesis (Springman et al. 2009; Domingo-Calap et al. 2012) than RNA viruses, suggesting that their mutation rates are far below the value that maximizes adaptability. Therefore, Drake’s rule may be a result of the interplay between mutational loads, the costs of fidelity, and the drift barrier.
Acknowledgments
We thank René Olsthoorn and Jim Bull for the virus and cells and members of the laboratory for technical assistance and useful comments. This work was supported by grants from the Spanish Ministerio de Economía y Competitividad (BFU2011-25271) and the European Research Council (ERC-2011-StG- 281191-VIRMUT).
Footnotes
Communicating editor: J. J. Bull
Literature Cited
- Anderson J. P., Daifuku R., Loeb L. A., 2004. Viral error catastrophe by mutagenic nucleosides. Annu. Rev. Microbiol. 58: 183–205. [DOI] [PubMed] [Google Scholar]
- André J. B., Godelle B., 2006. The evolution of mutation rate in finite asexual populations. Genetics 172: 611–626. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barton N., 1995. A general model for the evolution of recombination. Genet. Res. 65: 123–145. [DOI] [PubMed] [Google Scholar]
- Batschelet E., Domingo E., Weissmann C., 1976. The proportion of revertant and mutant phage in a growing population, as a function of mutation and growth rate. Gene 1: 27–32. [DOI] [PubMed] [Google Scholar]
- Bull J. J., Badgett M. R., Springman R., Molineux I. J., 2004. Genome properties and the limits of adaptation in bacteriophages. Evolution 58: 692–701. [DOI] [PubMed] [Google Scholar]
- Carrasco P., de la Iglesia F., Elena S. F., 2007. Distribution of fitness and virulence effects caused by single-nucleotide substitutions in Tobacco Etch virus. J. Virol. 81: 12979–12984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chao L., Rang C. U., Wong L. E., 2002. Distribution of spontaneous mutants and inferences about the replication mode of the RNA bacteriophage φ6. J. Virol. 76: 3276–3281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clune J., Misevic D., Ofria C., Lenski R. E., Elena S. F., et al. , 2008. Natural selection fails to optimize mutation rates for long-term adaptation on rugged fitness landscapes. PLoS Comput. Biol. 4: e1000187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coffey L. L., Beeharry Y., Bordería A. V., Blanc H., Vignuzzi M., 2011. Arbovirus high fidelity variant loses fitness in mosquitoes and mice. Proc. Natl. Acad. Sci. USA 108: 16038–16043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dawson K. J., 1998. Evolutionarily stable mutation rates. J. Theor. Biol. 194: 143–157. [DOI] [PubMed] [Google Scholar]
- de la Iglesia F., Martínez F., Hillung J., Cuevas J. M., Gerrish P. J., et al. , 2012. Luria-Delbruck estimation of turnip mosaic virus mutation rate in vivo. J. Virol. 86: 3386–3388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Paepe M., Taddei F., 2006. Viruses’ life history: towards a mechanistic basis of a trade-off between survival and reproduction among phages. PLoS Biol. 4: e193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Visser J. A., 2002. The fate of microbial mutators. Microbiology 148: 1247–1252. [DOI] [PubMed] [Google Scholar]
- Denison M. R., Graham R. L., Donaldson E. F., Eckerle L. D., Baric R. S., 2011. Coronaviruses: an RNA proofreading machine regulates replication fidelity and diversity. RNA Biol. 8: 270–279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Domingo, E., 2006 Quasispecies: Concept and Implications for Virology, Springer-Verlag, Berlin/Heidelberg, Germany/New York. [Google Scholar]
- Domingo E., Flavell R. A., Weissmann C., 1976. In vitro site-directed mutagenesis: generation and properties of an infectious extracistronic mutant of bacteriophage Qbeta. Gene 1: 3–25. [DOI] [PubMed] [Google Scholar]
- Domingo-Calap P., Cuevas J. M., Sanjuán R., 2009. The fitness effects of random mutations in single-stranded DNA and RNA bacteriophages. PLoS Genet. 5: e1000742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Domingo-Calap P., Pereira-Gómez M., Sanjuán R., 2012. Nucleoside analogue mutagenesis of a single-stranded DNA virus: evolution and resistance. J. Virol. 86: 9640–9646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drake J. W., 1991. A constant rate of spontaneous mutation in DNA-based microbes. Proc. Natl. Acad. Sci. USA 88: 7160–7164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drake J. W., Charlesworth B., Charlesworth D., Crow J. F., 1998. Rates of spontaneous mutation. Genetics 148: 1667–1686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drake J. W., Bebenek A., Kissling G. E., Peddada S., 2005. Clusters of mutations from transient hypermutability. Proc. Natl. Acad. Sci. USA 102: 12849–12854. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duffy S., Shackelton L. A., Holmes E. C., 2008. Rates of evolutionary change in viruses: patterns and determinants. Nat. Rev. Genet. 9: 267–276. [DOI] [PubMed] [Google Scholar]
- Eckerle L. D., Lu X., Sperry S. M., Choi L., Denison M. R., 2007. High fidelity of murine hepatitis virus replication is decreased in nsp14 exoribonuclease mutants. J. Virol. 81: 12135–12144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eckerle L. D., Becker M. M., Halpin R. A., Li K., Venter E., et al. , 2010. Infidelity of SARS-CoV Nsp14-exonuclease mutant virus replication is revealed by complete genome sequencing. PLoS Pathog. 6: e1000896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Furió V., Moya A., Sanjuán R., 2005. The cost of replication fidelity in an RNA virus. Proc. Natl. Acad. Sci. USA 102: 10233–10237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Furió V., Moya A., Sanjuán R., 2007. The cost of replication fidelity in human immunodeficiency virus type 1. Proc. Biol. Sci. 274: 225–230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- García-Villada L., Drake J. W., 2012. The three faces of riboviral spontaneous mutation: spectrum, mode of genome replication, and mutation rate. PLoS Genet. 8: e1002832. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giraud A., Matic I., Tenaillon O., Clara A., Radman M., et al. , 2001. Costs and benefits of high mutation rates: adaptive evolution of bacteria in the mouse gut. Science 291: 2606–2608. [DOI] [PubMed] [Google Scholar]
- Gnadig N. F., Beaucourt S., Campagnola G., Borderia A. V., Sanz-Ramos M., et al. , 2012. Coxsackievirus B3 mutator strains are attenuated in vivo. Proc. Natl. Acad. Sci. USA 109: E2294–E2303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hayden E. J., Ferrada E., Wagner A., 2011. Cryptic genetic variation promotes rapid evolutionary adaptation in an RNA enzyme. Nature 474: 92–95. [DOI] [PubMed] [Google Scholar]
- Holmes, E. C., 2009 The Evolution and Emergence of RNA Viruses. Oxford University Press, London/New York/Oxford. [Google Scholar]
- Jiang X., Mu B., Huang Z., Zhang M., Wang X., et al. , 2010. Impacts of mutation effects and population size on mutation rate in asexual populations: a simulation study. BMC Evol. Biol. 10: 298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson T., 1999. The approach to mutation-selection balance in an infinite asexual population, and the evolution of mutation rates. Proc. R. Soc. Lond. B Biol. Sci. 266: 2389–2397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson T., Barton N. H., 2002. The effect of deleterious alleles on adaptation in asexual populations. Genetics 162: 395–411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimura M., 1967. On the evolutionary adjustment of spontaneous mutation rates. Genet. Res. 9: 23–34. [Google Scholar]
- Lynch M., 2010. Evolution of the mutation rate. Trends Genet. 26: 345–352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynch M., 2011. The lower bound to the evolution of mutation rates. Genome Biol. Evol. 3: 1107–1118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Minskaia E., Hertzig T., Gorbalenya A. E., Campanacci V., Cambillau C., et al. , 2006. Discovery of an RNA virus 3′->5′ exoribonuclease that is critically involved in coronavirus RNA synthesis. Proc. Natl. Acad. Sci. USA 103: 5108–5113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orr H. A., 2000. The rate of adaptation in asexuals. Genetics 155: 961–968. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pfeiffer J. K., Kirkegaard K., 2005. Increased fidelity reduces poliovirus fitness and virulence under selective pressure in mice. PLoS Pathog. 1: e11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanjuán R., 2012. From molecular genetics to phylodynamics: evolutionary relevance of mutation rates across viruses. PLoS Pathog. 8: e1002685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanjuán R., Nebot M. R., Chirico N., Mansky L. M., Belshaw R., 2010. Viral mutation rates. J. Virol. 84: 9733–9748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schrag S. J., Rota P. A., Bellini W. J., 1999. Spontaneous mutation rate of measles virus: direct estimation based on mutations conferring monoclonal antibody resistance. J. Virol. 73: 51–54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sedivy J. M., Capone J. P., RajBhandary U. L., Sharp P. A., 1987. An inducible mammalian amber suppressor: propagation of a poliovirus mutant. Cell 50: 379–389. [DOI] [PubMed] [Google Scholar]
- Sniegowski P. D., Gerrish P. J., Lenski R. E., 1997. Evolution of high mutation rates in experimental populations of E. coli. Nature 387: 703–705. [DOI] [PubMed] [Google Scholar]
- Sniegowski P. D., Gerrish P. J., Johnson T., Shaver A., 2000. The evolution of mutation rates: separating causes from consequences. Bioessays 22: 1057–1066. [DOI] [PubMed] [Google Scholar]
- Springman R., Keller T., Molineux I., Bull J. J., 2009. Evolution at a high imposed mutation rate: adaptation obscures the load in phage T7. Genetics 184: 221–232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suárez P., Valcárcel J., Ortín J., 1992. Heterogeneity of the mutation rates of influenza A viruses: isolation of mutator mutants. J. Virol. 66: 2491–2494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sung W., Ackerman M. S., Miller S. F., Doak T. G., Lynch M., 2012. Drift-barrier hypothesis and mutation-rate evolution. Proc. Natl. Acad. Sci. USA 109: 18488–18492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ulferts R., Ziebuhr J., 2011. Nidovirus ribonucleases: structures and functions in viral replication. RNA Biol. 8: 295–304. [DOI] [PubMed] [Google Scholar]
- Vignuzzi M., Stone J. K., Arnold J. J., Cameron C. E., Andino R., 2006. Quasispecies diversity determines pathogenesis through cooperative interactions in a viral population. Nature 439: 344–348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagner A., 2011. The molecular origins of evolutionary innovations. Trends Genet. 27: 397–410. [DOI] [PubMed] [Google Scholar]