A Comparison of Ground Reaction Forces Determined by Portable Force-Plate and Pressure-Insole Systems in Alpine Skiing

Abstract

For the determination of ground reaction forces in alpine skiing, pressure insole (PI) systems and portable force plate (FP) systems are well known and widely used in previous studies. The purposes of this study were 1) to provide reference data for the vertical component of the ground reaction forces (vGRF) during alpine skiing measured by the PI and FP systems, and 2) to analyze whether the differences in the vGRF measured by the PI and the FP depend on a skier’s level, skiing mode and pitch. Ten expert and ten intermediate level skiers performed 10 double turns with the skiing technique “Carving in Short Radii” as High Dynamic Skiing mode and “Parallel Ski Steering in Long Radii” as Low Dynamic Skiing mode on both the steep (23 °) and the flat (15 °) slope twice. All subjects skied with both the PI and the FP system simultaneously. During the outside phase, the mean vGRF and the maximum vGRF determined by the FP are greater than the PI (p < 0.01). Additionally during the inside phase, the mean vGRF determined by the FP were greater than the PI (p < 0.01). During the edge changing phases, the mean vGRF determined by the FP were greater than the PI (p < 0.01). However, the minimum vGRF during the edge changing phases determined by the FP were smaller than the PI (p < 0.01) in the High-Steep skiing modes of Experts and Intermediates (p < 0.001). We have found that generally, the PI system underestimates the total vGRF compared to the FP system. However, this difference depends not only the phase in the turn (inside, outside, edge changing), but also is affected by the skier’s level, the skiing mode performed and pitch.

Key points.

• Typically, during the steering phases of the ski turns the total vGRFs measured by the pressure-insole system were lower compared to the portable force-plate system.

• However, in some skiing modes during the edge changing phase, the pressure-insole system overestimates the total vGRF compared to the portable force-plate system.

• Differences between the forces determined by the both systems depend on the phase in the turn (inside, outside, edge changing) and are affected additionally by the skier’s level, the performed skiing mode and pitch.

Introduction

In alpine skiing, as in most sports, the determination of the ground reaction forces provides important and useful information that can lead to injury prevention, the development of new equipment, and technique improvement.

For scientific investigations in alpine skiing, portable force plates (FP) and pressure insole systems (PI) have been widely used to measure the ground reaction forces (Babiel et al., 1997; Kiefmann et al., 2006; Kröll et al., 2006; Scheiber et al., 2006; Spitzenpfeil et al., 2009; Vaverka and Vodickova, 2009; Vodickova and Vaverka, 2009; Yoneyama et al., 2003). The most common portable force plate system was developed by Kistler (Winterthur, Switzerland), consists of three 3D dynamometers using piezoelectric sensors, and is able to measure three- dimensional (3D) forces and torques (Stricker et al., 2010). One of the most widely used pressure insole systems, which use capacitive sensors, was developed by Novel (Pedar, Novel, Munich, Germany). This pressure insole system measures one dimensional (only compressive) force.

These two measurement systems are considered to have both advantages and disadvantages. One of the advantages of PI is that insoles are thin (2.2 mm) and light (0.2 kg). Thus, the insoles have a minimal influence on a subject’s skiing performance. In contrast, one FP weighs 0.9 kg and is 36 mm high. Due to the weight and height of the FP system, their usability is limited. For example, in a high dynamic ski situation such as slalom racing or mogul skiing, a skier needs to perform dynamic movements. In these situations, FP may have a negative influence on a skier’s performance; therefore, a kinetic analysis may not be possible during high performance skiing.

Another advantage of PI is that subjects are able to use their own skis and bindings. On the other hand, FP is normally mounted between experimental skis and bindings; therefore, subjects cannot use their own skis and bindings. For both systems, subjects can use their own ski boots.

Stricker et al., 2010 compared a portable FP to a non-portable FP. The accuracy of the force measured by the portable FP was 4.6 % for lower forces (Fz < 292 N) and 0.3 % for high loads (Fz > 292 N) compared to the non­portable FP. Conversely, the accuracy of the force determined by the PI reported by Hurkmans et al., 2006 ranged from -2.2 % to 0.3 %, compared with Novel calibration device. Both experiments took place in static conditions in a laboratory. The findings of the two studies showed that when both systems are used in alpine skiing, the determined forces are different. Stricker et al., 2010 reported that during alpine skiing with one subject, PI underestimated the ground reaction force by 54 % (inner ski) and 21 % (outer ski) compared to the force determined by the FP system.

Even though both systems have been widely used for scientific investigations, it is still unclear how great the differences between PI and FP are in detail, and if those differences are additionally affected by other factors (such as steering phase, skier’s level, skiing mode, pitch, etc.). The development of a “correction model” for ground reaction forces determined by PI’s to estimate the “real ground reaction forces” would benefit the scientific community. Therefore, the first step was to provide detailed information on differences in the ground reaction forces determined by both systems. Consequently, the primary aims of this study were 1) to provide reference data for forces during alpine skiing measured by the PI and FP systems, and 2) to analyze if the differences between PI and FP depend on the skier’s level, skiing mode and pitch.

Methods

Experimental design & measurement materials

For the expert group “Atomic FIS GS” skis (length = 184 cm, radius = 23 m) and for the intermediate group “Atomic Drive Fibre Sport” skis (length = 169 cm, radius = 15 m) were used in this study. All subjects were allowed to use their own ski boots. To additionally evaluate the influence of ski boot stiffness on the determined forces the values of flex index units from each ski boot was notated. This was done based on the information given by the ski boots manufacturers.

Force plate system

One portable FP produced by Kistler (Winterthur, Switzerland) was mounted under the toe binding and the other was mounted under the heel binding (Atomic Race 1018). Each plate consisted of three piezoelectric sensors (Figure 1). A charge signal of the transducer from each FP was amplified and converted into a voltage signal. Amplifiers, their power supply, supply box and data loggers were carried in a backpack (in total 4 kg) and worn by subjects (Figure 2).

Figure 1.

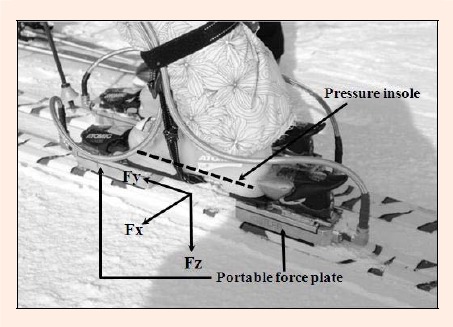
Experimental ski, the force plates and the image of the pressure insole. Two force plates were mounted between the experimental ski and bindings. One plate was located under the toe binding and the other was under the heel binding. Pressure insoles were set inside the subject's boot.

Figure 2.

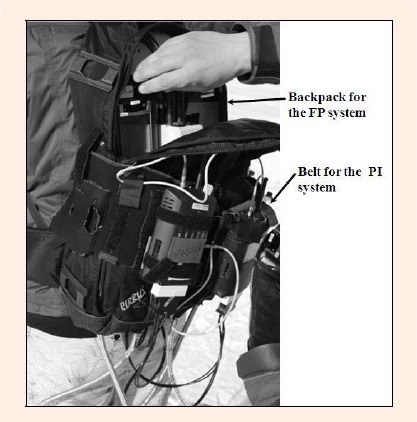
Experimental backpack and belt. Amplifiers, power supply, supply box and data loggers were carried in a backpack. The novel data logger, battery pack, and trigger switch were carried in a belt.

Pressure insole system

The Pedar PI (Pedar, Novel, Munich, Germany) was located inside the boots of all skiers. The optimal insole size for each subject’s inner boots was selected and inserted into inner ski boots in place of the normal insoles. The Novel data logger, battery pack, and trigger switch were carried in a belt (in total 1 kg) that was attached to the Kistler backpack. Before the field test, all pressure insoles were recalibrated in the laboratory using the standard calibration procedure from Novel (Novel manual p71~, 2007). The sampling frequency of both systems was at 100Hz which represents the maximum sampling rate of the Novel system. At the beginning and the end of each trial, subjects were asked to stomp the downhill ski once to synchronize force-time histories of the two kinetic systems and the video camera (HDR- HC1E, Sony, Tokyo, Japan), which was used for documentation and identification of turn phases.

Subjects & data collection

The subjects for this study were recruited based on a ski-course which took place prior to this project. In total twenty subjects were recruited and assigned to either the expert or the intermediate level group, based on Austrian Ski Teaching Concept (Wörndle et al., 2011). The expert level group consisted of ski racers or certified ski instructors. The intermediate level group consisted of advanced skiers, who are able to ski on flat and steep slopes with short and long radii turns.

Ten (8 males and 2 females) expert level skiers (Mean ± SD: Age = 25.7 ± 3. 9 years; Height = 1.79 ± 0.09 m; Weight = 75.7 ± 12.0 kg) and ten male intermediate level skiers (Mean ± SD: Age = 23.6 ± 3.0 years; Height = 1.77 ± 0.07 m; Weight = 71.7 ± 5.1kg) took part in this study. Prior to this test, all subjects were informed of the nature, risks and benefits of the investigation and written consent was obtained. The study was approved by the Ethics Committee of the University of Salzburg, Austria. Two different skiing modes were performed randomly on both a steep and a flat slope by all subjects (Figure 3).

Figure 3.

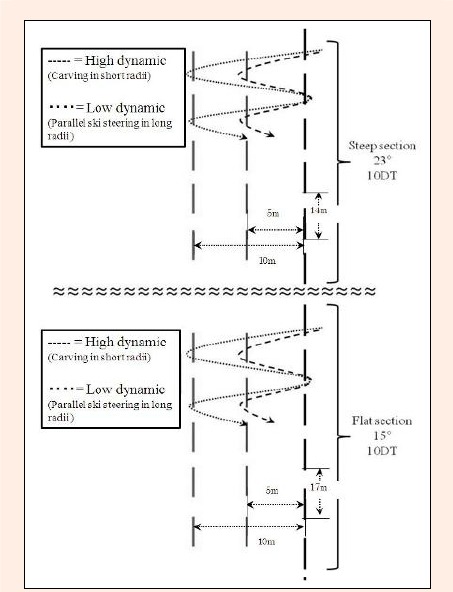
Course setting and skiing modes. Horizontal 5m setting is for the High Dynamic Skiing mode (Carving Short Radii), and 10m setting is for the Low Dynamic Skiing mode (Parallel Ski Steering in Long Radii).

The skiing technique “Carving in Short Radii” (Wörndle et al., 2011) was used for High Dynamic Skiing modes (which is characterized by a short radius turn and dynamic vertical movement) and the technique “Parallel Ski Steering in Long Radii” (Wörndle et al. , 2011) was used for Low Dynamic Skiing modes (which is characterized by a long radius skidded turn and less dynamic movement). Short poles were set into the slope as a land mark for turning and controlling the turn radius. All runs took place on a north-faced slope without any side hill sections. The slope where the tests occurred is also used as a training area for competitive athletes with a compact and hard layer of natural and artificial snow. The surface of the slope was daily groomed by a machine. The snow temperature was constant on all measurement days with a mean temperature of -1.1 ± 2.2 °C. The slope was divided into two sections based on pitch. The upper part of the run was termed “the steep section” with a pitch of 23 degrees, while the bottom part of the run was described as “the flat section” with a pitch of 15 degrees. Before measuring with both measurement systems, subjects performed a warm up run to become accustomed to skiing with all devices, the course settings, skiing techniques and pitches. All 20 subjects performed 10 double turns for each skiing mode on each pitch twice.

Data analysis

Alpine skiing can be defined as a continuous movement with alternating “loading” (steering phase) and “unloading” (edge changing phase) phases (Müller et al., 1998) and this characteristic is symmetric for both the right and the left legs.

Therefore, in the current study, a double turn was defined as follows: starting with the time point of edge changing, followed by one right turn (loading phase) and the edge changing phase (unloading) and a left turn (loading phase, see Figure 4).

Figure 4.

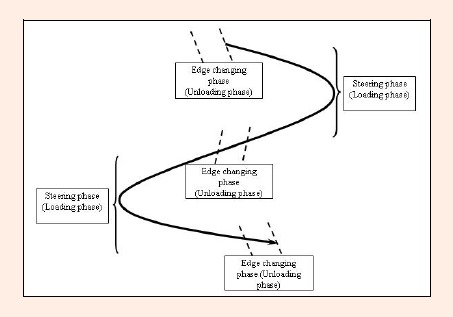
Illustration of continuous cycle of “loading” (steering) and “unloading” (edge changing) movement in alpine skiing.

Only the vertical component of the ground reaction force (vGRF) from the left leg was used for data comparison between the FP and PI systems. The forces were normalized by body weight (plus 5kg for the backpack) of each subject, separated as double turns and time-normalized. The timing of the edge change was defined at the minimum value of the vGRF, which was determined by the FP combined from both legs during edge changing movement. The time period from 0 % to 50 % was defined as the “outside phase” (Figure 5).

Figure 5.

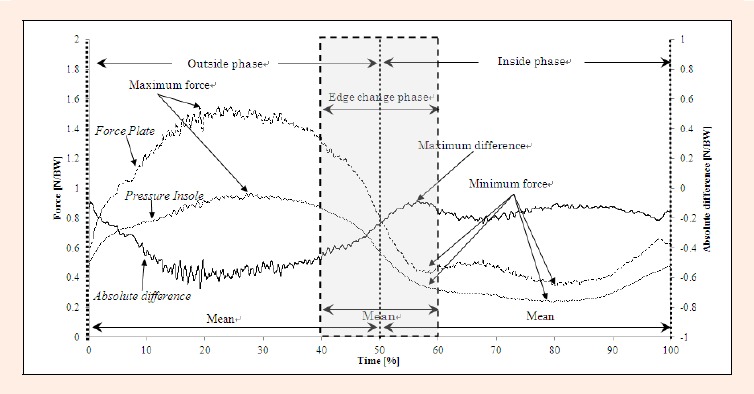
Definition of the variables and phases. From the outside phase, mean (vGRFmean) and maximum forces (vGRFmax) were calculated. From the inside phase, mean (vGRFmean) and minimum (vGRFmin) forces were calculated. During the edge changing phase, mean (vGRFmean) and minimum forces (vGRFmin) were calculated. Mean absolute differences of the outside and the inside phase and maximum absolute differences during the edge changing phase were calculated.

The “inside phase” was defined as the time period from 50 % to 100 %. From the outside phase, the mean and maximum values of vGRF were calculated, and from the inside phases the mean and minimum values were calculated. For the detailed analysis of the unloading phase, the time period from 40 % to 60 % was set as “edge changing phase” in this study. In this phase, the mean and minimum values of the vGRF were computed as well.

Moreover, to estimate the difference between the two systems, the absolute and relative difference between the vGRF of two systems were calculated by using the following equations:

Similar to the variables of the vGRF, the mean and maximum values of the absolute and relative differences were also computed.

Statistical analysis

For all data analysis, the software IkeMaster (Ike Software Solutions, Salzburg, Austria) was used. Statistical analysis was performed using SPSS v.18 software (SPSS, Chicago, IL). Repeated measures ANOVA were calculated 2 (Expert, Intermediate)×(2 systems, 2 skiing modes, 2 pitches) for global significance and to find the main effects of pitch, skier’s levels and skiing modes on the variable of absolute difference (PI-FP). When global significances for the factor “systems” were found, paired-sample t-test with Bonferroni adjustment was calculated as post hoc test. T-test was also used to compare the values between the outside and the inside phases.

Results

Descriptive data for vGRF in alpine skiing

Table 1 summarizes the analyzed variables vGRFmean, vGRFmax on the outside, vGRFmean, vGRFmin on the inside, vGRFmean and vGRFmin on the edge changing phase for all skiers’ levels, skiing modes and pitches.

Table 1.

Unilateral values (Mean ± SD) for the variables of vGRFmax, vGRFmean (outside phase); vGRFmin, vGRFmean (inside phase); vGRFmin, vGRFmean (edge changing phase) determined by pressure insoles (PI) and force plates (FP) depending on the test situations: expert (n=10) vs. intermediate (n=10) level skiers, low vs. high dynamic skiing modes, on 15° (flat) vs. 23° (steep) slopes. When global significances for the factor “system” were observed, paired-sample t-tests between the force determined by the FP and the PI were additionally carried out. Significant differences between the systems are indicated by

			Expert group				Intermediate group				Interaction		Interaction		Interaction
			High dynamic skiing mode		Low dynamic skiing mode		High dynamic skiing mode		Low dynamic skiing mode		System x level		System x mode		System x slope
Variable	Unit	System	Flat slope	Steep slope	Flat slope	Steep slope	Flat slope	Steep slope	Flat slope	Steep slope	p	ηp2	p	ηp2	p	ηp2
vGRFmean	[N/BW]	PI	.87 (.14)	.82 (.17)	.83 (.16)	.78 (.18)	.90 (.16)	.78 (.14)	.86 (.16)	.79 (.18)	.02	.29	.00	.39	.00	.79
		FP	1.26 (.08)*	1.15 (.08)*	1.27 (.08)*	1.18 (.10)*	1.18 (.13)*	1.01 (.11)*	1.15 (.11)*	1.04 (.10)*
vGRFmax	[N/BW]	PI	1.16 (.18)	1.22 (.21)	1.03 (.12)	1.06 (.18)	1.19 (.22)	1.11 (.21)	1.12 (.20)	1.09 (.25)	.00	.59	.39	.04	.06	.19
		FP	1.91 (.18)*	2.05 (.20)*	1.76 (.09)*	1.86 (.13)*	1.68 (.25)*	1.61 (.21)*	1.59 (.14)*	1.60 (.20)*
vGRFmean	[N/BW]	PI	.42 (.13)	.42 (.15)	.32 (.12)	.32 (.14)	.39 (.07)	.36 (.08)	.34 (.08)	.31 (.09)	.65	.01	.00	.42	.10	.15
		FP	.56 (.09)*	.62 (.13)*	.48 (.09)*	.49 (.13)*	.51 (.05)*	.53 (.06)*	.45 (.03)	.45 (.05)*
vGRFmin	[N/BW]	PI	.30 (.11)	.26 (.13)	.21 (.09)	.21 (.10)	.27 (.06)	.23 (.05)	.21 (.06)	.16 (.07)	.39	.04	.29	.07	.00	.44
		FP	.27 (.04)	.15 (.09)	.26 (.06)	.26 (.10)	.26 (.08)	.20 (.10)	.27 (.06)	.19 (.11)
vGRFmean	[N/BW]	PI	.60 (.13)	.49 (.14)	.58 (.19)	.49 (.19)	.54 (.12)	.41 (.12)	.49 (.11)	.42 (.11)	.04	.22	.00	.58	.01	.38
		FP	.76 (.09)*	.60 (.12)*	.83 (.22)*	.67 (.18*	.62 (.14)	.49 (.11)	.62 (.12)	.53 (.129
vGRFmin	[N/BW]	PI	.36 (.13)	.30 (.14)*	.31 (.16)	.26 (.12)	.33 (.10)	.23 (.08)*	.31 (.10)	.23 (.11)	.19	.10	.00	.58	.00	.60
		FP	.34 (.10)	.15 (.09)	.37 (.10)	.26 (.11)	.27 (.10)	.09 (.08)	.31 (.11)	.15 (.14)

* Interaction effects (2 skier’s groups ×(2 systems ∙2 skiing modes ∙2 pitches)) repeated ANOVA) are indicated by the level of significance (p) and effect size (ηp²). Data are means (±SD).

The force-time graphs measured by both systems and absolute differences are presented in Figure 6a-h.

Figure 6a-h.

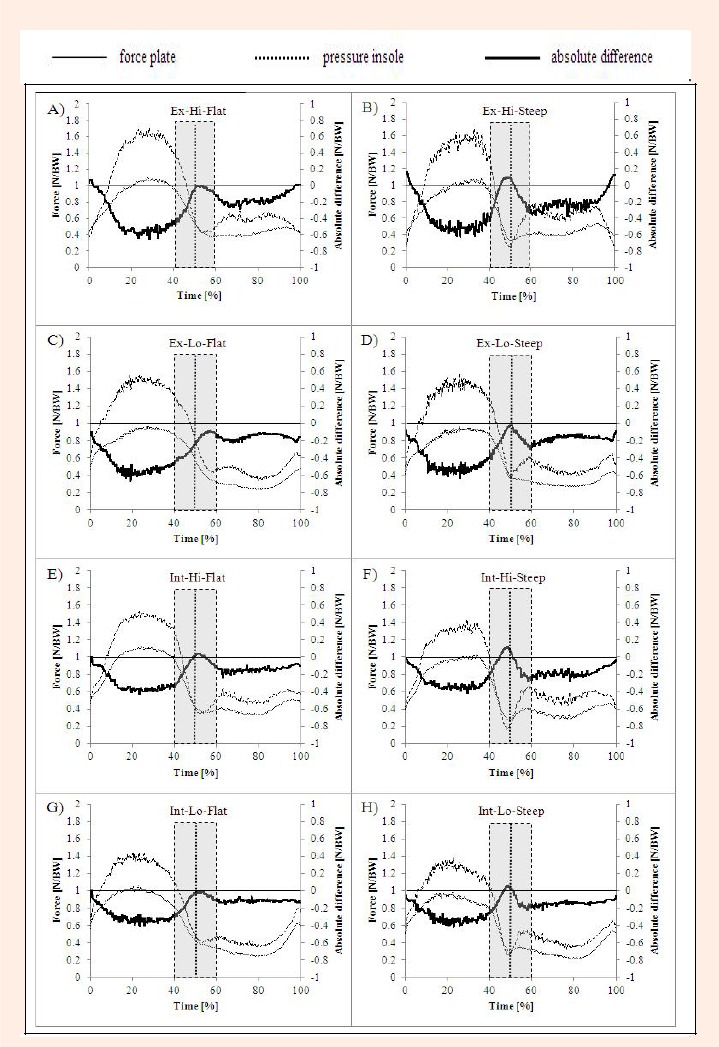
Graphs of mean forces, determined by force plates (dotted line) and pressure insoles (solid line), and mean absolute differences between the force plate and the pressure insole (thicker line) for expert level (n=10) and intermediate level (n=10); High and Low dynamic skiing modes; pitch of 15° (Flat) and 23° (Steep). Each skiing mode includes 20 double turns × n=10 subjects. A) Expert-High-Flat, B) Expert-High-Steep, C) Expert-Low-Flat, D) Expert-Low-Steep, E) Intermediate-High-Flat, F) Intermediate-High-Steep, G) Intermediate-Low-Flat, H) Intermediate-Low-Steep skiing mode. Negative (minus) absolute differences indicate that the forces determined by the FP are greater than the PI and positive (plus) absolute differences indicate that the forces determined by the FP are smaller than the PI.

vGRFmean for outside and inside phase

The vGRFmean measured by the FP ranged from 1. 04 to 1.28 N/Body Weight (BW) and the vGRFmean measured by the PI ranged from 0.78 to 0.90 N/BW for the outside phase for all skiing modes (Table 1). For the inside phase, the vGRFmean determined by the FP ranged from 0.45 to 0.62 N/BW and the vGRFmean determined by the PI ranged from 0.31 to 0.42 N/BW for all skiing modes. The vGRFmean (Table 1) measured by the FP are greater than the PI for both the outside and the inside phases (p < 0.01). Additionally the vGRFmean of the outside phase are greater compared to the inside phase in both measurement systems.

The maximum (vGRFmax) and minimum (vGRFmin) values

The vGRFmax determined by the FP ranged from 1.59 to 2.05 N/BW, and the vGRFmax determined by the PI ranged from 1.03 to 1.22 N/BW for the outside leg on all skiing modes. The vGRFmin during the inside phase determined by the FP ranged from 0.15 to 0.27 N/BW, and the vGRFmin determined by the PI ranged from 0.16 to 0.30 N/BW in all skiing modes. The vGRFmax during the outside phases measured by the FP were greater than the PI (p < 0.01).

During Edge changing phase

The vGRFmean measured by the FP ranged from 0.49 to 0.83 N/BW and the vGRFmean measured by the PI ranged from 0.41 to 0.60 N/BW in all skiing modes. The vGRFmin determined by the FP ranged from 0.09 to 0.37 N/BW, and the vGRFmin determined by the PI ranged from 0.23 to 0.36 N/BW. During the edge changing phases, the vGRFmean determined by the FP were greater than the PI in all skiing modes (p < 0.01). However, it is worthwhile noticing that the vGRFmin during the edge changing phases determined by the FP were smaller than the PI (p < 0. 01) in the High-Steep skiing modes of Experts and Intermediates (p < 0.001).

Difference between systems (FP vs. PI)

The mean absolute difference of the vGRFmean between the two systems ranged from -0.45 to -0.23 N/BW on the outside leg (Table 2 and Figure 6a-h) and from -0.19 to -0.10 N/BW on the inside leg. The mean absolute difference of the vGRFmax during the outside phases between the two systems ranged from -0.82 to -0.31 N/BW (Table 2 and Figure 6a-h) and the mean absolute difference of the vGRFmin during the inside phase ranged from -0.05 to 0.11 N/BW. The mean absolute difference of the vGRFmean during edge changing phase ranged from -0.25 to 0.13 N/BW. The maximum absolute difference of vGRFmin always occurred in the edge changing phase and ranged from -0.02 to 0.21 N/BW. The mean absolute differences of the vGRFmean during the outside phase were greater than the inside phase in all skiing modes other than Intermediate-High-Steep skiing mode (p < 0.006). The relative differences, see equation 2, between the vGRFmean (Table 1) on the outside phase ranged from 22.6 to 35.2 % and from 23.0 to 32.4 % on the inside phase. The relative differences between the vGRFmax (Table 1) on the outside phase ranged from 29.3 to 42.8 %. The relative differences between the vGRFmin (Table 1) on the inside phase ranged from -69.6 to 20.8 %. During the edge changing phase, the relative differences between the vGRFmean (Table 1) measured by both systems ranged from -29.7 to -13.9 % and the relative difference between the vGRFmax (Table 1) determined by both systems ranged from -15.8 to 160.3 %.

Table 2.

Results of the absolute difference of the vGRF between the FP and PI.

				Expert group				Intermediate group
				High dynamic skiing mode		Low dynamic skiing mode		High dynamic skiing mode		Low dynamic skiing mode
	Phase	Variable	Unit	Flat slope	Steep slope	Flat slope	Steep slope	Flat slope	Steep slope	Flat slope	Steep slope
Absolute	Outside	vGRFmean	[N/BW]	-.39 (.10)*	-.33 (.11)*	-.45 (.12)*	-.40 (.12)*	-.27 (.14)*	-.23 (.15)	-.27 (.13)*	-.25 (.15)*
		vGRFmax	[N/BW]	-.75 (.14)	-.82 (.14)	-.73 (.15)	-.80 (.15)	-.49 (.21)	-.50 (.19)	-.31 (.44)	-.51 (.22)
	Inside	vGRFmean	[N/BW]	-.14 (.10)	-.19 (.14)	-.15 (.09)	-.17 (.11)	-.12 (.08)	-.17 (.07)	-.10 (.10)	-.14 (.09)
		vGRFmin	[N/BW]	03 (.12)	.11 (.13)	-.05 (.09)	-.05 (.07)	.01 (.09)	.03 (.08)	-.03 (.11)	-.03 (.11)
	Edge changing	vGRFmean	[N/BW]	-.16 (.11)	-.11 (.09)	-.25 (.10)	-.19 (.08)	-.09 (.10)	-.08 (.08)	-.11 (.11)	.13 (.08)
		vGRFmin	[N/BW]	.06 (.09)	.21 (.10)	-.02 (.08)	.08 (.10)	.09 (.08)	.18 (.09)	.06 (.11)	.13 (.08)
Relative	Outside	vGRFmean	%	-30.7	-28.5	-35.2	-33.7	-23.2	-22.6	-25.1	-23.8
		vGRFmax	%	-39.1	-40.2	-41.6	-42.8	-29.4	-30.9	-29.3	-31.9
	Inside	vGRFmean	%	-24.4	-31.5	-32.4	-35.1	-23.0	-32.0	-25.4	-31.4
		vGRFmin	%	10.2	69.6	-20.8	-18.5	4.9	16.3	-20.4	-15.7
	Edge changing	vGRFmean	%	-21.3	-17.9	-29.7	-27.6	-13.9	-15.7	-20.0	-20.1
		vGRFmin	%	5.7	96.6	-15.8	.8	22.2	160.3	.4	47.4

* indicates significance difference in t-test between the absolute differences of the vGRFmean during the outside and inside phase. Negative values (minus) of the absolute and relative differences indicate the values determined by the FP are greater than the PI. Positive values (plus) of the absolute and relative difference indicate the values determined by the FP are smaller than the PI. Data are means (±SD).

The results of the interaction between system and skiers’ level, skiing mode and pitch calculated by repeated measures ANOVA are presented in Table 1. The differences of the vGRFmean on the outside and the edge changing phase were significantly influenced by the skier’s level, skiing mode and pitch (Table 1), while the differences of the vGRFmean on the inside phase were significantly influenced by the skiing mode. Additionally, the differences of the vGRFmax on the outside phase were significantly influenced by the skier’s level, even as the differences of the vGRFmin on the inside phase were significantly influenced by pitch. Finally, the differences of the vGRFmin on the edge phase were significantly influenced by both skiing mode and pitch.

Discussion

The aims of this study were 1) to provide data for vertical ground reaction forces (vGRF) during alpine skiing measured by pressure insoles (PI) and portable force plates (FP) as a reference for further scientific studies, and 2) to analyze whether the differences in the vGRF measured by the PI and the FP depend on a skier’s level, skiing mode and pitch. The main findings of this study were that the vGRF measured by the FP are generally greater than the PI. However, during the short term of the edge changing phase in some skiing modes, the vGRF determined by the PI is greater than the FP. These findings are similar to and coincided with the previous study by Stricker et al., 2010. Technically seen, the two systems differ in the location of system placement and the different measurement principle. From a sport scientific perspective, changes in skiing mode, pitch and different skier’s levels are also influencing factors on the variances in the vGRFs of the PI and the FP.

The next two sections explain the differences in the two measurement systems from a technical perspective.

One considerable difference is system placement. PIs are placed inside the ski boots, in additional to or in place of normal insoles, while FPs are placed between the skis and the bindings. As a result of their placement, FPs are able to measure the forces acting between the ski and the bindings, and therefore, to measure the force acting on the ski boot. In contrast, the PIs only are able to measure the vGRF beneath the skier’s foot, which is inside the boot. As presented in previous literature (Lüthi et al., 2005; Kersting et al., 2009; Scheiber et al., 2010; Stricker et al., 2010), a percentage of the total vGRF is transferred via the ski boot shank, and consequently, cannot be measured by the PI system.

Referring to the laboratory study by Barnett, et al. (2000), forces measured by the PI were found to be smaller than those determined by a non-portable force plate (Kistler Instruments, Hampshire, UK) placed in the laboratory floor resulting in a difference of 3 to 31 % with four different types of shoes. In our study, the mean relative differences of the outside and the inside phases ranged from 22.6 to 35.2 % (Table 2) and the relative differences of vGRFmax and vGRFmin forces ranged from 29.3 to 42.8 %. These differences are greater than those in Barnett’s study. One explanation for the differences between the two studies is that the shoes which were used in the Barnett study did not have the part above the ankle; therefore, they did not have supporting ankle stabilization function like ski boots have. Consequently, the forces transferred via the shank are smaller than in ski boots. In alpine skiing, tibia shank forces of 0.11 to 0.16 N/BW were found by Scheiber et al., 2010. Additionally, these authors reported a relationship among skiing styles, skiers’ levels and the shank forces.

The measurement principles of the sensors contained in both systems are fundamentally different. The portable FP system produced by Kistler contained rigid piezoelectric sensors inside of the plates (Bill, 2002), while the PI system used capacitive sensors covered by a soft protection layer (Barnett et al., 2000). The PI system is able to determine compressive forces by multiplying the pressure value with the area of each sensor. However, each pressure sensor has a minimum threshold of 20 kPa; consequently, pressure values lower than 2 N/cm2 are eliminated. In contrast, the piezoelectric sensors are able to measure these small forces, and moreover, the negative force as a negative value. In the current study, these small negative values of FP-forces were observed in the individual data analysis, but they disappeared when the mean values of groups were calculated. As a result, such small values cannot be found in the figure 6a-h.

From a biomechanical perspective, the reasons why skiers’ levels, certain turn phases, different skiing modes and pitches had significant effects on the differences are stated below.

According to the studies by Müller and Schwameder, 2003 and Schiefermüller et al., 2005, a skier’s center of gravity during skidded turns (low dynamic skiing mode) was found to be located nearly above or slightly forward (in anterior) to a skier’s ankle joint (average value during a turn). In contrast, a skier’s center of gravity in carved turns (high dynamic skiing mode) was located behind (posterior) the ankle joint. These findings are in agreement with the recommendation by the Austria Ski Teaching Concept (Wörndle et al., 2011). Additionally, the range of motion, as determined by the anterior-posterior movement of the center of gravity, is typically greater in skidded turns compared to carved turns. As a result, skiers may lean more on the boot shaft; hence, the support function of the ski boot may be greater in skidded turns compared to carved turns. Consequently, the force acting on the shank could be increased, resulting in an increased difference between the forces determined by the PI and the FP system.

It is not the relative, but the absolute time of steering phase in the low dynamic (skidded) skiing mode that is typically longer compared to the high dynamic (carved) skiing mode (Müller and Schwameder, 2003). The longer steering phases are needed for the drifted turning of the skis (Wörndle et al., 2011). Within this time period, skiers move in anterior direction (initial phase) and posterior direction (steering phase), which again results in increased forces transmitted via the boot shaft. There is no doubt that skiing with carved turns requires better sagittal plane balance abilities; skiers tend to keep the center of gravity in a middle position to be able to act and react to external disturbances (Müller and Schwameder, 2003; Schiefermüller et al., 2005; Wörndle et al., 2011). These middle positions potentially reduce the shank forces.

In this study, the subjects were allowed to use their own ski boots, instead of providing standardized boots. However, the flex index of each boot was recorded regarding to the flex information provided from the boot manufacturer. The mean value of flex index units in expert group was 123.0 ± 18.0 and 92.2 ± 18.6 in intermediate group. The flex index units of the different companies may be seen more as an indicator, than as total numbers. However, the fact the intermediate level skiers used softer boots than the expert level skiers may be another explanation of the interaction between systems and skiers’ levels because stiffer boots potentially result in greater shank forces.

During the edge changing phase, the vGRFmin determined by the FP were smaller than the PI forces. These differences were tended to be greater in the high versus low dynamic skiing mode and on steep versus flat pitches (Table 2). When skiers performed a high dynamic skiing mode, or ski on a steep pitch, they needed to use a more dynamic unloading movement compared to a low dynamic skiing mode or skiing on a flat pitch. These dynamic unloading movements led to negative vertical force (skis are lifted) measured by the FP, which was observed in the individual analyses of the force-time characteristic. However, these low negative forces, in particular, cannot be measured by the PI system, as reported above. According to the vGRFmin force values from the edge changing phase (Table 1), the force around 0.23 N/BW could be seen as a minimum cut-off point of the pressure insole system during alpine skiing.

Conclusion

The principal advantage of the FP system is to be able to measure 3D forces and moments, and the determined values are considered as standard. Nevertheless, the weight of all systems and increasing standing height of the FP are a notable disadvantage. Because of the mentioned advantages of the FP system, and as previously observed by Stricker et al., 2010, the FP system should be used whenever data of 3D forces and moments are needed (e.g. for inverse dynamics), and whenever the analyzed skiing situation “allows” the usage of this system. To measure the vGRF in mogul skiing, powder snow skiing or in any other high dynamic skiing situation (such as ski racing), the PI might be the more appropriate system.

The data of the current study provide a report on the vGRF in alpine skiing determined by the PF and the FP systems, and present the influence of a skier’s level, the skiing mode and the pitch on the differences in the vGRFs. We have found that typically, the PI system underestimates the total vGRF, as measured by the FP system. However, this difference depends on the phase in the turn (inside, outside, edge changing) and is affected additionally by the skier’s level, the performed skiing mode and pitch. All these factors seem to substantially influence the difference between the vGRF determined by both systems. In future scientific studies, these facts should be considered when the question of which system should be used for data collection arises. These data may be seen as a reference for further studies, dealing with kinetics in alpine skiing.

More data under specific conditions are needed for a better understanding of those differences and to be able to develop a “correction model” for the PI data. Then, it would be possible to determine kinetic data with the PI system, which does not influence the skiers technique, and estimate the real forces, based on this correction model.

Biographies

Kosuke Nakazato

Employment

PhD student at the Department of Sport Science and Kinesiology, and CD-Laboratory “Biomechanics in Skiing”, University of Salzburg, Austria.

Degree

MSc

Research interests

Biomechanics; Kinetics in alpine skiing

E-mail: kosuke.nakazato@sbg.ac.at

Peter Scheiber

Employment

Research assistant at the Department of Sport Science and Kinesiology, and CD-Laboratory “Biomechanics in Skiing”, University of Salzburg, Austria.

Degree

PhD

Research interests

Applied Biomechanics & Physiology, Alpine Skiing.

E-mail: peter.scheiber@sbg.ac.at

Erich Müller

Employment

Head of the Department of Sport Science and Kinesiology, and CD-Laboratory “Biomechanics in Skiing”, University of Salzburg, Austria.

Degree

PhD

Research interests

Biomechanics, Training and Coaching, Motor Learning

E-mail: erich.mueller@sbg.ac.at