Cytoplasmic streaming in plant cells emerges naturally by microfilament self-organization

Abstract

Many cells exhibit large-scale active circulation of their entire fluid contents, a process termed cytoplasmic streaming. This phenomenon is particularly prevalent in plant cells, often presenting strikingly regimented flow patterns. The driving mechanism in such cells is known: myosin-coated organelles entrain cytoplasm as they process along actin filament bundles fixed at the periphery. Still unknown, however, is the developmental process that constructs the well-ordered actin configurations required for coherent cell-scale flow. Previous experimental works on streaming regeneration in cells of Characean algae, whose longitudinal flow is perhaps the most regimented of all, hint at an autonomous process of microfilament self-organization driving the formation of streaming patterns during morphogenesis. Working from first principles, we propose a robust model of streaming emergence that combines motor dynamics with both microscopic and macroscopic hydrodynamics to explain how several independent processes, each ineffectual on its own, can reinforce to ultimately develop the patterns of streaming observed in the Characeae and other streaming species.

Cytoplasmic streaming pervades the vast spectrum of cell types, achieving great diversity to fulfill many varied goals. Drosophila oocytes use disorderly streaming to localize proteins without counterproductive backflows (1, 2); Caenorhabditis elegans couples cortical flow with bistable pattern formation for polarity determination (3); Elodea leaf cells circulate chloroplasts in response to illumination (4); and pollen tubes transport tip growth material in fountain-like flows (5, 6), to name four disparate examples. At their core, either as the end goal or within the mechanism itself, lies the biological pillar of pattern formation (7).

The different realizations of streaming can be effectively categorized by the degree of order inherent in the observed flow (4, 8). The most disordered instances often function as part of cellular patterning processes, as in Drosophila. In contrast, the orderly types must themselves already be the product of some pattern-forming process to exist at all. The basic paradigm that underlies streaming, motor proteins interacting with polymer filaments, has been seen to possess many pattern-forming behaviors in both theoretical (9–11) and experimental (11–14) settings, with recent work beginning to incorporate the effects of cylindrical cell-like domains (15, 16). However, such studies are often “bottom up,” taken out of context from concrete biological systems, and in particular no direct connection has been made to the development of cytoplasmic streaming.

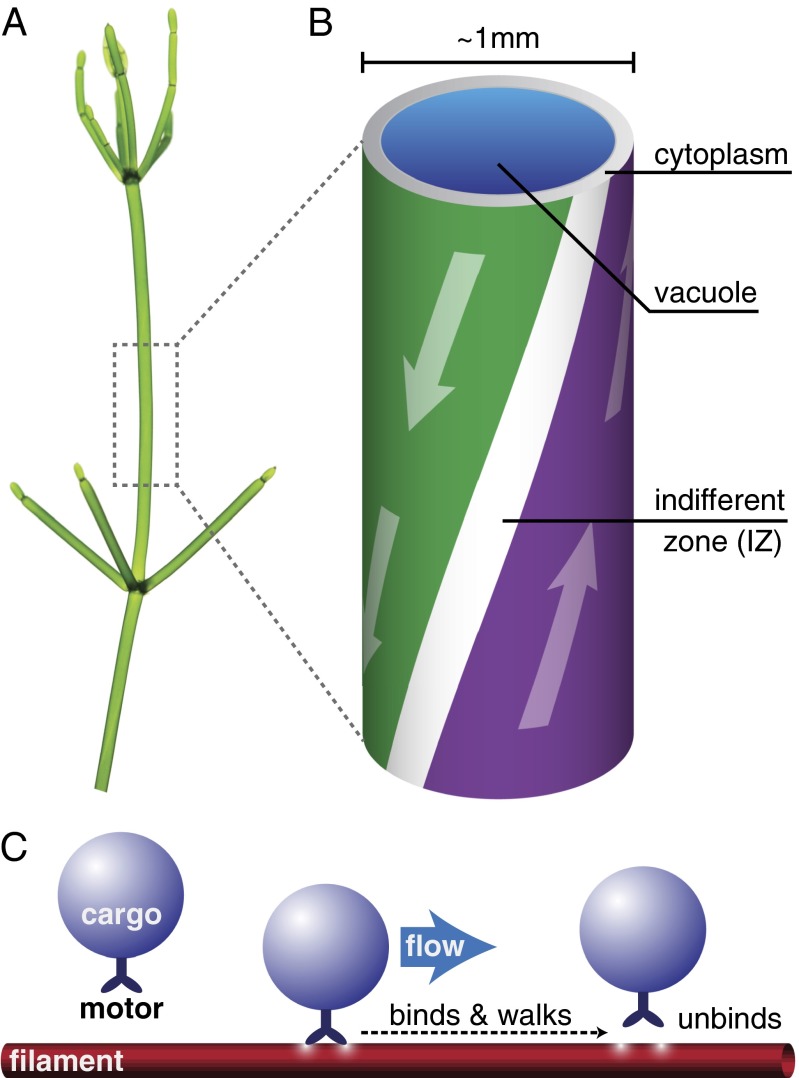
If we want to understand what fundamental dynamics drive the formation of orderly streaming and connect the microscopic with the macroscopic, an alternative “top-down” approach is warranted. To this end, we approach the problem by way of a concrete, prototype system. We adopt perhaps the most strikingly patterned example of all, the aquatic alga Chara corallina (Fig. 1A). The giant cylindrical internodal cells of Chara measure 1 mm in diameter and up to 10 cm in length. First observed in 1774 (17), its rotational streaming—termed “cyclosis”—is driven by vesicles (in the endoplasmic reticulum) coated with the motor protein myosin (18–20) sliding along two oppositely directed longitudinal stripes of many continuous, parallel actin filament cables (21, 22) (Fig. 1 B and C). Every cable is a bundle of many individual actin filaments, each possessing the same intrinsic polarity (23); myosin motors walk on a filament in a directed fashion, from its minus (pointed) end to its plus (barbed) end. These cables are bound to the cortically fixed chloroplasts at the cell periphery (24) in a “barber pole” twist, generating flow speeds of 50–100 μm/s (25–27). It is unclear how this simple yet striking pattern forms during morphogenesis; what process is responsible for forming two, and only two, precisely equal stripes? One could imagine it to be the result of complex chemical prepatterning, but experimental evidence suggests otherwise.

Fig. 1.

Cytoplasmic streaming in Chara corallina. (A) Internodes and branchlets of Chara. Individual internodes can grow up to 10 cm long. (B) Rotational streaming in a single internodal cell of Chara. The stripes indicate the polarity of actin cables at the periphery driving flow in the cytoplasm and vacuole. (C) Microscopic mechanism driving plant cell streaming. Cargo-carrying myosin motors bind to actin filaments and entrain flow as they walk.

Foissner and Wasteneys (28) introduced the agents cytochalasin D and oryzalin into young Chara cells to arrest streaming and completely disorganize the established actin cables. They found a gradual recovery process (Fig. 2) whereby streaming initially resumes in a disordered saltatory fashion. Over time, the filaments reorganize, first into locally ordered “streamlets,” until eventually the initial filament layout is reestablished. They note one crucial difference from the prearrest configuration: the so-called indifferent zone (IZ) (Fig. 1B) separating the up- and down-streaming stripes, initially identifiable by a line of missing chloroplasts, is often found in a new position. Put another way, the entire pattern has shifted around the central axis. Together with the local-to-global progression, also observed in other cell types (8, 29), a self-organization process is implicated.

Fig. 2.

Disruption, rearrangement, and resumption of streaming in Chara (28). Filament bundles disorganize and reform with the IZ in a new location.

Similar behavior has been induced in rotationally streaming Vallisneria leaf cells where flow handedness was preserved only if some “seed” filament bundles survived disintegration (30), a hallmark of a symmetry-breaking self-organization process. Healing of localized wounds in Characean cells also furnishes evidence, where the actin network regenerates in a gradually organizing process (31, 32). Even ex vivo experiments lend credence to such a theory: cytoplasmic droplets forcibly extracted from Chara cells can begin spontaneously circulating at a steady rate (8, 33, 34) likely owing to a self-organizing process (35). Furthermore, images of filament networks in very young Characean cells show long cables forming only after elongation begins, with just a disorderly meshwork at genesis (36).

In this work, we will unify this wealth of experimental evidence for a self-organization mechanism by constructing a simple theoretical model of streaming emergence during cell development. The model will couple the hydrodynamics of the cytoplasm with the dynamics of a microfilament suspension subject to a few key reorienting and organizing effects. We will then illustrate the model’s capacity for mimicking the emergence of Characean streaming by way of an example and a parameter space scan to identify regimes of robust cyclosis development. Finally, we will discuss the model in the context of pathologies and disruptions to understand the importance of each of the components of the filament dynamics.

Model

A young Chara cell is modeled as a cylinder of radius R with periodic boundaries at a distance L apart. The fixed chloroplasts lie at the edge, with the subcortical cytoplasm a thin cylindrical layer between the chloroplasts and the vacuolar membrane; the vacuole then comprises the bulk of the cell. The cytoplasm is taken to consist of a layer of short, initially disordered actin filaments beneath a layer of myosin-coated endoplasmic reticulum vesicles, which drive flow by forcing the cytoplasm as they process on the actin filaments (Fig. 1C). Because the subcortical layer is very thin compared with the vacuole, we approximate the cytoplasmic layer as a purely 2D cylindrical shell. We also assume that the effective viscosity contrast between cytoplasm and vacuolar fluid is sufficiently large to take vacuolar flow as purely passive, induced by cytoplasmic flow (25) but not affecting it. This yields a truly 2D problem.

Our final simplification is to neglect the helical twist in the streaming pattern (Fig. 1B). No discernible twist exists in young cells with developed actin cables (28), so its appearance is more likely connected to later development of the microtubule cytoskeleton (37) by a process of twisting growth once the main cables are established and bound to the cortical chloroplasts (38). The twist appears to be advantageous primarily for large, mature cells, where it enhances vacuolar mixing and nutrient uptake (25, 26).

We will now formalize the hydrodynamics. Endow the shell with cylindrical coordinates 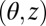and corresponding unit vectors 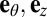. Let 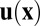be the velocity field of the suspending cytoplasmic fluid. The small velocity of streaming allows us to work in the zero Reynolds number limit. We then take 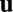to obey the forced Stokes equations with friction,

where 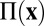is the 2D pressure and 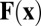is the filament-induced forcing, discussed shortly. The frictional term 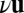captures the effect of the no-slip boundary proximity in our thin-shell approximation, in a manner similar to Hele–Shaw flow (SI Text).

There are two crucial constraints on the flow field that must be incorporated. First, because the tonoplast membrane, which separates the cytoplasm and vacuole, behaves as a 2D incompressible fluid (39), we must have incompressibility 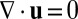. Second, the presence of end caps on the cell must be acknowledged, either through explicit modeling of the end geometry or, as we do here, qualitatively through the simple extra constraint of zero net flux 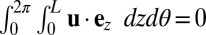, essentially due to the incompressibility of a finite domain in the 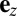direction. This is balanced by allowing a longitudinal pressure gradient 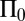and writing 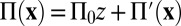, with 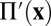the remaining fully periodic pressure field.

We now turn to the filament suspension, whose dynamics will incorporate several crucial effects. The filaments are taken to be restricted: passive advection and shear alignment in the flow 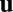is inhibited by a factor ϵ due to frictional or binding effects of the filaments on the chloroplasts or with cortical polymer networks. As a consequence of restriction, the filaments are non–self-advective: a vesicle walking forward on a filament will induce only a negligible backward propulsion of the filament itself. The filaments are also taken to spontaneously bundle: filaments will locally align with each other, controlled by a coupling constant 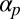(a rate constant for the exponential growth of small local polarization), mimicking the presence of bundling proteins. (Inhibiting the action of bundling proteins thus corresponds to setting .)

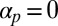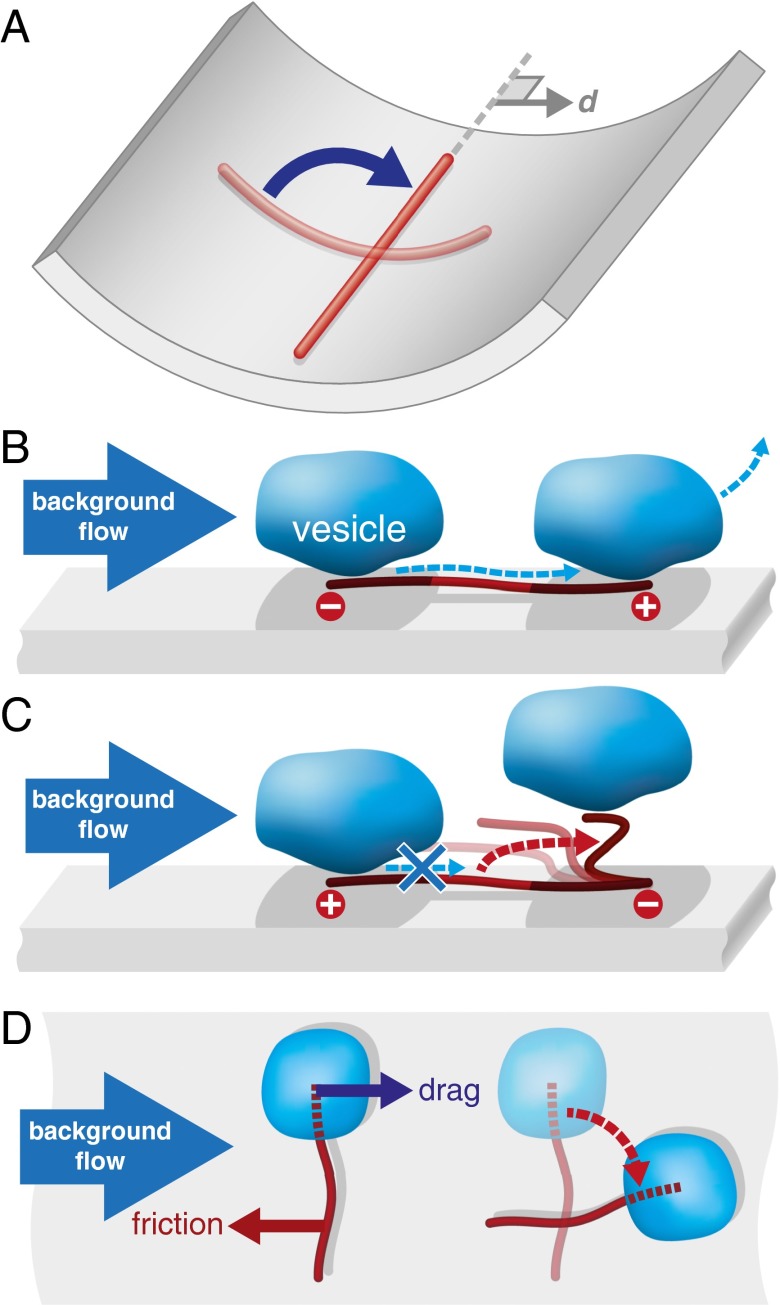
To represent nonspherical cellular geometry or substrate patterning we include a repulsive direction 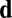, which filaments will preferentially avoid, with coupling constant κ (Fig. 3A); this will be set here to , the circumferential direction. Although apparently a strong assumption, there is remarkable experimental precedent for such an effect whereby filaments can reorient circumferentially around cells upon inhibition of binding or director components (40–42).

Fig. 3.

Filament reorganization mechanisms. (A) Repulsive direction: a filament preferentially reorients away from a direction 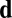either to minimize physical curvature or minimize interactions. (B–D) Polar flow reorientation: rather than aligning nematically with flow shear, filaments can align in a polar fashion with flow itself. Alignment with the plus end downstream is stable (B), but hydrodynamic drag on vesicles bound to the filament competes with friction from wall restriction when the motor is not free to walk downstream (C and D).

In the absence of any other contributing factors, the effects described above will tend to produce a uniformly polarized suspension in a direction perpendicular to 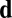. There is one more key factor: polar flow alignment, with coupling constant (encoding the linear growth rate of filament polarization with cytoplasm flow, similar to 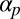). We argue that the presence of myosin-coated vesicles brings about alignment of the filaments with the flow field 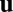itself in a truly polar fashion, minus end upstream and plus end downstream, supplementing traditional nematic alignment with flow shear 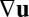. Suppose that a motor-laden vesicle approaches a filament, advected by a net background flow 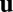from the action of other vesicles processing along filaments nearby. There are then three basic cases to consider for the filament orientation relative to the flow. If the vesicle approaches a microfilament oriented parallel with 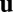—that is, minus end upstream so the myosin walk direction is with the flow—then the vesicle can bind, process along the filament at a speed 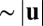, and unbind with little change to the filament (Fig. 3B). This implies parallel flow alignment is stable. Antiparallel alignment, with plus end upstream and walk direction against the flow, is unstable: a vesicle bound upstream on the filament will be impeded from walking by hydrodynamic drag, stall on the restricted filament, and twist it into the flow (Fig. 3C). Finally, perpendicular alignment induces reorientation either parallel or antiparallel to the flow upon binding of a vesicle, because a torque is generated by the competition of filament restriction against hydrodynamic drag (Fig. 3D). This effect is not unique to microfilaments: thin-film dumbbell microswimmers are subject to the same polar alignment, driven by asymmetric friction forces (43).

For this reorientation mechanism to occur and be robust (that is, stable when oriented parallel with the flow), there are two important conditions. First, the timescale 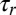for filament reorientation must be shorter than the timescale 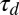for motor detachment after stalling (44) in order for any appreciable filament reorientation to occur in the flow-antiparallel and flow-perpendicular cases. Second, the timescale 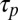for a motor to process along a flow-parallel filament must be shorter than the filament reorientation timescale 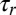, in order for orientation parallel with the flow to be stable; if this is not the case, then no orientation is stable, and the filament will writhe continuously over time irrespective of its orientation relative to the background flow. Thus, we require 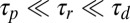. The sliding speed ∼100 μm/s (45) on ∼10μm filaments yields a quick procession timescale 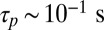. By contrast, it has been suggested that the very fast streaming may in fact be due to the action of many nonprocessive motors on one vesicle acting simultaneously (45, 46), which would likely yield a long stall detachment time 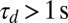due to the long dwell time of individual characean myosins (46). Microfluidic studies indicate that the reorientation timescale 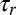lies in-between these two extremes (47), indicating that this reorientation mechanism is indeed viable.

To describe the microfilaments we use a formalism from the theory of active suspensions (35, 48). The full derivation of the dynamics can be found in SI Text; we summarize it here, as follows. At each point on the cylinder, define the angular distribution function 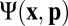of microfilaments with unit direction 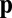. From this, we define the local filament concentration 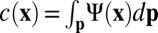and average orientation director 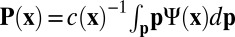. The distribution 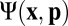obeys a Smoluchowski equation, whose orientational moments yield the dynamics of the concentration and director fields after applying a simple moment closure approximation, whose viability is discussed further in SI Text. Our non–self-advective supposition then reduces the concentration dynamics to pure advection-diffusion (SI Text), allowing us to neglect fluctuations and reduce to a uniform concentration .

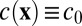The system is closed by defining the flow forcing 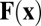. As the filaments are restricted by frictional forces with the outer wall, the primary contribution of a vesicle processing along a filament is a point force (i.e., a Stokeslet), suggesting a simple relationship 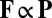. However, global streaming does not persist in the presence of filament unbundling agents, whereas the actin–myosin interaction remains uninhibited (28). Therefore, the flow does not play a role in the linear stability of a disordered suspension, implying that the force must be nonlinear in the local alignment 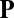(SI Text). We take the lowest nonlinear order permitted by symmetry and write 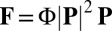. The proportionality constant 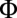encodes the force per unit area generated by vesicles processing along perfectly aligned filaments, and thus includes all information relating to vesicle number, procession speed, and binding rates.

The last step is to nondimensionalize all variables and coupling constants; we scale space by the radius R and choose rescalings to eliminate the friction coefficient ν and the forcing constant 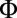(SI Text). The final dynamics for 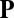read

where all coupling constants are now nondimensional. The parameters 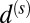and 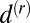are spatial and rotational diffusion constants, respectively. The final hydrodynamics read

subject to

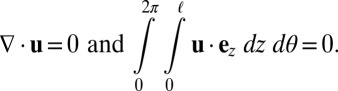All fields have periodic boundary conditions on 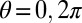and 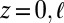, where 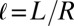is the nondimensional cell length.

Results

To test the model and understand more about the regimes of behavior it possesses, we ran numerical integrations of the system starting from initial conditions of randomly perturbed total filament disorder (Materials and Methods). The parameters 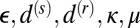were fixed at representative values 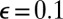, , 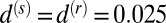, 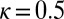and 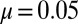to focus on the most important coupling constants 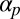and 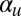. We also chose 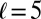as an appropriate radius-to-length ratio for a young cell with observably organized actin cables (36).

Time Progression.

Fig. 4 displays a typical time sequence for numerical integration of the model with an illustrative choice of the parameters 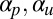. The experimentally observed regeneration progression (28) is clearly reproduced as it moves from disorder, through small patches of locally ordered “streamlets” caused by spontaneous polarization, and settles into fully developed cyclosis as the passive and active reorienting effects of flow reach full potency. Although the polar flow alignment is important for establishing the global streaming pattern, it is worth remarking that the traditional nematic shear alignment, though damped by the restriction factor ϵ, still plays a role: it acts to smooth out curved IZ boundaries between adjacent up- and down-streaming regions, where flow shear is high, into straight lines. This is seen in the later stages of the time evolution in Fig. 4.

Fig. 4.

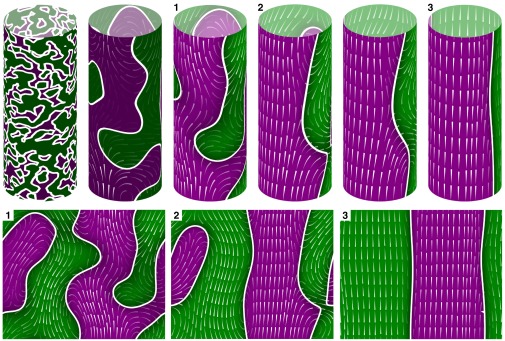
Cyclosis developing in our model for 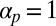and 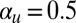, with other parameters fixed as in the text. Color coding corresponds to the z-component of the order vector 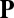, with purple for 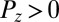and green for 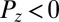, darker for lower magnitude. The white lines represent IZs separating up- and down-streaming regions. Superimposed are streamlines of the cytoplasmic flow 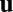induced by the filament field 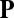, where the flow is directed from the thin end to the thick end of the individual lines. (Upper) Time sequence of six frames, showing progression from random disorder through local order to complete steady cyclosis. (Lower) “Unwrapped” streaming patterns of the three indicated frames.

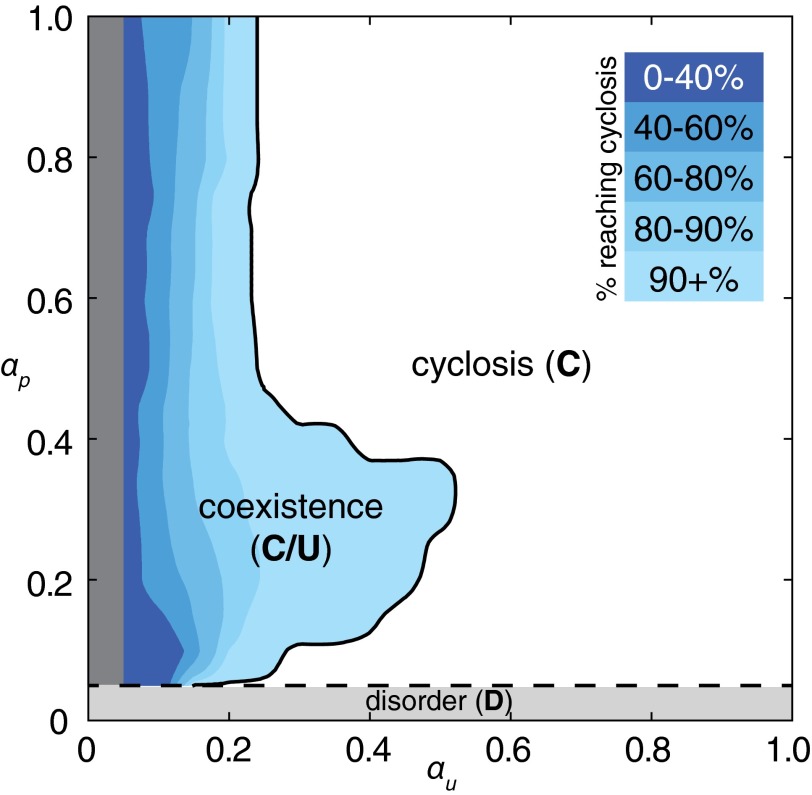
Cyclosis Parameter Scan.

To gauge the model’s robustness, we executed a numerical parameter sweep of nonzero 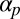and 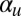both between 0.025 and 1. The parameter space was divided up into a 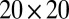grid, and the full set of parameters was simulated for each of 50 different instances of random initial conditions. Combined with a linear stability analysis (SI Text), this detects three distinct regimes (Fig. 5): disorder (D), cyclosis/unidirectional coexistence (C/U), and full cyclosis (C). Parameters in region D have 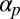too low for spontaneous order to flourish, where the disordered state 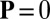is linearly stable. In region C/U, the system may evolve into either the cyclosis state or the unidirectional state 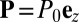(where 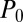is a constant). Which steady state is reached is dependent on the precise nature of the initial conditions, a consequence of coexistence of basins of attraction in the neighborhood of the Fourier space origin. Parameters in region C always developed the desired cyclosis solutions for all sets of initial conditions, indicating that the basin of attraction of the unidirectional state is now negligible. These regimes can be understood further by considering the simplified one-dimensional regime of z-independent and z-parallel alignment, i.e., 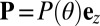(SI Text).

Fig. 5.

Results of a numerical parameter sweep over 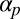and 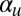between 0.025 and 1, with other parameters held fixed as in the text. The entire set of 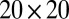parameters was simulated for 50 different random initial conditions, uncovering regions of cyclosis/unidirectional bistability (C/U) and fully robust cyclosis (C). Color coding in region C/U denotes the percentage of the initial conditions that developed into steady cyclosis states at each pair of parameters. Region D, where 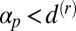, is linearly stable and develops no streaming.

Flow-Stabilized Pattern Formation.

The one-dimensional simplification also allows us to consider the model in the context of pattern formation theory. When 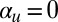, the system assumes nonconservative Allen–Cahn form, for which it can be shown that a spatially oscillating state is always unstable; consequently, fronts separating regions of upward and downward alignment will always eventually coalesce (49). However, 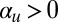introduces a difficult nonlocal term, which cannot be written as the gradient of some free energy functional. In fact, for 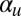above a small threshold, cyclosis solutions are stabilized by global flow alignment effects. The exact threshold as a function of 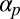can be determined by fixing 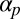and varying 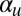to compute trajectories of eigenvalues of the nonlocal Sturm–Liouville problem induced by linear stability analysis. This is discussed further in SI Text.

Discussion

We have demonstrated the capability of this model for simulating the emergence of Characean streaming. For the computational study, we focused on the roles of the polarization and flow-coupling constants 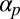and 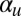. Perhaps the next most important parameter is the directional repulsion κ, which we have not investigated in detail here. The value we chose, 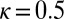, is a nice intermediate providing a definite preference for upward orientation, but not so strong as to completely dominate the early-time dynamics. However, if κ is too small, then little or no directional effects are felt, and the dynamics may be either unsteady or settle into circumferential flows.

In fact, studies of poor, malformed streaming induced in vivo hint at the true effects of removing directional preference. Conversely, a suitable model for streaming should be able to reproduce observed pathologies and experimental disruptions, at least qualitatively, and it is these we now briefly discuss. Total cable fragmentation (28, 30, 50) has already been mentioned and directly corresponds to setting 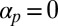to inhibit bundling effects. There is also the possibility of atypical reorganization of the actin cables; to our knowledge, such behavior has not yet been induced in Characean cells. Nevertheless, it has been documented in other types of orderly streaming plant cells, with which a direct comparison can be made owing to the generality of this approach. On inhibiting the binding of the cell membrane to the cell wall, actin cables in Vallisneria mesophyll cells can reorient from longitudinal to circumferential, running around the long axis (40). Similar reorientation can be induced in Lilium pollen tubes, where actin cables reorient circumferentially in regions lacking longitudinal microtubules (41). Both studies supply evidence for the restriction and repulsive direction components of our model. Even though these atypical streaming arrangements were not induced during cell development, such a configuration can be reproduced by choosing parameters appropriately (SI Text).

We have considered the bases of 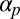(bundling), κ (geometric reorientation), and ϵ (restriction), but how might one experimentally account for the polar alignment coefficient 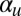? Setting 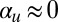corresponds to inhibiting the ability of myosin to walk on actin. In the Characeae, one would also have to disorganize the filament network (28) to observe its effect from a base state. We would then expect a unidirectional streaming pattern to emerge, or at least a metastable cyclosis with unequal widths of opposing streams, as the filaments bundle. Such an experiment would be an exciting test of the principal ideas on which this conceptually simple yet powerful self-organization model has been built.

Materials and Methods

Simulation Method.

Simulations were performed using spectral methods, evaluating gradients and evolving in time in Fourier space and moving into physical space to evaluate nonlinearities. The periodic boundary conditions were then implicit in choosing a Fourier basis. Explicit fourth-order Runge–Kutta integration was used for time evolution.

Initial Conditions.

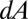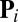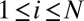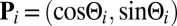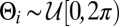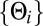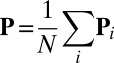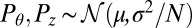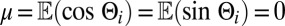For all simulations, the initial conditions were of total filament disorder as follows. Suppose in a small area there are filaments whose orientations , , are uniformly distributed, i.e., , where . Then because the are independent and identically distributed random variables, the central limit theorem applies to , giving that with and 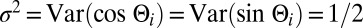. Therefore, to model an initial distribution of 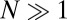filaments per grid square, initial conditions are drawn as 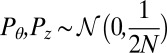. 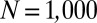was taken for all simulations.