Skip to main content
PMC home page
Journal of Sports Science & Medicine logoLink to Journal of Sports Science & Medicine
. 2010 Jun 1;9(2):282–287.

Analysis of the Vertical Ground Reaction Forces and Temporal Factors in the Landing Phase of a Countermovement Jump

Daniel Rojano Ortega 1,✉, Elisabeth C Rodríguez Bíes 1, Francisco J Berral de la Rosa 1
PMCID: PMC3761745  PMID: 24149697

Abstract

In most common bilateral landings of vertical jumps, there are two peak forces (F1 and F2) in the force-time curve. The combination of these peak forces and the high frequency of jumps during sports produce a large amount of stress in the joints of the lower limbs which can be determinant of injury. The aim of this study was to find possible relationships between the jump height and F1 and F2, between F1 and F2 themselves, and between F1, F2, the time they appear (T1 and T2, respectively) and the length of the impact absorption phase (T). Thirty semi-professional football players made five countermovement jumps and the highest jump of each player was analyzed. They were instructed to perform the jumps with maximum effort and to land first with the balls of their feet and then with their heels. All the data were collected using a Kistler Quattro Jump force plate with a sample rate of 500 Hz. Quattro Jump Software, v.1.0.9.0., was used. There was neither significant correlation between T1 and F1 nor between T1 and F2. There was a significant positive correlation between flight height (FH) and F1 (r = 0.584, p = 0.01) but no significant correlation between FH and F2. A significant positive correlation between F1 and T2 (r = 0.418, p < 0.05) and a significant negative correlation between F2 and T2 (r = -0.406, p < 0.05) were also found. There is a significant negative correlation between T2 and T (r = -0. 443, p < 0.05). T1 has a little effect in the impact absorption process. F1 increases with increasing T2 but F2 decreases with increasing T2. Besides, increasing T2, with the objective of decreasing F2, makes the whole impact absorption shorter and the jump landing faster.

Key points.

  • In the landing phase of a jump there are always sev-eral peak forces. The combination of these peaks forces and the high frequency of jumps during sports produces a large amount of stress in the joints of the lower limbs which can be determinant of injury.

  • In the most common two-footed landings usually appear two peak forces (F1 and F2) in the force-time curve and the second one is usually related to injury’s risk. In this article it is shown that increasing the time F2 appears decrease F2.

  • Increasing landing times could be counterproductive with respect to the goals of the sport. In this article it is shown that increasing the time F2 appears makes, however, the whole impact absorption shorter in du-ration.

Key words: Impact absorption, peak forces, vertical jump, injuries

Introduction

The vertical jump is an essential motor skill in many sports (McNitt-Gray, 1991). The success or failure of a sportive action strongly depends on the ability of the athlete to jump high and fast (McNitt-Gray, 1991; Reiser et al., 2006). This is the reason why many studies have analyzed the vertical jump from a physical point of view, to establish the factors that have to be improved to increase jump height (Aura and Viitasalo, 1989; Bobbert and Van Ingen Schenau, 1988; Cross, 1998; Dowling and Vamos, 1993; Innocenti et al., 2006; Linthorne, 2001; Offenbacher, 1970; Reiser et al., 2006; Tomioka et al., 2001; García et al., 2003). It is common in many sports to perform unloaded or loaded jump series with the objective of increasing jump height and explosive strength. However, not many athletes remember being coached on how to land these jumps.

Nonetheless, many activities in sports require landings from a jump (McNitt-Gray, 1991; Reiser et al., 2006). The vertical ground reaction forces (GRF) on the body during landing, can be determinants of injury, especially if the jumps are made very often and the GRF are high (Mizrahi and Susak, 1982; McNair et al., 2000). Coleman et al., 1984 reported that a United States volleyball team performed 300 to 500 spikes and block jumps in a four- hour session of training. Lian et al., 1996 reported that volleyball involved approximately 60 maximal jumps per hour of game play. McClay et al., 1994 found that elite basketball teams averaged 70 jumps per game. These data cannot be extrapolated to the entire sports world, but they give us a good idea of the relevance of jumping in many sports and the number of high impact forces that an elite athlete suffers during the practice of any of these sports.

Impact forces may contribute to optimal skeletal health (Fuchs et al., 2001; 2002). However, if the frequency of the impact forces is very high, it is advisable to decrease these impacts under certain limits to also decrease the risk of injury of the joints involved (Bressel and Cronin, 2005). Henry et al., 1982 and Zelisko et al., 1982 analyzed the injury rate in professional basketball. They affirmed that many players could not relate their injuries to one incident but complained rather of a problem that was chronic. Richie et al., 1985 analyzed the injury rate in aerobic dancers. They related the injury rate to factors like frequency of participation in aerobic dance, floor surfaces, shoes and participating in other sports such as running. These articles support the idea that it is the repetition of the impact forces, especially if these impact forces are high, which can be determinant of injury.

There are many different ways of landing a vertical jump (Chockley, 2006; Ozguven and Berme, 1988; Tillman et al., 2004). For bilateral landings, the literature differentiates basically between two types: one that is made with flat feet and one that is made first with the forefoot and then with the rearfoot. The last type is the most common when the landing is made consciously, and the vertical GRF are smaller for this type than for the flat-footed landing (Bressel and Cronin, 2005; Chockley, 2006; McClay et al., 1994; Ozguven and Berme, 1988; Self and Paine, 2001). The non-flat-footed bilateral landings show two peak vertical forces in the force-time curve, as it can be observed in Figure 1. The first is produced by the impact of the metatarsal heads, and the second by the impact of the calcaneus (Abián et al., 2006; 2008; Bressel and Cronin, 2005; McClay et al., 1994; Mizrahi and Susak, 1982; Ozguven and Berme, 1988; Seegmiller and McCaw, 2003; Zhang et al., 2005). Sometimes there is also a third peak usually much smaller than the other two. This third peak is normally related to the maximum dorsal flexion degree of the ankle, and the study of this third peak force is beyond the scope of this study.

Figure 1.

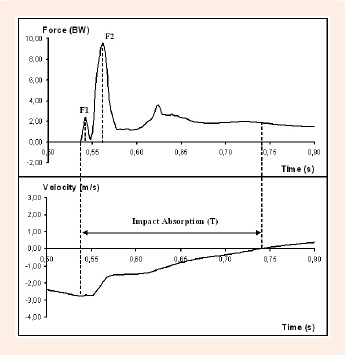
Figure 1.

Open in a new tab

Swimming performance in 25 m front crawl at the beginning of the protocol Force-time and velocity-time curves obtained with a force plate during the landing phase of a countermovement jump. F1 and F2 are the first and the second peak vertical forces. T is the length of the impact absorption.

The landings made first with the balls of the feet and then with the heels, produce smaller peak forces compared with the landings with the feet flat. However, even with the first type of landing, Bressel and Cronin, 2005 affirm that it is possible to have two bigger peaks in a small amount of time (hard landing) or two smaller peaks over a longer period of time (soft landing). Thus, making hard landings with a high frequency can also produce a great amount of stress in the joints of the lower limbs. This stress can be determinant of injury (Bressel and Cronin, 2005). Some studies have matched only the second peak, corresponding to the impact of the heel, with injury risk in sports (Dufek and Bates, 1991; McNair and Marshall, 1994; Mizrahi and Susak, 1982). Ferreti and Papandrea, 1992; Lian et al., 1996 and Richards et al., 1996 have found that good jumpers have a larger number of injuries because they have higher peak forces.

Therefore, it is recommended to improve landing technique by increasing the landing times to decrease impact forces (Bressel and Cronin, 2005; Ferreti and Papandrea, 1992; McNair et al., 2000; Reiser et al., 2006; Rubio et al., 2006). It is possible to increase landing time by flexing at the hip, knee and ankles with the proper coordination (Bressel and Cronin, 2005; Reiser et al., 2006; Rubio et al., 2006). However, increasing landing times could be counterproductive with respect to the goals of the sport. A slow landing after getting a basketball rebound, for example, can decrease effectiveness on the court. The aim of this study was to find possible relationships between jump height and the two peak vertical forces, and also between these two peaks, the time elapsed from the beginning of the landing phase to the appearance of each peak, and the duration of the impact absorption phase. The results obtained here can be useful for future investigations about the necessity of decreasing the first, the second or both peak forces and for the improvement of the coordination of the muscles involved in the process of absorbing impact forces, with the objective of decreasing the risk of injuries.

Methods

Subjects

A group of thirty semi-professional football players was studied and the countermovement jump was analyzed. All the players trained 8 hours per week on average and played in the Spanish Third Division. They had a mean age of 27.41 ± 3.99 years, a mean body mass of 76.62 ± 4.77 kg and a mean height of 1.75 ± 0.07 m. All the players gave informed consent according to the Declaration of Helsinki.

Study design

The jump made to evaluate the vertical GRF was a countermovement jump (CMJ) because the technique of this jump was easy to learn. The CMJ is a vertical jump made with the contribution of the stretch- shorten cycle. The subject starts from an upright standing position with the hands on the hips and begins with a preliminary downward movement by flexing at the knees and hips (eccentric phase) Then the knees and hips are immediately extended again to jump vertically (concentric phase). There is a minimum stop between the eccentric and the concentric phases to take advantage of the energy stored by the elastic elements of the muscles. In the exact protocol the knee angle at the end of the eccentric phase must be about 90° (Bosco, 1999; González and Ribas, 2002). However, following the actual trends, the knee angle was not controlled.

Two preparatory sessions took place the week before the data collection. In the first, the participants were instructed on the CMJ technique, and in the second they made several jumps on the force plate to become familiarized with it. The subjects performed five CMJs. They were instructed to use maximum effort and to land first with the balls of the feet and then with the heel. Only the jump with the greatest flight height was selected for analysis. It was assumed that the jumps were maximal, but this was not really necessary for our study.

Force-time curve analysis

All the data were collected using a Kistler Quattro Jump force plate with a sample rate of 500 Hz. Hori et al., 2009 found that the reliability assessed by intraclass correlation coefficient (ICC) for peak force (0. 92), peak velocity (0.98) and peak power (0.98) of a CMJ measured with a force plate like ours was very high. We used Quattro Jump Software, v.1.0.9.0. This program gave us the force-time, velocity- time and displacement-time curves. The force-time curve was obtained directly using the platform. The resultant force acting on the jumper’s center of mass was the ground reaction force obtained directly by the platform minus the weight of the jumper. The velocity-time curve was obtained by dividing the resultant force by the jumper’s body mass, obtaining the acceleration and then numerically integrating with respect to time using the trapezoid rule. The displacement of the center of mass was obtained by numerically integrating the velocity with respect to time, using again the trapezoid rule. Thus, the height of the centre of mass was obtained with a double integration method.

All these data were copied to a Microsoft Office Excel 2003 spreadsheet for the analysis. Within the curves, we measured the maximum height (MH), the flight height (FH), the two peak vertical forces in the landing phase (F1 and F2) normalized to the body weight, the moment the landing phase begins, the times at which F1 and F2 occur and the moment the center of mass velocity becomes zero, for the first time after the beginning of the landing, which is the moment we considered to represent the end of the landing phase.

The MH is the difference between the position of the subject’s centre of mass when standing upright and the subject’s center of mass at the highest part of the flight. The FH is the difference between the subject's center of mass at take-off (with the ankles extended) and the subject’s center of mass at the highest part of the flight. Thus, the flight height is always some centimeters smaller than the maximum height. From the temporal data collected we obtained the following values: the length of the impact absorption phase (T), the time elapsed between the two peak forces (TP) and the time elapsed from the beginning of the landing phase to F1 (T1) and to F2 (T2). In the type of landing of this study, impact absorption starts when the jumper’s toes touch the ground. This is the moment that the center of mass has maximal downward velocity and the moment that the velocity starts to decrease after the flight. The impact absorption is ended at the lowest position of the center of mass, when its velocity becomes zero.

Statistical analysis

The statistical analysis was made with the program SPSS for Windows, v. 13.0. We calculated the means and standard deviations of all the variables measured, and we analyzed the possible relationships between the variables using the Pearson correlation coefficient. Results were considered significant at p < 0.05.

Results

For all the variables of the thirty jumps analyzed, the mean values and the standard deviations were calculated (Table 1). Table 2 shows the Pearson correlation coefficient between MH, FH, F1 and F2 (Figure 1). There is a significant positive correlation between MH and F1 (r = 0.567, p < 0.01) and between FH and F1 (r = 0.584, p = 0.01). There is no significant correlation between any of the heights and F2. There is a significant positive correlation between MH and FH (r = 0.814, p < 0.01).

Table 1.

Descriptive statistic of the variables (n = 30) of the study.

Mean (±SD) Min Max
F1 (BW) 2.58 (.85) 1.10 5.86
F2 (BW) 9.92 (3.02) 4.50 17.19
TP (s) .030 (.011) .006 .062
T1 (s) .014 (.005) .008 .030
T2 (s) .045 (.013) .014 .078
T (s) .144 (.034) .080 .228
MH (cm) 45.2 (5.2) 37.4 60.5
FH (cm) 33.9 (3.5) 28.3 40.7
Open in a new tab

F1: first peak vertical force; F2: second peak vertical force; TP: time between peaks; T1: time F1 appears; T2: time F2 appears; T: length of the impact absorption phase; MH: maximum height; FH: flight height.

Table 2.

Pearson correlation coefficient between maximum height (MH) or flight height (FH) and peak vertical forces (F1 and F2) (n = 30).

F1 F2 MH FH
F1 Pearson Correlation 1 -.027 .567(**) .584(**)
Sig. (2-tailed) .886 .001 .001
F2 Pearson Correlation -.027 1 .157 .066
Sig. (2-tailed) .886 .406 .730
MH Pearson Correlation .567(**) .157 1 .814(**)
Sig. (2-tailed) .001 .406 .000
FH Pearson Correlation .584(**) .066 .814(**) 1
Sig. (2-tailed) .001 .730 .000
Open in a new tab

** Correlation is significant at the 0.01 level (2-tailed).

We also calculated the Pearson correlation coefficient between each of the following variables: F1, F2, T1, TP, T2 and T (Table 3). There is a significant positive correlation between F1 and TP (r = 0.412, p < 0.05) and between F1 and T2 (r = 0.418, p < 0.05). There is a significant negative correlation between F2 and TP (r = -0.417, p < 0.05) and between F2 and T2 (r = -0.406, p < 0.05). There is a significant positive correlation between TP and T2 (r = 0.939, p < 0.01) and a significant negative correlation between TP and T (r = -0.383, p < 0.05). There is a significant positive correlation between T1 and T2 (r = 0.545, p < 0.01) and there is a significant negative correlation between T2 and T (r = -0.443, p < 0.05).

Table 3.

Pearson correlation coefficient between peak vertical forces (F1 and F2) and the temporal factors: time F1 and F2 appear (T1 and T2), time between peaks (TP) and length of the impact absorption phase (T) (n = 30).

F1 F2 TP T1 T2 T
F1 Pearson Correlation 1 -.027 .412(*) .181 .418(*) -.124
Sig. (2-tailed) .886 .024 .338 .022 .513
F2 Pearson Correlation -.027 1 -.417(*) -.136 -.406(*) -.100
Sig. (2-tailed) .886 .022 .474 .026 .598
TP Pearson Correlation .412(*) -.417(*) 1 .225 .939(**) -.383(*)
Sig. (2-tailed) .024 .022 .233 .000 .037
T1 Pearson Correlation .181 -.136 .225 1 .545(**) -.321
Sig. (2-tailed) .338 .474 .233 .002 .084
T2 Pearson Correlation .418(*) -.406(*) .939(**) .545(**) 1 -.443(*)
Sig. (2-tailed) .022 .026 .000 .002 .014
T Pearson Correlation -.124 -.100 -.383(*) -.321 -.443(*) 1
Sig. (2-tailed) .513 .598 .037 .084 .014
Open in a new tab

* Correlation is significant at the 0.05 level (2-tailed).

** Correlation is significant at the 0.01 level (2-tailed).

Discussion

The mean values of F1 and F2 were 2.58 ± 0.85 BW and 9.92 ± 3.02 BW (times body weight), respectively. The mean values of MH and FH were 45.17 ± 5.18 cm and 33.88 ± 3.52 cm, respectively. Our values of F2 are higher than those found by Abián et al., 2008, who obtained 7.51 ± 2.38 BW for landings from 35.5 ± 4.5 cm height, height quite similar to that in our study (33.88 ± 3.52 cm). Their values are probably lower than ours because they analyzed jumps made by applicants to a faculty of sports sciences during the tests for application, and these applicants had prepared for the tests for a long time, so they were familiarized with the jump technique, including the landing phase.

The impact absorption phase lasted 144ms, with a standard deviation of 33 ms. These values agree with the results shown by Lees, 1981, who concluded that this phase lasted for only 150-200 ms. F1 and F2 appear at 15 ± 5 ms and 45 ± 13 ms, respectively, after the first contact of the toes. These values are in very good agreement with those found by McNitt-Gray, 1991 and Abián et al., 2008, who affirmed that F1 appeared approximately 10 ms after the first contact and F2 appeared at any instant between 30 and 70 ms, depending on the foot length and the activation of the plantar flexor muscles.

There was a significant positive correlation between MH and FH (r = 0.814 and p < 0.01). This is logical because a large percentage of MH comes from jump flight, and only a small percentage comes from the ankle extension before the take-off. The fact that there is a significant positive correlation between MH and F1 (r = 0.567 and p < 0.01) and between FH and F1 (r = 0.584 and p = 0.01) shows that, in a countermovement jump with our type of landing, F1 increases with increasing jump height. There was no correlation of F2 with any of the heights. We confirm, therefore, the conclusion of Rubio et al., 2006 that the landing technique must be the main responsible for decreasing this peak force.

There was neither significant correlation between T1 and F1 nor between T1 and F2. In addition, the mean value found for T1 (14 ± 5 ms) and the low variability found for it in other studies (McNitt-Gray, 1991; Abián et al., 2008), leads us to the conclusion that T1 is not easy to modify and has a little effect in the impact absorption process. The significant positive correlations between TP and F1 (r = 0.412 and p < 0.05) and between T2 and F1 (r = 0.418 and p < 0.05) suggest that F1 increases when any of these times is increased. The opposite happens with F2, because the significant negative correlations with TP (r = -0.417 and p < 0.05) and with T2 (r = -0.406 and p < 0.05), suggest that F2 decreases when any of these times is increased.

This means that even when we found no significant correlation between F1 and F2, the impact absorptions of the two peaks are not really independent processes because increasing T2 or TP with the objective of decreasing F2 can also increase F1. There was a very high significant positive correlation (r = 0.939 and p < 0.01) between TP and T2 which explain the similar behaviour of these two variables with regard to F1 and F2. There was a significant negative correlation between T2 and T (r = -0.443 and p < 0.05), which implies that T decreases with increasing T2, thereby resulting in a shorter whole impact absorption, with a lower F2 value.

Conclusion

Although the landing takes place over nearly 1 s, the impact absorption phase lasted for only 144 ± 33 ms. The rest of the time is concerned with the maintenance of the balance and the return of the center of mass to the standing position. It is possible to decrease F2 increasing T2. According to most studies which match F2 with the risk of injury (Dufek and Bates, 1991; McNair and Marshall, 1994; Mizrahi and Susak, 1982), this is very useful to decrease that risk. However, increasing T2 to decrease F2 can also increase F1.

It seems logical to think that increasing T2 (to decrease F2) would make the jump landing slower, being counterproductive with respect to the goals of the sport. However, in our study we have found that increasing T2 makes the whole impact absorption shorter and the jump landing faster. The knowledge of these results can be useful for future investigations about the process of absorbing impact forces. It can also be useful for coaches to improve the performance and decrease the risk of injuries.

Biographies

graphic file with name jssm-09-282-g002.gif

Daniel Rojano Ortega

Employment

Graduate in Physics, Master in High Sport Capacity, University Pablo de Olavide, Sevilla, Spain.

Degree

MSc.

Research interests

Biomechanics in sport.

E-mail: drojort@upo.es

graphic file with name jssm-09-282-g003.gif

Elisabeth C. Rodríguez Bíes

Employment

Graduate in Physical Education, Master in High Sport Capacity, University Pablo de Olavide, Sevilla, Spain.

Degree

MSc.

Research interests

Biomechanics in sport.

E-mail: ecrodbie1@upo.es

graphic file with name jssm-09-282-g004.gif

Francisco J. Berral de la Rosa

Employment

Doctor in Medicine and Surgery, Spe-cialist in Sport Medicine, University Pablo de Olavide, Sevilla, Spain.

Degree

MD, PhD.

Research interests

Medicine and sport.

E-mail: fjberde@upo.es

References

  1. Abián J., Alegre L.M., Lara A.J., Aguado X. (2006) Diferencias de sexo durante la amortiguación de caídas en tests de salto. Archivos de Medicina del Deporte 116, 441-449 (In Spanish: English abstract) [Google Scholar]
  2. Abián J., Alegre L.M., Lara A.J., Rubio J.A., Aguado X. (2008) Landing differences between men and women in a maximal vertical jump aptitude test. Journal of Sports Medicine & Physical Fitness 48, 305-310 [PubMed] [Google Scholar]
  3. Aura O., Viitasalo J.T. (1989) Biomechanical Characteristics of Jumping. International Journal of Sports Biomechanics 5, 89-98 [Google Scholar]
  4. Bobbert M.F., Van Ingen Schenau G.J. (1988) Coordination in Vertical Jump. Journal of Biomechanics 21(3), 249-262 [DOI] [PubMed] [Google Scholar]
  5. Bosco C. (1999) Strength Assessment with the Bosco’s Test. Rome: Italian Society of Sport Science.68 [Google Scholar]
  6. Bressel E., Cronin J. (2005) The Landing Phase of a Jump: Strategies to Minimize Injuries. Journal of Physical Education, Recreation & Dance 76(2), 31-47 [Google Scholar]
  7. Chockley C. (2006) Ground reaction force comparison between jumps landing on the full foot and jumps landing en pointe in ballet dancers. Paper presented at the 16th Annual Meeting of the International Association for Dance Medicine and Science, Palm Beach, USA. [PubMed] [Google Scholar]
  8. Coleman J., Adrian M.J., Yamamoto H. (1984) The teaching of the mechanics of jump landing. Paper presented at the Second National Symposium on Teaching Kinesiology and Biomechanics in Sport, Colorado Springs, USA. [Google Scholar]
  9. Cortes N., Onate J., Abrantes J., Gagen L., Dowling E., Van Lunen B. (2007) Effect of gender and foot-landing techniques on lower extremities kinematics during drop-jump landings. Journal of Applied Biomechanics 23(4), 289-299 [DOI] [PubMed] [Google Scholar]
  10. Cross R. (1998) Standing, walking, running and jumping on a force plate. American Journal of Physics 67(4), 304-309 [Google Scholar]
  11. Dowling J.J., Vamos L. (1993) Identification of kinetic and temporal factors related to vertical jump performance. Journal of Applied Biomechanics 9, 95-110 [Google Scholar]
  12. Dufek J.S., Bates B.T. (1991) Biomechanical factors associated with injury during landing in jump sports. Sports Medicine 12, 326-337 [DOI] [PubMed] [Google Scholar]
  13. Ferreti A., Papandrea P. (1992) Knee ligament injuries in volleyball players: A longitudinal evaluation. Journal of Sports Medicine & Physical Fitness 36, 35-42 [Google Scholar]
  14. Fuchs R.K., Bauer J.J., Snow C.M. (2001) Jumping improves hip and lumbar spine bone mass in prepubescent children: A randomized controlled trial. Journal of Bone & Mineral Research 16(1), 148-156 [DOI] [PubMed] [Google Scholar]
  15. Fuchs R.K., Cusimano B., Snow C.M. (2002) Box jumping: A bone-building exercise for elementary school children. Journal of Physical Education, Recreation & Dance 73(2), 22-25 [Google Scholar]
  16. García J., Peleteiro J., Rodríguez J.A., Morante J.C., Villa J.G. (2003) Validación biomecánica de un método para estimar la altura de salto a partir del tiempo de vuelo. Archivos de Medicina del Deporte 93, 28- 34 (In Spanish: English abstract) [Google Scholar]
  17. González J.J., Ribas J. (2002) Programación del Entrenamiento de Fuerza. Barcelona: INDE Publicaciones.327 [Google Scholar]
  18. Henry J.H., Lareau B., Neigut D. (1982) The injury rate in professional basketball. American Journal of Sports Medicine 10(1), 16-18 [DOI] [PubMed] [Google Scholar]
  19. Hori N., Newton R.U., Kawamori N., McGuigan M.R., Kraemer W.J., Nosaka K. (2009) Reliability of performance measurements derived from Ground Reaction Force data during Countermovement Jump and the influence of Sampling Frequency. Journal of Strength and Conditioning Research 23(3), 874-882 [DOI] [PubMed] [Google Scholar]
  20. Innocenti B., Facchielli D., Torti S., Verza A. (2006) Analysis of Biomechanical Quantities During a Squat Jump: Evaluation of a Perfomance Index. Journal of Strength & Conditioning Research 20(3), 709-715 [DOI] [PubMed] [Google Scholar]
  21. Lees A. (1981) Methods of impact absorption when landing from a jump. Engineering in Medicine 10, 207-211 [Google Scholar]
  22. Lian O., Engebretsen L., Ovrebo R.V., Bahr R. (1996) Characteristics of the leg extensors in male volleyball players with jumper’s knee. American Journal of Sports Medicine 24(3), 380-385 [DOI] [PubMed] [Google Scholar]
  23. Linthorne N.P. (2001) Analysis of standing vertical jumps using a force platform. American Journal of Physics 69(11), 1198-1204 [Google Scholar]
  24. McClay I.S., Robinson J.R., Andriacchi T.P., Frederic E.C., Gross T., Marin P., Valiant G., Williams K.R., Cavanagh P.R. (1994) A profile if ground reaction forces in professional basketball. Journal of Applied Biomechacics 10, 222-236 [Google Scholar]
  25. McNair P.J., Marshall R.N. (1994) Landing characteristics in subjects with normal and anterior cruciate ligament deficient knee joints. Archives of Physical Medicine & Rehabilitation 75, 584-589 [PubMed] [Google Scholar]
  26. McNair P.J., Prapavessis H., Callender K. (2000) Decreasing landing forces: effect of instruction. British Journal of Sports Medicine 34, 293-296 [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. McNitt-Gray J. (1991) Kinematics and impulse characteristics of drop landings from three heights. International Journal of Sports Biomechanics 7, 201-223 [Google Scholar]
  28. Mizrahi J., Susak Z. (1982) Analysis of parameters affecting impact force attenuation during landing in human vertical free fall. Engineering in Medicine 11, 141-147 [DOI] [PubMed] [Google Scholar]
  29. Offenbacher E.L. (1970) Physics and the Vertical Jump. American Journal of Physics 38(7), 829-836 [Google Scholar]
  30. Ozguven H.N., Berme N. (1988) An experimental and analytical study of impact forces during human jumping. Journal of Biomechanics 21(12), 1061-1066 [DOI] [PubMed] [Google Scholar]
  31. Reiser R.F., Rocheford E.C., Armstrong C.J. (2006) Building a better understanding of basic mechanical principles through analysis of the vertical jump. Strength & Conditioning Journal 28(4), 70-80 [Google Scholar]
  32. Richards D.P., Ajemain S.V., Wiley J.P., Zernicke R.F. (1996) Knee joint dynamics predict patellar tendonitis in elite volleyball players. American Journal of Sports Medicine 24(5), 676-683 [DOI] [PubMed] [Google Scholar]
  33. Richie D.H., Celso S.F., Bellucci P.A. (1985) Aerobic dance injuries: a retrospective study of instructors and participants. The Physician & Sportsmedicine 13(2), 130-140 [DOI] [PubMed] [Google Scholar]
  34. Rubio J.A., Abián J., Alegre L.M., Lara A.J., Sordoz S., Aguado X. (2006) Analysis of two jump tests and their landing phase in a group of school aged children. Poster presented at the 11th Annual Congress of the European College of Sport Science, Lausanne, Switzerland. [Google Scholar]
  35. Seegmiller J.G., McCaw S.T. (2003) Ground reaction forces among gymnasts and recreational athletes in drop landings. Journal of Athletic Training 38(4), 311-314 [PMC free article] [PubMed] [Google Scholar]
  36. Self B.P., Paine D. (2001) Ankle biomechanics during four landing techniques. Medicine & Science in Sports & Exercise 33(8), 1338-1344 [DOI] [PubMed] [Google Scholar]
  37. Tillman M.D., Hass C.J., Brunt D., Bennet G.R. (2004) Jumping and landing techniques in elite women’s volleyball. Journal of Sports Science & Medicine 3, 30-36 [PMC free article] [PubMed] [Google Scholar]
  38. Tomioka M., Owings T.M., Grabiner M.D. (2001) Lower extremity strength and coordination are independent contributors to maximum vertical jump height. Journal of Applied Biomechanics 17, 181-187 [Google Scholar]
  39. Zelisko J.A., Noble H.B., Porter M.A. (1982) Comparison of men’s and women’s professional basketball injuries. American Journal of Sports Medicine 10(5), 297-299 [DOI] [PubMed] [Google Scholar]
  40. Zhang S., Clowers K., Kohstall C., Yu Y.J. (2005) Effects of various midsole densities of basketball shoes on impact attenuation during landing activities. Journal of Applied Biomechanics 21, 3-17 [DOI] [PubMed] [Google Scholar]

Articles from Journal of Sports Science & Medicine are provided here courtesy of Dept. of Sports Medicine, Medical Faculty of Uludag University

RESOURCES