Abstract
A proper distance metric is fundamental in many computer vision and pattern recognition applications such as classification, image retrieval, face recognition and so on. However, it is usually not clear what metric is appropriate for specific applications, therefore it becomes more reliable to learn a task oriented metric. Over the years, many metric learning approaches have been reported in literature. A typical one is to learn a Mahalanobis distance which is parameterized by a positive semidefinite (PSD) matrix M. An efficient method of estimating M is to treat M as a linear combination of rank-one matrices that can be learned using a boosting type approach. However, such approaches have two main drawbacks. First, the weight change across the training samples maybe non-smooth. Second, the learned rank-one matrices might be redundant. In this paper, we propose a doubly regularized metric learning algorithm, termed by DRMetric, which imposes two regularizations on the conventional metric learning method. First, a regularization is applied on the weight of the training examples, which prevents unstable change of the weights and also prevents outlier examples from being weighed too much. Besides, a regularization is applied on the rank-one matrices to make them independent. This greatly reduces the redundancy of the rank-one matrices. We present experiments depicting the performance of the proposed method on a variety of datasets for various applications.
1 Introduction
The choice of an appropriate distance or similarity measure over the input space is critical to many computer vision and pattern recognition applications, including but not limited to clustering and classification [1–3], image retrieval [4], shape detection [5], face recognition [6–11], tracking [12]. There are many commonly used distance metrics, e.g. Euclidean distance, L1-norm distance, χ2 distance, and Mahalanobis distance etc. However, it is usually very hard to predict which distance measure is appropriate for a certain application with specific inputs. Therefore, it is more apt to develop a task-dependent metric based on the available knowledge of the inputs. It was shown [1, 3, 11] that a properly designed distance metric, compared with the standard distances, can significantly improve the performance for many applications.
There are a lot of metric learning algorithms in the literature. A good metric learning algorithm should be able to learn a metric that can amplify informative dimensions (feature) and squash non-informative dimensions. This is unlike Euclidean distance, which treats every dimension equally and does not consider the correlation between them.
In most cases, metric learning algorithms are derived from the labeled training datasets, and the goal of the algorithm is to learn a metric which can separate the instances of different classes apart, and bring together the instances belonging to the same class. To be specific, the labeling of the inputs can be provided mainly in three ways. First, the input constraint is (xi, yi) where xi ∈ ℝD is an instance and yi is its label. Second, the input constraint is ((xi, xj),yij) where yij indicates whether xi and xj are “similar” or “dissimilar” [13]. An even weaker representation often used in information retrieval [14] is the proximity relationship over triplets (i, j, k), meaning that xi is closer to xj than to xk. Proximity relationships are the most natural constraint for learning a metric, and are of the weakest representation because proximity triplets can be derived from the other kinds of constraints, but not vice versa.
In this paper, we propose a doubly regularized metric learning algorithm, termed by DRMetric. Our goal is to learn a Mahalanobis distance metric which tries to preserve the proximity relationships over the input. Mahalanobis distance metric is parameterized by a positive semidefinite (PSD) matrix [15, 16]1. It has been well studied and advantages were shown over some other metrics such as multidimensional scaling (MDS) [17], ISOMAP [18], and locally linear embedding (LLE) [19].
Several aspects of our DRMetric are novel. First, we use the total Kullbak-Leibler (tKL) divergence [20] to regularize the evolution of the weights on the training triplets. tKL is a recently proposed divergence which has been proved to be statistically robust [20]. The regularization automatically ensures that the weight of the examples is upper bounded, therefore, the weight can not be extremely large for outliers. Note that without regularization, the weight of an outlier example will keep increasing, which may lead to serious problems such as overfitting and inefficiency. Furthermore, for some noisy examples, their weight may depict severe oscillations. This not only hampers the convergence rate of the metric learning algorithm, but also leads to overfitting, and lowers the accuracy. Second, we regularize the rank-one PSD matrices to minimize the dependence between them. This regularization makes the rank-one matrices least correlated, and therefore least redundant, which greatly decreases the number of rank-one matrices needed and improves the efficiency.
The rest of the paper is organized as follows. In Section 2, we briefly review the metric learning literature. In Section 3, we present the doubly regularized linear programming metric learning algorithm, termed by DLMetric. In Section 4, we investigate DLMetric empirically by evaluating our algorithm on a number of datasets for various applications. We also compare our method with the state-of-the-art metric learning and other algorithms. Finally, we conclude the paper in Section 5.
2 Literature review
A good task dependent metric has attracted extensive attention recently. The machine learning community has done many researches to automatically learn a distance function from available knowledge of the dataset [15, 21, 22, 13]. Most existing works assume the metrics to be Mahalanobis distance, which are parameterized by PSD matrices.
Various techniques have been proposed to learn a PSD matrix from the dataset. Some techniques force the negative eigenvalues in the learned symmetric matrix to be zero as in [13]. Some others set the matrix to be the inverse of the covariance matrix of the centered data points in small subsets of points with known relevant information [15]. In [22], the matrix exponential gradient update was used which preserves symmetry and positive definiteness due to the fact that the matrix exponential of a symmetric matrix is always an SPD matrix. In [23], Iwasawa factorization was used to ensure the positive definiteness [23]. Most of these techniques are limited from a scalability or a computational complexity view point.
More recently, some researchers [1, 14] adapted the boosting technique to metric learning. This kind of metric learning is based on an important theorem that a PSD matrix with trace one can always be represented as a convex combination of multiple rank-one PSD matrices. This is a generalization of boosting [24] in the sense that the weak learner in these metric learning algorithms is a rank-one matrix instead of a classifier. The main idea behind these boosting-based metric learning algorithms is that at each iteration, they will learn a rank-one matrix from the training examples that follow a distribution. The weighted rank-one matrix is then added to the PSD matrix. This weight is typically related to the rank-one matrix's ability to discriminate the examples from different classes. The higher the discriminatory power, the larger the weight, and vise versa. After learning the rank-one matrix, the distribution of the examples is updated. The examples are reweighted according to the rule that misclassified examples tend to gain weight and correctly classified examples tend to lose weight. Therefore, the rank-one matrices to be learned will be focused more on the examples that were misclassified previously.
However, these methods are not statistically robust i.e., the learning process is sensitive to noisy data and outliers [25, 26]. The reason is that the weight of noisy examples might switch between severe increase and severe decrease frequently, which seriously slows down the convergence of the learning process. Furthermore, the weight of outliers might keep increasing, which largely affects the metric to be learned. To avoid these issues and inspired by the regularized boosting [25, 26] techniques, we propose a regularized metric learning algorithm, which regularizes the weight updating process involved in the training stage. Furthermore, in order to reduce the redundancy of the learned rank-one matrices, we add another regularization term to make the dependence between the learned rank-one matrices as small as possible. In this way, we can use much fewer number of rank-one matrices (i.e. much fewer number of iterations) to form the PSD matrix which parameterizes a suitable metric. Experimental results illustrate that for a dataset of D dimensions, DRMetric is able to learn a relatively good metric in D iterations.
3 Proposed method
Given a dataset X = {xi}, with xi ∈ ℝD, and its associated triplet set
 = {(i, j, k)}, with (i, j, k) meaning that xi is more similar to xj than to xk. Let N = |
= {(i, j, k)}, with (i, j, k) meaning that xi is more similar to xj than to xk. Let N = |
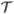 | denote the number of triplets in
| denote the number of triplets in
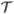 . The goal is to learn a Mahalanobis distance which preserves the relationship in
. The goal is to learn a Mahalanobis distance which preserves the relationship in
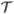 .
.
A Mahalanobis distance is parameterized by a PSD matrix M ∈ ℝD × D. The Mahalanobis distance between xi ∈ X and xj ∈ X based on M is
| (1) |
To remove the scalability effect of the distance resulting from M, we require tr(M) = 1. Since any trace-one PSD matrix can be decomposed as a convex combination of rank-one trace-one PSD matrices, i.e.,
| (2) |
To avoid notation clutter in later computations, we introduce a vector vn = [υnl], where υnl corresponds to ul and the nth triplet (i, j, k), and is defined as
| (3) |
A potentially appropriate M should be able to maximize the soft margin defined in the following linear programming,
| (4) |
where ζn is the slack variable, and α is a constant factor which penalizes the slack variables.
The Lagrangian dual problem of (4) is
| (5) |
where d, c, and q are non-negative regularizes. After some simple algebraic manipulation we arrive at the dual problem of (4) given by,
| (6) |
3.1 Regularization on d
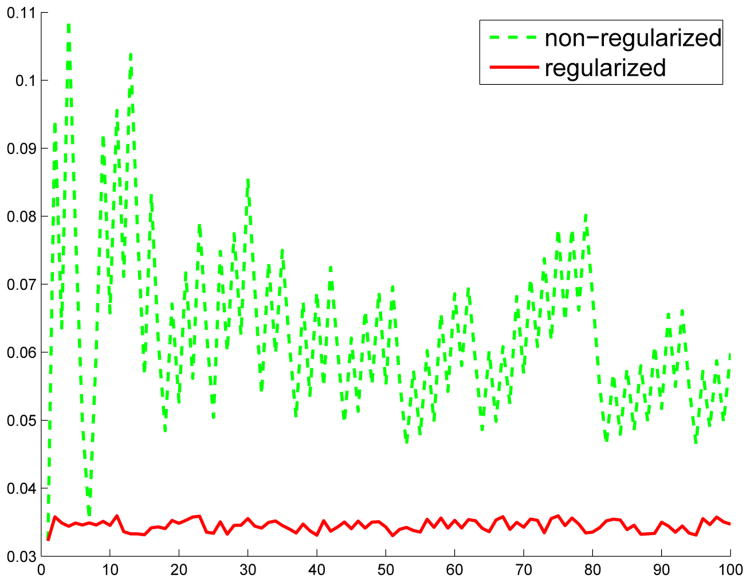
The regularization on d is very important because for the non-regularized metric learning algorithm, the weight of the training examples might change very severely, i.e., the weight of a training example might oscillate significantly when it is misclassified or correctly classified by the weak learners (rank-one matrices) as shown in Fig. 1. This instability will seriously affect the learning efficiency, accuracy, and also lead to overfitting. With regularization, severe oscillations and instabilities can be prevented, which makes the algorithm converge faster, i.e. need fewer number of rank-1 PSD matrices. Fig. 1 depicts that, using regularization, the resulting weight change of the training data is stable.
Fig. 1.
Change in the weight of a training example in the Heart disease dataset from the UCI repository, under metric learning without regularization and with regularization.
To overcome the aforementioned instabilities, we add a regularization term to the update of d in (6), i.e.,
| (7) |
where η is the regularization coefficient that balances the margin and the smoothness. η is set to be a fixed number 2 as in [25] to make the number of iterations upper bounded by a constant without hurting the accuracy. δ(d, d̂) is the tKL divergence [25, 27], and
| (8) |
Note that the regularization term δ(d, d̂) ensures that the evolution of d is smooth.
Here, d̂ can be chosen in different ways. In this paper, we set d̂ = d0, where d0 is the initialized distribution, this means d should not be far away from the initialized distribution. Since d0 is user defined, it is usually set according to the application problem and the data. One tends to initialize larger weight on the examples with more importance, so we use δ(d, d0) as the regularizer. Note that the dn is upper bounded by α as in (6), therefore the weight of the noisy examples and outliers is prevented from being too large leading to possible domination in the learning3.
To directly compute dt from (7) is complicated, instead, we will first find its Lagrangian and use it to compute dt. To find the Lagrangian, we rewrite (7) into the following form
| (9) |
The Lagrangian Ψ of (9) is given by,
| (10) |
where, ωl, l = 1, ⋯, t, ξn, n = 1, ⋯,N and γ are non-negative regularizers. Using some simple calculus and the KKT condition [28], we can simplify (10) and get the partial Lagrangian
| (11) |
Now differentiating Ψ with respect to d, setting it to 0, and normalizing d, we get,
| (12) |
and Zt is the normalization parameter to make . Here if , then we manually set .
3.2 Regularization on u
We put two constraints on u. First, we want it to maximize the margin. Second, we require u to be independent of the previously learned ul, l = 1, 2, ⋯, t, so that the learned {u} will not be redundant. Therefore, the number of rank-one matrices needed to form a good metric is reduced. The dependence between u and ul is measured by ║uT ul║2 ∈ [0, 1]. The larger ║uT ul║2 is, the more dependent they are. When ║uT ul║2 = 0, u and ul are independent.
The two constraints on u are described as
| (13) |
where λ is the regularization coefficient to penalize the dependence. (13) can be rewritten as
| (14) |
Let matrix , then ut+1 is the eigenvector corresponding to the largest eigenvalue of At.
The weight vector w for the rank-one matrices should satisfy the linear programming problem (4) which can be solved using column generation [29] or a gradient based method.
3.3 Building the Triplets
For each xi ∈ X, we first find the a instances which are in the same category as xi but are most different from xi. After that, we find the a nearest neighbors in a different category, then (i, j, k) will form a triplet. If the size of X is small, we will use a larger a, otherwise, we will use a smaller a. Furthermore, if the number of triplets is very large, we will randomly select 10 ∼ 50% of the triplets for training.
As a summary, the algorithm for the proposed DRMetric is presented in Algorithm 1. The proof of the convergence is very similar to the proof from Schapire and Singer [30].
4 Experimental Results
The proposed algorithm is evaluated on a number of public domain datasets for a variety of applications. We use the UCI machine learning repository [31] for classification, use the COREL image dataset for content based image retrieval, and use the Labeled Faces in the Wild (LFW) [32] dataset for face recognition. We compare our method with many state-of-the-art metric learning and other techniques. The results show that our proposed metric learning method is very promising for many applications.
| Algorithm 1 Doubly Regularized Metric Learning |
|
Input: Dataset X = {xi}, xi ∈ ℝD Triplet set 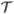 = {(i, j, k) | xi is closer to xj than to xk}. N = | = {(i, j, k) | xi is closer to xj than to xk}. N = |
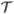 |, the number of triplets in |, the number of triplets in
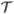 . .Output: , ul ∈ ℝD, ║ul║ = 1, w ∈ Δt, t is the number of iterations. Initialization: Initialize , the weight of the nth triplet, n = 1, ⋯, N, according to the importance, or set by default. for l = 1 to t do
end for Return . |
4.1 Classification
The classification experiments are performed on the UCI machine learning repository [31], which is a collection of datasets that have been extensively used for analyzing machine learning techniques. The repository contains a large variety of datasets, including very noisy datasets (e.g. the Optical Recognition of Handwritten Digits dataset, the wine dataset) as well as relatively clean datasets, which is optimal for testing the robustness and accuracy of classification algorithms. We selected 9 datasets from the UCI repository. The selected datasets include noisy and clean datasets, cover small size to large size datasets in terms of number of instances in the datasets, and range from low dimension to high dimension in terms of number of attributes per instance of the datasets. The description of the selected datasets is shown in Table 1.
Table 1.
Description of the selected UCI datasets.
| dataset | # instances | # attributes |
|---|---|---|
|
| ||
| Heart disease | 303 | 74 |
| Australian sign | 6650 | 14 |
| Blood transfusion service center | 748 | 5 |
| Artificial characters | 6000 | 7 |
| Glass identification dataset | 214 | 10 |
| Adult dataset | 48842 | 14 |
| Handwritten digits | 5620 | 64 |
| Wine dataset | 178 | 13 |
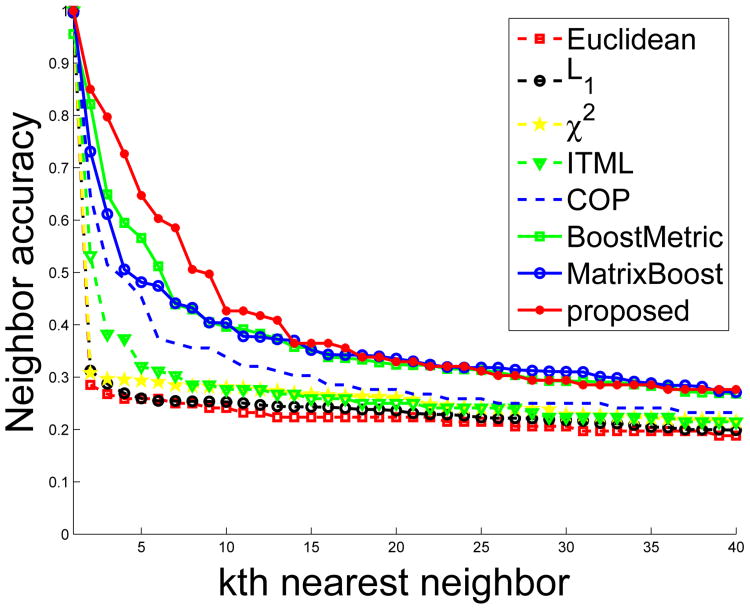
We use 5-fold cross validation to evaluate the proposed algorithm. The regu-larization parameters α, η and λ are determined during the training and validation stage, and they are set to be the numbers which maximize the performance on the training dataset. The final result is the average of the results obtained over the 5 runs. The proposed DRMetric is compared with many other non-metric learning and metric learning algorithms, including Euclidean distance, L1-norm distance, χ2 distance, BoostMetric [11], MatrixBoost [1], ITML [16], and COP [13]. The code for metric learning methods is obtained directly from the corresponding authors or downloaded from the authors' webpage. The classification performance is measured based on neighbor accuracy curves. The neighbor accuracy measures the percentage of correctly classified instances based on the kth (k = 1, 3, 5, 7, 9) nearest neighbor. The average neighbor accuracy is shown in Fig. 2. The comparison depicts that in general DRMetric yields higher classification accuracy.
Fig. 2.
The neighbor accuracy curves from different metrics on the Heart disease, Australian sign and Blood transfusion service center datasets in the UCI repository.
We also evaluate the 3-nearest-neighbor voting classification accuracy on several UCI datasets including the Glass Identification dataset, the Adult dataset, the Optical Recognition of Handwritten Digits dataset, and the Wine dataset. The classification results are shown in Table 2, which reflects that the proposed method outperforms the other methods.
Table 2.
Classification accuracy using different metrics on selected datasets from the UCI repository.
| dataset | Euclidean | L1 | χ2 | ITML | COP | BoostMetric | MatrixBoost | proposed |
|---|---|---|---|---|---|---|---|---|
|
| ||||||||
| Characters | 0.7235 | 0.7452 | 0.7651 | 0.9114 | 0.8889 | 0.9147 | 0.9049 | 0.9288 |
| Glass | 0.6114 | 0.6404 | 0.6479 | 0.7975 | 0.7850 | 0.8135 | 0.7991 | 0.8204 |
| Adult | 0.6017 | 0.6249 | 0.6284 | 0.7760 | 0.7752 | 0.7981 | 0.7894 | 0.8075 |
| Digits | 0.6865 | 0.7107 | 0.7284 | 0.7352 | 0.7473 | 0.8014 | 0.8148 | 0.8290 |
| Wine | 0.7240 | 0.7261 | 0.7602 | 0.8625 | 0.8958 | 0.9074 | 0.9152 | 0.9161 |
Besides, for DRMetric, we examined the relationship between the classification accuracy change and the number of iterations. The results are shown in Fig. 3, which implies that when the number of iterations is less than D (the dimension of the dataset), the classification accuracy increases at a higher rate. However, when the number of iterations is larger than D, the classification accuracy improves very slowly. This means that, using our method, D rank-one matrices can form a relatively high quality Mahalanobis distance.
Fig. 3.
The change of classification accuracy with related to the number of iterations using DRMetric on the Heart disease (left), Australian sign (middle), and Blood transfusion service center (right) datasets. The black disk corresponds the classification accuracy when the number of iterations equals to the number of attributes.
4.2 Content based image retrieval
The task for image retrieval is that given one image in a category, find the images in the same category. We use the COREL image database [33] to evaluate our method on content based image retrieval. The database contains 3400 real-world images with 34 different categories, and 100 images per category.
Each image is represented as a 33 dimensional feature vector, which is a combination of low level features including color features, edge features and texture features. For color features, we first represent the images in the HSV color space, and then compute the mean, variance, skewness of the HSV color to get a 9 dimensional feature vector. For edge features, the Canny edge detector [34] is first applied to images to detect the edges, and the histogram for edge direction was quantized into 9 bins of every 40 degrees, which resulted in 9 different edge features. For texture features, we use the multi-resolution simultaneous autoregressive (MASAR) model [35] to get 15 features. In total, there are 33 features for each image.
We use 10-fold cross validation to evaluate the proposed algorithm, i.e., 90% images are used to learn the metric, and 10% images are used for evaluation. We use every image in the test dataset as a query, if the retrieved image belongs to the same category as the query image, the retrieval is correct. We measure the retrieval performance based on the neighbor accuracy curves. Neighbor accuracy measures the percentage of correctly retrieved images in the kth nearest neighbors of the query images (k = 1, ⋯, 40 in our experiments).
We compared our method to many algorithms, including Euclidean distance, L1-norm distance, χ2 distance, BoostMetric [11], MatrixBoost [1], ITML [16], and COP [13]. The retrieval results are shown in Fig. 4. The results illustrate that our proposed method achieves a higher neighbor accuracy when using 1st ∼ 25th and 34th ∼ 40th nearest neighbors. However, it's a little worse than MatrixBoost when using the 26th ∼ 33rd nearest neighbors.
Fig. 4.
Comparison of using different metric learning methods for content based image retrieval on the COREL dataset.
We compare the computational time of BoostMetric [11], MatrixBoost [1], and DRMetric to learn the distance metric on the COREL database. All algorithms are run on a laptop with Intel(R) Core(TM)2 CPU L7500 @ 1.6GHz, 4GB memory, GNU Linux and MATLAB (Version R2011a). The average CPU time taken to converge for our algorithm is 167.68s, while BoostMetric takes 244.81s, and MatrixBoost takes 239.28s.
4.3 Face recognition
In this scenario, the goal for face recognition is to do pair matching: given two face images, determine if these two images belong to the same person. We use the Labeled Faces in the Wild (LFW) [32] dataset. This is a fairly difficult dataset for face recognition, because it has a large range of the variation (varying pose: straight, left, right, up; expression: neutral, happy, sad, angry; eyes: wearing glasses or not; clothes: wearing different clothes; size: small, medium or large) seen in real life. It includes 13233 images of 5749 people collected from news articles on the Internet. The number of images per person ranges from 1 to 530, and 1680 people have two or more distinct images in the dataset. This is a popular dataset which has been used by many researchers [6, 8, 36, 10, 37] to evaluate their face recognition frameworks.
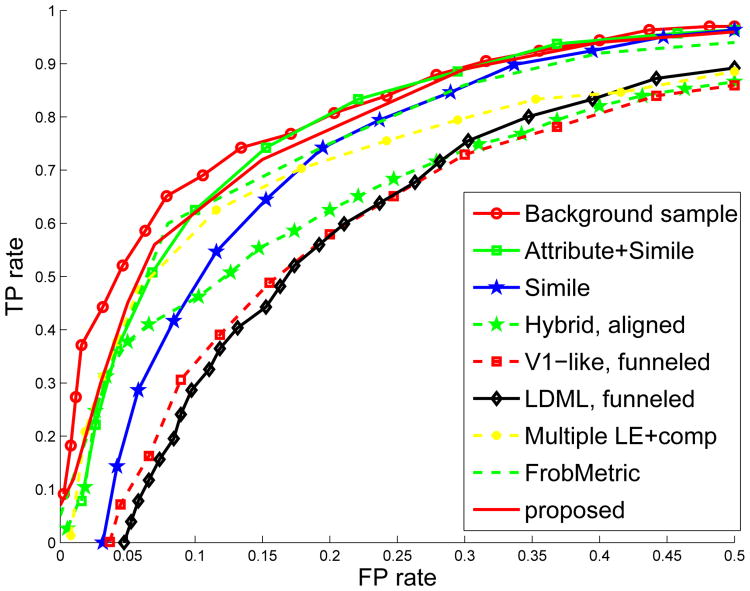
In this experiment, we have compared the proposed DRMetric to the state-of-the-art methods for the task of face pair-matching problem. To ensure fairness, we used the same features as used in the literature [6–11, 38]. Features of face images are extracted by computing the 3-scale, 128-dimensional SIFT descriptors [39], centered on 9 points of facial features extracted by a facial feature descriptor, as described in [7]. In this way, we get 3 × 128 × 9 = 3456 features in total for each image. PCA is then performed on the feature vectors to reduce the dimension to 400 (because the result in [11] showed that dimension 400 is a good compromise between performance and efficiency) for training. The triplets are built according to Section 3.3. The number of generated triplets is 44794, out of which, we use 20% (i.e. 8960) for training. We compared our method with LDML funneled [40], Hybrid aligned [38], V1-like funneled [10], Simile [8], Attribute + Simile [8], Background sample [41] Multiple LE + comp [6], and FrobMetric [11]. All these methods except FrobMetric are more complicated than our method, because they either use additional information, hybrid descriptors or combination of classifiers. The performance is described using an ROC curve 4 on which each point represents the average over the 10 runs of (false positive rate, true positive rate) for a fixed distance threshold. The results from all other techniques were taken from their latest published results. The comparison is shown in Fig. 5, which depicts that our method is only slightly worse than the two leading techniques (Attribute + Simile [8] and Background sample [41]) that are much more complicated. Furthermore, our method is comparable to or better than other state-of-the-art techniques on face recognition.
Fig. 5.
False positive (FP) rate versus true positive (TP) rate on face recognition using different metric learning methods on the LFW dataset.
5 Conclusions
We proposed an efficient and robust doubly regularized metric learning algorithm DRMetric. It has two regularization parts. First, we use tKL to regularize the update of the weight of the training examples. This avoids instabilities in the weight change, and consequently avoids overfitting and make it more robust to noisy data as well as outliers. Second, we add a regularization to the rank-one matrices enforcing them to be as independent as possible. In this way, the redundancy of the learned rank-one matrices as well as the number of necessary rank-one matrices are significantly reduced, which leads to higher efficiency. Furthermore, DRMetric is robust and capable of handling a variety of datasets for different applications. Though the idea behind DRMetric seems simple, its robustness and applicability can not be undervalued.
Footnotes
Strictly speaking, this matrix should be symmetric positive definite (SPD) in order for it to be a metric. However, we relax the requirement and allow two different instances to have zero distance.
, where N is the number of training samples, D is the dimension of each training sample, and ∊ is the error tolerance of the margin between different classes based on the learned metric [25].
To make such a d exist, we should require α ≥ 1/N. It was shown in [26] that α = 1/s, and s ∈ {1, ⋯, N} is a favorable choice.
If the distance, based on the learned metric, is above some threshold, the two images will be declared as not belonging to the same person, and vice versa. For each threshold, we get the corresponding FP/TPrate. By changing the thresholds, we get a set of {FP/TPrate}, which forms the ROC curve. Using ROC curve to evaluate face recognition methods is widely used in literature [40, 38, 8, 41, 10].
References
- 1.Bi J, et al. AdaBoost on low-rank PSD matrices for metric learning with applications in Computer Aided Diagnosis. IEEE CVPR. 2011:1049–1056. [Google Scholar]
- 2.Dollar P, Tu Z, Tao H, Belongie S. Feature mining for image classification. IEEE CVPR. 2007:1–8. [Google Scholar]
- 3.Hastie T, Tibshirani R. Discriminant adaptive nearest neighbor classification. IEEE TPAMI. 1996;18:607–616. [Google Scholar]
- 4.Yang L, et al. A Boosting framework for visuality-preserving distance metric learning and its application to medical image retrieval. TPAMI. 2010:30–44. doi: 10.1109/TPAMI.2008.273. [DOI] [PubMed] [Google Scholar]
- 5.Ong E, Bowden R. A boosted classifier tree for hand shape detection. IEEE Int Conf Automatic Face & Gesture Recogn; 2004; pp. 889–894. [Google Scholar]
- 6.Cao Z, Yin Q, Tang X, Sun J. Face recognition with learning-based descriptor. IEEE CVPR. 2010:2707–2714. [Google Scholar]
- 7.Guillaumin M, Verbeek J, Schmid C. Multimodal semi-supervised learning for image classification. IEEE CVPR. 2010:902–909. [Google Scholar]
- 8.Kumar N, Berg AC, Belhumeur PN, Nayar SK. Attribute and simile classifiers for face verification. IEEE ICCV. 2009:365–372. [Google Scholar]
- 9.Nowak E, Jurie F. Learning visual similarity measures for comparing never seen objects. IEEE CVPR. 2007 [Google Scholar]
- 10.Pinto N, DiCarlo JJ, Cox DD. How far can you get with a modern face recognition test set using only simple features? IEEE CVPR. 2009 [Google Scholar]
- 11.Shen C, Kim J, Wang L. A scalable dual approach to semidefinite metric learning. IEEE CVPR. 2011:2601–2608. [Google Scholar]
- 12.Jiang N, Liu W, Wu Y. Adaptive and Discriminative Metric Differential Tracking. IEEE CVPR. 2011 [Google Scholar]
- 13.Xing E, Ng A, Jordan M, Russell S. Distance metric learning, with application to clustering with side-information. NIPS. 2002;15:505–512. [Google Scholar]
- 14.Shen C, Kim J, Wang L, van den Hengel A. Positive semidefinite metric learning with boosting. NIPS. 2009 [Google Scholar]
- 15.Bar-Hillel A, Hertz T, Shental N, Weinshall D. Learning a mahalanobis metric from equivalence constraints. JMLR. 2005;6:937–965. [Google Scholar]
- 16.Davis J, Kulis B, Jain P, Sra S, Dhillon IS. Information-theoretic metric learning. ICML. 2007:209–216. [Google Scholar]
- 17.Cox M, Cox T. Multidimensional Scaling. Springer Handbooks Comp. Statistics. 2008:315–347. [Google Scholar]
- 18.Tenenbaum J, Silva V, Langford J. A Global Geometric Framework for Nonlinear Dimensionality Reduction. Science. 2000;290:2319–2323. doi: 10.1126/science.290.5500.2319. [DOI] [PubMed] [Google Scholar]
- 19.Roweis S, Saul L. Nonlinear dimensionality reduction by locally linear embedding. Science. 2000;290:2323–2326. doi: 10.1126/science.290.5500.2323. [DOI] [PubMed] [Google Scholar]
- 20.Vemuri BC, Liu M, Amari SI, Nielsen F. Total Bregman divergence and its applications to DTI analysis. IEEE TMI. 2011;30:475–483. doi: 10.1109/TMI.2010.2086464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Shalev-Shwartz S, Singer Y, Ng AY. Online and batch learning of pseudo-metrics. ICML. 2004 [Google Scholar]
- 22.Tsuda K, Rsch G, K Warmuth M. Matrix exponentiated gradient updates for on-line learning and bregman projection. JMLR. 2005;6:995–1018. [Google Scholar]
- 23.Jian B, Vemuri BC. Metric learning using iwasawa decomposition. IEEE ICCV. 2007:1–6. doi: 10.1109/ICCV.2007.4408846. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Saberian MJ, Vasconcelos N. Multiclass Boosting: Theory and Algorithms. NIPS. 2011 [Google Scholar]
- 25.Liu M, Vemuri BC. Robust and efficient regularized boosting using total bregman divergence. IEEE CVPR. 2011:2897–2902. doi: 10.1109/CVPR.2011.5995686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Warmuth MK, Glocer KA, Vishwanathan SV. Entropy regularized LPBoost. Int Conf Alg Learn Theory. 2008:256–271. [Google Scholar]
- 27.Liu M, Vemuri BC, Amari S, Nielsen F. Shape retrieval using hierarchical total bregman soft clustering. IEEE TPAMI. 2012 doi: 10.1109/TPAMI.2012.44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Boyd S, Vandenberghe L. Convex optimization. Cambridge University Press; Cambridge, England: 2004. [Google Scholar]
- 29.Demiriz A, Bennett KP, Shawe-Taylor J. Linear programming boosting via column generation. Mach Learn. 2002;46:225–254. [Google Scholar]
- 30.Schapire R, Singer Y. Improved boosting algorithms using confidence-rated predictions. Mach Learn. 1999;37:297–336. [Google Scholar]
- 31.Frank A, Asuncion A. UCI machine learning repository. 2010 [Google Scholar]
- 32.Huang GB, Ramesh M, Berg T, Learned-Miller E. Labeled faces in the wild: A database for studying face recognition in unconstrained environments. ECCV. 2008 [Google Scholar]
- 33.French J, Watson J, Jin X, Martin W. An exogenous approach for adding multiple image representations to content-based image retrieval systems. Int Sym Signal Processing App. 2003;1:201–204. [Google Scholar]
- 34.Canny J. A computational approach to edge detection. IEEE TPAMI. 1986;8:679–698. [PubMed] [Google Scholar]
- 35.Manjunath BS, Ma W. Texture features for browsing and retrieval of image data. IEEE TPAMI. 1996;18:837–842. [Google Scholar]
- 36.Nguyen HV, Bai L. Cosine similarity metric learning for face verification. ACCV. 2010 [Google Scholar]
- 37.Yin Q, Tang X, Sun J. An Associate-Predict Model for Face Recognition. IEEE CVPR. 2011:497–504. [Google Scholar]
- 38.Taigman Y, Wolf L, Hassner T, Tel-Aviv I. Multiple One-Shots for utilizing class label information. BMVC. 2009 [Google Scholar]
- 39.Lowe DG. Distinctive image features from scale-invariant keypoints. IJCV. 2004;60:91–110. [Google Scholar]
- 40.Guillaumin M, Verbeek J, Schmid C. Is that you? metric learning approaches for face identification. IEEE ICCV. 2009:498–505. [Google Scholar]
- 41.Wolf L, Hassner T, Taigman Y. Similarity scores based on background samples. ACCV. 2009 [Google Scholar]