Chemometric Resolution and Quantification of Four-Way Data Arising from Comprehensive 2D-LC-DAD Analysis of Human Urine

Abstract

Two-dimensional liquid chromatography (LC×LC) is quickly becoming an important technique for the analysis of complex samples, owing largely to the relatively high peak capacities attainable by this analytical technique. With the increase in the complexity of the sample comes a corresponding increase in the complexity of the collected data. Thus the need for chemometric methods capable of resolving and quantifying such data is ever more urgent in order to obtain the maximum information available from the data. To this end, we have developed a chemometric method that combines iterative key set factor analysis and multivariate curve resolution-alternating least squares analysis with a spectral selectivity constraint that is shown to be capable of resolving chromatographically rank deficient, non-multilinear data. (Spectrally rank deficient compounds can only be quantified if the peaks having the same spectra are chromatographically resolved.) Over 50 chromatographic peaks were found in a relatively small section of a LC×LC-diode array data set of replicate urine samples (a four-way data set) using the developed method. The relative concentrations for 34 of the 50 peaks were determined with % RSD values ranging from 0.09 % to 16 %.

1. Introduction

Comprehensive two-dimensional liquid chromatography (LC×LC) is potentially a very powerful separation technique for the quantitative analysis of multiple analytes in complex mixtures due to the high peak capacities that can be achieved. In comprehensive LC×LC methods, a sample is passed through two independent column systems such that all of the effluent from the first dimension separation is sequentially introduced into the second dimension separation system to achieve a separation [1,2]. A major drawback to the practical implementation of LC×LC is the extended run times necessary to achieve the desired increased peak capacities. Until recently, typical run times required for a single injection could be hours or even days [3]. However, considerable advancements in instrument design by Stoll et al. [4] have resulted in a significant reduction in single injection run times to as low as fifteen to thirty minutes. With the advantages of increased resolving power directly related to the orthogonality of LC×LC separations and of reduced run times currently achieved through the implementation of high temperatures on the second column, comes the ability to analyze very complex biological samples in a more efficient and effective manner.

Complex samples arising from genomic, proteomic and metabolomic studies are excellent candidates for analysis by fast LC×LC, due to the demand in these fields for resolution of hundreds or thousands of constituents with concentration ranges that can exceed nine or ten orders of magnitude [2,5]. A wide range of sample types (including cell cultures, microbes, body fluids and tissues, and plants) have been used in metabolomic studies which involve the collection of quantitative data for the characterization of metabolites; i.e., low molecular weight molecules [6,7]. Urine is replete in both endogenous and xenoboitic metabolites and the highly responsive nature of human urine to metabolic stressors such as disease or toxicity (a direct consequence of the body’s autonomic response to eliminate substances in an attempt to maintain homeostasis) offers several overwhelming advantages [8,9]. Due to this autonomic response, detection of the changes in the endogenous metabolites in urine has the potential to increase our understanding of the mechanisms of disease and drug action; and detection of the changes in the xenobiotic metabolites in urine has the potential to aid in the discovery of biomarkers for drug efficacy and toxicity and of biomarkers for disease risk [7,10,11]. LC and/or nuclear magnetic resonance (NMR) are techniques commonly employed in metabolomic profiling of urine centered around the identification of just a few known metabolites and/or the use of pattern recognition techniques applied to unidentified signals [12]. Non-targeted, global profiling of metabolites in human urine has been accomplished in recent studies using GS-MS [10,13,14].

Peak quantification is an important factor involved in metabolomic analysis. The ability to accurately quantify small metabolites present in a sample is essential in the identification of potential biomarkers in metabolomic studies where the biomarker signature is not the presence of unique compounds, but is rather the presences of unique concentrations or concentration ratios. While LC×LC is well reported and has been employed in the fields of proteomics [15] and metabolomics [3], and for the separation of polymers [16] and organic acids, [17] to date, there are only a few papers in the literature that broach the subject of peak quantification of data collected from comprehensive LC×LC analysis. Thekkudan and Rutan recently performed simulation experiments in which LC×LC chromatographic data were simulated varying both first dimension retention time and peak widths. The accuracy and precision of the determined simulated peak concentrations were evaluated by either summing the areas of the second dimension chromatograms or by fitting the first dimension peaks to Gaussian peak shapes [18] Peters et al. have developed an automated algorithm for peak detection for two-dimensional chromatography that provides quantitative results for the detected peaks [19]. Mondello et al. [20], Reichenbach et al. [21]and Marriott et al. [22] have also proposed algorithms for quantitative analysis of LC×LC data. However, none of these works have addressed the quantitative analysis of overlapped peaks, which is the focus of the present work.

The comprehensive LC×LC-DAD (diode array detection) data used in this work were determined to lack a quadrilinear structure; thus, we chose to employ multivariate curve resolution (MCR) techniques in the data analysis to aid in the determination of the number of spectral components and in the chemometric resolution of overlapped peaks. Due to areas of the data where there is a loss of the linear relationship between absorbance and concentration resulting from detector saturation, a section of the data where the detector was not saturated was chosen for chemometric analysis. In addition, due to the complexity and size of the data section, the data were further divided into thirty-four subsections. The subsequent steps involved rank determination (N = number of unique spectra) in the data subsection to be analyzed, followed by curve resolution of that subsection using an in-house MCR-alternating least squares (ALS) algorithm. Following curve resolution, relative peak concentrations were ascertained by a manual baseline determination method, and the % RSD values for the resolved peaks in replicate standard mixture samples and control urine samples were determined.

2. Theory

In the simplest case, the data from a single chromatographic experiment (1D-LC-DAD data, which gives rise to 2-way data) can be contained in a matrix X, which consists of absorbance values as a function of elution time and wavelength, and can be represented as follows:

$$\mathbf{X}=\mathbf{C}·{\mathbf{S}}^{\mathbf{T}}+\mathbf{E}$$ (1)

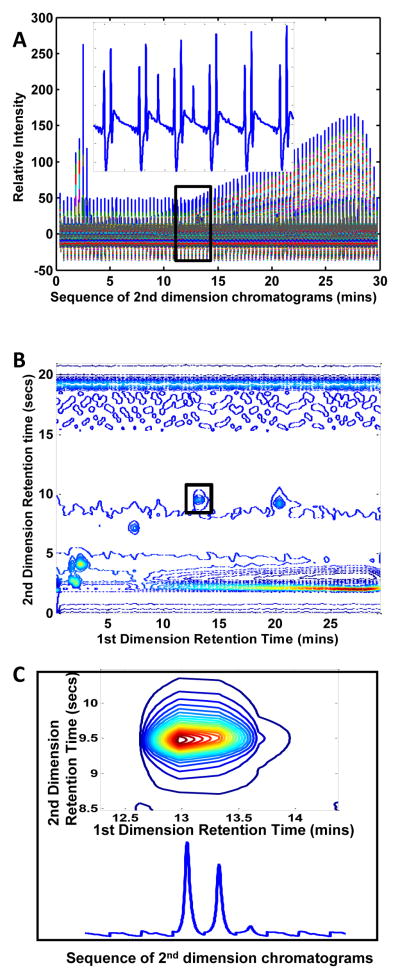
where C is the chromatographic matrix, S is the spectral matrix and E is an error matrix [23]. The columns of the data matrix X are absorbance measurements that vary with time (chromatograms) and the rows are intensity measurements that vary with wavelength (spectra). The columns of matrix C contain the chromatograms of the individual pure components present in the sample represented by matrix X, while the columns of matrix S contain the spectra of those components. In this work, the LC×LC-DAD data were collected by the instrument as 2-way data for each separate 1^st dimension injection as seen in Figure 1A in which all of the 2^nd dimension injection chromatograms are sequenced end to end. We can represent the data as either a two-way data matrix, X, with dimensions IJK×L (Figure 1A), or as a four-way data array with dimensions I×J×K×L (shown at one wavelength for one sample in Figure 1B). Here, I is the number of data points in each 2^nd dimension chromatogram, J is the number of data points in each 1^st dimension chromatogram, K is the number of different samples that were analyzed and L is the number of points in each spectrum.

Figure 1.

Several different types of plots for the 2^nd sample of the standards mixture raw data. (A) Plot of the two-way raw data as collected by the instrument, such that all 2^nd dimension injections of a corresponding sample injection are sequenced end-to-end. The insert shows an enlarged section of the sequenced data that was determined to encompass the corresponding peak illustrated in the contour plot at 216 nm of (B). Using the determined section dimensions, the same peak is shown as a contour plot at 216 nm in the box (C) along with its corresponding sequenced 2^nd dimension chromatograms.

2.1 Iterative Key Set Factor Analysis (IKSFA)

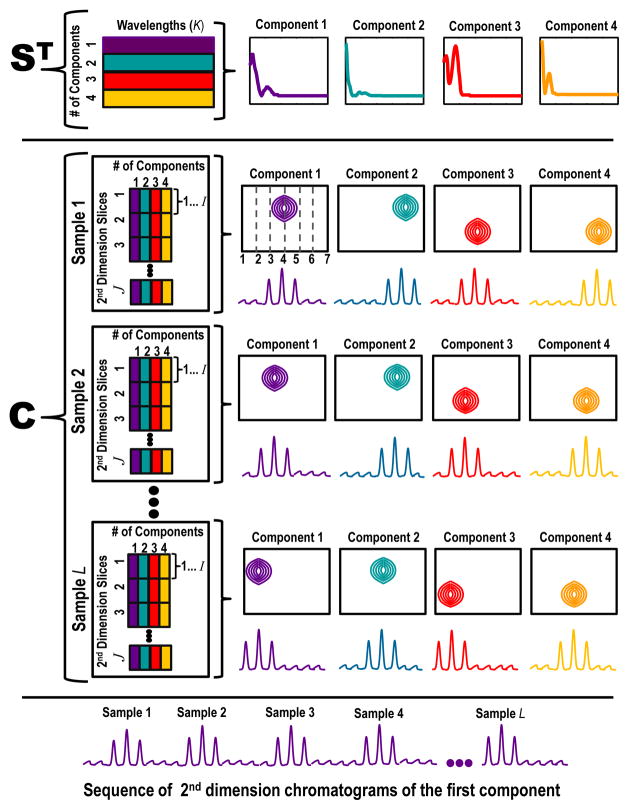
The IKSFA method was developed by Malinowski and is a preferred set selection method that assumes the purest spectra in the data set are mutually more dissimilar than the mixture spectra [24]. IKSFA is an iterative improvement over KSFA which seeks to find the minimum number (N) of spectra (out of IJK total spectra) required to represent the entire data set through the characterization of the most orthogonal spectra that typify the original data matrix [25,26]. This approach is not restricted to the spectral information of the data matrix; however, for simplicity the following discussion will focus only on the determination of the key set of spectra, because this is the method we used in our analysis. To determine the number of significant spectral factors (N) and to create a spectral initial guess for the curve resolution step, IKSFA was applied to the two-way data matrix X. Keep in mind that in our work, the columns of X are a combination of the first and second dimension chromatograms and the sample injections (IJK) and the rows of X are the spectra (L) as described above, refer to Figure 2 for a schematic representation of the unfolded data and the data decomposition. IKSFA first decomposes the data using singular value decomposition (SVD) such that

Figure 2.

Schematic illustration of the resolution results from the IKSFA-ALS-ssel analysis in which both the data structure and corresponding graphical representations of the resolved spectra and chromatograms are shown. The data structure as shown consists of J = 7 2^nd dimension slices and K samples (1^st dimension injections). Panel 1 illustrates the resolved spectral matrix. The dimensions of the resolved S^T data matrix in this example are four spectral components by the total number of wavelengths collected (L). The corresponding spectra for each of the four components are plotted such that the y-axis is relative intensity versus wavelength. Panel 2 illustrates the resolved chromatographic matrix. Recall that each 1^st chromatographic data point is equal to a 2^nd dimension slice and that a 2^nd dimension slice consists of I data points. The dimensions of the resolved C data matrix is unfolded to combine the 1^st chromatographic dimension (J), the 2^nd chromatographic dimension (I) and the number of samples (K) by the four spectral components. The four spectral components are color coordinated to correspond to their chromatographic counterpart. Each resolved chromatographic peak is graphically represented in two ways (1) by a contour plot of the 1^st chromatographic dimension by the 2^nd chromatographic dimension plotted for a given wavelength and a given sample and (2) a sequence of 2^nd dimension chromatograms. Panel 3 shows the corresponding sequence of 2^nd dimension chromatograms of component 1 for all samples (1-K).

$$\mathbf{X}=\mathbf{U}\mathbf{D}{\mathbf{V}}^{\mathbf{T}}$$ (2)

where U and V matrices contain the left and right singular vectors, and the D matrix is diagonal and represents the relative contribution of each principal component, i.e., the singular values. The search for a key set of orthogonal spectra uses the matrix U, that contains the left singular vectors. Each row vector, u_r, of the matrix, U, is first normalized to unit length

$${\stackrel{\sim }{\mathbf{u}}}_{\text{r}}=\frac{{\mathbf{u}}_r}{{\left({\displaystyle \sum _{n=1}^N}{\mathbf{u}}_{rn}^2\right)}^{\frac{1}{2}}}$$ (3)

where ũ_r is the normalized row vector and the denominator is the norm of the row vector, since only the directions (row vectors that are perpendicular) and not the magnitudes of the row vectors are of interest in determining the most orthogonal rows. It is important to note that this is row-wise normalization as opposed to column-wise normalization.

The first key row corresponds to the row whose ũ _r,1 value has the largest absolute value and we denote this row as ũ _key1. This is a deviation from IKSFA as utilized by Schostack and Malinowski [27] where the first key row contained the minimum of the ũ _r,1 value. This change was implemented due to the significance and uniqueness of the background spectra known to exist in the data set. A determinant is found for this key row and each remaining row, r, and the row with the maximum determinant

$$max\left(det\left|\left[\begin{array}{cc}{\stackrel{\sim }{\mathbf{u}}}_{\mathit{key}1,1}& {\stackrel{\sim }{\mathbf{u}}}_{\mathit{key}1,2}\\ {\stackrel{\sim }{\mathbf{u}}}_{r,1}& {\stackrel{\sim }{\mathbf{u}}}_{r,2}\end{array}\right]\right|\right)$$ (4)

is the second key row, ũ _{key 2} This procedure is continued by adding a third row and finding the row that gives the maximum 3 × 3 determinant, etc., until N key rows are identified. It is at this point that iteration begins. The first key row, ũ _key1 is replaced by the first row vector ũ₁. If the absolute value of the determinant for the new key set is greater than that of the initial key set, the first row vector replaces the initial first key row; if the value is less than that of the initial key set, the key set remains unchanged, and ũ _key1 is then replaced with the second row vector. This procedure is continued for the first key row for all r row vectors. The same logic is followed for all key rows completeing one iteration cycle. Iteration continues until no change in the key set occurs after the completion of one complete iteration cycle [25,28]. The key rows of X, key1 through keyN, are then used as an initial estimate for the MCR-ALS algorithm as follows.

$${\mathbf{S}}_{\mathit{initialestimate}}=\left[\begin{array}{c}{\mathbf{x}}_{\mathit{key}1}\\ {\mathbf{x}}_{\mathit{key}2}\\ ⋮\\ {\mathbf{x}}_{\mathit{keyN}}\end{array}\right]$$ (5)

2.2 Multivariate Curve Resolution-Alternating Least Squares (MCR-ALS)

MCR-ALS is a multivariate curve fitting technique that enables the analyst to mathematically separate chemical components in a data set by least squares optimization using data structure and the implementation of mathematical constraints that have a chemical significance [29]. These constraints can include nonnegativity, unimodality and multilinearity, among others. Equation 1 can be rearranged to solve for either the chromatographic matrix C (equation 6) or the spectral matrix S (equation 7) where the data matrix X is known. Either a spectral matrix estimate is used to solve for the chromatographic matrix or a chromatographic initial estimate is used to solve for the spectral matrix. The MCR-ALS algorithm then iterates between equations 6 and 7 to minimize the error matrix until one of the two input iteration criteria is met; i.e., until the fit error reaches a minimal improvement criterion or until a given maximum number of iterations has occurred [30].

$$\mathbf{C}=\mathbf{X}{({\mathbf{S}}^{\mathbf{T}}\mathbf{S})}^{-\mathbf{1}}\mathbf{S}$$ (6)

$${\mathbf{S}}^{\mathbf{T}}={({\mathbf{C}}^{\mathbf{T}}\mathbf{C})}^{-\mathbf{1}}{\mathbf{C}}^{\mathbf{T}}\mathbf{X}$$ (7)

Our implementation of the MCR-ALS algorithm allows for the flexible implementation of chemically valid constraints for carrying out mathematical resolution of the data set reducing ambiguity in the model. In the present work, we employ two types of constraints – nonnegativity and selectivity, which are described in more detail in the section 3.2. It is important to note that we do NOT use a multilinearity constraint in the present work (aside from the inherent bilinearity implied by the model given in eqn. (1)). This is due to the fact that we have found the degree of retention time shifting from sample to sample which occurs in both the first and second dimension chromatograms is significant enough to prevent the validity of either the trilinearity or quadrilinearity constraint. Because we do not employ this constraint, there is little to no sensitivity to retention time shifting or, just as importantly, to peak shape distortions due to phase shifting in the 1^st dimension sampling. However, the lack of multilinearity does mean that a unique, correct result will not necessarily be obtained. The use of the spectral selectivity and nonnegativity constraints will aid in ameliorating this limitation.

The implementation of the IKSFA-ALS-ssel for a subsection of raw data results in the assignment of chromatographic peaks to their corresponding spectral components. An idealized representation of this is shown in 2 for a four component model. The resolved S matrix has the dimensions of the number of wavelengths collected by four components (L ×N), while the resolved C matrix has the unfolded dimensions of the 1^st and 2^nd chromatographic dimensions and the number of samples by four components (IJK×N). Samples 1 and 2 through K are shown, such that each spectral component of S corresponds to its color coordinated resolved chromatographic peak of C. The resolved C matrix is represented in two ways, first as a contour plot and then as the corresponding sequence of 2^nd dimension chromatograms for each component. This illustration is idealized for simplicity and clarity, in that background component(s) are not represented, and each spectral component corresponds to a single, non-overlapped chromatographic peak. In the realm of real data, things are frequently not so straightforward. This point is clearly illustrated in section 4.2 by the results of the IKSFA-ALS-ssel analysis of a subsection of urine control data.

2.3 Quantification algorithm development (relative concentration determination)

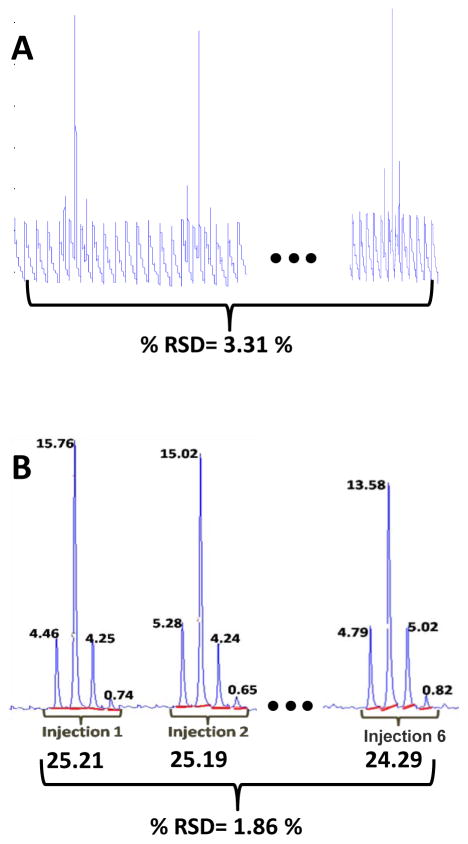
In LC×LC, a first dimension peak consists of several second dimension injections (slices across a first dimension peak consisting of J data points). Each second dimension injection (slice) will produce a second dimension chromatogram consisting of I data points. The volume determination algorithm is based on the premise that the sum of these second dimension peak areas is equivalent to the volume of that LC×LC peak [18,31]. Figure 3B illustrates this premise, in which the same single compound is present in six replicate sample injections. It can be seen that sample injection 1 consists of four sequential second dimension peaks. The areas under each of these four second dimension peaks are determined and are summed in order to ascertain the LC×LC peak concentration [32]. This procedure is followed for all six sample injections shown in Figure 3B and allows for the comparison of the relative concentrations of the single compound present in all six sample injections. This method will be referred to as the manual baseline method throughout this work and is equivalent to the area summation method described by Thekkudan et. al. [18].

Figure 3.

Comparison of the subsection for the standards mixture peak 1 showing the sequence of resolved 2^nd dimension chromatograms and the raw data for the injection of six replicate samples onto the 1^st dimension column. (A) A plot of the sequenced second dimension chromatograms of the raw data. Each 1^st dimension sample injection gives rise to seven 2^nd dimension injections with four of those injections containing the peak of interest and three injections consisting only of the background in this example. (B) The above data after the application of the devoloped chemometric method. The red line drawn under each 2^nd dimension peak shows the manually determined baseline, and the areas for each of the second dimension peaks (shown at the top of the peaks) are totaled (shown at the bottom of each peak grouping), giving the relative concentrations of peak 1 for each of the six sample injections and the % RSD showing the precision of the quantification.

For simplicity, Figure 3B represents an ideal case in which the peak has been well resolved from the background components using the developed chemometric method and only one compound is present in the section of the data analyzed, as opposed to Figure 3A, which shows a plot of the corresponding raw data. Unfortunately, the ideal case is not frequently observed and it is extremely likely that other components of the sample may have the same first dimension retention time but an earlier or later second dimension retention time. In such an instance, additional second dimension peaks will elute in the individual second dimension chromatograms either before or after the peak of interest. Any second dimension peaks not associated with the peak of interest are simply left unintegrated and thus do not contribute to the relative concentration calculation. For very simple mixtures, it is straightforward to determine which second dimension peaks comprise a given LC×LC peak, but for more complex mixtures, that are of interest in the present work, this can be challenging at best. The IKSFA/MCR-ALS curve resolution procedure is used in the present work to resolve all spectrally distinct components into individual LC×LC chromatograms, which are much simpler, and can therefore be more easily and precisely integrated using the above procedure. Often the method resolves weakly absorbing peaks that were not visually observable in the raw data and may not be spectrally distinct. The advantage of the manual baseline method is that spectral uniqueness is not necessary as long as the peaks in question are chromatographically resolved and a manual baseline can be drawn for integration.

3. Materials and Methods

3.1 Samples, instrumentation and software

Six injections of a standards mixture (Figure 4A) and fourteen injections of urine control sample (Figure 4B) were interspersed over the course of a 64 injection LC×LC run requiring over thirty hours of total run time. The standards mixture consists of nitrate, tryptophan, hydroxytryptophan, indole-3-acetic acid, indole-3-propionic acid, indole-3-acetonitrile and tyrosine. The data analyzed in this study were collected using a comprehensive LC×LC system developed by Stoll and Carr at the University of Minnesota [21,32]. The system employs the use of a dual gradient and employs the use of high temperature (110 °C) in the second dimension. This was accomplished through the use of an eluent preheater and a heating jacket placed around the second dimension reversed-phased carbon-clad zirconia column. The sample to be injected onto the first dimension system is preheated to 40 °C before passing through the first column, effluent from the first column is collected in 21-second fractions and then each fraction is injected onto the second column. Diode array detection (DAD) from 200 nm to 700 nm was employed after the second column. The acquired data consist of absorbance values in mAU units as the dependent variable, and the independent variables being retention on the first dimension column, retention on the second dimension column, UV-visible wavelength, and sample injection number. Thus for the standards mixture data the size of the array is 840 × 84 × 6 ×126 (2^nd chromatographic dimension, 1^st chromatographic dimension, number of sample injections, wavelength from 200 nm to 700 nm at 4 nm intervals) and the size of the array for the analyzed section for urine control data is 161 × 26 ×14× 126. The data were imported into the MATLAB environment using ACDLABS ChromProcessor 9.0 (Advanced Chemistry Development, Inc. Toronto, Canada). The data were analyzed using MATLAB software R2007a (Mathworks, Inc. Natick, MA) and a HP Pavilion dv9500 with 4GB RAM, an Intel® Core^™ 2 Duo CPU T7500 @ 2.20GHz processor operating with the Windows Vista Home Premium operating system. The MCR-ALS algorithm used for this analysis has been described previously by this group [30]. LCImage software (GC Image, LLC Lincoln, NE) was provided by S. Reichenbach [21].

Figure 4.

Contour plots at 216 nm of two different sample types within the 64 injection LC×LC-DAD run. (A). Contour plot of the third replicate injection of the standards mixture where peak 1 is indole-3-acetonitrile, peak 2 is indole-3-propionic acid, peak 3 is indole-3-acetic acid, peak 4 is tryptophan peak 5 is hydroxytryptophan and peak 6 is tyrosine. (B). Contour plot of the seventh replicate injection of the urine control standard. Inset shows the section of data selected for chemometric analysis.

3.2 Data analysis scheme

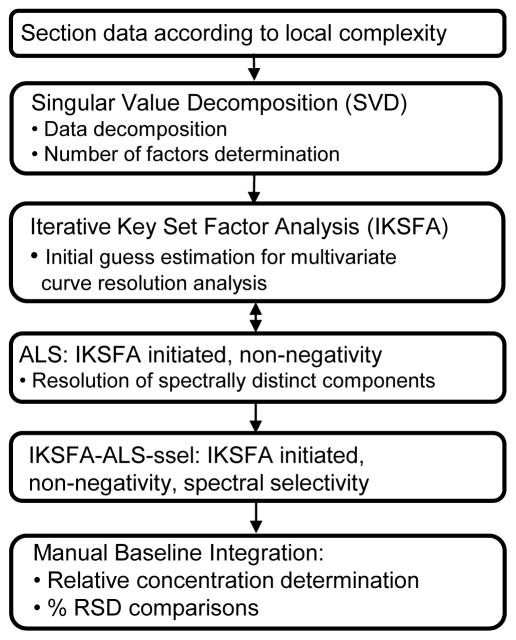
The data analysis procedure followed for the analysis of both the standards mixture data and the urine control data is outlined in Figure 5. Subsections were initially determined by creating contour plots to determine the 1^st and 2^nd dimension data point boundaries around a visually observable peak. Once a subsection was created, chemometric data analysis began with SVD and IKSFA of the data matrix X (dimensions IJK×L). The initial input parameter for IKSFA, the number of components (N), was to some extent subjectively determined using a combination of two visualization methods, a scree plot and a contour plot of the subsection to be analyzed. The initial N spectral components obtained from the IKSFA analysis are then used as an initial estimate for the initialization of the in-house MCR-ALS algorithm [30] which employs the non-negativity constraint in the chromatographic dimension. These two steps are repeated for several different possible numbers of components to ensure that as many possible components are found without over-fitting the data. (see section 4.4 for a more detailed description)

Figure 5.

Chemometric data analysis scheme used in the resolution and quantification of LC×LC data.

After the optimization of the number of components, a final MCR-ALS analysis step, referred to from here on as IKSFA-ALS-ssel, where ssel denotes the use of the spectral selectivity constraint, is performed in which three constraints are applied to the analysis: (1) chromatographic non-negativity, applied as in the previous analysis steps. (2) spectral selectivity, and (3) spectral non-negativity. Our implementation of spectral selectivity, constrains only the non-background components so that the last 51 spectral data points (corresponding to wavelengths 440 nm to 700 nm) were set to zero. The spectral non-negativity constraint was selectively applied to correspond to the parameters of the spectral selectivity constraint so that the background components are allowed to be negative but the compound spectra are constrained to be greater than or equal to zero. Which components require the application of constraints (2) and (3) were identified in the first MCR step.

The implementation of the IKSFA-ALS-ssel approach described above for a subsection of raw data results in the assignment of chromatographic peaks to their corresponding spectral components. The spectral component that contains the peak of interest is further analyzed to determine the relative concentrations of the resolved peak for each sample injection, and the % RSD was then calculated. This is accomplished by plotting the resolved chromatographic results for only the component of interest and for a given sample injection as a sequence of second dimension chromatograms. This allows for good baseline visualization of the component of interest in a given injection for implementation of the manual baseline method as was previously described. After the manual baseline method has been utilized to determine the relative concentrations of the component of interest, the % RSD for that peak was determined by dividing the standard deviation of the replicate sample injections by the average determined relative concentrations for all replicate sample injections and multiplying by 100. Due to the data structure (replicate injections without calibration injections) it was not possible to calculate the accuracy of the method, only the precision of the method can be discussed.

The above described procedure was followed for the eighteen data subsections that were created for the eighteen visually observable peaks. The analysis of these eighteen subsections revealed additional peaks not previously observed in the raw data contour plot of the entire section. New subsections were created for the analysis of the previously unobserved peaks as these peaks were detected, so that both observed and initially undetected peaks in the data were appropriately analyzed. A full discussion of the choices and reasoning behind why the authors followed the above steps is undertaken in section 4.4.

4. Results and Discussion

4.1 Standards mixture analysis (effects of subsection size and number of components)

The six replicate standard mixture injections (Figure 4A) were interspersed throughout a 64 injection run and contained six known compounds that were intended to be well resolved. However, multiple contaminants were found in close proximity to Peak 6 for all of the replicate sample injections. Therefore, this peak was not included in the following analyses, because the goal of this portion of the work was to limit possible interfering variables, such as chromatographic and spectral rank deficiencies, to obtain a better understanding of how the algorithm functions. The % RSD values for the concentrations of Peaks 1–5 for the raw data using the manual baseline method and the chemometrically resolved data using both the manual baseline method and LCImage software volume determination are shown in Table 1. Peaks 3 and 4 (indole-3-acetic acid and tryptophan as shown in Figure 4A) give the highest % RSD values for both data types and quantification methods. Peak 3 is a very weakly absorbing compound making it difficult to accurately determine the peak baseline from the high background in the raw data. The reason for the high % RSD for Peak 4 is that there is an overlapping contaminant found to be present only in injection 2. The IKSFA-ALS-ssel resolved data yields better results as compared with the raw, unresolved data, except for Peak 2. Overall, there is an average three-fold improvement in precision over integration of the raw data.

Table 1.

% RSD results for the precision of peak quantification of both raw and IKSFA-ALS-ssel-resolved data of the standards mixture injections for peak 1 through peak 5.

Standards Mixture Data	Manual Baseline		LC Image software
	Raw Data	IKSFA-ALS-ssel	IKSFA-ALS-ssel
Peak 1	3.31	1.60	9.07
Peak 2	1.75	2.16	10.5
Peak 3	12.6	4.71	34.5
Peak 4	13.1	3.47	19.4
Peak 5	5.21	1.40	1.30
Ave % RSD	6.53	2.61	15.0

The analysis of Peaks 1–5 using IKSFA-ALS-ssel for different subsection sizes was done to determine whether the size of the subsection chosen to encompass the peak of interest would have an effect on quantification. Due to large retention time shifting in the first retention time dimension, it is important that the subsection include all data points which reflect the presence of the compound of interest; however, after this criteria is met, is it in the best interest of the analysis for the subsection size to be small (just encompassing the peak of interest), as large as possible (allowing for additional data points that might allow for more accurate determination of the background component) or does subsection size have any effect on the % RSD values at all? Table 2 gives the % RSD values as determined after IKSFA-ALS-ssel analysis using the manual baseline method for five different subsection sizes for each of the Peaks 1–5. The first and second dimension coordinates for the maxima of the Peaks 1–5 were visually determined, and the peak was centered within each subsection so that the first dimension for all subsection sizes contained ten data points. This range of points in the first dimension ensured that the peaks are not cut off in the first retention time dimension. The number of data points in the second dimension for the five different subsection sizes were 200, 250, 300, 350 and 400 data points respectively. From Table 2 it is clear that as the subsection size increases, the % RSD decreases until a critical limit is reached, at which point the % RSD increases with increasing subsection size. This trend is directly related to the signal to noise ratio of the given subsection size for a specific component. We conclude that for smaller subsections, there are two contributing issues that lead to the higher % RSD values. For one, if the peak is large relative to the background component (such that the peak “overwhelms” the size of the subsection) the analysis method will have difficulty in accurately estimating the background contribution. Second, upon integration, the lack of data points on either side of the peak in the resolved sequenced chromatogram makes a consistent baseline determination more difficult. For the larger subsections, the issue is the opposite, particularly for weaker peaks; i.e., the method has difficulty in accurately estimating the peak contribution. In other words, the peak gets lost in the background. This is especially evident in Peak 3 for subsection sizes 4 and 5 in which the background was so large in comparison to the weak peak that the algorithm was unable to yield a resolution of the peak that was quantifiable. Therefore, the most appropriate subsection size is dependent on the relative intensity of the target compound within the subsection.

Table 2.

Effects of subsection size on the % RSDs of IKSFA-ALS-ssel analyzed standard mixture data for peak 1 - peak 5.

Size of subsection in data points	% RSD Values
	Peak 1	Peak 2	Peak 3	Peak 4	Peak 5
Subsection 1 (200 × 10)	2.71	2.16	4.71	CO	5.04
Subsection 2 (250 × 10)	2.22	2.30	7.76	5.33	4.08
Subsection 3 (300 × 10)	2.03	2.31	12.67	5.85	2.88
Subsection 4 (350 × 10)	1.60	2.68	NA	4.93	1.40
Subsection 5 (400 × 10)	1.86	7.59	NA	3.47	2.69

CO: the peak was clearly cut off for this subsection size.

NA: no available results due to very low peak to background ratio.

4.2 Urine control sample analysis (curve resolution and quantification)

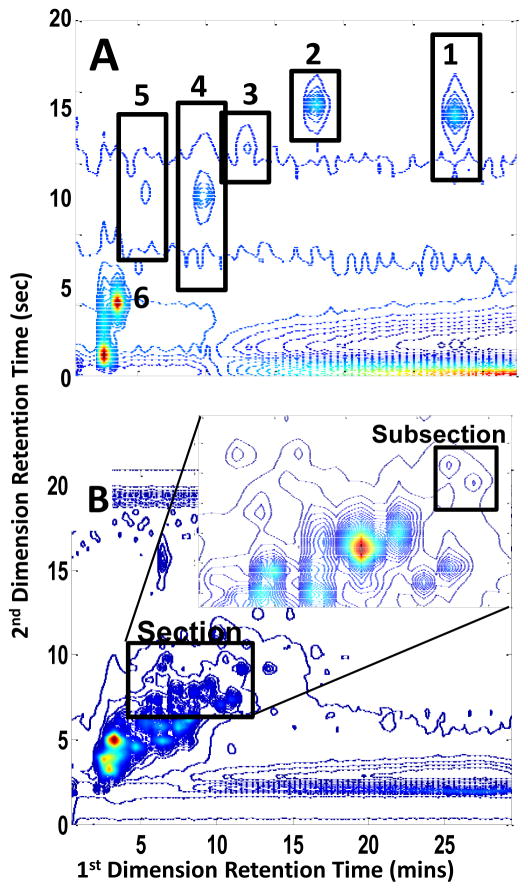
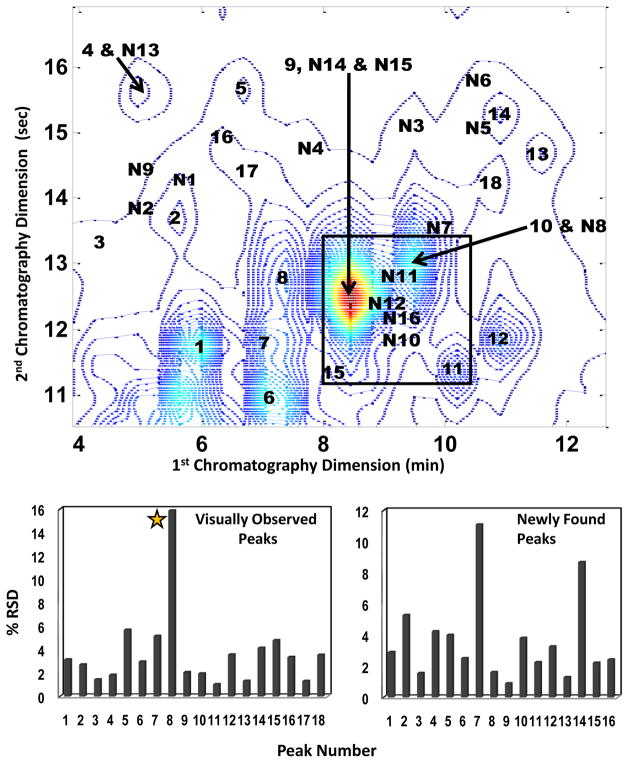
Over fifty peaks were found within the section of the urine control chromatogram that was analyzed in this work. Of these, thirty-four were resolved well enough for the determination of their relative concentrations. Figure 6 shows the location of the 34 resolved components, where the numbers 1–18 refer to the peaks initially detected upon visual inspection of the data, and number N1–N16 refer to the newly detected peaks.

Figure 6.

Contour plot of the urine control at 216 nm showing 34 resolved peaks. The N preceding 16 of the 34 resolved and quantified peaks signifies that those peaks were found and resolved only after application of the developed chemometric method (newly found) while the other 18 peaks were visually observable prior to chemometric analysis. The two bar graphs show % RSD values calculated for the corresponding peaks. The star on the visually observed peaks graph indicates that Peak 8 is considered to be a chemically unstable compound.

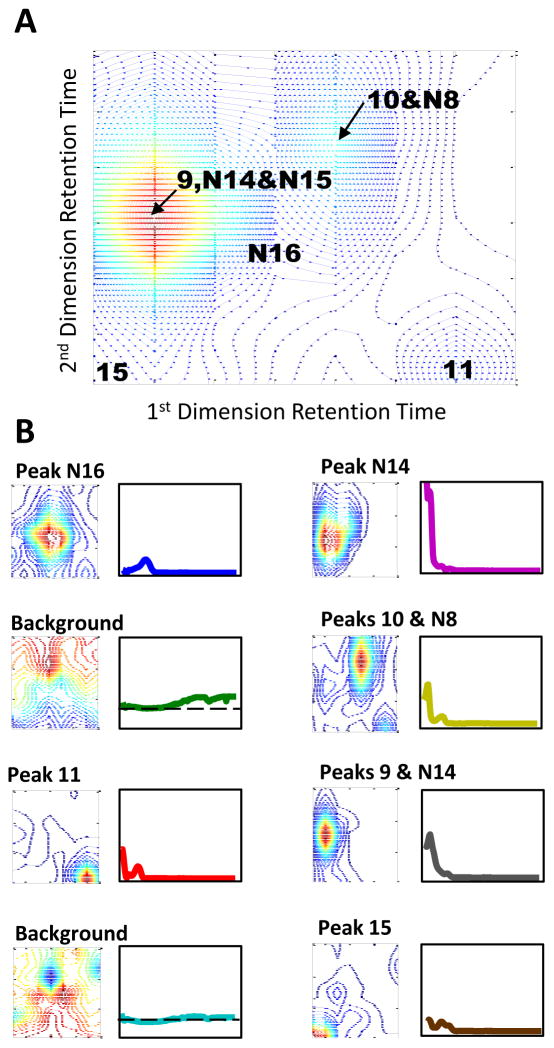
The indicated subsection of the chromatogram shown in Figure 6 was used to quantify peak N16. The spectral and chromatographic profiles obtained after implementation of IKSFA-ALS-ssel are shown in Figure 7. As can be seen in this figure, the IKSFA-ALS-ssel analysis revealed the presence of eight components in this subsection. Two of these components were identified as background components. It should be noted that the analysis of additional overlapping subsections in this region of the chromatogram permitted peaks 10 and N8, and peaks 9 and N15 to be resolved from one another, as well as resolving peaks N10, N11 and N12 from the background for a total of ten quantified peaks. While the above-mentioned peaks have the same first dimension retention times and very similar second dimension retention times, chemometric resolution was possible due to the unique spectra of the corresponding peaks. The ability of the algorithm to resolve chromatographically overlapped peaks having different spectral profiles was demonstrated in several areas of the data in which two or more peaks were found to be present, but only one peak was visually apparent. Evidence of several additional very weak peaks was also found in this subsection, but these peaks could not be reliably quantified.

Figure 7.

(A) Contour plot of a subsection of urine control data at 216 nm in which resolution and quantification of Peak N16 is the goal for the chemometric analysis. (B) The chromatographic and corresponding spectral results for each component of the 8 component IKSFA-ALS-ssel analysisl for the above subsection of raw data.

The bar graph in Figure 6 provides the % RSD values determined for the chemometrically resolved peaks. The % RSD values for the initially observed peaks ranged from 1.04 % for peak 11to 15.9 % for peak 8 with an average % RSD of 3.73 %. Peak 8 appeared to be a chemically unstable compound (its intensity consistently decreased over the course of the analysis) leading to the poor quantitative precision for that compound. The % RSD values for the sixteen additionally found peaks ranged from 0.90 % for peak N10 to 11.1 % for peak N7 with an average % RSD value of 3.56 % for this group of resolved peaks. This section for all fourteen replicate injections was also evaluated by LCImage software[21] using their blob detection tool (i.e. peak picking). The blob detection found on average 22 peaks using the default settings and 24 peaks after modification of the detection setting in the section of data analyzed in this work. The detected peaks for the fourteen replicate injections ranged from 20 to 28 depending on the injection and the setting used for detection. Of the 24 peaks found by the LCImage software for sample injection 7, three were also found by the IKSFA-ALS-ssel method but are cut off by the section parameters and therefore not included in the 34 quantified peaks. Also, two of the LCImage detected peaks for injection 7 are not detected in all fourteen injections.

The relative signal was evaluated and compared to the corresponding % RSD values for each quantitatively resolved peak to determine if a low signal response was correlated to a decrease in the precision of quantification as seen by an increase in % RSD values. The relative signal response was determined by multiplying the chromatographic maximum value of the 7^th sample injection by the spectral maximum value for each peak. This assumption can be made due to a relatively constant background response of the section of the data analyzed. We found that in the majority of cases where the % RSD of a given peak is above 4, a low signal response was not responsible for the observed poor precision, but rather other chromatographic phenomena such as spectral or chromatographic rank deficiencies (overlapped peaks) and unsatisfactory resolution of the peaks from the background. These issues will be discussed in more detail in a future publication. Peaks with % RSD values of less than 2 % were not affected by these issues.

4.3 Comparison to previous Rutan group work

Previously, Porter et al. analyzed four-way data arising from a comprehensive LC×LC analysis of maize seedlings[3]. The data was assumed to be approximately quadrilinear, as the total run time of all samples was only three hours. This assumption allowed Porter et al. to employ the PARAFAC model such that the results from PARAFAC were used to initiate the in-house ALS algorithm so that constraints could be applied selectively. The samples used for method comparison in this work consisted of two extracts of mutant orange pericarp maize seedlings and two extracts of wild-type maize seedlings.

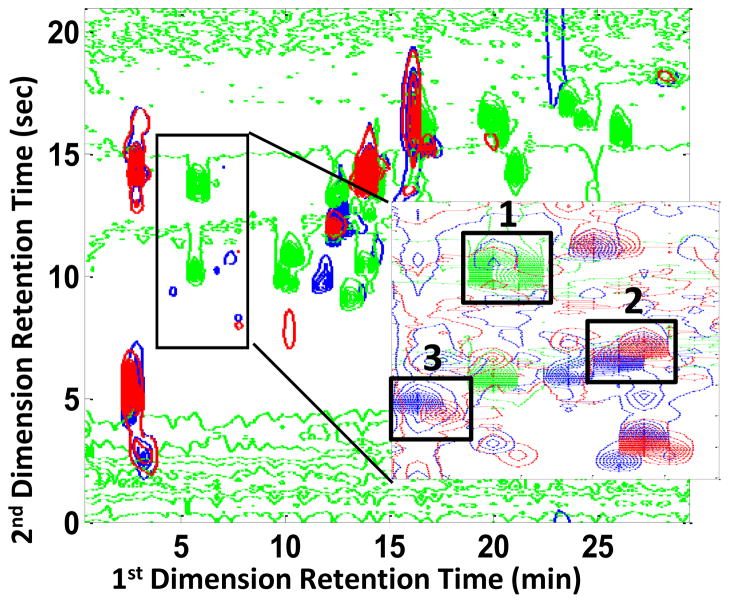
For method comparison purposes a small section of the previously analyzed data set, shown in Figure 8, was analyzed using the current IKSFA-ALS method with the exception that the spectral selectivity constraint was not employed due to insufficient wavelength collection during the LC×LC run of the maize data. Peaks labeled 1, 2, and 3 were chosen for % RSD comparison of the determined relative concentrations. These peaks were selected because they were present in both the mutant and wild type samples and were resolved using the PARAFAC-ALS method. The results in Table 3 show that for four out of the five comparisons made, IKSFA-ALS yields considerably lower % RSD values for these peaks than PARAFAC-ALS. It is of particular interest, that the IKSFA-ALS method chemometrically resolved an additional six peaks that were not detected by Porter et al. and was able to resolve several peaks that the PARAFAC-ALS method did not resolve due to the lack of multilinearity in the first retention time dimension. We also conclude from these results that, even for the relatively short three hour run, there were sufficient retention time shifts to decrease the precision of the PARAFAC- ALS analysis, relative to the IKSFA-ALS method.

Figure 8.

Overlaid contour plot of maize data analyzed by Porter et al. [3] The blue contour plot is the first injection of the mutant sample, the green contour plot is the indole standard mixture and the red contour plot in the second injection of the wild type sample. Adapted from ref. [3].

Table 3.

Comparison of % RSD values for duplicate samples resulting from PARAFAC-ALS method [4] and IKSFA-ALS-ssel methods in the analysis of maize data. NP: the compound was not present in the wild type samples

	PEAK 1		PEAK 2		PEAK 3
	PARAFAC- ALS	IKSFA- ALS-ssel	PARAFAC- ALS	IKSFA- ALS	PARAFAC- ALS	IKSFA- ALS
Mutant	40.1	5.4	141.0	14.6	5.1	1.4
Wild Type	NP	NP	26.4	2.5	21.8	82.0

NP=Not Present

4.4 Data analysis considerations

Due to the size of the urine control data set and to the large number of factors involved in the analysis of an entire chromatogram, it was first necessary to divide the data into sections. This enabled us to work with a more manageably sized section shown in Figure 4B from 3.85 to 12.6 minutes and 6.6 to 10.6 seconds; this section was chosen for further investigation since it is free of signals where the detector was saturated. The nature of the data (complex and lacking multilinear behavior because of the retention time shifts) limits the chemometric methods available, requiring that either prealignment data processing occurs before chemometric implementation of methods that require multilinearity can be employed, such as PARAFAC, or restriction of the data analysis to methods that are not affected by retention time shifting such as MCR-ALS. We chose the second option, employing an approach involving IKSFA and MCR-ALS, neither of which requires multilinearity. The authors recognize that the described method requires user intervention. While the number of components, N, determination step and the spectral selectivity constraints implementation require the user to make decisions based on visual inspection of the results before proceeding to the next step, these decisions are fairly straightforward and are not time consuming. In other words, this method can be easily taught and learned such that a great deal of expertise is not required to achieve good results. In addition, the method is shown in section 4.3 to be applicable to other data sets arising from LC×LC-DAD analysis and to be an improvement over a previously published method.

While the number of components (N) is somewhat subjectively determined, it is easily and quickly accomplished. Contour subplots of the subsection to be analyzed at different wavelengths allows for an approximate number of peak components to be determined by simply counting the peaks that are visually apparent. Due in large part to the large dynamic range of this data, chromatographic peaks are not always observable even when plotted at multiple key wavelengths. Hence, the comparison of the number of visually counted peaks to the number of principal components ascertained from the scree plot leads to a reasonable initial estimate of N that can be attained in less than a minute. It is important to keep in mind that there are also background components to be considered to obtain the final estimate for the number of spectrally distinct components, N. The determination of an appropriate final N parameter included the consideration of several factors: there should be no more than 3 background components following curve resolution, the value of the determinant for the final key set should be less than 0.1 and greater 0, and the fit error for the MCR-ALS step should be less than 5%. Addition of more components to reduce the fit error further usually resulted in overfitting, as evidenced by the appearance of the component profiles that did not make sense chromatographically or spectrally. A cross validation of the subsection used for the analysis of peak N16 in which a leave-seven-out approach was taken for component models of N= to 7, 8, and 9, confirmed that for this subsection the eight component model chosen using the above described method resulted in the best fitting model.

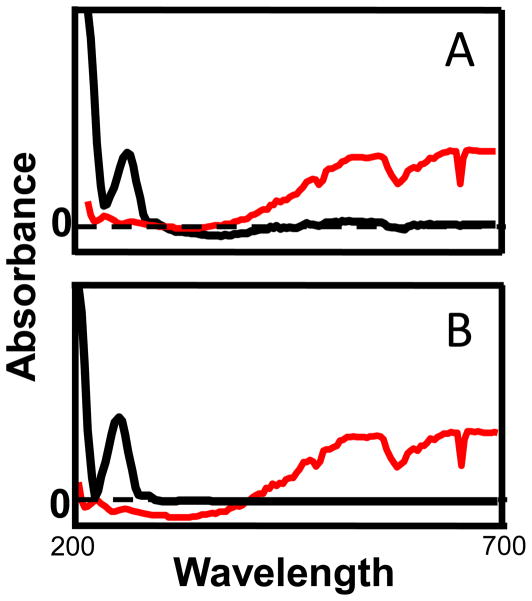
The second manual step that we employ is the implementation of the constraints. One of the advantages of the in-house MCR-ALS algorithm [30] is that each of the constraints can be selectively applied to individual components. An example of this is the selective application of the spectral selectivity constraint to only the non-background components such that the wavelengths from 440 nm to 700 nm were set to zero. This wavelength range was chosen due to the complete lack of corresponding spectral information above 440 nm to any components other than the background. This helps the algorithm resolve the background from actual components because the background spectra have a consistent increasing absorbance above 440 nm. Also, the manner in which the spectral selectivity constraint was employed, allowed for the selective application of the non-negativity constraint to the spectral dimension of all components except the background components. The implementation of the two spectral constraints aids in the spectral resolution of the background spectral components from non-background spectral components, as illustrated in Figure 9. Chemometric resolution of the background components provides substantial improvements in quantification using the manual baseline method for relative concentration determination Figure 2.

Figure 9.

Component spectra (blue) and background spectra (red) before (A) and after (B) implementation of the spectral selectivity and spectral non-negativity constraints. By zeroing the chemical component spectra after 440 nm, the algorithm is better able to resolve the background spectra from the compound spectra.

The unimodality constraint was not employed in this work for several reasons. Unimodality, as is currently employed in many MCR algorithms, sets a vertical at the valley of the non-unimodal peak and sets all of the data points of the peak with the smaller maximum to zero [29,30,33]. This, in essence, eliminates a possible smaller peak from the analysis results that the manual baseline method may be capable of integrating. Alternatively, dynamic unimodal regression may be used; however, in practice the smaller peak is still lost. It is important to remember that an incompletely resolved component may be non-unimodal in either the first dimension retention time, the second dimension retention time or it may exhibit non-unimodal behavior in both retention time dimensions. What would ultimately be required is the capability to employ the unimodality constraint for four-way data to selective components in a manner that adds an additional component to the result and assigns the smaller of the non-unimodal peaks to the “new” component so that no information is lost in the resulting answer. To the authors’ knowledge, this approach has currently not been investigated in the literature.

5. Conclusions

Most of the published peak detection methods for LC×LC data analysis [19–22] have been for chromatographically well-resolved peaks. Curve resolution procedures that have been useful for the analysis GC×GC data [1,34] for the most part have not been successfully applied to LC×LC, probably because of the same retention time reproducibility issues that we encountered in this work. Also, the modification of successful algorithms used for the analysis of 1D techniques to 2D chromatography is complicated due to the undersampling effect of the first dimension and the necessity of combining several second dimension peaks to represent the total LC × LC peak [19,35]. We have shown that the IKSFA-ALS-ssel method successfully resolves complex LC×LC-DAD data without requiring prealignment of the data to achieve multilinearity. Due to lack of retention time alignment, the previously developed PARAFC-ALS method showed higher % RSD values, assigned the same peak to different components and did not resolve peaks that were found to be present when compared to the IKSFA-ALS method. The current drawback to the IKSFA-ALS-ssel method is the lack of automation. However, the intervention that is required is straightforward and relatively simple, if somewhat tedious. For the standards mixture data, there is a 2.5 fold improvement in the % RSD values of the IKSFA-ALS-ssel analyzed data as compared to the raw data. The chemometric analysis of the urine control data revealed over fifty compounds, thirty-four of which were resolved sufficiently for quantitative analysis. The average % RSD of the quantified peaks of 3.5 %, while rather high for accepted 1D-LC analysis, is quite good for such a complex sample such as human urine but leaves room for improvements in quantification of LC×LC data.

Several issues associated with the quantification of this data arose during curve resolution, including phase shifting caused by retention time shifts in the first dimension, rank deficiency, large dynamic range issues and unsatisfactory curve resolution of the peaks from the background. These are several of the obstacles associated with achieving more precise quantification and will be addressed by the authors in future publications.