Lipid Droplets Purified from Drosophila Embryos as an Endogenous Handle for Precise Motor Transport Measurements

Abstract

Molecular motor proteins are responsible for long-range transport of vesicles and organelles. Recent works have elucidated the richness of the transport complex, with multiple teams of similar and dissimilar motors and their cofactors attached to individual cargoes. The interaction among these different proteins, and with the microtubules along which they translocate, results in the intricate patterns of cargo transport observed in cells. High-precision and high-bandwidth measurements are required to capture the dynamics of these interactions, yet the crowdedness in the cell necessitates performing such measurements in vitro. Here, we show that endogenous cargoes, lipid droplets purified from Drosophila embryos, can be used to perform high-precision and high-bandwidth optical trapping experiments to study motor regulation in vitro. Purified droplets have constituents of the endogenous transport complex attached to them and exhibit long-range motility. A novel method to determine the quality of the droplets for high-resolution measurements in an optical trap showed that they compare well with plastic beads in terms of roundness, homogeneity, position sensitivity, and trapping stiffness. Using high-resolution and high-bandwidth position measurements, we demonstrate that we can follow the series of binding and unbinding events that lead to the onset of active transport.

Introduction

Molecular motor proteins are responsible for long-range transport of vesicles and organelles in eukaryotic cells. In animal cells, motors of the kinesin family move cargo toward the plus ends of microtubules while cytoplasmic dynein carries the cargoes toward the minus ends, typically arranged at the centrosome. Much of our understanding of how molecular motors function has benefited from single-molecule measurements in vitro where individual motors are attached to microspheres nonspecifically. Yet transport of cargoes in living cells is very different: they carry multiple similar and dissimilar motors (1–4), as well as motor light chains and cofactors (5–7). The dynactin complex, a motor cofactor, is of particular interest as it bridges the cargo and the microtubule along which it diffuses without force generation (8). Dynactin can also interact with both polarity motors (9) and alter their function (10,11). Moreover, the organization and stoichiometry of the different proteins on the cargo, as well as the way they are attached to it, can be important in determining the ensuing dynamics. It is currently not possible to reconstitute such transport complexes on plastic beads. It is, therefore, important to study the native motor complex to understand transport beyond the isolated motor function.

Several recent studies have demonstrated the ability to make precision measurements on individual endogenous cargoes in living cells (3,12–15), and such measurements have been used to study the coordination of opposite polarity motors (1) and motor regulation (16). However, in vivo measurements suffer from three shortcomings that reduce the ability to dissect the details of motor dynamics and function with high precision. First, the heterogeneity of the cell can result in local changes in motor dynamics and compromise the high-precision detection. Second, the crowded cell and microtubule tracks limit the observation time of individual cargoes in isolation, as other cargoes can bump into them. Third, genetic manipulation can indirectly alter parts of the transport complex not targeted by the mutation, making it difficult to dissect function. For instance, we showed in a previous work that genetic reduction of kinesin results in a concurrent reduction of cargo-bound dynein, even though the overall cellular expression of dynein is not altered (3).

To circumvent these limitations, yet study the native transport complex, we reconstituted the motility of purified cargo ex vivo. We use the term ex vivo as opposed to in vitro to differentiate between the motility of purified organelles as discussed in this work and motility demonstrated in other works using isolated motors or motors attached to microspheres. Previous works using purified cargoes extracted from different systems have focused on vesicles (4,17–20), limiting their use for high-precision measurements in an optical trap, because a large laser power is necessary to manipulate them due to their small index of refraction. Sucrose-filled vesicles have been shown to be easily trapped without deforming, yet their nonendogenous nature limits their applicability to in vitro studies (21). Endogenous purified cargoes were recently shown to be amenable to optical trapping, albeit not high-precision measurements, yet their unidirectional kinesin-driven transport makes them not suitable to study bidirectional cargo transport and motor regulation (22). Here, we reconstitute ex vivo transport of lipid droplets purified from Drosophila embryos. Lipid droplets are refractile spheres of neutral lipids, and we have previously used them for optical trap measurements in vivo (1,3). Lipid droplets in yeast were used in conjunction with optical trapping to study cytosolic rheology (23). We use a high-bandwidth and high-precision optical trapping system to characterize their suitability for high-precision measurements ex vivo and monitor motor dynamics at an unprecedented bandwidth.

In our experiment, a single-beam trap is capable of tracking the position of a spherical tracer particle in three dimensions with nanometer spatial and microsecond temporal resolution (24). Moreover, it can follow sequential formation of bonds between the trapped tracer particle and a substrate (25). This allowed us to follow the dynamics of cargo-microtubule interaction with unprecedented detail. For example, by following the position of a microtubule-bound cargo, we show that the unbinding of one of the cargo-microtubule tethers correlates with the onset of transport.

Methods

Lipid droplet purification

Wild-type Drosophila embryos 0–3 h old were collected on yeast-agar plates, washed with ddH₂O, and dechorionated with 1:1 v/v bleach/water solution for 2–3 min. Embryos were gently homogenized with a Teflon pestle in lysis buffer (62.5 mM K₂-PIPES, 1 mM EGTA, and 5 mM MgCl₂, pH 7.2) supplemented with 1X protease inhibitor cocktail (cOmplete ULTRA mini, Roche, Basel, Switzerland) and 5 mM dithiothreitol (DTT). Embryo lysate was centrifuged for 10 min at 10,000 rpm at 4°C and the top layer of the postnuclear supernatant (PNS) was collected via a cold glass pipette. This fraction is enriched with lipid droplets. DTT and protease inhibitor supplements were added to the PNS fraction.

Motility assays

For lipid droplet motility, microtubules (unlabeled for DIC motility assays, or rhodamine fluorescent for optical trap measurements) grown at 37°C in growth buffer (80 mM PIPES, 2 mM Mg₂SO₄, and 1 mM EGTA supplemented with 1 mM GTP and 20 μM taxol) were deposited into flow chambers made with 0.02% poly-L-lysine-treated coverslips separated by a spacer. All surfaces were blocked using 5 mg/ml casein in blocking buffer (35 mM PIPES, 5 mM Mg₂SO₄, 1 mM EGTA, and 0.5 mM EDTA, pH 7.2) supplemented with 1 mM GTP and 20 μM taxol. Lipid droplet motility was observed in motility buffer (62.5 mM K₂-PIPES, 1 mM EGTA, and 5 mM MgCl₂, pH 7.2) supplemented with 1 mM ATP, 5 mM DTT, 20 μM taxol, and an oxygen-scavenging system consisting of 50 U/ml glucose oxidase, 500 U/mL catalase, and 12.5 mM glucose.

Polystyrene beads

Polystyrene beads certified by the National Institute of Standards and Technology were acquired from Bangs Laboratories (Fishers, IN); the beads, with diameters of d = 506 ± 6 nm and d = 990 ± 30 nm (mean ± SE), are henceforth referred to as 500 nm and 1 μm beads, respectively.

High-bandwidth and high precision optical trapping

Fig. 1 shows a schematic of our optical trap and three-dimensional position detector. The beam of a 1064 nm laser (Mephisto 500 mW, Innolight, Hannover, Germany) was expanded and focused through a water immersion objective lens (UPlanSApo 60×, Olympus, Tokyo, Japan), forming an optical trap in the focal plane of the lens. The sample chamber was mounted to an xyz-nanopositioning stage (P-561, Physik Instrumente, Karlsruhe, Germany) that allowed motion of the sample relative to the stationary trap. Light forward-scattered by a trapped nanoparticle, as well as unscattered light of the trapping laser, was collected by a condenser lens and projected onto a quadrant photodiode (QPD), where the two waves interfered with each other. This interference pattern on the QPD produced the position signal of the particle: the output voltages of the QPD can be related to the particle’s x-, y-, and z-positions relative to the center of the optical trap (26). The position voltages were sampled by a flexible-resolution digitizer (NI PXI 5922, National Instruments, Austin, TX) at a frequency of 100 kHz. The error of the position measurement was dominated by the position noise of the nanopositioning stage, which we measured to have a standard deviation of 1.5 nm in the lateral direction and 1 nm along the axial direction ((25) and data not shown).

Figure 1.

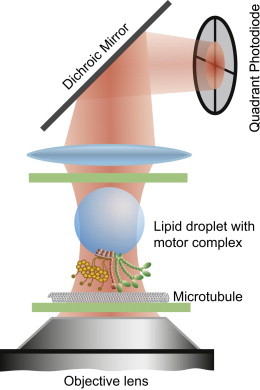
Schematic of the experimental setup. The laser is focused through a microscope objective and forms an optical trap. Lipid droplets purified from Drosophila embryos with their attached endogenous motor complex are trapped. Scattered and unscattered laser light is collected by the condenser lens and projected onto a quadrant photodiode. The electrical signal of the photodiode allows three-dimensional position tracking of the droplet at a sampling rate of 100 kHz.

Linearization of the detector

The relation between QPD response and particle position is approximately linear only close to the center of the trapping volume. For high-precision experiments, the detector’s response must be linearized. A method for linearizing and simultaneously calibrating the detector has been described previously (27). For calibration, this method relies on knowledge of the trapped particle's radius. However, here we are interested in calibrating the response of a diffusing lipid droplet whose radius is unknown. Thus, we do not know its diffusion constant, D, which is necessary to calculate the local slope of the detector's response curve using Eq. 7 of Tischer et al. (27). However, we can set the diffusion constant to any arbitrary value, which is equivalent to using arbitrary units for the diameter of the droplet. The linearization and calibration procedure described in Tischer et al. (27) then yields a transformation that linearizes the detector but transforms the detector's output voltage into arbitrary units of position. In other words, although we can linearize the detector, the resulting linearized position signal is still uncalibrated, and we will refer to it as the uncalibrated position signal. For each trapped particle, a 12-s-long time trace of its position fluctuations was recorded at 100 kHz at the beginning of each experimental run. From this time trace, we computed a transformation to linearize the detector response, as described in Tischer et al. (27). For all work described here, all recorded detector responses were first linearized into uncalibrated position signals, even if we do not explicitly mention it hereafter.

Calibration of position signal and determination of particle diameters

The uncalibrated position signal was calibrated as described by Tolić-Nørrelykke et al. (28), because their method of calibration does not require any knowledge of the radius of the trapped particle. In brief, four windows of 10 s each of linearized but uncalibrated position signal were recorded at a sampling frequency of 100 kHz, with simultaneous application of a sinusoidal lateral motion (amplitude 100 nm, frequency 40 Hz) to the sample chamber. The power spectral density (PSD) of each window was computed, and the four PSDs were averaged. From the power in the peak at the oscillation frequency and the corner frequency of the PSD (see below) the calibration (sensitivity) of the detector was determined.

A fit of the full hydrodynamic theory to the window- and block-averaged PSD (29) yields the corner frequency and the uncalibrated diffusion constant of the trapped particle. The full hydrodynamic theory requires knowledge of the diffusing particle’s mass density. We assumed that the mass density of lipid droplets is equal to 930 kg/m³. The density enters only as a correction factor in the fit. The particle size computed using the fit is effectively insensitive to the precise value of the density used: the measured size changes only by 0.1% when the density changes by 50%.

The goodness of fit is given by the weighted sum of square errors (SSE), which is defined, as in Berg-Sorensen and Flyvbjerg (29), as

$$\text{SSE}=n_w{n}_B\sum _{k=1}^{N^{\text{'}}}{\left(\frac{P_k^{Experiment}}{P_k^{Theory}}-1\right)}^2,$$

where n_w is the number of windows and n_B the number of points per block. The sum runs over all data points in the averaged and blocked PSD, and P_k is the measured or theoretical PSD, as indicated by the superscripts Experiment and Theory, respectively.

The uncalibrated diffusion constant found by the fit was calibrated using the sensitivity; the particle’s diameter, d, was found by the Stokes-Einstein relation (d = kT/3πηD), where D is the calibrated diffusion constant. We assumed the viscosity, η, of the buffer to be equal to the viscosity of water at 26°C.

Determination of spring constants

The spring constant of the optical trap can in principle be found from the corner frequency of the PSD and thus could be extracted from the calibration procedure described above. However, based on repeated measurements on the same trapped particle, this approach was empirically found to lead to a large scatter in determined spring constants.

It appears that the extraction of the spring constant by Boltzmann statistics from the spatial probability distribution of the trapped particle (30) leads to a more precise measurement. This method was chosen here.

For each measurement, a 12-s-long time trace of positions of the trapped particle was recorded at a sampling frequency of 100 kHz, linearized, and calibrated. From these data, one-dimensional spatial probability distributions were computed and the spring constants were extracted.

Results

Long-range motility of lipid droplets ex vivo

Lipid droplets in Drosophila embryos exhibit bidirectional motion along microtubules. It has previously been shown that the molecular motors kinesin-1 and cytoplasmic dynein, together with a multitude of motor cofactors, form the motor complex responsible for this transport of the lipid droplets in the embryos (1,3,31–34). To reconstitute cargo transport ex vivo, we purified lipid droplets from early Drosophila embryos (see Methods). To test whether the motors and motor cofactors remained attached to the lipid droplets after purification, we recorded simultaneous differential interference contrast (DIC) and immunofluorescence images of lipid droplets labeled with antibodies specific to kinesin-1, cytoplasmic dynein, and the P150^Glued subunit of the dynactin complex. As shown in Fig. S1 in the Supporting Material, fluorescence coincided with the lipid droplets for both motors and dynactin. No coinciding fluorescence was observed in control experiments lacking the specific primary antibody. Thus, isolating the lipid droplets left the motor-dynactin complex bound to the droplets.

To test whether the motor-cargo complexes attached to the purified droplets remain functional, lipid droplets were trapped with optical tweezers, positioned over a taxol-stabilized microtubule attached to a glass coverslip, and released from the trap. Lipid droplets attached specifically to microtubules and many moved several micrometers, often after multiple seconds of fluctuating over a short distance (see below and Fig. S2). Fig. 2 A shows an example of long-range motility of a lipid droplet measured by video microscopy. Fig. 2 B shows traces of other droplets moving with velocities of a few hundred nanometers per second, typical of both kinesin- and dynein-transported cargoes. These experiments demonstrate that motors attached to the droplets survive the purification process and remain functional.

Figure 2.

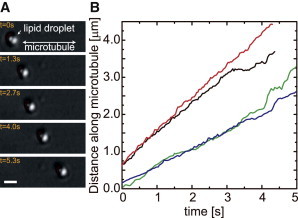
Purified lipid droplets can exhibit long-range transport in vitro. (A) Video frames showing a lipid droplet being transported along a microtubule attached to the microscope slide and imaged in DIC. Scale bar, 1 μm. (B) Position traces of various droplets show that they are transported at velocities of ∼400–1000 nm/s, characteristic of molecular motors.

Purified lipid droplets are suitable tracer particles for high-resolution experiments

Tracer particles for high-resolution optical trapping experiments need to be spherical, homogeneous, and stable over time. In addition, their index of refraction should be significantly higher than the surrounding medium. Since the droplets cause a strong contrast in DIC microscopy, the latter requirement is fulfilled. However, the other requirements are more difficult to confirm, because the images of the droplets are diffraction-limited and look perfectly homogeneous and round most of the time in bright-field and DIC. Another challenge is that their diameter varies and needs to be determined for calibrated force and position measurements.

Roundness and homogeneity of the droplets

If a droplet is not spherical, its rotational motion will cause artifacts in the position signal by scattering light in different directions depending on its rotational orientation. Due to the slow timescales of rotational diffusion in the weak trap, the power spectrum of an aspherical particle is expected to be elevated at low frequencies (35,36). A similar effect is expected for particles with a heterogeneous index of refraction. We thus inspected the power spectra of trapped droplets and compared them to the analytical expression for the spectrum of a spherical particle confined by a harmonic potential. To obtain the highest precision, we use the analytical expression derived from the full hydrodynamic theory (29) (see Methods). To quantify the agreement between the analytical theory and the data, we calculate the goodness of the fit, given by the weighted SSE (see Methods).

For reference, we first inspected the PSD of a 1-μm-diameter polystyrene bead, commonly used as a tracer particle in single-molecule experiments (Fig. 3 A, circles), and compared it to the analytical fit. The graph shows that the analytical expression fits the data exceptionally well, with an SSE of 0.027, which we will use as a reference for an excellent fit. Fig. 3 A shows the PSDs for two different lipid droplets (circles and stars). Visual inspection of the graphs clearly shows that the fit to the PSD of the first droplet is much better (SSE = 0.029) than the fit to the PSD of the second droplet (SSE = 0.175). For the latter, the fit fails, especially at low frequencies (dashed oval), as expected for a nonspherical and/or nonhomogeneous particle. Since it is possible that the roundness and the homogeneity of the lipid droplets depend on their diameter, we plotted the SSE of the fit versus the measured diameter (see Methods) for each droplet (Fig. 3 B). As a reference, the graph also shows SSEs of 500 nm and 1 μm beads (squares and triangles). Evidently, most lipid droplets (circles) have a goodness of fit comparable to that of the reference beads. Larger lipid droplets (>1 μm in diameter) tend to show significantly larger SSEs (stars) and therefore are problematic for high-resolution experiments. To establish an empirical standard, we accept all lipid droplets with an SSE falling within four standard deviations of that of the standard beads as suitable for high-resolution measurements.

Figure 3.

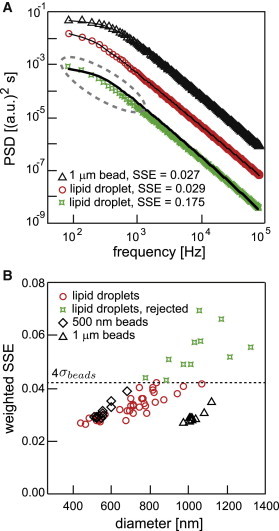
The goodness of fit to the PSD of the droplets reveals that most lipid droplets are spherical and homogeneous. (A) PSD plots of the thermal motion of an optically trapped 1-μm-diameter polystyrene bead (black triangles) and the thermal motion of optically trapped lipid droplets (red circles and green stars). Analytical fits of the full hydrodynamic theory for the diffusion of a spherical particle in a harmonic potential are shown as black lines. By visual inspection, it is clear that the theory fits the PSD of the bead (black triangles) and that of the first lipid droplet (red circles) very well, but it fails to fit the PSD of the second droplet (green stars). The PSD of an aspherical particle is elevated at low frequencies (dashed ellipse) and can no longer be correctly fit by the analytical theory. The traces indicate that the first droplet was as spherical and homogeneous as the polystyrene bead, whereas the second droplet was not. (B) The weighted SSE of the fit of the analytical theory to the PSD as shown in A is plotted versus diameter for lipid droplets (red circles and green stars) and reference beads of 500 nm diameter (black squares) and 1 μm diameter (black triangles), where the diameter was determined from the fit. Most droplets have SSEs comparable to the SSEs of the reference particles. The larger the droplet, the more likely it is to have a high SSE. We empirically set a cutoff at <SSE_beads> + 4σ_beads (dashed line). Droplets with SSEs above this cutoff were discarded and not used in further analysis.

Droplet size distribution

The diameter of purified lipid droplets varies significantly and therefore needs to be measured with sufficient precision for each droplet in situ. Fig. 4 shows the diameter distribution of all droplets that were found to be spherical and homogeneous by the criterion set in the previous paragraph. The distribution peaks at a diameter of ∼660 nm, and the mean diameter of all suitable droplets was 700 nm with a standard deviation of ±150 nm, which agrees reasonably well with previous observations in vivo (1) and (G.T. Shubeita,unpublished). The distribution appears to be cut off toward small droplet diameters. This is due to smaller droplets being more difficult to visualize in simple bright-field contrast as used in these experiments. Equipping the trapping system with dark-field illumination or DIC will make it possible to use small lipid droplets as tracer particles.

Figure 4.

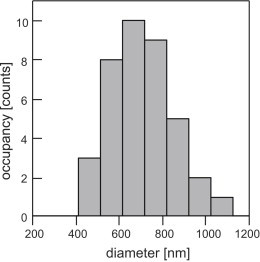
Lipid droplet size distribution. The diameter of all droplets was measured using the procedure outlined in Methods. Only droplets that met the criterion for a spherical and homogeneous particle are presented.

To determine the uncertainty in the size distribution, we measured the diameters of two different types of polystyrene beads (500 nm and 1 μm in diameter) and compared the mean measured diameter to the diameter provided by the manufacturer. For the 500 nm beads, the manufacturer reported the diameter as d = 506 ± 6 nm (mean ± SE), and we found experimentally d_exp = 558 ± 14 nm (N = 12 beads). For the 1 μm diameter beads, the manufacturer provided a diameter of d = 990 ± 30 nm, whereas we found experimentally d_exp = 1036 ± 48 nm (N = 11 beads). Our method thus systematically overestimates the particle diameter by ∼50 nm in this size range. The origin of the systematic error is currently not known. If higher accuracy is desired in the future, further measurements using reference beads could be made to correct for this small systematic error.

Detector sensitivity and spring constant of the optical trap

Two important parameters for high-resolution experiments are the position sensitivity, which quantifies the response of the detector signal to a change in position of the tracer particle within the trap, and the stiffness of the trapping potential. High position sensitivity ensures that the signal rises above the laser power noise and the noise of the electronics. In our detection scheme, the position sensitivity along the optical axis depends critically on the intensity of the forward-scattered laser light and with that on the diameter and the ratio of the indices of refraction of the trapped particle and of the medium that surrounds it.

Fig. 5 shows the dependence of lateral position sensitivity on particle diameter, both for lipid droplets (circles) and for two different sizes of polystyrene bead (500 nm beads (squares) and 1 μm beads (triangles). The sensitivity increases with increasing droplet and particle diameter. It is important to note that the position sensitivity for lipid droplets is only slightly smaller than that of 500 nm polystyrene particles, which qualifies them clearly for high-precision tracking experiments.

Figure 5.

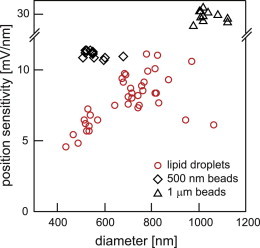
Comparison of the position sensitivities of lipid droplets and polystyrene beads. The lateral position sensitivity of lipid droplets (red circles) increases with diameter. It is comparable to, albeit smaller than, the position sensitivity of 500-nm-diameter (black squares) and 1-μm-diameter (black triangles) polystyrene beads.

Like the position sensitivity, the spring constant of the trapping potential that confines the tracer particle depends on the ratio of the indices of refraction of the particle and of the surrounding medium and the diameter of the particle. High trapping efficiency has two advantages: Less laser power is necessary to confine a particle with the same stiffness, and therefore, photodamage to the molecular motors and regulatory factors on the lipid droplets can be minimized (37). The second advantage is that high trapping stiffness increases the available force range, and a wider range of collective force generation by teams of motors can be probed.

Fig. 6 shows the spring constant for lipid droplets in the diameter range from 400 nm to 1 μm, as well as for 500 nm and 1 μm polystyrene beads. The spring constant of lipid droplets is slightly smaller than that of polystyrene beads of the same diameter. The spring constant for lipid droplets increases approximately linearly over the relevant size range from 400 nm to 800 nm diameter, consistent with earlier observations (1,38).

Figure 6.

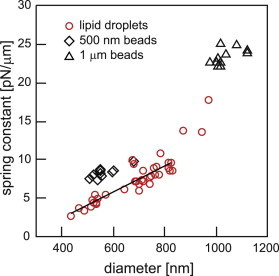
Comparison of the spring constant experienced by lipid droplets and polystyrene beads at the same laser power. As expected, trapped lipid droplets feel a stiffer confinement when their diameter increases. At diameters between 400 nm and 800 nm, this increase is approximately linear at a slope of 17 pN/μm² (black line). The confinement of 500-nm-diameter (black squares) and 1-μm-diameter (black triangles) polystyrene beads is stronger, but of the same order of magnitude.

We used a low laser power at the sample of ≈13 mW, which is well below the power that we have previously employed to trap lipid droplets in vivo without observing any photodamage (1,3). Nevertheless, a typical droplet of 700 nm diameter experiences a stiffness of 7.5 pN/μm even at this low laser power. The stiffness can easily be increased by increasing the laser power to what we have used for in vivo force measurements and by increasing the numerical aperture of the objective lens.

In summary, lipid droplets are comparable to plastic beads in terms of position sensitivity as well as trap stiffness and therefore are ideal for high-resolution experiments.

Lipid droplets in high-resolution binding and motility assays

We demonstrated at the beginning of this article that purified lipid droplets carry the endogenous motors, dynactin, and possibly other factors that regulate transport in vivo. Although motors move the purified droplets over several micrometers, as shown in Fig. 2, unlike lipid droplet transport in vivo, a large fraction of the traces display long-lived short-range bidirectional transport along the microtubules over a range of a few hundred nanometers, reminiscent of what has been reported for purified vesicles (17). Fig. S2 shows a few examples of these back-and-forth traces collected by video tracking. The position-scatter data show obvious elongation along the microtubule, which suggests motor activity in moving the droplets. A droplet with an immobile tether to the microtubule would produce a nearly symmetric distribution in position around its tethering point. However, with the resolution offered by video tracking, it is not possible to differentiate between back-and-forth motion due to rapid switching between the opposite-polarity motors on the one hand, and one-dimensional diffusion along the microtubule on the other. Hence, we opted to use the higher bandwidth offered by the optical-tweezers setup to follow the position of the droplet in three dimensions with high precision.

Fig. 7 A shows high-bandwidth time traces of binding and transport events for a lipid droplet that interacts with a microtubule. The coordinate system is oriented such that the x and y axes are parallel to the coverslip, and the z axis points into the direction of the optical axis. The microtubule is oriented along the x axis. Five regimes of behavior, labeled I–V, can be observed. In regime I, the droplet was positioned above the microtubule and its diffusion was confined by the optical trap in the x, y, and positive z direction. The accessible volume for diffusion toward the microtubule (negative z axis) is cut off due to collisions with the glass coverslip and the microtubule. The mean z-position of the droplet and the magnitude of its vertical fluctuations abruptly change at the transition from regime I to regime II. This indicates the binding of the droplet to the microtubule via a motor or a motor cofactor present on the lipid droplet (39). We excluded the possibility of nonspecific binding to the surface of each flow cell by bringing lipid droplets into contact with the glass surface away from any microtubule and monitoring the z trace for any binding event for at least 20 s. We consistently found that lipid droplets did not bind to blocked surfaces; bonds formed only when a droplet was placed directly above a microtubule.

Figure 7.

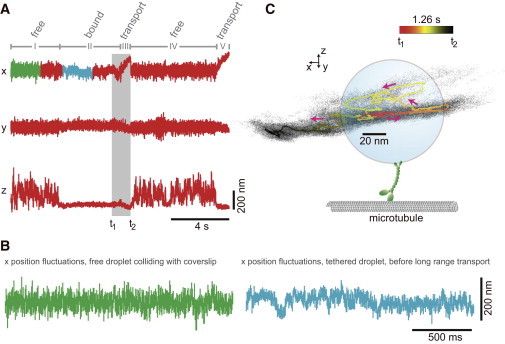
Motors and motor cofactors bind the microtubule dynamically. (A) The position of a lipid droplet in the sample plane (x, y) and along the optical axis (z) measured at a sampling rate of 100 kHz shows five different regimes of interaction with the microtubule. In regime I, the lipid droplet is held in the optical trap above a microtubule and allowed to collide with it as evidenced by the cutoff of the accessible volume for diffusion toward the negative z direction. In regime II, the droplet tethers to the microtubule. Its range of thermal motion along the z axis is dramatically reduced, and the center of its x and y fluctuations shifts. In regime III, transport along the microtubule results in a rapid increase in the mean of the x fluctuations, before the droplet detaches from the microtubule. In regime IV, the droplet has detached from the microtubule and is once again free to explore the top part of the trapping volume while colliding with the microtubule during thermal motion in the negative z direction. Thermal motion in the x and y directions shifts back toward the center of the trapping volume. In regime V, the droplet tethers again to the microtubule and immediately resumes directed motion along the x axis. (B) Comparison of short-timescale fluctuations along the x axis of the untethered (green) and tethered (teal) droplet during regime II. Even though no long-range transport is visible in regime II, the high-bandwidth data reveal transient changes in the mean of the fluctuations that are inconsistent with a single passive tether. The data for the tethered droplet suggest interplay between more than one tether bridging the droplet to the microtubule. (C) Three-dimensional scatter plot (black dots) and mean path of droplet positions for the transition from regime II to regime III (the gray-highlighted regime in A). The droplet is pulled in the negative x direction (red to orange) followed by a relaxation in the z direction which is indicative of the release of a tether (orange to yellow). Active transport along the microtubule then pulls the droplet in the positive x direction, and closer to the coverslip (yellow to black). Magenta arrows point in the direction of time. The droplet, motor, and microtubule are not drawn to scale.

Interestingly, no long-range motor-driven motion in the lateral directions is observed in regime II. This can be inferred from the x and y traces, since on the timescale of seconds there is no significant change in their mean values after the initial shift induced by the binding event. Thus, the droplet was tethered to the microtubule, but the tether was not generating active forces against the trap, even though the ATP concentration in solution was saturating (Methods). However, our high-bandwidth detector allows us to resolve the fast-timescale dynamics in regime II. Fig. 7 B shows an expanded view of 2 s of position data along the microtubule before the droplet was tethered to the microtubule (green trace) compared to 2 s of data after the droplet had tethered (teal trace). On fast timescales, the transient shifts in the mean that are visible for the tethered droplet are inconsistent with a single passive tether, which would lead to uniform position fluctuations over such a time interval (25,39). Rather, the data suggest that multiple tethers bridge the droplet to the microtubule and that their combined effect is the inhibition of long-range transport. Such antagonist tethers could be unregulated, active opposite-polarity motors, inactive motors, or a motor and dynactin, for example. Methods that make it possible to distinguish between these scenarios are presented in the Discussion. Several seconds after the initial binding event, the mean of the x trace rapidly increases, whereas the means of the y and z traces change only slightly (regime III). This is the signature of active transport of the droplet directed along the x axis, which is consistent with the orientation of the microtubule. A closer inspection of the transition from regime II to regime III supports the interpretation of regime II as resulting from more than one tether (Fig. 7 C). Immediately before active transport begins, the droplet is partially released from the microtubule, implying the release of a bond, as indicated by the average position trace (orange to yellow). The drastic change in the tethering is more clearly seen in the three-dimensional scatter plot of the position data (black dots). The volume accessible to the bead increases significantly just before the motor pulls the droplet along the positive x axis and directional transport begins; this is followed by a stronger restriction of its motion also along the z axis (yellow to black). Thus, the detailed analysis of the transition is consistent with the idea that the initial binding event was caused by more than one molecule and that directed transport was only initiated after one of them unbound from the microtubule.

The run of ∼200 nm with approximately constant velocity ends with the complete unbinding of the droplet from the microtubule, which can be seen from the large increase in axial fluctuations (regime IV) and is indicative of transport driven by only a single motor. Rebinding of the droplet to the microtubule in regime V leads to immediate transport of the droplet along the positive x axis. Here, the motor pulls the droplet out of the detection regime of the trap (data not shown).

Discussion

Typical in vitro samples in which highly purified motors are attached to plastic beads, glass surfaces, or, recently, to DNA scaffolds, can exhibit interesting dynamics when multiple copies of a similar or dissimilar motor are used (40–44). However, the lack of the endogenous cargo-binding domain, as well as necessary cofactors on these cargoes, can limit the applicability of the results of such assays in explaining in vivo observations. Indeed, it has previously been shown that motor activity is regulated by cargo binding and/or accessory proteins (45). The purified lipid droplets used in this work circumvent this obstacle. As demonstrated in the Results and Supporting Material, these purified cargoes preserve components of the endogenous transport machinery, in particular the motors kinesin-1 and cytoplasmic dynein, in addition to the motor cofactor dynactin, all of which are known to be key players in the transport of many distinct cargoes across different cell types and organisms (2,5–7,11,46). No additional sample preparation is required. Furthermore, although our understanding of motor function has greatly benefited from optical trapping experiments, until recently, artificial beads were the best available choice of cargoes. Their roundness and high index of refraction made trapping and precise position tracking possible. We showed that purified lipid droplets from Drosophila embryos are comparable to plastic beads in terms of trapping efficiency and roundness. Recently, purified lipid droplets from rat liver, as well as phagocytosed plastic beads in cells, have been used for force measurements (13,14,22) and could potentially serve as probe particles for high-resolution measurements, provided the droplets exhibit a similar shape uniformity and the phagosome membranes do not deform under the antagonistic forces of the trap and motors. However, lipid droplets from Drosophila facilitate the study of motor regulation, since the droplets carry both-polarity microtubule motors and have the added advantages of their extensively characterized transport in vivo (1,3,32–34), a published proteome (31), and the tractable genetics of the fly. Further, we have recently shown that lipid droplets can be used as a model to study neuronal transport, as some of the regulators of axonal cargoes regulate lipid droplets similarly (16).

We show here that the use of an endogenous cargo, with its high level of complexity, leads to much richer cargo dynamics than those exhibited during transport of plastic beads. Our lipid droplets portray a mixture of long-range transport spanning several micrometers in length and back-and-forth motion that does not go beyond a few hundred nanometers. Although a similar short-range bidirectional motion has been observed in vesicles purified from mouse brain (17), the suitability of the lipid droplets for high-precision position measurements enabled us to transcend the limitations of video tracking and helped us to dissect individual events of the transport dynamics, providing unprecedented detail of the interactions among different microtubule-binding tethers. Given that transport is a dynamic process and that multiple motors and cofactors are present that can interact with the microtubule at various timescales and in different order, experiments with high temporal and spatial resolution in three dimensions, as described in this work, are critical. The measurements in Fig. 7 A demonstrate the potential of these experiments to determine the different states of the transport complex dynamically.

However, the advantages of our approach present a new challenge. To dissect the entire process, from cargo binding to regulation of transport, it is important that the different binding states can be distinguished and ordered in time. The number of states that can be distinguished depends on the number of parameters that can be extracted from position time traces and the precision with which each parameter can be measured. As we have shown previously (25,39), passive binding events can be analyzed in detail, and parameters can be extracted that characterize each state. Such parameters include the stiffness of the tether along three axes, its length, and its resting position in three dimensions relative to the anchor point on the microtubule. The precision with which the parameters can be measured depends on the time spent in a particular state; long-lived states can be characterized with high precision. Being able to distinguish between states is a necessary condition for a systematic analysis of motor regulation. However, before we can understand the mechanistic details of motor regulation, it is important to identify all molecules (and their states) that determine the properties of a tether. This can be achieved by interplay between three different approaches: measurements on purified motors and cofactors attached individually to microspheres, measurements on lipid droplets for which specific factors have been inhibited, and measurements on droplets purified from different Drosophila mutants. Further, there are several ways to improve the assay, such as polarity labeling of the microtubules.

In addition to showing that we can identify various states of cargo-microtubule interaction, we have also demonstrated that transitions between states can be characterized by following the three-dimensional motion of the droplet (Fig. 7 C). The high-precision and high-bandwidth measurements provided unprecedented detail that allowed us to correlate the release of a tether with the onset of transport. Since the specific identity of the molecules that form the tether is not known at this time, the observed change could be the result of a single tether (motor) changing its state as opposed to the unbinding of one out of two tethers leaving the other unhindered to translocate along the microtubule. However, the latter possibility is consistent with the notion that the short-range back-and-forth motion (Fig. S2) results from an unregulated binding and unbinding of active opposite-polarity motors and cofactors in this purified system. Cataloging the mechanical properties of the various motors and cofactors present on the droplets as described above can resolve this ambiguity. Furthermore, novel methods for extracting tether (motor and cofactor) properties during transport will allow us to correlate the tether state with the velocity of the droplet and the force produced.

Finally, the genetics of Drosophila is tractable, and many well-characterized mutants are available. Mutants that lack factors important for motor-driven transport, and the lipid droplets purified from them, can be systematically studied. The correlation of the loss of these factors with changes in the states observed in ex vivo experiments will then provide insight into the function of each factor being investigated. The versatility of using Drosophila genetics offers a strong advantage over other in vitro assays with purified cargoes (13,17,18,47).

Conclusion

We have introduced an ex vivo assay that enables the study of molecular motor cooperativity and regulation of same and opposite-polarity motors with a higher level of complexity than attained via traditional in vitro studies. Our approach uses purified endogenous lipid droplets from Drosophila embryos as high-precision tracer particles for optical tweezers experiments. We show that, when carefully selected based on the goodness of the fit to their power spectrum at low frequency, these purified droplets are comparable to the plastic or silica beads typically used in in vitro studies. Furthermore, we present high-resolution position traces of droplets binding to and being transported along microtubules in vitro. We demonstrate the wealth of information that can be extracted from these traces, such as properties of the tether and the averaged path of the droplet, which facilitates the study of transitions that lead to the motile state. Finally, we discuss how high-resolution tracking data can be used to investigate motor cooperativity and regulation and how genetic manipulation of Drosophila embryos can be used to decipher the role of each factor in this complex process of motor-driven transport regulation.