Abstract
Recent studies show that minor and major centroidal axes (CA) of long bone cross sections provide valuable predictions of prevailing loading patterns in age and treatment matched cohorts of animals. Furthermore, using CA, we recently showed that the degree of mineralization and area of woven bone laid down in the first two weeks after creation of a critical sized bone defect relate inversely and correlate significantly to loading patterns. Here, we aim to determine how closely independent measures of the spatial distribution of bone apposition determined using the major and minor CA as reference points correlate to those using anatomically defined axes as reference points. In histological sections from the previous study, we found no statistically significant difference between the anatomical and centroidal axes with respect to the centroid location or axis rotation, but there is a significant albeit small difference in the average distance between centroids. Outcome measures calculated in areas of bone defined by 15°, 30°, 45°, 60° or 90° sectors when using the CA differ less than 5% from those calculated using anatomical axes as reference points. Hence, the major and minor CA provide objective reference points for comparison of mechanobiological outcome measures between animals in matched cohorts. Calculation of major and minor CA is automated, which reduces the potential for observer bias. A major advantage of using the major and minor CA as reference points is that it allows for direct relation of outcome measures to loading patterns in age and treatment matched cohorts, ultimately providing a tool to test mechanobiological hypotheses on histological cross sections of bone.
1. Introduction
Uncovering the mechanisms of mechanoadaptation in bone requires an understanding of structure - function relationships in systems that are by nature dynamic in space and time. Biological samples contain the environmental history of the cells for which they provide a habitat, a history defined by biological, chemical, electrical and mechanical events integrated over the lifetime of the organism from which the sample is taken. While imaging technology has grown in scope and sophistication over the past decade, we do not yet have the ability to assess structure - function relationships during de novo bone formation or during bone growth, healing, adaptation, and aging, in health or in disease, or over multiple length and time scales. Histological sections of bone tissue samples allow understanding of cellular contexts for tissue and organ length scale healing and adaptation.
A recent study from Lieberman et al. showed that the minor and major centroidal axes (CA) provide good predictions of prevailing loading patterns in age and treatment matched cohorts of animals [1]. The major and minor axes are cross-sectional geometric properties describing the axes of bending about which long bones are most and least likely to bend for a given bending force, respectively, like the orthogonal axes of an I-beam cross section. Although the major and minor CA provide valuable landmarks to identify areas of bone exposed to similar loading histories between animals in matched cohorts, they do not give reliable predictions of absolute loading magnitudes or direction (tension versus compression) [1]. Recently, we measured areas and density of bone laid down along the CA of femoral defect cross sections to test the hypothesis that mechanical loading patterns relate to de novo tissue generation and healing in critical sized defects surrounded in situ by periosteum [2]. We showed that degree of mineralization and area of woven bone laid down in the first two weeks after defect creation are inversely related and correlate significantly to loading patterns. Specifically, bone laid down along the major axis exhibits more total bone area albeit less mineralization than that laid down along the minor axis of the mid defect cross section, and vice versa. Similar trends were observed for measures of tissue perfusion at 16 weeks after surgery, when all defects had healed [2]. Furthermore, in a parallel study of massive autograft healing, we showed significant differences in early proliferative woven bone apposition between areas along the major and minor CA [3]. Finally, in a rat study, CA was shown to relate significantly to new bone apposition in response to lithotripsy treatment only in animals that were subjected to mechanical loading and not in hindlimb suspended (unloaded) animals [4].
Current methods to control for loading histories in cohorts of large and small animals in vivo include treadmill loading [5,6], exogenous loading using mechanical testing devices in small animals [7,8], and control of loading magnitude and distribution via implants in large and small animals (external fixators, plates, etc.) [9,10]. Typically, mechanical strains under bending loads are related to the neutral axis, which separates areas subjected to compression and tension. Determination of the neutral axis requires experimental strain gauging with rosette gauges to assess principal strain direction [1]. Furthermore, mechanical strains are typically reported in relation to anatomical references, i.e. anterioposterior and mediolateral axes, which can be difficult to infer accurately in cross sections of long bones prepared for histomorphometry. Hence, the impetus of this study was to test reference points that mark predominant retrospective loading patterns without the need for controlled loading schemes, experimental strain methods, and/or exact specification of anatomical landmarks.
Here, we compared how closely independent measures of the spatial distribution of bone apposition, determined using the major and minor CA, matched those determined using the anatomical axes as reference points. If no significant difference were to be found between the two measures, then the major and minor CA of bone cross sections would provide effectively equivalent reference points (100% would be consistent with perfect equivalence) about which biological outcome measures can be made to test mechanobiological hypotheses. Given the inherent variability of biological systems and their outcome measures, we hypothesized that the CA reference system serve as an accurate surrogate for anatomical axes if it predicts outcome measures within 5% of those made using anatomical axes.
2. Methods
Overview of ovine (sheep) femoral defect model
In brief, the critical sized defect (2.5 inches) was enveloped by periosteum retaining small, adherent bone chips on its internal surface. During surgery, the defect fills with haematoma and thereafter periosteum-derived cells ingress into the defect. Within two weeks the defect fills with proliferative woven bone [2, 11]. This early bone apposition is tagged using the mineral chelating fluorochrome calcein green. At the conclusion of the IACUC approved experiments (Canton of Grisons, Switzerland), treated femora (all from same side of animal) and surrounding soft tissues are resected and embedded in polymethylmethacrylate after dehydration and fixation. The bone remains undecalcified for assessment of bone apposition. For histomorphometric assessment, three to four, contiguous (circa 250 μm thick) sections are cut through the center of the 2.54 cm defect zone (Well Diamond Wire Saw Model 4240) and polished to 100 μm using increasingly fine grades of sand paper (Buehler Automet 2000 Polisher), after which sections are mounted (Eukitt) on custom sized glass slides and coverslipped for imaging (see [2,11] for full details of experimental protocols).
Imaging of bone cross section and new bone formation
Femoral block cross sections (n = 5 bones, 3-4 cross sections per bone) from the central defect zone of the previously described study (see [2] for details) are imaged using an epifluorescent, inverted microscope with motorized stage control and full color camera (Leica DMIRE2, Leica Microsystems GmbH, Wetzlar, Germany). Images are taken of the specimen, at 1.6× magnification, using an ultraviolet (UV) (Leica Filter System A, excitation filter broad pass 340-380 nm, dichroic mirror 400 nm, barrier filter low pass 430 nm) and FITC (fluorescein isothiocyanate) filter and collaged to show the entire specimen. The UV light excites autofluorescent collagens in muscle, bone and fibrous tissue, making visible the entire cross section of the sample (UV image). The FITC filter excites only the calcein green fluorochrome, which chelates to mineral laid down in the first weeks after surgery (initial bone image).
Determination of axes
The anteroposterior and mediolateral anatomical axes are determined on each three-dimensional (3D), femoral block, first by drawing a ray between the center of the intramedullary nail that stabilizes the defect zone during healing (following [11]) and the intersection of the trochanteric crest and the insertion of the quadratus femoris, an anatomical reference point which we used to define the middle of the posterior aspect (not visible on cross-sections, but on the proximal ends of the whole bone blocks). The anteroposterior mediolateral directions are derived from the posterior ray and validated using high-resolution radiographs and micro-computed tomography scans. As such, determination of the anatomical axes requires interpretation by the scientist and may contain inherent bias. The anatomical axes determined on the 3D block are easily transferrable to the two dimensional cross sections, because each section fits like a puzzle piece (albeit missing some of its thickness after polishing) into the missing sections of the block after cutting with the diamond wire saw.
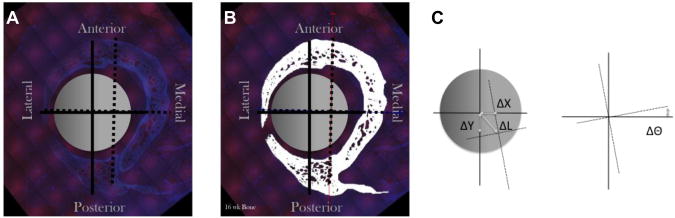
In contrast, the major and minor CA are calculated using an algorithm based on the bone cross-sectional geometry. The UV image of the bone cross section (Fig. 1A) is first segmented (Fig. 1B) using multiple image processing steps in an automated MatLab algorithm. Then the CA are calculated using the CA centroid and orientation functions in MatLab.
Figure 1.
Determination of the major and minor centroidal axes (CA) and the anteroposterior and mediolateral anatomical axes for the ovine femur cross sections, shown on the original epifluorescent digital image (A), the segmented image depicting bone in white (B) and a schematic diagram (C) showing how differences in location of the respective centroids were calculated (ΔX,ΔY,ΔΘ). The major and minor CA (dashed lines), anteroposterior and mediolateral anatomical axes (solid lines), intramedullary nail (gray circle). After[12], used with permission.
Comparison of anatomically determined axes and centroidal axes
Location and Rotation
The average difference in the location and rotation between the anatomical axes and centroidal axes should be close to zero if the major and minor CA provide accurate surrogates for anatomical axes as objective reference points for bone mechanoadaptation. To calculate the differences between the two, we first determine the average difference in the centroid location between the anatomic and the centroidal axes in the x- and y-directions, and we calculate the Euclidian distance (Fig. 1C). Next, the average difference in axial rotation is determined using the right-handed axes rule (Fig. 1D). By taking an average that incorporates all cross sections from each femoral block, we effectively eliminate issues related to unequal sample number.
Measuring Distribuition of Initial Bone Generated with Respect to Reference Axes
Thereafter, using each set of axes as a reference, we quantify the percent of the total initial bone generated that lies within a given sector; specifically, the amount of initial bone lying within a given 15°, 30°, 45°, 60°, or 90° sector is divided by the total bone laid down within the first two weeks after surgery. Different sized sectors are analyzed to determine how sensitive the measurements are to the size of the sector assessed. In sum, the percent of initial bone in each sector represents the spatial distribution of initial bone formation measured using a given reference axis system.
By quantifying the distribution of bone with reference to the anatomical axes and then with reference to the CA, both reference systems are represented equally per bone. We then calculate the absolute difference between distributions calculated using anatomical and centroidal axes for each sector to determine the error inherent to measurements made using the CA reference system. The absolute difference was chosen because the sector errors are not independent, i.e. if one sector's value increases then one or more sector's value(s) must decrease. Therefore, when the errors (positive and negative) are averaged they will always average out to approximately zero. By taking the absolute error, dependence is not eliminated but the mathematical possibility of a zero error is avoided. In fact, the error is overestimated because as one sector's value (or error) increases the distribution to other sectors is also counted as additional error. The absolute differences in measurement cannot be compared across sector sizes, because small sectors will yield small measurements and hence small differences, whereas large sector sizes will yield large measurements and hence large differences. For this reason, the measurements are also normalized by degrees in the sector.
Functional Equivalence
If the major and minor CA provide accurate surrogates for anatomical axes as objective reference points for bone mechanoadaptation, then we would expect the average difference in the location and rotation between the anatomical axes and centroidal axes to be close to zero. Also, the absolute error between bone distribution measurements made using the anatomical axes and the CA would be minimal. As mentioned previously, effective equivalence would be defined by a zero difference and would signify functional equivalence, allowing the use of CA as a surrogate for anatomical axes, was defined by a 5% or less difference.
Statistical Analysis
All data related to centroid location and rotation are presented as mean values with a 95% confidence interval. A t-test was used to compare the mean errors. P-values of less than 0.05 indicated significant differences from zero. All data comparing spatial distribution of data measured using anatomical versus CA are presented as mean values of absolute error with a 95% confidence interval. T-tests were used to compare values between anatomic and CA reference systems across all sectors and all animals, for a given sector size). P-values of less than 0.05 indicated significant differences from zero.
3. Results
On average, the centroids of the anatomical and CA are not perfectly colocalized. However, there is no significant, repeatable pattern of offset, indicating that the CA centroid location is approximately the same as the anatomical centroid location. There was no preference in the direction of anatomical and CA centroid offset, as the average differences in ΔX or ΔY (Table 1) were not significantly different from zero. However, the anatomical and CA centroid were offset by an average of 1.29 (0.93, 1.65) mm, which is less than approximately 5% of the total bone diameter, i.e. dividing the average ΔL by circa 3 cm (Table 1). The radial offset (ΔΘ) was also not significantly different from zero. (Table 1)
Table 1.
Average differences in axis location with respect to the center of the intramedullary nail. Refer to Fig. 1 for schematic representation of centroidal and anatomical axes and how measurements were made.
| Measure | Average Δ and (95% Confidence Interval) | p-Value |
|---|---|---|
| ΔX | 0.25 mm (-0.19, 0.69) | 0.247 |
| ΔY | 0.28 mm (-0.33, 0.88) | 0342 |
| ΔL | 1.29 mm (0.93, 1.65) | <0.001 |
| ΔΘ | -11.75° (-27.36, 3.84) | 00130 |
A small but statistically significant absolute error in initial bone apposition was observed between measures made using either CA or anatomical axes as reference points (Tables 2, 3). The mean absolute difference in percent initial bone measured in a sector, using either anatomical axes or CA as the reference axes, increased with increasing sector size (1.59-4.97%, Table 2). This was expected as the measurement per sector increases with increasing sector size. The mean absolute difference data normalized to the degrees per sector decreased with increasing sector size (0.1063-0.0552% per degree, Table 3). Again, this was expected as the ability to capture approximately the same distribution of bone increases with sector size; e.g. a sector of 360° should capture the exact same distribution with both axes systems.
Table 2.
Ninety-five per cent confidence interval for absolute error between initial bone measurements in a sector using either the anatomical axes or CA system and different degrees per sector and their significance (p-value). All mean differences are zero. Refer to Fig. 1 for graphical representation of these systems.
| °/sector | Mean Absolute Error & (95% Confidence Interval) | p-value |
|---|---|---|
| 15 | 1.59 (1.22, 1.96)% | 0 |
| 30 | 2.64 (1.80, 3.48)% | 0 |
| 45 | 2.56 (1.83, 3.38)% | 0 |
| 60 | 3.34 (2.07, 4.62)% | 0 |
| 90 | 4.97 (2.44, 7.50)% | 0.001 |
Table 3.
Ninety five percent confidence interval for the normalized absolute error between initial bone measurements in a sector using either the anatomical axes or CA system and different degrees per sector and their significance (p-value). Refer to Fig. 1 for graphical representation of these systems.
| °/sector | Mean Absolute Error and 95% CI for Normalized Error (% per °) | p-Value |
|---|---|---|
| 15 | 0.106 (0.082, 0.131) | 0 |
| 30 | 0.088 (0.061, 0.116) | 0 |
| 45 | 0.057 (0.039, 0.075) | 0 |
| 60 | 0.056 (0.035, 0.077) | 0 |
| 90 | 0.055 (0.027, 0.083) | 0.001 |
In sum, there is no significant difference between the anatomical and CA with respect to the centroid location (X,Y), or axis rotation. However, there is a small but significant difference in the average distance between centroids. On average the major/minor axis centroid is 1.29 (0.93, 1.65) mm away from the anatomical centroid. If the distributions are calculated using 15 - 90° sectors, there is a minimal albeit statistically significant difference in outcome measure when using the CA versus anatomical axes as reference points; for example, using 15° sectors, the maximum average difference is 1.59% and for 90° sectors the maximum average difference is 4.97% (Table 2). Since the difference between measures made using CA and anatomical axes is small but significant, they cannot be considered perfectly equivalent. However, the CA reference system serves as an accurate surrogate for anatomical axes, because outcome measures made with CA are no more than 5% different than those made using anatomical axes.
4. Discussion and Conclusion
These studies show that the major and minor CA predict outcome measures from 1.59 - 4.97% (within 5%) of those calculated using anatomical axes. Hence, major and minor CA provide objective reference points for comparison of outcome measures between animals in matched cohorts of animals. However, if the expected differences between experimental and control groups in a given study are smaller than 5%, precise definition of anatomical landmarks prior to sectioning may be advisable. Given the natural variation (even in anatomy) among study subjects, the major and minor CA provide several advantages over anatomical axes as reference systems. Since the major and minor CA are calculated using a software algorithm on images, measures can be automated. Thus, little potential for observer bias exists beyond that inherent to image processing procedures. In contrast, determination of the anatomical axes requires interpretation by the scientist and may contain inherent bias. Furthermore, the accuracy of anatomical axis determination was not measured in the current study and may be impossible to measure given the lack of an absolute anatomical reference point such as magnetic north in determination of absolute geographical orientation. Finally, in addition to providing objective structural reference points, the minor and major CA provide valuable functional reference points in a given bone, predicting loading patterns in age and treatment matched cohorts of animals [1]. Hence, although CA is not perfectly equivalent to anatomical axes, they serve as an unbiased surrogate for anatomical axes and are particularly advantageous for testing mechanobiological hypotheses.
Acknowledgments
The study was funded through grants from the AO Foundation. Specifically, the histological studies reported in the current study were supported through grants numbered F-07-99K and 04-K3. The original surgical study, approved through the animal review board of the Canton of Grisons, Switzerland, was funded through AO Grant No. 02-K83 and a grant from the Research Programs Council of The Cleveland Clinic (Grant No. 07316). Sara McBride was supported in part by an NIH training grant (NIAMS 5 T32 AR 007505-20). Scott Dolejs was supported in part by a grant from the National Science Foundation (EEC-0552804).
Footnotes
Conflict of interest statement: None of the co-authors has a conflict of interest with regard to this manuscript or the research study described therein.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Lieberman DE, Polk JD, Demes B. Predicting long bone loading from cross-sectional geometry. American Journal of Physical Anthropology. 2004;123:156–71. doi: 10.1002/ajpa.10316. [DOI] [PubMed] [Google Scholar]
- 2.Knothe U, Dolejs S, Miller RM, Knothe Tate ML. Effects of mechanical loading patterns, bone graft and proximity to periosteum on bone defect healing. Journal of Biomechanics. 2010;43:2728–37. doi: 10.1016/j.jbiomech.2010.06.026. [DOI] [PubMed] [Google Scholar]
- 3.Knothe Tate ML, Dolejs S, Miller RM, Knothe U. Role of mechanical loading in healing of massive bone autografts. Journal of Orthopaedic Research. 2010;28:1657–84. doi: 10.1002/jor.21190. [DOI] [PubMed] [Google Scholar]
- 4.Knothe Tate ML, Cai L, McNamara E, Knothe U. Bone resorption is mitigated by treatment with lithotripsy. Transactions of the Orthopaedic Research Society. 2010;35:0581. [Google Scholar]
- 5.Steck R, Gatzka C, Schneider E, Niederer P, Knothe Tate ML. Measurement of bone surface strains on the sheep metacarpus in vivo and ex vivo. Veterinary and Comparative Orthopaedics and Trumatology. 2003;16:38–43. [Google Scholar]
- 6.Rabkin BA, Szivek JA, Schonfeld JE, Halloran BP. Long-term measurement of bone strain in vivo: the rat tibia. Journal of Biomedical Materials Research. 2001;58:277–81. doi: 10.1002/1097-4636(2001)58:3<277::aid-jbm1017>3.0.co;2-t. [DOI] [PubMed] [Google Scholar]
- 7.Torrance AG, Mosley JR, Suswillo RF, Lanyon LE. Noninvasive loading of the rat ulna in vivo induces a strain-related modeling response uncomplicated by trauma or periosteal pressure. Calcified Tissue International. 1994;54:241–7. doi: 10.1007/BF00301686. [DOI] [PubMed] [Google Scholar]
- 8.Raab-Cullen DM, Akhter MP, Kimmel DB, Recker RR. Bone response to alternate-day mechanical loading of the rat tibia. Journal of Bone and Mineral Research. 1994;9:203–11. doi: 10.1002/jbmr.5650090209. [DOI] [PubMed] [Google Scholar]
- 9.Claes L, Laule J, Wenger K, Suger G, Liener U, Kinzl L. The influence of stiffness of the fixator on maturation of callus after segmental transport. Journal of Bone and Joint Surgery British. 2000;82:142–8. [PubMed] [Google Scholar]
- 10.Bishop NE, Schneider E, Ito K. An experimental two degrees-of-freedom actuated external fixator for in vivo investigation of fracture healing. Medical Engineering Physics. 2003;25:335–40. doi: 10.1016/s1350-4533(02)00250-3. [DOI] [PubMed] [Google Scholar]
- 11.Knothe Tate ML, Ritzman T, Schneider E, Knothe U. Testing of a new one-stage bone-transport surgical procedure exploiting the periosteum and bone transport for repair of long bone defects. Journal of Bone and Joint Surgery American. 2007;89:307–316. doi: 10.2106/JBJS.E.00512. [DOI] [PubMed] [Google Scholar]
- 12.McBride SH, Dolejs S, Brianza S, Knothe U, Knothe Tate ML. Net change in periosteal strain during stance shift loading after surgery correlates to rapid de novo bone generation in critically sized defects. Annals of Biomedical Engineering. 2011 doi: 10.1007/s10439-010-0242-9. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]