Measuring Electrostatic Fields in Both Hydrogen Bonding and non-Hydrogen Bonding Environments using Carbonyl Vibrational Probes

Abstract

Vibrational probes can provide a direct read-out of the local electrostatic field in complex molecular environments, such as protein binding sites and enzyme active sites. This information provides an experimental method to explore the underlying physical causes of important biomolecular processes such as binding and catalysis. However, specific chemical interactions such as hydrogen bonds can have complicated effects on vibrational probes and confound simple electrostatic interpretations of their frequency shifts. We employ vibrational Stark spectroscopy along with infrared spectroscopy of carbonyl probes in different solvent environments and in Ribonuclease S to understand the sensitivity of carbonyl frequencies to electrostatic fields, including those due to hydrogen bonds. Additionally, we carried out molecular dynamics simulations to calculate ensemble-averaged electric fields in solvents and in Ribonuclease S, and found excellent correlation between calculated fields and vibrational frequencies. These data enabled the construction of a robust field-frequency calibration curve for the C=O vibration. The present results suggest that carbonyl probes are capable of quantitatively assessing the electrostatics of hydrogen bonding, making them promising for future study of protein function.

I. Introduction

Vibrational (IR) probes are sensitive to their local electrostatic environment and can be as small as two atoms. Therefore, these probes are ideally suited to study the intricate architecture of proteins, whose electrostatic characteristics vary steeply over very small length scales.^1-3 Furthermore, the sensitivity of a vibrational frequency to an electrostatic field can be experimentally calibrated in an external well-defined electric field using vibrational Stark spectroscopy.^4,5 An ideal vibrational probe of electrostatics would allow one to read an electric field, $\overrightarrow{F}$, experienced by a vibration due to its surrounding environment directly from the infrared (IR) spectrum, according to:

$$\overrightarrow{F}·{\widehat{u}}_{\mathit{probe}}=\frac{\mathit{hc}({\overline{\nu }}_{\mathit{obs}}-{\overline{\nu }}_0)}{\left|\mathrm{\Delta }{\overrightarrow{\mu }}_{\mathit{probe}}\right|}$$ (1)

where ν̄_obs is the observed vibrational frequency, ν̄₀ is a reference frequency calibrated to zero electric field, $\left|\mathrm{\Delta }{\overrightarrow{\mu }}_{\mathit{probe}}\right|$ is the magnitude of the probe’s difference dipole – which is determined by measuring the vibrational Stark effect and defines the sensitivity of vibrational shifts to electric field, and $\overrightarrow{F}·{\widehat{u}}_{\mathit{probe}}$ is the electric field experienced by the vibration projected onto the difference dipole vector, $\mathrm{\Delta }{\overrightarrow{\mu }}_{\mathit{probe}}$. For the case of a decoupled vibrational mode that is confined to two atoms, û_probe is necessarily co-linear with the bond axis of the vibration, and aligned with the permanent bond dipole moment.⁶ This criterion implies that when a field is oriented in a manner that stabilizes the bond’s (difference) dipole, the vibration shifts to lower frequency.

The nitrile (C≡N) vibration has gained wide attention as an electrostatic probe in biophysical studies because it is intense, local, absorbs in an uncluttered region of the IR spectrum, and a number of approaches have been developed to introduce it into biological systems.^1-3,7-11 The goal to utilize Eq. 1 as a general tool to translate observed vibrational frequency shifts into electric fields is complicated by the possibility that the variation in a probe’s absorption frequency may not be entirely due to electrostatics. For example, C≡N frequencies exhibit a characteristic blue-shift upon accepting a hydrogen bond (H-bond) in a manner that is not described by the linear vibrational Stark effect.^12,13 It would be preferable to apply Eq. 1 uniformly across both H-bonding and non-H-bonding environments, because many cases where protein electrostatics are functionally relevant (ligand binding, enzyme catalysis, protein-protein recognition) involve H-bonding or a transition between non-H-bonding and H-bonding states.

The carbonyl (C=O) stretching mode is also very local, and generally more intense than nitriles.^14,15 Importantly, computational results have predicted that carbonyl frequencies vary linearly with electrostatic field in H-bonding environments.¹⁶ A limitation to the C=O probe is that its characteristic frequency (1700 cm^-1) overlaps with the densely populated amide I region, making it more challenging to detect in proteins. However, we have overcome this limitation by carefully selecting a reference sample that is almost identical to the vibrational-probe bearing sample, but alters the vibrational probe, and then calculating the difference spectrum.¹⁷ This technique further requires that transmission spectra of sample and reference be closely matched and that the protein concentration be low enough that some light can transmit through the amide I frequency range. The carbonyl probe can be installed into proteins via the unnatural amino acid, p-acetyl-L-phenylalanine (p-Ac-Phe), either through reassembly of a split protein, protein semi-synthesis, or nonsense suppression.¹⁸ Carbonyl groups are also often present on substrates, inhibitors, and drugs. In this study, we deployed the C=O probe into a protein by incorporating p-Ac-Phe as a residue into a polypeptide chain. To study a diverse range of solvents, we chose acetophenone as a solute because it maintains the same local structure around the C=O chromophore as p-Ac-Phe.

In this work, we test the viability of carbonyl vibrations as local electrostatic probes, with a focus on examining their response to strong interactions such as H-bonding. To do this, we performed vibrational Stark spectroscopy on C=O vibrations to determine the intrinsic sensitivity of the C=O vibrational frequency to an electrostatic field. We also obtained IR spectra of carbonyls in a variety of settings – such as in solvents of different polarities and H-bond donor strengths, and in the model protein Ribonuclease S (RNase S) – to see how their frequencies report on the local electrostatic fields of those environments. These observations were compared against molecular dynamics (MD) calculations of the electric fields in the respective environments, with which they displayed a remarkably high linear correlation. With this correlation, we developed a robust field-frequency calibration for carbonyl vibrations. Our results collectively indicate that carbonyl frequency shifts conform to the formalism in Eq. 1, and report on the relatively large electric fields that are created by H-bonding by way of a linear Stark effect. In particular, the latter feature makes them an attractive probe for future research in protein structure and function, and these applications will be described in future publications.

II. Results and Discussion for Solvents

1. Vibrational Stark Spectroscopy of Acetophenone

In vibrational Stark spectroscopy, the sensitivity of a vibration to an electric field is determined by applying a uniform field onto a vitrified sample with a high-voltage power source, and then observing the response of the IR spectrum.⁴ The absorption and Stark spectra of acetophenone, a model compound that contains a local C=O stretch, are displayed in Figure 1 and summaries of the spectral data are given in Table 1. Stark spectra are conventionally shown as the difference spectrum between the field-on and the field-off absorbances and are interpreted by numerically fitting the difference spectrum to contributions from the zeroth, first, and second derivatives of the absorption spectrum. Vibrational Stark spectra have been previously reported for the heme-bound CO in CO-myoglobin (wild-type and several mutants),¹⁹ for the C=O in acetone,²⁰ and for 6-propionyl-2-(dimethylamino)naphthalene,⁵ but not for a simple aromatic ketone like acetophenone.

Figure 1.

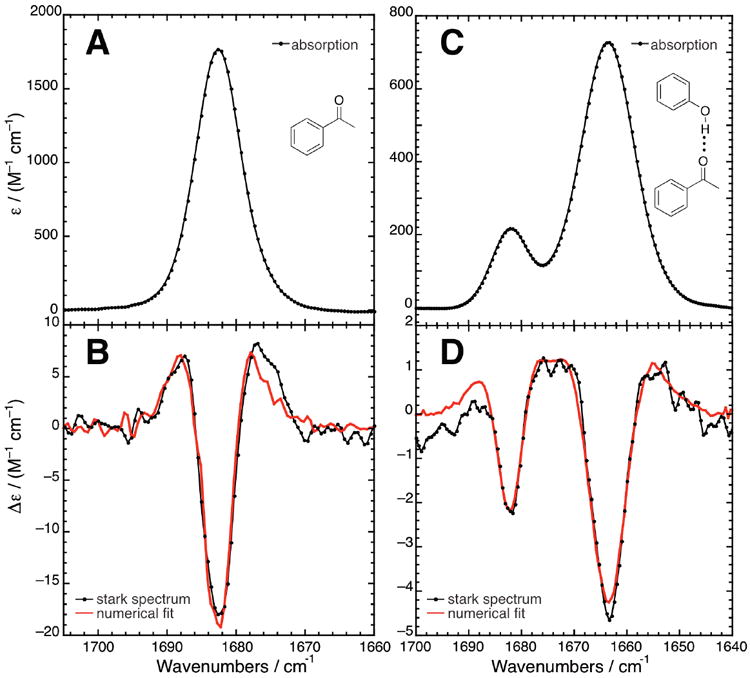
Vibrational Stark spectroscopy of the C=O stretch. Absorption (A, C) and Stark (B, D) spectra of acetophenone (50 mM) at 77 K in 2-methyltetrahydrofuran (A, B) and in toluene with 1.25 equivalents of phenol (C, D). Stark spectra are recorded at several applied fields from 0.5–1.4 MV/cm, but are scaled to 1 MV/cm here for comparison (note that the Stark signal scales with the square of the external field³³). In the Stark spectra, the black dots and trace is the experimental data and the red trace is a numerical fit, (consisting of contributions of the 0th, 1st, and 2nd derivatives of the absorption) from which Stark parameters are extracted (see Table 1).

Table 1.

Vibrational Stark effect data of acetophenone ^a

	Absorption			Stark
System	Peak Position / cm−1	FWHM / cm−1	Peak Area / M−1 cm−2	A	B / cm−1	C / cm−2	$\left|\mathrm{\Delta }\overrightarrow{\mu }\right|f$b / cm−1 / (MV/cm)
2-meTHF	1682.6	7.9	15,600	(−4.3 ± 2.4) × 10−4	(1.53 ± 1.03) × 10−3	(1.097 ± 0.032) ×10−1	1.05 ± 0.08
Toluene + 1.25 eq Phenol	1682.0	6.3	1,900	(−1.2 ± 0.1) × 10−3	(−2.1 ± 7.5) × 10−4	(1.136 ± 0.031) × 10−1	1.07 ± 0.08
	1663.7	10.9	9,800

^aData and fitting parameters correspond to absorption and Stark spectra in Figure 1 (see Refs. 4 and 6 for details on interpretation of fitting parameters).

^bDerived from the second derivative component, C. Assumes the angle between the vibration’s difference dipole and transition dipole is 0°.

The C=O stretch of acetophenone in 2-MeTHF has an intense peak molar extinction of 1800 M⁻¹ cm⁻¹ (Figure 1A, Table 1), and possesses a strong Stark signal (Figure 1B) whose lineshape is almost identical to the second derivative of the absorption spectrum. As shown in Table 1, the fitting coefficients for the zeroth and first derivative contributions are essentially zero within experimental error. The dominance of the second derivative contribution implies that the sensitivity of the vibration to electric field is determined almost exclusively by the C=O vibration’s difference dipole, $\left|\mathrm{\Delta }\overrightarrow{\mu }\right|$.^4,6 The difference dipole, also known as the Stark tuning rate, specifies the extent to which a vibrational frequency shifts linearly with respect to electrostatic field. From the second derivative fitting parameter (Table 1), we calculate that $\left|\mathrm{\Delta }\overrightarrow{\mu }\right|f=1.05\pm 0.08{\mathrm{cm}}^{­1}/(\mathrm{MV}/\mathrm{cm})$ where f is the local field correction factor, described further in section II.5 below and experimental methods section V.4.

To examine the effect of accepting an H-bond on the Stark tuning rate of C=O, acetophenone was dissolved in toluene along with 1.25 equivalents of phenol, an H-bond donor. The low-temperature absorbance (Figure 1C) consists of two well-resolved peaks, and the minor band’s peak position matches that of acetophenone when no phenol is present. The second peak is broader, has a peak frequency (1663.7 cm⁻¹) closer to that of acetophenone dissolved in water (1669.4 cm⁻¹), and increases in intensity upon increasing the concentration of phenol (data not shown). These observations confer strong evidence that acetophenone forms an H-bonding complex with phenol, and that the second peak corresponds to the H-bonded population. As seen in Figure 1D, a satisfactory fit to the Stark features of both the H-bonded and non-H-bonded populations was obtained with a single set of parameters (Table 1). Moreover, the Stark tuning rate determined from this fit (1.07 cm^-1/(MV/cm)) was nearly identical to that found in 2-MeTHF (1.05 cm⁻¹/(MV/cm)). These results strongly suggest that the carbonyl frequency’s intrinsic sensitivity to an electric field is the same in both non-H-bonding and H-bonding environments.²¹

In summary, the carbonyl vibration is more sensitive to electric fields than the nitrile vibration, whose Stark tuning rate is typically observed to be 0.6–0.7 cm^-1/(MV/cm).^4-6 Acetophenone’s Stark tuning rate is more than that of acetone (0.8 cm^-1/(MV/cm)²⁰), but less than that of 6-propionyl-2-(dimethylamino)naphthalene (1.8 cm^-1/(MV/cm)⁵), suggesting that for carbonyls, increasing the conjugation leads to larger sensitivity to electric field.

2. Vibrational Solvatochromism of Acetophenone

To explore the response of the C=O vibration to the effect of diverse condensed phase environments, we carried out vibrational solvatochromism studies on acetophenone. Acetophenone is miscible in a wide range of solvents and it can serve as a model compound for p-Ac-Phe, the unnatural amino acid that we employed to incorporate the carbonyl probe into proteins.

As shown in Figure 2A, the C=O stretching band in acetophenone progressively shifts to the red as it is dissolved in solvents of progressively greater polarity, with the peak frequency moving 14.4 cm⁻¹ from hexanes (1696.4 cm⁻¹) to dimethyl sulfoxide (DMSO, 1682.0 cm⁻¹). Full spectral data are given in Table S1. The peak frequency of acetophenone dissolved in chloroform (1683.3 cm⁻¹) possesses a value near to that of DMSO, which is striking given the relatively small dielectric constant of 4.7 for chloroform compared to DMSO’s dielectric constant of 47. As discussed further in the simulation section, we speculated that this peculiar shift could be attributed to H-bonding, because chloroform (as well as dichloromethane) possesses a polar H-atom unlike the other organic solvents examined, whose polar components only involve heavy atoms. The solvatochromic dispersion of acetophenone’s C=O band is greater than that of benzonitrile’s C≡N band, which while possessing the same qualitative trend of shifting to the red in solvents of greater polarity, only shifts 5.8 cm^-1 from hexanes to DMSO.²² When dissolved in water (water refers to D₂O), acetophenone’s C=O band shifts substantially to the red (to 1669.4 cm⁻¹) and broadens. According to Eq. 1, this behavior would be consistent with water exerting much larger electric fields compared to the other solvents, which can be rationalized by considering that an H-bond donor positions a large dipole very close to the reporter vibration due to the small van der Waals radius of hydrogen. This observation is suggestive that the C=O frequency reports on the electric fields in H-bonding environments. In contrast, the C≡N stretch of benzonitrile in water is strongly blue-shifted, and has a frequency higher than benzonitrile dissolved in hexanes. Figure 2A also indicates there is a strong correlation between the spectral linewidths (related to the spread in electric fields) and peak frequency (related to the overall electric field magnitude), as examined further in Figure S1.

Figure 2.

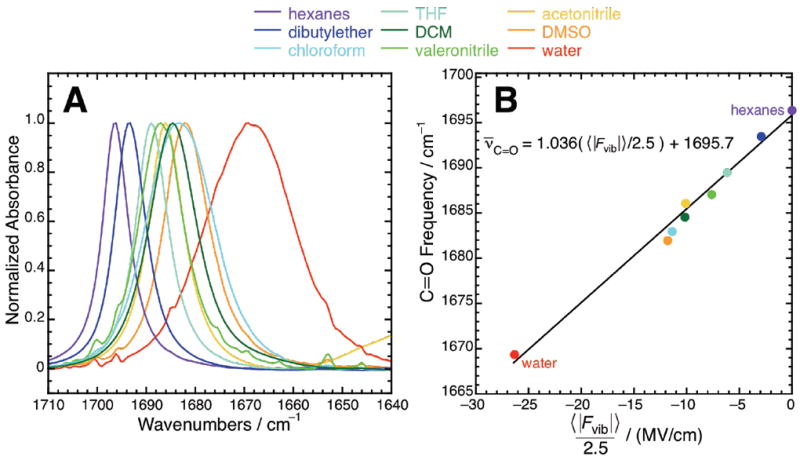
C=O vibrational frequencies shift due to solvent electric field. (A) Representative FTIR spectra of the C=O stretch band of acetophenone (10 mM) dissolved in a number of organic solvents and water. The spectra are colored from violet to red in order of increasing static dielectric constant. (B) Plot of acetophenone’s peak C=O frequency in nine solvents compared against the average electric field C=O experiences in each of those nine solvents, as calculated by MD simulation. Note that electric fields are rescaled by a factor of 2.5 (see main text). The best-fit linear model is ν̄_C=O =(1.036〈|F_vib|〉/2.5)+1695.7 with R² = 0.99.

3. Solvation Simulation Overview

Motivated by the importance to describe both H-bonding and non-H-bonding environments in a consistent fashion, we used an atomistic approach to calculate solvation fields by MD simulation. Pioneering work by Jorgensen and coworkers demonstrated the capability of classical force fields to recapitulate bulk properties of organic liquids like heat of vaporization, density, and radial distribution functions.^23,24 In the following, we show these models also can predict solvent-induced frequency shifts. The simulations were carried out with the General AMBER force field (GAFF),^{25, 26} following a recently published study²⁷ that benchmarked GAFF’s and OPLS/AA’s reliability for modeling a wide array of organic liquids including acetophenone. We chose to model solvent molecules with GAFF parameters to enable comparison to protein simulations that use AMBER force fields. Water was modeled using the TIP3P model.²⁸ In total, electric fields were calculated for nine solvents (acetonitrile, chloroform, dibutylether, dichloromethane, dimethyl sulfoxide, n-hexane, tetrahydrofuran, valeronitrile, and water). All simulations were set up and carried out in GROMACS version 4.5.3.²⁹ For each snapshot, the electric field exerted onto the C=O vibration of acetophenone by the solvation environment was calculated by projecting onto the C=O bond vector, and then averaging between the C-atom and at the O-atom. This quantity is denoted |F_vib| and referred to as the field experienced by the C=O vibration. Similarly, the electric field drop over the bond length (denoted |ΔF_vib| was calculated by taking the difference between those two quantities instead of averaging. In both cases, an ensemble average was determined by calculating the mean across all snapshots in the trajectory, denoted 〈|F_vib|〉 and 〈|ΔF_vib|〉. Simulation methodology and the method for calculating electric fields are described in detail in the computational methods sections IV.1–3.

4. MD Calculation of Solvation Fields

The ensemble electrostatic data for the C=O probe of acetophenone in various solvents are compiled in Table 2. These calculated fields display a strong correlation with solvent polarity: the more polar solvents exert an electric field of greater magnitude onto acetophenone’s C=O bond. The negative sign associated with all calculated fields implies that the environment interacts favorably with the carbonyl moiety of the solute. It is important to point out how the MD simulations handled the cases where the solvent can form H-bonds with the C=O probe. Interestingly, MD predicted that chloroform exercises an average electric field (−28.5 MV/cm) of nearly equal magnitude to DMSO (−29.6 MV/cm), even though their dielectric constants are very different. This result is consistent with the FTIR measurements (Figure 2A), where it was found that acetophenone’s C=O band has a very similar peak frequency when it is dissolved in DMSO and chloroform (1682.0 cm⁻¹ and 1683.3 cm⁻¹, respectively). Taken together, these observations suggest that chloroform’s (and dichloromethane’s) deviation from the correlation with solvent dielectric can be explained as a linear Stark effect when one accounts for the fact that chloroform’s H-bonding to the carbonyl group results in larger electric fields than would be predicted from a continuum descriptor like dielectric constant. This concept can be expanded further to the case of water. The C=O stretch of acetophenone is shifted 12.6 cm⁻¹ to the red in water relative to DMSO (Figure 2A). This large shift is recapitulated by the MD simulations, which indicate that the average electric field in water (−65.9 MV/cm) is more than two times the next largest field (−29.6 MV/cm, DMSO). Indeed, the stronger H-bonds furnished by water would be expected to exert larger electric fields onto the C=O bond. To further develop the concept that dichloromethane, chloroform, and water create increasingly large fields via H-bonds of increasing strength, we examined the trajectories and identified structural/dynamic properties that correlate with H-bonding capacity and strength. On average, the solvent atom closest to the O-atom of the C=O probe was able to get somewhat closer and stay the closest atom for longer in the H-bonding solvents (see Table S3). These features are both characteristic of H-bonding interactions.

Table 2.

MD electrostatic data for C=O bonds in solvents and proteins

	|Fvib| / (MV/cm) a		|ΔFvib| / (MV/cm) b
	mean	std. dev.	mean	std. dev.
hexanes	−0.115	0.77	−0.029	0.76
dibutylether	−7.40	6.42	−0.28	3.83
chloroform	−28.5	13.6	−13.7	12.7
tetrahydrofuran	−15.5	9.36	−0.19	6.09
dichloromethane	−25.5	15.9	−8.66	11.6
valeronenitrile	−19.2	12.0	−0.67	7.46
acetonitrile	−25.3	13.6	−3.73	9.58
dimethylsulfoxide	−29.6	11.5	−1.53	10.1
water (TIP3P)	−65.9	23.1	−40.7	25.7
[p-Ac-Phe]S-peptide	−63.6 [−61.9]c	39.6 [39.0] c	−38.1 [–38.6] c	33.1 [33.3] c
[p-Ac-Phe]RNase S	−13.4 [−11.5] c	7.05 [7.00] c	−3.44 [−4.00] c	4.90 [5.04] c

^aThe electric field experienced by the C=O vibration, as defined by Eq. 4.

^bThe electric field drop across the C=O vibration, as defined by Eq. 5.

^cFor the bottom two entries, the set of values in brackets reflect calculations that do count the probe-bearing residue’s backbone atoms as part of the environment (see text).

An additional comparison can be made between the observed linewidths of the solvatochromic spectra and the standard deviations of the calculated field distributions. These two variables correlate modestly well (with an R² of 0.72, see Figure S2 and accompanying analysis), but not perfectly. This is not surprising given that the linewidth is a dynamical property that depends on field correlations as well as field statistics.³⁰ Nonetheless, a qualitative connection between the range of the electric field distribution and IR linewidth is apparent.

We noticed there was a connection between H-bonding and the field drop, |ΔF_vib| (Table 2). For most of the solvents, the ensemble-averaged field drop was rather small, with absolute values clustered around and less than 1 MV/cm. Small field drops imply that the ensemble-averaged field is smooth and shallow, exactly as expected for fields that arise from nonspecific dielectric polarization. On the other hand, a rather steep field drop arises for the weak H-bonding hydrochlorocarbons and an enormous field drop (41 MV/cm) is manifested in water. These results are explained by the intuition that when an H-bond forms between the probe and a donor, it is only the H-bond accepting atom that enters into close contact with the H-bond donor’s dipole. In other words, the large field associated with the H-bond is strongly weighted by the contribution from the H-bond accepting atom, resulting in a precipitous field drop with respect to the more distal atom of the vibrational probe.

An important observation about the MD fields is that they are consistently large relative to what one would expect from the solvent-induced frequency shifts and the Stark tuning rate. For example, the calculated field dispersion from n-hexane to DMSO is ca. 30 MV/cm; however, the observed frequency dispersion over the same span in environments is only 14.4 cm⁻¹, and we expect a frequency shift of 1.05 cm⁻¹ for every 1 MV/cm change in electric field from the measured the Stark tuning rate. This finding suggests either that the MD simulations systematically over-estimate the magnitude of the environment’s electric fields, or that the Stark tuning rate is over-estimated. Possible origins for this discrepancy is discussed further in the following.

5. Discussion for Solvents

Plotting the observed C=O peak frequencies in the nine different solvents (Figure 2A) against the ensemble-average electric fields in those corresponding solvents (Table 2), we obtain a remarkable linear trend whose R² is 0.99 (Figure 2B). This excellent correlation provides strong evidence in support of the claim that solvation-induced frequency shifts are explained by the average electric fields created by the various solvents.³¹ This trend extends equally to cases in which H-bonding is present: both weak H-bonds (chloroform and dichloromethane) and moderately strong H-bonds (water), with their increasingly larger electric fields, are found to produce frequency shifts with a consistently linear pattern. This analysis suggests that C=O’s solvent-induced frequency variation can be essentially explained in terms of a model with a single electrostatic parameter (the average electric field, 〈|F_vib|〉, including cases with specific chemical interactions. The same cannot be said for nitriles, for which the field-frequency calibration curve only extends to non-H-bonding cases, and for which additional analysis is necessary to first determine that the nitrile is not H-bonded before one can translate a vibrational frequency to a field.²²

Despite this excellent linear correlation between observed frequency and calculated field, the slope of the regression line is 0.414 cm⁻¹/(MV/cm), which is significantly different from C=O’s observed Stark tuning rate of 1.05 cm⁻¹/(MV/cm) (Figure 1 and Table 1). In Figure 2B, we have rescaled the calculated electric fields uniformly by introducing a correction factor of 2.5. Consequently, the MD-calculated fields plotted in Figure 2B (〈|F_vib|〉/2.5) are 2.5 times smaller than the raw MD-calculated fields (〈|F_vib|〉) in Table 2. The resultant regression line is ν̄_C=O = 1.036(〈|F_vib|〉/2.5)+1695.7; importantly, the intercept and the correlation coefficient (0.99) are independent of the rescaling factor.

We have two hypotheses for the origin of the 2.5-fold discrepancy between the simulated fields and the observed Stark tuning rate. Fixed-charge force fields (such as GAFF) represent nuclear degrees of freedom explicitly, but do not represent electronic polarizability. In practice, the missing electronic degrees of freedom are compensated for by “pre-polarizing” the atomic charges, which are noticeably larger than atomic charges in high-level quantum population analyses.³² These larger charges would in turn lead to inflated electric fields. On the other hand, polarizable force fields use a more physical description of intermolecular interactions in the condensed phase, ³² so they might predict the scale of solvent fields differently (and presumably, more correctly). Use of polarizable models to calculate electric fields is the subject of ongoing work.

Another source of difference between experiment and theory could come from the local field correction to the Stark tuning rate, which refers to the uncertainty in the magnitude of the electric field experienced by a vibration in a Stark experiment owing to the difference between the externally applied field and the local field at the position of a chromophore.^4,33 The local field at a particular point (where a vibrational probe sits) will in general be somewhat larger (by a factor denoted f) than the external field, derived from the distance and applied voltage between the two electrodes, due to the extra contribution arising from the polarization of the surrounding environment.^33,34 The local field effect implies that the experimentally determined Stark tuning rate ( $\left|\mathrm{\Delta }\overrightarrow{\mu }\right|f$) will be larger than the microscopic Stark tuning rate ( $\left|\mathrm{\Delta }\overrightarrow{\mu }\right|$), which the slope of the field-frequency curve ought to reproduce. Classical electrostatic theory estimates the value of f of a frozen glass to be ~1.3 and largely independent of the glass-former’s polarity,³³ although its value could be larger. In summary, the factor of 2.5 discrepancy can be attributed both to overestimation of calculated solvent fields and to the local field correction factor.

A number of studies have now shown that a ~2-fold correction is needed to harmonize experimental vibrational Stark effect shifts with those calculated with electrostatic models, ^1,35,36 so the effect described above appears to be general. This factor was previously found to lead to better agreement between calculated and observed vibrational frequency shifts accompanying mutation and pH change,^1,35 as well as ultra-fast vibrational frequency shifts in response to photo-induced charge transfer in a nearby dye.³⁶ The key result illustrated in Figure 2B is that observed IR frequencies correlate linearly with the computed average value of the electric field, across solvents of very different dielectric and H-bonding properties. Some uncertainty remains regarding the overall scale of solvent fields, the resolution of which awaits further study; nevertheless, meaningful comparisons between solvents and proteins is still possible, as described in the following.

III. Results and Discussion for Ribonuclease S

1. Vibrational Probes in RNase S

The FTIR spectrum of p-Ac-Phe in D₂O, 20 mM HEPES, pD = 8.0 is shown in black in Figure 3A. The peak position matched perfectly with that of acetophenone in D₂O (full spectral data given in Table S2). This experiment demonstrates, as expected, that the C=O vibration in acetophenone is an appropriate model for the C=O vibration in p-Ac-Phe, and suggests that the two compounds possess identical vibrational frequencies when exposed to identical environments. It further demonstrates that the C=O stretch is indeed very local, and so its frequency is relatively independent of the distal parts of molecule in which it resides. In turn, this condition implies that acetophenone’s field-frequency calibration should be transferable onto p-Ac-Phe, as discussed below. With this in mind, we set out to install p-Ac-Phe as a residue into a peptide and a protein to examine biomolecular electrostatic environments.

Figure 3.

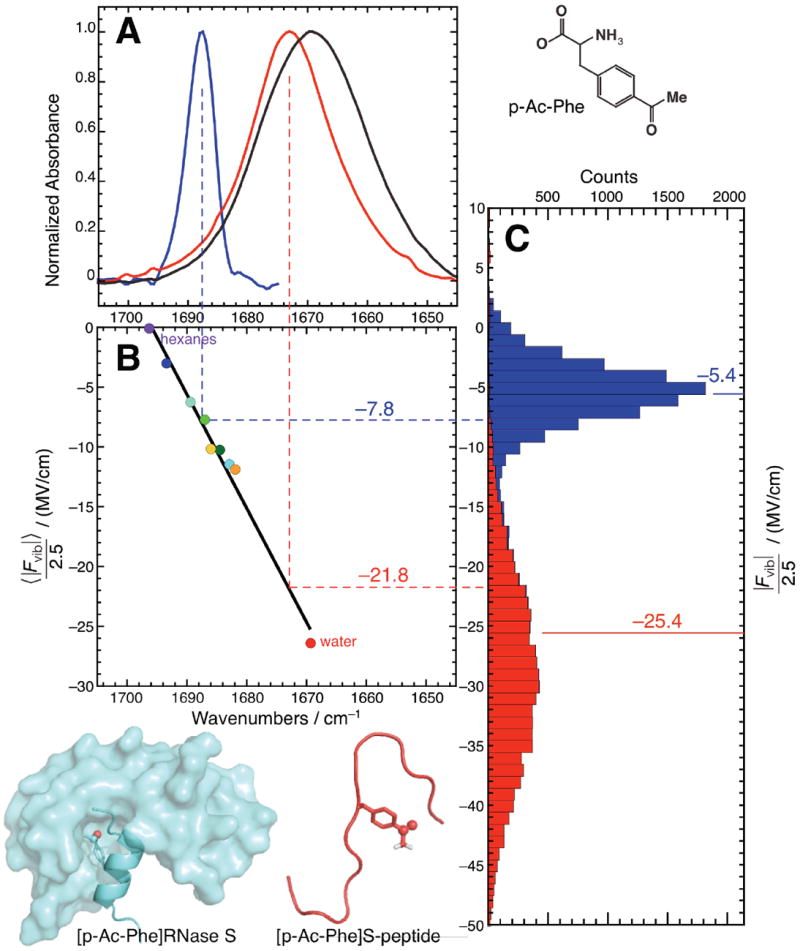
A solvatochromic model calibrates C=O vibrational frequency to electrostatic field. (A) FTIR spectra of p-Ac-Phe (black), [p-Ac-Phe]S-peptide (red) and [p-Ac-Phe]RNase S (blue). (B) The solvatochromic field-frequency correlation plot from Figure 2B (rotated by 90°) with rescaled fields used to convert the peak frequencies of the two spectra in (A) to predictions for ensemble-averaged electric fields (illustrated with dotted lines). This process yields values of − 21.8 MV/cm for [p-Ac-Phe]S-peptide and −7.8 MV/cm for [p-Ac-Phe]RNase S. (C) Histograms of |F_vib|/2.5 from the MD simulations of [p-Ac-Phe]S-peptide and [p-Ac-Phe]RNse S. The means (marked with solid lines) are −5.4 MV/cm and −25.4 MV/cm, which differ from their predicted values by 31% and 16% respectively.

RNase S is a split protein consisting of a peptide fragment (the S¹⁵-peptide, residues 1–15) and a protein fragment (the S-protein, residues 21–124).³⁷ The S¹⁵-peptide is strongly bound to the S-protein by non-covalent interactions,³⁸ such that the reassembled two-chain protein retains essentially the same structure and activity as the single-chain protein, RNase A.³⁹ Residues 16–20 are not as important for binding, structure, or function. As reported previously,³⁵ RNase S is an ideal system for facile insertion of vibrational probes, because the S¹⁵-peptide can be exploited to deliver a probe through an unnatural amino acid. In the present case, p-Ac-Phe was incorporated into a synthetic S¹⁵-peptide by replacing the natural Phe at position 8 with it. We refer to this construct as [p-Ac-Phe]S-peptide (Figure 3). Isolated S¹⁵-peptide is preponderantly a random coil in aqueous solution,⁴⁰ so the C=O probe from p-Ac-Phe in the S¹⁵-peptide is expected to be highly exposed to water. In contrast, when [p-Ac-Phe]S-peptide is combined with S-protein, the RNase S complex is formed (referred to as [p-Ac-Phe]RNase S, Figure 3) wherein the C=O is placed in a highly hydrophobic pocket. The procedure for preparing and purifying [p-Ac-Phe]RNase S is described in the experimental methods section V.2. Kinetic and thermodynamic parameters for RNase S catalysis and reassembly are provided in Table 3. Additional spectroscopic characterization and full data for the enzymological and calorimetric measurements are described in the supplementary information (Figures S3–S6 and accompanying analysis).

Table 3.

Kinetic and thermodynamic parameters for [p-Ac-Phe]RNase S compared to those of wild-type RNase

	Wild-type RNase a	[p-Ac-Phe]RNase S
Catalytic Activity b
kcat / s−1	2.8 ± 0.1	0.8 ± 0.03
KM / mM	1.25 ± 0.1	1.37 ± 0.2
R2	0.994	0.991
S-peptide Binding Thermodynamics c
KD	110 ± 20 nM d	12.7 ± 1 μM
ΔG°	−9.5 ± 0.1 kcal/mol d	−6.7 ± 0.1 kcal/mol
ΔH°	−39.3 ± 0.6 kcal/mol d	−16.7 ± 0.1 kcal/mol
ΔS°	−100 cal/(mol K) d	−33.6 cal/(mol K)

^aWild-type RNase refers to single-chain RNase A for activity measurements and the split-protein RNase S for binding measurements.

^bMichaelis-Menton kinetics for the hydrolysis of cyclic cytidine monophosphate. See Figure S3 for full data and analysis.

^cThermodynamics for the binding of S-peptide to S-protein to form RNase S at 25 °C as determined by isothermal titration calorimetry. See Figure S6 for full data and analysis.

^dData from Ref. 38.

The FTIR spectra for the two probe-bearing constructs ([p-Ac-Phe]S-peptide, red; [p-Ac-Phe]RNase S, blue) are displayed in Figure 3A. The C=O band position in the peptide is at 1673.1 cm⁻¹ – close to the value of acetophenone in water – and very broad (14.7 cm⁻¹). Both of these features signify H-bonding to water molecules. On the other hand, there is a large shift to the blue (to 1687.6 cm⁻¹) and band narrowing (to 5.6 cm⁻¹) accompanying the replacement of water around p-Ac-Phe with a protein environment. These features are consistent with the non-polar and structurally defined milieu characteristic of a protein interior. Under the same conditions except employing a nitrile as a probe (i.e., p-CN-Phe at position 8),²² we also observed a band narrowing upon formation of [p-CN-Phe]RNase S. However, unlike the C=O probe which underwent a large blue shift, the C≡N probe shifted 4.0 cm⁻¹ to the red. This shift was interpreted as a superposition of two competing factors: a blue-shift due to lower electric fields and a larger red-shift due to removing an H-bond.^22,41 In contrast, it appears that the C=O shift in RNase S can be rationalized purely with electrostatic arguments and without invoking a competing effect arising from H-bonding, highlighting the advantage of C=O probes when large changes in environment occur.

2. MD Calculation of Fields in RNase S

MD simulations were carried out on [p-Ac-Phe]S-peptide and [p-Ac-Phe]RNase S, and ensemble-average electric fields were calculated as described in computational methods section IV.3. In both cases, the calculated electrostatic fields are readily understood from qualitative arguments about the structure of the two systems and the IR frequencies observed for them. Just as [p-Ac-Phe]S-peptide places the carbonyl probe in a largely aqueous environment, the average field calculated for it (−63.6 MV/cm; −25. 4 MV/cm rescaled by 2.5) is quite close to the field acetophenone experiences in water. Furthermore, the calculations validate the prediction that the hydrophobic environment associated with a protein core would lead to a significant attenuation in the electric field. The calculated field experienced by the probe in [p-Ac-Phe]RNase S is −13.4 MV/cm (−5.4 MV/cm rescaled), similar to that of THF. These two extra points fall squarely along the field-frequency curve spanned by the solvatochromic series, and their inclusion only lowers R² from 0.99 to 0.97. This point supports the idea that proteins do not introduce any new idiosyncratic contributions to the vibrational frequency that cannot simply be attributed to electrostatics. Another interesting observation is that the pronounced narrowing of p-Ac-Phe’s C=O band (Figure 3A) upon formation of the RNase S complex is matched with a narrowing in the calculated electric field distribution (Figure 3C), supporting the link between field heterogeneity and linewidth established with the solvent series.

3. Discussion for RNase S

Our interest in solvation fields and solvent-induced frequency shifts stems from the possibility that the information can be used to construct a field-frequency calibration curve to semi-empirically convert C=O frequencies measured in proteins into the protein’s local electrostatic fields projected onto the probe’s bond.²² This strategy effectively applies Eq. 1 in the form of the regression line in Figure 3B. Using the peak frequencies found for the C=O probe in [p-Ac-Phe]S-peptide and in [p-Ac-Phe]RNase S, and applying the solvatochromic model described above, the average electric field for the C=O probe in these two environments is predicted to be −21.8 MV/cm and −7.8 MV/cm, respectively. The field-to-frequency conversion is illustrated in Figure 3. These predictions compare favorably with the average electric fields calculated for those two systems from direct MD simulation (−25.4 MV/cm and −5.4 MV/cm, respectively), differing on average by a factor of 1.2 (note that this comparison is independent of the value chosen for the correction factor). It is difficult to say whether the discrepancy between fields calculated by direct simulation versus by semi-empirical field-frequency mapping is due to force field accuracy, sampling error, or limitations in the solvatochromic calibration scheme. In any event, the correspondence is relatively robust, and invites the use of solvatochromic models to predict electric fields in cases where they would not otherwise be possible to calculate due to computational limitations arising from system size, sampling requirements, or force field accuracy.

Although C=O probes in proteins are not technically new, following early work on myoglobin^15,19,42 they have been largely discarded and viewed as intractable owing to their overlap with proteins’ amide I bands. Indeed, as local vibrational probes have seen greater use in protein science, possessing an absorption band in an uncluttered region has become accepted as sine qua non^3,5,7-11; the present work employing C=O in RNase S represents a departure from that axiom. We emphasize that C=O vibrations are observable amidst the protein background if one carefully selects a reference sample that is nearly identical to the vibrational-probe bearing construct, and leverages difference spectroscopy to bring buried bands into view. From a practical perspective, the experimental approach was not greatly limited by the transmission level in the amide I range, but mostly on how precisely the sample’s and the reference’s spectra were matched. We therefore expect this approach to generalize to larger and more complicated proteins, especially if one employs more sophisticated forms of difference spectroscopy that employ isotopic replacement (used to locate the buried N≡O band in NO-myoglobin⁴³) or photoactivation (used to locate buried vibrational bands in the reaction center⁴⁴ and bacteriorhodopsin⁴⁵). With this in mind, we believe C=O vibrational probes constitute a powerful tool to interrogate the whole range of biomolecular processes such as binding, catalysis, and self-assembly, because these are almost always mediated by H-bonds.

IV. Computational Methods

1. Solvation Simulation Methods

Acetophenone was placed at the center of a cubic box filled with solvent molecules. The size of the box was such that the distance between acetophenone and the box edge was 1.0 nm; between 370 molecules (for n-hexane) to 3500 molecules (for water) of solvent were required to fill the volume. The solvated system was energy minimized by 1000 steps of steepest descent, then equilibrated for 100 ps (2 fs time step) in an NPT ensemble with the temperature set to 300 K and the reference pressure set to 1 bar. The equilibration procedure employed the Bussi thermostat,⁴⁶ the Berendsen barostat, and the particle mesh Ewald (PME) method⁴⁷ for calculating long-range electrostatic interactions. The cut-off distances for Coulomb summation and for van der Waals interactions were both set to 1.0 nm. We constrained all bond vibrations with the LINCS algorithm.⁴⁸ Production dynamics were carried out for 2 ns (2 fs time step) in the NPT ensemble continuing from the final coordinates and velocities of the equilibration run. The temperature was set to 300 K and the reference pressure was set to 1 bar utilizing the Parrinello-Rahman barostat.⁴⁹ These simulations employed a stochastic dynamics (SD) integrator, as implemented in GROMACS.⁵⁰ Stochastic dynamics were chosen as a temperature-coupling mechanism because it allows equilibrium properties of the thermal ensemble to converge more quickly. A relatively short trajectory of 2 ns was deemed sufficient to capture the average electrostatic field of a bulk solvent because the dominant relaxation components operative in solvation are generally very fast (on the order of the Debye timescale, ca. 10 ps).⁵¹ All other settings were the same as the equilibration run.

2. Calculation of Solvation Fields

A new method was developed to calculate the electric field exerted onto the vibrational probe from each snapshot. Snapshots were recorded every 100 steps (200 fs), and consisted of full-precision coordinates and forces. First, the total force on the C-atom and on the O-atom of the carbonyl in acetophenone was extracted for each snapshot. Then, a charge-neutralized topology file was generated for the system, in which the partial charges for all of the solvent atoms are set to zero (but all of the solute’s atoms retain the same charges as used during dynamics), and all non-charge parameters are kept identical. The trajectory from the production dynamics was post-processed with the charge-neutralized topology using GROMACS’ rerun utility. In the resulting trajectory, different forces are present on each atom, due to the absence of any intermolecular electrostatic interaction. Likewise, the total force on the C- and O- atoms was extracted from each snapshot. With this information, the total electric field experienced by the vibration due to the environment in each snapshot was calculated with Eq. 2-4.

$${\overrightarrow{f}}_{\mathit{electro}}^i={\overrightarrow{f}}_{\mathit{tot}}^i-{\overrightarrow{f}}_{\mathit{non}-\mathit{electro}}^i$$ (2)

$${\overrightarrow{F}}^i={\overrightarrow{f}}_{\mathit{electro}}^i/q_i$$ (3)

$$\left|F_{\mathit{vib}}\right|=\frac{1}{2}({\overrightarrow{F}}^C·{\widehat{u}}_{\mathit{CO}}+{\overrightarrow{F}}^O·{\widehat{u}}_{\mathit{CO}})$$ (4)

In equations 2-4, i indexes over the C-atom and the O-atom of the carbonyl probe, $\overrightarrow{f}$ denotes force, and $\overrightarrow{F}$ denotes electric field. The subtraction of all non-electrostatic forces (as determined by re-running the trajectory with the charge-neutralized topology) from the total force results in a force exerted on a particular atom due only to electrostatic interactions (Eq. 2). The electrostatic force can be converted into an electrostatic field (Eq. 3) simply by dividing by the partial charge of the atom in question (either C or O of acetophenone or p-Ac-Phe). Finally, the electric field “experienced” by the vibration, |F_vib|, is calculated by projecting the field at either C or O onto the unit vector defining the vibration’s bond axis, and then averaging the two field projections between the two atoms (Eq. 4). |F_vib| as defined in this way, is operationally equivalent to $\overrightarrow{F}·{\widehat{u}}_{\mathit{probe}}$ in Eq. 1. The electric field experienced by the vibration is averaged over 10,001 snapshots taken over 2 ns to obtain the ensemble-averaged electric field, 〈|F_vib|〉. Other statistical measures of the field distribution, such as standard deviation (σ_|Fvib|), are calculated as well. Additionally, we calculated the electric field drop over the carbonyl bond, |ΔF_vib|, for each snapshot. This calculation involves the same first two steps as used to calculate |F_vib|, but the step in Eq. 4 is replaced with Eq. 5:

$$\left|\mathrm{\Delta }{F}_{\mathit{vib}}\right|=({\overrightarrow{F}}^O·{\widehat{u}}_{\mathit{CO}}-{\overrightarrow{F}}^C·{\widehat{u}}_{\mathit{CO}})$$ (5)

Similar to |F_vib|, the ensemble-average and standard deviation of the field drop distribution were calculated. Python scripts used to streamline these calculations are provided in the supplementary information (SI section S3.2).

3. Ribonuclease Simulation Methods

We calculated ensemble-averaged fields and field drops for the C=O probe in the S-peptide system and the RNase S system, using methods similar to those described for the simple solvents. All simulations employed the AMBER99SB-ILDN forcefield⁵² to describe the protein, and the TIP3P water model to describe the solvent. The p-Ac-Phe residue was parameterized and added to the force field using a simple procedure because of its high similarity to Phe. The details of this procedure are provided in the supplementary information (SI section S3.1).

To simulate [p-Ac-Phe]RNase S, the 1.5 Å-resolution crystal structure of the analog [p-CN-Phe]RNase S (PDB: 3OQY³⁵) was used to generate starting coordinates. To obtain starting coordinates for [p-Ac-Phe]S-peptide, the coordinates of the first chain from the corresponding RNase S structure were taken. In both cases, the PDB2GMX utility with its default options was employed to protonate the starting structures, assign disulfide linkages, and assign protonation states to ionizable moieties, except that all histidines were manually entered as protonated at the epsilon-nitrogen, as expected at pH 8.0 (the condition for all experiments).⁵³ The protein was solvated in a periodically replicated dodecahedral box filled with water, ensuring that the edges of the box were at least 1.0 nm separated from the ends of the protein. The system was neutralized and brought to a net ion concentration of ca. 20 mM (the experimental condition) by addition of sodium and chloride ions. Conditions for minimization and equilibration were similar to those stated for the solvation systems, vide supra. For the RNase S systems, equilibration was conducted first for 100 ps with 1000 kJ mol⁻¹ nm⁻¹ positional restraints applied isotropically to all protein atoms, and then for 20 ns without positional restraints. The long equilibration time allowed the local structure of the S-protein to relax around the acetyl group appended onto Phe8 of the S¹⁵-peptide. For the S-peptide system, equilibration runs were all 100 ps long. The second equilibration without positional restraints was conducted at 400 K and then at 300 K. The high-temperature equilibration step was meant to give the S-peptide an opportunity to relax non-intrinsic helical structure induced by its association with the S-protein.

Production dynamics were again performed in an NPT ensemble, with a stochastic integrator used for temperature-coupling. The only major difference was that the simulations were 20 ns long (rather than 2 ns), and full-precision snapshots with coordinates and forces were recorded every 1000 steps (rather than every 100 steps). Electric fields on the C- and O-atoms of the vibrational probe were determined in each snapshot, and used to calculate the electric field experienced by the vibration (Eq. 4) and the electric field drop over the bond (Eq. 5) as for the solvent simulations. To create the charge-neutralized topology file for these system, the charges on all the water molecules, the ions, and the residues other than the probe-containing residue were set to zero.

4. Additional Considerations of the Current MD Approach to Calculating Fields

The methodology we developed here differs somewhat from previous strategies to extract electric fields from MD trajectories, which have relied on calculating the Coulombic force on a virtual test-charge particle inserted into the MD trajectory.^35,54,55 A problem with this method is that the calculation of the Coulombic interaction omits interactions arising from outside the main simulation box in a simulation with periodic boundary conditions (personal communication, J. Chodera). Calculation of forces in Eq. 2 using GROMACS’ built-in functions assures that direct Coulomb and Particle Mesh Ewald contributions are calculated and combined (as they would be during normal dynamics) for the purposes of calculating electric fields.

Another important consideration that arises in these calculations is the choice of a zero-field reference state against which one chooses to define the electric field. We have chosen to define the electric field as the total field impinging onto a target atom from its environment. The environment refers to all atoms that are not part of the same molecule as the target atom. What is intentionally excluded from this definition is the self-field an atom experiences due to a molecule’s own nuclei and electronic density. Applying this definition, the electric field on any atom of any molecule in the gas phase is zero. The purpose for this exclusion is that we are ultimately interested in utilizing the electric field as a descriptor for intermolecular interactions. This description facilitates a mapping onto intermolecular energetics, so long as the interactions in question are electrostatic in nature. On this point, we note that the H-bonding interactions furnished by water and chlorohydrocarbons appear to be well explained purely in terms of electrostatics, as has been noted for weak H-bond complexes as well.⁵⁶ Implicit in our definition of the total field is a strict demarcation between a molecule and its environment, which is not enforceable in a rigorous quantum mechanical formalism, but which is readily adapted to MD force fields that systematically separate bonding (within the same molecule) from non-bonding (between molecules) interactions.

In practice, the valence terms in MD force fields (bonds, angles, and torsions) are only meant to capture local contributions to the bonding potential energy curve, and electrostatic interactions are allowed between two atoms of the same molecule, if they are separated by a certain number of bonds. This treatment of intramolecular electrostatics is meant to approximately recapture long-range quantum mechanical interactions and is an essential component of MD force fields. However, these contributions lie outside our chosen definition of the electric field as being limited to those due to the environment. A simple and general way to remove the intramolecular electrostatics from our electric field calculations is to retain the solute’s atomic charges in the charge-neutralized topology (we only zero the solvent’s charges), so that the intramolecular electrostatics cancels out in the difference of Eq. 2. This demarcation becomes subtler for calculations on proteins, where we must arbitrate where the probe molecule or fragment ends and the protein environment (even though it may be on the same molecule) begins. We chose to discount the self-field arising from the probe-bearing amino acid residue, and considered the other residues as well as solvent as the environment. Another possibility would be to additionally count the field arising from the probe-bearing residue’s backbone (see values in brackets in Table 2), which also gave reasonable (and not very different) results. The definition we chose is purely operational, and highlights a difficulty with unnatural amino-acid based probes (the same difficulty would not be encountered when a vibrational probe is delivered on a ligand). One reason why the current electric field calculation method presented here is preferable is that it provides a reliable way to control what interactions are to be included in the field by choosing which charges to zero out in the charge-neutralized topology.

5. Control Simulations for Solvation Electrostatics

To calculate solvation fields, the methodology described above used stochastic dynamics and the RESP-fitting method to determine solvent atomic charges, as carried out by Caleman et al.²⁷ We followed up those simulations with three additional control scenarios, to test how sensitive the resultant ensemble-average electric fields were to certain choices. In the first control, we used deterministic dynamics in place of stochastic dynamics to test whether the random force terms in the Langevin equation appreciably change the ensemble-average electrostatic quantities (Table S4). In the second control, we used the simplified AM1-BCC method²⁶ (as implemented by Antechamber in AmberTools12) to assign the charges to the solvent molecules’ atoms, rather than the RESP fitting procedure used by Caleman et al (Table S5).²⁷ This control was designed to examine the accuracy of the AM1-BCC method by testing how well it can recapitulate electrostatic quantities derived from RESP charges. In a final third control, we replaced all the (RESP) solvent charges with their values multiplied by 0.9 (Table S6). This control was designed to test the sensitivity of the calculated electric fields on the charge parameterization. Given that there is some error in any force field’s charge parameters, this simulation sheds light on to what degree that inaccuracy endangers the dependability of the calculated electric fields. All of these modifications resulted in minor changes to ensemble-average solvation fields (see Tables S4–S6 and accompanying discussion). An important conclusion from these control simulations is that the overall magnitude of the MD-calculated fields (which required the 2.5 rescaling factor for the slope of the field-frequency curve to agree with the measured Stark tuning rate) was not a consequence of a particular choice of how to parameterize the charges or run the dynamics.

V. Experimental Methods

1. Materials

Liquid acetophenone, 99% (Sigma Aldrich) was purchased and used without further purification. Anhydrous solvents including deuterium oxide (99.5% or higher) were purchased from Acros Organics and were used without further purification. Ribonuclease A from bovine pancreas and Subtilisin A from Bacillus licheniformis (Sigma) were purchased and used without further purification.

2. Synthesis of [p-Ac-Phe]RNase S and precursors

N-Fmoc-L-(p-Acetyl-Phe) was purchased from Peptech and used without further purification. To convert the N-protected amino acid into the free amino acid, we perform a solution-phase base-catalyzed Fmoc removal reaction with piperidine, according to previously established procedure.²² Material derived from this reaction was recovered in 75% yield, and was verified by ESI Mass Spec and ¹H NMR in D₂O. ¹H NMR(D₂O @ 300 MHz): δ 7.83 (d, J = 8 Hz, 2H, Hε), 7.29 (d, J = 8 Hz, 2H, Hδ), 3.87 (dd, J = 6 Hz, 5 Hz, 1H, Hα), 3.0–3.2 (m, 2H, Hβ), 2.51 (s, 3H, Hθ). LCMS: mass calc’d for [M] C₁₁H₁₃NO₃ is 207.2. Found: (+) 209.18 [M + 2] and (−) 206.16 [M − 1].

To prepare [p-Ac-Phe]S-peptide (KETAAAK[p-Ac-Phe]ERQHMDS), N-Fmoc-L-(p-Acetyl-Phe) was transferred to Elim BioPharm (Hayward, CA) which employed standard Fmoc-based solid-phase peptide synthesis to generate the S-peptide. The material was verified by HPLC and by ESI Mass Spec. HPLC: single peak detected by A₂₂₀, eluting at 8 min. LCMS: mass calc’d for [M] C₇₅H₁₁₉N₂₃O₂₆S is 1790.9. Found: (+) 1791.9 [M +1].

The S-protein fragment was isolated by combining 100 mg of RNase A (20 mg/mL) with 40 μL of subtilisin (10 mg/mL) in 100 mM Tris (pH = 8.0), and letting the digest proceed overnight on ice. Afterwards, the solution was acidified to pH 2 via drop-wise addition of concentrated HCl, and purified by HPLC as described previously.³⁵ To prepare [p-Ac-Phe]RNase S, [p-Ac-Phe]S-peptide (1.5 equiv) and the lyophilized S-protein fragment were dissolved in 20 mM HEPES (pH = 8.0) and combined. The resultant solution was purified by cation exchange chromatography with a Hi-Trap SP XL column (GE Healthcare) on an FPLC setup (buffer A = 20 mM HEPES; buffer B = 20 mM HEPES, 1.0 M NaCl), running a gradient from 0–100 %B over 15 column volumes. The S-peptide did not bind to the column, and the purified RNase S complex eluted between 15–28 %B. The material was verified by ESI Mass Spec. LCMS: two peaks eluted from the LC column at 4.64 min (S-peptide) and 6.90 min (S-protein). The RNase S complex is not stable under the acidic conditions of the LC column, but the existence of the S-peptide peak evidences that the RNase S complex was intact to begin with because S-peptide needed to be bound to S-protein to co-elute during cation exchange. Mass calc’d for S-peptide 1791; for S-protein 11542. Found at 4.64 min: (+) 1790; found at 6.90 min: (+) 11537 (masses reflect the most likely mass as determined by maximum entropy deconvolution). Additional biophysical characterization of the [p-Ac-Phe]RNase S construct is provided in the supplementary information: UV-Vis spectroscopy (Figure S4), circular dichroism spectroscopy (Figure S5), and isothermal titration calorimetric measure of the S-peptide/S-protein binding thermodynamics (Figure S6).

3. FTIR Spectroscopy

All spectra were recorded on a Bruker Vertex 70 FTIR spectrometer, in a fashion very similar to as described previously.¹⁷ In general, samples were loaded into a demountable liquid cell (Bruker) with two windows (CaF₂, .750” thick, Red Optronics). The windows were separated using two off-set semicircular mylar spacers (75 μm and 100 μm for solvatochromism; 50 μm and 75 μm for RNase S and precursors). For the solvatochromism experiments, a 5-minute delay was applied to purge gaseous CO₂, and then 64 scans were acquired and averaged to obtain each transmission interferogram. For experiments on RNase S and its precursors, all conditions were kept constant except the purging time was increased to 10 minutes and 256 scans were taken. Band positions and FWHMs were calculated using the OPUS software’s peak picker (Bruker) – which uses a second-derivative-based method – as well as fitting the curve with a Levenberg-Maquardt algorithm.

A background transmission spectrum was subtracted from the sample’s transmission to obtain absorption spectra. For the solvatochromism experiments, the background was simply the pure solvent itself without acetophenone. For the experiments on RNase S and its precursors, backgrounds were by necessity chosen more judiciously: (1) for p-Ac-Phe, the background was phenylalanine at the same concentration (5 mM); (2) for [p-Ac-Phe]S-peptide, the background was [p-CN-Phe]S-peptide at the same concentration (5 mM); (3) for [p-Ac-Phe]RNase S, the background was [p-CN-Phe]RNase S at the same concentration (2.5 mM). All of these experiments were conducted in the same buffer system, namely 20 mM HEPES in D₂O, pD =8.0.

4. Vibrational Stark Spectroscopy

Vibrational Stark spectra were recorded as previously described.⁴ Briefly, acetophenone was dissolved in the organic solvent to a concentration of 50 mM, loaded into a custom-made sample cell consisting of CaF₂ windows coated with a 4 nm-thick layer of nickel metal, and frozen in liquid nitrogen using a custom-designed cryostat. The sample serves as a dielectric between the two conducting plates, which are connected to a high-voltage power source; in other words, the sample cell acts overall as a parallel-plate capacitor. Fields were applied in the range of 0.2 – 1.0 MV/cm. Stark spectra were determined by calculating the difference between the field-on and field-off transmission spectra (64 scans apiece), and were repeated at three different field magnitudes. The linear Stark tuning rates were determined from a numerical fit of the Stark spectra with derivatives of the experimental absorption spectra.

Due to the residual dielectric response of a frozen solvent, the effective field exerted onto the solute is larger than the applied field by a small factor f, the local field correction factor.³³ For a particular frozen glass, f is expected to be a constant, and its value is estimated to be between 1.1 – 1.4. Because f is not independently measurable, we report the observed Stark tuning rate as a product between the true Stark tuning rate and the local field correction factor, $\left|\mathrm{\Delta }\overrightarrow{\mu }\right|f$.

5. Enzymology

Kinetic traces were obtained by measuring the UV absorption at 286 nm every second for five minutes on a Lamda 25 UV-Vis spectrometer (Perkin-Elmer) at room temperature. To obtain a trace, 50 μL of RNase (6 μM) in 20 mM Bis-Tris, 1.0 mM EDTA pH 6.0 was pipetted into an Eppendorf tube containing 250 μL of cyclic cytidine monophosphate (cCMP, Sigma-Aldrich) in 20 mM Bis-Tris, 1.0 mM EDTA pH 6.0 at concentrations ranging between 0.12–4.8 mM. The mixture was quickly aspirated, transferred to a 1.0-mm quartz cuvette, and placed into the spectrometer cuvette holder. The final mixture comprised of RNase at 1 μM, and substrate at 0.1–4.0 mM. The initial rate was determined by calculating the slope of the least-square regression line of the absorbance vs. time data during the 2nd minute, and converting from OD/min to mM/s using Δε₂₈₆(cCMP–CMP) = 1.22 cm⁻¹ mM⁻¹, as determined by letting an RNase-catalyzed reaction go to completion running overnight. The concentration of protein was determined using ε₂₈₀(RNase) = 9.63 cm⁻¹ mM⁻¹ (ExPASy Protein Parameter server). The non-linear fit of the data to the Michaelis-Menton equation was carried out in Kaleidagraph.

6. Calorimetry

Isothermal titration calorimetry (ITC) was used to measure the binding thermodynamics of [p-Ac-Phe]S-peptide to S-protein. The titration was carried out in a buffer of 50 mM sodium acetate, 100 mM sodium chloride, pH 6.0 at 25.0 °C, following previous conditions.³⁸ S-protein solution was de-salted and equilibrated into buffer using a PD-10 column (GE Healthcare), then diluted to 0.25 mM. 2 mL of this solution was used to fill the cell of a MicroCal VP-ITC system (GE Healthcare). [p-Ac-Phe]S-peptide was dissolved in 2 M triethylammonium acetate and lyophilized (to remove excess protons and prevent pH drops), and redissolved into the same buffer at a concentration of 4.5 mM, 300 μL of which was used to load the ITC micro-syringe. The titration proceeded with 60 injections of 5 μL apiece, allowing 270 s between injections. The data was processed using MicroCal LLC’s Origin package.

VI. Concluding Remarks

We have assembled data from FTIR spectroscopy, vibrational Stark spectroscopy, and MD simulation to validate C=O vibrations for use as electrostatic probes in molecular biophysics. Our results show that the C=O vibrational frequency varies linearly with electrostatic field in a wide range of conditions: from non-polar solvents and protein hydrophobic cores, to the highly polar environment of an H-bond. These observations suggest that C=O frequencies can be converted into ensemble-average electrostatic fields using a linear model (Eq. 1). The present findings relied on the use of atomistic methods to calculate electric fields. We found that these methods capably represent the electrostatic consequences that accompany specific chemical interactions, a significant advantage over continuum descriptions of electrostatics (see Figure S7 and accompanying analysis). Computational models and vibrational Stark effect measurements are in good agreement, up to an overall scaling factor of 2.5. Moreover, the need to invoke this rescaling parameter was independent of several choices in the simulation methodology (see computational methods section IV.5). The disagreement almost certainly reflects the role of polarization effects, which have not been accounted for in the solvent field calculations (which used a fixed-charge model) or in the Stark tuning rate (which is influenced by the local field correction⁵⁷). We surmise that the burden of error is borne by both of these factors, which points to the necessity of including explicit polarization to reproduce electrostatics at the level of detail accessible to vibrational spectroscopic measurements. Therefore, we anticipate vibrational probes will continue to play an important role in benchmarking electrostatic calculations. Finally, while RNase S served as a useful testing grounds to assess the ability of a solvatochromic calibration scheme to measure electric fields in proteins with vibrational probes, the concepts developed here can be more generally applied to measure fields more intimately involved in function, which will be described shortly.