Summary
Typical oncology practice often includes not only an initial, frontline treatment, but also subsequent treatments given if the initial treatment fails. The physician chooses a treatment at each stage based on the patient’s baseline covariates and history of previous treatments and outcomes. Such sequentially adaptive medical decision-making processes are known as dynamic treatment regimes, treatment policies, or multi-stage adaptive treatment strategies. Conventional analyses in terms of frontline treatments that ignore subsequent treatments may be misleading, because they actually are an evaluation of more than front-line treatment effects on outcome. We are motivated by data from a randomized trial of four combination chemotherapies given as frontline treatments to patients with acute leukemia. Most patients in the trial also received a second-line treatment, chosen adaptively and subjectively rather than by randomization, either because the initial treatment was ineffective or the patient’s cancer later recurred. We evaluate effects on overall survival time of the 16 two-stage strategies that actually were used. Our methods include a likelihood-based regression approach in which the transition times of all possible multi-stage outcome paths are modeled, and estimating equations with inverse probability of treatment weighting to correct for bias. While the two approaches give different numerical estimates of mean survival time, they lead to the same substantive conclusions when comparing the two-stage regimes.
Keywords: Causal inference, Clinical trial, Dynamic treatment regime, Treatment policy
1 Introduction
Confirmatory evaluation of a new cancer treatment often is based on a randomized clinical trial with overall survival (OS) time as the primary endpoint. Compared to intermediate outcomes that may be used because they are observed sooner, such as disease-free survival (DFS) time or tumor response, OS time is widely considered to be the “gold standard” for treatment evaluation because prolonging survival is the ultimate goal of cancer therapy. A fundamental problem with this paradigm is that, in typical oncology practice, a patient receives not only an initial, frontline treatment, but also one or more subsequent treatments, chosen adaptively by the physician based on the patient’s history of treatments and outcomes. Each patient’s OS time may depend on the entire sequence of treatments and the adaptive manner in which they were chosen, rather than only the frontline treatment. Consequently, a conventional statistical analysis of frontline treatment effects on OS that ignores subsequent treatments actually is an evaluation of more than just the frontline treatments.
This type of sequentially adaptive medical decision-making process is known as a dynamic treatment regime (DTR), treatment policy, or multi-stage treatment strategy. There is a substantial statistical literature on methods for analyizing observational data having this structure (Robins, 1986; Robins and Rotnitzky, 1992; Murphy, van der Laan and Robins, 2001; Lunceford, Davidian and Tsiatis, 2002; Murphy, 2003; Wahed and Tsiatis, 2004, 2006). There also is a growing literature on methods for designing clinical trials to evaluate DTRs (Lavori and Dawson, 2000, 2004; Thall, Millikan and Sung, 2000; Thall, Sung and Estey, 2002; Murphy, 2005; Zhao, Kosorok and Zeng, 2009).
The problem that motivates this paper, and that will play a central role in determining our models and analytical methods, arises from the therapeutic decisions that oncologists make when a patient’s frontline treatment has failed. In such cases, it is common clinical practice to administer a second line, “salvage” treatment that is different from the patient’s frontline treatment. The dataset that we will analyze arose from a randomized trial of four combination chemotherapies given as frontline treatments to patients with poor prognosis acute myelogenous leukemia (AML) or myelodysplastic syndrome (MDS). Chemotherapy (chemo) of AML/MDS proceeds in stages. A “remission induction” chemo combination is given first, with the aim to achieve a complete remission (CR), defined as the patient having < 5% blast cells, a platelet count > 105/mm3 and white blood cell (WBC) count > 103/mm3, based on a bone marrow biopsy. If the induction chemo does not achieve a CR, or a CR is achieved but the patient suffers a relapse, then a salvage chemo usually is given in a second attempt to achieve a CR. The AML/MDS trial used a 2×2 factorial design with chemo combinations fludarabine + cytosine arabinoside + idarubicin (FAI), FAI + all-trans retinoic acid (ATRA), FAI + granulocyte colony stimulating factor (G-CSF) and FAI + ATRA + G-CSF. The primary aim was to assess the effects of adding ATRA, G-CSF, or both to FAI on the probability of success, defined as the patient being alive and in CR at six months. Analyses of this dataset have been reported previously (Estey, Thall, Pierce at el., 1999), using conventional methods including logistic regression, Kaplan-Meier estimates, and Cox model regression, assuming that the only relevant treatments were the frontline therapies.
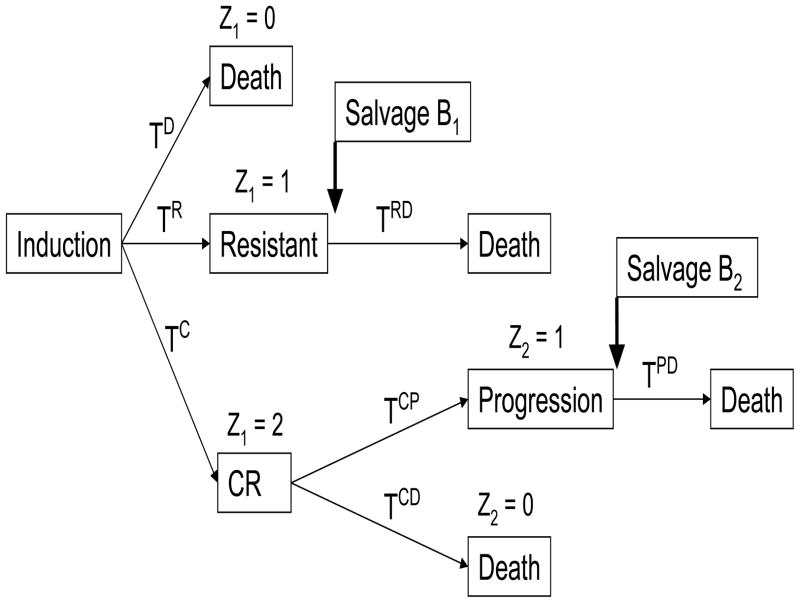
Consideration of both frontline and salvage therapies leads to a far more complex picture of the interplay between treatments and outcomes. The possible pathways that a patient’s actual course of therapy may have taken in the trial are illustrated in Figure 1, which shows that a patient may die (i) during induction therapy, (ii) following salvage therapy given if the disease is resistant to induction, (iii) while in CR, or (iv) following disease progression after CR. The reasons for these different types of death are complex. For example, a patient might die while in CR due to cumulative damage to the patient’s immune system and internal organs from either the chemo or the leukemia.
Figure 1.
Possible pathways of successive states, transition times and salvage therapy following induction treatment in acute leukemia patients.
Our primary goal is to evaluate the effects of (induction, salvage) strategies on OS. To do this, we will keep track of all transition times between states (Figure 1). We characterize treatment regimes by the triple d = (A, B1, B2), where A denotes induction therapy, B1 denotes salvage therapy for patients whose disease was resistant to induction, and B2 denotes salvage therapy for patients with disease progression following a CR achieved with induction. For regime (A, B1, B2), each patient received A only, (A, B1), or (A, B2). We will discuss this point further in Section 2. We focus on regimes rather than individual treatments because the optimal regime dopt = (A, B1, B2)opt may not correspond to what would be obtained by optimizing A, B1, and B2 separately at each stage of therapy. A common example in AML/MDS is that an aggressive frontline treatment may maximize Pr(CR), but it also may cause so much damage to the patient’s immune system that a rapid relapse is likely and any salvage therapy B2 given after relapse is unlikely to achieve a second CR. For example, suppose two induction regimens, A(1) and A(2), both provide 12 month mean OS if CR is achieved, Pr(CR|A(1)) = 0.60 and Pr(CR|A(2)) = 0.40, and both have induction death probabilities 0.10. While this suggests that A(1) is greatly superior to A(2), if A(1) is more immunosuppressive so that any salvage regimen B1 given following resistance to A(1) has 2 month mean OS compared to 12 months with salvage following resistance to A(2), then the overall mean OS is 0.60×12 + 0.30×2 = 7.8 months for (A(1), B1, B2) and 0.40×12 + 0.50×12 = 10.8 months for (A(2), B1, B2). For treating solid tumors, a particular frontline chemo A may be suboptimal as frontline chemo to eradicate the tumor, but have a high probability of debulking the tumor so that it is surgically resectable. Thus, the strategy (A, surgery) may be optimal to maximize OS. Such synergies may have profound implications for clinical practice, since a physician giving Aopt determined by considering only frontline treatments may unknowingly be setting patients on pathways that include only inferior regimes.
In the AML/MDS trial, patients were randomized among the four induction combinations to choose A, whereas the salvage treatments B1 and B2 were chosen subjectively by the attending physicians on a patient-by-patient basis. Consequently, considering the multi-course structure of the patients’ actual therapy, the data are observational because salvage treatments were not chosen by randomization. This motivates our use of inverse probability of treatment weighted (IPTW) estimation (Robins, Hernan, and Brumback, 2000), which accounts for the variation in receiving a specific treatment by weighting each observation by the inverse of the propensity (estimated probability) of receiving that treatment.
In Section 2 we describe the data structure and establish notation for the outcomes, treatment regimes and likelihoods. Families of parametric models for the transition times are given in Section 3. Analyses of the AML/MDS data aimed at estimating the effects of treatment regimes on OS are given in Section 4, including both a model-based approach and the use of estimating equations. The results are contrasted with those of conventional analyses that ignore salvage therapy. We close with a brief discussion in Section 5.
2 Data Structure and Likelihoods
To provide a framework for analyzing the treatment regimes actually used in the AML/MDS trial, we first establish notation for the transition times and their likelihoods. As shown by Figure 1, at the start of therapy the three possible events {death without the patient’s disease being declared resistant or achieving CR}, {disease resistant to induction treatment} and CR are competing risks, since at most one can occur. We denote the respective times to these events from the start of induction by TD, TR and TC. To keep track of which event occurred, denoting a ∧ b = minimum{a, b}, we define Z1 = 0 if T D < TR ∧ TC, Z1 = 1 if TR < TD ∧ TC, and Z1 = 2 if T C < TD ∧ TR. The transition time from the patient’s disease being declared resistant to death is denoted by TRD, which is defined only if Z1 = 1. For patients whose induction therapy achieved a CR, subsequent progressive disease and death in CR are competing risks, the transition times to these events are denoted by TCP and TCD, and we define the indicator Z2 = I(TCP < TCD) to record which of these two events occurred after CR. The transition time from disease progression to death is TPD, which is defined only if Z2 = 1. Similarly, TCP, TCD and Z2 are defined only if Z1 = 2. The distinction between a variable being well-defined and being potentially observable is important. For example, the potentially observable variable TR is not defined if Z1=0.
Aside from discontinuation of therapy due to a reason other than death, including administrative right censoring or drop-out, each patient’s observed sequence of transition times consisted of exactly one of the four vectors (TD), (TR, TRD), (TC, TCP, TPD), or (TC, TCD), with Z1 the only outcome variable observed for all patients. The seven transition times, Z2, and these four vectors may be thought of as counterfactual outcomes (Holland, 1986), in the sense that together they describe all possible outcome paths but each patient had only one outcome. Each patient’s OS time may be expressed formally as follows:
| (1) |
Table 1 summarizes the counts and median transition times for the seven possible events illustrated in Figure 1 for the leukemia data. These include the three induction therapy outcomes (indexed by Z1) for each treatment arm, and the four possible subsequent outcomes. Because there were many different salvage treatments, we classified salvage as either containing high dose ara-C (HDAC) or not. The small discrepancy between the treatment arm sample sizes in Table 1 and those reported by Estey et al. (1999, Table 1) are due to exclusion of five ineligible patients and correction of two patients’ treatment assignments. Although Table 1 does not account for covariates, it shows the generally poor outcomes in that only 48% of patients achieved a CR while 33% died during induction therapy, with this type of death very likely to occur in less than two months. The times to achieve CR or for the patient’s disease to be declared resistant to induction were similarly short, with all patients’ initial outcomes almost certainly known within 112 days from the start of therapy. For induction therapy outcomes, an apparent difference was that, in the two arms that included G-CSF, both Pr(Death) and Pr(CR) were higher and Pr(Resistant Disease) was lower compared to the two non-G-CSF arms. For the salvage therapy outcomes, while there did not appear to be any difference between HDAC and other treatments in terms of the probabilities of death following either resistant disease or progression after CR, both residual survival times in these cases were much longer for patients who received a non-HDAC regimen as salvage. However, these conclusions ignore the combined effect of (frontline, salvage) on OS, which cannot be determined either from the summaries in Table 1 or from conventional analyses based only on patient baseline covariates and frontline therapy.
Table 1.
Summary of outcomes following induction and salvage therapy, overall and by frontline treatment. The sample median of each transition time is given in days, with lower and upper 95% confidence interval limits subscripted on the left and right.
| Group | Initial Outcomes Following Induction Therapy
|
Total N | |||||
|---|---|---|---|---|---|---|---|
| Death | Resistant Disease | CR | |||||
| N (%) | TD | N (%) | TR | N (%) | TC | ||
| All Patients | 69 (33) | 222432 | 39 (19) | 515970 | 102 (48) | 303234 | 210 |
| FAI | 17 (31) | 212752 | 17 (31) | 416397 | 20 (37) | 293144 | 54 |
| FAI+ATRA | 15 (28) | 182244 | 13 (24) | 555976 | 26 (48) | 293144 | 54 |
| FAI+G | 20 (38) | 223245 | 4 (8) | 2777112 | 28 (54) | 293640 | 52 |
| FAI+G+ATRA | 17 (34) | 142130 | 5 (10) | 485170 | 28 (56) | 283238 | 50 |
| Outcomes Following CR or Resistant Disease
|
||||||||
|---|---|---|---|---|---|---|---|---|
| Death After Res | Death in CR | Prog After CR | Death After Prog | |||||
| N (%) | TRD | N (%) | TCD | N (%) | TCP | N (%) | TPD | |
| All Patients | 37 (95) | 6279148 | 9 (9) | 46293345 | 93 (91) | 190256329 | 83 (93) | 106128175 |
| HDAC | 25 (93) | 2765117 | – | – | – | – | 47 (89) | 6298253 |
| Other Trt | 12 (100) | 82130252 | – | – | – | – | 36 (90) | 122158191 |
As shown by Figure 1, all patients received induction, and a second decision to choose a salvage treatment was made if either Z1 = 1, for salvage B1 following resistant disease, or Z1 = 2 and Z2 = 1, for salvage B2 following progressive disease after CR. Under strategy (A, B1, B2), a patient cannot receive both B1 and B2 since achieving CR and having disease resistant to induction are disjoint events, and patients who die during induction receive neither B1 nor B2. Thus, each strategy is inherently outcome-adaptive. Denote the set of possible induction treatments by
 = {a1, ···, ak}, the possible salvage treatments for patients with resistant disease by
= {a1, ···, ak}, the possible salvage treatments for patients with resistant disease by
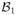 = {b1,1, ···, b1,l1}, and the possible salvage treatments for patients with disease progression after CR by
= {b1,1, ···, b1,l1}, and the possible salvage treatments for patients with disease progression after CR by
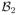 = {b2,1, ···, b2,l2}. In typical practice, the oncologist chooses each patient’s induction regimen based on diagnostic information, such as the cytogenetic abnormality characterizing the leukemia, WBC count, platelet count, age, and performance status. In contrast, the AML/MDS dataset arose from a randomized trial of four induction treatments {a1, a2, a3, a4} in the 2×2 factorial design described earlier, with
for each j = 1, 2, 3, 4. The salvage treatments were not assigned by randomization, but rather were chosen subjectively by each patient’s attending physician. Denoting the interim data for a patient with resistant disease by
= {b2,1, ···, b2,l2}. In typical practice, the oncologist chooses each patient’s induction regimen based on diagnostic information, such as the cytogenetic abnormality characterizing the leukemia, WBC count, platelet count, age, and performance status. In contrast, the AML/MDS dataset arose from a randomized trial of four induction treatments {a1, a2, a3, a4} in the 2×2 factorial design described earlier, with
for each j = 1, 2, 3, 4. The salvage treatments were not assigned by randomization, but rather were chosen subjectively by each patient’s attending physician. Denoting the interim data for a patient with resistant disease by
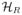 and the data for a patient with progressive disease after CR by
and the data for a patient with progressive disease after CR by
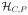 , the salvage treatment decisions are functions B1:
, the salvage treatment decisions are functions B1:
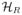 →
→
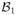 and B2 :
and B2 :
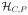 →
→
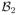 . Salvage treatment in the first case is given at time TR, and in the second case at time TC + TCP. One may formulate d more generally as a two-stage regime (A, B) in which B is a function from the set of all possible interim data {
. Salvage treatment in the first case is given at time TR, and in the second case at time TC + TCP. One may formulate d more generally as a two-stage regime (A, B) in which B is a function from the set of all possible interim data {
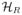 ∪
∪
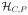 } that would require salvage therapy
} that would require salvage therapy
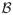 =
=
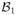 ∪
∪
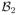 . We consider it more informative to distinguish between the two types of salvage treatment, B1 and B2, because they are given following qualitatively different patient histories. A treatment in
. We consider it more informative to distinguish between the two types of salvage treatment, B1 and B2, because they are given following qualitatively different patient histories. A treatment in
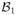 is an attempt to save a patient whose induction therapy failed, whereas a treatment in
is an attempt to save a patient whose induction therapy failed, whereas a treatment in
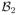 is an attempt to re-induce CR after it was achieved initially but the patient’s disease later progressed.
is an attempt to re-induce CR after it was achieved initially but the patient’s disease later progressed.
Each of the following distributions varies with patient covariates, X = (X1, ···, Xq). To reduce notation, we suppress this dependence when no meaning is lost. For initial outcome j = D, R, or C, denote by hj(t|A) the instantaneous risk of j at time t. To accommodate right-censoring, we denote the time from start of induction to last follow up by T0, the time to initial outcome j or right-censoring by Uj = Tj ∧ T0, and δj = I(Uj = Tj). Note that at most one of UD, UR or UC may be observed for each patient. We also assume, from here onwards, that censoring is conditionally independent of the transition times given prior transition times and other covariates including prior treatment (for example, the probability of being censored after resistance is independent of time from resistance to death given X and TR). In this case, the likelihood contribution for the initial outcome is
| (2) |
where , and . For patients with resistant disease, where Z1 =1 and TR is observed, denote URD = TRD ∧ (T0 − TR) and δRD = I(TRD = URD). Thus,
Denote the instantaneous risk of death at time t following resistance (Z1 = 1), given the time to resistance TR, by hRD|R(t|TR, A, B1) for patients receiving A as induction, becoming resistant to A, and receiving B1 as salvage. The likelihood contribution of such patients is
| (3) |
where
| (4) |
and
| (5) |
Similarly, for patients achieving CR, so that Z1 = 2 and T C is observed, define UCD = TCD ∧ (T0 − TC), δCD = I(TCD = UCD), if there is no progression in disease (death or censoring occurs after remission), and UCP = TCP ∧ (T0 − TC), and δCP = I(TCP = UCP), if death does not occur before disease progression or censoring. Denote the instantaneous risk of death following remission for patients receiving induction treatment A at time t before disease progression by hCD|C(t|TC, A). Similarly, define hCP|C(t|TC, A) as the instantaneous risk of progression prior to death following remission at time t, given TC and A. For patients who suffer progressive disease after CR, so that Z = (2,1), define TPD,0 = TPD ∧ {T0 − (TC+TCP)} and δPD = I(TCD = UCD). Denote the conditional instantaneous risk of death following progression at time t for patients who achieve CR at time TC with frontline A, then suffer progressive disease at time TC +TCP and are given salvage B2 by hPD|CP(t|TC,TCP, A, B2).
The contribution to the likelihood from a patient who achieves remission is therefore
| (6) |
where each pair fj(·|·) and F̄j(·|·) are defined based on hj(·| ·) similarly to the definitions given in the Equations (4) and (5).
Combining expressions (2), (3), and (6), the overall likelihood is
| (7) |
3 Parametric Models
For each of the seven transition times, TD, TR, TRD, TC, TCD, TCP, and TPD, we used parametric regression models to account for effects of the baseline covariates and the treatment or treatments received prior to the noted event. For example, to model TD when Z1 = 0, the time to death during induction therapy, we fit members of the class of accelerated failure time (AFT) regression models given by
To obtain a good fit to the data we assumed, in turn, that εi followed an extreme value, standard extreme value (with fixed scale), logistic, or normal distribution. These give, respectively, Weibull, exponential, log-logistic, or log-normal distributions for TD. The log of any transition time observed prior to the transition time variable being modeled was included in X along with the baseline covariates. Specifically, the model for [TRD|TR] included log(TR), for [TCP|TC] included log(TC), for [TCD|TC] included log(TC), and for [TPD|TC, TCP] included log(TC) and log(TCP) as covariates. For each of the seven transition times, we compared the fits of the four AFT regression models in terms of their Bayes information criterion (BIC, Schwarz, 1978) values, and we used this to choose a best model. We compared the different treatment strategies by combining the fitted regression models to estimate mean OS time for the distribution of [T|A, B1;, B2].
4 Evaluating Treatment Policies
The departure of our analyses from conventional evaluation of the effects of the induction treatments on OS or progression-free survival time begins with recognition of the facts that patients whose disease was resistant to induction, Z1 = 1, or whose disease progressed after CR, Z = (2, 1), received salvage therapy. Our primary goal is to estimate and compare the effects of the strategies (A, B1, B2) on OS time while also accounting for baseline covariate effects. We will address this in two ways, one model-based and the other utilizing IPTW estimating equations. Let θ(A, B1, B2) denote the summary parameter for the regime (A, B1, B2). For example, θ(A, B1, B2) could be P(T > t*|A, B1, B2), the survival probability beyond a particular time t* that is clinically meaningful, or E(T|A, B1, B2), the mean OS time under regime (A, B1, B2). In our analyses, we use the latter. Mean OS can be expressed in terms of the parameters of counterfactual survival times, as follows:
| (8) |
where X represents the baseline covariates, X(R) denotes post baseline covariates observed at or before treatment resistance, including log(TR), X(C) denotes post baseline covariates observed at or before observing CR, including log(TC), and X(P) denotes the post-remission covariates observed at or before disease progression, including log(TP). For j ∈ {D, R, RD, C, CP, CD, PD}, θj(·) is the conditional expectation of Tj given the arguments and other necessary conditions for the existence of Tj. For example, θPD(A, B2, X, X(C), X(P)) = E[TPD|Z = (2, 1), A, B2, X, X(C), X(P)]. The measures μ(X) and μ(X(j)) are defined by the probability distribution of the covariates, and we estimate these using the empirical measures. Equation (8) is an application of Robins’ g-formula (Robins et al., 2000) for estimating the effects of time-varying treatment regimes.
Once the component models are fit, we substitute them into the expressions above to obtain the estimates for θ(A, B1, B2). In contrast with the likelihood-based equation (8), the IPTW estimates for strategy-specific overall mean survival is
| (9) |
where
| (10) |
In equation (10), K̂(·) is a consistent estimator of the censoring time survival distribution, δi is the indicator of whether death was observed for the ith patient, Ii(E) is an indicator function taking the value 1 if ith patient receives treatment E and the value 0 otherwise, and I(Ei) takes value 1 if the event Ei is true, and 0 otherwise. Under certain assumptions, such as consistency (observed data equals the counterfactual data under consistent treatment assignment) and the sequential randomization assumption, which states that the probability of receiving treatment at a specific stage is independent of unobserved failure times given the covariates observed prior to treatment assignment, the above estimator has been shown to be consistent (Robins and Rotnitzky, 1992).
Secondary aims are to assess the effects of salvage treatments on the patient’s remaining survival time, after resistant or progressive disease is observed, as a function of past history. Specifically, we will evaluate and compare the effects of B1 on T RD given A and TR, and the effects of B2 on T PD given A, TC and TCP.
5 Analyses of the Leukemia Data
It is well-known that age and type of cytogenetic abnormality (cyto) are highly reliable predictors of the probability of CR and OS time in AML/MDS. In particular, cyto (−5, −7), characterized by missing portions of the 5th and 7th chromosomes, and older age both are strongly associated with a lower probability of CR and shorter OS. Because this trial’s entry criteria required patients to have at least one unfavorable prognostic characteristic, the distributions of age and cyto were different from those seen in the population of newly diagnosed AML/MDS patients. E.g., only 4 patients had the comparatively favorable cyto inv-16, an inversion of the 16th chromosome, or t(8,21), a translocation between chromosomes 8 and 21. Consequently, to take advantage of cyto as a prognostic variable in our regression analyses, we grouped cyto into three categories: poor = {(−5,−7)}, intermediate = {diploid, -Y, or insufficient metaphases to classify} or good = {+8, 11q, inv-16, t(8,21), other}. We used covariates for two different purposes: (i) to model the transition times (e.g. time to death, time between complete remission and death, etc.) in the likelihood-based method, and (ii) to model the probability of receiving each salvage treatment in the IPTW method (using logistic regression). To realize the first objective, we fit AFT models for each of the seven failure times (TD, TR, TC, TRD, TCD, TCP, and TPD), assuming various parametric hazard models (exponential, Weibull, log-logistic, and lognormal), as described in Section 3. For some of these event times the data were quite variable, and included a small number of outliers that were extremely large compared to the other sample values. Consequently, to ensure stability of the model fits, six of the seven component models were fit by restricting the time to the particular event to a fixed upper limit, with the limits set by first examining the observed distribution of each event time. Specifically, the variables TD, TC, TRD, TCD, TCP, and TPD were restricted to 100, 110, 1408, 692, 1326, and 2274 days, respectively. The Bayesian information criterion (BIC) for the 28 model combinations are shown in Table 2. For each time component, the best model was chosen to be that minimizing the BIC among the four AFT distributions noted above. The best models were exponential for TRD and TCD, Weibull for TD, log-logistic for TC and TCP, and lognormal for TR and TPD (Table 2), regardless of whether the outliers were included or excluded in the model fitting. We present details of the model fits without outliers.
Table 2.
Bayesian information criterion (BIC) for each of four different models fit to each transition time in the leukemia dataset. For each transition time, the minimum BIC is underlined.
| Time to | Exponential | Weibull | Log-logistic | Log-normal |
|---|---|---|---|---|
| death (TD) | 204.9 | 197.4 | 199.3 | 205.5 |
| resistance (TR) | 108.7 | 65.9 | 63.1 | 60.8 |
| CR (TC) | 247.5 | 131.3 | 91.5 | 92.6 |
| death from resistance (TRD) | 157.5 | 161.4 | 166.5 | 171.8 |
| death from CR (TCD) | 28.0 | 31.9 | 29.4 | 29.2 |
| disease progression from CR (TCP) | 271.2 | 259.3 | 248.4 | 251.8 |
| death from disease progression (TPD) | 288.9 | 297.0 | 284.9 | 282.7 |
5.1 Death During Induction Therapy
Unfortunately, many AML patients undergoing chemo to induce CR die during this process, before either CR is achieved or it can be determined that the patient’s disease is resistant to the induction chemo. While such deaths may be attributed to either the leukemia or the chemo, so called “regimen-related death,” due to the fact that both the disease and the treatment cause low WBC counts and other adverse events it often is very difficult to identify a sole cause of death. The patients in this study were especially susceptible to induction death due to their poor prognosis at trial entry, with overall rate of death during induction chemo 33% (69/210), varying from 28% to 38% across the four induction regimens (p-value = 0.70, generalized Fisher exact test). In the fitted model for the three induction event times (Table 3), no baseline covariate was significantly associated with TD. There did not appear to be any significant difference between the induction treatment effects on TD, although ATRA may have had a slightly deleterious effect in that, among the 69 patients who died during induction, the patients in the two ATRA arms died a few days sooner, on average.
Table 3.
Maximum likelihood estimates from AFT model for time to death, resistance, and complete remission during induction stage. Each parameter estimate is given with 95% confidence interval limits subscripted on the left and right.
| Distribution | Time to
|
||
|---|---|---|---|
| Death Weibull | Resistance Log-normal | CR Log-logistic | |
| Intercept | 2.803.794.80 | 3.674.365.05 | 3.103.383.65 |
| Frontline Therapy | |||
| FAI | −0.150.290.73 | −0.230.130.50 | −0.130.050.22 |
| FAI+ATRA | −0.400.080.56 | −0.220.170.57 | −0.21 − 0.050.11 |
| FAI+G | −0.290.230.60 | −0.420.090.59 | −0.110.050.22 |
| FAI+G+ATRA | ref | - | - |
| Age (per year) | −0.02 − 0.0050.01 | −0.016 − 0.0070.002 | −0.0015 0.00230.006 |
| Cytogenetic Group* | |||
| 0 vs. 2 | −0.57 − 0.130.30 | −0.22 − 0.110.43 | −0.22 − 0.080.05 |
| 1 vs. 2 | −0.57 − 0.170.24 | −0.130.040.21 | |
| σ | 0.540.650.79 | 0.300.380.47 | 0.150.170.20 |
0 = (“DIP,-Y”, “IM”), 1= “−5,−7”, 2=(“+8”, “11Q”, “INV16”, “T(8,21)”, “MISC”).
5.2 Resistance and death following resistance
Resistance to induction treatment occurred in 39 (18.6%) patients, relatively more frequently among patients receiving FAI and FAI+ATRA (31% and 24% respectively) compared to those who received FAI+G or FAI+ATRA+G (7.8% and 10% respectively). The times to treatment resistance were similar across the four induction treatments, but with greater variability in the FAI + G arm (Table 3).
Among the 39 patients who were resistant to frontline treatment, 27 were given HDAC as salvage treatment. Two patients in this cohort were censored prior to observing death. Using likelihood ratio tests, factors that were associated with time from induction treatment resistance to death were age, log(TR), frontline therapy, HDAC as salvage (B1) and their interaction (Table 4). Patients with older age, shorter TR, frontline therapy FAI+G+ATRA, or salvage with HDAC died more quickly following their disease being declared resistant. Among patients given non-HDAC salvage, TRD was significantly greater if they received FAI+ATRA or FAI+G compared to those who received FAI+G+ATRA as the induction treatment. Also, for patients receiving FAI+G as induction and HDAC as salvage following treatment resistance, TRD was significantly larger than those who received FAI+G but no HDAC or FAI+G+ATRA either with or without HDAC salvage.
Table 4.
Maximum likelihood estimates from AFT models for residual time to death following disease being declared resistant to induction (TRD), time to disease progression following complete remission (TCP), and time to death from progression (TPD). Each parameter estimate is given with 95% confidence interval limits subscripted on the left and right.
| Distribution | Time
|
||
|---|---|---|---|
| TRD Exponential | TCP Log-logistic | Lognormal TPD | |
| Intercept | −6.31 − 1.323.68 | 6.498.119.73 | −0.721.253.23 |
| Frontline therapy | |||
| FAI vs. FAI+G+ATRA | −0.570.641.85 | −0.420.170.76 | −0.86 − 0.210.45 |
| FAI+ATRA vs. FAI+G+ATRA | 0.551.833.10 | −0.280.290.86 | −0.090.501.09 |
| FAI+G vs. FAI+G+ATRA | 0.872.834.80 | 0.030.621.21 | −0.300.270.84 |
| Cytogenetic Group* | |||
| 0 vs. 2 | −0.770.291.36 | −0.340.030.41 | −0.56 − 0.050.45 |
| 1 vs. 2 | −0.460.491.44 | −0.95 − 0.52−0.10 | −0.90 − 0.320.26 |
| Age (per year) | −0.05 − 0.010.03 | −0.006 − 0.0040.014 | −0.04 − 0.03−0.01 |
| log(Time to resistance) | 0.111.202.30 | – | – |
| log(Time to CR) | – | −1.29 − 0.83−0.37 | – |
| log(Time to disease progression) | – | – | 0.550.851.16 |
| Salvage therapy | |||
| HDAC ( vs. others) | −4.07 − 1.610.85 | −0.94 − 0.340.27 | −0.84 − 0.390.06 |
| Interaction between induction and salvage therapy | |||
| FAI−HDAC (vs others) | −2.310.282.88 | −0.13 − 0.801.73 | |
| [FAI+ATRA]−HDAC (vs others) | −0.991.664.31 | −0.220.641.51 | |
| [FAI+G]−HDAC (vs others) | 1.024.257.48 | 0.371.202.03 | |
| Scale | 0.340.400.49 | 0.850.991.15 | |
0 = (“DIP,-Y”, “IM”), 1=“−5,−7”, 2=(“+8”, “11Q”, “INV16”, “T(8,21)”, “MISC”).
5.3 Complete remission, progression and death after remission and progression
About half (48.6%) of the 210 patients achieved CR, with CR rates of 37, 48, 53, and 56% in the FAI, FAI+ATRA, FAI+G and FAI+G+ATRA arms, respectively. Time to achieve CR did not differ significantly with frontline therapy (Table 3). Of the 102 patients who achieved CR, 93 (91%) had disease progression before death or being lost to follow-up. Among these, 53 (57%) received HDAC as salvage treatment. Since there were only 9 patients who died in CR, an intercept-only exponential AFT model was used for modeling TCD. On the other hand, to model time between CR and progression (TCP), a log-logistic model gave the best fit based on BIC values. Results for this fitted model are provided in Table 4.
Cytogenetics and TC were associated with TCP. The longer it took to achieve CR, the shorter the period of time the patient remained in CR, a well-known phenomenon in chemotherapy for AML/MDS (Shen and Thall, 1998; Estey, Shen and Thall, 2000). Recall that cytogenetic abnormalities were classified as good (“+8”, “11Q”, “INV16”, “T(8,21)”, “MISC”), intermediate (diploid, -Y or inevaluable), or poor (−5/−7). Patients with a “good” cytogenetic abnormality were more likely to stay in CR longer than those in the intermediate or poor categories.
Residual time to death from disease progression after achieving CR was associated with age at entry, time to disease progression following CR, and slightly with HDAC salvage. Older patients were likely to have shorter residual life once disease progressed, compared to younger patients. Longer time to disease progression was associated with longer time between disease progression and death.
5.4 Strategy effects
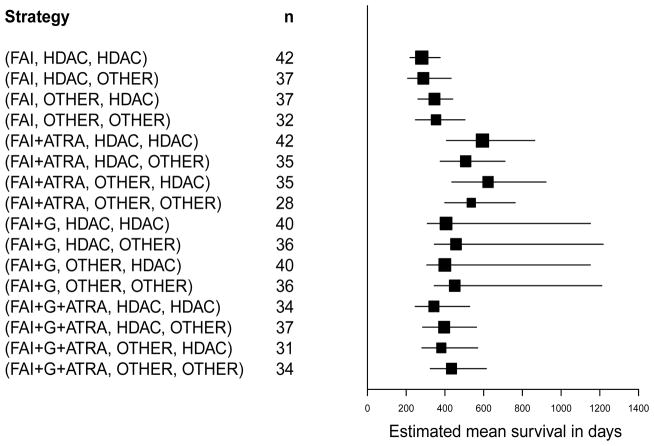
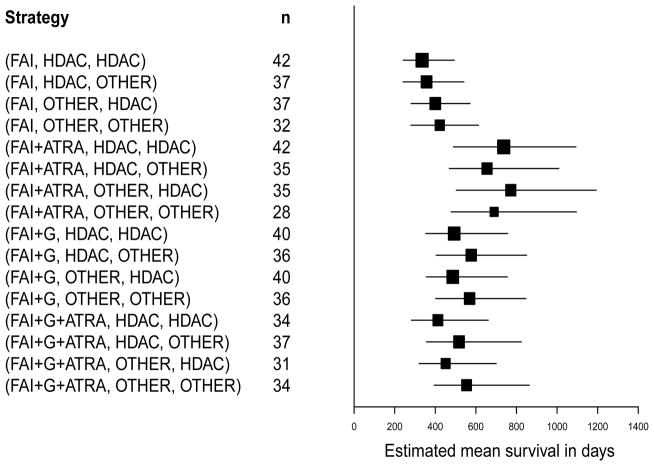
Mean OS time estimates under each of the 16 different strategies in the leukemia data were calculated using both the likelihood-based method and the IPTW method, from formulas (8) and (9), respectively. Confidence intervals for these estimates were calculated using a non-parametric bootstrap method based on 500 with-replacement samples. The results are presented in Table 5.4. The likelihood-based bootstrap confidence intervals are illustrated in Figure 2 using the data with outliers removed, and in Figure 3 using the entire dataset.
Figure 2.
Overall mean survival estimates and 90% non-parametric bootstrap confidence intervals for estimators under the likelihood method, excluding outliers. Strategies such as (FAI,HDAC,HDAC) stand for “Give FAI as induction, but if the patient’s disease is resistant to therapy, or if relapse occurs after achieving complete remission, then give HDAC as salvage.” For each strategy, the effective sample size n is the total number of patients in the study whose treatment regime was consistent with the strategy.
Figure 3.
Overall mean survival estimates and 90% non-parametric bootstrap confidence intervals for estimators under the likelihood method based on all observations in the dataset including putative outliers. Strategies such as (FAI,HDAC,HDAC) stand for “Give FAI as induction, but if the patient’s disease is resistant to therapy, or if relapse occurs after achieving complete remission, then give HDAC as salvage.” For each strategy, the effective sample size n is the total number of patients in the study whose treatment regime was consistent with the strategy.
It is clear from Table 5 that the two methods give very different estimates for mean OS time, with the likelihood-based estimator larger than the corresponding IPTW estimator for all strategies. The conference intervals for the likelihood-based estimators were wider for 10 strategies and narrower for 6 strategies. These differences are not entirely surprising, since the two methods are very different. The likelihood-based method defines OS time in terms of the seven transition times via (1), it uses regression models to account for effects of patient covariates and previous transition times, in addition to treatments, on each transition time, and it marginalizes over the covariate distributions to obtain θ(A, B1, B2). Thus, the likelihood-based method estimates many covariate effects, which may be considered nuisance parameters. In contrast, the IPTW estimator ignores this structure and uses the covariates very differently, to estimate the strategy probability weights. Additionally, modeling each time-to-event variable separately reduces the effective sample size for each model fit and thus increases the overall variability of the strategy mean estimates, whereas the IPTW estimates are calculated from the overall sample, where time to death is the main source of random variation.
Table 5.
Strategy-specific estimates of mean overall survival time, in days, based on the IPTW and Likelihood-based methods. Each estimate is given with 90% confidence interval limits subscripted on the left and right.
| Strategy
|
Estimators
|
||
|---|---|---|---|
| (A, B1, B2) | IPTW | Likelihood-Based Excluding Outliers | Likelihood-Based Including Outliers |
|
|
|
||
| (FAI, HDAC, HDAC) | 149189229 | 220281375 | 242335494 |
| (FAI, HDAC, OTHER ) | 129258397 | 207289432 | 241357541 |
| (FAI, OTHER, HDAC) | 162214283 | 261346441 | 281400571 |
| (FAI, OTHER, OTHER) | 147275422 | 248354504 | 280422613 |
| (FAI + ATRA, HDAC, HDAC) | 334524751 | 408594864 | 4897371093 |
| (FAI + ATRA, HDAC, OTHER ) | 263460707 | 376507710 | 4696551009 |
| (FAI + ATRA, OTHER, HDAC) | 342529749 | 436623922 | 5037721193 |
| (FAI + ATRA, OTHER, OTHER) | 269465713 | 399536763 | 4786901095 |
| (FAI + G, HDAC, HDAC) | 251337445 | 3094061151 | 353493757 |
| (FAI + G, HDAC, OTHER) | 217307408 | 3454571217 | 404577850 |
| (FAI + G, OTHER, HDAC) | 253338445 | 3064001151 | 355486755 |
| (FAI + G, OTHER, OTHER) | 218309410 | 3454511210 | 402569847 |
| (FAI + G + ATRA, HDAC, HDAC) | 169328514 | 246343528 | 282413661 |
| (FAI + G + ATRA, HDAC, OTHER) | 215294367 | 285396563 | 356517824 |
| (FAI + G + ATRA, OTHER, HDAC) | 187351546 | 281381569 | 320451700 |
| (FAI + G + ATRA, OTHER, OTHER) | 236318392 | 324434614 | 395554863 |
The substantive conclusions regarding the comparative effects of the 16 strategies are essentially the same for the two methods, however. Under both methods, the mean survival time estimates were smallest for the four strategies with FAI as frontline regardless of salvage, with the exception that under the likelihood-based analysis the strategy (FAI+G+ATRA, HDAC, HDAC) was slightly inferior to the strategies (FAI, OTHER, HDAC) and (FAI, OTHER, OTHER), and the confidence intervals were smallest for these inferior strategies. As shown by Figures 2 and 3 for the likelihood-based approach, the mean overall survival estimates were largest for the four strategies with FAI+ATRA as frontline. With the likelihood-based approach, Figures 2 and 3 together show that the substantive conclusions were insensitive to whether the outliers were included or not, although using all of the data gave much smaller bootstrap confidence intervals for the means associated with the four strategies (FAI+G, B1, B2). Most importantly, all approaches showed that, among the four best strategies, (FAI+ATRA, B1, HDAC) was superior to (FAI+ATRA, B1, Other) regardless of B1. These results suggest that (i) FAI+ATRA was the best remission induction therapy, (ii) if the patient’s disease was resistant to FAI+ATRA as induction therapy then it was irrelevant whether the salvage therapy contained HDAC, and (iii) if the patient achieved CR with FAI+ATRA and later relapsed then salvage with HDAC was superior These conclusions, while not confirmatory, are in sharp contrast with those given by Estey et al. (1999) based on conventional Cox regression model analyses and hypothesis testing, which were that none of the three adjuvant combinations FAI+ATRA, FAI+G, or FAI+ATRA+G were significantly different from FAI alone with respect to either survival or event-free survival time, considering only the frontline therapies.
An exhaustive formal comparison of the 16 strategies based on our analyses would require 120 pairwise tests, an unavoidable multiple comparisons problem that arises when evaluating multi-stage strategies. The trial was not designed to identify multi-stage strategies, and no clinical study can be powered to reliably conduct so many pairwise tests. With regard to estimation of strategy-specific mean survival times, however, although the 90% confidence intervals in Table 5 have a large degree of overlap, in terms of the estimated means it is striking that the two strategies (FAI+ATRA, HDAC, HDAC) and (FAI+ATRA, OTHER, HDAC) appear to be superior, with (FAI+ATRA, HDAC, OTHER) and (FAI+ATRA, OTHER, OTHER) ranked third and fourth, based on both of the two very different analytic approaches that we have taken here.
6 Discussion
We have re-analyzed a dataset from a four-arm clinical trial designed to assess the effects of adding ATRA, G, or both to FAI for treatment of newly diagnosed AML or high risk MDS. The purpose of our analysis has been to account for the multi-stage, adaptive nature of the therapy actually received by the patients, which in particular included salvage therapies given if either the patient’s disease was resistant to initial remission induction therapy or the patient relapsed after achieving a CR. This motivated evaluation of 16 possible two-stage strategies for choosing induction and salvage therapies. We employed two very different methods of analysis. The first was based on a detailed likelihood that accounted for all possible outcome paths, the transition times between successive states, and effects of covariates on each transition time. The second method employed IPTW-based estimating equations, and was much simpler, using covariates only to estimate the probabilities of the different strategies. While the two methods gave numerically different estimates of OS time, they agreed with regard to the worst and best strategies. Perhaps the most important conclusion was that these analyses both identified two strategies that appeared to be superior, a conclusion not seen earlier when only frontline treatments were evaluated. The trial was motivated by the idea that retinoids, such as ATRA, might improve outcome for AML/MDS patients when given with chemotherapy, since it was well established at the time this trial was initiated that ATRA has substantive anti-disease activity in treating acute promyelocytic leukemia (Estey, et al., 1997). Based on our re-analyses of this dataset, it seems that this idea for treatment of AML/MDS may have been correct. While our results cannot be considered confirmatory, it seems that analyses of the types presented here, had they been carried out in 1999, might have altered subsequent decisions of what combinations to study next, as well as showing the value of considering two-stage strategies. An open question that now seems important is whether the addition of ATRA to currently used frontline and salvage chemotherapy combinations for AML/MDS may improve OS time. More generally, our analyses of this dataset strongly suggest that a great deal of valuable information may be lost when using conventional methods based on initial treatment alone to analyze clinical trials.
Acknowledgments
The authors thank two referees, an Associate Editor, and Editor for their constructive comments and suggestions. Re-analysis of this dataset was approved by the M.D. Anderson Institutional Review Board under Exempted Research Protocol PA11-0730. Peter Thall’s research was partially supported by NCI grant RO1-CA-83932.
Appendix: Proof of the g-formula in Equation (8)
First note that the overall survival time T is a mixture of component transition times:
| (11) |
| (12) |
| (13) |
Suppose first that there are no covariates. Then to find the mean of T under a given treatment strategy (A, B1, B2), one would take the expectation of the components on the right hand side of the above equation under treatment assignment consistent with this strategy.
Therefore,
| (14) |
Now, using covariates to model the conditional probabilities and expectations on the right hand side of the above equation, and integrating over the respective covariate distributions, we obtain the g-formula in Equation (8).
References
- Estey EH, Thall PF, Pierce S, Cortes J, Beran M, Kantarjian H, Keating MJ, Andreeff M, Freireich E. Randomized phase II study of fludarabine + cytosine arabinoside + idarubicin ± granulocyte colony-stimulating factor in poor prognosis newly diagnosed acute myeloid leukemia and myelodysplastic syndrome. Blood. 1999;93(8):2478–2484. [PubMed] [Google Scholar]
- Estey EH, Thall PF, Pierce S, Kantarjian H, Keating M. T Treatment of newly diagnosed acute promyelocytic leukemia without cytarabine. J Clinical Oncology. 1997;15:483–490. doi: 10.1200/JCO.1997.15.2.483. [DOI] [PubMed] [Google Scholar]
- Estey EH, Shen Y, Thall PF. Effect of time to complete remission on subsequent survival and disease-free survival in AML, RAEB-t, and RAEB. Blood. 2000;95(10):72–77. [PubMed] [Google Scholar]
- Holland P. Statistics and causal inference. Journal of the American Statistical Association. 1986;81:945–960. [Google Scholar]
- Lavori P, Dawson R. A design for testing clinical strategies: biased individually tailored within-subject randomization. Journal of the Royal Statistical Society, A. 2000;163:29–38. [Google Scholar]
- Lavori P, Dawson R. Dynamic treatment regimes: practical design considerations. Clinical Trials. 2004;1:9–20. doi: 10.1191/1740774s04cn002oa. [DOI] [PubMed] [Google Scholar]
- Lunceford J, Davidian M, Tsiatis AA. Estimation of the survival distribution of treatment policies in two-stage randomization designs in clinical trials. Biometrics. 2002;58:48–57. doi: 10.1111/j.0006-341x.2002.00048.x. [DOI] [PubMed] [Google Scholar]
- Murphy SA. Optimal dynamic treatment regimes (with discussion) Journal of the Royal Statistical Society, B. 2003;65:331–366. [Google Scholar]
- Murphy SA. An experimental design for the development of adaptive treatment strategies. Statistics in Medicine. 2005;24:1455–1481. doi: 10.1002/sim.2022. [DOI] [PubMed] [Google Scholar]
- Murphy SA, van der Laan, Robins JM, CPPRG Marginal mean models for dynamic treatment regimes. Journal of the American Statistical Association. 2001;96:1410–1424. doi: 10.1198/016214501753382327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robins JM. A new approach to causal inference in mortality studies with sustained exposure periods - application to control of the healthy survivor effect. Mathematical Modeling. 1986;7:1393–1512. [Google Scholar]
- Robins JM. Causal Inference from Complex Longitudinal Data Latent Variable Modeling and Applications to Causality. In: Berkane M, editor. Lecture Notes in Statistics. 120. NY: Springer Verlag; 1997. pp. 69–117. [Google Scholar]
- Robins JM, Hernan MA, Brumback B. Marginal structural models and causal inference in epidemiology. Epidemiology. 2000;11:550–560. doi: 10.1097/00001648-200009000-00011. [DOI] [PubMed] [Google Scholar]
- Robins JM. Optimal structural nested models for optimal sequential decisions. In: Lin DY, Heagerty P, editors. Proceedings of the Second Seattle Symposium on Biostatistics. New York: Springer; 2004. [Google Scholar]
- Robins JM, Rotnitzky A. Recovery of information and adjustment for dependent censoring using surrogate markers. In: Jewell N, Dietz K, Farewell, editors. AIDS epidemiology, methodological issues. Boston, MA: Birkhauser; 1992. pp. 297–331. [Google Scholar]
- Robins JM, Orellana L, Hernan M, Rotnitzky A. Estimation and extrapolation of optimal treatment and testing strategies. Statistics in Medicine. 2008 doi: 10.1002/sim.3301. To appear. [DOI] [PubMed] [Google Scholar]
- Schwarz G. Estimating the dimension of a model. Annals of Statistics. 1978;6:461–464. [Google Scholar]
- Shen Y, Thall PF. Parametric likelihoods for multiple non-fatal competing risks and death. Statistics in Medicine. 1998;17:999–1016. doi: 10.1002/(sici)1097-0258(19980515)17:9<999::aid-sim785>3.0.co;2-3. [DOI] [PubMed] [Google Scholar]
- Thall PF, Millikan R, Sung HG. Evaluating multiple treatment courses in clinical trials. Statistics in Medicine. 2000;19:1011–1028. doi: 10.1002/(sici)1097-0258(20000430)19:8<1011::aid-sim414>3.0.co;2-m. [DOI] [PubMed] [Google Scholar]
- Thall PF, Sung H-G, Estey EH. Selecting therapeutic strategies based on efficacy and death in multi-course clinical trials. Journal of the American Statistical Association. 2002;97:29–39. [Google Scholar]
- Thall PF, Logothetis C, Pagliaro L, Wen S, Brown MA, Williams D, Millikan R. Adaptive therapy for androgen independent prostate cancer: A randomized selection trial including four regimens. Journal of the National Cancer Institute. 2007;99:1613–1622. doi: 10.1093/jnci/djm189. [DOI] [PubMed] [Google Scholar]
- Wahed AS, Tsiatis AA. Optimal estimator for the survival distribution and related quantities for treatment policies in two-stage randomization designs in clinical trials. Biometrics. 2004;60:124–133. doi: 10.1111/j.0006-341X.2004.00160.x. [DOI] [PubMed] [Google Scholar]
- Wahed AS, Tsiatis AA. Semiparametric efficient estimation of survival distribution for treatment policies in two-stage randomization designs in clinical trials with censored data. Biometrika. 2006;93:163–177. [Google Scholar]
- Zhao Y, Kosorok MR, Zeng D. Reinforcement learning design for cancer clinical trials. Statistics in Medicine. 2009;28:3294–3315. doi: 10.1002/sim.3720. [DOI] [PMC free article] [PubMed] [Google Scholar]