Gain control of synaptic response function in cerebellar nuclear neurons by a calcium activated potassium conductance

Abstract

Small conductance Ca²⁺ activated potassium (SK) current provides an important modulator of excitatory synaptic transmission, which undergoes plastic regulation via multiple mechanisms. We examined whether inhibitory input processing is also dependent on SK current in the cerebellar nuclei (CN), where inhibition provides the only route of information transfer from the cerebellar cortical Purkinje cells. We employed dynamic clamping in conjunction with computer simulations to address this question. We found that SK current plays a critical role in the inhibitory synaptic control of spiking output. Specifically, regulation of SK current density resulted in a gain control of spiking output, such that low SK current promoted large output signaling for large inhibitory cell input fluctuations due to Purkinje cell synchronization. In contrast, smaller non-synchronized Purkinje cell input fluctuations were not amplified. Regulation of SK density in the CN therefore would likely lead to important consequences for the transmission of synchronized Purkinje cell activity to the motor system.

INTRODUCTION

The cerebellar nuclei (CN) provide a critical bottleneck in the output processing of the cerebellum. The GABAergic output from at least a 10-fold higher number of Purkinje cells (PC) than cells present in the CN is integrated here before the cerebellum can affect other brain areas [1, 2]. Several concepts have been proposed for how the CN integrate PC input, ranging from simple rate coding [3, 4] to responses to synchronized pauses in PC firing triggering spikes [5–7] and postinhibitory rebound responses [8–10] mediated by fast T-type current [11, 12] and a slower persistent sodium current [13]. A distinct mechanism for coding output likely also exists for synchronized complex spike input from PCs [6, 14, 15], which themselves receive highly synchronized olivary inputs [16–18]. Neurons in the CN are characterized by several active properties that are likely important in the mechanism(s) by which PC input is decoded. Besides the rebound currents mentioned above there are considerable components of hyperpolarization activated cyclic - nucleotide gated (HCN) current [8, 13, 19, 20] and small conductance Ca²⁺ activated potassium (SK) current present [13, 19]. These currents are known to be involved in the spike response coding following excitatory input in other types of neurons. Notably the HCN current can contribute to sharpening synaptic responses [21] and phase resetting [22], whereas the SK current has been implicated in regularizing spiking [23, 24] through forming a medium-duration spike-afterhyperpolarization (mAHP), suppressing bursts [25] and reducing sensitivity to small input fluctuations [24]. The role of these currents in the processing of inhibitory input is much less studied, however, and in the case of the CN, in which GABA inhibition carries the entire signal from the cerebellar cortical input stream, this question becomes particularly important. . In this study we examined the role of SK current in the synaptic coding of spike output in the CN using a dynamic clamp approach in rat brain slice recordings [5, 26] in conjunction with computer simulations. In order to determine the role of different amounts of SK current in an individual neuron we first compared responses to inhibitory dynamic clamp input patterns before and after blocking SK with the highly selective drug apamin. We then titrated a varying amount of artificial SK current back into the blocked state by using a new dynamic clamping approach that allows simulating the calcium-gated SK conductance in the dynamic clamp loop through the inclusion of voltage-gated calcium currents and an intracellular calcium pool in the dynamic clamp algorithm. The results of these experiments and associated computer simulations indicate that SK current indeed plays a crucial role in the spike responses to inhibitory PC input, which can be summarized as a gain function. In this gain function, a high amount of SK current leads to single spike responses to transient inhibitory input reduction in a considerable range of amplitudes, whereas a low amount of SK current results in much stronger multi-spike responses associated with larger transient reductions in PC input. Therefore, a low SK conductance state promotes a higher contrast between responses to small and large input transients and an increased output gain.

MATERIALS AND METHODS

Cerebellar Brain Slices

Slices were obtained from Sprague-Dawley rats aged P15-P20. The animals were anesthetized with isoflurane and decapitated. The cerebellum was removed within 1 minute and placed in an artificial cerebral spinal fluid (ACSF) consisting of (in mM) 124 NaCl, 3 KC1, 1.9 MgSO₄, 1.2 KH₂PO₄, 26 NaHCO₃, 2 CaCl₂, 20 glucose, bubbled with 95% O₂ and 5% CO₂ to obtain a pH of 7.4. The cerebellum was then mounted on a vibratome and 300 µm-thick sagittal slices were made. The slices were incubated in ACSF at 32 °C for at least 75 minutes before recording. All procedures were approved by the Emory IACUC and complied with the NIH Guide on Animal Use.

Electrophysiology

Cerebellar slices were placed in a recording chamber perfused with ACSF, containing 1mM Kynurenic Acid (Sigma-Aldrich) and 100 µM picrotoxin (Sigma-Aldrich) to prevent synaptic transmission, and maintained at 32 °C. The slices were visualized using a Zeiss Axioskop microscope and CN neurons were identified using a 60x water-immersion objective. Glass pipette electrodes were pulled from 1.5 mm borosilicate glass (Sutter Instruments Co., Novato, CA, USA) and were filled with an intracellular solution consisting of (in mM) 140 Potassium Gluconate, 6 NaCl, 10 HEPES, 0.2 EGTA, 2 MgCl₂, 0.05 Spermine, 5 Glutathione, 4 NaATP, 0.4 NaGTP. Whole cell patch clamp recordings were performed using a Multiclamp 700B amplifier (Molecular Devices, Sunnyvale, CA). To block SK current, 100 nM apamin (Sigma-Aldrich) and 1% bovine serum albumin to keep the apamin in solution were added to the perfusion solution. Current clamp recordings were sampled at 10 kHz using an NI PCI-6052E DAQ card (National Instruments, Austin, TX) and custom data-acquisition software written in LabVIEW 8 (National Instruments). Recordings were obtained from neurons identified in all three deep cerebellar nuclei, with no observed differences in physiological characteristics between nuclei.

In Vivo-Like Background Synaptic Input Applied Via Dynamic Current Clamp

We constructed an artificial synaptic conductance G_syn consisting of a constant level of excitatory conductance (G_ex) and a fluctuating inhibitory conductance (G_in) derived by simulating 400 stochastic Purkinje cell input trains. The stimulus design with constant excitatory conductance allows the isolation of inhibitory PC input dynamics in the control of CN output spiking. Unitary inhibitory inputs (g_in) were simulated as a dual exponential function as previously described [5]. We used the intermediate synchronicity and gain conditions from our previous study throughout, i.e. the 400 Purkinje cells were divided into 10 groups of 40 synchronous cells and the mean combined inhibitory input conductance was 8 nS. These stimuli were directly taken from our previously published study [5] to allow direct comparison of synaptic coding of spiking with our previous data. Therefore, they do not reflect some recent updates on Purkinje cell IPSCs in the cerebellar nuclei [27, 28], indicating that individual IPSCs are shorter and larger than earlier data on which our synaptic input parameters were based [29]. However, in our stimuli several thousand IPSCs are summed every second, and the summed conductance results in very similar spiking output when large fast-decaying or small slow-decaying IPSC shapes are used in a CN neuron model [30].

Dynamic clamp in this study was implemented with LabVIEW 8 on a PXI-8176 real-time controller mounted on a PXI-1002 Chassis (National Instruments). See the supplemental material for the equations which describe the synaptic input conductance.

CN Morphological Model Simulation

Morphology, passive properties, and active conductances: The morphological reconstruction, fitting of passive parameters, and tuning of active membrane conductances for this model have been previously described [30, 31]. Briefly, the model has a total membrane resistance of 271 MΩ and contains a somatic compartment, 485 dendritic compartments, and a 30 compartment artificial axon to provide a spike initiation zone. It features a full complement of membrane channels based on published analyses of CN neuron conductances [19, 20, 32, 33] and implemented using the Hodgkin-Huxley formalism in GENESIS 2.3 [34]. The channels consist of a fast sodium current (NaF), fast Kv3 family (fKdr) and slow Kv2 (sKdr) family delayed rectifiers, a tonic non-specific cation current (TNC), a high-voltage activated (HVA) calcium current, a purely calcium-gated potassium current (SK), a low-voltage activated T-type calcium current (CaT), a hyperpolarization activated (IH) current, and a persistent sodium current (NaP). The density of active conductances in the model is not uniform but varies between four major partitions of the model: axonal, somatic, proximal dendritic, and distal dendritic. All channel kinetics were adjusted to a temperature of 32°C as used for the slice recordings by applying a Q10 value for all Hodgkin-Huxley rate constants and the intracellular calcium concentration was modeled as a diffusion shell. The model has a spontaneous firing rate of 11.17 ± 0.15 Hz.

The synaptic input to the model matches the design of the experimental dynamic clamp stimuli such that both use exact same conductance waveforms [35]. The reversal potentials of the excitatory and inhibitory synaptic conductances were initially set to 0 mV and −70 mV, respectively, as in our slice recordings. Since the slice recordings were not corrected for a 10 mV junction potential during dynamic clamping, the reversal potentials in the model were shifted downward by 10 mV. They were then further shifted by −4.4 mV to match the same offset from the mean subthreshold membrane potential between slice recordings and simulations and therefore the mean driving force for synaptic excitation and inhibition [35]. To simulate dynamic clamp in the model, the synapses were focalized completely on the soma, which is the site of current injection with a somatic whole cell recording. Our previous modeling study showed, however, that a dendritic distributed source of synaptic conductance yields very similar results [35].

To simulate repeated trials of the dynamic clamp stimuli, we introduced a fluctuating somatic current injection to the soma of the model as previously described [35]. The model without noise fires at 11.20 Hz and at 11.17 ± 0.15 Hz (N=6 noise trials) with noise. Six waveforms of frozen noise were obtained using different random seeds and used to simulate six presentations of the same dynamic clamp stimulus.

Artificial SK Conductance Applied Via Dynamic Current Clamp

We constructed an artificial SK conductance (G_SK-art) by simulating a high voltage activated (HVA) L-type Ca²⁺ current, an intracellular Ca²⁺ pool, and Hill equation-based Ca²⁺-binding SK channel activation [36]. The resulting SK conductance was applied via dynamic current. We simulated Ca²⁺ inflow to the intracellular pool as being carried by a simulated HVA current that we modeled with Hodgkin-Huxley kinetics and dependent on the recorded V_M in real time. The HVA current kinetics and the SK current kinetics were directly taken from our computer simulation study and adjusted to a temperature of 32°C. See the supplemental material for the equations that describe this artificial SK conductance model.

Data Analysis

We analyzed recordings with Mathworks MATLAB 2007b. Spike detection was performed by searching for peaks defined by three consecutive time sample increases in V_M preceding three consecutive time sample decreases in V_M and occurring above a spike threshold of −10 mV. Interspike interval histograms were assembled by searching for spike times and then recording the time intervals between successive spikes. These time intervals were then formed into a histogram with 10 ms bins. Spike precision across repeated trials of the same dynamic clamp waveform was computed as described in our previous study [5], i.e. a cross-correlation analysis was performed and the percentage of all spikes recurring within a specified precision time window above chance level across trials was scored. Statistical analysis consisted of two tailed paired t-tests and two tailed two sample t-tests. The paired t-tests were used to test for a significant change in measured characteristics in spike response patterns such as precision, inter-spike interval (ISI), coefficient of variation (CV), and spike rate (SR).

RESULTS

In-vivo like synaptic conductances block apamin induced burst firing in CN neurons

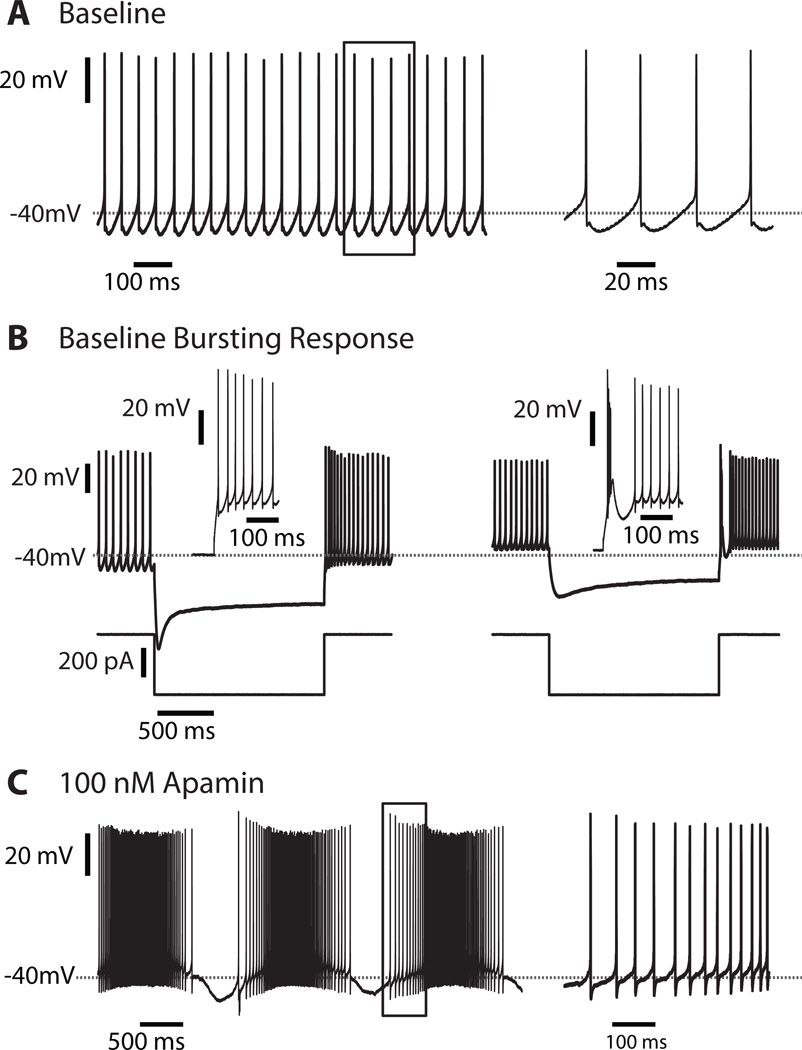
To explore the contribution of the SK current to synaptic processing in CN neurons, we chose to use the selective blocker apamin, which has been shown to abolish the SK-dependent mAHP and induce a switch from rhythmic pacemaker activity to spontaneous bursting activity in CN neurons [19, 36] (Fig. 1C) and in other neurons with SK channels [37–39]. Electrophysiological recordings were made from CN neurons in rat cerebellar slices before and after SK block, as described in the Materials and Methods section. With native AMPA/NMDA and GABA synaptic input blocked, we observed tonic spontaneous regular spiking at frequencies ranging from ∼7 to 15.2 Hz before apamin block (Fig. 1A). Recordings were obtained from a total of 17 neurons from all three cerebellar nuclei. Negative current injection pulses revealed that our sampled neurons consisted of both transient (Fig. 1B, right trace) and weak burst rebound phenotypes (Fig. 1B, left trace) [10, 40]. However, rebound behavior was not further addressed in our study, and the effect of apamin was not assessed. We also observed 3 neurons without a fast AHP preceding the mAHP, likely corresponding to GABAergic neurons as previously reported [9]. However, the SK- dependent mAHP depth was not significantly different between cells with different rebound or fAHP types. After the application of 100 nM apamin, we observed the abolishment of the mAHP, and subsequent bursting behavior in all cells (Fig. 1C). Therefore, for the remainder of this study concerned with effects of SK current on the synaptic transfer function, all recorded cell types are treated as a single population.

Figure 1. SK Block by 100 nM Apamin alters the spontaneous behavior of CN neurons.

A: Membrane voltage of baseline spontaneous activity of a CN neuron. On the right is an expanded inset of the boxed area. Note the pronounced mAHP waveform. B: Voltage response of a weak rebound burster (left) and a transient rebound burster (right) to −400 pA current pulse injections. C: Membrane voltage of spontaneous activity of neuron from (A) after superfusion of 100 nM apamin. On the right is an expanded inset of the boxed area. Note that the mAHP is fully blocked.

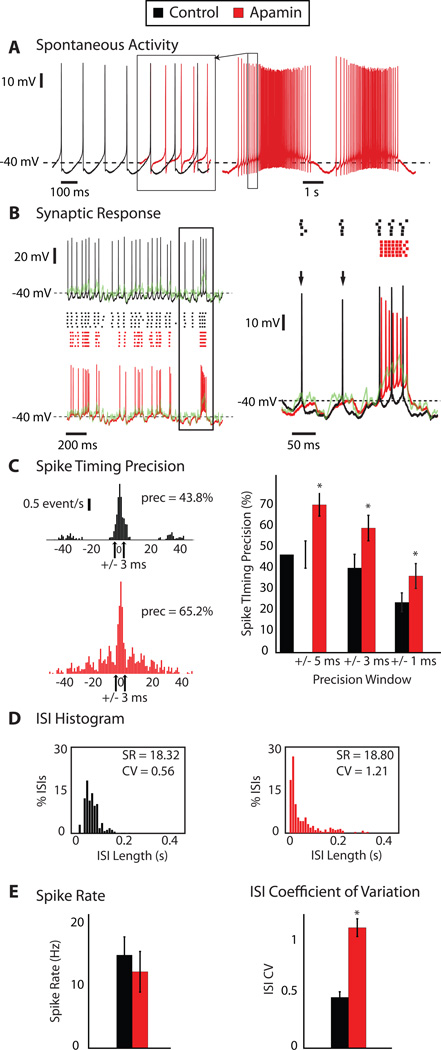
To examine the effect of SK channels on CN spike coding of PC inputs, we applied a dynamic clamp stimulus of an in-vivo like PC input pattern during whole cell recording in slice while maintaining excitation at a constant baseline conductance. The inhibitory input patterns were kept identical to our previous study [5], to allow a direct comparison of the results. Our previous study showed that the timing of CN spikes with such input is precisely related to transient decreases in inhibitory input. During subthreshold behavior the CN neuron closely follows the temporal waveform of the reversal potential of the combined excitatory and inhibitory input conductance [5] resulting in a precisely repeating response pattern for repeated stimulations with the same waveform. Our present sample of cells (N=17) showed the same response properties as previously observed, and we proceeded to determine the effect of SK block on the observed spike responses (Fig. 2). After apamin block resulted in a transition from regular pacemaking to pronounced bursting (Fig. 2A) we applied the same dynamic clamp input that we also tested prior to apamin application (Fig. 2B). Several important observations can be made from these data. First, the apamin-induced burst pattern was stopped by the application of a synaptic conductance input pattern (Fig. 2B) because the ongoing baseline of GABA conductance forced the membrane potential (Vm) close to the chloride reversal potential, here set at −70 mV with the dynamic clamp. This effect shows the advantage of dynamic clamping over a current waveform application without real-time feedback, as only dynamic clamping includes the changing driving forces with changing Vm that result in this critical feature of stabilizing Vm by a high-conductance input pattern. The second important observation was that the output spike pattern with the same synaptic input pattern had changed (Fig. 2B), indicating a strong influence of the SK current on the synaptic transfer function of CN neurons. Specifically, stronger depolarizing transients in the input waveform due to a transient reduction in inhibition resulted in a much stronger high-frequency spike response after apamin block than before (Fig. 2B, right panel), because blocking the mAHP allowed much faster spike trains in the depolarized state. Note, however, that the faster spiking was not uncontrolled as the overall level of spike precision for repeated applications of the same input pattern remained high, and among a sample of 8 neurons quantitatively analyzed was actually significantly increased after SK block (Fig. 2C, right panel). A second effect that we observed in this condition is that the spike responses to weaker depolarizing input transients were diminished (Fig. 2B, right panel) in that spikes reliably triggered by such transients before apamin application were missing afterwards. Both effects taken together resulted in a synaptic transfer function that showed an increase in both shorter and longer inter-spike intervals, while showing diminished ISIs of intermediate duration (Fig. 2D) that were set by the pacemaker properties of the SK dependent mAHP. These effects led to a significant increase in the coefficient of variation of the ISI distribution (ISI CV), which changed from 0.48 to 1.10 after apamin presentation (Fig. 2E, p=0.0002, n=10 neurons analyzed). As a result of the combination of the opposing effects described above, however, the spike rate (SR) was not significantly altered (14.3 to 12.3 Hz) (Fig. 2E, p=0.38, n=10). The overall function of the SK current could be described as a lowered a ‘contrast function’ by which weak and strong input transients were able to control output spiking, resulting in stronger spike responses to large input transients and weaker ones for small input transients when SK is downregulated.

Figure 2. SK Block by apamin alters the spike response pattern elicited by synaptic input applied via dynamic clamp.

A: Spontaneous activity of a CN neuron before (black) and after superfusion of 100 nM apamin (red). A segment of the spike train after apamin block was superposed on the control spike train to allow direct comparison of the AHP waveform at a comparable spike rate (red overlay demarcated by box) B: Stimulus aligned voltage responses to a synaptic conductance input pattern applied via dynamic clamping on the left before (black) and after apamin (red) superfusion. Spike raster plots for 5 stimulus repetitions are shown in the center and the temporal waveform of the combined reversal potential of inhibition and excitation (E_syn) is shown in green. On the right is an expanded inset of the boxed area overlaying the voltage traces. The loss of certain isolated spike events (arrows) and the presence of fast frequency spiking with a large depolarizing stimulus event are evident after the application of apamin. C: Spike timing cross-correlograms reveal time-locked responses to specific input events across trials. On the left are cross-correlograms of the spike responses across 5 repeated applications of the same synaptic conductance waveform applied both before (top) and after apamin presentation (bottom). For a precision window of +/− 3 ms, this neuron had 43.8% of spikes repeated at the same time across trials in the baseline condition and 65.2% following apamin. On the right are the percentages of aligned spikes for +/− 5, 3, and 1 ms precision windows for 8 recorded neurons. For all tested precision windows, the SK blocked condition yielded significant higher spike precision values (p < 0.05, N=8). D: Histograms of inter-spike intervals (ISIs), with a 10 ms bin, of a neuron’s responses to dynamic clamp-applied synaptic input. High frequency bursts elicited by larger depolarizing events lead to an increase in the percentage of the shorter ISIs (that of the 10 ms or less bin rises from zero to ∼18%). The loss of some responses to smaller synaptic events leads to an increase in the number of longer ISIs as well. The shift in the ISI distribution leads to a large change in the coefficient of variation (ISI-CV), from 0.535 to 1.21, while the SR is nearly unchanged after apamin presentation (18.32 Hz vs. 18.8 Hz). E: For all 8 quantitatively analyzed neurons, SR remains statistically unchanged while ISI-CV increases significantly (p < 0.001) after apamin presentation as a result of the combination of the antagonistic effects seen in (B) and (D).

Computer simulations can replicate the observed SK dependence of the synaptic transfer function, but only with an added negative bias current

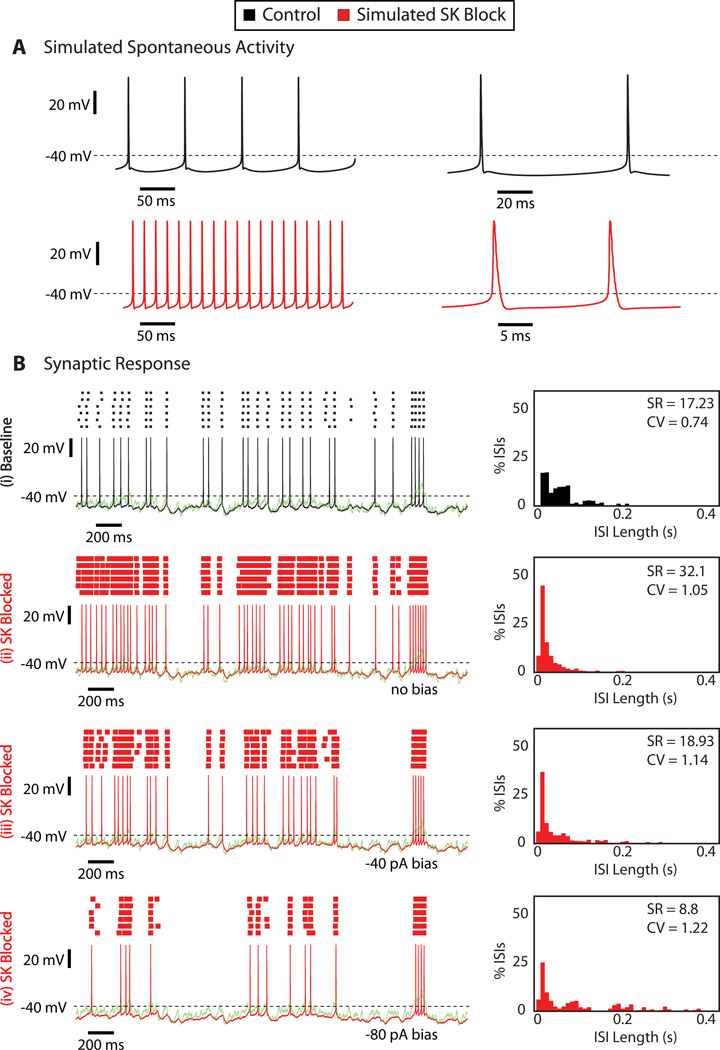
We used computer simulations to replicate the mechanisms underlying the changed synaptic response function after SK block. While we had a clear hypothesis that the increased spike response to strong input transients are explained by an abolished mAHP, the reduction of responses of weaker transients is hard to explain by a reduced potassium current that should result in a more depolarized Vm. We hypothesized that a plausible mechanism for this effect was an increased steady-state inactivation of the fast voltage-gated Na channel (NaF) and a concomitant increase in spike threshold. The NaF conductance in CN neurons was previously shown to have a high component of steady-state inactivation at baseline [20]. However, in our experimental data we could not determine a clear depolarized shift in spike threshold after SK block (data not shown). A small shift that is experimentally hard to determine could have been missed, and one goal of our computer simulations that included NaF conductance with steady-state inactivation to match the experimental data was to ascertain this effect.

The CN computer model was taken from a previous study [30] and adapted with a somatic noise source [35] to closely match the dynamic clamp data in the presence of SK current described in our previous experimental study [5]. In the absence of any synaptic input, the model exhibits spontaneous tonic firing (Fig. 3A, top, in black). The effect of apamin was simulated by setting the SK conductance in the model to a value of zero. This block resulted in a considerable speedup in spiking and the loss of the mAHP (Fig. 3A, bottom, in red). However, a burst pattern of spiking was not observed, presumably because the model does not include important slow dynamic variables such as calcium buffering and ionic pumps. As previously analyzed in detail [35], the model closely matched the experimentally observed spike response to our dynamic clamp input pattern when SK was present (Fig. 3B(i)). Removing the SK conductance in the model resulted in a two-fold increase in SR and a pronounced increase in the ISI-CV from 0.74 to 1.05. As in the experiments an increased spike response to large input transients and an increase in short ISIs was observed (Fig. 3B(ii)). However, the reduction of spiking for weak input transients was not observed, and NaF inactivation was not sufficiently increased to elevate the spike threshold to make such an effect possible. As an alternative explanation to reduced spiking with weak input transients we posed the hypothesis that a constant negative bias current was present in addition to SK conductance block. Application of just −40 pA (Fig. 3B(iii)) bias current indeed lowered the model’s responses to weak input transients, while maintaining an elevated response to strong transient reductions in inhibition. In fact, the results obtained with −40 pA bias current resulted in SR and CV changes that were close to experimentally obtained values (Fig. 2D).

Figure 3. Computer simulations using a full morphological CN neuron model suggest that two distinct mechanisms are required for observed effects of SK block on synaptic spike response function.

A: Spontaneous activity of the CN model neuron before (black) and after (red) simulated SK block. To simulate apamin application, SK channel density was reduced to zero in the CN model neuron. B: Stimulus aligned voltage response of the CN model to simulated dynamic clamp stimuli with and without SK conductance and varying levels of somatic bias current. SK block alone resulted in an increase of spike responses to weak and strong transient reductions in PC input. Adding an additional negative bias current of −80 pA (bottom trace) abolished the response to weak transients, while the response to strong transients remained above baseline excitability. The ISI histograms for trials with negative bias show a widening of the ISI distribution and increase in CV similar to that observed in the experiments.

Burst suppression prevented the reduction in responsiveness to weak input transients

Our computer simulations predicted that the observed effects on the synaptic transfer function could be explained with two distinct mechanisms: An increased responsiveness to large input transients due to blocking the mAHP, and a decrease in responsiveness to smaller input transients due to an overall hyperpolarizing shift. What mechanism in the real cells, however, could result in a hyperpolarizing shift upon blocking SK current with apamin? One potential cause for such a shift could be given by the pronounced bursting pattern induced by apamin that was developing for several minutes before we tested cells with dynamic clamp input. The extreme spike rates and depolarized potential during the bursts might lead to a compensatory hyperpolarization for example by calcium inflow - induced intracellular processes. To test this hypothesis we performed recordings from another set of cells (N=7), in which we voltage-clamped CN neurons at −60 mV as soon as apamin started to result in an irregular spike pattern (Fig. 4A) prior to full blown bursting. We kept this burst suppression (BS) on at all times except when dynamic clamp conductances were applied in current clamp. A fast switching of voltage clamp and current clamp modes is possible in the Axon Multiclamp 700B amplifier used in this study. We observed that when CN neurons were burst suppressed after apamin presentation, responses to larger depolarizing input transients were still enhanced and often consisted of short high frequency bursts (Fig. 4B, in red). However, in contrast to the observed reduction in responses to small input transients seen in freely bursting (FB) CN neurons (Fig. 2B), responses to smaller depolarizing input transients were not reduced after apamin presentation, but were in fact slightly enhanced as well (Fig. 2B). The ISI histogram of the neuron shown in Fig. 2B confirms that these changes shifted the overall spike distribution in that the number of short intervals was increased, with a concomitant left-shift of the modal interval, but at the same time the tail of long intervals also increased (Fig. 4C). Across the sample of recording, the spike timing precision remained unchanged (Fig. 4D, N=7 cells), but the ISI-CV was significantly increased as in the freely bursting cells (Fig. 4D). The SR showed a trend towards increase, which did not reach significance, however. (Fig. 4D). These data are in fact similar to those seen with a pure SK block in the computer simulations. Therefore, apamin induced bursting is likely responsible for an overall hyperpolarizing shift in the recorded neurons that could be induced by an increased tonic K⁺ conductance or a decreased tonic non-specific cation current present in CN neurons [20]. In the absence of such a hyperpolarizing shift the role of SK current with respect to synaptic integration can be described by a gain control function: An overall decrease in responsiveness to input transients that in particular reduces the maximal spike frequency for strong depolarizing input transients. As the predominant signal stream is expected to originate with inhibitory inputs from PCs, such transients would be given by synchronous pauses in a population of PCs. Nevertheless, transient increases in mossy fiber excitation could also result in similar spike responses [26].

Figure 4. Suppression of spontaneous bursting after SK Block prevents loss of responses to weak depolarizing input events applied with dynamic clamping.

A: Spontaneous activity of a CN neuron before (black) and after superfusion of 100 nM apamin (red). A portion of the apamin spike pattern is superposed on the control spike train at the matching time scale to allow a direct comparison of spikes (red overlay demarcated by box). This burst suppressed (BS) neuron was voltage-clamped to a holding potential of −60 mV to prevent spontaneous high frequency bursting. The neuron was released from voltage clamp only during the time of dynamic clamp stimulus application. B: Stimulus aligned voltage responses of a BS neuron to a synaptic conductance input pattern applied via dynamic current clamp on the left before (black) and after apamin (red) presentation. Raster plots are shown in the center and E_syn is depicted in green. BS neuron responses to weak depolarizing events were almost never reduced, unlike that seen for FB neurons (Fig. 2B), but fast frequency burst responses were still only associated with large depolarizing events. On the right is an expanded inset of the boxed area. C: ISI histograms of the same BS neuron responses to dynamic clamp-applied synaptic input. The increase in responses to both large and small depolarizing events lead only to an increase in the shorter ISIs. Both the SR (10.6 Hz to 14.4 Hz) and ISI-CV (0.422 to 0.687) of the BS neuron depicted in (B) increase after apamin presentation. D: The data from all 7 BS neurons show a maintained spike time precision during in responses to dynamic clamp stimuli, but a significant increase in ISI-CV (paired t-test, p < 0.001) and a non-significant increase in SR (paired t-test, p = 0.1).

Artificial SK conductance (G_SK-art) inserted via dynamic clamp restored the mAHP and spike responses to inhibitory input patterns

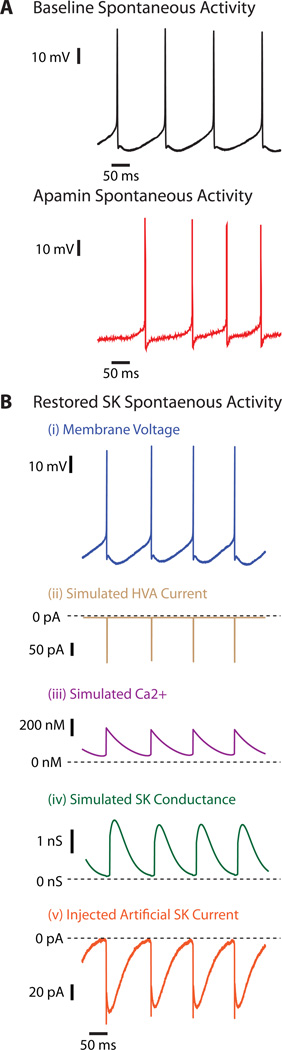
We next asked whether our understanding of the SK conductance could fully account for the observed gain changes in the synaptic transfer function. To address this question we added back a fully controlled artificial SK conductance with dynamic clamping after blocking the intrinsic conductance with apamin. To apply an artificial version of SK current (I_SK-art) with dynamic clamping, several steps were necessary (Fig. 5). First, the intrinsic SK conductance was fully blocked with apamin (Fig. 5A). Then the real-time loop of the dynamic clamp algorithm was expanded to include a simulated voltage-dependent source of calcium into a simulated calcium pool, as well as a mechanism of exponential decay from this pool. An artificial SK conductance, as also implemented in our compartmental computer model [30, 35] was then linked to this simulated calcium pool and the resulting I_SK-art was applied back to the recorded neuron [36](Fig 5B). Previous experimental work has indicated that high-voltage-activated (HVA) calcium current in CN neurons is the only source of calcium driving SK activation [41]. We used the same Hodgkin-Huxley HVA calcium kinetics as was also used in our CN computer model [30, 35] but the voltage driving the activation function was taken in real-time from our recording.

Figure 5. Artificial SK Conductance (G_SK-art) inserted via dynamic clamp can recover spontaneous behavior of CN neurons after SK block by apamin.

A: Spontaneous activity of a CN neuron before (black) and after presentation of 100 nM apamin (red). B: Restored spontaneous activity by artificial SK conductance (G_SK-art) applied via dynamic clamp following apamin superfusion. From top to bottom, locked in time: (i) voltage response (blue) similar to baseline spontaneous activity, (ii) simulated high voltage activated (HVA) Ca²⁺ current (brown), (iii) simulated intracellular [Ca²⁺] (purple), (iv) simulated G_SK-art (green), and (v) injected artificial SK current (I_SK-art) (orange).

Indeed, when our artificial SK conductance was applied to recordings, in which apamin blocked the intrinsic I_SK, we were able to restore an mAHP waveform and to recover regular pacemaking activity (Fig. 5B). To achieve good matches between the recordings with I_SK-art and the pre-apamin mAHP shape and depth, individual tuning of the calcium pool decay time constant as well as the maximal SK conductance was required for each recorded cell (N=5 BS recordings). After tuning G_SK-art for each SK-blocked BS neuron, we repeated the application of the dynamic clamp PC input pattern, this time with the additionally inserted G_SK-art, to determine whether G_SK-art could replicate the original baseline synaptic response function.

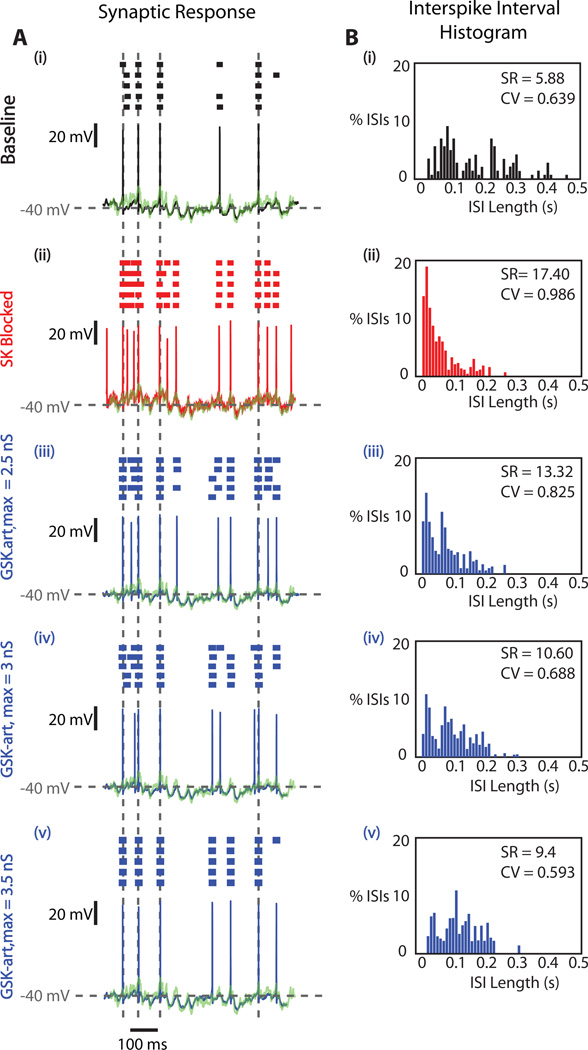
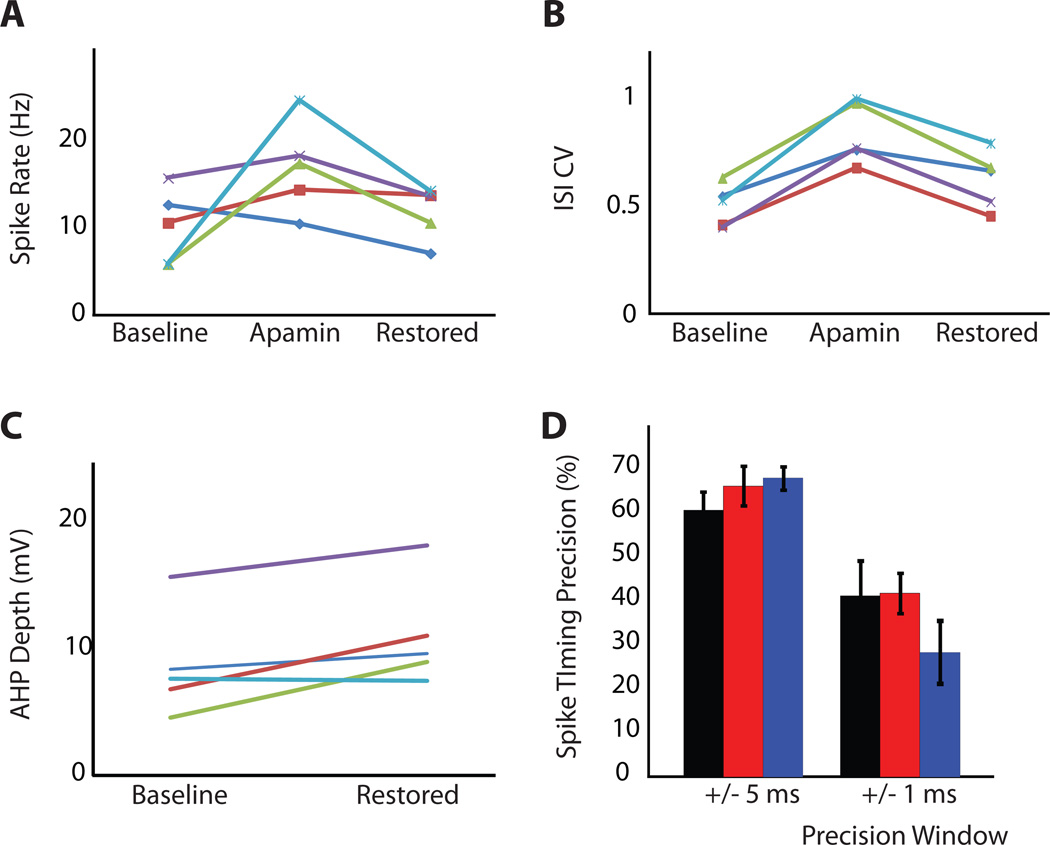
As depicted in Fig. 6 for a single neuron, the responses to PC input patterns began to resemble the original pre-SK block pattern as an increasing amount of G_SK-art was applied. For a value of 3.5 nS maximal G_SK-art responses to large depolarizing transients in the synaptic input (indicated by vertical grey dotted lines in Fig. 6A) had fully reverted from spike bursts to single spikes (Fig. 6A(v)) and were similar to the pre-apamin baseline case (Fig. 6A(i)). The ISI histogram distributions (Fig. 6B) for an entire 10 s stimulation period also demonstrated a reversal towards the pre apamin block data as increasing amounts of G_SK-art were applied. Notably, the CV decreased from its peak value with apamin block close to its pre- SK block low and the SR decreased as well, although it did not quite reach the pre-SK block value. These effects were consistent in a set of 5 BS cells recorded with the full set of stimulus conditions (Fig. 7). In each cell the amount of G_SK-art was adjusted to result in best matches with the pre-apamin spike responses based on on-line visual response inspection. This manipulation resulted in a range of G_SK-art application from 2.5 to 4.5 nS (mean = 3.48 ± 0.78 nS, N=5). In all cells the SR was reduced with G_SK-art and in most cells came close to the pre-apamin rate (Fig. 7A, mean control SR = 10.2 Hz, mean restored SR = 11.9 Hz, p = 0.52, paired t-test). The significant increase in CV of spiking induced by apamin application (control CV = 0.51, apamin CV = 0.84, p = 0.002, paired t-test, N=5) was almost fully reversed by G_SK-art (Fig. 7B, restored CV = 0.63, p = 0.13, paired t-test, N=5). The spike precision remained high throughout apamin application and restoration with dynamic clamping (Fig. 7D), and did not differ significantly between conditions for a precision window of either 5 ms or 1 ms (Fig. 7D, P > 0.1; paired t-test, N=5). Thus, a comparable level of synaptic control of spike timing was maintained throughout. Interestingly, these values of synaptic response matching were achieved with a level of G_SK-art that resulted in somewhat deeper mAHPs than the intrinsic SK current had showed (Fig. 7C, control AHP depth = 8.7 mV, restored AHP depth = 11.2 mV, p = 0.048, paired t-test, N=5) despite a remaining slight elevation in SR in several cells. This finding may point towards some amount of intrinsic SK conductance in an axonal spike initiation zone that needed to be compensated with an increased amount of somatic G_SK-art.

Figure 6. Recovering the Synaptic Response Function with G_SK-art after SK block.

A: Stimulus aligned voltage responses of a BS neuron to the input pattern applied via dynamic current clamp before apamin presentation (black), after apamin presentation (red), and with G_SK-art added (blue) after apamin application at multiple levels of maximal conductance (G_SK-art,max). Raster plots are shown above each voltage trajectory and E_syn is shown in green. The SK-blocked response patterns resembled the baseline patterns most closely for the G_SK-art,max level of 3.5 nS (iii). This is particularly noticeable at the time points indicated by the dotted grey lines, as apamin-induced bursting responses were greatly reduced by the insertion of G_SK-artB: ISI histograms of the neuron’s response patterns from (A). After apamin superfusion, the ISI distribution shifted towards the left, as a result of the high frequency burst responses. The percentage of the shortest ISIs decreased with the increasing levels G_SK-art,max.

Figure 7. Recovery of the original behavior with G_SK-art.

A: SR during synaptic input applied via dynamic clamp increased after SK block and decreased after the insertion of G_SK-art. Each line corresponds to one BS neuron. B: ISI-CV during synaptic input also increased after SK block and decreased after the insertion of G_SK-art C: The mAHP depth observed during spontaneous activity was restored by the insertion of G_SK-art. After SK block, the intrinsic mAHP depth was reduced to nearly 0 mV (not shown). D: Spike timing precision during synaptic input before (black) and after superfusion of 100 nM apamin (red) and following insertion of G_SK-art (blue) for precision windows of +/−5, +/−3, and +/−1 ms. Precision is not significantly affected by the presence or absence of SK current.

Overall, these results indicate that a spike-associated inflow of calcium via HVA calcium channels and the SK conductance triggered by this calcium inflow is fully sufficient to account for an important gain shift in the synaptic transfer function

DISCUSSION

Previous studies have highlighted the involvement of SK current in excitatory synaptic processing at the site of the synapse itself; and a significant SK contribution to EPSP reduction has been shown in hippocampal pyramidal cells [42, 43]. This contribution could be modulated through SK downregulation via cholinergic M1 receptor activation [42, 43]. In cerebellar Purkinje cells SK current reduces excitability, regularizes the spike trains, and reduces dendritic calcium transients [44–46], and this effect could be reduced by SK downregulation via parallel fiber LTP induced excitability plasticity [46]. This excitability plasticity was in part mediated by protein phosphatase 2B (PP2B), and another study recently showed that PC specific PP2B knockout mice exhibit increased regularity in PC spiking as well as deficits in motor learning [47].

We addressed for the first time the question of how SK current may be involved in the control of spiking mediated by GABAergic synaptic inhibition, which in the CN provides the only pathway of information transfer from the cerebellar cortex. In previous dynamic clamp studies we showed that synchronized Purkinje cell spiking resulting in strong transients in CN input conductance in particular could effectively control CN SR as well as spike time precision [5, 26]. Here we used the identical stimulus configuration in order to address the effect of SK conductance on synaptic coding. As seen in many other cell types [38, 48, 49] and in CN neurons [19, 41] before, SK block with apamin resulted in the abolishing of the mAHP waveform and in highly irregular or burst firing. When we applied in-vivo like synaptic PC input patterns, the effect of the abolished mAHP waveform was an enhanced spike response to synchronization in PC inputs. Spike synchronization in vivo could occur due to various processes. Synchronous pauses in PC activity have been found in anesthetized rats and hypothesized to be a potential code for PC to CN signal transmission [5, 7, 50]. Synchronized spiking followed by pauses would also occur due to precise complex spike synchronization taking place in cerebellar cortex [17, 18]. A reduction of SK would therefore increase the gain of these modes of transmission. Less synchronous PC activity results in a more steady-state inhibitory synaptic conductance, and in fact weak input transients were not amplified in our data, pointing to a selective enhancement of strong input transients by a reduction in SK current. We termed our dynamic clamp synaptic input ‘in-vivo like’ [5, 26] because it consists of a constant barrage of synaptic input creating a high-conductance state with important consequences for cellular dynamics as also described in neocortex[51, 52]. It should be noted, however, that we chose a synthetic approach to construct PC spike trains in which different degrees of synchronization were superposed on a completely random Poissonian background. Thus, additional aspects of PC activity modulation that might be present in awake animals during behavior, such as strong coordinated rate changes or synchronized climbing fiber responses, could elicit response mechanisms at the level of the CN not seen in the present study. The most obvious of these is given by rebound dynamics following strong inhibitory transients. However, the presence of synaptically evoked CN rebounds in behaving animals is currently under intense debate [15, 53–55] and remains uncertain. The same uncertainty could in fact be stated about the presence of precise PC synchronization in vivo or the presence of other mechanisms generating synchronized PC pauses in awake animals that have been observed in anesthesia [7]. Beyond a reasonable degree of confidence that rate coding does in fact work and take place in the cerebellar cortico-nuclear connection [4, 56, 57] we actually know very little about population coding in the cerebellum, and this study might best be taken as a pointer that such considerations are of vital importance in order to determine cerebellar function and more experimental work should be dedicated towards synchronous recordings from multiple PCs during behavior.

A high degree of spike time precision of CN responses to PC input was maintained at all levels of SK, indicating that PC input can effectively control CN spike patterns regardless of SK current. While apamin block without burst suppression actually lead to an increase in the level of precision, this effect was not seen when apamin induced burst activity was suppressed. We did not investigate how bursting activity may reduce subsequent spike time variability, and this effect is not likely to occur in vivo where SK reduction would occur gradually without induced strong burst patterns. The high spike time precision levels we found are in accordance with our previous dynamic clamp studies, and suggest that synchronously patterned PC activity can support a temporal output code from the CN [5, 26, 27].

While we did not pursue the question of which signaling pathway in CN neurons results in a reduction of SK current, the presence of such pathways in other cell types by protein phosphatases linked to cholinergic transmission [42, 43], LTP induction [46] or metabotropic receptor activation [58] points to a likely plasticity of SK current in CN neurons as well. In fact, while recordings from young rodents (<20 days) show a relatively consistent large mAHP amplitude, the results for adult mice are more variable (see supplemental materials) and often the mAHP was near absent in adult mouse CN during spontaneous pacemaking. This observation favors the speculation that in young pre-weanling animals a high level of SK current promotes responsiveness to small input transients while preventing burst responses, whereas in adult animals excitability plasticity has stabilized large responses to functionally relevant large input transients originating from behaviorally meaningful synchronized PC activity.

We made the unexpected observation that apamin induced burst firing itself in CN neurons leads to a reduction of general excitability, which our computer simulations suggest could be due to an increased outward bias in the mean intrinsic currents. This additional apamin induced excitability regulation resulted in a change of the synaptic response function, such that small input transients failed to trigger any spike responses. The combined effect of reduced excitability and increased responsiveness to large input transients is best described as tuning a synaptic response contrast function, in that the contrast between responses to small and large input transients was highly increased after apamin when cells were allowed to burst. The question of whether intrinsic downregulation of SK conductance would also result in an overall reduction in excitability by a tonic increase in outward bias remains to be addressed. However, many if not all cell types show homeostatic plasticity of spike rates such that regulatory processes counteract a tonic increase in spike rate [59, 60] and can be mediated by the adaptive regulation of a voltage-insensitive K⁺ current [61]. In fact the rapid onset of reduced excitability with apamin induced bursting may present just a exaggerated form of such an otherwise more gradual process. Apamin induced bursting could also lead to increased calcium levels and a consequent increase in BK calcium-dependent K⁺ current, which has been recently shown to regulate the excitability and firing rate of CN neurons [62].

The strong involvement of SK current in shaping the synaptic spike response function is overall another clear example that intrinsic dynamic properties of neurons make an important contribution to network processing [63–66], and should be carefully considered in network simulations of neural function. The direct consequences of SK function for motor control remains to be determined. Our results suggest that a general gain increase in responsiveness of cerebellar circuits could be mediated by cell-specific SK downregulation, which would allow selective activation of learnt behaviors. Recently it is becoming clear that considering the detailed mechanisms of intrinsic channel properties and their regulation is also important in understanding and treating neural dysfunction [67]. Several specific mutations in Purkinje cell channels such as P/Q type Ca channel mutation in tottering mice [68], or ataxia resulting from NaV 1.6 [69] or large-conductance voltage- and calcium-activated potassium (BK) channel [70, 71] knockout result in altered patterns of PC activity that notably include reduced firing rates and rhythmic bursting. Pathological PC bursting and synchrony also underlies some forms of cerebellar dystonia [72, 73], which in turn results in enhanced bursting in CN activity [74, 75] as would be expected from our results as well. The SK current has been implicated as a potential modulator of cerebellar ataxia, and enhancing SK current with a pharmacological activator reduces disease symptoms [76, 77]. This effect could be in part mediated by a reduction of burst responses in the CN that are induced by the pronounced PC synchronization in these disorders. Therefore, previous work in conjunction with our new results point squarely at the SK current as an important regulator in the synaptic processing of normal and dysfunctional cerebellar output and SK activators as a promising drug target for disorders with abnormally high response gains.