On the evolution of intergenerational division of labor, menopause and transfers among adults and offspring

Abstract

We explain how upward transfers from adult children to their elderly parents might evolve as an interrelated feature of a deepening intergenerational division of labor. Humans have a particularly long period of juvenile dependence requiring both food and care time provided mainly by younger and older adults. We suggest that the division of labor evolves to exploit comparative advantage between young and old adults in fertility, childcare and foraging. Eventually the evolving division of labor reaches a limit when the grandmother's fertility reaches zero (menopause). Continuing, it may hit another limit when the grandmother's foraging time has been reduced to her subsistence needs. Further specialization can occur only with food transfers to the grandmother, enabling her to reduce her foraging time to concentrate on additional childcare. We prove that this outcome can arise only after menopause has evolved. We describe the conditions necessary for both group selection (comparative steady state reproductive fitness) and individual selection (successful invasion by a mutation), and interpret these conditions in terms of comparative advantages.

1. Introduction

This paper considers the evolution first of menopause, and then of upward transfers from younger to older adults, and offers a formal analysis of how these rare phenomena among species can arise along with the evolution of an intergenerational division of labor. In East Asian cultures upward transfers of this sort are referred to as “filial piety,” a term we will use as a convenient shorthand in what follows.

The behavior pattern in which young adults support and make sacrifices for their old parents may be unique to humans. In modern human societies much of the wealth is held by the older generation, so one might wonder whether adults' upward transfers to their old parents are merely in exchange for the old parents' anticipated bequest or inter-vivos gifts (Cox, 1987). But the fact that people were willing to sacrifice resources to bury their parents thousands of years ago when life was so difficult suggests that emotional factors are involved, which may have arisen from evolutionary forces. Could evolutionary selection sustain an emotional drive for costly care of the elderly during their lives? Other factors surely contributed to its emergence in various cultures, and our analysis also suggests that this would be advantageous, but we will argue that biological forces also played a role.

What about contemporary societies? According to the National Transfer Accounts project (Lee and Mason, 2011), a large cross-national study of both public and private intergenerational transfers, in a number of Asian countries with relatively weak public pension programs net private transfers flow upwards from younger adults to the elderly. Although in most other countries the elderly age 65 and over make net downward private transfers to younger people, above age 75 the elderly are increasingly likely to receive net private transfers. In all rich countries and many poor ones, pervasive public sector support for the elderly (pensions, health care and long term care) obscures private motivations (Lee, 2013). Yet these public programs are themselves arguably an expression of filial piety, and they render private upward transfers largely redundant. Perhaps most relevant are practices in hunter-gatherer societies, which we will discuss later.

From an evolutionary point of view, the emergence of menopause also requires an explanation because natural selection would not forfeit a female's fecundity unless her sterility somehow favored her genes, and hence the grandmothers' menopause must be connected to some indirect help they provide to their offspring. One theory (Williams, 1957) suggests that menopause evolved because the mortality risks of childbearing at older ages threatened the survival of younger offspring still dependent on maternal care, although later studies discount this possibility (Shanley and Kirkwood, 2001; Rogers, 1993; Hill and Hurtado, 1996). Another theory argues that post-reproductive individuals continue to promote the survival and reproduction of their offspring and grandoffspring, thus raising their own extended fitness, leading to selective pressure for their continuing survival. Were older individuals still reproductive, they would be less able to lend this material support to their descendants. The grandmother hypothesis is the leading version of this theory (Hawkes et al., 1997). Here we will give a rigorous analysis of the conditions necessary for menopause to evolve in this way.

Similarly, young adults' devoting resources to old parents (filial piety) also requires an explanation. However, finding an explanation here is more difficult: the post-reproductive survival of a grandmother helps the contemporary grandchildren, whereas a young adult who provides an upward transfer incurs a reduction in her reproduction without any immediate gain; hence a genetic mutation for filial piety could hardly invade successfully. Our analysis must find a way to resolve these difficulties.

While filial piety may be a phenomenon we observe only in humans, several other mammals also have long post-reproductive survival (PRS), including short-finned pilot whales and killer whales (Cohen, 2004; Mann et al., 2000; Levitis, 2009; Levitis and Bingaman-Lackey, 2011). Sperm whales and some other whales appear likely to have long PRS, but this has not been proven. To explain why a few species have menopause and humans have both menopause and filial piety, the argument must involve characteristics that are particular to these species. We will suggest that an intensive division of labor and a long period of juvenile dependency are the two keys behind the evolution of both menopause and filial piety, and that these two evolutionary events occur in a particular order.

Several scientists (Carey and Gruenfelder, 1997; Sherman, 1998; Peccei, 2001) have discussed menopause and PRS in non-human species. Carey and Gruenfelder studied the case of post-reproductive dolphins and whales, in which the older males or females appear to guard or train their offspring, allowing the younger parents to forage. The exact relations between the adults and young for these species are not clear (Mann et al., 2000), but we do know that babysitting and guarding the young interfere with foraging by the adult and thus are costly. If prey is then shared with the babysitting older adult, that would exemplify filial piety in a non-human species, but we know of no evidence that this occurs. Sperm whales are known to bring squid parts to the surface, but it is not known whether babysitting elders consume them. For hunter-gatherer humans, child care is often done by the mother, while the post-reproductive grandmother, grandfather and perhaps other relatives forage and provide food for the mother (Williams, 1957; Rogers, 1993; Hill and Hurtado, 1996; Hawkes et al., 1997; Peccei, 2001; Shanley and Kirkwood, 2001; Kaplan and Robson, 2002; Lee, 2003, 2008; Hawkes, 2003; Gurven and Kaplan, 2006; Kaplan et al., 2010, see also Pavard and Branger, 2012, for preindustrial populations). The broader sharing of work beyond mothers and daughters for humans is consistent with our modeling approach, which assumes that intergenerational transfers are constrained by the average population age distribution in a cooperative breeding group rather than by particular relationships (Hrdy, 2009; Sear and Mace, 2008; Hill and Hurtado, 2009).

The remainder of this paper is arranged as follows. Section 2 describes three different stages of the division of labor, and helps the reader grasp the conceptual idea of our later analytics. Section 3 presents the mathematical model of overlapping generations, and analyzes the equilibrium of cooperative breeding. The fourth section moves on to discuss the first phase of the division of labor, and how evolution can facilitate its realization. Sections 5 and 6 discuss the second and third phases of the division of labor, resulting in menopause and filial piety respectively. The last section provides conclusions and discussions.

2. Evolution of division of labor: three stages

Here we set up a life history model in which age-specific fertility and survival are “choice” variables, that is, subject to natural selection and evolution. For the species we consider, children (the term we use for all pre-adult offspring of any species) need to receive transfers of food and inputs of adult time to survive and grow. Their probability of surviving to adulthood depends on these adult transfers of food and time. The opportunity cost of the parental time spent caring for children is the foregone food from hunting/foraging (henceforth foraging). Given this opportunity cost structure, we explore the possibility of an intergenerational division of labor and explain how the division of labor may evolve as various corner solutions are reached. We suggest that our analysis can explain the evolution of two important features of human life history: menopause and filial piety.

We consider a cooperative breeding species in which the younger and older adults provide energy and time inputs to the children jointly.³ From an evolutionary perspective, however, the objectives of these “cooperative” adults diverge: in a two-sex model, a mother cares about her children and her nieces differently, and if the grandmother and mother both have new-born children, the mother will treat her child and her new-born sister the same only when the mother and her sister have the same father. Because of this divergence in objectives among agents, the base-line structure of cooperative breeding we consider is, in fact, the equilibrium of a non-cooperative game, where each adult provides their share (of time and energy) to the co-residing group without any coordination, and the pool is shared by all children evenly. Basic economics tells us that there will be some inefficiency in this scenario, for each adult may have the incentive to free-ride on other adults, and let others support the common pool. The Nash equilibrium of this non-cooperative game involves a strategic combination of adults at various ages where each agent chooses her optimal contribution simultaneously but independently, given other agents' choices.

Going beyond this base-line structure, we consider evolutionary forces that may change this inefficient base-line structure, leading to an intergenerational division of labor between adults of various ages. Because there are two tasks (childcare and foraging-hunting), as long as there are comparative advantages in these tasks among co-residing family members of different ages, it is more efficient for different age groups to carry out different tasks (Gurven and Kaplan, 1996). In other words, from the perspective of an optimal life history, a division of labor will generate a larger Euler–Lotka parameter. Horan et al. (2005) argued that division of labor and trade were the main reasons why human beings drove away Neanderthals, a species with larger body and brain size. We will show that if there is a strong demand for transfers of both food and care time for children, a mutation that causes a change in the division of labor between foraging care time across ages may successfully out-compete the wild type gene line. Thus evolution will indeed tend toward an efficient first stage division of labor.

The crux of our reasoning is that since an agent is at a Nash equilibrium, she unilaterally chooses a strategy that maximizes the expected reproduction of her own gene line or of her gene line adjusted for relatedness. Calculus tells us that around this maximum a unilateral marginal change of life-history choices along the boundary of the feasible set does not change the fitness, and this implies that a mutant's own fitness does not decline. In the next period when this mutant has adult children of her own, the situation may improve because she and some of her children complete the division of labor jointly, and thereby may produce more offspring. This conclusion is qualified by the assumption that the number of other wild-type individuals in the cooperative breeding group, who may take advantage of the efficiency gains from the division-of-labor mutants, is relatively small.

When the division of labor between care-time and foraging advances, it eventually will reach a state where further sharing of tasks is not possible. Specifically, either the grandmother cannot do more child care or the mother and her sisters cannot do more foraging. However, we will show that this constraint on the division of labor can be reached only after some corner solutions of choice variables have been reached first. This corner solution is likely to occur when the grandmother's fertility is pushed to zero. This is what we call the second stage division of labor. We show that if the efficient division of labor requires more care time from the grandmother, then she would have to reduce her fertility in order to further reduce her foraging time. The exercise at this stage is to see whether a further division of labor would be efficient, and whether evolution can make it happen. We show that even if the condition for sustaining an efficient group division of labor is satisfied, an individual mutation for this efficient division of labor may not be selected. We then derive the conditions under which an individual mutation could successfully invade and be selected, which basically requires that the benefit created by the partial-task-sharing between the grandmother and some of her adult children is not compromised by the existence of other adult children and co-residing members who do not carry this mutation and continue to share tasks in the old way.

The young of many species are dependent on energy transfers from other adults, typically the mother. When the young also require intensive adult time for care such as guarding, warming, ventilating, or training, then the possibility arises of an intergenerational division of labor. We argue that the evolution of both menopause and filial piety is driven by this intensive demand. It is possible that when the need for adult support is very strong, even a corner solution for grandmaternal fertility is not enough. At this stage, the grandmother has already reduced her fertility to zero (menopause), and she uses a small amount of her time to forage to sustain her own survival while devoting her remaining time to child care. However, if the children still would benefit from more grandmaternal care time, she can provide it only if someone else provides the energy needed for her sustenance, and this “someone” is likely to be her adult children. We call this transfer from adult children to the grandmother an “upward transfer.” This is the third stage division of labor.

This upward transfer, however, would be a more difficult evolutionary step in the division of labor than the previous two. If young adults were to provide upward transfers, these would represent an immediate loss of energy, and the donors' fitness index would be likely to decline if the energy-recipients were genetically different than themselves. For this reason a mutation of this sort would be unable to invade the wild gene line. In terms of calculus, giving away energy is not moving along the budget hyperplane, therefore our original reasoning cannot hold. If a mutation for this upward transfer did occur, all the mutant would get in return for giving away her energy is the expectation of receiving the same upward transfer from half of her own adult children (who inherit the mutation) in the next period. But since the mutant already gave away energy in the present period, her own fitness would decline. Upward transfers of energy from adult children to grandparents are called “filial piety” in many cultures. Despite these difficulties, we will explain how filial piety may have evolved.

Suppose that the grandmother already has reached menopause, so that her period of post-reproductive survival is used only to care for her grandchildren. Then all the energy she acquires through foraging is by definition used to sustain her own survival. In this case, any extra upward transfer to her only relaxes her energy constraint, and thereby enables her to provide more care time. In other words, since a post-reproductive female does not have any life purpose of her own in the evolutionary sense, the extra energy she receives can be used only for her grandchildren. This is why a mutation of filial piety can invade in this situation. We therefore argue that the prior evolution of menopause is a precondition for the evolution of filial piety.

Fig. 1 provides a schematic representation of these steps in the intensification of the division of labor, and the order in which they occur.

Fig. 1.

Stages of the division of labor. 0 (No. division of labor): coresiding adults choose their time allocation (foraging and child-caring) as if they play a non-cooperative Nash game. 1 (Pure division of labor): an age-specific division of labor occurs, with the age-1 devoting more time to foraging and the age-2 devoting more time to child-care. 2 (Menopause): a further division of labor occurs, when the age-2 becomes sterile and thereby avoids the energy expenditure of giving birth. This enables her to switch more time from foraging (generating energy) to child-care. 3 (Filial piety): a further division of labor occurs, when the age-2 reduces or stops foraging to acquire energy for her own subsistence. This enables her to switch even more time from foraging to child-care.

3. An overlapping generations model

Since the implementation of an intergenerational division of labor by definition involves overlapping generations, our simple model of optimal life history explicitly characterizes the species' age structure, along the lines of Samuelson (1958). In our discussion of group selection, we do not have to emphasize two-sex reproduction, hence we mainly consider the life history of females and use terms such as “her,” “she,” and “sisters.” In our discussion of individual selection, spelling out a two-sex reproduction structure is necessary, and we will be more specific in using terms.

Consider a species whose members live either one, two or three periods. We need at least one period of child growth to justify adult care, and we need at least two potentially fertile periods in order to make the possible survival past the menopausal age meaningful. Thus we require at least three age groups for our analysis. The first age is spent growing prior to maturity with zero fertility, and the following two mature ages are potentially fertile. This three-age setting is, of course, a simplification rather than a premise of our analysis.

In models of life history in which growth as well as fertility and mortality are endogenous, it has been shown that if the energy budget constraint is linear, then the optimal life history has an initial stage of positive somatic growth while fertility is at the zero corner, followed by a second stage of positive fertility while somatic growth is at the zero corner (Taylor et al., 1974; Vaupel et al., 2004). This pattern, which is approximately characteristic of mammals and many other animals, is called determinate growth. Although for simplicity we do not include explicit somatic growth in our analysis here, we nonetheless impose zero fertility as a prior constraint for the first age group. If it is optimal to have zero fertility in old age together with a positive probability of surviving to that age, then we have an adaptive menopause with postre-productive survival.

3.1. Age-specific energy constraints

In our notation a = 0, 1, 2 will refer to the age interval [a, a + 1). “Child” refers to age 0, “young adult” to age 1, and “old adult” to age 2. The probability that a person survives from age a to age a + 1 is denoted p_a, a = 0, 1. The number of births per female at age-a is denoted m_a.

Adults at ages a = 1, 2 are endowed with 1 unit of time which they allocate between care-time (t_a) and foraging (1−t_a). We will measure this unit of time as net of the minimum necessary time commitment by the mother for lactation so that the lower bound of t_a is zero. Given production efficiency θ_a (a = 1,2), adults can acquire an amount of energy from foraging given by θ_a · (1−t_a). The energy will be used in several ways: maintenance for surviving to the next age if possible (p_a), reproduction (m_a), transfers to children (T_a) and transfer to other adults (F_a). We will explain these item by item below.

The survival probability p₁ depends positively on the amount of energy devoted to bodily maintenance and repair at age 1. Here we will assume a linear relationship; for a more general approach, see Chu et al. (2008). Let b₁ be the energy required to achieve a one-unit increase in p₁, so that b₁p₁ is the total energy needed for an individual to obtain a survival probability p₁, where p₁ is between 0 and 1. The end of age-2 is assumed to be the upper bound of life, hence p₂≡0, and individuals do not invest in further survival. The specification of p₀ will be discussed shortly. Let c_a be the linear cost coefficient associated with fertility, so the energy devoted to fertility is c_am_a, a = 1,2. This linear structure of energy consumption is also found in Abrams and Ludwig (1995), Cichon (1997), Vaupel et al. (2004), and Chu and Lee (2006).

In addition to the energy costs of fertility and survival, there is a fixed cost of living and preserving functionality at each adult age, E₁ and E₂ resp. Without this expenditure of energy, an adult might survive but would not be able to perform the functions of fertility, child-care or energy acquisition. If E_a = 0, individuals aged a could care for their grandchildren with no energy intake at all, which is not reasonable. Finally, we assume that a child is unable to forage (acquire energy), so her energy comes entirely as transfers from adults.

The last possible energy use is downward transfers by adults. Note that since the age-2 grandmother and the age-1 mother share only half their genes in a two sex model, in general it does not make sense for them to transfer energy to one another. In most of our discussion the only transfer age-a adults will provide is T_a, which goes into the common pool for the survival of co-residing children. However, we will show later that a transfer between adults will evolve in some special cases.

Leaving aside the possible energy transfer between adults, the energy budget constraints for age-1 and age-2 can then be written as

$$E_1+b_1{p}_1+c_1{m}_1+T_1={\theta }_1·(1-t_1)$$ (1)

$$E_2+c_2{m}_2+T_2={\theta }_2·(1-t_2).$$ (2)

In (2) there is no energy expenditure on prolonging survival for age-2 because by assumption that is the maximum age to which an individual can survive.

3.2. Child survival probabilities

The probability of child survival, p₀, depends on inputs per child of parental care-time and energy transfer (food). To calculate food and care time available per child, we first have to specify the resource pooling structure. Note that in a 2-sex model with three generations, the genetic relationships may be very complicated as we will discuss later. For analytical purposes, we assume that at a given time the coresident members consist of N₂ age-2 members (grandmothers), N₁ age-1 sisters (mothers), and their N₀ newborn age-0 children. In this cooperative breeding group, the role of males is assumed away. This assumption can be justified if males only provide genes, and after mating they do not participate in hunting or rearing activities (Chu, 2010).

Given that there are N₂ age-2 and N₁ age-1 cooperatively breeding adults, the aggregate care time in this group is N₁t₁ + N₂t₂, and the aggregate energy transfer is N₁T₁ + N₂T₂. Ignoring the possibility that some child care may have the property of public goods, each child gets an equal share of this energy and care time. Child survival probability p₀ is then specified as

$$p_0=f(\frac{N_1{T}_1+N_2{T}_2}{N_1{m}_1+N_2{m}_2},\frac{N_1{t}_1+N_2{t}_2}{N_1{m}_1+N_2{m}_2}).$$ (3)

3.3. Absolute and comparative advantages

We assume that c₁ < c₂, which implies that young females can produce babies more efficiently than older females, for example, due to higher quality eggs for younger mothers, fewer miscarriages, faster conception, and lower risks to the mother's health (Kaplan et al., 2010 discuss additional factors). This is an “absolute” advantage for the young. We also assume that θ₁ > θ₂, meaning that young females are more efficient in producing food (Kaplan et al., 2010 report that peak foraging productivity per hour occurs in the mid-40s for both men and women in two hunter-gatherer groups, the Ache and Tsimane). These assumptions appear to be realistic for humans, but they are not necessary for our results. We make these assumptions only for simplicity of analysis and clarity of expostion.

However, Ricardo (1817) advised us long ago that as long as there are comparative advantages, it would be more efficient to have a division of labor between the young and old adults. What is necessary for our results is that young adults have a “comparative advantage” in production relative to old adults, in the sense that θ₁/c₁ > θ₂/c₂. Older adults could be more efficient both in fertility and in production, and our results would still follow provided that the advantage of older over younger in fertility was greater than the advantage in production.

Note that these parametric assumptions could be reversed, and none of our arguments would be affected, except that the pattern of the division of labor between ages 1 and 2 would be changed. The key question is whether an efficient division of labor between young and old adults may arise from evolution.

The order of events is assumed to be as follows. At the beginning of a period there are (N₀, N₁, N₂) individuals in the population. Suppose an adult reserves t_a of her time for possible child care. The remaining (1−t_a) of time generates θ_a · (1−t_a) energy from foraging. This energy is then allocated to various uses. The survival probabilities p₀ and p₁ are then determined. Given these survival probabilities (p₀, p₁), p₀N₀ and p₁N₁ individuals survive to bear children in the next period. So the next period starts with a population vector (m₁p₀N₀ + m₂p₁N₁, p₀N₀, p₁N₁). It is a well-known theorem in demography (Leslie, 1945) that these dynamics will converge to a stable population.

3.4. Individual interactions and Nash equilibrium

Suppose a group of individuals faces the constraints in (1)–(3). To model evolutionary group selection, one often assumes that the species maximizes reproductive fitness as measured by the steady-state Euler–Lotka parameter, subject to the constraints of (1)–(3). In our two sex model, however, mother and daughters have different genes and hence different fitness measures as objectives. Therefore, to analyze individual selection, one has to discount different offspring by gene relatedness. For instance, if a female's children are valued 1/2, then her sisters' children (nieces) will be valued 1/4.

To simplify our algebra we assume that in terms of relatedness there are only two adult gene types in a family, with fitness objective functions ϕ₁ and ϕ₂ respectively, which attach different fitness values to the life history traits and behaviors of individuals in the group. For a more explicit development of these fitness objective functions, see Chu and Lee (2012, Eq. (2), p.357). This will be the case, for instance, if a mother who is approaching age 2 disperses to found a new stem family with all her surviving offspring. She will become the age-2 grandmother in this new stem family, and the age-1 group will be her adult children. As Pennisi (2009, p. 1197) pointed out, “for most human history, small related groups were the norm.” Relaxing this assumption would not yield new insights, but would make the algebra more tedious. Later we will discuss how more complicated genetic configurations would affect the evolutionary pattern of the division of labor.

Let the control variables for age-1 be a vector X₁ = (p₁, m₁, t₁, T₁) and those for age-2 be X₂ = (m₂, t₂, T₂). Note that ϕ₁ and ϕ₂ are affected by both X₁ and X₂ because of the cooperative breeding constraint (3). Even among the age-1 sisters (mothers), their objectives are different, for they only share 1/2 their genes. For analytical purposes, we sometimes spell out our X₁ vector as X₁ = (X₁₁, …, X_1k) if there are k sisters residing together, where X_1j is adult j's control vector. For each age-1 mother j, her selfish gene seeks to maximize ϕ₁(X_1j, X_1j′, X₂) over X_1j, subject to (1) and (3), given others' choice of X_1j′ and X₂, where j′ refers to age-1 adults other than j. For the age-2 grandmother, her objective is to maximize ϕ₂(X₁, X₂) over X₂ subject to (2) and (3), given the age-1's choices of X₁.

In this cooperative breeding group, as we mentioned, members are actually playing a non-cooperative game, mainly because there is no ex ante coordination between members. A Nash equilibrium is characterized by a vector of strategies $(X_1^{*},X_2^{*})$ among these members such that ${\varphi }_1(X_{1j}^{*},X_{1j\prime }^{*},X_2^{*})\ge {\varphi }_1(X_{1j},X_{1j\prime }^{*},X_2^{*})$ ∀X_1j satisfying (1) and (3), ${\varphi }_2(X_1^{*},X_2^{*})\ge {\varphi }_2(X_1^{*},X_2)$ ∀X₂ satisfying (2) and (3). However, a coordinated deviation from $(X_1^{*},X_2^{*})$ may improve both ϕ₁ and ϕ₂.

As long as $X_1^{*}$ and $X_2^{*}$ are interior solutions, the first order conditions for such a Nash equilibrium indicate that

$$d{\varphi }_1(X_1^{*},X_2^{*})\equiv {\varphi }_1(X_1^{*}+d{X}_1^{*},X_2^{*})-{\varphi }_1(X_1^{*},X_2^{*})=0$$ (4)

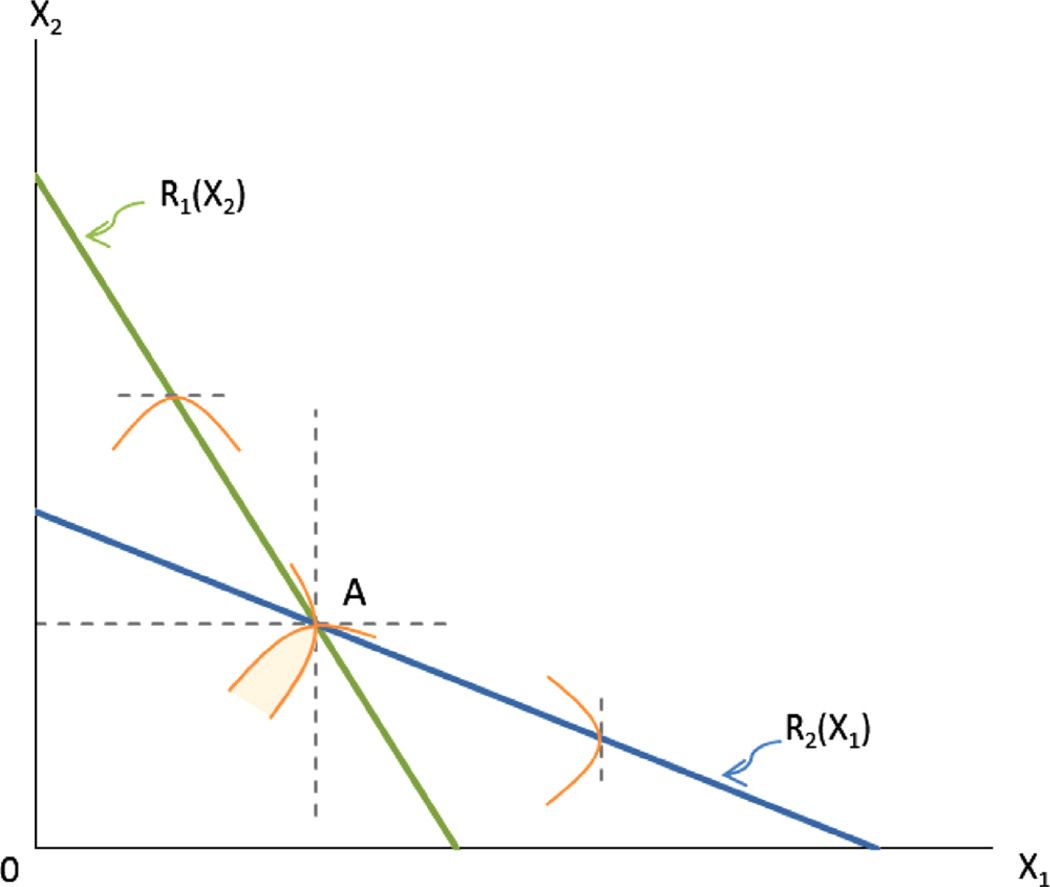
for variations of dX₁ around the neighborhood of $X_1^{*}$ along the hyperplane spanned by (1) and (3). Similarly, we also have $d{\varphi }_2(X_1^{*},X_2^{*})=0$ for variations of dX₂ around the neighborhood of $X_2^{*}$ along the hyperplane spanned by (2) and (3). In Fig. 2, we draw the best-response functions for individuals 1 and 2, R₁(X₂) and R₂(X₁), for the case when the choice variable is one-dimensional. As one can see, any unilateral marginal move by age-a around $(X_1^{*},X_2^{*})$ does not affect age-a's fitness, but a joint move into and through the shaded section improves the fitness of both ages. A move to the noncooperative equilibrium A in Fig. 2 can be achieved through natural selection acting on a series of mutations which affect X₁ or X₂ separately. By contrast, natural selection acting on mutations that cause simultaneous deviations in both X₁ and X₂ in ways that deepen the division of labor can move the species into the shaded fitness area, mimicking cooperative behavior.

Fig. 2.

The straight lines indicate the choices of X that an age 1 or age 2 individual would make in response to a choice by the other. Where the two lines cross at point A the responses would be consistent with both individuals continuing to choose the X values that define point A, so A is a Nash equilibrium. The curved lines are isofitness lines for Ages 1 and 2 individuals, derived from the ϕ₁ and ϕ₂ fitness functions. Higher fitness values are found closer to the axes. At point A, any small unilateral change in X₁ by the Age 1 individual or in X₂ by the Age 2 individual would leave the fitness of each unaffected where as a larger move would reduce fitness, since their isofitness curves are tangent to the vertical or horizontal axes at A. Without cooperative action, the system will settle at point A. With cooperative choices, which in our case would be governed by an appropriate mutation affecting the choices of both younger and older adults, Age 1 and 2 individuals could both achieve higher fitness by moving toward the origin within the shaded area. We might think of A as the equilibrium in which Age 1 and Age 2 individuals are each fertile and each feeds and cares for her own offspring. However, with specialization and division of labor, both can achieve higher fitness by assisting one another according to their age-specific comparative advantages.

4. Moving toward the division of labor

We now investigate whether a division of labor between age-1 and age-2 that improves child-rearing efficiency can arise as a result of evolution. Note that individuals make their choices independently in this common-pool Nash game, so there is no coordination between these co-residing members. For instance, if the foraging time and caring time of an age-1 individual are altered, the new values must still conform to (1), and similarly the age-2 individual's adjustment must conform to (2).

4.1. Sexual Diploid Reproductions

We assume that individuals' age-specific strategies (X₁, X₂) are controlled by genes. For sexual diploid species, every individual carries two genes at each locus, one from the mother and one from the father.

Suppose that the wild type population has reached an equilibrium consisting of homozygotes at a locus governing the traits of interest, here X₁ and X₂. All of them have the gene pair (a, a) while a mutant has (a, A). If a mutant mates with a wild type, the genetic type for children is determined by the following matrix:

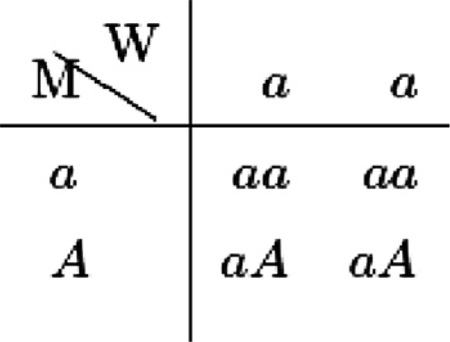where W refers to wild type and M indicates mutation.

The wild type is assumed to be at a Nash equilibrium, and its chosen strategy is denoted $(X_1^{*},X_2^{*})$. Suppose A is dominant over a so that a heterozygote mutant (a,A) chooses (X′₁, X′₂). For recessive mutations, the probability of offspring adopting strategy X′ will be different, and we will briefly discuss it in Appendix A. According to the above matrix, if an (a,A) female meets a wild type male of (a,a), there is 50% chance that their children will choose X′ and 50% chance they will choose X*.

Consider a mutation that causes an individual to make the following marginal adjustments: (I) At age-1, within the constraint set spanned by (1), X₁ deviates a little bit from $X_1^{*}$ to ${X\prime }_1=X_1^{*}+d{X}_1$. (II) At age-2 within the constraint set spanned by (2), X₂ deviates a little bit from $X_2^{*}$ to ${X\prime }_2=X_2^{*}+d{X}_2$.

In the beginning periods after this mutation appears, since the majority population is composed of the wild type (a,a), a female will carry this A mutation if one of her parents has (a,A). In this case, on average half of her sisters will carry A and choose X′. If this mutation does successfully invade the wild type, then in the future, there are three cases (to be specified soon) to be considered in her offspring stem families. If we can show that the mutant line experiences some fitness improvement in at least one of these three cases, and no deterioration in the others, then the mutant line will out-compete the original wild type. Let us discuss these three cases of the stem family one by one.

Case (α), the grandmother is of type (a,a) and adopts $X_2^{*}$, and so are her age-1 daughters (the co-residing mothers). The behavior and fitness for families in this case will be the same as the wild-type family. So there is no fitness loss in this case.

Case (β), the grandmother is of type (a,a) and chooses $X_2^{*}$, but half of her female age-1 children choose X′₁ while the other half choose $X_1^{*}$. This will happen when the (a,a) grandmother mated with an (a,A) male at her age-1. Since at the original Nash equilibrium the mutant age-1 was maximizing her ϕ₁ subject to the constraint in (1), by (4) any marginal change from $X_1^{*}$ to X′₁ moving on the plane spanned by (1) is not going to change ϕ₁. So all we need to check here is whether ϕ₂ for the age-2 and ϕ₁ for other age-1 siblings who choose $X_1^{*}$ are not affected by the marginal change of the age-1 mutant.

Case (γ) is when the grandmother is of type (a,A) and adopts X′, and more than half of her children adopt X′. This happens after several periods of the mutation invasion, when some of the grandfathers are also of type (a,A), or even (A,A). In this case, there is a stronger intergenerational division of labor within the family, and we want to make sure that it raises fitness at both ages.

4.2. The invasion of first-stage division of labor

Consider a mutation for the first kind of division of labor, task sharing between t_a and T_a: (a) The age-1 agent decreases t₁ a little bit so that her foraging time increases a bit, (b) she transfers this increased energy from foraging to the common pool for children (increasing T₁), (c) at age-2 the agent increases t₂ a little bit, and (d) because her foraging time (1−t₂) is reduced, she decreases her transfer to children correspondingly (reducing T₂). If there were coordination, (a) and (b) would be done by the contemporary age-1, and at the same time (c) and (d) would be done by the contemporary age-2. The fact that θ₁ > θ₂ tells us that a coordinated change like the above must be efficient (see Section 3.3), therefore the group selection condition is fulfilled. In our non-cooperative game, however, (a)–(d) can be exercised only by the same individual, not across contemporaneous age groups. Can a mutation for independent changes (a)–(d) invade the wild type successfully? This is a question about individual selection.

Since the mutant family line has three possibilities in the future, we will discuss them one by one. For case (α), the grandmother and mothers jointly adopt $(X_1^{*},X_2^{*})$. The situation is the same as the wild type, and so is the fitness index.

Case (β) is slightly more complicated: the grandmother adopts $X_2^{*}$, and half of her age-1 children adopt X′₁ while the other half adopts $X_1^{*}$. In this case, because the grandmother still adopts the original $X_2^{*}$, she may be hurt by the unilateral strategy change of some of her age-1 children. Note, however, that the adjustment of dT₁ and dt₁ described in (a) and (b) above only affects fitness through p₀ in (3). Let η≡1/(N₁m₁ + N₂m₂). It is easy to see from (3) that if K of the co-residing age-1 adults unilaterally adopt (a) and (b), the change in p₀ is

$$d{p}_0=K\eta (f_{1}d{T}_1+f_{2}d{t}_1)=K\eta (-{\theta }_1{f}_1+f_2)d{t}_1,$$

where the last equality holds because the energy constraint in (1) suggests dT₁ = −θ₁dt₁.

Since at the original Nash equilibrium an age-1 individual j maximizes her fitness with respect to X_1j, her corresponding first-order condition implies⁴

$$\frac{f_1\eta }{f_2\eta }=\frac{1}{{\theta }_1}.$$

Substituting the above condition into the dp₀ formula, we see that

$$d{p}_0{|}_{\mathit{\text{age}}-1}=0$$ (5)

must be true, where the subscript “age-1” of dp₀ means that the change is caused by the unilateral adjustment of dT₁ and dt₁ by the age-1 alone subject to her constraint in (1). Thus, unilateral marginal changes by these K young adults would not affect p₀. This is essentially what is described in (4). Because other family members can possibly be affected by the unilateral change of some of the age-1 only through p₀, the fact that dp₀ = 0 says that the age-1 mutant children would not affect the fitness of other family members. As such, case (β) is cleared.

For case (γ), the grandmother adopts X′₂, and more than half of her age-1 children (mothers) adopt X′₁ while the other adopt $X_1^{*}$. The scenario is a partial division of labor in this family. As in Bergstrom (1995), we propose the following assumption.

Assumption 1 (HEDL). Suppose in a stem family the grandmother has n surviving age-1 adult children. Let the ones who choose X′₁ be ordered first, and the ones who choose $X_1^{*}$ be ordered later. We have a half-group efficient division of labor within the family if for a = 1,2

$${\varphi }_a({X\prime }_{11},\dots ,{X\prime }_{1j},X_{1j+1}^{*},\dots X_{1,n}^{*},{X\prime }_2)\ge {\varphi }_a(X_1^{*},X_2^{*}),\forall j\ge n/2.$$ (6)

In the above equation, the right hand side is the fitness value which the wild type obtains by choosing $(X_1^{*},X_2^{*})$, and the left hand side is the fitness of a mutant stem family in which at least half of the age-1 mothers choose X′₁, while the grandmother adopts X′₂. Although the mutation leads to a changed strategy for both ages, at least in the beginning periods after the mutation appears, there are some children in the family who will still choose the original $X_1^{*}$. Inequality (6) says that the division of labor by age-2 and at least half of age-1 is efficient.

The HEDL assumption is just a compact way to write down the efficiency of a partial division of labor. For instance, suppose n = 6 and the grandmother adopts X′₂. Depending on whether the grandfather carries the mutant gene, on average there will be three or more mothers adopting X′₁. The HEDL assumption says that the existence of mothers who still adopt $X_1^{*}$ does not interfere with the division of labor between the grandmother and the mutant mothers who adopt X′₁. This assumption of non-interference seems to be reasonable in the cooperative breeding scenarios that we usually observe.

If HEDL is fulfilled, in case (γ) the mutant family improves its members' fitness. Then, because the mutant lines in cases (α), (β) and (γ) all fare better, this mutant line's fitness is improved, and should dominate the wild gene line. Note that in our discussion the mutant-line males do not take care of the children by assumption, but some proportion of them do have the gene (a, A). As time goes by, this increases the probability of newborns adopting X′. If HEDL is satisfied, eventually this mutant gene will out-compete the wild type and go to fixation in the population. Thus, a mutation satisfying HEDL will break the common-pool problem of cooperative breeding and gain efficiency. In this sense, natural selection does the coordination and solves the common pool problem.

Cooperative breeding can be treated as a special kind of common pool problem. It is well known that a group of people is more likely to overcome the common pool problem and move toward efficiency when internal monitoring and imposition of penalties against violators are easier. From our analysis, it seems that gene connection is one particular way to pass on to the next generation a “norm” of coordination (division of labor). Because nature favors the species that explores more options for efficiency, the penalty for deviating from coordination is in fact the loss of fitness. In this sense, evolutionary forces seem to provide a good incentive to overcome the inefficiency of the common pool problem. The norm in a genetically related group may well be a hard-wired command that imposes a specific cooperative strategy.

The more complicated cases for less highly interrelated groups and recessive genes are briefly discussed in Appendix A.

5. Second-stage division of labor: menopause

The preceding discussion established that as long as θ₁ > θ₂, a mutation causing (a)–(d) in Section 4.2 can sustain group selection toward t_a−T_a task-sharing, and if the HEDL assumption is satisfied, the mutation can also succeed through individual selection. Because the energy constraints in (1) and (2) are linear, once there is a marginal division of labor, the forces of selection will progressively increase task specialization. However, in view of (1) and (2), this division of labor cannot go on forever. Because the left hand sides of (1) and (2) are always positive, before either t₁ or t₂ reaches zero, some choice variable must hit its lower bound first. For the cases of humans, killer whales and some dolphins, the most interesting scenario arises when m₂ hits the bound m₂ = 0, that is menopause. But when will this happen? And can this phenomenon be supported by evolution?

Our discussion in Section 4 concentrated on a mutation promoting a swap between care time and food or energy, t_a and T_a, a = 1,2. An alternative swap is the following: (i) An age-1 female decreases her t₁ a bit and forages more, (ii) she uses this increased energy to increase fertility (m₁) and/or downward transfers (T₁), (iii) on reaching age-2 she increases her t₂ a bit, and (iv) she compensates for this energy loss due to decreased foraging by reducing her fertility, m₂. Focusing on this swap between t_a and m_a, note that at age-2 the opportunity cost of m₂ and t₂ are respectively c₂ and θ₂, so the relative cost of the t₂−m₂ tradeoff is θ₂/c₂. Similarly, the age-1 female's relative cost of trading off m₁ and t₁ is θ₁/c₁. Evidently, the group selection condition will be satisfied if θ₁/c₁ > θ₂/c₂. This condition tells us that continued fertility by older adults would be inefficient, an inefficiency that can be lessened by reduced fertility until eventually it reaches zero and menopause has been reached. To sustain individual selection, however, the situation is more complicated. As in the previous section, case (α) is not important, so we start by checking the individual selection condition under case (β), that the age-2 grandmother adopts $X_2^{*}$, and half of the age-1 females adopt X′₁.

For case (β) we know that any change of energy allocation by the age-1 female that satisfies the constraint in (1) does not alter her fitness index at the margin, so we focus on the fitness of other co-residing members. An age-2 grandmother who has (a,a) will stick to her $(m_2^{*},T_2^{*},t_2^{*})$ choice. Given that the only interaction between the age-1 and age-2 females is the child survival function p₀, the grandmother and the $X_1^{*}$-adopting sisters will not fare worse if the unilateral change of X′₁ by the age-1 does not change p₀ = f marginally. Thus, by (3) individuals in case (β) will have the same fitness index if

$$d{p}_0{|}_{\mathit{\text{age}}-1}\equiv \zeta [\frac{\partial f}{\partial T_1}d{T}_1+\frac{\partial f}{\partial t_1}d{t}_1+\frac{\partial f}{\partial m_1}d{m}_1+\frac{\partial f}{\partial p_1}d{p}_1]=0,$$ (7)

where ζ is some constant related to the current population size (N₁, N₂). Eq. (7) restricts the domain of free changes for the age-1 mutant, which originally can move so as to satisfy (1), that is, to make

$$b_{1}d{p}_1+c_{1}d{m}_1+d{T}_1+{\theta }_{1}d{t}_1\le 0.(1\prime )$$ (8)

However, the degree of freedom for the changes (dT₁, dt₁, dm₁, dp₁) is in general large enough to avoid any conflict between (1′) and (7). Or, one can simply imagine that the age-1 females make some marginal changes in the direction for which dp₀|_age−1 = 0.

Now we consider case (γ). To investigate the conditions on parameters for selection to take place, without loss of generality we will consider the following combinations of special changes: (1) for any given dm₂ < 0, dm₁ is such that d(m₁ + p₁m₂) = 0; (2) for any given dt₂ > 0, dt₁ < 0 is such that d(t₁ + p₁t₂) = 0; (3) dT₂ = 0; (4) absorb the energy gain by an age-1 female (since her foraging time (1−t₁) has increased) by dT₁ > 0. Because the energy transfer increases and the care time is held unchanged in (1)–(4) above, in view of (3), we see that dp₀ > 0.

In Appendix B we establish conditions for both d(m₁ + p₁m₂) = 0 and d(m₂f) > 0 to hold. On the one hand, given that d(m₁ + p₁m₂) = 0, the age-1 female is better off because her expected fertility is unchanged while the probability of child survival (p₀ = f) has increased. On the other hand, if f increases by more than compensating reduction in m₂ so that d(m₂f) > 0, then the age-2 female is also better off because she has more expected live births. Appendix B derives inequality (8)

$$d(m_{2}f)=(-d{m}_2)f\left[\frac{m_2{f}_1{p}_1{c}_1}{(m_1+p_1{m}_2)f}\right(\frac{{\theta }_1{c}_2}{{\theta }_2{c}_2}-1)-1]>0.$$ (9)

From (8), since −dm₂ > 0, we see that the larger is the age-1 female's comparative advantage in foraging relative to age-2 females (θ₁c₂/θ₂c₁), or the larger is the marginal productivity of energy for child survival (f₁), the more room there is for the mutation to invade the wild type and to exercise this efficient division of labor. This is indeed intuitively appealing. In summary, let us assume.

Assumption 2. Let the original wild-type equilibrium be $(X_1^{*},X_2^{*})$. Assume that at $(X_1^{*},X_2^{*})$, the parametric condition is such that inequality (8) is satisfied.

Note that under our linear structure of energy expenditure, the comparative advantage θ₁c₂/θ₂c₁ is a constant, independent of the current extent of task-sharing. However, if instead there is the usual property of diminishing returns, then f₁ would be a decreasing function of transfer inputs to children. For (8) to remain positive after considerable transfers have already been made, it must be the case that the children need a lot of transfers so that diminishing returns have not yet set in. This is indeed the case for species like humans or orcas that have a long period of juvenile dependence.

Assumption 2 guarantees that a further division of labor at the cost of sacrificing fertility at age-2 is good for both ages in case (γ). However, this only satisfies the group selection condition for both ages to fare better. Since there are multi-member interactions in this cooperative breeding group, for the mutant to be able to out-compete the wild type, we still need the HEDL Assumption 1, which as we explained concerns the non-interference of other co-residing members. In summary, if Assumptions 1 and 2 hold, then a mutation for further division of labor which pushes the age-2 female to increase her child-care time at the cost of her fertility will be selected.

6. Third-stage division of labor: filial piety

Now let us consider whether we can push the scenario a step further. Suppose that for the age-2 females, both T₂ and m₂ have already been squeezed to zero. In this case, the age-2 grandmothers' only job is child-rearing, using t₂ of their time. They support their basic maintenance energy E₂ by doing minimal foraging, using time 1−t₂ = E₂/θ₂ (see Eq. (2), by setting m₂ = T₂ = 0). If more child care time is needed, can the intergenerational cooperation be implemented any further?

If the game is a cooperative one, then there is one way: the age-1 female transfers some energy to her grandmother, enabling the grandmother to reduce the time she spends in inefficient foraging, and instead to use this saved time to increase her time spent caring for grandchildren. But could evolutionary forces lead to this scenario?

If the age-1 female gives away some energy, this move would not be along the hyperplane spanned by (1), so the envelope theorem cannot be applied as it was in the previous section. A reduction of energy at age 1 might cause a first-degree loss of fitness. If she does not know in advance how the age-2 grandmother will use the additional energy transferred to her, the age-1's upward transfer might reduce the expected survival of her children. Hence a gene promoting this upward transfer could not be expected to invade successfully.

Suppose, however, that the division of labor already makes the age-2 female have T₂ = 0 and m₂ = 0 (menopause). In this case, if the grandmother is given some energy F from her age-1 adult children, her energy constraint in (2) would now be

$$E_2={\theta }_2·(1-t_2)+F.$$ (10)

When F increases, according to (9) there is nothing else the age-2 grandmother can do but to increase her child-care time. In this case, a mutation that causes the adult child to make an upward transfer would automatically complete the division of labor, as if the mother were buying the grandmother's childcare time by paying her a unit cost of θ₂, which is smaller than the mother's own opportunity cost θ₁. Note that this is possible only when all choice variables that could be used to increase the age-2 female's own fitness have already been reduced to zero. In particular, if m₂ > 0 is still true, then transferring energy from the age-1 mother to the age-2 grandmother would cost the age-1 female some fertility in exchange for an increase in new-born sisters (born by the grandmother at age-2). This is not worthwhile, for c₂ > c₁ by assumption, and the age-1 female would rather bear her own children, who are even more similar genetically if the fathers are not the same.

If we interpret filial piety as a kind of upward transfer from adult children to their old mother, then what we have shown above is that this can arise through evolution. But our prediction is that this is likely to arise only after menopause, that is, when the age-2 female has already reduced her m₂ to zero. Then and only then would an upward transfer be equivalent to a further step toward the efficient division of labor. And of course, the HEDL assumption is still needed for individual selection.

7. Conclusions and discussions

This is the most recent in a series of papers by the authors that analyze the evolution of intergenerational transfers and the way these co-evolve with other aspects of the life history. These papers have examined the relation of intergenerational transfers to age patterns of mortality, fertility, “time preference” (tradeoffs between current and future energy), menopause, and sexual dimorphism.

This paper goes beyond these to consider ways in which a division of labor between older and younger adults in use of time for foraging versus for offspring care can enhance reproductive fitness. While such a division of labor can initially be implemented through different kinds of transfers from older and younger adults to offspring and grandoffspring, and through the evolution of menopause, as this division of labor proceeds further it may come to involve transfers between the older and younger adults as well. While the results in this paper relying on group selection could have been derived in a one-sex model, those that rely on individual selection and the invasion of a mutation require the separate treatment of males and females. While we analyze many features of males and females in our paper on sexual dimorphism (Chu and Lee, 2012), we do not discuss the age specific division of labor by sex. And this paper goes beyond our earlier treatment of menopause to consider further age specific division of labor even after menopause has evolved.

We have explored the evolution of the intergenerational division of labor among co-residing family members. As long as there exist comparative advantages between adults of different ages, there is room for the invasion of a mutation promoting a more efficient intergenerational division of labor. However, in a two-sex scenario, the condition for successful invasion is stronger for individual selection than for group (comparative steady state) selection. We have derived conditions for both these selection scenarios.

We separate the intergenerational division of labor into three stages. In the first stage group members share foraging and childcare tasks. In the second stage old adults reduce their energy use and foraging time by reducing their fertility to zero. This leaves them more time for child care which enhances the survival of their grandoffspring. In the third stage, grandmothers are already menopausally sterile and have exhausted all means to increase their childcare time. Increased childcare time by the grandmother is possible only if her adult children transfer some energy to her so she can further reduce her time spent foraging to satisfy her own energy needs. This upward transfer is what we call filial piety. A mutation promoting this upward transfer by younger mothers can invade only if grandmothers are incapable of directly propagating their own genes. For this reason the evolution of filial piety can potentially happen only after the evolution of menopause.

Our theory for the evolution of the division of labor applies regardless of whether young women specialize in childcare and old women specialize in foraging, or the reverse. However, our theory for the subsequent evolution of filial piety requires that old women specialize in providing childcare, and receive upward transfers of food from younger women. What specialization pattern is observed in the real world? A study of forager time use by Gurven and Kaplan (2006, pp. 34, 40) indicates that younger women tend to stay in camp and care for their children, while older women forage. However, because the focus of their study is not on the elderly, the model Gurven and Kaplan fitted to the raw data constrained child care time to decline monitonically at older ages, so the fitted curves could not show an increase in childcare at later ages even were it to occur in the data. Other studies do report such an increase. According to Hill and Hurtado, “Later, when they [grandmothers] are too old to engage in physically taxing activities, they baby-sit grandchildren and enable their daughters or daughters-in-law to work uncencumbered…. Finally, grandfathers, like grandmothers, become dedicated babysitters, freeing up younger individuals to forage far away from camp, often on short overnight trips” (1996, pp. 235–236). Biesele and Howell (1981) give a similar account for the !Kung, as does Simmons (1945) for a broad array of groups. This scenario, while not literally in accord with our theory (this would require a model with three adult age groups), is consistent with its thrust.

Cox (1987) asked whether transfers to the elderly are motivated by altruism or by exchange. From the point of view of evolution, upward transfers to the elderly could evolve precisely because they were paired with downward transfers from the elderly of care time for children. It is tempting to say that from an evolutionary perspective this is an evolved pattern of exchange that improves reproductive fitness. But from the point of view of human motivation we suggest that it evolved not as an exchange but rather as a pair of altruistically motivated transfers. We suggest that the adult offspring (here daughters) are moved by an evolved impulse to provide food for their elderly mothers, and that the elderly mothers have an ancient evolved impulse to care for their children and grandchildren. That leads them to provide additional care time once their daughters' transfers mean that they need less time to forage for their own subsistence. Since the impulse toward care for an elder parent is altruistic, it is muted by public care for the elderly, public care which may itself be motivated by the altruistic impulse of the adult children. Thus filial piety is less obvious in the rich industrial societies, but may nonetheless play an important role in them.

HIGHLIGHTS.

• Dynamic optimization finds optimal division of labor between young and old adults.

• We give conditions for an optimizing mutation to invade in a two sex model.

• Menopause occurs as a complete division of labor between fertility and foraging.

• Continuing specialization reduces foraging to own needs, raising care time.

• Further specialization in care requires food transfers from younger to older adults.

Appendix A. Complications for less highly interrelated coresidential groups

The discussion in the text is restricted to the simplest case of a stem family, where a grandmother co-resides with her age-1 adult children. If the co-residing family is larger and forms a joint family, perhaps including cousins or members of other degrees of relatedness, then the Nash equilibrium is composed of strategies of several groups. For instance, there may be several grandmothers adopting different strategies. When the co-residential group is large, the benefit from the division-of-labor between a grandmother and her young adults is diluted by the large more weakly related group, hence condition (6) should be modified accordingly. It is possible that during the long period before the mutant line begins to dominate in the population, another mutant strategy X″ that dominates X′ arises, rendering less relevant the dominance of X′ over X*. In particular, the X″ strategy could involve cheating and free-riding. This has been shown to happen in the case of microbes, for example (Pennisi, 2009).

We conjecture that a small and highly interrelated cooperative breeding group is more likely to fulfill the HEDL assumption, and hence to move through natural selection toward an efficient division of labor. On the one hand, a small group limits the dilution of efficiency gain within the limited number of mutant relatives. On the other hand, high interrelatedness makes the Nash interaction among co-residing members less complicated.

Another complication is the case of recessive genes. If the mutation is recessive relative to the wild type, then only a homozygote will change to X′, even if X′ is a more efficient strategy than X*. In this case the mutation invades the population at a slower pace, and the HEDL assumption will have to be replaced by stronger conditions. We will not discuss this case further here, and refer readers to Bergstrom (1995) for a discussion of the invasion of recessive genes in the case of sibling cooperation.

Appendix B. Establishing condition (8) in Section 5

We consider t_a−m_a swaps by both age-1 and age-2. For any given dm₂ < 0, by (2) we know that dt₂ = −c₂dm₂/θ₂. Assuming dp₁ = 0, to make dt₁ + p₁dt₂ = 0, dt₁ must be dt₁ = p₁c₂dm₂/θ₂. This increases the age-1 energy by e₁≡−θ₁p₁c₂dm₂/θ₂. Assuming dp₁ = 0, to make dm₁ + p₁dm₂ = 0, dm₁ must equal −p₁dm₂, which costs the age-1 e₂≡−c₁p₁dm₂ energy. Because θ₁/c₁ > θ₂/c₂, there is some energy gain from the above t_a−m_a swap, and this energy difference by design is all used in T₁:

$$d{T}_1=e_1-e_2=p_1{c}_1(-d{m}_2)(\frac{{\theta }_1{c}_2}{{\theta }_2{c}_1}-1).$$

From our assumption of d(m₁ + p₁m₂) = d(t₁ + p₁t₂) = dT₂ = 0, we see from (3) that, for any given N₁ and N₂, the change in f only comes from the change in dT₁. As long as θ₁c₂/θ₂c₁ > 1, dT₁ > 0 must be true. We have argued in the text that for a mutation causing (1)–(4) to be selective in the individual sense, we must have

$$d(m_{2}f)=m_{2}df+fd{m}_2=m_2\frac{f_{1}d{T}_1}{m_1+p_1{m}_2}+fd{m}_2>0$$

Substituting in the formula of dT₁ derived above, we obtain condition (8) in the text.