Temporal changes of neocortical high-frequency oscillations in epilepsy

Abstract

High-frequency (100–500 Hz) oscillations (HFOs) recorded from intracranial electrodes are a potential biomarker for epileptogenic brain. HFOs are commonly categorized as ripples (100–250 Hz) or fast ripples (250–500 Hz), and a third class of mixed frequency events has also been identified. We hypothesize that temporal changes in HFOs may identify periods of increased the likelihood of seizure onset. HFOs (86,151) from five patients with neocortical epilepsy implanted with hybrid (micro + macro) intracranial electrodes were detected using a previously validated automated algorithm run over all channels of each patient's entire recording. HFOs were characterized by extracting quantitative morphologic features and divided into four time epochs (interictal, preictal, ictal, and postictal) and three HFO clusters (ripples, fast ripples, and mixed events). We used supervised classification and nonparametric statistical tests to explore quantitative changes in HFO features before, during, and after seizures. We also analyzed temporal changes in the rates and proportions of events from each HFO cluster during these periods. We observed patient-specific changes in HFO morphology linked to fluctuation in the relative rates of ripples, fast ripples, and mixed frequency events. These changes in relative rate occurred in pre- and postictal periods up to thirty min before and after seizures. We also found evidence that the distribution of HFOs during these different time periods varied greatly between individual patients. These results suggest that temporal analysis of HFO features has potential for designing custom seizure prediction algorithms and for exploring the relationship between HFOs and seizure generation.

high-frequency oscillations (HFOs) have received increasing interest as a promising biomarker for epileptogenic tissue. HFOs are discrete electrophysiological events that stand out from background activity and are seen in normal as well as epileptic tissue (Engel et al. 2009). They occur in the 100- to 500-Hz frequency range and generally last on the order of tens of milliseconds. HFOs have conventionally been separated into two classes by frequency: ripples (100–250 Hz) and fast ripples (250–500 Hz), although a third class of mixed frequency events has been automatically identified in human neocortical epilepsy (Blanco et al. 2010). Ripples were first identified during normal brain functions such as memory consolidation (Buzsaki 1998; Grenier et al. 2001; Siapas and Wilson 1998) but were later identified in epileptic tissue as well (Bragin et al. 2002a).

The study of HFOs may help elucidate mechanisms of seizure generation (Demont-Guignard et al. 2012; Jefferys et al. 2012). Many investigations have focused on the mechanisms generating ripples (Bragin et al. 2004, 2007; Ylinen et al. 1995) and fast ripples (Dzhala and Staley 2004; Foffani et al. 2007; Ibarz et al. 2010; Menendez de la Prida and Trevelyan 2011). Fast ripples have been more closely linked to pathological activity and localize to the seizure onset zone (Bragin et al. 2002b; Urrestarazu et al. 2007). However, investigations of human intracranial recordings indicate that HFOs in both frequency ranges increase in epileptogenic brain regions (Jacobs et al. 2010; Worrell et al. 2008). Like seizures, HFOs increase after medication reduction, indicating a close link between the two phenomena (Zijlmans et al. 2009). These studies investigated HFOs primarily as a spatial biomarker, as they appear to have great potential for delineating epileptogenic brain. Removal of HFO-generating tissue has been shown to correlate with better outcomes of resective surgery (Akiyama et al. 2011; Jacobs et al. 2010). However, one of the primary challenges in HFO research remains how to distinguish between normal and abnormal HFOs (Engel et al. 2009; Traub 2003); merely identifying fast ripples and ripples is not specific enough, as all types of HFOs are present even in normal human brain tissue (Blanco et al. 2011).

One method of characterizing HFOs that has received relatively little attention is a detailed analysis of their temporal properties in the periods during and surrounding seizures. The seminal research on this subject has been encouraging. An in vitro study demonstrated increased ripple and fast ripple activity before seizures (Khosravani et al. 2005). Later human studies showed increased HFO activity 10 s before seizure onset (Zijlmans et al. 2011) and increased high-frequency power 8 s before seizure onset (Khosravani et al. 2009). Another investigation analyzing 15 min preceding seizures found preictal changes in HFO rates and HFO-band power in all patients. However, the magnitude and direction of these changes were variable, and there were no clear systematic trends across patients and seizures (Jacobs et al. 2009). The majority of these analyses focused on counting the number of HFOs and determining the peak spectral content to classify them as ripples or fast ripples. We hypothesize that quantifying other features of HFO signals and evaluating them with more robust statistics provides information critical to characterizing HFOs. This information could lead to new algorithms capable of predicting seizures or identifying abnormal areas of brain tissue.

The current study evaluates HFOs as a temporal biomarker for seizures, analyzing 86,151 events from five patients with neocortical epilepsy. HFOs were detected using an automated algorithm and grouped with unsupervised clustering (Blanco et al. 2010). This method allows for processing massive datasets in a manner that minimizes human bias (Gardner et al. 2007). Using this data set, we quantified waveform morphology using several signal processing features. These features were the basis for comparing the dynamics of HFOs in the epochs surrounding seizures, using several supervised classifiers and nonparametric statistical tests. The temporal changes in the rates of each type of HFO were also evaluated. We find that each patient has unique, statistically significant temporal changes in HFO rates and features in the 30-min period before and after seizures.

METHODS

Patient selection and data acquisition.

We used a previously published HFO dataset (Blanco et al. 2010). Nine patients diagnosed with medically refractory epilepsy were implanted with subdural electrodes (Ad-Tech Medical Instruments, Racine, WI). As the goal of the analysis was to characterize HFOs at different times relative to seizure onset, for inclusion in the study we required the presence of at least one HFO during an electrographic seizure. Five of the nine patients met this study criterion. Three of those excluded did not have any seizures, and the fourth did experience any HFOs during the single seizure. Table 1 shows the clinical characteristics and electrode type for each of the five included patients. The experimental protocol involved medication taper but not sleep staging.

Table 1.

Patient summary

Subject	Age	Sex	Pathology	Electrodes	Electrode Placement
A	35	F	Frontal neocortical	Standard: 6 × 6	Right: frontal, motor cortex
(SZ01)			oligodendroglioma	Micro: 1 × 8
B	24	M	Frontal cortical dysplasia	Standard: 6 × 6	Left: frontal, frontoparietal
(SZ02)				Micro: 4 × 6
C	39	F	Temporal neocortical gliosis	Standard: 6 × 6, 1 × 8, 1 × 8, 1 × 4, 1 × 4, 1 × 4	Left: temporal, inferior frontal, superior frontal, anterior temporal, posterior temporal, anterior, posterior
(SZ04)				Micro: 1 × 4
D	42	F	Frontal cortical dysplasia	Standard: 6 × 8, 3 × 8, 1 × 4	Right: frontal, temporal, anterior temporal, inferior temporal, posterior temporal
(SZ07)				Micro: 1 × 4, 1 × 8
E	38	F	Temporal neocortical gliosis	Standard: 6 × 6	Left: temporal, anterior temporal, middle temporal, posterior temporal
(SZ08)				Standard depth: 1 × 4
				Micro depth: 1 × 4, 1 × 4

Summary of patient clinical characteristics and electrode placement. Parentheses are labels used in prior study; see Table 1 in Blanco et al. (2011) for further details. F, female; M, male.

Electrodes were modified versions of standard grid and strip electrodes with added arrays of nonpenetrating, 40-μm platinum-iridium “micro” wires (Van Gompel et al. 2008). Besides intracranial electrodes, all patients received a limited montage of standard gold scalp electrodes, as well as other electrodes placed on the chin and anterior surface of the tibialis muscle to record electromyographic activity. Stainless steel surgical sutures (Ethicon, Somerville, NJ) located at the vertex region of the head served as the reference and ground for the intra- and extracranial electrodes. Data were acquired on a Digital Lynx Data Acquisition System (Neuralynx, Bozeman, MT) continuously at 32,556 samples per second with 18-bit resolution in up to 144 channels per patient, with a 9-kHz low-pass antialiasing filter.

HFOs were previously extracted from raw EEG data, as described by Blanco et al. (2010). Briefly, we used a well-known HFO detector (Staba et al. 2002) to identify candidate events and then clustered them using an unsupervised algorithm that did not presuppose the number of subpopulations of HFOs. This algorithm identified four clusters of HFOs, corresponding roughly to ripples, fast ripples, mixed events, and artifact. Events classified as artifacts were removed, and all remaining detected HFOs in each patient were used in the analysis. It is important to point out that the clustering algorithm removed filtering artifacts (Benar et al. 2010) and other nonphysiological waveforms with a success rate that was similar to trained human reviewers, who reviewed over 4,700 individual HFOs in raw and filtered form. The algorithm was used on the entire dataset without modification for ictal vs. interictal period. The present work is comprised of all HFOs that were detected and validated in the previous paper (Blanco et al. 2010), excluding the artifacts. The EEG data, as well as the HFO markings, are freely available at www.ieeg.org (see appendix a).

Feature extraction.

Eight quantitative measures were calculated from each of the 86,151 remaining HFOs, a process known as feature extraction. The features wereas follows: 1) fast ripple/ripple band power ratio; 2) spectral centroid; 3) spectral peak; 4) line length after spectral equalization; 5) bandpassed line length; 6) zero-crossings per sample length; 7) maximum amplitude; and 8) number of peaks per sample. The first four features characterize the frequency content of each event. The remaining four features capture elements of waveform morphology that distinguish HFO classes in published literature (see appendix b). After calculating all features, we found that the data from features 7 and 8 were highly correlated with others (correlation >0.84), but that the remaining 1–6 provided unique information. To reduce computational complexity, we used the reduced set of six features for all analyses except the initial classification (see HFO ictal/nonictal classification).

HFO ictal/nonictal classification.

We used three standard supervised machine-learning techniques to attempt to distinguish between HFO events occurring during ictal vs. nonictal periods: logistic regression, k-nearest neighbors (k-NN), and a support vector machine (SVM). Each of these techniques uses a different algorithm to classify data. The goal is to determine how to label HFOs automatically in subsequent data. We used two labels (ictal and nonictal) in the first test to assess whether classification was feasible and if more complex classification experiments aimed at seizure prediction would be possible. Information from all eight features was used to inform the classifiers, and we performed principal components analysis (PCA) to lessen the computational burden on the learning algorithms. This reduced the eight features to five components while retaining 96.3% of the data variance. We ran the experiments on the aggregate patient data and on an individual patient basis. However, it is important to note that conclusive analyses were performed on the full feature set, rather than just PCA data (see below). We split each set of samples into equally sized sets of training and testing data.

To further simplify the initial test of the classifiers, we first trained them on data from each patient individually, with a segregated partition of testing data. We also trained and tested on data from all patients in aggregate. In each case, we created 10 random partitions from the training and testing data sets, reserving 25% of the samples in each data set for cross validation. appendix c describes the details of the cross validation for the three methods. We assessed classifier performance on the testing data using the F₁ measure (Eq. 1), the harmonic mean of sensitivity and precision:

$$\begin{array}{c}\text{S}=\frac{\text{TP}}{\text{TP}+\text{FN}}\\ \text{P}=\frac{\text{TP}}{\text{TP}+\text{FP}}\\ {\text{F}}_1=\frac{2*\text{S}*\text{P}}{\text{S}+\text{P}}\end{array}$$ (1)

where S is sensitivity, P is precision, TP is true positive, TN is true negative, and FP is false positive. We used a permutation test to compare the testing set results to those generated by randomly assigned ictal/nonictal labels. This tested the null hypothesis that the classification was no better than randomly assigning the labels. After permuting the labels of the training data, we retrained the classifiers and then reclassified the testing data. We repeated this procedure for 10,000 trials for each patient and for 10,000 trials of the aggregate of all five patients. We compared the original F₁ performance of the classifiers to the expected performance under the null hypothesis (the distribution of F₁ from the random permutations) at a significance level α = 0.05 (Bonferroni corrected α = 0.001).

Temporal distribution of HFO features.

After calculating all features, each HFO can be represented as a unique point in “feature space” that has as many dimensions as the number of features. We divided the HFOs into four time epochs: preictal, ictal, postictal, and interictal. Pre- and postictal windows were defined as 10 min before and after a seizure, respectively. Interictal was defined as >10 min from a seizure for this test. We tested whether the distribution of HFOs within the feature space in each epoch was non-random. The null hypothesis was that the scattered distribution of features of all HFOs in each epoch was no different than if the HFOs were randomly assigned to an epoch. The centroid of features 1–6 was calculated (7–8 were not included due to high correlation with the other features). We measured the Euclidean distance of each HFO feature to the centroids, grouped HFOs according to epoch and used the median distance as the measure of dispersion for that epoch. We first calculated the dispersion using the original labels. We then randomly permuted the epoch labels, determined a new centroid for each of the four epochs, and recalculated the dispersion of all relabeled HFOs within that epoch, repeating this procedure >10,000 trials. The probability of the null hypothesis (i.e., that the observed dispersion in each epoch was that of a random sample of all HFOs) was the proportion of permutations with dispersion values more extreme than the real data, tested with a significance level of 0.05. Similar analyses were done with pre/postictal periods of several other durations from 2–120 min; results of this analysis were similar.

Temporal evolution of HFO features.

We assessed changes in the morphology features before and after seizures using two nonparametric statistical tests that are resistant to outliers and/or skewed data. We first performed PCA in each patient to reduce the set of HFO features to two dimensions for the purpose of visualization. We divided the four epochs above into smaller 5- to 10-min “stages” (10 total) between 0 and 30 min before and after seizures. Interictal for these analyses was defined as >30 min from a seizure. We made scatter plots of the HFOs in the first two PCA dimensions for each stage. The Kruskal-Wallis Test of the first two PCA components determined whether the two-dimensional PCA distributions from the different stages were unique vs. samples of the same distribution. We then evaluated temporal changes of the six individual morphology features (see previous paragraph) using Spearman's rank correlation, the nonparametric equivalent of the Pearson correlation. This test, which used six features explicitly, served as a more robust analysis of the conclusions in the PCA data. This test determines whether there is a monotonic relationship between time and each feature. HFOs before the first seizure or after the last were excluded from this analysis, as their relationship to previous or subsequent seizures could not be determined.

Stereotyped responses in different seizures.

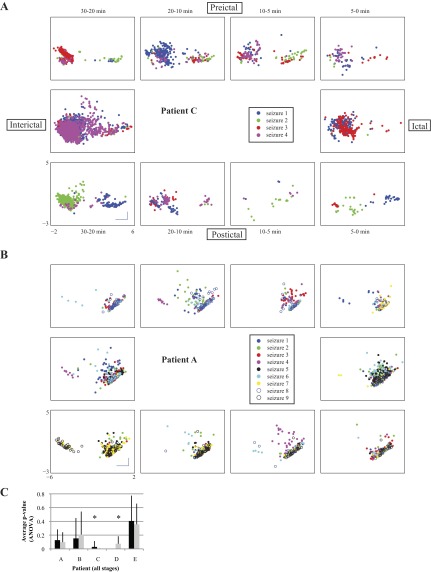
We evaluated whether the temporal changes above were consistent from seizure to seizure within each patient with an ANOVA on the first two PCA components in each of the 10 stages. We calculated the variance of each component in each temporal stage for each seizure and then computed the ANOVA across all seizures in each patient. The ANOVA P values were averaged across each patient and across each stage: high P values indicate that the distributions are similar from seizure to seizure, i.e., that the response is stereotyped.

Temporal evolution of HFO rate and class.

To analyze temporal changes in the rates and proportions of each of the three HFO classes [ripples, fast ripples, and mixed events (Blanco et al. 2010)], we calculated the average rate (events/min) and percentage of total events from each HFO class within each of the 5- to 10-min stages described above. To quantify the relationship between HFO class and latency to seizure, we performed a Kruskal-Wallis test comparing the rank order of each class with time to nearest seizure, aggregating all seizures. This was done twice, evaluating time to next and time to previous seizure. A significant P value (<0.05) indicates that the three clusters have different distributions, in other words that each class tends to occur at different times in relation to the nearest seizure. We tested whether the preictal rates of each class change significantly from interictal baseline with a χ² test, comparing the proportion of each type of HFO during interictal vs. the combination of all preictal stages (0–30 min).

RESULTS

HFO ictal/nonictal classification.

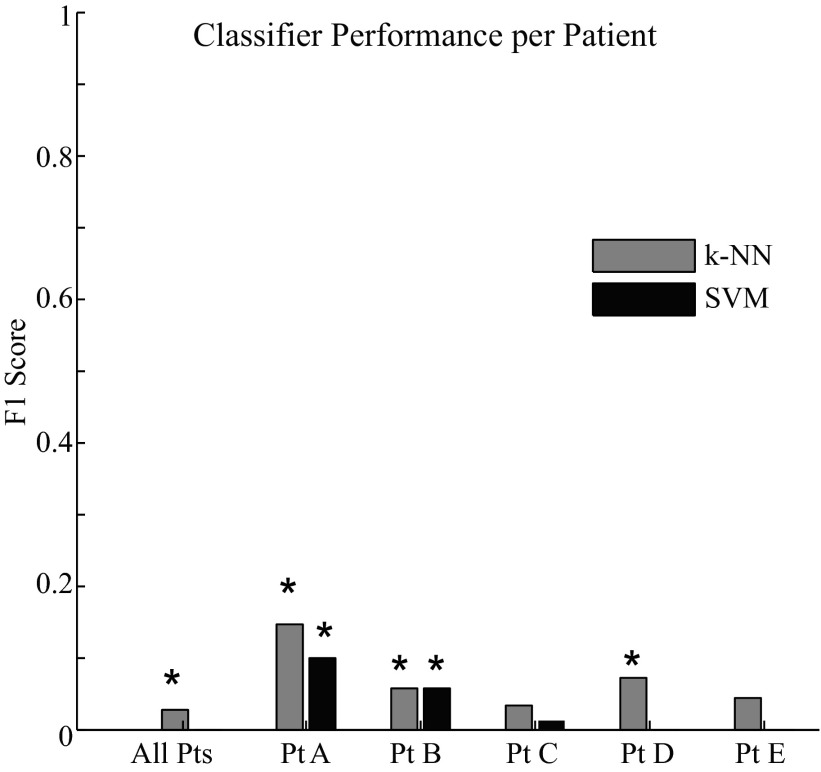
The first analysis tested three classifiers to determine whether they could distinguish HFOs occurring during seizures (ictal) from those occurring at other times (nonictal, including interictal, postictal, and preictal). Figure 1 shows how well each classifier was able to separate the morphology of ictal and nonictal HFOs, which we quantified using the F₁ measure. The logistic regression classifier is not included in the figure because it did not make a single true positive identification. A higher F₁ score indicates a larger number of true positives relative to false positives and false negatives. The highest possible score is 1, resulting from perfect sensitivity and precision. The classifiers had limited success in separating the ictal and nonictal HFOs. This is in part due to the fact that the proportion of nonictal HFOs was much greater than ictal in the training data. The k-NN and SVM classifiers were statistically superior to random classification (0.05 significance, Bonferroni correction P < < 0.001) in patients A and B, and the k-NN was superior to random classification in patient D and in the aggregate of all five patients. Thus, in certain patients, it was possible to distinguish ictal from nonictal HFOs better than random; however, the actual F₁ scores were all <0.2, suggesting the classification was not very sensitive nor precise.

Fig. 1.

Classifier performance for the aggregate patient data and for individual patients as measured by the F₁ score, the harmonic mean of sensitivity and precision (max = 1). *Statistical significance at the level of α = 0.05 (Bonferroni corrected α = 0.001). Results from the logistic regression classifier are not shown because the F₁ score was zero in every trial. SVM, support vector machine; k-NN, k-nearest neighbor.

Temporal distribution of HFO features.

To evaluate whether any feature characteristics varied over time, we further subdivided the nonictal period into postictal, preictal, and interictal epochs. Table 2 displays the number of HFOs in each epoch. Seizures were a mean of 120 min apart (range 9.5 to 839 min). In three patients, some seizures occurred less than 1 h apart, causing pre- and postictal periods to overlap. HFOs occurring during these overlaps were counted as both pre- and postictal events, which may introduce bias into some of the following analyses. However, this involved a small number of HFOs (15% of HFOs in patient A, none in B and C, and 1% in D and E) and removing them from analysis did not change any of the conclusions (see Temporal evolution of HFO features). In each patient, we tested whether the distribution of HFOs in feature space was different during each epoch than what would be expected from a random sample of HFOs from all epochs in that patient. Figure 2 displays a plot of all HFOs from one patient, projected into two-dimensional feature space via PCA, with raw data from several HFOs displayed to demonstrate the varied appearance across the PCA space. Figure 3 displays the same data separated into time epochs, showing that the HFO distribution in each epoch (i.e., the “shape” of the scattered HFOs) differs from the shape of the population as a whole. Similar findings were found in the other patients, although the distributions and rates of each HFO type were very different from this patient (see Fig. 6). Although it cannot be displayed graphically, the HFO distributions using all six features have similar temporal differences. When analyzing the data in six dimensions (one for each feature), the distributions were significantly different than random: there were specific characteristics during the different epochs, demonstrated by a difference in cluster dispersion as measured by Euclidean distance (P < 0.05). We made similar temporal comparisons for each feature individually and found great interpatient variability. Table 3 shows the P values for two example features, the line length after spectral equalization and power band ratio. The other features demonstrated similar interpatient variability and were significant in some, but never all, of the five patients. These results imply that HFO distributions vary during different peri-ictal epochs and involve complex relationships between several features but that these changes are unique to individual patients. Thus samples from different times, especially across different patients, will likely have different feature distributions.

Table 2.

HFO and seizure counts

Patient	Total Seizures	Total HFOs	Inter-ictal	Preictal	Ictal	Postictal
A	9	2,552	1,487	314	371	380
B	3	9,905	9,237	280	139	249
C	4	12,417	11,585	329	317	186
D	7	53,015	49,519	1,787	433	1,276
E	2	8,262	7,210	493	46	513
All	25	86,151	79,038	3,206	1,306	2,604

Counts of high-frequency oscillations (HFOs) in each time epoch for dispersion analysis. Preictal and postictal epochs were defined as 10 min before and after seizures, respectively.

Fig. 2.

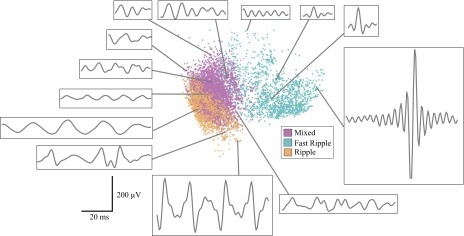
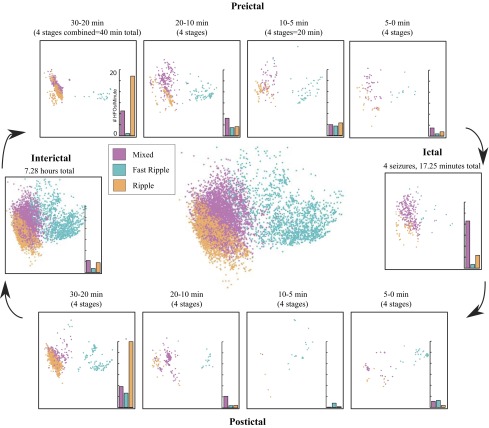
Scatter plot of all high-frequency oscillations (HFOs) in patient C in the first 2 dimensions of the principal components analysis (PCA) space. Each dot represents one HFO and is colored according to HFO cluster as determined by (Blanco et al. 2010). Localization of each dot corresponds to the first and second PCA components plotted in x–y coordinates. Representative waveforms from different regions of the PCA feature space provide examples of the morphology at each location.

Fig. 3.

Outside: scatter plots of the HFOs in each time stage for patient C in the first 2 dimensions of the PCA space. Color indicates HFO cluster as in Fig. 2. Bar graphs show the average rate (events per minute) for each cluster. Center: scatter plot of all HFOs from patient C.

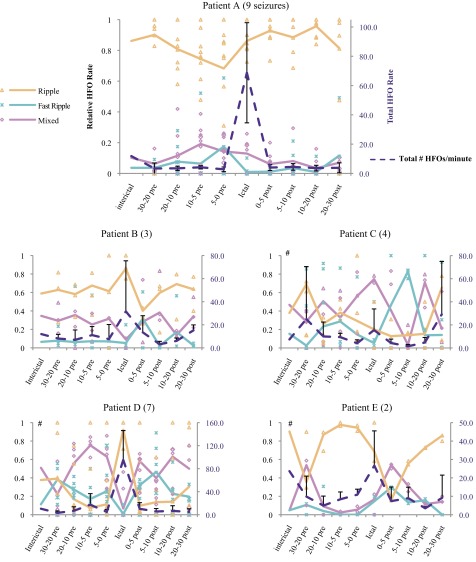
Fig. 6.

Graphs of the relative rates of HFOs in each frequency cluster (orange, blue, and pink lines; left axis) and the total HFO rate (dotted dark line; right axis). Rates of each HFO cluster during individual seizures are indicated with indicated symbols; lines indicate mean across all seizures. Error bars: standard deviation of total rate. Lack of any consistent trends among different patients implies that there is marked interpatient variability in HFO rates before and after seizures. Clustering of datapoints from different seizures indicates stereotyped responses, most prominent in patients A, B, and D. #χ² testing indicated that proportions of each HFO cluster are significantly different from interictal in the patients C, D, and E. Parentheses next to patient name indicate number of seizures in each patient.

Table 3.

Dispersion P values from 2 features

	Pt A	Pt B	Pt C	Pt D	Pt E	All
Feature 3 (line length)
Interictal	0.0018	*	*	*	0.0011	*
Preictal	0.3713	0.0615	*	*	0.0002	0.2242
Ictal	0.0426	0.0007	*	0.3148	0.0155	*
Postictal	0.0983	*	*	0.0038	*	*
Feature 4 (power band ratio)
Interictal	*	0.2285	*	*	*	0.1398
Preictal	0.0442	0.4916	*	*	0.4208	*
Ictal	*	0.0001	*	*	*	*
Postictal	*	0.1059	*	*	*	0.3285

P values from the epoch dispersion analysis. Values were calculated by dividing the number of permutation test trials with results more extreme than the true values by the total number of permutation test trials (10,000). Italics indicate values that were not statistically significant. The combination of all (6) features was significant in all patients (Pt A–E). Each patient had different trends with the individual features.

^*Highly significant (P < 1e-6).

Temporal evolution of HFO features.

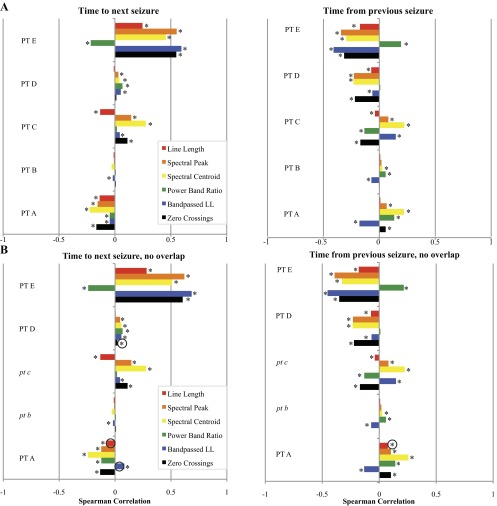
The previous section tested whether each epoch had a different distribution from random. We next sought to test the time dependency of HFO features. The first step was to compare the distributions in each stage in the two-dimensional PCA plots (e.g., Fig. 3 for patient C). The Kruskal-Wallis test demonstrated that for all patients there were highly significant differences between stages (P ≪ 0.0001). We then evaluated how the individual features changed temporally, using time before or after seizure as a continuous variable rather than constraining the analysis to categorical epochs. We used the Spearman correlation to assess whether there was any time dependence for each of the six individual features. The Spearman correlation determines strength and direction of any monotonic relationship between a feature and time; in this case, it assesses how much of a measureable, progressive change the HFO features have as a function of time prior or subsequent to seizure. Figure 4 shows the Spearman correlations for each patient. Correlations closer to ±1 indicate stronger relationships. In most cases, several features demonstrated weak but statistically significant correlations with both time to next seizure and time from previous seizure. Interestingly, certain features showed a significant positive correlation with time in some patients and a significant negative correlation with time in others. These analyses were repeated in patients A, D, and E with the overlapping HFOs removed, and there were no substantive changes to the conclusions: Kruskal Wallis tests were still all significant, and there were minor changes to the Spearman correlations (Fig. 4B).

Fig. 4.

A: bar graphs showing the Spearman correlations for morphology features and time to next seizure (left) and time from previous seizure (right). *Statistically significant correlations (α = 0.05). B: Repeat analysis when overlapping HFOs are removed. Patients B and C had none so the analysis was unchanged (italics). Black circles indicate subtle differences from A, most notably that 2 values in patients A and D become significant (P < 0.05). Kruskal Wallis tests all remained P < 0.001 when overlappers were removed (not shown).

In order for these temporal changes to be helpful in the development of customized seizure prediction algorithms, they must be consistent from seizure to seizure. Looking at each patient individually, we evaluated the seizure to seizure variability by running ANOVA on the first two PCA components in each peri-ictal stage across all seizures. In this analysis, when the P value is “insignificant” (>0.05), it corresponds to a similar distribution of the PCA values in subsequent seizures, i.e., the response is stereotyped and thus the ANOVA fails to find a difference between them. Conversely, a “significant” P value indicates there are differences across seizures, so the distributions of PCA are not stereotyped. An example of each case is shown in Fig. 5. These plots demonstrate that some patients are stereotyped while others are not, but do not capture all of the temporal changes described in previous paragraphs. The HFO distributions are quite similar from different seizure periods; for example, there are a large number of HFOs 20–30 min before seizure 3 with different morphology, so it would be difficult to predict seizure onset in this patient based on these data. We calculated the ANOVA of the PCA distributions across different seizures in every stage for every patient to determine if the changes were stereotyped. We found that three of the patients (A, B, and E) had stereotyped responses across all stages (P > 0.05; Fig. 5C). In the other two patients (C and D), the ANOVA found that at least one of the PCA components was significantly different between different seizures, meaning it would be hard to predict how the distribution would look in later seizures. Taken together, these data demonstrate that several HFO features are correlated with time, that these changes are often stereotyped, but that there is significant interpatient variability.

Fig. 5.

Temporal HFO distributions are stereotyped across different seizures in some patients. HFOs are displayed by their first 2 principle components and stratified by seizure. Plot is similar in organization to Fig. 3, but coloring corresponds to nearest seizure. A: in patient C, there are distinct patterns seen before or after certain seizures, such as 30–20 min preictally in seizure 3. This patient does not have stereotyped HFO distributions (P < 0.05). B: patient A has very similar distribution across all seizures in every stage, a stereotyped response (P > 0.1). All plots have same axes and scale, shown at bottom left (bars: 1 unit). C: P values for the ANOVA of the first 2 PCA components. Bar graphs of average P value across all stages except interictal in each patient. Bars indicate 1 SD (n = 9 stages). *Statistical significance (P < 0.05) Insignificant P values correspond to similarity in the distributions.

Temporal evolution of HFO rate and class.

Although it is clear from these analyses that a wide set of features is helpful to describe HFOs and their temporal dynamics, the data also suggest that the relative rate of each HFO cluster (ripple, fast ripple, and mixed event) may differ between different stages. Constraining each HFO to one of three cluster labels removes most information about its dynamic features but is also the most common way they are currently studied. To evaluate any changes descriptively, we first plotted the relative rates of each HFO cluster, as well as the total HFO rate, for each patient in each stage (Fig. 6). We observed distinct patient-specific trends in the evolution of rates and proportions of each cluster before and after seizures. In three of the patients (A, B, and D), the total number of HFOs is relatively constant until an increase during the ictal period, an effect less pronounced in patient B. However, the individual HFO clusters behave quite differently in these three patients. In patient A, there is a subtle drop in the proportional of ripples just before the seizures. Patient B has a similar effect postictally. In patient D, mixed events dominate preictally but disappear during the seizures. Observing the datapoints from individual seizures shows that similar findings are seen at each seizure. Patients C and E have much smaller changes in total HFO rate, sometimes having fewer HFOs during seizures. The only consistent change in patient C is increased mixed events and loss of ripples during seizures. Patient E is difficult to evaluate with only two seizures but tends to have a predominance of ripples preictally and mixed events immediately postictally. We tested whether the HFO rates changed significantly from baseline by comparing the proportion of each HFO cluster in the interictal stage with the aggregate of the four preictal stages. Patients C, D, and E had very significant changes from baseline, while patients A and B did not (P < <0.0001, χ²-square).To quantify the relationships between each type of HFO and time to seizure in Fig. 6, we compared the firing times of every HFO with a Kruskal-Wallis test using time to the previous and subsequent seizure as continuous variables. This assesses by rank order whether there are trends in the temporal distribution of each HFO cluster in each patient. A significant result (P < 0.05) indicates that the firing times of the three clusters are unlikely to be randomly distributed: that at least one type of HFO (ripple, fast ripple, and mixed event) is more likely to occur at specific times between seizures. We found that HFO times both before and after seizures were significantly different in all patients and times (Table 4, Kruskal-Wallis Test, P < 0.05). Thus, in each patient, specific types of HFOs became more or less likely to occur in the pre- and postictal periods. These findings demonstrate the strong temporal relationships HFOs have with seizures as well as the disparate patterns found in different patients.

Table 4.

P values of temporal rank

	Time to Next	Time From Previous	Closest Cluster (Next)
Pt A	<.0001*	<.0001*	FR, M
Pt B	0.013*	<.0001*	M, R
Pt C	<.0001*	<.0001*	FR, R
Pt D	<.0001*	<.0001*	FR, R
Pt E	<.0001*	<.0001*	R

P values from the second Kruskal-Wallis Test used to assess whether an HFO near a seizure was more likely to be of a specific cluster. Third column indicates which clusters were closest to the next seizure (R, ripple; M, mixed; and FR, fast ripple).

^*Statistical significance.

DISCUSSION

Peri-ictal HFO distributions vary greatly among patients.

Our current analysis evaluates properties of three classes of HFOs in four epochs (inter-, pre-, postictal, and ictal), collecting a large number of events in five patients. This allowed a thorough comparison of the statistical characteristics of HFOs during these epochs. Our use of three classes of HFO is a slight departure from previous work on these types of oscillations in patients with epilepsy. The first two classes are very similar to ripple and fast ripples, which are commonly recognized in the literature and were originally identified based on their peak oscillation frequency. In this work, we have included mixed events that were identified by an unsupervised algorithm (Blanco et al. 2010) as a third class, as their power spectra contain features of both ripples and fast ripples.

Our results show that the relative and absolute rates of each class of HFO changed in the periods before and after seizures and that these effects varied greatly among patients (Fig. 6). The ictal period was most variable in terms of the number and type of HFOs. The total HFO rate increased in three of the patients during seizures, while in the other two patients it decreased in the preictal period. Such disparities in preictal HFO rates have been identified previously (Jacobs et al. 2009); to our knowledge this is the first work evaluating the postictal and interictal periods as well. Interestingly, not all patients exhibited their highest total HFO rate during seizures. Fast ripple and mixed event rate increased beginning from 20 to 30 min before seizures in all patients but B. Fast ripple rates increased postictally in patients B–E. Ripples were predominant in three patients, although the ratio of ripples to fast ripples changed significantly in the 5 min before and after seizures. The time between seizures was highest in patients B and C, but there are no clear patterns that distinguish these two patients from the others. It is notable that there were no trends consistent among all five patients. With such a small patient sample size identifying so many differences between individuals, it is likely a common occurrence for patients to have unique HFO distributions. The cause of these findings is not clear. There are two main possibilities. The first is that behavior of HFOs during, between, and after periods of seizure generation may be unique to a patient's epileptic network or mechanism of epilepsy. Our analysis of PCA features (Fig. 5) revealed that at least three of the patients had unique responses that were stereotyped in different seizures, suggesting this may be true in some patients. Another possibility is that these individualized patterns may be due in part to sampling error, as there is no uniform implant strategy for all patients, and the microwires that detected many of the HFOs are dispersed unevenly in the implanted grids. These questions could be explored further by a larger sample with different implantation strategies that maximize high-resolution electrode coverage in the brain or perhaps by guiding electrode placement through intraoperative mapping of HFO generating regions to augment standard electrode placement strategies. Whatever the cause, our findings suggest that each patient must be evaluated individually when using HFO rates as an electrical seizure biomarker.

One intriguing possibility for future work lies in comparing the results from patients B and D, which had the most similar ictal responses in Fig. 6 (increased rate of HFO and ripples during seizure). These two patients both had frontal cortical dysplasia (Table 1). Although this sample size is small, this result suggests that future work should aim to stratify patients by epileptic pathology and perhaps common trends could be identified. Adding patients with other types of epilepsy (e.g., mesial temporal sclerosis) would also provide crucial information. Such work would likely also benefit from additional features that were not present in the current analysis.

HFO features during the ictal period, and seizure prediction.

We tested three machine learning algorithms with a large dataset of automatically detected HFOs to determine whether supervised classification could be used to identify differences between ictal and nonictal HFOs. With the use of the measurements described in appendix b, none of the algorithms obtained an F1 score >0.2, which is fairly poor performance. This finding suggests that, at least with these tools and features, it is difficult to distinguish any HFO signal features that are specific to the ictal period.

Despite the low performance, two methods did beat random chance, so we further investigated the temporal changes in HFOs in the peri-ictal period to determine the source of the differences. The first step was to analyze the HFO features in “feature space.” When the HFOs were grouped together based on stage, each patient's HFO distribution had a unique shape in feature space that changed over time. We found that these changes continued to evolve as much as 30 min before or after seizures. We tested these changes in several different ways: comparing the distributions of their PCA-reduced features, comparing their six-dimensional distributions to the distributions of random samples, and determining the Spearman correlation of each feature with time before and after seizures. In each case, there was strong statistical evidence of measureable temporal changes in HFO features.

These findings have significant implications for developing automated seizure prediction or warning algorithms. Although this analysis did not attempt to develop such an algorithm, it was performed on an unbiased sample of continuous EEG, thus simulating the “real-world” conditions necessary for such an algorithm to be successful. Additionally, it is well known that classification algorithms used for seizure detection and prediction usually perform better with input from multiple orthogonal features; most of our analyses were based on single or PCA-reduced features. Future attempts to develop seizure prediction algorithms based on combinations of these and other features may be very useful but will need to be rigorously tested using independent testing and training sets with prolonged continuous intracranial EEG, comparing against chance predictors using established methods (Mormann et al. 2007; Snyder et al. 2008). Furthermore, these data also suggest that these algorithms will be most effective if they are personalized for individual patients based on their unique features (Stacey and Litt 2008). For example, certain features might be relevant for one patient but not another, or the correlation of certain features with seizures might differ in strength or direction between patients. This will require a thorough analysis of HFO data on a per-patient basis before adjusting and applying the prediction algorithm. It will be critical to identify appropriate patients for such algorithms, and likewise not to abandon these techniques if they fail in some patients.

Identifying abnormal, epileptic HFOs.

As HFOs have been identified in both normal and abnormal brain, it is imperative that any clinical decisions based on them are able to distinguish whether they are markers of abnormal activity or not (Engel et al. 2009). To date, the primary clinical strategies proposed are to identify the electrodes with the highest number of HFOs (Jacobs et al. 2010) or to stratify HFOs into different categories based on peak frequency (i.e., ripples 100–250 Hz, fast ripples >250 Hz; Akiyama et al. 2011). While such strategies are promising, they were based on selected retrospective data, and there is considerable risk in basing prospective clinical decisions upon such data. The primary concern is that HFOs also occur outside the seizure onset zone, even in patients who do not have epilepsy at all (Blanco et al. 2011). It is quite possible that any patient can have a region with a relatively higher HFO density but that the increase could be due to local edema, physiological variation, or various other nonepileptic causes. It is therefore crucial to develop a method of characterizing HFOs that are true markers of epileptic tissue.

One characteristic of HFOs that has received relatively little attention is their temporal variation. A recent study evaluated HFOs and sharp waves with respect to seizures and found that, unlike sharp waves, HFO incidence changes similar to seizures (Zijlmans et al. 2009). This finding is intriguing in light of recent work investigating the mechanisms of abnormal HFOs and seizures. Ripples were originally described in normal tissue (Ylinen et al. 1995) and are considered to be the product of fast synchronous firing of inhibitory potentials. Conversely, later work in epileptic tissue has shown that “abnormal” HFOs are comprised of population spikes (Bragin et al. 2011). This difference has led to a great deal of research to determine how epileptic HFOs are made (Jefferys et al. 2012). However, detailed physiological studies into these phenomena are extremely difficult with current technology. Therefore, computational modeling has been used to confirm the role of population spikes in ripples (Stacey et al. 2009, 2011; Wendling et al. 2012) and fast ripples (Demont-Guignard et al. 2012; Ibarz et al. 2010; Roopun et al. 2010). In each case, epileptic pathologies (i.e., increased excitation, decreased inhibition, abnormal coupling) cause the abnormal HFO to occur. Wending et al. (2012) demonstrated that HFO characteristics change on a continuum from normal activity to seizure, depending upon the parameters. These realistic modeling studies suggest that epileptic pathologies will alter the appearance of HFOs and predict that a wide range of parameters (Demont-Guignard et al. 2012; Stacey et al. 2009) can be responsible. Our data demonstrate clinical evidence supporting this: that there are temporal changes in HFO morphology leading into seizures. These data likely represent a change in underlying physiology that is not yet quantified, which suggests that a robust feature analysis of HFOs may be able to illuminate future research into the underpinnings of this phenomenon.

If one assumes that there is an underlying process that alters the network parameters before and after seizures and that it affects both seizures and HFOs, it follows that HFOs may have different features in the time surrounding seizures. Until technology is able to characterize these network phenomena on smaller scales, our best method is to analyze EEG data. In this study, we analyze an unbiased sample of intracranial EEG and find that there are indeed temporal changes in HFO characteristics. However, the differences were relatively small and were highly variable between patients. Further work evaluating different signal features, recording EEG on different spatial and temporal scales, and comparing HFOs from “normal” and “abnormal” regions may be better able to distinguish these changes and lead to understanding of the mechanisms involved in generating both HFOs and seizures.

Conclusion.

With increasing interest in and evidence for HFOs as an electrical seizure biomarker, it is crucial to develop automated methods to identify and classify them that are not operator dependent, and that can be applied to a wide range of patients as well as animal models. With the use of data from an automated HFO detection algorithm, this study provides statistical evidence that some patients demonstrate temporal changes in the distribution of HFOs in the periods before and after seizures. Initially, these findings can be the basis of further experimental algorithms to explore temporal phenomena such as seizure generation, prediction, and epileptogenesis. With further validation, they may also provide a basis for algorithms capable of identifying periods of increased risk of seizure onset. Perhaps the most important finding from this study is that individual patients have vastly different HFO patterns related to seizures; these findings suggest that any clinical decision based on HFO analysis must be customized to each individual patient.

GRANTS

A. Pearce was supported by the Rachleff Scholars Program in Engineering at the University of Pennsylvania. University of Pennsylvania students and investigators were supported by National Institute of Neurological Disorders and Stroke (NINDS) Grants 2R01-NS0-41811-06 and 1-U24-NS-063930-02, Citizens United for Research in Epilepsy, and Dr. Michel and Mrs. Anna Mirowski Discovery Fund for Epilepsy Research. W. C. Stacey was supported by NINDS Grant 1K08-NS-069783-02.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: A.P., D.W., J.A.B., B.L., and W.C.S. conception and design of research; A.P., D.W., J.A.B., and W.C.S. performed experiments; A.P., D.W., A.K., B.L., and W.C.S. analyzed data; A.P., A.K., B.L., and W.C.S. interpreted results of experiments; A.P. and W.C.S. prepared figures; A.P. and W.C.S. drafted manuscript; A.P., A.K., B.L., and W.C.S. edited and revised manuscript; A.P., D.W., J.A.B., A.K., B.L., and W.C.S. approved final version of manuscript.

APPENDIX A: ONLINE ACCESS TO DATA AT WWW.IEEG.ORG

The EEG data and HFO markings used in this study have been posted by the authors of (Blanco et al. 2011) for viewing and analysis on the International Epilepsy Electrophysiology Portal (IEEG)-Portal (https://www.ieeg.org). This free online database allows the user to view, download, and annotate EEG data and has been established to allow datasharing and collaboration. The five studies used in this manuscript can be accessed with the following names: patient A: I001_P034_D01; patient B: I001_P011_D01; patient C: I001_P015_D01; patient D: I001_P014_D01; and patient E: I001_P017_D02.

APPENDIX B: FEATURE EQUATIONS

1. Power band ratio (250–500 Hz)/(100–200 Hz): the ratio of estimated power in the hypothesized “fast-ripple” band to that in the hypothesized “ripple” band, computed on the band-passed data; frequency-input domain.

   $$\begin{array}{c}\text{power}\text{\hspace{0.17em}band}\text{\hspace{0.17em}ratio}={\widehat{\text{P}}}_{[250,000]}/{\widehat{\text{P}}}_{[100,200]}\\ \text{where}\\ {\widehat{\text{P}}}_{[a,b]}={\displaystyle \sum _{\left\{\text{k}\in \text{Z}|\zeta (a)\le \text{k}\le \zeta (b)\right\}}{\left|{\text{M}}_{\text{k}}\right|}^2,(a<b)\in (0,\frac{{\text{F}}_{\text{s}}}{2})}\end{array}$$

   where and M_k is a multitaper power spectral density estimate. For more details, see Blanco et al. 2010.
2. Spectral centroid: the frequency corresponding to the “center of mass” of the spectrum, computed on the band-passed data; frequency-input domain.

   $$\text{spectral\hspace{0.17em}centroid}=\frac{{\displaystyle {\sum }_{k=0}^{\text{N}/2}\frac{k}{\text{NT}}{\left|{\text{M}}_{\text{k}}\right|}^2}}{{\displaystyle {\sum }_{k=0}^{\text{N}/2}{\left|{\text{M}}_k\right|}^2}}$$
3. Spectral peak: the frequency corresponding to the peak of the estimated power spectral density, computed on raw data; frequency-input domain.

   $$\text{spectral\hspace{0.17em}peak}=\frac{1}{\text{NT}}\underset{k}{\arg \max }{\left|{\text{M}}_{\text{k}}\right|}^2,k\in \{0,1,\dots \frac{N}{2}\}$$
4. Line length after spectral equalization: detections are first detrended and energy normalized by dividing by their Euclidean lengths and by sample length, computed on raw data after first-order backward differencing; time-domain input.

   $$\text{line}\text{\hspace{0.17em}length}=\frac{1}{L}{\displaystyle \sum _{i=0}^{L-2}\left|x_{i-l}-x_i\right|}$$
5. Line length (bandpassed) per sample length: line length of the 100- to 500-Hz bandpassed HFO waveform divided by the total length of the sample

   $$\text{line\hspace{0.17em}length\hspace{0.17em}(bandpassed)\hspace{0.17em}per\hspace{0.17em}sample\hspace{0.17em}length}=\frac{1}{N}{\displaystyle \sum _{i=2}^N\left|x_i-x_{i-1}\right|}$$
6. Zero-crossings per sample length: the number of times the sample crosses its mean divided by the total length of the sample, which is zero-meaned

   $$\text{zero\hspace{0.17em}crossings\hspace{0.17em}per\hspace{0.17em}sample}=\frac{1}{N}{\displaystyle \sum _{i=2}^N\text{sign}(x_{i-l})\ne \text{sign}(x_i)}$$
7. Maximum amplitude range: the difference between the maximum and minimum values of a sample

   $$\text{max}\text{.\hspace{0.17em}amplitude\hspace{0.17em}range}=\max (x)-\min (x)$$
8. Number of peaks per sample length: the total number of local maxima in a sample divided by the total length of the sample

   $$\text{no}\text{.}\text{\hspace{0.17em}peaks}\text{\hspace{0.17em}per}\text{\hspace{0.17em}sample}=\frac{1}{N}{\displaystyle \sum _{i=2}^{N-1}(x_i>x_{i-1}^x_i>x_{i+1})}$$

APPENDIX C: CLASSIFIER CROSS VALIDATION

The k-NN classifier requires specification of the value for k, the number of nearest neighbors to use. We determined the optimal k by calculating the average performance of the classifier for a range of k values (from 1 to 20) over the 10 partitions of training and validation data and selecting the input parameter that corresponded to the best average performance. We similarly obtained optimal parameters for the SVM classifier, which requires specification of 1) a cost parameter, C, that controls the tradeoff between reducing training errors and controlling the complexity of the model, and 2) a parameter, γ, that controls the width of the Gaussian kernel. The latter two classifiers were retrained on the augmented training and validation data using these optimal parameters. We did not optimize any parameters for the logistic regression classifier.