Effects of spectral and temporal disruption on cortical encoding of gerbil vocalizations

Abstract

Animal communication sounds contain spectrotemporal fluctuations that provide powerful cues for detection and discrimination. Human perception of speech is influenced both by spectral and temporal acoustic features but is most critically dependent on envelope information. To investigate the neural coding principles underlying the perception of communication sounds, we explored the effect of disrupting the spectral or temporal content of five different gerbil call types on neural responses in the awake gerbil's primary auditory cortex (AI). The vocalizations were impoverished spectrally by reduction to 4 or 16 channels of band-passed noise. For this acoustic manipulation, an average firing rate of the neuron did not carry sufficient information to distinguish between call types. In contrast, the discharge patterns of individual AI neurons reliably categorized vocalizations composed of only four spectral bands with the appropriate natural token. The pooled responses of small populations of AI cells classified spectrally disrupted and natural calls with an accuracy that paralleled human performance on an analogous speech task. To assess whether discharge pattern was robust to temporal perturbations of an individual call, vocalizations were disrupted by time-reversing segments of variable duration. For this acoustic manipulation, cortical neurons were relatively insensitive to short reversal lengths. Consistent with human perception of speech, these results indicate that the stable representation of communication sounds in AI is more dependent on sensitivity to slow temporal envelopes than on spectral detail.

animal communication sounds are composed of spectral and temporal cues that each contribute to detection and discrimination. The perceptual relevance of temporal modulations of amplitude is suggested by the prominent representation of modulation frequencies <16 Hz in natural sounds, including speech (Drullman et al. 1994; Elliott and Theunissen 2009; Xu and Pfingst 2008). In fact, modulation frequencies <50 Hz are sufficient to support robust speech recognition, even when the spectral information is reduced to only four bands of noise (Shannon et al. 1995). Conversely, speech recognition is reduced when temporal information is disrupted by iteratively time-reversing speech segments of >50 ms (Saberi and Perrott 1999). These findings are consistent with the theory that temporal coherence, including low-frequency amplitude modulations, are critical for extracting an auditory stream in a noisy environment (Shamma et al. 2011). This theory predicts that disrupting temporal cues would have a greater impact on the neural encoding of vocalizations than would disruption of spectral cues. Here, we tested this idea by characterizing the response of auditory cortex (AC) neurons in awake gerbils to species-specific vocalizations in which spectral or temporal cues were altered.

A number of studies have examined the effect of temporal disruption on responses at different levels of the auditory system by fully time-reversing species-specific vocalizations. These investigations have mainly focused on changes to overall firing rate, with contradictory results. In the marmoset AC, this manipulation reveals a firing rate selectivity for forward vocalizations that was not present when marmoset vocalizations were tested in cat AC, suggesting a species specificity (Wang and Kadia 2001; Wang et al. 1995). In contrast, forward selectivity was not observed in cat AC even when cat vocalizations were used as stimuli (Gehr et al. 2000). Likewise, there was no effect of species-specific vocalization reversal on firing rate in the AI of squirrel monkeys (Glass and Wollberg 1983; Pelleg-Toiba and Wollberg 1991). In the guinea pig inferior colliculus (IC), some neurons preferred natural guinea pig vocalizations and some preferred the reversed versions (Suta et al. 2003). In the auditory thalamus, no preference for forward vocalizations was found for rats (Philibert et al. 2005) or guinea pigs (Philibert et al. 2005; Suta et al. 2007). Thus this forward-selectivity may be specific to marmoset AC.

A few studies have also examined the effects of other spectral and temporal disruptions on cortical vocalization processing. Lewicki and Arthur (1996) investigated temporal context sensitivity in the songbird auditory forebrain by disrupting song syllable order and found that most neurons responded equally well to normal and temporally manipulated songs. However, neurons in this region were sensitive to low-pass filtering of the spectral and temporal modulations found in songs, as revealed by functional MRI (Boumans et al. 2007). Gehr et al. (2000) examined multiunit spike count in response to nine versions of a cat meow, which were time compressed, time expanded, low-pass- or high-pass filtered, and/or reversed. The authors found that ∼65% of stimulus pairs could be distinguished by spike count in the onset and/or sustained part of the response. Gourevitch and Eggermont (2007) tested many of the same stimuli, as well as meows in which the carrier frequency was up- or downshifted. The investigation focused on overall changes in firing rate during the response and on a comparison across different auditory cortical regions. In the mouse IC, a region upstream of AI, temporal disruption of mouse vocalizations by removal of amplitude modulations or by time-compression or -stretching heterogeneously altered the response patterns of most neurons by changing the spike rate and/or spike pattern (Holmstrom et al. 2010). The results of these studies point to a need for a more detailed examination of cortical response changes induced by spectral and temporal stimulus disruption.

The Mongolian gerbil has a repertoire of communication sounds containing temporal modulations primarily <8 Hz (Ter-Mikaelian et al. 2012). This modulation frequency range is well correlated with the sensitivity of gerbil AI neurons to amplitude-modulated (AM) tones (Ter-Mikaelian et al. 2007), consistent with a broad literature on AM processing (Joris et al. 2004). However, neural responses to natural sounds may not be easily predicted by the responses to simple synthetic stimuli (Holmstrom et al. 2010; Portfors et al. 2009; Theunissen et al. 2000; Woolley et al. 2006). Therefore, we tested the spectral and temporal processing windows of single AI neurons with two complementary manipulations of natural vocalizations: 1) spectral information was reduced by replacing the frequency-specific information with 4–16 bands of noise, while retaining the amplitude cues; and 2) temporal information was disrupted by time-reversing segments over a range of timescales, while maintaining spectral content. These manipulations were designed to parallel those of Shannon et al. (1995) and Saberi and Perrott (1999). Our observations show that single AI neuron responses were relatively robust to spectral degradation and temporal disruption at time scales >20 ms.

METHODS

Animal Preparation and Electrophysiological Recording

All procedures relating to the care and use of animals in this study were approved by the University Animal Welfare Committee at New York University. The methodology for chronic recordings in awake gerbils has been described in detail previously (Ter-Mikaelian et al. 2007). Briefly, adult animals were medicated (ketoprophen, 1.5 mg/kg intranasal, and dexamethasone, 0.35 mg/kg ip) and hydrated (normosol, 1.5 ml sc) before surgery, which was performed while animals were under isoflurane anesthesia. A head cap containing a head post was affixed to the skull for stabilization of the head during recording, and a craniotomy was performed over the left temporal cortex, permitting electrode access to AI. During recording, animals stood comfortably on a platform while the head was held in position by the head post. Animals exhibiting agitation (as evident from piloerection or frequent fidgeting) were administered the relaxant medetomidine at the beginning of the recording session (∼0.1–0.3 mg/kg, intranasal), supplemented as necessary. At this dosage, medetomidine does not appear to affect neural response magnitude in the cortex as assessed by functional MRI (Nasrallah et al. 2012). Behaviorally, medetomidine lowers motivation but does not affect attention or response accuracy in rats performing a short-term memory task (Ruotsalainen et al. 1997). Gerbils trained to detect amplitude modulation in our laboratory are also able to perform the task after medetomidine administration (unpublished observations, Sanes DH).

For electrophysiological recording, tungsten electrodes with 1.5- to 2.5-MΩ impedance (Microprobe, Gaithersburg, MD) were advanced ventrolaterally through the craniotomy at an angle of ∼14° lateral to vertical. Electrode insertion distances spanned a range of ∼0.3–3 mm (median 1.37). In all experiments, the location of the electrode in AI was determined based on a tonotopic progression matching that previously described for gerbil AI (Thomas et al. 1993). An attempt was made to sample from different tonotopic locations within each animal; thus the neurons in our study had a wide range of frequency tuning (see Fig. 9). Single-unit activity was recorded extracellularly using experimenter-controlled spike discrimination (MALab, Kaiser Instruments, Irvine, CA), and the times of action potential occurrence were stored for later analysis. Five animals (two females and three males aged 63–87 postnatal days) were used for chronic awake recording experiments. Between 3 and 10 recording sessions were done with each animal. A total of 103 cells were recorded; of these, 61 were lost before the presentation of the disrupted stimulus set could be completed. The remaining 42 neurons comprise the partially overlapping sets of neurons tested in the spectral disruption and temporal disruption experiments. Cortical cells typically had low rates of spontaneous activity (means ± SE: 3.4 ± 0.5 spikes/s for cells where spontaneous firing was explicitly assessed; n = 27).

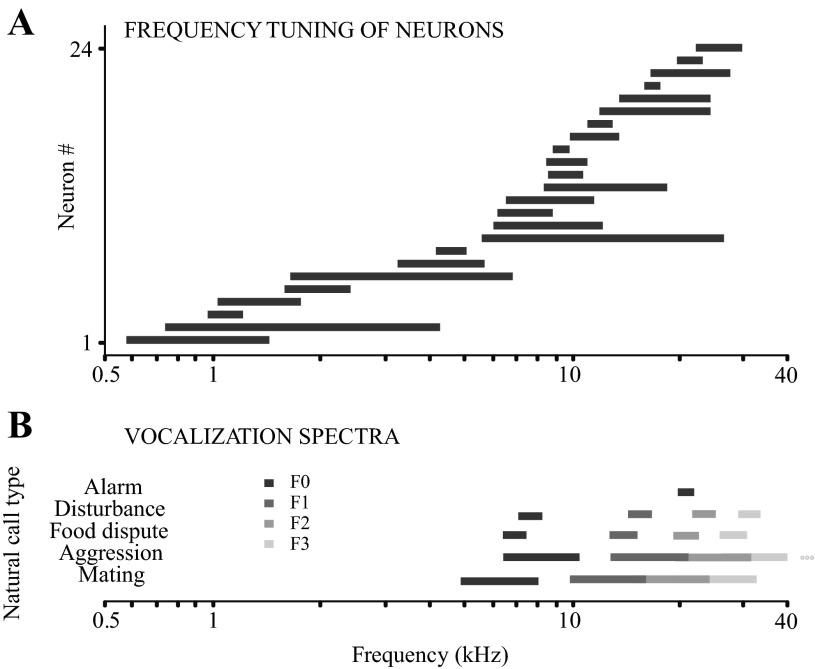
Fig. 9.

Frequency response areas of the sampled neurons in relation to the frequency content of the natural call stimuli. A: frequency tuning bandwidths for 24 neurons of the 42 used in the spectral and/or temporal experiment. These were the neurons for which rigorous tone frequency-tuning functions were available. Frequency tuning bandwidth was calculated as the width of the rate-vs.-frequency tuning function at half-height. B: frequency ranges of the fundamental and harmonics for the 5 standard natural calls. Frequency ranges of the 1st and 2nd, and 2nd and 3rd harmonics overlap for the aggression and mating calls.

Acoustic Stimulation

Cells were assessed with several simple synthetic stimuli as well as natural and manipulated gerbil vocalizations. All experiments were performed in a sound-attenuated chamber (Industrial Acoustics, Bronx, NY). The system used for generation, calibration, and presentation of synthetic sounds has been described in a previous publication (Malone and Semple 2001). Briefly, stimuli were presented via electrostatic earphones (STAX Lambda) in custom housings (Custom Sound Systems) fitted to ear inserts. Sounds were always presented binaurally at equal sound pressure level (SPL). Before each experiment, a previously calibrated probe tube and condenser microphone (4134; Brüel and Kjær) was used to calibrate the SPL expressed in decibels (dB, re: 20 mPa) at each ear for level and phase from 40 Hz to 40 kHz, under computer control.

The vocalization stimuli used were original or altered versions of adult gerbil calls, which were previously high-pass filtered and analyzed. Calls were edited and presented using Cool Edit Pro (version 1.2, Syntrillium Software, Phoenix, AZ). A 20-ms synchronizing pulse which coincided with the call onset was simultaneously input to the custom data acquisition hardware (MALab; Kaiser Instruments). The digital sound signal generated by Cool Edit Pro was fed to two five-band parametric equalizers (551E; Symetrix), one for each ear, to flatten the amplitude transfer function of the speakers. This manipulation resulted in a relatively flat output up to 10 kHz, while higher frequencies were generally somewhat attenuated (∼10–20 dB).

Standard call set.

In a typical recording session, each cell was first assessed for frequency tuning between 0.5 and 35 kHz by obtaining an iso-intensity function at 10–30 dB above threshold. This was followed by a standard set of five gerbil calls, each representing one class of vocalization (aggression, alarm, food dispute, mating, and disturbance; Ter-Mikaelian et al. 2012). The standard set was formed by selecting one call that closely matched the acoustic characteristics of the median call in each behavioral class from the repertoire of recorded gerbil vocalizations in our laboratory. Each of the 5 standard calls, ranging in duration from 180 to 376 ms, was repeated 25 times at a rate of 1/s. The rationale for presenting calls at 1/s was twofold. First, this is about the average rate of call repetition in a seminatural context (Ter-Mikaelian et al. 2012), although significant variability exists in the repetition rates of calls within a series. Second, by testing a variety of repetition rates in a subset of the cells (data not shown), we found that with a trial length of 1 s, minimal adaptation in firing rate occurs.

Relative responsiveness to each call was scored by visual assessment, and from the five call types, two to three which elicited the most robust responses were chosen for more detailed testing of the cell. Each call in this study was presented at a fixed level for all recorded neurons to permit population comparisons and analyses. Spectrum level of all calls was between 67 and 74 dB for the spectral disruption experiment and between 71 and 79 for the temporal disruption experiment. The full stimulus protocol required ∼35 min per cell. Cells tested with spectrally and temporally disrupted calls comprise partially overlapping sets.

Stimulus set for the spectral disruption experiment.

While the terms “spectral” and “temporal” are used variously by different investigators, for the purposes of this study, we define temporal properties as the amplitude envelopes of vocalizations and spectral properties as the overall spectral content and power of a vocalization.

Five standard calls (aggression, alarm, food dispute, mating, and disturbance) were used for the spectral disruption experiment. For each call, three disrupted versions were generated: 16-channel, 8-channel, and 4-channel vocoded versions. To create these stimuli, we used a freeware vocoding program (TigerCis version 1.04.03; Qian-Jie Fu). The frequency range for spectral information was defined as 2–40 kHz, in accordance with the range of call fundamental frequencies. Channel boundaries were assigned using a logarithmic distribution or Greenwood function (Greenwood 1991). It should be noted that vocoding the calls changes not only the spectral, but also the high-frequency temporal information due to the introduction of band-passed noise, which contains more energy at high frequencies than the original calls do.

The full stimulus set consisted of the five natural calls, the five 4-channel calls, the five 8-channel calls, and the five 16-channel calls. (The results for the 8-channel stimuli were intermediate to the 4-channel and 16-channel versions and are thus omitted from detailed discussion in this report.) Each call was presented 25 times consecutively at a rate of 1/s, with a silent interval of 1 s between each set of 25. The spectrograms and oscillograms of the natural and vocoded versions of three example calls are shown in results (see Fig. 3). Notice that the spectrograms of the disrupted calls look grossly different from the natural counterparts.

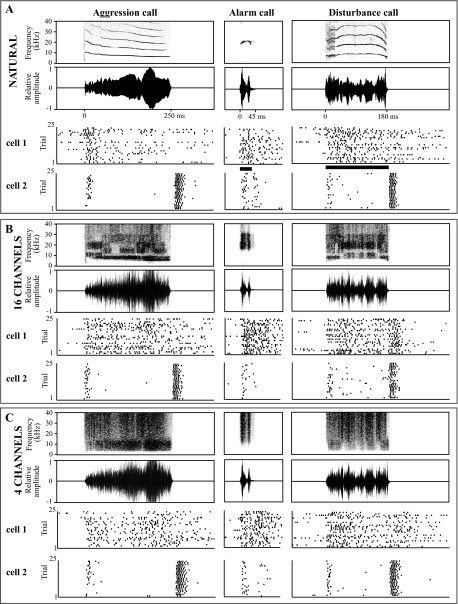
Fig. 3.

Example responses of neurons to spectrally disrupted calls. Spectrograms (top rows in A–C) and oscillograms (second rows in A–C) of 3 example vocalizations are followed by the responses of 2 example neurons (cell 1 and cell 2). A: natural calls. B: spectrally disrupted calls with 16 spectral channels. C: spectrally disrupted calls with 4 channels.

Stimulus set for the temporal disruption experiment.

One of the standard calls (usually, the longest one eliciting a robust response) was used for the temporal disruption experiment. Manipulated vocalizations were created by dividing the call into equal segments of specified length and locally time reversing all segments. The reversal was performed without smoothing the transitions between adjacent segments, as in the original study of the perception of locally time-reversed speech (Saberi and Perrott 1999). Tested segment lengths were 5, 10, 20, 30, 50, 100, 150, and 200 ms. For calls with duration <200 ms, the last value was not tested. If the call duration was not divisible by a particular segment length, the remainder of the waveform after the call segmentation was not time reversed, as this would necessitate including a shorter reversed segment, or incorporating silence within the call waveform. Either approach would have confounded the interpretation of the results. In the final manipulation, the entire call was time reversed. Each stimulus, the natural call, the locally time-reversed calls, and the fully time-reversed call, were presented 25 times consecutively at a rate of 1/s, with a silent interval of 1 s between each set of 25. It should be noted that this local reversal procedure results in discontinuities in the frequency signal, creating a local broadband noise artifact at the segment borders.

The temporal disruption test was usually accompanied by a sinusoidally amplitude-modulated (SAM) tone test paradigm as an independent assessment of the temporal characteristics of the cell, as described previously (Ter-Mikaelian et al. 2007). SAM tones were presented at the approximate best frequency of the neuron and at the SPL that produced the strongest synchronized response. The following modulation frequencies were tested as encompassing the range of AI neuron temporal sensitivity (Ter-Mikaelian et al. 2007): 0.5, 1, 2, 3, 4, 10, 20, and 30 Hz. An unmodulated tone at the same frequency and SPL and of the same duration as the SAM tones was also included as a control stimulus.

Data Acquisition and Analysis

For analysis of vocalization responses, spike times and the occurrence of the synchronizing pulse signaling the onset of a call stimulus were acquired in parallel. The data were subsequently exported to Matlab (version 7.1; MathWorks, Natick, MA), and the spike time arrays were aligned according to stimulus start times. This permitted the generation of raster plots and peristimulus time histograms for individual cells as well as across subpopulations of cells (“pooled histograms”). We did not exclude onset responses, as is sometimes done in the analysis of responses to long, arbitrary waveforms.

Several quantitative methods of comparing response patterns to complex stimuli were employed during within-cell as well as across-cell and across-population comparisons. Each of these methods implicitly assumes that a downstream neuron or neuronal population is “reading” the output of AI cells, and each requires a timescale or bin size parameter to define the resolution at which this readout is performed. Although all the methods operate on similar principles, not all are equally well-suited to single-cell or population level analysis, and each is associated with specific disadvantages. Thus different approaches were employed depending on the issue under examination.

Analysis of population responses: K-means clustering using Euclidean distance.

The first method used in this study is K-means clustering (implemented in Matlab), which can be performed either with single cell peristimulus time histograms or with pooled histograms from a cell population. This procedure permits the partitioning of a set of observations into a specified number of mutually exclusive clusters using a specified metric of dissimilarity. Each observation is handled as an object in a multidimensional space; the algorithm aims to set the centroids of each cluster so as to minimize the distance (in terms of the specified metric) between observations within each cluster and to maximize the distance between adjacent clusters.

In this study, each observation was a pooled histogram, represented as a vector with each value denoting the number of spikes in one bin. A range of bin sizes was tested (1, 2, 5, 10, 20, and 50 ms). The dissimilarity of these vectors was determined by calculating the Euclidean distance between them. Alternative dissimilarity measures, for example, one minus the sample correlation between histograms, or one minus the cosine of the included angle formed between two vectors, were also considered, and produced qualitatively similar results for several tested cells (data not shown). Euclidean distance was chosen because it assesses differences both in the relative distribution of spikes among bins as well as in the absolute numbers of spikes in each bin.

The clustering algorithm was set to search for a solution that minimized the sum of distances from each observation to its cluster centroid over 200 iterations. Nonetheless, it was possible that the solution found was a local minimum that did not produce the best separation between responses. To protect against this possibility, 100 repetitions of the iterative clustering were executed, and the best solution among all repetitions was used. Note that the number of solution improvements over 100 repetitions generally did not exceed 5. The results were checked to verify that there were no empty clusters.

VP spike timing distance.

A disadvantage of using a Euclidean distance-based metric of dissimilarity is the necessity of prebinning responses, thus artificially introducing categorical separations between adjacent time bins. This problem is avoided by another spike timing-based measure (Victor and Purpura 1997), which will hereafter be referred to as “VP spike timing distance.” This metric compares a pair of spike trains in terms of the minimal “cost” of converting one train into the other. This cost is defined as the absolute difference in the total number of spikes between the trains (i.e., the number of spike additions or deletions that must be performed for the trains to match in firing rate), plus the magnitude of lateral movements of spikes necessary to perfectly align the remaining spikes in the two trains. The latter is calculated as the absolute time difference in the occurrence of the spikes to be aligned, multiplied by the cost of the movement, which is in turn defined as:

$$Cost=1/timescale$$

where the timescale is expressed in milliseconds. Thus, at large timescales of analysis, the cost of spike movement becomes small, and the absolute difference in the total spike count determines the dissimilarity between two trains. The VP spike timing distance then becomes primarily an assessment of rate coding on the basis of average firing rate. Conversely, at very small analysis timescales, the cost of moving spikes becomes significant, and spike timing plays a greater role than total spike count in determining spike train similarity. To confirm this, for several cells, VP spike timing analysis was performed at a very large timescale of 100,000 ms and compared with the results of differentiating responses purely on the basis of total spike count. Results were identical (data not shown).

Classification algorithm using VP spike timing distance.

Since VP spike timing distance operates on a pair of spike trains at a time, it is necessary to establish a method of comparing entire sets of responses, such as responses to two different calls, A and B, containing 25 trials each. One possibility is to determine the VP spike timing distances between all possible pairs of trials in A and plot these as a probability distribution. One can then calculate the distances between all possible A–B pairs of trials and also plot these as a probability distribution. The region of overlap between these two distributions denotes the proportion of cases where trials from B can be erroneously identified as belonging to A. This method is sufficient for quantifying the differences between two groups of responses. However, because both the temporal disruption experiment and the spectral disruption experiment aim at understanding what perceptual decisions can be made on the basis of AI neuron firing, it is important to define a procedure for deciding whether a specific trial belonged to A or B.

One possible decision method is to select one spike train from A and one spike train from B to serve as template responses and assign all other spike trains to A or B based on which template is closer in VP spike timing distance. The drawback of this approach is that, if responses within each set show significant variability, the performance of the algorithm will depend significantly on the particular choice of template.

The classification algorithm implemented in this study is an extension of the probability distribution concept. Suppose that a given spike train occurred in response to stimulus A. The procedure is to calculate the VP spike timing distance (at a specific timescale) between this spike train and all other spike trains from set A in a pairwise fashion and obtain a mean value. Similarly, the pairwise distances are calculated between this spike train and all spike trains from set B to obtain a second mean. The train is then assigned to the set with the lower mean value of VP spike timing distance, meaning that the spike train is less dissimilar from the responses in that set. For two sets of responses, A and B, with 25 trials each, this procedure is repeated to produce 50 perceptual “decisions,” and the results are summarized in a 2 × 2 confusion matrix of the form depicted in Fig. 1B. A percent correct value is determined by adding the values along the diagonal (correct assignments; Fig. 1B, top left to bottom right) and dividing by the total number of trials.

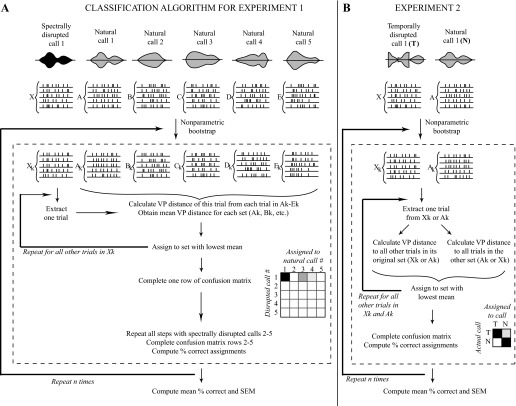
Fig. 1.

Procedure for comparing response sets to natural and disrupted stimuli using VP spike timing distance. A: classification algorithm used in experiment 1. Responses to spectrally disrupted calls were quantitatively compared with those to natural calls using VP spike timing distance. The response to each trial of a disrupted call was assigned to the set of natural call responses that were least different according to this metric, allowing the completion of a confusion matrix, where the strength of shading corresponds to the percentage of calls assigned. Perfect classification performance would result in a confusion matrix with darkly shaded squares along the diagonal from top left to bottom right, with all other squares unshaded. B: classification algorithm used in experiment 2. Responses to a temporally disrupted call were compared with those to the natural version of the same call using a similar procedure as in experiment 1. If the response to a disrupted call was fully confusable with that to the natural call, ∼50% of trials would be assigned incorrectly, resulting in an evenly shaded 2 × 2 confusion matrix. Perfect classification would result in a 2 × 2 matrix with the top left and bottom right square fully shaded, and the other 2 squares unshaded. In both A and B, n refers to the number of iterations of bootstrapping (refer to methods).

Nonparametric bootstrapping.

Since the presence of unrepresentative deviant trials in sets A or B could produce misleading classification results, nonparametric bootstrapping was used to estimate the reproducibility of the percent correct value. Nonparametric bootstrapping is a statistical inference procedure that treats the set of available spike trains as approximating the real-world distribution of spike trains produced by the given cell in response to a given stimulus. It then samples from this set with replacement to create new samples of spike trains. For each such sample, the classification procedure described above is repeated to generate a new confusion matrix and calculate the corresponding percent correct. Finally, the results from all bootstrap samples are averaged to determine a mean percent correct, and the standard error of the mean is calculated to assess its reliability. The number of bootstrap samples was empirically set at 1,000 for comparisons of two data sets with 25 trials each, as this reduced the standard error to <0.2%. When larger response sets (50 or 75 trials) were compared (as was done whenever possible for the natural call response; see Full classification algorithm for temporal disruption experiment), 1,500 bootstrap samples were used; again, this achieved standard error values of <0.2%.

Full classification algorithm for spectral disruption experiment.

A schematic of the full comparison procedure of responses to five natural calls and their spectrally disrupted counterparts using VP distance is provided in Fig. 1A. For simplicity, the response sets to natural calls 1–5 are called A, B, C, D, and E (each containing 25 trials) and the response set to the disrupted version of call 1 is named X.

Quantitative analysis parameters for spectral disruption experiment.

For analysis of the responses of individual cells to spectrally disrupted calls, only the portion of the spike train corresponding to stimulation was considered. First-spike latency in response to the natural call was determined by averaging the time of the first spike after stimulus onset over 25 trials and rounding to the nearest millisecond. The analysis window was set to include all spikes from stimulus onset to stimulus offset plus latency, plus an additional 10 ms to allow for jitter in the response latency. A standard set of analysis timescales (2, 8, 16, 32, 64, 256, and 1,024 ms) was used for VP spike timing analysis of all cells (see below). Mid-range resolutions of 16–64 ms allowed the best differentiation of spike trains for most cells.

Full classification algorithm for temporal disruption experiment.

A schematic of the full comparison procedure of two sets A and X using VP distance is shown in Fig. 1B. For the temporal disruption experiment, set A was always the set of spike trains in response to the natural call; set X was the set of responses to the call locally time reversed at a particular reversal length. Thus, for each cell, results consisted of a curve of mean percent correct as a function of the pairwise comparison (i.e., response to natural call vs. 5-ms-reversed call, response to natural call vs. 10-ms-reversed call, etc.).

Since all comparisons rely on reference set A, it is important that set A is truly representative of responses to the natural call. To maximize this probability, responses to the natural call from other test paradigms, such as the standard call set were added to A whenever possible. Often, the natural call in these additional test paradigms was presented significantly earlier or later in the recording session compared with the natural call in the “local time reversals” experiment. In some cases, this time difference corresponded to an apparent change in the cell's excitability; while isolation of the spike by the electrode remained identical, a significant increase or decrease in firing rate and occasionally in response pattern occurred. For such cells, only the natural call responses from the temporal disruption paradigm were included in response set A for the quantitative analysis; the decision to do so was based on a qualitative response patterns assessment.

Quantitative analysis parameters for temporal disruption experiment.

As in the Spectral Disruption experiment, the analysis window was set to include all spikes from stimulus onset to stimulus offset plus latency, plus an additional 10 ms to allow for jitter in the response latency. Initially, an exponential series of analysis timescales (1, 2, 4, 8, 16, 32, 64, 128, 256, 512, and 1,024 ms) was tested on a subset of cells. The performance of the algorithm at each timescale was assessed by calculating the total percent correct across all pairwise comparisons. It was found that discrimination between natural and locally time-reversed stimuli was generally poor at 1, 2, and 4 ms regardless of reversal length; best performance was generally achieved at 16 or 32 ms, and discrimination declined dramatically by 256 ms. Since each comparison required significant computational time due to the iterative bootstrapping process, the standard set of timescales was reduced to 2, 8, 16, 32, 64, 256, and 1,024 ms for VP spike timing analysis of all cells. Mid-range resolutions of 16–64 ms allowed the best differentiation of spike trains for most cells.

Analysis of SAM tone responses.

Responses to SAM tones were analyzed for synchrony to the stimulus period. The first 100 ms, corresponding to the onset response, were excluded to make the results comparable to our earlier work (Ter-Mikaelian et al. 2007). A period histogram was created for each modulation rate with 100 bins per period. This period histogram was used to calculate a vector strength value at each modulation frequency, which was the basis of calculating a modified Rayleigh statistic

$$z=2\times N\times {\text{VS}}^2,$$

where N is the number of spikes in the region of interest and VS is the vector strength. Modified Rayleigh statistic values of 13.8 or higher correspond to statistically significant synchrony to the modulation period at a 0.1% confidence level (Liang et al. 2002). Thus a SAM synchrony cutoff frequency was determined by interpolating within the Rayleigh statistic curve to the modulation frequency associated with this value. The reciprocal of a neuron's SAM synchrony cutoff was our estimate of its temporal integration window for synthetic stimuli.

RESULTS

Individual Neurons and Small Neuron Populations Are Able to Classify Natural Calls

We first examined the ability of AI neurons to uniquely represent the five natural gerbil call types used in this study (Fig. 2A). The responses of individual neurons (n = 24, the same neurons used in the spectral experiment) to the calls were analyzed using a classification algorithm similar to that shown in Fig. 1A. The responses of each cell to single trials of natural calls were compared with its responses to other natural calls using a spike timing-based metric (see methods). The classification algorithm attempted to match responses to a specific call to other trials of responses to the same call. Mistakes resulted when the responses to two different natural calls failed to be differentiated. The confusion matrix in Fig. 2B shows the proportion of responses to each call that were correctly classified. The average performance of individual neurons on the classification of the five natural calls was 54.6% correct, well above the 20% chance level.

Fig. 2.

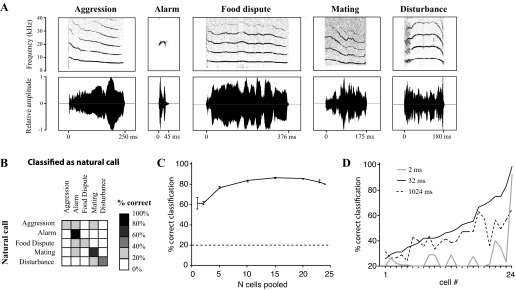
Classification of natural calls by auditory cortex (AI) cells. A: spectrograms (top row) and oscillograms (bottom row) of the 5 natural calls used as stimuli in this study. B: averaged performance of individual AI neurons on the classification of the 5 natural calls. Each neuron performance was measured at its best analysis timescale (see methods). Sample consists of the same neurons tested in the spectral disruption experiment (n = 24). C: performance of the boosting algorithm at classifying natural call responses as a function of the number of cells whose responses were pooled. Points represent mean classification performance ± SE. The last point (at x = 24) does not have error bars, as it represents the pool of all tested cells. Dashed line indicates chance performance of the classification algorithm. D: percent correct classification of natural calls by individual neurons when spike trains were analyzed at 3 different VP timescales: 2 ms (“precise spike timing,” gray line), 1,024 ms (“rate code,” dashed line), and 32 ms (a mid-range timescale, solid black line). Cells are ranked by percent correct classification at 32 ms.

To determine the number of neurons required for robust classification of natural calls, we tested the performance of randomly selected subpopulations of these 24 neurons (Fig. 2C). Since the number of possible combinations can be quite large (e.g., almost 2 million combinations for 10 cells), for points in the middle of the graph (i.e., selecting 5, 10, or 15 neurons out of the population), 600 combinations were randomly selected, and the performance of these 600 cases was averaged. The responses of the selected cells were analyzed using a boosting algorithm, in which each cell's highest-probability classification of the cell for a given stimulus was obtained. For instance, if applying the VP spike timing-based classification algorithm to a given neuron's response produced a confusion matrix in which 60% of trials corresponding to the aggression call were correctly classified as the aggression call, then the neuron would assign that stimulus to the aggression call category. If, on the other hand, the neuron confusion matrix showed that the aggression call was most commonly classified as the mating call, then the neuron's assignment would reflect this. The boosting algorithm tallied up the assignments of the individual cells in the subpopulation and categorized each stimulus according to the majority assignment. If there were an equal number of cells assigning a given stimulus to, for instance, an aggression call and a mating call, a choice was made randomly among the equally frequent assignments.

Figure 2C shows that the performance of the cells improved gradually with increasing population size until it reached a plateau at around 20 cells. The best classification performance was achieved by 15 cells at 86.6% correct. Increasing the sample necessitated including neurons that did not differentiate well among the stimuli and whose assignments added noise to the classification. These may be cells that are not normally involved in this type of task. We found no sex differences in the processing of natural calls (data not shown).

Spectral Disruption Does Not Prevent Call Discrimination

Single AI neurons (n = 24) were tested with natural and spectrally disrupted calls. Raster plots showing the response to an aggression, an alarm, and a disturbance call are presented for two cells (Fig. 3). For a single vocalization, if natural and spectrally disrupted variants elicit similar neural responses, this implies that fine spectral detail is not critical for call representation in AI.

To quantify the degree of similarity between AI cell representations of natural and spectrally manipulated vocalizations (Fig. 3), responses of individual cells to single trials of disrupted calls were compared with responses to natural calls using a spike timing-based metric (see methods). For the 4-channel and 16-channel stimuli, the classifier attempted to match the responses to these disrupted stimuli to the respective natural call responses. Mistakes resulted when, for example, a response to disrupted call 1 was more similar to the response to natural call 2 than to natural call 1. For the five natural calls, the classification algorithm attempted to match responses to a specific call to other trials of responses to the same call. Mistakes resulted when the responses to two different natural calls were confusable. Based on pair-wise comparisons between individual response trials to disrupted and natural calls, each disrupted call response was classified as belonging to one of the five call types.

As illustrated in Fig. 1A, a confusion matrix was constructed for each neuron and stimulus condition (4- or 16-channel, and natural calls) showing the spectrally disrupted stimulus (vertical axis), and the natural call to which responses to that stimulus were assigned (horizontal axis). Shading indicates the percentage of responses assigned to a particular stimulus. A confusion matrix illustrating perfect performance would contain black squares along the diagonal from top left to bottom right, with all other squares unshaded. This analysis was performed at a standard range of timescales for every cell (see methods): unless otherwise noted, results reported are for the timescale that produced the best classification for each cell.

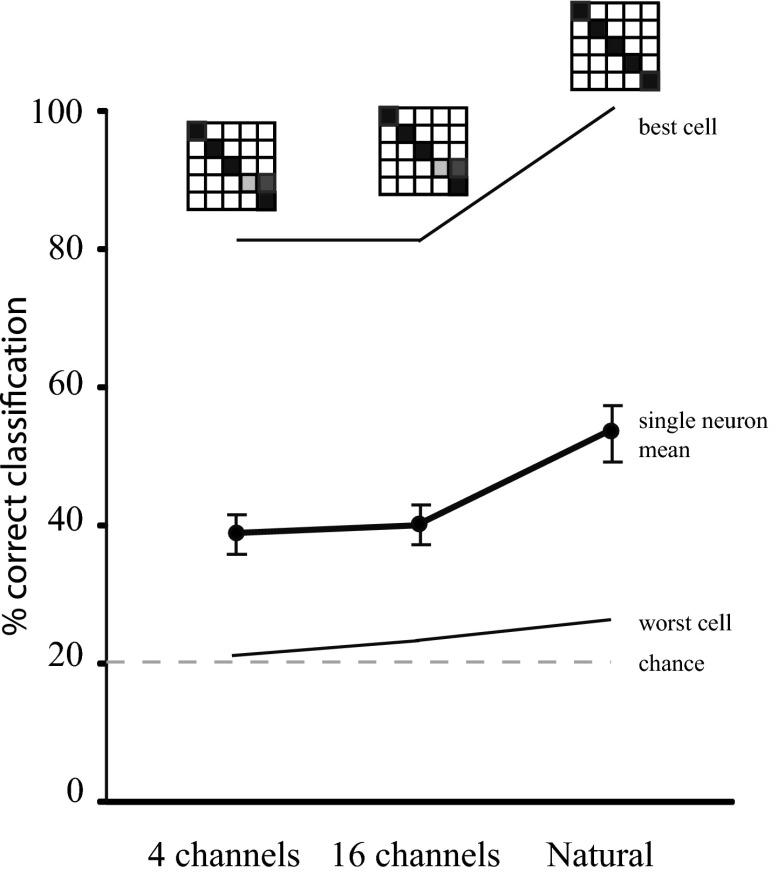
Figure 4 shows the outcome of applying this classification algorithm to the responses of two single neurons (the best and worst encoders). The first two points (4- and 16-channel) reflect how similar the responses to the disrupted stimuli are to responses to each of the five natural stimuli. The third point (natural) reflects the similarity in the responses to the unmanipulated natural calls (i.e., calls with an arbitrarily large number of spectral channels). It is clear that spike timing information in individual responses to four-channel calls was sufficiently similar to that in natural call responses to permit classification well above chance in all except one neuron (labeled “worst cell”).

Fig. 4.

Responses to spectrally disrupted calls are predicted by temporal call characteristics. Results of classification of the responses of single neurons to spectrally disrupted and natural calls; 20% correct represents chance performance. The best and worst performing neuron in the population are shown. A confusion matrix for each condition is displayed above the respective point on the graph for the best neuron. The mean classification performance for all sampled AI cells (n = 24) is shown in bold.

This analysis was performed for all cells, and results were averaged across the sample. Figure 4 (bold line) shows that the mean classification performance was well above chance for the three stimulus conditions. There was no significant improvement between the 4-channel and 16-channel stimulus conditions, suggesting that increased spectral detail in the stimulus had a minimal effect on spike timing (two-tailed paired t-test, P = 0.4698; n = 24 pairs). The final point on the graph demonstrates the results of using the classification algorithm to compare the responses to the five base natural calls, demonstrating a significant improvement when compared with the 4-channel stimulus (two-tailed Wilcoxon matched-pairs signed rank test, P = 0.0003; n = 24 pairs; means 38.4% correct and 52.8% correct, respectively).

Population Response Accurately Classifies Spectrally Disrupted Calls

To assess call representation among a small population of AI neurons, we pooled the discharge pattern of all cells to each natural and spectrally disrupted call. Spike trains were aligned by stimulus onset, binned at 5 ms, and summed. The population histograms displayed no striking differences between the responses to natural and spectrally disrupted versions of three calls (Fig. 5A). To quantify how robust population representations of the calls are to spectral disruption, we used a classification algorithm, Euclidean distance between population histograms to cluster the responses to natural and spectrally altered calls into five call types based on similarity. To make the classification task more challenging, responses to eight-channel stimuli were included in the test pool. This method resulted in 95% correct classification of 20 population histograms (5 call types, 4 spectral conditions) into 5 classes. This suggests that in spite of major disruptions in spectral content, a relatively small population of AI neurons is sufficient to classify variants of five species-specific vocalizations.

Fig. 5.

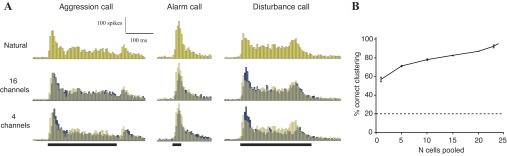
Temporal call features are preserved in AI population representation of spectrally disrupted calls. A: histograms showing pooled responses of all sampled AI cells (n = 24) to 3 natural and spectrally disrupted calls. Responses were aligned by stimulus onset and binned at 5 ms. Solid rectangles below each natural call indicate stimulus duration. Note that stimuli are depicted aligned to the response onset for ease of visual inspection. The natural call response has been made semitransparent and superimposed on the locally time-reversed call responses for ease of comparison. B: performance of the Euclidean distance-based clustering algorithm at clustering responses to natural and disrupted calls together, as a function of the number of cells whose responses were pooled. Responses of individual cells were binned by 25 ms before pooling. Points represent mean classification performance ± SE. The last point (at x = 24) does not have error bars, as it represents the pool of all tested cells. Dashed line indicates chance performance of the clustering algorithm.

To determine the number of neurons required for robust classification, the clustering algorithm was tested on the pooled responses of randomly selected subpopulations of the 24 recorded neurons (Fig. 5B). For points in the middle of the graph (i.e., selecting 5, 10, or 15 neurons out of the population), 600 combinations were randomly selected, and the performance of the clustering algorithm for these 600 cases was averaged. Figure 5B shows that performance is significant even with as few as five cells and improves gradually with increasing population size. It should be noted that the clustering algorithm performs better than the spike timing distance-based method with one cell (Fig. 4); however, as it is relatively less flexible and less rigorous (see methods), it was not the method of choice for the other single-cell analyses in this study.

Temporal Disruptions Degrade Call Representation

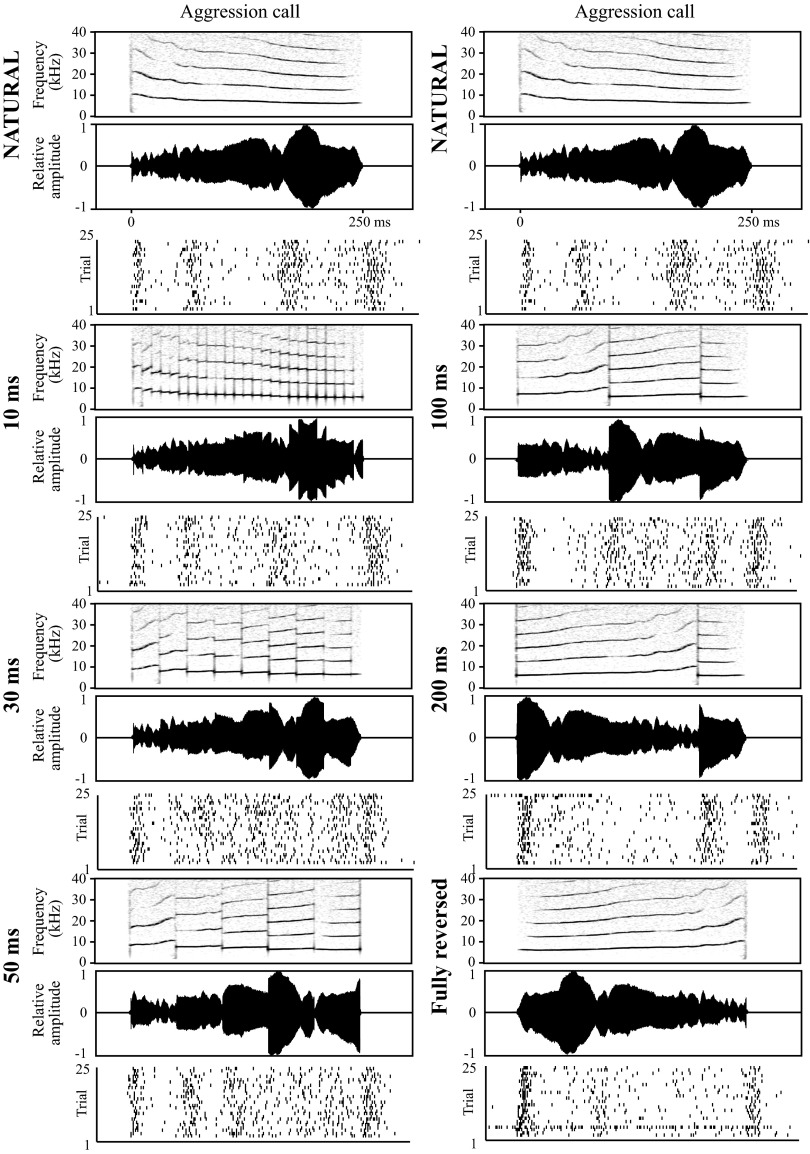
Temporally disrupted calls were tested on 37 AI cells. Example responses of one neuron to the aggression call are shown in Fig. 6. For this neuron, an onset and strong offset response are observed for each stimulus independent of reversed segment length, but there are many unique response features, particularly for disruption timescales ≥30 ms. While the cell responded to reversals that were associated with large changes in stimulus amplitude, it did not appear to respond to the many noise transients when reversal time scale was small.

Fig. 6.

Example responses to temporally disrupted calls. Responses of a representative AI neuron to the natural and temporally disrupted aggression call. Reversal length is indicated to the left of each stimulus. Conventions as in Fig. 3. For convenience, the natural call and the neuron response to it are shown at the top of both columns as a reference point. Note that stimuli are depicted aligned to the response onset for ease of visual inspection.

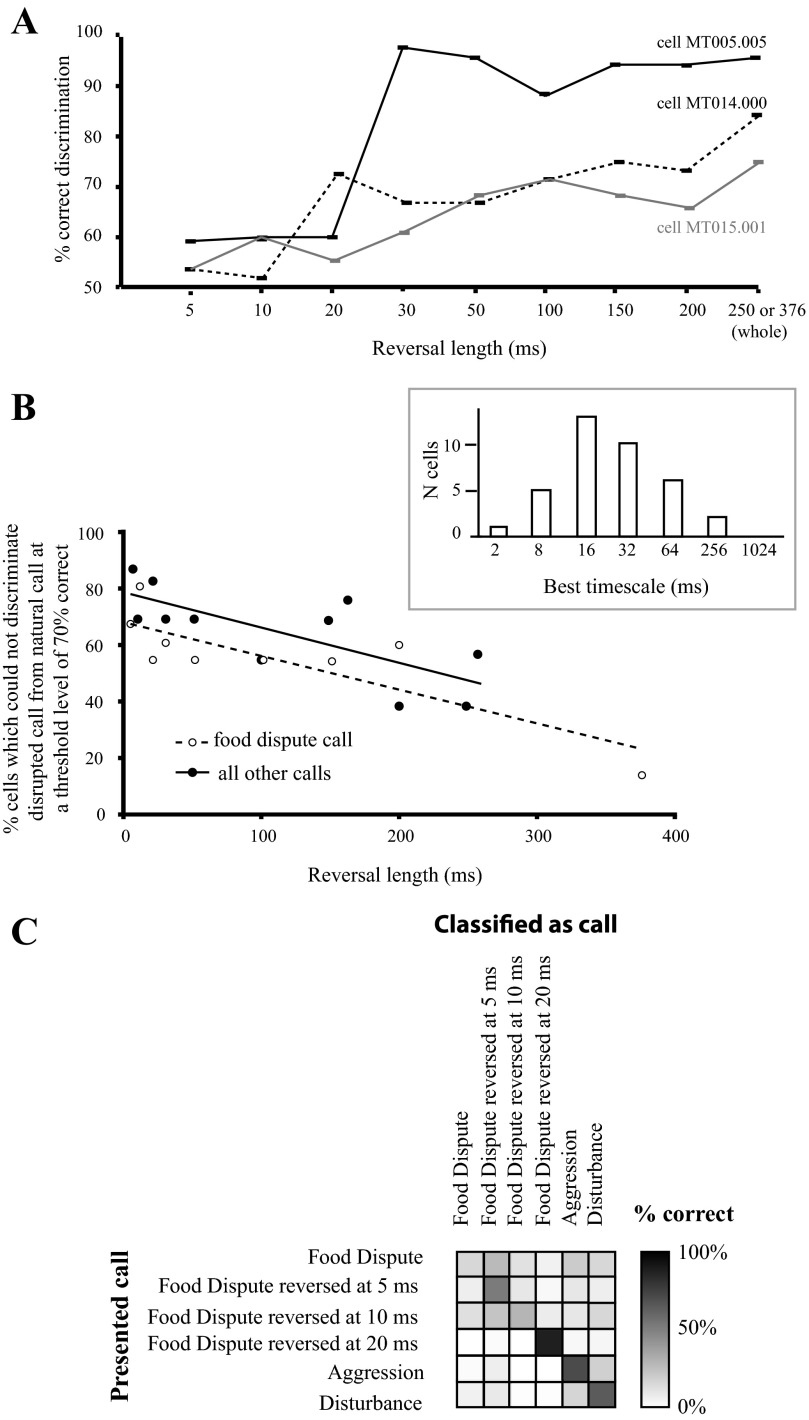
As for the spectral disruption experiment, a classification algorithm based on spike timing distance was used to determine the similarity between single AI neuron representations of disrupted vs. natural calls. For a single vocalization, if natural and temporally disrupted variants elicit similar neural responses, this implies that temporal information at that particular time scale is not essential for call encoding. Individual spike trains for each time scale (5-ms reversal, 10-ms reversal, etc.) were compared pairwise to those for the respective natural call; thus confusion matrixes were 2 × 2. Figure 7A shows the results of applying this classification algorithm to the responses of three cells. These examples suggest that temporal disruption at timescales ≈30 ms and above elicits relatively large changes in the discharge pattern of single AI neurons. Nonetheless, even at reversal lengths of 5–20 ms, classification performance was significantly better than chance, suggesting that the cell responses could occasionally differentiate between natural and temporally disrupted calls.

Fig. 7.

Temporal disruptions severely alter call representation by AI cells. A: quantitative comparison of responses of 3 example cells to locally time-reversed and natural calls. Results of utilizing the method depicted in Fig. 1B to analyze the responses of individual cells to the aggression call (cell MT005.005) or the food call (cells MT014.000 and MT015.001). Note that the durations of these 2 calls are different. In all cases, responses to the locally time-reversed call are compared with those to the natural call; 50% corresponds to chance performance. Values represent mean performance over bootstrapping iterations, and error bars represent SE. B: percentage of tested cells which failed to discriminate the disrupted call from the natural call at a level of 70% correct or above as a function of reversal segment length. Results for the food dispute call, which contained minimal FM, are separated from the results for the other call types. The points in each group were fit using a linear regression (food dispute call: R² = 0.69, P = 0.009; other calls: R² = 0.55, P = 0.005). Inset: histogram of best timescale for comparing call responses in the temporal disruption experiment. The best timescale for each cell corresponds to the timescale at which the highest total percent correct could be achieved for comparisons of natural and locally reversed calls across all reversal lengths. This represents the timescale at which each cell firing pattern is best differentiated; n = 37 cells. C: confusion matrix showing the average performance of a sample of AI neurons on the classification of food dispute calls that were temporally disrupted at short timescales as well as other natural calls in the same frequency range. The classification scheme was similar to that shown in Fig. 1A; n = 10 cells.

Figure 7B shows the percentage of tested cells that failed to discriminate temporally disrupted calls from natural calls at a level of 70% correct for each reversal length. The 70% criterion was chosen because it is generally employed as a threshold value in psychophysics experiments (Levitt 1971). The cells probed with the food dispute call, which contains minimal frequency modulation (FM), were separated from those probed with other call types, which do contain significant FM, to assess the contribution of reversed FM to reversal detection. In both samples, the vast majority (70–80%) of AI neurons failed to discriminate calls reversed at a 5-ms time scale from natural calls, but as the reversal length was increased, more neurons detected the difference. Since detection functions varied among recorded neurons, the population curves declined smoothly (linear regression, food dispute call: R² = 0.69, P = 0.009; other calls: R² = 0.55, P = 0.005); by reversal lengths of 100 ms, only 54% of cells still “confused” the disrupted call with the natural call. Interestingly, while the slopes of the population curves are almost identical, the curve for the cells probed with the food dispute call is downshifted relative to that for the other calls, indicating that AI neurons were somewhat better at detecting reversals of a call that did not contain FM. This is the opposite of the effect expected if reversed FM was an important factor in temporal disruption detection.

Another possibility is that some neurons responded to the noise artifacts created by the reversal procedure and that these responses contributed to the discrimination of temporally disrupted calls from natural ones. If so, then one would expect stimuli disrupted on a short timescale (e.g., 5–20 ms) to cause larger changes in the neural response, compared with stimuli disrupted on long timescales (e.g., 100 ms), since the former contain many more of these noise artifacts. This is the opposite of what we observe (Fig. 7, A and B), suggesting that the contribution of noise artifacts to the observed differences in call discrimination is relatively small.

To further test the idea that temporal disruptions up to ∼20 ms do not dramatically alter call representation by AI neurons, we examined the ability of a small sample of neurons (n = 10) to classify natural food dispute calls, food dispute calls disrupted at 5, 10, or 20 ms, and two other natural call types in a similar frequency range (Fig. 7C). We found significant confusion among the natural, 5-ms-reversed, and 10-ms-reversed food dispute calls, suggesting that the response patterns were not sufficiently different when the call was disrupted on these short timescales. However, the neurons classified the 20-ms-reversed food dispute call correctly on 90% of trials. Likewise, the natural aggression and disturbance calls were correctly assigned most of the time. This lends further weight to the idea that temporal disruptions on a timescale of 20 ms or more severely alter call representation in AI.

To assess call representation among a small population of AI neurons, we pooled the discharge patterns of all cells to each natural and temporally disrupted call. Figure 8A shows population histograms of the responses to the food call and its temporally disrupted versions. (Note: since stimuli were selected to maximize responsiveness, not all 37 tested cells were probed with the same call. Figure 8A shows the pooled response of the 15 cells tested with the natural food call and its locally time-reversed copies.) Responses to the natural call and manipulated calls with the shortest reversal lengths appear to have similar patterns, whereas responses to calls reversed at longer timescales are divergent.

Fig. 8.

Temporal disruptions alter population responses to locally reversed calls. A: pooled response of 15 cells to the locally reversed food call sequence. Peristimulus time histograms of individual cells were aligned by stimulus onset, binned at 5 ms, and summed; reversal lengths are indicated to the left of each histogram. The natural call response has been made semitransparent and superimposed on the locally time-reversed call responses for ease of comparison. Right: quantitative comparison of pooled population responses to natural and locally reversed calls. B: food call; n = 15 cells. C: aggression call; n = 8 cells. D: disturbance call; n = 10 cells. Pooled histograms of population responses were binned at 5 ms, and Euclidean distance was calculated between the response to each manipulated call and the natural call response. Points were fit with a power function (R² = 0.78, 0.58, and 0.80 for B, C, and D, respectively). Due to a small sample size (n = 4 cells), pooled responses to the final tested call, the mating call, were not analyzed.

To quantify differences in the population representation, we computed Euclidean distance (see methods) between the reversed call response and the natural call response for each reversal length (Fig. 8B). Points were fit with a power function, as this emphasizes the transition that occurs with increasing reversal length (R² = 0.78). Differences between the natural call and calls disrupted at the shortest timescales of 5 and 10 ms were on the same order of magnitude as the difference between two samples of the natural call response (data not shown). The population response difference then increases dramatically for 20-ms reversal length and continues to increase gradually with increasing reversal length. A similar outcome was observed for pooled responses to the other tested natural calls and their manipulated versions (Fig. 8, C and D), with dramatic increases at reversal lengths of 20 and 100 ms, respectively. In both cases, differences between the natural and manipulated call responses for two or more of the shortest reversal lengths are of a similar order of magnitude as the difference between two samples of the natural call response (data not shown). This suggests that AI population output does not distinguish between the natural call, the 5-ms-reversed call, and the 10-ms reversed call, but reversals of 20 ms or more can produce a significantly different population response pattern.

Relationship Between Call Processing and Basic Response Properties

An interesting question is whether the responses we have observed to natural and disrupted vocalizations are correlated with the responses observed for synthetic stimuli. Figure 9 shows the relationship between the tone frequency response areas of most of the sampled neurons and the frequency content of the calls used in this study. The spectra of the calls were within the excitatory receptive fields for most of the neurons except the first five cells, which would not be expected to respond to the calls based on their frequency tuning (Fig. 9A). However, low-frequency-tuned cells may respond to higher-frequency vocalizations due to difference tones arising from simultaneous combinations of frequencies in the calls (Portfors et al. 2009). In addition, many studies have found that responses to pure tones do not always predict the responses to complex sounds (deCharms et al. 1998; Theunissen et al. 2000). In fact, these five neurons did respond to the vocalizations.

We also examined the correspondence between neuron responses to SAM tones, where available, and their sensitivity to temporal call disruption. Although there was only a weak linear relationship between the highest modulation frequency to which cells could follow SAM and the shortest detected call reversal (data not shown), there was nonetheless a consistent pattern in these two measures of temporal integration. Neurons whose temporal integration window, as assessed by SAM cutoff, was <120 ms tended to detect reversals of 10 ms or shorter at the criterion level of 70% correct (median shortest detected reversal 5 ms, n = 10 cells). On the other hand, neurons with SAM temporal integration windows exceeding 120 ms generally did not detect reversals <30 ms at the criterion level (median shortest detected reversal 50 ms, n = 11). The shortest detected reversals in the two groups were found to be significantly different from each other (two-sample t-test assuming unequal variances, two-tailed P = 0.01).

Average Firing Rate Does Not Encode Stimulus Condition

It is possible that call identity is encoded by average firing rate rather than spike timing in AI neurons. To test this possibility, firing rate indices were computed for each cell in both experiments as follows:

$$(F{R}_i-F{R}_{ag1})/(F{R}_i+F{R}_{ag1})$$

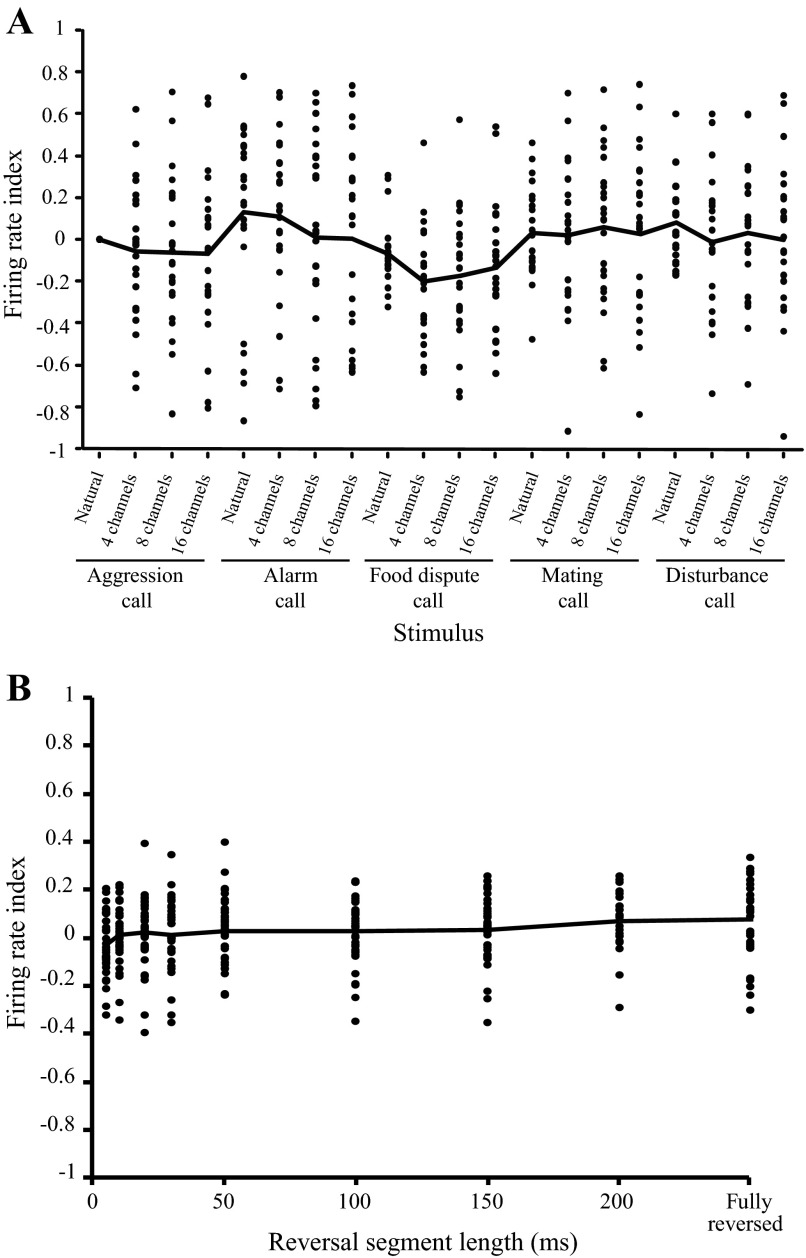
where FR_i is that average firing rate for any natural or spectrally disrupted call and FR_ag1 is the average firing rate for the natural aggression call. The average firing rate was calculated over a region of interest corresponding to the stimulus duration with an additional 50 ms to allow for response latency and jitter. Results are shown in Fig. 10 where each data point represents an individual neuron. The mean firing rate index as a function of stimulus condition is flat for both experiments.

Fig. 10.

Firing rate does not encode differences between natural and disrupted calls. A: experiment 1. Firing rate index as a function of stimulus condition for all tested cells. Firing rate index for each call was calculated relative to the response for the natural aggression call. Black line denotes the population mean; n = 24. B: experiment 2. Firing rate index as a function of reversal length for all tested cells. Firing rate index was calculated as (FR_rev − FR_nat)/(FR_rev + FR_nat), where FR_nat is the average firing rate for the natural call and FR_rev is the firing rate for the locally time-reversed call. Each data point corresponds to one cell. Black line denotes the population mean; n = 37.

To further explore the coding scheme employed by AI neurons, we compared the classification of natural calls when the spike trains of individual neurons were analyzed at three different VP timescales (see methods): 2 ms (corresponding to a precise spike timing code), 1,024 ms (corresponding to a rate code), and 32 ms (a mid-range timescale). Figure 2D shows that the mid-range timescale typically permitted the best classification of natural calls. Similarly, analysis timescales of 16–32 ms allowed the best discrimination of natural and temporally disrupted calls for the majority of neurons (Fig. 7B, inset). These timescales correspond to a spike timing code with significant jitter. Interestingly, performance worsened more steeply for the shortest analysis timescale than for the longest timescale (Fig. 2D), ruling out a neural code based on precise spike timing.

DISCUSSION

Temporal and spectral cues each play a distinct role in the perception of animal communication sounds. However, behavioral performance is robust to a significant reduction of acoustic information. Here, we asked whether these principles apply to the neural representation of natural and acoustically degraded gerbil vocalizations. Our findings demonstrate that even severe loss of spectral information did not prevent AI neurons from correctly classifying individual calls. However, temporal disruptions degraded call representation significantly. Disruptions at timescales of ∼20 ms and above reliably altered AI responses. Therefore, the stable representation of communication sounds by AI neurons is more dependent on sensitivity to slow temporal envelopes than on spectral fine structure.

Representation of Natural Vocalizations by Neurons in AI

We found that the temporal response patterns of individual AI neurons permitted relatively good classification of natural gerbil calls (Fig. 2), while call selectivity as assessed by average firing rate was low (Fig. 10). This accords well with what has been found by other investigators. For example, the spiking patterns of neuron responses in ferret AI permitted phoneme classification that closely resembled human perceptual performance (Mesgarani et al. 2008). However, unlike in the avian song system, where a small population of cells was found to be selective for specific songs (Margoliash 1983), early attempts to find similar “call detectors” in the AC were unsuccessful (Creutzfeldt et al. 1980; Newman and Wollberg 1973; Wollberg and Newman 1972). Recent findings throughout the ascending auditory pathway are also in agreement with our observations. For example, in the mouse IC, the majority of neurons responded to ∼80% of the various vocalizations presented (Portfors et al. 2009). Similarly, in the IC of guinea pigs, the majority of neurons responded to all four guinea pig calls that were presented (Suta et al. 2003). Auditory cortical neurons in the bat also responded with similar peak firing rates to multiple social calls, but the temporal structure of the responses was unique for each call (Medvedev and Kanwal 2008). In the auditory thalamus of rats and guinea pigs, half of the sampled cells were not very selective and responded to all four presented vocalizations (Philibert et al. 2005).

Our findings based on the limited data we collected with synthetic sounds indicate that while there is a broad correlation between these basic response properties and the responses to natural and disrupted calls, synthetic stimulus responses are a relatively poor predictor of responses to natural stimuli. This accords well with what has been found by many prior investigations (deCharms et al. 1998; Theunissen et al. 2000; Woolley et al. 2006). This may be due to the fact that the neurons are tuned to respond to some nonlinear combination of multiple spectrotemporal features (Andoni and Pollak 2011; Sadagopan and Wang 2009).

It should be noted that because the animals did not have the opportunity to orient to stimuli or to exhibit other voluntary responses, variation in attention is an uncontrolled variable in this study. Since each stimulus was presented at least 25 consecutive times, it is likely that any attention to the stimulus would have habituated, thereby minimizing the effects of variation in attention on the phenomena observed.

Impact of Spectral Disruption of Calls on Cortical Representation

Our findings indicated that when spectral information in gerbil calls is degraded to only four channels of bandpassed noise, AI neurons were still able to reliably classify calls. This finding is consistent with human performance on a speech discrimination task in which subjects could identify vocoded syllables with only four spectral bands (Shannon et al. 1995). In contrast, human discrimination of more challenging Mandarin syllables containing significant FMs is further improved with 16 bands (Kong and Zeng 2006). The lack of improvement between 4- and 16-channel conditions in our experiment suggests that the performance of AI neurons probably depends on the acoustic attributes of the test stimuli; that is, the spectral content of gerbil calls may not have been sufficiently complex to differentiate between 4 and 16 channels. While it is not known how gerbils perceive spectrally impoverished calls, rats discriminate speech syllables degraded to four spectral channels with nearly 80% accuracy (Ranasinghe et al. 2012). Additionally, cotton-top tamarins exhibit the same behavioral responses to natural and spectrally reduced calls (Ghazanfar et al. 2002) and zebra finches are able to discriminate between spectrally reduced songs at a high level of accuracy (Vernaleo and Dooling 2011). Each of these findings suggest that nonhuman animals rely more heavily on temporal than spectral cues. Additionally, some neurons in the AC of bats also respond robustly to vocalizations that are missing many spectral details (Ohlemiller et al. 1996).

Although the responses of individual neurons in AI can be surprisingly good at matching spectrally disrupted calls to the respective natural calls (Fig. 4, “best cell”), the performance of most single cells could not explain the sort of behavioral performance displayed by humans on spectrally reduced speech (Kong and Zeng 2006; Shannon et al. 1995). On the other hand, the pooled responses of small populations of AI neurons permit ∼90% correct classification (Fig. 5B). This suggests that while individual AI neurons are unlikely to support perceptual classification of calls, a downstream population of neurons receiving input from a subset of AI neurons could do so (Gifford et al. 2005; Russ et al. 2007).

The notion that a population of neurons is required to accurately classify communication sounds is supported by findings in songbird. Thus populations of neurons are necessary to achieve song discrimination accuracy at the level observed in behavioral experiments (Ramirez et al. 2011; Schneider and Woolley 2010). Likewise, phoneme classification by ferret AI neurons increases with population size (Mesgarani et al. 2008). Population encoding of vocalization identity also appears to be a coding strategy in the AC of bats and primates (Kanwal and Rauschecker 2007).

Impact of Temporal Disruption of Calls on Cortical Representation

Our experiment was originally suggested by an analogy with human speech processing. Here, it is found that locally reversing speech on a timescale of 100 ms or more impedes recognition (Saberi and Perrott 1999). However, it is likely that listeners can distinguish speech reversed in 5- to 50-ms segments from natural speech (personal observations). This suggests that humans process the locally reversed stimuli at two perceptual levels: one is determined by the acoustic dissimilarity between waveforms, and the second is language based. Since it is unknown how locally reversed species-specific calls are perceived by Mongolian gerbils, it is unclear whether our physiological results reflect the animal's perception of acoustic dissimilarity or call recognition.

Perhaps a closer behavioral correlate to our findings is the observation that zebra finches can discriminate perfectly between natural songs and songs with a single reversed syllable when that syllable is >100 ms, but their performance appears to degrade gradually for shorter syllables (Vernaleo and Dooling 2011). Specifically, we found that there was a gradual reduction in the percentage of AI neurons that could not discriminate between reversed and natural calls as reversal length increased (Fig. 7B).

Our findings indicate that reversed FM is not a significant contributor to AI neuron ability to discriminate temporally disrupted vocalizations from natural ones (Fig. 7B); instead, there seems to be a general correlation between reversal detection and AM sensitivity. The opposite has been observed in the AC of bats, where reversal of FM but not of asymmetric AM partly explained the decrease in gamma oscillations caused by call reversal (Medvedev and Kanwal 2008). This may be due to the relatively greater importance of FM selectivity to the representation of vocalizations in the bat cortex (Fuzessery et al. 2011).

Perception of Species-Specific Calls by Mongolian Gerbils

The extent to which Mongolian gerbils assign a meaning to conspecific vocalizations or associate them with a specific response is not well studied, but these vocalizations have been associated with a specific behavioral context (Ter-Mikaelian et al. 2012). At a minimum, it is clear that gerbils can discriminate alarm calls from food dispute calls and react with alarm behavior to the former (Yapa 1994). Likewise, it is not known how gerbils perceive locally time-reversed or fully reversed calls, although evidence that they can discriminate upward and downward frequency sweeps (Ohl et al. 2001) suggests that such perturbations should affect perception. Experiments with rhesus macaques reveal a particular behavioral response to conspecific vocalizations, and reversed vocalizations do not elicit this response, suggesting that the perception of reversed calls is categorically different (Ghazanfar et al. 2001).

The stable representation of communication sounds in AI appears to be more dependent on sensitivity to slow temporal envelopes than on spectral content. Individual AI neurons can categorize spectrally disrupted calls, and a small population is required to attain high performance. The implication of this result is that temporal envelope must be important for proper categorization. In principle, the responses of AI neurons to temporal disruption of the calls are consistent with this idea. Large temporal disruptions that would be expected to degrade slow temporal envelopes were associated with better discrimination between natural and disrupted waveforms, implying that accurate categorization would be more difficult.

GRANTS

This work was supported by National Institute of Deafness and Other Communications Disorders Grant DC-009237 and New York University Research Challenge Fund.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: M.T.-M., M.N.S., and D.H.S. conception and design of research; M.T.-M. performed experiments; M.T.-M. analyzed data; M.T.-M., M.N.S., and D.H.S. interpreted results of experiments; M.T.-M., M.N.S., and D.H.S. prepared figures; M.T.-M. drafted manuscript; M.T.-M. and D.H.S. edited and revised manuscript; M.T.-M., M.N.S., and D.H.S. approved final version of manuscript.