Vestibular benefits to task savings in motor adaptation

Abstract

In everyday life, we seamlessly adapt our movements and consolidate them to multiple behavioral contexts. This natural flexibility seems to be contingent on the presence of movement-related sensorimotor cues and cannot be reproduced when static visual or haptic cues are given to signify different behavioral contexts. So far, only sensorimotor cues that dissociate the sensorimotor plans prior to force field exposure have been successful in learning two opposing perturbations. Here we show that vestibular cues, which are only available during the perturbation, improve the formation and recall of multiple control strategies. We exposed subjects to inertial forces by accelerating them laterally on a vestibular platform. The coupling between reaching movement (forward-backward) and acceleration direction (leftward-rightward) switched every 160 trials, resulting in two opposite force environments. When exposed for a second time to the same environment, with the opposite environment in between, subjects showed retention resulting in an ∼3 times faster adaptation rate compared with the first exposure. Our results suggest that vestibular cues provide contextual information throughout the reach, which is used to facilitate independent learning and recall of multiple motor memories. Vestibular cues provide feedback about the underlying cause of reach errors, thereby disambiguating the various task environments and reducing interference of motor memories.

motor adaptation is the process of regaining or retaining a given level of motor performance (Shadmehr and Wise 2005). It has been shown that subjects readily adapt reaching movements to visual or force perturbations, suggesting that the brain forms and updates an internal model of the body and its interactions with the world (Brashers-Krug et al. 1996; Caithness et al. 2004; Howard et al. 2010; Izawa et al. 2008; Nozaki et al. 2006; Shadmehr and Mussa-Ivaldi 1994). However, it is unclear how many internal models can be formed without interfering.

Daily life experience suggests no limit. In tennis we do not forget the forehand swing when learning the backhand stroke. Thus we seem capable of simultaneously representing different dynamics associated with different contexts, suggesting multiple internal models can be formed, adapted, and consolidated independently (Kawato 1999). This, however, is at odds with laboratory findings.

Experiments with haptic interfaces have shown that the memory of one task is lost (Brashers-Krug et al. 1996; Caithness et al. 2004) or cannot be recalled (Criscimagna-Hemminger and Shadmehr 2008; Pekny et al. 2011) after learning an opposing task. Associating each task with a different context by adding static visual (Gandolfo et al. 1996) or haptic cues (Cothros et al. 2008) does not improve recall of the memory. However, if tasks are distinguished by dynamic sensorimotor contextual cues, there is evidence for learning and storage of multiple internal models (Hirashima and Nozaki 2012; Howard et al. 2008, 2010, 2012; Malone et al. 2011; Nozaki et al. 2006). For example, when unimanual and bimanual tasks are linked to opposing force fields, interference is reduced in the arm that is involved in both tasks (Nozaki et al. 2006). Likewise, different limb configurations, such as wrist postures (Gandolfo et al. 1996) or starting hand positions (Hwang et al. 2006a), can aid in learning. Recently, different targets in the visual domain (Hirashima and Nozaki 2012) or different cueing premovements (Howard et al. 2012) also were discovered to provide sufficient sensorimotor context to permit parallel learning of opposing force fields.

The key difference between static visual or haptic cues and dynamic sensorimotor cues is that the former do not affect the motor plan. This lack of task involvement may explain why such cues do not improve retention. In other words, they are not directly implicated in the circuits mediating online sensorimotor control and as a result do not provide sensorimotor context.

So far, however, the sensorimotor cues that have been studied were all presented prior to movement execution. Here we ask the question whether sensorimotor cues that are only available during the execution of a task can also aid in learning and retaining two internal models.

In the present study, we exploit the natural sensorimotor link between the vestibular system and motor system. Because of its specialized organs (semicircular canals, otoliths) for detecting rotational and linear accelerations, the vestibular system may well serve in detecting different inertial force environments and aid in attributing them to distinct internal models. To date, however, experiments on adaptation of reaching movements have typically been performed in body-stationary subjects (Brashers-Krug et al. 1996; Caithness et al. 2004) or under constant-velocity whole body rotation where the vestibular system no longer indicates movement (Dizio and Lackner 1995; Lackner and Dizio 1994).

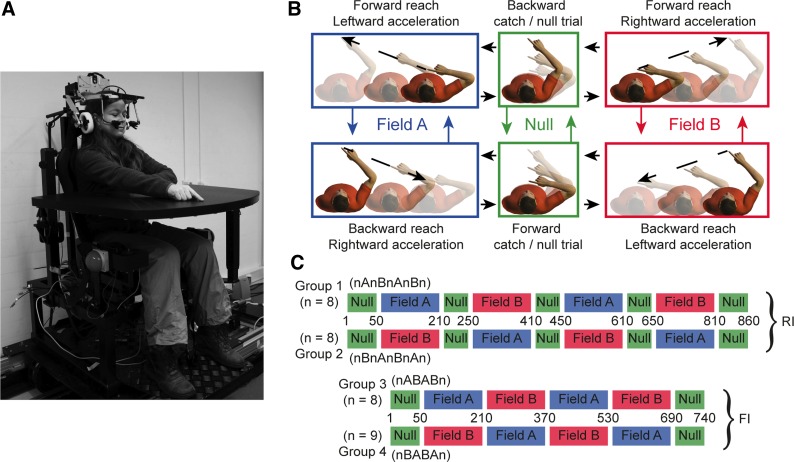
We tested subjects making forward and backward reaches while their whole body was linearly accelerated either leftward or rightward on a vestibular platform (see Fig. 1A). The coupling between reaching and whole body acceleration made vestibular information only available during arm movement execution. Reaches were made between the same initial and final hand positions, irrespective of the vestibularly detected direction of body motion. We show that the vestibular system (i.e., otoliths) not only facilitates the estimation of the imposed forces but also provides a contextual signal aiding in learning and recalling multiple internal models.

Fig. 1.

Experimental setup and paradigms. A: subjects were seated on a linear sled and performed right-hand reaching movements to visual targets presented on a sled-mounted table. B: force pairings. Pairing A (blue) consists of forward reaches linked to leftward accelerations and backward reaches linked to rightward accelerations. Pairing B (red) consists of forward reaches linked to rightward accelerations and backward reaches linked to leftward accelerations. During null and catch trials (green) the sled remained stationary. Arrows indicate possible trial transitions. C: experimental paradigms. In the reduced interference (RI) paradigm, force pairings are interspersed with 40 null trials. In the full interference (FI) paradigm, force fields follow directly after each other.

MATERIALS AND METHODS

Participants

Experiments were conducted under the general approval for behavioral experiments by the institutional ethics committee. Thirty-eight right-handed naive subjects gave their written consent to participate in the experiments. Reimbursement was provided in terms of course credit or payment. All subjects had normal, or corrected-to-normal, vision and had no known motor deficits. Five subjects were excluded from the analyses based on their failure to develop internal models of the tested task environments (see Catch trials for further details).

Setup

Subjects performed reaching movements with their right arm while sitting on a linear sled that moved along a magnetic track. The sled, powered by a linear motor (TB15N; Technotion, Almelo, The Netherlands), was controlled by a Kollmorgen S700 drive (Danaher, Washington, DC). The sled chair was configured such that participants were seated with the interaural axis aligned with the sled's motion axis. Participants were restrained using a five-point seat belt, and their head was firmly fixated using an ear-fixed mold. Integrated earphones provided auditory instructions and feedback during the experiments. Emergency buttons at either side of the sled chair enabled subjects to stop the sled motion immediately if needed.

The tip of the right index finger and the sled position were recorded at 250 Hz using an Optotrak Certus system (Northern Digital Instruments, Waterloo, Canada) and stored for off-line analysis. Reach start and target positions were body-fixed and indicated by green and red light-emitting diodes (LEDs), integrated into a table. This stimulus table was mounted on the sled, in front of the subject, and further served as an armrest in between trials (Fig. 1A).

During the experiment, the sled accelerated laterally with a bell-shaped velocity profile of 650-ms duration and 30-cm amplitude with a maximum acceleration of 4.1 m/s². Sled movement was triggered by the initiation of the reaching movement, derived from real-time Optotrak data recorded at 100 Hz (maximum loop delay 40 ms). This results in a time-dependent force environment. Time-dependent force fields have been shown to be (mis)interpreted as state-dependent fields, which makes them more difficult to learn (Conditt and Mussa-Ivaldi 1999; Karniel and Mussa-Ivaldi 2003). The setup and experiment was controlled using custom software written in Delphi.

Task

Subjects had to perform 35-cm alternating forward and backward reaching movements. Inertial forces were introduced by lateral sled accelerations. Start and target positions were indicated using a green (start) and red (target) LED, which were aligned with the subject's midsagittal plane. During the sled movement, the start and target LEDs moved with the subject, i.e., they were body-fixed.

Participants initiated a trial by positioning their right index finger onto the green start location. A go beep was given after the finger had been within a circle with a radius of 1.5 cm centered at the start location and its speed had stayed below 2.5 cm/s for 500 ms. The start of the reach was determined as the first time point after the go beep at which the finger speed exceeded 2.5 cm/s. The endpoint of the reach was defined as the first point where finger speed was below 2.5 cm/s. If this point was outside the target area (radius of 1.5 cm), participants received auditory feedback that they missed the target (“please, aim better”). If this point was inside the target area, participants received auditory feedback about whether their reach time was below (“move faster”), within (“well done”), or above (“move slower”) the required time window of 600–800 ms.

During the perturbation trials, the lateral sled accelerations resulted in inertial forces on the subject's arm and body. Subjects were instructed to perform reaches as naturally as possible, not to slide their finger or arm over the table surface, and to stay within the allowed time window. Experiments were performed under dimmed light to improve saliency of the body-fixed targets. Subjects could not make use of any visual anchoring points to assess amplitude or direction of the chair displacement.

Experimental Paradigms

Our main interest is the degree of interference and retention of motor memories when learning two dynamical environments. Two opposing force environments were created by changing the couplings of the reach direction (forward and backward) and acceleration direction of the sled (leftward and rightward). By testing two reach directions, instead of just forward reaches, the overall learning rate is decreased, which allows scrutinizing the characteristics of adaptation in more detail. Furthermore, using two reach directions also improved the flow of the experimental paradigm as the sled moved back and forth on its rail from trial to trial, staying within its limited movement range.

Pairing A consisted of a forward reach combined with a leftward acceleration and a backward reach combined with a rightward acceleration. For pairing B these couplings of reach direction and acceleration direction were reversed (Fig. 1B). To ensure that observed effects are not due to the order of presented force environments, each paradigm included two subject groups tested with the opposite order of force pairings. We further manipulated the amount of potential interference by using two paradigms: a reduced interference (RI) and a full interference paradigm (FI) (Fig. 1C).

RI paradigm.

Subjects performed a familiarization block (50 reaches) without sled accelerations (null trials). This block was followed by four perturbation blocks (160 reaches each) with alternating force pairings: one pairing for perturbation blocks 1 and 3 and the opposite pairing for blocks 2 and 4. Retrograde interference occurs when learning of a force environment interferes with the memory of a previously learned environment; interference is anterograde when learning of the first environment interferes with the learning of the second. The latter was minimized here by interspersing the perturbation blocks with blocks of 40 washout trials (null trials). Each perturbation block included 14 catch trials, in which the sled unexpectedly remained stationary (similar to the null trials, Fig. 1B). Catch trials were implemented on seven forward and seven backward reaches. They were randomly introduced with a minimum separation of five trials. Furthermore, catch trials evoke forward and backward reaching movements randomly at either side of the sled, even though sled motion alternates. This reduces the likelihood of subjects being able to use an explicit strategy based on sled position to dissociate between the two force pairings. The initial 20 trials of a perturbation block were catch trial free, and every subsequent bin of 10 trials contained 1 catch trial. After the final perturbation block, a de-learning block followed (50 reaches), which was equivalent to the familiarization block (null).

FI paradigm.

As we show in results, in the RI paradigm subjects were able to retain the learned dynamics after having learned the opposite force pairing in between. Therefore, we set out to explore whether this observation also holds when both retrograde and anterograde interference are involved. The structure of this FI paradigm was equivalent to the RI paradigm except that the four perturbation blocks directly followed after each other without intervening blocks of washout trials (Fig. 1C).

Analyses

Data were analyzed off-line using Matlab (The MathWorks). Fingertip positions were first preprocessed. Missing data points, which were the result of an occlusion of an Optotrak marker during the reach, were reconstructed using spline interpolation. Position data were subsequently filtered using a fifth-order, 12-Hz low-pass bidirectional Butterworth filter. All trials were used for analysis.

As we show in the results, the deviation of the reaching movement from a straight line joining start and target position changes over the course of a block of trials. To quantify this deviation, we computed the signed hand-path error (E), defined as:

$$E={\displaystyle \underset{t_0}{\overset{t_{\text{f}}}{\int }}x(t)\cdot \dot{y}(t)\text{d}t,}$$ (1)

where x(t) is defined as the time-varying perpendicular distance between the actual trajectory and a straight line from the start to target position, weighted by the signed velocity $\dot{y}(t)$ of the movement in the direction from start to target (Franklin et al. 2003). Note that by using this measure we do not suggest that subjects intended to make straight-line reaching movements in our paradigms. We used signed x(t) and signed $\dot{y}(t)$ in the calculation of E such that forward and backward errors have the same sign in each of the force fields. Because errors differ in magnitude between forward and backward reaches, likely caused by differences in limb inertia, we collapsed forward and backward errors into pairs.

As a first step in testing our retention hypothesis, we computed the relative difference in E between the first and second exposure to the second force pairing (perturbation blocks 2 and 4) at three different stages of adaptation (initial, early, and final). We tested whether the obtained values deviated from zero using one-sample t-tests.

Furthermore, to quantify learning over time in each subject, hand-path error in each block of trials was fitted with a single rate exponential function:

$$E(n)=E_0\cdot e^{-\frac{n}{\tau }}+E_{\text{f}},$$ (2)

in which E₀ + E_f represents the error at the beginning of learning, τ is the time constant of adaptation, E_f is the offset representing the learning plateau, and n refers to a pair of trials. If a pair of trials contained a catch trial, the whole pair was excluded from the fit. All other pairs were included in the analyses. Fit parameters served to test the retention hypothesis that subjects learn a force environment faster during the second exposure. More specifically, this means that τ should be smaller for the second exposure but that neither E₀ + E_f nor E_f should differ between the first and second exposure. To test this statistically, we log-transformed the values of the fit parameters to ensure normal distributions and compared values of first and second exposure to a force environment using paired t-tests.

Catch trials.

Over the course of learning, subjects dynamically compensate for perturbing forces, resulting in a decrease in hand-path error. If these perturbations are unexpectedly removed (catch trials), compensation leads to an error in the opposite direction. Because of this reverse relationship, the hand-path errors in the catch trials reveal whether subjects establish an internal model during adaptation, by showing an increase over the course of learning. If hand-path errors during perturbation trials decrease with trial number but are not paralleled with an increase of the error in the catch trials, subjects probably use an alternative strategy, for example, an impedance control strategy (Franklin et al. 2003).

We used linear regression to test whether the error in catch trials increased with trial number in a perturbation block and only included subjects that did show a significant positive slope in exposure blocks 2–4. On the basis of this criterion, which is not related to any of our outcome measures, 5 of 38 subjects were excluded from further analysis. Three of them were from group 1; the other two were from groups 2 and 3.

RESULTS

We evaluated the adaptation and retention of human reaching movements in response to inertial force perturbations induced by whole body lateral accelerations. Subjects were tested in two opposing force pairings, A and B, in which the direction of the reaching movement (forward-backward) was uniquely associated with the acceleration direction of the body (leftward-rightward) (Fig. 1B). We used these pairings in two different interference paradigms (Fig. 1C): reduced (RI) and full interference (FI). Within each paradigm, two subject groups were tested to balance for the order of the force pairings. We hypothesize that the vestibular system provides a strong contextual cue, which is independent of the reach error. This cue reduces task interference and therefore enables learning of the two opposing force environments. We start the description of the results by depicting the development of the reach trajectories over the course of learning. We will focus our analyses on perturbation blocks 2 and 4 because they have the same immediate history of force environments and therefore offer the fairest comparison.

Reach Trajectories During Adaptation

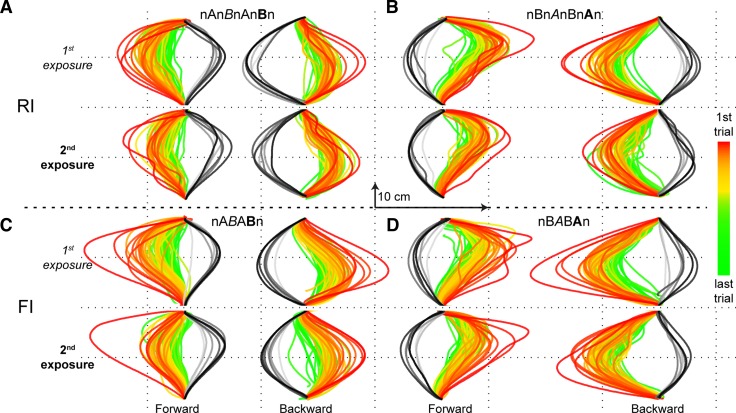
Figure 2 shows group average trajectories (forward and backward) for all trials, for all four subject groups (2 paradigms × 2 force pairings) separately, color-coded by trial number. In all conditions, initial trajectories (red) in the first and second exposure blocks match closely, suggesting that adaptation started at the same level. The same holds for the final trajectories (green), suggesting that subjects reach the same level of adaptation in the first and second exposure block. However, the red-to-green color gradient (orange-yellow), characterizing the time course of adaptation, is clearly different for the first and second exposure: In the second exposure block the trajectories converged faster toward the final adapted trajectory compared with the first exposure block.

Fig. 2.

All forward and backward reach trajectories during the 1st and 2nd exposure block, averaged across subjects. Exponential color transition from red (initial trials) via yellow to green (final trials) is indicated. A and B: RI paradigm. C and D: FI paradigm.

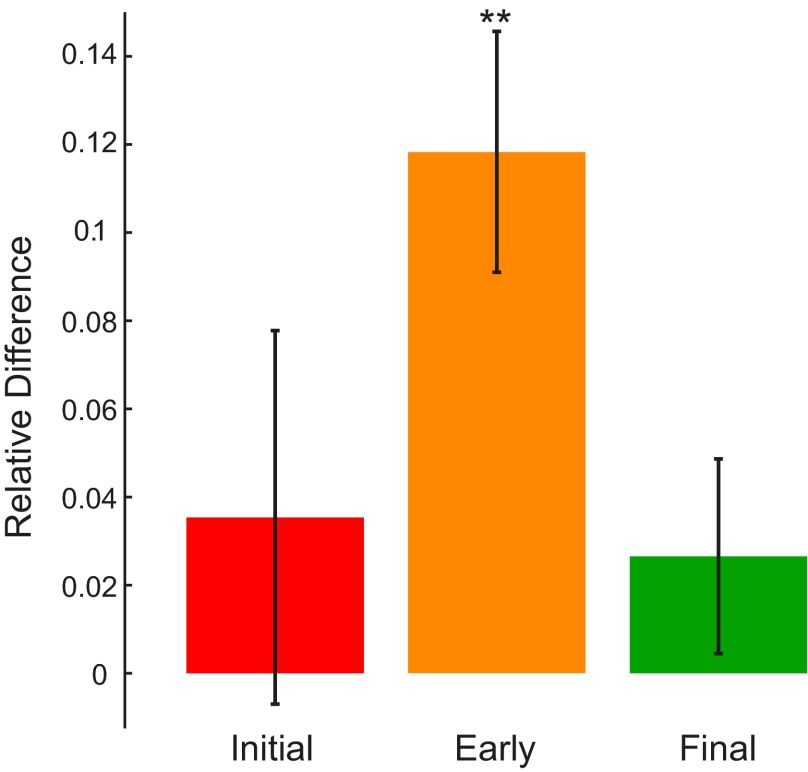
To validate the adaptation effects, we computed the signed hand-path error E (see materials and methods) to quantify trial-by-trial changes of the reach trajectories. We examined the relative difference between E at three phases of the first and second exposure blocks: the initial trials (trials 1 and 2), the early trials (trials 9–13), and the final trials (trials 140–160). Figure 3 shows the mean (±SE) of the relative difference across all paradigms. One-sampled t-tests did not reveal a significant difference from zero for the initial (P = 0.41) and final (P = 0.24) reaches. By contrast, for the early reaches (orange bar), the relative difference was significantly larger than zero (P < 0.001), meaning E was significantly smaller for the second than the first exposure. This systematic difference suggests that during the second exposure to the same force environment, subjects more quickly regained the performance level at which they ended the first exposure.

Fig. 3.

Relative difference (1st vs. 2nd exposure) of initial, early, and final hand-path errors (E; Eq. 1) across all subject groups. Bars denote SE. The relative difference only differs from zero for the early reaches.

A noteworthy observation in Fig. 2 is that the final adapted trajectory (green) does not match a straight trajectory that is usually observed in initial control trials during which no perturbations are imposed (Izawa et al. 2008). The final trajectories are curved with a consistent maximum deviation of about 1–2 cm from a straight line. This suggests that subjects do not fully compensate for the imposed forces early in the reach and exploit the inertial forces, caused by the deceleration, to bring their hand on target (Izawa et al. 2008).

Learning Curves

In the above we only assessed retention at specific time points in the learning process (Figs. 2 and 3). To capture the temporal characteristics of reach adaptation, we examined the signed hand-path error E (see Eq. 1) in each block, as a function of trial pair. The blue and red dots in Fig. 4 show these data, as an average across subjects, for the two force pairings of each paradigm. The black dots represent E of catch trials, which is discussed below. Consistent with the observations in Figs. 2 and 3, hand-path error gradually decreases over the course of a perturbation block. We fit single-decaying exponential functions (see materials and methods) to each subject's data to estimate the learning curves. R² values ranged from 0.45 to 0.71 for all paradigms (P < 0.001). The parameters of the individual fits of perturbation blocks 2 and 4 are presented in Table 1. The time constant τ of the exponential fits quantifies the rate of adaptation from initial error (E₀ + E_f), observed during the first trials (Fig. 2, red trajectories) to the final error (E_f) that remains during the final trials (Fig. 2, green trajectories). Thus τ provides a measure of the speed of learning. Retention would be indicated by a faster error-reduction rate, and thus a smaller time constant τ, for relearning (second exposure) compared with naive learning (first exposure).

Fig. 4.

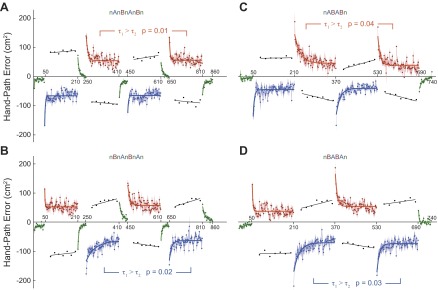
Hand-path error as a function of trial pair (dots), averaged across subjects. Shaded areas denote SE. A single rate exponential function (solid lines), fitted to the perturbation errors, suggests faster relearning at reexposure. Green, null trial; blue, force pairing A; red, force pairing B. Black dots represent catch trials, and black solid line presents their best fit line. A: subject group 1. Comparison of field B exposures (RI). B: subject group 2. Comparison of field A exposures (RI). C: subject group 3. Comparison of field B exposures (FI). D: subject group 4. Comparison of field A exposures (FI).

Table 1.

Mean and standard error values of exponential fit parameters

	1st Exposure (Block 2)		2nd Exposure (Block 4)
	Mean	SE	Mean	SE	P Value
nAnBnAnBn
E0 + Ef	136.6	12.6	139.5	9.1	0.77
Ef	51.4	5.9	55.6	6.3	0.22
τ	10.9	5.4	1.9	0.5	0.01
nBnAnBnAn
E0 + Ef	−148.4	7.9	−138.6	5.9	0.36
Ef	−64.5	4.6	−59.6	4.2	0.19
τ	20.2	4.3	10.7	4.4	0.02
nABABn
E0 + Ef	170.4	21.3	156.2	17.4	0.46
Ef	34.6	7.9	34.5	13.4	0.99
τ	21.9	10.3	7.6	5.2	0.04
nBABAn
E0 + Ef	−202.2	13.9	−212.2	10.9	0.13
Ef	−64.1	6.2	−74.1	8.3	0.13
τ	15.6	6.7	4.9	1.1	0.03

Values are means and SE of exponential fit parameters: E₀ + E_f represents the error at the beginning of learning, in cm²; E_f is the offset representing the learning plateau, in cm²; and τ is the time constant of adaptation, in forward and backward pairs.

With regard to the RI paradigm (Fig. 4, A and B), both subject groups show a significantly smaller τ (P_{field B} = 0.01; P_{field A} = 0.02), and thus faster relearning in the second exposure. The FI paradigm (Fig. 4, C and D) shows similar results (P_{field B} = 0.04; P_{field A} = 0.03) for both groups, with a smaller τ for the second than the first exposure. In contrast, regardless of paradigm type and subject group, the error on the first trial (represented by E₀ + E_f) did not differ between the first and second exposure, suggesting that subjects were naive to the force environment switch in both cases. Additionally, the remaining error at the end of adaptation (represented by E_f) did not differ between first and second exposure, indicating that on the first exposure block subjects had reached full adaptation and that no further improvement occurred in the second block.

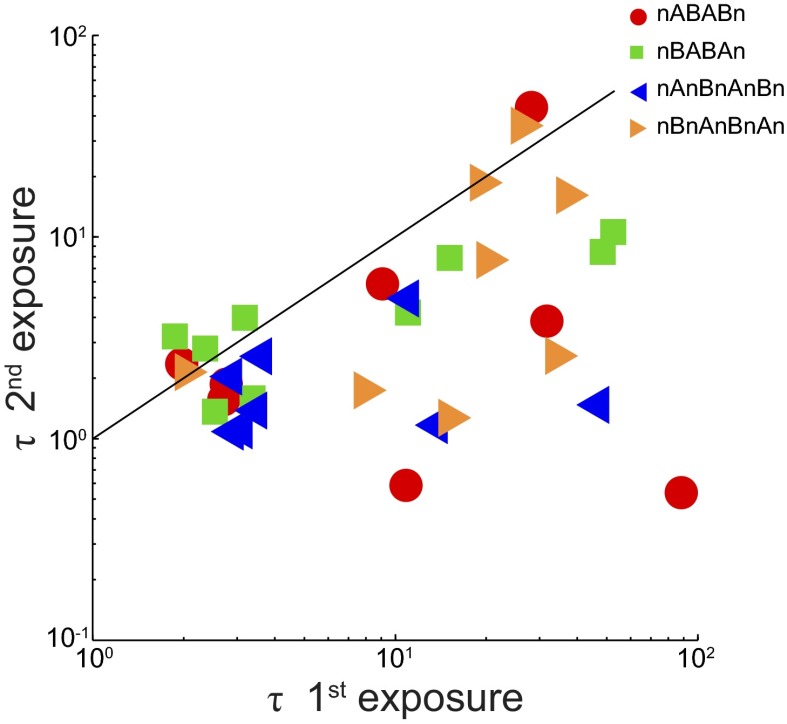
Figure 5 summarizes the results for all paradigms, plotting τ of the first exposure vs. that of the second exposure, for each subject separately. Symbols indicate the different paradigms. The majority of points are below the identity line, showing that relearning is faster during the second exposure for most subjects.

Fig. 5.

Time constants (τ) of the 1st exposure vs. time constants of the 2nd exposure of individual subjects.

Taken together, in contrast to previous work with body-stationary subjects interacting with robot-generated force fields (Brashers-Krug et al. 1996; Caithness et al. 2004; Shadmehr and Mussa-Ivaldi 1994), all our analyses show that subjects are able to retain a previously established internal model of force pairings induced by whole body acceleration after being exposed to an interfering perturbation block. This observation holds regardless of force environment or interference level.

Catch Trials

Finally, it is important to demonstrate that learning of an internal model occurred in our paradigms. The catch trials, in which the force was unexpectedly removed by not moving the sled during the reach, served this purpose. If an internal model is established, catch trials will show aftereffects due to the compensation for expected forces that are not present. The more the subject has adapted to the new force environment, the greater the aftereffect in the catch trials (Shadmehr and Mussa-Ivaldi 1994). Hence, to demonstrate learning, the size of the hand-path error in the catch trials should increase with the number of trials performed in a block. Figure 2 shows the trajectories of the interspersed catch trials, color-coded by trial number using a light-to-dark grayscale. They show increasing deviation from a straight line, in the direction opposite that of the field trials, with progressing level of adaptation.

To quantify these deviations, the black data points in Fig. 4, together with their fit lines, show the average E on the catch trials for each block and paradigm. The slope of the fit lines was not significantly different from zero (P = 0.83) across paradigms during the first perturbation block, indicating an overall lack of internal model formation. Once our subjects got more acquainted to our setup (blocks 2–4), E in the catch trials started to increase over the course of a perturbation block (P < 0.001). Because of the lack of internal model formation in the first perturbation block and because the immediate history of force environments is only equivalent for blocks 2 and 4, we only assessed our retention hypothesis for these blocks.

DISCUSSION

We studied the adaptation of reaching movements to two opposing dynamic environments, induced by whole body accelerations on a vestibular platform. Our results show that subjects are able to retain and recall the learned dynamics during reaches after adapting their reaches to the opposing force environment. This result held even with full levels of anterograde and retrograde interference between the two force pairings. Our results suggest that the vestibular system, as part of the sensorimotor loop, disambiguates the force environment, allowing subjects to learn and readily recall two opposing force environments linked to the same movement goal. Furthermore, none of the subjects reported a switch in force pairings during the experiment, making an explicit strategy unlikely. We next discuss the implications of our results.

Motor adaptation results in the formation of a memory that contains the control strategies (internal model) for reaching in the new environment. Previous work in body-stationary subjects learning force fields induced by robotic interfaces showed that the memory of a single force field can be retained, even when a period without a force field (“null field”) has intervened (AnA paradigm; Caithness et al. 2004). However, when the null field is replaced by the opposite field of A, as tested in the ABA paradigm, the motor memory of A seems to have disappeared after the learning of field B. Even when static visual or haptic cues are provided to indicate the change in force fields, subjects fail to show task savings in the relearning of A (Cothros et al. 2008; Gandolfo et al. 1996). Only when the two opposing force fields are interspersed with a long delay (i.e., a day) or by extensive training (Krakauer et al. 2005), with random or frequent switches of fields, can they be learned (Osu et al. 2004).

Whereas static visual and haptic cues may fail in supporting retention, our results suggest a role for vestibular cues in the independent formation and retrieval of multiple internal models or motor memories. The important difference compared with standard visual and haptic cues is that the vestibular system is an integral part of the sensorimotor loop, in that its signals are involved in online feedback control of the movement (Bresciani et al. 2005).

Recently, Howard et al. (2012) showed that a dynamic visual cue is able to serve as contextual information, and reduce interference, if incorporated into the sensorimotor loop by dynamically timing and aligning it with the onset of the movement. Similarly, using two opposite visuomotor rotations, Hirashima and Nozaki (2012) trained subjects to physically perform the same movement in the context of two distinct visual targets (thus 2 motor plans). Next, they added two opposing curl force fields linked to the two motor plans and showed that subject could learn to compensate for the two fields without interference. In contrast to both studies (Hirashima and Nozaki 2012; Howard et al. 2012), our study does not artificially create a connection between visual input and motor execution but makes use of the natural, direct link between the vestibular and motor system, providing a cue within and not before the execution of the reach. We show that this can also disambiguate two contexts, enabling the system to readily select the appropriate internal model. The vestibular system directly senses the underlying accelerative cause of the perturbing forces, enabling immediate corrective responses and providing important information about the dynamic environment.

To our knowledge, we are the first to show the contribution of a vestibular cue to multiple task savings and recall in force environments. In the present study, subjects adapted to two opposite force environments, even though the visual context remained the same, i.e., the reach target was the same. In other words, two distinct internal models can be learned and retrieved while having only one movement intention. Thus, in our case, retention is not facilitated through a difference in the visual (Hirashima and Nozaki 2012) or motor plan (Hwang et al. 2006a; Howard et al. 2008, 2010, 2012; Malone et al. 2011; Nozaki et al. 2006) but by contextual coupling of internal models through vestibular cues during task execution.

Although we attribute the retention effect to the vestibular input, the whole body acceleration also activates cutaneous receptors due to the pressure and shear forces. We cannot dissociate their contribution from the vestibular contribution to retention (Clemens et al. 2011). In contrast, it is unlikely that proprioceptive signals have cued the opposing force environments. Previous studies have shown that when reach goal and initial limb configuration are the same, proprioceptive feedback signals throughout the reach do not induce retention. Therefore, in the current study, in which reach goal and limb configuration are the same for the force environments, other signals (i.e., vestibular and/or cutaneous sensory signals) have provided relevant contextual cues to distinguish the imposed force environments.

Why would proprioceptive error signals from a perturbed reach, that are essential for adaptation, fail to serve as contextual cues for learning two opposite perturbations (see e.g., Caithness et al. 2004)? We suggest that the important difference with vestibular signals is that such time-varying proprioceptive signals represent a mixture of cause and effect. In contrast, vestibular signals solely reflect the cause of error but not the actual error signal itself. If the brain cannot dissociate the underlying causes of the errors (Berniker and Kording 2008), it is also unable to attribute them to separate internal models. In contrast, time-varying proprioceptive signals from a precueing movement [i.e., movements before perturbation exposure (Howard et al. 2012), initial limb configuration (Nozaki et al. 2006), and movement intentions (Hirashima and Nozaki 2012; Howard et al. 2008, 2010)] do dissociate the two contexts, and as a result two separate internal models are formed and retained.

Two theories have been proposed in the literature on the mechanism by which a contextual cue could enable savings. One theory suggests that memories can be in an active or inactive state. During the formation of a memory, the information is first coded in an active and readily available state. The memory can turn over to an inactive state when no further events occur on which the memory is based or if no further actions occur. An inactive memory needs to be reactivated to return to an active state if it is to be used in guiding behavior (Nader et al. 2000; Nader 2003). It requires task-dependent contextual cues to decide when and which motor memory should be reactivated. If there are no such cues, the memory remains in the latest, active state and is constantly modified, even if the dynamics of the environment change (Caithness et al. 2004). Recently, this idea was implemented in a model using multiple states that are operated by contextual cues (Lee and Schweighofer 2009). Although this model is agnostic as to the nature of these contextual cues, here we suggest they must be task-related cues, of sensorimotor origin, to operate the switch.

A second theory is that in the learning of field A, followed by the learning of field B, two distinct memories are formed. The memory of A is not modified by B. Instead, both memories coexist, but the most recently stored memory masks the other. This explains why in the ABA paradigm there is no faster relearning at reexposure of field A, when no task-dependent contextual cues are provided. In other words, this theory suggests that multiple motor memories are encoded, but the retrieval of the correct memory for a specific task requires task-dependent contextual cues. Behaviorally, both theories yield the same outcome: no faster relearning at reexposure of field A in an ABA paradigm, in the absence of contextual cues (Criscimagna-Hemminger and Shadmehr 2008; Pekny et al. 2011).

In both the RI and FI paradigm, contextual cues mediate switching between motor memories by activating or unmasking them. The result is observed as savings. It has been suggested that savings are improved if anterograde interference is reduced by the use of washout trials (Miall et al. 2004). However, our data showed retention both when anterograde inference was minimized (RI paradigm, using intervening washout trials) and when there were full levels of anterograde and retrograde interference (FI paradigm). In both paradigms, learning took place significantly faster during the second exposure to the same force pairing compared with the first exposure (see Figs. 2–4), suggesting that the vestibular cue distinguishes among fields A, B, and null.

To our knowledge, there are no reports that tested reach adaptation to inertial forces induced by linear whole body accelerations. Changes in control strategies in response to perturbation of gravitational forces, through micro- or hypergravity, have been reported (Crevecoeur et al. 2009, 2010). In those experiments vestibular signals certainly played a role, but retention was not tested in terms of an ABA paradigm. In other previous literature, adaptation to Coriolis forces has been studied in subjects reaching during constant-speed body rotations (Lackner and Dizio 1998). However, in such experiments the vestibular system no longer indicates movement. Also, in Hwang et al. (2006b) the vestibular system was not involved, since they studied reaches in the presence of inertial forces created by a haptic manipulandum. They found that the trajectories of the adapted reaches did not converge to straight movements, but curved 1–2 cm away from a straight line. We made similar observations in our paradigm (see Fig. 2). These findings do not imply that adaptation was incomplete. The view that adaptation is about canceling kinematic effects of a perturbation, thus that movements return to near baseline (unperturbed) conditions (e.g., a straight line), was recently challenged by Izawa et al. (2008). They suggest that motor adaptation is a process of reoptimization, possibly resulting in a different trajectory in the new environment (Chib et al. 2006; Izawa et al. 2008). Our results support this notion. Subjects exploited the force field by using a control policy that initially counteracts the inertial forces imposed by the accelerating body and then, after the hand has reached peak velocity, uses the body's deceleration to pull the hand back to target.

Finally, we note the difference between the observed learning rates with the use of a haptic manipulandum (Shadmehr and Mussa-Ivaldi 1994) compared with use of a rotating room (Lackner and Dizio 1998) or linear accelerations to introduce a force field. In the first setup, in which there are contact forces on the reaching hand, subjects need about 80 trials to reach a stable state. When there are no contact forces, as in the latter two setups, learning seems to occur about twice as fast, suggesting that contact-free inertial forces acting on the entire arm are taken into account more readily than contact forces acting on a single point.

Taking all findings into account, we suggest that the vestibular system plays an important role in coding and decoding multiple motor memories. This system provides information about the environmental dynamic changes and a strong contextual cue for different types of force fields. Such cues, if an integral part of the sensorimotor loop, substantially reduce interference and improve the formation and selection of multiple memories.

GRANTS

This research was supported by The Netherlands Organization for Scientific Research Grants 451-10-017 (to L. P. Selen), 400-07-003 (to W. P. Medendorp), 453-11-001 (W. P. Medendorp), a starting grant from the European Research Council (to W. P. Medendorp), and a grant from the Radboud University Medical Centre (to L. P. Selen and W. P. Medendorp).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

A.M.S., L.P.S., and W.P.M. conception and design of research; A.M.S. performed experiments; A.M.S. and L.P.S. analyzed data; A.M.S., L.P.S., and W.P.M. interpreted results of experiments; A.M.S. prepared figures; A.M.S. drafted manuscript; A.M.S., L.P.S., and W.P.M. edited and revised manuscript; A.M.S., L.P.S., and W.P.M. approved final version of manuscript.