Abstract
The Monty Hall Dilemma (MHD) is a well-known probability puzzle in which players try to guess which of three doors conceals a prize. After selecting a door, players are shown that there is no prize behind one of the remaining doors. Players then are given a choice to stay with their door or switch to the other unopened door. Most people stay, even though switching doubles the probability of winning. The MHD offers one of the clearest examples of irrational choice behavior in humans. The present experiment investigated how monkeys and humans would behave when presented with a computerized version of the MHD. Specifically, we were interested in whether monkeys were more likely to engage in a switching strategy than humans and whether both species could learn to switch with repeated trials. Initially, humans and monkeys showed indifference between the two options of either staying with their initial choice or switching. With experience, members of both species learned to use the switch strategy at above chance levels, but there were individual differences with only approximately half of the participants in each species learning to choose the more optimal response. Thus, humans and monkeys showed similar capacity to adjust their responding as a result of increased experience with this probabilistic task.
Keywords: Monty Hall Dilemma, rhesus monkeys, Macaca mulatta, Probability game
Recent interest has emerged in searching for the evolutionary foundations of human economic decision-making. In part, this has been the result of accumulating evidence indicating that humans are not as optimal in their decision-making as once was thought (e.g., Shanks, Tunney, & McCarthy, 2002). Humans frequently make decisions that fail to produce the most optimal outcomes in situations in which risks and rewards are compared (e.g., Tversky & Kahneman, 1974), in situations in which goods are distributed among various partners (e.g., Henrich et al., 2006), in situations in which past and future costs are weighed (e.g., Arkes & Blumer, 1985), and in situations in which probabilities of outcomes must be estimated (e.g., Kahneman & Tversky, 1973). Cumulatively, this evidence indicates that the human species should be demoted from its honorary title of Homo economicus to a more realistic position as a species in which multiple non-relevant contextual and experiential aspects interfere with decision-making. Recent evidence suggests that some nonhuman species also show suboptimal behaviors in situations where maximization can occur but does not (e.g., Beran, Evans, & Harris, 2008) but in other situations, nonhuman species are more rational maximizers than humans (e.g., Jensen, Call, & Tomasello, 2007). It is also important to note that, even when behavior appears to be suboptimal, or even “irrational,” this behavior could be a by-product of an otherwise rational decision strategy that simply does not apply well to a given task because of the nature of the task itself.
The 3 Door Problem offers one of the clearest examples of irrational behavior in humans. The problem originated from a variation of a game that was part of a popular TV game show hosted by Monty Hall and is therefore often referred to as the Monty Hall Dilemma (MHD), although the MHD does not exactly follow the course of events used in the game show. In the MHD variation of the game show, participants choose one of three doors. One of the doors conceals a valuable prize (e.g., a car) while the other two doors conceal worthless prizes known as “zonks” (e.g., goats). After contestants make a selection, one of the unselected doors is opened, and that door always reveals a zonk. Participants then are asked if they want to stay with their original selection or switch to the unopened door before all doors are opened and the location of the prize is revealed.
Intuitively, one might assume that it does not matter whether one switches or stays with the original selection. With two doors remaining, one might assume that the probability of winning is .50 either way. However, Selvin (1975) showed that employing a switching strategy improves the probability of winning from .33 to .67. The reason this strategy is optimal is not always intuitive. If, at the beginning the game, the contestant picks one of the two doors that has a zonk behind it (which they will do in 2 out of 3 games), they will always win the prize by switching as the other zonk cannot be picked because it has to be revealed. However, if the door with the prize behind it is selected (which will happen on average in only 1 game in 3), the player will not win after switching. So, if the player always switches, the player wins 2 games of 3 (67%) as the player has a 2 in 3 chance of originally picking a zonk. Despite this fact, empirical studies consistently show that when faced with the MHD, most people fail to switch (Friedman, 1998; Granberg & Brown, 1995; Granberg & Dorr, 1998), and this effect occurs across cultures (Granberg, 1999a). For example, Friedman found that when faced with a card problem analogous to the MHD, fewer than 10% of the participants switched on the first trial. Thus, adult humans appear to act irrationally and in a suboptimal manner when faced with the MHD, perhaps because they do not understand the causal nature of the task (Burns & Wieth, 2004).
However, most of the research with the MHD has focused on the initial response to the problem and has aimed to increase the probability of switching by employing confederates (Granberg & Dorr, 1998), providing additional information about the problem (Friedman, 1998), or changing the probabilities (Granberg, 1999b). Most of these manipulations fail to show rational behavior on the part of human participants. One possibility, however, is that this irrational behavior may change with experience, and in particular, with experience that provides concrete feedback in the form of winning and losing outcomes. There is evidence that humans do increase use of a switching strategy when they make repeated responses and receive feedback (e.g. Granberg & Dorr, 1998). However, the number of repeated trials is usually small in studies with human participants (< 50; but see Herbranson & Schroeder, 2010) and use of the switch strategy tends to stabilize at just over .50.
The MHD is interesting for several reasons. First, it is interesting because the solution is not intuitive. It has been stated that no other statistical puzzle comes so close to fooling all of the people all of the time (Krauss & Wang, 2003). Second, the problem involves a two-step decision-making process whereby participants can make an initial tentative decision, receive new information and then decide whether they want to commit to their original choice or change their minds. In this way, researchers can use the MHD to investigate how commitment, regret, and dissonance affect decision-making (Granberg, 1999b). Finally, when presented with the MHD, humans tend to behave irrationally. Although the most efficient strategy is to switch, most people (erroneously) believe that they have a 50 percent chance of winning when asked whether they want to switch or stay. Therefore, one would predict that switch rates should mirror this probability. However, most people opt to stay with their original choice (Burns & Wieth, 2004). Although it is not known exactly why people show a stay bias, it has been hypothesized that people find switching and losing more aversive than staying and losing (Gilovich, Medvec, & Chen, 1995). To test this hypothesis, Granberg and Brown (1995) gave participants a hypothetical test of choices (switch or stay) and outcomes (win or lose) and asked them to describe how they would feel in each situation. Participants reported that they would feel worse about losing if they switched from a door that concealed a prize than if they lost by staying with a door that concealed a zonk. A subsequent study provided some evidence that the reluctance to switch could also be explained by an illusion of control that accompanied the initial selection (see Granberg & Dorr, 1998).
Only one experiment to date has given the MHD to a nonhuman species (Herbranson & Schroeder, 2010). In that study, pigeons were given an operant version of the task, and repeated exposure to the game over long periods of time. Pigeons came to respond optimally, switching their choice on the vast majority of trials, and this behavior remained optimal even as the researchers manipulated the probability of reinforcement for the switching response. Humans, however, did not show such optimal performance, suggesting a clear species difference.
The purpose of the present study was to investigate how nonhuman primates behaved when presented with the MHD. Specifically, we were interested in whether monkeys would be more likely to switch than humans (looking more like pigeons) or would show the same response biases shown by humans. We also were interested in whether humans and monkeys eventually could learn to use a switching strategy (regardless of any initial response biases) with repeated opportunities to solve the problem. Therefore, we compared the performance of rhesus monkeys and humans on identical versions of a computerized MHD task. This comparison is an interesting one because rhesus monkeys are more closely related to humans than are pigeons (the only other species given the MHD game), and so there is some expectation that monkeys might show more of the biases that humans show in the task. This might be expected given that other comparisons of humans and pigeons on identical probability-based tasks have also shown large differences in performance, and specifically suboptimal responding by humans relative to pigeons (Herbranson, Fremouw, & Shimp, 1999 Herbranson, Fremouw, & Shimp, 2004).
Our predictions were as follows. First, we expected all subjects to initially show a stay bias (humans) or show indifference to the two options (monkeys). For humans, this would be consistent with previous studies that presented a relatively small number of trials, and for monkeys we expected that some number of trials would be needed to teach them the nature of the task given that verbal instructions were impossible. Given the large number of trials presented in our experiment, however, we expected subjects to change their strategy as a result of trial by trial feedback. Their initial behavior would result in reinforcement either 33% of the time (for a stay bias) or 50% of the time (for indifference), which would presumably be low enough that subjects would investigate alternative strategies (i.e., switching) and eventually learn to behave optimally, exclusively using a switch strategy.
The MHD is difficult for humans because of the conflict between what is intuitively believed about the task (i.e., that there is a .50 probability of winning) and what is actually experienced (i.e., the results of actually employing switching and staying responses). Presently, it is not known whether monkeys would suffer that same faulty decision-making or whether they would look more like pigeons (Herbranson & Schroeder, 2010). What is known is that human children become progressively less efficient at the MHD as they get older (e.g., DeNeys, 2007). Specifically, they become more likely to assume the chances are equal for either of the two remaining doors containing the prize, and they become more likely to adopt a strategy of sticking with their original choice. This developmental trend may well be influenced by increased experience with formal mathematics and probability outcomes, something that monkeys would not have as much experience with. Therefore, we predicted that monkeys would outperform humans in the repeated MHD game, suggesting that animals are less likely to suffer from faulty probability estimation in the face of clear feedback.
Method
Participants
We tested 15 adult humans, all of whom were undergraduate students attending Georgia State University. The participants included 4 males (mean age = 22.75 years; SD = 6.29), and 11 females (mean age = 20.00 years; SD = 1.61). These participants were recruited from various psychology courses and received partial course credit for their involvement.
We also tested 7 rhesus monkeys (Macaca mulatta), all housed at the Language Research Center of Georgia State University. The rhesus monkeys were all males (mean age = 15.43 years; SD = 8.94), and they were all individually housed with continuous visual and auditory access to other monkeys. All monkeys had 24-hour access to water and were fed a daily diet of fruit, vegetables, and manufactured chow. All monkeys were highly experienced with making joystick responses to digital stimuli with the employed apparatus, and they all had previously been tested in a variety of computerized cognitive and psychomotor tasks. Relevant to the current task, the monkeys successfully completed a previous quantity conservation task in which they made multiple responses to the same stimuli within each trial, indicating that they recognized that the trial had continued rather than starting anew (Beran, 2007).
Apparatus
The test program was created using Microsoft Visual Basic version 6.0. The input device was the directional button of a digital gamepad, which was fitted with a metal joystick. The monkeys manipulated the joystick outside of their home cage by reaching through their cage mesh. The joystick controlled a cursor on a computer monitor, and participants used this cursor to select task stimuli by bringing it into contact with those stimuli. Monkeys were rewarded automatically with 97 mg fruit flavored pellets for correct responses. Incorrect responses led to no food reinforcement. Human participants were given visual feedback for their correct and incorrect responses in the form of flashing on-screen words “Winner” and “Loser.” Humans and monkeys also received differential auditory feedback from the computer for correct and incorrect responses.
Procedure
The goal of the test program was for the participant to locate a small green square (1.9 cm by 1.9 cm) that was the prize located behind one of three large black squares (5.3 cm by 5.3 cm) that served as the doors. The position of the green square was randomly determined at the start of each trial, independent of where it has been located during previous trials. Behind each of the other two black squares was a small red square (1.9 cm by 1.9 cm) that represented an incorrect response (i.e., a zonk). At the beginning of the trial a cursor appeared in the center of the computer screen and the three black squares appeared in three of the four corners of the computer screen (the three chosen positions were randomly determined for each trial). This arrangement was chosen rather than a linear array because it decreased the chances of accidental touches to stimuli closer together on the screen that could have occurred if a linear array was used. Spacing stimuli in the corners of the screen was a common procedure for many of the previous experiments that these monkeys had completed. The participant initiated a trial by moving the cursor into contact with any one of the three black squares. The cursor then was fixed to the selected black square while one of the other two black squares moved upwards to reveal a small red square. The red square and the black square that had covered it then disappeared, and the cursor returned to the center of the screen. Next, the participant chose between the previously selected black square (the stay response) and the third black square (the switch response), and the “content” of the participant’s second choice then was revealed. The participant then received appropriate feedback (positive feedback if the green square was revealed, and negative feedback if a red square was revealed). Each new trial began after a short inter-trial interval (5s for the monkeys and 1s for the humans).
The human program differed from the monkey program in that it began with the following written instructions:
Thank you for your participation today. In the following experiment, you will be trying to locate the hiding location of a green square among three different locations. At the start of each trial, you will choose one of the three squares by using the joystick to move the red dot on the screen. After your choice, the computer will provide you with additional information about where the green square is NOT located. Then, you will make another response and find out if you win or lose and where the green square really was hidden. After a very short break, the next trial will begin. There is nothing tricky about the experiment. Please try your best to find the green square on each trial. When you are ready to begin, press the space bar. All responses after that will be made with the joystick.
These instructions were necessary because many human participants had never completed a task such as this, and the instructions gave them the basic parameters of the game without providing any instructions as to how to play the game strategically. Thus, there was no mention of switching or staying, and no mention of the Monty Hall Dilemma game. After completing the experiment (500 trials or the end of the experimental period, whichever came first), the human participants were presented with the following request on the computer screen:
One Last Request: Please use the box below to provide a written summary of any strategy that you might have used to play this game. Please be as detailed as possible regarding why you responded the way that you did. When you are finished, click the “Finished” button, and the experiment then is complete.
Participants completed a single 60-minute session during which they completed as many trials as possible. The rhesus monkeys each completed 500 trials. They had 4-hour access to the task each test day. Some monkeys were able to complete all 500 trials in the first session, but other monkeys required multiple sessions.
Analysis
For each completed trial, the computer program recorded whether the participant stayed or switched, and whether they won or lost the trial. We assessed the frequency of first-trial switch responses in human participants, as a group, using a binomial sign test with an alpha probability of .05 (we did not analyze the first-trial responses in monkeys because they were naïve as to the structure of the task on trial 1). Additionally, we analyzed the frequency of switch responses made by each individual of each species after 10 trials, and well as for each block of 100 trials (or as many 100 trial blocks were completed during the one hour session for human participants) using individual binomial sign tests with an alpha probability of .01. This alpha level was calculated using a Bonferroni correction for multiple comparisons within an individual (.05 / 5 trial-blocks = .01). These statistical tests indicated whether or not individuals significantly preferred a particular response pattern (switch or stay). However, they did not indicate whether statistically significant response patterns were optimal, as the only optimal pattern was to choose to switch in 100% of trials. See Figures 1 and 2 for the degree of each individual’s preferred response bias.
Figure 1.
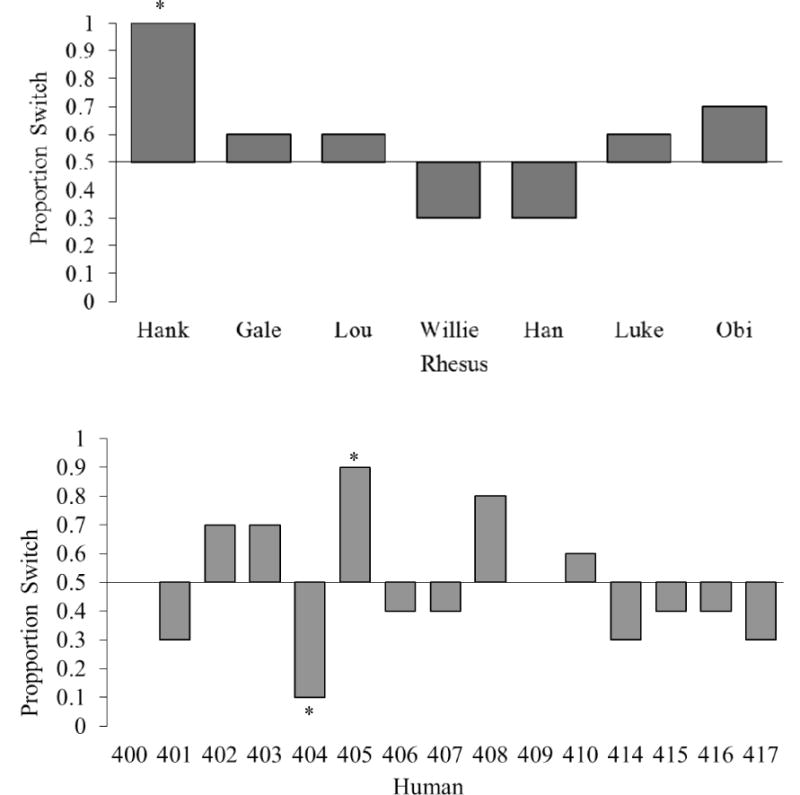
The percentage of switch choices for each participant across the first 10 trials. An asterisk located above or below a bar indicates a significant switch or stay bias, respectively.
Figure 2.
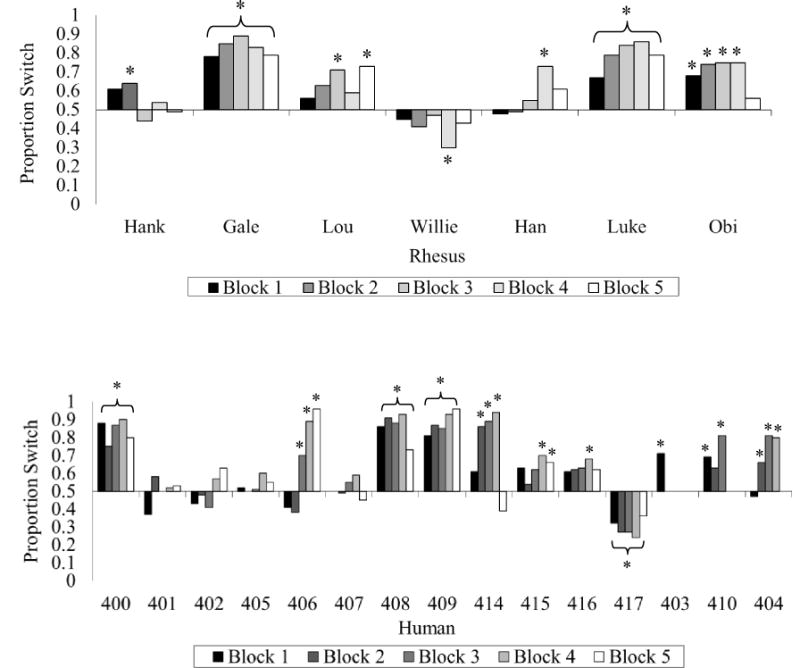
The percentage of switch choices for each participant across all trials completed (divided into 100-trial blocks). An asterisk located above or below an individual bar indicates a significant switch or stay bias, respectively. An asterisk located above or below a bracket indicates an experiment-wide significant switch or stay bias, respectively.
Results
Nine human participants completed the 500-trial test block in their single session. The other six completed between 191 and 490 trials (Mean = 470.53, SD = 80.06) before the session ended. All 7 monkeys completed the 500-trial test block, and they required between 1 and 7 sessions to do so (Mean = 2.86, SD = 1.95). Figure 1 shows all participants’ performance at the end of their first 10 trials. Figure 2 shows performance across all trials, divided into 100-trial blocks.
On the first trial, 10 of the 15 human participants chose to stay with their original selection. However this was not a significant group level preference (p = .302). After the first 10 trials, only two humans showed statistically significant selection biases. One individual chose to stay and one individual chose to switch (both p = .022; Figure 1). Also, only one monkey exhibited a significant individual selection bias for the switch response (p < .05; Figure 1).
After 100 trials, 5 of 15 humans exhibited a significant bias to switch whereas only 1 individual exhibited a significant bias to stay with their original choice (all p < .01; Figure 2). After 100 trials, 3 of 7 individual rhesus monkeys exhibited a significant bias to switch (all p < .01; Figure 2) and no monkeys exhibited a significant bias to stay. For each successive block of 100 trials, the number of participants in each species that exhibited a significant bias is shown in Figure 2. As seen in the figure, there were individual differences, with approximately half of the participants in each species showing a significant bias (p < .01) to switch for any given 100-trial block, and very few individuals who showed a preference to stay.
Discussion
This experiment provides a comparative assessment of performance on a computerized version of the MHD using humans and rhesus monkeys. On average, at the outset of the testing, both species showed indifference between the two options of either staying with their initial choice or switching. However, within the first 100 trials, and then for all remaining blocks of trials, approximately half of the subjects of each species showed a significant bias to switch. Therefore, at the behavioral level, these two groups responded very similarly. Neither species, however, approached the optimal levels of responding exhibited by pigeons (Herbranson & Schroeder, 2010). As noted by one of the reviewers of this paper, pigeons often are faced with probabilistic situations in which they must be sensitive to probabilities in order to maximize reinforcement (e.g., Arkes & Ayton, 1999; Bullock & Bitterman, 1962; Shimp, 1973). This may not be as true for monkeys, and especially monkeys that have extensive experience on tasks that mainly offer 100% probability for food reward with “correct” responding. The monkeys in this experiment have participated almost exclusively in experiments in which all correct responses produced food reward with 100% probability, and all incorrect responses produced either no food or a timeout period with 100% probability. This may explain why monkeys looked more like human than did pigeons.
Typically, when humans are given only one chance to play the MHD game, they show either indifference or a bias to stay with their original selection despite the fact that neither of those strategies is optimal, and we saw the same pattern in this experiment. There also were individual differences in the extent to which participants of each species changed their behavior throughout the experiment (Figure 2). One might expect that learning might occur in which the switch strategy was employed more and more frequently as the experiment progressed, but this was true only for a few monkeys (e.g., Lou and Luke) and a few humans (#404, #406, #409, #414). Even rarer among these individuals were the large changes in switch responses that might reflect more explicit recognition of the optimal response strategy (e.g., perhaps human participants #406 and #414, although even they did not shift to 100% switching). Only one participant explicitly stated a response strategy that was optimal – “First, I clicked on a random box. After one of the boxes disappeared, I clicked on the third box.” This participant (#409) switched most often of all human participants (88% of trials; Figure 2). Another participant (#414) stated the same general strategy but expressed little confidence in that strategy (“It seemed that I had the highest win percentage when I would go for the box in the middle first, then the remaining box I had not tried before. That may have just been luck though.”). This participant also had a lower percentage of switching (74%; Figure 2). Two participants (#415 and #417) reported that they used the results of a previous trial to dictate future responses on new trials on the basis of door location (a variation of the win-stay, lose-shift strategy). These two participants switched on 63% and 52% of the trials overall (Figure 2).
There were two participants (#400 and #417) who claimed to have no strategy other than random responding, although in actuality these two participants were heavily biased to switch (84% of trials switched) or stay (71% of trials stayed) with their first selection. The remaining nine participants offered no response to the question about strategy or just restated the goal. Therefore, despite a minority of participants showing behavioral changes over the course of the experiment, nearly none of the human participants explicitly stated that they used a clear rule. Their changing response patterns seemingly emerged from implicit recognition that the correct strategy was to switch choices within each trial. This could be similar to the way in which human children and adults have been reported to learn artificial grammars in laboratory tests despite being unable to verbalize the grammatical rules (e.g., Braine, 1963; Reber, 1967). Further, the performance here may relate to the kind of implicit learning shown in weather prediction tasks (i.e., learning that certain arbitrary stimuli are predictive of particular weather conditions); in both cases participants gradually learn appropriate responses while being unable to articulate the actual rules of the task (for a review, see Janacsek & Nemeth, 2012).
This is the first time that monkeys have been presented with the MHD, and their performance indicates a strong comparative similarity with human responding. This was contrary to our prediction that monkeys would outperform humans when both were given repeated experience with the task. Initially, the monkeys had no strategy other than random responding, but with experience approximately half of the monkeys learned that switching was a more effective strategy, and this proportion matched that of the subset of humans who also came to switch more often than chance. However, it is important to note that with much more experience, both species may have shown more optimal responding, in line with that seen in pigeons that were given many days of testing (Herbranson & Schroeder, 2010), although for many of the participants 500 trials was not sufficient to show more optimal responding with experience.
In conclusion, with repeated trials some monkeys and some humans learned to rely more on a switching strategy when faced with the MHD task. Despite showing early indifference and sub-optimal responding, learning did occur for these individuals. Most human participants who improved did so without explicitly stating why they performed the way that they did. This suggests that recognition of statistical probabilities within this game occurred implicitly if it was occurring at all. We did not directly ask participants if they knew what the probabilities for each response type were in terms of finding the prize, and so more research is needed to better understand whether participants fail to optimize their wins because of lack of understanding of the probabilities of the game or because of choice of response strategies that do not best match those probabilities.
The issue of individual differences in responding remains to be more thoroughly assessed, in both species. A larger sample of participants might provide a clearer picture of what accounts for the initial biases, the likelihood of changing strategies with experience, and the likelihood of finding the optimal strategy. We considered carefully a number of things that might account for the differences in the monkeys’ performance, but at present we do not have any viable hypotheses. What we can state is that, at least for the monkeys, there is no ranking of these animals in terms of their strategy (switch, stay, or random) that matches how we might rank those animals in age, years performing computer tests, general productivity on computer tests (e.g., trials per day output), or even our own subjective sense of their “brightness.” Monkeys Gale and Hank, for example, are the same age, started in research at the same time, and have very similar testing histories, for much of which they looked very similar in performance. And yet here they differed substantially in their response choices. Much work remains on the issue of individual differences in comparative cognition (see Kemp & Kaplan, 2011; Matzel, Wass, & Kolata, 2011; Mercado, 2011; Vonk & Povinelli, 2011).
These results also indicate the need to expand the phylogenetic assessment of responding in this task. If this form of learning how to maximize one’s number of winning responses occurs implicitly, it should occur as well in many other species. Specifically, it should be evident in those species that have shown an affinity for tracking reward rates and probabilities given multiple schedules or response types (such as the pigeons that have shown such high levels of optimal responding in the MHD; Herbranson & Schroeder, 2010). Success of nonhuman animals on the MHD also may have important implications for other areas of investigation into psychological phenomena such as cognitive dissonance (see Chen, 2008; Egan, Santos, & Bloom, 2007). Thus, additional investigations of the MHD will better outline the phylogenetic emergence of probability learning and the relative role of explicit and implicit knowledge in decision making across species.
Acknowledgments
This research was supported by National Institute of Child Health and Human Development Grants HD-38051, HD-060563, and National Science Foundation Grant BCS-0924811. The authors thank Audrey Parrish for her helpful comments on an earlier draft of this paper.
References
- Arkes HR, Ayton P. The sunk cost and Concorde effects: Are humans less rational than lower animals? Psychological Bulletin. 1999;125:591–600. [Google Scholar]
- Arkes HR, Blumer C. The psychology of sunk costs. Organizational Behavior and Human Decision Processes. 1985;35:124–140. [Google Scholar]
- Beran MJ. Rhesus monkeys (Macaca mulatta) succeed on a computerized test designed to assess conservation of discrete quantity. Animal Cognition. 2007;10:37–45. doi: 10.1007/s10071-006-0028-5. [DOI] [PubMed] [Google Scholar]
- Beran MJ, Evans TA, Harris EH. Perception of food amount by chimpanzees based on the number, size, contour length, and visibility of items. Animal Behaviour. 2008;75:1793–1802. doi: 10.1016/j.anbehav.2007.10.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Braine MDS. On learning the grammatical order of words. Psychological Review. 1963;70:323–348. doi: 10.1037/h0047696. [DOI] [PubMed] [Google Scholar]
- Bullock DH, Bitterman ME. Probability-matching in the pigeon. American Journal of Psychology. 1962;75:634–639. [PubMed] [Google Scholar]
- Burns BD, Wieth M. The Collider Principle in causal reasoning: Why the Monty Hall Dilemma is so hard. Journal of Experimental Psychology. 2004;133:434–449. doi: 10.1037/0096-3445.133.3.434. [DOI] [PubMed] [Google Scholar]
- Chen MK. Rationalization and cognitive dissonance: Do choices affect or reflect preferences? (Cowles Foundation Discussion Paper No 1669) New Haven, CT: Yale University Cowles Foundation for Research in Economics; 2008. [Google Scholar]
- Egan LC, Santos LR, Bloom P. The origins of cognitive dissonance. Psychological Science. 2007;18:978–983. doi: 10.1111/j.1467-9280.2007.02012.x. [DOI] [PubMed] [Google Scholar]
- De Neys W. Development of decision making: The case of the Monty Hall Dilemma. In: JA Elsworth., editor. Psychology of decision making in education, behavior, and high risk situations. Hauppauge, NY: Nova Science Publishers; 2007. pp. 271–281. [Google Scholar]
- Friedman D. Monty Hall’s three doors: Construction and deconstruction of a choice anomaly. The American Economic Review. 1998;88:933–946. [Google Scholar]
- Gilovich T, Medvec VH, Chen S. Commission, omission, and dissonance reduction: Coping with regret in the “Monty Hall” problem. Personality and Social Psychology Bulletin. 1995;21:182–190. [Google Scholar]
- Granberg D. Cross-cultural comparison of responses to the Monty Hall Dilemma. Social Behavior And Personality. 1999a;27:431–438. [Google Scholar]
- Granberg D. A new version of the Monty Hall dilemma with unequal probabilities. Behavioural Processes. 1999b;48:25–34. doi: 10.1016/s0376-6357(99)00066-2. [DOI] [PubMed] [Google Scholar]
- Granberg D, Brown TA. The Monty Hall dilemma. Personality and Social Psychology Bulletin. 1995;21:711–723. [Google Scholar]
- Granberg D, Dorr N. Further exploration of two-stage decision making in the Monty Hall dilemma. American Journal of Psychology. 1998;111:561–579. [Google Scholar]
- Henrich J, McElreath R, Barr A, Ensminger J, Barrett C, Bolyanatz A, Cardenas JC, Gurven M, Gwako E, Henrich N, Lesorogol C, Marlowe F, Tracer D, Ziker J. Costly punishment across human societies. Science. 2006;312:1768–1770. doi: 10.1126/science.1127333. [DOI] [PubMed] [Google Scholar]
- Herbranson WT, Fremouw T, Shimp CP. The randomization procedure in the study of categorization of multidimensional stimuli by pigeons. Journal of Experimental Psychology: Animal Behavior Processes. 1999;25:113–135. [PubMed] [Google Scholar]
- Herbranson WT, Fremouw T, Shimp CP. Categorizing a moving target in terms of its speed, direction, or both. Journal of the Experimental Analysis of Behavior. 2002;78:249–270. doi: 10.1901/jeab.2002.78-249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herbranson WT, Schroeder J. Are birds smarter than mathematicians? Pigeons (Columba livia) perform optimally on a version of the Monty Hall Dilemma. Journal of Comparative Psychology. 2010;124:1–13. doi: 10.1037/a0017703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Janacsek K, Nemeth D. Predicting the future: From implicit learning to consolidation. International Journal of Psychophysiology. 2012;83:213–221. doi: 10.1016/j.ijpsycho.2011.11.012. [DOI] [PubMed] [Google Scholar]
- Jensen K, Call J, Tomasello M. Chimpanzees are rational maximizers in an Ultimatum Game. Science. 2007;318:107–109. doi: 10.1126/science.1145850. [DOI] [PubMed] [Google Scholar]
- Kahneman D, Tversky A. On the psychology of prediction. Psychological Review. 1973;80:237–257. [Google Scholar]
- Kemp C, Kaplan G. Individual modulation of anti-predator responses in common marmosets. International Journal of Comparative Psychology. 2011;24:112–136. [Google Scholar]
- Krauss S, Wang XT. The psychology of the Monty Hall problem: Discovering psychological mechanisms for solving a tenacious brain teaser. Journal of Experimental Psychology: General. 2003;132:3–22. doi: 10.1037/0096-3445.132.1.3. [DOI] [PubMed] [Google Scholar]
- Matzel LD, Wass C, Kolata S. Individual differences in animal intelligence: Learning, reasoning, selective attention and inter-species conservation of a cognitive trait. International Journal of Comparative Psychology. 2011;24:36–59. [Google Scholar]
- Mercado E., III Mapping individual differences in learning capacity. International Journal of Comparative Psychology. 2011;24:4–35. [Google Scholar]
- Reber AS. Implicit learning of artificial grammars. Journal of Verbal Learning and Verbal Behavior. 1967;6:855–863. [Google Scholar]
- Selvin S. A problem in probability. The American Statistician. 1971 Feb;29:67. [Google Scholar]
- Shanks DR, Tunney RJ, McCarthy JD. A re-examination of probability matching and rational choice. Journal of Behavioral Decision Making. 2002;15:233–250. [Google Scholar]
- Shimp CP. Probabilistic discrimination learning in the pigeon. Journal of Experimental Psychology. 1973;97:292–304. [Google Scholar]
- Tversky A, Edwards W. Information versus reward in binary choices. Journal of Experimental Psychology. 1966;71(5):680–683. doi: 10.1037/h0023123. [DOI] [PubMed] [Google Scholar]
- Tversky A, Kahneman D. Judgment under uncertainty: Heuristics and biases. Science. 1974;185:1124–1131. doi: 10.1126/science.185.4157.1124. [DOI] [PubMed] [Google Scholar]
- Vonk J, Povinelli D. Individual differences in long-term cognitive testing in a group of captive chimpanzees. International Journal of Comparative Psychology. 2011;24:137–167. [Google Scholar]


