Polyethylene glycol binding alters human telomere G-quadruplex structure by conformational selection

Abstract

Polyethylene glycols (PEGs) are widely used to perturb the conformations of nucleic acids, including G-quadruplexes. The mechanism by which PEG alters G-quadruplex conformation is poorly understood. We describe here studies designed to determine how PEG and other co-solutes affect the conformation of the human telomeric quadruplex. Osmotic stress studies using acetonitrile and ethylene glycol show that conversion of the ‘hybrid’ conformation to an all-parallel ‘propeller’ conformation is accompanied by the release of about 17 water molecules per quadruplex and is energetically unfavorable in pure aqueous solutions. Sedimentation velocity experiments show that the propeller form is hydrodynamically larger than hybrid forms, ruling out a crowding mechanism for the conversion by PEG. PEGs do not alter water activity sufficiently to perturb quadruplex hydration by osmotic stress. PEG titration experiments are most consistent with a conformational selection mechanism in which PEG binds more strongly to the propeller conformation, and binding is coupled to the conformational transition between forms. Molecular dynamics simulations show that PEG binding to the propeller form is sterically feasible and energetically favorable. We conclude that PEG does not act by crowding and is a poor mimic of the intranuclear environment, keeping open the question of the physiologically relevant quadruplex conformation.

INTRODUCTION

The highly conserved repetitive DNA sequence 5′-d(TTAGGG)_n is found within the telomeres of all human chromosomes (1). Hundreds of copies of the sequence are found in the telomere, predominantly in duplex form, but with ∼200 nt as a single-stranded 3′ overhang (2). This overhang is an unusual example of a functional single-stranded element within the human genome. In the presence of monovalent cations, at least four repeats of the TTAGGG sequence can fold into quadruplex structures comprising stacked G-quartets having a variety of loop topologies (3–7). A designed quadruplex-specific ligand, 360 A, binds preferentially to terminal regions of chromosomes in both normal and tumor cells (8), supporting the hypothesis that quadruplex ligands can induce or stabilize quadruplex structures within telomeres of human cells. Studies using a structure-specific antibody show that G-quadruplex formation at specific locations in the genome, including telomeres, may be modulated during cell-cycle progression in human cells (9). The extensive literature on the chemistry and biology of human telomere DNA has been recently reviewed (10).

The telomeric TTAGGG repeat sequence can fold into numerous quadruplex structures depending on the cations present and on nucleotide additions to the ends of the sequence. In Na⁺-containing solutions, an anti-parallel basket conformation was identified by nuclear magnetic resonance (NMR) (11). This structure features three stacked G-quartets, two lateral loops and one diagonal loop. In K⁺-containing crystals, a novel parallel-stranded ‘propeller’ structure was observed (12), featuring all-parallel strand segments and three stacked G-quartets linked by three chain-reversal ‘side’ loops. A variety of chemical and biophysical approaches has revealed that the propeller structure is not the predominant form in K⁺-containing solutions (13–17). Subsequently, two types of anti-parallel ‘hybrid’ or ‘3 + 1’ forms were determined by NMR (18–21). These structures feature three stacked G-quartets, two lateral loops and one side loop, where the location of the side loops differs in forms 1 and 2. Recently, an anti-parallel basket form with only two stacked G-quartets was identified in K⁺ solution by NMR (22). Which of these structures exist in the cell (if any) is of great interest and a matter of some debate.

Quadruplex structures are dependent on solution conditions. Addition of small molecule co-solvents or macromolecular co-solutes is commonly used to perturb conformational equilibria. There are four main mechanisms by which additives can influence conformation, namely, macromolecular crowding (which acts on shape and size differences), osmotic stress (which acts by hydration differences), differential binding (general solvation effects) and by general electrostatics (e.g. dielectric effect on ionic activities). The propeller quadruplex conformation was found to form in solution under dehydrating conditions (23,24), in high concentrations of polyethylene glycol (PEG) (14,23,25), and in a non-aqueous high-viscosity deep eutectic solvent (26). The cell and its compartments are certainly crowded, with macromolecules occupying ∼30% of the total volume in eukaryotes (27,28). The resultant excluded volume effects can drastically influence biochemical reactions by driving equilibria in the direction of species with the minimal volume (29–33). Efforts to mimic the intracellular environment of quadruplexes have relied on solute crowding reagents, typically PEGs of various molecular weights (MWs).

Hydration is a fundamentally important aspect of biochemical reactions, as hydration significantly impacts macromolecule stability and conformation (34,35), and water is an active participant in many biochemical reactions (34,36,37). However, the properties of the aqueous environment in the cell are a matter of some debate (34,37). The structure of water in the cell is inhomogeneous: the hydration layers around macromolecules differ from bulk water, and ‘free’ water also differs in some properties, including viscosity and diffusion coefficients. Processes such as macromolecular folding that involve differentially hydrated conformations depend on the activity of the water such that a reduction in water activity favors the less hydrated species (35). However, the exact water activity throughout the cell is poorly defined (38).

Crowding and hydration effects on reactions are distinct phenomena with different underlying physical principles, although an experimental separation of the effects can be complicated (38). Experimental studies of hydration using osmotic stress (36,39) or of macromolecular crowding (40,41) both rely on the addition of neutral co-solutes intended primarily to alter either water activity or excluded volume, respectively. Because any co-solute affects both of these solution properties to variable degrees, separating the dominant influence poses a challenge. Typically, water activity is changed by the addition of small neutral organic compounds [e.g. alcohols, sugars, ethylene glycol (EG)], whereas excluded volume is altered by addition of large polymers (e.g. PEGs, dextrans, proteins). In both approaches, it is essential that the added solutes are inert and do not interact with either reactants or products of the reaction under study. By convention, properly designed hydration or crowding studies typically use a number of different solutes to show that any observed effects are independent of the chemical properties of the individual solute additives (42).

One early example studied hydration and crowding effects on the stability of DNA triplex and duplex structures (42). The small osmolytes EG, glycerol, acetamide and sucrose were found to exert similar quantitative effects, decreasing water activity and destabilizing both duplex and triplex DNA. The results showed that the helical forms are more hydrated than the denatured single strands. In contrast, addition of the volume-excluding polymers PEG 400, 1000, 3400 and 10 000 stabilized both duplex and triplex DNA. Quantitative analysis of a large set of thermal denaturation data demonstrated that the effects of the polymers could be correlated with geometric models for excluded volume, and that their effects were due primarily to crowding. In this case, hydration changes and crowding effects could be clearly separated.

In contrast to DNA duplexes and triplexes, decreased water activity stabilizes quadruplexes and increases their melting temperature (24,40,43–45). This indicates that folded quadruplexes are less hydrated than their unfolded single strands, and that water is released on folding. Initial quantitative estimates using PEG suggest 13–18 water molecules per G-quartet are released on folding (44,46). Decreased water activity also drives a conformational transition of the human telomeric quadruplex in potassium solutions from a hybrid to a propeller form (23,24), indicating that these particular quadruplex conformations differ in their hydration.

Recent investigations have focused on the ability to perturb a variety of quadruplex equilibria through the addition of co-solvents. PEG 200 facilitates the folding of the sequence 5' G₃(T₂AG₃)₃ into an anti-parallel form in the absence of cation (47,48). In addition, PEG drives the formation of a quadruplex from an initial duplex formed by (TTAGGG)₄ and its complementary strand (49,50). Both of these cases are potentially consistent with a crowding mechanism, which demands that the reaction be driven in the direction that reduces the total excluded volume of the system, yielding more compact species. In these cases, the starting reactants (single strand, duplex) have larger hydrodynamic volumes than the final folded quadruplex product.

PEG has been reported to drive a transition between the anti-parallel hybrid and all-parallel propeller conformations of the human telomere sequence. This was first reported qualitatively in an attempt to rationalize why the solution structure differed from the structure observed in crystals (14). More detailed studies followed (25,48,51), including the determination of a high-resolution structure by NMR (23). In none of these cases were the contributions from hydration and crowding clearly separated and quantitatively accounted for. A puzzling aspect of these studies is why crowding should drive the transition of the more compact folded hybrid form to the hydrodynamically larger propeller form (24) because this violates the fundamental basis of macromolecular crowding. Other crowding agents that also have minimal effects on water activity, including BSA, Ficoll 70 and Ficoll 400 did not drive the hybrid to parallel quadruplex transition (24,51,52) nor was the propeller conformation observed by circular dichroism (CD) or NMR in a Xenopus laevis egg extract, which represents perhaps the best mimic of the crowded intracellular environment currently available (52,53). For a true crowding mechanism, the perturbation of the equilibrium should be independent of the chemical nature of the crowding agent. Macromolecular crowding therefore is an unlikely mechanism by which PEG alters quadruplex conformation, and additional studies are needed to understand how it acts.

The use of PEG in macromolecular crowding studies has been discouraged (32). A strict demand on a crowding reagent is that it is inert, with no binding to either the reactants or products of the reaction under study. Several studies have shown that the stabilization of protein by PEG cannot be described quantitatively in terms of excluded volume alone, but rather that there is an attractive interaction between PEG and non-polar or hydrophobic side chains on the protein surfaces (32). These attractive interactions make quantitative analysis of crowding effects difficult and compromise the use of PEG in crowding experiments. Further, PEG behaves like a weak organic solvent, and not simply as an inert volume excluder (54). For these reasons, it has been suggested PEG be avoided for crowding studies (55).

Crowding studies using PEG have been used to support the existence of a parallel conformation for telomeric DNA in vivo and to argue that it is the most relevant conformation to serve as a target for drug discovery (23,25,56). To assess these claims, it is important to understand the underlying mechanism by which PEG alters quadruplex conformation, and in particular to separate and quantify the contributions of hydration and crowding. An analytical strategy for the separation of preferential interactions and excluded volume effects was recently described (57). The analysis requires a study of the effects of a full series of monomeric to polymeric EGs on the ‘m-value’, the derivative of the observed free energy change for the reaction with respect to solute concentration. Such a systematic approach has not been previously used to study quadruplex structure and stability. The goals of this work are to evaluate the contributions of hydration, crowding or other interactions on the conformational transition between the hybrid and propeller forms and to understand the mechanism by which PEG influences the transition. Our results will show that PEG is not acting as a macromolecular crowding agent, making suppositions about the conformation of the quadruplex in the cell based on studies using PEG suspect.

MATERIALS AND METHODS

Oligodeoxynucleotides and co-solvent preparation

The 22-nt human telomeric G-quadruplex forming oligodeoxynucleotide 5′-d(AGGG(TTAGGG)₃) was purchased from Integrated DNA Technologies (Coralville, IA). DNA was purchased on a 10-μmol scale with standard desalting. All DNA is quality checked by commercial sources by the use of either MALDI-TOF or Electrospray Ionization mass spectrometry. All purchased DNA was used without further purification. Before use, DNAs were diluted into folding buffer [10 mM tetrabutylammonium phosphate, 1 mM EDTA acid (pH 7.0)] to a stock concentration of 1 mM and stored at 4°C. This folding buffer is designed to prevent structure formation before the addition of cation. Acetonitrile and all PEGs were purchased from Sigma at the highest available grade. PEGs arrived as either a solid or premade 100% (w/v) or 50% (w/v) solutions. Acetonitrile and premade PEG solutions were used without further purification. Solutions of 50% (w/v) PEGs were prepared by dilution of 125 g PEG into 250 ml of total volume using purified water. In some cases, gentle heating was required to aid in dissolving the PEG before dilution to final volume. Molar concentrations were calculated for all PEG solutions, and densities were used to normalize all solutions to percentage (v/v) for pipette mixing of solutions. We observed that addition of PEG may decrease the pH of solutions. Control CD experiments established that these slight pH changes have no significant effect on quadruplex structures.

CD and absorbance spectroscopies

Simultaneous CD and absorbance (Abs) spectra were collected using a Jasco J-815 spectropolarimeter equipped with a Peltier temperature controller. CD/Abs spectra were collected from 220 to 340 nm with 1 nm steps and standard sensitivity while maintained at a constant 20°C. Scan rate was set to 200 nm/min with a 2-s integration time. A total of four scans were collected and averaged. Before each scan, blank spectra were collected using the corresponding solvent conditions without the addition of DNA. For direct comparison of all collected CD spectra, scans were normalized to delta epsilon (Δε) through the use of Equation (1), where θ_λ is the observed CD in millidegrees at wavelength λ, M is DNA strand concentration in molar and L is pathlength in cm. Normalization was done using Microsoft Excel software, and all plots were constructed using Origin 7.0 software.

(1)

Co-solvent titrations

Isothermal co-solvent titrations were conducted using 18 individually prepared samples over a co-solvent range of 0–42.5% (v/v) measured at a constant temperature of 20°C. DNA samples were prepared to a final volume of 2 ml by mixing of DNA, premade co-solvents, 10× concentrated buffer components and purified water to a final buffer concentration of 25 mM KCl, 10 mM tetrabutylammonium phosphate, 1 mM EDTA (pH 7.0) (25 mM KCl-folding buffer) with 0–42.5% (v/v) co-solvent. Co-solvents were added based on volume through manual pipetting. Samples were prepared at 4 μM strand concentration and annealed by placing in 1 l of boiling water for 20 min followed by reduction of heat to room temperature and slow cooling. Samples were allowed to cool slowly in the water bath overnight before use. CD/Abs scans were collected on all individually prepared samples and on buffered co-solvent solutions in the absence of DNA to ensure no significant background was present. Data were exported for all titration points as millidegrees and normalized to Δε using Equation (1).

Water activities

Water activities for all co-solvents were obtained from published values (58–60). Whenever possible, water activities were checked using a Vapro vapor pressure osmometer 5520 (Wescor Inc., Logan, UT). Published and experimentally obtained values differed by at most 5% for the instrumental range of 3200 mmol/kg. Vapor pressures were converted to water activities using Equation (2) (61), where mOsm is the vapor pressure measured in mmol/kg, α_w is the water activity and M₁ is the MW of water.

(2)

Analytical ultracentrifugation

AUC was carried out in a Beckman Coulter ProteomeLab XL-A analytical ultracentrifuge (Beckman Coulter Inc., Brea, CA) at 20°C for 24 h at 50 000 rpm in standard double sector cells. Data were analyzed using Sedfit (free software: www.analyticalultracentrifugation.com) and DCDT+ (version 2.3.2, John Philo, Thousand Oaks CA). Values for S_20,w obtained by the two analysis methods agreed within 5% until 30% (v/v) PEG was used, where DCDT+ failed to yield a result owing to the low value of the uncorrected sedimentation coefficient in this high viscosity solution (62). Buffer density was determined on a Mettler/Paar Calculating Density Meter DMA 55 A at 20°C, and buffer viscosity was determined using an Anton Parr Automated Micro Viscometer AMVn at 20°C. For the calculation of frictional ratios, 0.55 ml/g was used for partial specific volume (63), and 0.3 g/g was assumed for the amount of water bound (64).

Molecular modeling

The propeller form of the human telomere (PDB entry 1KF1) and hybrid 1 form (PDB entry 2HY9) were used to examine PEG 200 and 600 binding. The hybrid 1 form was truncated to the same 22 bases as the parallel form (2HY9-t). Four PEG 200 or 600 molecules were manually docked to the groove regions of 1KF1 and in two separate systems to the groove regions and quartet backbone of 2HY9-t. The PEG 200 and 600 molecule partial charges were calculated using Antechamber and AM1-BCC methods and parameters from the GAFF force field. An explicitly solvated model with potassium counter ions were generated with the parm99SB.dat Amber force field using the following protocol: (i) two unsolvated potassium ions were placed between the G-quartet tetrads for stabilization; (ii) the system was solvated by the addition of a rectangular box of TIP3P water at 15 Å; (iii) neutralizing solvated potassium ions were added randomly around the quadruplex:PEG 200 or 600 structure using Amber 11 leap rules for counter ions. The system was heated slowly and equilibrated for 600 ps using the following protocol: minimize water holding the DNA:PEG 200 or 600 (100 kcal mol⁻¹ Å⁻¹), minimize the complete system, 50 ps molecular dynamics (heating to 300 K) holding the DNA:PEG 200 or 600 fixed (100 kcal mol⁻¹ Å⁻¹), and (iv) unrestrained molecular dynamics for 300 ns. Simulations were performed in the isothermal isobaric ensemble (P = 1 atm, T = 300 K). Periodic boundary conditions and the Particle-Mesh-Ewald algorithm were used. A 2.0 fs time step was used with bonds involving hydrogen atoms frozen using SHAKE. For the equilibration steps and the production steps, molecular dynamics calculations were carried out using AMBER 11 program sander and the cuda version of pmemd, respectively.

The 50% (v/v) acetonitrile system was investigated using the propeller form of the human telomere (PDB entry 1KF1) with 4199 acetonitrile and 8398 TIP3P water molecules using periodic box conditions. All atom parameters for acetonitrile were used from the Manchester Amber Parameter Database (http://www.pharmacy.manchester.ac.uk/bryce/amber#org). The 2HY9-t model was solvated in rectangular box of TIP3P water at 15 Å. The same protocol as aforementioned was used with restraints only on the quadruplex DNA for 60 ns to allow for equilibrium of the solvent mixture with production runs of 500 ns for the acetonitrile:water:propeller quadruplex and 100 ns for the water:hybrid 1 quadruplex. The final imaged snapshots of the production trajectories were used for solvation shell analysis.

RESULTS AND DISCUSSION

Acetonitrile and EG cause a shift in quadruplex conformation in potassium solutions through changes in hydration

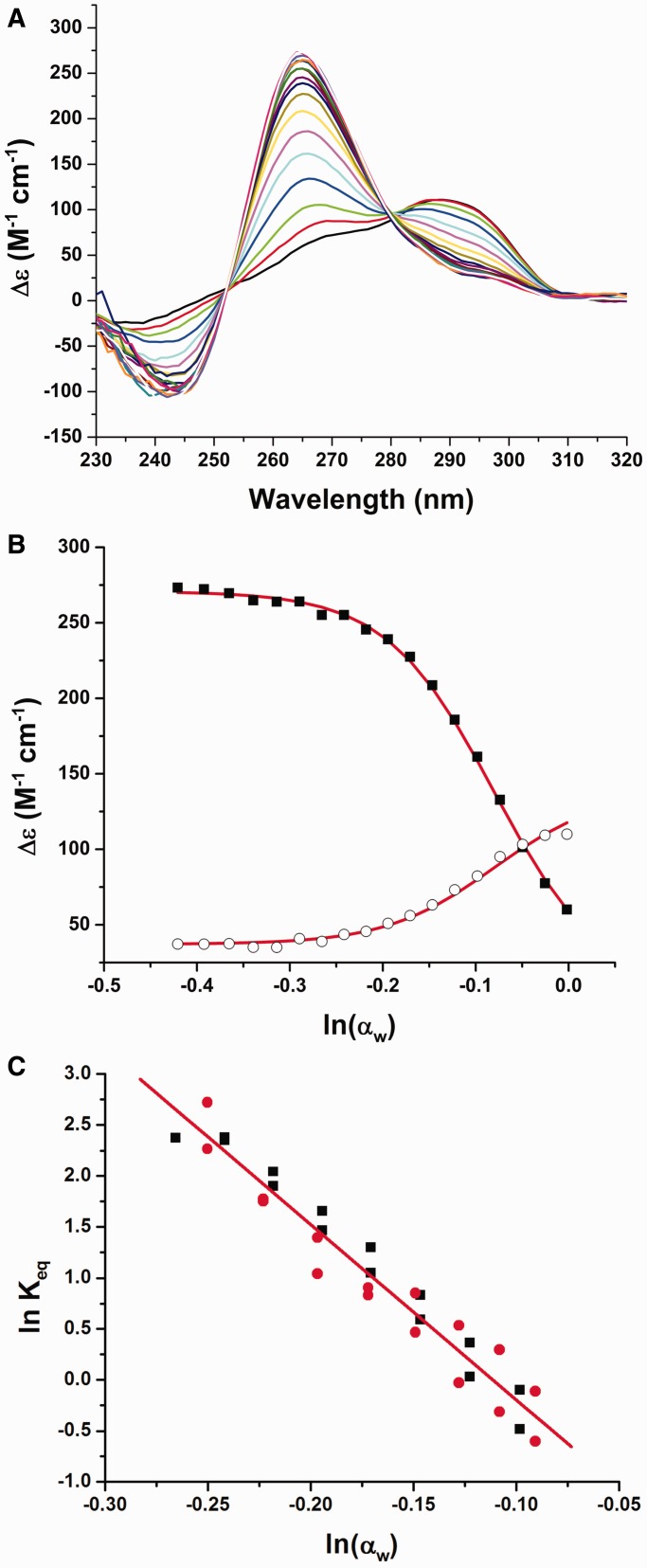
The conformational change of the 22-nt human telomeric quadruplex (hTel22) in the presence of potassium was monitored by changes in CD spectra over a range of 0–42.5% (v/v) acetonitrile at 20°C (Figure 1A). In the absence of acetonitrile, hTel22 showed a major peak near 290 nm with a shoulder at 265 nm consistent with a hybrid conformation (65). The addition of acetonitrile caused a shift in its CD spectrum to a major peak near 265 nm and a shoulder at 290 nm consistent with formation of a parallel propeller conformation (65). CD spectra were collected at intervals of 2.5% (v/v) acetonitrile and were used to construct a data matrix representing the spectral changes as a function of water activity. Changes in CD intensity at 265 and 290 nm can be used to monitor the appearance of the propeller form and the disappearance of the starting hybrid quadruplex, respectively (Figure 1B). Evaluation of the titration curves demonstrates 50% conversion of the hTel22 is obtained at ln(α_w) of −0.12 (α_w = 0.886) with complete conversion at −0.25 (α_w = 0.778) and lower. The observation that decreased water activity favors the propeller form indicates that it is less hydrated than the hybrid form.

Figure 1.

Conformational change of hTel22 driven by decreased water activity in the presence of potassium at 20°C. (A) CD spectra obtained as a function of acetonitrile concentration. Addition of acetonitrile causes a shift in the CD spectrum from a major peak at 290 nm to a major peak at 265 nm. (B) The conformational change of the quadruplex monitored at 290 nm (circles) and 265 nm (solid squares) as a function of the natural logarithm of the water activity. The 295 nm signal monitors the loss of initial hybrid structure while the 265 nm signal arises from the appearance of parallel quadruplex. (C) Data for acetonitrile (black) and EG (red) plotted according to Equation (5) for determination of K_eq,0 and Δn_w. Global best-fit line (shown in red) for acetonitrile and EG was determined to be ln(K_eq) = −1.91 − 17.2ln(α_w).

Singular value decomposition (SVD) was applied to the data matrix to evaluate the number of significant spectral species involved in the quadruplex conformational transition (66). SVD results (Supplementary Figure S1) show that only two significant spectral species were needed to describe the data matrix, indicating that the reaction is effectively two-state within the limitations of the information content of CD spectra. The presence of only two significant spectral species indicates that the conformational change can be modeled as a simple equilibrium between two hydrated quadruplex conformations. Mechanism 1 is a minimal reaction scheme that accounts for a shift in conformation from the initial hybrid form (Q_Hyb) to the converted propeller form (Q_P) accompanied by a change in hydration (Δn_w = x − y).

(Mechanism 1)

The two-state reaction mechanism defines an apparent equilibrium constant (K_eq) that can be estimated at each acetonitrile concentration by Equation (3),

(3)

where θ is the fraction of quadruplex converted. Equation (4) was used to calculate θ for each acetonitrile concentration,

(4)

where Δε₀ is the CD signal from the starting hybrid conformation, Δε_F is the signal from fully converted quadruplex and Δε_i is the CD signal at the i-th acetonitrile concentration. A linear dependence of Δε_F on acetonitrile concentration was assumed to account for the slopes evident in the ends of the titration curves in Figure 1B. Plots were constructed of ln(K_eq) against ln(α_w) (Figure 1C) to estimate the hydration change that accompanies the conformational transition [Equation (5)].

(5)

Data obtained for a second osmolyte, EG, which has different chemical properties, are also included in Figure 1C. The data for the two solutes are in excellent agreement. Linear regression using the collective data in Figure 1C yields the best-fit line ln(K_eq) = −1.91 − 17.2ln(α_w) providing an estimate of Δn_w = −17.2 ± 0.8 from the slope with a 95% confidence interval of −18.7 to −15.6 (36). The negative sign of the Δn_w demonstrates that the conformational change of the hTel22 is accompanied by a significant decrease in hydration, with the release of ∼17 waters per quadruplex. The equilibrium constant (K_eq,0) for the conversion of the hybrid form to the propeller form in pure water was determined from the intercept at ln(α_w) = 0 to be 0.147 with a 95% confidence interval of <0.112; 0.194>. This indicates that ∼14% of the quadruplex exists as the propeller structure in the absence of acetonitrile or EG. The free energy change for the transition, ΔG_25°C = −RTln(K_eq,0), is +1.1 kcal mol⁻¹ at 25°C with a 95% confidence interval of <1.0; 1.3>. This value indicates that the hybrid form is thermodynamically favored, although a significant amount of the propeller form exists in aqueous solution. More complex models that assumed multiple hybrid conformations were explored but offered no better fits to the experimental CD data. These models required additional fitting parameters, but yielded an estimate for the total number of water molecules released in the hybrid-to-propeller transition that was similar to the value obtained using the simpler two-state model.

Our findings are consistent with previous studies that have reported multiple quadruplex conformational forms in solution, although none of these have provided quantitative character of the equilibria. NMR studies of the two-repeat telomere sequence d(TAGGGTTAGGGT) showed that the bimolecular parallel and anti-parallel quadruplexes could coexist in K⁺ solutions, with the anti-parallel form strongly favored at 20°C (67). A pulsed EPR study concluded that the four-repeat unimolecular human telomere quadruplex existed in solution as a nearly 1:1 mixture of hybrid and propeller form (68). Similarly, ¹²⁵I radio probing experiments (13,69) suggested that unimolecular basket, chair, hybrid and propeller conformations coexisted in K⁺ solution. We caution that both of these studies were done at extremely low temperatures (−233.15°C for EPR and −80°C for the radioprobing) that would surely perturb both folding and conformational equilibria. Recent thermodynamic studies report a heat capacity change of about −300 cal mol⁻¹ deg⁻¹ for the folding of telomeric quadruplex, a value that indicates cold denaturation would complicate any studies done at extremely low temperatures (70). NMR evidence (24,71) shows that the hTel22 sequence consists of two major non-parallel species in aqueous solution.

Molecular dynamics simulations were performed to examine the water release from the hydrated hybrid 1 form to the acetonitrile hydrated propeller form. The hybrid 1 form had solvation shells at 4, 5 and 6 Å comprising 369, 486 and 598 water molecules, respectively. The acetonitrile hydrated propeller form had solvation shells at 4, 5 and 6 Å comprising 342, 463 and 568 water molecules and 68, 87 and 115 acetonitrile molecules, respectively. Therefore, the Δn_w values at 4, 5 and 6 Å are −27, −23 and −30, respectively. These values confirm that the parallel form is less hydrated than the hybrid forms, and the values are reasonably consistent with the measured experimental value. The equilibrated molecular dynamics simulation of the acetonitrile-hydrated propeller form also indicates that there is no preferential binding of acetonitrile to the quadruplex, as the acetonitrile composition of the solvation shells is 16–17% compared with 33% for the bulk solvent composition.

Polyethyleneglycols do not alter quadruplex conformation by osmotic stress

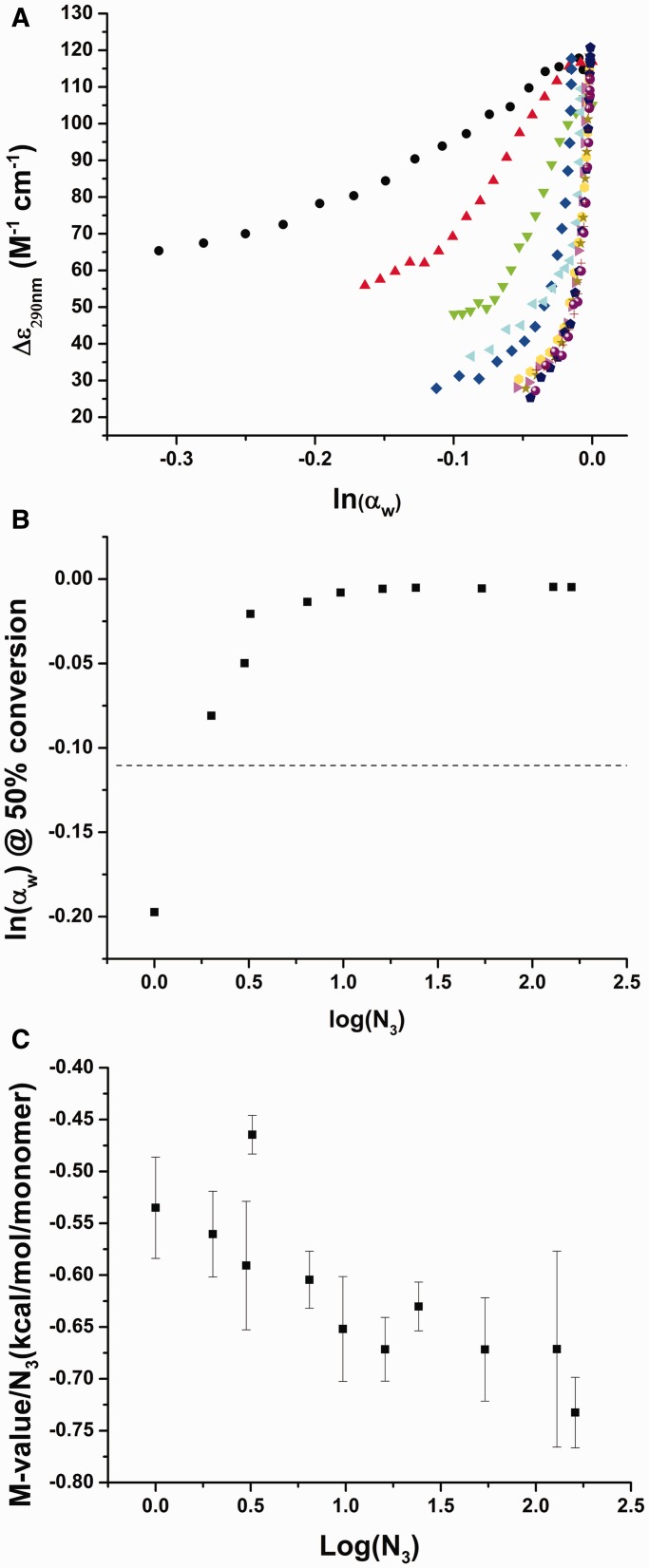
The conformational change of the hTel22 was studied by isothermal titrations using a set of increasing MW glycols. The series included EG, diethylene glycol (diEG), triethylene glycol (triEG) and PEGs of MW 200, 400, 600, 1000, 1500, 3350, 8000 and 10 000. Titrations over the range of 0–42.5 % (v/v) were monitored by CD. All glycols were found to drive the conformational change of the hTel22 to a parallel form. Analysis of spectral changes by SVD showed that only two significant spectral species were needed to describe the data matrix. At the highest glycol concentration used, a CD spectrum with a major peak at 265 nm and a shoulder at 290 nm is observed (Figure 2A). Conversion of the quadruplex by different MW glycols results in similar transition curves (Figure 2B). The magnitude of CD changes was found to be dependent on the MW, with EG, diEG and triEG having lower values compared with the higher MW PEGs. This difference in CD perhaps results from binding interactions between the high MW PEGs and the quadruplex. The high MW PEGs showed Δε₂₉₀ and Δε₂₆₅ plateau regions of 28.6 ± 2.5 and 274.0 ± 21.9 M⁻¹ cm⁻¹, respectively.

Figure 2.

Isothermal titrations of hTel22 with a series of increasing MW PEGs. Colors correspond to EG (black), diEG (red), triEG (green), PEG 200 (blue), PEG 400 (cyan), PEG 600 (magenta), PEG 1000 (yellow), PEG 1500 (dark yellow), PEG 3350 (dark blue), PEG 8000 (purple, and PEG 10 000 (wine). (A) Comparison of hTel22 CD spectra obtained at the titration end point. These spectra demonstrate that all glycols cause conversion to a parallel conformation. (B) CD titration curves for each glycol studied. Arrow indicates the direction of increasing MW.

For comparison with acetonitrile titrations, the reduction in water activity caused by the addition of different MW PEGs was measured. The change in water activity observed for the complete transition was found to decrease with increasing PEG MW (Figure 3A). For PEG 400 and larger, the transition midpoint is ln(α_w) ≈ −0.02 (α_w ≈ 0.98), and the transition is complete at ln(α_w) ≈ −0.05 (α_w ≈ 0.95). These values are dramatically different from the values seen for acetonitrile and EG and suggest that these PEGs are not greatly perturbing water activity and are not therefore acting by osmotic stress and dehydration. This point is emphasized in Supplementary Figure S2 that compares the effect of acetonitrile to PEG 600. The effect of PEG 600 on the transition is complete before the effect of acetonitrile has barely begun. The two agents must act by different underlying mechanisms.

Figure 3.

(A) Transformed titration curves obtained from the primary data shown in Figure 2B. (B) Change in the transition midpoint as a function of the MW of PEG. (C) M-value plot (see text) for the conversion of the hTel22 demonstrates an increase in magnitude suggesting preferential interactions significantly contribute to the conversion of the human telomeric G-quadruplex. M-value averages and standard deviations were obtained from the analysis of multiple wavelengths. PEG 400 data were analyzed using the first half of the titration owing to non-linearity at high PEG 400 concentrations.

EG behaves similarly to acetonitrile, as shown in Figure 1C. Data for EG and acetonitrile superimpose within experimental error, suggesting that both reagents are acting by the same mechanism to perturb quadruplex hydration. Both compounds yield estimates of Δn_w of about −17. In contrast, if the data for PEG 400 and greater (Figure 3A) are assumed to act by an osmotic stress mechanism, estimates of Δn_w of about −1200 are obtained. These estimates for the number of water molecules are unrealistically large and physically unreasonable. Because a water molecule covers about 7–10 Ų (72), a Δn_w value of −1200 suggests the loss of ≈12 000 Ų of solvent accessible surface on conversion of the hybrid quadruplex to the propeller form. However, as the folded quadruplexes have total solvent accessible surface areas of 3500–4000 Ų (24), this number is absurd.

The conformational change induced by PEGs does not occur through a molecular crowding mechanism: evaluation of preferential interactions and excluded volume effects

Record and coworkers recently proposed an analytical method for separating hydration and excluded volume effects on folding equilibria (57). The approach requires data obtained for the concentration-dependent effects on the reaction of interest using a complete series of solutes differing in MW, from monomer to polymer. In our case, we used EG through polymeric PEGs (Figures 3 and 4). The effect of solutes is quantified through ‘m-values’, the derivative of the observed free energy changes with respect to solute concentration (Supplementary Figure S3). For the case of duplex or hairpin DNA thermal denaturation, Record and coworkers observed a dramatic effect of solute MW on m-values, with a change in sign (from negative to positive) from the monomer EG to the higher MW PEGs. The dramatic difference was attributed to the dominance of excluded volume effects (‘crowding’) for the high MW PEGs on duplex denaturation. We observe the opposite behavior for the quadruplex conformational change studied here.

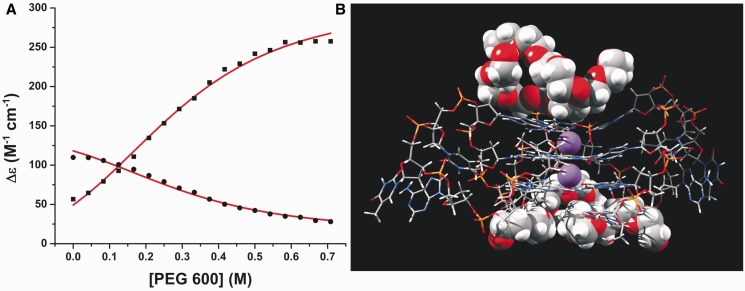
Figure 4.

Conformational selection by differential binding of PEG to the propeller quadruplex. (A) Representative fit of titration data obtained for PEG600 to Equation (7) (squares, 265 nm; circles, 290 nm). Optimized parameters were K_eq,0 = 0.147, n = 4 and K_B = 0.41 ± 0.01 M for the binding affinity of PEG 600. (B) Molecular dynamics shows PEG 600 interacts favorably with the planar G-tetrad faces of the propeller structure.

M-values were determined based on changes in the Gibbs free energy owing to a shift in the quadruplex conformation with respect to increasing MW PEGs. M-value plots quantify solute effects on a process through the derivative of the standard Gibbs free energy change (ΔG_obs) with respect to solute (m₃) concentrations [Equation (6)] (57).

(6)

Titration results for each MW PEG were transformed to plots of ΔG_obs versus monomolar PEG concentration. Monomolar concentration refers to the molar concentration of equivalent monomer subunits in solution and normalizes the concentration with respect to the number of repeating EG units (N₃) to normalize for different MW. The fraction of converted quadruplex was calculated using Equation (4), where the i-th component now refers to the i-th PEG concentration. The equilibrium constant was estimated using Equation (3) and ΔG = −RTln(K) calculated at 25°C. Linear regression of the Gibbs free energy change against monomolar PEG concentration results in a monomer m-value for each glycol studied (Supplementary Figure S3). The resulting monomer m-values were plotted against log(N₃) to evaluate distinct energy changes based on the MW of the PEG solution (Figure 3C). The conversion of the hTel22 was found to have monomer m-values that increase in magnitude with the MW of the glycols. This behavior stands in sharp contrast to what was observed by the Record laboratory (57) for crowding effects on duplex stability, in which m-values changed from negative to positive over the same range of glycol MWs. Our data indicate that excluded volume effects are minimal for the hTel22 conformational transition driven by PEGs. Indeed, m-values are greater for the larger PEGs than for the monomer EG, which indicate enhanced preferential interactions with the altered quadruplex conformation.

The propeller conformation is hydrodynamically larger than hybrid forms and would not be favored by macromolecular crowding

Heddi and Phan (23) determined that hTel22 adopts an all-parallel ‘propeller’ conformation in PEG solutions that is similar to the conformation originally solved by X-ray crystallography (12). The proposed mechanism for the conformational transition was molecular crowding, which requires that a reaction be driven to more compact states owing to a decrease in available volume (32). For molecular crowding to exert an effect on the hTel22 equilibrium, the propeller form must be more compact than the hybrid conformation. HYDROPRO software was used to calculate the hydrodynamic parameters of several hTel22 conformations based on their published structures. Bead models were constructed, and the parameters describing the size and shape of the structures were calculated (Table 1). Evaluation of the hydrodynamic parameters demonstrates that the propeller conformation is not the most compact of the available solution conformations, having a larger Stokes’ radius and radius of gyration than other known hTel22 conformations. These computed values were validated by experimental sedimentation velocity studies (Table 2). The data show S_20,w values consistent with a hybrid form in the absence of PEG and a propeller form at high PEG concentrations. S_20,w values were found to decrease from 1.99 in the absence of PEG 600 to 1.69 in 30% (v/v) PEG 600. The S_20,w values agree well with the HYDROPRO calculations for the hybrid and propeller conformations, respectively. The measured frictional ratios show that with addition of PEG 600, the hTel22 conformation shifts to a more elongated structure (with the frictional ratio increasing from 1.01 to 1.19) assuming 0.3 g/g for the amount of water bound (64). The higher frictional ratio indicates a larger hydrodynamic volume in PEG, which is incompatible with a molecular crowding mechanism.

Table 1.

Hydrodynamic properties of hTel22 conformers calculated using HYDROPRO software

	Stokes’ radius	Radius of gyration	S20,w
	(10−7 cm)	(10−7 cm)	(Svedbergs)
propeller	1.602	1.322	1.744
hybrid 1	1.430	1.089	1.953
hybrid 2	1.515	1.172	1.843
basket	1.479	1.105	1.888

Table 2.

Hydrodynamic parameters determined from sedimentation velocity experiments

PEG 600 %(v/v)	S20,w (Svedbergs)	Frictional ratio	MW ± SEa
0	1.99	1.013	7347 ± 77
10	1.99	1.013	7110 ± 79
20	1.93	1.044	7269 ± 188
30	1.69	1.192	7214 ± 220

^aThe sedimentation coefficients were determined by extrapolation to zero concentration using five concentrations of hTel22 in the range of 2.0–7.6 μM. The true MW assuming 2 K⁺ bound of 7045 was used for the calculation of frictional ratios assuming 0.3 g/g water bound. MW ± SE was determined from the analysis of five concentrations of hTel22 for each concentrations of PEG using Sedfit software.

Aggregation of the hTel22 does not occur on the addition of PEG

PEG could exert a type of crowding effect if the hybrid-to-propeller conformational transition were coupled to aggregation of the propeller form. Crowding facilitates aggregation if the volume of the aggregate is less than the sum of the volumes of monomer units. If such aggregation occurs during the conformational change, the PEG titration curves should be dependent on DNA concentration. The results of PEG titrations conducted at 10-fold higher hTel22 concentrations show identical behavior compared with low DNA concentrations (Supplementary Figure S4), indicating the conversion of the quadruplex is independent of concentration in the range studied. Higher quadruplex concentrations could not be evaluated owing to potential self-aggregation of the human telomeric quadruplex in the absence of PEG (73). Sedimentation velocity experiments were conducted in solutions of 0, 10, 20 and 30% (v/v) PEG 600 and show no aggregation on conversion of hTel22 (Supplementary Figure S5). It was determined from AUC experiments that the addition of PEG alters the hydrodynamic properties of hTel22, but that no higher-order species were formed (Table 2). The probability that observed changes in hydrodynamic behavior are due to nonideality introduced by 30% PEG is minimized by extrapolation of S_20,w to zero concentration (Table 2). These studies show that PEG does not exert a crowding effect to produce an aggregated quadruplex state with an altered conformation.

Differential binding of PEG can explain the hybrid to propeller conformational change

If molecular crowding or coupled aggregation cannot explain how PEGs alter the conformation of hTel22, what mechanism can? Evaluation of water activities clearly shows hydration is not a major determinant of the conformational change using high MW PEG solutions, and aggregation was not observed from AUC and DNA concentration-dependent titrations. Investigation of m-values indicated a mechanism where preferential interactions between PEG and the quadruplex seemed to be a strong driving force behind the conformational change. Figure 4A show the titration of hTel22 with PEG 600. The titration curve is sigmoidal, suggesting a cooperative transition between the two quadruplex forms. Global fitting of data for both wavelengths to a simple Hill equation

yields a Hill coefficient h = 4.2 ± 0.5 and dissociation constant K_d = 0.65 ± 0.02. This value of the Hill coefficient confirms a highly cooperative process and indicates that binding of greater than 4 PEG molecules is coupled to the conformational transition. The Hill coefficient, however, is a macroscopic parameter that does not reflect a physically meaningful reaction scheme (74,75). We therefore derived a more physically meaningful mechanistic model to analyze the data in Figure 4A.

Differential binding of PEG to the propeller form (Q_P) compared with the hybrid form (Q_Hyb) can account for the action of PEGs. A plausible mechanism is that PEG binding is coupled to the hybrid to propeller transition:

(Mechanism 2)

This mechanism requires an equilibrium between the propeller and hybrid quadruplex conformations in the absence of PEG (K_eq,0), as already indicated by the acetonitrile titrations described earlier in the text. Differential binding of PEG to the propeller conformation shifts the equilibrium to the preferred form, describing a conformational selection mechanism (32). This model is a restricted form of the classic Monod–Wyman–Changeux model (76) and assumes that that the interaction of PEG with hybrid conformations is negligible and that microstates of hybrid bound by PEG are unpopulated (See discussion in Supplementary Information). Equation (7) is derived from the model and can be used to fit PEG titration data as shown in Figure 4.

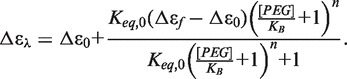(7)

Data are fit to an equilibrium constant between the aqueous and PEG conformations in aqueous solution (K_eq,0), the moles of PEG bound (n) and a dissociation constant for the binding of PEG to the propeller conformation (K_B). A global analysis of titration results from 265 and 290 nm was conducted to improved analysis but required parameter constraints. The value of K_eq,0 was fixed at 0.147 based on the estimates obtained from osmotic stress experiments (Figure 1C). Error analysis using the method of Saroff (77) showed that the estimates of parameters K_B and n were highly correlated (Supplementary Figure S6), and that only the lower limit of the value of n ≥ 2 can be defined. The number of bound molecules must be at least 2 or greater to properly match the sigmoidal nature of the titration. The Saroff analysis and molecular modeling (see later in the text) indicates a reasonable upper limit of 4. Model analysis results in an estimated dissociation constant for PEG 600 of K_B = 0.41 ± 0.01 M, with a fixed value of 4 PEG molecules bound per quadruplex (Figure 4A), as described later in the text. The value of 4 PEG molecules is consistent with fits to the Hill equation described earlier in the text. The free energy of PEG binding can be estimated to be ΔG_PEG = −RTln(1/K_B) ≈ −0.5 kcal mol⁻¹ at 25°C.

The conformational selection model describes a mechanism in which PEG binding is coupled to the hybrid to propeller conformational transition with preferential binding to the latter form. The differential binding of PEG to the propeller conformation is a plausible driving force for the conversion of the human telomeric quadruplex. The energetic difference between the hybrid forms and propeller conformation was determined by isothermal titrations to be a modest +1.1 kcal mol⁻¹. This energetic difference between the hybrid and propeller conformations could be driven by a conformational selection model, where the preferential binding of PEG to the propeller conformation over the hybrid conformation shifts the quadruplex solution population. The estimated binding energy of −0.5 kcal mol⁻¹ for each PEG 600 bound to the quadruplex illustrates that binding of three or more molecules can overcome the energetic differences between the two conformations.

The results of the analysis were used to initiate a molecular dynamics study on the ability of PEG to interact with the propeller quadruplex conformation 1KF1 and the hybrid 1 form 2HY9-t. PEG 200 and 600 were initially placed in the side grooves of the propeller structure and in the grooves and quartet backbone regions of 2HY9-t. Simulations with the propeller quadruplex form show that after initial minimization, both PEG 200 and 600 do not remain in the groove regions, but that they relocate to interact favorably with the planar region of the G-tetrad faces (Figure 4B) with long lived (greater than 300 ns) contact. In the hybrid 1 simulations, in contrast, both PEG 200 and 600 relocate to the bulk solvent with only transient interactions with the quadruplex over the 300 ns production trajectory. These simulations show differential binding interactions for PEG with the propeller and hybrid forms, consistent with the assumed mechanism described earlier in the text. As the preferred binding site of the PEG molecules was the tetrad face, four PEG 200 and two PEG 600 could be accommodated in the preferred site of the propeller quadruplex. This is consistent with the lower limits of the binding stoichiometry estimated earlier in the text and provides a rationalization for the value of n given in Figure 4A. The interaction of the PEG units with hydrophobic regions of the nucleic acid structure is a similar to previously published protein interactions with PEG (32). PEGs have been shown to interact with hydrophobic amino acid residues. The potential for this interaction with the exposed hydrophobic G-tetrads rationalizes a conformational selection model, where PEG units cause a shift in a conformation through an exposed binding site on the propeller quadruplex.

Sedimentation velocity measurements have the potential to detect bound PEG. Unfortunately, there are too many unknowns in the sedimentation velocity experiments to unambiguously establish the extent of PEG binding. As PEG 600 has a significantly larger partial specific volume than quadruplex DNA, the partial specific volume of the complex depends on binding stoichiometry. Increased PEG binding would increase the MW of the complex but decrease the buoyant density term in the Svedberg equation (78). An additional unknown is the effect of PEG binding on the frictional coefficients. The MWs reported in Table 2 were calculated assuming no change in partial specific volume. Thus, the reported MWs (Table 2) in the presence of PEG are not necessarily the true MW of a potential hTel22-PEG complex, and without knowing the exact stoichiometry of PEG binding and the shape of the complex, the MW cannot be established.

It may be argued that we have not provided ‘direct’ evidence for PEG binding to the parallel quadruplex. Characterization of weak interactions is notoriously difficult and presents a significant challenge to any analytical approach (79). ‘Direct’ characterization of binding requires distinguishing the physical properties of the free and bound ligand forms within an equilibrium mixture. For the data in Figure 4, this means that the properties of ≈16 µM bound PEG (four equivalents of PEG bound to the quadruplex at 4 µM) must be distinguished from the properties of free PEG present at ≈0.7 M. This amounts to one part of 43 750, a task beyond the physical capabilities of most available analytical tools. Our analysis of the data in Figure 4 by fitting to a mathematical model derived from a physically meaningful reaction mechanism follows an accepted strategy for characterization of a binding equilibria (80). The agreement between the model and experimental data fulfills the primary goal of binding studies, which is to obtain an adequate thermodynamic description of the reaction with evaluated parameters that can accurately predict the composition dependence of the binding response under the experimental conditions. We have not only succeeded in that but have, using molecular dynamics simulations, provided a plausible structural basis for the conformational selection model.

Explanatory power of the conformational selection mechanism

A curious observation is that although addition of PEG converts the hybrid to the parallel form in K⁺-containing solutions, it does not alter the anti-parallel basket structure to the parallel form in Na⁺ solution (14,81). The crowding mechanism cannot explain this observation, as the basket and hybrid forms have similar hydrodynamic volumes and ought to be driven by crowding to a similar extent. Furthermore, as these two forms are more compact than the parallel structure, the crowding agents should stabilize them to a similar extent (24). The conformational selection model provides an explanation. We found that in Na⁺ solution, the free energy cost of converting the basket to the hybrid form was an unfavorable +1.4 to +2.4 kcal mol⁻¹. As the energy cost of the hybrid to parallel conformation change is ∼1.1 kcal mol⁻¹, a free energy cycle dictates that the energy cost of the basket to parallel conversion in Na⁺ would be +2.5 to +3.5 kcal mol⁻¹ (82). Enough PEG would need to bind to provide favorable free energy to overcome that higher unfavorable cost of the conformational change, but the amount needed (>6) is larger than the maximum binding stoichiometry and is also incompatible with the space available on the DNA surface. Our conformational selection model can thus explain phenomenon the crowding model cannot, demonstrating its utility and power.

CONCLUSIONS

These results show that the conversion of the human telomere hybrid quadruplex to a propeller form by PEG cannot be adequately explained by ‘crowding’, by excluded volume or by hydration changes resulting from osmotic stress. The conversion instead most likely results from differential PEG binding coupled to the conformational transition between the two forms. Although the binding affinity of PEG for the propeller conformation is modest, it is sufficient to drive conformational selection at high PEG concentrations. These results raise doubts about claims based on studies using PEG that the propeller conformation is the ‘physiologically relevant’ form because it is favored under crowding conditions that mimic the intracellular milieu. PEG is not ‘crowding’ in this case but instead is acting by a different mechanism.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online: Supplementary Figures 1–6, Discussion of Equation 7 and Supplementary Reference [83].

FUNDING

The National Institutes of Health [CA35635], [GM077422] and NCRR [5P20RR018733]; The James Graham Brown Foundation; The Kentucky Challenge for Excellence. Funding for open access charge: [CA35635 and GM077422].

Conflict of interest statement. None declared.