A Three-dimensional Polymer Scaffolding Material Exhibiting a Zero Poisson’s Ratio

Abstract

Poisson’s ratio describes the degree to which a material contracts (expands) transversally when axially strained. A material with a zero Poisson’s ratio does not transversally deform in response to an axial strain (stretching). In tissue engineering applications, scaffolding having a zero Poisson’s ratio (ZPR) may be more suitable for emulating the behavior of native tissues and accommodating and transmitting forces to the host tissue site during wound healing (or tissue regrowth). For example, scaffolding with a zero Poisson’s ratio may be beneficial in the engineering of cartilage, ligament, corneal, and brain tissues, which are known to possess Poisson’s ratios of nearly zero. Here, we report a 3D biomaterial constructed from polyethylene glycol (PEG) exhibiting in-plane Poisson’s ratios of zero for large values of axial strain. We use digital micro-mirror device projection printing (DMD-PP) to create single- and double-layer scaffolds composed of semi re-entrant pores whose arrangement and deformation mechanisms contribute the zero Poisson’s ratio. Strain experiments prove the zero Poisson’s behavior of the scaffolds and that the addition of layers does not change the Poisson’s ratio. Human mesenchymal stem cells (hMSCs) cultured on biomaterials with zero Poisson’s ratio demonstrate the feasibility of utilizing these novel materials for biological applications which require little to no transverse deformations resulting from axial strains. Techniques used in this work allow Poisson’s ratio to be both scale-independent and independent of the choice of strut material for strains in the elastic regime, and therefore ZPR behavior can be imparted to a variety of photocurable biomaterial.

Introduction

Poisson’s ratio describes the degree to which a material contracts (expands) transversally when axially strained. A material that contracts transversally when stretched has a positive Poisson’s ratio (PPR). Vice versa, a material that expands in tandem in both the axial and transverse directions has a negative Poisson’s ratio (NPR). A zero Poisson’s ratio means that there is no transverse deformation resulting from an axial strain. Unlike NPR or PPR structures, which form doubly curved surface [1, 2] and saddle shaped surfaces respectively as an axial strain is applied, a ZPR structure demonstrates no change in the lateral dimensions.

Though Poisson’s ratio can take on positive, negative, and zero values, it is positive for most naturally occurring and artificial material. It has been shown, however, that the Poisson’s ratio of man-made materials can be tuned by patterning polymers with an artificial lattice of rib-containing unit-cells (pores), which control their shape and deformation mechanisms. [1, 3–9] Materials of this sort have been coined, cellular or hinged materials, owing to the fact that their constitutive pore structure can have a sizable effect on their mechanical behavior. In a porous elastic polymer, Poisson’s ratio depends on its porosity, the intrinsic properties of the material making up the cavity walls, and any anisotropic behavior due to the presence of the pores [10]. Moreover, so long as the in-plane deformations of these scaffolds remain elastic, the modified Poisson’s ratio behavior is controlled solely by the structure of the pores and not the intrinsic properties of the material making up the ribs. [11] Thus, the unusual elastic behavior of cellular materials is both scale-independent and independent of the choice of rib material for strains in the elastic regime.

It has been shown that a conventional honeycomb unit-cell yields a positive and magnified in-plane Poisson’s ratio and a re-entrant honeycomb structure yields a negative Poisson’s ratio. Another variation of the honeycomb model, the semi re-entrant honeycomb, has been shown to implement a zero Poisson’s ratio [12]. Although several biological tissues including cartilage, ligament, corneal, and brain are known to possess Poisson’s ratios of nearly zero [13–16], the Poisson’s ratio of soft tissues are often not explored. Though we previously reported polyethylene glycol (PEG) materials having tunable negative Poisson’s ratios, to our knowledge, biomaterials having a zero Poisson’s ratio (ZPR) due to the implementation of precise pore geometries at the microscale level has never been reported. [17] Thus, here we report a 3D PEG scaffolds exhibiting in-plane Poisson’s ratios of zero for large values of axial strain. We use digital micro-mirror device projection printing (DMD-PP) to create single- and double-layer scaffolds composed of semi reentrant pores whose arrangement and deformation mechanisms contribute to the zero Poisson’s ratio. We chose to use PEG hydrogel because of their wide spread application as scaffolds for three-dimensional cell culture and tissue engineering of soft tissues. [18–20]. Strain experiments prove ZPR behavior in the single- and double-layered constructs that is accurately predicted by the analytical semi re-entrant model.

Results and Discussion

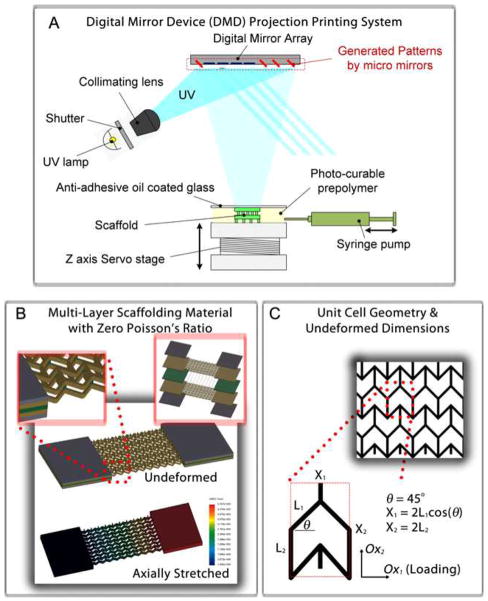
Figure 1A shows a schematic of the DMD-PP system used to fabricate the PEG scaffolds. 2D graphics models of the scaffold layers were designed in computer-aided design software and converted into standard bitmap graphics files, which were used as virtual photomasks during the DMD layer-by-layer photocuring process. The fabrication process has been described in detail in the Methods Section. Figures 1B, C highlight the geometry and relevant dimensions of the semi reentrant unit-cells patterned in the PEG. The material walls, denoted as ribs, have a rectangular cross-section of approximately 40 microns width and 100 microns depth. Rectangular slabs of material were incorporated at the ends of each porous sheet (layer) to make it easier to handle the material during strain testing. The ribs are arranged to form the semi re-entrant shape and the associated pore geometry. Figure 1B shows stress-strain finite element simulations conducted to determine the theoretical deformation behavior of the semi re-entrant scaffolding, taking material properties into account (refer to the Supplementary Information for movies showing ZPR behavior in real-time). Figure 2 shows SEM images of the semi-reentrant scaffolding.

Figure 1.

(A) Schematic of the digital micromirror device micro-stereolithography projection printing system (DMD-PP). (B) Stress-strain simulations of a ZPR PEG construct. Insets include a magnified and layer-by-layer assembly view of a double-layer scaffold assembled by stacking single- layer sheets (Layers C₁ and C₂) with a connecting layer of vertical posts (Layer P). (C) Unit-cell geometry and relevant parameters. The walls of the unit-cells are approximately 40 μm wide and 100 μm deep.

Figure 2.

Scanning electron microscope (SEM) images of a (A) single- and (B) double-layer ZPR PEG scaffold. Rectangular Blocks of PEG were patterned at the ends of the scaffold to provide mechanical stability in handling and strain testing.

The position and arrangement of the ribs, relative to one another, engender the zero Poisson’s ratio by virtue of a combination of rib bending (flexure), stretching, and hinging (angular deformations) [1, 10, 11, 21]. The degree to which each mode of deformation contributes to the elastic properties of a cellular meshwork, in general, depends on unit-cell geometry and the material properties of the ribs. Poisson’s ratio is usually strain-dependent for cellular materials, but unit-cell shape and orientation relative to the direction of loading (angle θ in Figure 1C) also plays a critical role in the magnitude and polarity of the Poisson’s ratio. The way the constitutive unit-cell of a cellular material responds to shear loads is known as the off-axis elastic response of the unit-cell [22]. The semi re-entrant structure is formed by changing the four side angles (angle θ) between the vertices (ribs) in a six-sided honeycomb (hexagon), with some additional modifications [11, 21]. Two of the angles have a positive angle, +θ, and the opposite two angles have a negative angle, −θ. Two rib lengths, L₃and L₃, and angle θ completely constrain the dimensions of the unit-cell. The size of the unit-cell is defined by X₃ and X₃, where X₃ = 2L₃ cos θ and X₃ = 2L₃. Attard and Grima [12] showed that the semi re-entrant mesh is isotropic, exhibiting a zero Poisson’s ratio for any in-plane normal stresses (σ_x, σ_y) regardless of their directionality. Expressions for true strain were derived from physical interpretations of deformation (for an infinite surface) taking into account all three possible modes of deformation including stretching, hinging, and flexing. Their analysis indicated a zero Poisson’s ratio for each mode of deformation, considered in isolation, for strain in both the O_X1 and O_X2 directions (Fig. 1C); in some cases, analytical models could not be derived due to anatomical hindrances in the way that the semi re-entrant model was perceived to deform. Even considering the more realistic and general case where each of the deformation modes act together, Poisson’s ratio remains zero since such a model is simply a corollary to the superposition of the individual modes taken in isolation. Thus, Poisson’s ratio remains zero regardless of whether one mode dominates over the other or they each contribute equally to the overall deformation of the unit-cell. It is noteworthy to point out that the proposed theory assumes an infinite surface, and edge effects and defects could, indeed, alter Poisson’s ratio. However, for all intents and purposes, the Poisson’s ratio of the semi re-entrant structure is both isotropic and strain-independent in the elastic regime for a real semi re-entrant surface away from any edges (as indicated by our experiments).

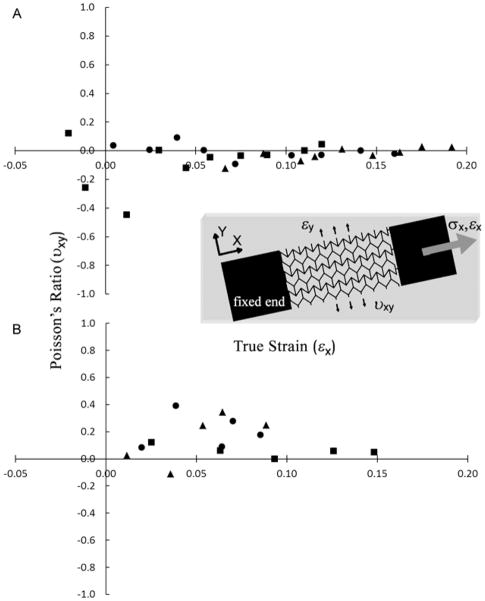
To determine if the addition of multiple layers would alter the Poisson’s ratio, we fabricated double-layer scaffolds using the fabrication approach depicted in Figure 1B. In the double-layer construct, separate semi re-entrant layers (Layers C₁ and C₂) are connected by an alternating layer of vertical posts (Layer P). The SEM images in Figures 2C, D show the separation of the layers and the connection by the vertical posts. The Poisson’s ratio of the scaffold was evaluated using a custom-made strain measurement system. The rectangular slab on one side of the scaffold was affixed to an immovable stage while the opposite slab was hitched to a movable single-axis nano-positioning stage (moving in the axial direction). A “pulling” axial tensile stress was applied to the scaffold causing it to stretch in the axial direction. In-plane movement of the scaffold in both the axial and transverse directions was recorded using a CCD camera system. The Poisson’s ratio was estimated as described in the Methods Section. Figures 3A, B shows optical images of a construct undergoing axial stretching. Figure 4 shows plots of the Poisson’s ratio of both the single- (Figure 4A) and double-layer (Figure 4B) scaffolds as a function of true strain, calculated from measurements of the overall strains in the x- and y-directions (Equations 1, 2 in the Methods Section). The experimental Poisson’s ratios show no ascertainable change for increasing values of axial strain from 0 to 0.2. The strain tests demonstrate that the addition of the second semi re-entrant layer appeared to have little influence on the Poisson’s ratio, implying that scaffolds having multiple layers are possible without markedly diminishing the special elastic properties of the material.

Figure 3.

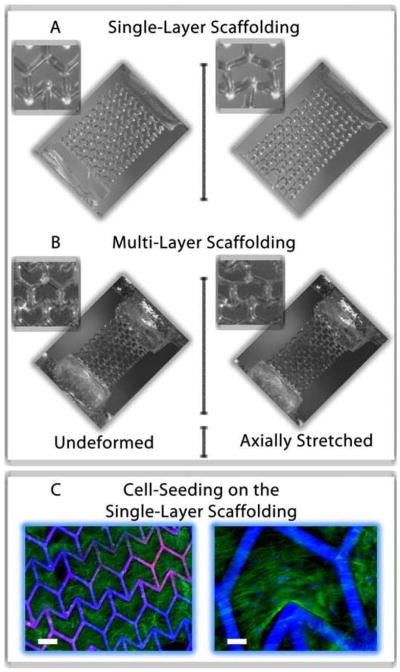
Optical images showing the deformation of a (A) single- and (B) double-layer ZPR PEG scaffold in response to an axial strain. The images show the scaffolds in their undeformed (left) and deformed (right) strain states. (C) Images of human mesenchymal stem cells (hMSCs) seeded on a single-layer ZPR PEG scaffold after one week of culture. hMSCs adhere and proliferate within and across the ZPR geometry. Scale bars represent (left) 200 μm and (right) 50 μm. The green stain is F-actin and blue stain labels the cell nuclei and scaffold.

Figure 4.

Plots of Poisson’s ratio as a function of true strain for a (A) single-layer and (B) double-layer scaffolds. Three strain-dependent experiments were performed for each type of scaffold and each test was conducted with a different sample.

Figure 3C shows images of human mesenchymal stem cells (hMSCs) cultured on a single-layer ZPR scaffold. hMSCs are an important cell source for the regeneration of a wide array of biological tissues as they have the ability to differentiate into phenotypes specific to bone, muscle, cartilage and fat. [23] The hMSCs were found to readily attach to the scaffold and grow along the ribs and into the interconnected pores. The results of our work with the hMSCs demonstrate the feasibility of utilizing the PEG-based scaffolds for biological applications which require little to no transverse mechanical necking (contracting) or bulging (expanding) due to axially-applied strains.

The Poisson’s ratio of soft tissues has been investigated very little, though it is commonly assumed to be ≤ 0.5. An optical and mechanical determination of the Poisson’s ratio of articular cartilage was found to be 0.185 and 0.174, respectively. [15] Another study revealed local variations in the Poisson’s ratio of the knee of a canine, with Poisson’s ratios varying significantly from region to region within the knee (~0.07 in the patellar groove and ~0.236 in the tibial plateau). This variation strongly suggests that spatial variations in mechanical properties should be incorporated in tissue engineering scaffolds aiding in the growth of soft tissues. [14] Thus, the tunability of Poisson’s ratio is needed to accurately design active scaffolds for tissue regeneration. The technique described in this paper, allows for the precise spatial tuning of Poisson ratio to an almost zero value in photocurable biomaterials [11]. Multi-layer ZPR scaffolds combined with embedded cells, drugs, and/or growth factor could be useful for several biomedical applications.

Experimental

Preparation of photocurable precursors

Poly (ethylene glycol) diacrylate (PEGDA, Mn= 700), acrylic acid (AA), and 2,2,6,6-tetramethylpiperidine 1-oxyl (TEMPO, free-radical quencher) were obtained from Sigma-Aldrich. Photoinitiator Irgacure 2959 and TINUVIN 234 UV-dye were obtained from Ciba Chemistry. TINUVIN 234 is a UV-absorbing agent, which was used to reduce the curing depth of the precursors and adjust the thickness of the microstructures in the DMD-based layer-by-layer fabrication process. TEMPO, on the other hand, enhances the contrast of the UV-curing process and optimizes feature resolution at the projection plane. Irgacure 2959 [1% (w/v)], TINUVIN 234 [0.15% (w/v)], and TEMPO [0.01% (w/v)] were added to the PEGDA oligomer and mixed thoroughly.

Digital micro-mirror array device projection printing (DMD-PP)

Figure 1A shows a schematic of the DMD-PP system used to fabricate the PEGDA scaffolds. 2D graphic models of the scaffold layers were designed in computer-aided drafting (CAD) software (AutoCAD LT 2006; Autodesk, Inc., San Raphael, CA, USA). CAD models in the drawing interchange format (DXF file extension, outputted from AutoCAD) were converted into standard bitmap format (BMP file extension) and exported to LabVIEW software (National Instruments, Austin, TX, USA), which was used to control the DMD system. The bitmap graphic files were used as virtual photomasks during the DMD layer-by-layer photocuring process.

A servo-stage was positioned 100 μm below a transparent quartz plate (quartz microscope slide), leaving a 100 μm gap between the plate and the stage. Photocurable precursor (10 μL) was injected into the gap with a syringe pump. The gap-spacing controlled the thickness of the photo-polymerized layer of PEG. Light emitted from the UV source was passed through a projection lens down to the projection plane, which was coplanar with the bottom side of the quartz substrate (Figure 1A). The light was spatially modulated at the projection plane by a digital micro-mirror (DM) array controlled by the virtual software masks. Precursor was exposed with a 50 mW cm⁻² dose of UV light for 11 sec to solidify select locations of the PEG.

After an individual layer was patterned, the stage was translated downwards 300 μm, pulling the solidified micropatterned sheet of PEG off the quartz substrate so that it only remained attached to the servo-stage. The release process was aided by coating the substrate with a silane (tridecafluoro-1,1,2,2-tetrahydrooctyl-1 trichlorosilane) (United Chemical Technologies, Inc., Bristol, PA, USA), which gave the surface a low surface energy (or high contact angle) [24, 25]. After a layer was fabricated, uncured precursor was washed away with deionized water. To create a second layer, the stage was translated slightly upwards until the top of the previously formed structure was approximately 100 μm below the quartz substrate, leaving another 100-μm gap. Once again, fresh precursor was pumped into the 100-μm gap, and the polymer was selectively cured using another software mask. The steps were repeated using a combination of software masks until a three-dimensional multi-layer scaffold was constructed.

Calculation of Poisson’s Ratios

To calculate Poisson’s ratios, we evaluated the overall transverse elastic deformation of the scaffolds resulting from axial strains. We determined Poisson’s ratios using equation 1 [26].

$${\upsilon }_{\text{xy}}=-\frac{{\epsilon }_{\text{y}}}{{\epsilon }_{\text{x}}}$$ (1)

where ε_y is transverse strain resulting from an axial strain ε_x. The subscripts x and y denote the axial and transverse strain directions, respectively, in a two-dimensional Cartesian coordinate system with orthogonal x- and y-axes. We note that we calculated in-plane values of Poisson’s ratio resulting from in-plane strains. Poisson’s ratio was determined from values of true strain. Total true strain, ε i, was calculated by equation (2) (for any in-plane coordinate direction).

$${\epsilon }_{\text{i}}=ln\left(\frac{{\text{L}}_{\text{i}}}{{\text{L}}_0}\right)=\sum _{\text{i}}\left[ln\left(\frac{{\text{L}}_{\text{i}}}{{\text{L}}_{\text{i}-1}}\right)+{\epsilon }_{\text{i}-1}\right]$$ (2)

where i = 1, 2, 3,…,n and denotes the current strain state, L₁ is the current specimen length for strain state i, and L₀ is the initial undeformed specimen length

Strain testing for the determination of Poisson’s ratios

The PEG scaffolds were loaded into a homemade strain measurement system by fixing one of their ends (at the rectangular blocks, see Figure 1 in main text) on an immovable stage while fixing the other end on a movable single-axis (axial direction) nano-positioning stage. The stage was connected to a motorized servo-actuator (CMA-25CCCL Closed-Loop DC Servo-actuator, Newport Corp., Irvine, CA, USA) that was capable of providing motion in 200-nm incremental steps. The actuator was driven and controlled by an axis-motion controller (ESP300 Axis Motion Controller and Driver, Newport Corp., Irvine, CA, USA) that provided stable and precise movement along with a programmable Lab View interface (LabView^™, National Instruments, Austin, TX, USA). A “pulling” axial tensile stress was applied to the end of the PEG scaffolds, attached to the movable stage, by the motion of the actuator while the other end of the PEG constructs, which were fixed to the immovable stage, remained still. The axial stresses exerted on the scaffolds ultimately caused them to strain in the axial direction. In-plane movement of the construct in the axial and transverse directions was observed with a color CCD camera system with magnifying optics (CV-S3200P CCD camera, JAI Inc., San Jose, CA, USA; magnifying camera optics, Edmund Industrial Optics, Barrington, NJ, USA).

Still images were recorded with the CCD camera for precise levels of travel of the actuator stage. Axial and transverse strains were estimated by measuring the displacement in the axial and transverse directions, respectively. Digitizer software (GetData Graph Digitizer 2.24, http://www.getdata-graph-digitizer.com) was used to digitize the optical images so that the displacements could be accurately determined based on the undeformed in-plane dimensions of the constructs. Digitized SEM images were used to determine the undeformed dimensions.

Scaffold functionalization

Pendant carboxyl groups on the poly(ethylene glycol)-co-poly(acrylic acid) scaffolds were activated by incubating the scaffolds in a working solution of 0.15M 1-ethyl-3-[3-dimethylaminopropyl] carbodiimide hydrochloride (EDC) and 0.12M N-hydoxysuccinimide (NHS) in 2-[morpholino]ethanesulfonic acid (MES) buffer at pH 5 for 2 hours. Scaffolds were briefly rinsed with phosphate-buffered saline (PBS) (pH 7.4) to remove any residual NHS and EDC and immersed in a 10 μg/ml solution of human plasma fibronectin (GIBCO) in PBS for 24 hours at 4°C to allow for fibronectin conjugation to the pendant carboxyl groups. Scaffolds were then briefly rinsed with PBS and sterilized by exposure to a germicidal UV lamp for 30 minutes.

Cell culture and seeding

Human bone marrow derived mesenchymal stem cells (Health Sciences Center, Texas A & M University) were cultured in growth medium consisting of high glucose DMEM (GIBCO), 10% fetal bovine serum (Hyclone, Atlanta Biologicals), 1% L-glutamine (GIBCO) and 50 units/ml penicillin/streptomycin, and passaged at 60–70% confluence. Cells were cultured at 37°C, 5% CO₂.

After 4 passages, cells were seeded on the fibronectin-conjugated scaffolds at 500,000 cells/ml (30 μl or 15,000 cells per sample) and allowed to attach for 3 hours. Cell-seeded scaffolds were then cultured in growth medium for 1 week.

Immunofluorescent staining

After 1 week of culture, cell-seeded scaffolds were fixed in 4% paraformaldehyde in PBS for 10 minutes. Samples were blocked/permeabilized in blocking buffer consisting of 3% bovine serum albumin, 0.1% Triton-X 100 in PBS for 30 minutes. Samples were then incubated with Alexa Fluor 488 phallodin (Invitrogen) (diluted 1:50 in blocking buffer) to stain filamentous actin, for 1 hour at room temperature in the dark. After briefly washing the samples in PBS to remove unbound antibody, samples were mounted on glass slides with mounting medium containing 4′,6-diamidino-2-phenylindole (DAPI) (Vectashield, Vector Laboratories) to stain nuclei. Samples were visualized by fluorescence microscopy using a Zeiss Observer A1 microscope equipped with an X-Cite 120 (EXFO) mercury lamp.

Scanning Electron Microscopy (SEM)

The scaffolds were sputter coated with 8nm thick Iridium using Emitech K575X, and examined in the Field Emission Environmental scanning electron microscope, FEI XL30 ESEM FEG operated at 10 kV using high vacuum mode.

Conclusions

We constructed single-layer and double-layer PEG scaffolds, which exhibit tunable in-plane zero Poisson’s ratio (ZPR) behavior, in accordance with existing analytical models found in the literature. The double-layer scaffolds were fabricated by assembling single-layer constructs in a layer-by-layer fashion, in top-bottom configuration with 100% interconnected structures as desired in scaffolds for tissue engineering. Human mesenchymal stem cells adhere and proliferate within the scaffolds, thereby demonstrating the feasibility of utilizing the ZPR scaffolds for tissue engineering and other biological applications. As long as the deformations to the material remain elastic, Poisson’s ratio is controlled solely by the structure of the pores and not by the intrinsic properties of the material making up the geometry. Poisson’s ratio of ZPR scaffolds is both scale-independent and independent of the choice of strut material for strains in the elastic regime, and therefore ZPR behavior can be achieved using a variety of photocurable material, with potential applications in biomedical applications which requires unique strain characteristics.