Calculating the sensitivity and robustness of binding free energy calculations to force field parameters

Abstract

Binding free energy calculations offer a thermodynamically rigorous method to compute protein-ligand binding, and they depend on empirical force fields with hundreds of parameters. We examined the sensitivity of computed binding free energies to the ligand’s electrostatic and van der Waals parameters. Dielectric screening and cancellation of effects between ligand-protein and ligand-solvent interactions reduce the parameter sensitivity of binding affinity by 65%, compared with interaction strengths computed in the gas-phase. However, multiple changes to parameters combine additively on average, which can lead to large changes in overall affinity from many small changes to parameters. Using these results, we estimate that random, uncorrelated errors in force field nonbonded parameters must be smaller than 0.02 e per charge, 0.06 Å per radius, and 0.01 kcal/mol per well depth in order to obtain 68% (one standard deviation) confidence that a computed affinity for a moderately-sized lead compound will fall within 1 kcal/mol of the true affinity, if these are the only sources of error considered.

1. Introduction

In recent years free energy calculations have been used to examine protein-ligand binding in many different proteins, from blind tests of affinity prediction in model binding sites^1,2 to detailed examinations of binding in more complicated biological receptors^3,4. Unlike simplified docking methods used in virtual screening, free energy calculations use simulations to compute a rigorous statistical-mechanical binding free energy within the context of a given force field⁵. It seems likely that these force fields must be highly accurate in order to predict accurate binding affinities, and force field inaccuracy may help explain why binding affinities have historically proven very difficult to predict^6,7,8,9. Still, the actual sensitivity of simulated binding free energies to the underlying force field parameters has rarely been examined quantitatively, perhaps due to the computational expense of the calculations^10,11.

The sensitivity of simulated binding free energies to force field parameters is of particular interest for several reasons. Firstly, by examining how sensitive binding affinities are to parameters, we learn how accurate force field parameters need to be for free energy calculations to produce accurate binding affinities. Secondly, this parameter sensitivity is useful for improving more simplified models of binding. Free energy calculations compute binding affinities using a fundamentally different approach from docking and scoring calculations. Phenomena such as dielectric screening and the hydrophobic effect arise naturally from the simulation, instead of being directly parameterized by surface tension or effective dielectric constant parameters¹². One strategy for improving docking calculations could therefore be to ensure the overall sensitivity to force field parameters mimics the more physically grounded sensitivity from free energy calculations, because these sensitivities cannot be directly compared with experiment. Thirdly, it has been pointed out that many force fields commonly used in condensed-phase simulations have significantly different interaction strengths between fragments than the interaction strengths from high level gas-phase ab initio calculations on the same fragments, potentially introducing large errors in predicted affinities¹³. It is important to determine whether or not these differences necessarily limit the ability of simplified force fields to predict overall binding affinities. Lastly, several physical mechanisms, described in more detail below, may make binding free energies moderately robust to the strengths of individual interactions. Examining the parameter sensitivity of binding free energy calculations can provide quantitative insight into these mechanisms and their effects on binding.

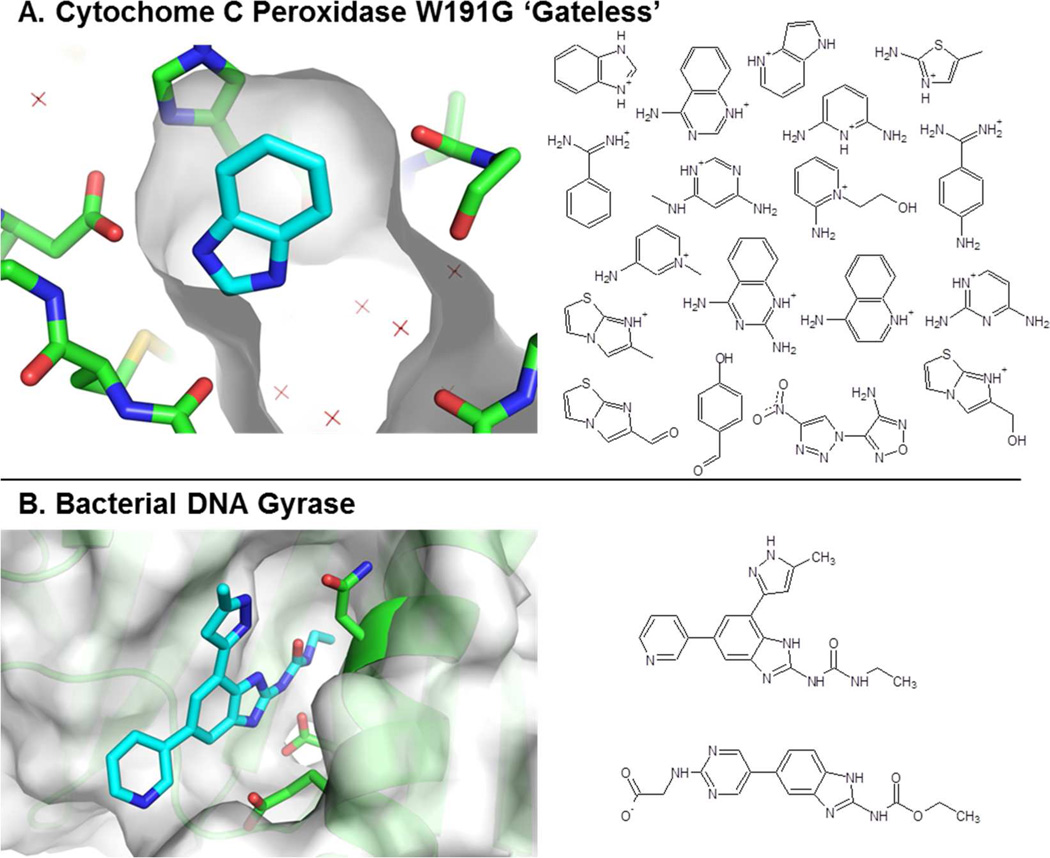
Here, we examine the sensitivity of simulated protein-ligand binding free energies to the nonbonded force field parameters of the ligands. For our main analysis, we studied a set of fragments binding to a highly enclosed, engineered binding site in yeast Cytochrome C Peroxidase (CCP)¹⁴, which we have previously studied with free energy calculations¹⁵ (Figure 1a). To test the generality of our conclusions, we also examined two ligands binding to the more realistic, pharmaceutically relevant binding site in bacterial DNA Gyrase (Figure 1b)¹⁶. For each ligand, we exhaustively made small perturbations to all ligand charge and van der Waals (vdw) parameters, and determined the change in the overall binding free energy for each perturbation.

Figure 1. Binding sites and compounds studied.

(A) Cytochrome C Peroxidase W191G ‘Gateless’ binding site bound to benzimidazole, from PDB 1KXM. Benzimidazole has an axis of symmetry: one symmetric amine hydrogen bonds with a protein Aspartate (left), while the other points at solvent (right). (B) Bacterial DNA Gyrase bound to an inhibitor shown at left. Binding site images generated using PyMOL 1.4.1, Schrödinger, LLC.

After determining the overall sensitivity of binding free energies to parameters, we then investigated three mechanisms, described below, which we hypothesized could lead to robust binding affinities: dielectric screening, cancellation of effects in solution and in the protein, and nonadditivity. We quantitatively measure these effects and describe their individual impacts on the robustness of binding free energies.

Dielectric screening

Electrostatic interactions in water are eighty fold weaker than in the gas phase, and interactions in proteins may be 2–40 fold weaker due to the effect of dielectric relaxation of the environment¹² . This reduces the sensitivity of binding affinities to electrostatics.

Cancellation of effects in solution and in the protein

Binding free energy is the free energy difference between the protein-ligand complex (ΔG_Complex) and the protein and ligand free in solution (ΔG_Wat). Most changes to ligand properties affect both of these free energies in the same direction, which buffers the overall size of the effect.

Non-additivity

If x is the effect on binding free energy of changing one interaction, y the effect of changing a second, and z the effect of changing both at once, then if z = x + y we say the effects are independent, and the total effect of n random independent changes should grow with $\sqrt{n}$. If | z | > | x + y |, the effects are cooperative, and if this is true on average for many perturbations, the total effect of n random changes may grow faster than $\sqrt{n}$. If instead | z | < | x + y |, the effects are buffering, and if this is true on average for many perturbations, the total effect of n random changes may grow more slowly than $\sqrt{n}$. If perturbations to interaction strengths most often buffer one another, then overall protein-ligand binding affinities will be more robust to interaction strengths¹⁷

2. Results

2.1 Exhaustive perturbation of ligand parameters

We simulated 18 fragment-sized compounds in vacuum, in TIP3P water, and in complex with yeast Cytochrome C Peroxidase (CCP) W191G ‘Gateless’¹⁴, for which they have experimental affinities between −3 and −7.1 kcal/mol (Figure 1a)¹⁵. Fifteen compounds were charged, three were neutral, and three do not actually bind to the protein at measurable concentrations, but do at least sterically fit into the binding site and were included to add compound diversity. Several compounds were considered in multiple orientations in the binding site, but each orientation was treated separately; in other words, we recorded the effects of all changes to ligand parameters on all orientations, rather that considering how changes to ligand parameters would shift the populations of different ligand orientations. We also simulated two lead-sized compounds in vacuum, in solvent, and bound to bacterial DNA Gyrase¹⁶, to which they have experimental affinities of −6.7 and −8.3 kcal/mol (Figure 1b). One Gyrase compound was neutral and one was charged.

With these simulations, we used the Zwanzig equation (1):

$$\Delta G(\mathit{\text{Ref}}\to \mathit{\text{New}})=-k_{B}T\text{ln}\langle \text{exp}(-\frac{E_{\mathit{\text{New}}}-E_{\mathit{\text{Ref}}}}{k_{B}T})\rangle \mathit{\text{Ref}}$$ (1)

to determine the free energy change ΔG (Ref ➔ New) for a given state caused by the change in parameters, where 〈…〉_Ref represents an ensemble average of snapshots from that state simulated using the reference parameters, E is the potential energy of a snapshot, k_B is Boltzmann’s constant and T the absolute temperature. By calculating ΔG (Ref ➔ New) for (a) the free ligand in vacuum, (b) the free ligand in solution, and (c) the ligand in complex with the protein, we were able to determine ΔΔG_Wat, the change in the vacuum ➔ water transfer free energy caused by the change in parameters, and ΔΔG_Complex, the change in the vacuum ➔ solvated protein transfer free energy caused by the change in parameters.

$$\mathrm{\Delta }\mathrm{\Delta }{\mathrm{G}}_{\text{Wat}}=\mathrm{\Delta }\mathrm{G}{(\mathit{\text{Ref}}\to \mathit{\text{New}})}_{\text{Wat}}-\mathrm{\Delta }\mathrm{G}{(\mathit{\text{Ref}}\to \mathit{\text{New}})}_{\text{Vac}}$$ (2)

$$\mathrm{\Delta }\mathrm{\Delta }{\mathrm{G}}_{\text{Complex}}=\mathrm{\Delta }\mathrm{G}{(\mathit{\text{Ref}}\to \mathit{\text{New}})}_{\text{Complex}}-\mathrm{\Delta }\mathrm{G}{(\mathit{\text{Ref}}\to \mathit{\text{New}})}_{\text{Vac}}$$ (3)

Finally, from ΔΔG_Wat and ΔΔG_Complex, we determined ΔΔG_Bind, the change in the binding affinity caused by the change in parameters, using equation 4:

$$\mathrm{\Delta }\mathrm{\Delta }{\mathrm{G}}_{\text{Bind}}=\mathrm{\Delta }\mathrm{\Delta }{\mathrm{G}}_{\text{Complex}}-\mathrm{\Delta }\mathrm{\Delta }{\mathrm{G}}_{\text{Wat}}$$ (4)

We examined the sensitivity to charge parameters by taking each bond on each ligand and redistributing 0.1e of charge from one bonded atom to the other in each direction, for a total of two perturbations per bond. Each charge perturbation only alters the local dipole of a single bond; less localized perturbations or perturbations to the overall net charge of the ligands are not considered. For van der Waals parameters, we added and subtracted 0.3 Å from the Lennard-Jones radius σ for each atom, and added and subtracted 0.04 kcal/mol from the well depth ε, for a total of four perturbations per atom. We excluded van der Waals perturbations which lowered σ or ε to zero. The perturbations are similar in size to the average root-mean-squared deviation (RMSD) in amino acid parameters between commonly used protein force fields (Table 1): the average RMSD for charge parameters is 0.09e, for sigma parameters is 0.34 Å, and for epsilon parameters is 0.036 kcal/mol. The starting (reference) ligand parameters came from the General AMBER force field (GAFF)^18,19 using the AM1-BCC charge model^20,21.

Table 1. Root-mean-squared deviation in amino acid force field parameters between commonly used protein force fields.

Parameters were counted considering every atom in the 20 genetically encoded amino acids separately, i.e. backbone atoms are counted 20 times each even if atom types are identical between amino acids. N- and C-terminal atoms are counted a total of once each. All four force fields use a geometric combination rule for ε. AMBER and CHARMM use an arithmetic combination rule for σ while OPLS uses a geometric rule.

Charge (e)	AMBER9922	AMBER0323	CHARMM2724	OPLSAA-200125
AMBER99	0.000	0.068	0.109	0.103
AMBER03		0.000	0.108	0.102
CHARMM27			0.000	0.059
OPLSAA-2001				0.000
Sigma (Å)		AMBER99/03	CHARMM27	OPLSAA-2001
AMBER99/03		0.000	0.360	0.389
CHARMM27			0.000	0.272
OPLSAA-2001				0.000
Epsilon (kcal/mol)		AMBER99/03	CHARMM27	OPLSAA-2001
AMBER99/03		0.000	0.046	0.025
CHARMM27			0.000	0.036
OPLSAA-2001				0.000

Because we compute ΔΔG_Bind using simulations that only directly sampled the reference state, we may incorrectly calculate ΔΔG_Bind for rare cases where the important phase space in the new state significantly differs from the reference state. However, because these parameter perturbations are so miniscule and have such small effects on ΔΔG_Bind, ΔΔG_Complex, and ΔΔG_Wat, this error should have only a minor effect on the main conclusions.

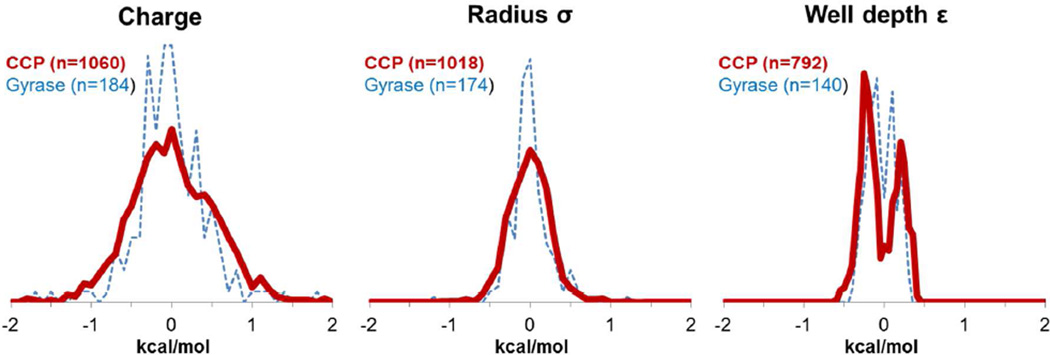
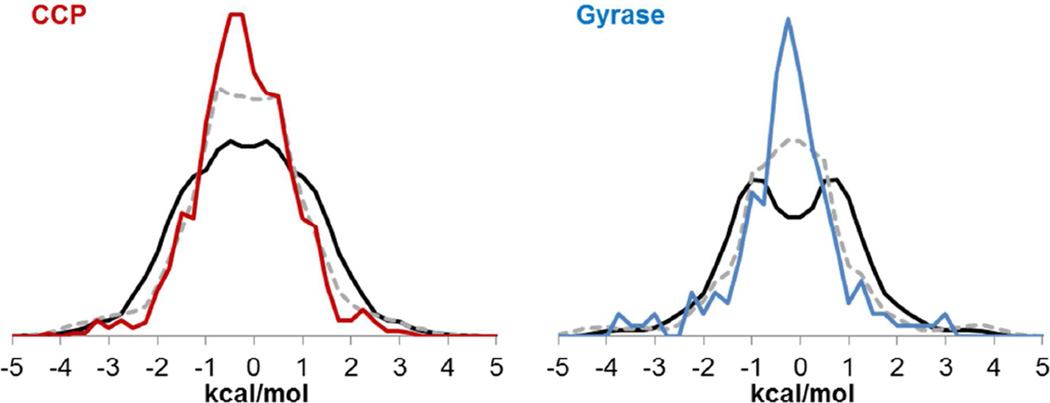
The ΔΔG_Bind values for all perturbations are shown in histogram form in Figure 2. In our analysis, we consider only the perturbations in CCP, although the Gyrase histograms show that the results are similar for the case of a more realistic binding site. The histograms are centered near zero because all perturbations are done in both directions (one direction likely increasing ΔΔG_Bind and the other likely decreasing it). For these compounds, changes to parameters weaken binding slightly on average: the 〈ΔΔG_Bind〉 values for charge, σ, and ε perturbations are 0.058 ± 0.016 kcal/mol, 0.040 ± 0.008 kcal/mol, and 0.030 ± 0.006 kcal/mol (uncertainties are the standard error of the mean, or SEM, and angled brackets are now used to indicate an average over all parameter perturbations). Though random charge perturbations weaken binding on average, they strengthen protein-ligand interactions (〈ΔΔG_Complex〉= −0.072 ± 0.031 kcal/mol) and ligand-solvent interactions (〈ΔΔG_Wat〉 = −0.130 ± 0.022 kcal/mol). (ΔΔG_Complex and ΔΔG_Wat do not include changes in internal energies of the compounds, because these effectively cancel between the vacuum and protein- or solvent-interacting states.) We interpret the difference to indicate the greater ability of the solvent to react to an arbitrary introduction of charge separation on the ligand. To simplify the analysis, we do not further consider this small average effect, and instead use the average absolute value of ΔΔG_Bind, indicated as〈|ΔΔG_Bind|〉, to measure the overall sensitivity of ΔG_Bind to ligand parameters. For CCP compounds, the 〈|ΔΔG_Bind|〉 values for charge, σ, and ε perturbations are 0.41 ± 0.01 kcal/mol, 0.20 ± 0.01, and 0.21 ± 0.01 kcal/mol for van der Waals perturbations (Figure 2).

Figure 2. Distribution of ΔΔG_Bind values for charge and van der Waals parameter perturbations in CCP (red) and Gyrase (blue).

Charge and σ histograms binned at 0.1 kcal/mol; ε histograms binned at 0.05 kcal/mol. For each parameter type (charge, σ, and ε), CCP and Gyrase results are normalized to each other to show relative frequencies. Charge, σ, and ε histograms are not normalized to each other.

2.2 For small perturbations, ΔΔG_Bind is proportional to perturbation size

The magnitude of 〈|ΔΔG_Bind|〉 depends on the size of the perturbations chosen. To examine how 〈|ΔΔGBind|〉 scales with the size of the individual perturbations, we also calculated ΔΔG_Bind values for perturbations which were 25%, 50%, and 75% as large as those used for the main analysis. Table 2 shows that 〈|ΔΔG_Bind|〉 grows linearly with the size of the perturbations for charge, σ, and ε perturbations. Because we compute free energies by reanalyzing trajectories simulated in the reference state, we are limited in the size of perturbations we can examine, and did not examine perturbations larger than 0.1 e, 0.3 Å, and 0.04 kcal/mol.

Table 2. The sensitivity of binding affinity to parameters is proportional to the size of the change in parameters.

We calculated the relative change in 〈|ΔΔG_Bind|〉 for full parameters perturbations (bottom row, ×4) compared with smaller perturbations. Values are normalized to the smallest perturbation size (0.025 e, 0.075 Å, and 0.01 kcal/mol). Uncertainties were calculated by bootstrapping (recalculating the fold-change in ΔΔG_Bind for 50,000 resamplings of the original data).

Pert. Size	Charge (n=1060)	σ (n=1018)	ε (n=792)
×1	1	1	1
×2	2.005 ± 0.068	1.970 ± 0.079	1.988 ± 0.049
×3	3.015 ± 0.103	2.940 ± 0.116	2.968 ± 0.073
×4	4.042 ± 0.137	3.949 ± 0.156	3.946 ± 0.097

2.3 Charge perturbations depend on bond type; van der Waals perturbations depend on parameter type

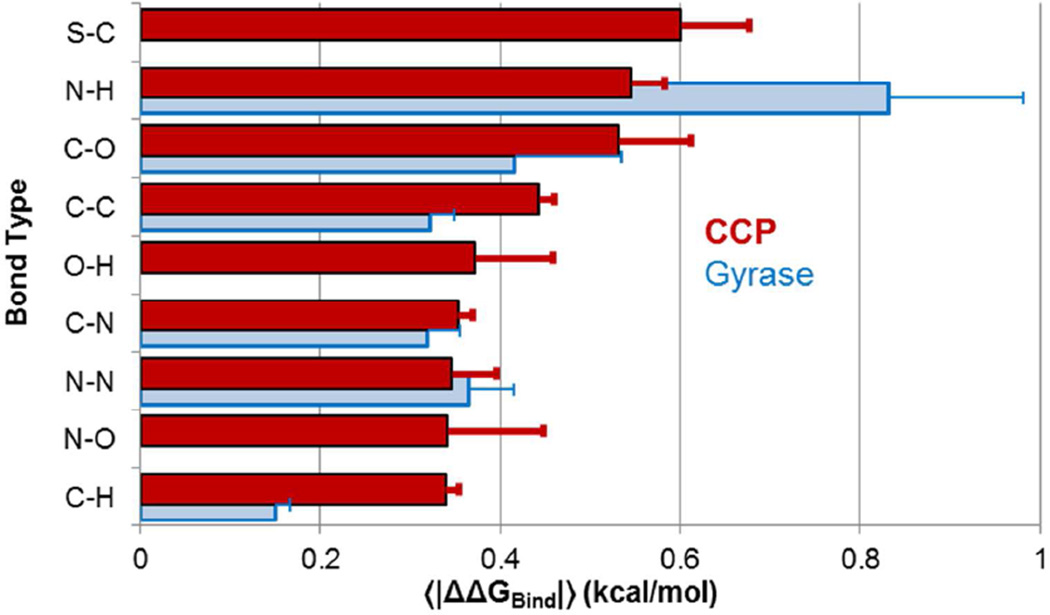
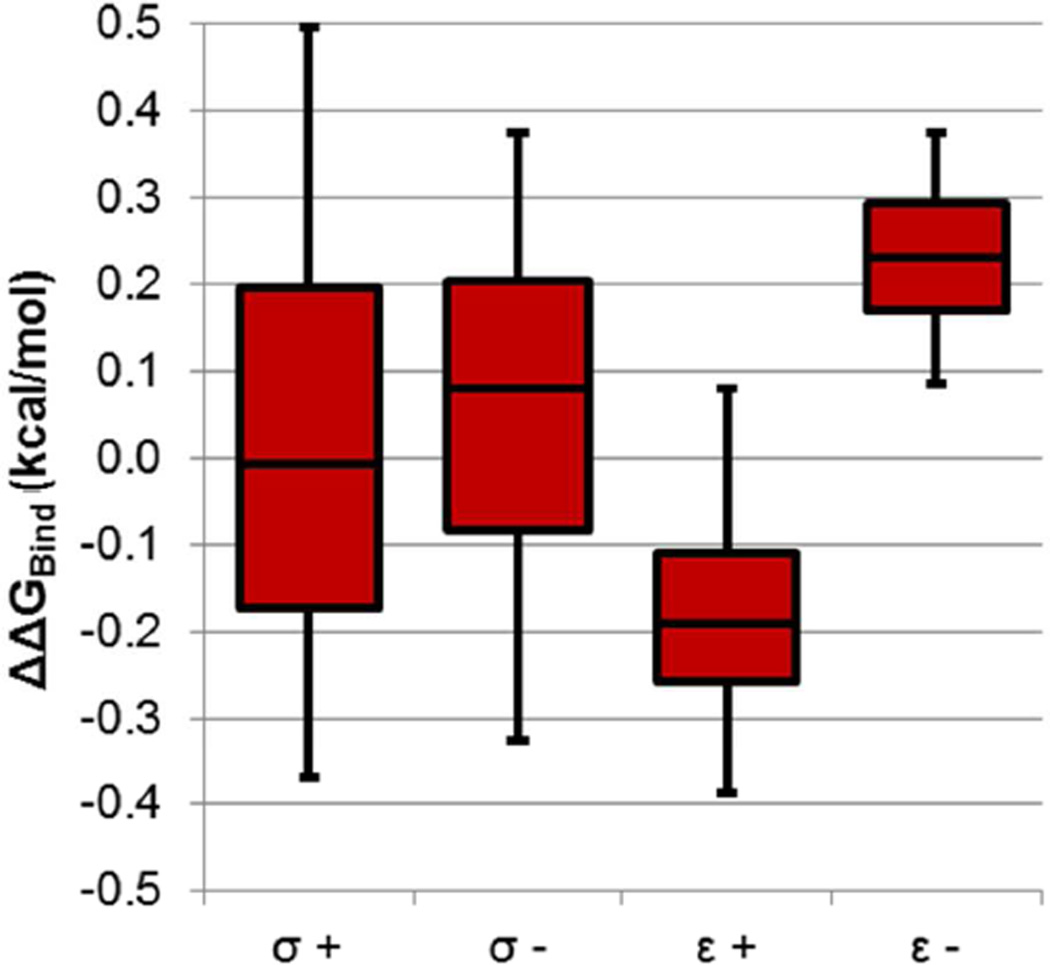
To more closely examine which charge and van der Waals parameters most affected ΔG_Bind, we separated our analysis based on which atoms were being perturbed and which perturbation was applied. For charge perturbations, we calculated individual 〈|ΔΔG_Bind|〉 values for each set of bonded elements (Figure 3). Both the CCP and Gyrase results show a similar trend, with polar S-C, N-H, and C-O bonds as most sensitive to charge parameters and C-H bonds as least sensitive. The errors bars for individual bond types do not overlap between CCP and Gyrase because of important differences between the binding sites: a greater fraction of N-H bonds in the Gyrase ligands point at ionized residues than in CCP, and a smaller fraction of C-H bonds in the Gyrase ligand are in polar binding site regions than in CCP. When changing van der Waals parameters, changing sigma may increase or decrease binding, while increasing epsilon almost always strengthens binding and decreasing epsilon almost always weakens binding (Figure 4).

Figure 3. Different bonds are differently sensitive to charge parameters.

We calculated 〈|ΔΔG_Bind|〉for charge perturbations along each type of bond; uncertainties show the standard error of the mean for 〈|ΔΔG_Bind|〉. Red: CCP results; blue: Gyrase results.

Figure 4. Different types of van der Waals perturbations have different effects on binding.

We separated the van der Waals perturbations into increasing and decreasing sigma and epsilon, and show in box plot form the 5^th, 25^th, 50^th, 75^th, and 95^th %ile values of ΔΔG_Bind.

2.4 Different ligands are similarly sensitive to parameters

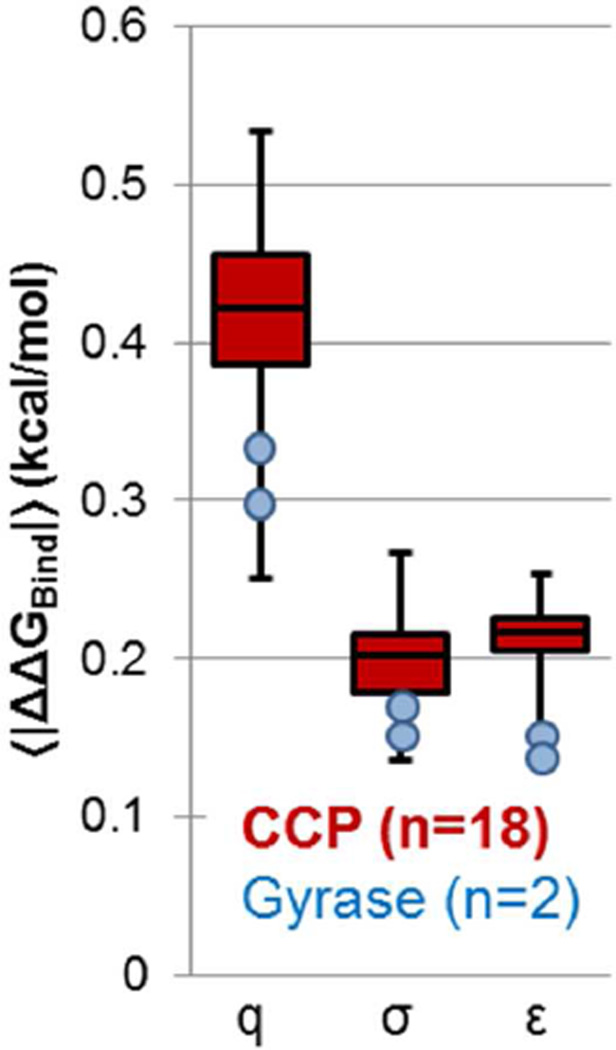
To examine whether 〈|ΔΔG_Bind|〉 significantly varied from ligand to ligand, we calculated individual 〈|ΔΔG_Bind|〉 values for each ligand, and show the results in Figure 5. The distributions are relatively narrow compared to the values of 〈|ΔΔG_Bind|〉, and the sensitivities of the Gyrase ligands fall within the distributions established by the CCP compounds. There is no clear difference in sensitivity to charge parameters between the three neutral CCP compounds and the remaining charged CCP compounds: the neutral compounds have 〈|ΔΔG_Bind|〉 values of 0.41 kcal/mol, 0.45 kcal/mol, and 0.51 kcal/mol, essentially in the middle of the distribution in Fig. 5.

Figure 5. Different ligands show similar sensitivity to charge and van der Waals parameters.

We calculated individual values of 〈|ΔΔG_Bind|〉for each ligand, and show here the minimum, first quartile, median, third quartile, and maximum 〈|ΔΔG_Bind|〉 values for the 18 CCP compounds in box plot form (red). Charge (q), radius (σ) and well depth (ε) perturbations are shown separately. 〈|ΔΔG_Bind|〉 values for the two Gyrase compounds are shown as blue circles.

2.5 Dielectric screening partially buffers affinities

Gas-phase interaction energies are often used as a reference state to consider the accuracy of force field parameters^13,26. However, binding affinities calculated in solution should be more robust to force field parameters, because the strength of electrostatic interactions is weakened by dielectric relaxation^12,27. For the ligand interacting with the protein, there are three sources of dielectric relaxation: electronic polarization, solvent reorganization, and protein reorganization, which we consider to include movement of the protein and ligand relative to each other. Our free energy calculations lack electronic polarization, but we can quantify the magnitudes of the other two effects by comparing free energy calculations to Poisson-Boltzmann (PB) calculations with defined amounts of dielectric relaxation^28,29,30.

We compared ΔΔG_Complex values for charge perturbations between the free energy calculations (dielectric relaxation from both protein and solvent) and two other systems: first, a single snapshot of the protein-ligand complex in vacuum (no dielectric relaxation at all), and second, a PB calculation using a single snapshot of the protein-ligand complex with ε_ext = 97 and ε_int = 1 (solvent dielectric relaxation equal to the dielectric of TIP3P water³¹, but no protein dielectric relaxation at all) (Figure 6, Table 3). Each PB ΔΔG_Complex value is calculated based on a single snapshot, though to ensure that the results are not overly dependent on the snapshot chosen, we calculated 50 separate PB ΔΔG_Complex values using 50 different structural snapshots from the original 1 ns simulations of each ligand pose. By calculating each PB ΔΔG_Complex value from a single snapshot, we ensure the only dielectric relaxation in the ΔΔG_Complex calculation is the applied continuum solvent dielectric of ε_ext = 97. (If all snapshots were used to calculate a single overall PB ΔΔG_Complex value with the Zwanzig equation (1), the protein reorganization between the original and new parameters would introduce additional screening.) These ΔΔG_Complex values, both from free energy calculations and PB calculations, exclude the change in the ligand’s internal energy due to perturbed parameters – only the change in protein-ligand interaction is considered.

Figure 6. Dielectric screening reduces the magnitude of 〈|ΔΔG_Complex|〉 for charge perturbations.

Red (left, CCP) and blue (right, Gyrase): distribution of 1060 (CCP) or 184 (Gyrase) ΔΔG_Complex values for charge perturbations from free energy calculations. Black: distribution of ΔΔG_Com_plex values for charge perturbations calculated using a single snapshot of the protein-ligand complex in vacuum, and including 50 snapshots per perturbation (CCP) or 200 snapshots per perturbation (Gyrase). Grey dashes: distribution of ΔΔG_Complex values for charge perturbations calculated using a Poisson-Boltzmann calculation on a single snapshot of the protein-ligand complex with ε_int=1, ε_ext=97, using the number of snapshots as above. All distributions are shown as normalized histograms binned at 0.25 kcal/mol.

Table 3.

Summary of comparisons between free energy and Poisson-Boltzmann ΔΔG_Complex values.

	CCP	Gyrase
n Perturbations	1060	184
〈|ΔΔG Complex|〉 (kcal/mol)
Vacuum (single structure)	1.08 ± 0.01	1.05 ± 0.05
PB εint=1, εext =97 (single structure)	0.95 ± 0.01	0.95 ± 0.01
Free Energy	0.77 ± 0.02	0.75 ± 0.01
Poisson-Boltzmann single fit εint for all perturbations
Optimal εint	2.58 ± 0.01	2.92 ± 0.61
RMSE vs Free Energy (kcal/mol)	0.50	0.52
R2	0.75	0.77

Figure 6 shows that the distribution of ΔΔG_Complex values narrows in CCP and Gyrase when solvent dielectric relaxation is added (black to dashed grey lines), and narrows further when protein dielectric relaxation is added by computing ΔΔG_Complex using free energy calculations (dashed grey to colored lines). This is reflected in the values of 〈|ΔΔG_Complex|〉 shown in Table 3. In CCP and Gyrase, relaxation of the protein and solvent buffers 30% of the effect of parameter changes on ΔΔG_Complex.

2.6 Dielectric screening in free energy calculations is protein- and environment-dependent

How much protein dielectric relaxation is observed in the free energy calculations? Poisson-Boltzmann calculations commonly model the protein as a uniform homogenous dielectric, which, while a significant oversimplification, provides an easily understood means to quantify relaxation. Using PB calculations on a single structure of each protein-ligand complex, we calculated ΔΔG_Complex values for all charge perturbations with ε_ext = 97 (representing TIP3P water) and ε_int varying between 1 and 80. We then interpolated each ΔΔG_Complex value as a function of ε_int using a cubic spline, and determined an optimal value of ε_int for each protein to reproduce the ΔΔG_Complex values from the free energy calculations (Table 3). The CCP and Gyrase ΔΔG_Complex values were best reproduced with a homogenous ε_int of 2.58 ± 0.01 and 3.03 ± 0.01 respectively (Table 3, uncertainties were computed based on 1,000 bootstrapping selections from the ΔΔG_Complex values). A dielectric of 2.0 is close to the minimum one would expect from electronic relaxation alone³². Our simulations, which feature (modest) structural relaxation and no electronic relaxation, hardly exceed this low level of total relaxation.

How much does the protein environment modulate the amount of dielectric screening? In our previous free energy study of ligand binding to CCP, we constructed an artificial ‘miniature binding site’ in silico, made of all CCP residues which contact the ligands, fixed in space by harmonic position restraints¹⁵. This miniature binding site is surrounded by bulk solvent rather than protein, which should raise the effective dielectric in the site. Comparing 〈|ΔΔG_Complex|〉 between the full CCP protein and the miniature site allows us to directly observe how the binding site environment (low dielectric protein vs. high dielectric solvent) modulates sensitivity to charge parameters. Because not all ligand poses were simulated in the miniature site, we look here at a smaller set of charge perturbations (n = 744). This smaller set of charge perturbations has 〈|ΔΔG_Complex|〉 = 0.81 ± 0.02 kcal/mol and an optimal ε_int of 2.12 ± 0.01, which are similar to 0.77 ± 0.02 kcal/mol and 2.58 ± 0.01 observed in the full set of 1060 perturbations, though with slightly less screening. When the 744 perturbations are made in the miniature site, 〈|ΔΔG_Complex|〉 is 0.73 ± 0.02 kcal/mol and the optimal ε_int is 3.15 ± 0.01, both showing increased screening compared with the same perturbations made in the full protein. This ε_int was calculated by comparing the free-energy calculated ΔΔG_Complex values in the miniature site with PB-calculated ΔΔG_Complex values in the full protein. It thus represents the homogenous internal dielectric which, when used in PB calculations on the full protein, best reproduces the parameter sensitivity observed in free energy calculations in the miniature site.

How accurately can PB calculations predict the effects of charge parameter changes in free energy calculations? The RMSE (using the optimally fit ε_int) between PB calculations and free energy calculations was 0.50 kcal/mol in CCP and 0.52 kcal/mol in Gyrase, compared with the standard deviations of the underlying distributions of 0.99 and 1.07 kcal/mol in each protein (Table 3). In both systems, the PB calculations with a homogenous protein dielectric constant explain 75% of the variability of the free energy-computed ΔΔG_Complex values. The remaining variability cannot be explained using a single homogenous protein dielectric constant, because different points on the ligands have different levels of flexibility themselves and feel different amounts of protein relaxation^33,34.

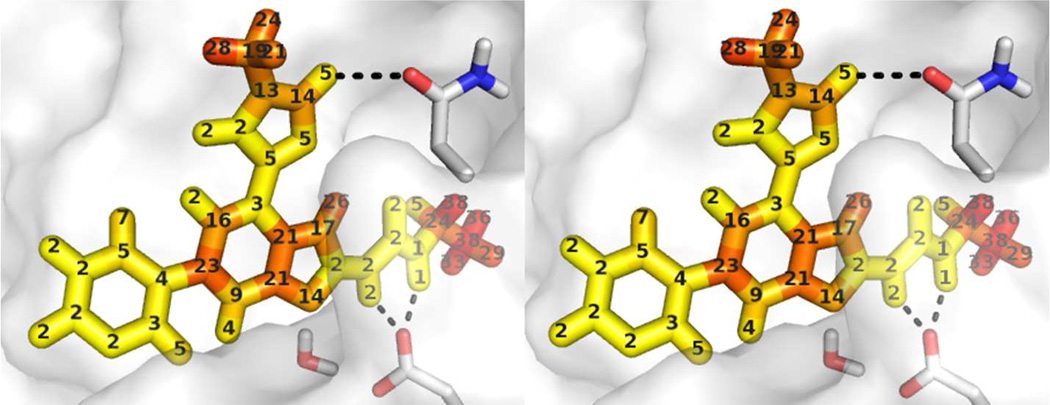
To gain a deeper insight into why different positions on the ligands feel differing amounts of protein dielectric relaxation, we examined how the optimal ε_int varied spatially throughout the ligand atoms. Rather than determining an overall optimal ε_int for the set of all charge parameter perturbations, we determined an individually optimal ε_int for each perturbation. The perturbations were originally applied to bonds, so we mapped these perturbations to the ligand atoms by averaging the optimal ε_int values for all bonds around a given atom. These optimal ε_int values are shown for one Gyrase ligand in Figure 7. These ε_int values represent the optimal homogenous protein dielectric constant for PB calculation to reproduce free energy calculations which slightly redistribute charge at a given position. They do not represent the total effective dielectric, because all PB calculations were performed with ε_ext = 97 and only varied ε_int. Still, these numbers show interesting spatial variability in the amount of protein dielectric relaxation in free energy calculations. In particular, several atoms in contact with the protein surface on the central benzimidazole moiety of the ligand are best modeled in PB calculations with high (above 10) protein dielectric constants, which may relate to the presence of an adjacent buried water molecule in the free energy calculations.

Figure 7. Effective protein dielectric constant, probed from different ligand atoms in Gyrase.

For each ligand bond, an optimal protein ε_int for PB calculations was determined which matched the ΔΔG_Complex values from free energy calculations. For each ligand atom, the optimal ε_int was defined as the average of the optimal ε_int values for each bond to that atom. Ligand atoms are colored by the optimal ε_int value. Residues Asn46 and Asp73 are shown explicitly, as is a water molecule from the free energy calculations which may raise the protein dielectric constant required for optimal PB calculations.

2.7 Cancellation of effects in solvent and in the protein strongly buffers affinities

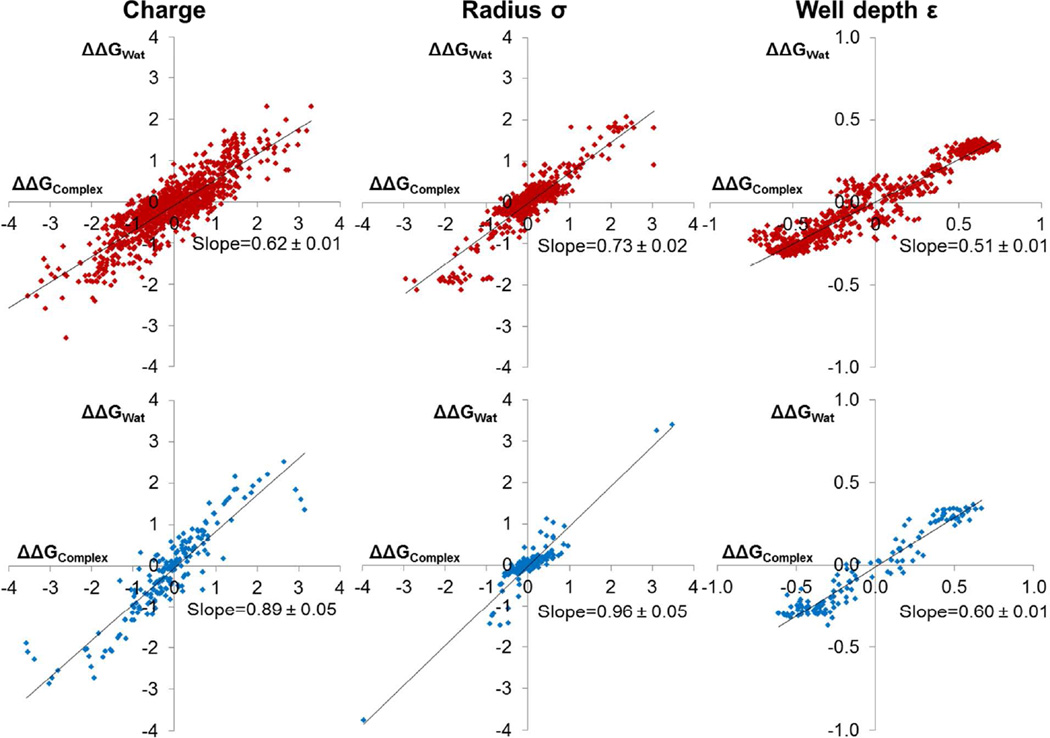
Dielectric screening appears to reduce the magnitude of 〈|ΔΔG_Complex|〉 by 30% compared with gas-phase calculations. The magnitude of 〈|ΔΔG_Bind|〉 is then further reduced by cancellation of effects between ΔΔG_Complex and ΔΔG_Wat, because parameter perturbations typically strengthen or weaken both protein-ligand and ligand-solvent interactions at the same time (Figure 8). For charge, σ, and ε perturbations in the CCP compounds, 〈|ΔΔG_Bind|〉 is 53%, 49%, and 67% as large as 〈|ΔΔG_Complex|〉. The compensation is even stronger in Gyrase, because a larger fraction of each Gyrase ligand is exposed to solvent, and perturbing parameters on these atoms causes essentially equal changes in ΔG_Complex and ΔG_Wat. The 30% reduction in 〈|ΔΔG_Complex|〉 compared with gas-phase calculations, combined with a further 35–50% reduction in 〈|ΔΔG_Bind|〉 compared with 〈|ΔΔG_Complex|〉 constitute a sizable buffering effect. This also suggests that it may be easier to predict accurate binding free energies than to predict accurate solvation free energies, because errors in parameters will cancel substantially between the protein-ligand interaction and the protein-solvent and ligand-solvent interactions.

Figure 8. Cancellation of effects in solvent and in the protein buffers the overall ΔG_Bind to changes in parameters.

In CCP (top, red), ΔΔG_Wat buffers 35–50% of the change in ΔΔG_Complex (despite slopes of 0.6–0.7), while in Gyrase (bottom, blue) this buffering is even stronger. Best fit lines are shown in black. Slope uncertainties represent one standard deviation from bootstrapping calculations.

2.8 Multiple perturbations show some non-additivity, but do not buffer each other

To examine whether non-additivity buffers the overall affinity in response to multiple parameter perturbations, we exhaustively calculated ΔΔG_Bind values for all pairs of charge perturbations and all pairs of van der Waals perturbations. Perturbations to σ and ε were mixed together for this analysis, although we did not include perturbing both σ and ε on the same atom. We also calculated ΔΔG_Bind values for 100 triple perturbations per ligand, chosen by randomly selecting three single perturbations (all charge or all van der Waals) to perform together. As expected, the overall effect of multiple combined perturbations is larger than the effect of single perturbations (Figure 9). We then calculated ΔΔΔG_Non-add as the difference between the actual ΔΔG_Bind for multiple perturbations and the expected ΔΔG_Bind based on additivity:

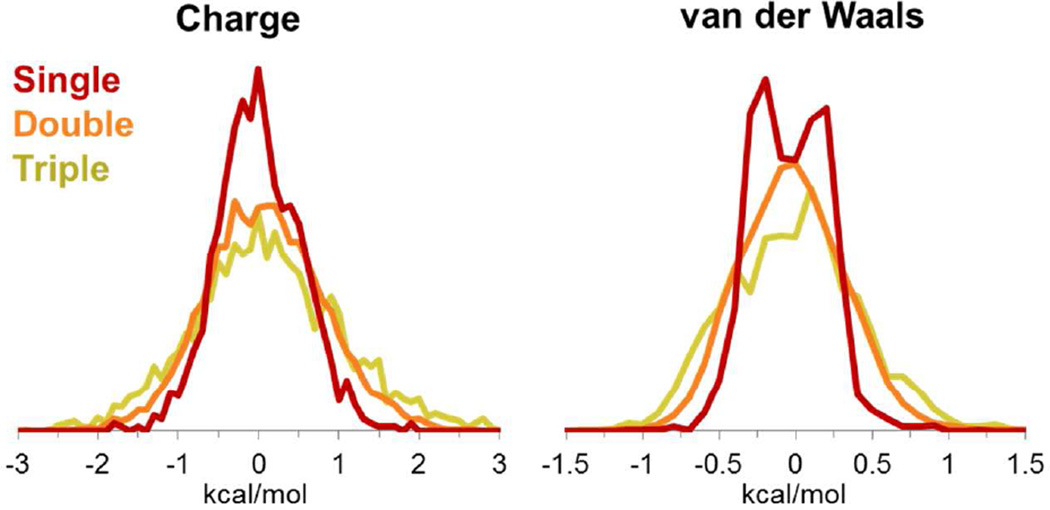
Figure 9. Multiple simultaneous perturbations lead to a broader distribution of ΔΔG_Bind values.

ΔΔG_Bind distributions in CCP for single (red), double (orange), and triple (yellow) simultaneous perturbations are shown binned at 0.1 kcal/mol. Histograms for single, double, and triple perturbations are normalized to each other; charge and van der Waals histograms are normalized separately.

For double perturbations:

$$\mathrm{\Delta }\mathrm{\Delta }\mathrm{\Delta }{\mathrm{G}}_{\text{Non-add}}=\mathrm{\Delta }\mathrm{\Delta }{\mathrm{G}}_{\text{Bind},\text{Simult}}-(\mathrm{\Delta }\mathrm{\Delta }{\mathrm{G}}_{\text{Bind},1}+\mathrm{\Delta }\mathrm{\Delta }{\mathrm{G}}_{\text{Bind},2})$$ (5)

In Eq. 5, ΔΔG_Bind,Simult is the free energy of perturbing parameters 1 and 2 simultaneously, and ΔΔG_Bind,1 and ΔΔ_GBind,2 are the free energies of perturbing parameters 1 and 2 individually.

For triple perturbations:

$$\mathrm{\Delta }\mathrm{\Delta }\mathrm{\Delta }{\mathrm{G}}_{\text{Non-add}}=\mathrm{\Delta }\mathrm{\Delta }{\mathrm{G}}_{\text{Bind},\text{Simult}}-(\mathrm{\Delta }\mathrm{\Delta }{\mathrm{G}}_{\text{Bind},1}+\mathrm{\Delta }\mathrm{\Delta }{\mathrm{G}}_{\text{Bind},2}+\mathrm{\Delta }\mathrm{\Delta }{\mathrm{G}}_{\text{Bind},3})$$ (6)

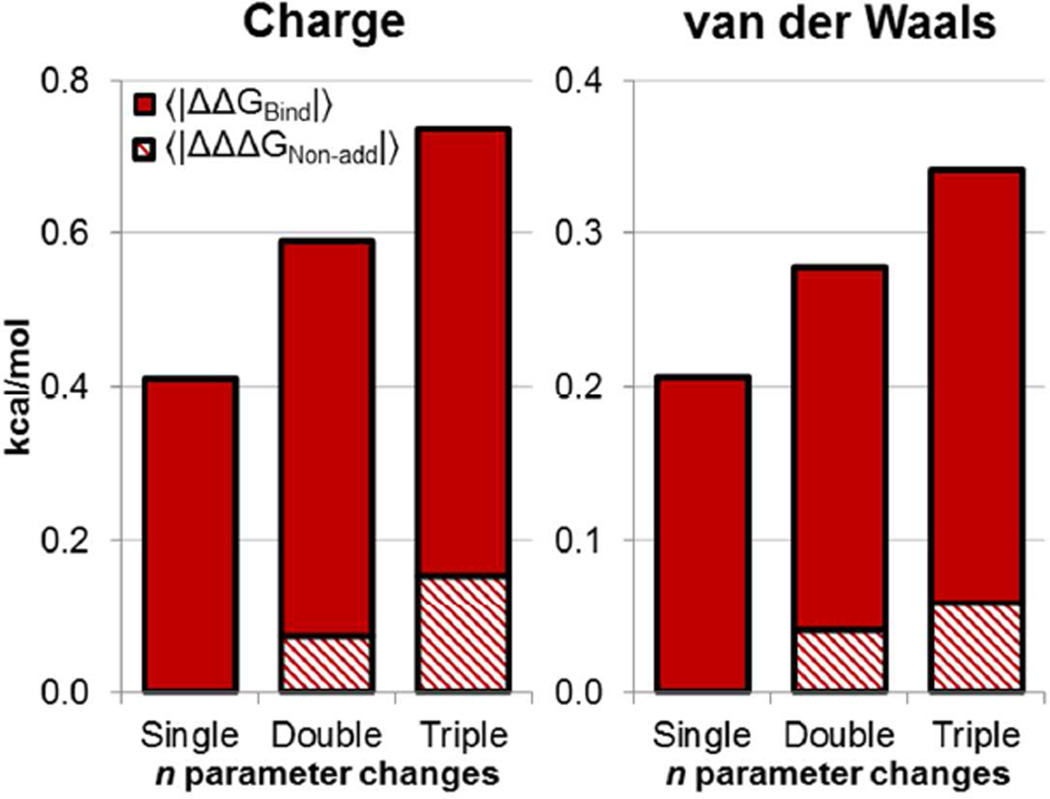
The combined effect of multiple small parameter perturbations is generally additive, though the amount of non-additivity increases with additional perturbations. We determined the relative amount of nonadditivity by comparing 〈|ΔΔG_Bind,Simult|〉 and 〈|ΔΔΔG_Non-add|〉 (Figure 10). For double and triple charge perturbations, 〈|ΔΔΔG_Non-add|〉 is 12% and 21% as large as 〈|ΔΔG_Bind,Simult|〉, and 15% and 17% as large for double and triple van der Waals perturbations. Free energy calculations do therefore contain an important non-additive element which may be missed by simpler scoring functions. However, this non-additivity will only buffer the overall magnitude of ΔΔG_Bind,Simult if ΔΔΔG_Non-add and ΔΔG_Bind,Simult are oppositely signed. To examine this, we collected the magnitudes of all ΔΔΔG_Non-add values, and assigned each one a negative sign if ΔΔG_Bind,Simult was smaller in magnitude than ΔΔG_Bind,1 + ΔΔG_Bind,2 (ΔΔΔG_Non-add buffers ΔΔG_Bind,Simult), or assigned it a positive sign if ΔΔG_Bind,Simult was larger than ΔΔG_Bind,1 + ΔΔG_Bind,2 (ΔΔΔG_Non-add adds to ΔΔG_Bind,Simult). With this sign convention, the average ΔΔΔG_Non-add values for double and triple charge perturbations are −0.0026 ± 0.0007 and −0.0025 ± 0.0039 kcal/mol, and the average ΔΔΔG_Non-add values for double and triple van der Waals perturbations are 0.0015 ± 0.0003 and 0.0011 ± 0.0019 kcal/mol. These average ΔΔΔG_Non-add are very close to zero, meaning that multiple perturbations neither buffer each other nor are cooperative on average.

Figure 10. Multiple simultaneous perturbations show a small amount of non-additivity.

Solid bars show 〈|ΔΔG_Bind|〉 for single, double, and triple perturbations. The shaded regions shows 〈|ΔΔΔG_Non-add|〉, which is the average amount of non-additivity in ΔΔG_Bind for multiple perturbations (see equations 5 and 6).

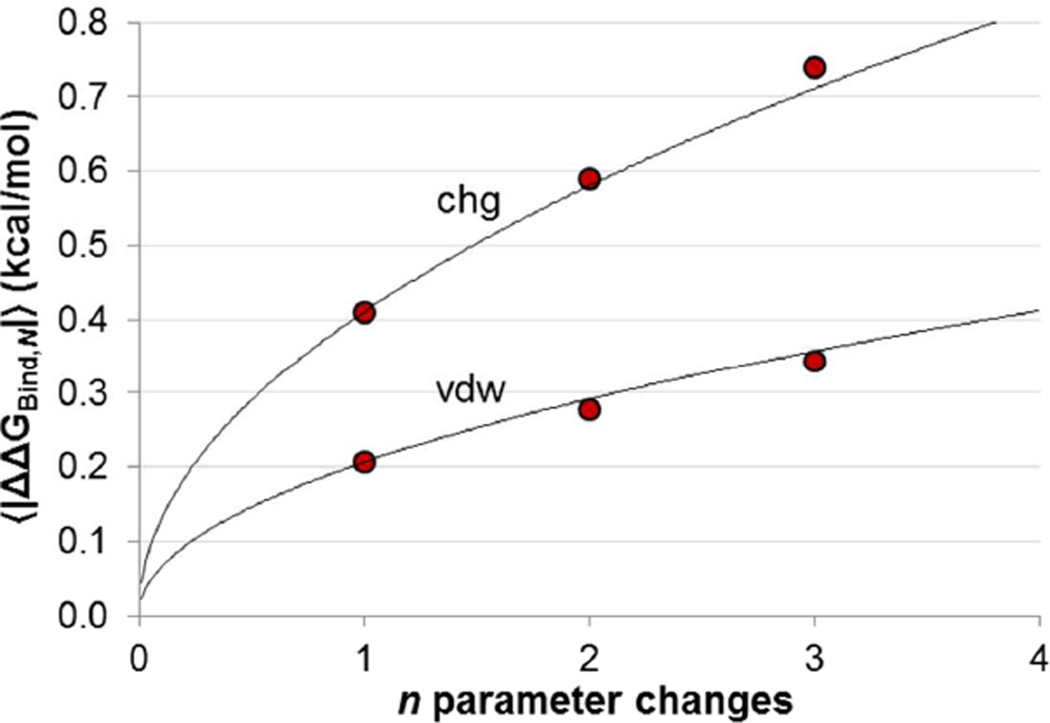
Because multiple perturbations combine additively on average (even though there is non-additivity in any individual case), the growth in 〈|ΔΔG_Bind|〉 with n perturbations should be predictable as if the perturbations were independent ,We show this in Figure 11, where each point is a 〈|ΔΔG_Bind|〉 value computed from the distributions in Figure 9. The black lines show the predicted 〈|ΔΔG_Bind|〉 values based on the single perturbation data, assuming that 〈|ΔΔG_Bind|〉 for n perturbations is n times 〈|ΔΔG_Bind|〉 for one perturbation. The prediction is very accurate for both n = 2 and n = 3, though the 〈|ΔΔG_Bind|〉 value for triple charge perturbations is slightly larger than the prediction.

Figure 11. Growth in 〈|ΔΔG_Bind|〉 for n parameter changes.

Red points: 〈|ΔΔG_Bind|〉 from CCP ΔΔG_Bind data for multiple simultaneous parameter changes. Bootstrapped uncertainties are shown but are smaller than the visual appearance of the data points. Black lines: expected 〈|ΔΔG_Bind|〉 growth for n random, independent simultaneous perturbations based on single perturbation data, growing as $\sqrt{n}$.

The small overall amount of non-additivity we observed results in part from our treatment of ligand symmetry. Because we treated symmetric ligand atoms as unique and considered each ligand in a fixed orientation in the binding site (though no restraints were applied), we obtained a higher resolution view of which interactions contributed to affinity, because otherwise identical atoms are distinguished from each other by the interactions they make. For example, for benzimidazole bound to CCP (shown in Figure 1 a), one symmetric imidazole amine forms a hydrogen bond with a protein aspartate residue, while the other symmetric amine hydrogen bonds with solvent. By treating the two amines differently, we can observe that the depolarizing the amine N-H (moving 0.1e of charge from the H to the N) which points at the aspartate weakens binding by 1.45 kcal/mol, while depolarizing the opposite amine has little effect on binding (0.02 kcal/mol). However, if one N-H bond were depolarized in a true binding calculation, the ligand would orient to point the more polar amine toward the aspartate and the less polar amine away, and the overall effect on binding (based on combining our data from both perturbations) for depolarizing one amine would be only 0.30 kcal/mol. By considering each amine separately, we calculated a larger average ΔΔG_Bind for depolarizing a benzimidazole amine (the average of 1.45 kcal/mol and 0.02 kcal/mol vs. the average of 0.30 kcal/mol and 0.30 kcal/mol). Just as our treatment of symmetry leads to a larger 〈|ΔΔG_Bind|〉 for depolarizing these amines, it also leads to a smaller 〈|ΔΔG_Bind|〉 for increasing the polarity of the amines, and the effect on 〈|ΔΔG_Bind|〉 for the entire dataset somewhat cancels because all perturbations were tested in both directions. However, our treatment of symmetry does decrease the amount of nonadditivity we observe. By considering each amine separately, we calculated a more additive ΔΔG_Bind,Simult for depolarizing both amines together: the combined ΔΔG_Bind,Simult is 1.46 kcal/mol, which is nearly the sum of 1.45 kcal/mol and 0.02 kcal/mol. If, alternatively, ΔΔGBind for depolarizing each amine is calculated as 0.30 kcal/mol because of ligand reorientation, then the combined ΔΔG_Bind,Simult appears highly non-additive (1.46 kcal/mol vs 0.60 kcal/mol), because only when both amines are depolarized together is the aspartate-ligand interaction weakened. Likewise, we observed a more additive ΔΔG_Bind,Simult for increasing the polarity of both amines as well. Overall, by re-analyzing simulations of ligands in fixed orientations and treating symmetry-related atoms as unique, our results underestimate the amount of nonadditivity resulting specifically from symmetric ligands, or groups which do not normally rotate in simulations but could if they were given asymmetric parameters, such as primary amines.

2.9 Differences between parameter sets may be correlated

The previous analysis considered the sensitivity of ΔG_Bind to random changes in ligand parameters. However, parameterization methods for force fields produce parameters which are coupled to each other: if some parameters were to change slightly, others could change in a compensatory fashion and produce a force field of similar quality, according to the objective function used for parameterization. As a result, even though ΔΔG_Bind becomes larger as a larger number of random parameter perturbations are applied (Figure 11), actual differences between force fields are not likely to be collections of random perturbations.

To examine how correlations between parameters lead to overall smaller ΔΔG_Bind values, we compared two sets of charge parameters for our CCP ligands: the original AM1-BCC parameters used as the reference parameters in this study, and new parameters derived by electrostatic potential (ESP) fitting to ab initio MP2 calculations, referred to as QM ESP parameters. These QM ESP parameters were also taken from ref. 15. The differences between AM1-BCC charges and QM ESP charges are correlated with each other, because AM1-BCC charges are also designed to reproduce the ESP around a given molecule, though fitting to the ESP itself often leads to underdetermined atomic partial charges.

For each CCP compound, we decomposed the overall atomic charge differences between AM1-BCC parameters and QM ESP parameters into multiple individual bond perturbations, where a bond perturbation consists of transferring a specific amount of charge from one bonded atom to its bonded neighbor. When all of these bond perturbations are added to the original AM1-BCC parameters, the molecule is fully perturbed from AM1-BCC charges to QM ESP charges. Because we have already calculated ΔΔG_Bind for each individual bond perturbation on its own (assuming the linear relationship in Table 2 holds), we can predict an expected overall ΔΔG_Bind,Simult for perturbing a compound from AM1-BCC to QM ESP charges, using the assumption of exact additivity. (We use this assumption because we wish to examine the effect of correlations in parameters, and not non-additivity.) This expected ΔΔG_Bind,Simult includes any effect of correlation in the differences between AM1-BCC parameters and QM ESP parameters. The magnitudes of these expected ΔΔG_Bind,Simult values are shown in Figure 12 (red), with the values for each compound ordered from smallest (left) to largest (right).

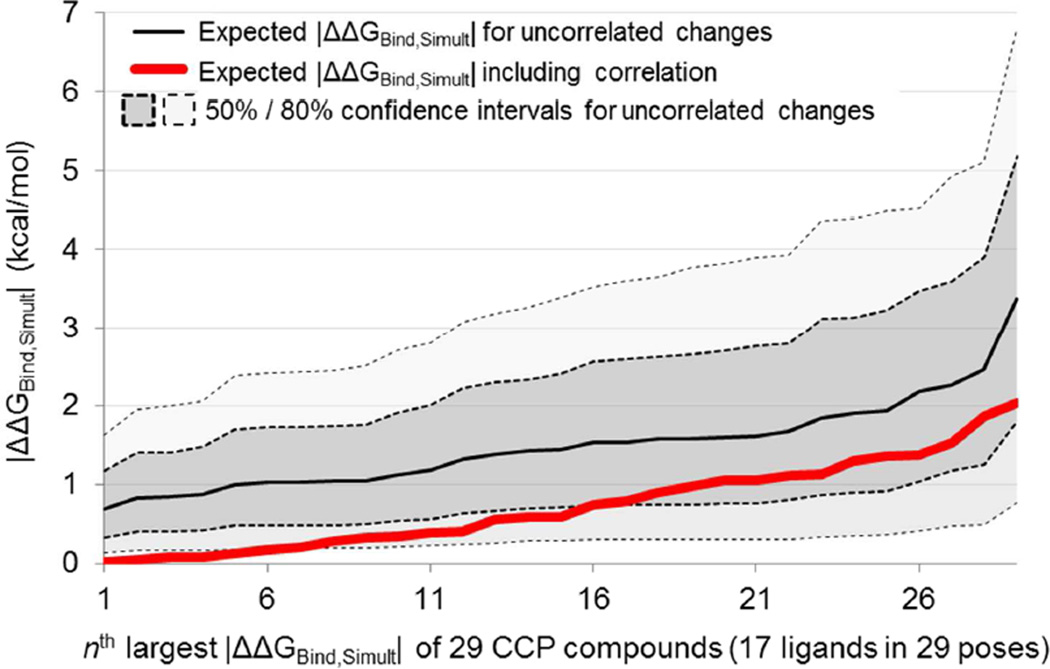
Figure 12. Force fields with similar parameterization objective functions can lead to smaller |ΔΔG_Bind,Simult| values for many simultaneous parameter perturbations.

Red: expected |ΔΔG_Bind,Simult| values for perturbing the charges along each bond in CCP compounds until AM1-BCC charges have been transformed into QM ESP charges, based on measured sensitivities for single bond perturbations and assuming exact additivity, ordered from smallest (left) to largest (right). Black: expected |ΔΔG_Bind,Simult| values for perturbing the charges along each bond in CCP compounds randomly until the same overall magnitude of perturbation has been applied as the difference between AM1-BCC charges and QM ESP charges (see text), again based on measured sensitivities for single bond perturbations and assuming exact additivity. Shaded regions indicate 50% confidence and 80% confidence windows for the randomly assigned bond perturbations based on 10,000 trials. Ligands have no specific order in the 10,000 trials; different ligands end up as “least perturbed” and on the far left in each different trial, and the black line represents the average over all trials of the least perturbed ligands for a given trial (far left), the second least perturbed ligands for a given trial (second from left), and so forth

To remove any effect of correlation in the differences between parameter sets, we generated thousands of variant parameter sets of the original AM1-BCC parameters. Each variant parameter set (10,000 per compound) was generated by taking the magnitudes of the AM1-BCC-to-QM ESP bond perturbations and assigning each magnitude to a random bond in a random direction, each magnitude being used once and each bond being perturbed once. Each of these variant parameter sets is thus equally different from the original AM1-BCC parameters as the QM ESP parameter are, except that the difference is randomly distributed instead of distributed in a correlated fashion. By again using the ΔΔG_Bind values for single perturbations and assuming exact additivity, we predicted expected ΔΔG_Bind,Simult values for each variant parameter set. Using all the variant parameter sets for all the compounds, we produced a background distribution of |ΔΔG_Bind,Simult| for perturbations of the same magnitude as the difference between AM1-BCC and QM ESP, but without correlations in which parameters change simultaneously. These expected |ΔΔG_Bind,Simult| values are shown in black in Figure 12, along with the 50% and 80% confidence intervals. Figure 12 indicates that the actual differences between AM1-BCC and the QM ESP parameters (red) result in smaller changes in affinity 〈|ΔΔG_Bind,Simult|〉 than would be expected if the parameters were randomly perturbed by an amount equal in magnitude to the overall difference between the AM1-BCC and QM ESP parameter sets (black). Some ligands are not expected to change affinity at all (leftmost ligands, red) between AM1-BCC and QM ESP parameters 〈|ΔΔG_Bind,Simult| < 0.1 kcal/mol〉, even though the magnitude of the parameter changes being made would suggest that whichever ligand changes least would change by 0.7 kcal/mol (leftmost ligands, black).

3 Discussion

3.1 How accurate do force field parameters need to be?

The force fields used in binding calculations suffer from inherent inaccuracies: the force field itself uses a simplified, classical-mechanical functional form^36,37, a limited number of atom types are used to represent the breadth of chemical space¹⁸, the experimental data available for selecting parameters is incomplete and leaves parameters underdetermined, and the “correct” parameters will often depend on the chemical environment in ways which are still challenging to capture , These approximations can introduce errors in simulated binding affinities, though the magnitude of these errors depends on the sensitivity of computed binding affinities to the force field parameters. Here, we find that dielectric screening reduces this sensitivity by 30% compared with the strength of molecular interactions in the gas phase (Figure 6 and Table 3), and that cancellation of effects between protein-ligand interactions and solvent-ligand interactions reduces the sensitivity by a further 35–50% (Figure 8).

Despite these buffering effects, the $\sqrt{n}$ scaling of 〈|ΔΔG_Bind|〉 with n parameter perturbations may pose a serious challenge to obtaining accurate binding affinities for drug-size molecules. This scaling has previously been hypothesized by Merz, who applied it to calculate the expected error in a computational affinity prediction between Indinavir (molecular weight 613.8 g/mol, 45 heavy atoms) and HIV protease³⁵. Here, we re-consider this problem for binding free energy calculations in light of our results. We start by assuming the overall error in a free energy calculation for Indinavir binding results from the combined effects of many small errors in force field parameters, that these parameter errors impact the binding affinity primarily through modulating interaction strengths, and not through altering the protein or ligand conformation, and that these errors consist of random independent inaccuracies in parameters compared with their “true” values which would produce the correct affinity. Actual errors in force fields are certainly not entirely independent, as Figure 12 suggests. However, some fraction of the overall error will behave in this manner, and it is useful to estimate how much random error is tolerable. Indinavir has 96 bonds which can have incorrect charge distributions, and 92 atoms which can each have two erroneous van der Waals parameters. As a first approximation, we can consider the binding site to have an identical number of relevant charge and van der Waals parameters, doubling the effective number of errors.

If we begin by assuming the same average parameter errors which we have examined in this study – 0.1e per bond, 0.3 Å per radius, 0.04 kcal/mol per well depth and – the combined effects of 192 random independent errors in bond charges, 184 errors in well depths and 184 errors in radii leads to an expected 6.9 kcal/mol error in the affinity prediction, based on the distribution of ΔΔG_Bind values from the CCP data in Figure 2. To obtain a free energy prediction with 68% confidence (one standard deviation) of being within 1 kcal/mol of the true affinity, the upper limit on random errors in individual parameters is nearly ten-fold smaller than the perturbation magnitudes considered here: 0.01e per bond, 0.03 Å per radius, and 0.004 kcal/mol per well depth. The exceptionally large size of Indinavir makes it an extreme case, though the results are similar for more moderately-sized lead-like ligands: a similar analysis of the 48 bonds and 41 atoms in the Gyrase ligand in Figure 1b using the Gyrase van der Waals data in Figure 2 and the Gyrase bond-type specific charge data in Figure 3 leads to an expected 4.1 kcal/mol error in affinity prediction, implying that parameter errors must be five-fold smaller than those considered here for 68% confidence in a predicted affinity. These targets for accuracy are substantially smaller than the RMS differences between the commonly used protein force fields shown in Table 1. However, the parameter differences between these force fields are likely correlated, making binding affinities more similar between these force fields than would be expected from the parameter differences alone, as in Figure 12. Assessing the extent of this correlation and its effect on ligand binding affinity is beyond the scope of this work, though it is important for guiding force field development.

Several caveats apply to this analysis. Importantly, we assume above that only random errors (like our parameter perturbations) affect the binding affinities, and not systematic errors, which could lead to greater inaccuracy¹³. We also neglect possible errors in conformational parameters such as torsions, which may be widespread in force fields. This is a reasonable approximation for the relatively rigid CCP ligands, but error in torsional parameters could cause even larger errors in calculations on drug-size compounds than our present analysis predicts. Finally, the sensitivity of binding affinity to parameters will depend on the force field itself. Different force fields might agree on a particular binding affinity, yet display different sensitivities to parameters, and understanding these differences should be useful in developing robust physics-based methods for predicting binding affinity.

3.2 How can force fields be improved?

Our results identify several directions for improvements in force fields. The perturbation sizes we examined − 0. 1e for charges, 0.3 Å for radii, and 0.04 kcal/mol for well depths ߝ are roughly proportional to the RMS difference between AMBER, CHARMM, and OPLSAA parameters in Table 1 (111%, 88%, and 111% respectively). With this rough normalization, 〈|ΔΔG_Bind|〉 for charge parameters is about twice as large as 〈|ΔΔG_Bind|〉 both van der Waals parameters (Figures 2 and 5). This suggests that charge parameters may be a larger source of inaccuracy. The significant sensitivity to charge parameters may result from an effective protein dielectric which is too low. We observed an effective protein dielectric near 2.5 in CCP and below 3 in Gyrase, while a dielectric of at least 2 is expected from electronic relaxation alone³². Adding explicit polarizability to force fields may help correct this, and a similar sensitivity analysis in a polarizable system would be especially informative regarding the effect of screening. Still, the true impact of the difference in charge parameters between protein force fields is likely smaller than would be expected from the RMS difference in parameters, due to the types of correlations shown in Figure 12, and correlations between σ and ε and between the van der Waals and charge parameters likely exist as well.

The variation between force fields in van der Waals parameters can also have an important impact on binding affinities. For example, CHARMM²⁴ and OPLSAA-2001²⁵ well depths are on average 0.009 kcal/mol (12%) and 0.004 kcal/mol (5%) smaller than AMBER²² well depths. Importantly, this average difference in epsilon will cause a systematic difference in affinities between the force fields, growing linearly with the number of atoms, because differences in epsilon consistently affect binding in the same direction (Figure 4). While this difference between force fields was calculated using amino acid parameters, we can still use our data examining sensitivity to ligand parameters to estimate the importance of this systematic difference. A change in well depth of 0.04 kcal/mol on a single ligand atom generally changes binding affinity by more than 0.2 kcal/mol (Figure 4). This suggests the well-depth difference between AMBER and CHARMM can easily cause a 1 kcal/mol difference in a system with 15 ligand atoms and only 15 relevant protein atoms, if the affinity is equally sensitive to both ligand parameters and protein parameters. For a ~100 atom compound like Indinavir, the difference could be 8 kcal/mol. Correlations between van der Waals parameters and electrostatic parameters could mitigate these effects, though similarly sized ligands can have different levels of polarity, making it difficult for these effects to compensate consistently.

4. Conclusion

We quantified the sensitivity of binding free energy calculations to ligand parameters by measuring ΔΔG_Bind for tens of thousands of small parameter perturbations. This quantitative measure of sensitivity can be used to interpret differences between force fields at computing the same compound’s binding affinity, and can also be used to gain chemical intuition into which properties of a molecule are most important for its affinity. ΔΔG_Bind in solution is 65% less sensitive to parameters than would be expected from vacuum calculations, but the $\sqrt{n}$ growth in random error in binding calculations may make affinities difficult to predict. This smaller sensitivity may contribute to the increased accuracy of free energy calculations compared with docking and scoring methods, and similar sensitivity analyses of other methods should be useful in examining this further. Based on our measured sensitivities, we calculated the tolerable random error in force field interaction parameters for large drug-sized or medium-sized lead compounds to be 0.01–0.02e per charge, 0.03–0.06 Å per radius, and 0.004–0.008 kcal/mol per well depth, which is significantly smaller than the variation in amino acid parameters in several commonly used protein force fields. We expect that theoretical and experimental studies in simplified binding sites will be critical toward achieving this level of accuracy, because the number of parameters contributing to affinity is already quite large even in these small systems.

Appendix: Methods

Free energy calculations

Software

All simulations of the protein-ligand complexes, the Gyrase ligands in solution, and all simulation reprocessing was performed using the FEP branch of the GROMACS 4.5⁴⁰ git repository, accessed after June 2011 and kindly provided by Michael Shirts. Simulations of the free CCP ligands in solution were performed using GROMACS 3.3.4.

Force fields

CCP and Gyrase were each parameterized using the AMBER99SB force field⁴¹. Ligands were parameterized using Generalized Amber Force Field (GAFF)^18,19 parameters generated using Antechamber 1.27, with AM1-BCC charges^20,21 generated using the OEChem toolkit version 1.5. Heme parameters and charges were taken from the Hemoglobin model in Amber 8, and an additional +1 charge was added to the iron to form Fe(III), as in Banci et al.⁴². The Fe-Nε bond between the Heme and His175 and the four Heme N-Fe-Nε angles were parameterized using force constants taken from Banci et al.⁴², with equilibrium lengths and angles generated based on averaging the existing crystal structures of CCP W191G, as in ref. 15 and ref. 43. Protonation states of titratable residues were selected using MCCE 2.2^44,45, with a reference pH of 4.5 for CCP (model 1KXN with the Heme removed) and pH 7.0 for Gyrase. Simulations were performed using the TIP3P water model.

Simulation parameters

All simulations (new and reprocessed existing simulations) were performed using Langevin dynamics at constant volume, a temperature of 300 K, inverse friction constant of 1.0 ps, and 2 fs step size. Lennard-Jones interactions were smoothly switched off after 8 Å and truncated at 9 Å. The neighborlist was set to 1 nm and updated every 10 steps. Electrostatic interactions were calculated using the particle-mesh Ewald (PME) method with tinfoil boundary conditions, a real space cutoff of 1 nm, a spline order of 6, a Fourier spacing of 1 Å, and a relative tolerance between long- and short-range energies of 10⁻⁶. Bonds to hydrogen were constrained using LINCS. Simulations of the free ligands in vacuum were performed using cut-off electrostatics with a 2 nm cut-off distance.

Equilibration of free ligands in solvent

Ligands were equilibrated in solvent using the protocol taken from ref. 46. Briefly, ligands were solvated in a truncated dodecahedral box with a 1.2 nm distance between the ligand and the box edge, energy minimized, and equilibrated for 10 ps at constant volume and 100 ps at constant pressure.

Equilibration of protein-ligand complexes

The CCP protein-ligand complexes were equilibrated using the protocol taken from ref. 15. Briefly, PDB structure 1KXN¹⁴ was solvated in a truncated dodecahedral box with a 1.2 nm distance between the protein and the box edge, along with 5 neutralizing Cl⁻ ions and an additional 100 mM ionic strength of NaCl. The solvent and ions were then equilibrated for 2 ns at constant volume while the protein coordinates were held fixed. The protein was then energy minimized and equilibrated for 2 ns as in ref. ⁴⁷. Each ligand was inserted into this equilibrated, solvated protein system in several conformations chosen by docking, and water molecules within 2.0 Å of the inserted ligand were removed, creating several separate systems for each ligand, each with an individual ligand pose. These systems were simulated for 1 ns each to identify metastable ligand poses using the method described in ref. 15, and additional 1 ns simulations were initiated from each metastable pose. These last simulations, in which the ligand remained in its metastable pose through the simulation, were reprocessed for this study.

The Gyrase protein-ligand complex coordinates were directly provided by Vertex Pharmaceuticals. Each complex was then solvated in a truncated dodecahedral box with 1.2 nm distance between the protein and the box edge, along with 9 neutralizing Na⁺ ions and no additional ionic strength. Following minimization of the protein and solvent, the system was equilibrated for 50 ps at constant volume and 200 ps at constant pressure. 1-ns production runs were then performed which were used here for re-analysis. Both ligands remained approximately in their starting orientations throughout these runs.

Reprocessing

All ΔΔG_Wat values were calculated using at least 1000 snapshots from a simulation of 1 ns or longer (longer simulations were used for ligands with more flexibility). All ΔΔG_Complex values for single perturbations were calculated using at least 100 snapshots from a simulation of 1 ns or longer, and ΔΔG_Complex values for double and triple perturbations were calculated using at least 1000 snapshots.

Poisson-Boltzmann calculations

PB calculations were performed using APBS 1.3⁴⁸ in a cubic box with 9.2 nm edge length, 0.575 Å grid spacing (161 grid points in each direction), and no ionic strength at 300 K. The linearized Poisson-Boltzmann equation was solved using the 4-level multigrid method, with multiple Debye-Huckel sphere boundary conditions, and a “molecular” surface definition with a 1.4 Å solvent probe and harmonic average smoothing. A total of 50 (CCP) or 200 (Gyrase) evenly spaced snapshots were taken from the MD trajectories used for reprocessing, stripped of all water residues and ions and analyzed with the ligand centered in the box. Optimal ε_int values were calculated based on interpolating calculations using ε_int values of 1, 2, 3, 4, 6, 8, 10, 12, 15, 20, 30, 40, and 80.