Bayesian semiparametric regression models for evaluating pathway effects on continuous and binary clinical outcomes

Abstract

Many statistical methods for microarray data analysis consider one gene at a time, and they may miss subtle changes at the single gene level. This limitation may be overcome by considering a set of genes simultaneously where the gene sets are derived from prior biological knowledge. Limited work has been carried out in the regression setting to study the effects of clinical covariates and expression levels of genes in a pathway either on a continuous or on a binary clinical outcome. Hence, we propose a Bayesian approach for identifying pathways related to both types of outcomes. We compare our Bayesian approaches with a likelihood-based approach that was developed by relating a least squares kernel machine for nonparametric pathway effect with a restricted maximum likelihood for variance components. Unlike the likelihood-based approach, the Bayesian approach allows us to directly estimate all parameters and pathway effects. It can incorporate prior knowledge into Bayesian hierarchical model formulation and makes inference by using the posterior samples without asymptotic theory. We consider several kernels (Gaussian, polynomial, and neural network kernels) to characterize gene expression effects in a pathway on clinical outcomes. Our simulation results suggest that the Bayesian approach has more accurate coverage probability than the likelihood-based approach, and this is especially so when the sample size is small compared with the number of genes being studied in a pathway. We demonstrate the usefulness of our approaches through its applications to a type II diabetes mellitus data set. Our approaches can also be applied to other settings where a large number of strongly correlated predictors are present.

1. Introduction

Many statistical methods have been developed to analyze microarray data based on single genes [1, 2]. However, these methods are not able to model the dependencies among genes when genes are analyzed marginally. Therefore, they may not be able to detect coordinated changes among a set of genes where each gene only shows modest changes. One way to address the limitation of single gene-based analysis is to analyze gene sets derived from prior biological knowledge to uncover patterns among the genes within a set. A number of methods and programs have been developed to consider gene groupings, for example, Gene Ontology [3]. These methods have been successful to detect subtle changes in expression levels, which could be missed using single gene-based analysis [4, 5]. Because each gene set is often associated with a certain biological function, such analyses may also help to generate biological hypotheses for follow-up studies. In our following discussion, we call a pathway as a predefined set of genes that serve a particular cellular or physiological function.

One motivating example of our methodology development is a type II diabetes study [4], where a microarray expression data from 22,283 genes were measured in 17 male patients with normal glucose tolerance and 18 male samples with type II diabetes mellitus. A pathway-based analysis revealed that a number of pathways were enriched for genes with different expression levels, which could not be detected using single gene-based analysis. Mootha et al. [4] used gene expression profile data to find pathways distinguishing between two groups. Incorporating continuous outcomes, such as glucose level, and incorporating clinical covariates, such as age, in a regression setting might more efficiently detect subtle differences in gene expression profiles. This is the focus of our paper, and we will consider both continuous and binary clinical outcomes.

A number of methods have been proposed to identify pathways relevant to a particular disease. Goeman et al. [6] proposed a global test derived from a random effects model. Gene Set Enrichment Analysis (GSEA) proposed by Subramanian et al. [7] examined the overall strength of top signals in a given pathway. Whereas global test and GSEA mainly focused on the detection of differentially expressed pathways associated with binary outcomes, a Random Forests approach proposed by Pang et al. [8] is applicable to both continuous and binary outcomes. Liu et al. [9] proposed a semiparametric regression model for pathway-based analysis. Whereas the pathway effects are included in a covariance matrix by Goeman et al. [6] and Liu et al. [9], the Bayesian approach proposed by Stingo et al. [10] modeled the pathway effects through a parametric mean function. In our study, we model the pathway effect through a covariance matrix of random variable by using Gaussian process under a semiparametric regression model.

Liu et al. [9] studied a single pathway with five genes on pre-surgery prostate-specific antigen level for prostate cancer with the following model:

$$Y=\mathbf{X}\mathit{\beta }+\mathbf{r}(\mathbf{Z})+\mathit{\epsilon },$$

where Y is an n × 1 vector denoting the continuous outcomes measured on the n subjects, X is an n × q matrix representing q clinical covariates of these subjects, β is a q × 1 vector of regression coefficients for the covariate effects, Z is a p × n matrix denoting the gene expression matrix for p genes (p ≫ n), z_i is the ith column vector of Z, r(Z) = {r(z₁), …, r(z_n)} ~ N(0, τK) with r(·) following a Gaussian process with mean 0 and covariance cov{r(z), r(z′)} = τK(z, z′), τ is an unknown positive parameter, K(·, ·) is a kernel function, which implicitly specifies a unique function space spanned by a particular set of orthogonal basis functions, K is an n × n matrix with the ijth component K(z_i, z_j), i, j = 1, …, n, and ε ~ N(0, σ²I). By connecting a least squares kernel machine [11] with a restricted maximum likelihood (REML), Liu et al. [9] estimated the nonparametric pathway effects of multiple gene expressions, r(Z) under a fixed model and variance component parameters under a linear mixed model. They derived score equations and information matrix of variance component parameters treating the estimated β̂ as if it was the true parameter. They also derived score test, which was performed using its asymptotic distribution, requiring a large sample. However, in practice, the sample size is typically small in many microarray studies. In addition, some of the variance components parameters were not identifiable in certain situations so that their approach was numerically unstable. These have motivated us to develop our Bayesian approach. In the rest of the paper, we refer the approach of Liu et al. as LLG’s approach.

The goals of our study were (i) to propose more flexible approaches for parameter inference and for incorporating prior information into analysis, (ii) to model covariance structure with different kernels, including the Gaussian, polynomial, and neural network kernels, and (iii) to propose a Bayesian inference for identifying significant pathways and ranking genes within a significant pathway. To achieve these goals, we propose to adopt a Bayesian approach, which is more flexible because it allows direct estimation of the parameters of variance components and the nonparametric pathway effects without connecting the least squares kernel machine estimates with REML. It is also easy to incorporate prior knowledge into Bayesian hierarchical modeling and analysis and to make inference by using the posterior samples.

We organize this article as follows. In Section 2, we briefly review LLG’s likelihood-based approach and provide the motivation of our Bayesian approach. In Section 3, we describe two Bayesian models to be developed: one for continuous outcomes and the other for binary outcomes. In Section 4, we propose to use the Bayes factor (BF) as well as resampling to identify significant pathways and to rank important genes within a significant pathway. In Section 5, we consider kernel selection as a model selection problem within the kernel machine framework and use the BF for kernel selection. In Section 6, we report the simulation results comparing our Bayesian approach with LLG’s likelihood-based approach. In Section 7, we apply our method to the type II diabetes data set analyzed by Mootha et al. [4]. Section 8 contains concluding remarks.

2. Likelihood-based approach

In this section, we briefly review LLG’s approach and provide the motivation to our Bayesian approaches. Because Liu et al. [9] developed their approach for continuous outcomes, we first start with Y as a continuous outcome and then further discuss binary outcomes in Section 3.

Liu et al. [9] proposed a likelihood-based approach by connecting a least squares kernel machine under a fixed nonparametric model with an REML under a linear mixed model. They estimated the β and r(·) by maximizing the scaled penalized likelihood function with smoothing parameter λ

$$L\{\mathit{\beta },\text{r}(·)\}=-\frac{1}{2}\sum _{i=1}^n{\{y_i-{\mathbf{x}}_i\mathit{\beta }-\text{r}({\mathbf{z}}_i)\}}^2-\frac{1}{2}\lambda {\left|\right|\mathbf{r}\left|\right|}^2.$$

By using the dual formulation [11] to reduce the high-dimensional problem into a low-dimensional one, they estimated parameters β and r(·), β̂ = {X^T (I + λ⁻¹K)⁻¹X}⁻¹X^T (I + λ⁻¹K)⁻¹y and r̂ = λ⁻¹K(I + λ⁻¹K)⁻¹ (y − Xβ̂).

For estimating variance components parameters, Liu et al. [9] used a linear mixed model formulation with the assumption that the nonparametric function r(·) follows a Gaussian process with mean 0 and covariance cov{r(z), r(z′)} = τK(z, z′) = τ exp(−||z − z′||²/ρ), where ρ is an unknown positive scale parameter. With the use of the marginal distribution of y ~ N(Xβ, Σ), the regression coefficient estimator β̂ can be also obtained from the weighted least squares estimator β̂ = (X^T Σ⁻¹X)⁻¹X^T Σ⁻¹Y, where Σ = σ²I + τK.

The variance components parameters, Θ = (τ, ρ, σ²), can be estimated through the REML, a commonly used approach for estimating variance components in a linear mixed model, and the smoothing parameter can be obtained from λ = τ⁻¹σ². Their REML is

$$l_1(\mathrm{\Theta })=-\frac{1}{2}{(\mathbf{y}-\mathbf{X}\widehat{\mathit{\beta }})}^T{\mathrm{\sum }}^{-1}(\mathbf{y}-\mathbf{X}\widehat{\mathit{\beta }})-\frac{1}{2}log\mid {\mathbf{X}}^T{\mathrm{\sum }}^{-1}\mathbf{X}\mid -\frac{1}{2}log\mid \mathrm{\sum }\mid ,$$

and they derived the score equations and information matrix of Θ = (τ, ρ, σ²) at given β̂. They used the Newton–Raphson method to estimate Θ and derived the score test to make an inference.

In our simulations and real data analysis, we found that this approach was numerically unstable. It was especially difficult to obtain joint convergence for both τ and ρ. This is because the Fisher information matrix and the asymptotic distributions of τ̂ and ρ̂ are the same and are degenerated when ρ → 0 and τ → 0. We provide a more detailed explanation in Supplementary Material A.^‡ In addition, ρ and τ are not identifiable under one of the following conditions: (i) τ → 0, (ii) ρ → 0 and $\tau ~O(\frac{1}{{\rho }^m})$ for any positive m, or (iii) $\frac{1}{\rho }\to 0$. This is because of the marginal distribution of Y, f (Y|τ) = f (Y|ρ) ~ N(0, σ²I) under conditions (i) and (ii) and f (Y|τ) = f (Y|ρ) ~ N(0, σ²I + τJ) under condition (iii). A simple way to avoid this problem is to estimate ρ by using a grid search within a specified range. However, find-ing this pre-specified range is nontrivial in practice. In addition, because the score test derived by Liu et al. [9] relies on the asymptotic distribution, thus requiring a large sample, it may not be appropriate for microarray data, which typically have small sample size.

To overcome the limitations of this likelihood-based approach, we propose a Bayesian hierarchical modeling approach, which is more flexible and stable. Our Bayesian approach can allow direct estimation of the parameters of variance components and the nonparametric pathway effects without connecting the least squares kernel machine estimates with REML. It is also easy to incorporate prior knowledge into modeling and to make inference by using the posterior samples for both small and large sample size cases.

3. Bayesian approach

In this section, we develop two Bayesian models based on Bayesian hierarchical model formulations. One is for continuous outcomes, and the other is for binary outcomes.

3.1. Bayesian hierarchical model for continuous outcome

We start with a Bayesian hierarchical model formulation:

$$\begin{array}{l}[Y\mid \mathbf{X},\text{r}(\mathbf{Z})]~N\{\mathbf{X}\mathit{\beta }+\text{r}(\mathbf{Z}),{\sigma }^{2}I\},\\ \text{r}(\mathbf{z})~\text{GP}\{0,\tau K(\mathbf{z},{\mathbf{z}}^{\prime })\},\\ \tau ~\text{IG}(a_{\tau },1/b_{\tau }),\end{array}$$ (1)

where r(Z) = {r(z₁), r(z₂), …, r(z_n)} ≡ r and K is an n × n matrix with the ijth component K(z_i, z_j), i, j = 1, …, n. We consider the following kernels for K(·, ·):

• the dth-order polynomial kernel, K(z, z′) = (zz′ + c)^d, d = 1, 2, where c = 0 if d = 1 and c = 1 if d = 2;

• the Gaussian kernel, $K(\mathbf{z},{\mathbf{z}}^{\prime })=exp(-\frac{{\left|\right|\mathbf{z}-{\mathbf{z}}^{\prime }\left|\right|}^2}{\rho })$, where ${\left|\right|\mathbf{z}-{\mathbf{z}}^{\prime }\left|\right|}^2={\sum }_{k=1}^p{(z_k-z_k^{\prime })}^2$ and ρ is an unknown scale parameter;

• the neural network kernel, K(z, z′) = tanh(z · z′).

For all these kernels, if two samples have ‘similar’ expression profiles for genes in a pathway, this pathway has similar effects on their clinical outcomes. However, their ‘similarity’ is measured differently through different kernels. Their similarity in the Gaussian kernel is measured using the Euclidean distance between z_i and z_j. The smaller the distance, the higher the similarity. The polynomial kernel quantifies similarity through inner product. The neural network kernel uses the hyperbolic tangent (tanh) function to quantify similarity.

The parameters of interest are (β, σ, r, τ, ρ). We assumed that these parameters have the following prior distributions: β ~ N(0, Σ_β), σ² ~ IG(a_σ², b_σ²), r ~ N(0, τK), τ ~ IG(a_τ, 1/b_τ), and ρ ~ Unif[C₁, C₂], where ${\mathrm{\sum }}_{\beta }={\sigma }_{\beta }^{2}I$ with a fixed large value ${\sigma }_{\beta }^2$, fixed values a_σ², b_σ², for hyperprior of σ², and a fixed positive small value C₁ and large value C₂ with the assumption C₂ ~ O {E(||z − z′||²)}. In our analysis, we chose the prior parameters to be proper but vague, with ${\sigma }_{\beta }^2=100$, a_σ² = 2.01, b_σ² = 1, a_τ = 2.0001, b_τ = 10, C₁ = 10⁻⁵, C₂ = 10 × E(||z − z′||). We varied the values of hyperpriors somewhat, with minor changes in the results. We further discuss the sensitivity to prior and proposal distributions in Section 7.1.

Let Ψ denote the vector of all the parameters. Under the Gaussian kernel, Ψ = (β, σ², r, τ, ρ), and for other kernels, Ψ = (β, σ², r, τ). The conditional distribution of (y, r) and the marginal distribution of y are

$$\begin{array}{l}[\mathbf{y}\mid \mathbf{X},\mathbf{Z},\mathbf{r},\mathrm{\Psi }][\mathbf{r}\mid \mathrm{\Psi }]~\frac{1}{{(2\pi )}^n{({\sigma }^2)}^{n/2}{\tau }^{n/2}\mid \mathbf{K}\mid }exp\{-\frac{{(\mathbf{y}-\mathbf{X}\mathit{\beta }-\mathbf{r})}^T(\mathbf{y}-\mathbf{X}\mathit{\beta }-\mathbf{r})}{2{\sigma }^2}\}exp\{-\frac{{\mathbf{r}}^T{\mathbf{K}}^{-1}\mathbf{r}}{2\tau }\},\\ [\mathbf{y}\mid \mathbf{X},\mathbf{Z},\mathrm{\Psi }]~N(\mathbf{X}\mathit{\beta },\mathrm{\sum }).\end{array}$$

The complete conditional distributions of ‰ under the Gaussian kernel are

$$\begin{array}{l}[\mathit{\beta }\mid \mathbf{y},\mathbf{X},\mathbf{Z},\mathbf{r},{\sigma }^2,\tau ,\rho ]~N\{{\sigma }^{-2}{({\mathrm{\sum }}_{\beta }^{-1}+{\sigma }^{-2}{\mathbf{X}}^T\mathbf{X})}^{-1}{\mathbf{X}}^T(\mathbf{y}-\mathbf{r}),{({\mathrm{\sum }}_{\beta }^{-1}+{\sigma }^{-2}{\mathbf{X}}^T\mathbf{X})}^{-1}\},\\ [{\sigma }^2\mid \mathbf{y},\mathbf{X},\mathbf{Z},\mathbf{r},\mathit{\beta },\tau ,\rho ]~\text{IG}[\frac{n}{2}+a_{{\sigma }^2},\frac{{\{\mathbf{y}-(\mathbf{X}\mathit{\beta }+\mathbf{r})\}}^T\{\mathbf{y}-(\mathbf{X}\mathit{\beta }+\mathbf{r})\}}{2}+b_{{\sigma }^2}],\\ [\mathbf{r}\mid \mathbf{y},\mathbf{X},\mathbf{Z},\mathit{\beta },{\sigma }^2,\tau ,\rho ]~N[{\sigma }^{-2}{\{{(\tau \mathbf{K})}^{-1}+{\sigma }^{-2}I\}}^{-1}(\mathbf{y}-\mathbf{X}\mathit{\beta }),{\{{(\tau \mathbf{K})}^{-1}+{\sigma }^{-2}I\}}^{-1}],\\ [\tau \mid \mathbf{y},\mathbf{X},\mathbf{Z},\mathbf{r},\mathit{\beta },{\sigma }^2,\rho ]~\text{IG}[\frac{n}{2}+a_{\tau },{\{\frac{{\mathbf{r}}^T\mathbf{K}{(\rho )}^{-1}\mathbf{r}}{2}+b_{\tau }\}}^{-1}],\\ [\rho \mid \mathbf{y},\mathbf{X},\mathbf{Z},\mathbf{r},\mathit{\beta },{\sigma }^2,\tau ]\propto \frac{1}{{(2\pi )}^{n/2}{\mid \tau \mathbf{K}(\rho )\mid }^{1/2}}exp\{-\frac{{\mathbf{r}}^T\mathbf{K}{(\rho )}^{-1}\mathbf{r}}{2\tau }\}.\end{array}$$

We draw samples from the joint posterior distribution [Ψ|y, X, Z] by using MCMC.

• We can sample β and σ² from their complete conditional distributions by using Gibbs sampling.

• For τ and r, we use the Metropolis–Hastings (MH) algorithm because K is sometimes a singular matrix so that we cannot obtain K⁻¹.

  • If K is nonsingular, we can directly sample from their complete conditional distributions.

  • Otherwise, we sample [r|rest] from the MH algorithm with the proposal distribution N(σ⁻² ([τ{δI + K(ρ)}]⁻¹ + σ⁻² I)⁻¹ (y − Xβ), ([τ{δI + K(ρ)}]⁻¹ + σ⁻² I)⁻¹ with small value of δ following the uniform distribution within a small range, for example, δ ∈ [0.0001, 0.01].

  • We also sample [τ|rest] from the MH algorithm with the proposal distribution $\text{IG}[\frac{n}{2}+a_{\tau },\frac{{\mathbf{r}}^T{\{\delta I+\mathbf{K}(\rho )\}}^{-1}\mathbf{r}}{2}+b_{\tau }]$ with small value of δ following the uniform distribution within a small range.

• Because the full conditional distribution for ρ does not have a closed form, we sample [ρ|rest] from the MH algorithm. We derive the proposal distribution in the following way. Let $S={\sum }_{i=1}^n\text{r}({\mathbf{z}}_i)\text{r}{({\mathbf{z}}_i)}^{\prime }$ and then S ~ W_n{1, τ K(ρ)} is a Wishart distribution with n degrees of freedom. Let L_n×1 = (1, …, 1)^T. The $L^{\prime }SL={\sum }_{i=1}^n{\sum }_{j=1}^n\text{r}({\mathbf{z}}_i)\text{r}({\mathbf{z}}_j)~{\sigma }_L^2{\chi }_n^2$, where ${\sigma }_L^2=L^{\prime }\tau \mathbf{K}(\rho )L=\tau {\sum }_{i=1}^n{\sum }_{j=1}^{n}K(i,j\mid \rho )$. Therefore, we have

  $$\begin{array}{l}\frac{{\sum }_{i=1}^n{\sum }_{j=1}^n\text{r}({\mathbf{z}}_i)\text{r}({\mathbf{z}}_j)}{\tau {\sum }_{i=1}^n{\sum }_{j=1}^{n}K(i,j\mid \rho )}~{\chi }_n^2=\text{Gamma}\left(\frac{n}{2},2\right),\\ \frac{1}{{\sum }_{i=1}^n{\sum }_{i=1}^{n}K(i,j,\mid \rho )}~\text{Gamma}\{\frac{n}{2},\frac{2\tau }{{\sum }_{i=1}^n{\sum }_{j=1}^n\text{r}({\mathbf{z}}_i)\text{r}({\mathbf{z}}_j)}\},\\ \sum _{i=1}^n\sum _{j=1}^{n}K(i,j,\mid \rho )~\text{IG}\{\frac{n}{2},\frac{1}{(\frac{2\tau }{{\sum }_{i=1}^n{\sum }_{j=1}^n\text{r}({\mathbf{z}}_i)\text{r}({\mathbf{z}}_j)})}\}.\end{array}$$

Let $k^{\ast }~\text{IG}[\frac{n}{2},{\{\frac{2\tau }{{\sum }_i^n{\sum }_j^n\text{r}({\mathbf{z}}_i)\text{r}({\mathbf{z}}_j)}\}}^{-1}]$ and then set ${\sum }_{i=1}^n{\sum }_{j=1}^{n}exp(-\frac{a_{ij}}{\rho })=k^{\ast }$, where $a_{ij}={\sum }_{k=1}^p{(z_{ik}-z_{jk})}^2$. Then ${\rho }_{\text{prop}}=\frac{{\sum }_{i=1}^n{\sum }_{j=1}^n{a}_{ij}}{n^2-k^{\ast }}$ if $\frac{{\sum }_{i=1}^n{\sum }_{j=1}^n{a}_{ij}}{\rho }\ll n^2$. If $\frac{{\sum }_{i=1}^n{\sum }_{j=1}^n{a}_{ij}}{\rho }\gg n^2$, then we ignore some terms such that $\frac{a_{ij}}{\rho }\gg 1$ because $exp(-\frac{a_{ij}}{\rho })\ll 1$. Therefore, if a_ij is defined as ${\sum }_{k=1}^p{(z_{ik}-z_{jk})}^2$, the proposal distribution of ρ_prop is

$$\frac{b_k^{a_k}}{\gamma (a_k)}{\left(n^2-\frac{{\sum }_{i=1}^n{\sum }_{j=1}^n{a}_{ij}}{{\rho }_{\text{prop}}}\right)}^{-a_k-1}exp\left\{-\frac{b_k}{n^2-(\frac{{\sum }_i^n{\sum }_j^n{a}_{ij}}{{\rho }_{\text{prop}}})}\right\}\sum _i^n\sum _j^n{a}_{ij},$$

where a_k = n/2 and $b_k={\{\frac{2\tau }{{\sum }_i^n{\sum }_j^n\text{r}(z_i)\text{r}(z_j)}\}}^{-1}$.

For other kernels, K does not depend on ρ. The complete conditional distributions of β, σ², r, and τ are the same as those of the Gaussian kernel.

Another hierarchical model that we consider is under the same setting of the previous model (1) except for using the following mixture model:

$$\text{r}(\mathbf{z})~\pi \text{GP}\{0,\tau K(\mathbf{z},{\mathbf{z}}^{\prime })\}+(1-\pi ){\delta }_0(\text{r}),$$ (2)

where δ₀(r) represents the point mass density at zero and π ∈ [0, 1]. With an additional prior for π, for example, uniform prior π ~ Unif[0, 1] or beta prior π ~ B(a_π, b_π), the samples from the joint posterior distribution are drawn using the MH algorithm in a similar way, which we explain using previous model. In many single gene-based analyses, many genes do not play an important role in differentiating the disease and non-disease groups. Similarly, in pathway analysis, we expect that many pathways are not involved. This mixture prior might be useful to incorporate such characteristics in the analysis. For prior knowledge to be incorporated into our Bayesian analysis, the prior of π can be established from historical knowledge. We can choose the beta distribution, B(a_π, b_π), for the prior of π. We can select hyperpriors a_π and b_π to have large mean value, for example, 0.7, and variance as 2 × mean value for pathways identified by Mootha et al. [4], whereas for pathways that were not identified, we choose small mean value, for example, 0.3, and variance as 2 × mean value. Laud and Ibrahim [12] used such informative prior elicitation.

3.2. Bayesian hierarchical latent model for binary outcome

Let Y_i be the binary response variable, i = 1, …, n. Let Y_i = 1 denote that sample i has one phenotype, for example, diseased, and Y_i = 0 denote that sample i has the other phenotype, for example, normal. The Bayesian hierarchical model with a binary outcome Y, a clinical covariate X, and a gene expression matrix Z is

$$\begin{array}{l}Pr\{Y=1\mid \mathbf{X},\mathbf{r}(\mathbf{Z})\}=\mathrm{\Phi }\{\mathbf{X}\mathit{\beta }+\mathbf{r}(\mathbf{Z})\},\\ \mathbf{r}(\mathbf{Z})~N\{\mathbf{0},\tau \mathbf{K}(\mathbf{Z})\},\\ \tau ~\text{IG}({\alpha }_{\tau },1/b_{\tau }),\end{array}$$ (3)

where Φ (·) is the standard normal cumulative density function. On the basis of the work of Albert and Chib [13], we define latent variables T = (T₁, T₂, …, T_n)^T with T ~ N {Xβ + r(Z), I} such that Y_i = 1 if T_i ≥ 0 and Y_i = 0 if T_i < 0, where Pr{T_i ≥ 0|x_i, r(z_i)} = Pr{Y_i = 1|x_i, r(z_i)} and Pr{T_i < 0|x_i, r(z_i)} = 1 − Pr{T_i ≥ 0|x_i, r(z_i)}. On the basis of this setting, we can derive the joint posterior distribution as

$$[T,\mathit{\beta },\mathbf{r},\tau \mid \mathbf{y},\mathbf{X},\mathbf{Z}]\propto \prod _{i=1}^n(I_{T_i\ge 0}{I}_{y_i=1}+I_{T_i<0}{I}_{y_i=0})\times \prod _{i=1}^{n}N(T_i;{\mathbf{x}}_i\mathit{\beta }+{\text{r}}_i,1)\times N\{\mathbf{r};\mathbf{0},\tau \mathbf{K}(\mathbf{Z})\}\times \text{Gamma}({\tau }^{-1};a_{\tau },b_{\tau })\times N(\mathit{\beta };0,{\mathrm{\sum }}_{\beta }^{-1}),$$

where I_(A) is an indicator function, which is equal to 1 if A is true and is equal to 0 otherwise. This Bayesian hierarchal latent model allows us to have closed forms of the full conditional distributions for (T_i, β, r, τ) except for ρ under the Gaussian kernel as follows:

$$\begin{array}{l}[T_i\mid y_i=0,\mathit{\beta },{\text{r}}_i,\tau ,\rho ]\propto I_{T_i<0}{I}_{y_i=0}N(T_i;{\mathbf{x}}_i\mathit{\beta }+{\text{r}}_i,1),\\ [T_i\mid y_i=1,\mathit{\beta },{\text{r}}_i,\tau ,\rho ]\propto I_{T_i\ge 0}{I}_{y_i=1}N(T_i;{\mathbf{x}}_i\mathit{\beta }+{\text{r}}_i,1),\\ [\mathit{\beta }\mid T,\mathbf{r},\tau ,\rho ]~N\{{({\mathrm{\sum }}_{\beta }^{-1}+{\mathbf{X}}^T\mathbf{X})}^{-1}{\mathbf{X}}^T(T-\mathbf{r}),{({\mathrm{\sum }}_{\mathit{\beta }}^{-1}+{\mathbf{X}}^T\mathbf{X})}^{-1}\},\\ [\mathbf{r}\mid T,\mathit{\beta },\tau ,\rho ]\propto \text{MN}({[\mathbf{I}+{\{\tau \mathbf{K}(\mathbf{Z})\}}^{-1}]}^{-1}(T-\mathbf{X}\mathit{\beta }),{[\mathbf{I}+{\{\tau \mathbf{K}(\mathbf{Z})\}}^{-1}]}^{-1}),\\ [\tau \mid T,\mathit{\beta },\mathbf{r},\rho ]\propto \text{IG}\left[a+\frac{n}{2},{\{b+\frac{1}{2}{\mathbf{r}}^T{\{\mathbf{K}(\mathbf{Z})\}}^{-1}\mathbf{r}\}}^{-1}\right],\\ [\rho \mid T,\mathit{\beta },\mathbf{r},\tau ,\rho ]\propto \frac{1}{{(2\pi )}^{n/2}{\mid \tau \mathbf{K}(\rho )\mid }^{1/2}}exp\{-\frac{{\mathbf{r}}^T\mathbf{K}{(\rho )}^{-1}\mathbf{r}}{2\tau }\}.\end{array}$$

The full conditional distributions for T_i are truncated normal distribution. Because the full conditional distributions for all parameters except for ρ have closed forms, we sample from the joint posterior distributions by using MH algorithm and Gibbs sampling.

Another hierarchical latent model is the use of the mixture model (2) under the same setting of the Bayesian hierarchal latent model (3). We can draw the samples from the joint posterior distribution by using the MH algorithm and the Gibbs sampling in a similar way.

4. Identifying significant pathways and ranking genes within a significant pathway

With the Gaussian kernel, the null hypothesis H₀: {r(Z) is a point mass at zero} ∪ {r(Z) has a constant covariance matrix as a function of Z} is equivalent to $H_0:\frac{\tau }{\rho }=0$ or ρ = 0. We provide the proof of this equivalence in Supplementary Material B. For the polynomial and neural network kernels, we test H₀ : τ = 0.

4.1. Identifying significant pathways

We make an inference based on two approaches: one is a Bayesian inference by using the BF, and the other is a resampling-based inference.

4.1.1. Bayesian inference

We estimate the BF in favor of the alternative hypothesis H₁ versus the null hypothesis H₀ as follows:

$$\text{BF}=\frac{m_1(\mathbf{y})}{m_0(\mathbf{y})}=\frac{\int f(\mathbf{y}\mid {\mathit{\theta }}_1,H_1)\pi ({\mathit{\theta }}_1\mid H_1)\text{d}{\mathit{\theta }}_1}{\int f(\mathbf{y}\mid {\mathit{\theta }}_0,H_0)\pi ({\mathit{\theta }}_0\mid H_0)\text{d}{\mathit{\theta }}_0},$$

where f (y|θ_l, H_l) is the density function of data y under H_l given the model-specific parameter vector θ_l, l = 0, 1, and π (θ_l|H_l) is the prior density of θ_l. Using the approach proposed by Newton and Raftery [14], we estimate m̄_l (y):

$${\widehat{m}}_l(\mathbf{y})={\left\{\frac{1}{S}\sum _{s=1}^S\left(\frac{1}{f(y\mid {\mathit{\theta }}_l^{(s)},H_l)}\right)\right\}}^{-1}$$

where $\{{\mathit{\theta }}_l^s\}\equiv \{{\mathit{\theta }}_l^1,\dots ,{\mathit{\theta }}_l^S\}$ are S draws from the posterior density π (θ_l|y, H_l)obtained using an MCMC method.

Large values of the BF are in favor of H₁. This means that the data indicate that H₁ is more strongly supported by the data under consideration than H₀. Following Jeffreys’s [15] suggestion, we interpret the value of the BF as weak favor if BF ≤ 3, positive favor if 3 < BF ≤ 12, strong favor if 12 < BF ≤ 150, and decisive favor if BF > 150. This Bayesian inference is applicable for both continuous and binary outcomes.

4.1.2. Resampling-based inference

In addition to using the BF, we also use the following simulation procedure to test statistical significance with continuous and binary outcomes, respectively.

Continuous outcomes

Under the Gaussian kernel, we first estimate τ/ρ, ρ, τ by using the observed data by fitting the semiparametric model and calculate the residuals ε̂_0i from y_i = x_i β + ε_0i. We then permute the residual ${\widehat{\epsilon }}_{0i}^{\ast }$ and simulate outcomes as $y_i^{\ast }=x_i\widehat{\beta }+{\widehat{\epsilon }}_{0i}^{\ast }$. On the basis of y^*, x, and z, we fit the semiparametric model by using either the likelihood-based approach or the Bayesian approach and then estimate τ̂^*/ρ̂^*, ρ̂^*, and τ̂^*.

For each pathway, we estimate the statistical significance by the percentage of times either τ̂^*/ρ̂^* > τ̂/ρ̂ or ρ̂^* > ρ̂, where τ̂/ρ̂, ρ̂, τ̂ are the estimated values from the observed data. We can select sig-nificant pathways based on this percentage by using the empirical distribution of test statistics. For the polynomial and neural network kernels, we use a similar procedure by estimating τ.

Binary outcomes

The only difference for a binary outcome is to use the Bayesian hierarchical latent model (3). Under the polynomial and neural network kernels, we first estimate τ by using the observed data by fitting model (3). We then generate $y_i^{\ast }$ by using Pr(Y_i = 1|X_i). On the basis of y^*, x, and z, we fit the Bayesian hierarchical latent model and estimate τ̂^*. We then estimate the statistical significance by the percentage of times τ̂^*> τ̂.

4.2. Ranking genes within a significant pathway

Continuous outcomes

To rank the importance of genes and gene pairs within a significant pathway related to a clinical outcome, we consider the following models:

• a semiparametric mixed model based on all genes except the gth gene,

  $$Y=\mathbf{X}\mathit{\beta }+\mathbf{r}\{{\mathbf{Z}}_{-(g)}\}+\epsilon ;$$ (4)
• a semiparametric mixed model based on all genes except the gth and g′th genes,

  $$Y=\mathbf{X}\mathit{\beta }+\mathbf{r}\{{\mathbf{Z}}_{-(g,g^{\prime })}\}+\epsilon .$$ (5)

For the Bayesian approach, we use the posterior samples of parameters after burn-in time, ${\widehat{\tau }}_{\text{Bay},(-g)}^s,{\widehat{\rho }}_{\text{Bay},(-g)}^s$, and ${(\widehat{\tau }/\widehat{\rho })}_{\text{Bay},(-g)}^s$ by fitting model (4), where s = 1, …, S, for example, S = 5, 000. Then we calculate the absolute value of difference, $\mid {\widehat{\tau }}_{\text{Bay},(-g)}^s-\widehat{\tau }\mid ,\mid {\widehat{\rho }}_{\text{Bay},(-g)}^s-\widehat{\rho }\mid$, and $\mid {(\frac{\widehat{\tau }}{\widehat{\rho }})}_{\text{Bay},(-g)}^s-(\frac{\widehat{\tau }}{\widehat{\rho }})\mid$, under the Gaussian kernel. For the other kernels, we only need to calculate the absolute value of difference $\mid {\widehat{\tau }}_{\text{Bay},(-g)}^s-\widehat{\tau }\mid$. We rank the importance of the genes by the mean absolute difference, $\frac{1}{S}{\sum }_{s=1}^S\mid {\widehat{\tau }}_{\text{Bay},(-g)}^s-\widehat{\tau }\mid$. If a gene plays an importance role in a pathway, then this difference will be large. To study the importance of gene pairs, we perform the same procedure based on model (5) by calculating $\mid {\widehat{\tau }}_{\text{Bay},-(g,g^{\prime })}^s-\widehat{\tau }\mid ,\mid {\widehat{\rho }}_{\text{Bay},-(g,g^{\prime })}^s-\widehat{\rho }\mid$, and $\mid {(\frac{\widehat{\tau }}{\widehat{\rho }})}_{\text{Bay},-(g,g^{\prime })}^s-(\frac{\widehat{\tau }}{\widehat{\rho }})\mid$ under the Gaussian kernel. For the other kernels, we obtain only $\mid {\widehat{\tau }}_{\text{Bay},-(g,g^{\prime })}^s-\widehat{\tau }\mid$. We can rank the top gene pairs by the absolute difference.

For the likelihood-based approach, we can bootstrap the samples B times. For each bootstrapped sample, we estimate ${\widehat{\tau }}_{(-g)}^b,{\widehat{\rho }}_{(-g)}^b$, and ${(\widehat{\tau }/\widehat{\rho })}_{(-g)}^b$ by fitting model (4), where b = 1, …, B. We calculate the absolute value of difference in a similar way.

Binary outcomes

To rank the importance of genes and gene pairs within a significant pathway related to a binary outcome, we fit the Bayesian hierarchical latent model (3) after removing one gene or two genes at a time. We perform a similar procedure as previously mentioned to calculate the absolute value of difference.

5. Kernel selection

We have considered four kernels to model the covariance matrix of pathway effects. A question in practice is how to choose the kernel appropriately. Little work has been carried out in this area in the literature.

We consider kernel selection as a model selection problem within the kernel machine framework. We estimate the BF in favor of kernel K_i versus kernel K_j as follows:

$${\text{BF}}_K=\frac{m_{K_i}(\mathbf{y})}{m_{K_j}(\mathbf{y})}=\frac{\int f(\mathbf{y}\mid {\mathit{\theta }}_i,K_i)\pi ({\mathit{\theta }}_i\mid K_i)\text{d}{\mathit{\theta }}_i}{\int f(\mathbf{y}\mid {\mathit{\theta }}_j,K_j)\pi ({\mathit{\theta }}_j\mid K_j)\text{d}{\mathit{\theta }}_j}.$$

Similarly, we define f (y|θ_l, K_l) to be the density function of data y under kernel K_l given the model-specific parameter vector θ_l, l = i, j, and π (θ_l|K_l) to be the prior density of θ_l. We then estimate m̂_Kl(y):

$${\widehat{m}}_{K_l}(\mathbf{y})={\left\{\frac{1}{S}\sum _{s=1}^S\left(\frac{1}{f(\mathbf{y}\mid {\mathit{\theta }}_l^{(s)},K_l)}\right)\right\}}^{-1},$$

where $\{{\mathit{\theta }}_l^s\}\equiv \{{\mathit{\theta }}_l^1,\dots ,{\mathit{\theta }}_l^S\}$ are S draws from the posterior density π (θ_l|y, K_l) obtained using an MCMC method [14]. We interpret a large value of BF_K as in favor of kernel K_i.

6. Simulation studies

We conducted simulations to compare LLG’s likelihood approach [9] and our Bayesian approach. In our simulations, we consider both continuous and binary outcomes.

6.1. Continuous outcomes

For the assessment of type I error, we considered the following Case 0 and simulated 1000 data sets with two sets of n and p values. One set is (n, p) = (60, 5) with a relatively large sample size compared with the number of genes, and the other set is (n, p) = (60, 200) with a relatively small sample size compared with the number of genes.

• Case 0: y_0i = βx_i + ε_i with β = 1, x_i = 3 cos(π/6) + 2u_i with u_i ~ N(0, 1) and ε_i ~ N(0, σ²)

Using these y₀, x, and any z generated in Cases 1–5, which are explained in the succeeding text, we estimated the type I error rate by the proportion of samples having p-values smaller or equal to the 0.05 cutoff.

For power, we considered the following five cases and simulated 1000 data sets with the same two sets of n and p values discussed previously.

• Case 1: y_i = βx_i + r(z_i1, z_i2, …, z_ip) + ε_i with β = 1, x_i = 3 cos(z_i1) + 2u_i with u_i being independent of z_i1 and following N(0, 1), z_ij ~ Uniform(0, 1), and $\text{r}(\mathbf{z})=10cos(z_1)-15z_2^2+10exp(-z_3)z_4-8sin(z_5)cos(z_3)+20z_1{z}_2$.

• Case 2: the same setting as that of Case 1 except that the true r(z) ~ GP{0, τK_g(ρ)}, where K_g(ρ) (z, z′) = exp(−||z − z′||²/ρ).

• Case 3: the same setting as that of Case 1 except that r(z) ~ GP(0, τK_p2), where K_p2(z, z′) = (zz′ + 1)².

• Case 4: the same setting as that of Case 1 except that r(z) ~ GP(0, τK_p1), where K_p1(z, z′) = (zz′)¹.

• Case 5: the same setting as that of Case 1 except that the r(z) was generated using simulator within the boost R package [16]; this simulator allows us to retain the pathway correlation structure from real data. We chose for this case a pathway, Oxidative phosphorylation, from Mootha et al. [4] with the most significant.

We consider Case 1 because the nonparametric function r(z_i1, z_i2, …, z_ip) is allowed to have a complex form with nonlinear functions of the z’s and interactions among the z’s. It allows for x_i and (z_i1, …, z_ip) to be correlated. It also compares how two approaches detect unknown pathway effects. We choose Cases 2–4 to investigate how accurately the two approaches capture pathways effects under different kernels. We consider Case 5 to study more realistic settings.

For each case, we fitted the semiparametric regression model by using LLG’s likelihood-based approach and our Bayesian approach. We considered both the Gaussian kernel and the polynomial kernel with d = 1, 2. We made an inference based on both resampling-based method as well as using the BF with a cutoff value of 150 in favor of H₁. We summarize the estimated type I error and power in Table I. We calculated the power at the 0.05 significance level as well as the BF larger than 150. We also calculated the standard deviations of the estimated type I error and power. Because their standard deviations are similar among different kernels, we listed their standard deviations when the Gaussian kernel was considered in Supplementary Material Table 1. We also calculated the mean squared error (MSE) of the parameter estimates as well as the coverage probabilities. We show the MSEs and the coverage probabilities for Cases 2–4 in Table II and summarize the parameter estimates for Cases 2–4 in Supplementary Material Tables 2–4.

Table I.

Estimated type I error rate and power on a continuous clinical outcome.

		Case	GK			Kernel (K) P2K			P1K
			LIKE	BHM	BHM (BF)	LIKE	BHM	BHM (BF)	LIKE	BHM	BHM (BF)
n = 60 p = 5	Type I Power	0	0.04	0.04	0.05	0.04	0.04	0.05	0.04	0.04	0.05
		1	0.99	0.99	1	0.97	0.98	1	0.97	0.98	1
		2	0.90	0.94	0.97	0.85	0.86	0.89	0.65	0.66	0.70
		3	0.86	0.89	0.91	0.91	0.93	0.95	0.86	0.87	0.89
		4	0.84	0.86	0.89	0.77	0.80	0.82	0.92	0.93	0.95
		5	0.77	0.78	0.81	0.73	0.74	0.78	0.72	0.73	0.77
n = 60 p = 200	Type I Power	0	0.03	0.03	0.04	0.03	0.03	0.04	0.03	0.03	0.04
		1	0.84	0.85	0.89	0.83	0.85	0.89	0.82	0.83	0.87
		2	0.81	0.82	0.87	0.74	0.77	0.81	0.56	0.60	0.61
		3	0.77	0.79	0.81	0.80	0.82	0.84	0.74	0.79	0.79
		4	0.73	0.73	0.77	0.63	0.64	0.66	0.80	0.84	0.88
		5	0.72	0.73	0.76	0.71	0.72	0.75	0.70	0.72	0.75

LIKE = LLG’s likelihood-based approach with kernel K by using a resampling-based inference; BHM = Bayesian approach on hierarchical model by using a resampling-based inference; BHM (BF) = Bayesian approach on hierarchical model by using an inference based on the Bayes factor; GK = Gaussian kernel; P2K = quadratic kernel; P1K = linear kernel.

Table II.

The coverage probability (cvpr) of confidence intervals and average mean squared error values (MSE) of parameter estimates on a continuous clinical outcome.

	K	Method	Case		β	σ	τ	ρ
n = 60 p = 5	GK	LIKE	2	cvpr ×100	97	96	91	90
				MSE	0.0053	0.0247	0.0483	0.0623
		BHM		cvpr ×100	98	96	93	91
				MSE	0.0044	0.0149	0.0295	0.0452
	P2K	LIKE	3	cvpr ×100	98	93	95	N/A
				MSE	0.0053	0.0485	0.0252	N/A
		BHM		cvpr ×100	98	94	96	N/A
				MSE	0.0050	0.0478	0.0224	N/A
	P1K	LIKE	4	cvpr ×100	97	93	95	N/A
				MSE	0.0051	0.0104	0.0165	N/A
		BHM		cvpr ×100	97	93	95	N/A
				MSE	0.0043	0.0089	0.0132	N/A
n = 60 p = 200	GK	LIKE	2	cvpr ×100	89	87	87	80
				MSE	0.0321	0.0436	0.0424	0.1261
		BHM		cvpr ×100	89	89	88	81
				MSE	0.0282	0.0264	0.0372	0.1095
	P2K	LIKE	3	cvpr ×100	86	63	87	N/A
				MSE	0.0478	0.4683	0.0388	N/A
		BHM		cvpr ×100	86	64	88	N/A
				MSE	0.0461	0.4368	0.0313	N/A
	P1K	LIKE	4	cvpr ×100	86	65	82	N/A
				MSE	0.0486	0.2984	0.0583	N/A
		BHM		cvpr ×100	87	67	85	N/A
				MSE	0.0381	0.2328	0.0550	N/A

LIKE = LLG’s likelihood-based approach with kernel K; BHM = Bayesian approach on hierarchical model with kernel K; GK = Gaussian kernel; P2K = quadratic kernel; P1K = linear kernel.

We can see that the estimated type I error rates from the two approaches are similar to each other. When n > p, they are all close to the nominal level, but when n < p, both methods differ from the nominal level. However, the estimated power of the Bayesian approach is larger than that of the likelihood approach. The power for Case 1 is larger than that of the other cases because the fixed nonparamet-ric model of Z in Case 1 induces a stronger pathway effect than the random effects model of Z in the other cases. When n > p, the estimated power is in the range of [0.65, 0.98], whereas it is in the range of [0.56,0.85] when n < p. For Case 2, as expected, the power calculated by fitting the model with the Gaussian kernel is higher than that obtained by fitting the model based on the polynomial kernels with d = 1, 2. Overall, when n < p, the Bayesian approach performs better than the likelihood-based approach, whereas when n > p, both approaches are comparable with each other. This simulation result implies that the Bayesian approach is more preferable in real application because most microarray data sets have a relatively small sample size compared with the number of genes in a pathway.

When n > p, the Bayesian approach has better coverage performance than the likelihood-based approaches for σ with mostly nominal level 95% (all above 90%) and has smaller MSE than the likelihood-based approach. When n < p, the coverage percentage reduces to the range of [65%, 89%]. In this case, the Bayesian approach also has better coverage performance than the likelihood-based approaches.

6.2. Binary outcome

For binary outcome, we conducted similar simulation studies except for using a semiparametric logistic regression. We considered the following Case 6 for the assessment of type I error and Cases 7–9 for power. We also simulated 1000 data sets with two sets of n and p values.

• Case 6: logit{Pr(y_i = 1)} = βx_i, x_i = 3 cos(π/6) + u_i /2 with u_i ~ N(0, 1).

• Case 7: logit{Pr(y_i = 1)} = {βx_i + r(z_i1, z_i2, …, z_ip)}, x_i = z_i1 + u_i /2 with u_i being independent of z_i1 and following N(0, 1), z_ij ~ Uniform(0, 1), and $r(\mathbf{z})=1.8{(z_1-z_2)}^2+0.9z_2{z}_3+2.7sin(2z_3)z_4+0.9z_5^2+1.8cos(z_4)z_5$.

• Case 8: the same setting as that of Case 7 except that the true r(z) ~ GP{0, τK_g(ρ)}, where K_g(ρ) (z, z′) = exp(−||z − z′||²/ρ).

• Case 9: the same setting as that of Case 7 except that r(z) were similarly generated to Case 5.

The results on a binary outcome are similar to those on a continuous outcome. We summarize the estimated type I error and power in Table III. We also summarize the standard deviations of power and type I error in Supplementary Material Table 5. The estimated type I error rates from the two approaches are similar to each other. When n > p, they are all close to the nominal level, but when n < p, both methods differ from the nominal level. We also observe that the estimated power of Bayesian approach is larger than that of the likelihood approach.

Table III.

Estimated type I error rate and power on a binary outcome.

		Case	GK			Kernel (K) P2K			P1K
			LIKE	BHLM	BHLM (BF)	LIKE	BHLM	BHLM (BF)	LIKE	BHLM	BHLM (BF)
n = 60 p = 5	Type I Power	6	0.044	0.044	0.053	0.044	0.045	0.054	0.044	0.044	0.051
		7	1	1	1	1	1	1	1	1	1
		8	0.92	0.95	1	0.86	0.87	0.91	0.66	0.68	0.72
		9	0.78	0.78	0.82	0.74	0.74	0.78	0.73	0.74	0.78
n = 60 p = 200	Type I Power	6	0.037	0.037	0.042	0.036	0.036	0.041	0.038	0.038	0.04
		7	0.85	0.86	0.89	0.84	0.86	0.89	0.83	0.83	0.89
		8	0.82	0.82	0.87	0.76	0.77	0.81	0.57	0.60	0.64
		9	0.73	0.73	0.77	0.72	0.72	0.75	0.71	0.72	0.75

LIKE = LLG’s likelihood-based approach with kernel K by using a resampling-based inference; BHLM = Bayesian approach on hierarchical latent model with kernel K by using a resampling-based inference; BHLM (BF) = Bayesian approach on hierarchical latent model by using the Bayes factor; GK = Gaussian kernel; P2K = quadratic kernel; P1K = linear kernel.

6.3. Kernel and gene selections

We also conducted a simulation study to assess the performance of our kernel and gene selection approaches.

For kernel selection, we reconsidered Cases 1 and 2, discussed previously, because we can count how many times the kernel selection approach selects the correct kernel. We summarize the results in Table IV. Our kernel selection approach was able to identify the true kernels in Case 2, whereas assigned the unknown kernel to the Gaussian kernel 60% of the time and the quadratic kernel 40% of the time.

Table IV.

The number of counts out of 1000 simulated data sets that our kernel selection approach assigns unknown kernel to kernels we considered under Case 1 and detects true Gaussian kernel under Case 2, respectively.

	Case	GK	Kernel		NNK
			P1K	P2K
n = 60, p = 5	1	603	0	397	0
	2	1000	0	0	0
n = 60, p = 200	1	512	0	488	0
	2	1000	0	0	0

GK = Gaussian kernel; P2K = quadratic kernel; P1K = linear kernel; NNK = neural network kernel.

For gene selection, we considered the following Cases 10–11 and simulated 1000 data sets with the same two sets of n and p values.

• Case 10: the same setting as that of Case 1 except that the true $\text{r}(\mathbf{z})=10cos(z_1)-15z_2^2+20z_1{z}_2$.

• Case 11: the same setting as that of Case 1 except that the true r(z) = exp(−z₃)z₄ − 8 sin(z₅) cos(z₃).

In Case 10, we expect that the two genes (z₁ and z₂) are top ranked, whereas in Case 11, the other three genes (z₃, z₄, and z₅) are top ranked. For each case, we count how many times our gene selection approach detects these genes ranked as top genes. We summarize the results in Table V. As we expect, our gene selection approach was able to detect top genes correctly.

Table V.

The number of counts out of 1000 simulated data sets that our gene selection approach detects two genes ranked as top genes under Case 10 and other three genes ranked as top genes under Case 11, respectively.

	Case	Are genes z1 and z2 in top two ranked genes?	Are genes z3, z4, z5 in top three ranked genes?
n = 60, p = 5	10	1000	0
	11	1000	0
n = 60, p = 200	10	0	1000
	11	0	1000

7. Application

We applied our Bayesian approach to a microarray expression data set on type II diabetes [4], which was described in Section 1. We studied a total of 278 pathways consisting of 128 KEGG pathways and 150 curated pathways. The KEGG pathway database (http://www.genome.jp/kegg/pathway.html) is a collection of curated pathways representing our knowledge on the molecular interaction and reaction networks for metabolism, genetic information processing, environmental information processing, cellular processes, and human diseases. The 150 curated pathways were constructed from known biological experiments by Mootha and colleagues. Our interest on pathways is to understand the overall pathway effect rather than the effects of individual genes.

In our analysis, we considered two cases: one is for a continuous Y outcome, where Y is the log-transformed glucose level, and the other is for a binary outcome, where Y represents the diabetes status. Let X be the age and Z be the p × n gene expression levels within each pathway, where n is 35 and p varies from 4 to 200 across the pathway considered. Our goal was to identify pathways that affect the glucose level related to diabetes after adjusting for the age effect and to identify pathway to distinguish between two binary groups. We then rank genes within a significant pathway. To identify significant pathways, we used LLG’s likelihood-based approach and our Bayesian approach.

7.1. Sensitivity analysis

For the Bayesian approach, we fitted Bayesian hierarchical model (1) and Bayesian hierarchical latent model (3). We used several convergence strategies [17–19]. We ran parallel MCMC chains with diverse starting values generated from priors distribution with different prior parameters; these converged to the same range of values for each parameter. We also calculated Gelman and Rubin’s statistics [17]. These values were within 0.93 and 0.99, which are close to 1 and suggest good convergence. We also applied the Geyer’s convergence strategy [18]. We calculated lag 1 autocorrelation and then use it to obtain a confidence interval of mean of MCMC samples. The MCMC samples were within this interval, which also indicates MCMC convergence.

On the basis of iterations plots, all parameters appeared to mix satisfactorily. We sampled all parameters except ρ by using Gibbs sampling. For sampling ρ, we used the MH algorithm. We first used a proposal distribution using Gamma distribution with mean from the previous MCMC chain value and with variance of 100. The acceptance rate was slow (0.09), but the MH algorithm with our proposal distribution derived in Section 3 gave faster convergence. The acceptance rate varied between 0.21 and 0.43 based on the starting values.

To investigate the sensitivity of these prior choices, we varied the values of hyperpriors: we varied the value of ${\sigma }_{\beta }^2$ from 10 to 1000, where large value represents more noninformative prior. We varied the value of a_σ² from 2.01 to 2.001 with b_σ² = 1, which means that the prior mean of σ² was 1 but that the variance was altered from 98 to 998. We varied the value of b_τ from 10 to 100 and varied the value of a_τ from 2.001 to 2.00001, which means that the prior mean of τ was changed from 0.00099 to 0.099 and that the variance was altered from 98 to 0.099. We varied the value C₁ from 10⁻⁵ to 10⁻¹ and varied C₂ from 1 × E(||z−z′||) to 100 × E(||z−z′||). We ran the MCMC with different prior distributions and found that there were no appreciable changes in the result. However, ρ was sensitive when C₁ was less than 10⁻⁶. The results presented here are from a single chain of 2000 posterior samples after 50,000 burn-in times when ${\sigma }_{\beta }^2=100$, a_σ² = 2.01, b_σ² = 1, a_τ = 2.0001, b_τ = 0.1, C₁ = 10⁻⁵, C₂ = 10 × E(||z−z′||).

7.2. Identifying significant pathways

7.2.1. Continuous outcome

Using the Bayesian inference based on the BF, we selected pathways with BF larger than 150. We found 53, 59, 51, and 32 pathways by using the polynomial kernel with d = 1, 2, the Gaussian kernel, and the neural network kernel, respectively. For the mixture Bayesian hierarchical model, we established the prior of π from historical knowledge from Mootha et al. [4]. We used the beta distribution B(a_π, b_π), where a_π and b_π were selected to have relatively large mean 0.7 and variance 2 × mean for pathways identified by Mootha et al. [4] whereas they were chosen to have small mean 0.3 and variance 2 × mean for pathways that were not identified. We found that for pathways with large BF, the estimated mixing proportion π of the mixture Bayesian hierarchical model was all larger than 0.82. Using prior π ~ Unif[0, 1], we also found that the mixing proportion π for these pathways was all larger than 0.89.

Using a resampling-based inference, for each pathway, we estimated the statistical significance by the percentage of times either τ̂^*/ρ̂^* > τ̂ /ρ̂ or ρ̂^* > ρ̂, where τ̂/ρ̂, ρ̂, τ̂ are the estimated values from the observed data. We selected significant pathways based on of this percentage by using the empirical distribution of test statistics. We chose the 0.05 cutoff for the statistical significance by the percentage, which was described in Section 4. We found 58, 57, 55, and 23 significant pathways by using the polynomial kernel with d = 1, 2, the Gaussian kernel, and the neural network kernel, respectively. We also applied existing multiple comparison methods [20, 21] to our pathway data, although our pathways are not independent of each other because of shared genes and interactions among pathways. The FDR q-values were between 0.081 and 0.303. We note that FDR q-values were developed in single gene-based analysis, which assumes that genes are independent of each other or are positively dependent.

We selected the top 50 pathways from the Bayesian approach and the likelihood-based approach for each kernel. The proportions of overlap between the Bayesian inference based on the BF and the resampling-based inference were between 0.34 and 0.46. We summarize these proportions in Supplementary Material Table 6.

A total of 22 pathways were common among the four kernels by using the Bayesian-based inference, whereas seven pathways were common by using the resampling-based inference. They include Alanine and aspartate metabolism, Oxidative phosphorylation, and RNA polymerase pathways. These seven pathways are all in the top 20 pathways having the large BF values and are summarized in Table VI. We summarize the overlapped genes among these seven pathways in Supplementary Material Figures 1–3. We also summarize pathways that are common among the four kernels by using the Bayesian-based inference in Table VII.

Table VI.

The seven pathways identified by both Bayesian inference based on the Bayes factor and resampling-based inference by using the four kernels.

Pathway ID	Name	No. of genes	Selected kernel	Bayes factor
4	Alanine and aspartate metabolism	18	P2	2.82e+213
140	MAP00252_Alanine_and_aspartate_metabolism	21	P2	5.80e+69
36	c17_U133_probes	116	G	9.81e+215
133	MAP00190_Oxidative_phosphorylation	58	P2	5.30e+213
229	Oxidative phosphorylation	113	P2	2.41e+158
209	MAP03020_RNA_polymerase	21	G	1.62e+07
254	RNA polymerase	25	G	1.46e+09

Table VII.

Pathways identified by Bayesian inference based on the Bayes factor.

Pathway ID	Name	No. of genes	Selected kernel	Bayes factor
201	MAP00860_Porphyrin_and_chlorophyll_metabolism (user defined)	19	P2	3e+216
230	OXPHOS_HG-U133A_probes (user defined)	121	P2	2E+162
228	Oxidation phosphorylation (user defined)	48	P1	3E+94
51	c3_U133_probes (user defined)	185	G	1E+94
46	c25_U133_probes (user defined)	36	P1	1E+82
49	c28_U133_probes (user defined)	188	G	2.59E+56
11	Amyotrophic lateral sclerosis (ALS)	15	G	1.62e+38
13	Apoptosis	92	P2	4e+35
194	MAP00670_One_carbon_pool_by_folate (user defined)	13	G	2.22E+23
59	c5_U133_probes (user defined)	194	P2	2E+21
40	c20_U133_probes (user defined)	240	G	1.62e+21
16	ATP synthesis	49	P1	1.41e+20
32	c13_U133_probes (user defined)	157	P2	4.62e+19
109	Integrin-mediated cell adhesion	91	P2	1.96e+19
37	c18_U133_probes (user defined)	235	P1	6e+18

Two of them, namely pathways 4 and 140, where pathway 4 is a subset of pathway 140, are related to the Alanine and aspartate metabolism pathway, which has been studied in type II diabetes [22]. Two other pathways, pathways 133 and 229, are related to the Oxidative phosphorylation, which is known to be associated with diabetes [4]. This is a process of cellular respiration in humans (or in general eukary-otes). The pathway contains coregulated genes across different tissues and are related to insulin/glucose disposal. Researchers have found that oxidative phosphorylation expression is coordinately decreased in human diabetic muscle. It consists of ATP synthesis, a pathway involved in energy transfer. We note that all genes in the Oxidative phosphorylation pathway were not significant using single gene-based analysis. All genes except one in pathway 133 belong to pathway 229. The other two pathways, pathways 209 and 254, are related to RNA polymerase, which catalyzes the synthesis of RNA directly DNA as a template and makes an RNA chain with a sequence complementary to the template strand. All genes except two genes in pathway 209 belong to pathway 254. Among all the pathways, pathway 36, c17_U133_probes, is the most significant one under the Gaussian kernel. This pathway plays a role in cellular behavioral changes [23] and is also one of the seven pathways that are common among the four kernels. Only one gene in pathway 36 is included in pathway 254. We found that pathway 36, c17_U133_probes, contains several genes, for example, CAP1, MAPP2K6, ARF6, and SGK, related to human insulin signaling [24]. These genes were not significant using single gene-based analysis. We also note that all genes in the Oxidative phosphorylation pathway were not significant using single gene-based analysis. Only one gene, GAD2, in pathways 4 and 140 is significant using single gene-based analysis.

7.2.2. Binary outcome

We calculated the prediction accuracy based on leave-one-out cross-validation for each of these seven pathways. We provide the prediction accuracy in Table VIII based on several classification methods including discriminant analysis, support vector machines, k-nearest neighbor classifier, and neural network classifier. We found that pathway 36, c17_U133_probes, gave the best prediction accuracy among all the pathways considered.

Table VIII.

Leave-one-out cross-validation prediction rates of seven pathways by using several prediction methods.

Pathway ID	Name	No. of genes	LDA	Prediction SVML	Method SVMP	KNN (K = 1)	NNet
4	Alanine and aspartate metabolism	18	0.57	0.60	0.57	0.69	0.54
140	MAP00252_Alanine_and _aspartate_metabolism	21	0.57	0.74	0.57	0.66	0.63
36	c17_U133_probes	116	0.71	0.66	0.57	0.60	0.69
133	MAP00190_Oxidative _phosphorylation	58	0.49	0.49	0.49	0.51	0.40
229	Oxidative phosphorylation	113	0.49	0.63	0.57	0.45	0.54
209	MAP03020_RNA _polymerase	21	0.63	0.60	0.60	0.63	0.66
254	RNA polymerase	25	0.57	0.60	0.60	0.57	0.71

LDA = linear discrimination analysis; SVML = support vector machine with linear kernel; SVMP = support vector machine with polynomial kernel; KNN = k-nearest neighbor classifier; NNet=neural network classifier.

We fitted Bayesian hierarchical latent model (3) and compared the top 50 pathways identified by global test [6] and GSEA [7]. Global test is based on a random effects model, which does not include covariates and uses a linear kernel. GSEA calculates enrichment score, which is weighed function of correlation among genes in a pathway. This GSEA method cannot include covariate information into this enrichment score value.

In Supplementary Material Table 7, we calculated and summarized the proportions of overlap among global test, GSEA, and Bayesian inference based on the BF. The proportions of overlap between global test and GSEA was 0.36. The largest proportion among GSEA and Bayesian approaches was 0.43 using the quadratic kernels. These results suggest that the proportions of overlap among different methods were small, which means that they detected different pathways. When the Bayesian approach was used with four different kernels, the largest overlap was 0.91 between linear and quadratic kernels.

Global test and GSEA approaches found that pathways 4, 140, and 229 are significant. But they could not detect pathways 36, 133, and 254, whereas our Bayesian approach detects them all. Our Bayesian approach also detects other pathways that were not detected by other methods. We summarize these pathways in Table IX.

Table IX.

Pathway names that are identified by Bayesian inference based on the Bayes factor larger than 150 by using the four kernels but that are not detected from global test, GSEA, and resampling-based methods.

Pathway ID	Name	No. of genes
44	c23_U133_probes (user defined)	67
213	MAPK signaling pathway	274
107	Inositol phosphate metabolism	52
50	c29_U133_probes (user defined)	119
38	c19_U133_probes (user defined)	174
94	Glycerolipid metabolism	96
221	N-Glycans biosynthesis	38
41	c21_U133_probes (user defined)	191
34	c15_U133_probes (user defined)	154
138	MAP00240_Pyrimidine_metabolism (user defined)	45
54	c32_U133_probes (user defined)	203
96	GLYCOGEN_HG-133A_probes (user defined)	26
155	MAP00380_Tryptophan_metabolism (user defined)	60
246	Purine metabolism	112
186	MAP00620_Pyruvate_metabolism (user defined)	49
47	c26_U133_probes (user defined)	220
148	MAP00310_Lysine_degradation (user defined)	24
75	Dentatorubropallidoluysian atrophy (DRPLA)	23
115	Lysine degradation	44
67	Cholera - Infection	72
219	Neurodegenerative disorders	33
70	Citrate cycle (TCA cycle)	39
248	Pyrimidine metabolism	61
259	Starch and sucrose metabolism	54
257	Sphingoglycolipid metabolism	55
105	Huntington’s disease	46
71	Complement and coagulation cascades	47
82	Fatty acid metabolism	79
238	Phosphatidylinositol signaling system	58

7.3. Kernel selection

By considering kernel selection as a model selection problem, we select the kernel that provides the largest BF, suggesting that the data indicate that the kernel with the largest BF is more strongly supported by the data under consideration of the other kernels. In our application, pathway 36, c17_U133_probes, has the largest BF value in favor of the Gaussian kernel versus the other kernels, whereas pathways 4, Alanine and aspartate metabolism, and 229, Oxidative phosphorylation, have the largest values in favor of the quadratic kernel among the four kernels. Pathway 254, RNA polymerase, has the largest value in favor of the neural network kernel among the four kernels. We also note that for a given Gaussian kernel, pathway 36 has the largest BF among all pathways. Pathways 4, 36, and 229 have the largest values among all pathways in favor of the quadratic kernel. Pathways 4, 36, 133, and 229 are in the top 20 pathways having large BF values for all pathways with all the kernels.

7.4. Pathways Oxidative phosphorylation and c17_U133_ probes

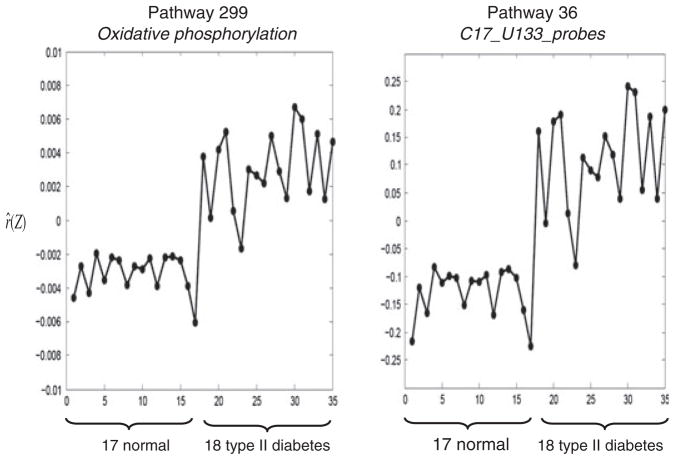
In our analysis, we found that pathway 36, c17_U133_probes, was the most significant and gave the best prediction accuracy. This pathway plays a role in cellular behavioral changes [23]. We further compared pathway 36 with pathway 229, Oxidative phosphorylation. On the basis of the gene expression data from pathway 36, we estimated and plotted r̂ against 35 samples, which consisted of 17 normal samples and 18 with type II diabetes samples. We conducted a similar analysis for pathway 229. The two plots in Figure 1 show that the two groups (17 normal and 18 with diabetes) can be discriminated very well based on the expression profiles in these two pathways. These two plots are very similar to each other but have different ranges of r̂ with that of pathway 36, much wider than that of pathway 229. We note that the value of ρ of pathway 36 is larger than that of pathway 229, whereas the value of ρ of pathway 36 is smaller than that of pathway 229. However, the ratio τ̂/ ρ̂ is 69.65 and 0.12 for pathways 36 and 229, respectively. The ratio value of pathway 36 is much larger than that of pathway 229, which indicates that c17_U133_probes pathway identifies the glucose level related to diabetes better than the Oxidative phosphorylation pathway. There are no common genes between these two pathways. The Pearson correlations between gene pairs, with one gene from pathway 36 and the other gene from pathway 229, were calculated. A total of 39 genes pairs have strong positive correlation values (>0.7), and six gene pairs have strong negative correlation values (<−0.7). This result indicates that although these two pathways contain very different genes, the overall effects between the two pathways are similar to each other.

Figure 1.

Plot between r̂(Z) and 35 samples with 17 normal and 18 with diabetes by using pathway 229, Oxidative phosphorylation, and pathway 36, c17_U133_probes, where r̂ (Z) was estimated by fitting Bayesian hierarchical model.

7.5. Ranking genes within pathway c17_U133_ probes

We used the method described in Section 4 to rank important genes and gene pairs within pathway 36, c17_U133_probes. In Table X, we show the top 20 genes that gave large mean absolute difference values calculated using posterior samples. We calculated the mean absolute difference values by fitting Bayesian hierarchical model (3) after removing one gene at a time. Genes MEF2C, NR4A1, SOX1, and TPS1 are known to be related to glucose [25, 26]. Gene CAP1 is related to human insulin signaling [24]. We also show the top 20 gene pairs in Supplementary Material Table 8. This list includes genes MAP2K6, ARF6, and SGK, which are known to be related to human insulin signaling [24]. Gene ARF6 has been reported to play a role in the activation of protein kinase and phospholipase under high glucose condition that was hypothesized to be an important intracellular event linked to diabetic nephropathy [27]. The SGK haplotype was significantly higher in individuals with type II diabetes than in healthy volunteers in the Romanian population [28]. Boini et al. [29] reported in the journal Diabetes that salk intake decreases SGK-dependent glucose uptake, and thus, SGK plays a role in glucose intolerance in mice. The aforementioned findings can help scientists identify potential biomarkers and drug targets and generate further biological hypothesis for testing.

Table X.

Top genes, within pathway 36, c17_U133_probes, ranked by the mean of the absolute values of the difference $\frac{1}{S}{\sum }_{s=1}^S\mid \widehat{\tau }-{\widehat{\tau }}_{\text{Bay},(-g)}^s\mid$, where τ̂ and ρ̂ are the means of posterior samples obtained by fitting Bayesian hierarchical model (3) by using the observed data and where ${\widehat{\tau }}_{\text{Bay},(-g)}^s$ and ${\widehat{\tau }}_{\text{Bay},(-g)}^s$ are the sth posterior samples obtained by fitting Bayesian hierarchical model (3) after removing gene g.

Gene ID	Gene name	$\frac{1}{S}{\sum }_{s=1}^S\mid {\widehat{\tau }}_{\text{Bay},(-g)}^s-\widehat{\tau }\mid$	$\frac{1}{S}{\sum }_{s=1}^S\mid {\widehat{\rho }}_{\text{Bay},(-g)}^s-\widehat{\rho }\mid$	$\frac{1}{S}{\sum }_{s=1}^S\mid {(\frac{\widehat{\tau }}{\widehat{\rho }})}_{\text{Bay},(-g)}^s-(\frac{\widehat{\tau }}{\widehat{\rho }})\mid$
202305_s_at	FEZ2	13.73	1.25	58.59
203138_at	HAT1	6.79	0.61	58.47
215000_s_at	FEZ2	6.18	1.13	64.13
215489_x_at	HOMER3	5.90	0.73	61.50
220966_x_at	ARPC5L	3.63	1.13	66.37
202569_s_at	MARK3	2.72	1.12	67.18
208903_at	RPS28	2.67	0.34	61.70
207968_s_at	MEF2C	2.02	1.13	67.79
217150_s_at	NF2	1.44	0.01	37.30
217852_s_at	SBNO1	1.38	0.20	62.54
207741_x_at	TPS1	1.18	0.07	51.24
205963_s_at	DNAJA3	1.12	0.22	64.23
38918_at	SOX13	0.91	0.16	63.45
217161_x_at	AGC1	0.82	0.05	52.59
217780_at	PTD008	0.81	0.19	65.02
208904_s_at	RPS28	0.77	0.20	65.57
213798_s_at	CAP1	0.68	0.18	65.58
202804_at	ABCC1	0.63	0.19	65.96
215148_s_at	RAB3D	0.59	0.17	65.75
218188_s_at	RPS5P1	0.51	0.02	46.01

8. Discussion

In an earlier pathway-based analysis for diabetes, Mootha et al. [4] used gene expression profile data to find pathways distinguishing between diabetic and non-diabetic groups. Incorporating continuous outcome, such as glucose level, and clinical covariates, such as age, into analysis might more efficiently detect subtle differences in gene expression profiles. This has motivated us to develop statistical methods under a regression setting to study the effects of clinical covariates and expression levels of genes in a pathway on continuous and binary clinical outcomes.

In addition to assessing the overall effect of a single pathway, we have further considered ranking the importance of genes and gene pairs within a significant pathway related to clinical outcomes. We have developed both BF-based method and resampling-based method for identifying important pathways and ranking genes in a pathway. The advantages of our Bayesian approach versus the previously proposed likelihood-based approach by Liu et al. [9] are the following: (i) unlike the likelihood-based approach, our Bayesian hierarchical modeling approach allows direct estimation of the parameters of variance components and the nonparametric pathway effects without connecting the least squares kernel machine estimates with REML; (ii) it can easily incorporate prior knowledge into modeling and analysis; (iii) the Bayesian approach is especially attractive when a pathway contains a relatively large number of genes compared with the number of available samples. Our general approach can be applied to other settings where a large number of strongly correlated predictors are available, for example, associations between disease phenotypes and a large number of markers within a genomic region.

For convergence diagnostics of our Bayesian approach, we used the approaches proposed by Gelman and Rubin [17] and Geyer [18]. It is important to theoretically show that the MCMC samples are from the correct joint posterior distribution.

As discussed in Section 5, the choice of an appropriate kernel poses a significant practical issue. We have considered kernel selection as a model selection problem within the kernel machine framework and used the BF for selecting kernels selection. Our simulation results suggest that our method works well. More general and flexible methods on variable selection methods for covariance matrix estimation [30] may be explored here and are worth future research.

We note that we have analyzed each pathway separately in our analysis. It is known that pathways are not independent of each other because of shared genes and interactions among pathways, which makes it difficult to adjust the p-value for resampling-based inference, and Bayesian inference based on the BF does not consider multiple comparisons. A proper analysis of the data should take this aspect of the multiple testing problem into account. Developing such multiple comparison method for pathway-based analysis will be an interesting and challenging problem because of the complex dependence structure among pathways.

Last but not least, although some of the pathways with large BF values are identified to distinguish diabetes, they need to be further validated biologically.