Sample Size Considerations of Prediction-Validation Methods in High-Dimensional Data for Survival Outcomes

Abstract

A variety of prediction methods are used to relate high-dimensional genome data with a clinical outcome using a prediction model. Once a prediction model is developed from a data set, it should be validated using a resampling method or an independent data set. Although the existing prediction methods have been intensively evaluated by many investigators, there has not been a comprehensive study investigating the performance of the validation methods, especially with a survival clinical outcome. Understanding the properties of the various validation methods can allow researchers to perform more powerful validations while controlling for type I error. In addition, sample size calculation strategy based on these validation methods is lacking. We conduct extensive simulations to examine the statistical properties of these validation strategies. In both simulations and a real data example, we have found that 10-fold cross-validation with permutation gave the best power while controlling type I error close to the nominal level. Based on this, we have also developed a sample size calculation method that will be used to design a validation study with a user-chosen combination of prediction. Microarray and genome-wide association studies data are used as illustrations. The power calculation method in this presentation can be used for the design of any biomedical studies involving high-dimensional data and survival outcomes.

Introduction

One of the main objectives for conducting microarray studies and genome-wide association studies (GWASs) in cancer clinical trials is the development of a statistical model to predict patient’s clinical outcome, such as time to progression or survival, using genomic markers. As high-throughput technology becomes more mature, translating genomics research findings from bench side to clinic in assisting with medical decisions is now a trend. However, biological samples for these high-throughput experiments are costly and usually difficult to obtain. Having too many samples will waste valuable resources, while having too few samples may lead to no meaningful scientific conclusions. Therefore, it is necessary for us to develop a method for sample size calculations with the appropriate prediction-validation methods for censored outcomes.

A few methods have been developed for building genomic classifiers. Most methods are focused on sample size calculations for predicting classes and are not applicable to censored outcomes data, also called survival data, directly. Some have considered sample size estimations for biomarker discovery with control of the false discovery rate, which is defined as the expected proportion of falsely discovered biomarkers. For example, Jung [2005] derives a sample size formula for the Storey’s [2002] procedure under the weak dependence assumption. Liu and Hwang [2007] propose similar sample size formulae that can be used for comparison of multiple independent samples. Others have also considered power and sample size calculations under FDR control, e.g., Tong and Zhao [2008]. Dobbin and Simon [2007] presented analytical formulae for determining the number of biological replicates needed for developing a predictive classifier. Murcray et al. [2011] have considered sample size requirements to detect gene-environment interactions in GWAS. Matsui and Noma [2011] developed sample size and power assessment methods based on nonparametric hierarchical mixture models. Simon et al. [2011] provided a nice evaluation of cross-validation (CV) strategy for the assessment of model prediction in the survival setting. However, none of these publications provide a comprehensive investigation of sample size estimation for prediction of censored survival outcomes or a prediction method jointly with a validation method. With high-dimensional genomic data, we cannot separate development of a prediction model from its validation.

Apart from not being able to handle censored outcomes, most of these published methods do not take into account the underlying correlation structure among genes or single nucleotide polymorphisms (SNPs). Jung et al. [2005] and Jung and Young [2012] provide some of the first attempts to incorporate the complicate correlation structure of microarray in deriving an accurate sample size for biomarker discovery while controlling the family-wise error rate in the classification setting. Since genes or SNPs are unlikely independent of each other, having a sample size calculation method that takes it into account is more practical. We have taken this into considerations in our proposed sample size calculation strategy because the performance of prediction and validation methods are heavily dependent on the true correlation structure.

Transcriptome microarray or genotype data are now commonly collected from patients in clinical trials. These data provide valuable information in identifying biomarkers for patients’ prognosis. Sample size calculation is a critical procedure when designing microarray study and GWAS for the development of a prediction model and its validation. Without independent validation data, a common approach to assess prediction accuracy is based on some form of resampling the original data. These techniques include (1) dividing the data into a training set and a test set, (2) k-fold CV, and (3) leave-one-out CV (LOOCV). Some of these methods are coupled with permutation for assessing model significance. The current literature lacks a comprehensive comparison of validation methods for censored outcomes in the genomic settings. This paper provides an extensive investigation of this issue and derives a sample size calculation strategy for prediction and validation using high-dimensional prognostic genomic markers and a survival outcome.

This paper is organized as follows. In Section “Methods,” we present the different validation methods compared, simulations setup, and an algorithm for sample size calculations. We provide our results of simulation and real data sample size calculations for validation in Section “Results.” This is followed by a discussion in Section “Discussion.”

Methods

In the survival prediction setting, suppose we have n observations or subjects. For observation i(= 1, …, n), we have a corresponding measure of time to an event T_i, such as tumor recurrence or death. The event time may be censored due to loss to follow-up or study termination. Therefore, we observe X_i = min(T_i, C_i) with an event indicator δ_i = I (T_i ≤ C_i), where C_i is the censoring time which is independent of T_i given the genomic predictors. The methods described below can be applied to any type of high-throughput genome data, such as SNPs taking values (0, 1, or 2) in GWAS. However, for simplicity, we will describe our method in terms of gene expression data. Let Z_ij denote the gene expression measurement for gene j (= 1, …, p) of subject i from a microarray experiment. The goal in survival prediction is to build a model with input from Z = (Z₁, …, Z_p) in order to predict T or its distribution. Using this model, the survival distribution of a future subject can be predicted based on its corresponding gene expression measures. These models can be built via proportional hazards regression model by Cox [1972] or random survival forests [Ishwaran et al., 2008; Pang et al., 2010].

In this paper, we will mainly focus on inference from the Cox’s proportional hazards regression model. The hazard function at time t for a subject i with gene expression values Z_i = (Z_i1, …, Z_ip)^T is given by

$${\lambda }_i(t)={\lambda }_0(t)\mathit{exp}({\beta }^T{Z}_i),$$

where λ₀(t) is an unspecified baseline hazard function and β = (β₁, …, β_p)^T is a set of unknown regression parameters. As in most high-dimensional genomic data, the number of genes p is much larger than the number of subjects n. Therefore, the standard regression analysis method does not work. Penalized methods have been widely investigated to overcome the large-p -small-n problem, including ridge regression [Hoerl and Kennard, 1988], lasso [Tibshirani, 1996], and elastic net [Zou and Hastie, 2005]. These methods require intensive computations. In this paper, we consider a simple prediction method for heavy computation, specially for simulations, and focus on the evaluation of validation methods (rather than prediction methods) and sample size algorithm that can be applied to any combination of prediction and validation methods.

Prediction

Before we apply a prediction method to microarray data, we standardize the expression data of each gene by subtracting the sample mean and dividing by sample standard deviation. For the selection method in the training set, we use the univariate method to choose the top m genes in terms of marginal P-value associating each gene with survival time. We test the effect of gene expression value of each gene on survival. For gene j, a univariate Cox regression with hazard function λ(t | Z_j) = λ_0j (t)exp (β_j Z_j) is fitted, and testing the null hypothesis of β_j = 0 vs. β_j ≠ 0 is conducted using the partial likelihood test. The genes are then ranked according to their P-values in an ascending order.

We fit a multivariate Cox regression model from the training data using the chosen m genes as covariates to perform prediction on the test set. Let (β̂₁, …, β̂_m) denote the regression estimates from a fitted prediction model and (Z₁, …, Z_m) the expression data of the corresponding genes. We call S = β̂₁Z₁ + ···+ β̂Z_m a risk score, a large value representing a short survival time.

For validation that is described in the following section, we standardize the gene expression data in the test set using the sample means and sample standard deviations from the training set. Using the prediction model fitted from training set, we partition the subjects in the test set into high-risk group and low-risk group using the median for their risk score values as a cutoff value in this paper. We may choose a different cutoff depending on how large high-risk patient group we want. We may not even dichotomize the risk score and validate the prediction model by regressing the survival time on the continuous risk score as a single covariate using test set.

Validation

Resampling Methods

Assessing the accuracy of a fitted prediction model based on the same data set that was used to develop the model can result in an overly optimistic performance assessment of the model for future samples, which is called overfitting bias. To alleviate or remove this bias, validation methods such as bootstrapping, CV, and permutation can be employed. We describe below the resampling techniques that we consider in this paper.

Hold-out or split sample method

The hold-out method or split sample method is the simplest of all the resampling methods considered in this paper. It involves a single random split or partition of the data into a training set with proportion P and a test set with proportion 1 − P. We have chosen to use 50% for the training set and the rest as the test set. Another choice for the split is 70% training and 30% testing. Because we do not reuse the training set for test, no overfitting is involved in this case.

k -fold CV

The k-fold CV method consists of splitting the data set randomly into k partitions that are close to equal in size. At each of the k-th iteration, k − 1 partitions will be used as the training set and the left out partition will be used as the test set. Fivefold and 10-fold CVs are commonly used. In this paper, in addition to those two resampling k-fold schemes, we also investigated twofold CV. A twofold CV is essentially a 50% hold-out method with the training set role being switched with the test set.

LOOCV

LOOCV is a special case of k-fold CV in which the k = n, the sample size of the data set. At each of the n iterations, the whole data set is used as the training except one sample which is left out as test set. Because it requires the largest number of iterations, it is the most computationally expensive resampling method introduced here.

Log-Rank Test for Validation

As mentioned in Section “Prediction,” we partition the patients in the test set into high-risk and low-risk groups using median as a cutoff value for their risk scores. Because the gene expression data are standardized, we expect about 50-50 allocation between the two patient groups. In order to validate the fitted prediction model (or the risk score) from the training set, we compare the survival distributions of the training set patients between the two groups using the log-rank test [Peto and Peto, 1972]. Let n₁ and n₂ denote the number of patients in the high (k = 1) and low (k = 2) risk groups, respectively. For patient i in group k, let X_ki denote the minimum of the survival and censoring times and δ_ki the event indicator. Also, for group k(= 1, 2), let $N_k(t)={\sum }_{i=1}^{n_k}{\delta }_{ki}I(X_{ki}\le t)$ and $Y_k(t)={\sum }_{i=1}^{n_k}I(X_{ki}\ge t)$ denote the event process and the at-risk process, respectively. Then the log-rank statistic to test the difference in survival distributions between the two groups is given by:

$$W={\int }_0^{\infty }\frac{Y_2(t)}{Y_1(t)+Y_2(t)}{dN}_1(t)-{\int }_0^{\infty }\frac{Y_1(t)}{Y_1(t)+Y_2(t)}{dN}_2(t).$$

If the two groups have the same survival distributions in the held-out test set, W is asymptotically normal with mean 0 and variance σ² that can be consistently estimated by

$${\widehat{\sigma }}^2={\int }_0^{\infty }\frac{Y_1(t)Y_2(t)}{{\{Y_1(t)+Y_2(t)\}}^2}\{{dN}_1(t)+{dN}_2(t)\}.$$

With a two-sided type I error rate α, we conclude the validation of the fitted prediction model by the hold-out resampling method if |W/β̂| > z_1−α/2, where z_1−α denotes the 100(1 − α) percentile of the standard normal distribution.

CV with Permutation

Among the above resampling methods to split the whole data of size n into training and test sets, only the hold-out method is free of overfitting bias because the resulting training and validation sets are mutually exclusive. All other methods reuse part of the whole data for training. In order to remove the overfitting bias of the latter resampling methods, we use a permutation method as follows.

• From a resampling of the original data {(X_i, δ_i), (Z_i1, …, Z_ip) : i = 1, …, n} calculate the log-rank P-value, p₀, comparing the survival distributions between high- and low-risk patient groups of test set.

• Generate the b-th permutation data by shuffling the survival data {(X_i, δ_i) : i = 1, …, n} and randomly matching them with the microarray data {(z_i1, …, z_ip) : i = 1, …, n}.

• At the b-th permutation, apply the prediction-validation procedures, which are used for the original data, to the permuted data, and calculate the log-rank P-value, p_b.

• Repeat B permutations, and estimate an unbiased P-value for validation by

  $$P-\text{value}=B^{-1}\sum _{b=1}^{B}I(p_b\le p_0).$$

  For a prespecified type I error rate α, we conclude a positive validation of the prediction if P-value < α.

Sample Size Calculation

Suppose that we want to estimate the sample size for a microarray study or GWAS that will be analyzed to develop a prediction model and validate it as described above. At the design stage of such study, we have to (1) specify a certain number of candidate prognostic genes or SNPs, say genes or SNPs j = 1, …, m, and (2) their effect sizes (or regression coefficients) β₁, …, β_m to specify a hypothetical prediction model

$$\lambda ={\lambda }_{0}exp({\beta }_1{Z}_1+\cdots +{\beta }_m{Z}_m),$$

where the baseline hazard rate λ₀ can be estimated from the survival distribution for the whole patient population assuming an exponential survival distribution. Once, a prediction model is specified, we estimate the sample size for the study using a simulation method by generating a large number of gene expression (or genotype) and clinical outcome data of any size until we find a size that guarantees a certain power for the selected prediction and validation methods. The efficiency of any prediction-validation procedure is heavily dependent on the correlation structure of microarray or genotype data. So, in sample size calculation, it is a challenge to generate a large number of high-dimensional microarray or genotype data that have the same correlation structure as the real data to be collected from the new study. The sample size calculation method we present can be used for any high-dimensional data, but we describe it in terms of microarray data as in the previous sections.

In real genome data the dependency structure of the gene expression or genotype data will be very complex. So, it is difficult to model the true dependency. To overcome this difficulty, we propose to use a two-stage procedure in sample size calculation of a real microarray study. At the first stage, we conduct a microarray experiment for a small number of patients, say 50. Using the first stage gene expression or genotype data, we can generate as many microarray data as we want that have the same correlation structure observed from the stage 1 data. Let 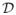= {(x_i1, …, x_ip), i = 1, …, n} denote the stage 1 data, and, for gene j (= 1, …, p), x̄_j and s_j denote the sample mean and standard deviation. Suppose that we want to generate a microarray data of size N(> n). For ε₁, …, ε_N ~ i.i.d. N(0, 1) random variables, we generate simulated microarray data

$$\stackrel{\sim }{\mathcal{D}}=\{(z_{i1},\dots ,z_{ip}),i=1,\dots ,N\},$$ (1)

where z_ij = (x_i′j − x̄_j)ε_i/s_j and i′ is a randomly chosen number from (1, …, n). It is easy to show that, the correlation coefficients 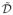conditioning on 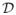is asymptotically identical to those of the marginal distribution of 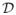, refer to Jung and Young [2012].

In the second stage, we generate a large number of simulated microarray data of size N together with the survival data from the specified prediction model, and apply the chosen prediction-validation algorithm to each simulation set to see if the chosen N provides a reasonable power or not.

More specifically, our sample size calculation procedure can be described as follows:

1. Specify the design parameters

   • (α, 1 − β) = type I error rate and power

   • m = number of candidate prognostic genes

   • (1̃, …, m̃) = gene IDs of candidate prognostic genes

   • β_j̃ = effect size for candidate gene j̃

   • λ₀ = baseline hazard rate estimated from the population survival distribution

   • Accrual period a and additional follow-up period f

   • n = stage 1 sample size

   • Prediction and validation (resampling) methods to be used for the final data analysis

2. Stage 1: Conduct a microarray experiment to collect pilot data of size n, 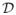= {(x_i1, …, x_ip), i = 1, …, n}

3. Stage 2:

   1. For a given sample size N, generate a large number of simulation microarray data sets {(z_i1, …, z_ip), i = 1, …, N} by (1)

   2. For each simulation microarray data set, generate censoring variable C_i = f + aU_i and survival time T_i from the exponential distribution with hazard rate λ_i = λ₀ exp(β_1̃z_1̃ + ··· + β_m̃z_m̃), where U₁, …, U_N are i.i.d. U(0, 1) random variables

   3. Apply the chosen prediction-validation method to each simulation data set {(X_i, δ_i, z_i1, …, z_ip), i = 1, …, N}

   4. Estimate the power for N, 1 − β̂_N, by the proportion of simulation data sets for which the prediction is validated

   5. Continue stage 2 until 1 − β̂_N ≈ 1 − β

A target sample size N can be obtained using the bisection method in stage 2. Note that all the design parameters except n are used only in stage 2. If survival data are available for the patients included in stage 1, we may refine the values of design parameters m and β_1̃, …, β_m̃ before starting stage 2.

Results

Simulation Studies

If the survival times are exponentially distributed, the translation of the regression coefficients from the hazard to survival time is simple as the baseline hazard is constant. Let λ₀ be the scale parameter for the exponential distribution and U be uniformly distributed on the interval from 0 to 1. The hazard function of the exponential model is λ(t | Z_i) = λ₀exp (β^TZ_i). Then survival times for the exponential model can be generated with the following:

$$T_i=-\frac{log(U)}{{\lambda }_{0}exp({\beta }^T{Z}_i)}.$$ (2)

We investigate the performance of the various validation methods to understand these approaches under the null and alternative hypotheses. We generate gene expression data from a multivariate normal distribution, MVN(0, Σ). The covariance matrix is a block-diagonal matrix Σ with size 200 × 200 with each of the blocks of size 20 × 20 of autocorrelation structure, i.e.,

$$\begin{array}{l}\mathrm{\sum }={\left(\begin{array}{cccccc}{\mathrm{\sum }}_{\rho }& 0& \dots & \dots & \dots & ⋮\\ 0& {\mathrm{\sum }}_{\rho }& 0& \ddots & \ddots & ⋮\\ ⋮& 0& {\mathrm{\sum }}_{\rho }& 0& \ddots & ⋮\\ ⋮& \ddots & 0& {\mathrm{\sum }}_{\rho }& 0& ⋮\\ ⋮& \ddots & \ddots & 0& {\mathrm{\sum }}_{\rho }& ⋮\\ \dots & \dots & \dots & \dots & \dots & \dots \end{array}\right)}_{200\times 200},\\ {\mathrm{\sum }}_{\rho }={\left(\begin{array}{ccccc}1& \rho & \dots & {\rho }^{18}& {\rho }^{19}\\ \rho & 1& \ddots & \dots & {\rho }^{18}\\ ⋮& \ddots & \ddots & \ddots & ⋮\\ {\rho }^{18}& \dots & \ddots & 1& \rho \\ {\rho }^{19}& {\rho }^{18}& \dots & \rho & 1\end{array}\right)}_{20\times 20}.\end{array}$$

This covariance setup is similar to Pang et al. [2009]. The survival time is generated from exp(λ), where λ = exp(β₁Z₁ + β₂Z₂ + β₃Z₃) for the alternative case and λ= 1 for the null case. We consider p = 20; n = 200; ρ = 0.2; censoring of 15%, 30%, or 50%. Censoring time is generated from U(0, c₀) with c₀ chosen for 50% censoring. With c₀ fixed at this value, a censoring variable for 30% or 50% of censoring is generated from U(c₁, c₀ + c₁) by choosing the appropriate c₁ value. Univariate gene selection as described in Section “Prediction” is repeated for every training set. We choose the top three or six genes in terms of univariate P-values to fit a prediction model in our simulations. A 100 simulations are performed under each design setting. For the hold-out method, we obtain the number of simulation samples having the log-rank P-values from the test sets are smaller than α = 0.05. For the k-fold CV and LOOCV methods, the validation of fitted prediction models is assessed by a permutation P-value from B = 200 permutations and a type I error rate of α= 0.05.

At first we investigate the performance of the validation method using different resampling methods. For the null case where β₁ = β₂ = β₃ = 0, under the simulation setup described above, we obtained the results given in Table 1. With top three genes selected, among the different CV methods, 10-fold CV with permutation has the best type I error control at the α = 0.05 level. Under 30% censoring, the 50-50 hold-out method and LOOCV both have slightly inflated type I error. With 100 simulations, the limits of 95% confidence interval are ±0.043. The 70-30 hold-out method appears to work well in terms of type I error control. With top six genes selected, we observe a similar pattern.

Table 1.

Empirical type I error rate from 100 simulation data sets under p = 200, n = 200, block compound symmetry correlation structure with a block size of 20 and a correlation coefficient of ρ= 0.2, and a censoring proportion of 15%, 30%, or 50%. Prediction models including top three or six genes are validated using various resampling methods. The type I error rate for CV methods are approximated by 200 permutations.

Censoring proportion	Resampling method	Select top
		Three genes	Six genes
15%	50-50 hold-out	0.06	0.03
	70-30 hold-out	0.04	0.05
	Twofold CV	0.03	0.05
	Fivefold CV	0.03	0.03
	10-fold CV	0.05	0.05
	LOOCV	0.06	0.06
30%	50-50 hold-out	0.09	0.04
	70-30 hold-out	0.05	0.05
	Twofold CV	0.05	0.08
	Fivefold CV	0.09	0.03
	10-fold CV	0.05	0.03
	LOOCV	0.11	0.07
50%	50-50 hold-out	0.07	0.05
	70-30 hold-out	0.08	0.06
	Twofold CV	0.08	0.10
	Fivefold CV	0.08	0.02
	10-fold CV	0.05	0.06
	LOOCV	0.06	0.08

Table 2 reports empirical power (and mean number of true selections within the prediction models within the parentheses) from 100 simulation data sets under β₁ = β₂ = β₃ = 0.3. As the censoring proportion of the survival outcomes increases, both the validation power and the number of true selections decreases. The power of LOOCV steeply decreases in the censoring proportion. Among the resampling methods, LOOCV has the lowest power, while its mean true selections is highest. By selecting more genes for prediction than the number of true prognostic genes (i.e., select top six genes), we have a larger true selections, but a lower power. By selecting six top genes, each prediction model will include at least three unassociated genes, which represents random noises in prediction. So, selecting a large number of genes in prediction not necessary leads to a higher prediction power. Note that fivefold and 10-fold CVs are clear winner in terms of power and are second to LOOCV in terms of true selections.

Table 2.

Empirical power (and mean number of prognostic genes selected in the prediction models) from 100 simulation data sets under β₁ = β₂ = β₃ = 0.3, p = 200, n = 200, and block compound symmetry correlation structure with a block size of 20 and a correlation coefficient of ρ = 0.2. The power for CV methods are approximated by 200 permutations.

Censoring proportion	Resampling method	Select top
		Three genes	Six genes
15%	50-50 hold-out	0.63 (1.81)	0.51 (2.22)
	70-30 hold-out	0.63 (2.23)	0.59 (2.74)
	Twofold CV	0.86 (1.83)	0.81 (2.33)
	Fivefold CV	0.95 (2.50)	0.90 (2.79)
	10-fold CV	0.95 (2.61)	0.88 (2.87)
	LOOCV	0.92 (2.74)	0.62 (2.94)
30%	50-50 hold-out	0.62 (1.69)	0.54 (2.11)
	70-30 hold-out	0.63 (2.07)	0.50 (2.51)
	Twofold CV	0.71 (1.55)	0.71 (2.11)
	Fivefold CV	0.88 (2.28)	0.87 (2.67)
	10-fold CV	0.83 (2.43)	0.79 (2.78)
	LOOCV	0.46 (2.54)	0.44 (2.83)
50%	50-50 hold-out	0.38 (1.15)	0.33 (1.84)
	70-30 hold-out	0.39 (1.72)	0.35 (2.30)
	Twofold CV	0.52 (1.18)	0.47 (1.78)
	Fivefold CV	0.66 (1.84)	0.57 (2.42)
	10-fold CV	0.62 (2.00)	0.57 (2.55)
	LOOCV	0.22 (2.20)	0.21 (2.68)

Both 50-50 hold-out and twofold CV partition the whole data into two subsets of equal size. The former uses one subset only for training and the other subset only for test, but the latter uses both subsets for training and test. As such, twofold CV has much higher power than 50-50 hold-out despite having similar true selections. Between the two hold-out methods, 70-30 has a larger true selections because it uses a larger training set, but they have similar validation power. The hold-out methods have low power and small true selections in general.

The power of a combination of prediction and validation methods will depend on how accurate the predicted model is and how large an independent test set is. In the hold-out methods, by increasing the size of the training set, we can improve the efficiency of the fitted predicted models (i.e., partially reflected by the true selections), but lose the power of the log-rank test for validation because the size of test set will decrease. On the other hand for k-fold CV methods, both the size of test sets and the amount of overlap between training sets and test sets increase as k increases. Hence, the validation power decreases while the number of true selections increases in k. Recall that LOOCV is n-fold CV.

Real Data Examples

Example 1

Beer et al. [2002] used oligonucleotide microarrays to generate gene expression data for p = 4,966 genes from n = 86 patients with lung adenocarcinoma. We calculate a sample size for a project using the published data as stage 1 data.

At first, we choose 10-fold CV combined with 100 permutations for validation. We calculated the power of various sample sizes with two-sided type I error of α = 0.05 for validation, see Table 3. The survival data are generated using parameter values λ₀ = 0.004684, β₁ = −1.157, β₂ = 0.582, β₃ = 0.455 estimated from the stage 1 data by fitting a proportional hazards regression model based on exponential distribution. The censoring variables are generated from U(3, 5), mimicking a 2-year accrual and a 3-year additional follow-up of the study. Table 3 shows that at N = 172, we can achieve an approximate power of 81% for the prediction method using Cox’s regression method combined with the 10-fold CV.

Table 3.

Sample size calculation for Beer et al. [2002] microarray project for prediction by selecting top three genes and validation using 10-fold CV under α = 0.05

Sample size	Power
N = 100	0.45
N = 150	0.69
N =, 172	0.81
N = 200	0.94

In order to compare the performance of different resampling methods for validation, we calculated the power of the prediction method with N = 172 combined with various validation methods. Consistent with the simulation results, we observe that the 10-fold CV with permutation method outperforms other validation strategies, see Table 4. The fivefold CV is the second best.

Table 4.

Power analysis for Beer et al. [2002] microarray project with N = 172 for prediction by selecting top three genes and validation using various resampling methods under α = 0.05

Resampling method	Power
50-50 hold-out	0.46
70-30 hold-out	0.38
Twofold CV	0.69
Fivefold CV	0.77
10-fold CV	0.81
LOOCV	0.44

In order to investigate the impact of the correlation structure among genes in the power, we estimated sample size for the prediction method combined with validation by 10-fold CV under the independence assumption among genes. We use the same design parameter values as above but ignore the dependencies among the genes by generating i.i.d. N(0, 1) random variable for gene expression data. The required sample size for 81% in this case is about 180. The impact of ignoring the dependencies among genes is not so big in this project.

Example 2

Avet-Loiseau et al. [2009] used GeneChip Human Mapping 500K Array Set to characterize malignant plasma cells from 192 multiple myeloma patients and to identify SNPs associated with survival. They provided insights into how chromosomal aberrations might have prognostic implications for multiple myeloma patients. We applied our sample size calculation method using part of their data (n = 50) as stage 1 data.

Based on the results from the simulation results, we have chosen 10-fold CV as the default for sample size calculations. The overfitting bias for the 10-fold CV was adjusted by 100 permutations. We calculated the power of various sample sizes with two-sided type I error of α = 0.05 using 100 simulations, see Table 5. The survival data are generated using parameter values λ₀ = 0.03373, β₁ = −1.241, β₂ = 1.892, β₃ = 1.974 that are estimated from a Cox-exponential model using the stage 1 data. Censoring times are generated from U(5, 7) reflecting a 5-year accrual and a 2-year follow-up of their project. Table 5 shows that the project requires N = 212 for a power of 88%. Note that this sample size is very close to their sample size 192, so that their original project seems to be appropriately powered.

Table 5.

Sample size calculation for Avet-Loiseau et al. [2009] GWAS project for prediction by selecting top three SNPs and validation using 10-fold CV under α = 0.05

Sample size	Power
N = 100	0.30
N = 200	0.70
N = 212	0.88
N = 218	0.90
N = 240	0.95

Discussion

As the need to validate developed clinical cancer biomarkers continues, understanding the statistical properties of prediction-validation methods in analyzing survival outcomes is essential. Amount of censoring and gene (or SNP) selection can affect the performance of these prediction and validation methods. We have investigated these factors and also presented a sample size calculation algorithm for the design of biomarker-based prediction-validation study. We illustrate our sample size calculation algorithm using a microarray data set for patients with lung cancer and a GWAS data set for multiple myeloma patients. As illustrated in the review presented in the introductory section, most published literature focus on sample size calculations for gene discovery associated with binary outcomes. None of these papers perform a comprehensive comparison of validation methods for a fitted prediction model and present sample size calculation strategy for prediction validation. It is well known that genes/SNPs work together in groups [Pang et al., 2011]. Therefore, to reflect real data, our simulations and sample size calculation algorithm take into account the correlation among genes. The algorithm of our sample size method can be used for any combination of a prediction method and a validation method. It can be further extended to any types of traits (clinical outcomes), such as dichotomous, continuous variables, or (right, left, or interval) censored variables, as long as we have regression methods for the trait types.

In our simulation and real example studies, the hold-out methods, 50-50 split, 70-30 split, and twofold CV with permutations perform poorly. One of the reasons is that the mean number of selected true genes is relatively lower among these validation strategies. Despite LOOCV with permutation being able to select most number of correct genes, it did not perform well when the censoring proportion becomes high. The 10-fold CV proves to be the most effective validation strategy among all the validation methods investigated. It controls type I error close to the nominal rate and has the best power given a certain sample size across a variety of settings. This is consistent with the real data analysis. The fivefold CV follows closely behind but does not perform as well probably because of the lower average number of true genes selected. As a reviewer pointed out, however, these comparisons may depend on a chosen prediction model. In a real project, we may choose a more efficient prediction method, such as lasso or elastic net, calculate the required sample sizes for all different kind of validation methods from pilot (first stage) data, and choose the one requiring the smallest sample size for the whole project.

We partitioned the test set into two risk groups using the median of the risk score values from the training set as a cutoff. We can choose a different cutoff value depending on the objective of the project. For example, if we want to identify a small group of low-risk patients, we may use the first quartile or the 33 percentile of the risk score values. If we want to validate a prediction model without limiting to a specific cutoff value, we may fit a Cox regression model to the test set using the continuous risk scores as a covariate.

Due to the computational intensiveness of the simulation studies, we chose a simple prediction method and a small number of permutations to estimate an unbiased validation P-value for k-fold CV resampling methods. These can certainly be expanded to any prediction and validation algorithms, and a larger number of permutations, especially in designing a real study. Due to the same reason, we have written a parallelized sample size algorithm that takes advantage of multicore processing for this purpose.

In a future work we will investigate the effect of how gene (or SNP) selection method may play an important role in the performance of these validation methods. Also, we will look at other high-throughput data types such as proteomics data.